Machine Learning-Assisted Synergistic Optimization of 3D Printing Parameters for Enhanced Mechanical Properties of PLA/Boron Nitride Nanocomposites
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Design by Statistical Analysis (DOE)
2.3. Sample Fabrication
2.3.1. Filament Extrusion
2.3.2. Sample Preparation
2.4. Mechanical Testing
2.4.1. Tensile Testing
2.4.2. Impact Testing
2.5. Statistical Analysis
2.5.1. Analysis of the Signal-to-Noise (S/N) Ratio
2.5.2. Analysis of Variance (ANOVA)
2.6. Machine Learning
2.6.1. Linear Regression (LR)
2.6.2. Random Forest Regression (RFR)
- Top of form;
- Bottom of form.
2.6.3. Extreme Gradient Boosting (XGBoost)
2.6.4. CatBoost Regression (CBR)
2.6.5. Gaussian Process Regression (GPR)
2.6.6. Model Interpretability
SHAP Analysis
3. Results and Discussion
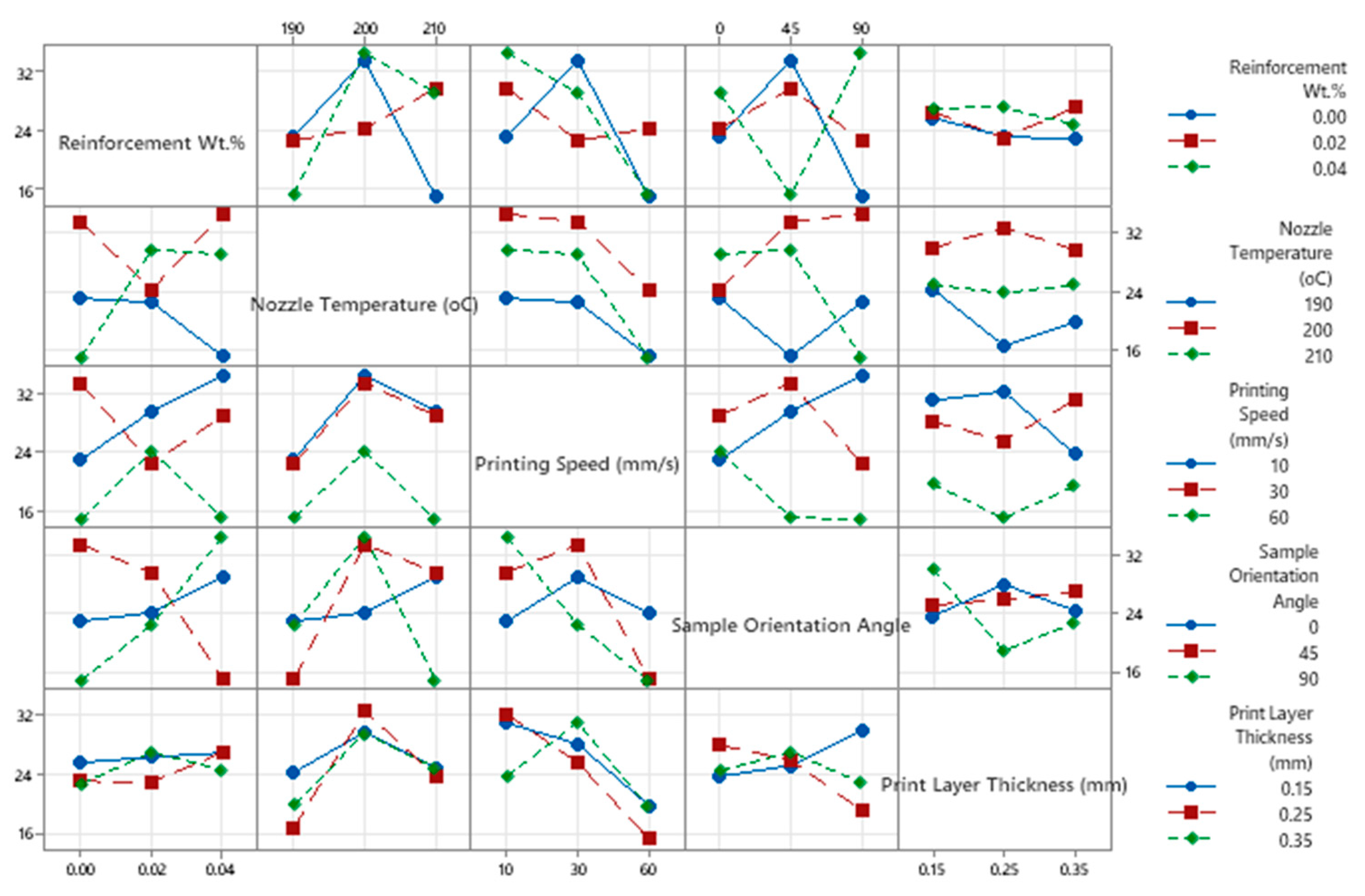
3.1. Statistical Analysis of Experimental Design (DOE)
3.2. Experimental Results
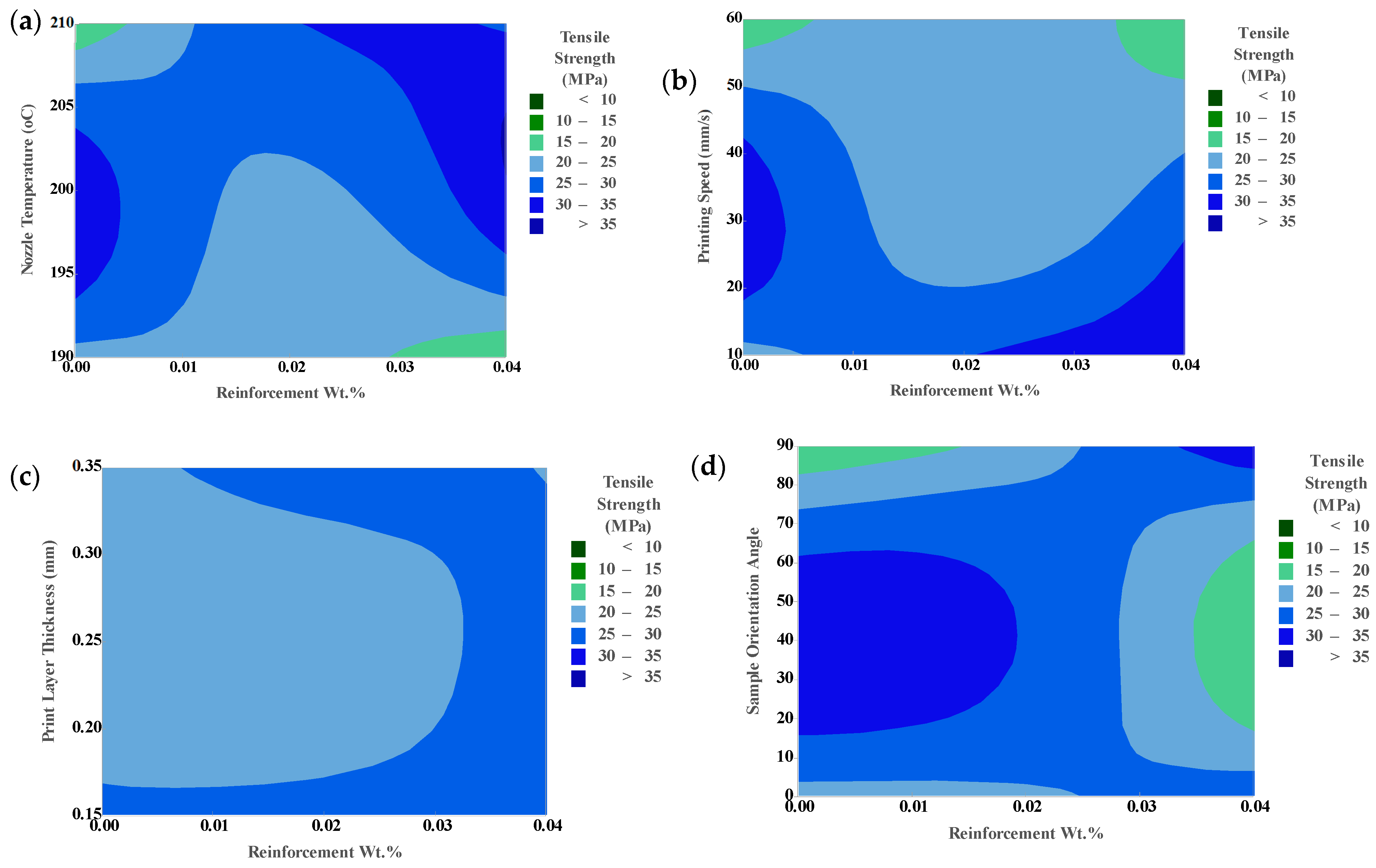
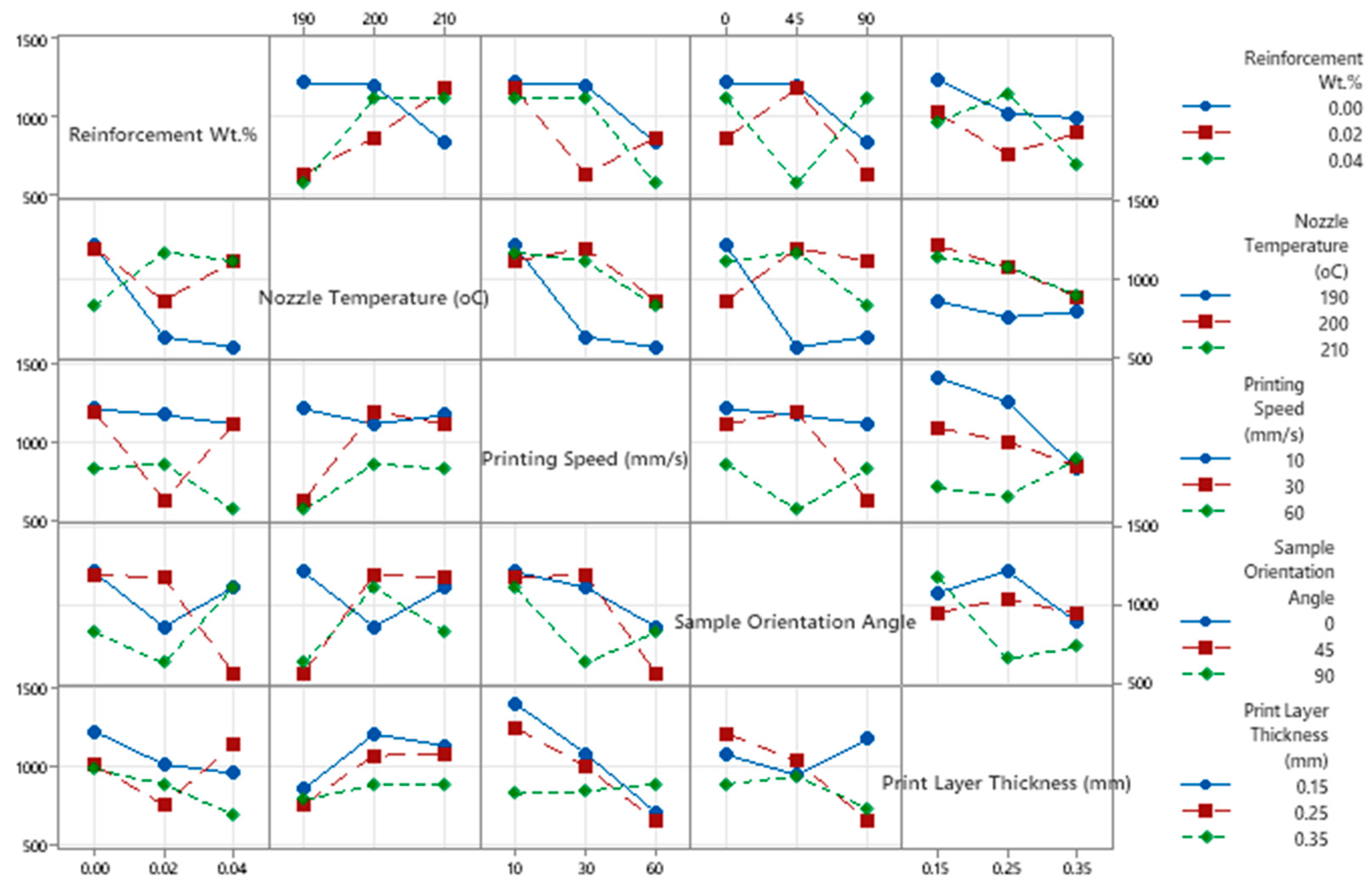
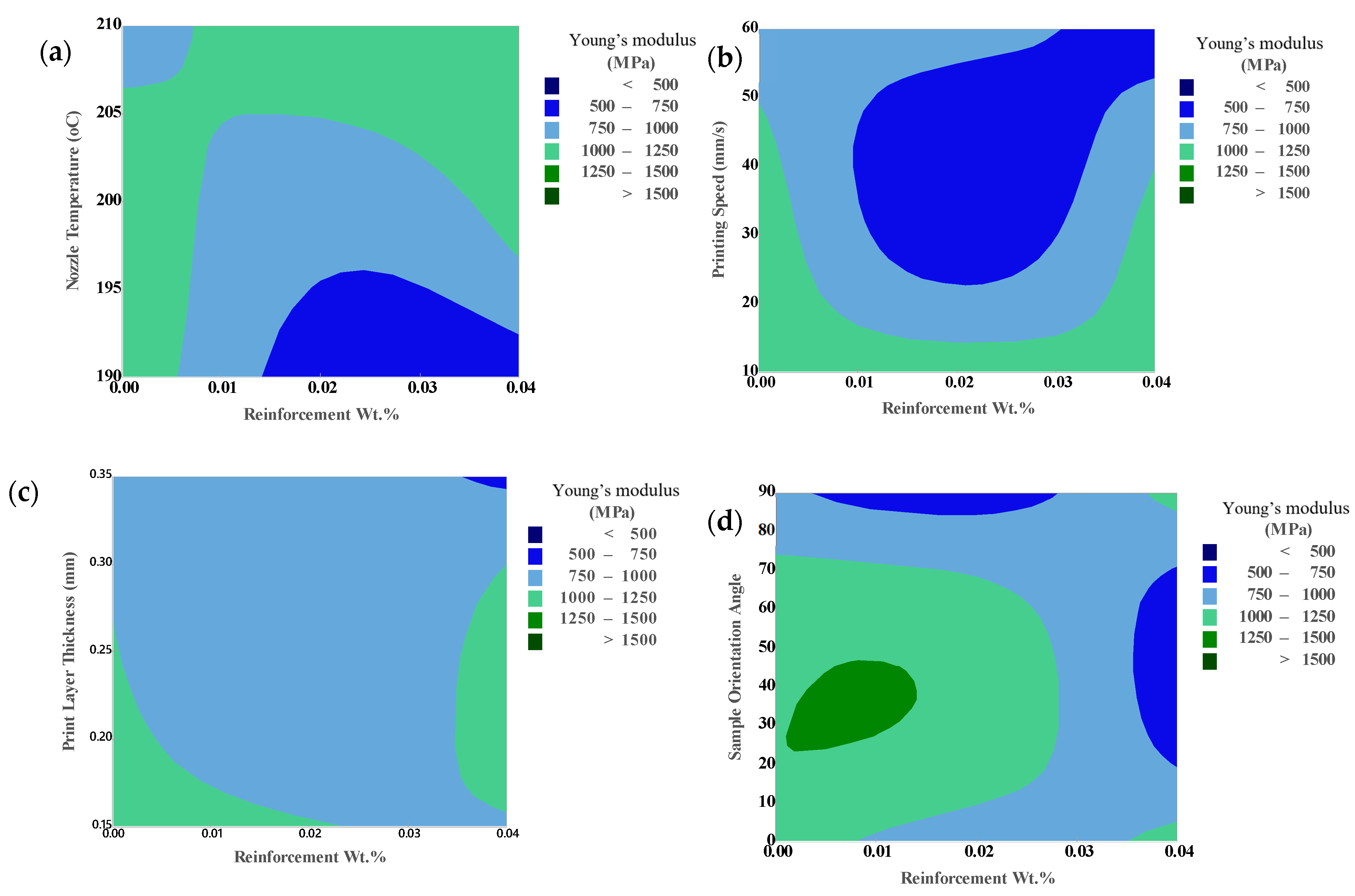
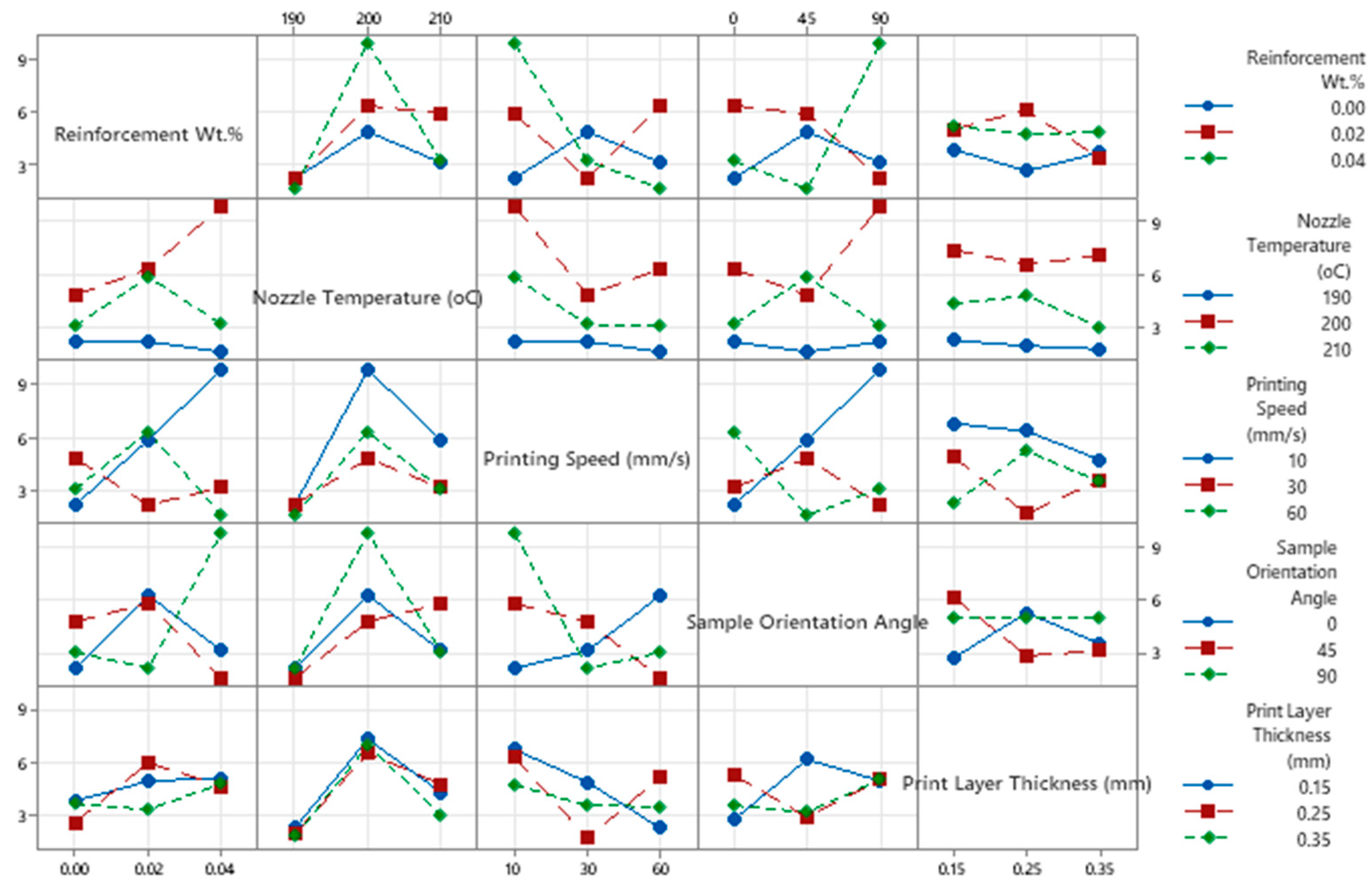
3.2.1. Tensile Properties
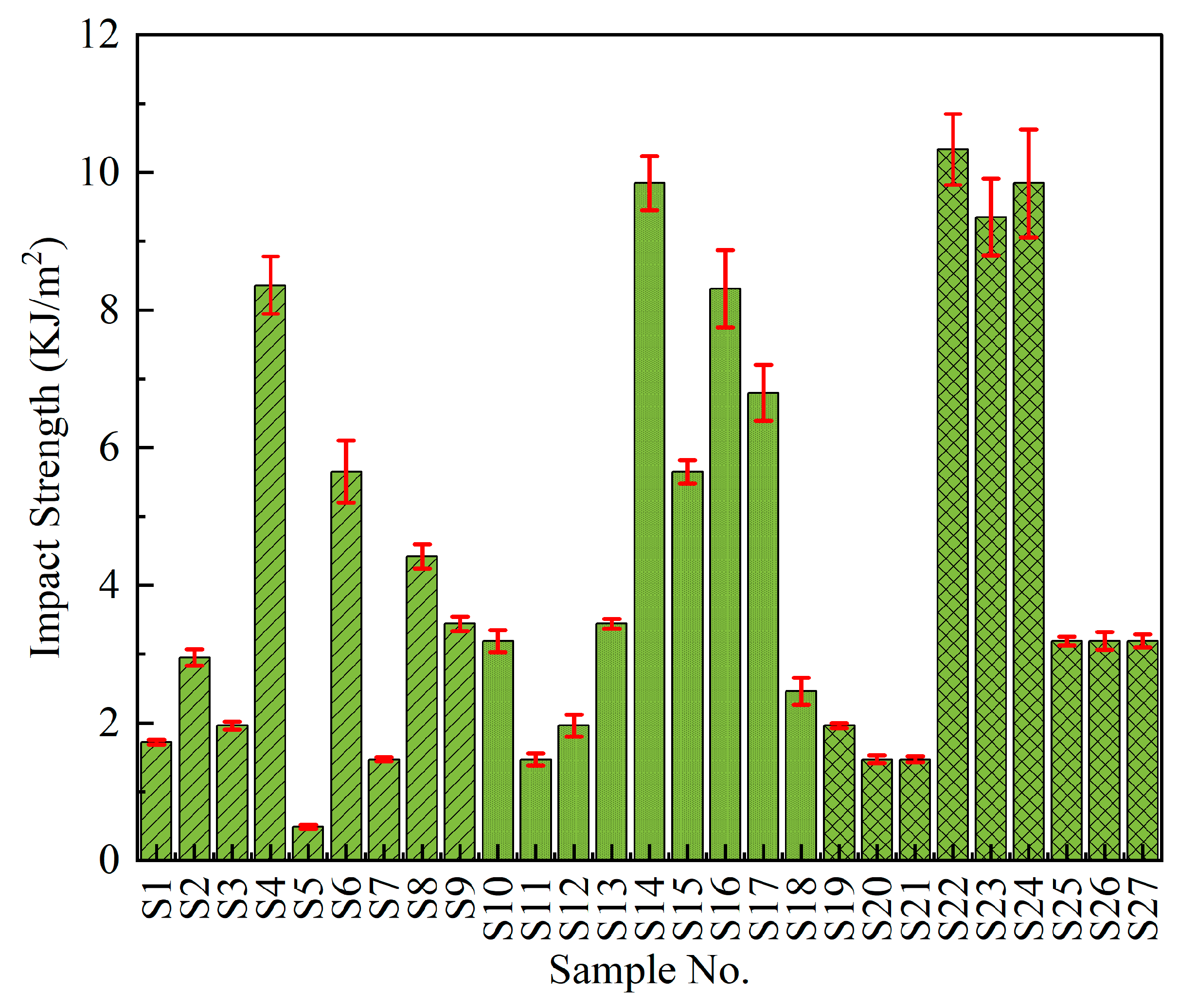
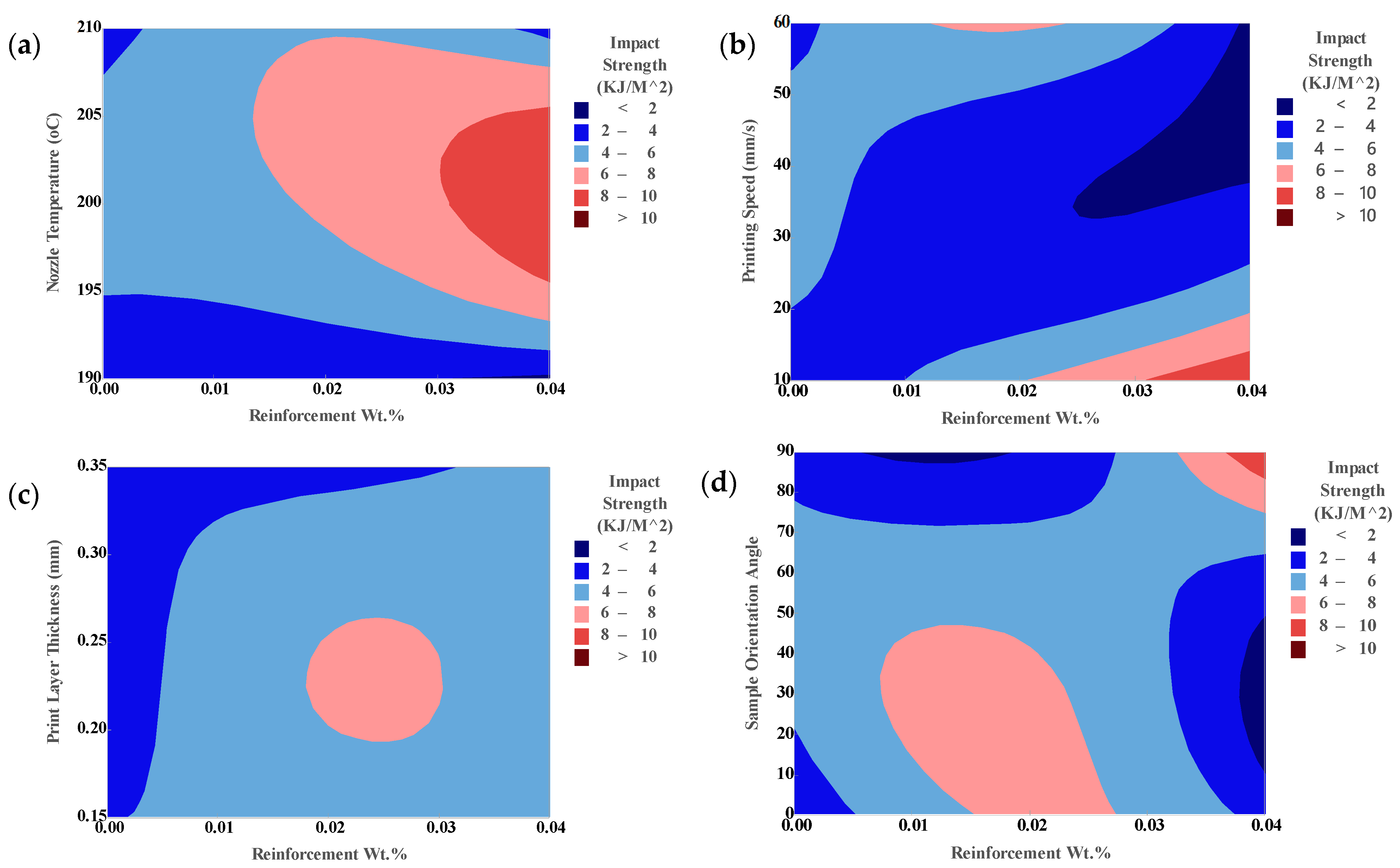
3.2.2. Impact Strength
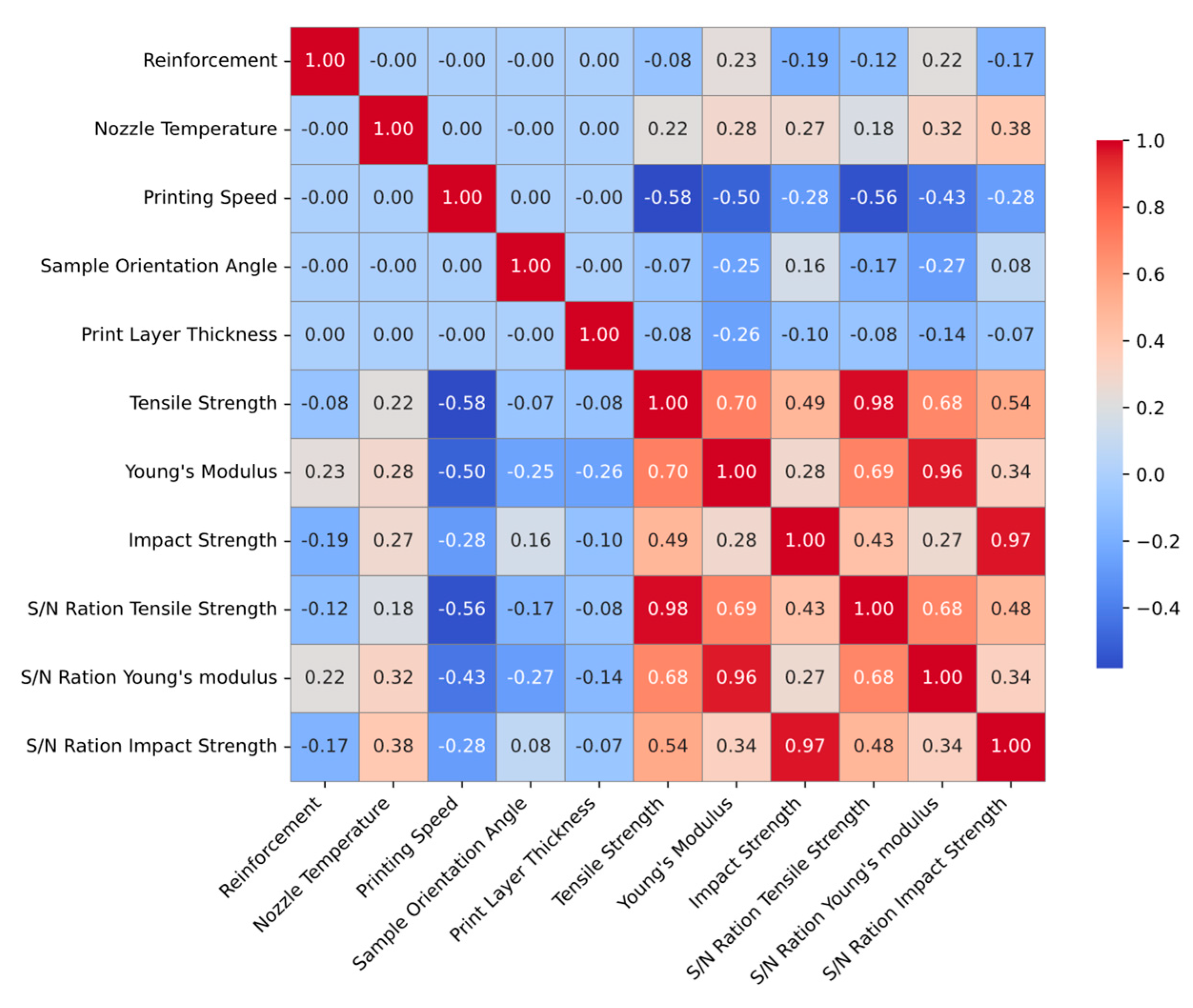
3.3. Statistical Analysis
3.3.1. Signal-to-Noise (S/N) Ratio Analysis
3.3.2. Taguchi Analysis
Taguchi Analysis for Tensile Strength
Taguchi Analysis for Young’s Modulus
Taguchi Analysis for Impact Strength
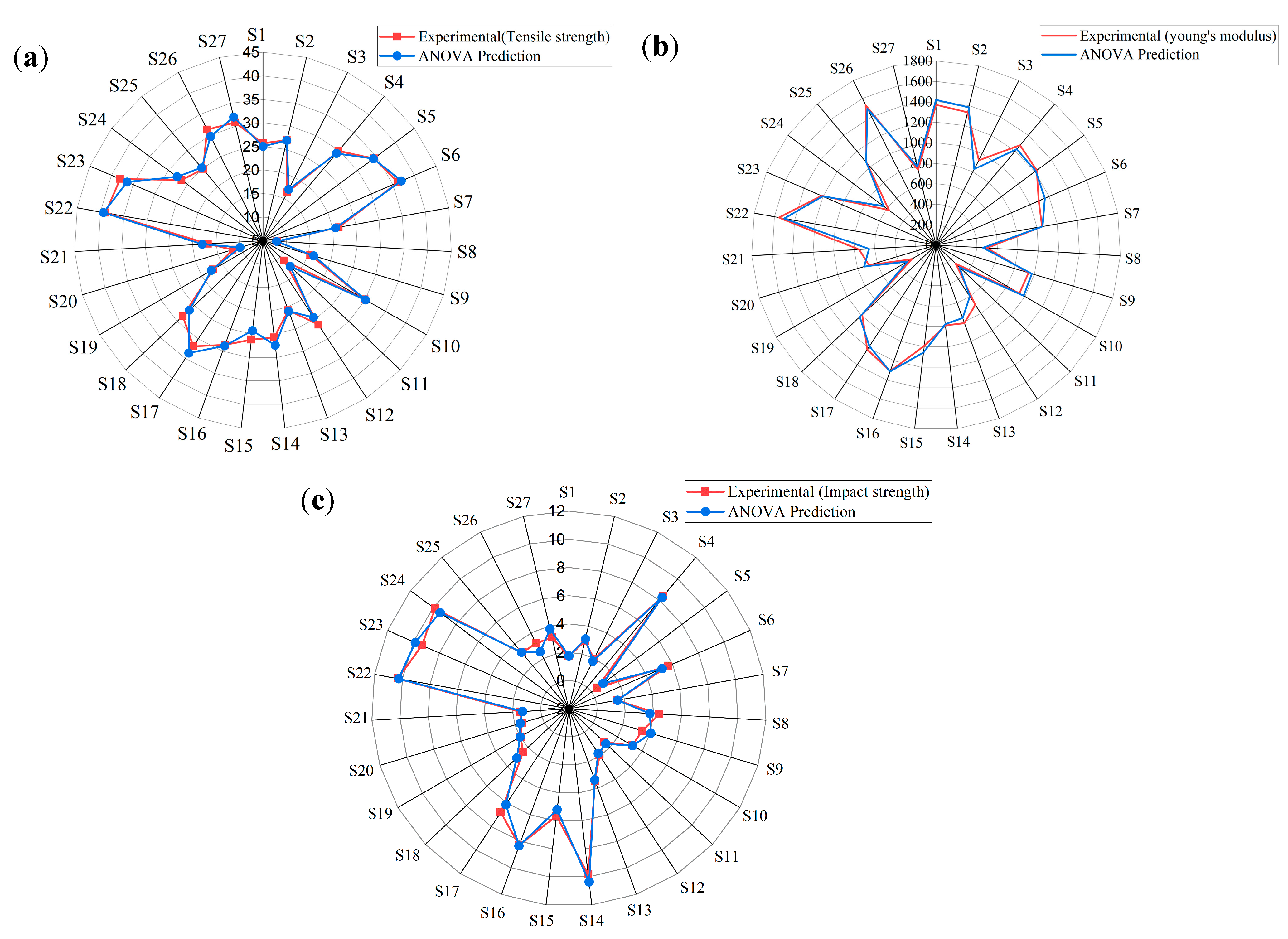
3.3.3. Analysis of Variance (ANOVA)
ANOVA for Tensile Strength
| Tensile strength = 25.159 − 1.350 C10.00+0.286 C10.02 + 1.064 C1_0.04 − 4.914 C2190 | (19) |
| + 5.553 C2200 − 0.639 C2210+ 3.886 C310+ 3.164 C330 − 7.050 C360 + 0.253 C40 + 0.941 C445 − 1.194 C490 + 1.1 | |
| 75 C50.15 − 0.805 C50.25 − 0.370 C50.35 + 2.85 C2190 × C50.15 − 2.81 C2190 × C50.25 − 0.04 C2190 × C50.35 − 2.05 C2200 × C50.15 | |
| + 2.76 C2200 × C50.25 − 0.71 C2200 × C50.35 − 0.79 C2210 × C50.15 + 0.05 C2210 × C50.25 + 0.75 C2210 × C50.35 + 0.85 C310 × C50.15 | |
| + 4.06 C310 × C50.25 − 4.91 C310 × C50.35 − 1.30 C330 × C50.15 − 1.88 C330 × C50.25 + 3.18 C330 × C50.35 + 0.45 | |
| C360 × C50.15 − 2.18 C360 × C50.25 + 1.73 C360 × C50.35 − 2.85 C40 × C50.15 + 3.43 C40 × C50.25 − 0.57 C40 × C50.35 − | |
| 2.04 C445 × C50.15 + 0.67 C445 × C50.25 + 1.37 C445×C50.35 + 4.89 C490 × C50.15 − 4.10 C490 × C50.25 − 0.79 C490 × C50.35 |
ANOVA for Young’s Modulus
| Young’s modulus (MPa) = | (20) |
| 967.0 + 111.8C10 − 77.3C10.02 − 34.6C10.04 − 163.0C2190 + 91.5C2200 + 71.5C2210 + 198.9C310 | |
| + 14.2C330 − 213.0C360 + 95.8C40 + 12.2C445 − 108.0C490 + 103.7C50.15 + 5.8 C50.25 − 109.6C50.35 + 49.2 | |
| C10* × C50.15 − 66.8C10 × C50.25 + 17.6C10 × C50.35 + 25.8C10.02 × C50.15 − 137.6C10.02 × C50.25 | |
| + 111.9 C10.02 × C50.35 − 74.9 C10.04 × C50.15 + 204.4 C10.04 × C50.25 − 129.5 C10.04 × C50.35 + 141.3 C310 × C50.15 | |
| + 84.7 C310 × C50.25 − 226.0 C310 × C50.35 + 5.3 C330 × C50.15 + 18.8 C330 × C50.25 − 24.1 C330 × C50.35 − 146.6 | |
| C360 × C50.15 − 103.5 C360 × C50.25 + 250.1 C360 × C50.35 − 87.5 C40 × C50.15 + 148.8 C40 × C50.25 − 61.3 C40 | |
| × C50.35 − 131.0 C445 × C50.15 + 57.0 C445 × C50.25 + 74.0 C445 × C50.35 + 218.5 C490 × C50.15 − 205.8 C490 × C50.25 | |
| − 12.7 C490 × C50.35 |
ANOVA for Impact Strength
| Impact Strength (KJ/m2) | = | 4.354 − 0.970 C10 + 0.436 C10.02 + 0.534 C10.04 − 2.338 C2190 + 2.640 C2200 − 0.303 C2210 | (21) |
| + 1.614 C310 − 0.944 C330 − 0.670 C360 − 0.451 C40 − 0.247 C445 + 0.698 C490 + 0.309 C50.15 | |||
| + 0.087 C50.25 − 0.396 C50.35 + 0.156 C10 × C50.15 − 0.852 C10 × C50.25 + 0.695 C10 × C50.35 − 0.120 | |||
| C10.02 × C50.15 + 1.157 C10.02 × C50.25 − 1.037 C10.02 × C50.35 − 0.037 C10.04 × C50.15 − 0.305 C10.04 × C50.25 + 0.342 C10.04 × C50.35+ 0.509 C310 × C50.15 + 0.309 C310 × C50.25 | |||
| − 0.819 C310 × C50.35+ 1.194 C330 × C50.15 − 1.781 C330 × C50.25 + 0.586 C330 × C50.35 | |||
| − 1.704 C360 × C50.15+ 1.471 C360 × C50.25+ 0.232 C360 × C50.35 − 1.429 C40 × C50.15 | |||
| + 1.336 C40 × C50.25+ 0.093 C40 × C50.35+ 1.794 C445 × C50.15 − 1.276 C445 × C50.25 | |||
| − 0.517 C445 × C50.35 − 0.365 C490 × C50.15 − 0.060 C490 × C50.25+ 0.424 C490 × C50.35 | |||
| − 12.7 C490 × C50.35 |
3.4. Machine Learning
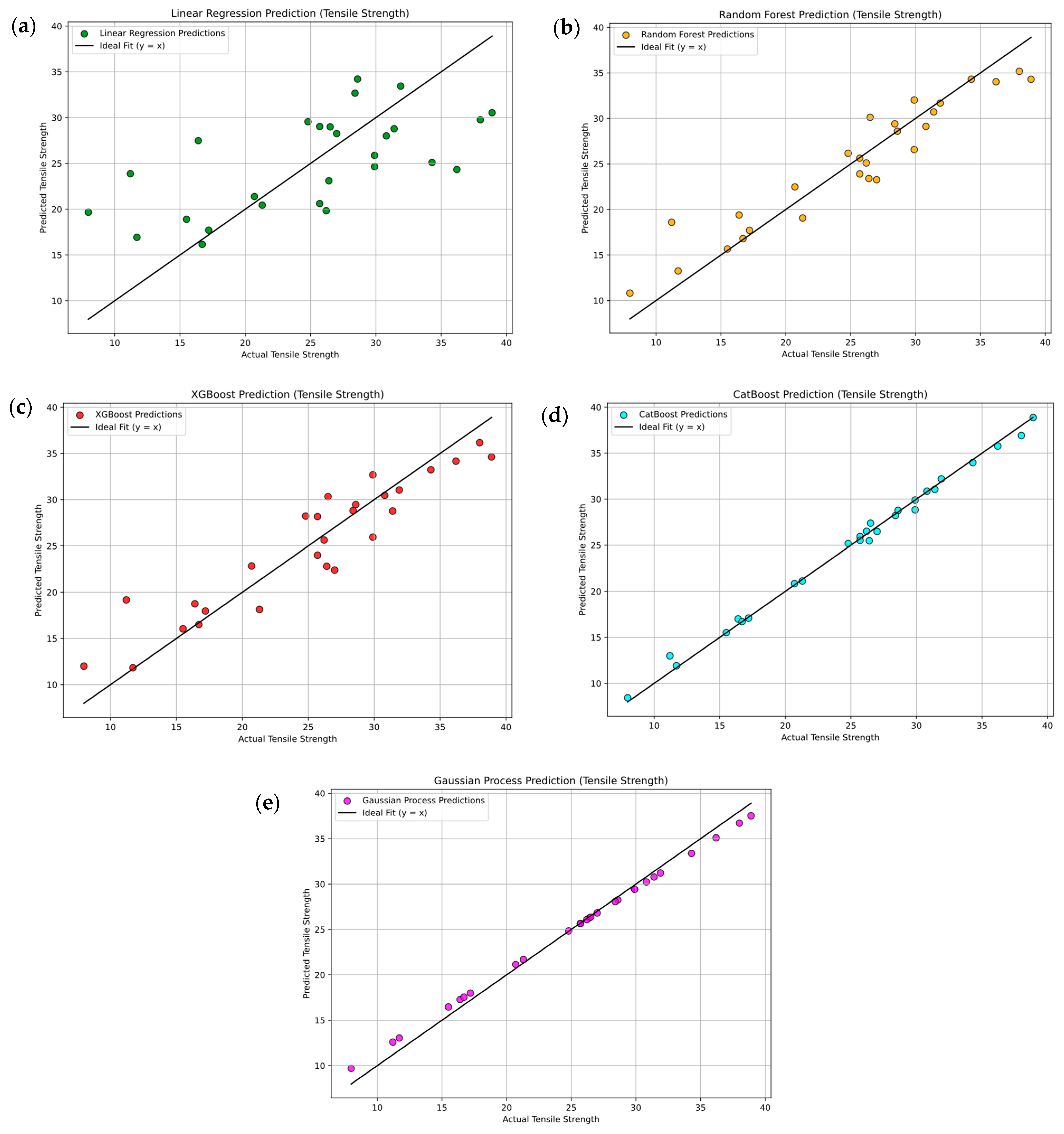
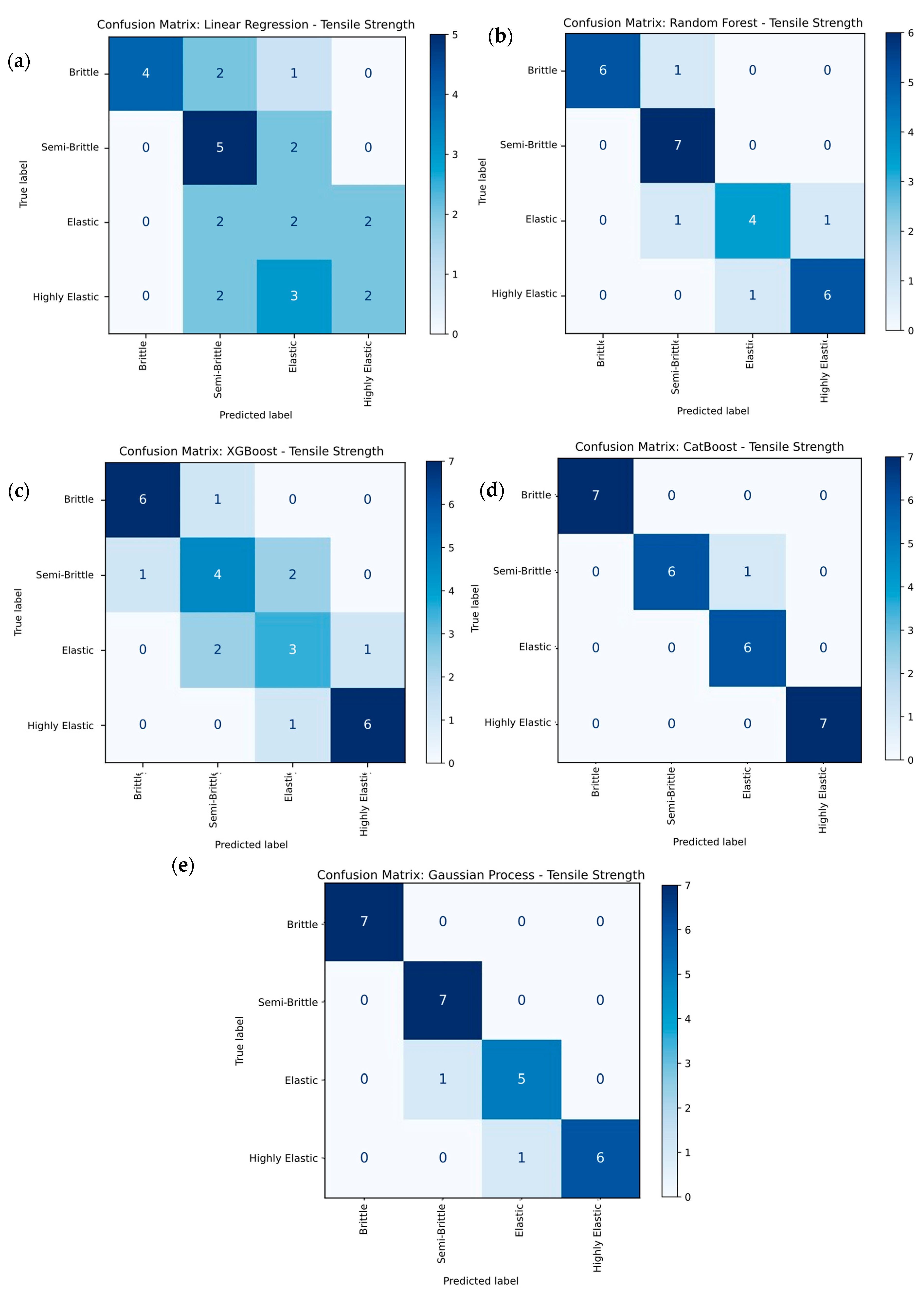
3.4.1. Machine Learning for Tensile Strength
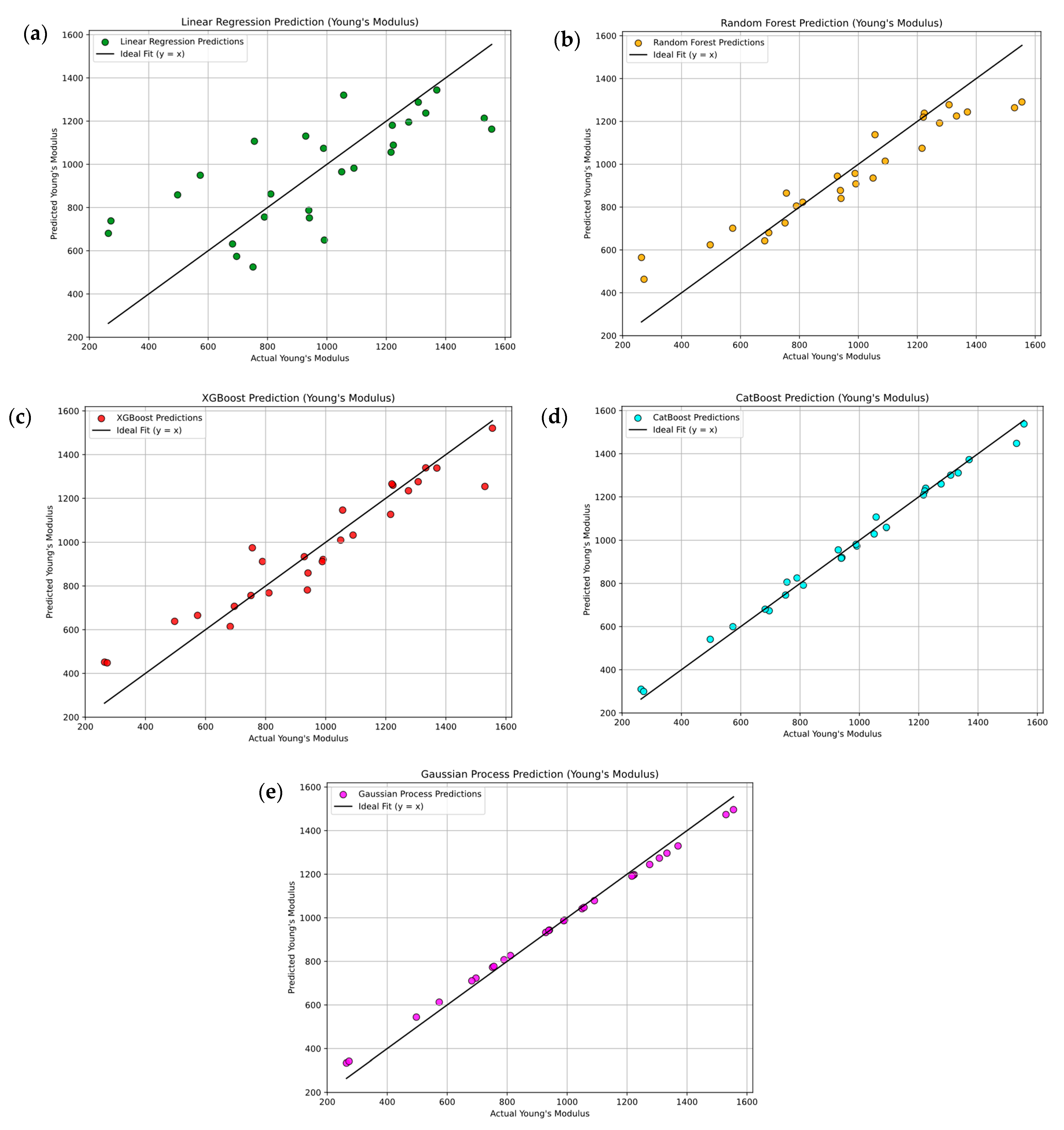
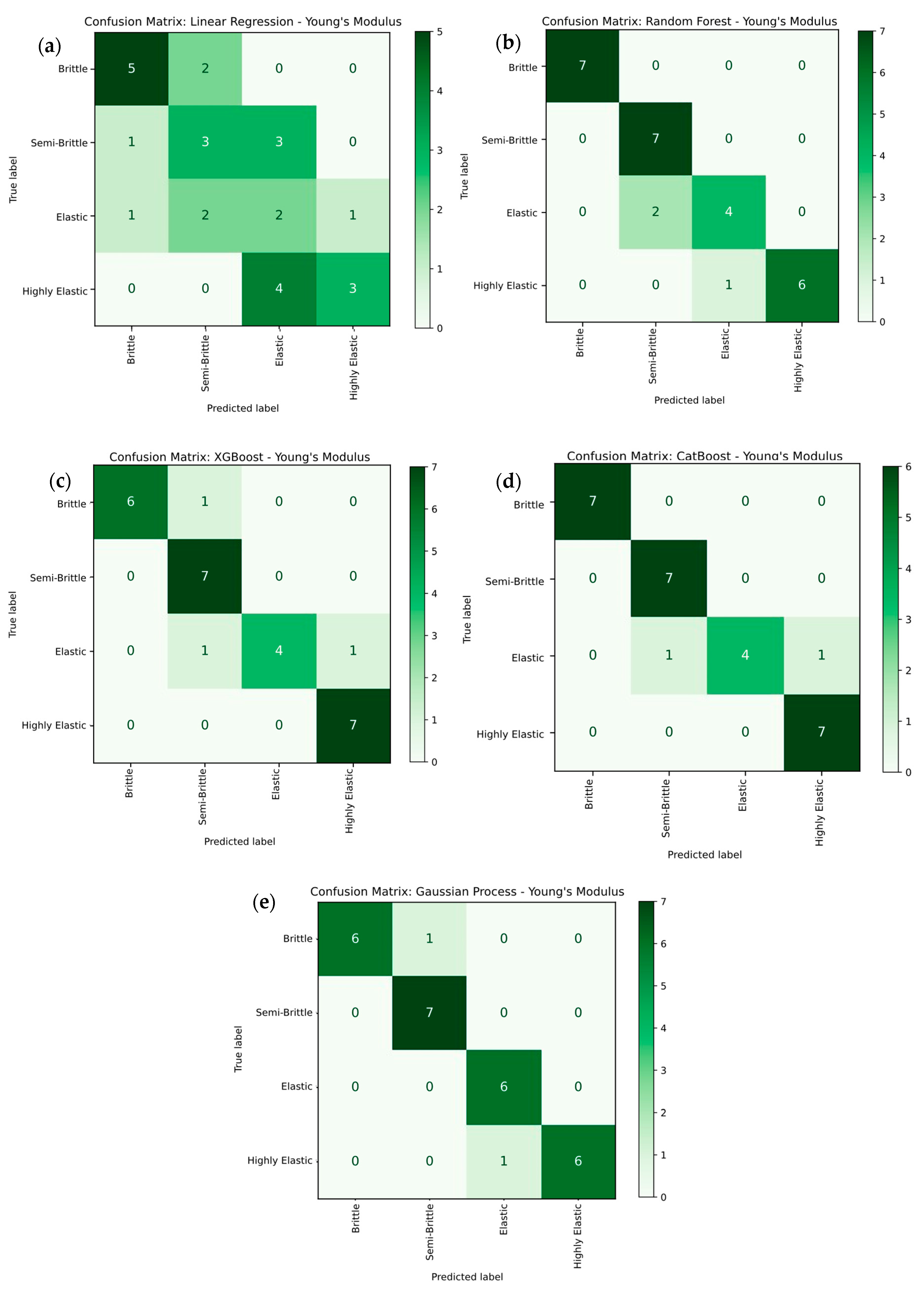
3.4.2. Machine Learning for Young’s Modulus
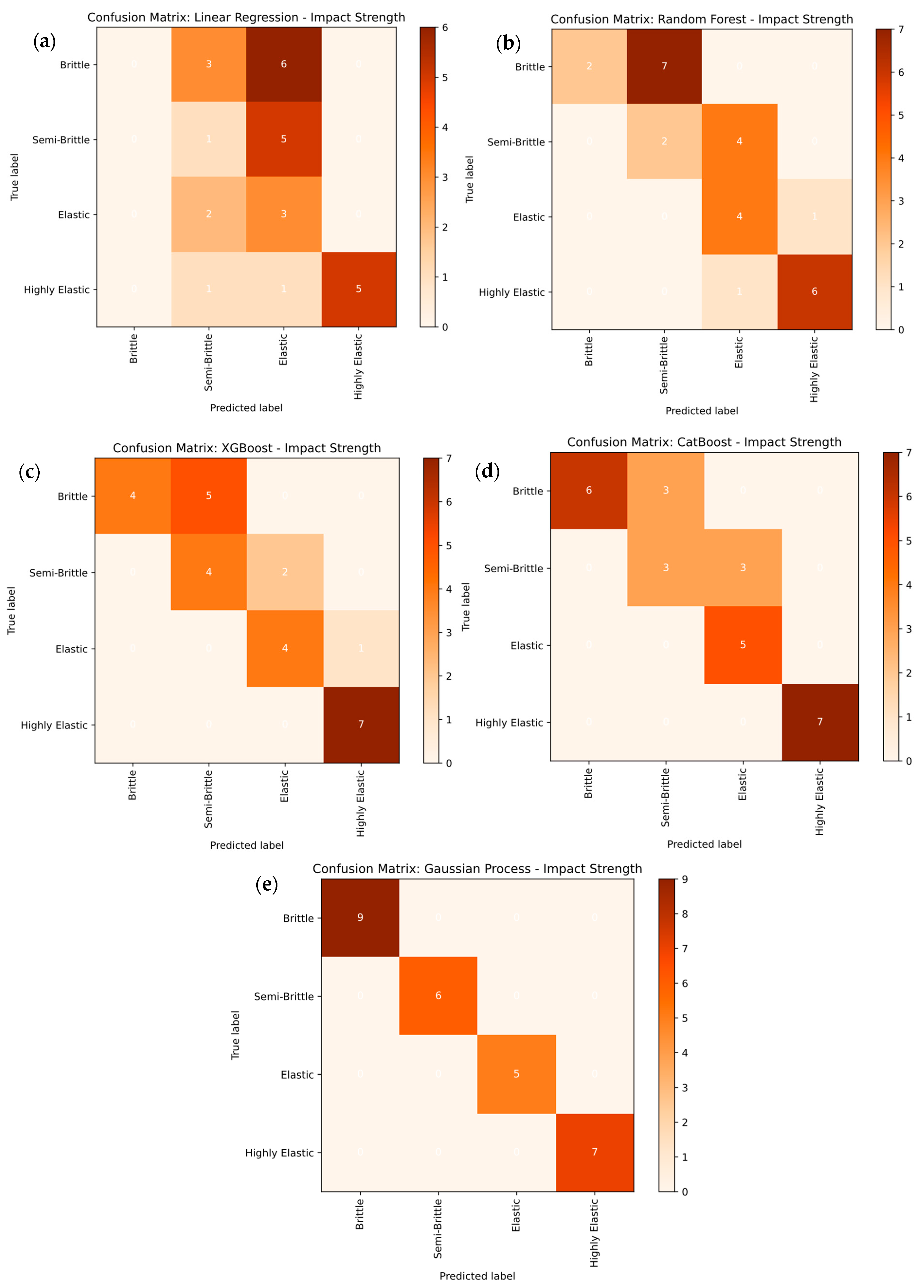
3.4.3. Machine Learning for Impact Strength
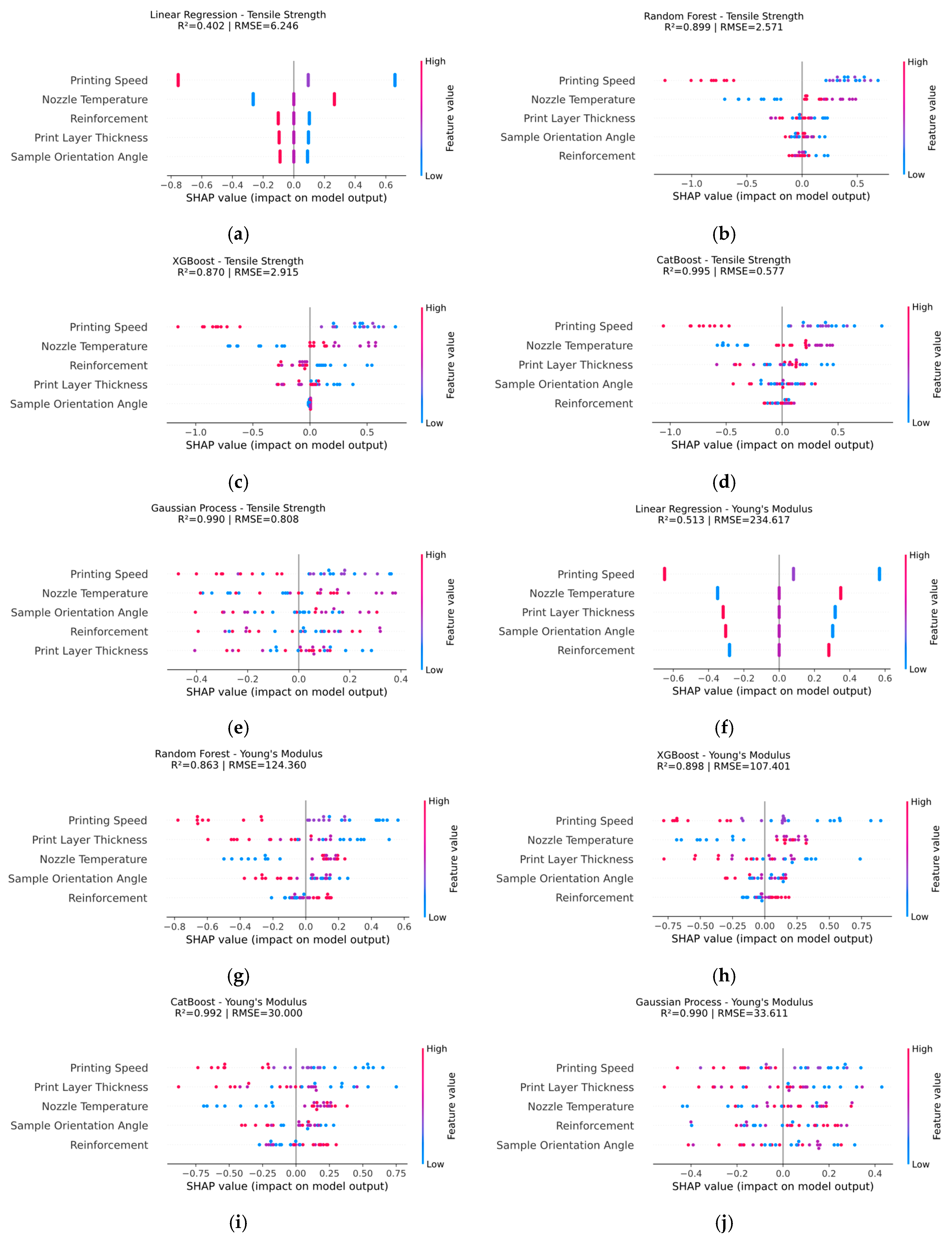
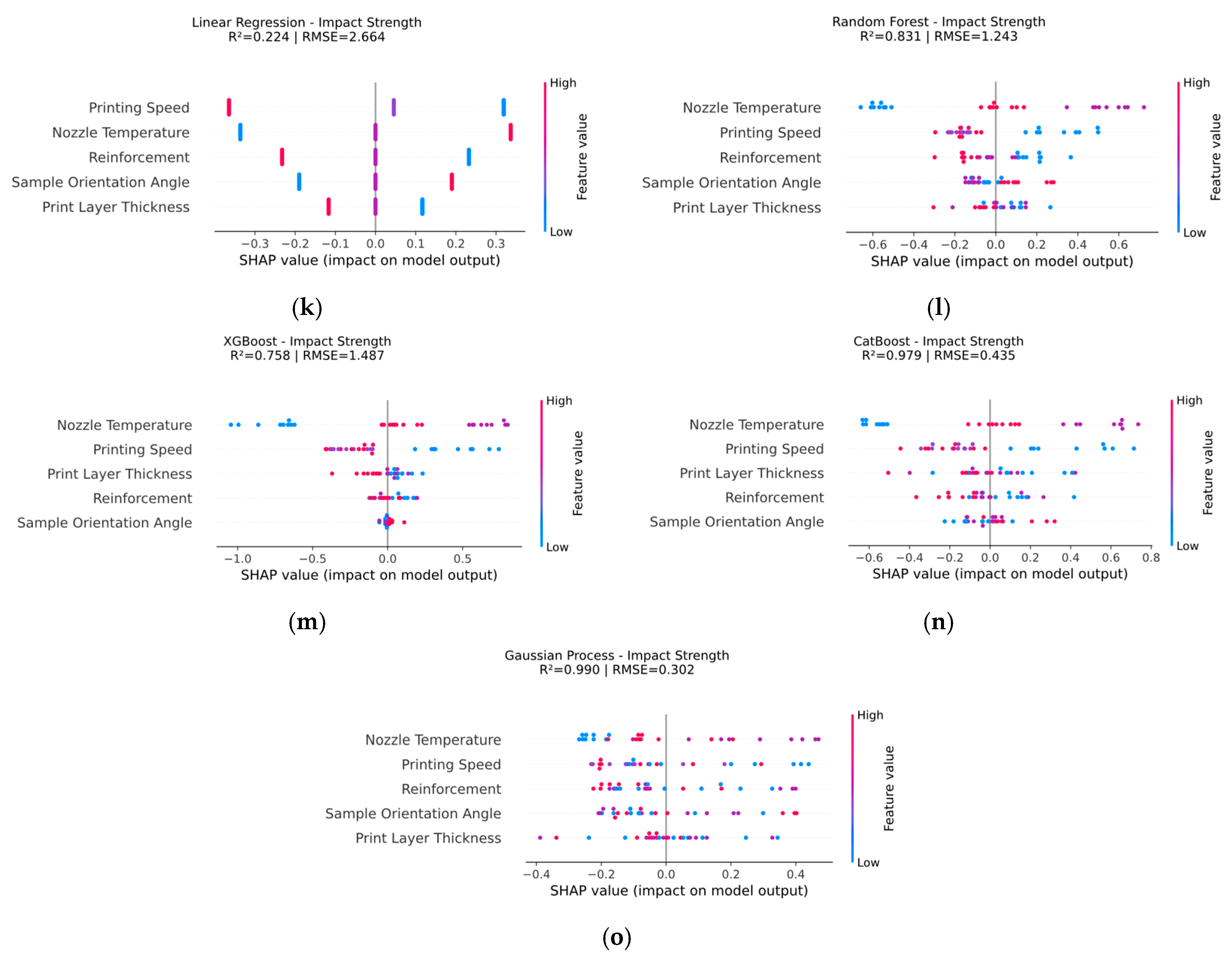
3.5. Model Evaluation by SHAP Analysis
4. Conclusions
- Incorporating 0.04 wt.% BNNP led to remarkable improvements: tensile strength increased by 44.2%, Young’s modulus by 45.5%, and impact strength by over 500% compared to pure PLA.
- Taguchi and ANOVA analyses identified printing speed and nozzle temperature as the most dominant factors for optimizing mechanical properties, while sample orientation and layer thickness had minor effects.
- CatBoost and Gaussian process regression models consistently delivered R2 values above 0.98 and mean absolute percentage errors below 4%, outperforming linear regression, Random Forest, and XGBoost models; their reliability was confirmed through parity plots and multi-class classification breakdowns.
- SHAP analysis reinforced the critical importance of printing speed and nozzle temperature, showing localized and global effects on predictive outputs, with SHAP values reaching up to 0.6.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PLA | Polylactic acid |
| BNNP | Boron nitride nanoplatelets |
| FDM | Fused deposition modeling |
| wt.% | Weight percent |
| ANOVA | Analysis of variance |
| ML | Machine learning |
| GPR | Gaussian process regression |
| SHAP | Shapley Additive Explanations |
| TEM | Transmission electron microscopy |
| UTM | Universal Testing Machine |
| DOE | Design of Experiments |
| S/N | Signal-to-noise |
| MSE | Mean squared error |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| RFR | Random Forest Regression |
| XGBoost | Extreme Gradient Boosting |
| CBR | CatBoost Regression |
| RBF | Radial Basis Function |
References
- Islam, M.A.; Mobarak, M.H.; Rimon, M.I.H.; Al Mahmud, M.Z.; Ghosh, J.; Ahmed, M.M.S.; Hossain, N. Additive manufacturing in polymer research: Advances, synthesis, and applications. Polym. Test. 2024, 132, 108364. [Google Scholar] [CrossRef]
- Blasiak, S.; Bochnia, J.; Takosoglu, J.; Kozior, T.; Nowakowski, L.; Skrzyniarz, M.; Krzysztofik, I.; Blasiak, M.; Dindorf, R.; Wos, P. 3D/4D Printing in Advanced Robotics Systems—Recent Developments and Applications. Sustainability 2024, 16, 11174. [Google Scholar]
- Alzyod, H.; Kónya, G.; Ficzere, P. Integrating Additive and Subtractive Manufacturing to Optimize Surface Quality of MEX Parts. Results Eng. 2025, 25, 103713. [Google Scholar]
- Raja, M.; Krishnan, S.G.; Harish, J.S. The future of 3D printing in manufacturing (innovative technology revolutionizing manufacturing processes and products). Int. J. Sci. Res. Eng. Manag. 2024, 8, 1–6. [Google Scholar]
- Herranz, G.; Berges, C.; Hidalgo, J. Material Extrusion Additive Technologies: Benefits, Challenges, and Niche Applications. In Additive Manufacturing—Present and Sustainable Future, Materials and Applications; IntechOpen: London, UK, 2025. [Google Scholar]
- Prashar, G.; Vasudev, H. Additive Manufacturing. In Advanced Manufacturing Processes; CRC Press: Boca Raton, FL, USA, 2025; pp. 1–8. [Google Scholar]
- Elhady, S.; Ellatif, I.A.B.D.; Abdelrahman, K.M.; Mostaf, A.S.; Fahim, I.S. Innovations in 3D Printing-Assisted Biopolymers for Biomedical Applications. In Sustainable 3D Printing for Innovative Biopolymer Production and Applications; Sharma, B., Pani, B., Shekhar, S., Okolie, J.A., Eds.; Wiley: Hoboken, NJ, USA, 2025; pp. 95–116. [Google Scholar]
- Rogachuk, B.E.; Okolie, J.A. Economic and Environmental Assessment of Sustainable Polymer-Based 3D Printing. In Sustainable 3D Printing for Innovative Biopolymer Production and Applications; Sharma, B., Pani, B., Shekhar, S., Okolie, J.A., Eds.; Wiley: Hoboken, NJ, USA, 2025; pp. 233–243. [Google Scholar]
- Liu, H. Research Progress in the Synthesis and Modification of Polylactic Acid. Highlights Sci. Eng. Technol. 2024, 84, 35–41. [Google Scholar] [CrossRef]
- Kaptan, A.; Kartal, F. Advancements in Polylactic Acid Research: From Material Properties to Sustainable Applications. Eur. Mech. Sci. 2024, 8, 104–114. [Google Scholar] [CrossRef]
- Khamvongsa, M.; Milton, K.; Faisal, T.R. Mechanical Characterization of Low-Cost 3D FDM Printed Scaffolds Fabricated with Synthesized PLA/HA Bio-Composite Filament. Ann. 3D Print. Med. 2025, 18, 100194. [Google Scholar]
- Arunkumar, P.; Balaji, D.; Radhika, N.; Rajeshkumar, L.; Mavinkere Rangappa, S.; Siengchin, S. Effect of Infill Pattern on Mechanical Properties of 3D Printed PLA-Zn Composites for Drone Frame Structures: A Topology Optimization Integrated Application Study. Results Eng. 2025, 25, 104107. [Google Scholar] [CrossRef]
- Firoz, A.B.; Rybakov, V.; Fetisova, A.A.; Shlapakova, L.E.; Pariy, I.O.; Toropkov, N.; Lozhkomoev, A.S.; Mukhortova, Y.R.; Sharonova, A.A.; Wagner, D.V.; et al. 3D-Printed Biodegradable Composite Poly(Lactic Acid)-Based Scaffolds with a Shape Memory Effect for Bone Tissue Engineering. Adv. Compos. Hybrid Mater. 2025, 8, 95. [Google Scholar]
- Bakhtiari, A.; Madaah Hosseini, H.R.; Alizadeh, R.; Mohammadi, M.; Zarei, M. Enhancing Mechanical and Biological Properties of 3D-Printed Polylactic Acid Scaffolds by Graphitic Carbon Nitride Addition for Bone Tissue Engineering. J. Mater. Res. Technol. 2025, 35, 308–316. [Google Scholar] [CrossRef]
- Mohammed, O.K.; Hassani, A.; Zolfaghari, A.; Diwan, A.A. Mechanical Performance of 3D Printed Polylactic Acid/MWCNT Brackets: Effects of CNT Concentration and Printing Orientation on Stress-Strain Behavior and Deflection Characteristics. Int. J. Eng. 2025, 38, 1782–1792. [Google Scholar] [CrossRef]
- Nataraj, G.; Babu, S.R. Enhancing mechanical properties of PLA-based bio composite filament reinforced with horse gram filler for 3D printing applications. J. Vinyl Addit. Technol. 2025, 31, 453–468. [Google Scholar] [CrossRef]
- Jasiński, W.; Szymanowski, K.; Nasiłowska, B.; Barlak, M.; Betlej, I.; Prokopiuk, A.; Borysiuk, P. 3D Printing Wood–PLA Composites: The Impact of Wood Particle Size. Polymers 2025, 17, 1165. [Google Scholar] [CrossRef]
- Mishra, D.K.; Giri, J.; Sathish, T.; Kanan, M.; Prajapati, D. Influence of 3D printing process parameters on mechanical properties of PLA-based ceramic composite parts. Results Eng. 2025, 25, 104488. [Google Scholar] [CrossRef]
- Li, H.; Yu, Z.; Liu, B.; Gao, Y.; Liu, M.; Zhang, J.; Zhu, Y.; Chen, S.; Yu, B.; Wang, B. A Highly Ductile Composite of 3D-Printed Poly (Lactic Acid) With InSe Particles and Flakes as a Filler. SmartMat 2025, 6, e1316. [Google Scholar] [CrossRef]
- Neto, T.S.; Maia, L.S.; Zanata, L.; Conceição, M.O.; Medeiros, S.F.; Faria, M.I.S.; Mulinari, D.R. A promising pullulan/PLA composite: Influence of pullulan on the scaffolds’ morphology constructed by 3D printing. J. Appl. Polym. Sci. 2025, 142, e56389. [Google Scholar] [CrossRef]
- Koyunbakan, M.; Uslugil, Y.; Ekrem, M.; Eser, Ü. Investigation of the mechanical properties of aramid fiber-reinforced hybrid nanocomposites with BNNP-enhanced epoxy matrix. Compos. Interfaces 2025, 1–17. [Google Scholar] [CrossRef]
- Rasul, M.G.; Kiziltas, A.; Arfaei, B.; Shahbazian-Yassar, R. 2D boron nitride nanosheets for polymer composite materials. NPJ 2D Mater. Appl. 2021, 5, 56. [Google Scholar] [CrossRef]
- Badgayan, N.D.; Sahu, S.K.; Samanta, S.; Sreekanth, P.S.R. Assessment of bulk mechanical properties of HDPE hybrid composite filled with 1D/2D nanofiller system. Mater. Sci. Forum 2018, 917, 12–16. [Google Scholar] [CrossRef]
- Alahmad, H.; Alamir, R.; Asadzadeh, M.; Daood, U.; Qasim, S.S.B. Enhancing PMMA properties: A comprehensive study of nanographene oxide and Boron nitride impact through In-Vitro analysis. BMC Oral Health 2025, 25, 659. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Auffray, L.; Gouge, P.-A.; Hattali, L. Design of experiment analysis on tensile properties of PLA samples produced by fused filament fabrication. Int. J. Adv. Manuf. Technol. 2022, 118, 4123–4137. [Google Scholar] [CrossRef]
- Mishra, V.; Negi, S.; Bharat, N.; Veeman, D.; Kumar, V. Effect of FFF parameters on PLA/WD composite properties: Comparative analysis using Taguchi and GRA approach. J. Reinf. Plast. Compos. 2025, 44, 1314979. [Google Scholar] [CrossRef]
- Vidakis, N.; Petousis, M.; Mountakis, N.; Papadakis, V.M. Glass Fillers in Three Different Forms Used as Reinforcement Agents of Polylactic Acid in Material Extrusion Additive Manufacturing. Appl. Sci. 2023, 13, 6471. [Google Scholar] [CrossRef]
- Tosto, C.; Pergolizzi, E.; Vitiello, L.; Filippone, G.; Cicala, G. Production of PLA-milled carbon fiber (MCF) filled filaments for Fused Filament Fabrication (FFF) printing. Macromol. Symp. 2022, 404, 2100417. [Google Scholar]
- Sapre, M.; Jatti, A.V.; Khedkar, N.K.; Jatti, V.S. Mechanical Properties of 3D-Printed Components Using Fused Deposition Modeling: Optimization Using the Desirability Approach and Machine Learning Regressor. Appl. Syst. Innov. 2022, 5, 112. [Google Scholar] [CrossRef]
- Daly, M.; Tarfaoui, M.; Chihi, M.; Bouraoui, C. FDM technology and the effect of printing parameters on the tensile strength of ABS parts. Int. J. Adv. Manuf. Technol. 2023, 126, 5307–5323. [Google Scholar] [CrossRef]
- Hemanth, R.; Sekar, M.; Suresha, B. Effects of fibers and fillers on mechanical properties of thermoplastic composites. Indian J. Adv. Chem. Sci. 2014, 2, 28–35. [Google Scholar]
- Uddin, M.S.; Sidek, M.F.R.; Faizal, M.A.; Ghomashchi, R.; Pramanik, A. Evaluating Mechanical Properties and Failure Mechanisms of Fused Deposition Modeling Acrylonitrile Butadiene Styrene Parts. J. Manuf. Sci. Eng. 2017, 139, 081018. [Google Scholar] [CrossRef]
- Ul-Hamid, A. Synthesis, microstructural characterization and nanoindentation of Zr, Zr-nitride and Zr-carbonitride coatings deposited using magnetron sputtering. J. Adv. Res. 2021, 29, 107–119. [Google Scholar]
- Pernica, J.; Vodák, M.; Šarocký, R.; Šustr, M.; Dostál, P.; Cerny, M.; Dobrocky, D. Mechanical Properties of Recycled Polymer Materials in Additive Manufacturing. Manuf. Technol. 2022, 22, 200–203. [Google Scholar] [CrossRef]
- Boangmanalu, E.P.D.; Pratama, A.B.; Qadry, A.; Saragi, J.F.H.; Sinaga, F.T.H. Charpy and Izod Method Impak Strength Analysis on ST 37 Steel with Temperature Variations. J. Sci. Technol. 2023, 2, 7074. [Google Scholar]
- Kacem, M.A.; Zekri, A.; Ben Ouada, A.; Abderrazek, H.; Smaoui, N.; El Cafsi, M.; Bouhamed, A. Development and 3D printing of PLA bio-composites reinforced with short yucca fibers and enhanced thermal and dynamic mechanical performance. J. Mater. Res. Technol. 2025, 36, 1243–1258. [Google Scholar] [CrossRef]
- Mecha, P.; Zhu, R.; Zhang, J.; Awuah, E.; Soomro, S.A.; Chen, K. Optimization of chanterelle mushroom drying kinetics under heat pump dryer using Taguchi design method. Int. J. Agric. Biol. Eng. 2024, 16, 273–279. [Google Scholar] [CrossRef]
- Ong, N.R. Use of Taguchi Method-Based Design of Experiments (DOE) in the Optimization of the Drilling Parameters of Structural A572 Steel. Int. J. Adv. Mech. Eng. 2023, 13, 578. [Google Scholar]
- Zheng, M.; Wen, Q.; Xu, F.; Wu, D. Regional Forest Carbon Stock Estimation Based on Multi-Source Data and Machine Learning Algorithms. Forests 2025, 16, 420. [Google Scholar] [CrossRef]
- Khalfa, M.A.; Manai, L.; Mchara, W. Advanced artificial intelligence model for solar irradiance forecasting for solar electric vehicles. Int. J. Dyn. Control 2025, 13, 101. [Google Scholar]
- Sundarasetty, H.; Sahu, S.K. Tribological behavior of PLA reinforced with boron nitride nanoparticles using Taguchi and machine learning approaches. Results Eng. 2025, 26, 104772. [Google Scholar] [CrossRef]
- Yang, L.; Shen, D. Algebraic and Statistical Properties of the Partially Regularized Ordinary Least Squares Interpolator. arXiv 2024, arXiv:2411.06593. [Google Scholar] [CrossRef]
- Liu, T.; Sun, Y.; Han, H.; Wu, G.; Zhang, X.; Ren, W.; Chen, Y.; Li, Z. Identification of the primary pollution sources and dominant influencing factors of soil heavy metals using a random forest model optimized by genetic algorithm coupled with geodetector. Ecotoxicol. Environ. Saf. 2025, 290, 117731. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Xie, J.; Xiong, X.; Wang, L.; Chang, X. Prediction of peak particle vibration velocity based on intelligent optimization algorithm combined with XGBoost. Expert Syst. Appl. 2025, 280, 127654. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Du, D.; Yu, Z.; Ma, T.; Liang, Q. A Fusion XGBoost Approach for Large-Scale Monitoring of Soil Heavy Metal in Farmland Using Hyperspectral Imagery. Agronomy 2025, 15, 676. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, C.; Dai, X.; Xiong, X. Research on mining land subsidence by intelligent hybrid model based on gradient boosting with categorical features support algorithm. J. Environ. Manag. 2024, 354, 120309. [Google Scholar] [CrossRef] [PubMed]
- Dalmasso, M.; Civera, M.; De Biagi, V.; Chiaia, B. Gaussian Process Regression (GPR)-based missing data imputation and its uses for bridge structural health monitoring. Appl. Biomater. Eng. Nanotechnol. 2025, 6, 23. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, X.; Lin, Z. Improving soil moisture prediction using Gaussian process regression. Smart Agric. Technol. 2025, 11, 100905. [Google Scholar] [CrossRef]
- Ponce-Bobadilla, A.V.; Schmitt, V.; Maier, C.S.; Mensing, S.; Stodtmann, S. Practical guide to SHAP analysis: Explaining supervised machine learning model predictions in drug development. Clin. Transl. Sci. 2024, 17, e70056. [Google Scholar] [CrossRef] [PubMed]
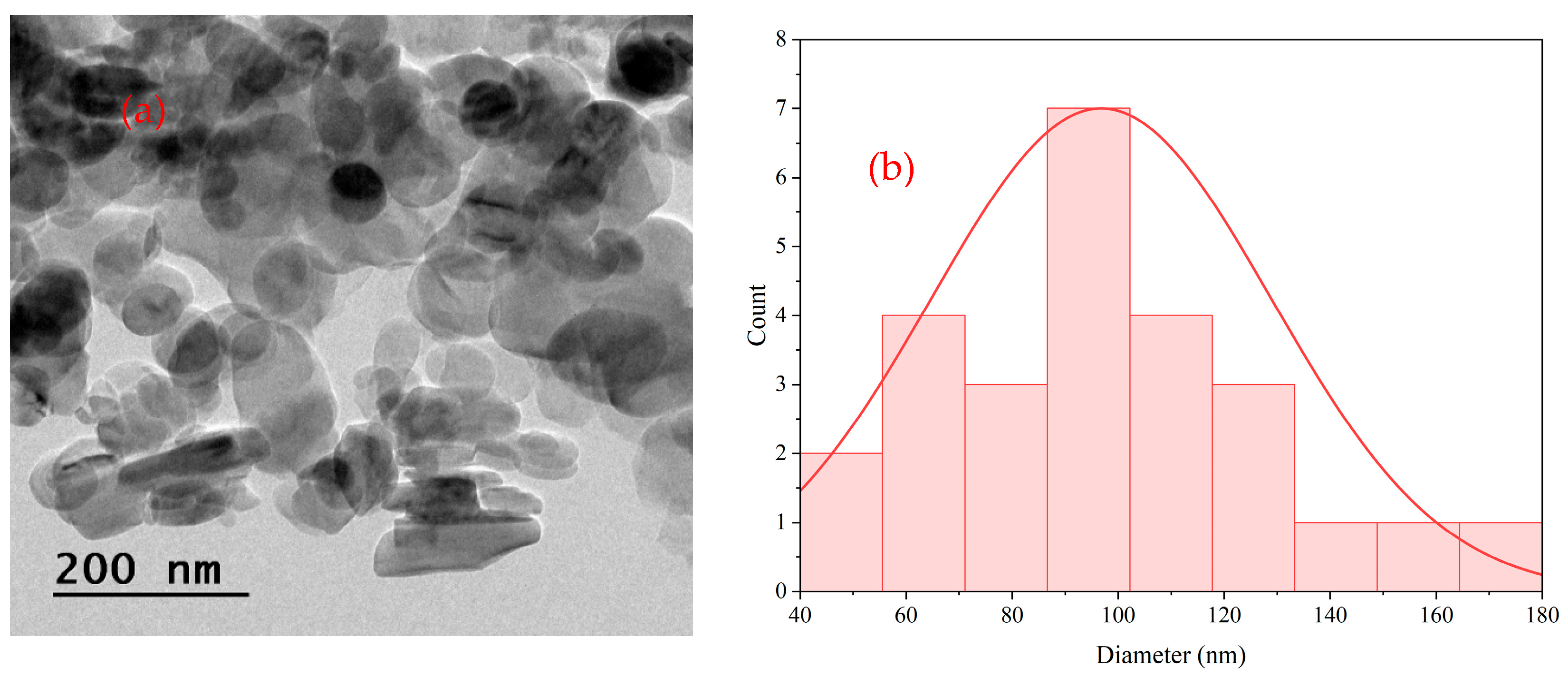

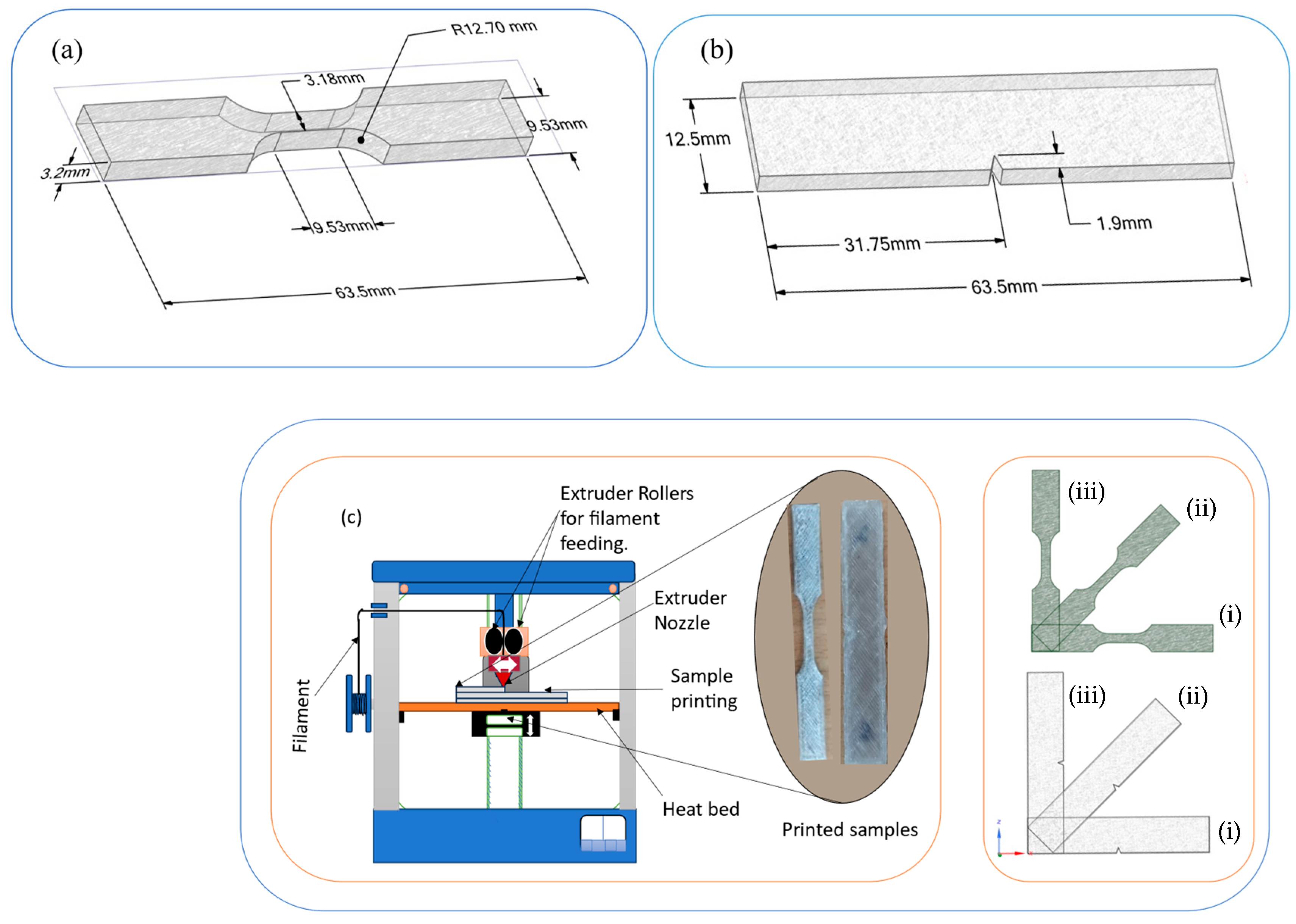


| Processing Parameters | Level-1 | Level-2 | Level-3 |
|---|---|---|---|
| Reinforcement wt.% (C1) | Pure PLA | 0.02 | 0.04 |
| Nozzle Temperature (°C) (C2) | 190 | 200 | 210 |
| Printing Speed (mm/s) (C3) | 10 | 30 | 60 |
| Sample Orientation Angle (C4) | 0 | 45 | 90 |
| Print Layer Thickness (mm) (C5) | 0.15 | 0.25 | 0.35 |
| Exp. No. | Sample. No | Reinforcement wt.% | Nozzle Temperature (°C) | Printing Speed (mm/s) | Sample Orientation Angle | Print Layer Thickness (mm) |
|---|---|---|---|---|---|---|
| 1 | S1 | Pure | 190 | 10 | 0 | 0.15 |
| 2 | S2 | Pure | 190 | 10 | 0 | 0.25 |
| 3 | S3 | Pure | 190 | 10 | 0 | 0.35 |
| 4 | S4 | Pure | 200 | 30 | 45 | 0.15 |
| 5 | S5 | Pure | 200 | 30 | 45 | 0.25 |
| 6 | S6 | Pure | 200 | 30 | 45 | 0.35 |
| 7 | S7 | Pure | 210 | 60 | 90 | 0.15 |
| 8 | S8 | Pure | 210 | 60 | 90 | 0.25 |
| 9 | S9 | Pure | 210 | 60 | 90 | 0.35 |
| 10 | S10 | 0.02 | 190 | 30 | 90 | 0.15 |
| 11 | S11 | 0.02 | 190 | 30 | 90 | 0.25 |
| 12 | S12 | 0.02 | 190 | 30 | 90 | 0.35 |
| 13 | S13 | 0.02 | 200 | 60 | 0 | 0.15 |
| 14 | S14 | 0.02 | 200 | 60 | 0 | 0.25 |
| 15 | S15 | 0.02 | 200 | 60 | 0 | 0.35 |
| 16 | S16 | 0.02 | 210 | 10 | 45 | 0.15 |
| 17 | S17 | 0.02 | 210 | 10 | 45 | 0.25 |
| 18 | S18 | 0.02 | 210 | 10 | 45 | 0.35 |
| 19 | S19 | 0.04 | 190 | 60 | 45 | 0.15 |
| 20 | S20 | 0.04 | 190 | 60 | 45 | 0.25 |
| 21 | S21 | 0.04 | 190 | 60 | 45 | 0.35 |
| 22 | S22 | 0.04 | 200 | 10 | 90 | 0.15 |
| 23 | S23 | 0.04 | 200 | 10 | 90 | 0.25 |
| 24 | S24 | 0.04 | 200 | 10 | 90 | 0.35 |
| 25 | S25 | 0.04 | 210 | 30 | 0 | 0.15 |
| 26 | S26 | 0.04 | 210 | 30 | 0 | 0.25 |
| 27 | S27 | 0.04 | 210 | 30 | 0 | 0.35 |
| Exp. No | Sample No | Tensile Strength | Young’s Modulus | Impact Strength | S/N Ratio Tensile Strength | S/N Ratio Young’s modulus | S/N Ratio Impact Strength |
|---|---|---|---|---|---|---|---|
| 1 | S1 | 25.7 | 1370 | 1.72 | 28.19 | 62.73 | 4.71 |
| 2 | S2 | 27 | 1333 | 2.95 | 28.63 | 62.49 | 9.39 |
| 3 | S3 | 16.4 | 928.71 | 1.96 | 24.29 | 59.36 | 5.85 |
| 4 | S4 | 29.9 | 1275.45 | 8.36 | 29.51 | 62.11 | 18.44 |
| 5 | S5 | 34.3 | 1223.64 | 0.49 | 30.71 | 61.75 | 6.19 |
| 6 | S6 | 36.2 | 1091.03 | 5.65 | 31.17 | 60.76 | 15.04 |
| 7 | S7 | 21.3 | 1049.84 | 1.47 | 26.57 | 60.42 | 3.35 |
| 8 | S8 | 7.98 | 497.16 | 4.42 | 18.04 | 53.93 | 12.91 |
| 9 | S9 | 15.5 | 941.02 | 3.44 | 23.81 | 59.47 | 10.73 |
| 10 | S10 | 29.9 | 938.98 | 3.19 | 29.51 | 59.45 | 10.08 |
| 11 | S11 | 11.2 | 263.94 | 1.47 | 20.98 | 48.43 | 3.35 |
| 12 | S12 | 26.4 | 695.96 | 1.96 | 28.43 | 56.85 | 5.85 |
| 13 | S13 | 20.7 | 810.97 | 3.44 | 26.32 | 58.18 | 10.73 |
| 14 | S14 | 25.7 | 789.61 | 9.84 | 28.19 | 57.95 | 19.86 |
| 15 | S15 | 26.2 | 991.38 | 5.65 | 28.37 | 59.93 | 15.04 |
| 16 | S16 | 28.6 | 1307.78 | 8.31 | 29.13 | 62.33 | 18.39 |
| 17 | S17 | 31.9 | 1220.32 | 6.79 | 30.07 | 61.73 | 16.64 |
| 18 | S18 | 28.4 | 988.76 | 2.46 | 29.07 | 59.90 | 7.82 |
| 19 | S19 | 17.2 | 272.59 | 1.96 | 24.71 | 48.71 | 5.85 |
| 20 | S20 | 11.7 | 682.16 | 1.47 | 21.36 | 56.68 | 3.34 |
| 21 | S21 | 16.7 | 751.10 | 1.47 | 24.45 | 57.51 | 3.35 |
| 22 | S22 | 38.9 | 1554.93 | 10.33 | 31.79 | 63.83 | 20.28 |
| 23 | S23 | 38 | 1215.99 | 9.35 | 31.59 | 61.69 | 19.42 |
| 24 | S24 | 26.5 | 573.45 | 9.84 | 28.46 | 55.17 | 19.85 |
| 25 | S25 | 24.8 | 1056.39 | 3.19 | 27.88 | 60.48 | 10.07 |
| 26 | S26 | 31.4 | 1529.91 | 3.19 | 29.94 | 63.69 | 10.08 |
| 27 | S27 | 30.8 | 755.74 | 3.19 | 29.77 | 57.57 | 10.08 |
| Source | DF | Seq. SS | Adj. SS | Adj. MS | F-Value | p-Value | Contribution |
|---|---|---|---|---|---|---|---|
| Reinforcement wt.% | 2 | 27.31 | 27.31 | 13.656 | 1.54 | 0.320 | 1.55% |
| Nozzle Temperature | 2 | 498.48 | 498.48 | 249.242 | 28.06 | 0.004 | 28.29% |
| Printing Speed (mm/s) | 2 | 673.26 | 673.26 | 336.630 | 37.89 | 0.003 | 38.21% |
| Sample Orientation Angle | 2 | 21.38 | 21.38 | 10.692 | 1.20 | 0.390 | 1.21% |
| Print Layer Thickness (mm) | 2 | 19.49 | 19.49 | 9.743 | 1.10 | 0.417 | 1.11% |
| Nozzle Temperature (°C) * Print Layer Thickness (mm) | 4 | 88.54 | 88.54 | 22.136 | 2.49 | 0.199 | 5.03% |
| Printing Speed (mm/s) * Print Layer Thickness (mm) | 4 | 193.71 | 193.71 | 48.428 | 5.45 | 0.065 | 10.99% |
| Sample Orientation Print Layer Thickness (mm) | 4 | 204.29 | 204.29 | 51.073 | 5.75 | 0.059 | 11.59% |
| Error | 4 | 35.54 | 35.54 | 8.884 | 2.02% | ||
| Total | 26 | 1762 | 100% | ||||
| R-Sq: 97.98% R-Sq(adj): 86.89% | |||||||
| Source | DF | Seq. SS | Adj. SS | Adj. MS | F-Value | p-Value | Contribution |
|---|---|---|---|---|---|---|---|
| Reinforcement wt.% | 2 | 177,079 | 177,079 | 88,540 | 4.98 | 0.082 | 5.81% |
| Nozzle Temperature | 2 | 360,388 | 360,388 | 180,194 | 10.13 | 0.027 | 11.82% |
| Printing Speed (mm/s) | 2 | 766,204 | 766,204 | 383,102 | 21.54 | 0.007 | 25.12% |
| Sample Orientation Angle | 2 | 188,951 | 188,951 | 94,476 | 5.31 | 0.075 | 6.19% |
| Print Layer Thickness (mm) | 2 | 205,214 | 205,214 | 102,607 | 5.77 | 0.066 | 6.73% |
| Reinforcement wt.% * Print Layer Thickness (mm) | 4 | 310,335 | 310,335 | 77,584 | 4.36 | 0.091 | 10.17% |
| Printing Speed (mm/s) * Print Layer Thickness (mm) | 4 | 521,768 | 521,768 | 130,442 | 7.33 | 0.040 | 17.11% |
| Sample Orientation Print Layer Thickness (mm) | 4 | 449,124 | 449,124 | 112,281 | 6.31 | 0.051 | 14.72% |
| Error | 4 | 71,138 | 71,138 | 17,784 | 2.33% | ||
| Total | 26 | 3,050,201 | 100% | ||||
| R-Sq: 97.67% R-Sq(adj): 84.84% | |||||||
| Source | DF | Seq. SS | Adj. SS | Adj. MS | F-Value | p-Value | Contribution |
|---|---|---|---|---|---|---|---|
| Reinforcement wt.% | 2 | 12.74 | 16.024 | 12.74 | 6.37 | 6.23 | 5.16% |
| Nozzle Temperature (°C) | 2 | 112.738 | 111.589 | 112.738 | 56.369 | 55.16 | 45.67% |
| Printing Speed (mm/s) | 2 | 35.509 | 45.860 | 35.509 | 17.755 | 17.37 | 14.38% |
| C4 | 2 | 6.764 | 5.948 | 6.764 | 3.382 | 3.31 | 2.74% |
| Print Layer Thickness (mm) | 2 | 2.343 | 4.864 | 2.343 | 1.172 | 1.15 | 0.95% |
| Reinforcement wt.% * Print Layer Thickness (mm) | 4 | 11.623 | 37.651 | 11.623 | 2.906 | 2.84 | 4.71% |
| Printing Speed (mm/s) * Print Layer Thickness (mm) | 4 | 33.262 | 39.894 | 33.262 | 8.315 | 8.14 | 13.47% |
| Sample Orientation Print Layer Thickness (mm) | 4 | 27.799 | 12.239 | 27.799 | 6.95 | 6.8 | 11.26% |
| Error | 4 | 4.087 | 5.196 | 4.087 | 1.66% | ||
| Total | 26 | 246.865 | 100.00% | ||||
| R-Sq: 98.34% R-Sq(adj): 89.24% | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harishbabu, S.; Alrasheedi, N.H.; Louhichi, B.; Sreekanth, P.S.R.; Sahu, S.K. Machine Learning-Assisted Synergistic Optimization of 3D Printing Parameters for Enhanced Mechanical Properties of PLA/Boron Nitride Nanocomposites. Machines 2025, 13, 949. https://doi.org/10.3390/machines13100949
Harishbabu S, Alrasheedi NH, Louhichi B, Sreekanth PSR, Sahu SK. Machine Learning-Assisted Synergistic Optimization of 3D Printing Parameters for Enhanced Mechanical Properties of PLA/Boron Nitride Nanocomposites. Machines. 2025; 13(10):949. https://doi.org/10.3390/machines13100949
Chicago/Turabian StyleHarishbabu, Sundarasetty, Nashmi H. Alrasheedi, Borhen Louhichi, P. S. Rama Sreekanth, and Santosh Kumar Sahu. 2025. "Machine Learning-Assisted Synergistic Optimization of 3D Printing Parameters for Enhanced Mechanical Properties of PLA/Boron Nitride Nanocomposites" Machines 13, no. 10: 949. https://doi.org/10.3390/machines13100949
APA StyleHarishbabu, S., Alrasheedi, N. H., Louhichi, B., Sreekanth, P. S. R., & Sahu, S. K. (2025). Machine Learning-Assisted Synergistic Optimization of 3D Printing Parameters for Enhanced Mechanical Properties of PLA/Boron Nitride Nanocomposites. Machines, 13(10), 949. https://doi.org/10.3390/machines13100949









