A Research Method to Investigate the Effect of Vibration Suppression on Thin-Walled Parts of Aluminum Alloy 6061 Based on Cutting Fluid Spraying (CFS)
Abstract
1. Introduction
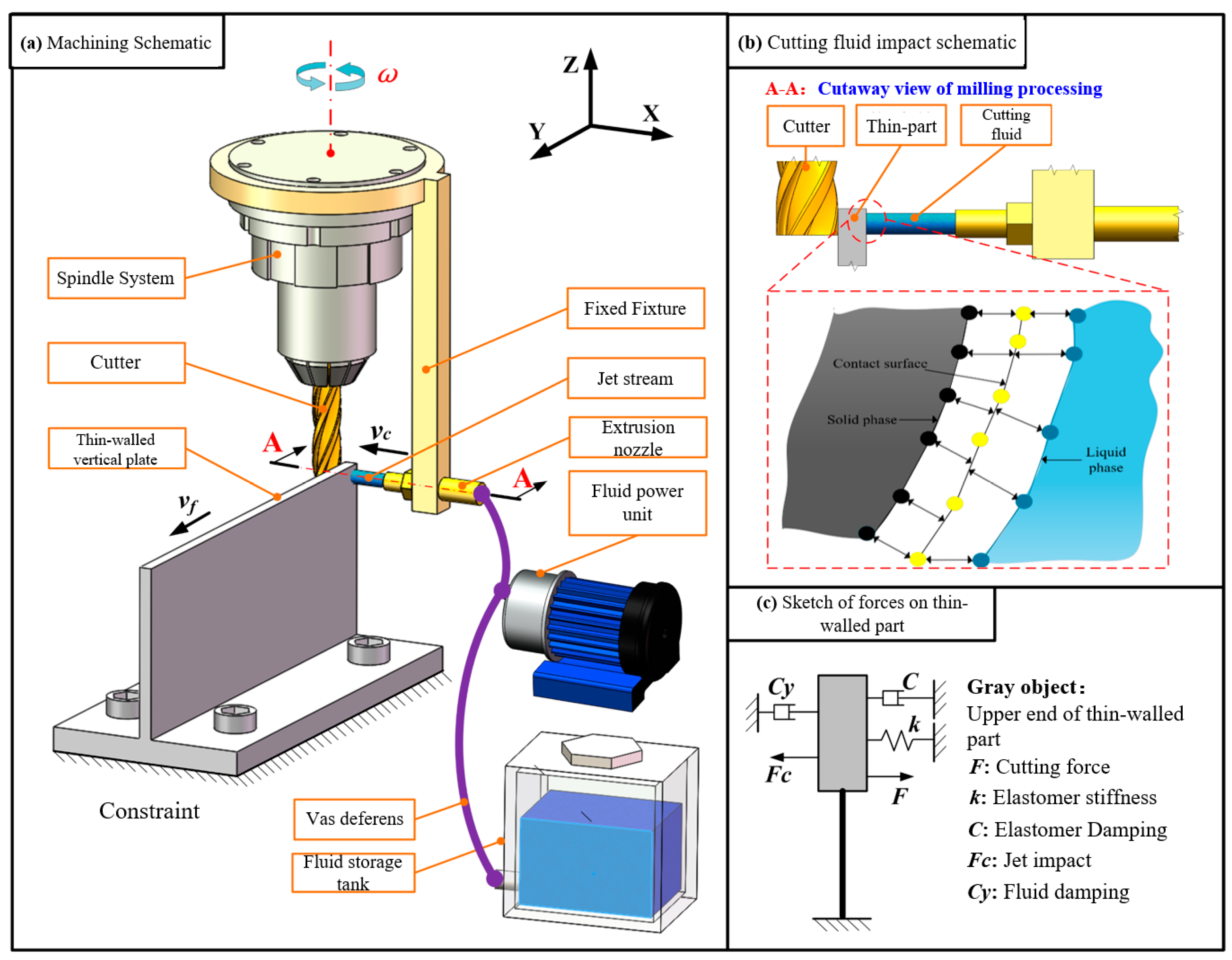
2. Cutting and Machining Methods for Thin-Walled Parts Under CFS
3. Platform Construction and Experimental Program
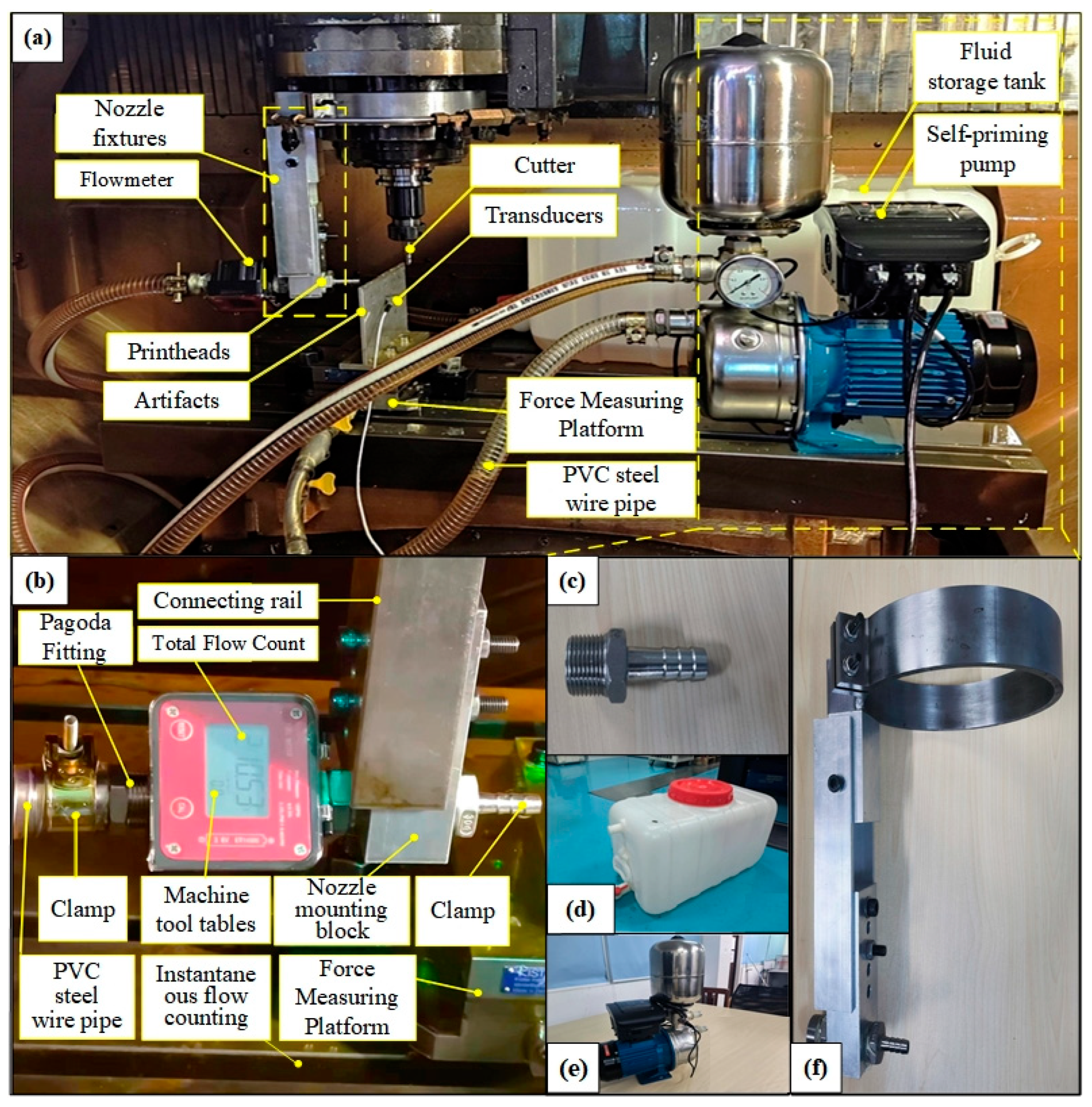
3.1. Experimental Platform Construction
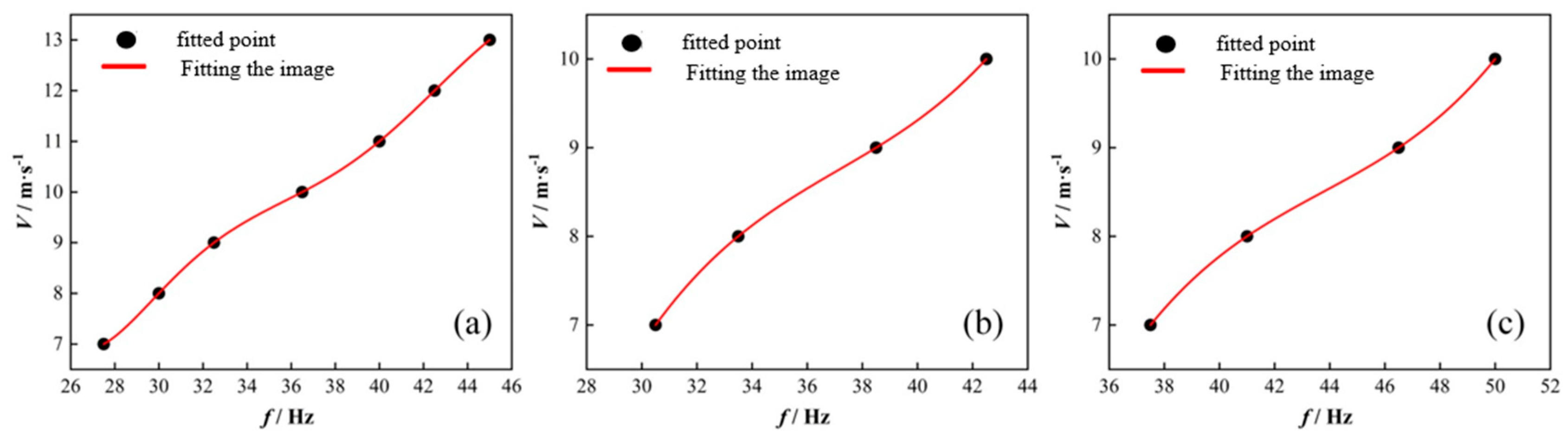
3.2. Debugging of the Experimental Platform
3.3. Experimental Materials
3.4. Experimental Program
3.4.1. Hammering Test
3.4.2. Milling Test
4. Experimental Results Analysis
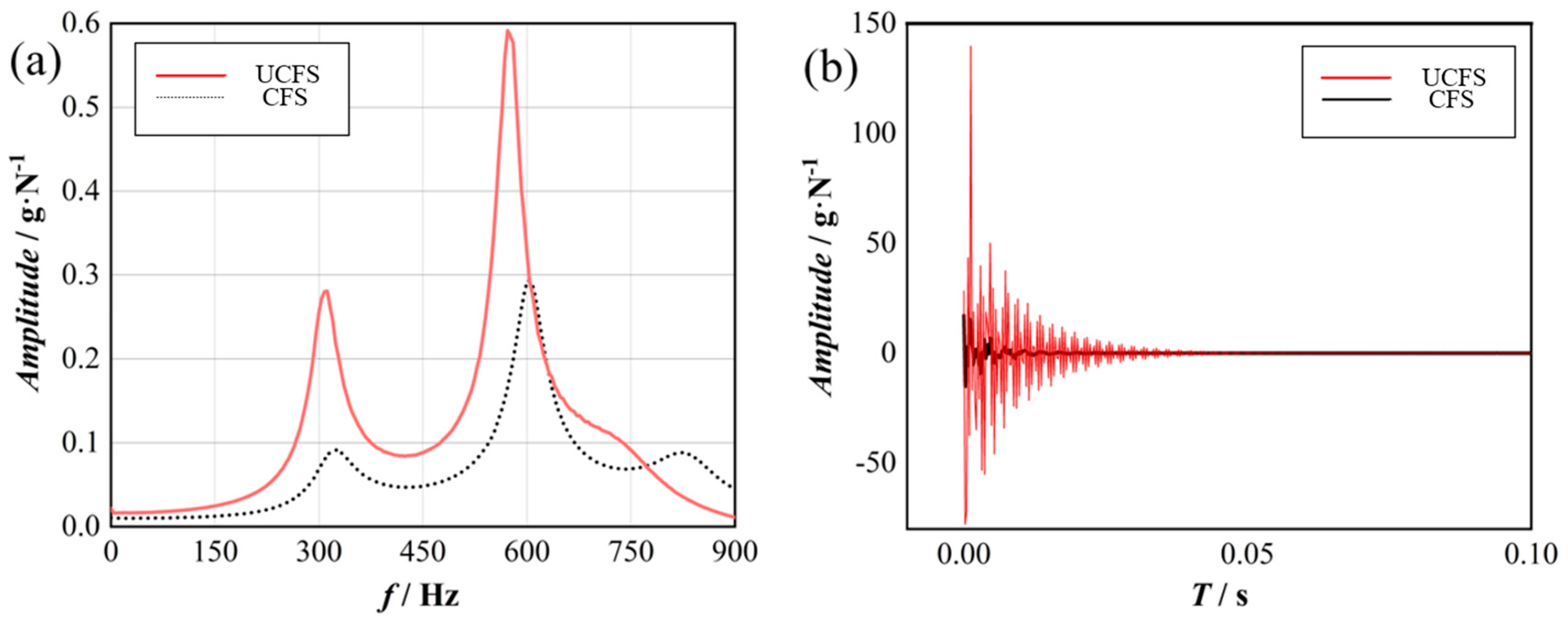
4.1. Analysis of Hammering Experiment Results
4.2. Cutting Experiment Results Analysis
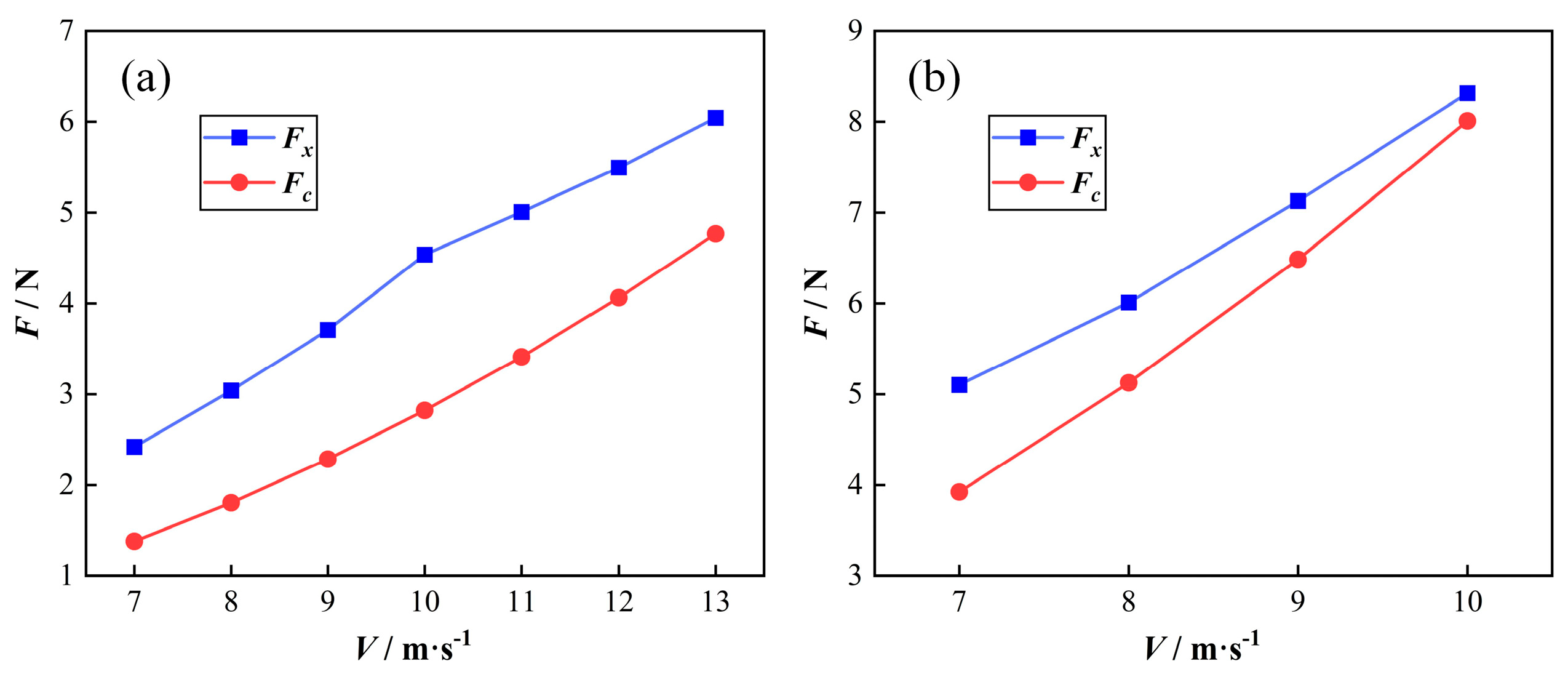
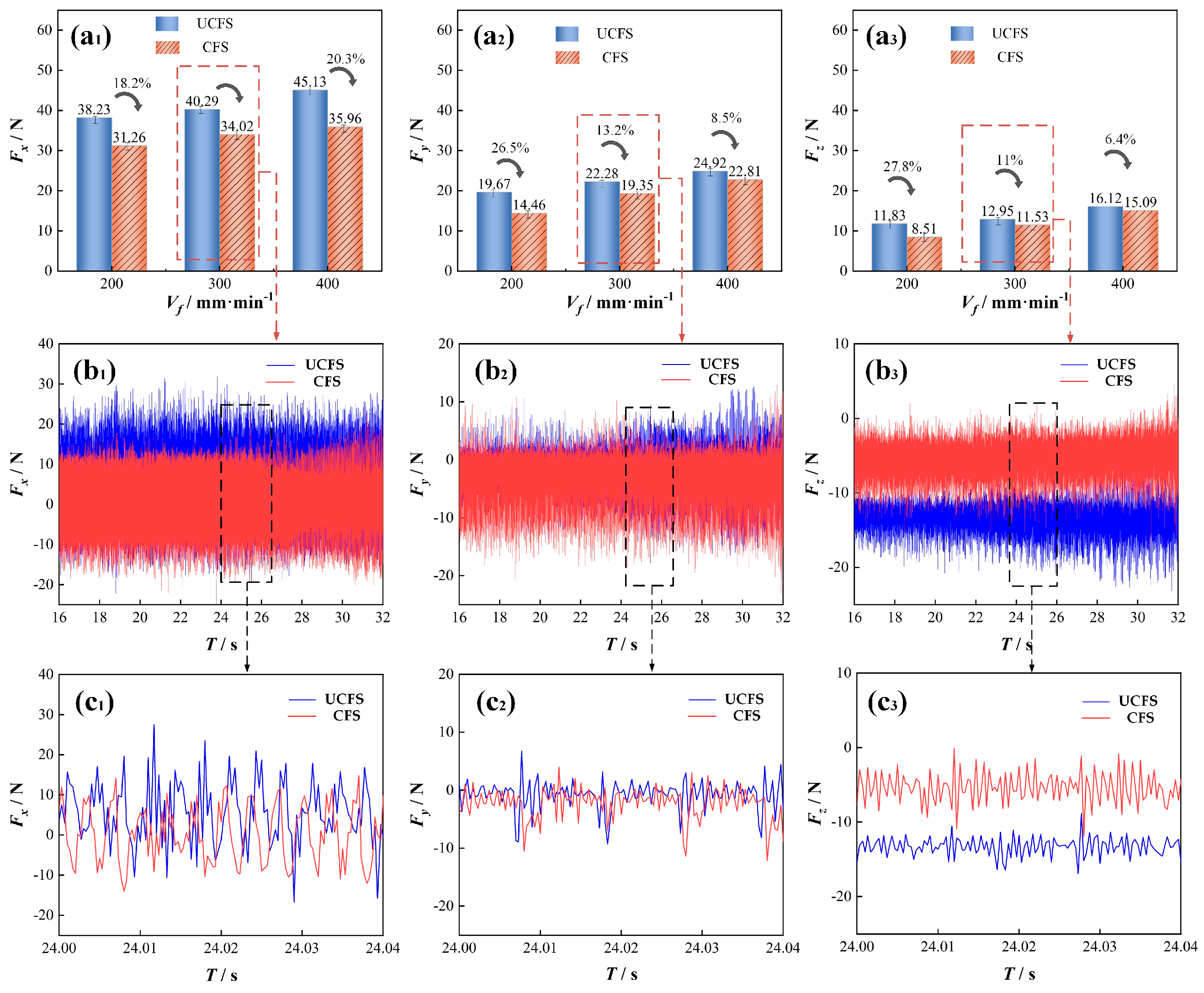
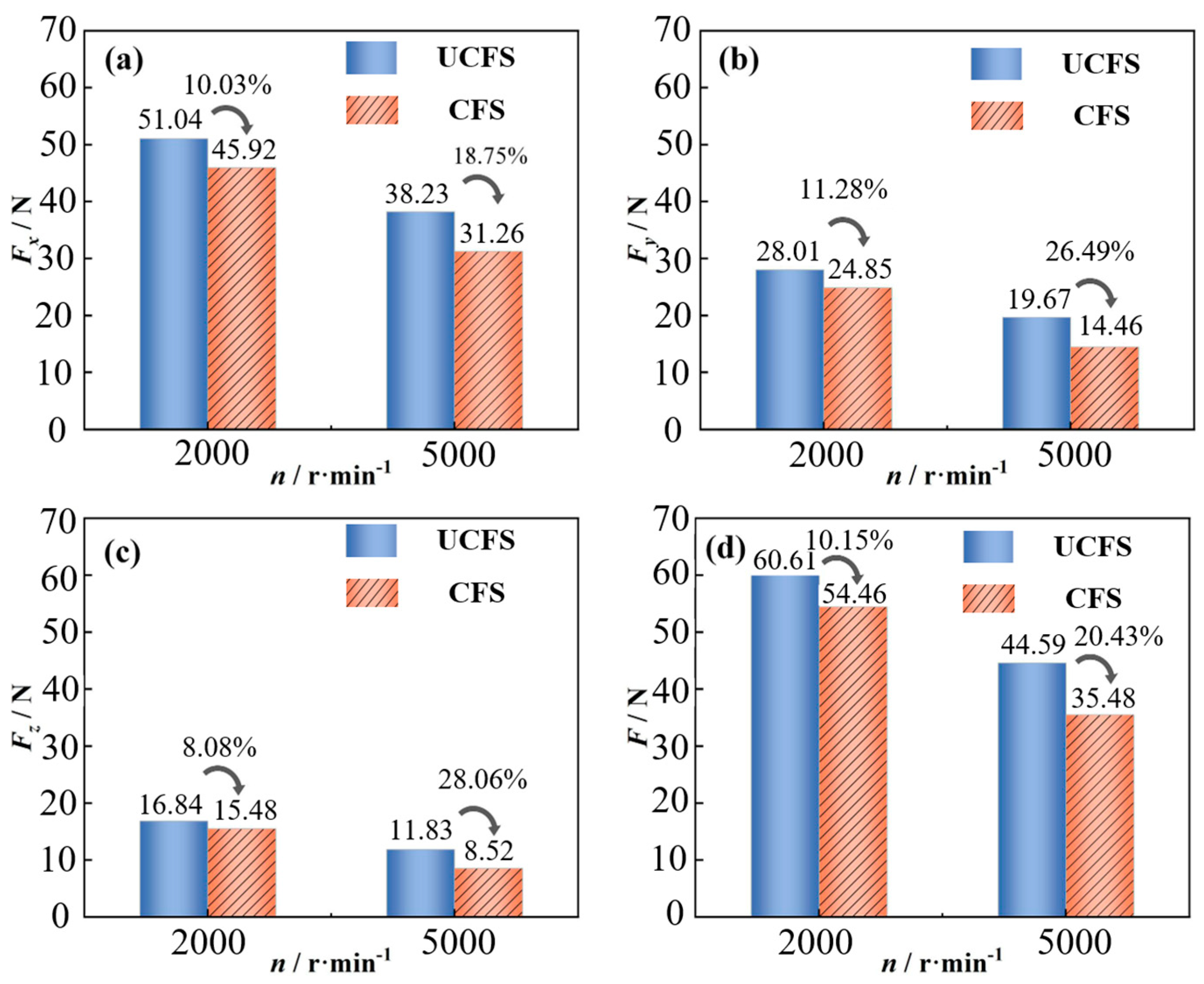
4.2.1. Cutting Forces Analysis
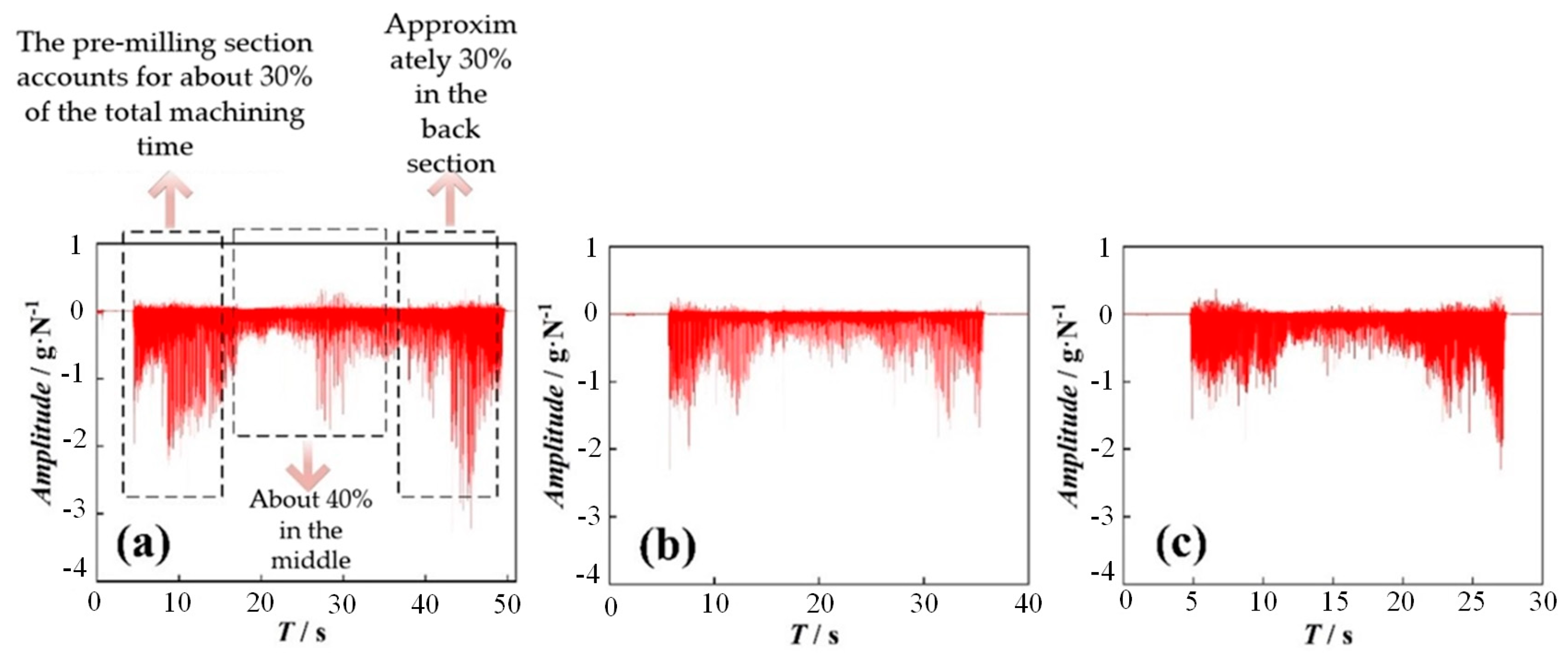
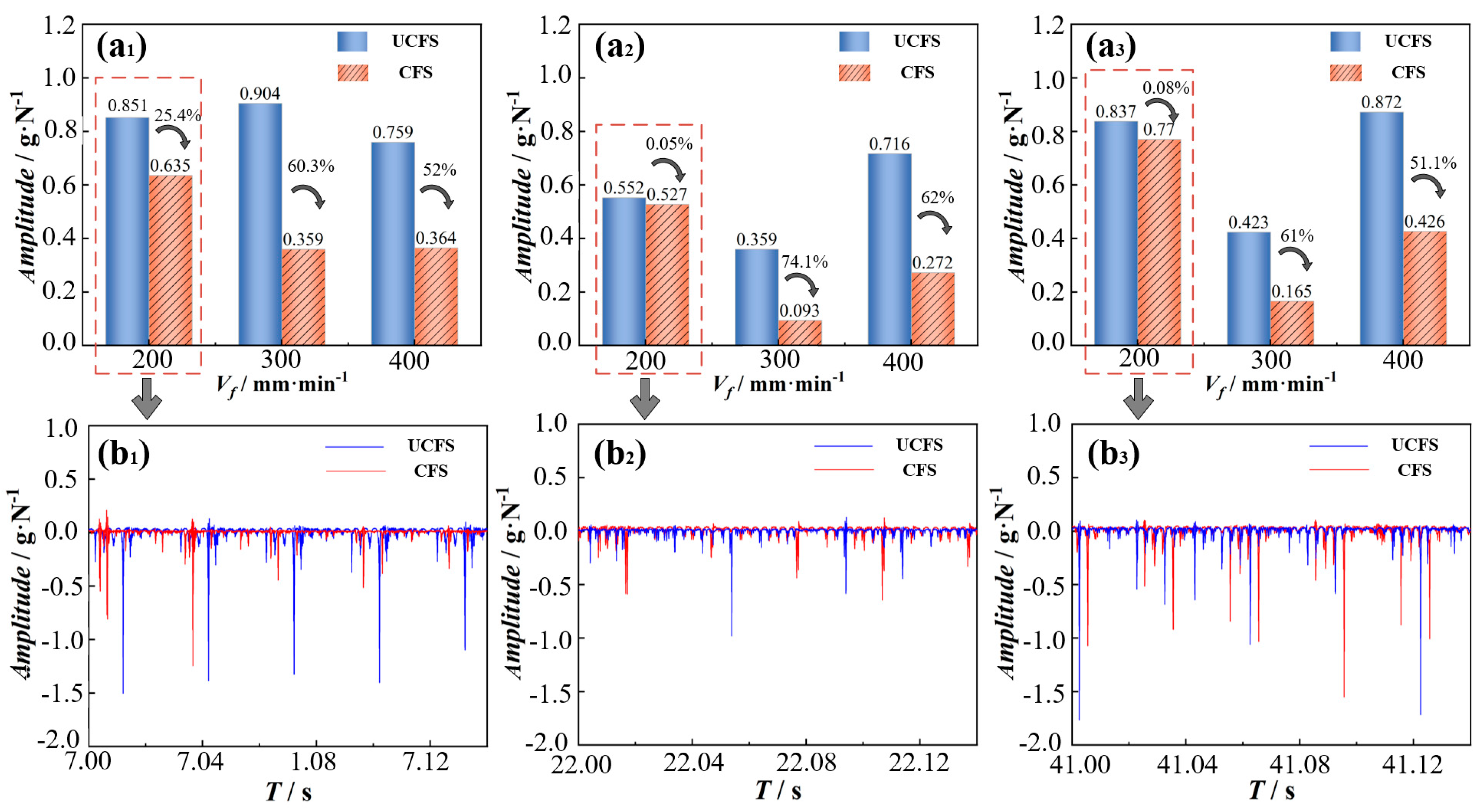
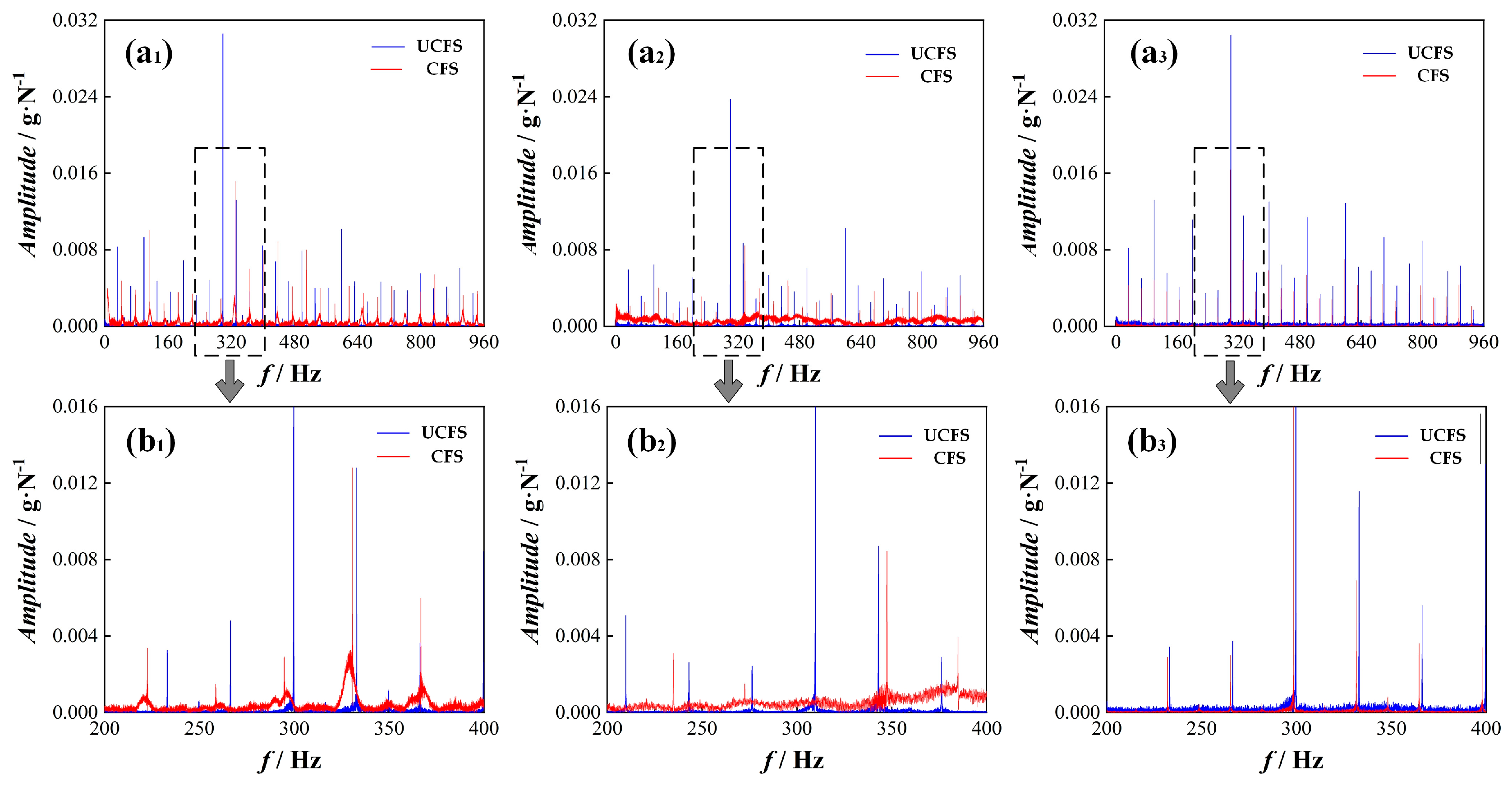
4.2.2. Vibration Analysis for Milling of Thin-Walled Parts
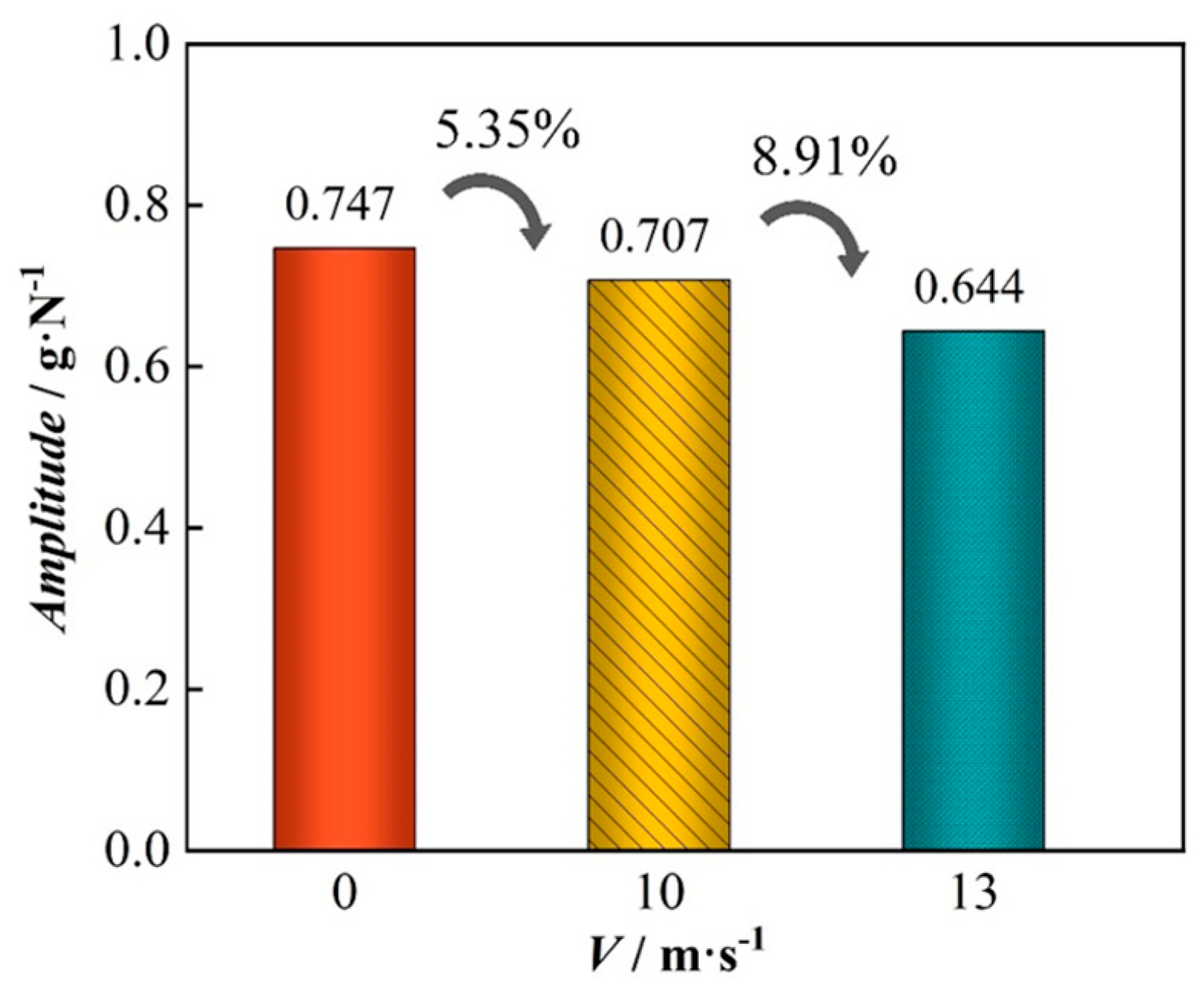
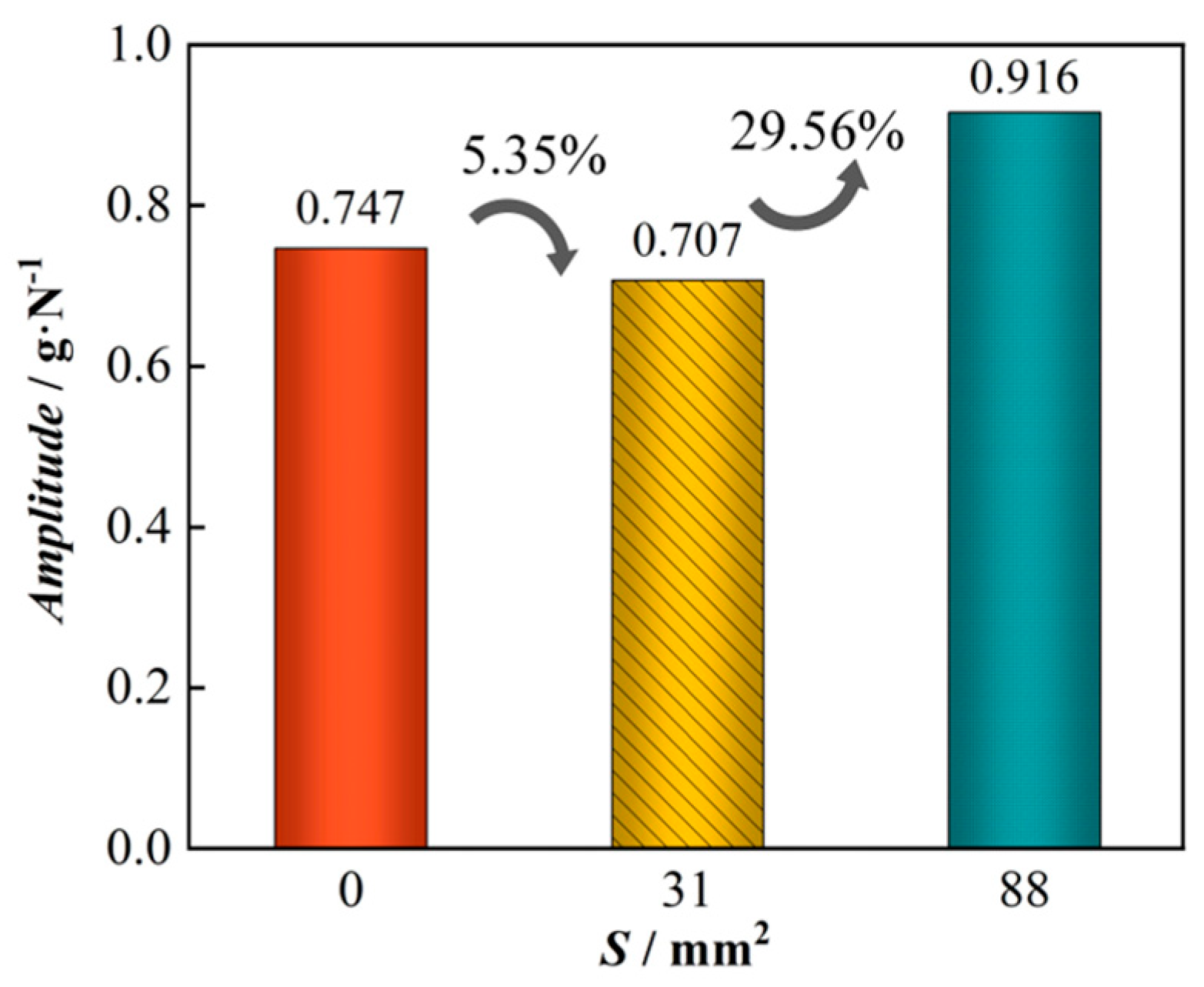
4.2.3. Analysis of Impact Factors and Comparative Discussion
5. Conclusions
- (1)
- Compared with the non-injected condition, the workpiece force and vibration amplitude of the cutting fluid injection condition are significantly reduced, and under the machining parameters, the size of the milling force on the workpiece is in the order of Fx > Fy > Fz, and the effect of the cutting fluid injection to reduce the milling force of Fx becomes greater with an increase in the feed rate, while the effect of the reduction in the milling force of Fy and Fz becomes less with an increase in the feed rate. Furthermore, the effect of the milling force of Fy and Fz becomes less with an increase in the feed rate when the feed rate is increased by Vf = 300 mm/min. When Vf = 300 mm/min and Vf = 400 mm/min, the vibration suppression effect caused by cutting fluid injection is more obvious.
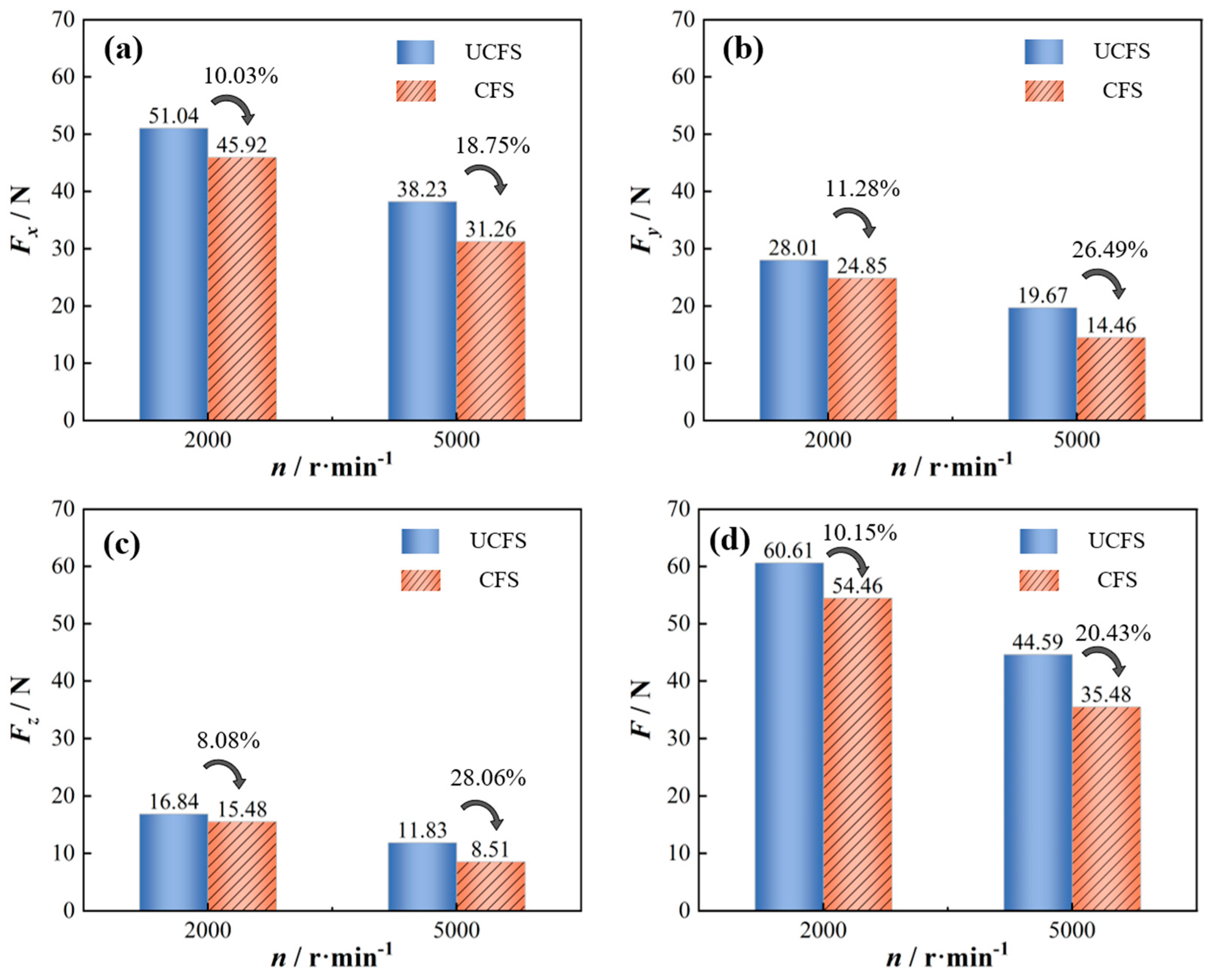
- (2)
- Compared with the non-injected condition, the force on the workpiece under the cutting fluid injection condition is reduced significantly. When n = 2000 r/min, the force and combined force on the workpiece in the X, Y, and Z directions is reduced by 10.03%, 11.28%, 8.08%, and 10.15%, respectively.
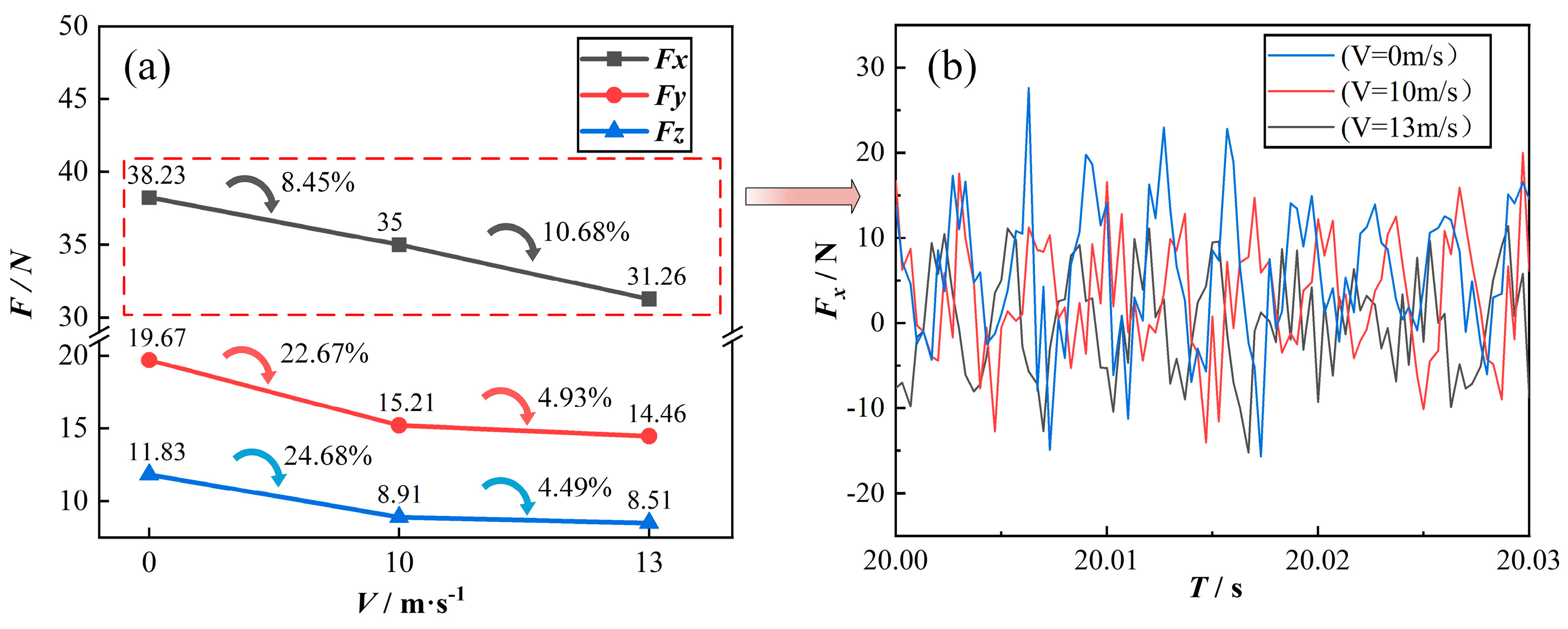
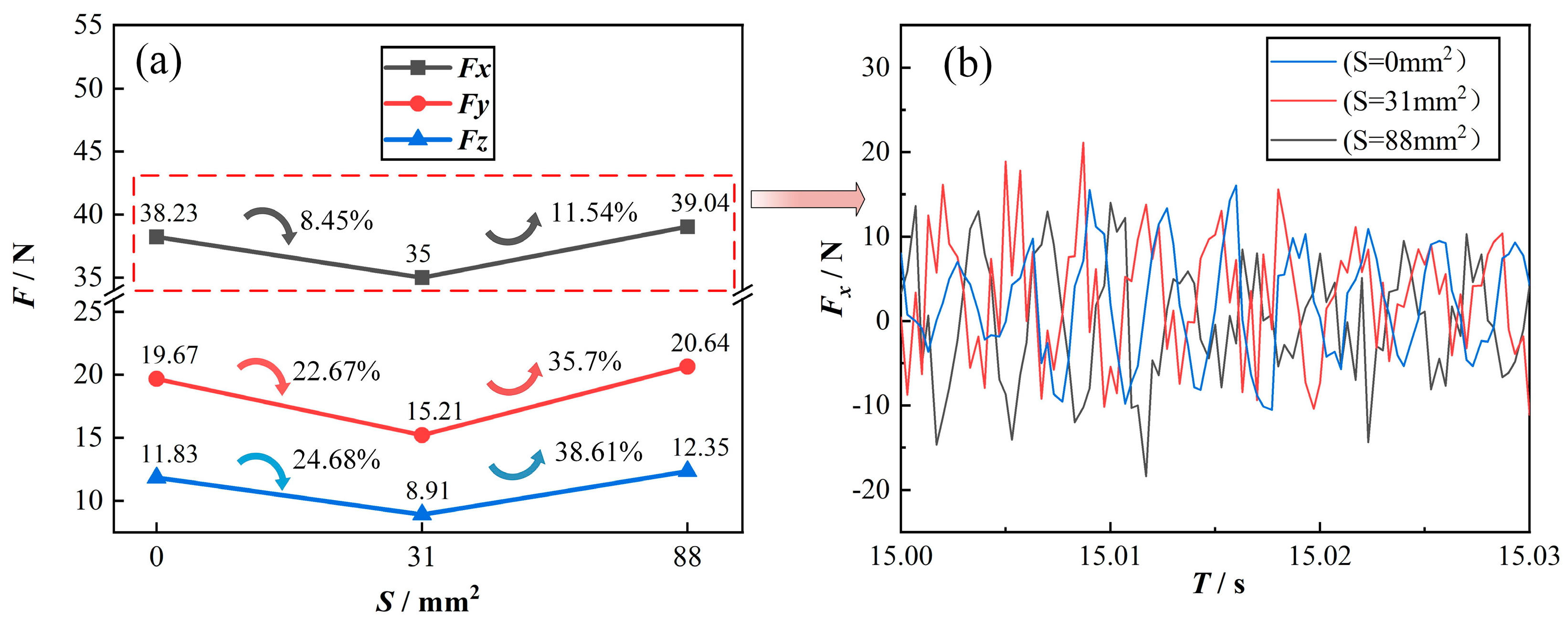
- (3)
- By comparing and analyzing the effects of the different injection flow rates of cutting fluid on the workpiece force and the amplitude of machining vibration, we can surmise that with an increase in injection speed, the workpiece force is gradually reduced, in which the reduction in Fx is the most obvious and almost linear, and the overall amplitude of vibration of the workpiece is gradually reduced.
- (4)
- The object of this paper was aluminum alloy 6061T-type planar thin-walled parts. Whether the methodology of this paper is applicable to complex thin-walled parts needs to be discussed in depth. At the same time, it is also necessary to carry out further research on titanium alloys and other material thin-walled parts.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Muxuan, G.; Lida, Z.; Boling, Y. Research on the Milling Stability of Thin-walled Parts Based on the Semi-discretizationMethod of Improved Runge-Kutta Method. Int. J. Adv. Manuf. Technol. 2021, 115, 2035. [Google Scholar] [CrossRef]
- Chigbogu, G.O. Polynomial Tensor-Based Stability Identification of Milling Process: Application to Reduced Thin-Walled Workpiece. In IUTAM Bookseries, Proceedings of the IUTAM Symposium on Model Order Reduction of Coupled Systems, Stuttgart, Germany, 22–25 May 2018; Springer: Berlin/Heidelberg, Germany, 2019; Volume 209, p. 220. [Google Scholar] [CrossRef]
- Mehran, M.; Mohammad, R.; Movahhedy Amir, J. Three dimensional prediction of stability lobes in end milling of thin-walled structures based on tool and workpiece dimensions. Sci. Iran. 2021, 29, 41–52. [Google Scholar] [CrossRef]
- Song, Q.H.; Liu, Z.Q.; Wan, Y. Application of Sherman–Morrison–Woodbury formulas in instantaneous dynamic of peripheral milling for thin-walled component. Int. J. Mech. Sci. 2015, 97, 79–90. [Google Scholar] [CrossRef]
- Wang, X.J.; Song, Q.H.; Wang, Q. Dynamic model and stability prediction of thin-walled component milling with multi-modes coupling effect. J. Mater. Process. Technol. 2021, 288, 116869. [Google Scholar] [CrossRef]
- Gao, H.N.; Liu, X.L. Stability Research Considering Non-Linear Change in the Machining of Titanium Thin-Walled Parts. Materials 2019, 12, 2083. [Google Scholar] [CrossRef]
- Wang, B.S.; Li, J.B.; Gao, H.B. Vibration Modal Analysis of Thin-walled Component with Variable Curvature Based on Finite Element. DEStech Trans. Eng. Technol. Res. 2017, 23, 1005–1008. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, Y.Q.; Han, C.J. Microstructure and mechanical properties of GH4169 thin-walled parts fabricated by ultrasonic vibration assisted laser directed energy deposition/milling hybrid process. Thin-Walled Struct. 2024, 205, 112349. [Google Scholar] [CrossRef]
- Jia, F.; Wan, M.; Gao, T.Q. Mechanism of process damping in milling of thin-walled workpiece. Int. J. Mach. Tools Manuf. 2018, 134, 1–19. [Google Scholar] [CrossRef]
- Zhuo, Y.; Han, Z.Y.; Dong, H.Y. Surface topography prediction in peripheral milling of thin-walled parts considering cutting vibration and material removal effect. Int. J. Mech. Sci. 2021, 211, 106797. [Google Scholar] [CrossRef]
- Li, W.S.; Jin, G.; Tian, Y.J. Analysis of cutting vibration of aluminum alloy 6061 thin-walled parts. In Proceedings of the 2022 International Symposium on Control Engineering and Robotics, Changsha, China, 18–20 February 2022; Volume 1, pp. 83–86. [Google Scholar] [CrossRef]
- Wu, Q.; Li, L.; Zhang, Y.D. Simulations and Experiments on Vibration Control of Aerospace Thin-Walled Parts via Preload. Shock. Vib. 2017, 1, 1–7. [Google Scholar] [CrossRef]
- Kasper, R.; Yaser, M.; Christian, H. Optimization of Material Removal Rate in Milling of Thin-walled Structures Using Penalty Cost Function. Int. J. Mach. Tools Manuf. 2019, 145, 103430. [Google Scholar] [CrossRef]
- Serhii, K.; Sergey, D.; Yevheniia, B. Adaptive Fluid Jet Support Technique for Variable Stiffness Thin-Walled Parts End Milling. Lect. Notes Mech. Eng. 2024, 1, 223–239. [Google Scholar] [CrossRef]
- Wang, S.; Chong, H.; Li, J.G. Vibration-free surface finish in the milling of a thin-walled cavity part using a corn starch suspension. J. Mater. Process. Technol. 2021, 290, 116980. [Google Scholar] [CrossRef]
- Wang, Q.L.; Wang, W.; Zheng, L.Y. Force control-based vibration suppression in robotic grinding of large thin-wall shells. Robot. Comput.-Integr. Manuf. 2021, 67, 102031. [Google Scholar] [CrossRef]
- Butt, M.A.; Yang, Y.Q.; Pei, X.T. Five-axis milling vibration attenuation of freeform thin-walled part by eddy current damping. Precis. Eng. 2018, 51, 682–690. [Google Scholar] [CrossRef]
- Li, C.; Li, X.; Huang, S. Ultra-precision grinding of Gd3Ga5O12 crystals with graphene oxide coolant: Material deformation mechanism and performance evaluation. J. Manuf. Process. 2021, 61, 417–442. [Google Scholar] [CrossRef]
- Hu, S.R.; Zhang, P.R.; Du, J.H. Suppression of cutting vibration in side milling of laser cladded layer on thin-walled parts with interfacial structures. J. Manuf. Process. 2024, 111, 32–44. [Google Scholar] [CrossRef]
- Zhao, X.; Lianyu, Z.; Fan, W.; Lu, Y. Real-time vibration data-driven adaptive optimization of flat milling process parameters for thin-walled parts. J. Mech. Eng 2020, 56, 172–184. [Google Scholar]
- Paweł, D.; Stefan, B.; Karol, M. Increasing Damping of Thin-Walled Structures Using Additively Manufactured Vibration Eliminators. Materials 2020, 13, 2125. [Google Scholar] [CrossRef]
- Li, Z.H.; Xu, W.; Wang, C. Investigation on Vibration Characteristics of Thin-Walled Steel Structures under Shock Waves. Materials 2023, 16, 4748. [Google Scholar] [CrossRef]
- Shi, Z.M.; Li, B.Z.; Sun, Z.H. Residual stress superposition in milling process of thin-walled parts and comprehensive deformation control method. Res. Sq. 2023, 1, 10–13. [Google Scholar] [CrossRef]
- Ding, H.J.; Zhou, B.; Xue, K. Research on Variable Milling Process Parameters of Thin-walled Parts Based on Cutting Force Control. Modul. Mach. Tool Autom. Manuf. Tech. 2020, 9, 117–122. [Google Scholar]
- Zhang, S.F.; Ma, J.H.; Wang, S. Milling force prediction of inclined rib with low rigidity in milling process of hollow thin-walled structural parts. Int. J. Adv. Manuf. Technol. 2023, 127, 815–830. [Google Scholar] [CrossRef]
- Chen, Z.T.; Yue, C.X.; Liu, X.L. Surface Topography Prediction Model in Milling of Thin-Walled Parts Considering Machining Deformation. Materials 2021, 14, 7679. [Google Scholar] [CrossRef] [PubMed]
- Mohammad, R.S.; Selim, G.; Jian, L. Vibration suppression and surface quality enhancement in milling thin-walled structures using shear thickening fluids. J. Manuf. Process. 2024, 131, 2219–2229. [Google Scholar] [CrossRef]
- Tong, J.L.; Zhang, Z.P.; Chen, P. Study on surface morphology of titanium alloy curved thin-walled parts by longitudinal-torsional composite ultrasonic assisted milling. J. Manuf. Process. 2022, 84, 316–326. [Google Scholar] [CrossRef]
- Fei, J.X.; Lin, B.; Xiao, J.L. Investigation of moving fixture on deformation suppression during milling process of thin-walled structures. J. Manuf. Process. 2018, 32, 403–411. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Li, H.N.; Rüdiger, S. Disturbance rejection control for vibration suppression of piezoelectric laminated thin-walled structures. J. Sound Vib. 2014, 333, 1209–1223. [Google Scholar] [CrossRef]
- Liu, D.S.; Luo, M.; Urbikain, P.G. Position-oriented process monitoring in milling of thin-walled parts. J. Manuf. Syst. 2021, 60, 360–372. [Google Scholar] [CrossRef]
- Sun, Y.X.; Xiang, Z.H. A natural perturbation method with symmetric secant stiffness for stability analyses of quasi-perfect thin-walled structures. Thin-Walled Struct. 2021, 164, 107870. [Google Scholar] [CrossRef]
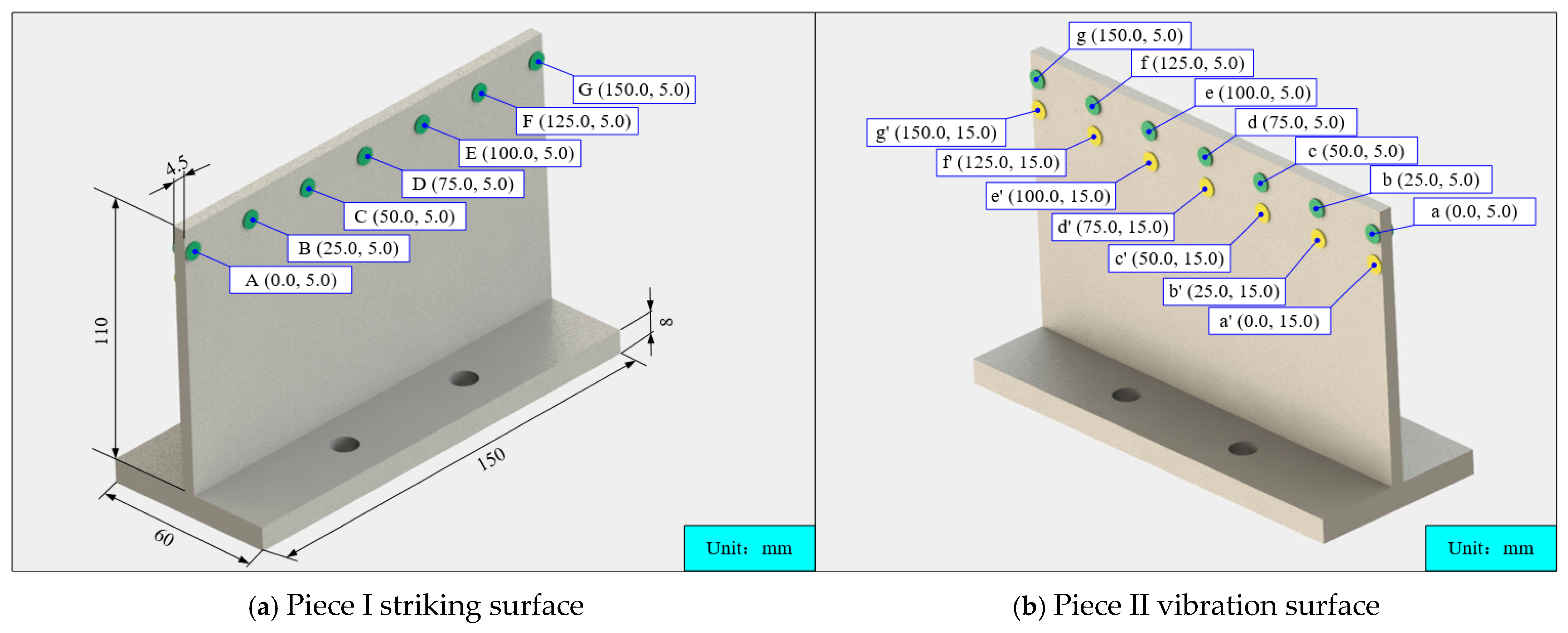
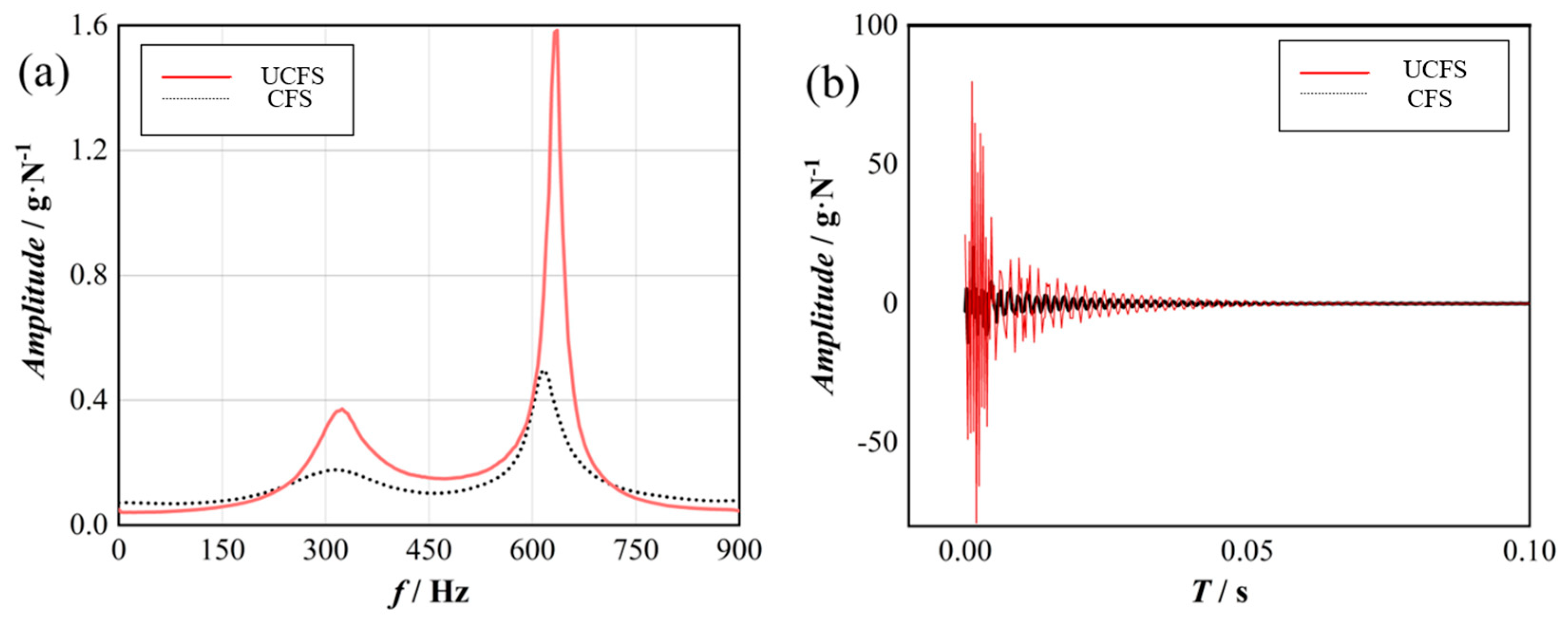
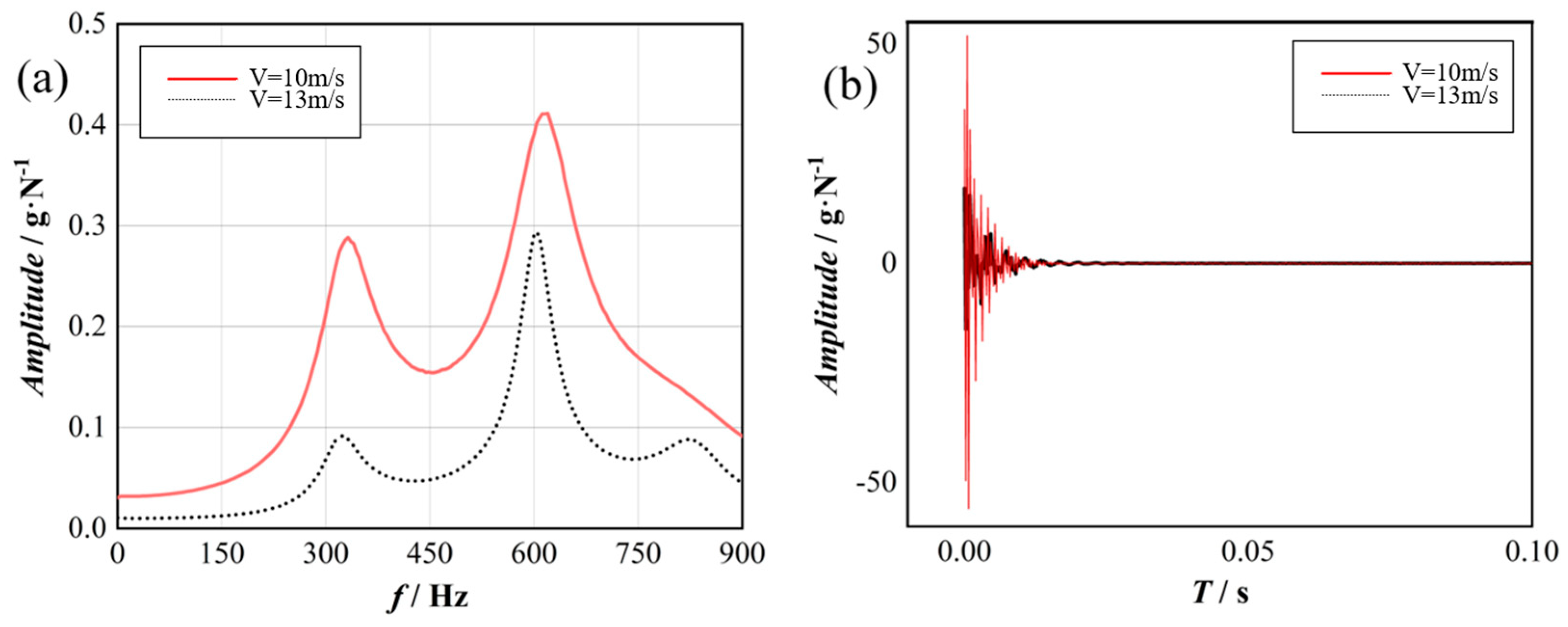
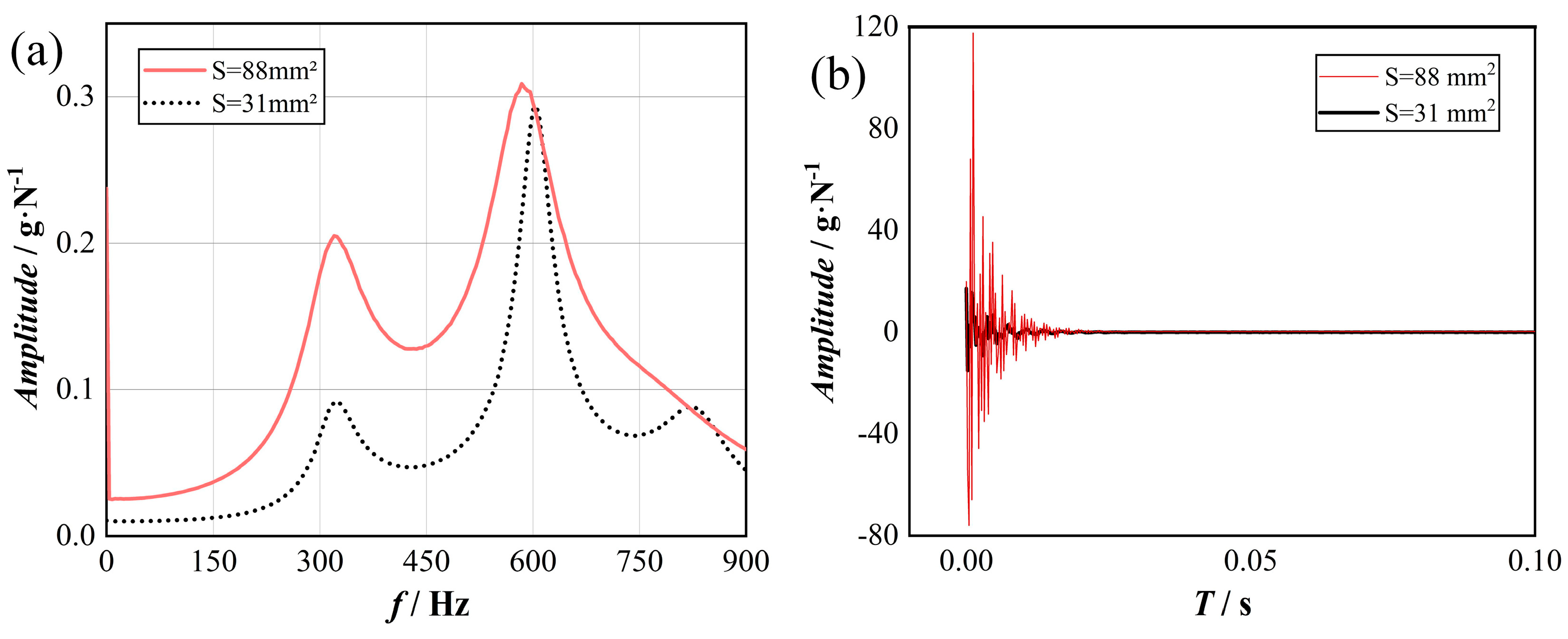
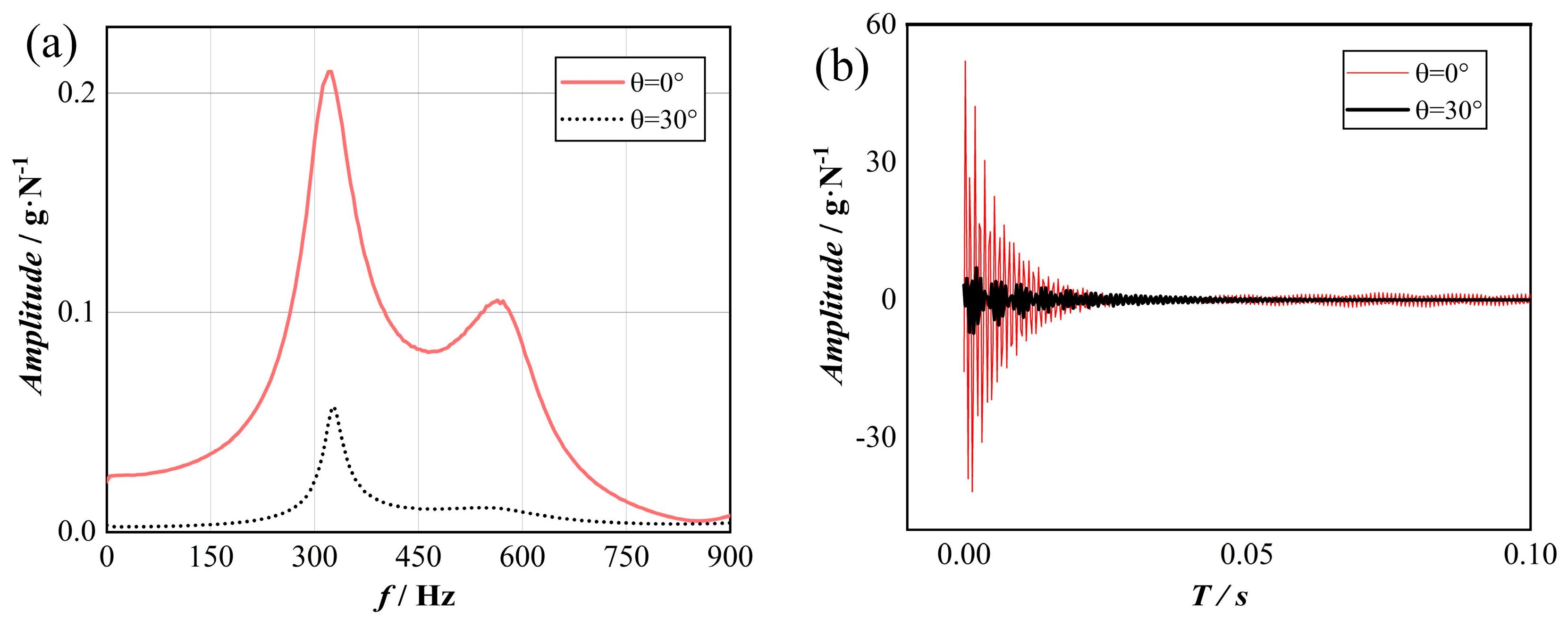
| Artifacts | Experiment Number | Hammer Point | Point of Measurement |
|---|---|---|---|
| Pieces I | 1,2,3,4,5,6,7 | A,B,C,D,E,F,G | a,b,c,d,e,f,g |
| Part II | 8,9,10,11,12,13,14 | A,B,C,D,E,F,G | a,b,c,d,e,f,g |
| Experiment Number | Hammer Point | Point of Measurement | Injection Point | Spraying Speed (m/s) | Nozzle Radius/Area (mm/mm2) | Spray Angle |
|---|---|---|---|---|---|---|
| 15 | A | a | g′ | 10 | 3.1/31 | 0° |
| 16 | B | b | g′ | 10 | 3.1/31 | 0° |
| 17 | C | c | g′ | 10 | 3.1/31 | 0° |
| 18 | D | d | g′ | 10 | 3.1/31 | 0° |
| 19 | A | a | a′ | 10 | 3.1/31 | 0° |
| 20 | B | b | b′ | 10 | 3.1/31 | 0° |
| 21 | C | c | c′ | 10 | 3.1/31 | 0° |
| 22 | D | d | d′ | 10 | 3.1/31 | 0° |
| 23 | E | e | e′ | 10 | 3.1/31 | 0° |
| 24 | F | f | f′ | 10 | 3.1/31 | 0° |
| 25 | G | g | g′ | 10 | 3.1/31 | 0° |
| 26 | A | a | a′ | 13 | 3.1/31 | 0° |
| 27 | D | d | d′ | 13 | 3.1/31 | 0° |
| 28 | A | a | a′ | 10 | 5.3/88 | 0° |
| 29 | D | d | d′ | 10 | 5.3/88 | 0° |
| 30 | D | d | d′ | 10 | 3.1/31 | 30° |
| Experiment Serial Number | Spindle Speed n (r/min) | Feed Rate Vf (mm/min) | CFS Speed V (m/s) | CFS Area S (mm2) |
|---|---|---|---|---|
| A1 | 5000 | 200 | 0 | 0 |
| A2 | 5000 | 200 | 10 | 31 |
| A3 | 5000 | 200 | 13 | 31 |
| A4 | 5000 | 200 | 10 | 88 |
| A5 | 5000 | 300 | 0 | 0 |
| A6 | 5000 | 300 | 13 | 31 |
| A7 | 5000 | 400 | 0 | 0 |
| A8 | 5000 | 400 | 13 | 31 |
| A9 | 2000 | 200 | 0 | 0 |
| A10 | 2000 | 200 | 13 | 31 |
| Experiment Number | Fx (N) | Fy (N) | Fz (N) | (N) |
|---|---|---|---|---|
| A1 | 38.23 | 19.67 | 11.83 | 44.59 |
| A2 | 35.00 | 15.21 | 8.91 | 39.19 |
| A3 | 31.26 | 14.46 | 8.51 | 35.48 |
| A4 | 39.04 | 20.64 | 12.35 | 45.85 |
| A5 | 40.29 | 22.28 | 12.95 | 47.83 |
| A6 | 34.02 | 19.35 | 11.53 | 40.80 |
| A7 | 45.13 | 24.92 | 16.12 | 54.01 |
| A8 | 35.96 | 22.81 | 15.09 | 43.60 |
| A9 | 51.04 | 28.01 | 16.84 | 60.61 |
| A10 | 45.92 | 24.85 | 15.48 | 54.46 |
| Experiment Number | Mean Value of Acceleration Amplitude at Different Stages (g-N−1) | |||
|---|---|---|---|---|
| A1 | 0.851 | 0.552 | 0.916 | 0.747 |
| A2 | 0.784 | 0.536 | 0.801 | 0.707 |
| A3 | 0.635 | 0.527 | 0.77 | 0.644 |
| A4 | 0.835 | 0.658 | 1.255 | 0.916 |
| A5 | 0.904 | 0.359 | 0.423 | 0.562 |
| A6 | 0.359 | 0.093 | 0.165 | 0.206 |
| A7 | 0.759 | 0.716 | 0.872 | 0.782 |
| A8 | 0.364 | 0.272 | 0.426 | 0.354 |
| A9 | 0.893 | 0.794 | 0.822 | 0.836 |
| A10 | 0.759 | 0.716 | 0.714 | 0.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Min, Y.; Liu, X.; Hu, G.; Jin, G.; Ma, Y.; Bian, Y.; Xie, Y.; Hu, M.; Li, D. A Research Method to Investigate the Effect of Vibration Suppression on Thin-Walled Parts of Aluminum Alloy 6061 Based on Cutting Fluid Spraying (CFS). Machines 2025, 13, 594. https://doi.org/10.3390/machines13070594
Min Y, Liu X, Hu G, Jin G, Ma Y, Bian Y, Xie Y, Hu M, Li D. A Research Method to Investigate the Effect of Vibration Suppression on Thin-Walled Parts of Aluminum Alloy 6061 Based on Cutting Fluid Spraying (CFS). Machines. 2025; 13(7):594. https://doi.org/10.3390/machines13070594
Chicago/Turabian StyleMin, Yonglin, Xiao Liu, Gaofeng Hu, Gang Jin, Yuanhao Ma, Yipu Bian, Yihan Xie, Mengpan Hu, and Desheng Li. 2025. "A Research Method to Investigate the Effect of Vibration Suppression on Thin-Walled Parts of Aluminum Alloy 6061 Based on Cutting Fluid Spraying (CFS)" Machines 13, no. 7: 594. https://doi.org/10.3390/machines13070594
APA StyleMin, Y., Liu, X., Hu, G., Jin, G., Ma, Y., Bian, Y., Xie, Y., Hu, M., & Li, D. (2025). A Research Method to Investigate the Effect of Vibration Suppression on Thin-Walled Parts of Aluminum Alloy 6061 Based on Cutting Fluid Spraying (CFS). Machines, 13(7), 594. https://doi.org/10.3390/machines13070594







