Self-Regulating Fuzzy-LQR Control of an Inverted Pendulum System via Adaptive Hyperbolic Error Modulation
Abstract
1. Introduction
1.1. Literature Review
1.2. Proposed Methodology
- Formulation of the proposed CS-FLQR scheme for the SLRIP. The baseline LQR law is decomposed into CSE and CSED variables, which are processed through an FIS to enhance the control system’s resilience against exogenous perturbations.
- Integration of pre-calibrated CHTFs for adaptive preprocessing of CSE and CSED variables to normalize them within ±1 and to create selective attenuation and amplification regions for improved control efficiency.
- Augmentation of the CHTFs with model-free adaptive tuning principles to dynamically adjust the said function’s variation rate and hence the magnitudes of compounded error variables to further enhance the controller’s adaptability.
- Performance validation of the proposed self-regulating CS-FLQR against baseline CS-FLQR and classical LQR via customized experimental trials conducted on the Quanser rotary pendulum platform [39].
2. System Description
2.1. System’s Mathematical Model
2.2. Baseline LQR Strategy
3. Proposed Control Methodology
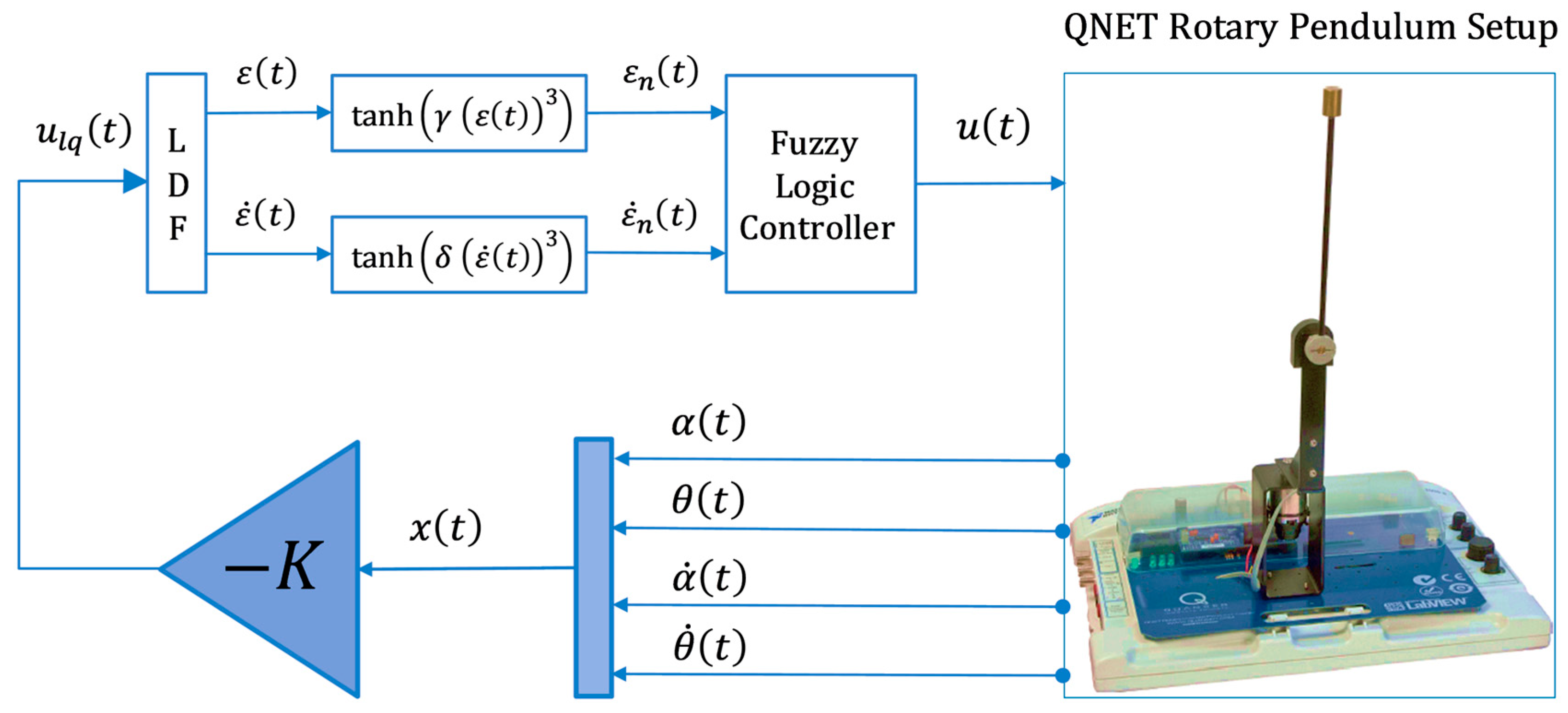
3.1. Fuzzy-Based Linear Quadratic Regulator (FLQR)
- Amplify the control effort when the system deviates from the desired state.
- Reduce the control effort as the system approaches the stable equilibrium.
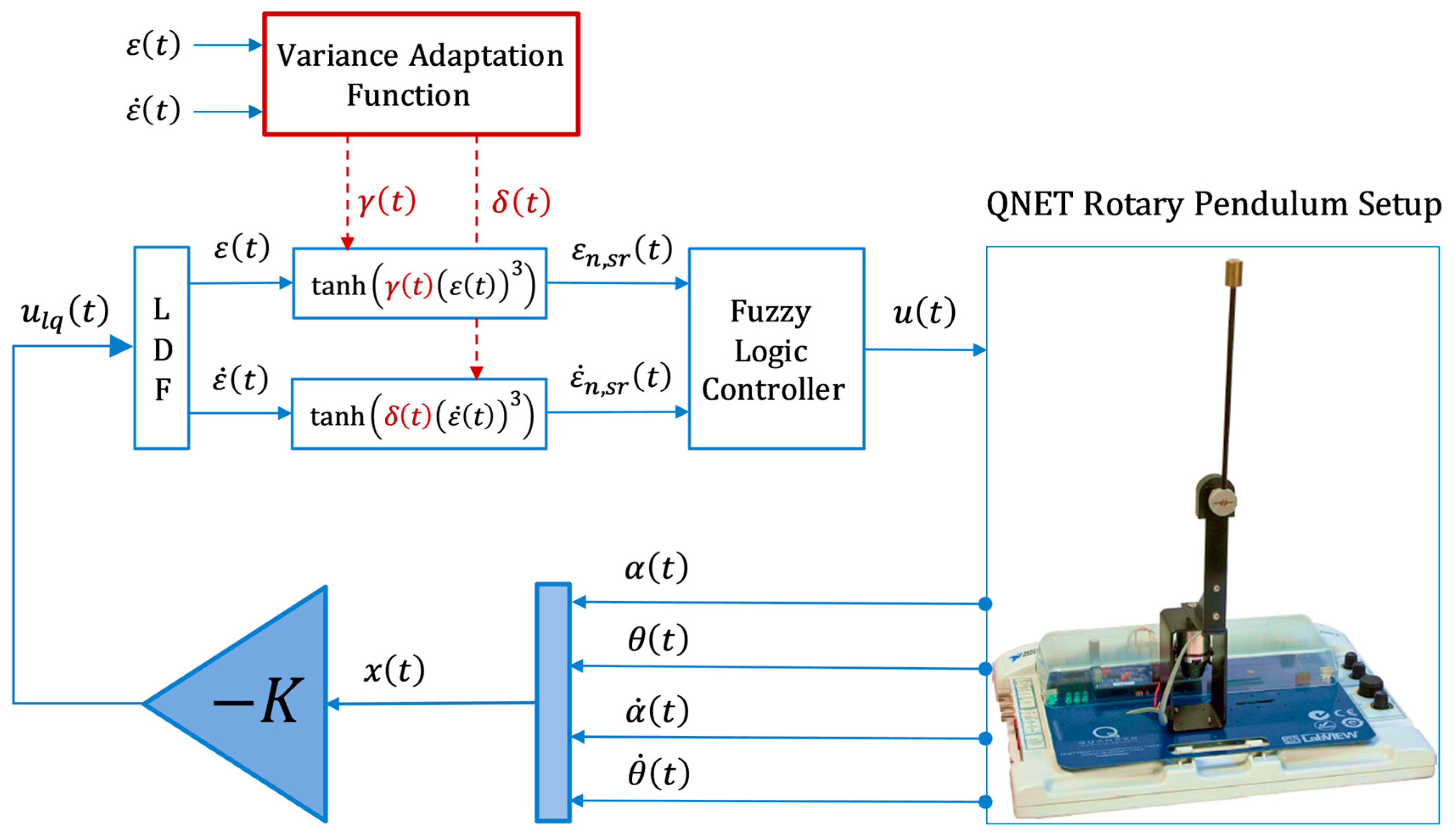
3.2. Self-Regulating FLQR Law
| Dissipative term: | Anti-dissipative term: |
- Dissipative term: Reduces the variation rate under small error conditions, ensuring gentle settlement of the response as it approaches reference, reducing steady-state fluctuations, and preventing wind-up.
- Anti-dissipative term: Amplifies the variation rate when the state error increases, promoting an aggressive control action to suppress overshoots, while speeding up the transient recovery response.
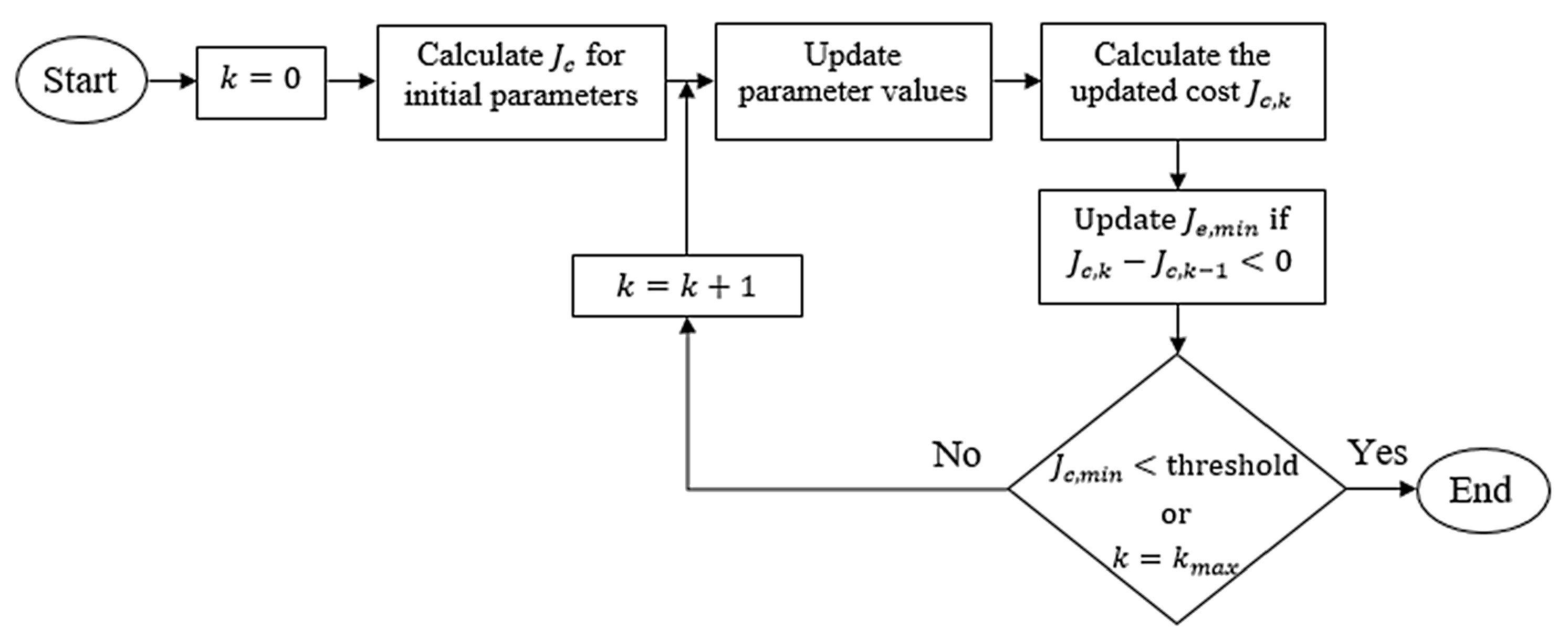
4. Parameter Optimization Method
4.1. Tuning Algorithm
4.2. Controller Parameterization
5. Experimental Results and Discussions
5.1. HIL Implementation
5.2. Experimental Validation
- A.
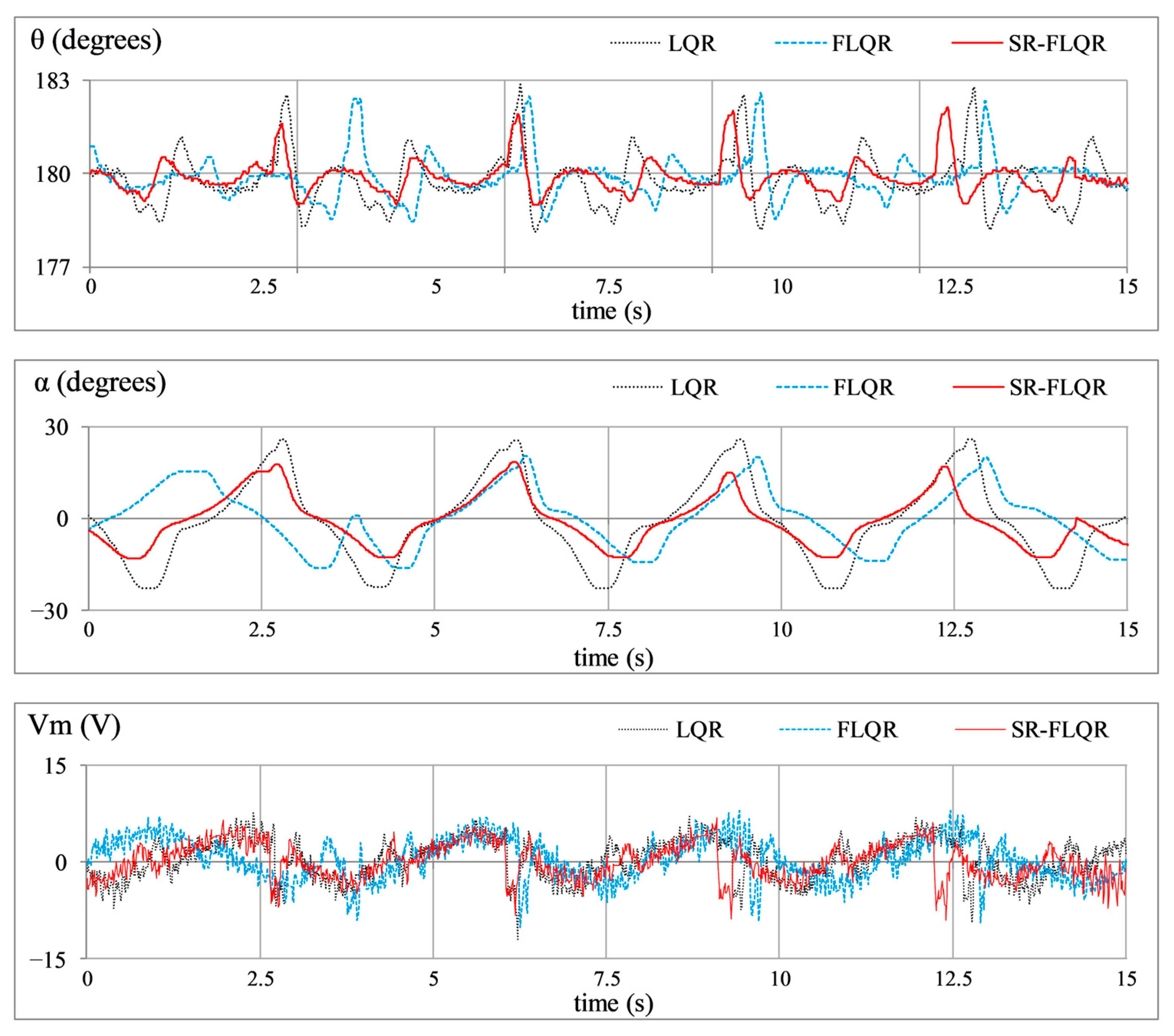
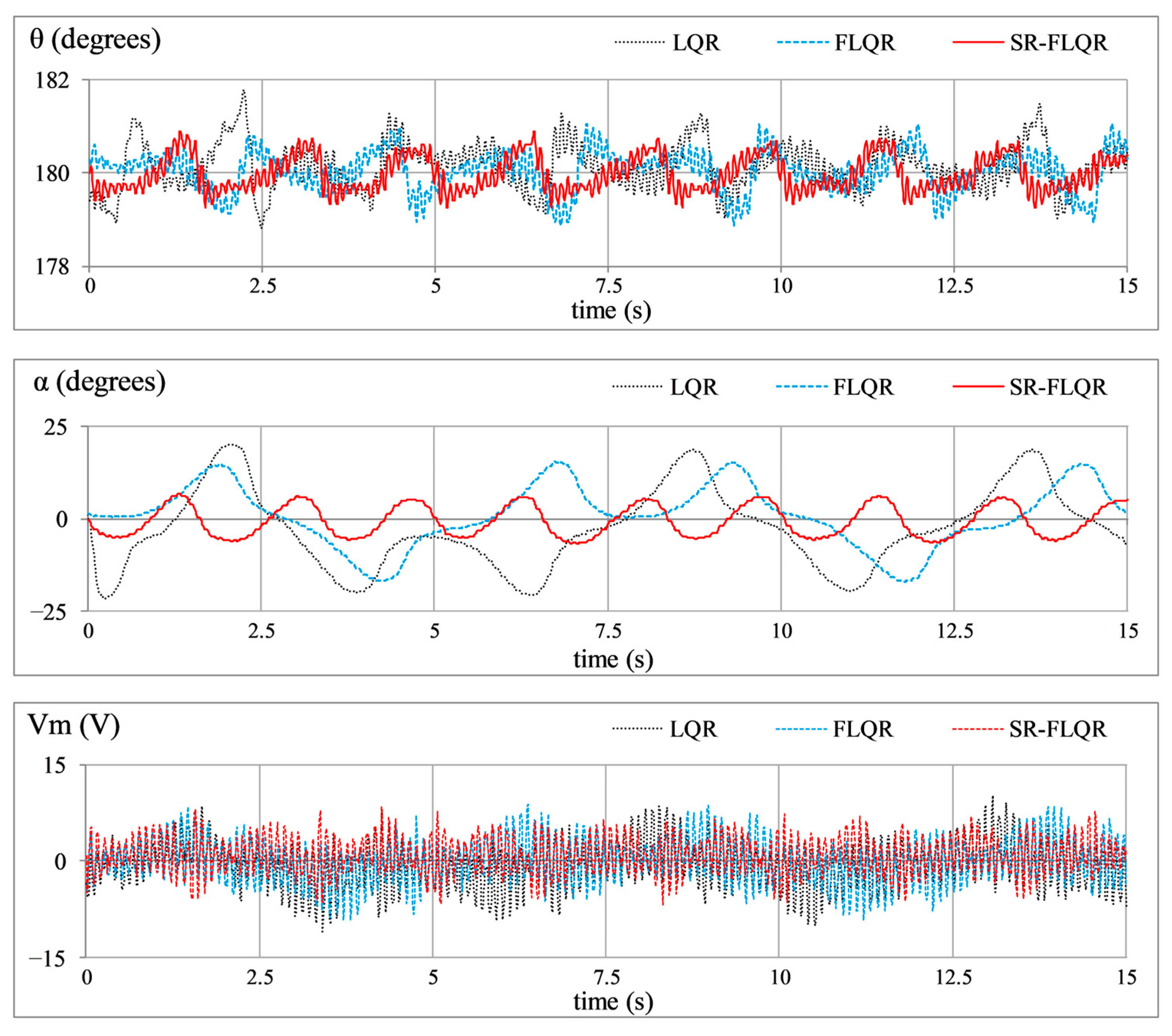
- Position Regulation: This baseline experiment evaluates the system’s ability to maintain its reference positions without external disturbances. It replicates real-world scenarios where a robotic system or an industrial manipulator must remain stable under normal operating conditions. The time-domain profiles of , , and are manifested in Figure 9.
- B.
- Impulse Disturbance Rejection: This experiment is conducted to evaluate the system’s response to transient impacts. An impulse disturbance is injected into the control input to assess the system’s capability to recover from sudden external shocks, such as power transients, abrupt mechanical impacts, sudden hardware failures, or seismic forces in engineering applications. A simulated 5.0 V pulse, having a span of 100 ms, is applied whenever the horizontal arm reaches its maximum position. The corresponding profiles of , , and are illustrated in Figure 10.
- C.
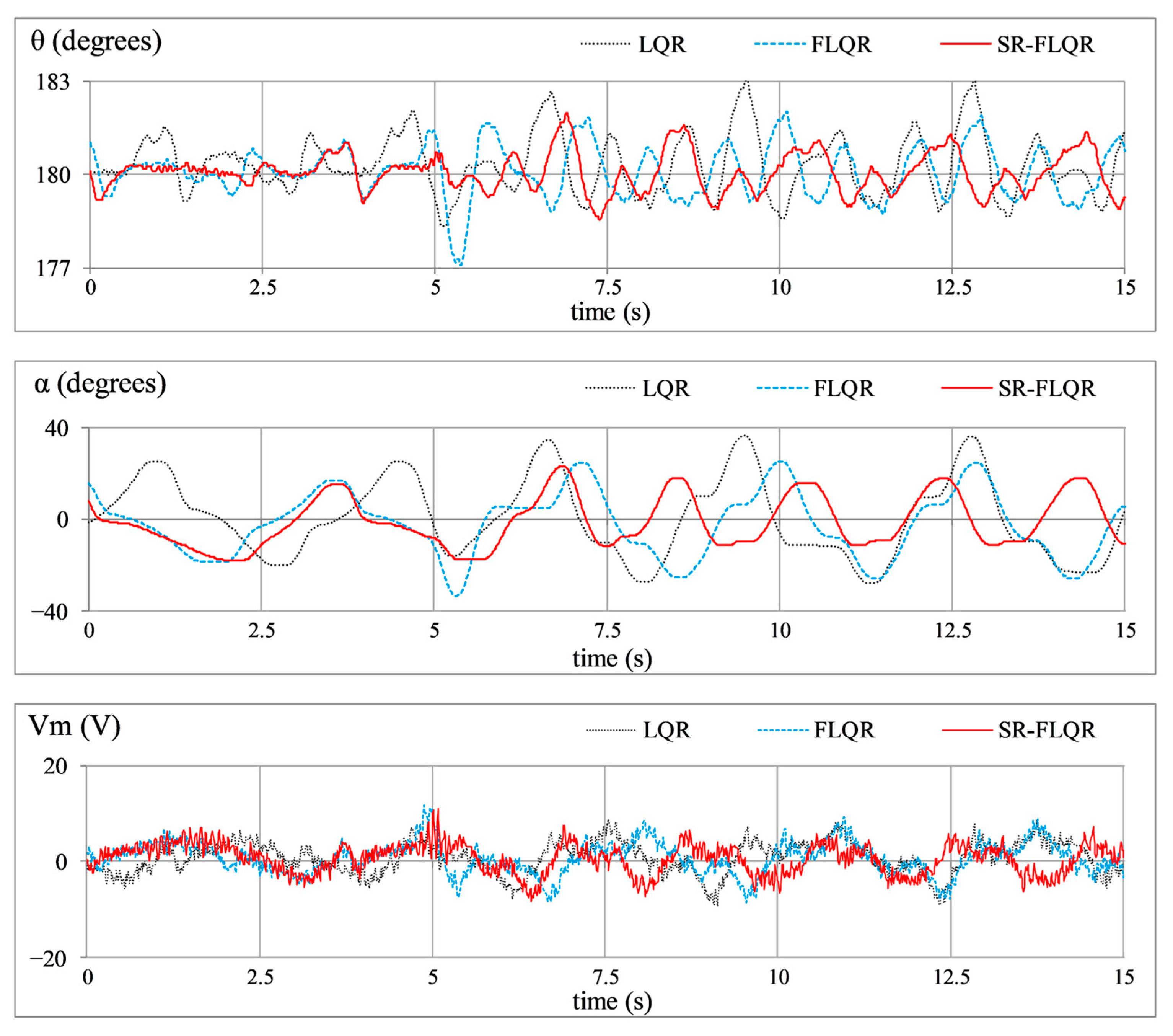
- Step Disturbance Compensation: This experiment evaluates the effect of a sudden and sustained external force, similar to wind gusts on aircraft, ocean currents affecting marine vessels, or sustained mechanical loads on industrial robots. A −5.0 V step input is introduced in the control signal at t = 10 s to examine the control scheme’s ability to manage abrupt but constant disturbances. The resulting variations in , , and are depicted in Figure 11.
- D.
- Sinusoidal Disturbance Attenuation: This test examines the control system’s resilience against periodic disturbances and mechanical vibrational effects, which are very common in robotics, aerospace, and automotive control systems. Although real disturbances such as sensor noise, friction, and backlash are non-periodic in nature, a sinusoidal disturbance is employed for this test case as a structured input to systematically test the controller’s robustness. The sinusoidal disturbance provides a repeatable and well-defined disturbance with continuous excitation across time, which makes it suitable for stressing both the tracking and regulation capabilities of the controller [48]. Moreover, stochastic disturbances are inherently present during the hardware experiments, meaning the proposed controller was simultaneously exposed to realistic non-periodic perturbations as well. A sinusoidal disturbance signal of the form, , is injected into the control signal to evaluate robustness. The corresponding responses of , , and are shown in Figure 12.
- E.
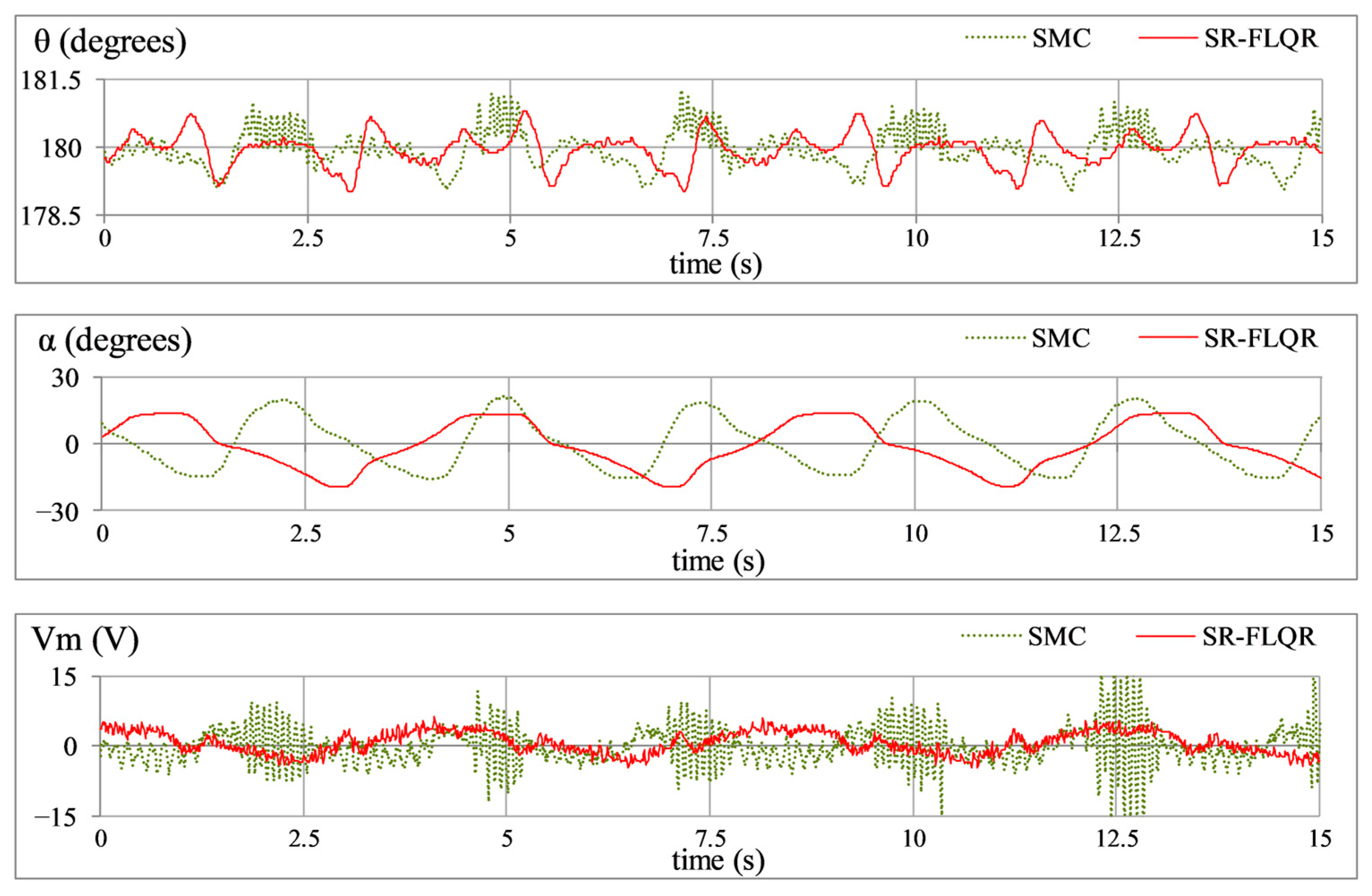
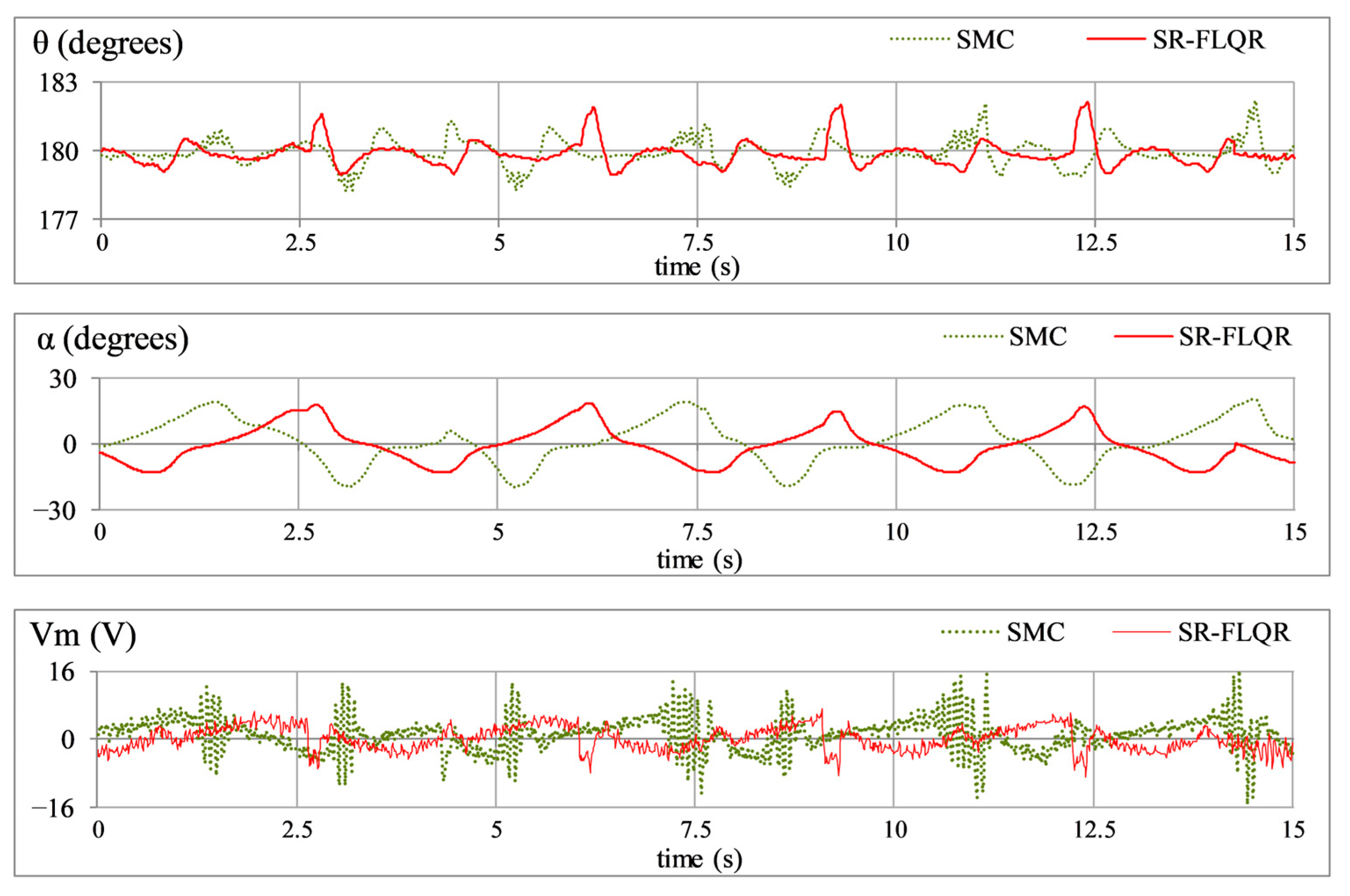
- Model Error Rejection: This scenario assesses the controller’s capacity to compensate for model inaccuracies and parametric variations, which occur in real-world applications where the system dynamics evolve/alter over time. To simulate this effect, a 0.1 kg mass is attached beneath the pendulum link, creating a mismatch between the real and modeled system dynamics. The system’s adaptability to this perturbation is investigated via the time domain profiles of , , and shown in Figure 13.
5.3. Analysis and Discussions
- RMSEz—Root mean square (RMS) error in the pendulum link and arm positions.
- Mp,θ—Peak overshoot magnitude of the rod following a disturbance.
- Ts,θ—Time required for the pendulum link to settle within ±5% of π rad. reference of the pendulum (~0.157 rad.) after a transient disturbance.
- αoff—Offset in the horizontal arm’s position after disturbance application.
- αp-p—Peak-to-peak magnitude of oscillations in the arm after disturbance application.
- MSVm—Mean squared value of the motor control voltage.
- Vp—Maximum control voltage after disturbance application.
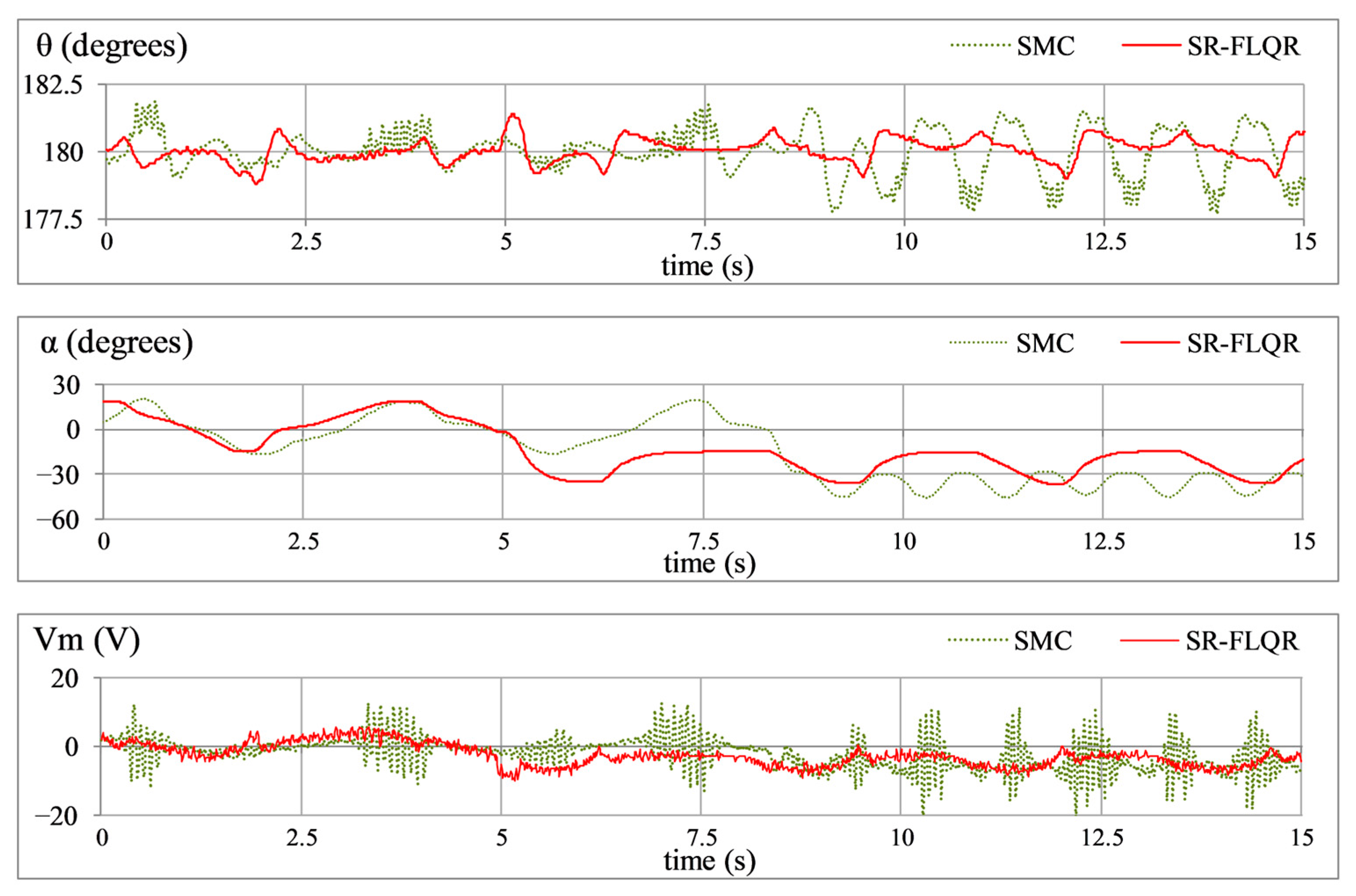
5.4. Comparison with a Robust SMC Controller
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aguilar-Avelar, C.; Moreno-Valenzuela, J. A composite controller for trajectory tracking applied to the Furuta pendulum. ISA Trans. 2015, 57, 286–294. [Google Scholar] [CrossRef] [PubMed]
- Costanzo, M.; Mazza, R.; Natale, C. Digital Control of an Inverted Pendulum Using a Velocity-Controlled Robot. Machines 2025, 13, 528. [Google Scholar] [CrossRef]
- Ramírez-Neria, M.; Sira-Ramírez, H.; Garrido-Moctezuma, R.; Luviano-Juarez, A. Linear active disturbance rejection control of underactuated systems: The case of the Furuta pendulum. ISA Trans. 2014, 53, 920–928. [Google Scholar] [CrossRef]
- Gritli, H.; Belghit, S. Robust feedback control of the underactuated Inertia Wheel Inverted Pendulum under parametric uncertainties and subject to external disturbances: LMI formulation. J. Frankl. Inst. 2018, 355, 9150–9191. [Google Scholar] [CrossRef]
- Kim, S.; Kwon, S. Nonlinear optimal control design for underactuated two-wheeled inverted pendulum mobile platform. IEEE/ASME Trans. Mechatron. 2017, 22, 2803–2808. [Google Scholar] [CrossRef]
- Wang, F.-C.; Chen, Y.-H.; Wang, Z.-J.; Liu, C.-H.; Lin, P.-C.; Yen, J.-Y. Decoupled Multi-Loop Robust Control for a Walk-Assistance Robot Employing a Two-Wheeled Inverted Pendulum. Machines 2021, 9, 205. [Google Scholar] [CrossRef]
- Saleem, O.; Mahmood-ul-Hasan, K. Adaptive State-space Control of Under-actuated Systems Using Error-magnitude Dependent Self-tuning of Cost Weighting-factors. Int. J. Control Autom. Syst. 2021, 19, 931–941. [Google Scholar] [CrossRef]
- Prasad, L.B.; Tyagi, B.; Gupta, H.O. Optimal control of nonlinear inverted pendulum system using PID controller and LQR: Performance analysis without and with disturbance input. Int. J. Autom. Comput. 2014, 11, 661–670. [Google Scholar] [CrossRef]
- Boubaker, O. The Inverted Pendulum Benchmark in Nonlinear Control Theory: A Survey. Int. J. Adv. Robot. Syst. 2013, 10, 233. [Google Scholar] [CrossRef]
- Wang, J.J. Simulation studies of inverted pendulum based on PID controllers. Sim. Mod. Pract. Theory 2011, 19, 440–449. [Google Scholar] [CrossRef]
- Wang, J.J.; Kumbasar, T. Optimal PID control of spatial inverted pendulum with big bang–big crunch optimization. IEEE/CAA J. Autom. Sin. 2018, 7, 822–832. [Google Scholar] [CrossRef]
- Saleem, O.; Mahmood-ul-Hasan, K. Robust stabilisation of rotary inverted pendulum using intelligently optimised nonlinear self-adaptive dual fractional-order PD controllers. Int. J. Syst. Sci. 2019, 50, 1399–1414. [Google Scholar] [CrossRef]
- Batiha, I.M.; Momani, S.; Batyha, R.M.; Jebril, I.H.; Judeh, D.A.; Oudetallah, J. DC motor speed control via fractional-order PID controllers. Int. J. Fuzzy Log. Intell. Syst. 2024, 24, 74–82. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, D.; Zhang, J.; Guo, F. Controlling and synchronizing a fractional-order chaotic system using stability theory of a time-varying fractional-order system. PLoS ONE 2018, 13, e0194112. [Google Scholar] [CrossRef]
- Nguyen-Vinh, Q.; Pham-Tran-Bich, T. Sliding mode control of induction motor with fuzzy logic observer. Electr. Eng. 2023, 105, 2769–2780. [Google Scholar] [CrossRef]
- Saleem, O.; Alsuwian, T.; Amin, A.A.; Ali, S.; Alqarni, Z.A. Stabilization control of rotary inverted pendulum using a novel EKF-based fuzzy adaptive sliding-mode controller: Design and experimental validation. Automatika 2024, 65, 538–558. [Google Scholar] [CrossRef]
- Chu, T.D.; Chen, C.K. Design and Implementation of Model Predictive Control for a Gyroscopic Inverted Pendulum. Appl. Sci. 2017, 7, 1272. [Google Scholar] [CrossRef]
- Waheed, F.; Yousufzai, I.K.; Valášek, M. A TV-MPC Methodology for Uncertain Under-Actuated Systems: A Rotary Inverted Pendulum Case Study. IEEE Access 2023, 11, 103636–103649. [Google Scholar] [CrossRef]
- Le, H.D.; Nestorović, T. Integral Linear Quadratic Regulator Sliding Mode Control for Inverted Pendulum Actuated by Stepper Motor. Machines 2025, 13, 405. [Google Scholar] [CrossRef]
- Xue, D.; Chen, Y.Q.; Atherton, D.P. Linear Feedback Control: Analysis and Design with MATLAB; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Saleem, O.; Iqbal, J. Phase-Based Adaptive Fractional LQR for Inverted-Pendulum-Type Robots: Formulation and Verification. IEEE Access 2024, 12, 93185–93196. [Google Scholar] [CrossRef]
- Saleem, O.; Abbas, F.; Iqbal, J. Complex Fractional-Order LQIR for Inverted-Pendulum-Type Robotic Mechanisms: Design and Experimental Validation. Mathematics 2023, 11, 913. [Google Scholar] [CrossRef]
- Szuster, M.; Hendzel, Z. Intelligent Optimal Adaptive Control for Mechatronic Systems; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Zabihifar, S.H.; Yushchenko, A.S.; Navvabi, H. Robust control based on adaptive neural network for Rotary inverted pendulum with oscillation compensation. Neural Comput. Appl. 2020, 32, 14667–14679. [Google Scholar] [CrossRef]
- Ochoa, P.; Peraza, C.; Melin, P.; Castillo, O.; Geem, Z.W. Type-3 Fuzzy Dynamic Adaptation of the Crossover Parameter in Differential Evolution for the Optimal Design of Type-3 Fuzzy Controllers for the Inverted Pendulum. Machines 2025, 13, 450. [Google Scholar] [CrossRef]
- Moness, M.; Mahmoud, D.; Hussein, A. Real-time Mamdani-like fuzzy and fusion-based fuzzy controllers for balancing two-wheeled inverted pendulum. J. Ambient Intell. Humaniz. Comput. 2022, 13, 3577–3593. [Google Scholar] [CrossRef]
- Nguyen, T.V.A.; Dao, Q.T.; Bui, N.T. Optimized fuzzy logic and sliding mode control for stability and disturbance rejection in rotary inverted pendulum. Sci. Rep. 2024, 14, 31116. [Google Scholar] [CrossRef]
- Hazem, B.Z.; Bingül, Z. A comparative study of anti-swing radial basis neural-fuzzy LQR controller for multi-degree-of-freedom rotary pendulum systems. Neural Comput. Appl. 2023, 35, 17397–17413. [Google Scholar] [CrossRef]
- Hazem, B.Z.; Fotuhi, M.J.; Bingül, Z. Development of a Fuzzy-LQR and Fuzzy-LQG stability control for a double link rotary inverted pendulum. J. Frankl. Inst. 2020, 357, 10529–10556. [Google Scholar] [CrossRef]
- Shang, W.W.; Cong, S.; Li, Z.X.; Jiang, S.L. Augmented Nonlinear PD Controller for a Redundantly Actuated Parallel Manipulator. Adv. Robot. 2009, 23, 1725–1742. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Huang, J. Tank-level robust control of LNG carrier based on hyperbolic tangent function nonlinear modification. Transp. Saf. Environ. 2024, 6, tdae010. [Google Scholar] [CrossRef]
- Qasem, O.; Gutierrez, H.; Gao, W. Experimental validation of data-driven adaptive optimal control for continuous-time systems via hybrid iteration: An application to rotary inverted pendulum. IEEE Trans. Ind. Electron. 2023, 71, 6210–6220. [Google Scholar] [CrossRef]
- Unluturk, A.; Aydogdu, O. Machine learning based self-balancing and motion control of the underactuated mobile inverted pendulum with variable load. IEEE Access 2022, 10, 104706–104718. [Google Scholar] [CrossRef]
- Lee, T.; Ju, D.; Lee, Y.S. Transition Control of a Double-Inverted Pendulum System Using Sim2Real Reinforcement Learning. Machines 2025, 13, 186. [Google Scholar] [CrossRef]
- Oh, Y.; Lee, T.; Ryoo, S.; Koh, K.C.; Han, S.; Lee, Y.S. Reinforcement Learning to Achieve Real-time Control of a Quadruple Inverted Pendulum. Int. J. Control Autom. Syst. 2025, 23, 2797–2806. [Google Scholar] [CrossRef]
- Israilov, S.; Fu, L.; Sánchez-Rodríguez, J.; Fusco, F.; Allibert, G.; Raufaste, C.; Argentina, M. Reinforcement learning approach to control an inverted pendulum: A general framework for educational purposes. PLoS ONE 2023, 18, e0280071. [Google Scholar] [CrossRef]
- Hernandez, R.; Garcia-Hernandez, R.; Jurado, F. Modeling, simulation, and control of a rotary inverted pendulum: A reinforcement learning-based control approach. Modelling 2024, 5, 1824–1852. [Google Scholar] [CrossRef]
- Razmjooei, H.; Palli, G.; Abdi, E.; Strano, S.; Terzo, M. Finite-time continuous extended state observers: Design and experimental validation on electro-hydraulic systems. Mechatronics 2022, 85, 102812. [Google Scholar] [CrossRef]
- Saleem, O.; Iqbal, J.; Afzal, M.S. A robust variable-structure LQI controller for under-actuated systems via flexible online adaptation of performance-index weights. PLoS ONE 2023, 18, e0283079. [Google Scholar] [CrossRef] [PubMed]
- Balamurugan, S.; Venkatesh, P. Fuzzy sliding-mode control with low pass filter to reduce chattering effect: An experimental validation on Quanser SRP. Sadhana 2017, 42, 1693–1703. [Google Scholar] [CrossRef][Green Version]
- Astom, K.J.; Apkarian, J.; Karam, P.; Levis, M.; Falcon, J. Student Workbook: QNET Rotary Inverted Pendulum Trainer for NI ELVIS; Quanser Inc.: Waterloo, ON, Canada, 2011. [Google Scholar][Green Version]
- Peláez, G.; Izquierdo, P.; Peláez, G.; Rubio, H. A Multibody-Based Benchmarking Framework for the Control of the Furuta Pendulum. Actuators 2025, 14, 377. [Google Scholar] [CrossRef]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Lupu, D.; Necoara, I. Exact representation and efficient approximations of linear model predictive control laws via HardTanh type deep neural networks. Syst. Control Lett. 2024, 186, 105742. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Song, Y.; Rong, X. The Influence of the Activation Function in a Convolution Neural Network Model of Facial Expression Recognition. Appl. Sci. 2020, 10, 1897. [Google Scholar] [CrossRef]
- Alagoz, B.B.; Ates, A.; Yeroglu, C.; Senol, B. An experimental investigation for error-cube PID control. Trans. Inst. Meas. Control 2015, 37, 652–660. [Google Scholar] [CrossRef]
- Saleem, O.; Rizwan, M.; Iqbal, J. Adaptive optimal control of under-actuated robotic systems using a self-regulating nonlinear weight-adjustment scheme: Formulation and experimental verification. PLoS ONE 2023, 18, e0295153. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Ajmeri, M. Robust stabilization and tracking control of spatial inverted pendulum using super-twisting sliding mode control. Int. J. Dyn. Control 2023, 11, 1178–1189. [Google Scholar] [CrossRef]
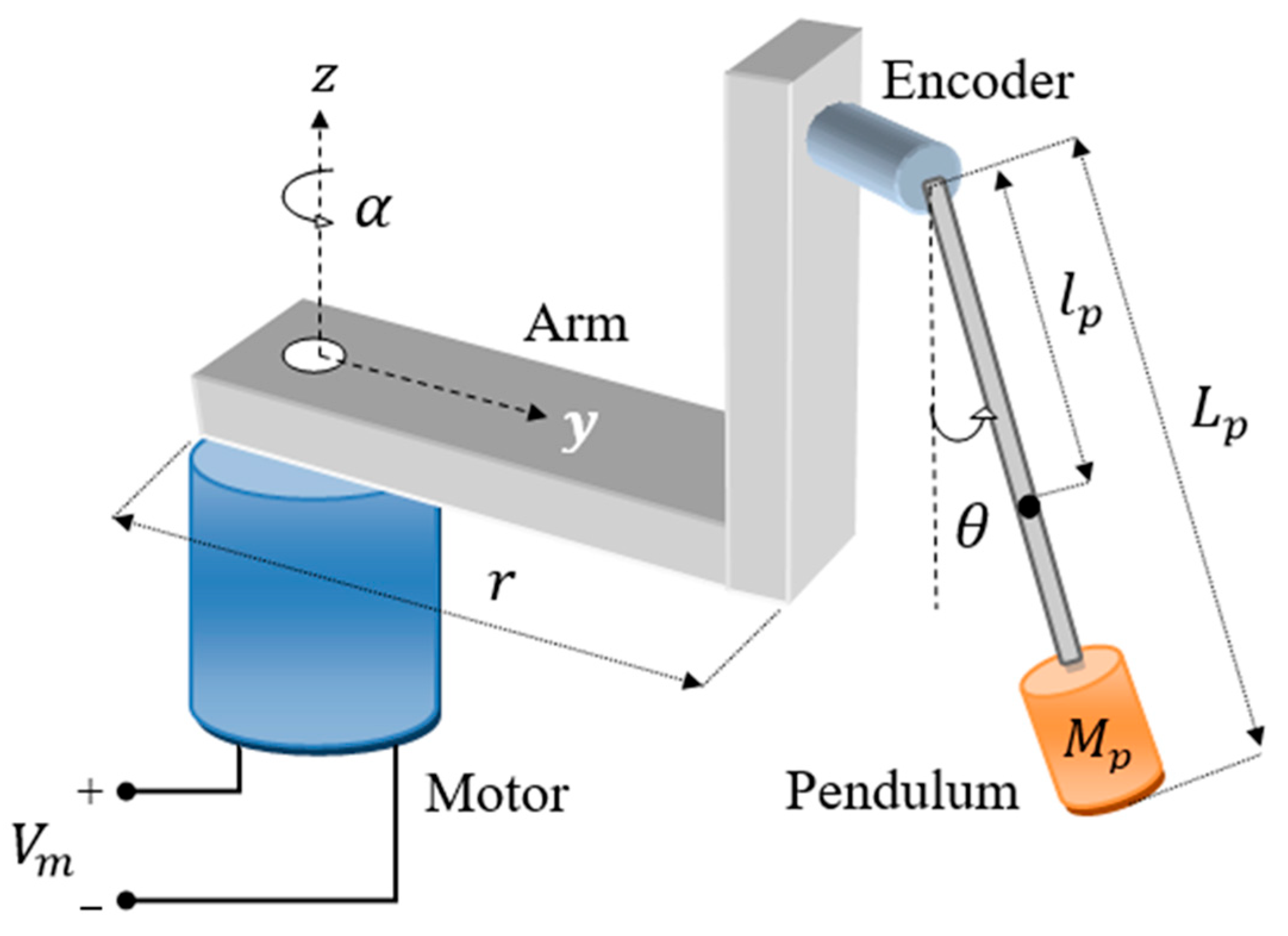
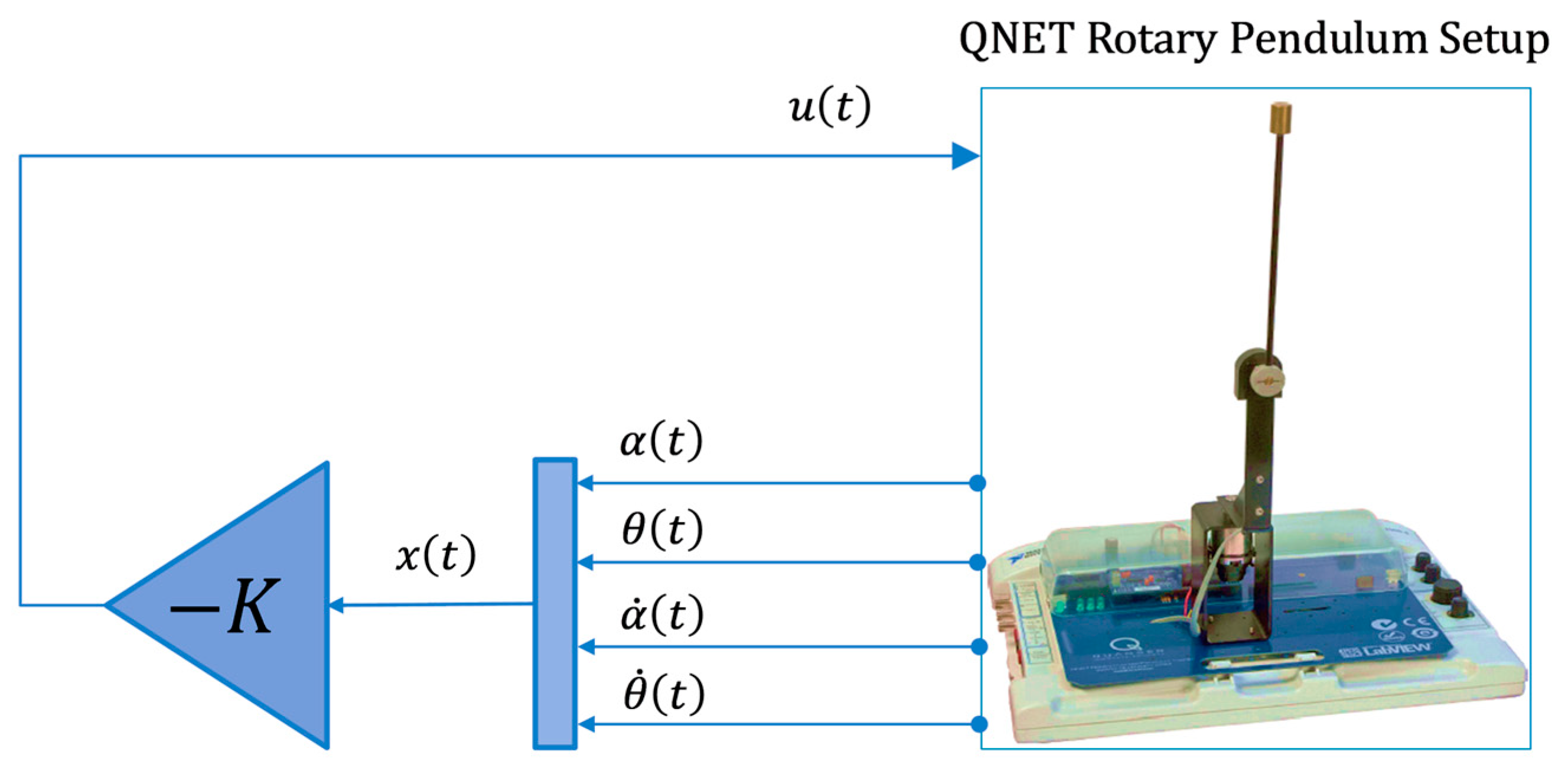
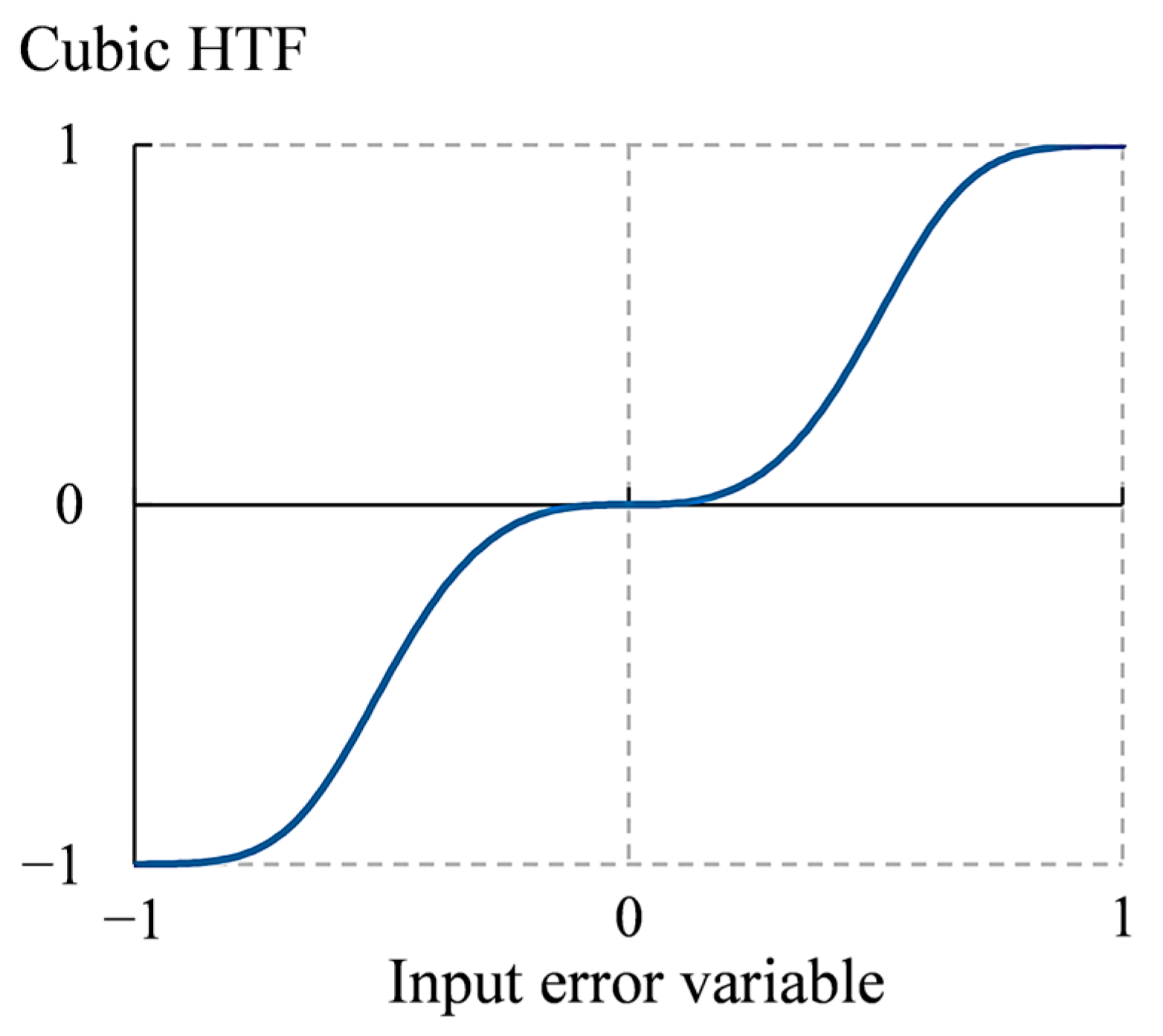
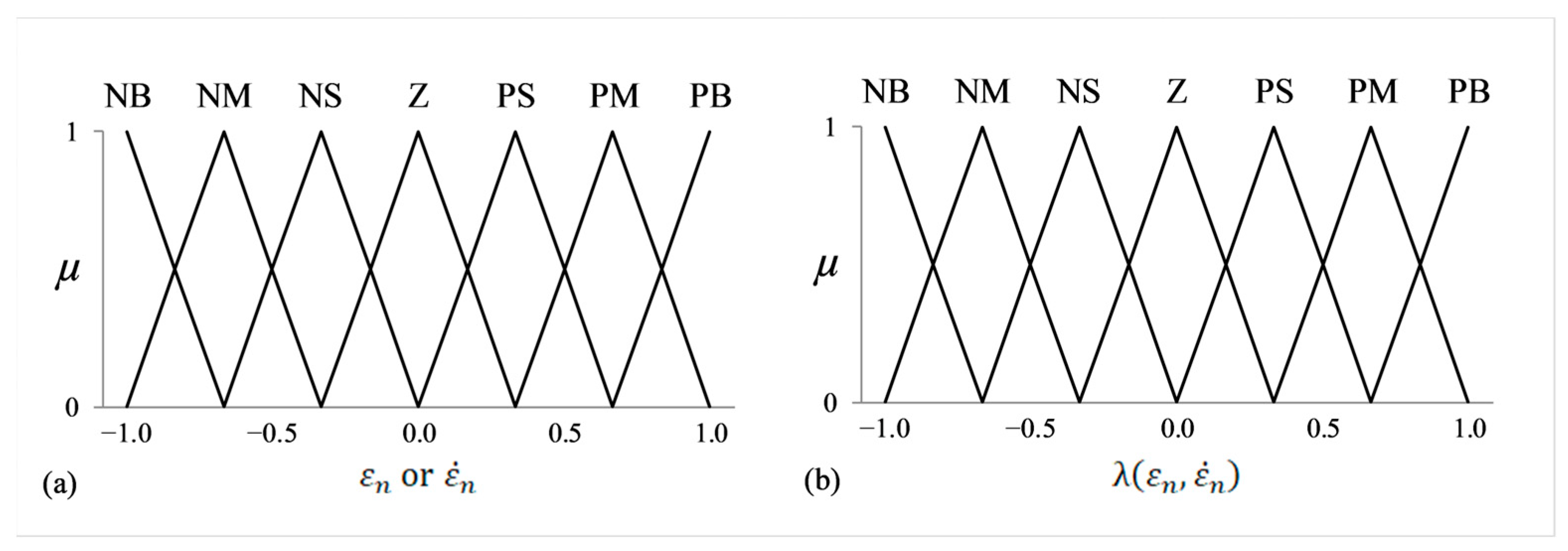





| Parameter | Description | Value | Unit |
|---|---|---|---|
| Mp | Pendulum’s mass | 0.027 | kg |
| lp | Pivot to pendulum’s center distance | 0.153 | m |
| Lp | Pendulum link length | 0.191 | M |
| r | Horizontal arm length | 0.083 | M |
| Marm | Arm’s mass | 0.028 | Kg |
| g | Acceleration due to gravity | 9.810 | m/s2 |
| Je | Moment about motor shaft | 1.23 × 10−4 | kgm2 |
| Jp | Moment about pendulum | 1.10 × 10−4 | kgm2 |
| Rm | Motor’s armature resistance | 3.30 | Ω |
| Lm | Motor’s armature inductance | 47.0 | mH |
| Kt | Motor torque coefficient | 0.028 | Nm |
| Km | Back-EMF coefficient | 0.028 | V/(rad/s) |
| Tm | Maximum torque | 0.14 | Nm |
| / | NB | NM | NS | Z | PS | PM | PB |
| NB | NB | NB | NB | NB | NM | NS | Z |
| NM | NB | NB | NB | NM | NS | Z | PS |
| NS | NB | NB | NM | NS | Z | PS | PM |
| Z | NB | NM | NS | Z | PS | PM | PB |
| PS | NM | NS | Z | PS | PM | PB | PB |
| PM | NS | Z | PS | PM | PB | PB | PB |
| PB | Z | PS | PM | PB | PB | PB | PB |
| Experiment | QPM | Control Scheme | |||
|---|---|---|---|---|---|
| Symbol | Unit | LQR | FLQR | SR-FLQR | |
| A | RMSEθ | deg. | 0.49 | 0.43 | 0.38 |
| RMSEα | deg. | 14.64 | 13.38 | 10.81 | |
| MSVm | V2 | 7.53 | 7.09 | 5.87 | |
| B | RMSEθ | deg. | 0.82 | 0.66 | 0.52 |
| Mp,θ | deg. | 2.87 | 2.58 | 2.15 | |
| Ts,θ | s. | 0.78 | 0.61 | 0.52 | |
| RMSEα | deg. | 13.74 | 9.82 | 8.42 | |
| MSVm | V2 | 10.06 | 10.19 | 7.52 | |
| Vp | V | −11.94 | −10.05 | −8.99 | |
| C | RMSEθ | deg. | 0.96 | 0.68 | 0.45 |
| RMSEα | deg. | 34.81 | 26.98 | 21.31 | |
| αoff | deg. | −42.12 | −29.92 | −25.40 | |
| αp-p | deg. | 30.78 | 33.88 | 21.37 | |
| MSVm | V2 | 27.70 | 21.01 | 17.98 | |
| D | RMSEθ | deg. | 0.51 | 0.47 | 0.38 |
| RMSEα | deg. | 10.93 | 8.21 | 4.29 | |
| MSVm | V2 | 13.21 | 11.34 | 8.57 | |
| E | RMSEθ | deg. | 1.01 | 0.83 | 0.62 |
| RMSEα | deg. | 16.84 | 14.22 | 11.18 | |
| MSVm | V2 | 11.29 | 12.42 | 10.03 | |
| Experiment | QPM | Control Scheme | Improvement in SR-FLQR (%) | ||
|---|---|---|---|---|---|
| Symbol | Unit | SMC [7] | SR-FLQR | ||
| A | RMSEθ | deg. | 0.40 | 0.38 | 5.0 |
| RMSEα | deg. | 11.85 | 10.81 | 8.8 | |
| MSVm | V2 | 19.71 | 5.87 | 70.2 | |
| B | RMSEθ | deg. | 0.61 | 0.52 | 14.8 |
| Mp,θ | deg. | 2.20 | 2.15 | 2.3 | |
| Ts,θ | s. | 0.72 | 0.52 | 27.8 | |
| RMSEα | deg. | 10.34 | 8.42 | 18.6 | |
| MSVm | V2 | 14.71 | 7.52 | 48.9 | |
| Vp | V | −16.02 | −8.99 | 43.9 | |
| C | RMSEθ | deg. | 0.91 | 0.45 | 50.5 |
| RMSEα | deg. | 27.70 | 21.31 | 23.1 | |
| αoff | deg. | −35.91 | −25.40 | 29.3 | |
| MSVm | V2 | 30.33 | 17.98 | 40.7 | |
| D | RMSEθ | deg. | 0.44 | 0.38 | 13.6 |
| RMSEα | deg. | 8.69 | 4.29 | 50.6 | |
| MSVm | V2 | 19.94 | 8.57 | 57.0 | |
| E | RMSEθ | deg. | 1.06 | 0.62 | 41.5 |
| RMSEα | deg. | 12.42 | 11.18 | 10.0 | |
| MSVm | V2 | 22.54 | 10.03 | 55.5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleem, O.; Iqbal, J.; Alharbi, S. Self-Regulating Fuzzy-LQR Control of an Inverted Pendulum System via Adaptive Hyperbolic Error Modulation. Machines 2025, 13, 939. https://doi.org/10.3390/machines13100939
Saleem O, Iqbal J, Alharbi S. Self-Regulating Fuzzy-LQR Control of an Inverted Pendulum System via Adaptive Hyperbolic Error Modulation. Machines. 2025; 13(10):939. https://doi.org/10.3390/machines13100939
Chicago/Turabian StyleSaleem, Omer, Jamshed Iqbal, and Soltan Alharbi. 2025. "Self-Regulating Fuzzy-LQR Control of an Inverted Pendulum System via Adaptive Hyperbolic Error Modulation" Machines 13, no. 10: 939. https://doi.org/10.3390/machines13100939
APA StyleSaleem, O., Iqbal, J., & Alharbi, S. (2025). Self-Regulating Fuzzy-LQR Control of an Inverted Pendulum System via Adaptive Hyperbolic Error Modulation. Machines, 13(10), 939. https://doi.org/10.3390/machines13100939








