Curing Deformation Prediction and Compensation Methods for Large-Sized CFRP Components

Abstract

The residual stresses induced by the curing process for carbon fiber-reinforced polymers (CFRPs) lead to inevitable deformation, which seriously affects manufacturing accuracy, especially for large-sized CFRP components. Furthermore, deformation may cause damage or failure of components during subsequent assembly. More attention needs to be paid to improving the curing accuracy for large-sized CFRP components. In this study, a normal direction compensation algorithm based on node deformation is proposed based on the mold profile. Firstly, a finite element model was constructed to simulate the curing process of CFRPs and validated with a small-sized test piece. The results showed the effectiveness of the simulated and compensation methods. Secondly, to meet the precision requirements of large-sized CFRP components, a neural network was used to establish a mapping between curing process parameters and curing deformation, and the parameters were then optimized with a genetic algorithm for subsequent analysis. Finaly, a 15 m CFRP component was used to explore the effect of compensation methods in reducing curing deformation of large-sized CFRP components. The verified results showed that the maximum deformation after compensation was 0.99 mm in the normal direction, which was superior to the 1.258 mm compensation in the connecting direction.

1. Introduction

Carbon fiber-reinforced polymer (CFRP) composites are extensively used in the aerospace industry due to their high specific strength and stiffness, corrosion resistance, and lightweight characteristics [1,2,3]. The large-sized, integrated design of main load-bearing CFRP structures has become an important development trend, aimed at meeting the requirements of high load capacity, long range, and high performance for next-generation aerospace vehicles. However, large-sized composite components exhibit uneven deformation after demolding, mainly due to thermal expansion differences between the fiber–resin interface and the CFRP, as well as between the CFRP and the mold [4,5]. These differences, combined with complex temperature variations on the large-sized mold surface, uneven internal stress distribution, and the release of residual stresses, contribute to deformation [6,7,8,9,10]. In aerospace composites with varying curvatures and thicknesses, non-uniform structural deformation during assembly leads to internal damage or even component failure [11,12,13]. Therefore, mold profile compensation is essential for improving the accuracy of large-sized CFRP composite components during the curing process.

Extensive research has focused on optimizing residual stress, process parameters, mold structure, and mold profile compensation. Rennick and Radford [14], Radford and Diefendorf [15], and Nelson and Cairns [16] reported that the curing deformation of CFRP laminates, both in-plane and through-thickness, results from mismatched thermal expansion and chemical shrinkage of the constituent materials. Svanberg and Holmberg [17] proposed a linear viscoelastic model accounting for thermal expansion, chemical shrinkage, and exothermic reactions during different stages of resin curing. The results indicated that the novel model improved computational efficiency and accuracy compared with conventional viscoelastic models. Prasatya et al. [18] used thermo-viscoelastic modeling to calculate the curing deformation of composites and concluded that resin cure shrinkage contributed over 30% to residual stresses. Zhu et al. [19] predicted residual stresses generated during curing and examined their effects on composite manufacturing accuracy. White and Hahn [20,21] developed a residual stress model to predict the curing process for composite laminates. Viscoelastic analysis revealed that chemical strains contributed less than 4% to residual stress in a typical cure cycle. Msallem et al. [22] calculated residual stresses developed during curing using finite element simulation. The results underscore the importance of characterization accuracy and model selection. Feng et al. [23] developed a multi-scale, non-orthogonal viscoelastic model to capture the constitutive behavior of preformed braided CFRP components during the curing process. Wang et al. [24] proposed a physics-based numerical model to predict and compensate for deformation induced during machining of three-dimensional woven composites.

Process parameters of CFRP composites also have a significant impact on curing deformation. Sorrentino and Tersigni [25] reported that for thick composite components, the degree of cure differs between the core and the surface, causing structural and geometric deviations. These issues mainly result from improper curing process design, underscoring the need for curing cycle design and optimization. Hui et al. [26] used a neural network to replace the conventional curing kinetics model, identify kinetics parameters, and derive the curing process of CFRP composites. The neural network model substantially improved prediction accuracy for curing behavior. Zhang et al. [27] derived the optimal compensation profile by establishing a coordinate model linking curing process parameters with mold profile compensation. Comparative results indicated that composite panel distortion was reduced by 86.2%.

In addition, curing deformation is effectively reduced by mold profile compensation. Li et al. [28] established a simple mathematical model to predict the spring-in and warpage of T-shaped structures. The results revealed that cure shrinkage and thermal expansion were the primary drivers of deformation. Fernlund et al. [29] investigated the curing process of C-shaped and L-shaped CFRP components and found that C-shaped components exhibited greater spring-in than L-shaped ones, which is attributed to the “geometric locking” effect of the part on the tooling. Furthermore, the differences in the thermal expansion coefficient between the mold and the CFRP critically influence curing-induced deformation. Wang et al. [30] integrated a finite-volume numerical model with a GA to optimize mold support structures, achieving a 17.21% improvement in curing uniformity. Dong et al. [31] proposed a compensation algorithm multiplying nodal deformation on the mold surface by a compensation factor, and the method effectively reduced curing deformation of CFRP components. Zein et al. [32] introduced a method for adjusting the mold profile with a reduced spectral basis to eliminate curing deformation. Liu et al. [33] developed a discrete curvature-based displacement adjustment method for mold profile compensation, which achieved dimensional accuracy for a composite skin in a single iteration, with a maximum surface deviation of 0.3 mm.

Most existing studies have addressed deformation prediction and compensation for small-sized CFRP components. However, methods such as profile compensation, mold structure optimization, and forming parameter optimization are inefficient and require numerous iterations for large-sized components. Traditional solutions rely on empirically determined curing parameters, followed by iterative adjustments and mold surface machining to control deformation. However, such iterative correction increases time and costs, hinders accurate mold surface design, restricts modifications to formed molds, and depends heavily on operator experience. In contrast, mold profile compensation based on node deformation remains one of the most effective and feasible approaches for controlling composite curing deformation. The purpose of this paper is to propose a curing deformation compensation method for large composite components in aerospace applications. The structure of this paper is as follows: Section 2 presents the mold profile compensation method based on node deformation. Section 3 presents the numerical analysis of CFRP curing deformation. Section 4 discusses the optimization of curing process parameters. Section 5 provides a compensation case for large-sized CFRP skin curing deformation. Finally, Section 6 concludes the paper.

2. Research on Mold Profile Compensation Based on Node Deformation

2.1. Compensation Principle

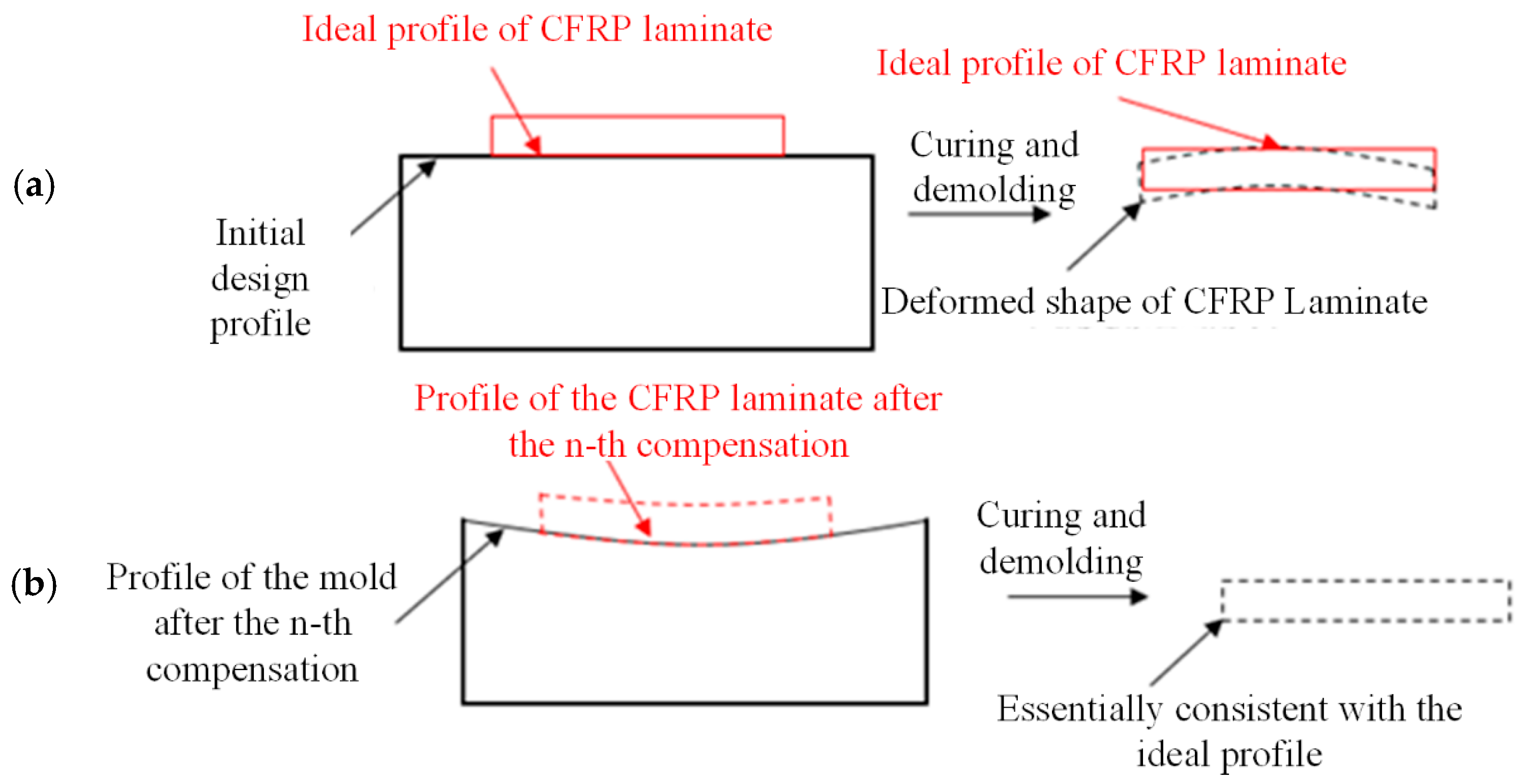
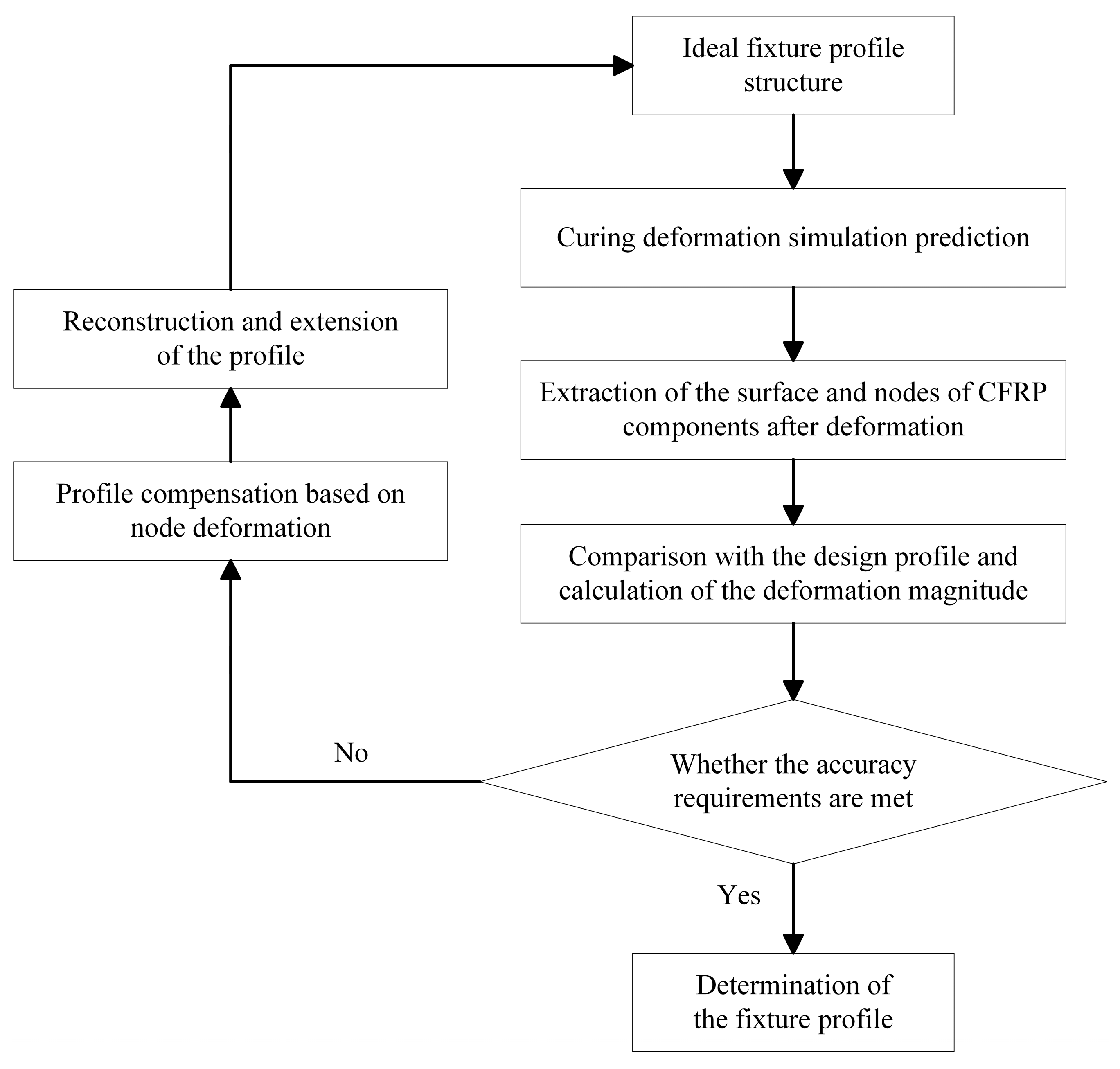
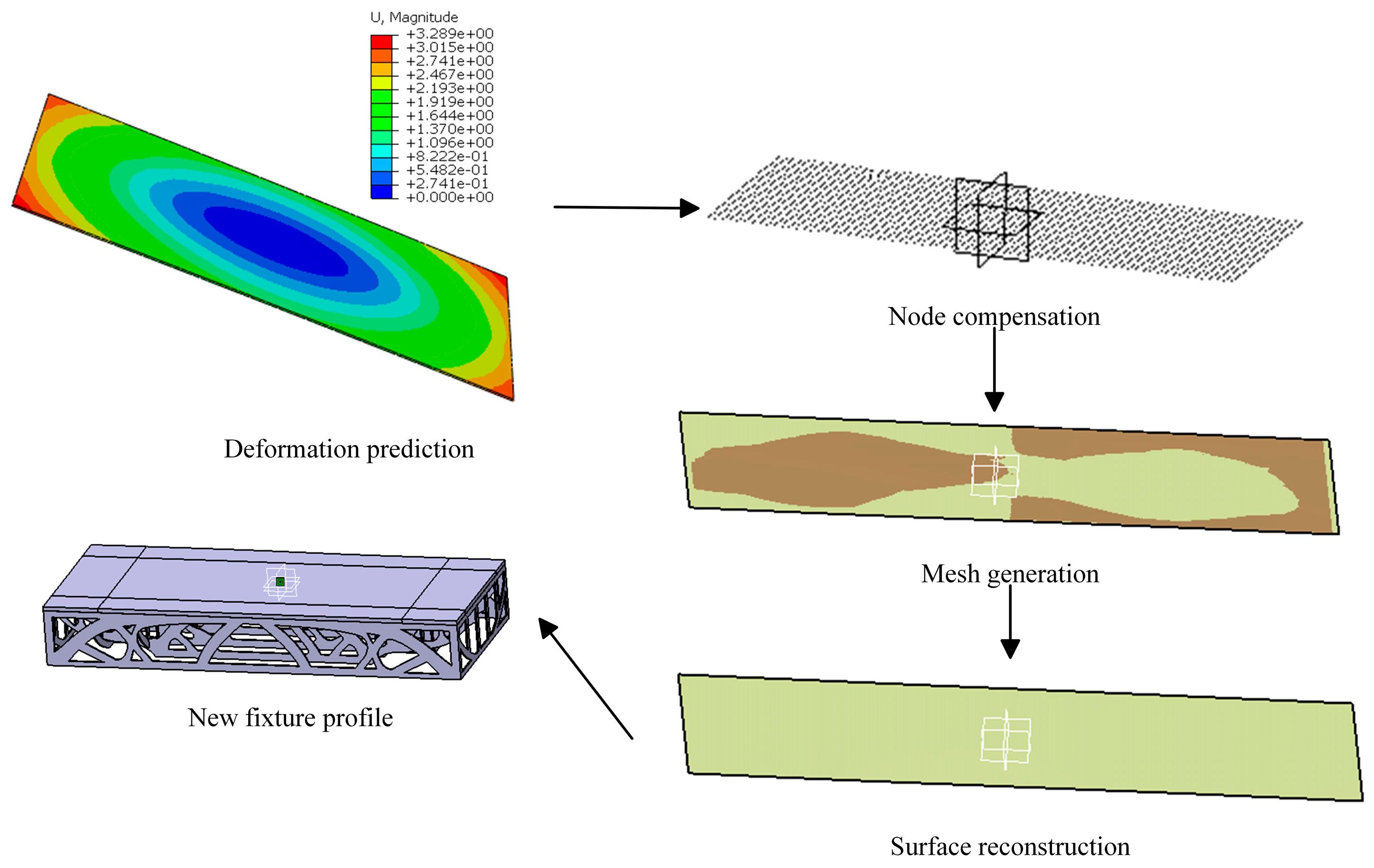
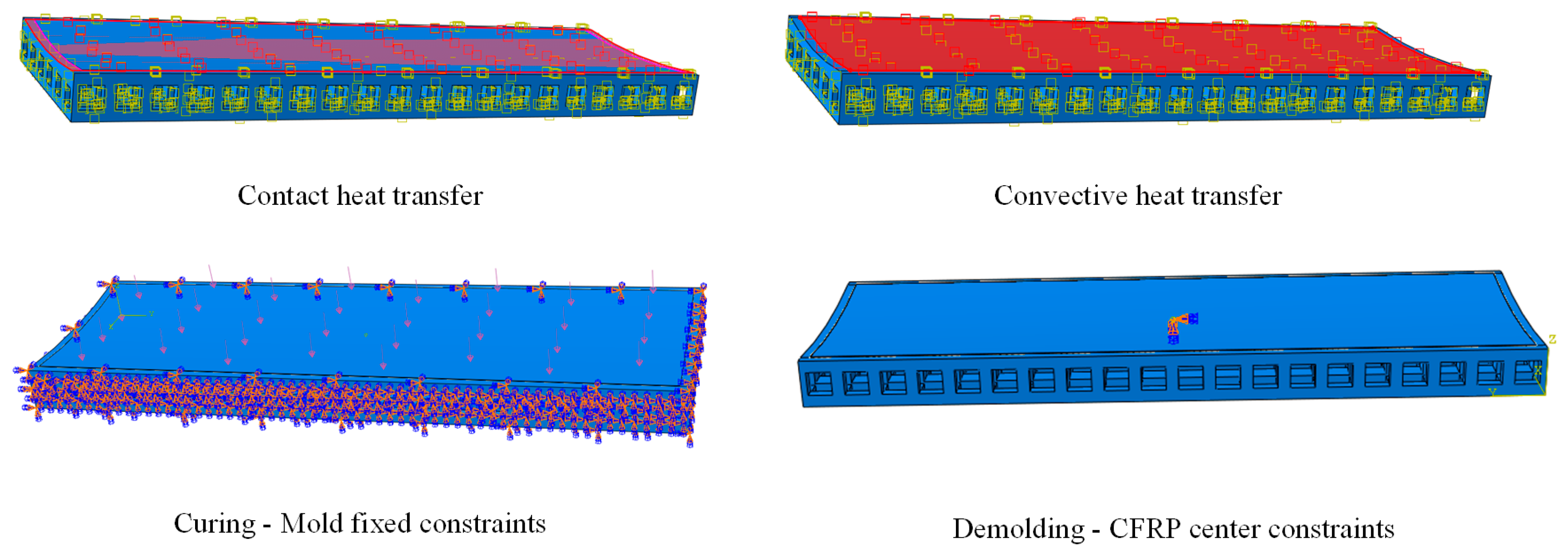
The processes of the mold profile compensation method based on node deformation are as follows: first, coordinate data for all surface nodes in both the undeformed and deformed states are obtained; then, displacement variations between the two states are calculated; finally, compensation is executed using the mold profile compensation algorithm based on deformation magnitude and direction. The resulting profile is extended to the mold boundary to account for deformation caused by the CFRP curing process, ensuring that the deformed shape aligns with the ideal profile. The compensation principle is shown in Figure 1, and the process is illustrated in Figure 2.

2.2. Mold Profile Compensation Algorithm Based on Node Deformation

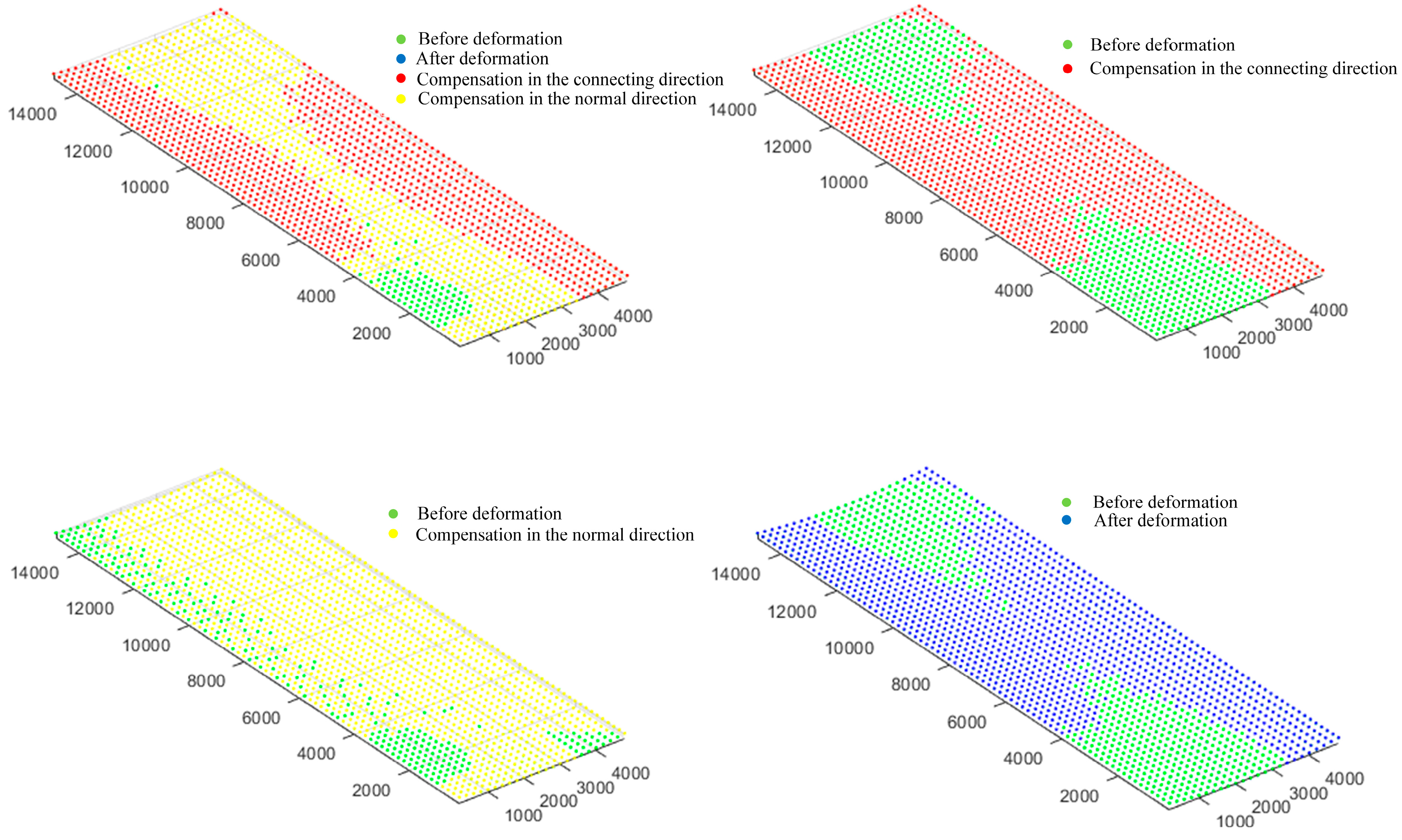
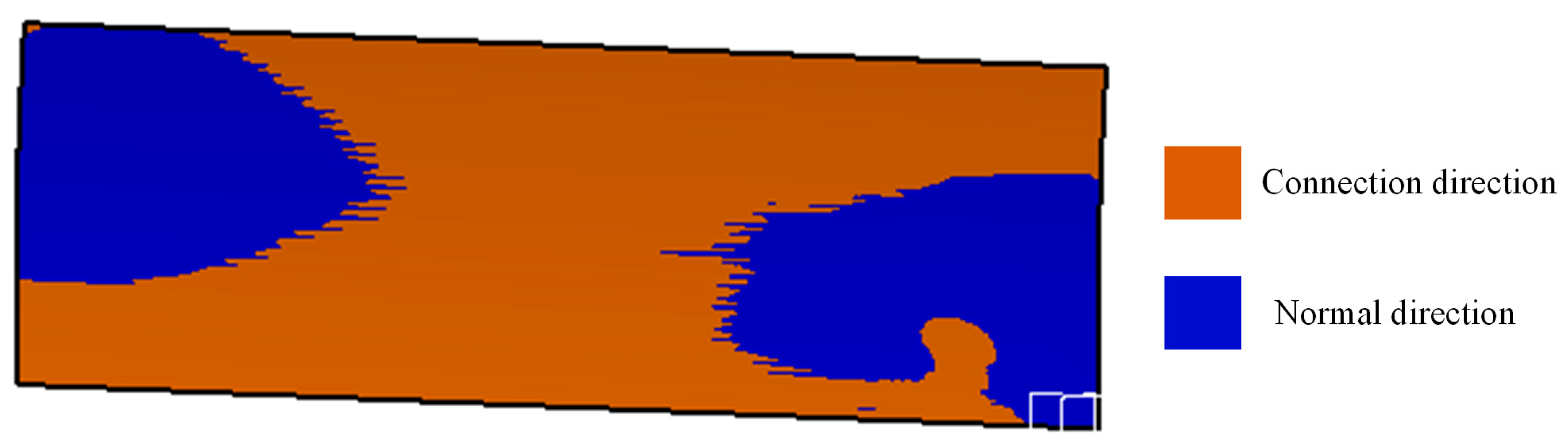
The inverse deformation compensation principle was applied using curing deformation prediction data to redesign the mold profile. The method involved post-processing numerical predictions for CFRP curing deformation. The coordinates of all nodes on the lower surface, along with their deformed displacements in the x, y, and z directions, were extracted for both the pre-deformation and post-deformation states. The mold was then compensated in both the connecting and normal directions to achieve the desired deformation control for the CFRP component.

(1)

Compensation process in the connecting direction

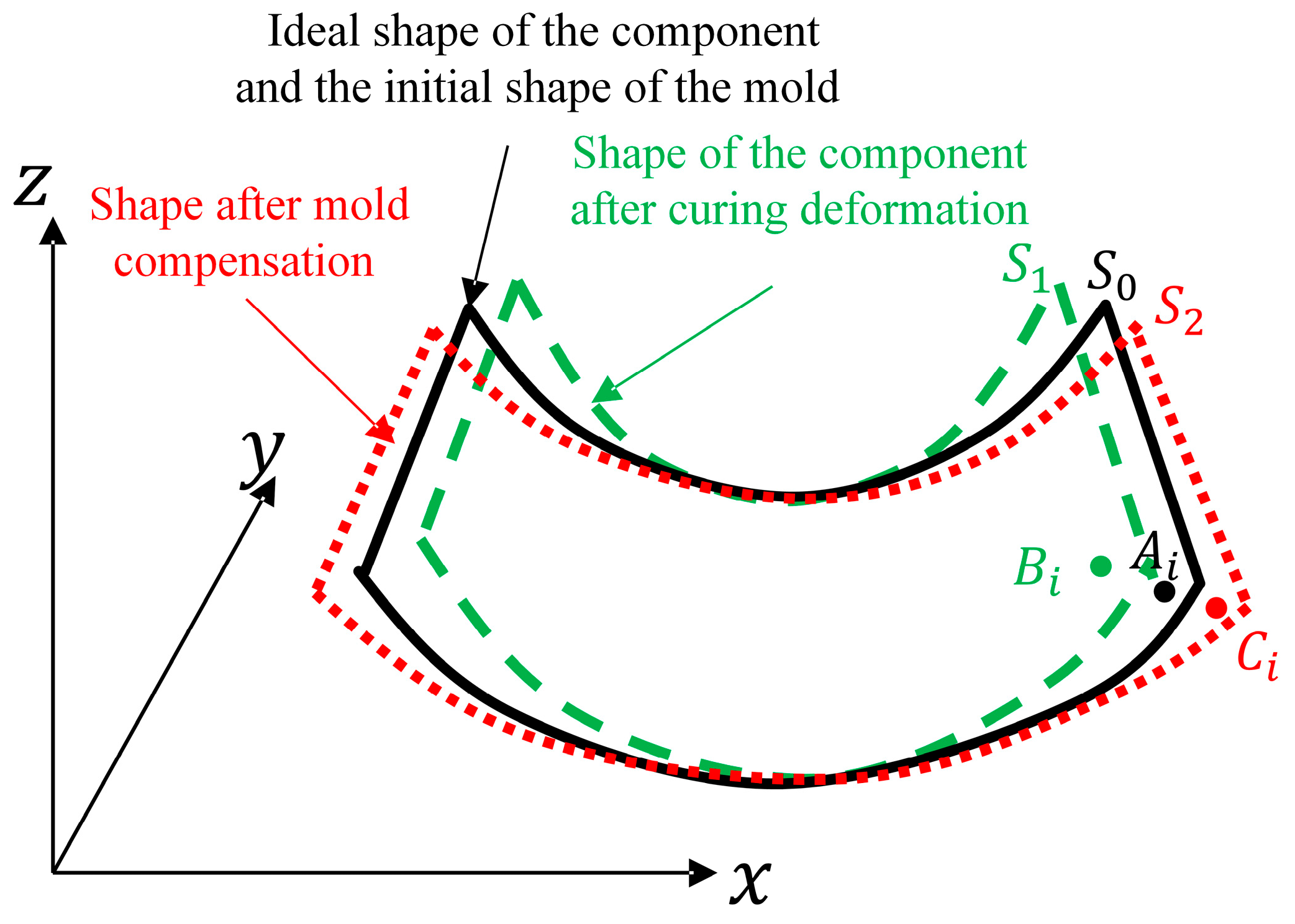
As shown in Figure 3, $S_0$ represents the initial profile of the component and the mold, which is the ideal profile of the component. And the node coordinates on the ideal surface were denoted as $A_i\left(x_i,y_i,z_i\right)$. $S_1$ represents the profile of the component after curing deformation, with the node coordinates on the surface denoted as $B_i\left({x_i}^{\prime },{y_i}^{\prime },{z_i}^{\prime }\right)$. $S_2$ represents the final profile of the compensated mold, and the node coordinates on the surface were denoted as $C_i\left({x_i}^{″},{y_i}^{″},{z_i}^{″}\right)$.

$$\left.\begin{array}{c}\Delta x={x_i}^{\prime }-x_i\\ \Delta y={y_i}^{\prime }-y_i\\ \Delta z={z_i}^{\prime }-z_i\end{array}\right\}$$

(1)

$$C_i(x^{″},y^{″},z^{″})=A_i\left(x,y,z\right)-k\left(\Delta x+\Delta y+\Delta z\right)$$

(2)

All nodes on the lower surface of the CFRP component in the finite element model were processed according to the compensation equation $k\overrightarrow{A_i{B}_i}=\overrightarrow{C_i{A}_i}$ (where k is the compensation factor, taken as 1 for the convenience of this study). The set of all compensated nodes $V_c=\left\{C_i\left(x_i^{\prime \prime },y_i^{\prime \prime },z_i^{\prime \prime }\right)\left|i=\mathrm{1,2},\dots ,n\right.\right\}$ (where n is the total number of nodes) was fitted to a new surface, which was used as the new mold profile. The carbon fiber prepreg was laid on the mold with the new profile, and the cured CFRP component was checked to determine whether the condition $\left|\overrightarrow{B_{i}A}\right|\le \xi$ (where $\xi$ is the dimensional accuracy of the part) was satisfied. The profile $S_2$ was considered as the final mold configuration when this condition was satisfied. In contrast, the optimization process of profile compensation for the mold was repeated until the accuracy of the cured CFRP component met the accuracy requirements.

(2)

Compensation process in the normal direction

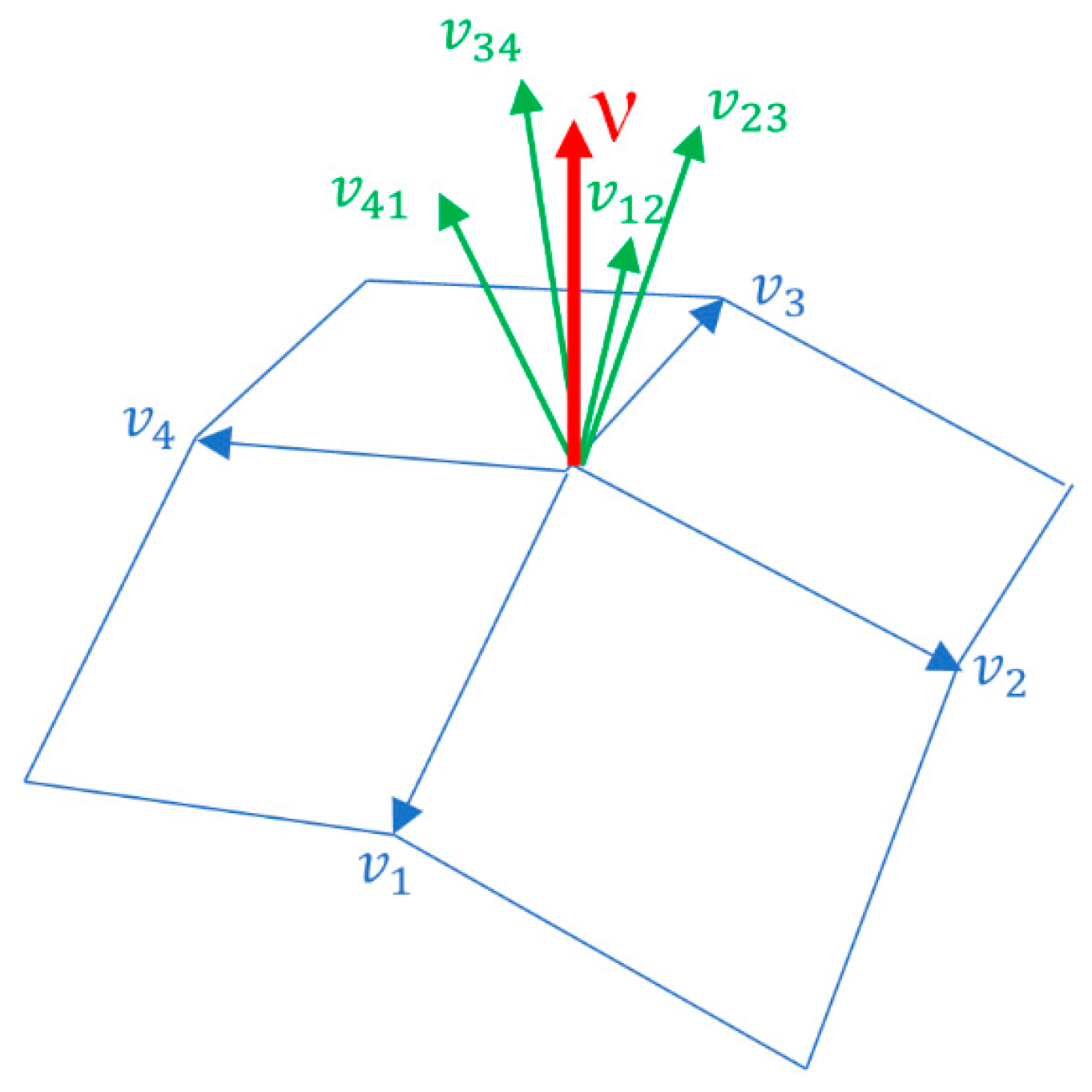
In normal direction compensation, the four mesh elements shared by each node were first identified, and the normal vectors of these elements were calculated. Next, the normal vector of each quadrilateral element was computed from three of its nodes, owing to the planar nature of the hexahedral mesh. Finally, these element vectors were aggregated to determine the normal direction for each node. The normal vectors of adjacent elements were summed and normalized to yield the nodal normal vector, as depicted in Figure 4, where, $v_1,v_2,v_3,{\mathrm{a}\mathrm{n}\mathrm{d}v}_4$ denote the four edges that form a node; $v_{12}$ represents the normal vector of the plane formed by $v_1\mathrm{a}\mathrm{n}\mathrm{d}{v}_2$; $v_{23}$ represents the normal vector of the plane formed by $v_2\mathrm{a}\mathrm{n}\mathrm{d}{v}_3$; $v_{34}$ denotes the normal vector of the plane formed by $v_3\mathrm{a}\mathrm{n}\mathrm{d}{v}_4$; $v_{41}$ represents the normal vector of the plane formed by $v_4\mathrm{a}\mathrm{n}\mathrm{d}{v}_1$; and $v$ is the vector sum of $v_{12},v_{23},v_{34},{\mathrm{a}\mathrm{n}\mathrm{d} v}_{41}$, the normal vector of the node.

The normal vector of each node is $v_i(a,b,c)$, and the compensated coordinates $C_i\left({x_i}^{″},{y_i}^{″},{z_i}^{″}\right)$ of each node are computed as follows:

$$\left.\begin{array}{c}{x}^{″}=x-{\displaystyle \frac{k\Delta x·a}{\sqrt{a^2+b^2+c^2}}}\\ y^{″}=y-{\displaystyle \frac{k\Delta y·b}{\sqrt{a^2+b^2+c^2}}}\\ z^{″}=x-{\displaystyle \frac{k\Delta z·c}{\sqrt{a^2+b^2+c^2}}}\end{array}\right\}$$

(3)

Based on the above algorithm, a MATLAB™ (2022) script was developed to implement the compensation process. For the process of connecting direction compensation, only the deformation and compensation vector along this direction were calculated for each node, and the deformation was applied along the connection direction of the corresponding node. In contrast, for normal direction compensation, the normal vector of each node was required, and the deformation was subsequently applied along the normal direction to complete the compensation.

3. Numerical Analysis of CFRP Curing Deformation

Temperature variations and exothermic heat from the curing reaction influenced the temperature distribution within the CFRP component. The complex temperature distribution resulted in varying degrees of curing across different locations of the component. Therefore, uneven stress distribution during cooling and stress release during demolding resulted in component deformation, a phenomenon particularly pronounced in large, curved composite structures. A numerical model of the curing deformation for CFRP components was established, and the predicted results were then validated through experiments.

3.1. Curing Deformation Prediction for CFRP Components

3.1.1. Construction of a Finite Element Model

The curing deformation model for CFRP components was established using Abaqus^TM (2022), with the following as primary considerations: ① The exothermic heat of the curing reaction. During the curing process, the resin underwent an exothermic curing reaction, which caused temperature variations within the mold. ② Non-uniform thermal expansion coefficients. The resin curing reaction kinetics model was incorporated into the thermal field simulation to simulate the thermo-chemical–mechanical coupled heat transfer process for the CFRP component. ③ CFRP curing shrinkage. When the curing degree failed to reach the gel point, both the curing shrinkage coefficient and curing shrinkage strain remained unchanged. In contrast, curing shrinkage and curing strain then commenced. The detailed information on the constitutive materials, curing kinetics equations, and resin cure parameters could be found in Sections S1–S4 of the Supplementary Materials.

The T700/5051 CFRP laminates were fabricated with a stacking sequence of ${\left[45/0/-45/0/45/90/-45/0/45/-45\right]}_s$. The basic material parameters [34] were $v_m=0.35$, $CH{T}_1=0.6\times {10}^{-6}$, $CH{T}_2=28\times {10}^{-6}$, $E_{f1}=139000 \mathrm{MPa}$, $E_{f2}=8150 \mathrm{MPa}$, $G_{f12}=4430 \mathrm{MPa}$, $G_{f23}=3550 \mathrm{MPa}$, $v_{f12}=0.2$, and $v_{f13}=0.2$, and for 6061 aluminum $E=68900 \mathrm{MPa}$ and $v=0.33$.

The geometric model of the mold and CFRP component are shown in Figure 5. The translational and rotational displacements at the center of the lower surface were constrained to prevent rigid motion of the CFRP component. Since this location failed to coincide with a mesh node, direct constraint application was not feasible. Given that the CFRP component was centrally positioned during modeling, the constraint was applied by restraining the four surrounding mesh nodes at the center. As shown in Figure 5, the yellow circle marks the center of the component, and the four red points denote the nodes closest to its center. The employed element was a 3D stress element. The mold was meshed with C3D4 four-node linear tetrahedral elements, while the CFRP laminates used C3D8 eight-node linear hexahedral elements.

3.1.2. Simulation Results for the CFRP Component

The simulation model was developed to simulate the curing and demolding processes for CFRP components. The prediction outcome is shown in Figure 6. Deformation at the center of the CFRP component was minimal after demolding, while maximum deformation occurred at the four top corners, with a maximum of 3.289 mm.

3.2. Experimental Verification

The prepreg was first cut to specified dimensions using a cutting machine, then hand-laid with strict alignment to the mold datum. Upon completing the layup process, the component underwent vacuum bagging to eliminate air pockets and surplus resin, followed by curing under programmed thermal cycles.

After the cured CFRP was removed and demolded, the component was measured to obtain deformation data. The point cloud data acquisition system consisted of a Handyscan700 3D scanner (resolution: 0.05 mm, accuracy: 0.025 mm), a computer processing system, and point cloud software for profile scanning. The point cloud scanning process for CFRP components after demolding is shown in Figure 7.

The imported point cloud model was aligned with the ideal plane to achieve the best fit. The profile deviations between CFRP components and the ideal profile are presented in Figure 8. The comparison of finite element deformation (Figure 6) and the scanning point cloud showed that the deformation trends of the experimental and simulated results were consistent. Specifically, the deformation at the center of the component was minimal, while the largest deformation occurred at the four corners.

The deformation of the CFRP component after curing manifested as warping at the four top corners, and the maximum deformation occurred at one of the top corners.

Table 1. Comparison of simulation and experimental results for deformation at top corner.

Vertex	1	2	3	4
Simulation value	3.007 mm	3.289 mm	3.024 mm	3.252 mm
Experimental value	2.926 mm	3.046 mm	2.820 mm	2.964 mm
Error	0.081 mm	0.243 mm	0.204 mm	0.288 mm
Relative error	2.7%	7.3%	6.7%	8.8%

presents the comparison results for the deformation at the four corners of the CFRP component after curing. The results indicated a maximum deviation of 0.288 mm between the experimental measurements and simulated predictions, demonstrating the accuracy of the proposed CFRP curing deformation prediction method. Given the negligible deformation observed, curing process parameter optimization was deemed unnecessary, thus allowing for the direct study of profile compensation for the mold.

3.3. Analysis of Inverse Deformation Compensation

3.3.1. Deformation Compensation for the CFRP Component

The normal inverse deformation compensation method was applied to validate the effectiveness of the normal compensation method. The coordinates of all lower surface nodes for the CFRP component were extracted from the inp file generated via Abaqus^TM post-processing. The node coordinates of the compensated surface were derived by applying the normal compensation algorithm implemented in MATLAB™, then the node data were imported into CATIA for fitting and extension to generate the new forming mold profile. The updated mold was used for curing simulations and experiments on the CFRP component, yielding both predicted and experimental values of curing deformation. The compensation process for the CFRP component is shown in Figure 9.

3.3.2. Results After Compensation

The compensated mold was used to simulate the curing and deformation processes for the CFRP component. The simulation results for curing deformation for the CFRP component after mold profile compensation are presented in Figure 10.

The same CFRP, layup method, and curing process were adopted for the curing and molding experiments after compensation. Figure 11 illustrates the point cloud scanning process of the compensated CFRP components. The profile deviations between CFRP components and the ideal profile are shown in Figure 12. The comparison of the simulated and experimental results after compensation showed that the maximum deformation in the simulation was 0.8273 mm, differing by 0.0953 mm from the experimental value of 0.732 mm. The compensation method reduced the curing deformation from 3.252 mm to 0.8273 mm, representing a 74.56% reduction.

4. Optimization of Curing Process Parameters Based on BP Neural Network and GA

Given the unclear relationship between process parameters and curing deformation, extensive simulations were conducted to generate sufficient data for establishing a mapping between curing parameters and the deformation. This mapping was subsequently applied to optimize the curing process parameters.

4.1. Construction of Curing Deformation Prediction Model Based on BP Neural Network

4.1.1. Sample Acquisition and Normalization

To avoid inconsistencies in the orders of magnitude for input variables and to reduce the occurrence of erroneous sample data, the samples were normalized to a [0, 1] range prior to neural network training. Afterward, the output vectors were denormalized to restore them to their actual values as follows:

$$z={\displaystyle \frac{x-x_{min}}{x_{max}-x_{min}}}$$

(4)

where $x_{max}\mathrm{a}\mathrm{n}\mathrm{d}{x}_{min}$ represent the maximum and minimum values of $x_i$, respectively, and z represents the normalized value of variable $x_i$.

The input parameters are shown in Figure 13, where $a_1/\left(°\mathrm{C}·\mathrm{m}\mathrm{i}\mathrm{n}\left(\right)\right)$ is the rate during the first heating process, $a_2/\left(°\mathrm{C}·\mathrm{m}\mathrm{i}\mathrm{n}\left(\right)\right)$ is the rate during the second heating process, $t_1/\mathrm{m}\mathrm{i}\mathrm{n}$ is the time of the first holding platform, $t_2/min$ is the time of the second holding platform, $T_1/°\mathrm{C}$ is the temperature of the first holding platform, and $T_2/°\mathrm{C}$ is the temperature of the second holding platform. The output parameter deform represents curing deformation, and $T_{cure}$ denotes total curing time. The sample data are detailed in Appendix A.

4.1.2. Optimization Results

The input test set was processed with the established neural network, and the results were then inversely normalized. These inverted normalized results were compared with the real output values of the test set for error analysis. The prediction results are shown in Figure 14. The predicted and simulated values of curing deformation are shown in

Table 2. Comparison of predicted and simulated values of curing deformation.

No.	Curing Deformation Test Value/mm	Curing Deformation Predicted Value/mm	Relative Error
1	7.303	7.617	4.3%
2	9.548	9.996	4.7%
3	7.279	7.529	3.4%
4	7.531	7.594	0.8%
5	7.347	7.740	5.3%
6	8.082	7.943	1.7%
7	10.693	10.332	3.4%
8	8.293	8.018	3.3%

, and the predicted and simulated values of curing time are shown in

Table 3. Comparison of predicted and simulated values of curing time.

No.	Curing Time Test Value/s	Curing Time Predicted Value/s	Relative Error
1	16,962	16,351	3.6%
2	15,415	15,889	3.1%
3	15,565	14,846	4.6%
4	14,806	14,783	0.2%
5	14,295	14,510	1.5%
6	16,578	15,889	4.2%
7	20,192	21,136	4.7%
8	16,377	15,974	2.5%

.

The graphical error curves and data comparison results showed that the maximum error for both curing deformation and curing time between the predicted data and the test set was less than 5%, which confirmed the effectiveness of the neural network in predicting curing deformation and curing time.

4.2. Optimization of Curing Process Parameters Based on GA

4.2.1. Algorithm Parameter Setting

To facilitate subsequent genetic operations, the solution set of the actual problem was encoded into a representation compatible with the solution space of the genetic algorithm. In this study, binary encoding was employed to convert real-valued solutions within the solution set range into binary strings consisting of 0 and 1, which facilitated the implementation of subsequent crossover and mutation operations. To avoid the loss of valuable genes due to improper selection by the fitness function, $F_{min}$ (the minimum value of fitness) was introduced to enhance the classical roulette selection method as follows:

$$P_i^{\prime }={\displaystyle \frac{F_i-F_{min}}{{\sum }_{i=1}^{N-1\sum }{F}_i-F_{min}}}$$

(5)

A mutation operator was introduced to prevent the algorithm from converging to a local optimum during the iteration process, enabling feasible solutions selected via the selection operation to undergo mutation with a specified probability. An excessively high mutation probability causes the genetic algorithm to degenerate into a random search, while an excessively low mutation probability inhibits the generation of new individuals. Therefore, the algorithm was improved by using an adaptive crossover mutation probability. The mathematical formulation of this relationship is expressed as follows:

$$P_c=\left\{\begin{array}{cc}{\displaystyle \frac{k_1(f_{\max }-f)}{f_{\max }-f_{avg}}},& f\ge f_{avg}\\ k_2,& f<f_{avg}\end{array}\right\}$$

(6)

$$P_m=\left\{\begin{array}{cc}{\displaystyle \frac{k_3(f_{\max }-f^{\prime })}{f_{\max }-f_{avg}}},& f^{\prime }\ge f_{avg}\\ k_4,& f^{\prime }<f_{avg}\end{array}\right\}$$

(7)

where $P_c\mathrm{a}\mathrm{n}\mathrm{d}{P}_m$ are the crossover probability and mutation probability, respectively; $f_{max}\mathrm{a}\mathrm{n}\mathrm{d}{f}_{avg}$ refer to the maximum fitness and average fitness of the population; $f$ is the greater fitness value of the two parent individuals participating in the crossover operation; $f_{\prime }$ is the fitness value of the individuals undergoing the mutation operation; and $k_1,k_2,k_3,\mathrm{a}\mathrm{n}\mathrm{d}{k}_4$ are constants that needs to satisfy the condition $k_1<k_2$ and $k_3<k_4$. The parameter settings for the genetic algorithm are shown in

Table 4. Parameter settings for the genetic algorithm.

Population Size	Maximum Number of Generations	Generation Gap	Crossover Probability	Mutation Probability	Binary Bit Length
40	200	0.95	0.7	0.05	10

.

4.2.2. Optimization Results

As shown in Figure 15, the optimization iterations of the genetic algorithm are illustrated. These iterations demonstrated that the population progressively converged to the optimum by the 100th generation. The optimized results are presented in

Table 5. Optimization results.

Parameter Variable	Before Optimization	After Optimization	Magnitude of Change
${\mathrm{a}}_1/\left(°\mathrm{C}·\mathrm{m}\mathrm{i}\mathrm{n}\left(\right)\right)$	2	2.11	5.5%
${\mathrm{a}}_2/\left(°\mathrm{C}·\mathrm{m}\mathrm{i}\mathrm{n}\left(\right)\right)$	2	1.99	0.5%
${\mathrm{t}}_1$	1200	917	−23.58%
${\mathrm{t}}_2$	5400	1588	−70.59%
${\mathrm{T}}_1/°\mathrm{C}$	80	68	−15%
${\mathrm{T}}_2/°\mathrm{C}$	120	125	41.67%
Deformation/mm	8.834	5.253	−40.54%
${\mathrm{T}}_{\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{e}}$/s	12,300	8453	−31.28%

. The results indicated that the curing time was reduced to 8453 s, which was 31.28% lower than the curing time of 12,300 s for the original model.

5. Case Study

5.1. Curing Deformation of Large-Sized CFRP Skin

The forming mold consisted of 20 partitions along the length direction, each measuring 425 × 425 mm, and 6 partitions along the width direction, each measuring 500 × 500 mm. A curved skin with a length of 14,600 mm, a width of 4600 mm, a curvature of 5.18 × $10^{-5}$, and a thickness of 10 mm was established. The geometric model of the forming mold and the geometric model of the curved CFRP component are shown in Figure 16.

The CFRP composite employed in this study was T700/5051, and the mold was fabricated from Invar steel. The performance parameters of the invar steel material are provided in

Table 6. The performance parameters of invar steel.

Performance	Value
Thermal conductivity coefficient	$11 \mathrm{W}/\left(\mathrm{m}·°\mathrm{C}\right)$
Density	$\mathsf{\rho }=8100 \mathrm{k}\mathrm{g}·{\mathrm{m}}^{-3}$
Specific heat capacity	$515 \mathrm{J}/\left(\mathrm{k}\mathrm{g}·°\mathrm{C}\right)$
Modulus	$\mathrm{E}=\mathrm{142,000} \mathrm{M}\mathrm{P}\mathrm{a}$
Poisson’s ratio	$\mathsf{\nu }=0.25$

.

As shown in Figure 17, the lower surface of the CFRP component and the upper surface of the mold were defined for contact heat transfer, while the outer surface of the composite and the outer surface of the mold were defined for convective heat transfer with the surroundings. The mold was fully constrained during curing analysis, while the central node of the composite skin was restrained during demolding analysis.

5.2. Results Analysis

The simulation results for curing deformation for the large-sized CFRP component are presented in Figure 18. It was observed that the maximum deformation of the original model was 8.834 mm, while the molding accuracy requirement specified a maximum deformation of no more than 2 mm. The difference between the simulation results and the required molding accuracy was substantial. Direct compensation would have required a large correction to the mold profile, potentially causing internal defects in the CFRP. Therefore, it was necessary to optimize the curing process parameters for further reduction in the deformation.

The simulated curing deformation obtained using the optimized process parameters is presented in Figure 19. In terms of addressing curing deformation, the first holding time (t₁) and the second holding time (t₂) exert a negative influence on deformation. Specifically, extending t₁ and t₂ contributes to reduced deformation, and a moderate increase in their durations further enhances this deformation-reducing effect. In contrast, the heating rate (a₁) exerts a positive influence on deformation: a lower a₁ helps mitigate deformation, while an increase in a₁ leads to a corresponding rise in deformation [35,36,37]. The results indicated that the optimized curing deformation was 5.153 mm, representing a 41.67% reduction compared to the original model’s curing deformation of 8.834 mm. These results demonstrated that the optimization method effectively reduced curing deformation while considering curing time. Although the optimized curing process parameters reduced the deformation of the composite skin, the resulting accuracy remained below the required threshold. As a result, additional compensation of the mold profile was required.

The coordinates of the lower surface nodes of the CFRP skin were obtained using the method described in Section 3.3. These coordinates were then compensated using the connecting direction compensation algorithm and the normal direction compensation algorithm outlined in Section 2.2. The compensated results are shown in Figure 20 and Figure 21, respectively.

The compensated results for the normal direction and connecting direction are shown in Figure 22 and Figure 23, respectively. The compensation data for large-sized components are shown in

Table 7. The compensation data.

Optimization Project	Before Optimization (mm)	After Optimization (mm)	Magnitude of Change
Curing process parameters	8.834	5.153	41.67%
Normal direction	5.153	0.9934	80.7%
Connecting direction	5.153	1.258	75.5%

. They indicated that the application of the normal direction compensation algorithm reduced the maximum curing deformation to 0.9934 mm, representing an 80.7% decrease from the original 5.153 mm and meeting the required molding accuracy for the CFRP component. However, the maximum curing deformation after applying the connecting direction compensation algorithm remained at 1.258 mm, reflecting a 75.5% reduction from the deformation before compensation. Therefore, the mold compensation in the normal direction is more effective for large-sized CFRP components.

6. Conclusions

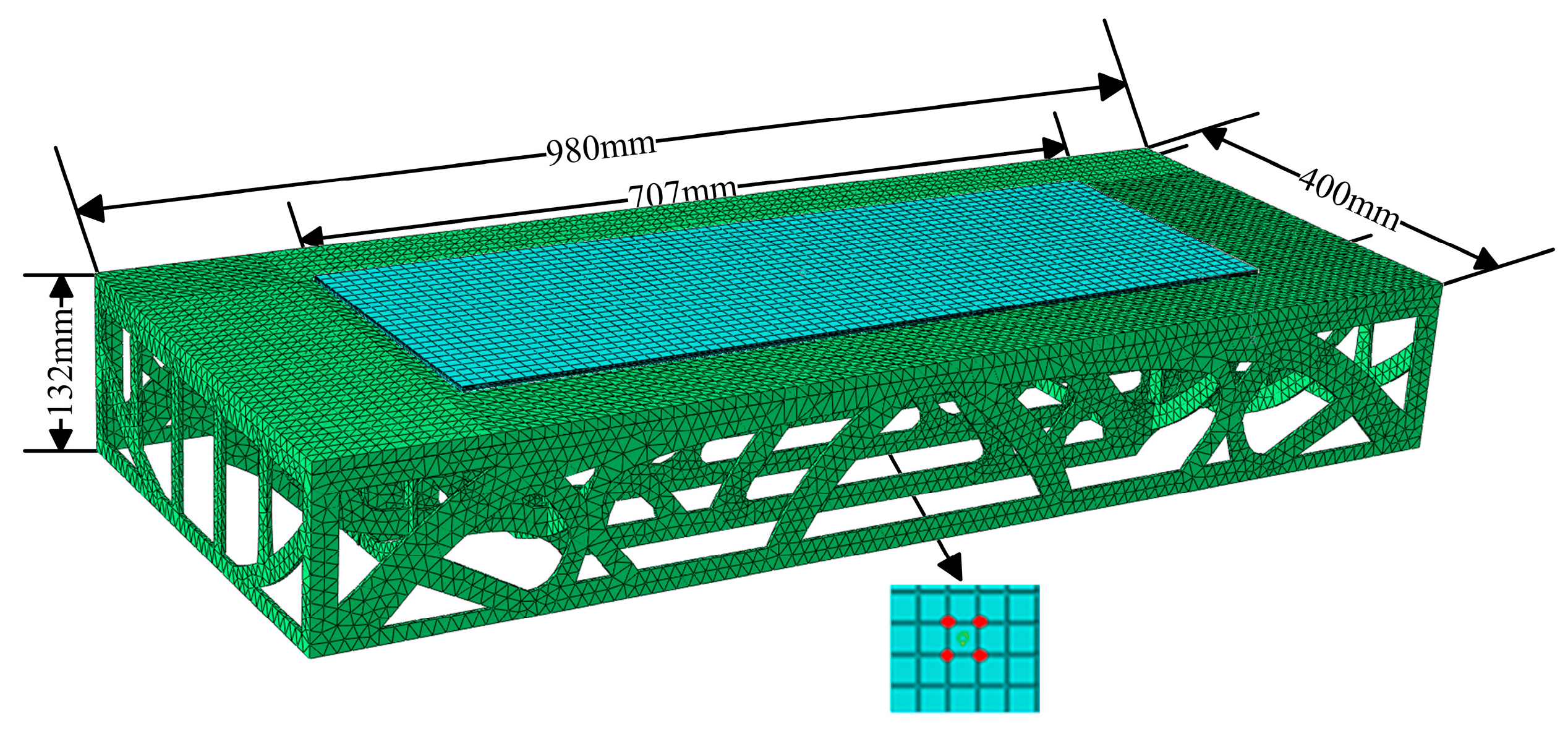
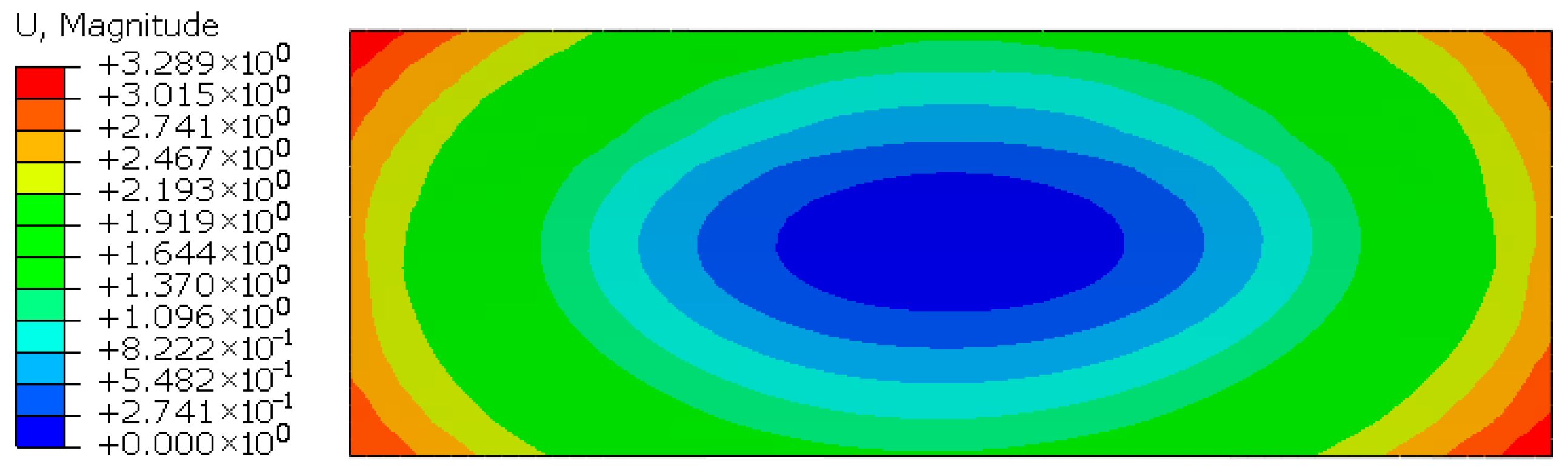
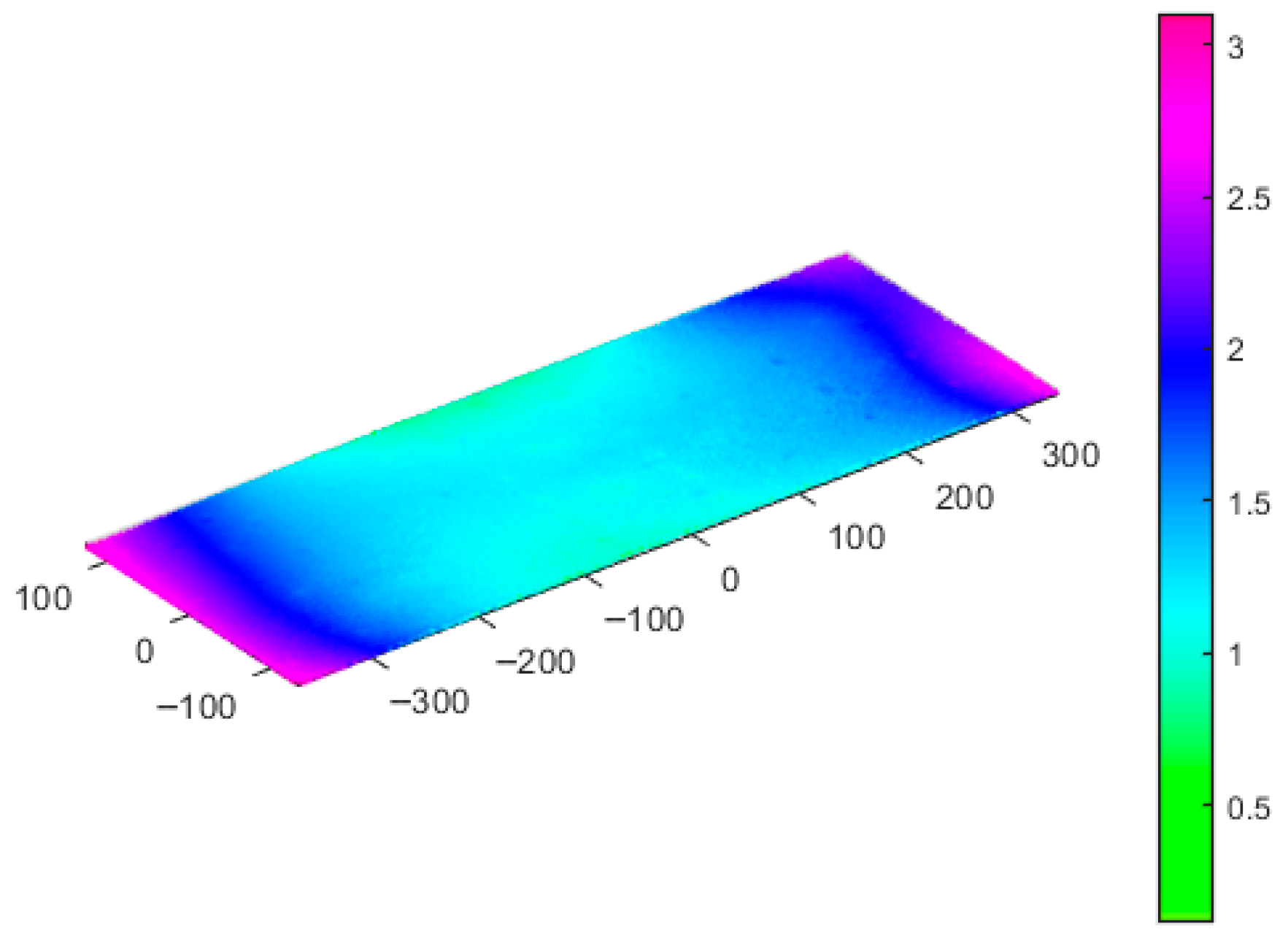
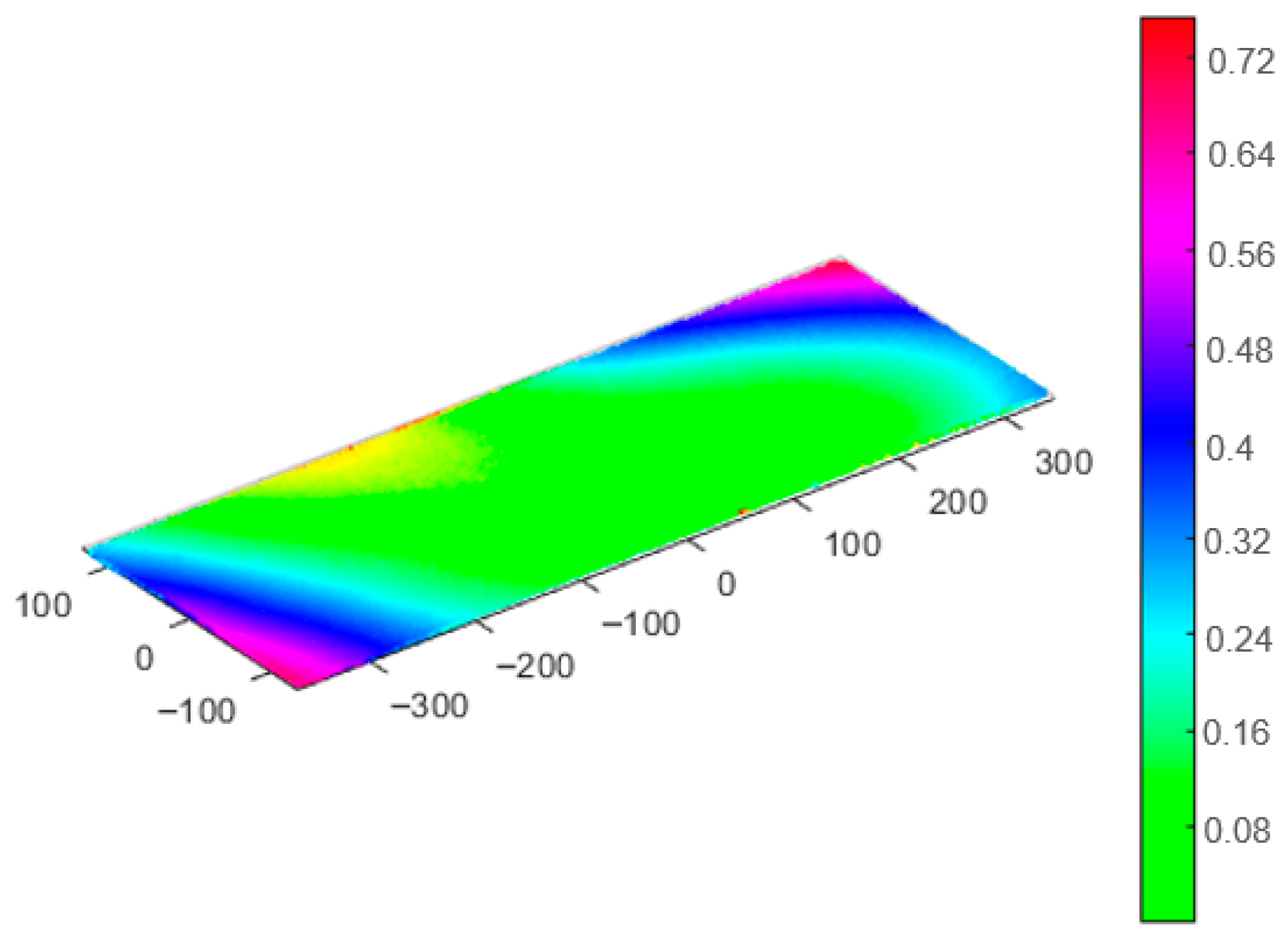
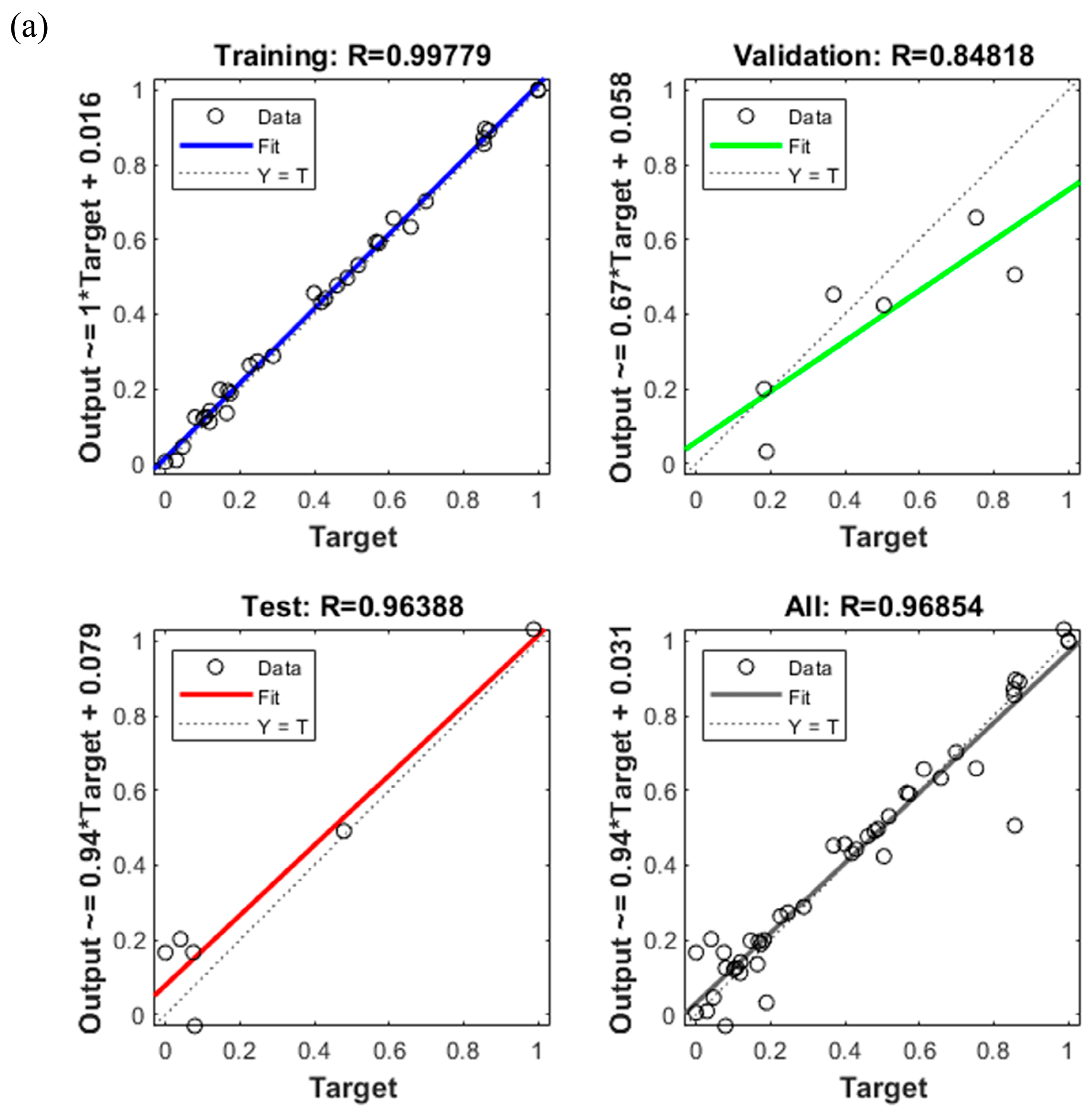
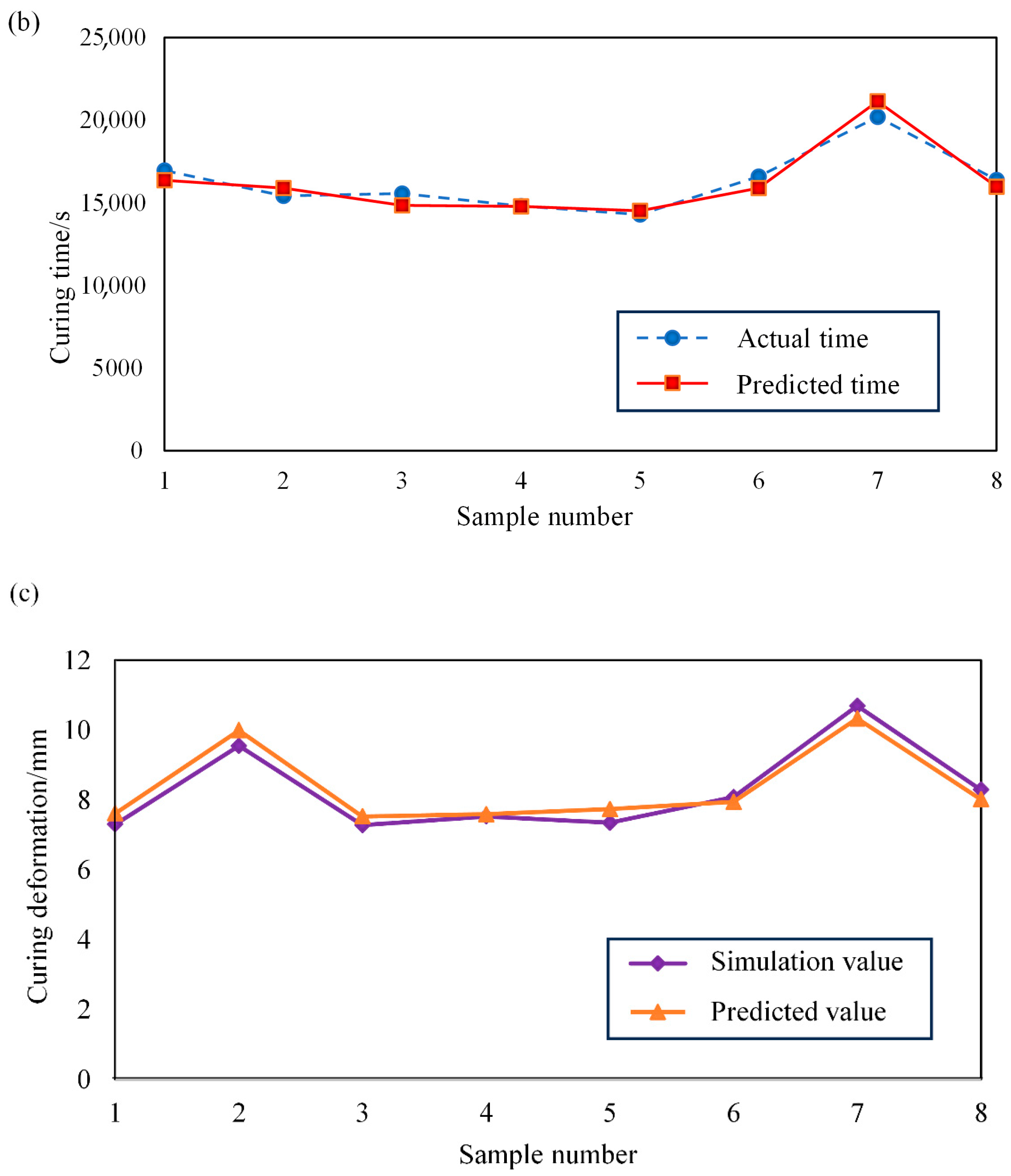
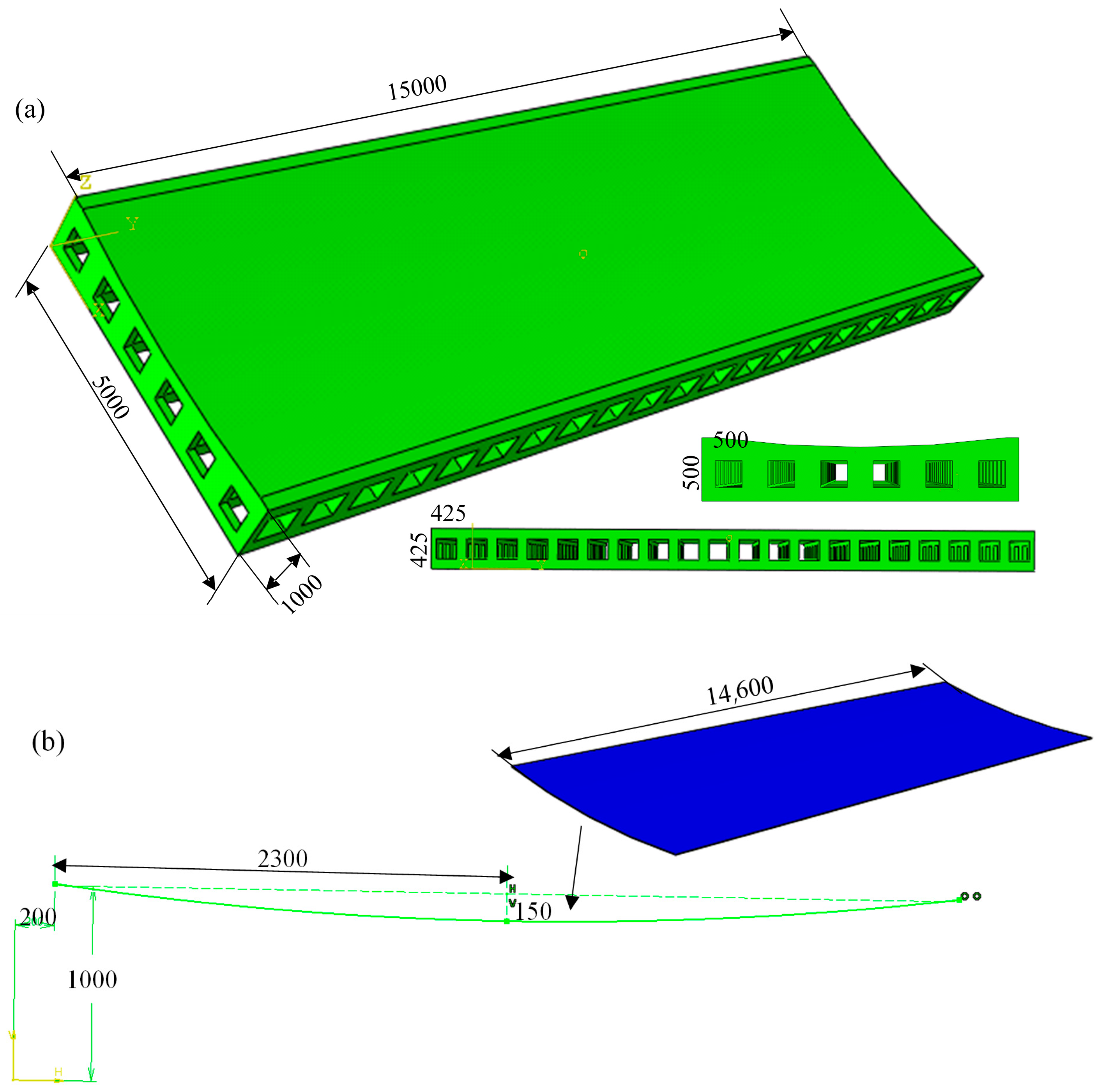
In this study, a normal direction compensation algorithm based on node deformation was proposed to establish an effective model for predicting and compensating for the deformation of large-sized CFRP components. Initially, the compensation process and the mold profile compensation algorithm based on node deformation were introduced. Subsequently, a finite element model was established to analyze the curing deformation of small-sized CFRP components and validated with a small-sized test piece. A maximum deformation of 3.252 mm was predicted by the numerical simulation, compared to an experimental measurement of 2.964 mm, yielding a deviation of 0.288 mm. The results validate the accuracy of the deformation prediction model. Next, a neural network model capturing the relationship between process parameters and curing deformation was established. A multi-objective optimization of the curing process parameters was conducted using the neural network model in combination with a genetic algorithm, with curing deformation and curing time both taken into consideration. Finally, a simulation model was developed to predict the curing deformation of 15 m CFRP components. The maximum deformation after optimization was reduced to 5.153 mm, representing a 41.67% reduction relative to the value prior to optimization. Further compensation showed that the maximum deformation in the normal direction after compensation was 0.9934 mm, demonstrating a significantly better compensation effect compared to the connection direction. Although the curing process was effectively simulated and deformation was controlled, certain limitations persisted, including limited simulation datasets and insufficient experimental validation for large-sized components. Most existing studies focus solely on curing deformation while neglecting deformation induced by demolding. Further research is needed to integrate demolding forces and methods into curing deformation analysis, thereby improving model accuracy for large CFRP components and enabling more precise deformation prediction.