Prediction and Optimization of Interference Fit Level in Slug Riveted Structure with Deep Learning Enhanced Genetic Algorithm
Abstract
1. Introduction
2. Basic Prediction and Optimization Framework
2.1. Modeling Process
2.2. Analysis of Process Parameters
2.3. Construction of Regression Model
2.4. Parameter Optimization Design
3. Prediction and Optimization Process of Interference Fit Level
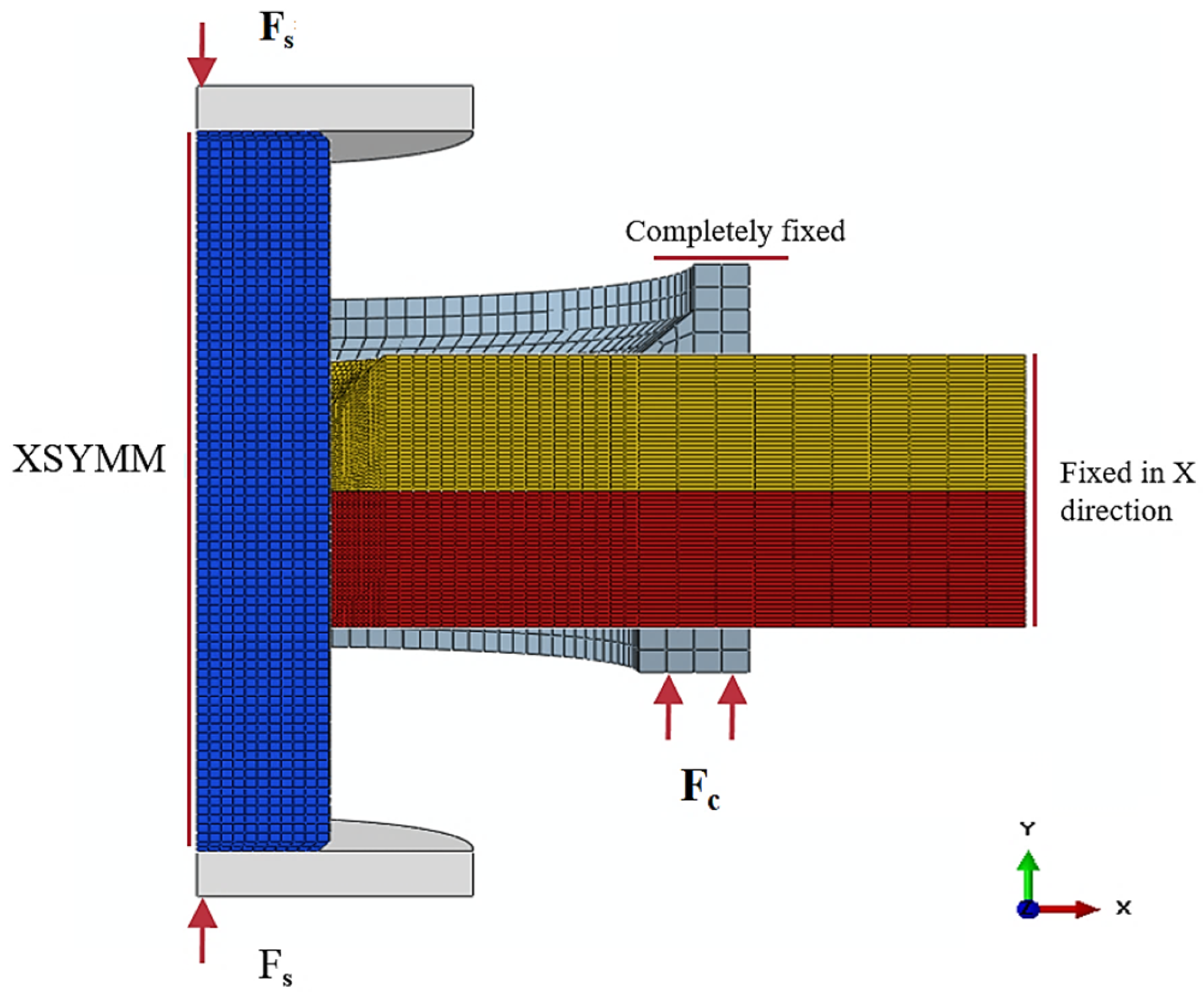
3.1. Modeling of FEM
3.2. Orthogonal Experiment Design
3.3. Construction of DNN Model
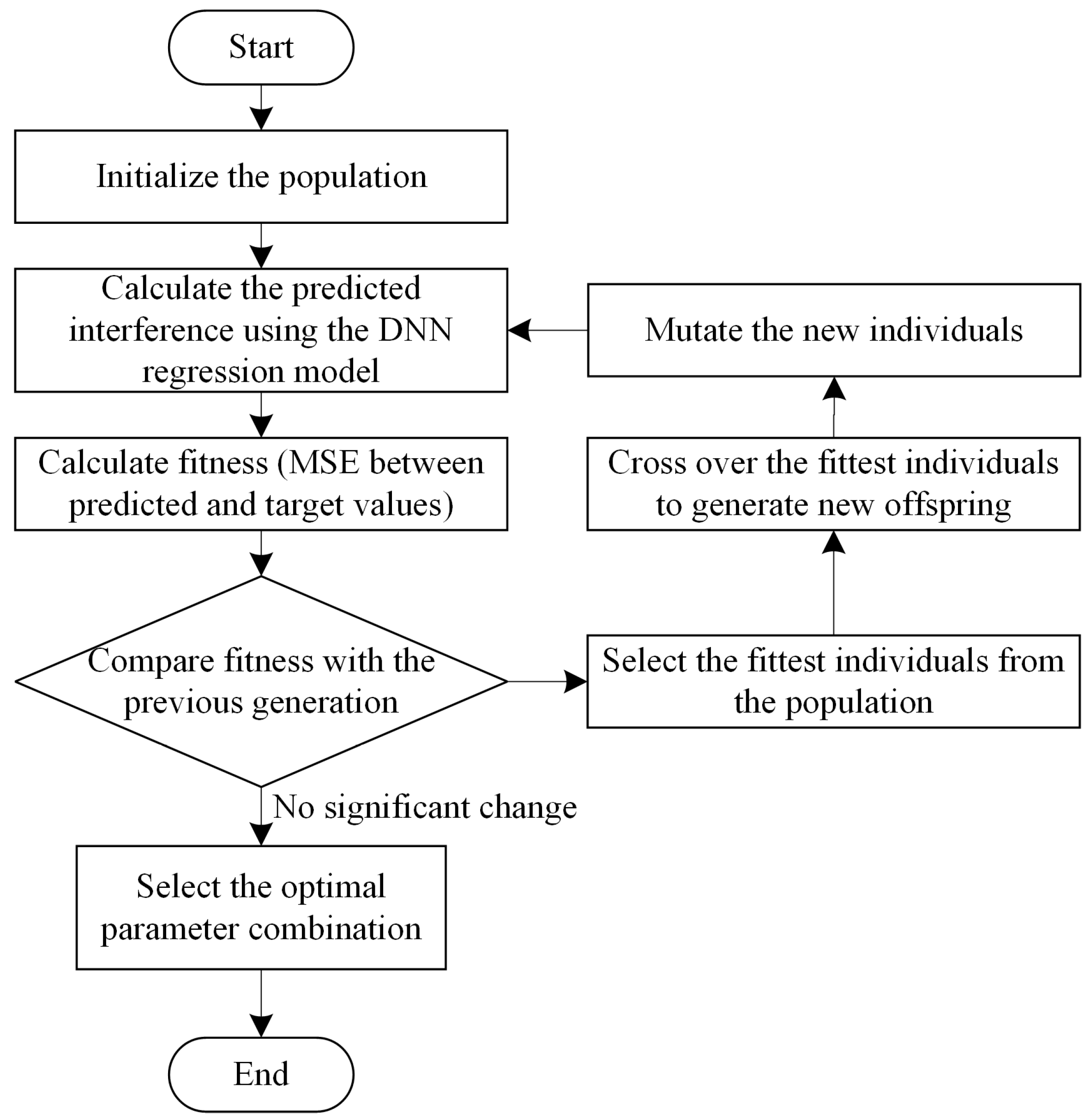
3.4. GA Optimization of Riveting Process
4. Results and Discussion
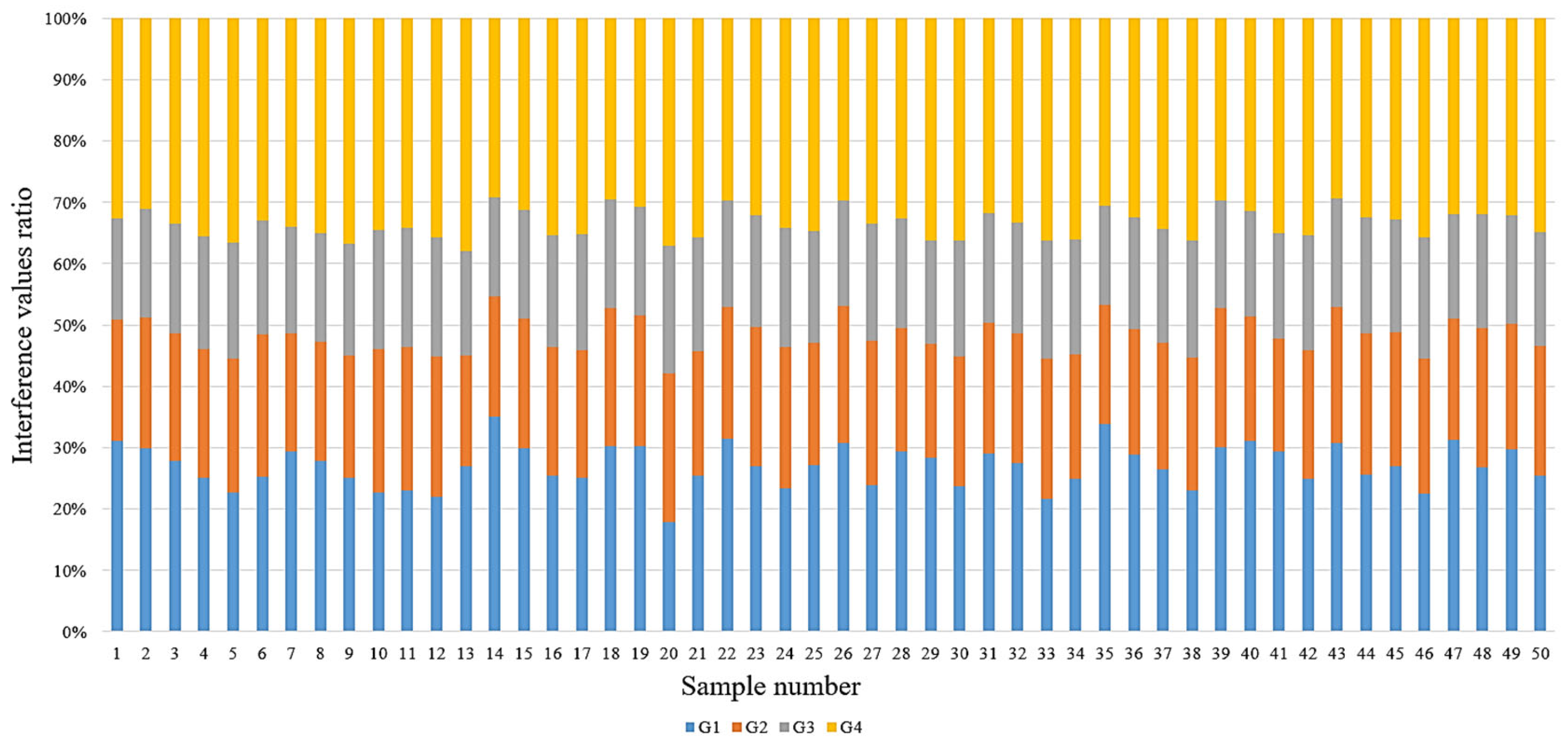
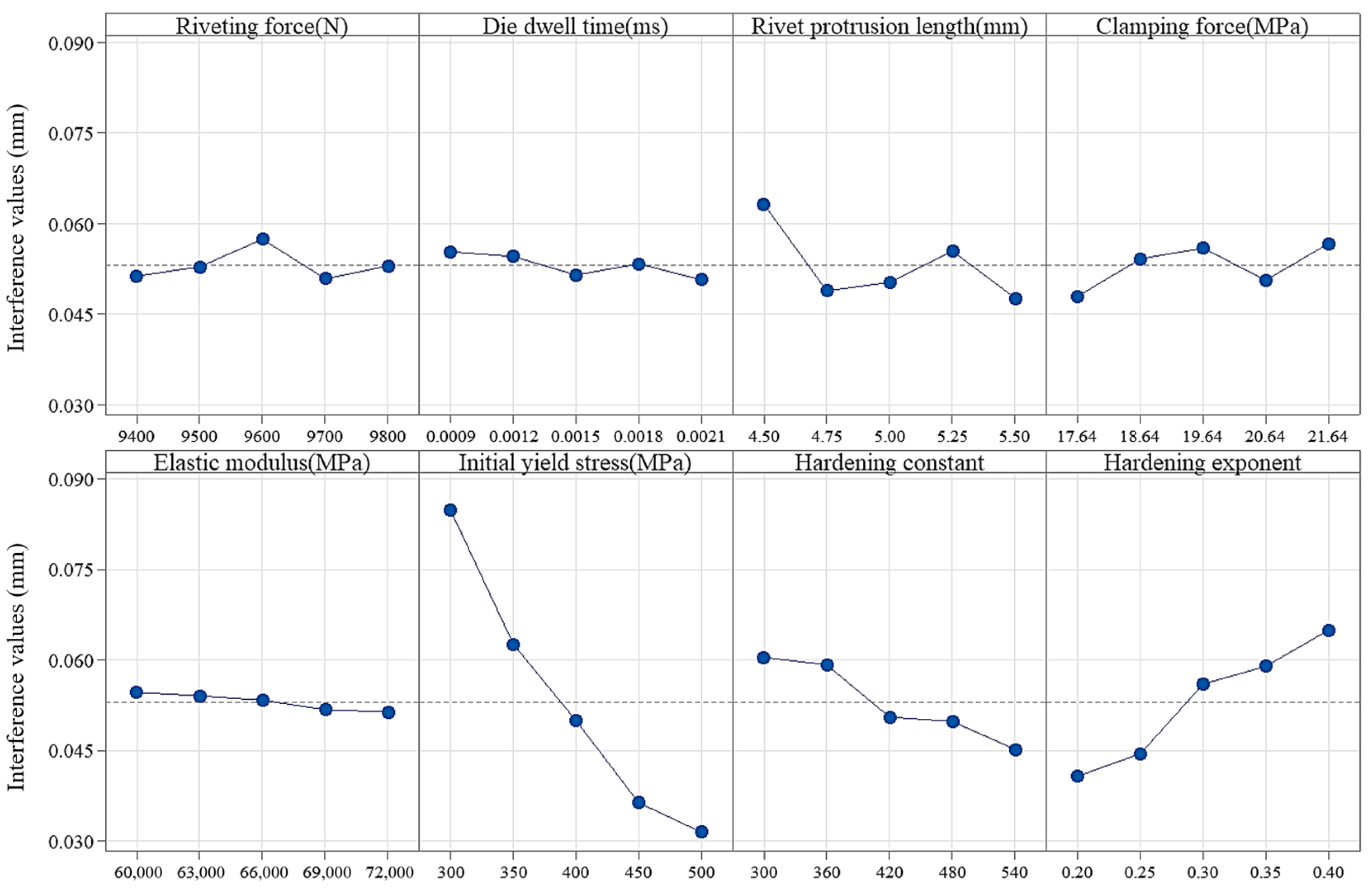
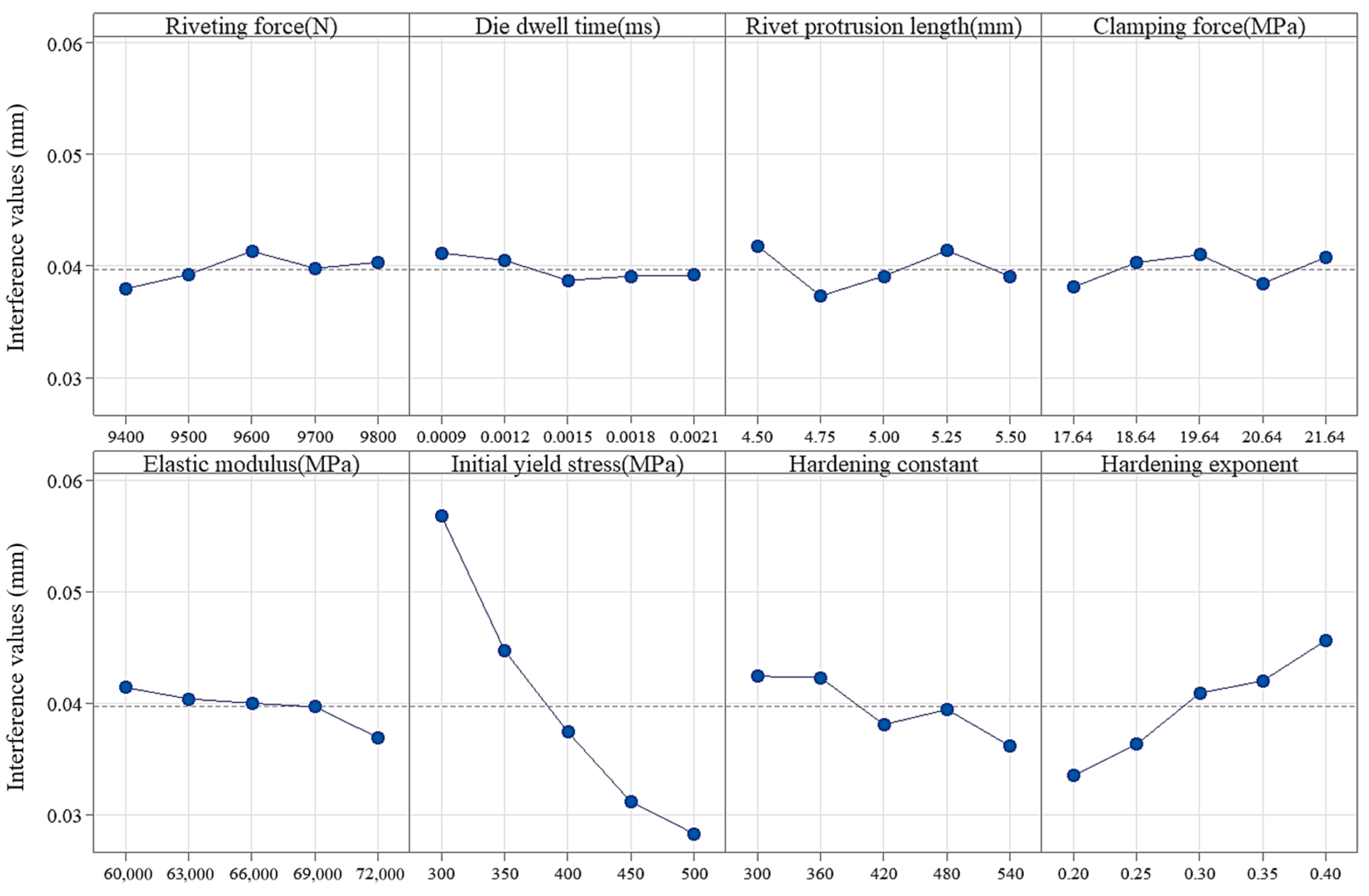
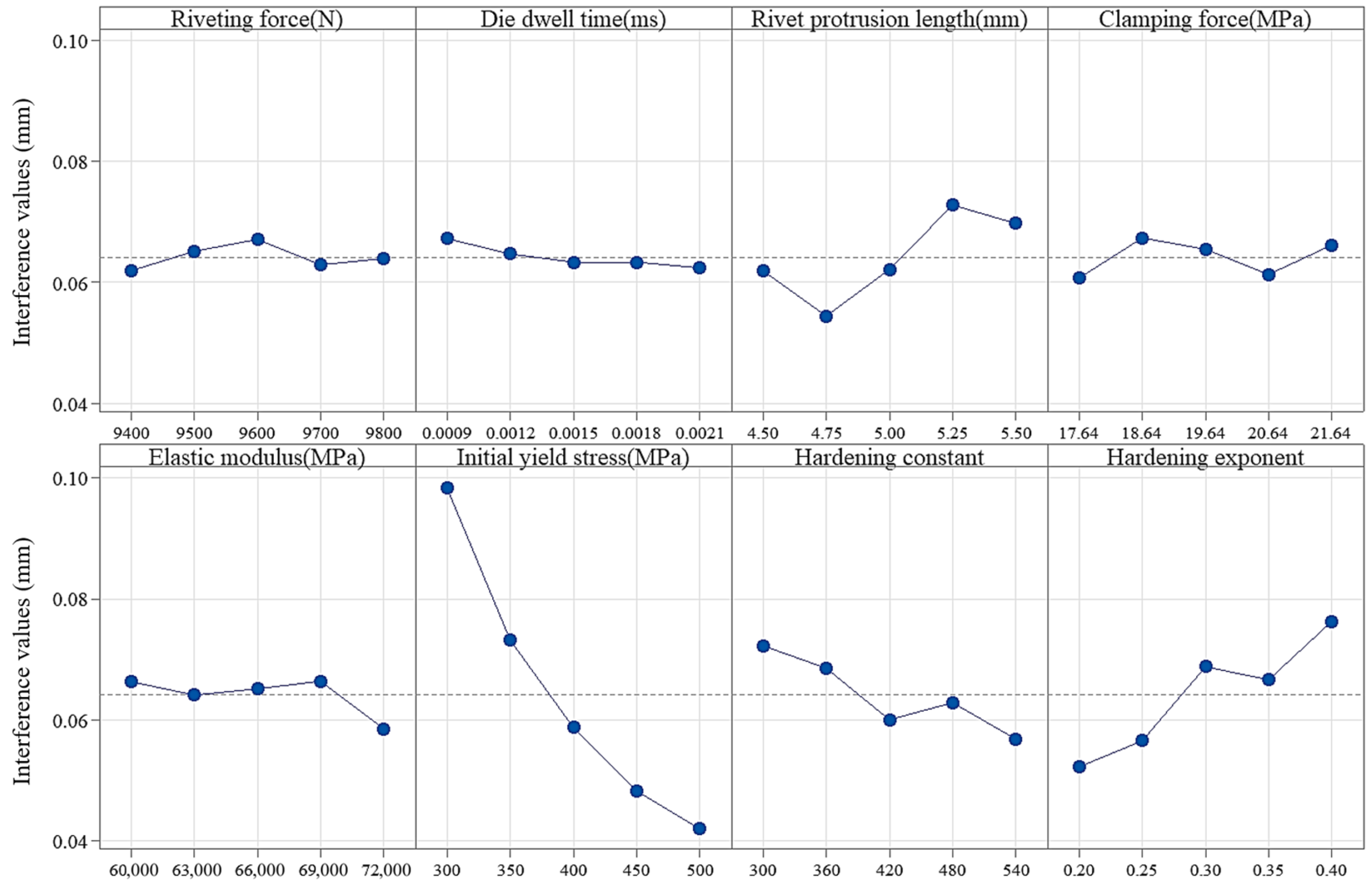
4.1. Analysis of Orthogonal Test Result
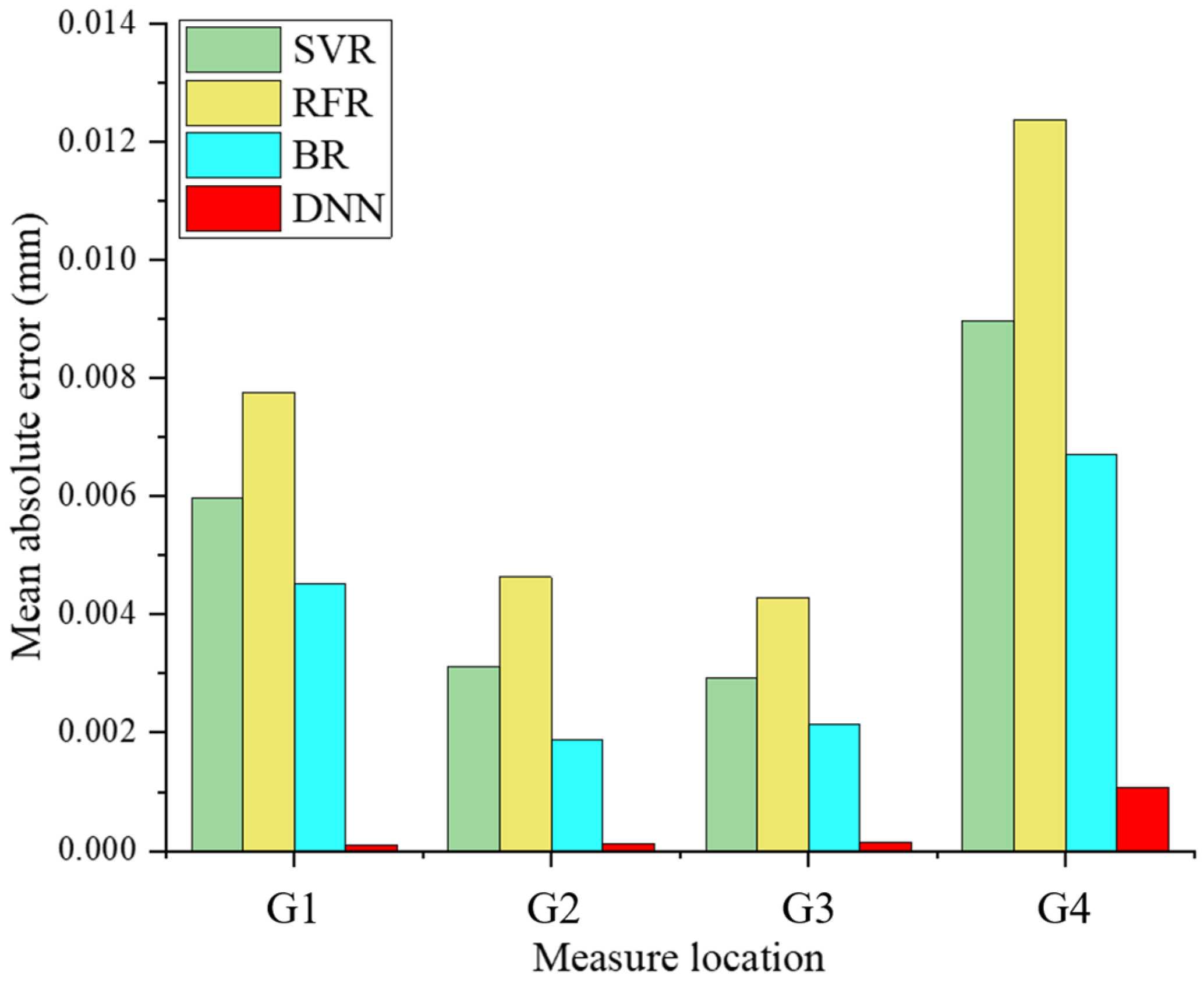
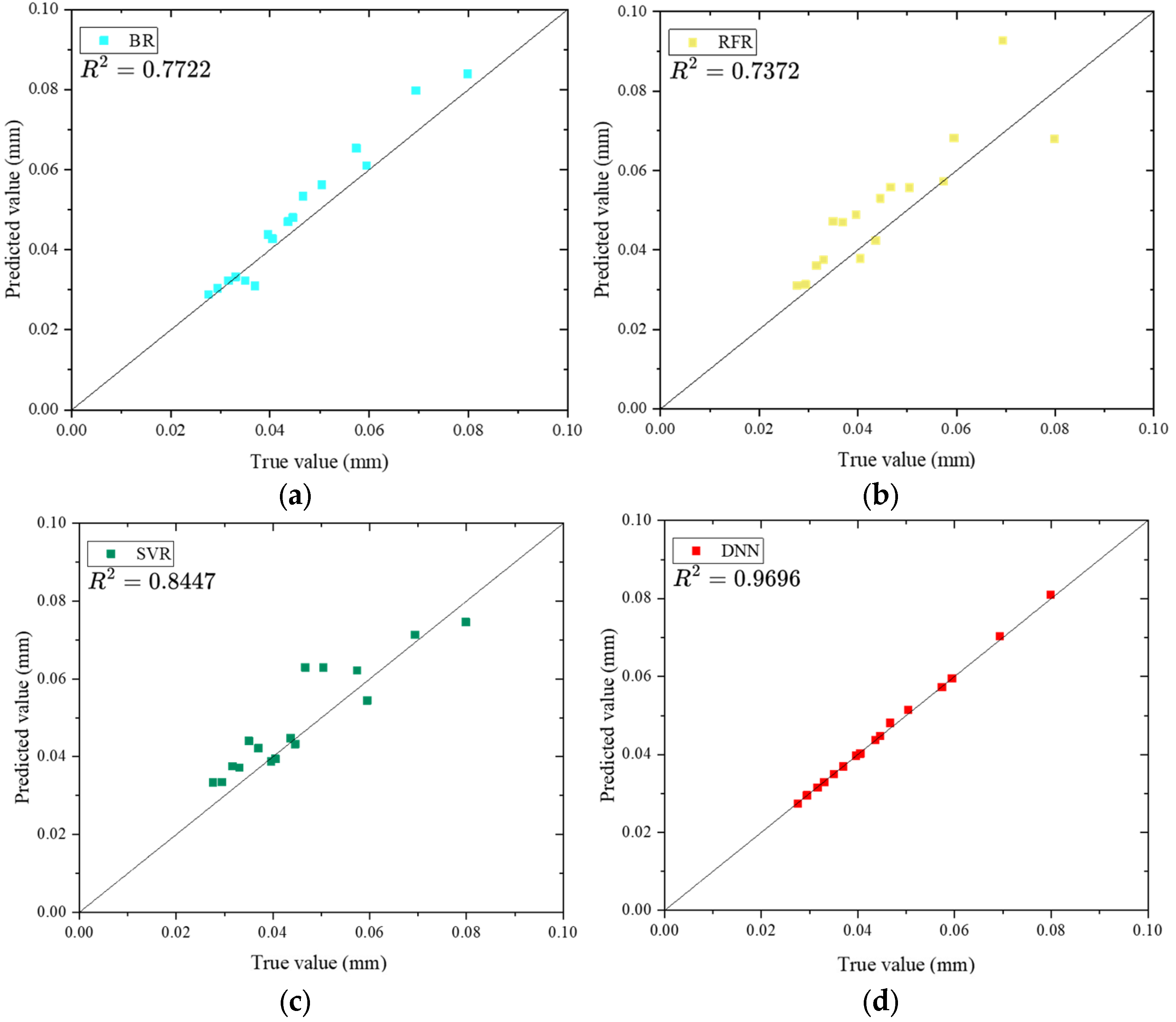
4.2. Verification of DNN Model Prediction Performance
4.3. Optimized Results of Process Parameters
5. Conclusions
- (1)
- A parametric finite element model for the riveting process of the slug rivet was established and subsequently validated through experiments. The verification demonstrated that the constructed FE model could predict riveting interference value accurately.
- (2)
- Orthogonal experiments were designed to investigate the effect of riveting parameters on the interference value. It was found that the initial yield stress of the connected plates had the most significant influence.
- (3)
- A regression prediction model based on DNN was proposed, and its predicted results were compared with three other traditional regression models (support vector machine regression, random forest regression, and Bayesian regression). The results showed that the proposed DNN regression model revealed a superior capability for fitting the multivariate nonlinear relationship between riveting process parameters and the interference value, which achieved a determination coefficient R-squared of 0.9696 and a mean absolute error of 0.00035 mm.
- (4)
- The riveting process parameters were optimized with a DNN-enhanced GA algorithm. Compared with simulated results, the target interference value showed a maximum relative error of 9.75%.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Chang, Z.; Guo, F.; Kang, Y.; Li, H.; Luo, Q.; Liu, B. Interference-Fit slug Rivet Joining Technology for Large-Aircraft Skin Panels. Aeronaut. Manuf. Technol. 2015, 34–39. [Google Scholar] [CrossRef]
- Liu, L.; Li, X.; Wang, Z.; Li, W. Experimental Investigation of an Automated Drilling-Riveting Process for slug Rivets. J. Northwestern Polytech. Univ. 2013, 31, 77–82. [Google Scholar]
- Lei, C.; Bi, Y.; Li, J.; Ke, Y. Experiment and Numerical Simulations of a Slug Rivet Installation Process Based on Different Modeling Methods. Int. J. Adv. Manuf. Technol. 2018, 97, 1481–1496. [Google Scholar] [CrossRef]
- Lv, G.; Li, C.; Zhao, C.; Jia, D.; Zhang, X.; Zhang, H.; Huang, W. Research on Theoretical Prediction Method of Rivet-Forming Quality Considering Different Riveted Structure Parameters. Int. J. Adv. Manuf. Technol. 2024, 132, 2333–2345. [Google Scholar] [CrossRef]
- Liang, Q.; Zhang, T.; Zhu, C.; Bi, Y. Effect of Riveting Angle and Direction on Fatigue Performance of Riveted Lap Joints. Coatings 2021, 11, 236. [Google Scholar] [CrossRef]
- Tian, S.; Li, C.; Dai, W.; Jia, D.; Zhang, H.; Xu, M.; Yuan, Y.; Liu, Y.; Zhang, Y. Effect of the Countersunk Hole Depth on Tensile-Tensile Fatigue Behavior of Riveted Specimens of AA2024-T3 Alloy. Eng. Fail. Anal. 2020, 115, 104639. [Google Scholar] [CrossRef]
- Derijck, J.; Homan, J.; Schijve, J.; Benedictus, R. The Driven Rivet Head Dimensions as an Indication of the Fatigue Performance of Aircraft Lap Joints. Int. J. Fatigue 2007, 29, 2208–2218. [Google Scholar] [CrossRef]
- Huang, L.; Shi, Y.; Guo, H.; Su, X. Fatigue Behavior and Life Prediction of Self-Piercing Riveted Joint. Int. J. Fatigue 2016, 88, 96–110. [Google Scholar] [CrossRef]
- Casolaro, A.; Capone, V.; Iannuzzo, G.; Camastra, F. Deep Learning for Time Series Forecasting: Advances and Open Problems. Information 2023, 14, 598. [Google Scholar] [CrossRef]
- Yang, G.R.; Wang, X.-J. Artificial Neural Networks for Neuroscientists: A Primer. Neuron 2020, 107, 1048–1070. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Belhouchet, K.; Bayadi, A.; Bendib, M.E. Artificial Neural Networks (ANN) and Genetic Algorithm Modeling and Identification of Arc Parameter in Insulators Flashover Voltage and Leakage Current. In Proceedings of the 2015 4th International Conference on Electrical Engineering (ICEE), Boumerdes, Algeria, 13–15 December 2015; pp. 1–6. [Google Scholar]
- Wang, Z.; Jia, Y.; Fu, P.; Li, H.; Song, L.; Yang, B.; Zhang, L.; Yuan, L.; Shi, K. Research on the Online Evaluation of the Straightness Error of Hydrostatic Guideways Based on Deep Learning. Int. J. Adv. Manuf. Technol. 2024, 134, 2023–2034. [Google Scholar] [CrossRef]
- Deshpande, S.; Venugopal, V.; Kumar, M.; Anand, S. Deep Learning-Based Image Segmentation for Defect Detection in Additive Manufacturing: An Overview. Int. J. Adv. Manuf. Technol. 2024, 134, 2081–2105. [Google Scholar] [CrossRef]
- Sun, H.; Cui, J.; Li, G.; Jiang, H. Genetic Sampling for Surrogate-Assisted Topology Optimization in Electromagnetic Riveting Device Design. Mater. Des. 2024, 237, 112527. [Google Scholar] [CrossRef]
- Masoudi Nejad, R.; Sina, N.; Ma, W.; Song, W.; Zhu, S.P.; Branco, R.; Macek, W.; Gholami, A. Artificial Neural Network Based Fatigue Life Assessment of Riveted Joints in AA2024 Aluminum Alloy Plates and Optimization of Riveted Joints Parameters. Int. J. Fatigue 2024, 178, 107997. [Google Scholar] [CrossRef]
- Michalewicz, Z.; Schoenauer, M. Evolutionary Algorithms for Constrained Parameter Optimization Problems. Evol. Comput. 1996, 4, 1–32. [Google Scholar] [CrossRef]
- Tomar, V.; Bansal, M.; Singh, P. Metaheuristic Algorithms for Optimization: A Brief Review. In Proceedings of the RAiSE-2023, Dubai, United Arab Emirates, 13 March 2024; p. 238. [Google Scholar]
- Shi, S.; Cheng, W.; Wang, Z. Intelligent Rivet Selection Technology for Interference-Fit Magnitude Control. Aeronaut. Manuf. Technol. 2021, 64, 74–79+85. [Google Scholar] [CrossRef]
- Choudhary, A.; Kumar, M.; Gupta, M.K.; Unune, D.K.; Mia, M. Mathematical Modeling and Intelligent Optimization of Submerged Arc Welding Process Parameters Using Hybrid PSO-GA Evolutionary Algorithms. Neural Comput. Appl. 2020, 32, 5761–5774. [Google Scholar] [CrossRef]
- Rajendran, S.; Ganesh, N.; Čep, R.; Narayanan, R.C.; Pal, S.; Kalita, K. A Conceptual Comparison of Six Nature-Inspired Metaheuristic Algorithms in Process Optimization. Processes 2022, 10, 197. [Google Scholar] [CrossRef]
- Ni, J.; Tang, W.C.; Xing, Y. Assembly Process Optimization for Reducing the Dimensional Error of Antenna Assembly with Abundant Rivets. J. Intell. Manuf. 2018, 29, 245–258. [Google Scholar] [CrossRef]
- Wu, P.; He, Y.; Li, Y.; He, J.; Liu, X.; Wang, Y. Multi-Objective Optimisation of Machining Process Parameters Using Deep Learning-Based Data-Driven Genetic Algorithm and TOPSIS. J. Manuf. Syst. 2022, 64, 40–52. [Google Scholar] [CrossRef]
- Da Costa Oliveira, A.L.; Britto, A.; Gusmão, R. Machine Learning Enhancing Metaheuristics: A Systematic Review. Soft Comput. 2023, 27, 15971–15998. [Google Scholar] [CrossRef]
- Demmel, F.; Hennet, L.; Jakse, N. The Intimate Relationship between Structural Relaxation and the Energy Landscape of Monatomic Liquid Metals. Sci. Rep. 2021, 11, 11815. [Google Scholar] [CrossRef]
- Li, X.; Chang, Z.; Gao, Y.; Huo, Y.; Song, J.; Wang, Z. Prediction of slug Rivet Interference-Fit Magnitude Using a Multivariate Nonlinear Regression Model. J. Xi’an Jiaotong Univ. 2024, 58, 157–166. [Google Scholar]
- Novac, O.-C.; Chirodea, M.C.; Novac, C.M.; Bizon, N.; Oproescu, M.; Stan, O.P.; Gordan, C.E. Analysis of the Application Efficiency of TensorFlow and PyTorch in Convolutional Neural Network. Sensors 2022, 22, 8872. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, Y.; Zhang, H. Recent Advances in Stochastic Gradient Descent in Deep Learning. Mathematics 2023, 11, 682. [Google Scholar] [CrossRef]
- Hong, D.; Chen, D.; Zhang, Y.; Zhou, H.; Xie, L. Attacking Robot Vision Models Efficiently Based on Improved Fast Gradient Sign Method. Appl. Sci. 2024, 14, 1257. [Google Scholar] [CrossRef]
- Kumar, H.; Manna, R.; Khan, D. Evaluation of Johnson–Cook Material Model Parameters for Fe–30Mn–9Al–0.8C Low-Density Steel in Metal Forming Applications. J. Mater. Sci. 2023, 58, 8118–8129. [Google Scholar] [CrossRef]
- Li, M.; Liu, Z.; Huang, L.; Chen, Q.; Tong, C.; Fang, Y.; Han, W.; Zhu, P. Automatic Identification Framework of the Geometric Parameters on Self-Piercing Riveting Cross-Section Using Deep Learning. J. Manuf. Process. 2022, 83, 427–437. [Google Scholar] [CrossRef]
- Zhu, J.; Yuan, W.; Peng, F.; Fu, Q. Interaction of Stress Relaxation Aging Behavior and Microstructural Evolution in Inconel 718 Alloy with Different Initial Stress Status. J. Mater. Sci. 2021, 56, 13814–13826. [Google Scholar] [CrossRef]

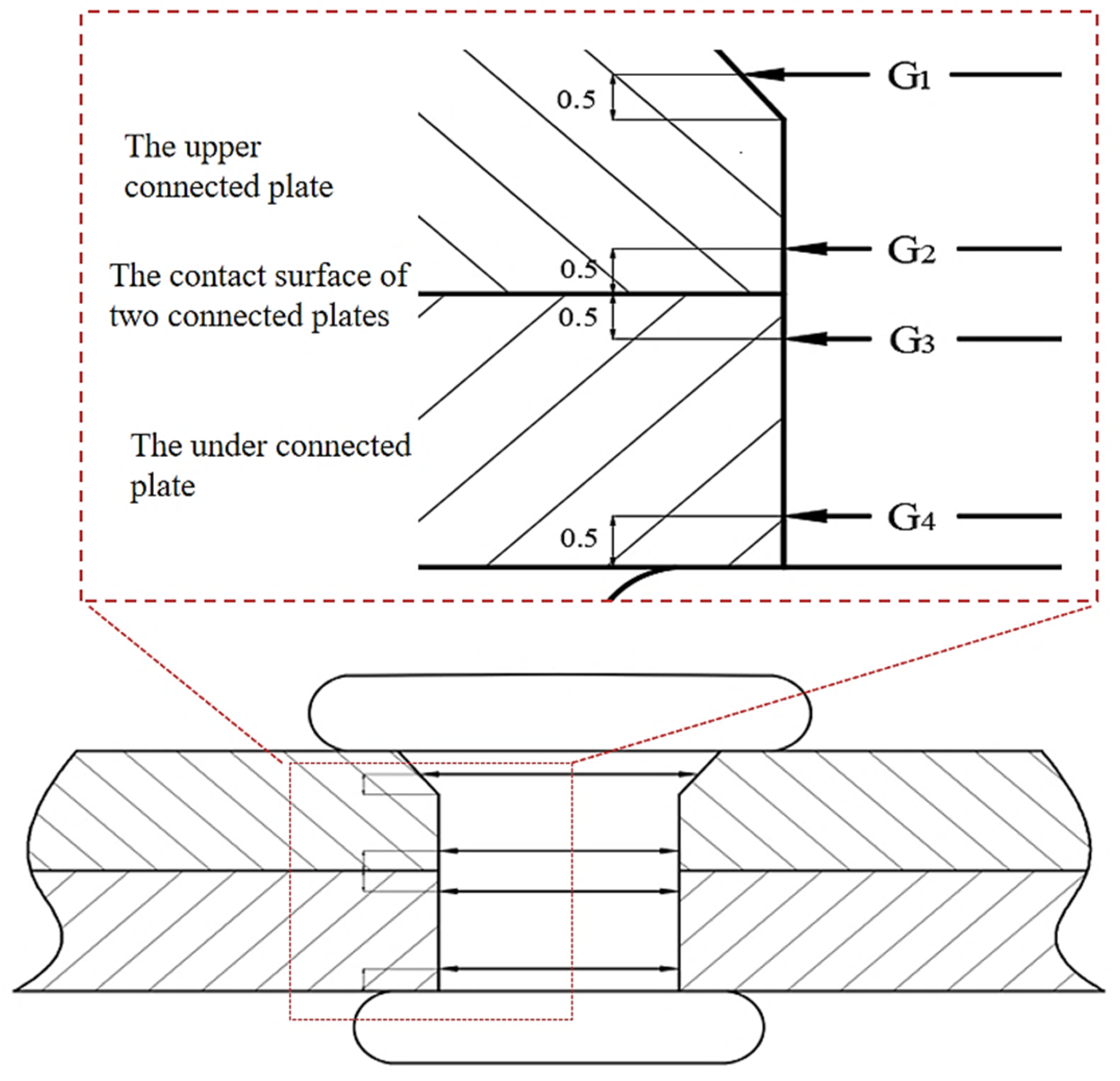



| Characterization of Interference Quantity | 2024-T351 | 7055-T76511 | ||||
|---|---|---|---|---|---|---|
| Experiment (mm) | Simulation (mm) | Error (mm) | Experiment (mm) | Simulation (mm) | Error (mm) | |
| G1 | 0.275 | 0.286 | 0.011 | 0.111 | 0.115 | 0.004 |
| G2 | 0.150 | 0.136 | 0.014 | 0.069 | 0.065 | 0.004 |
| G3 | 0.121 | 0.124 | 0.003 | 0.056 | 0.057 | 0.001 |
| G4 | 0.217 | 0.219 | 0.002 | 0.103 | 0.094 | 0.009 |
| Parameter | Elastic Modulus (MPa) | Initial Yield Stress (MPa) | Hardening Constant (MPa) | Hardening Exponent |
|---|---|---|---|---|
| Maximum value | 72,000 | 500 | 540 | 0.4 |
| Minimum value | 60,000 | 300 | 300 | 0.2 |
| Parameter | Rivet protrusion length (mm) | Riveting force (N) | Die dwell time (s) | Clamping force (MPa) |
| Maximum value | 5.5 | 9800 | 0.0021 | 21.64 |
| Minimum value | 4.5 | 9400 | 0.0009 | 17.64 |
| Riveting Force (N) | Die Dwell Time (s) | Rivet Protrusion Length (mm) | Clamping Force (MPa) | Elastic Modulus (MPa) | Initial Yield Stress (MPa) | Hardening Constant (MPa) | Hardening Exponent |
|---|---|---|---|---|---|---|---|
| 9400 | 0.0009 | 4.5 | 17.64 | 60,000 | 300 | 300 | 0.2 |
| 9400 | 0.0012 | 4.75 | 18.64 | 63,000 | 350 | 360 | 0.25 |
| 9400 | 0.0015 | 5 | 19.64 | 66,000 | 400 | 420 | 0.3 |
| 9400 | 0.0018 | 5.25 | 20.64 | 69,000 | 450 | 480 | 0.35 |
| 9400 | 0.0021 | 5.5 | 21.64 | 72,000 | 500 | 540 | 0.4 |
| 9500 | 0.0009 | 4.75 | 19.64 | 69,000 | 500 | 300 | 0.25 |
| 9500 | 0.0012 | 5 | 20.64 | 72,000 | 300 | 360 | 0.3 |
| 9500 | 0.0015 | 5.25 | 21.64 | 60,000 | 350 | 420 | 0.35 |
| 9500 | 0.0018 | 5.5 | 17.64 | 63,000 | 400 | 480 | 0.4 |
| 9500 | 0.0021 | 4.5 | 18.64 | 66,000 | 450 | 540 | 0.2 |
| 9600 | 0.0009 | 5 | 21.64 | 63,000 | 450 | 480 | 0.2 |
| 9600 | 0.0012 | 5.25 | 17.64 | 66,000 | 500 | 540 | 0.25 |
| 9600 | 0.0015 | 5.5 | 18.64 | 69,000 | 300 | 300 | 0.3 |
| 9600 | 0.0018 | 4.5 | 19.64 | 72,000 | 350 | 360 | 0.35 |
| 9600 | 0.0021 | 4.75 | 20.64 | 60,000 | 400 | 420 | 0.4 |
| 9700 | 0.0009 | 5.25 | 18.64 | 72,000 | 400 | 540 | 0.3 |
| 9700 | 0.0012 | 5.5 | 19.64 | 60,000 | 450 | 300 | 0.35 |
| 9700 | 0.0015 | 4.5 | 20.64 | 63,000 | 500 | 360 | 0.4 |
| 9700 | 0.0018 | 4.75 | 21.64 | 66,000 | 300 | 420 | 0.2 |
| 9700 | 0.0021 | 5 | 17.64 | 69,000 | 350 | 480 | 0.25 |
| 9800 | 0.0009 | 5.5 | 20.64 | 66,000 | 350 | 480 | 0.3 |
| 9800 | 0.0012 | 4.5 | 21.64 | 69,000 | 400 | 540 | 0.35 |
| 9800 | 0.0015 | 4.75 | 17.64 | 72,000 | 450 | 300 | 0.4 |
| 9800 | 0.0018 | 5 | 18.64 | 60,000 | 500 | 360 | 0.2 |
| 9800 | 0.0021 | 5.25 | 19.64 | 63,000 | 300 | 420 | 0.25 |
| 9400 | 0.0009 | 4.5 | 20.64 | 72,000 | 450 | 420 | 0.25 |
| 9400 | 0.0012 | 4.75 | 21.64 | 60,000 | 500 | 480 | 0.3 |
| 9400 | 0.0015 | 5 | 17.64 | 63,000 | 300 | 540 | 0.35 |
| 9400 | 0.0018 | 5.25 | 18.64 | 66,000 | 350 | 300 | 0.4 |
| 9400 | 0.0021 | 5.5 | 19.64 | 69,000 | 400 | 360 | 0.2 |
| 9500 | 0.0009 | 4.75 | 17.64 | 66,000 | 400 | 360 | 0.35 |
| 9500 | 0.0012 | 5 | 18.64 | 69,000 | 450 | 420 | 0.4 |
| 9500 | 0.0015 | 5.25 | 19.64 | 72,000 | 500 | 480 | 0.2 |
| 9500 | 0.0018 | 5.5 | 20.64 | 60,000 | 300 | 540 | 0.25 |
| 9500 | 0.0021 | 4.5 | 21.64 | 63,000 | 350 | 300 | 0.3 |
| 9600 | 0.0009 | 5 | 19.64 | 60,000 | 350 | 540 | 0.4 |
| 9600 | 0.0012 | 5.25 | 20.64 | 63,000 | 400 | 300 | 0.2 |
| 9600 | 0.0015 | 5.5 | 21.64 | 66,000 | 450 | 360 | 0.25 |
| 9600 | 0.0018 | 4.5 | 17.64 | 69,000 | 500 | 420 | 0.3 |
| 9600 | 0.0021 | 4.75 | 18.64 | 72,000 | 300 | 480 | 0.35 |
| 9700 | 0.0009 | 5.25 | 21.64 | 69,000 | 300 | 360 | 0.4 |
| 9700 | 0.0012 | 5.5 | 17.64 | 72,000 | 350 | 420 | 0.2 |
| 9700 | 0.0015 | 4.5 | 18.64 | 60,000 | 400 | 480 | 0.25 |
| 9700 | 0.0018 | 4.75 | 19.64 | 63,000 | 450 | 540 | 0.3 |
| 9700 | 0.0021 | 5 | 20.64 | 66,000 | 500 | 300 | 0.35 |
| 9800 | 0.0009 | 5.5 | 18.64 | 63,000 | 500 | 420 | 0.35 |
| 9800 | 0.0012 | 4.5 | 19.64 | 66,000 | 300 | 480 | 0.4 |
| 9800 | 0.0015 | 4.75 | 20.64 | 69,000 | 350 | 540 | 0.2 |
| 9800 | 0.0018 | 5 | 21.64 | 72,000 | 400 | 300 | 0.25 |
| 9800 | 0.0021 | 5.25 | 17.64 | 60,000 | 450 | 360 | 0.3 |
| G1 (mm) | G2 (mm) | G3 (mm) | G4 (mm) |
|---|---|---|---|
| 0.278743737 | 0.209038047 | 0.182087466 | 0.330130749 |
| Group | G1 (mm) | G2 (mm) | G3 (mm) | G4 (mm) |
|---|---|---|---|---|
| 1 | 0.084 | 0.063 | 0.054 | 0.099 |
| 2 | 0.112 | 0.084 | 0.072 | 0.132 |
| 3 | 0.10 | 0.08 | 0.07 | 0.12 |
| Parameter | R (G1)/mm | R (G2)/mm | R (G3)/mm | R (G4)/mm | R (Average)/mm |
|---|---|---|---|---|---|
| Riveting force | 0.00656 | 0.00338 | 0.00321 | 0.00519 | 0.004585 |
| Die dwell time | 0.00462 | 0.00246 | 0.00216 | 0.00485 | 0.0035225 |
| Rivet protrusion length | 0.01554 | 0.00449 | 0.00612 | 0.01836 | 0.0111275 |
| Clamping force | 0.00872 | 0.00290 | 0.00272 | 0.00665 | 0.0052475 |
| Elastic modulus (E) | 0.00324 | 0.00451 | 0.00440 | 0.00789 | 0.00501 |
| Initial yield stress (A) | 0.05321 | 0.02852 | 0.02701 | 0.05644 | 0.041295 |
| Hardening constant (B) | 0.01523 | 0.00628 | 0.00571 | 0.01545 | 0.0106675 |
| Hardening exponent (n) | 0.02413 | 0.01216 | 0.01138 | 0.02409 | 0.01794 |
| Group | Riveting Force (N) | Die Dwell Time (s) | Rivet Protrusion Length (mm) | Clamping Force of the Pressure Feet (MPa) |
|---|---|---|---|---|
| 1 | 9869.440 | 0.00098496 | 5.1256 | 21.1568 |
| 2 | 10,002.356 | 0.00035664 | 4.508316 | 18.3692 |
| 3 | 9964.080 | 0.00060456 | 4.7575 | 17.63762 |
| Interferometric Measurement Position | Optimal Values (mm) | Targeted Values (mm) | Relative Deviation | |
|---|---|---|---|---|
| 1 | G1 | 0.090707899 | 0.084 | 7.99% |
| G2 | 0.066179493 | 0.063 | 5.05% | |
| G3 | 0.0591217 | 0.054 | 9.48% | |
| G4 | 0.105208 | 0.099 | 6.27% | |
| 2 | G1 | 0.121151878 | 0.112 | 8.17% |
| G2 | 0.083218121 | 0.084 | 0.93% | |
| G3 | 0.0693104 | 0.072 | 3.74% | |
| G4 | 0.124837 | 0.132 | 5.43% | |
| 3 | G1 | 0.104535649 | 0.10 | 4.54% |
| G2 | 0.074297139 | 0.08 | 7.13% | |
| G3 | 0.0631781 | 0.07 | 9.75% | |
| G4 | 0.111384 | 0.12 | 7.18% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, K.; Wan, L.; Hui, N.; Shan, D.; Zhao, Y.; Chang, Z. Prediction and Optimization of Interference Fit Level in Slug Riveted Structure with Deep Learning Enhanced Genetic Algorithm. Machines 2025, 13, 936. https://doi.org/10.3390/machines13100936
Yan K, Wan L, Hui N, Shan D, Zhao Y, Chang Z. Prediction and Optimization of Interference Fit Level in Slug Riveted Structure with Deep Learning Enhanced Genetic Algorithm. Machines. 2025; 13(10):936. https://doi.org/10.3390/machines13100936
Chicago/Turabian StyleYan, Kanghe, Lichao Wan, Nana Hui, Donghe Shan, Yang Zhao, and Zhengping Chang. 2025. "Prediction and Optimization of Interference Fit Level in Slug Riveted Structure with Deep Learning Enhanced Genetic Algorithm" Machines 13, no. 10: 936. https://doi.org/10.3390/machines13100936
APA StyleYan, K., Wan, L., Hui, N., Shan, D., Zhao, Y., & Chang, Z. (2025). Prediction and Optimization of Interference Fit Level in Slug Riveted Structure with Deep Learning Enhanced Genetic Algorithm. Machines, 13(10), 936. https://doi.org/10.3390/machines13100936






