A New Method for Displacement Modelling of Serial Robots Using Finite Screw
Abstract
1. Introduction
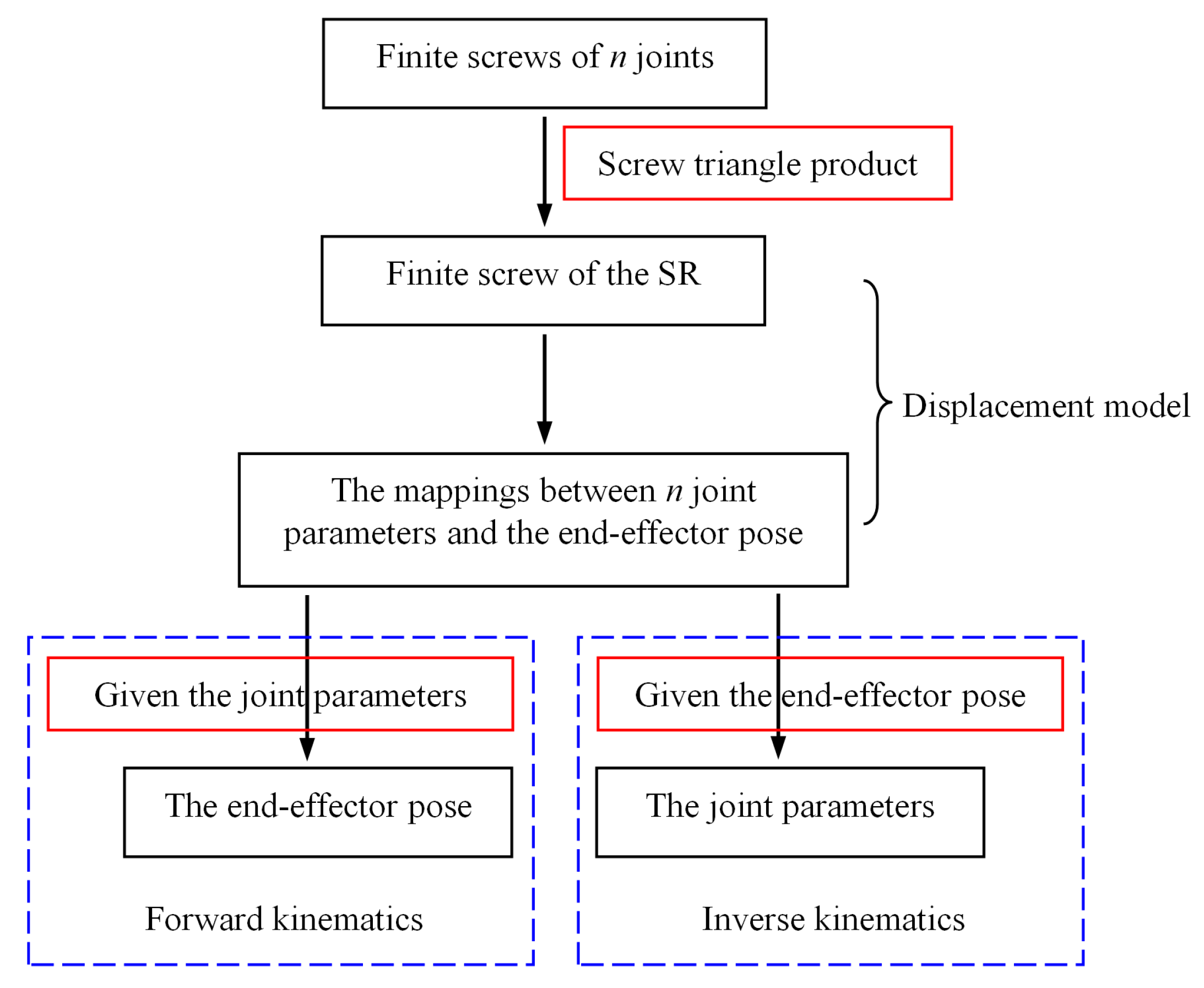
2. Displacement Modelling Using Finite Screw
3. Kinematics Using Finite Screw
4. Examples
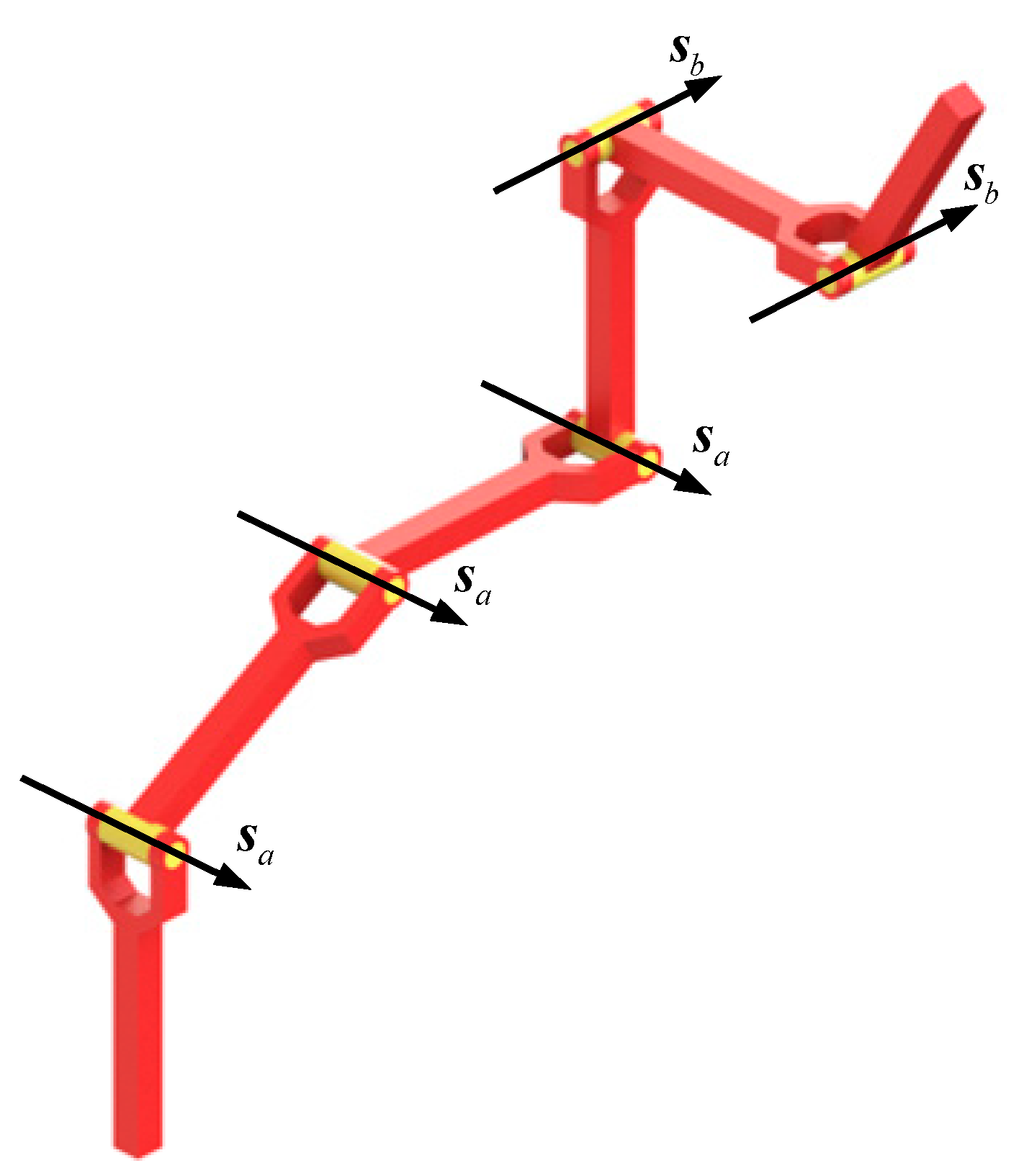
4.1. P1P2P3RaRb Robot
4.2. RaRaRaRbRb Robot
5. Matlab Simulation
5.1. P1P2P3RaRb
5.2. RaRaRaRbRb
6. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, S.J.; Ong, S.K.; Nee, A.Y.C. Optimal pass planning for robotic welding of large-dimension joints with deep grooves. Procedia CIRP 2016, 56, 188–192. [Google Scholar] [CrossRef]
- Curiel, D.; Veiga, F.; Suarez, A.; Villanueva, P.; Aldalur, E. Automatic trajectory determination in automated robotic welding considering weld joint symmetry. Symmetry 2023, 15, 1776. [Google Scholar] [CrossRef]
- Jia, G.; Huang, H.; Li, B.; Wu, Y.; Cao, Q.; Guo, H. Synthesis of a novel type of metamorphic mechanism module for large scale deployable grasping manipulators. Mech. Mach. Theory 2018, 128, 544–559. [Google Scholar] [CrossRef]
- Jia, G.; Huang, H.; Wang, S.; Li, B. Type synthesis of plane-symmetric deployable grasping parallel mechanisms using constraint force parallelogram law. Mech. Mach. Theory 2021, 161, 104330. [Google Scholar] [CrossRef]
- Song, Y.; Kang, X.; Dai, J.S. Instantaneous mobility analysis using the twist space intersection approach for parallel mechanisms. Mech. Mach. Theory 2020, 151, 103866. [Google Scholar] [CrossRef]
- Huo, X.; Song, Y. Finite motion analysis of parallel mechanisms with parasitic motions based on conformal geometric algebra. Adv. Appl. Clifford Algebras 2018, 28, 21. [Google Scholar] [CrossRef]
- Huo, X.; Lian, B.; Wang, P.; Song, Y.; Sun, T. Topology and dimension synchronous optimization of 1T2R parallel robots. Mech. Mach. Theory 2023, 187, 105385. [Google Scholar] [CrossRef]
- Di Gregorio, R. Singularity Analysis of spatial single-DOF mechanisms based on the locations of the instantaneous screw axes. Mech. Mach. Theory 2023, 189, 105438. [Google Scholar] [CrossRef]
- Hu, B.; Bai, P. Type synthesis of serial kinematic chains with screw type terminal constraints based on an adding joint method. Mech. Mach. Theory 2023, 184, 105277. [Google Scholar] [CrossRef]
- Song, Y.; Ma, X.; Dai, J.S. A novel 6R metamorphic mechanism with eight motion branches and multiple furcation points. Mech. Mach. Theory 2019, 142, 103598. [Google Scholar] [CrossRef]
- Sun, T.; Huo, X. Type synthesis of 1T2R parallel mechanisms with parasitic motions. Mech. Mach. Theory 2018, 128, 412–428. [Google Scholar] [CrossRef]
- Lian, B.; Sun, T.; Song, Y.; Wang, X. Passive and active gravity compensation of horizontally-mounted 3-RPS parallel kinematic machine. Mech. Mach. Theory 2016, 104, 190–201. [Google Scholar] [CrossRef]
- Feng, H.; Chen, Y.; Dai, J.S.; Gogu, G. Kinematic study of the general plane-symmetric Bricard linkage and its bifurcation variations. Mech. Mach. Theory 2017, 116, 89–104. [Google Scholar] [CrossRef]
- Shen, F.; Yang, S.; Wang, H.; Dai, J.S. Twist and finite twist analysis of 2UPR-SPR parallel mechanism based upon screw theory. Mech. Mach. Theory 2023, 184, 105276. [Google Scholar] [CrossRef]
- Wang, K.; Dai, J.S. The dual Euler-Rodrigues formula in various mathematical forms and their intrinsic relations. Mech. Mach. Theory 2023, 181, 105184. [Google Scholar] [CrossRef]
- Chen, K.; Wang, R.; Niu, Z.; Wang, P.; Sun, T. Topology design and performance optimization of six-limbs 5-DOF parallel machining robots. Mech. Mach. Theory 2023, 185, 105333. [Google Scholar] [CrossRef]
- Feng, H.; Peng, R.; Ma, J.; Chen, Y. Rigid foldability of generalized triangle twist origami pattern and its derived 6R linkages. J. Mech. Robot. 2018, 10, 051003. [Google Scholar] [CrossRef]
- Gao, C.; Huang, H.; Li, B.; Jia, G. Design of a truss-shaped deployable grasping mechanism using mobility bifurcation. Mech. Mach. Theory 2019, 139, 346–358. [Google Scholar] [CrossRef]
- Yang, Q.; Hu, K.; Zhang, Y.; Lian, B.; Sun, T. Design and experiment of multi-locomotion tensegrity mobile robot. Mech. Mach. Theory 2024, 198, 105671. [Google Scholar] [CrossRef]
- Wang, S.; Huang, H.; Jia, G.; Li, B.; Guo, H.; Liu, R. Design of a novel three-limb deployable mechanism with mobility bifurcation. Mech. Mach. Theory 2022, 172, 104789. [Google Scholar] [CrossRef]
- Dai, J.S. An historical review of the theoretical development of rigid body displacements from Rodrigues parameters to the finite twist. Mech. Mach. Theory 2006, 41, 41–52. [Google Scholar] [CrossRef]
- Dai, J.S. Finite displacement screw operators with embedded Chasles’ motion. J. Mech. Robot. 2012, 4, 041002. [Google Scholar] [CrossRef]
- Dai, J.S.; Holland, N.; Kerr, D.R. Finite twist mapping and its application to planar serial manipulators with revolute joints. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1995, 209, 263–271. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, H.; Zhang, M.; Li, B.; Liu, Q.; Dong, C. Elasto-dynamic performance evaluation of a 6-DOF hybrid polishing robot based on kinematic modeling and CAE technology. Mech. Mach. Theory 2022, 176, 104983. [Google Scholar] [CrossRef]
- Jin, Y.; Yang, Q.; Liu, X.; Lian, B.; Sun, T. Type synthesis of worm-like planar tensegrity mobile robot. Mech. Mach. Theory 2024, 191, 105476. [Google Scholar] [CrossRef]
- Sun, T.; Song, Y.; Dong, G.; Lian, B.; Liu, J. Optimal design of a parallel mechanism with three rotational degrees of freedom. Robot. Comput.-Integr. Manuf. 2012, 28, 500–508. [Google Scholar] [CrossRef]
- Jia, G.; Li, B.; Huang, H.; Zhang, D. Type synthesis of metamorphic mechanisms with scissor-like linkage based on different kinds of connecting pairs. Mech. Mach. Theory 2020, 151, 103848. [Google Scholar] [CrossRef]
- Sun, T.; Lian, B.; Song, Y.; Feng, L. Elastodynamic optimization of a 5-DoF parallel kinematic machine considering parameter uncertainty. IEEE/ASME Trans. Mechatron. 2019, 24, 315–325. [Google Scholar] [CrossRef]
- Ding, X.; Yang, Y.; Dai, J.S. Topology and kinematic analysis of color-changing ball. Mech. Mach. Theory 2011, 46, 67–81. [Google Scholar] [CrossRef]
- Huo, X.; Lian, B.; Wang, P.; Song, Y.; Sun, T. Dynamic identification of a tracking parallel mechanism. Mech. Mach. Theory 2021, 155, 104091. [Google Scholar] [CrossRef]
- Gan, D.; Dai, J.S.; Dias, J.; Seneviratne, L.D. Variable motion/force transmissibility of a metamorphic parallel mechanism with reconfigurable 3T and 3R motion. J. Mech. Robot. 2016, 8, 051001. [Google Scholar] [CrossRef]
- Sun, T.; Liu, C.; Lian, B.; Wang, P.; Song, Y. Calibration for precision kinematic control of an articulated serial robot. IEEE Trans. Ind. Electron. 2021, 68, 6000–6009. [Google Scholar] [CrossRef]
- Kang, R.; Guo, Y.; Chen, L.; Branson, D.T.; Dai, J.S. Design of a pneumatic muscle based continuum robot with embedded tendons. IEEE/ASME Trans. Mechatron. 2017, 22, 751–761. [Google Scholar] [CrossRef]
- Liu, H.; Dai, J. An approach to carton-folding trajectory planning using dual robotic fingers. Robot. Auton. Syst. 2003, 42, 47–63. [Google Scholar] [CrossRef]
- Sun, T.; Lian, B.; Song, Y. Stiffness Analysis of a 2-DoF over-constrained RPM with an articulated traveling platform. Mech. Mach. Theory 2016, 96, 165–178. [Google Scholar] [CrossRef]
- Sun, T.; Wu, H.; Lian, B.; Qi, Y.; Wang, P.; Song, Y. Stiffness modeling, analysis and evaluation of a 5 degree of freedom hybrid manipulator for friction stir welding. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 4441–4456. [Google Scholar] [CrossRef]
- Tang, G.; Yang, Q.; Lian, B. Design and experimentation of tensegrity jumping robots. Appl. Sci. 2024, 14, 3947. [Google Scholar] [CrossRef]
- Zhao, J.-S.; Wang, J.-Y.; Chu, F.; Feng, Z.-J.; Dai, J.S. Structure synthesis and statics analysis of a foldable stair. Mech. Mach. Theory 2011, 46, 998–1015. [Google Scholar] [CrossRef]
- Yan, S.J.; Ong, S.K.; Nee, A.Y.C. Stiffness analysis of parallelogram-type parallel manipulators using a strain energy method. Robot. Comput.-Integr. Manuf. 2016, 37, 13–22. [Google Scholar] [CrossRef]
- Aimedee, F.; Gogu, G.; Dai, J.S.; Bouzgarrou, C.; Bouton, N. Systematization of morphing in reconfigurable mechanisms. Mech. Mach. Theory 2016, 96, 215–224. [Google Scholar] [CrossRef]
- Wang, R.; Song, Y.; Dai, J.S. Reconfigurability of the origami-inspired integrated 8R kinematotropic metamorphic mechanism and its evolved 6R and 4R mechanisms. Mech. Mach. Theory 2021, 161, 104245. [Google Scholar] [CrossRef]
- Yan, S.J.; Ong, S.K.; Nee, A.Y.C. Optimization design of general triglide parallel manipulators. Adv. Robot. 2016, 30, 1027–1038. [Google Scholar] [CrossRef]
- Dai, J.S.; Jones, J.R. A linear algebraic procedure in obtaining reciprocal screw systems. J. Robot. Syst. 2003, 20, 401–412. [Google Scholar] [CrossRef]
- Mentrasti, L.; Cannella, F.; Pupilli, M.; Dai, J.S. Large bending behavior of creased paperboard. I. Experimental investigations. Int. J. Solids Struct. 2013, 50, 3089–3096. [Google Scholar] [CrossRef]
- Hunt, K.H. Kinematic Geometry of Mechanisms; Oxford University Press: Oxford, UK, 1978. [Google Scholar]
- Qin, Y.; Dai, J.S.; Gogu, G. Multi-furcation in a derivative queer-square mechanism. Mech. Mach. Theory 2014, 81, 36–53. [Google Scholar] [CrossRef]
- Gan, D.; Liao, Q.; Dai, J.S.; Wei, S.; Seneviratne, L.D. Forward displacement analysis of the general 6–6 Stewart mechanism using Gröbner bases. Mech. Mach. Theory 2009, 44, 1640–1647. [Google Scholar] [CrossRef]
- Ball, R.S. A Treatise on the Theory of Screws; Cambridge University Press: Cambridge, UK, 1900. [Google Scholar]
- Hamilton, W.R. Elements of Quaternions; Longmans, Green, & Company: London, UK, 1886. [Google Scholar]
- Rodriguez Leal, E.; Dai, J.S. From origami to a new class of centralized 3-DOF parallel mechanisms. In Proceedings of the ASME 2007 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Las Vegas, NV, USA, 4–7 September 2007; pp. 1183–1193. [Google Scholar] [CrossRef]
- Saglia, J.A.; Tsagarakis, N.G.; Dai, J.S.; Caldwell, D.G. Inverse-kinematics-based control of a redundantly actuated platform for rehabilitation. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2009, 223, 53–70. [Google Scholar] [CrossRef]
- Saglia, J.A.; Tsagarakis, N.G.; Dai, J.S.; Caldwell, D.G. Control strategies for ankle rehabilitation using a high performance ankle exerciser. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 2221–2227. [Google Scholar] [CrossRef]
- Kang, X.; Feng, H.; Dai, J.S.; Yu, H. High-order based revelation of bifurcation of novel Schatz-inspired metamorphic mechanisms using screw theory. Mech. Mach. Theory 2020, 152, 103931. [Google Scholar] [CrossRef]
- Huo, X.; Yang, S.; Lian, B.; Sun, T.; Song, Y. A survey of mathematical tools in topology and performance integrated modeling and design of robotic mechanism. Chin. J. Mech. Eng. 2020, 33, 62. [Google Scholar] [CrossRef]
- Tang, T.; Fang, H.; Luo, H.; Song, Y.; Zhang, J. Type synthesis, unified kinematic analysis and prototype validation of a family of Exechon inspired parallel mechanisms for 5-axis hybrid kinematic machine tools. Robot. Comput.-Integr. Manuf. 2021, 72, 102181. [Google Scholar] [CrossRef]
- Tang, T.; Luo, H.; Song, Y.; Fang, H.; Zhang, J. Chebyshev inclusion function based interval kinetostatic modeling and parameter sensitivity analysis for Exechon-like parallel kinematic machines with parameter uncertainties. Mech. Mach. Theory 2021, 157, 104209. [Google Scholar] [CrossRef]
- Chen, X.; Feng, H.; Ma, J.; Chen, Y. A plane linkage and its tessellation for deployable structure. Mech. Mach. Theory 2019, 142, 103605. [Google Scholar] [CrossRef]
- Wang, T.; Lin, Y.-H.; Spyrakos-Papastavridis, E.; Xie, S.Q.; Dai, J.S. Stiffness evaluation of a novel ankle rehabilitation exoskeleton with a type-variable constraint. Mech. Mach. Theory 2023, 179, 105071. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Q.; Jia, G.; Dai, J.S. Sylvester’s dialytic elimination in analysis of a metamorphic mechanism derived from ladybird wings. Mech. Mach. Theory 2023, 179, 105102. [Google Scholar] [CrossRef]
- Guo, F.; Sun, T.; Wang, P.; Liu, S.; Song, Y. Synchronous design method of stiffness and topology for parallel flexible mechanisms with various joints. Mech. Mach. Theory 2023, 180, 105137. [Google Scholar] [CrossRef]
- Salerno, M.; Zhang, K.; Menciassi, A.; Dai, J.S. A novel 4-DOFs origami enabled, SMA actuated, robotic end-effector for minimally invasive surgery. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2844–2849. [Google Scholar] [CrossRef]
- Yao, L.; Gu, B.; Haung, S.; Wei, G.; Dai, J.S. Mathematical modeling and simulation of the external and internal double circular-arc spiral bevel gears for the nutation drive. J. Mech. Des. 2010, 132, 021008. [Google Scholar] [CrossRef]
- Huijuan, F.; Jiayao, M.; Yan, C. Rigid folding of generalized waterbomb origami tubes. J. Mech. Eng. 2020, 56, 143. [Google Scholar] [CrossRef]
- Sun, T.; Song, Y.; Li, Y.; Liu, L. Dimensional synthesis of a 3-DOF parallel manipulator based on dimensionally homogeneous Jacobian matrix. Sci. China Ser. E Technol. Sci. 2010, 53, 168–174. [Google Scholar] [CrossRef]
- Yao, W.; Dai, J.S. Dexterous manipulation of origami cartons with robotic fingers based on the interactive configuration space. J. Mech. Des. 2008, 130, 022303. [Google Scholar] [CrossRef]
- Aldalur, E.; Suárez, A.; Curiel, D.; Veiga, F.; Villanueva, P. Intelligent and adaptive system for welding process automation in T-shaped joints. Metals 2023, 13, 1532. [Google Scholar] [CrossRef]
- Feng, H.; Lv, W.; Ma, J.; Chang, W.; Chen, Y.; Wang, J. Helical structures with switchable and hierarchical chirality. Appl. Phys. Lett. 2020, 116, 194102. [Google Scholar] [CrossRef]
- Feng, H.; Ma, J.; Chen, Y.; You, Z. Twist of tubular mechanical metamaterials based on waterbomb origami. Sci. Rep. 2018, 8, 9522. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Dai, J.S. Screw-system-variation enabled reconfiguration of the Bennett plano-spherical hybrid linkage and its evolved parallel mechanism. J. Mech. Des. 2015, 137, 062303. [Google Scholar] [CrossRef]
- Zhao, T.S.; Dai, J.S.; Huang, Z. Geometric synthesis of spatial parallel manipulators with fewer than six degrees of freedom. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2002, 216, 1175–1185. [Google Scholar] [CrossRef]
- Sun, T.; Yang, S.; Huang, T.; Dai, J.S. A way of relating instantaneous and finite screws based on the screw triangle product. Mech. Mach. Theory 2017, 108, 75–82. [Google Scholar] [CrossRef]
- Song, C.-Y.; Feng, H.; Chen, Y.; Chen, I.-M.; Kang, R. Reconfigurable mechanism generated from the network of Bennett linkages. Mech. Mach. Theory 2015, 88, 49–62. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, F.; Fang, Z.; Song, J.; Liu, Q.; Yang, S. A New Method for Displacement Modelling of Serial Robots Using Finite Screw. Machines 2024, 12, 658. https://doi.org/10.3390/machines12090658
Xue F, Fang Z, Song J, Liu Q, Yang S. A New Method for Displacement Modelling of Serial Robots Using Finite Screw. Machines. 2024; 12(9):658. https://doi.org/10.3390/machines12090658
Chicago/Turabian StyleXue, Feiyang, Zhengjun Fang, Jiahao Song, Qi Liu, and Shuofei Yang. 2024. "A New Method for Displacement Modelling of Serial Robots Using Finite Screw" Machines 12, no. 9: 658. https://doi.org/10.3390/machines12090658
APA StyleXue, F., Fang, Z., Song, J., Liu, Q., & Yang, S. (2024). A New Method for Displacement Modelling of Serial Robots Using Finite Screw. Machines, 12(9), 658. https://doi.org/10.3390/machines12090658






