Abstract
Shape memory alloys (SMAs) have emerged as promising materials for self-centering seismic applications due to their unique properties of superelasticity and shape memory effect. This review article examines recent advancements in the use of SMAs for self-centering seismic devices, focusing on their mechanical properties, damping characteristics and applications in structural engineering. The fundamental principles of SMAs are discussed, including their phase transformations and hysteretic behavior, and their performance under various loading conditions is analyzed. The article also explores different SMA-based damping systems, with a particular emphasis on innovative self-centering friction dampers. Furthermore, the influence of factors such as alloy composition, heat treatment and loading parameters on the seismic performance of SMA devices is investigated. The review concludes by highlighting the potential of SMAs in improving the seismic resilience of structures and identifying future research directions in this field.
1. Introduction
Earthquakes pose a significant threat to civil infrastructure, causing severe damage and potential loss of life. Traditional seismic design approaches have primarily focused on preventing structural collapse, often neglecting the post-earthquake recovery aspect [1]. This limitation has driven the development of innovative materials and systems that can not only dissipate seismic energy but also provide self-centering capabilities, reducing residual deformations and facilitating rapid post-earthquake restoration [2].
In recent years, the concept of seismic resilience has gained considerable traction in structural engineering. This shift extends beyond mere collapse prevention, encompassing the ability to maintain operational continuity and facilitate swift post-disaster recovery [3]. Within this context, shape memory alloys (SMAs) have emerged as promising materials for seismic applications due to their unique properties of superelasticity and shape memory effect [4].
SMAs offer several advantages for seismic protection. Their ability to undergo substantial deformations and return to their original shape results in large recoverable strains, which minimizes residual displacements. The hysteretic behavior of SMAs allows them to dissipate seismic energy effectively. Furthermore, SMAs exhibit self-centering properties, helping structures return to their initial position after seismic events, which in turn reduces repair costs and downtime. These combined characteristics make SMAs particularly suitable for applications in seismic-resistant structural systems.
The integration of SMAs into structural systems has led to the development of various devices and components, including self-centering connections, dampers and braces. Recent research has explored applications ranging from building frames to bridge structures. For instance, Karmakar et al. [4] investigated a novel self-centering friction damper (SCFD) that combines the energy dissipation capabilities of friction dampers with the recentering properties of SMAs. Norouzi Ojaey et al. [5] proposed an innovative lateral load-resisting system for tall reinforced concrete (RC) frames, incorporating a hybrid friction damper with superelastic SMA wires. Rahmzadeh and Alam [6] explored the feasibility of using superelastic SMAs in plastic hinge regions of steel bridge columns to minimize residual drifts.
While SMAs have shown great promise, researchers continue to explore other innovative approaches to seismic protection. These include the variable friction damper (VFD) introduced by Ferrotto et al. [7], which offers a unique approach to modulating dissipative capacity, and optimized tuned mass dampers (TMDs) that consider soil–structure interaction effects, as investigated by Vanshaj et al. [8].
Despite the promising attributes of these innovative systems in enhancing seismic resilience, their practical deployment in the industry remains limited. Challenges such as temperature sensitivity, high costs for SMAs and the need for precise calibration in some devices have hindered widespread adoption. However, ongoing research continues to address these issues and explore innovative applications that could lead to more widespread implementation.
This review article aims to explore recent advancements in the use of SMAs for self-centering seismic applications. It analyzes the fundamental principles governing SMA behavior, examines their mechanical and damping properties, and discusses various SMA-based seismic damping systems. Special attention is given to innovative self-centering friction dampers that incorporate SMAs. Additionally, the review discusses the influence of factors such as alloy composition, heat treatment and loading parameters on the seismic performance of SMA devices.
The structure of this review is as follows: Section 2 provides an overview of conventional seismic damping devices and their limitations; Section 3 introduces the basic principles of SMAs; Section 4 examines the mechanical properties and damping characteristics of SMAs in seismic engineering; Section 5 discusses various SMA-based damping systems; Section 6 explores the testing and validation methods for SMA-based seismic devices; Section 7 analyzes the influence of various factors on SMA performance in seismic applications; Section 8 outlines future research directions and unexplored areas in the field of SMAs for seismic applications and Section 9 concludes the review.
By systematically exploring these aspects, this review aims to provide a comprehensive understanding of the current state and future potential of SMAs in seismic engineering, contributing to the development of more resilient and sustainable built environments.
2. Conventional Seismic Damping Devices
Before delving into SMA-based systems, it is essential to understand the current state of seismic damping technology. This section provides an overview of conventional seismic damping devices, categorized into active and passive systems.
2.1. Active Control Systems
Active control systems in seismic engineering involve the use of external energy sources to modulate the dynamic response of structures during earthquakes. These systems typically consist of sensors, controllers, and actuators that work together to counteract seismic forces [9].
2.1.1. Active Mass Drivers (AMDs)
Active mass drivers are the most common active control systems used in seismic engineering. They consist of a large mass that can move in one or more directions, driven by a mechanical actuator capable of generating significant forces. AMDs are typically installed at the top of buildings to reduce oscillations [10], as illustrated in Figure 1.
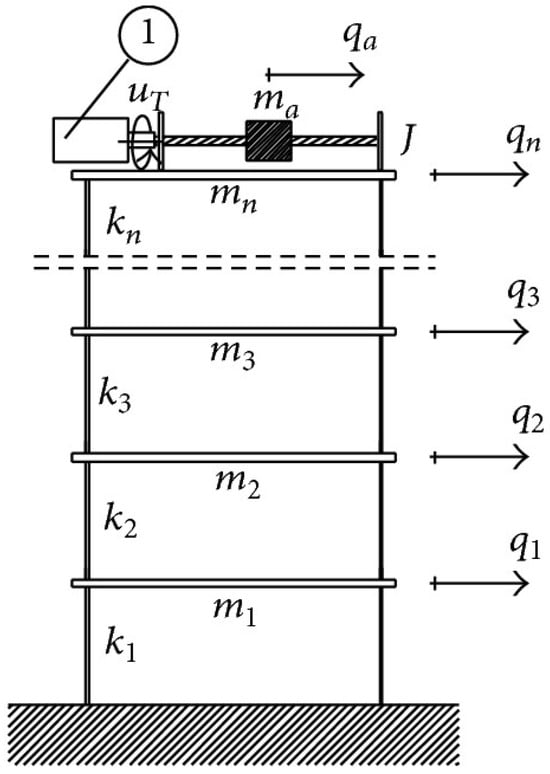
Figure 1.
Schematic representation of an AMD made of an electric torsional servomotor [11].
2.1.2. Active Tendon Systems
Active tendon systems are another type of active control device, usually installed on the ground floor of buildings. These systems consist of cables whose tension is regulated by a central control unit based on the structure’s needs during a seismic event [12], as depicted in Figure 2.
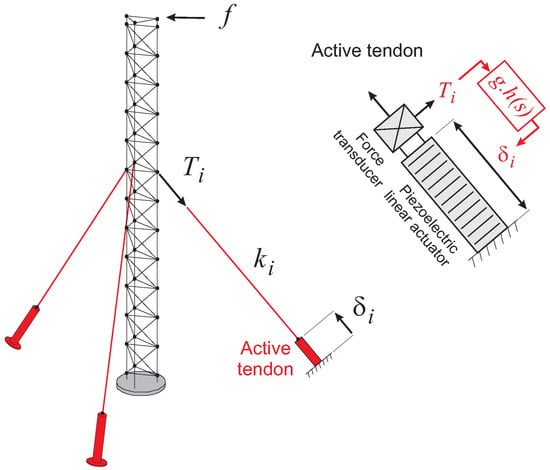
Figure 2.
Cable structure system with active tendons and decentralized control [13].
While active control systems offer the advantage of adapting in real-time to excitation conditions, making them more efficient than passive systems, they also have significant drawbacks. These include the need for a continuous external power source and uncertainty about their long-term reliability, which necessitates frequent and costly maintenance [14].
2.2. Passive Control Systems
Passive control systems, unlike their active counterparts, do not require external power sources. They work by either limiting the input energy from environmental loads or quickly damping their effects. Current passive control applications are based on two main techniques: isolation and energy dissipation through specially designed devices [15].
2.2.1. Base Isolators
Base isolators, illustrated in Figure 3, are passive control systems consisting of rubber–steel support systems placed at the base of the structure. They are designed to have optimal horizontal stiffness and equivalent damping values, which reduce the seismic energy transmitted to the building by decoupling the superstructure from the ground [16,17].
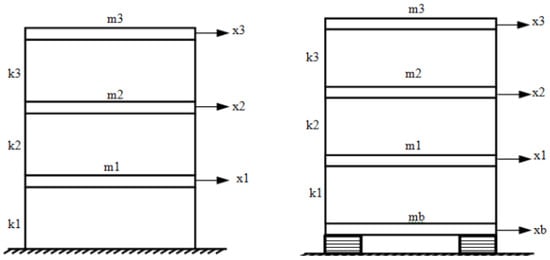
Figure 3.
(Left): a model of fixed base building; (Right): base isolated building [18].
2.2.2. Tuned Mass Dampers
Tuned mass dampers are another family of passive dampers widely used in civil engineering. As depicted in Figure 4, they consist of a mass–spring–damper system that mitigates vibrations by transferring the kinetic energy from the primary structure to self-damping components for dissipation [19].
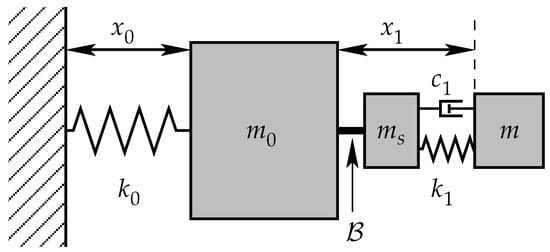
Figure 4.
Simple tuned mass damper. The TMD works by imposing a reaction force through the rigid bar labeled B [20].
2.2.3. Hysteretic Dampers
Hysteretic dampers exert their dissipative action through the characteristic stress–strain cycle (hysteresis cycle), in which the absorbed kinetic energy is transformed into thermal energy. These dampers are inserted into the building structure to increase stability and lateral load capacity, reduce the impact of cyclic stresses and structural damage, reduce functional loss caused by earthquakes, meet reinforcement and stiffness requirements, and provide additional damping through local deformation [21].
Hysteretic dampers can be further categorized based on their material and functioning principle into yielding metallic dampers, friction dampers, viscoelastic dampers and fluid viscous dampers. Each of these damper types has its own advantages and limitations. Figure 5 schematize a classical passive fluid viscous damper.
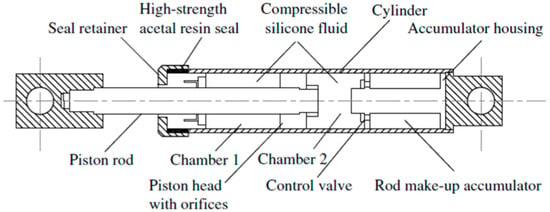
Figure 5.
Scheme of a classical passive fluid viscous damper [22].
While conventional dampers have proven effective in improving seismic performance, they often suffer from permanent deformation after strong seismic events, necessitating replacement and resulting in high repair costs and downtime. This limitation has driven researchers to explore new materials and systems that can provide both energy dissipation and self-centering capabilities, leading to the development of SMA-based seismic devices [23].
3. Fundamentals of Shape Memory Alloys
Shape memory alloys (SMAs) are a unique class of smart materials that exhibit two distinct properties: the shape memory effect and superelasticity. These properties arise from a reversible solid-state phase transformation between two crystal structures: austenite and martensite [24].
More in detail, SMAs have two primary phases: austenite (the high-temperature, more ordered phase) and martensite (the low-temperature phase). The transformation between these phases, schematically represented in Figure 6, occurs at specific temperatures, which are critical parameters for SMA behavior [25].
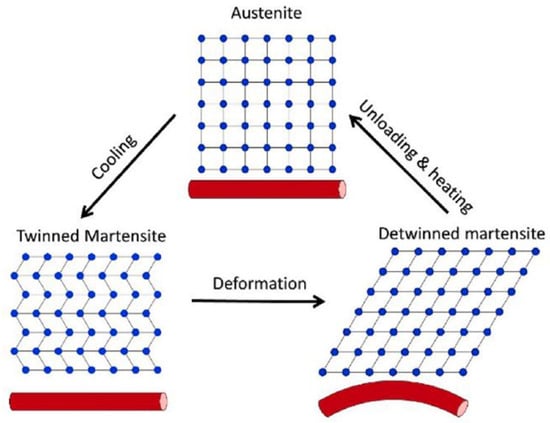
Figure 6.
Schematic representation of SMA phase transformations [26].
The shape memory effect allows SMAs to “remember” their original shape and return to it after deformation when heated. Superelasticity, on the other hand, occurs when an SMA is deformed above its austenite finish temperature, allowing it to undergo large deformations and return to its original shape upon unloading. The superelastic behavior of SMAs is characterized by a non-linear stress–strain relationship, which can be divided into several distinct regions [27]. The superelastic effect makes SMAs ideal for self-centering seismic applications [28], resulting in the hysteretic behavior, which is a key factor in SMA’s energy dissipation capabilities. The stress–strain curve of a superelastic SMA under cyclic loading typically exhibits a flag-shaped hysteresis loop, as visible in Figure 7, which represents the energy dissipated during a loading–unloading cycle [29].
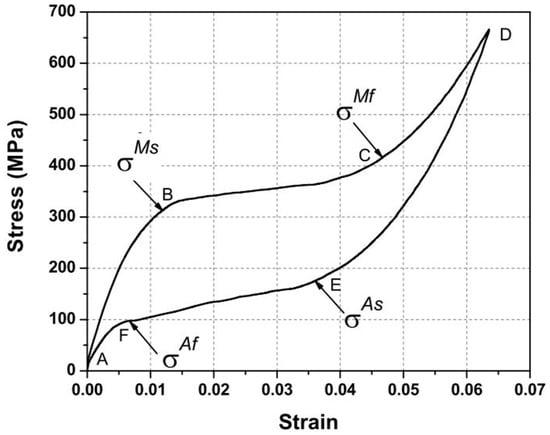
Figure 7.
Stress–strain curve illustrating hysteretic behavior os SMAs in superelastic field [26].
4. Mechanical Properties and Damping Characteristics of SMAs
The application of SMAs in seismic engineering relies heavily on their unique mechanical properties and damping characteristics. This section explores these properties in detail, focusing on their relevance to seismic applications.
4.1. Recovery Strain, Strength and Stiffness
SMAs exhibit significant recovery strain, typically ranging from 4% to 8% for common alloys like NiTi. This large recovery strain is crucial for accommodating substantial structural displacements during seismic events while maintaining the ability to return to the original position [30].
The strength and stiffness of SMAs vary depending on the alloy composition and thermomechanical treatment. For example, NiTi alloys can achieve ultimate tensile strengths up to 1000 MPa, with Young’s moduli ranging from 30 to 90 GPa depending on the phase [31].
4.2. Damping Characteristics
The damping capacity of SMAs is one of their most important features for seismic applications. The damping properties of SMAs are evaluated according to parameters such as the equivalent damping ratio and the loss factor.
The equivalent damping ratio () is a common measure of a SMA’s ability to dissipate energy. It can be calculated using the following equation [19]:
where:
- is the energy dissipated per cycle
- is the equivalent stiffness
- is the maximum strain
Studies have shown that the equivalent damping ratio of SMAs can range from 2% to 10%, depending on the alloy composition and loading conditions [32].
The loss factor () is another parameter used to quantify the damping capacity of SMAs. It is related to the ratio of the energy dissipated to the maximum strain energy stored in a cycle [33]:
where
- is the total strain energy;
- is the loss tangent.
4.3. Experimental Tests for Evaluating Material Damping Capacity
To quantitatively assess the damping capabilities of materials, researchers primarily employ three experimental tests: superelasticity (SE) tests, nanoindentation tests and dynamic mechanical analysis (DMA).
The thermomechanical superelastic experiment is the classical method for measuring the damping capacity of SMAs. SMAs are heated to a temperature above Af and subjected to a tension (or compression) loading–unloading cycle at a constant temperature. Since the loading and unloading paths differ, a closed curve known as the hysteresis loop is formed. From this, a value can be extracted, known as mechanical hysteresis or hysteresis load. This parameter is directly related to the energy dissipation capacity, and the area between the loading and unloading curves represents the damped energy. The damping energy can thus be determined as [23]:
DMA is another widely used method for determining internal friction in conventional metals and SMAs. In this test, the specimens are subjected to flexural loading by a sinusoidal load that can be described as:
where is the stress amplitude and is the angular frequency. The resulting strain from such a loading is also sinusoidal and is given by:
where is the strain amplitude and is the phase difference between stress and strain.
Based on the above, two moduli and can be defined. represents the storage modulus and is associated with the ability to store energy during load application; closely related to material stiffness, it is also known as the dynamic Young’s modulus. is the loss modulus and expresses the material’s propensity to dissipate energy, which is related to internal friction. Therefore, the ratio between and (/) is a measure of damping and quantifies a material’s ability to absorb and dissipate energy. This ratio is also known as the tangent of the phase angle [26]:
The third test for evaluating material damping capacity is the nanoindentation experiment. This test is used to obtain the mechanical properties of SMAs at the microscale and is particularly suitable for measuring the damping capacity of materials where it is not possible to produce test samples for DMA.
For this type of experiment, indentation parameters must be considered, including the load applied to the indenter tip and the duration of indentation. Often, the spherical indenter is preferred over others, as its use provides a uniform stress and strain gradient in the volume, making it easier to limit plasticity and promote superelastic response. Important indentation parameters are recoverable energy (), total deformation energy (), and dissipation energy (). is defined as the area under the loading curve. The non-recoverable work or dissipated energy () is the area between the loading and unloading curves [34]. The specific damping coefficient can be defined using the following formula:
Using the load–depth curve of nanoindentation, it is also possible to calculate a loss factor equivalent to the parameter obtained through DMA tests:
The equation can be modified for the condition of a positive stress–strain cycle as:
These experimental methods provide crucial insights into the damping properties of SMAs, allowing researchers to quantify and compare their performance for various applications, including seismic protection systems.
Understanding these factors is crucial for designing effective SMA-based seismic devices and optimizing their performance under various conditions.
5. SMA-Based Damping Systems
The unique properties of SMAs have led to the development of various damping systems for seismic applications. This section discusses some of the most promising SMA-based damping systems, with a focus on self-centering capabilities.
5.1. SMA Braces and Dampers
SMA braces and dampers typically consist of SMA wires or bars incorporated into traditional bracing systems or damping devices, as schematized in Figure 8 and Figure 9. The superelastic behavior of the SMA elements allows these systems to undergo large deformations during an earthquake and return to their original position after the event [35,36].
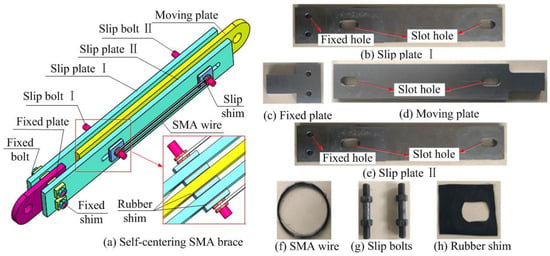
Figure 8.
Schematic diagram of a SMA brace system [37].
Dolce et al. developed two types of SMA-based braces for the seismic control of buildings and bridges. Their experimental results showed that SMA braces improve seismic performance at least as much as steel braces while providing the additional benefit of self-centering [38].
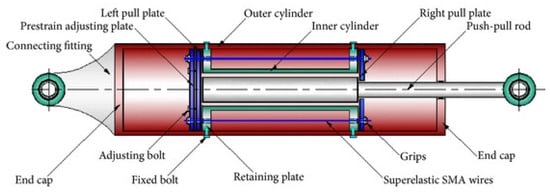
Figure 9.
Conceptual design of a SMA wire damper [39].
5.2. SMA-Based Base Isolation Systems
SMAs have been incorporated into base isolation systems to enhance their performances. For example, Wilde et al. proposed an intelligent isolation system that combines a laminated rubber bearing with an SMA device for highway bridges. These systems can limit displacement and dissipate energy during seismic events. The addition of SMA elements to traditional base isolators can provide additional energy dissipation and help control the displacement of the isolated structure [40].
5.3. Self-Centering Friction Damper (SCFD)
The self-centering friction damper (SCFD) is an innovative damping system that combines the benefits of SMAs and friction dampers. This device leverages the synergy between friction plates and SMA bars to dissipate input energy while providing strong self-centering capability [41].
The SCFD, as depicted in Figure 10 and Figure 11, consists of a friction system (composed of friction plates) and a self-centering system (consisting of SMA bars). Under both tension and compression, the friction plates move in opposite directions, generating friction forces that dissipate seismic energy. The SMA bars provide a restoring force to reduce residual displacement, returning the damper to its initial position.
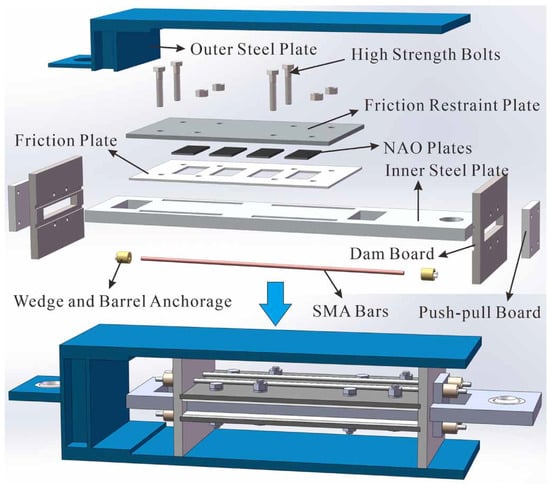
Figure 10.
An example of self-centering friction damper (SCFD) [42].
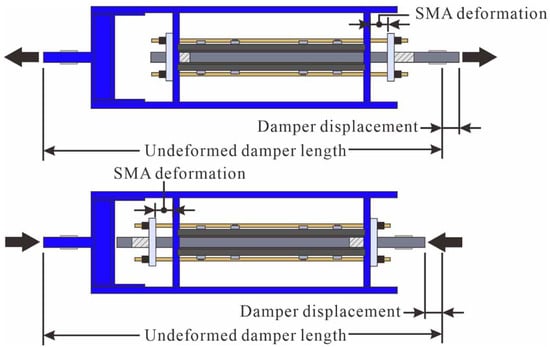
Figure 11.
SCFD working mechanism [42].
These SMA-based damping systems demonstrate the potential of SMAs to enhance the seismic performance of structures by providing both energy dissipation and self-centering capabilities. The choice of system depends on the specific requirements of the structure and the seismic hazard level.
6. Testing and Validation of SMA-Based Seismic Devices
Ensuring the reliability and effectiveness of SMA-based seismic devices is crucial for their widespread adoption in structural engineering. To this end, various testing and validation methods are employed to evaluate the performance of these devices. Experimental testing is a fundamental approach in this process, with several methods commonly used to assess their behavior under seismic conditions. Cyclic loading tests, for instance, simulate seismic loading conditions to evaluate the energy dissipation capacity and self-centering properties of SMA devices, as highlighted by DesRoches et al. (2004) [43]. Shake table tests involve subjecting full-scale or scaled structural models fitted with SMA devices to simulated earthquake ground motions, thereby allowing for the evaluation of their performance under realistic seismic conditions, as demonstrated in the study by Ozbulut et al. (2011) [30]. Additionally, fatigue testing is conducted to assess the long-term durability and stability of SMA devices over numerous loading cycles, providing insights into their longevity, as discussed by Tobushi et al. (2000) [44].
Alongside experimental methods, numerical simulation and modeling play a critical role in the testing and validation process. Advanced constitutive models have been developed to accurately represent the complex behavior of shape memory alloys (SMAs) under various loading conditions. These models are typically incorporated into finite element analysis software, enabling researchers to simulate the response of structures equipped with SMA devices during seismic events, as highlighted by Lagoudas et al. (2012) [45]. Auricchio et al. (2014) [46] further illustrate how these simulations contribute to predicting and optimizing the performance of SMA devices in various structural applications.
Performance-based evaluation is another important method used to assess the effectiveness of SMA devices in seismic design. This approach involves evaluating the likelihood of meeting specific performance objectives, such as immediate occupancy or life safety, under different levels of seismic hazard. Researchers compare the performance of structures with and without SMA devices to quantify the benefits of these systems, which include reduced damage, enhanced functionality, and lower life-cycle costs, as demonstrated by Taflanidis et al. (2009) [47] and Ozbulut et al. (2011) [48].
Finally, the field monitoring of SMA-based devices is becoming more prevalent, though it is still somewhat limited. In these studies, researchers implement SMA devices in actual structures and monitor their performance over time, which provides valuable data on their long-term behavior and reliability under real-world environmental and loading conditions, as noted by Song et al. (2006) [49]. Such field studies are crucial in bridging the gap between laboratory testing and real-world applications, ultimately advancing the adoption of SMA-based seismic devices in structural engineering.
7. Influence of Various Factors on SMA Performance in Seismic Applications
The performance of SMAs in seismic applications is influenced by various factors, including material composition, thermomechanical treatment, and loading conditions. Understanding these influences is crucial for optimizing SMA-based devices for seismic protection.
7.1. Effect of Alloy Composition
The composition of SMAs plays a significant role in determining their mechanical properties and transformation temperatures, which affect their seismic performance [31,50]. For example, the Ni content in NiTi alloys, which is the most widely used and studied SMA for seismic applications [33], significantly influences their properties. Increasing Ni content generally lowers transformation temperatures [51], enhances strength [52] and raises superelastic plateau stress. Moreover, the addition of third or fourth elements to NiTi alloys can further modify their properties, such as increasing transformation temperatures, improving stability, and widening the hysteresis loop, useful for certain damping applications [53].
7.2. Influence of Thermomechanical Treatment
Heat treatment and mechanical processing significantly affect the properties of SMAs. Solution treatment followed by water quenching is often used to homogenize the microstructure and set the initial shape of SMA components [54]. Aging can introduce precipitates that modify transformation behavior and mechanical properties. Cold working followed by annealing can be used to improve the strength and functional properties of SMAs. The degree of cold work and subsequent annealing temperature affect the final properties [55].
7.3. Loading Parameters
The response of SMAs under seismic loading is influenced by several loading parameters [43]. Larger strain amplitudes generally lead to increased energy dissipation [56]. However, very large strains may cause the accumulation of plastic deformation and degradation of properties. The loading rate affects the stress–strain behavior of SMAs [57]: lower rates allow more time for heat transfer, resulting in isothermal conditions; higher rates can lead to self-heating/cooling effects, altering the apparent transformation temperatures. Moreover, SMAs may exhibit some degradation in properties under cyclic loading: the stress amplitude decreases with increasing number of cycles, stabilizing after a certain number of cycles; the residual strain accumulates in the initial cycles but tends to stabilize with further cycling. Pre-straining or “training” of SMAs can help stabilize their behavior for seismic applications.
7.4. Temperature Effects
The operating temperature relative to the SMA’s transformation temperatures significantly affects its behavior. Temperatures above the austenite finish temperature are ideal for most seismic applications, resulting in a full superelastic field. It is important to note that the transformation temperatures can shift under applied stress, known as the Clausius–Clapeyron effect [58].
7.5. Size Effects
The size of SMA elements can influence their behavior. Thin wires typically exhibit more consistent properties due to their highly drawn microstructure, while larger bars may show more variability in properties but offer higher load-bearing capacity.
Understanding these influencing factors is crucial for designing effective SMA-based seismic devices and predicting their performance under various conditions. The proper selection of alloy composition, thermomechanical treatment, and operating conditions can optimize the behavior of SMAs for specific seismic applications.
8. Future Research Directions and Unexplored Areas
While significant progress has been made in the development of SMA-based seismic devices, several areas require further research and exploration. The ongoing development of new SMA compositions with improved properties for seismic applications remains a key focus, including high-temperature SMAs for extreme environments, SMAs with reduced temperature sensitivity and more cost-effective compositions to promote wider adoption [31,59,60]. Researchers are also exploring the potential of multi-functional SMA devices that could combine seismic protection with energy harvesting or structural health monitoring capabilities [61]. The integration of SMA-based devices with other smart structural technologies, such as active control systems or semi-active dampers, presents opportunities for creating hybrid systems with enhanced performance and adaptability [62]. Beyond primary structural elements, there is growing interest in expanding the use of SMAs to protect non-structural components, which often account for a significant portion of earthquake-related damages and losses [63]. To fully understand the long-term performance of these innovative systems, more extensive full-scale testing and monitoring of SMA-based seismic devices in real structures over extended periods is necessary. This will provide crucial data on their reliability, durability and effectiveness under various environmental conditions and seismic events [30]. The development of comprehensive design guidelines and optimization techniques for SMA-based seismic devices is another critical area, including standardized procedures for selecting appropriate SMA compositions, determining optimal device configurations, and integrating these devices into overall structural design processes [64]. Researchers are also investigating the potential of SMA-based systems to enhance structural resilience against multiple hazards beyond earthquakes, such as high winds, blast loading, or tsunamis, which could lead to more comprehensive and efficient protective systems [65]. Sustainability is another key consideration, with ongoing research into the life-cycle assessments of SMA-based seismic systems, considering their environmental impact, long-term economic benefits, and overall sustainability compared to conventional systems. This research could help justify the higher initial costs of SMA devices by demonstrating their long-term value [66]. Finally, novel applications in geotechnical engineering are being explored, such as using SMAs in foundation systems or soil improvement techniques, opening up new avenues for mitigating seismic risk at the soil–structure interface [67].
9. Conclusions
This review has explored the recent advancements in the use of shape memory alloys (SMAs) for self-centering seismic applications. The unique properties of SMAs, particularly their superelasticity and energy dissipation capabilities, make them promising materials for innovative seismic protection systems. Key conclusions from this review include:
- SMA-based devices, such as braces, dampers and isolation systems, have demonstrated significant potential in improving the seismic performance of structures by providing both energy dissipation and self-centering capabilities.
- The self-centering friction damper (SCFD), which combines SMAs with friction elements, shows promising performance in terms of energy dissipation and residual displacement reduction.
- The behavior of SMAs in seismic applications is influenced by various factors, including alloy composition, thermomechanical treatment, loading parameters and environmental conditions. Understanding these influences is crucial for optimizing SMA-based devices.
- NiTi-based alloys remain the most widely used SMAs for seismic applications, but ternary and quaternary alloys offer opportunities for property customization.
- The proper design and conditioning of SMA elements can mitigate issues related to cyclic degradation and temperature sensitivity, enhancing their long-term reliability in seismic applications.
Despite the promising results, several challenges remain in the widespread adoption of SMA-based seismic devices. These include the need for more comprehensive long-term performance data, the development of cost-effective manufacturing processes and the establishment of standardized design and testing procedures. Addressing these challenges through continued research and development efforts will be crucial in realizing the full potential of SMAs in seismic engineering.
As the field of earthquake engineering continues to evolve towards performance-based design approaches, the integration of smart materials like SMAs is likely to play an increasingly important role. The unique capabilities of SMAs offer the potential to create structures that not only withstand seismic events with minimal damage but also facilitate rapid recovery and continued functionality in the aftermath of earthquakes. This aligns well with the growing emphasis on seismic resilience and sustainable infrastructure development.
Future research directions, as outlined in this review, point towards exciting possibilities for expanding the application of SMAs in seismic engineering. From the development of advanced multi-functional devices to the exploration of novel applications in geotechnical engineering, there are numerous avenues for innovation. By addressing the identified research gaps and leveraging emerging technologies, researchers and engineers can continue to push the boundaries of what is possible in seismic protection, ultimately contributing to the creation of more resilient and sustainable built environments.
Author Contributions
Conceptualization: all the authors; methodology: all the authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Billah, A.H.M.M.; Alam, M.S. Seismic performance of concrete columns reinforced with hybrid shape memory alloy (SMA) and fiber reinforced polymer (FRP) bars. Constr. Build. Mater. 2012, 28, 730–742. [Google Scholar] [CrossRef]
- Koutsoloukas, L.; Nikitas, N.; Aristidou, P. Passive, semi-active, active and hybrid mass dampers: A literature review with associated applications on building-like structures. Dev. Built Environ. 2022, 12, 100094. [Google Scholar] [CrossRef]
- Lu, X.; Sun, W.; Xu, L. Experimental investigation on seismic behavior of damaged self-centering friction beam-column joints after repair. Eng. Struct. 2024, 310, 118135. [Google Scholar] [CrossRef]
- Karmakar, S.; Kumar, A.; Kolay, C. Development, characterization, and seismic application of a shape memory alloy-based self-centering damper. Soil Dyn. Earthq. Eng. 2024, 183, 108797. [Google Scholar] [CrossRef]
- Norouzi Ojaey, F.; Dashti Naserabadi, H.; Jamshidi, M. Seismic assessment of tall RC frames with hybrid friction damper and SMA designed by PBPD method. Rev. Int. Métod. Numér. Cálc. Diseño Ing. 2021, 37, 46. [Google Scholar] [CrossRef]
- Rahmzadeh, A.; Alam, M.S. Feasibility of using superelastic shape memory alloy in plastic hinge regions of steel bridge columns for seismic applications. Earthq. Eng. Struct. Dyn. 2024, 53, 2988–3008. [Google Scholar] [CrossRef]
- Ferrotto, M.F.; Di Paola, M.; Cavaleri, L. Seismic behavior of structures equipped with variable friction dissipative (VFD) systems. Bull. Earthq. Eng. 2021, 19, 4623–4639. [Google Scholar] [CrossRef]
- Vanshaj, K.; Shukla, A.K.; Shukla, M.; Mishra, A. Jellyfish search optimization for tuned mass dumpers for earthquake oscillation of elevated structures including soil–structure interaction. Asian J. Civ. Eng. 2023, 24, 779–792. [Google Scholar] [CrossRef]
- Ubertini, F.; Venanzi, I.; Comanducci, G. Considerations on the implementation and modeling of an active mass driver with electric torsional servomotor. Mech. Syst. Signal Process. 2015, 58–59, 53–69. [Google Scholar] [CrossRef]
- Mei, G.; Kareem, A.; Kantor, J.C. Model Predictive Control of Structures under Earthquakes using Acceleration Feedback. J. Eng. Mech. 2002, 128, 574–585. [Google Scholar] [CrossRef]
- Venanzi, I.; Ubertini, F. Free Vibration Response of a Frame Structural Model Controlled by a Nonlinear Active Mass Driver System. Adv. Civ. Eng. 2014, 2014, 745814. [Google Scholar] [CrossRef]
- Zheng, H.; Miao, L.; Xiao, P.; Lei, K.; Wang, Q. Novel metamaterial foundation with multi low-frequency bandgaps for isolating earthquakes and train vibrations. Structures 2024, 61, 106070. [Google Scholar] [CrossRef]
- Preumont, A. Active Damping, Vibration Isolation, and Shape Control of Space Structures: A Tutorial. Actuators 2023, 12, 122. [Google Scholar] [CrossRef]
- Xu, X.; Yuan, Y.; Zhang, T.; Li, K.; Wang, S.; Liang, C.; Zhu, H. A silanized MCNT/TPU-based flexible strain sensor with high stretchability for deformation monitoring of elastomeric isolators for bridges. Constr. Build. Mater. 2022, 338, 127664. [Google Scholar] [CrossRef]
- Li, C.; Pan, H.; Cao, L. Pendulum-type tuned tandem mass dampers-inerters for crosswind response control of super-tall buildings. J. Wind. Eng. Ind. Aerodyn. 2024, 247, 105706. [Google Scholar] [CrossRef]
- Xu, G.; Guo, T.; Li, A.; Wang, S.; Zhang, R.; Zhu, R.; Xu, J. Review on self-centering damper for seismic resilient building structures. Structures 2023, 54, 58–77. [Google Scholar] [CrossRef]
- Xu, W.; Cai, Y.; Liu, Y.; Zhang, T.; Lu, Y. Experimental and numerical study of a metal-friction hybrid damper. Structures 2024, 62, 106256. [Google Scholar] [CrossRef]
- Tolani, S.; Sharma, A. Effectiveness of Base Isolation Technique and Influence of Isolator Characteristics on Response of a Base Isolated Building. Am. J. Eng. Res. (AJER) 2016, 5, 198–209. [Google Scholar]
- Guo, W.; Wang, X.; Yu, Y.; Chen, X.; Li, S.; Fang, W.; Zeng, C.; Wang, Y.; Bu, D. Experimental study of a steel damper with X-shaped welded pipe halves. J. Constr. Steel Res. 2020, 170, 106087. [Google Scholar] [CrossRef]
- Tophøj, L.; Grathwol, N.; Hansen, S.O. Effective Mass of Tuned Mass Dampers. Vibration 2018, 1, 193–206. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Tagawa, H. Beam-to-column connection with double-stage yield buckling-restrained steel bar dampers. J. Constr. Steel Res. 2024, 212, 108278. [Google Scholar] [CrossRef]
- Zoccolini, L.; Bruschi, E.; Cattaneo, S.; Quaglini, V. Current Trends in Fluid Viscous Dampers with Semi-Active and Adaptive Behavior. Appl. Sci. 2023, 13, 10358. [Google Scholar] [CrossRef]
- Toker, G.P.; Saedi, S.; Acar, E.; Ozbulut, O.E.; Karaca, H.E. Loading frequency and temperature-dependent damping capacity of NiTiHfPd shape memory alloy. Mech. Mater. 2020, 150, 103565. [Google Scholar] [CrossRef]
- Sidharth, R.; Mohammed, A.S.K.; Abuzaid, W.; Sehitoglu, H. Unraveling Frequency Effects in Shape Memory Alloys: NiTi and FeMnAlNi. Shape Mem. Superelast. 2021, 7, 235–249. [Google Scholar] [CrossRef]
- Gong, Z.H.; Zhang, J.; Song, S.T.; Wang, C.L. Hysteretic behavior and recoverability research on the shape memory effect of SMA bars under cyclic loading. Constr. Build. Mater. 2023, 387, 131553. [Google Scholar] [CrossRef]
- Rashidi, K.; Sulong, A.B.; Muhamad, N.; Fayyaz, A.; Foudzi, F.M.; Basir, A. Martensitic transformation characteristics, mechanical properties and damping behavior of Cu–Al–Ni shape memory alloys: A review of their modifications and improvements. J. Mater. Res. Technol. 2024, 29, 2732–2749. [Google Scholar] [CrossRef]
- Acar, E.; Karaca, H.E.; Tobe, H.; Noebe, R.D.; Chumlyakov, Y.I. Characterization of the shape memory properties of a Ni45.3Ti39.7Hf10Pd5 alloy. J. Alloys Compd. 2013, 578, 297–302. [Google Scholar] [CrossRef]
- Juan, J.M.S.; Gómez-Cortés, J.F.; Nó, M.L. Ultra-high mechanical damping during superelastic bending of micro pillars and micro beams in Cu-Al-Ni shape memory alloys. J. Alloys Compd. 2022, 929, 167307. [Google Scholar] [CrossRef]
- Acar, E. Dynamic mechanical response of a Ni 45.7 Ti 29.3 Hf 20 Pd 5 alloy. Mater. Sci. Eng. A 2015, 633, 169–175. [Google Scholar] [CrossRef]
- Ozbulut, O.E.; Hurlebaus, S.; Desroches, R. Seismic response control using shape memory alloys: A review. J. Intell. Mater. Syst. Struct. 2011, 22, 1531–1549. [Google Scholar] [CrossRef]
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Cismaşiu, C.; Amarante dos Santos, F.P. Numerical simulation of superelastic shape memory alloys subjected to dynamic loads. Smart Mater. Struct. 2008, 17, 025036. [Google Scholar] [CrossRef]
- Janke, L.; Czaderski, C.; Motavalli, M.; Ruth, J. Applications of shape memory alloys in civil engineering structures—Overview, limits and new ideas. Mater. Struct. 2005, 38, 578–592. [Google Scholar] [CrossRef]
- Saedi, S.; Acar, E.; Raji, H.; Saghaian, S.E.; Mirsayar, M. Energy damping in shape memory alloys: A review. J. Alloys Compd. 2023, 956, 170286. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, S. A shape memory alloy-based reusable hysteretic damper for seismic hazard mitigation. Smart Mater. Struct. 2007, 16, 1603–1613. [Google Scholar] [CrossRef]
- Ozbulut, O.E.; Hurlebaus, S. Evaluation of the performance of a sliding-type base isolation system with a NiTi shape memory alloy device considering temperature effects. Eng. Struct. 2010, 32, 238–249. [Google Scholar] [CrossRef]
- Jia, Y.; Zhang, B.; Zeng, S.; Tang, F.; Hu, S.; Chen, W. Effect of Loading Rate and Initial Strain on Seismic Performance of an Innovative Self-Centering SMA Brace. Materials 2022, 15, 1234. [Google Scholar] [CrossRef]
- Speicher, M.; DesRoches, R.; Leon, R.T. Experimental results of a NiTi shape memory alloy (SMA)-based recentering beam-column connection. Eng. Struct. 2011, 33, 2448–2457. [Google Scholar] [CrossRef]
- Qian, H.; Li, H.; Song, G.; Guo, W. Recentering Shape Memory Alloy Passive Damper for Structural Vibration Control. Math. Probl. Eng. 2013, 2013, 1–13. [Google Scholar] [CrossRef]
- Ghassemieh, M.; Mostafazadeh, M.; Sadeh, M.S. Seismic control of concrete shear wall using shape memory alloys. J. Intell. Mater. Syst. Struct. 2012, 23, 535–543. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Wang, J.; Yu, H.; Ma, K.; Zhang, X.; Ji, W.; Li, R. Experimental investigation on the seismic behavior of a novel self-centering friction damper. J. Build. Eng. 2023, 76, 107384. [Google Scholar] [CrossRef]
- Han, M.; Chang, Z.; Xing, G.; Peng, P.; Liu, B. Cyclic behavior and seismic control performance of SMA friction damper. Smart Mater. Struct. 2023, 32, 075010. [Google Scholar] [CrossRef]
- DesRoches, R.; McCormick, J.; Delemont, M. Cyclic properties of superelastic shape memory alloy wires and bars. J. Struct. Eng. 2004, 130, 38–46. [Google Scholar] [CrossRef]
- Tobushi, H.; Shimeno, Y.; Hachisuka, T.; Tanaka, K. Thermomechanical properties of shape memory alloys. J. Intell. Mater. Syst. Struct. 2000, 11, 682–692. [Google Scholar] [CrossRef][Green Version]
- Lagoudas, D.C. Shape Memory Alloys: Modeling and Engineering Applications; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Auricchio, F.; Bonetti, E.; Scalet, G.; Ubertini, F. Shape memory alloys: From constitutive modeling to finite element analysis. Comput. Methods Appl. Mech. Eng. 2014, 281, 1–19. [Google Scholar]
- Taflanidis, A.A.; Beck, J.L. Life-cycle cost optimal design of passive dissipative devices. Struct. Saf. 2009, 31, 508–522. [Google Scholar] [CrossRef]
- Ozbulut, O.E.; Hurlebaus, S.; Desroches, R. Application of vibration control systems in civil engineering structures: Recent developments and advanced implementation issues. J. Vib. Control 2011, 17, 2001–2015. [Google Scholar]
- Song, G.; Ma, N.; Li, H.J. Application of shape memory alloy wire actuators for control of a flexible beam. Smart Mater. Struct. 2006, 15, 1332. [Google Scholar]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti–Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Frenzel, J.; George, E.P.; Dlouhy, A.; Somsen, C.; Wagner, M.F.X.; Eggeler, G. Influence of Ni on martensitic phase transformations in NiTi shape memory alloys. Acta Mater. 2010, 58, 3444–3458. [Google Scholar] [CrossRef]
- Pelton, A.R.; DiCello, J.; Miyazaki, S. Optimisation of processing and properties of medical grade Nitinol wire. Minim. Invasive Ther. Allied Technol. 2000, 9, 107–118. [Google Scholar] [CrossRef]
- Kim, J.I.; Liu, Y.; Miyazaki, S. Ageing-induced two-stage R-phase transformation in Ti–50.9at.%Ni. Acta Mater. 2006, 52, 487–499. [Google Scholar] [CrossRef]
- Tadesse, Y.; Thayer, N.; Priya, S. Tailoring the Response Time of Shape Memory Alloy Wires through Active Cooling and Pre-stress. J. Intell. Mater. Syst. Struct. 2010, 21, 19–40. [Google Scholar] [CrossRef]
- Huang, W.M.; Su, J.F.; Hong, M.H.; Yang, B. Pile-up and sink-in in micro-indentation of a NiTi shape-memory alloy. Scr. Mater. 2003, 49, 261–266. [Google Scholar] [CrossRef]
- Dolce, M.; Cardone, D.; Marnetto, R. Implementation and testing of passive control devices based on shape memory alloys. Earthq. Eng. Struct. Dyn. 2000, 29, 945–968. [Google Scholar] [CrossRef]
- Dayananda, G.N.; Subba Rao, M. Effect of strain rate on properties of superelastic NiTi thin wires. Mater. Sci. Eng. A 2007, 486, 96–103. [Google Scholar] [CrossRef]
- Buehler, W.J.; Gilfrich, J.V.; Wiley, R.C. Effect of low-temperature phase changes on the mechanical properties of alloys near composition TiNi. J. Appl. Phys. 1963, 34, 1475–1477. [Google Scholar] [CrossRef]
- Ma, J.; Karaman, I.; Noebe, R.D. High temperature shape memory alloys. Int. Mater. Rev. 2010, 55, 257–315. [Google Scholar] [CrossRef]
- Fang, C.; Wang, W. Recent developments in design of plasticity-based dampers for seismic protection of steel structures. J. Constr. Steel Res. 2019, 154, 253–266. [Google Scholar]
- Huang, W.M.; Yang, B.; Zhao, Y.; Ding, Z. Multifunctional shape memory alloy composites for self-healing, self-sensing, and energy harvesting. Mater. Today 2017, 20, 159–163. [Google Scholar]
- Casciati, S.; Marzi, A. Experimental studies on the fatigue life of shape memory alloy bars. Smart Struct. Syst. 2008, 4, 317–331. [Google Scholar] [CrossRef]
- Moradi, S.; Alam, M.S. Seismic response of non-structural components in buildings. Front. Struct. Civ. Eng. 2014, 8, 224–234. [Google Scholar]
- Torra, V.; Tachoire, H.; Auguet, C. A complete thermomechanical description of shape memory alloys: Understanding large plates of NiTi. Int. J. Therm. Sci. 2013, 64, 168–178. [Google Scholar]
- McCormick, J.; DesRoches, R.; Zaurin, R.; Ziehl, P. Analytical and experimental studies of semi-active control strategies for seismic protection of structures. In Proceedings of the 8th US National Conference on Earthquake Engineering, San Francisco, CA, USA, 18–22 April 2006; pp. 18–22. [Google Scholar]
- Dolce, M.; Cardone, D.; Bixio, A. Passive seismic protection of buildings by shape memory alloy devices. In Proceedings of the Smart Structures and Materials 2005: Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, San Francisco, CA, USA, 7–10 March 2005; Volume 5765, pp. 651–662. [Google Scholar]
- Qian, S.; Zhang, Y.; Qian, J.; Qu, J. Shape memory alloy-based self-healing concrete for civil infrastructure: Investigation of crack healing using a novel splicing technique. Smart Mater. Struct. 2018, 27, 085023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).