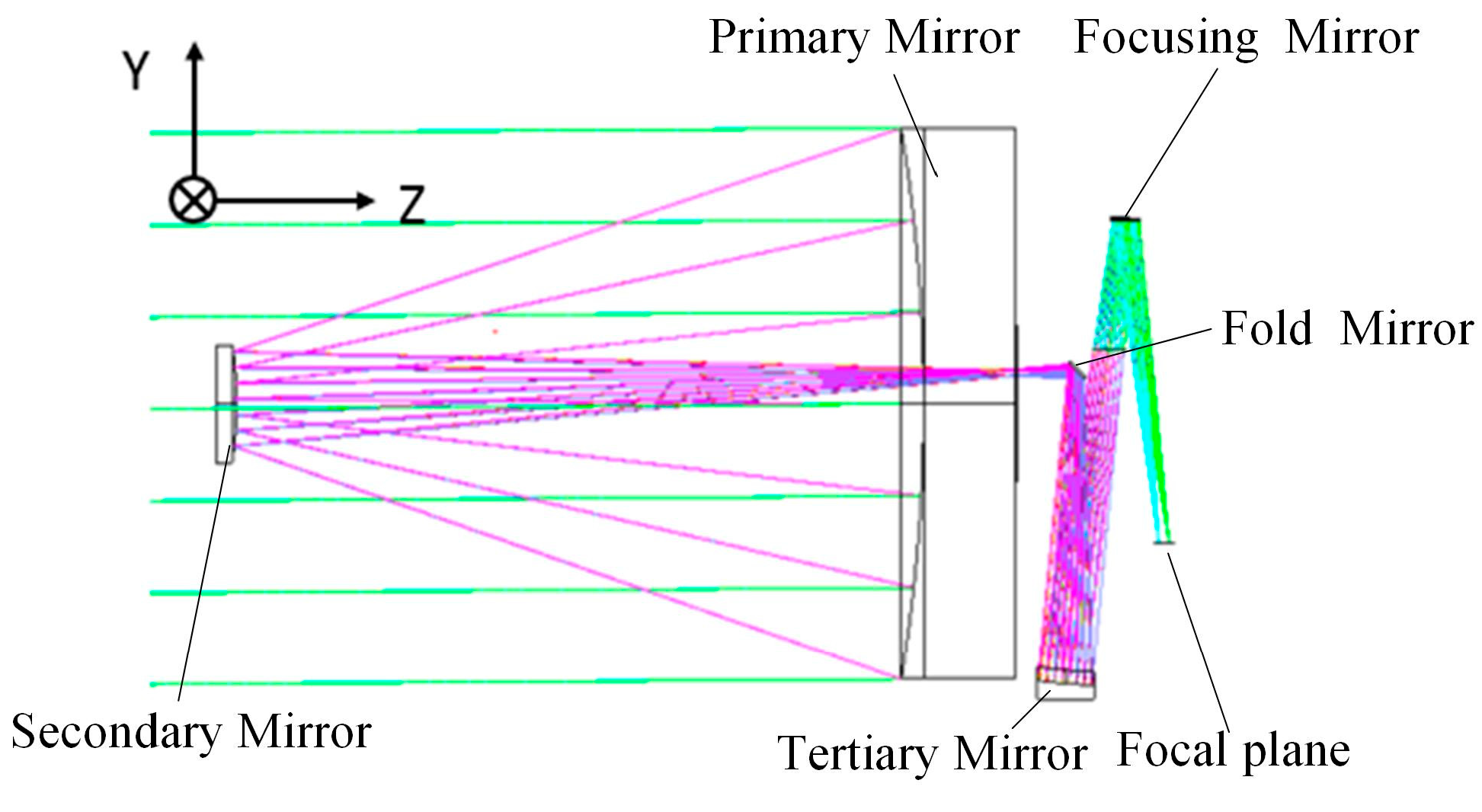
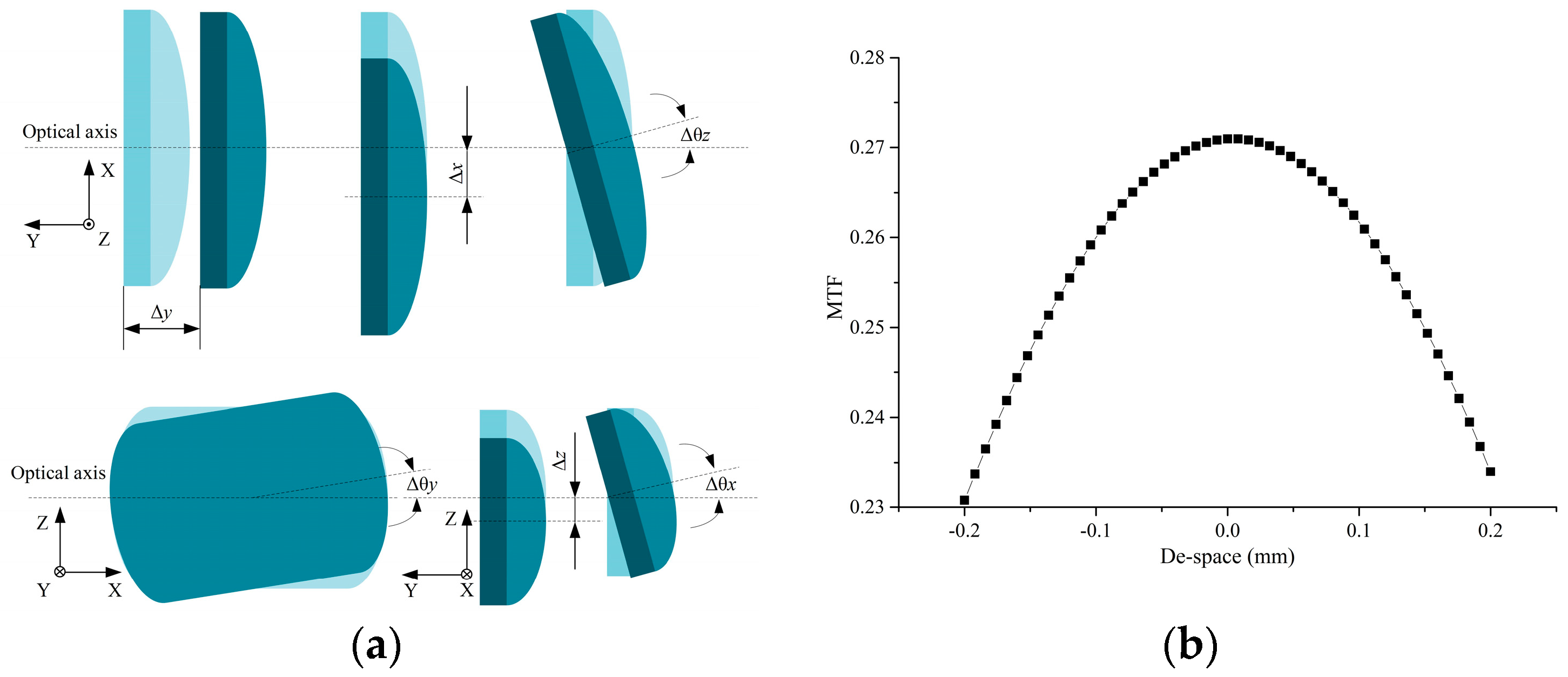
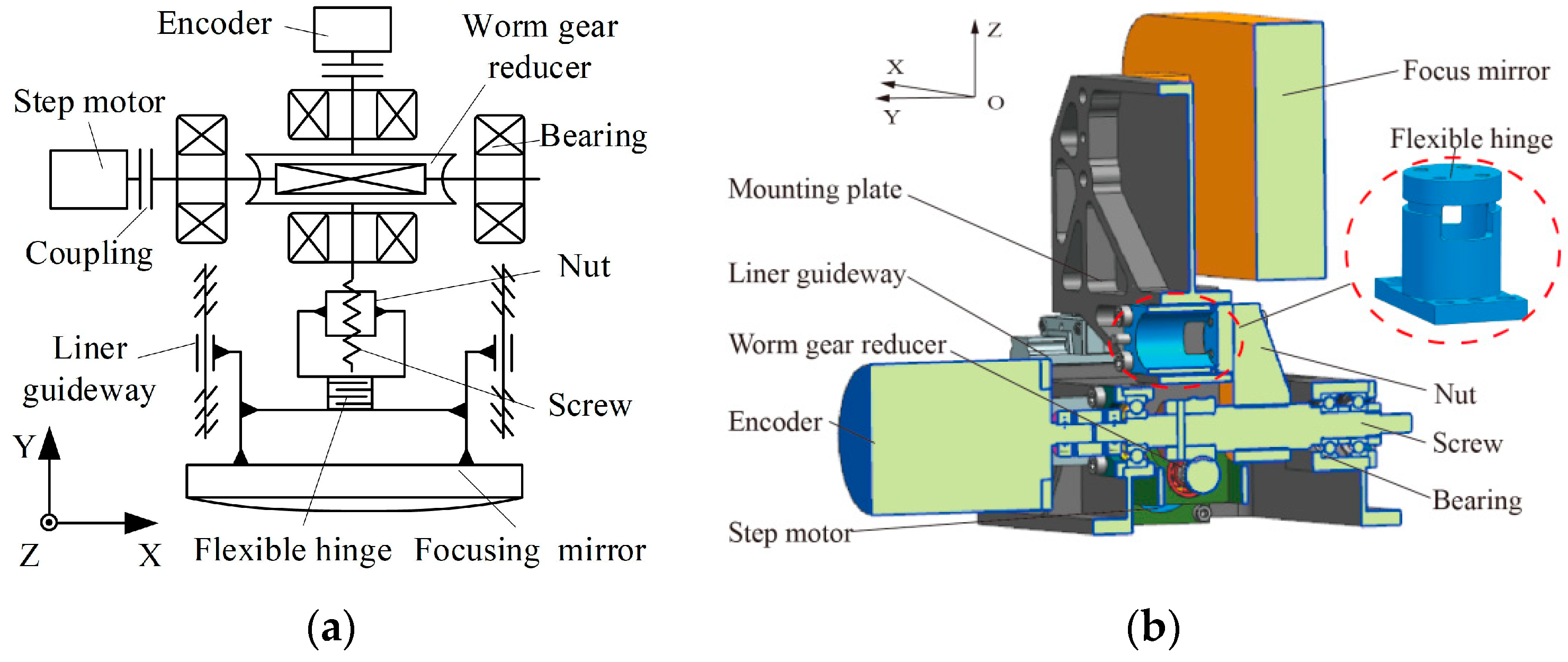
1. Introduction
Space cameras are essential instruments for obtaining ground information and are widely used in meteorology, geological exploration, agriculture, forestry, environmental monitoring, military operations, disaster relief, and other fields [
1,
2,
3]. After launch, due to changes in environmental conditions (atmospheric pressure, temperature, gravity, etc.), impact, vibration, overload, and other factors during transportation, as well as hygroscopic expansion of carbon fiber materials, the focal plane position of the optical system will change, and the image quality will eventually decline [
4]. To ensure the image quality of the space camera, it is necessary to design a focusing mechanism to fine-tune the position of the focal plane in the optical system, compensate for the defocus amount, and make the target image accurate on the detector surface. In addition, using a focusing mechanism can also relax the requirements on the installation position and change of each mirror in the optical system, which is conducive to the integration of the optical–mechanical system [
5].
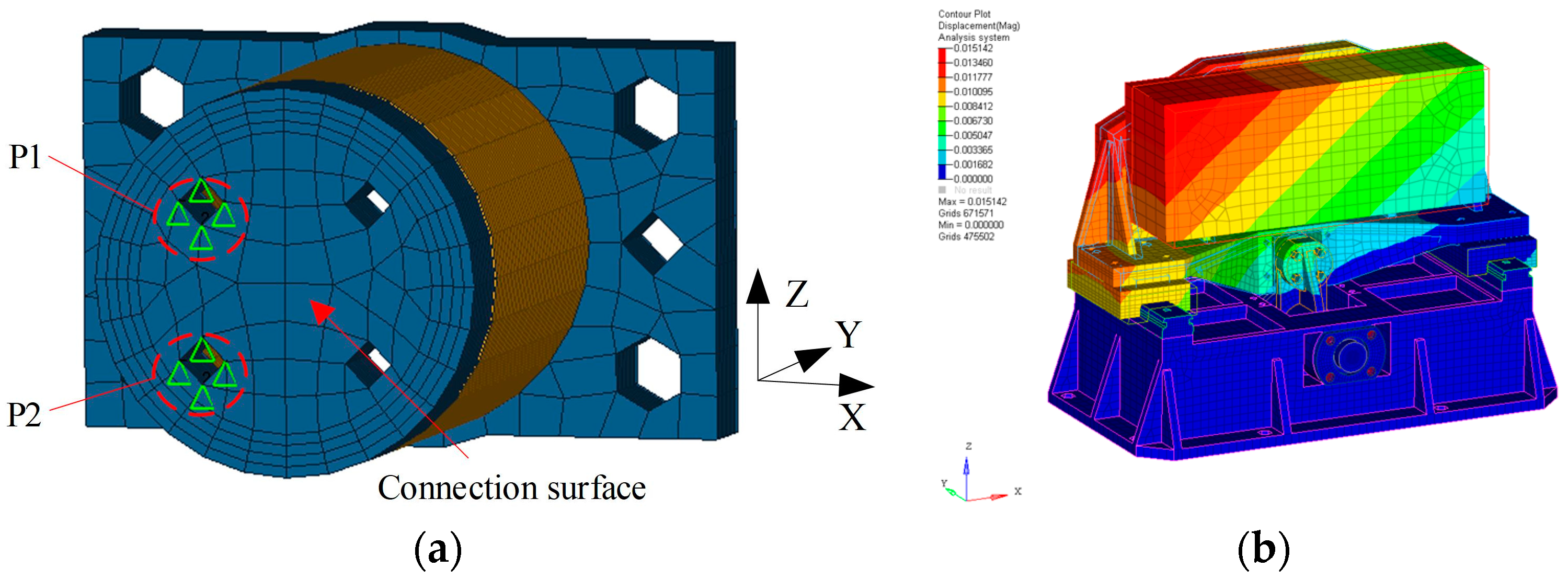
The sinusoidal excitation of the space camera during launch mainly comes from the thrust pulsation changes caused by the unsteady combustion of the launch vehicle engine and the unbalanced rotation of the rotating equipment. The frequency range is about 5 Hz–100 Hz. In addition, the random excitation frequency range caused by the ground transportation environment is roughly 0.5 Hz–100 Hz. If the fundamental frequency of the focusing mechanism is less than 100 Hz, it may lead to resonance under the action of vibration excitation in the ground transportation and launch flight stage, and it is faced with the risk of damage and loosening of the structural parts, stagnation of the focusing mechanism, and misalignment of the optical system. Therefore, the fundamental frequency of the focusing mechanism component is generally required to be higher than 100 Hz, and if the fundamental frequency is higher, it means that the likelihood of resonance is lower.
In recent years, the technology of space cameras has developed rapidly, and domestic and foreign researchers have conducted more and more research on focusing mechanisms. According to the driving principle of focusing mechanisms, focusing mechanisms can be roughly divided into mechanical focusing and thermal focusing. Mechanical focusing is more widely used. Jinwon Jung et al. [
5] proposed a novel focusing mechanism with a flexible hinge driven by a step motor to compensate for the defocusing of the optical system by moving the secondary mirror. The scheme can achieve 2.39 × 10
−3 mm travel, but the tilt error is 18.25″. On the other hand, Xiaozhe Ma et al. [
6] proposed a new focusing mechanism for a space telescope, which uses a flexible hinge rod to adjust the position of the secondary mirror. After analysis, this scheme is expected to reach no less than 9.4 × 10
−3 mm travel. To reduce the mass of the focusing mechanism and simplify the structure, Li et al. [
7] designed a focusing mechanism driven by piezoelectrics and based on the principle of a two-stage flexure hinge lever with a travel range of up to 2 mm, but its tilt error was not studied. Lu et al. [
8] designed a three-degree-of-freedom piezoelectric-driven flexible focusing mechanism whose fundamental frequency could reach 121.5 Hz. Kai W et al. [
9] developed a focusing mechanism combining spiral and worm gear transmission, ensuring precise linear motion by linear guideway. The focusing range was ±3 mm, and the positioning accuracy was better than ±6 × 10
−3 mm. Ziqing J et al. [
10] designed a new high-precision focusing mechanism composed of a worm gear and cam slider. A linear guideway also ensured precision linear motion; the focusing displacement error was better than 5.86 × 10
−3 mm, and the tilt error was less than 14″. There are relatively few studies on thermal focusing, mainly because thermal focusing tends to have minor travel and requires additional power consumption to maintain the position after focusing. In addition, thermal focusing has a slower response speed, so it is not as widely used as mechanical focusing [
11,
12,
13].
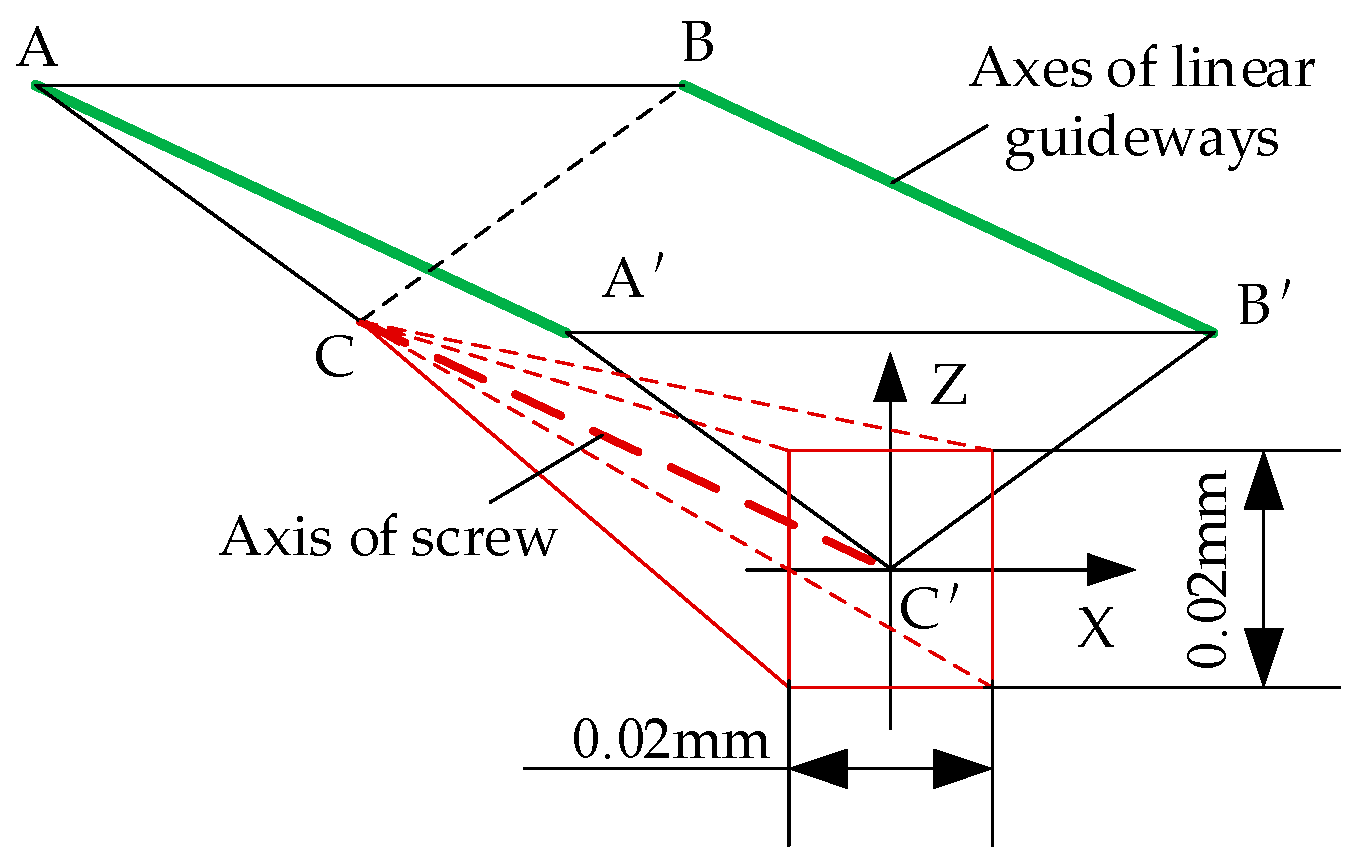
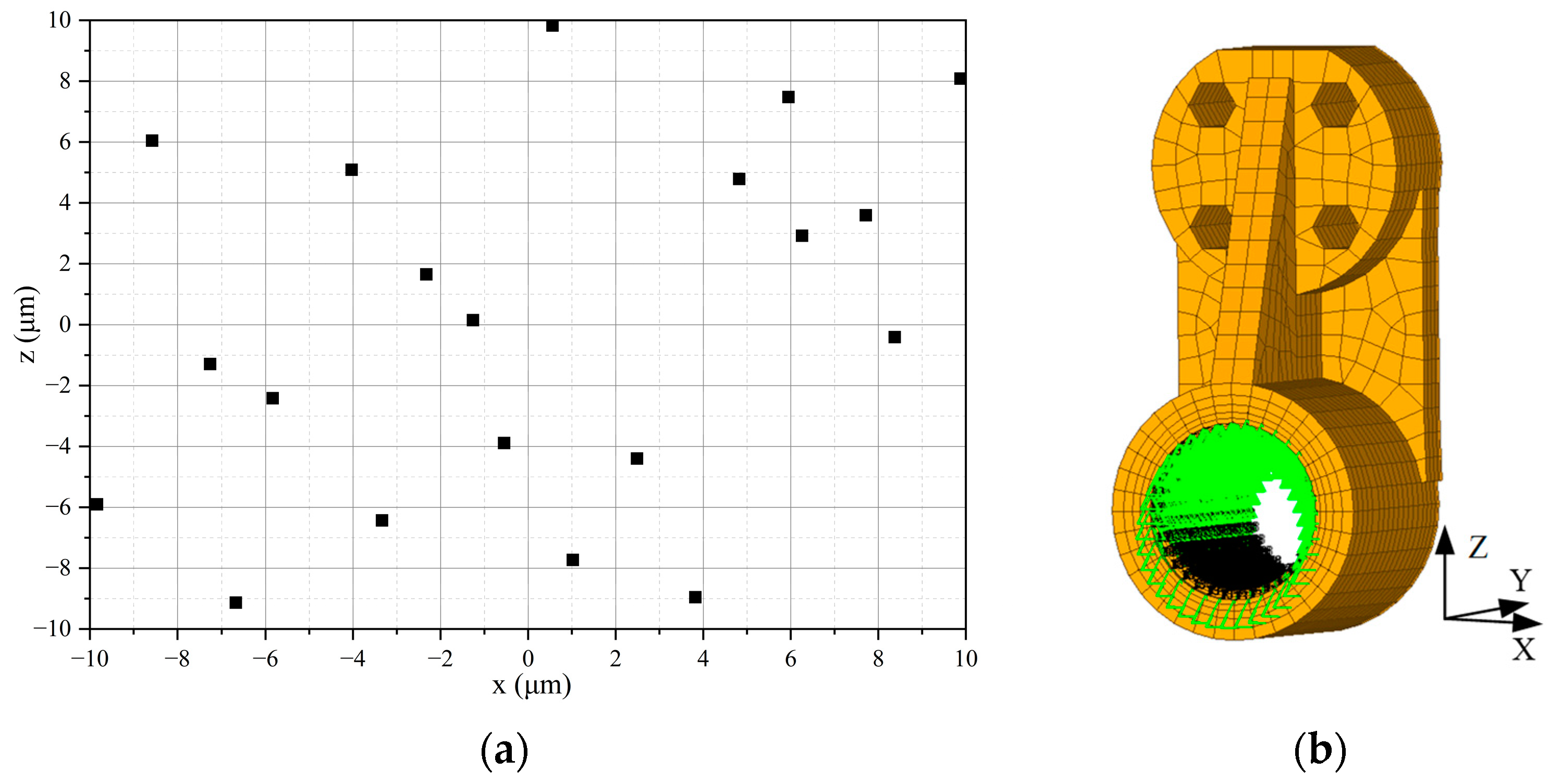
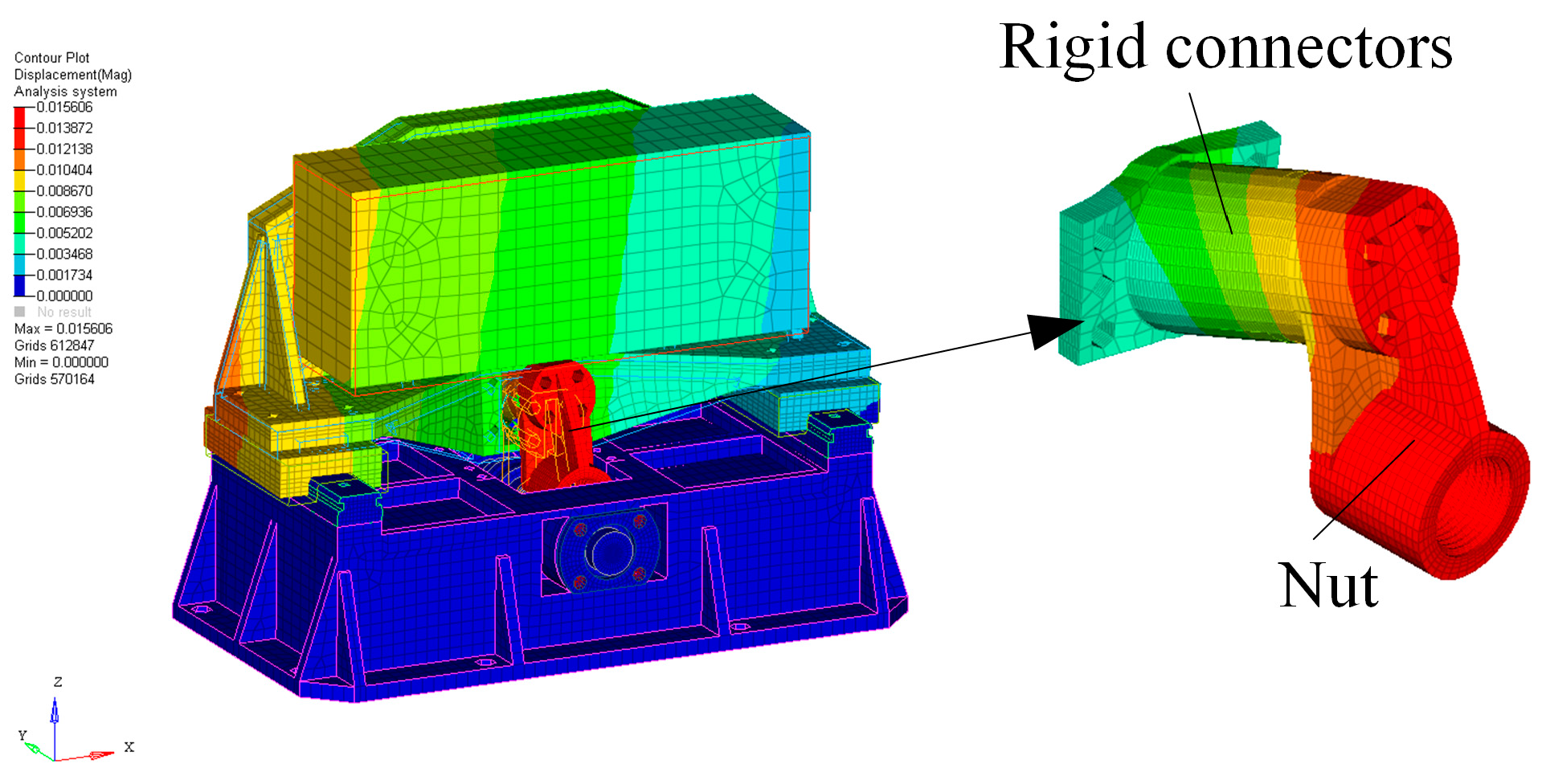
According to the above research, we can find that the research on mechanical focusing technology at home and abroad is mainly limited to the transmission mode, the form of the flexible hinge, etc., and there are few studies on how to improve the tilt accuracy of the focusing mechanism. Even though some individual literature has tested the tilt error of the focusing mechanism, the test results reached 12″–18″. It is challenging to meet the strict tilt error requirements of optical systems. Therefore, it is worth further research and exploration to study the factors that affect the tilt error of the focusing mechanism, improve the design scheme, and reduce the tilt error of the focusing mechanism. To study the causes of the tilt error of the focusing mechanism, it is often necessary to use the finite element method to model the system. As the core component of the focusing mechanism, the accuracy of the modeling of the linear guideway directly affects the conclusion of the analysis. Pawełko P et al. [
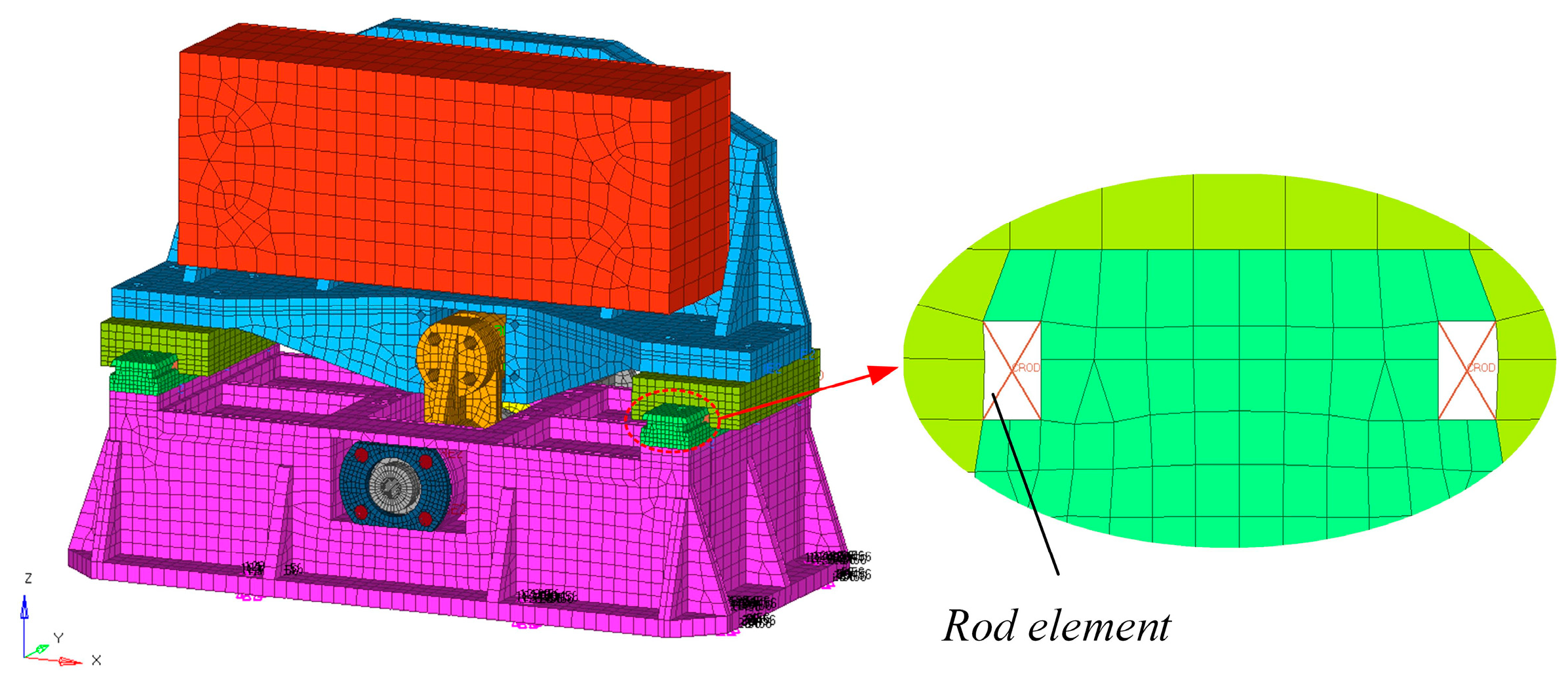
14] proposed using rod elements to model the linear guideway. Calculation efficiency is greatly improved by ensuring accuracy. This paper will also use the theory to build and verify a model.
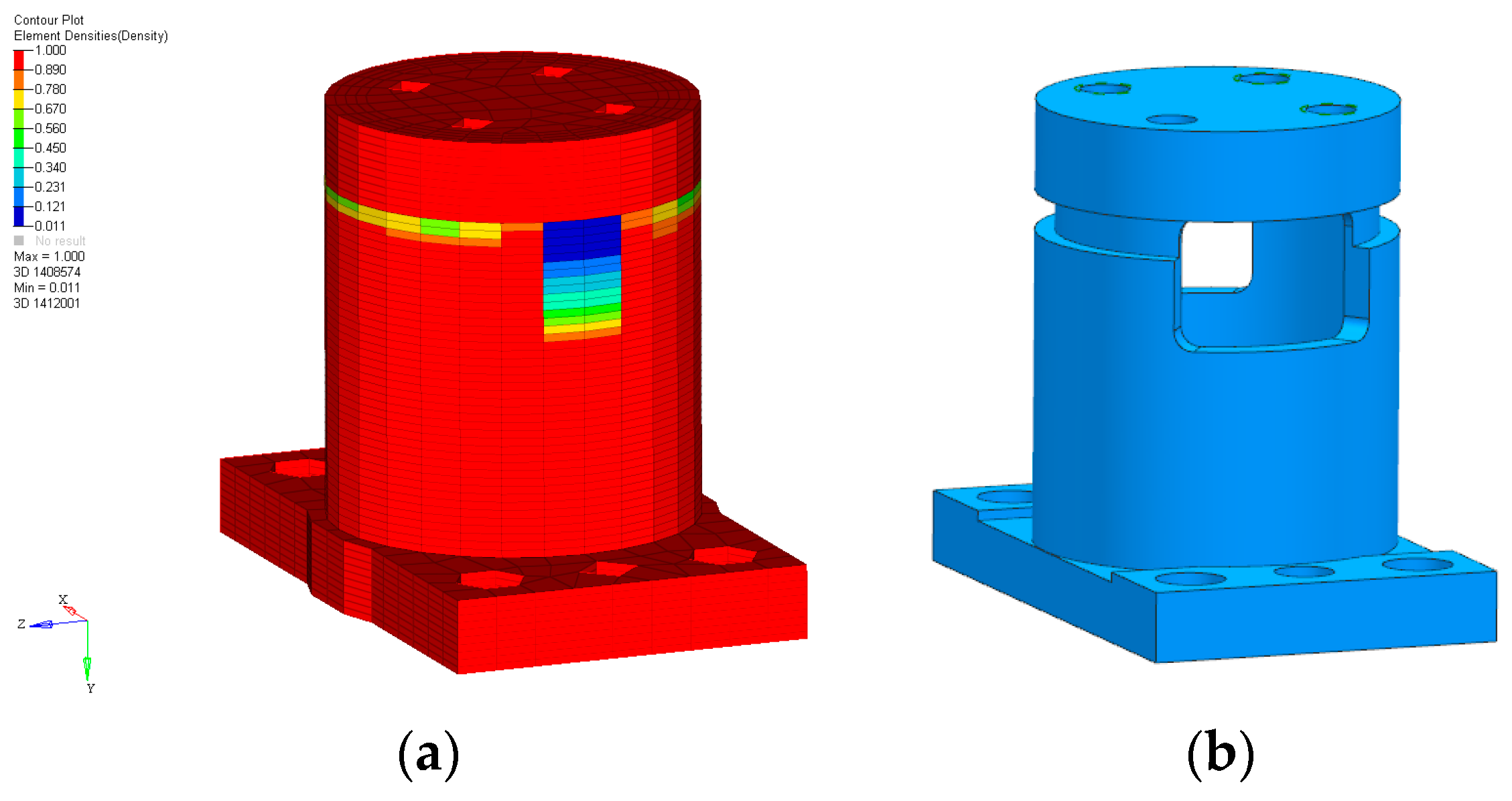
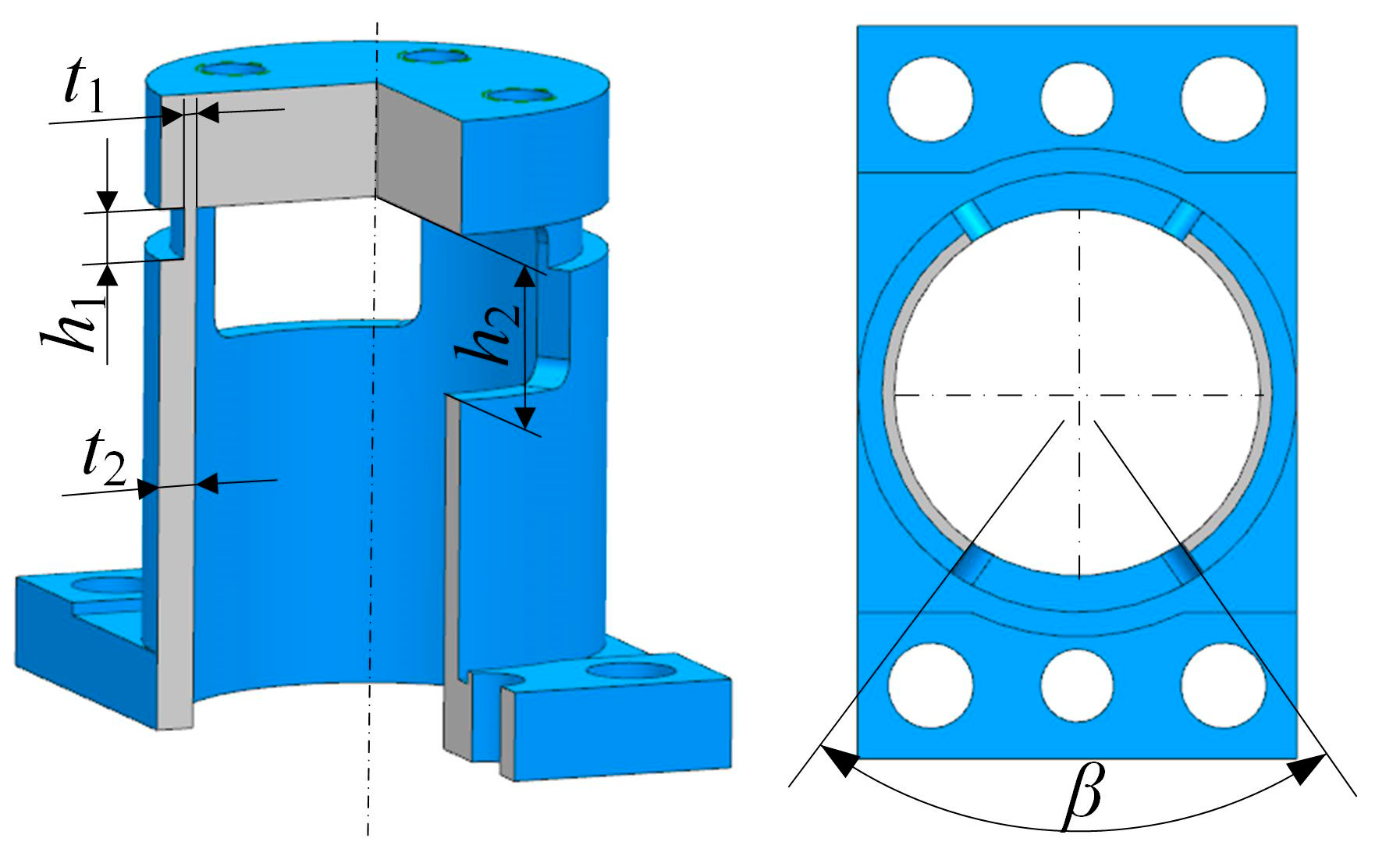
Within focusing mechanism studies, the flexible hinge is mainly used as a “guiding element” to ensure linear motion. In the field of mirror research, the flexible hinge, as a part of the support structure of the mirror, is usually used to reduce the influence of factors such as temperature change and uneven mounting surfaces on the reflective mirror type [
15,
16]. The interference between the guide and drive elements directly affects the focusing mechanism’s tilt accuracy. Therefore, by combining the flexible hinge with the focusing mechanism, this paper proposes using the flexible hinge to decouple the interference between the guide element and the drive element, which can provide a new idea for improving the tilt accuracy of the focusing mechanism. In the optimization design process of flexible hinges, to efficiently find the flexible hinge size with the best performance, this paper adopts the combination of topology optimization and integration optimization to optimize, and topology optimization was used to find the optimal structural configuration that meets the requirements quickly. Based on the optimal configuration, the integrated optimization method automatically facilitates data interaction and optimization among various models to attain the global optimal design of the system [
17].
The remaining sections of this paper are organized as follows:
Section 2 comprehensively explains the requirements, scheme, and finite element modeling simulation of the focusing mechanism.
Section 3 explicitly addresses the flexible hinge’s topology and integration optimization in the focusing mechanism.
Section 4 evaluates the overall functioning of the focusing mechanism through appropriate tests and inspections.