Research on Dynamic Modelling, Characteristics and Vibration Reduction Application of Hot Rolling Mills Considering the Rolling Process
Abstract
1. Introduction
- A torsional-vertical-horizontal coupled dynamic model of a rolling mill considering the rolling process is established and validated by simulation and field experiment.
- The influence rules of some typical parameters of the rolling process on the vibration of the rolling mill are revealed.
- Based on the theoretical findings, an application is performed for a hot continuous finishing mill on site to suppress its vibration.
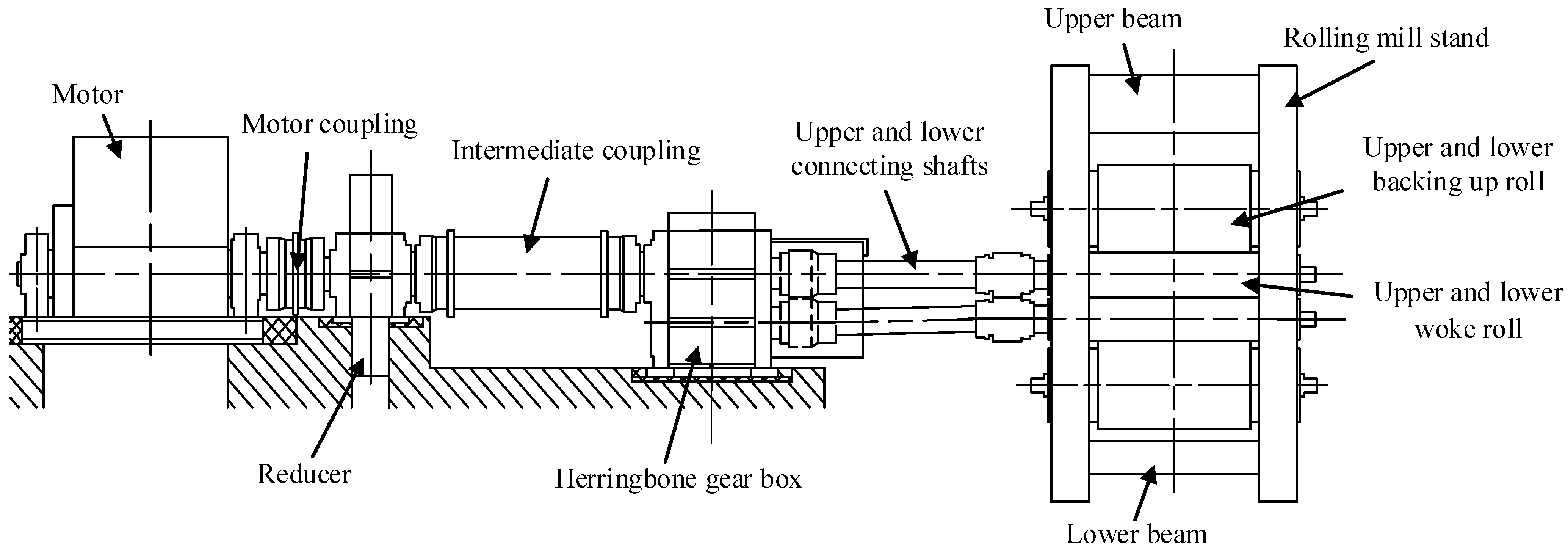
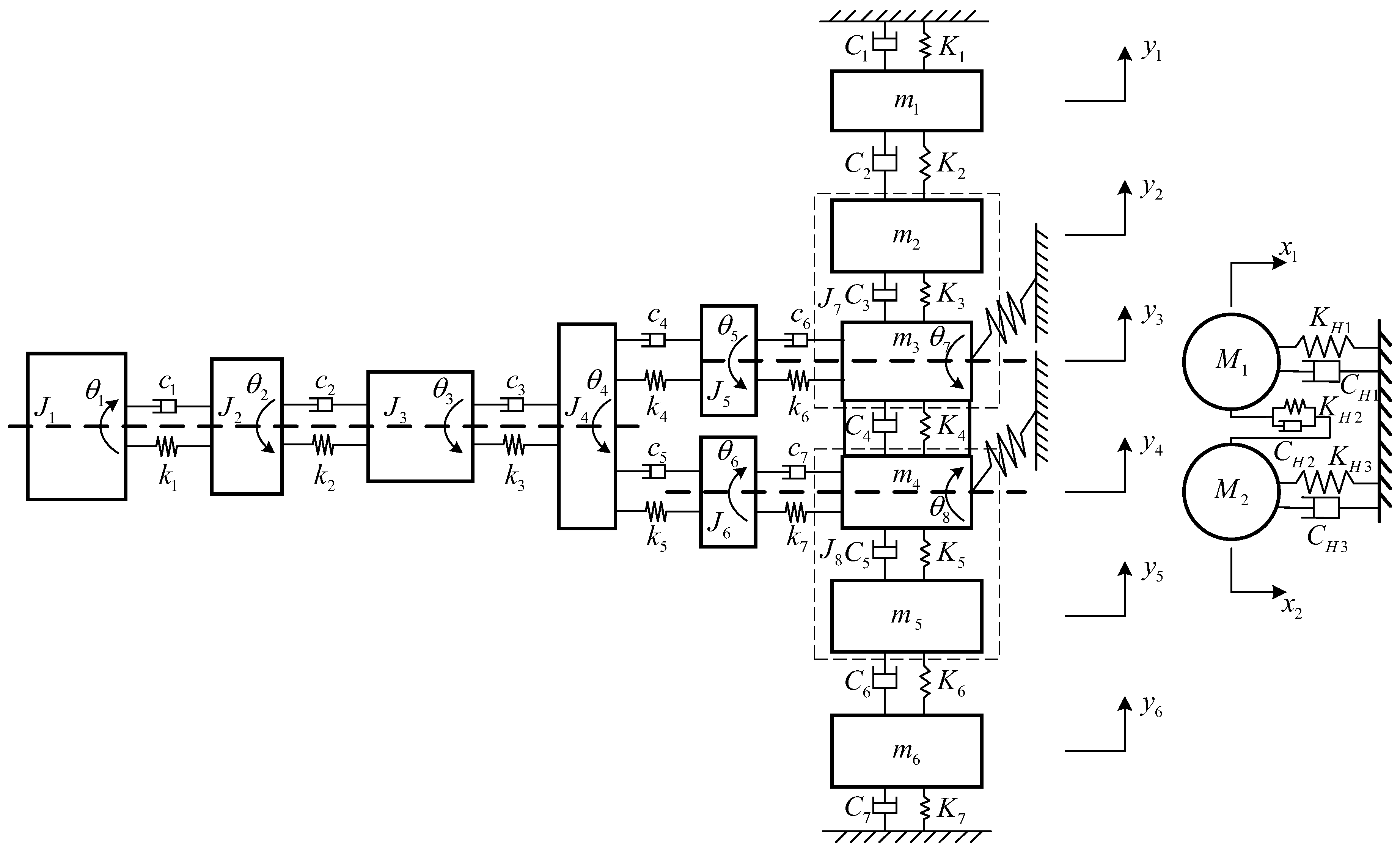
2. Dynamic Model Establishment and Verification
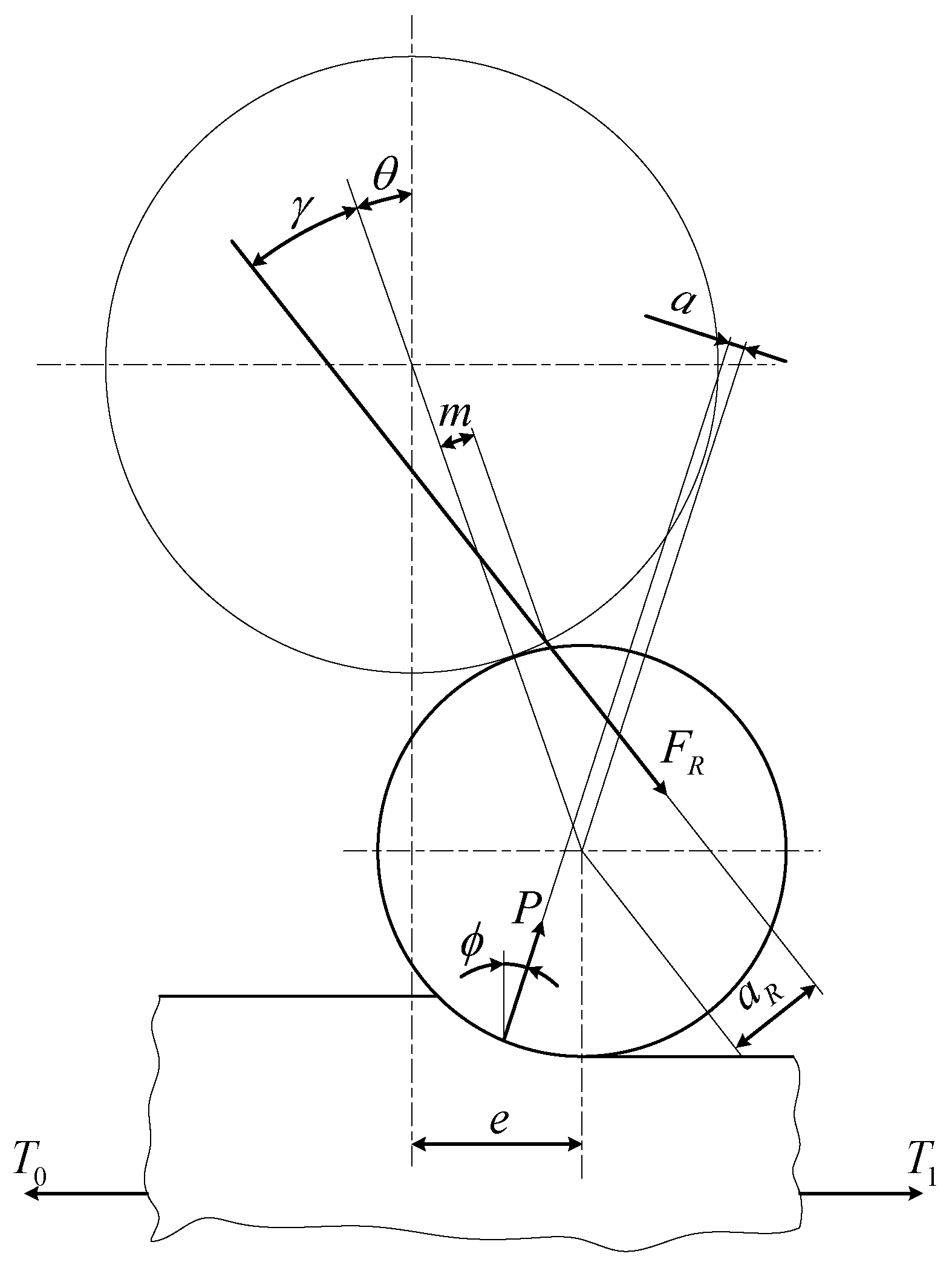
2.1. Coupled Dynamic Model
2.2. Model Verification
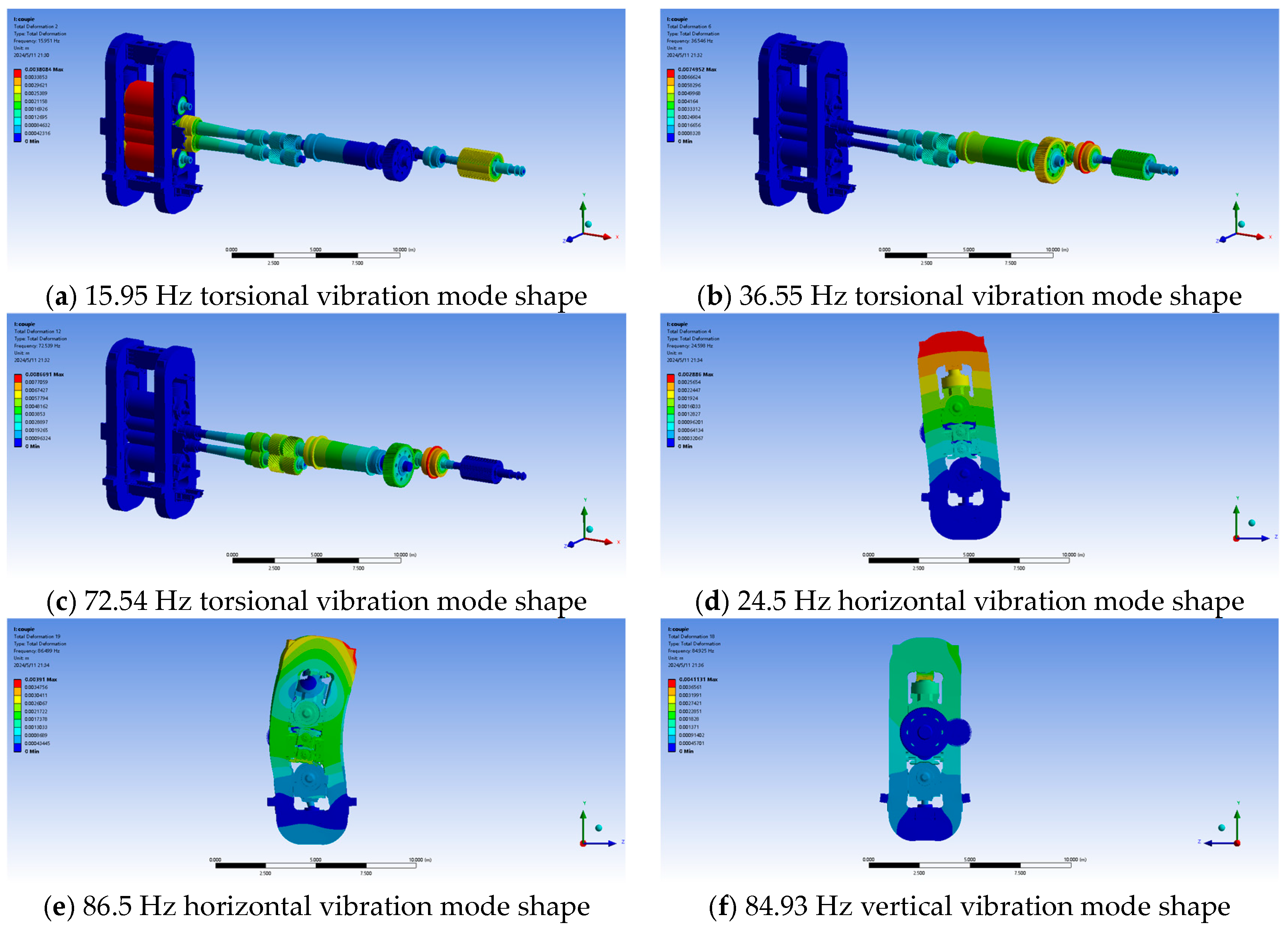
2.2.1. Finite Element Simulation Verification
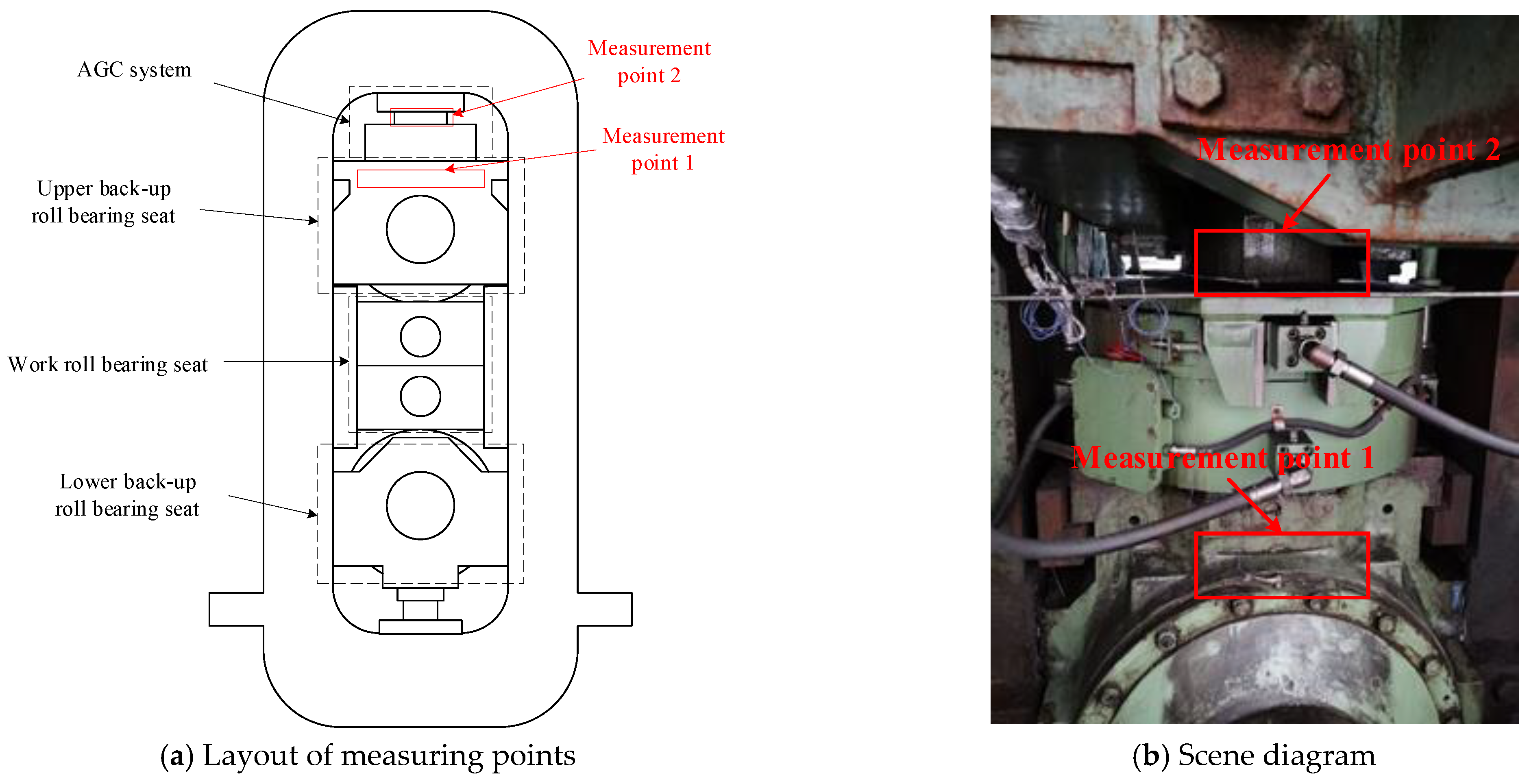
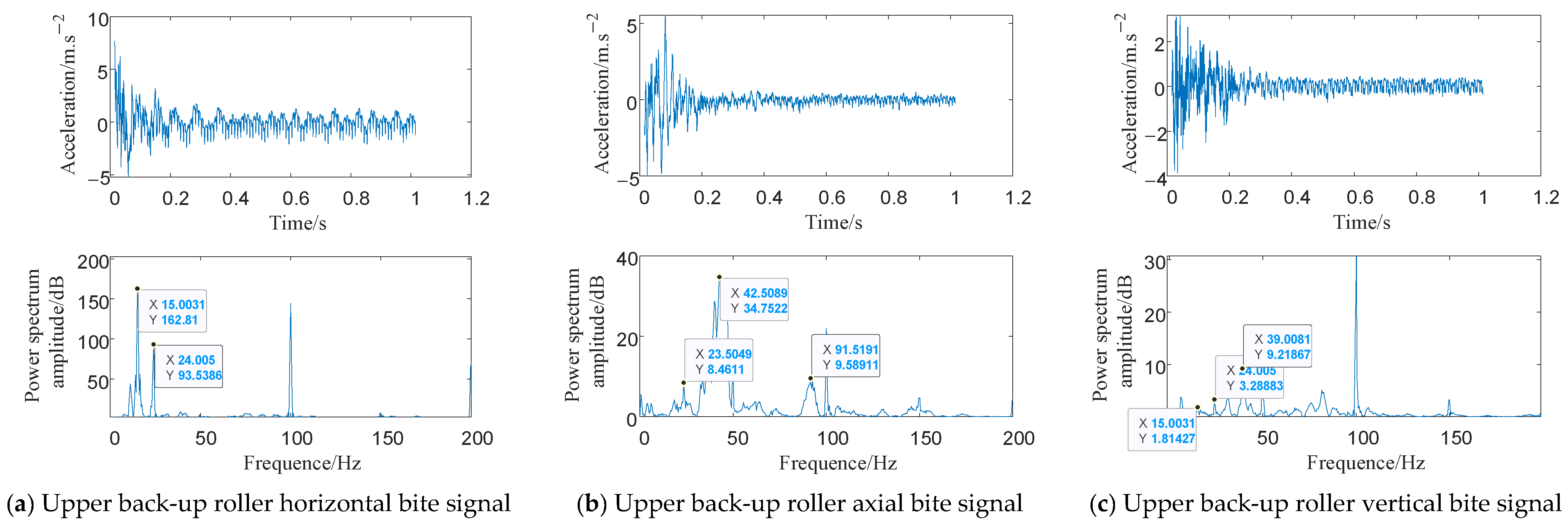
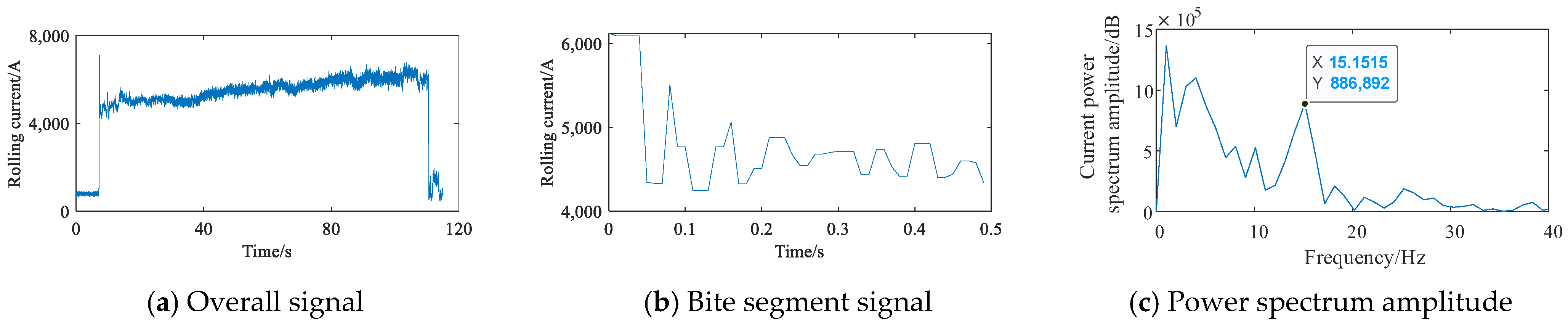
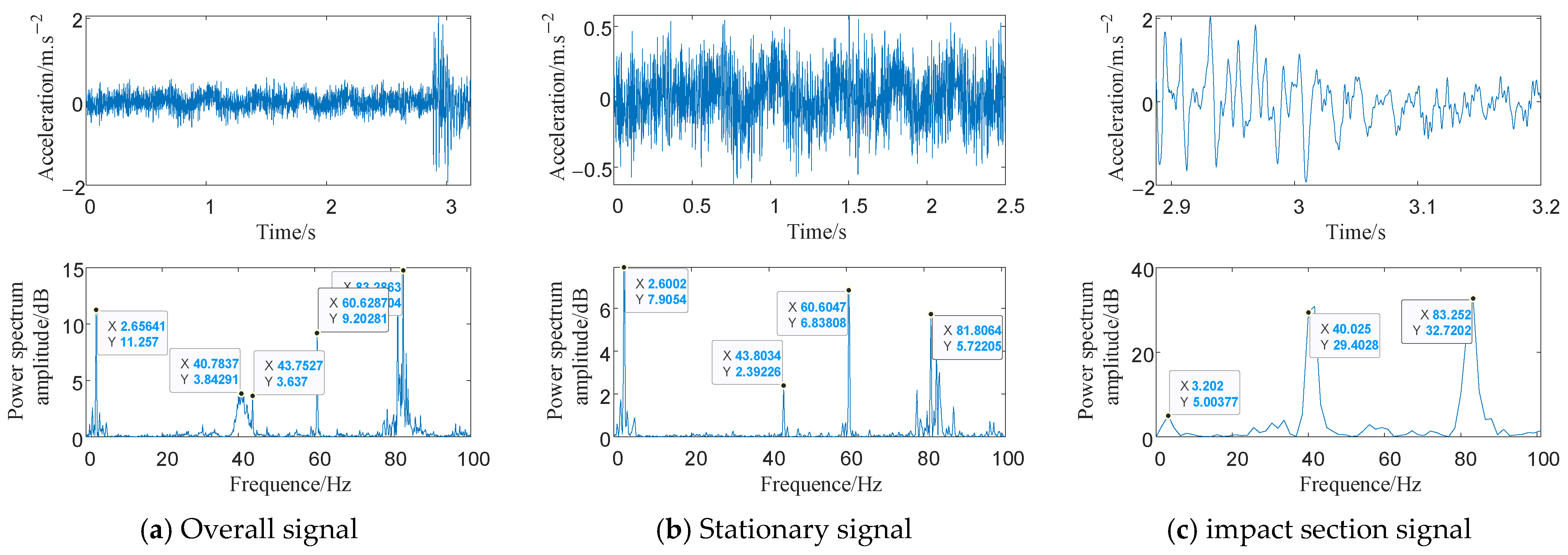
2.2.2. Experimental Verification
3. Analysis of Dynamic Response of the Rolling Mill System
3.1. Relationship between Rolling Excitations and Rolling Process Parameters
3.2. Research on the Influence of Rolling Process Parameters
4. On-Site Vibration Reduction Application in Rolling Mills
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, G.; Bao, J.; Li, W.; Wang, Z.; Meng, X. Coupled vibration characteristics analysis of hot rolling mill with structural gap. Shock Vib. 2021, 2021, 5581398. [Google Scholar] [CrossRef]
- Hou, D.; Sun, Z.; Mu, J.; Shi, P. Vertical Vibration Characteristics of strip rolling mill under compound roll bearing failure. ISIJ Int. 2022, 62, 179–190. [Google Scholar] [CrossRef]
- Qi, J.-B.; Wang, X.-X.; Yan, X.-Q. Influence of mill modulus control gain on vibration in hot rolling mills. J. Iron Steel Res. Int. 2020, 27, 528–536. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, R.; Zhang, H.; Peng, Y. Vibration prediction and analysis of strip rolling mill based on XGBoost and Bayesian optimization. Complex Intell. Syst. 2023, 9, 133–145. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, T.; Huang, Q.-X. Resonance Analysis of Horizontal Nonlinear Vibrations of Roll Systems for Cold Rolling Mills under Double-Frequency Excitations. Mathematics 2023, 11, 1626. [Google Scholar] [CrossRef]
- Kimura, Y.; Sodani, Y.; Nishiura, N.; Ikeuchi, N.; Mihara, Y. Analysis of chatter in tandem cold rolling mills. ISIJ Int. 2003, 43, 77–84. [Google Scholar] [CrossRef]
- Fan, X.; Zang, Y.; Jin, K. Rolling process and its influence analysis on hot continuous rolling mill vibration. Appl. Phys. A 2016, 122, 1–8. [Google Scholar] [CrossRef]
- Zeng, L.; Zang, Y.; Gao, Z. Multiple-Modal-Coupling Modeling and Stability Analysis of Cold Rolling Mill Vibration. Shock Vib. 2016, 2016, 2347386. [Google Scholar] [CrossRef]
- Peng, R.; Zhang, X.; Shi, P. Vertical–horizontal coupling vibration of hot rolling mill rolls under multi-piecewise nonlinear constraints. Metals 2021, 11, 170. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, S.; Wang, X.; Yan, X. Research on Multi-System Coupling Vibration of a Hot Tandem Mill. Machines 2024, 12, 302. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Ma, J. Dynamical responses for a vertical vibration model of a four-roller cold rolling mill under combined stochastic and harmonic excitations. Probabilistic Eng. Mech. 2023, 73, 103480. [Google Scholar] [CrossRef]
- Wu, J.; Yan, X. Coupling vibration model for hot rolling mills and its application. J. Vibroeng. 2019, 21, 1795–1809. [Google Scholar] [CrossRef]
- Qian, C.; Zhang, L.; Hua, C.; Bai, Z. Adaptive fuzzy vertical vibration suppression control of the mechanical-hydraulic coupling rolling mill system with input dead-zone and output constraints. IEEE Access 2020, 8, 85793–85801. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, Y. Dynamic rolling model based on uniform deformation. J. Manuf. Process. 2020, 58, 1334–1347. [Google Scholar] [CrossRef]
- Wang, L.; Yan, X.; Jia, X.; Wang, X. Dynamic Amplitude-Frequency Characteristics of Vertical–Torsional Coupling System with Harmonic Response in Hot Tandem Mill. Electronics 2022, 11, 3031. [Google Scholar] [CrossRef]
- Xu, H.; Cui, L.-L.; Shang, D.-G. A study of nonlinear coupling dynamic characteristics of the cold rolling mill system under different rolling parameters. Adv. Mech. Eng. 2017, 9, 1687814017713706. [Google Scholar] [CrossRef]
- Jia, X.; Wang, S.; Yan, X.; Wang, L.; Wang, H. Research on dynamic response of cold rolling mill with dynamic stiffness compensation. Electronics 2023, 12, 599. [Google Scholar] [CrossRef]
- Sun, C.; Zhao, W.; Huang, D.; Zhang, H. Stability of nonlinear vibrations induced by rolling force in a precise cold mill system. Appl. Math. Model. 2023, 119, 196–217. [Google Scholar] [CrossRef]
- He, D.-P.; Xu, H.-D.; Wang, M.; Wang, T.; Ren, C.-R.; Wang, Z.-H. Application of dynamic vibration absorber for vertical vibration control of corrugated rolling mill. J. Iron Steel Res. Int. 2023, 30, 736–748. [Google Scholar] [CrossRef]
- Wang, M.; Xu, H.; He, D.; Wang, T.; Zhang, J. Design of a damped vibration absorber to control the resonant vibration of roll. Mech. Syst. Signal Process. 2022, 178, 109262. [Google Scholar] [CrossRef]
- Xu, H.; Wang, M.; He, D.; Wang, T. Vibration transmission and energy dissipation of roll controlled by particle damping absorber. Int. J. Mech. Sci. 2023, 249, 108264. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, W.; Huang, D.; Sun, C.; Fan, J. Vertical nonlinear vibration analysis of cold rolling mill considering structural gap and dynamic rolling force. J. Manuf. Process. 2023, 108, 280–291. [Google Scholar] [CrossRef]
- Lu, X.; Sun, J.; Wei, Z.; Li, G.; Zhang, D. Effect of minimum friction coefficient on vibration stability in cold rolling mill. Tribol. Int. 2021, 159, 106958. [Google Scholar] [CrossRef]
- Jia, X.; Yan, X.; Wang, L. Influence Factors of Inherent Characteristics of F5 Cold-Rolling Mill’s Main Drive System. Math. Probl. Eng. 2022, 2022, 2082210. [Google Scholar] [CrossRef]
- Lu, X.; Sun, J.; Li, G.; Wang, Q.; Zhang, D. Dynamic analysis of vibration stability in tandem cold rolling mill. J. Mech. Work. Technol. 2019, 272, 47–57. [Google Scholar] [CrossRef]
- Wright, J. Mill drive system to minimize torque amplification. Iron Steel Eng. 1976, 53, 56–60. [Google Scholar]
- Yuan, G.M.; Wang, J.; Xiao, H.; Li, M.L. Research on online model of vertical rolling force in hot strip roughing trains. Adv. Mater. Res. 2011, 145, 198–203. [Google Scholar] [CrossRef]
- Arnold, R.R.; Whitton, P.W. Spread and roll force in rod rolling. Met. Technol. 1975, 2, 143–149. [Google Scholar] [CrossRef]
- Sims, R.B. The Calculation of roll force and torque in hot rolling mills. Proc. Inst. Mech. Eng. 1954, 168, 191–200. [Google Scholar] [CrossRef]

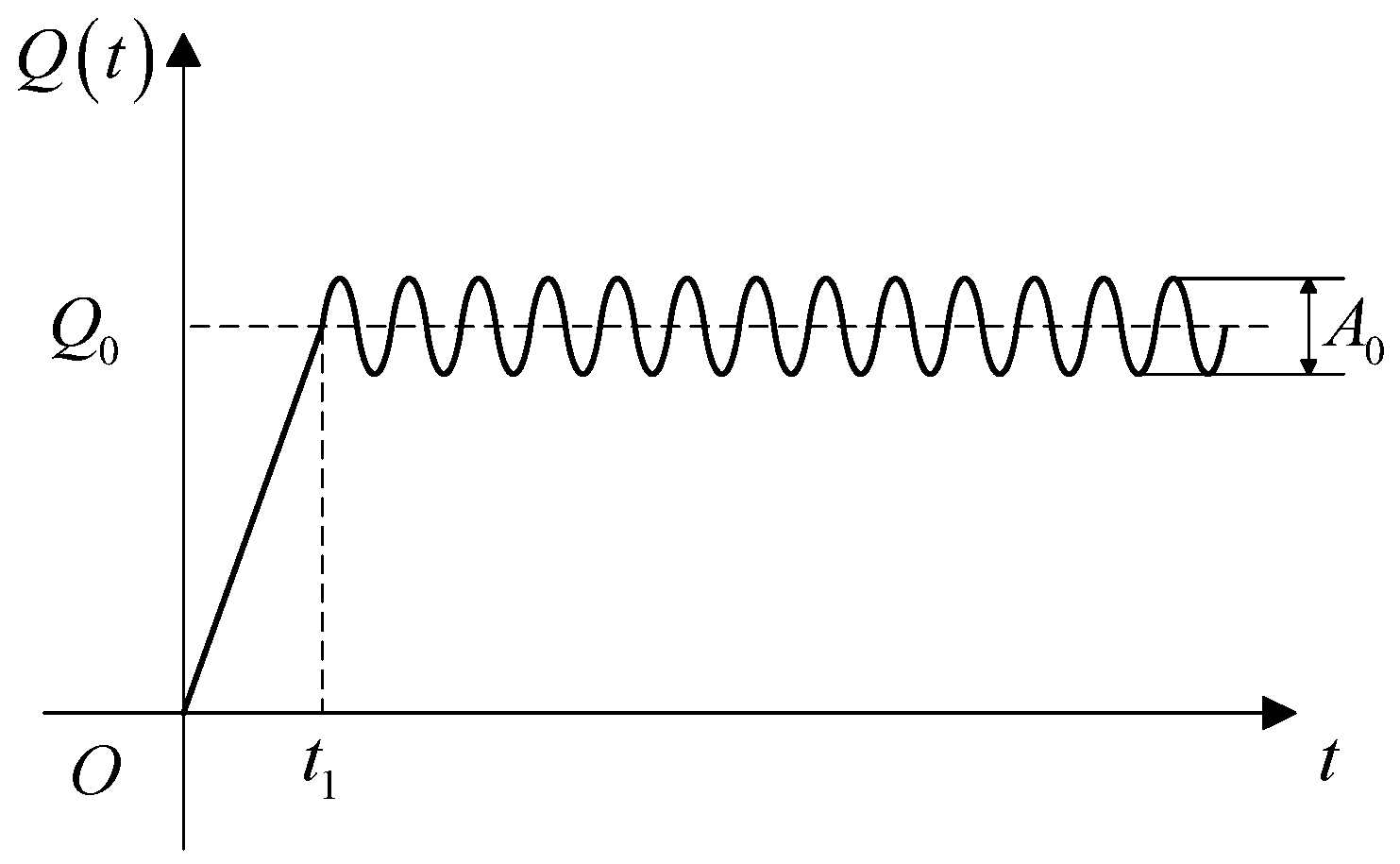
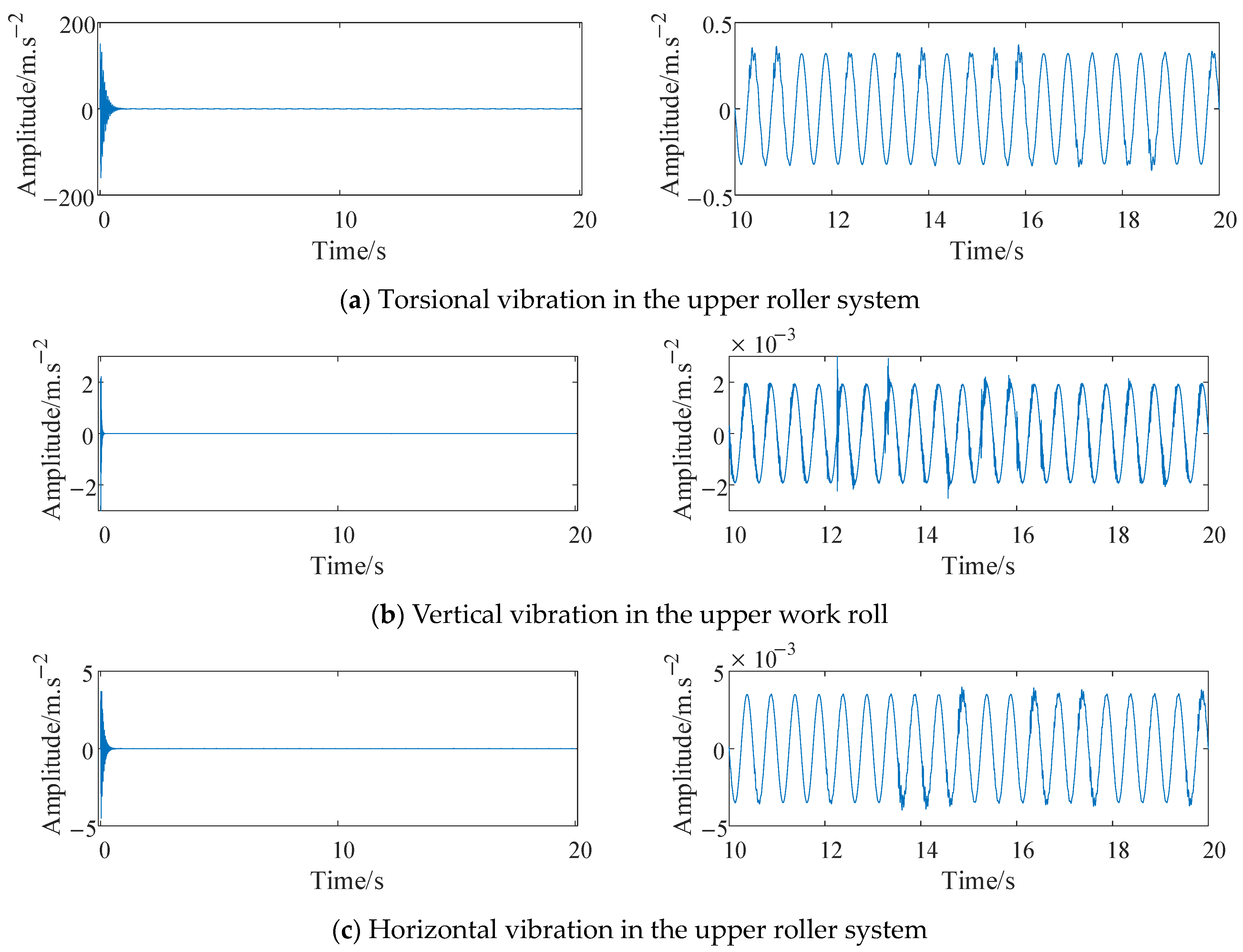
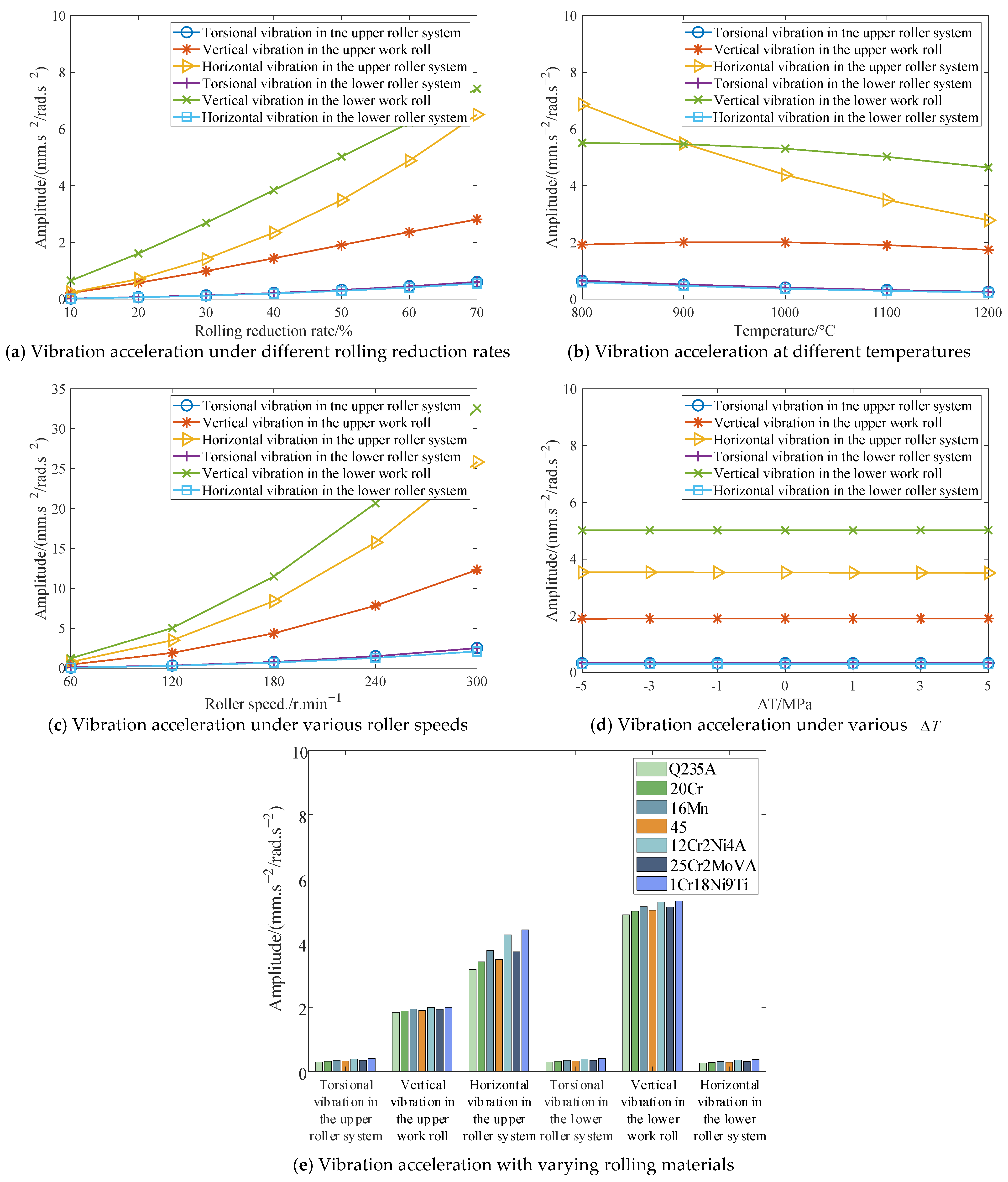
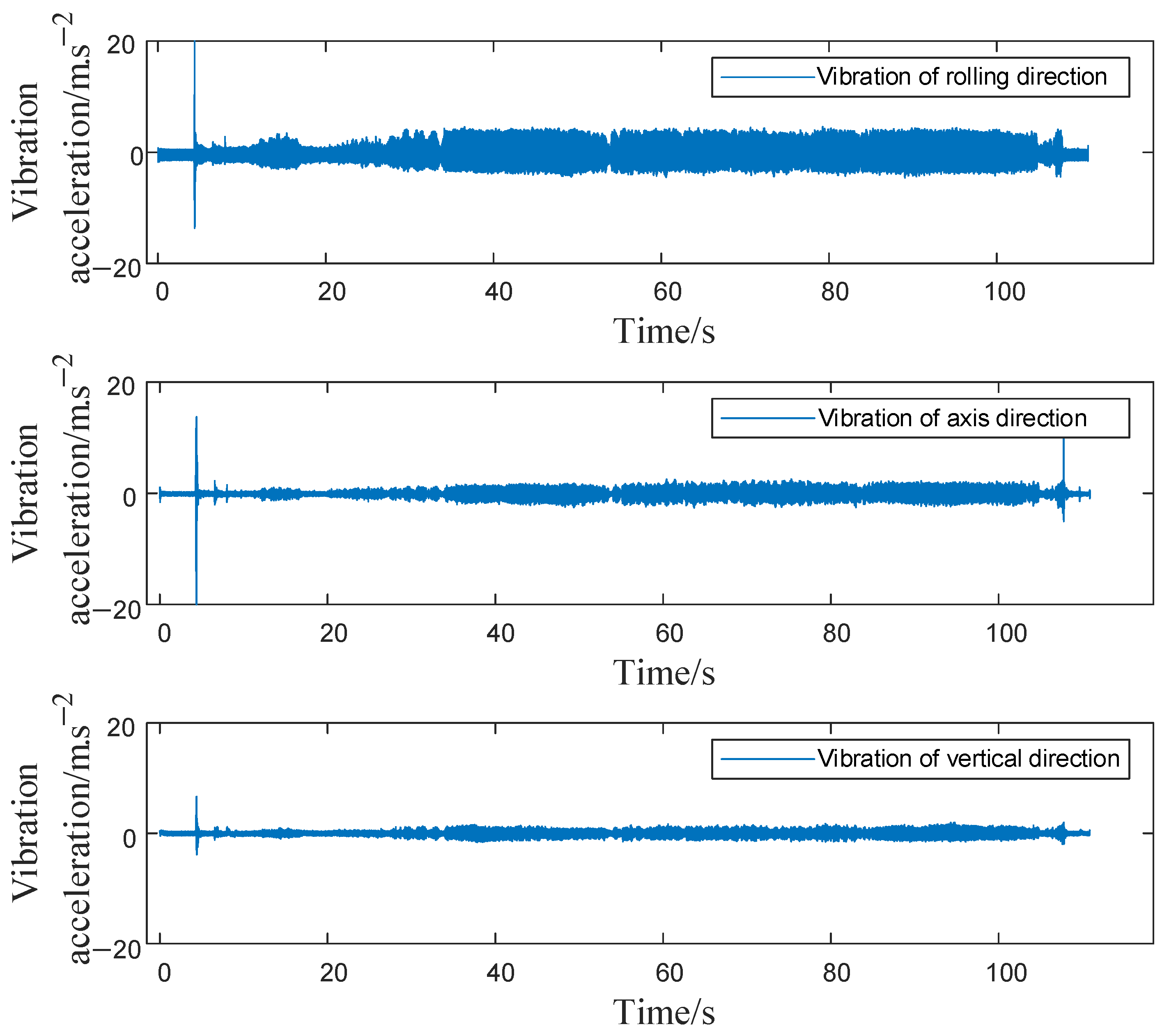
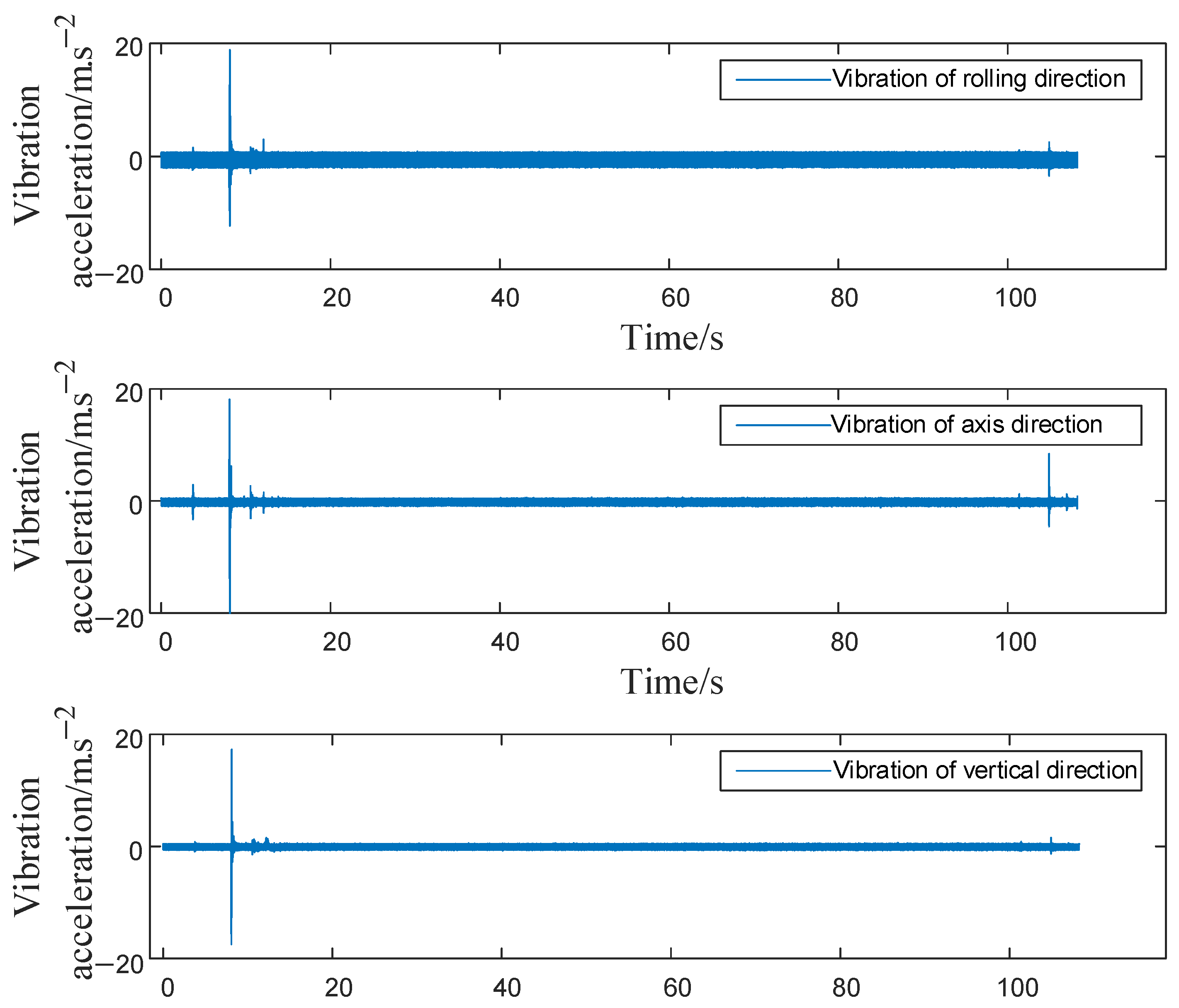
| Moment of Inertia/(kg·m2) | Effective Mass/(kg) | Effective Stiffness/(N·m/rad) | Effective Stiffness/(N·m−1) |
|---|---|---|---|
| — | |||
| — | — | — |
| NF | Value (Hz) | NF | Value (Hz) |
|---|---|---|---|
| 1st-order torsional mode | 15.8 | 1st-order vertical mode | 84.6 |
| 2nd-order torsional mode | 35.5 | 2nd-order vertical mode | 132.8 |
| 3rd-order torsional mode | 72.5 | 3rd-order vertical mode | 191.6 |
| 4th-order torsional mode | 112 | 1st-order horizontal mode | 25.6 |
| 5th-order torsional mode | 146.7 | 2nd-order horizontal mode | 91.1 |
| NF | Theory Model (Hz) | Finite Element Model (Hz) | Error Rate (%) |
|---|---|---|---|
| 1st-order torsional | 15.8 | 15.95 | 0.95 |
| 2nd-order torsional | 35.5 | 36.55 | 2.96 |
| 3rd-order torsional | 72.5 | 72.54 | 0.001 |
| 1st-order horizontal | 25.6 | 24.5 | 4.49 |
| 2nd-order horizontal | 91.1 | 86.5 | 5.05 |
| 1st-order vertical | 84.6 | 84.93 | 0.39 |
| 2nd-order vertical | 132.8 | — | — |
| Parameter | Value |
|---|---|
| Base deformation resistance (45 steel) | 162 MPa |
| Deformation resistance formula coefficients (45 steel) | A = 3.539; V = −2.78; C = −0.157; J = 0.226; E = 1.37; N = 0.342 |
| Work roll radius | 0.425 m |
| Billet temperature | 1100 °C |
| Reduction rate | 50% |
| Friction circle radius | 0.0322 m |
| Backup roll radius | 0.8 m |
| Force arm | 0.0326 m |
| Rolling speed | 120 r/min |
| Rolled piece dimension | 6 mm × 1250 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Zhou, D.; Yu, D.; Xiao, H. Research on Dynamic Modelling, Characteristics and Vibration Reduction Application of Hot Rolling Mills Considering the Rolling Process. Machines 2024, 12, 629. https://doi.org/10.3390/machines12090629
Lu Z, Zhou D, Yu D, Xiao H. Research on Dynamic Modelling, Characteristics and Vibration Reduction Application of Hot Rolling Mills Considering the Rolling Process. Machines. 2024; 12(9):629. https://doi.org/10.3390/machines12090629
Chicago/Turabian StyleLu, Zhiwen, Duolong Zhou, Danfeng Yu, and Han Xiao. 2024. "Research on Dynamic Modelling, Characteristics and Vibration Reduction Application of Hot Rolling Mills Considering the Rolling Process" Machines 12, no. 9: 629. https://doi.org/10.3390/machines12090629
APA StyleLu, Z., Zhou, D., Yu, D., & Xiao, H. (2024). Research on Dynamic Modelling, Characteristics and Vibration Reduction Application of Hot Rolling Mills Considering the Rolling Process. Machines, 12(9), 629. https://doi.org/10.3390/machines12090629





