A Semi-Analytical Loaded Contact Model and Load Tooth Contact Analysis Approach of Ease-Off Spiral Bevel Gears
Abstract
1. Introduction
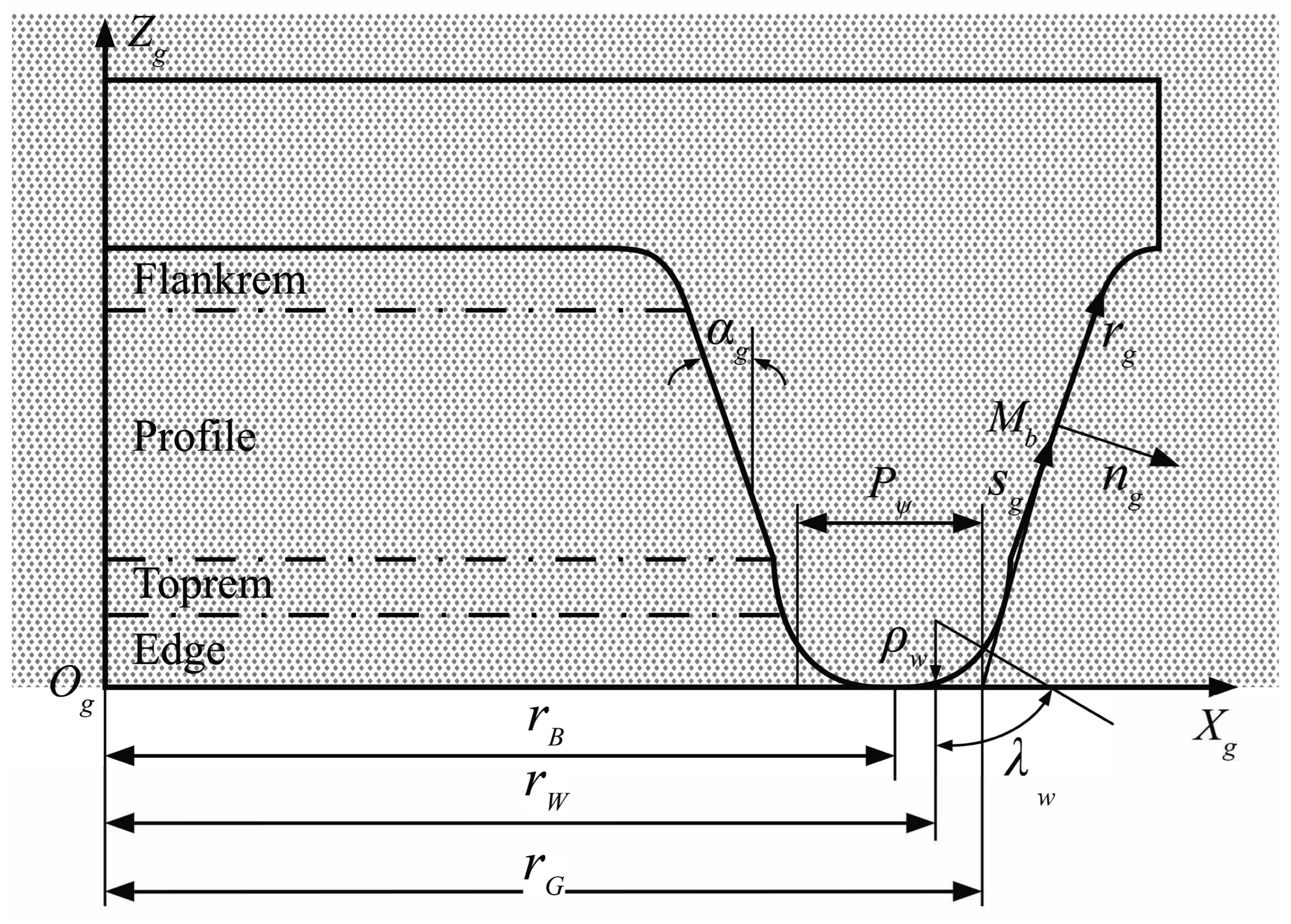
2. Generation of Gear Tooth Profiles
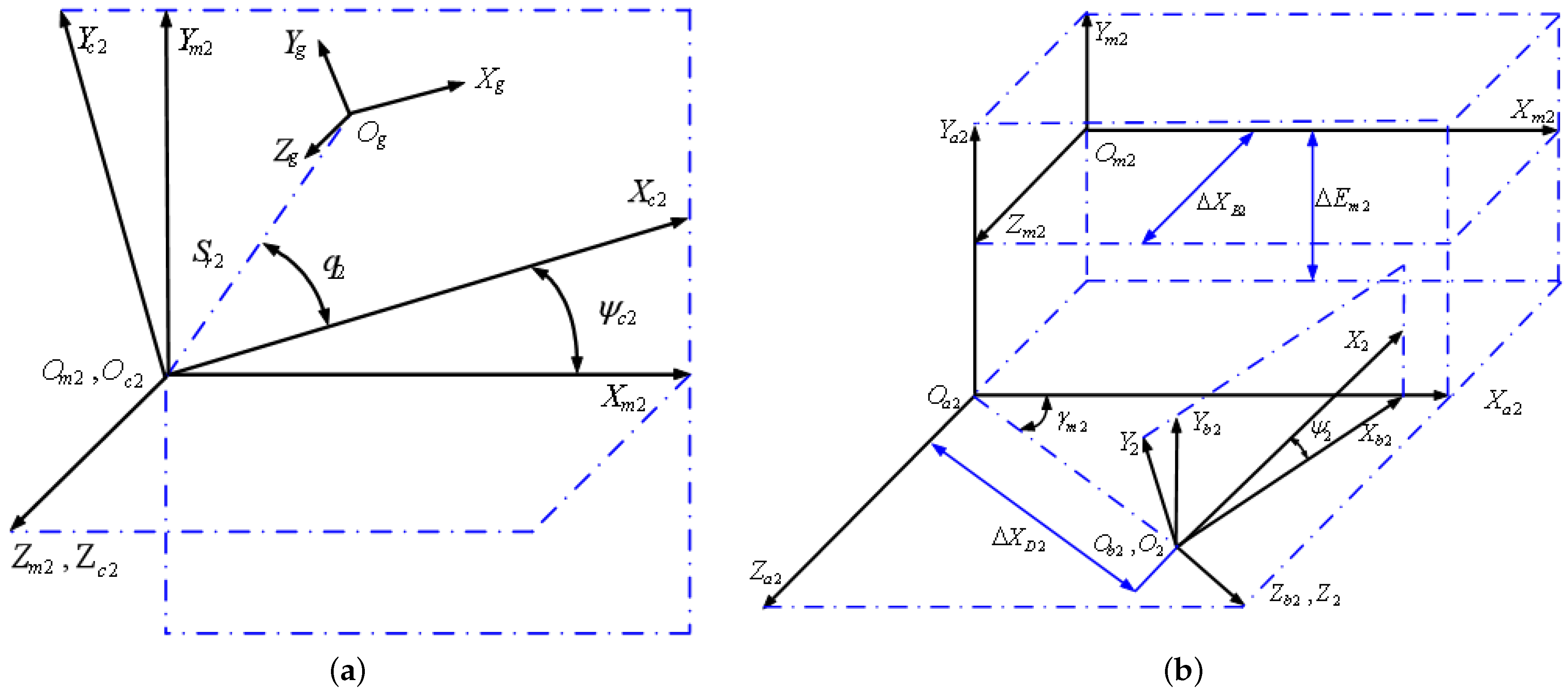
2.1. The Dimensional Configuration of Spiral Bevel Gears
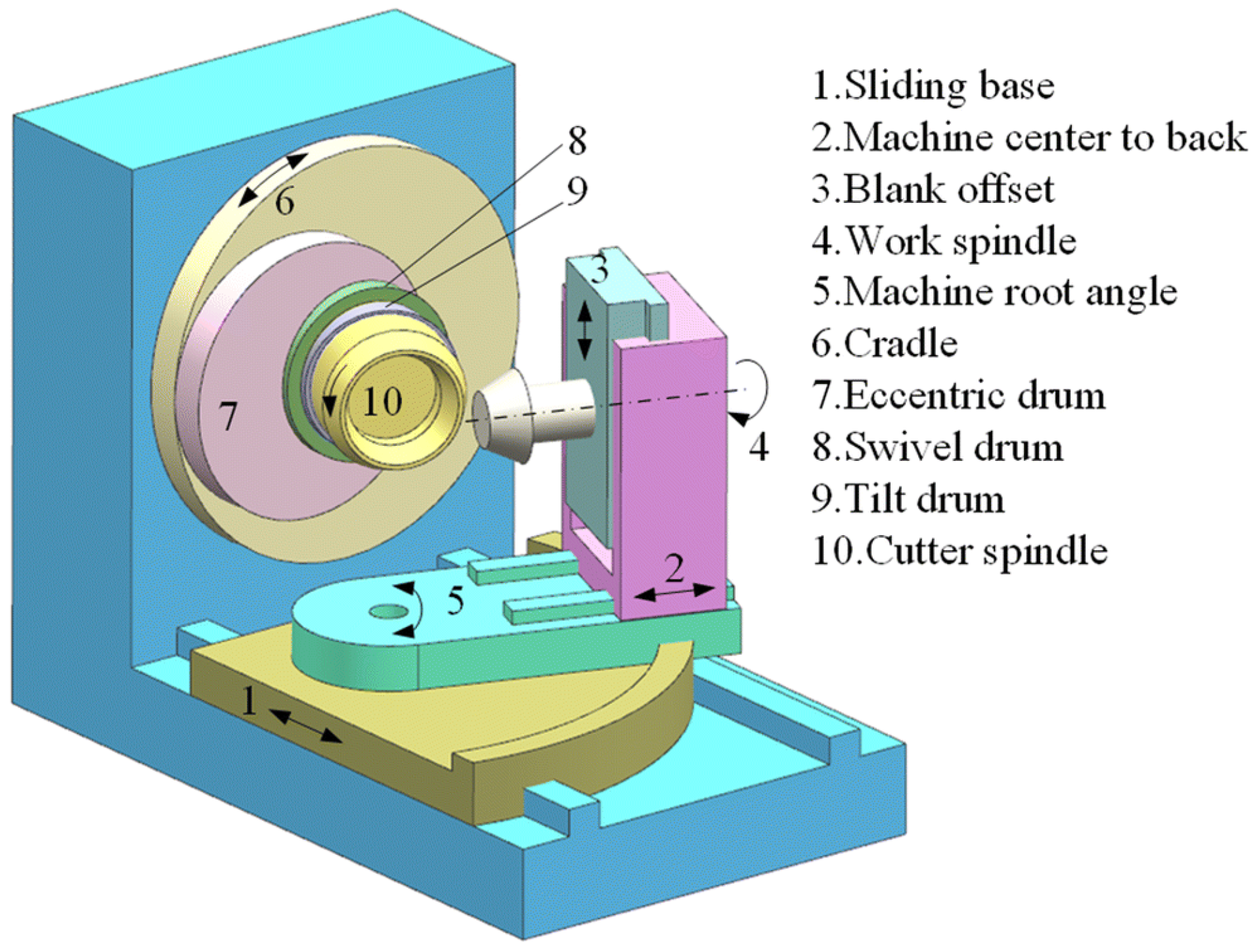
2.2. The Geometry of Cutting Tools and Their Relative Movement
2.3. Kinematics of Universal Motion Concept (UMC)
2.4. The Simulation of Generation Process
3. Semi-Analytical Loaded Contact Model Based on Ease-Off Topography
3.1. Theoretical Ease-Off Topography
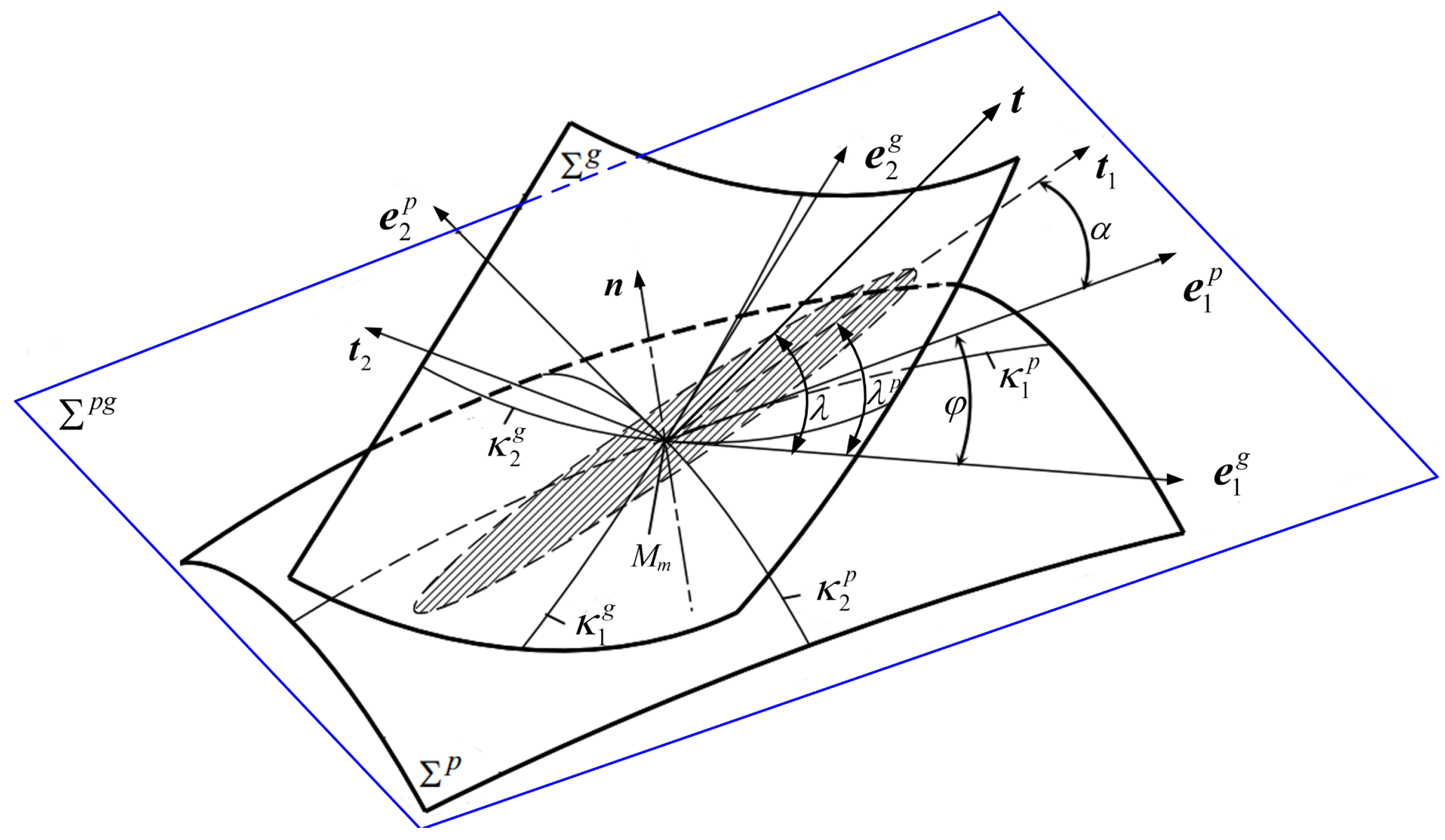
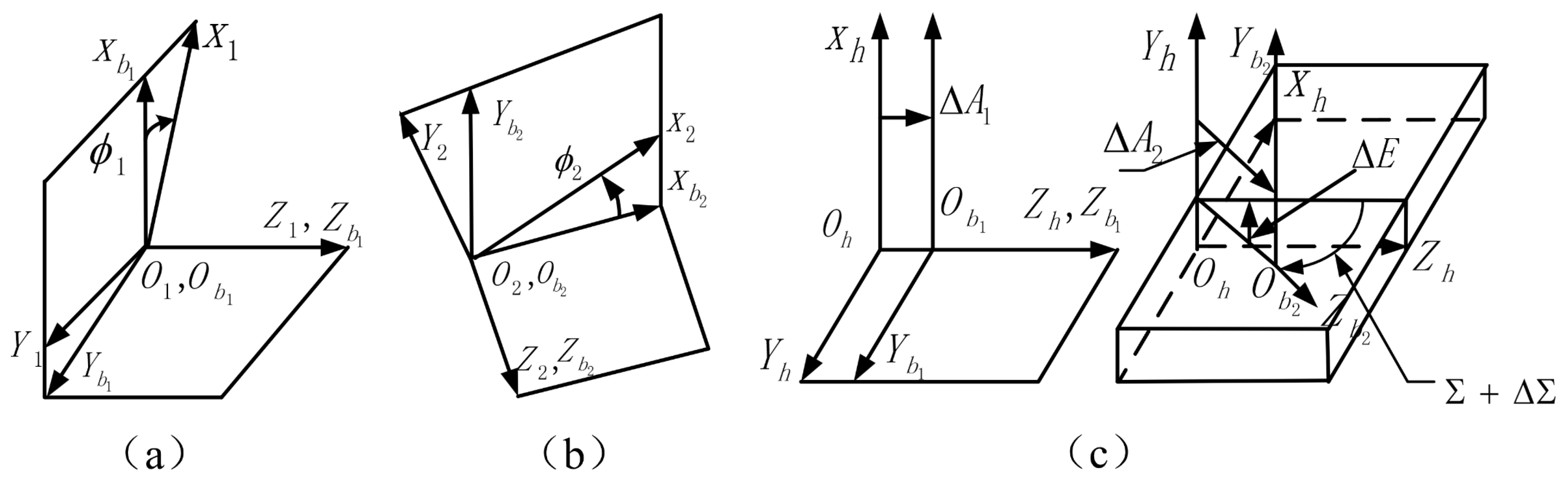
3.2. Calculation of the Contact Line Direction
3.3. Deformation Coordination Equation of a Contact Ellipse
3.4. Semi-Analytical Contact Model for Loaded Tooth Contact Analysis
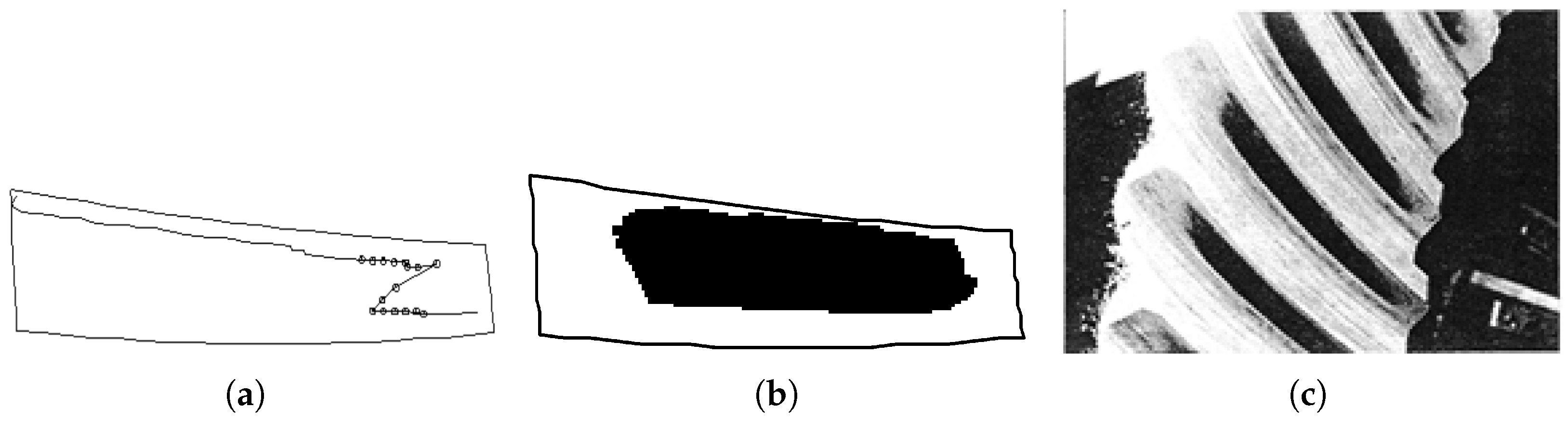
4. Validation of the LTCA Model by Using CNC-Generated Tooth Surfaces
4.1. Misalignments and Load Distribution of Spiral Bevel Gears
4.2. Validation of the LTCA Model by Simulating Various Misalignment Scenarios and Comparing Results with LTCA Software Analysis
4.3. Influence of Gear Ring Axial Displacement
4.4. Influence of Gear Shaft Spacing Deviation
4.5. Influence of Gear Angular Deviation
4.6. Comparison with LTCA Software
5. Conclusions
- The UGM describes the microgeometry and contact properties of ease-off surfaces, and the error-variation equation is developed to reflect the inherent relationships between errors and variations in machine tool settings.
- Advanced semi-analytical LTCA method is developed based on the ease-off spiral bevel gears with misalignments. The results of semi-analytical LTCA illustrate an investigation of the influence of misalignments on the path of contact and contact pattern.
- Through the application of the semi-analytical LTCA method, it is feasible to introduce misalignments during the ease-off process, to relocate the center of the contact pattern to a specific, pre-determined location on the tooth surface.Using the semi-analytical LTCA method, misalignments could be introduced during the ease-off process to move the contact pattern center to a certain predetermined position on the tooth surface.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, G.; Zhu, W. A Review on Up-to-Date Gearbox Technologies and Maintenance of Tidal Current Energy Converters. Energies 2022, 15, 9236. [Google Scholar] [CrossRef]
- Li, G.; Zhu, W. Design and power loss evaluation of a noncircular gear pair for an infinitely variable transmission. Mech. Mach. Theory 2021, 156, 104137. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Zhu, W.; Kubo, A. A function-oriented active form-grinding method for cylindrical gears based on error sensitivity. Int. J. Adv. Manuf. Technol. 2017, 92, 3019–3031. [Google Scholar] [CrossRef]
- He, D.; Ding, H.; Tang, J. A new analytical identification approach to the tooth contact points considering misalignments for spiral bevel or hypoid gears. Mech. Mach. Theory 2018, 121, 785–803. [Google Scholar] [CrossRef]
- Chen, P.; Wang, S.; Zou, H. Efficient semi-analytic method for single tooth contact analysis of loaded spiral bevel gears. Appl. Math. Model. 2024, 129, 754–779. [Google Scholar] [CrossRef]
- Temirkhan, M.; Amrin, A.; Spitas, V.; Spitas, C. Convergence and accuracy problems of the conventional TCA model–Critical analysis and novel solution for crowned spur gears. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 724–736. [Google Scholar] [CrossRef]
- Marciniec, A.; Pacana, J.; Pisula, J.M.; Fudali, P. Comparative analysis of numerical methods for the determination of contact pattern of spiral bevel gears. Aircr. Eng. Aerosp. Technol. 2018, 90, 359–367. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Kubo, A. The modeling approach of digital real tooth surfaces of hypoid gears based on non-geometric-feature segmentation and interpolation algorithm. Int. J. Precis. Eng. Manuf. 2016, 17, 281–292. [Google Scholar] [CrossRef]
- Simon, V.V. Multi-objective optimization of hypoid gears to improve operating characteristics. Mech. Mach. Theory 2020, 146, 103727. [Google Scholar] [CrossRef]
- Moslem, M.; Zippo, A.; Iarriccio, G.; Bergamini, L.; Pellicano, F. Loaded and unloaded tooth contact analysis of spiral bevel gears in consideration of misalignments. Insight-Non-Test. Cond. Monit. 2022, 64, 442–446. [Google Scholar] [CrossRef]
- Li, G.; Wang, Z.; Zhu, W. Prediction of surface wear of involute gears based on a modified fractal method. ASME J. Tribol. 2019, 141, 031603. [Google Scholar] [CrossRef]
- Jiang, J.; Luo, Q.; Wang, L.; Qiao, L.; Li, M. Review on logarithmic spiral bevel gear. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 400. [Google Scholar] [CrossRef]
- Ghionea, A.; Constantin, G.; Predincea, N.; Sandu, C. Adjustemnt Aspects of Gear Hobbing Machines in Diagonal Milling. In Proceedings of the 16th International Conference on Manufacturing Systems—ICMaS, Bucharest, Romania, 7–8 October 2007; pp. 73–76. [Google Scholar]
- Simon, V.V. Improvements in the mixed elastohydrodynamic lubrication and in the efficiency of hypoid gears. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 795–810. [Google Scholar] [CrossRef]
- Liu, Z.; Li, F.; Xu, Z.; He, Q. Semi-analytical loaded tooth contact analysis method for spiral bevel gears. Int. J. Mech. Sci. 2023, 253, 108329. [Google Scholar] [CrossRef]
- Li, F.; Wang, S.; Chen, P.; Li, Z.; Li, L.; Peng, Q. Multi-objective variable parameter optimization algorithm for spiral bevel gear tooth surface considering meshing efficiency and contact performance. J. Mech. Sci. Technol. 2022, 36, 3547–3559. [Google Scholar] [CrossRef]
- Ding, H.; Zhou, Y.; Tang, J.; Zhong, J.; Zhou, Z.; Wan, G. A novel operation approach to determine initial contact point for tooth contact analysis with errors of spiral bevel and hypoid gears. Mech. Mach. Theory 2017, 109, 155–170. [Google Scholar] [CrossRef]
- Fu, Y.; Zhuo, Y.; Zhou, X.; Wan, B.; Lv, H.; Wang, Z. Theoretical and experimental study on contact characteristics of spiral bevel gears under quasi-static and large loading conditions. Appl. Sci. 2020, 10, 5109. [Google Scholar] [CrossRef]
- Ding, H.; Li, H.; Shao, W.; Tang, J. Prediction and control for local bearing contact-based collaborative grinding of non-orthogonal aerospace spiral bevel gears. Mech. Syst. Signal Process. 2021, 160, 107841. [Google Scholar] [CrossRef]
- Kolivand, M.; Kahraman, A. A load distribution model for hypoid gears using ease-off topography and shell theory. Mech. Mach. Theory 2009, 44, 1848–1865. [Google Scholar] [CrossRef]
- Simon, V.V. Multi-objective optimization of the manufacture of face-milled hypoid gears on numerical controlled machine tool. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 235, 1120–1130. [Google Scholar] [CrossRef]
- Stanasel, I.; Ghionea, A.; Ghionea, I.; Ungur, P.; Stanasel, O. The Mathematical Model for the Generation of the Cylindrical Gear With Curved Cycloidal Teeth. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Las Vegas, NV, USA, 4–7 September 2007; Volume 48086, pp. 279–287. [Google Scholar]
- Vivet, M. Advanced Techniques for Numerical Contact Analysis in Spiral Bevel Gears. Ph.D. Thesis, Università della Calabria, Heverlee, Italy, 2019. [Google Scholar]
- Mathur, T.D.; Smith, E.C.; Bill, R.C. A novel loaded tooth contact analysis procedure with application to internal–external straight bevel gear mesh in a pericyclic drive. J. Tribol. 2021, 143, 101201. [Google Scholar] [CrossRef]
- Li, G.; Zhu, W. An Active Ease-Off Topography Modification Approach for Hypoid Pinions Based on a Modified Error Sensitivity Analysis Method. ASME J. Mech. Des. 2019, 141, 093302. [Google Scholar] [CrossRef]
- Efstathiou, C.; Tapoglou, N. Simulation of spiral bevel gear manufacturing by face hobbing and prediction of the cutting forces using a novel CAD-based model. Int. J. Adv. Manuf. Technol. 2022, 122, 3789–3813. [Google Scholar] [CrossRef]
- Gabiccini, M. A twist exponential approach to gear generation with general spatial motions. Mech. Mach. Theory 2009, 44, 382–400. [Google Scholar] [CrossRef]
- Simon, V.V. Influence of tooth modifications on tooth contact in face-hobbed spiral bevel gears. Mech. Mach. Theory 2011, 46, 1980–1998. [Google Scholar] [CrossRef]
- Simon, V.V. Manufacture of optimized face-hobbed spiral bevel gears on computer numerical control hypoid generator. J. Manuf. Sci. Eng. 2014, 136, 031008. [Google Scholar] [CrossRef]
- Doe, J. Simulation of hypoid gears dynamic performance. J. Mech. Eng. 2020, 45, 123–135. [Google Scholar]
- GB 11365-89; Terms for Resistance Strain Gauges. China Standards Press: Beijing, China, 1989.






| Parameter | Pinion | Gear |
|---|---|---|
| number of teeth | 6 | 37 |
| face angle | 16°3′ | 78°26′ |
| root angle | 11°15′ | 73°31′ |
| direction | left | right |
| shaft angle/ | 90 | 90 |
| module | 8.243 | 8.243 |
| face width/mm | 45.12 | 40 |
| face apex to crossing point/mm | −3.14 | 1.4 |
| pitch angle | 11°43′ | 77°58′ |
| pitch apex to crossing point/mm | 0.71 | 1.4 |
| root apex to crossing point/mm | −7.59 | 1.39 |
| outer cone distance/mm | 155.35 | 155.92 |
| outside diameter/mm | 84.07 | 305.52 |
| pitch diameter/mm | 304.99 | 304.99 |
| Error Value | FEA Results (Torque = 100 N·m) |
|---|---|
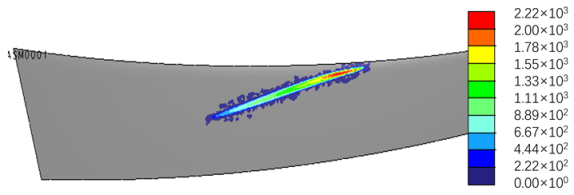 | |
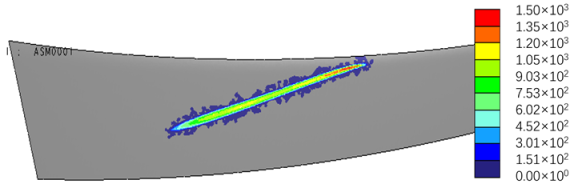 | |
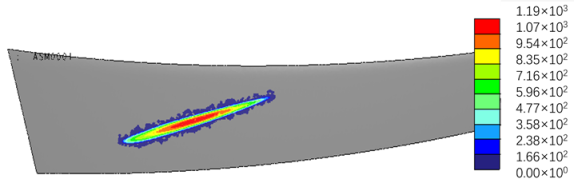 |
| Error Value | FEA Results (Torque = 100 N·m) |
|---|---|
 | |
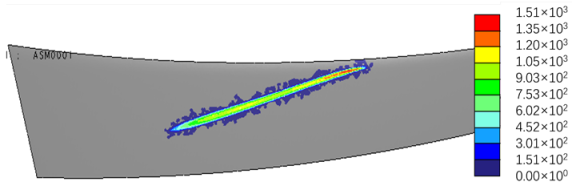 | |
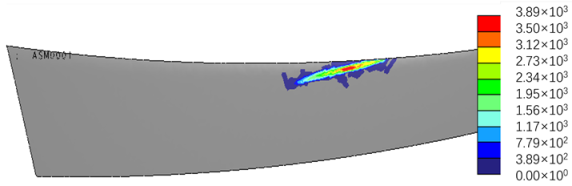 |
| Error Value | FEA Results (Torque = 100 N·m) |
|---|---|
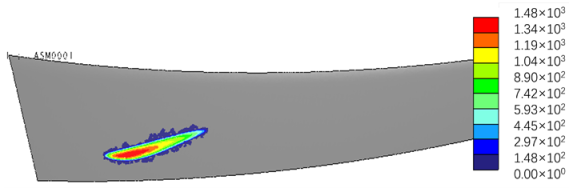 | |
 | |
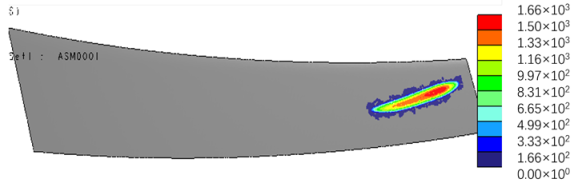 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, L.; Mao, X.; Shangguan, D. A Semi-Analytical Loaded Contact Model and Load Tooth Contact Analysis Approach of Ease-Off Spiral Bevel Gears. Machines 2024, 12, 623. https://doi.org/10.3390/machines12090623
Liu Y, Chen L, Mao X, Shangguan D. A Semi-Analytical Loaded Contact Model and Load Tooth Contact Analysis Approach of Ease-Off Spiral Bevel Gears. Machines. 2024; 12(9):623. https://doi.org/10.3390/machines12090623
Chicago/Turabian StyleLiu, Yuhui, Liping Chen, Xian Mao, and Duansen Shangguan. 2024. "A Semi-Analytical Loaded Contact Model and Load Tooth Contact Analysis Approach of Ease-Off Spiral Bevel Gears" Machines 12, no. 9: 623. https://doi.org/10.3390/machines12090623
APA StyleLiu, Y., Chen, L., Mao, X., & Shangguan, D. (2024). A Semi-Analytical Loaded Contact Model and Load Tooth Contact Analysis Approach of Ease-Off Spiral Bevel Gears. Machines, 12(9), 623. https://doi.org/10.3390/machines12090623






