Integrated Dynamic Modeling and Simulation of Wheeled Vehicle with Outer-Rotor In-Wheel Motors and Key Units
Abstract
1. Introduction
2. In-Wheel Motor-Drive Vehicle System
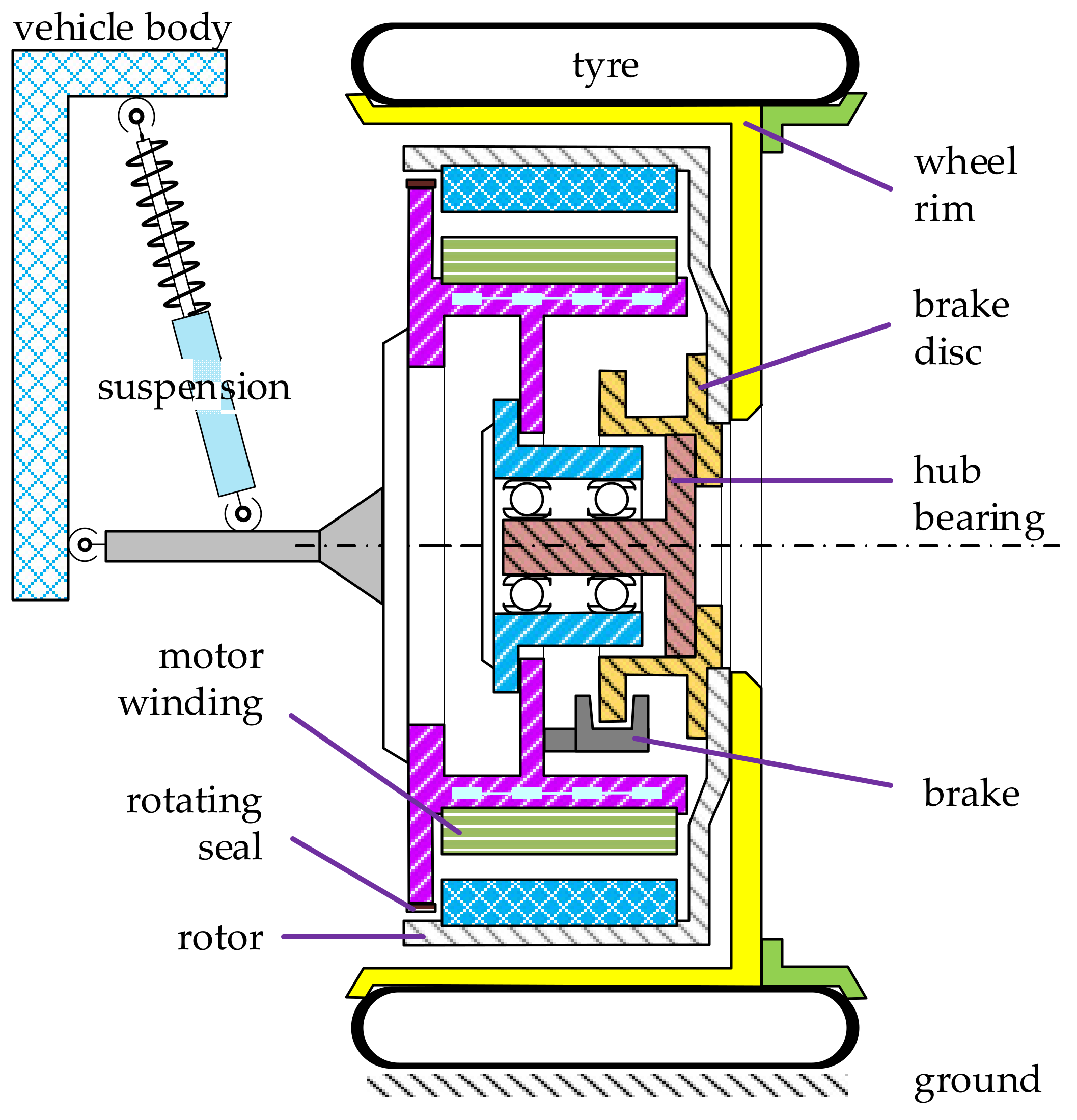
2.1. Direct Drive In-Wheel Motors
- Power: The IWM should have higher power output to meet the demands of vehicle acceleration, climbing, and high-speed driving.
- Efficiency: The motor design should be highly efficient, minimizing energy loss to maximize the vehicle’s driving range.
- Cooling: A well-designed and reliable cooling system is essential to prevent performance degradation or damage due to motor overheating.
- Durability: The IWM should offer an extended motor life and reliable performance, with particular emphasis on the robustness of critical components, such as the bearing unit, which should be designed to minimize the risk of damage.
2.2. Special-Wheeled Vehicle
3. Multi-Body Dynamics Modeling of Vehicle
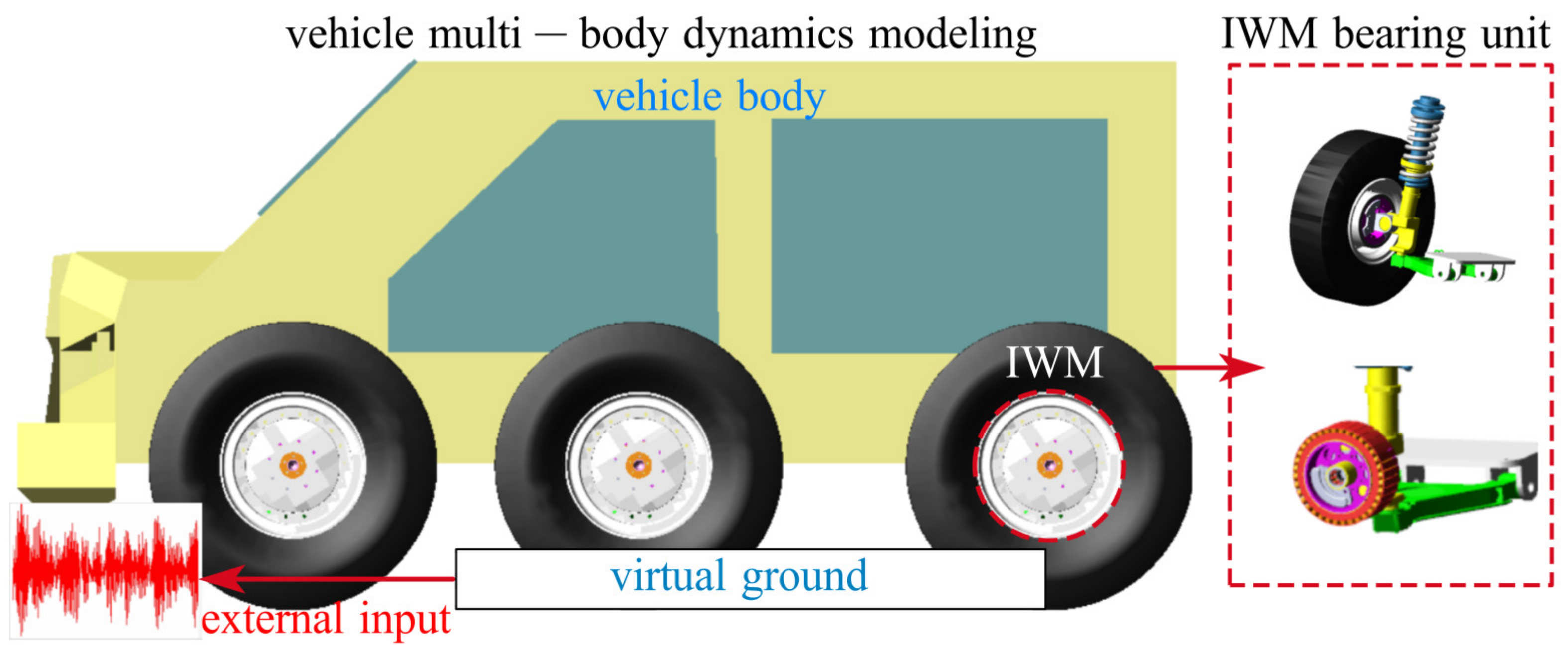
3.1. Modeling of Vehicle in ADAMS
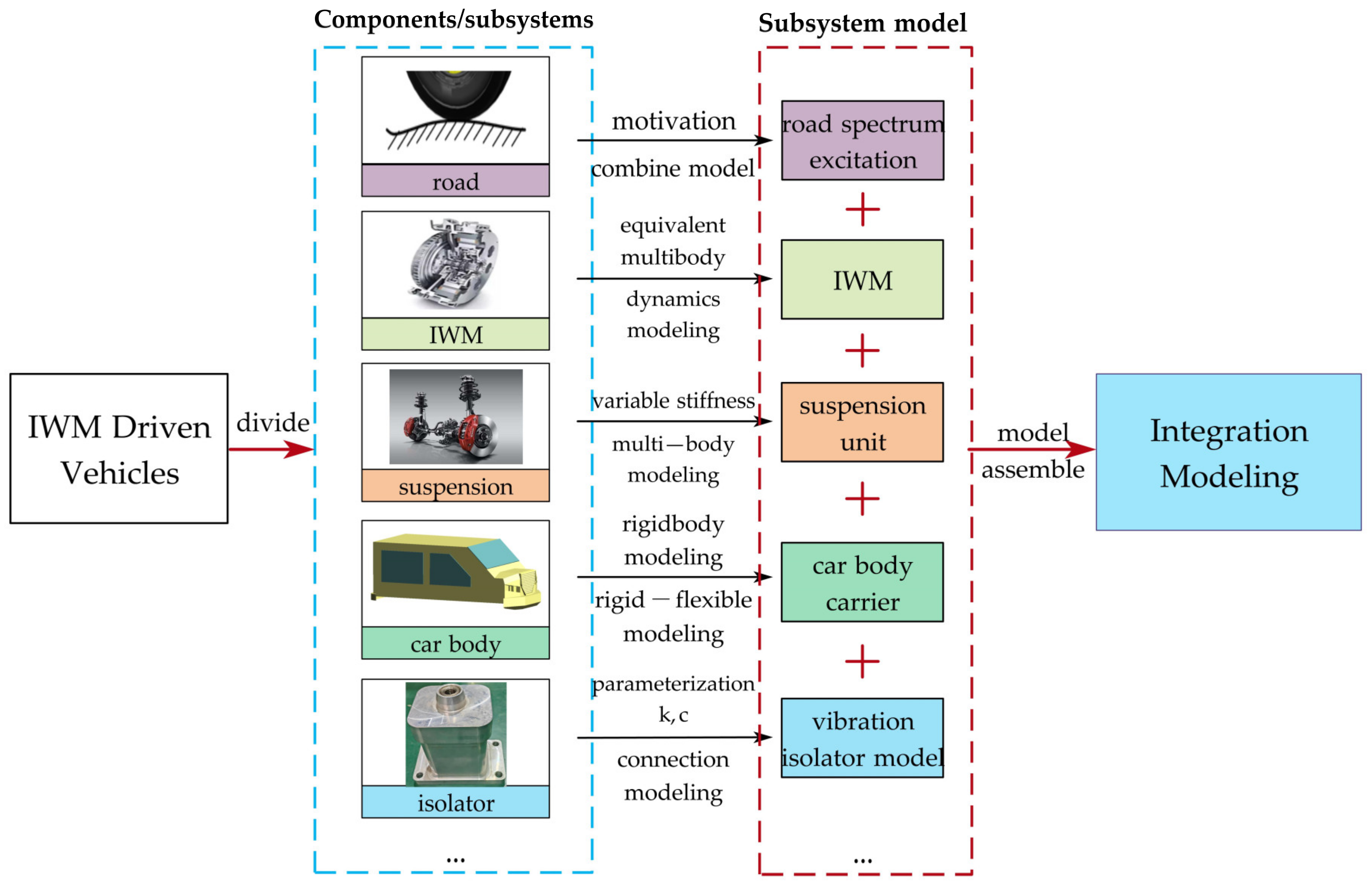
3.1.1. Vehicle-Integrated Modeling Strategy
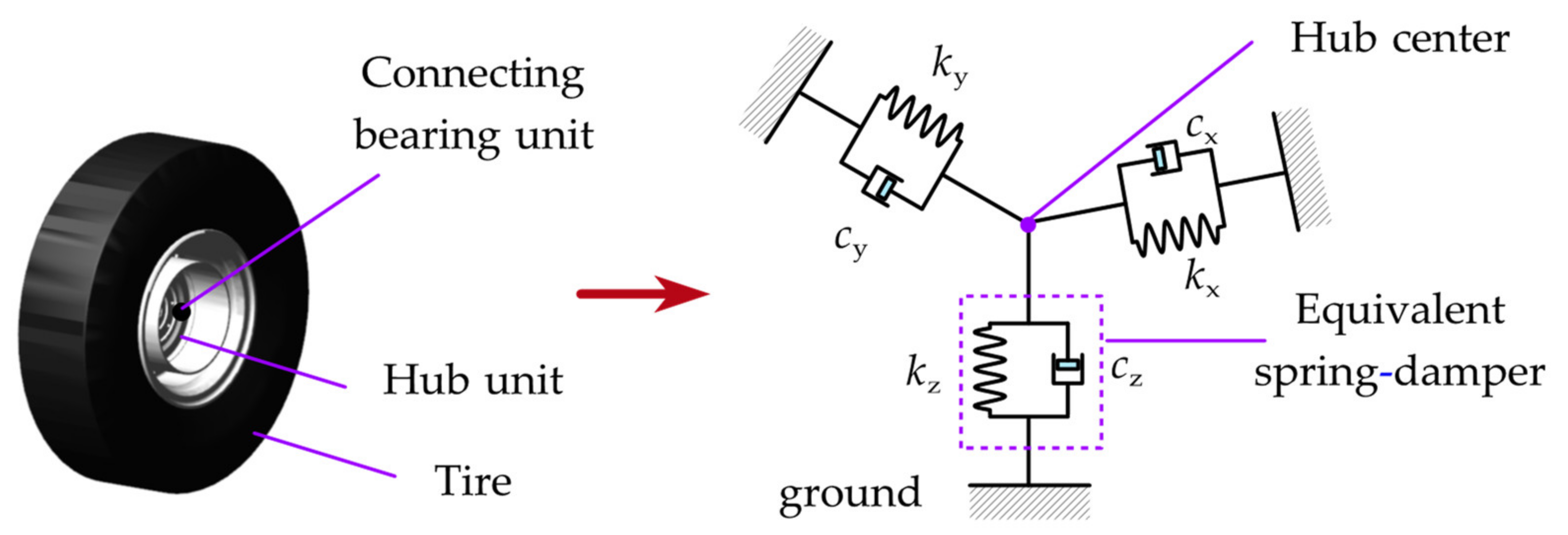
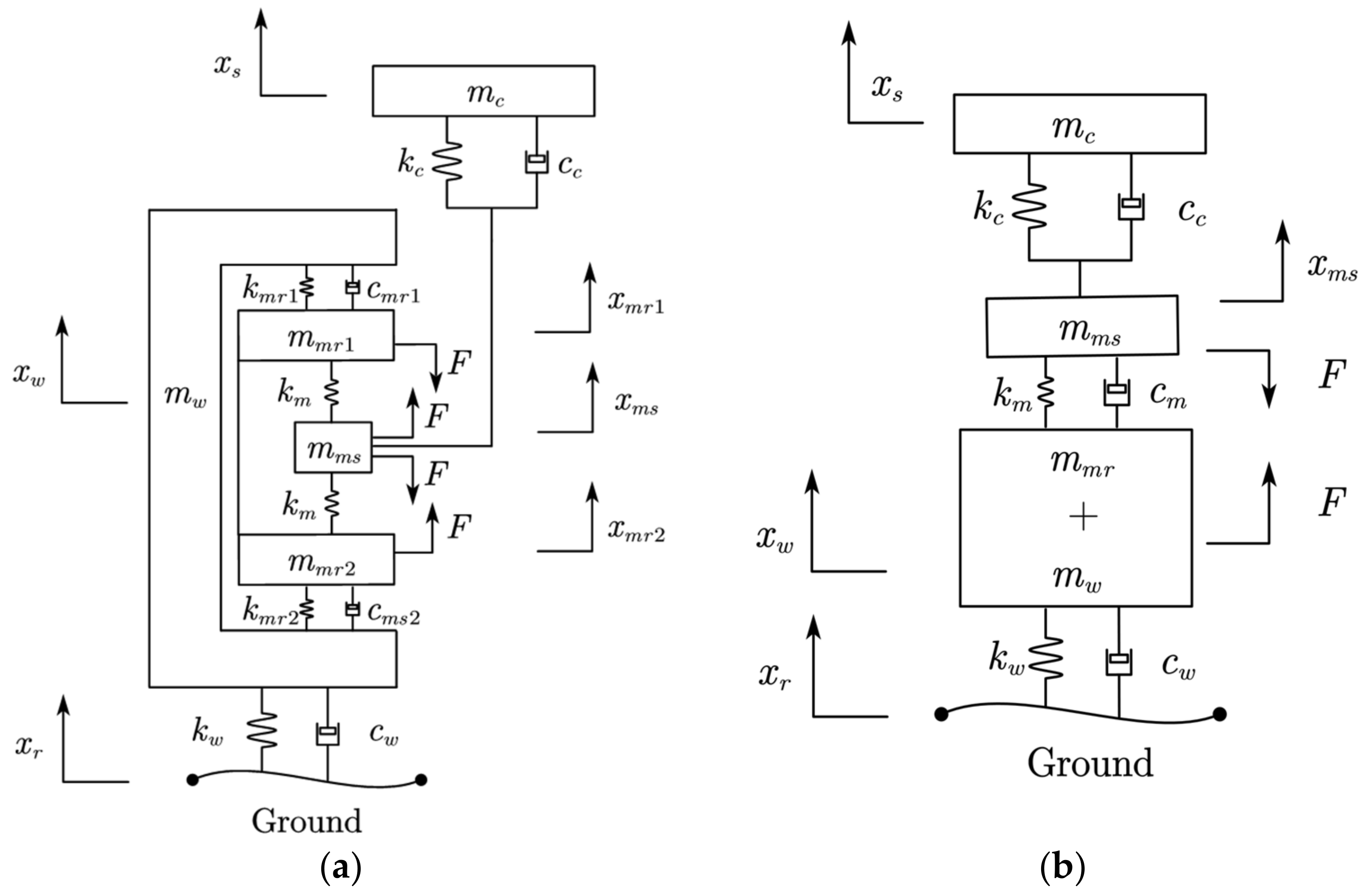
3.1.2. Modeling of In-Wheel Motor
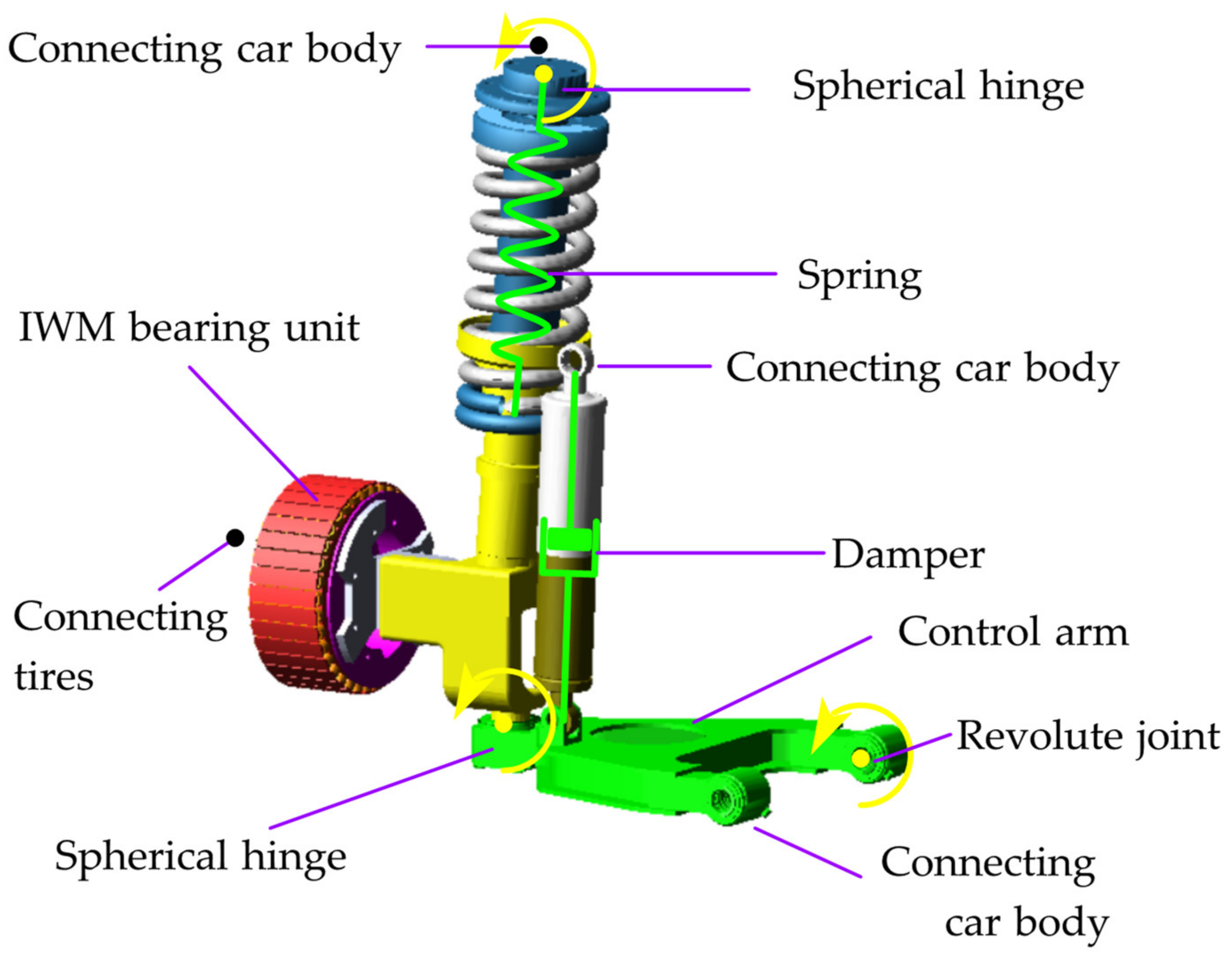
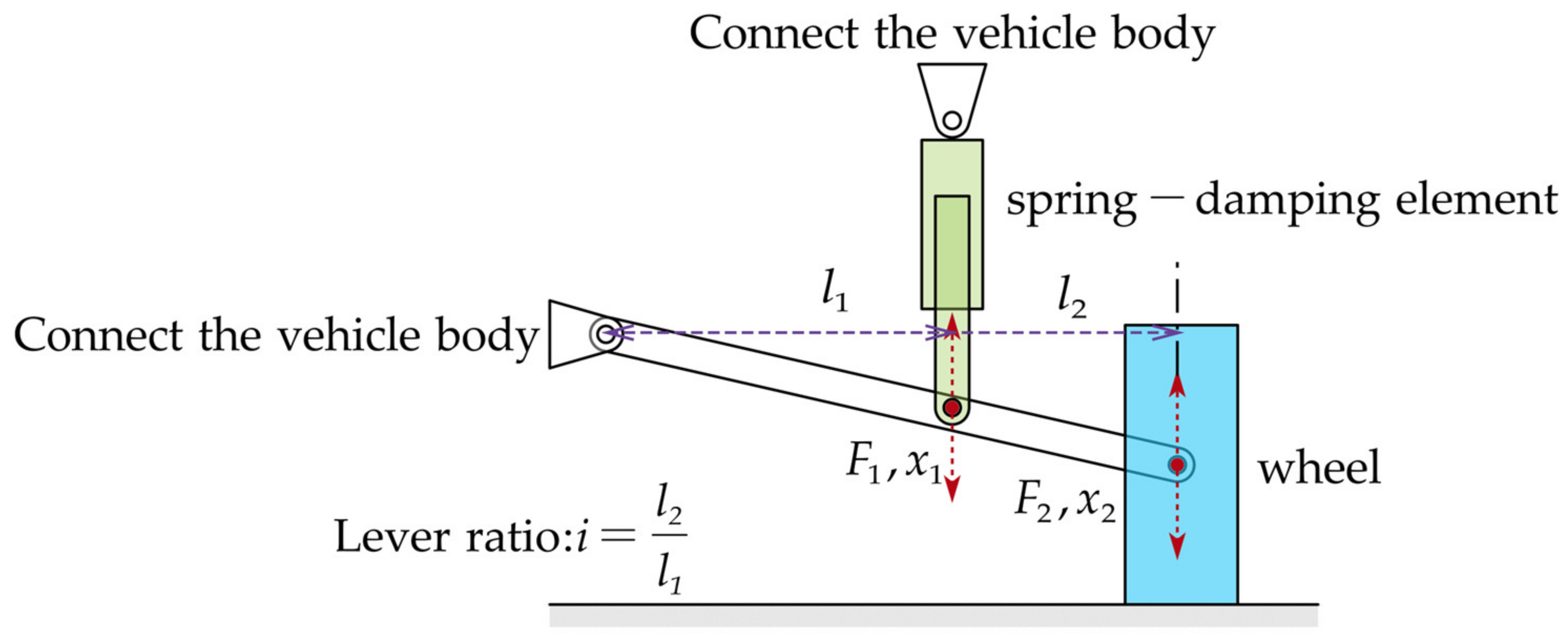
3.1.3. Modeling of Key Subsystems
3.1.4. Comprehensive Vehicle Dynamics Modeling
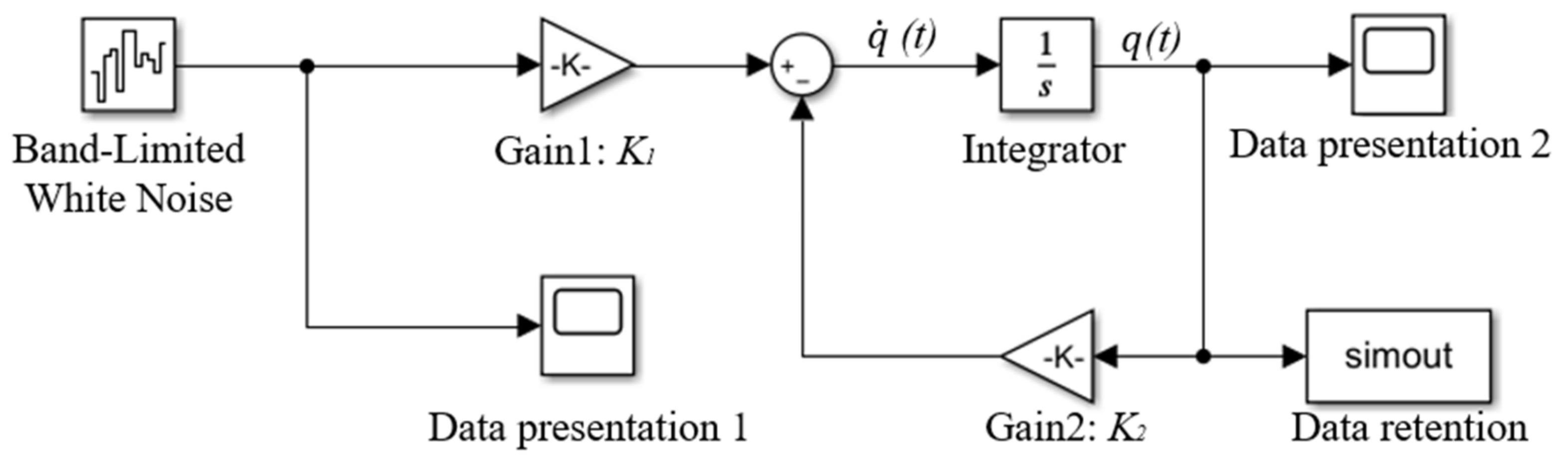
3.2. Modeling of Vehicle in MATLAB
4. Analysis of Vehicle Dynamics
4.1. Frequency-Domain Characteristic Analysis
4.1.1. Natural Frequency
- Vehicle
- Rotor and Stator
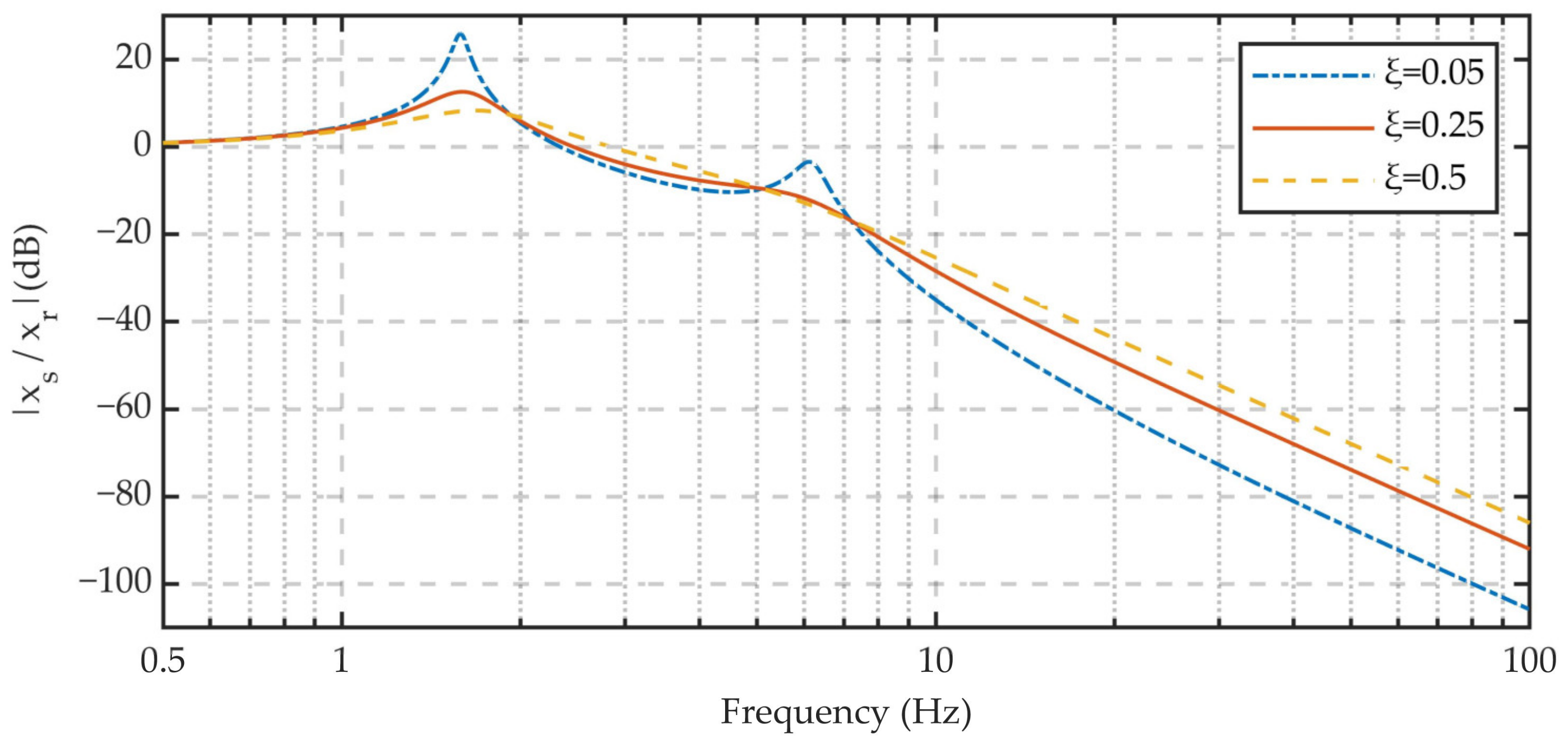
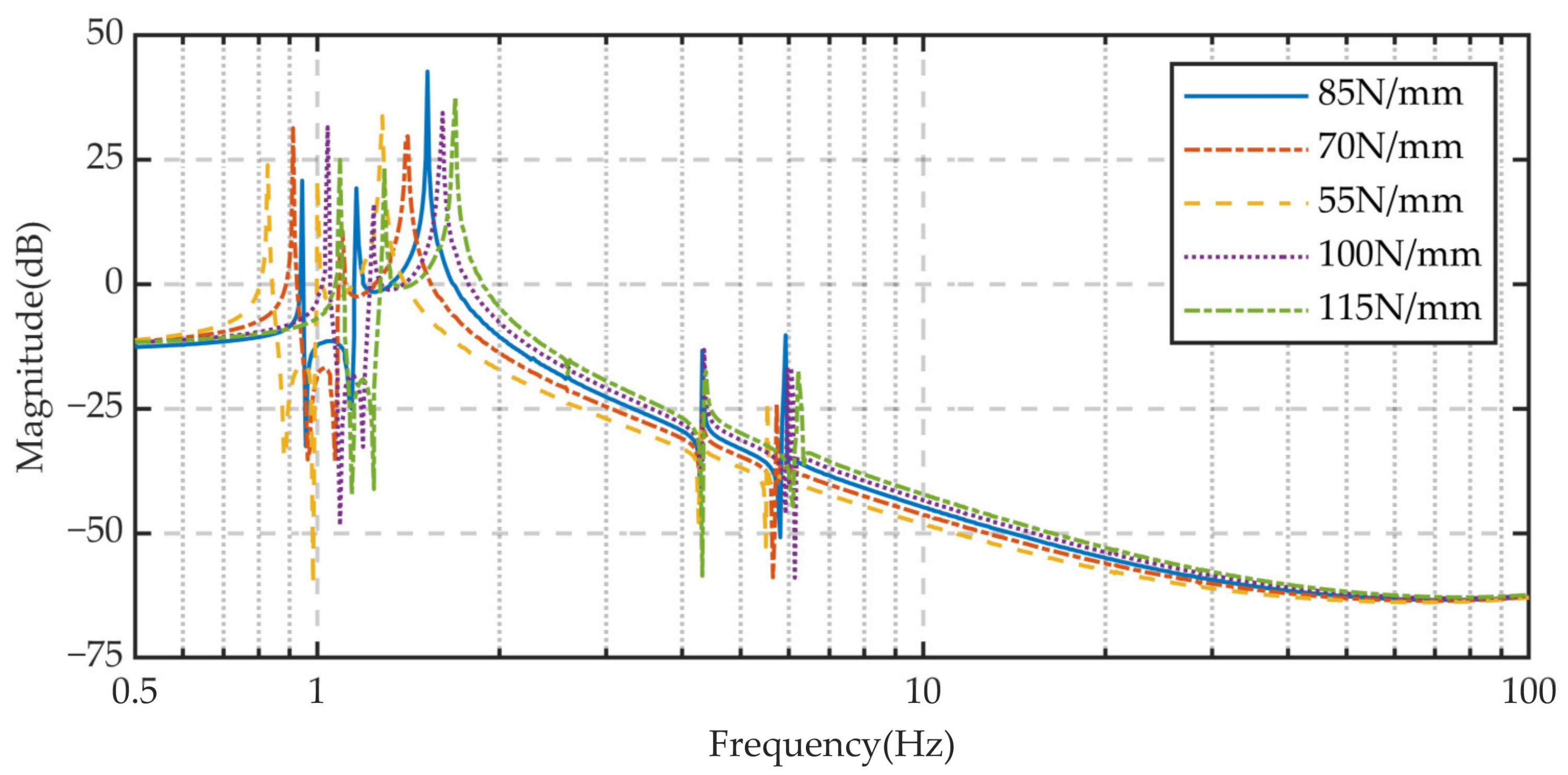
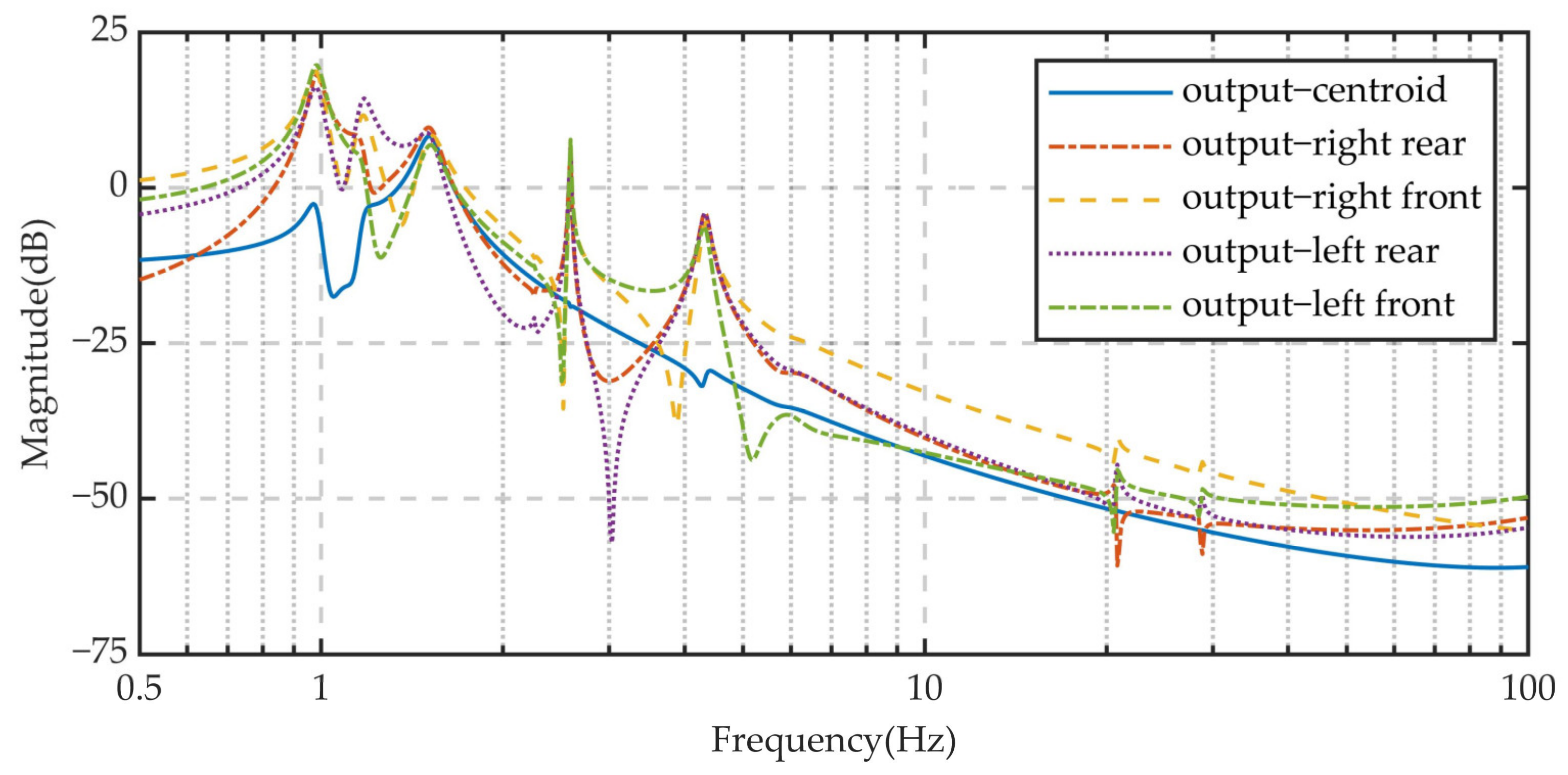
4.1.2. Vibration Transmissibility
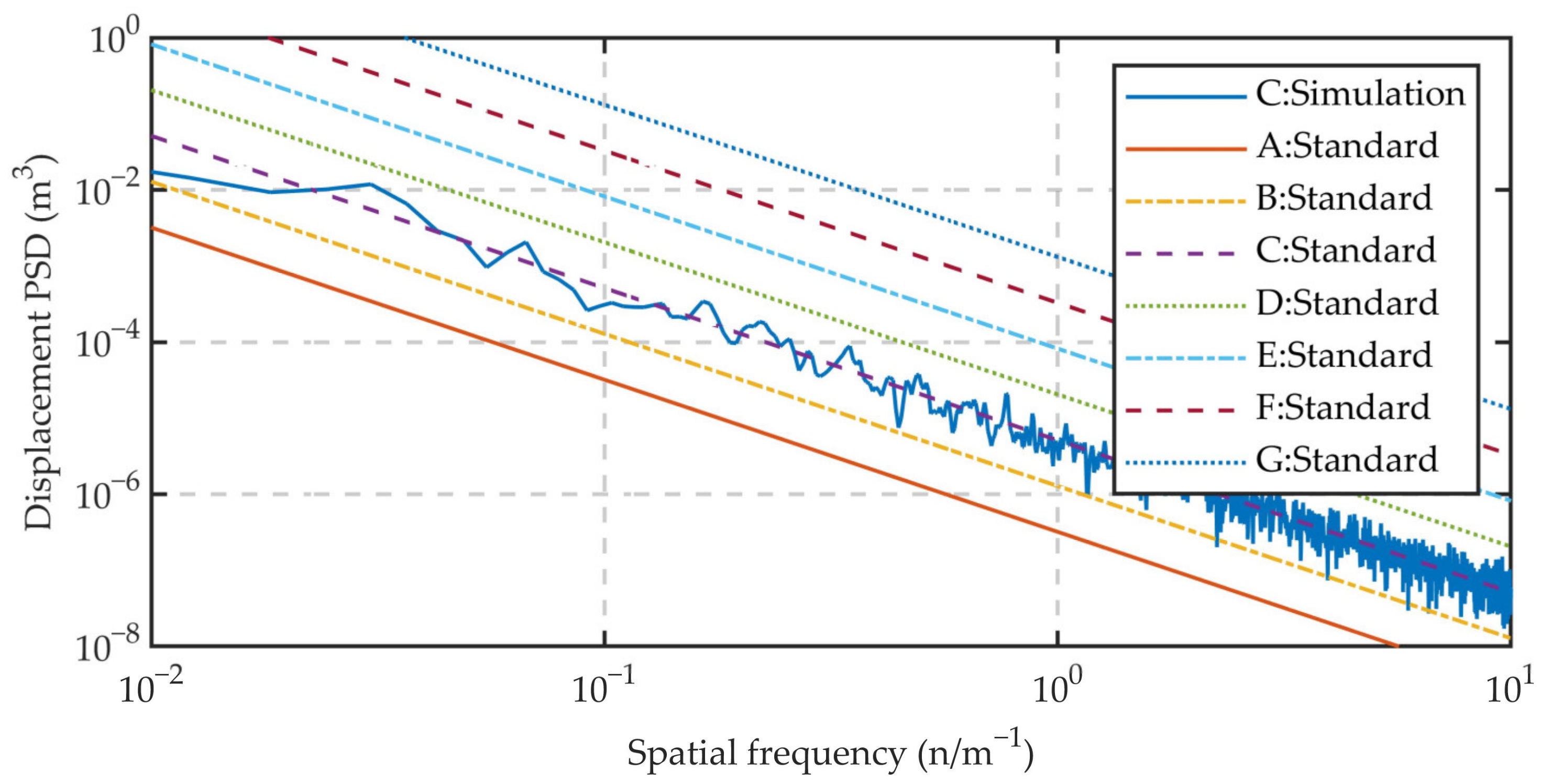
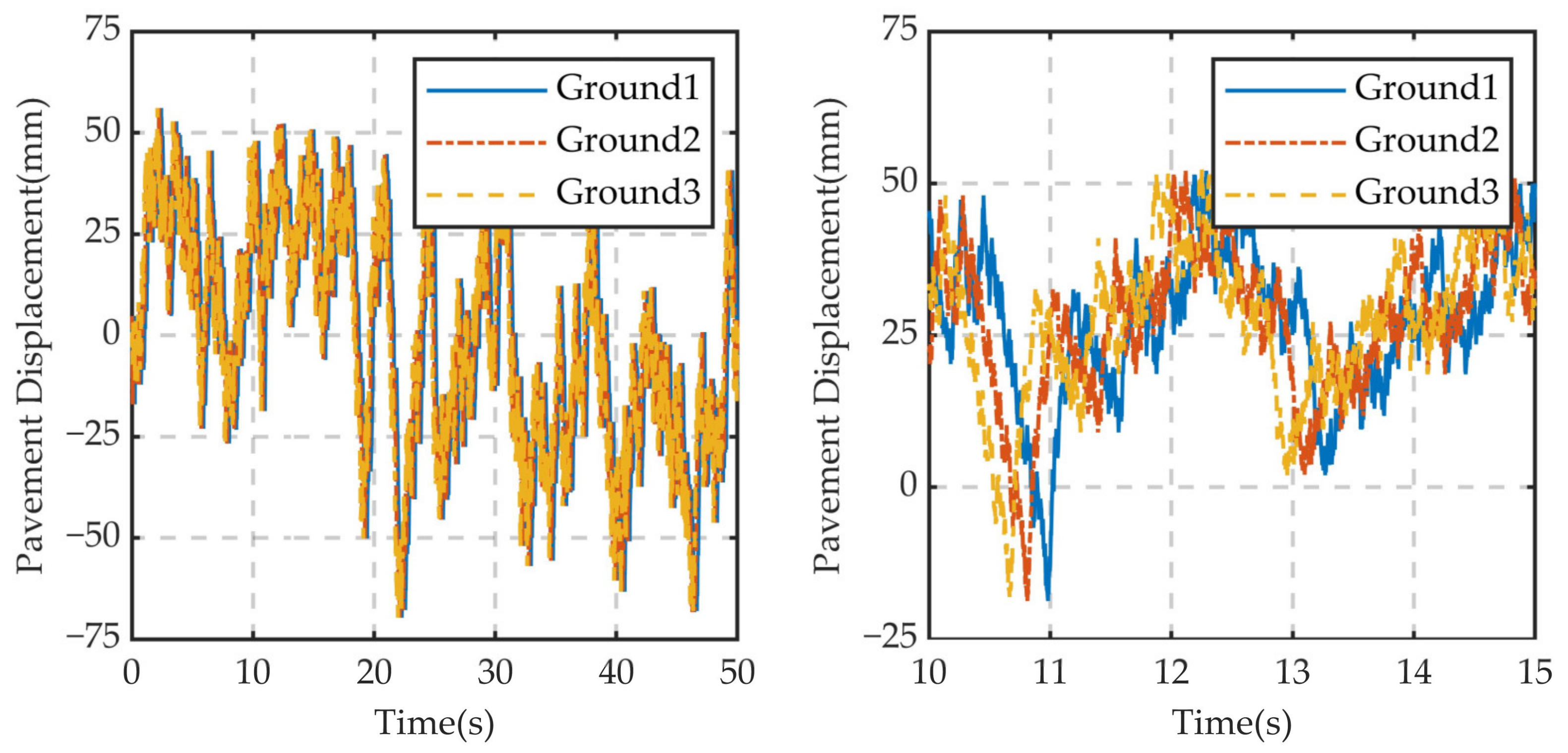
4.2. Road Spectrum Model Establishment and Excitation Input
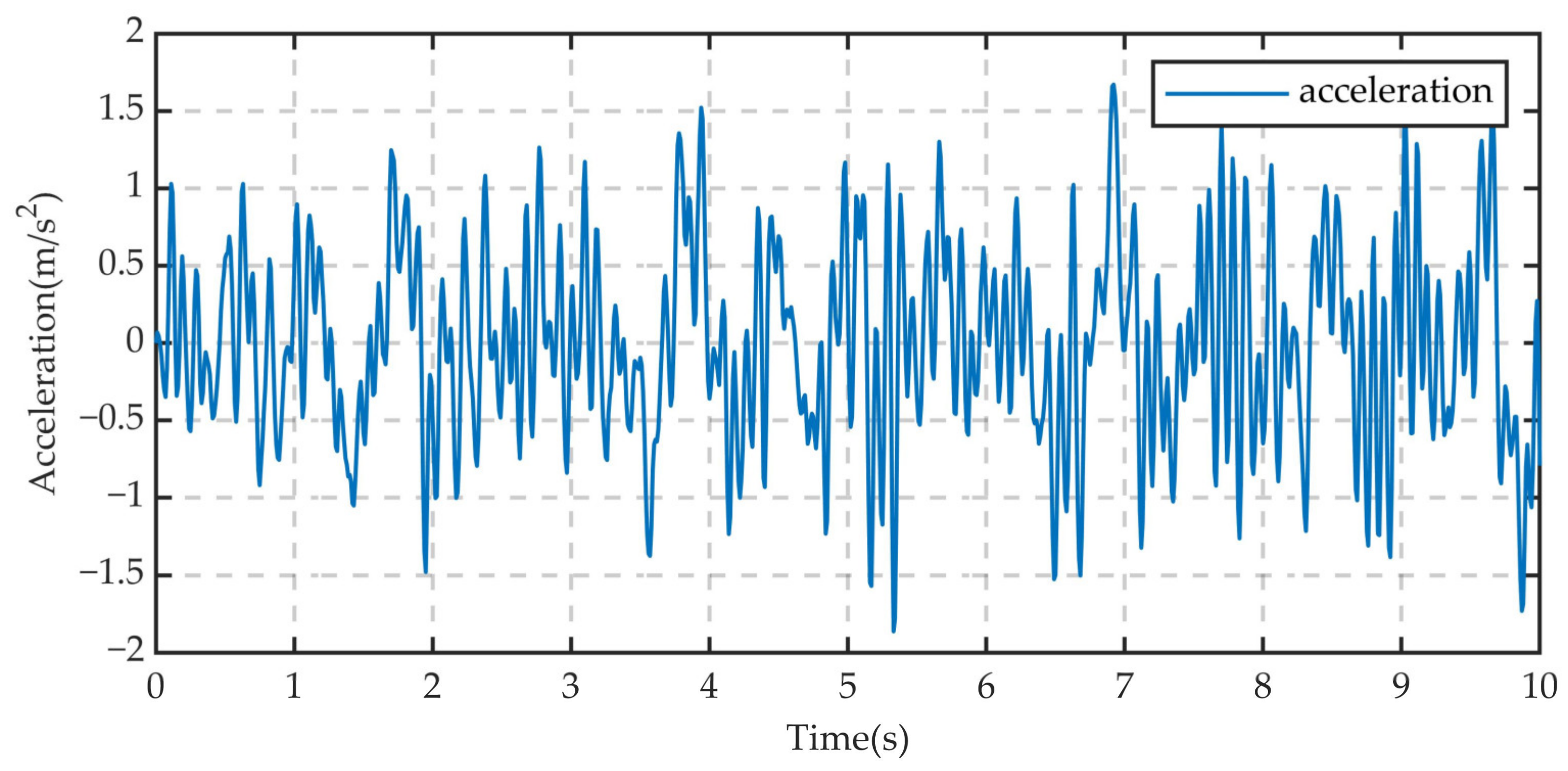
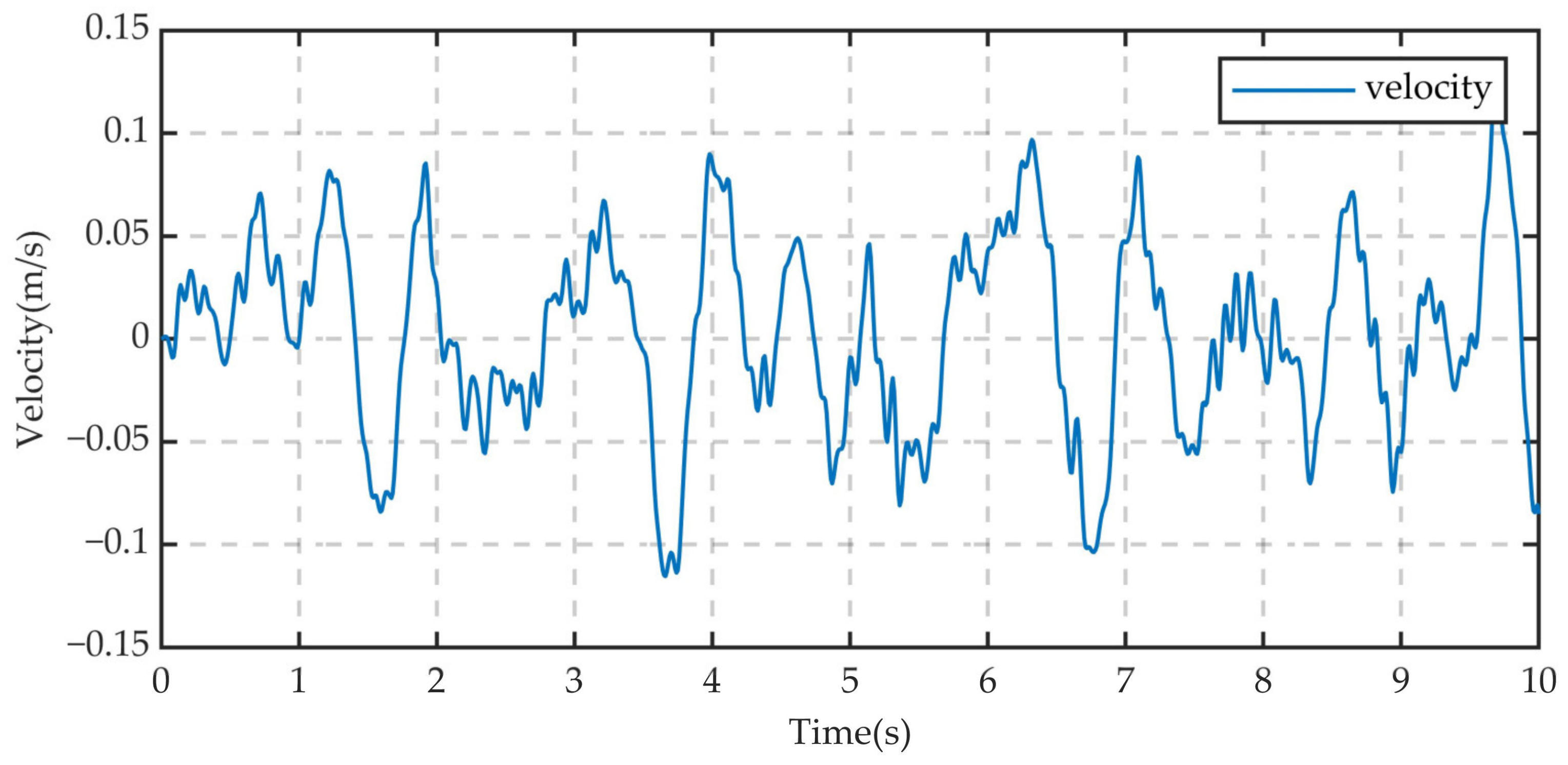
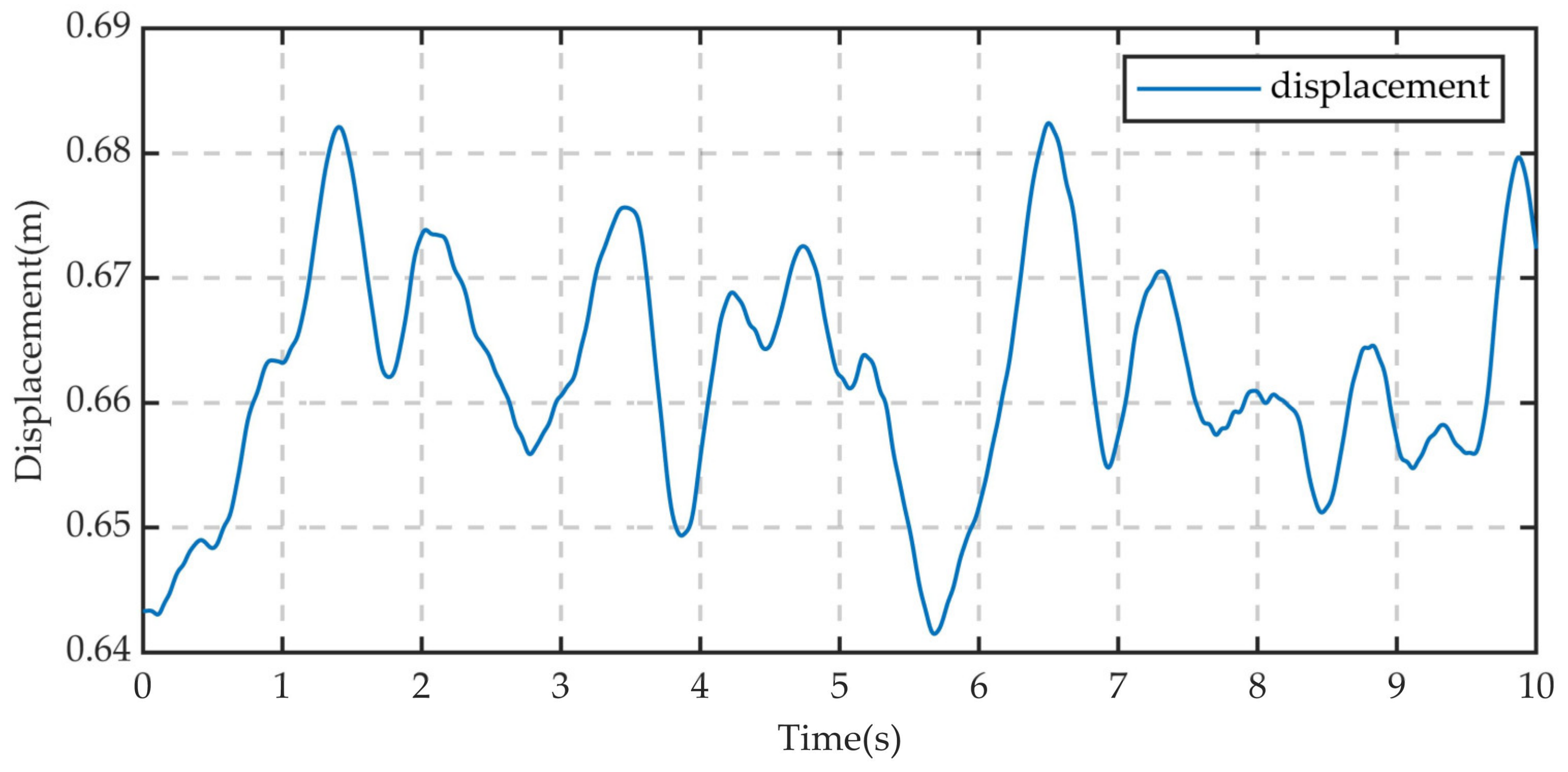
4.3. Time-Domain Characteristic Analysis
5. Conclusions
- Proposes a system-integrated modeling strategy and method for dynamic design of IWM.
- 2.
- Constructs the key subsystem of IWM bearing unit and the vehicle dynamics model.
- 3.
- Establishes a multi-source dynamic load characterization method and analyzed the vibration characteristics of the vehicle.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IWM | in-wheel motor |
| MM | magnet motor |
| NVH | noise, vibration, and harshness |
| WBV | whole-body vibration |
| MMG | motor magnetic gap |
| DDUGV | Distributed-Drive Unmanned Ground Vehicle |
| DOF | degree of freedom |
| CAE | Computer-Aided Engineering |
| IRI | International Roughness Index |
| PSD | power spectral density |
| RMS | Root Mean Square |
References
- Satoshi, M. Innovation by in-wheel-motor drive unit. Veh. Syst. Dyn. 2012, 50, 807–830. [Google Scholar]
- Wagh, K.; Dhatrak, P. A review on powertrain subsystems and charging technology in battery electric vehicles: Current and future trends. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 479–496. [Google Scholar] [CrossRef]
- Kumar, P.; Chakrabarty, S. Total cost of ownership analysis of the impact of vehicle usage on the economic viability of electric vehicles in India. Transp. Res. Rec. 2020, 2674, 563–572. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, L.; Ren, Y.; Li, Y.; Xiong, Z. Multi-objective optimization of active suspension system in electric vehicle with In-Wheel-Motor against the negative electromechanical coupling effects. Mech. Syst. Signal Process. 2019, 116, 545–565. [Google Scholar] [CrossRef]
- Deepak, K.; Frikha, M.A.; Benômar, Y.; El Baghdadi, M.; Hegazy, O. In-Wheel Motor Drive Systems for Electric Vehicles: State of the Art, Challenges, and Future Trends. Energies 2023, 16, 3121. [Google Scholar] [CrossRef]
- He, S.; Fan, X.; Wang, Q.; Chen, X.; Zhu, S. Review on torque distribution scheme of four-wheel in-wheel motor electric vehicle. Machines 2022, 10, 619. [Google Scholar] [CrossRef]
- Qatu, M.; Sirafi, M.; Johns, F. Robustness of powertrain mount system for noise, vibration and harshness at idle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2002, 216, 805–810. [Google Scholar] [CrossRef]
- Nagaya, G.; Wakao, Y.; Abe, A. Development of an in-wheel drive with advanced dynamic-damper mechanism. JSAE Rev. 2003, 24, 477–481. [Google Scholar] [CrossRef]
- Yane, Z.; Jianwu, Z.; Xu, H. Design and study on the dynamic-damper mechanism for an in-wheel motor individual drive electric vehicle. Mech. Sci. Technol. 2008, 27, 395. [Google Scholar]
- Ahmad, I.; Ge, X.; Han, Q.L. Decentralized dynamic event-triggered communication and active suspension control of in-wheel motor driven electric vehicles with dynamic damping. IEEE/CAA J. Autom. Sin. 2021, 8, 971–986. [Google Scholar] [CrossRef]
- Yoon, D.S.; Choi, S.B. Adaptive Control for Suspension System of In-Wheel Motor Vehicle with Magnetorheological Damper. Machines 2024, 12, 433. [Google Scholar] [CrossRef]
- Nam, K.; Fujimoto, H.; Hori, Y. Lateral stability control of in-wheel-motor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors. IEEE Trans. Veh. Technol. 2012, 61, 1972–1985. [Google Scholar]
- Zhang, H.; Wang, R.; Wang, J. Robust H∞ Output-Feedback Yaw Control for In-Wheel Motor-Driven Electric Vehicles with Differential Steering. In Robust Gain-Scheduled Estimation and Control of Electrified Vehicles via LPV Technique; Springer Nature Singapore: Singapore, 2023; pp. 131–152. [Google Scholar]
- Belrzaeg, M.; Ahmed, A.A.; Khaleel, M.M.; Alsharif, A.; Rahmah, M.M.; Alarga, A.S.D. Suspension system control process for Buses with In-Wheel Motors. Eng. Proc. 2023, 29, 4. [Google Scholar] [CrossRef]
- Rudiger, H. Technical Potential of in-Wheel Motors. ATZ Worldw. 2012, 114, 4–9. [Google Scholar]
- Li, C.; Guo, X.; Fu, J.; Fu, W.; Liu, Y.; Chen, H.; Wang, R.; Li, Z. Design and analysis of a novel double-stator double-rotor motor drive system for in-wheel direct drive of electric vehicles. Machines 2021, 10, 27. [Google Scholar] [CrossRef]
- Chan, C.C. An overview of electric vehicle technology. Proc. IEEE 1993, 81, 1202–1213. [Google Scholar] [CrossRef]
- Matsugaura, S.; Kawakami, K.; Shimizu, H. Advanced Direct Drive System for New Concept Electric Vehicle “KAZ”. In Proceedings of the 18th International Electric Vehicle Symposium (EVS18), Berlin, Germany, 20–24 October 2001. [Google Scholar]
- Yoshida, H.; Shimizu, H. Transportation and Safety in Japan: “Ellica”-the 370 km/h Maximum Speed Electric Vehicle. IATSS Res. 2005, 29, 75. [Google Scholar] [CrossRef][Green Version]
- Zhao, Z.; Taghavifar, H.; Du, H.; Qin, Y.; Dong, M.; Gu, L. In-wheel motor vibration control for distributed-driven electric vehicles: A review. IEEE Trans. Transp. Electrif. 2021, 7, 2864–2880. [Google Scholar] [CrossRef]
- Qin, Y.; Rath, J.J.; Hu, C.; Sentouh, C.; Wang, R. Adaptive nonlinear active suspension control based on a robust road classifier with a modified super-twisting algorithm. Nonlinear Dyn. 2019, 97, 2425–2442. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, Z.; Xiang, C.; Hashemi, E.; Khajepour, A.; Huang, Y. Speed independent road classification strategy based on vehicle response: Theory and experimental validation. Mech. Syst. Signal Process. 2019, 117, 653–666. [Google Scholar] [CrossRef]
- Zirkohi, M.M.; Lin, T.C. Interval type-2 fuzzy-neural network indirect adaptive sliding mode control for an active suspension system. Nonlinear Dyn. 2015, 79, 513–526. [Google Scholar] [CrossRef]
- Qin, Y.; He, C.; Shao, X.; Du, H.; Xiang, C.; Dong, M. Vibration mitigation for in-wheel switched reluctance motor driven electric vehicle with dynamic vibration absorbing structures. J. Sound Vib. 2018, 419, 249–267. [Google Scholar] [CrossRef]
- Shao, X.; Naghdy, F.; Du, H.; Qin, Y. Coupling effect between road excitation and an in-wheel switched reluctance motor on vehicle ride comfort and active suspension control. J. Sound Vib. 2019, 443, 683–702. [Google Scholar] [CrossRef]
- Múčka, P. International roughness index thresholds based on whole-body vibration in passenger cars. Transp. Res. Rec. 2021, 2675, 305–320. [Google Scholar] [CrossRef]
- Kumar, R.; Sharma, R.; Kumar, V.; Khan, A.A. Predictors of whole-body vibration exposure among Indian bus and truck drivers. J. Phys. Conf. Ser. 2021, 1854, 012033. [Google Scholar] [CrossRef]
- Svendenius, J.; Gäfvert, M. A semi-empirical dynamic tire model for combined-slip forces. Veh. Syst. Dyn. 2006, 44, 189–208. [Google Scholar] [CrossRef]
- Luo, Y.; Tan, D. Study on the dynamics of the in-wheel motor system. IEEE Trans. Veh. Technol. 2012, 61, 3510–3518. [Google Scholar]
- Jin, X.; Wang, J.; He, X.; Yan, Z.; Xu, L.; Wei, C.; Yin, G. Improving vibration performance of electric vehicles based on in-wheel motor-active suspension system via robust finite frequency control. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1631–1643. [Google Scholar] [CrossRef]
- Nah, J.; Yim, S. Vehicle stability control with four-wheel independent braking, drive and steering on in-wheel motor-driven electric vehicles. Electronics 2020, 9, 1934. [Google Scholar] [CrossRef]
- Drexler, D.; Hou, Z. Simulation analysis on vertical vehicle dynamics of three in-wheel motor drive configurations. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 238, 2105–2119. [Google Scholar] [CrossRef]
- Jin, X.; Wang, J.; Yan, Z.; Xu, L.; Yin, G.; Chen, N. Robust vibration control for active suspension system of in-wheel-motor-driven electric vehicle via μ-synthesis methodology. J. Dyn. Syst. Meas. Control. 2022, 144, 051007. [Google Scholar] [CrossRef]
- Ma, Y.; Deng, Z.; Xie, D. Control of the active suspension for in-wheel motor. J. Adv. Mech. Des. Syst. Manuf. 2013, 7, 535–543. [Google Scholar] [CrossRef]
- Liu, M.; Gu, F.; Zhang, Y. Ride comfort optimization of in-wheel-motor electric vehicles with in-wheel vibration absorbers. Energies 2017, 10, 1647. [Google Scholar] [CrossRef]
- Lu, S.; Xu, X.; Wang, W. Coupling dynamic model of vehicle-wheel-ground for all-terrain distributed driving unmanned ground vehicle. Simul. Model. Pract. Theory 2023, 128, 102817. [Google Scholar] [CrossRef]
- Wang, W.H.; Xu, X.J.; Xu, H.J.; Zhou, F.-L. Enhancing lateral dynamic performance of all-terrain vehicles using variable-wheelbase chassis. Adv. Mech. Eng. 2020, 12, 1–19. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, X.; Zhang, L. Heading tracking of 6WID/4WIS unmanned ground vehicles with variable wheelbase based on model free adaptive control. Mech. Syst. Signal Process. 2021, 159, 107715. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, G.; Li, Z.; Qiu, X.; Guo, S. Design and control of a foldable and reconfigurable multi-terrain vehicle with variable wheelbase. J. Mech. Robot. 2023, 15, 024501. [Google Scholar] [CrossRef]
- Yamada, S.; Beauduin, T.; Fujimoto, H.; Kanou, T.; Katsuyama, E. Active Model-Based Suppression of Secondary Ride for Electric Vehicles with In-Wheel Motors. IEEE/ASME Trans. Mechatron. 2022, 27, 5637–5646. [Google Scholar] [CrossRef]
- Tseng, H.E.; Hrovat, D. State of the art survey: Active and semi-active suspension control. Veh. Syst. Dyn. 2015, 53, 1034–1062. [Google Scholar] [CrossRef]
- Wang, F.; Easa, S. Analytical evaluation of ride comfort on asphalt concrete pavements. J. Test. Eval. 2016, 44, 1671–1682. [Google Scholar] [CrossRef]
- Qin, Y.; Zhao, Z.; Wang, Z.; Li, G. Study of longitudinal–vertical dynamics for in-wheel motor-driven electric vehicles. Automot. Innov. 2021, 4, 227–237. [Google Scholar] [CrossRef]
- Múčka, P. Proposal of road unevenness classification based on road elevation spectrum parameters. J. Test. Eval. 2016, 44, 930–944. [Google Scholar] [CrossRef]
- Davis, B.R.; Thompson, A.G. Power spectral density of road profiles. Veh. Syst. Dyn. 2001, 35, 409–415. [Google Scholar] [CrossRef]
- Kong, Y.; Zhao, D.; Yang, B.; Han, C.; Han, K. Non-fragile multi-objective static output feedback control of vehicle active suspension with time-delay. Veh. Syst. Dyn. 2014, 52, 948–968. [Google Scholar] [CrossRef]
- Salehi, M.; Bamimohamadi, G. An enhanced adaptive neuro-fuzzy vehicle suspension control in different road conditions. Int. J. Dyn. Control 2019, 7, 701–712. [Google Scholar] [CrossRef]











| Structural Parameters | Values | Electrical Parameters | Values |
|---|---|---|---|
| Rotor outer diameter | 384 mm | Rated current | 57.7 A |
| Stator inner diameter | 298 mm | Rated voltage | 380 V |
| Number of slots | 36 | Rated torque | 450 Nm |
| Number of poles | 32 | Rated speed | 750 rpm |
| Air gap length | 1 mm | Rated power | 35.3 kW |
| Permanent magnet pole arc coefficient | 0.86 | Overload current | 130 A |
| Winding turns | 14 | Overload torque | 900 Nm |
| Lead wire diameter | 0.88 mm × 13 | Maximum efficiency | 95.52% |
| Slot space-factor (pure copper) | 0.68 | Electric load | 26.2 A/mm |
| Permanent magnet material | N40 EH | Current density | 7.36 A/mm2 |
| Material of iron core | B35A250 | D-Q inductance and resistance | 0.970 mH/0.0646 Ω |
| No. | Object | Value | Quantity | Unit | |
|---|---|---|---|---|---|
| 1 | Motor system | Rotor | 32.47 | 6 | kg |
| 2 | Stator | 46.63 | 6 | kg | |
| 3 | Gear trains | Gear trains | 115.50 | 6 | kg |
| 4 | Suspension system | Control arm | 68.20 | 6 | kg |
| 5 | Suspension | 34.43 | 6 | kg | |
| 6 | Car body | Car body | 3505.6 | 1 | kg |
| Material | Poisson’s Ratio | Density (g/cm3) | Modulus of Elasticity (GPa) |
|---|---|---|---|
| RbFeB | 0.25 | 7.5 | 160 |
| Stainless steels | 0.28 | 7.85 | 210 |
| No. | Parameter Category | Object | Parameter Name | Numerical | Units |
|---|---|---|---|---|---|
| 1 | Quality parameter | Motor system | Motor system quality | Table 1 Component quality parameter | kg |
| 2 | Gear train | Gear train quality | kg | ||
| 3 | Suspension system | Suspension system quality | kg | ||
| 4 | Vehicle body | Vehicle body quality | kg | ||
| 5 | Kinetic parameter | Suspension | Suspension spring | 85 | N/mm |
| 6 | Suspension damping | 1 | N.S/mm | ||
| 7 | Gear train | Tire radial stiffness | 1000 | N/mm | |
| 8 | Tire radial damping | 0.2 | N.S/mm | ||
| 9 | Tire side stiffness | 250 | N/mm | ||
| 10 | Tire side damping | 0.2 | N.S/mm | ||
| 11 | Tire circumferential stiffness | 1000 | N/mm | ||
| 12 | Tire circumferential damping | 0.2 | N.S/mm |
| Step Mode | Vibration Mode Description | Damp Ratio | Frequency (Hz) |
|---|---|---|---|
| 1 | The car body rotates around the Z axis | 0.025 | 0.94 |
| 2 | The car body rotates around the X axis | 0.027 | 1.14 |
| 3 | The car body translation around the Y axis | 0.038 | 1.47 |
| 4 | The whole vehicle rotates around the Y axis | 0.004 | 2.26 |
| 5 | The whole vehicle rotates around the Z axis | 0.002 | 2.58 |
| 6 | The whole vehicle rotates around the X axis | 0.016 | 4.30 |
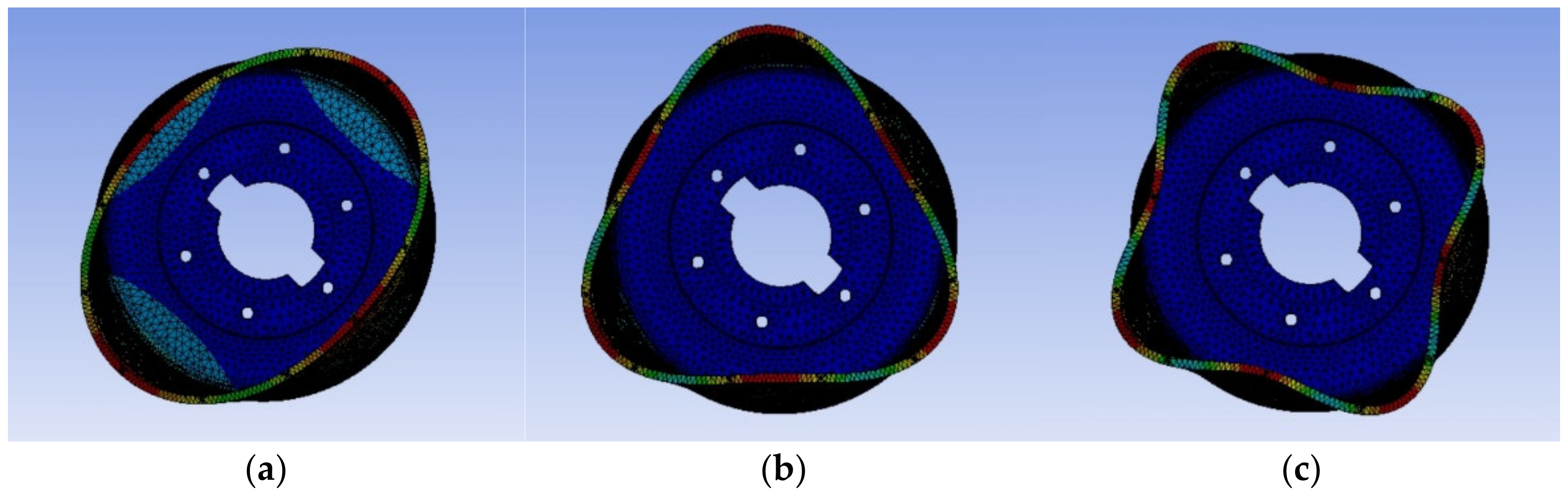
| Order | Simulation Frequency (Hz) | Vibration Pattern |
|---|---|---|
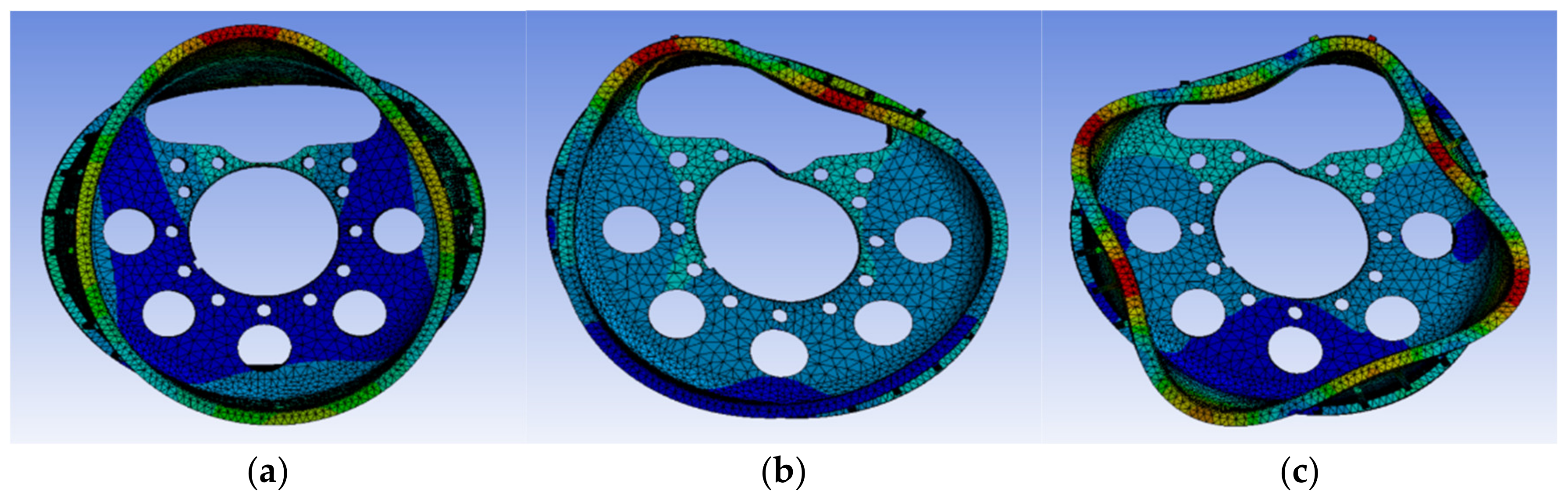
| 1 | 263.24 | Ellipses |
| 2 | 612.72 | Hexagon |
| 3 | 1045.30 | Octagon |
| Order | Simulation Frequency (Hz) | Vibration Pattern |
|---|---|---|
| 1 | 821.94 | Ellipses |
| 2 | 1403.00 | Quadrilateral |
| 3 | 2365.20 | Octagon |
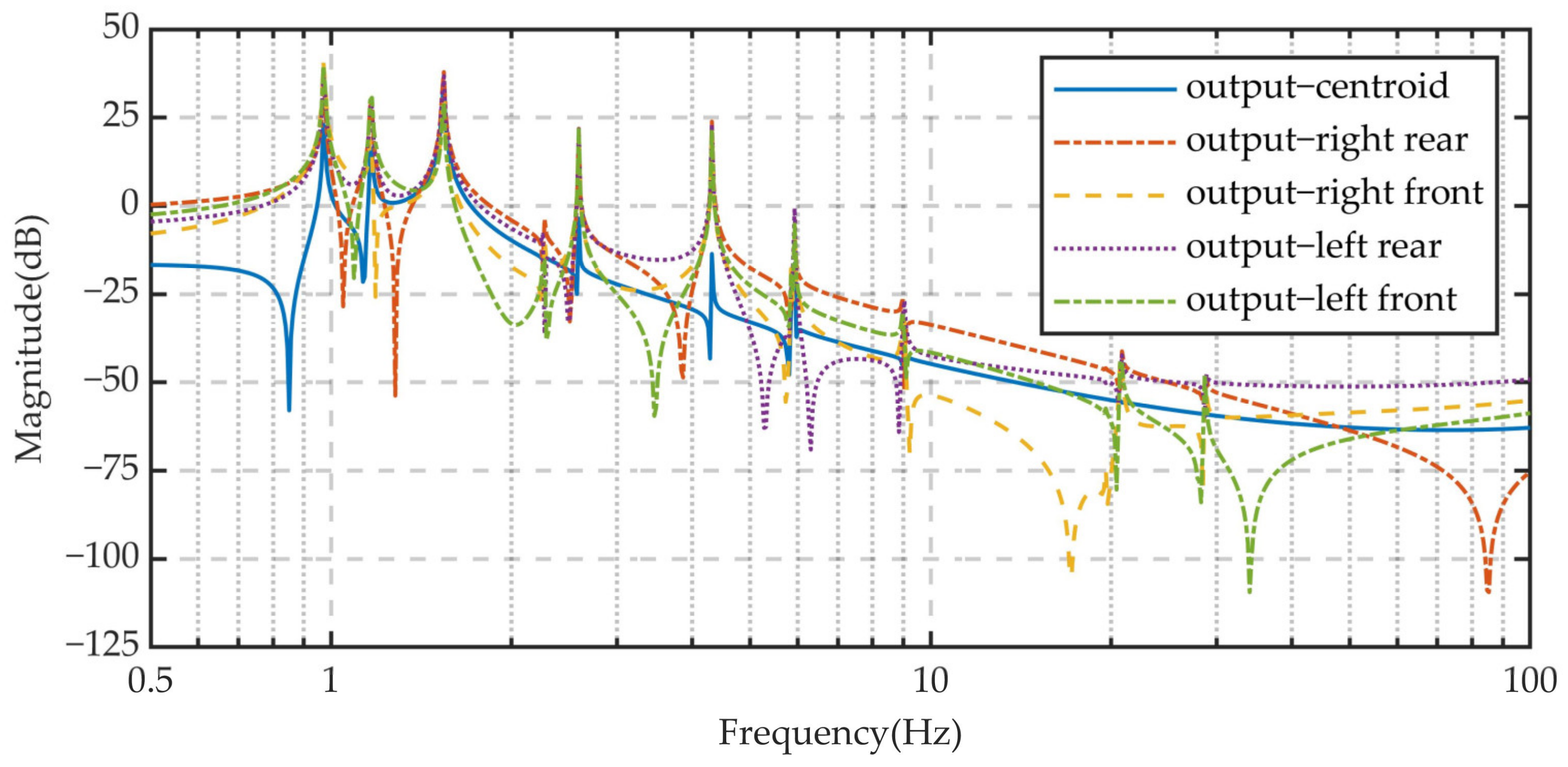
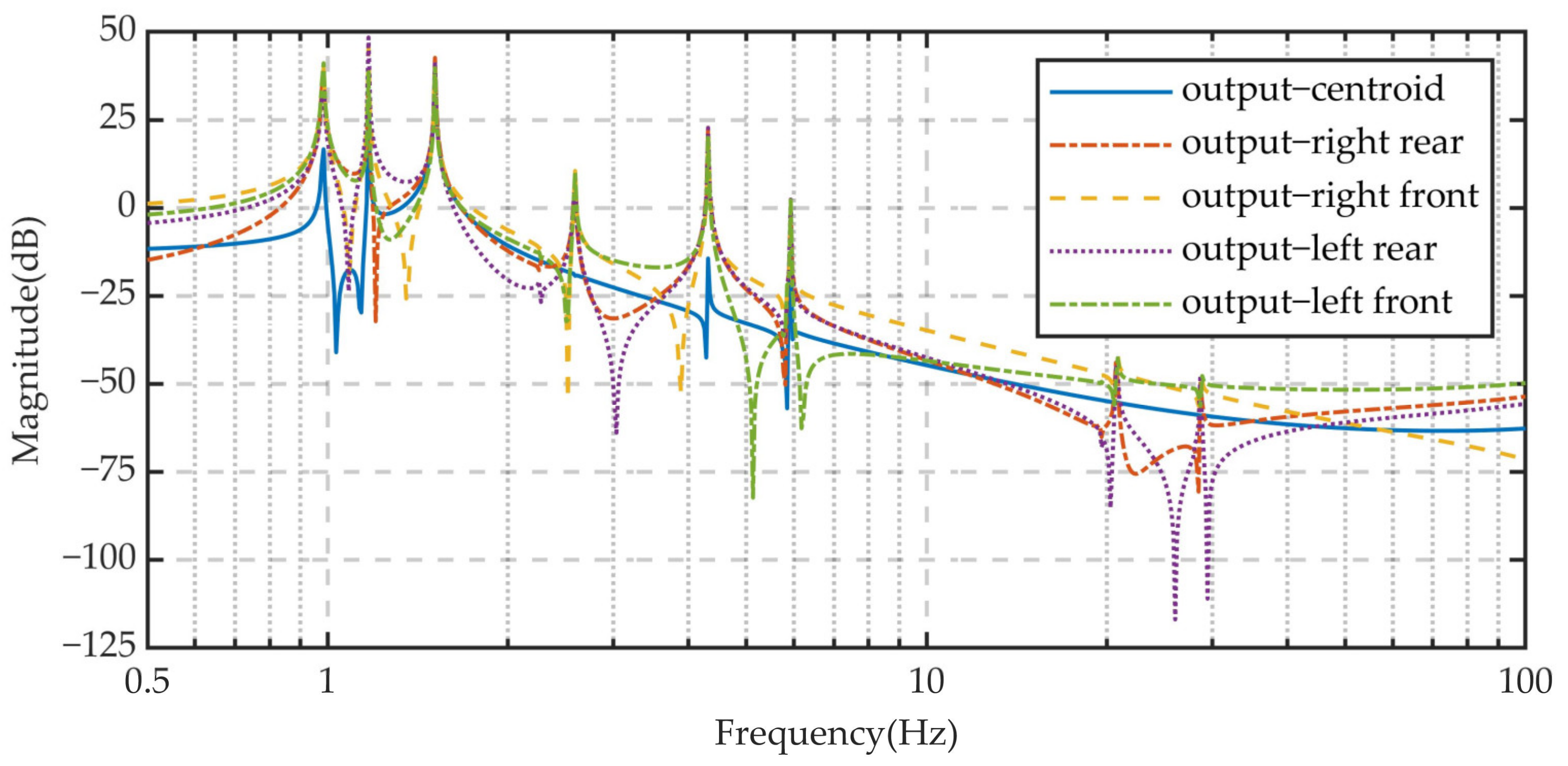
| Measurement Reference Point | Position |
|---|---|
| Output—right rear | Farthest rear right point of the vehicle |
| Output—right front | Farthest front right point of the vehicle |
| Output—left rear | Farthest rear left point of the vehicle |
| Output—left front | Farthest front left point of the vehicle |
| Output—centroid | Center of mass of the vehicle |
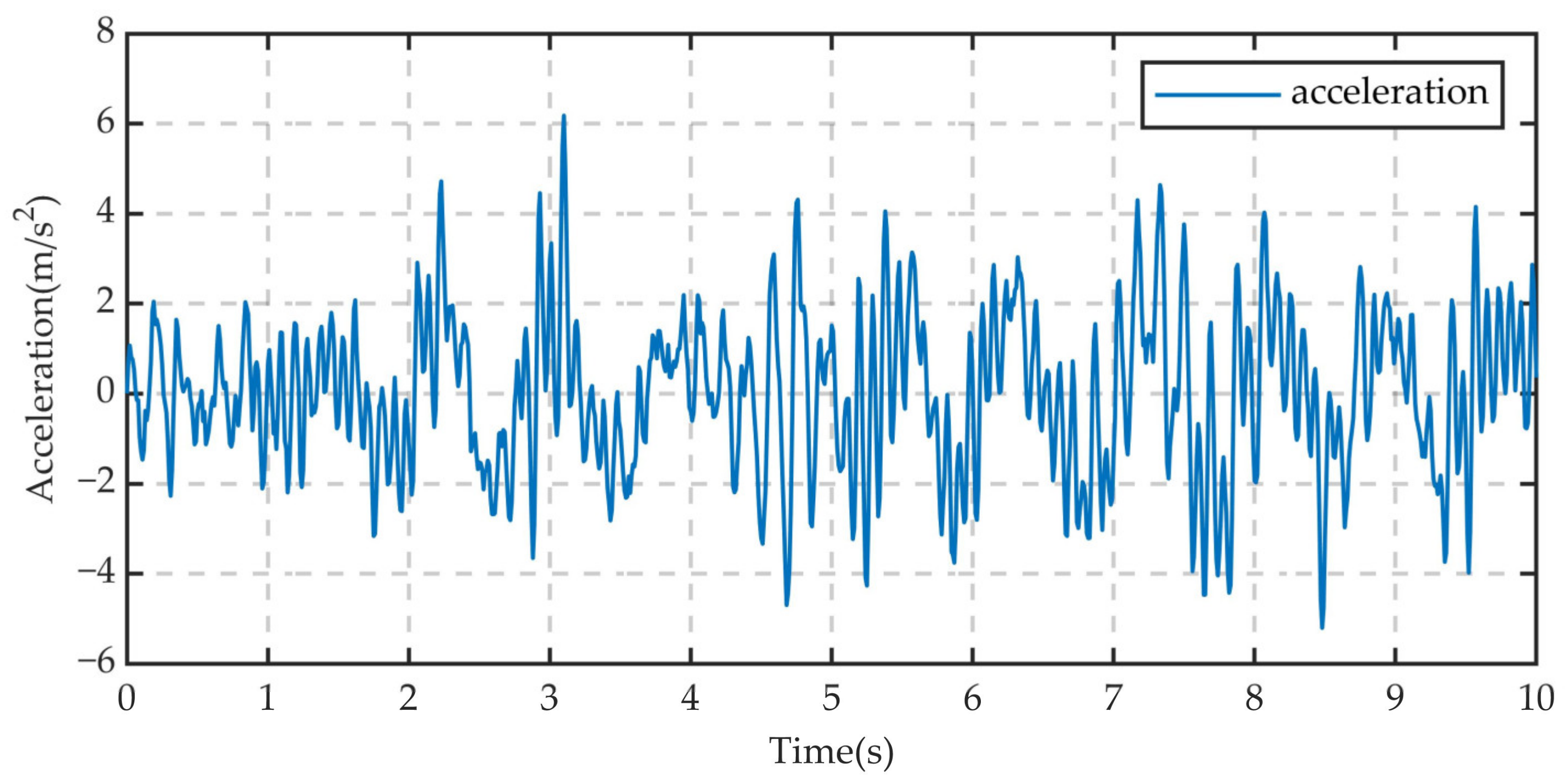
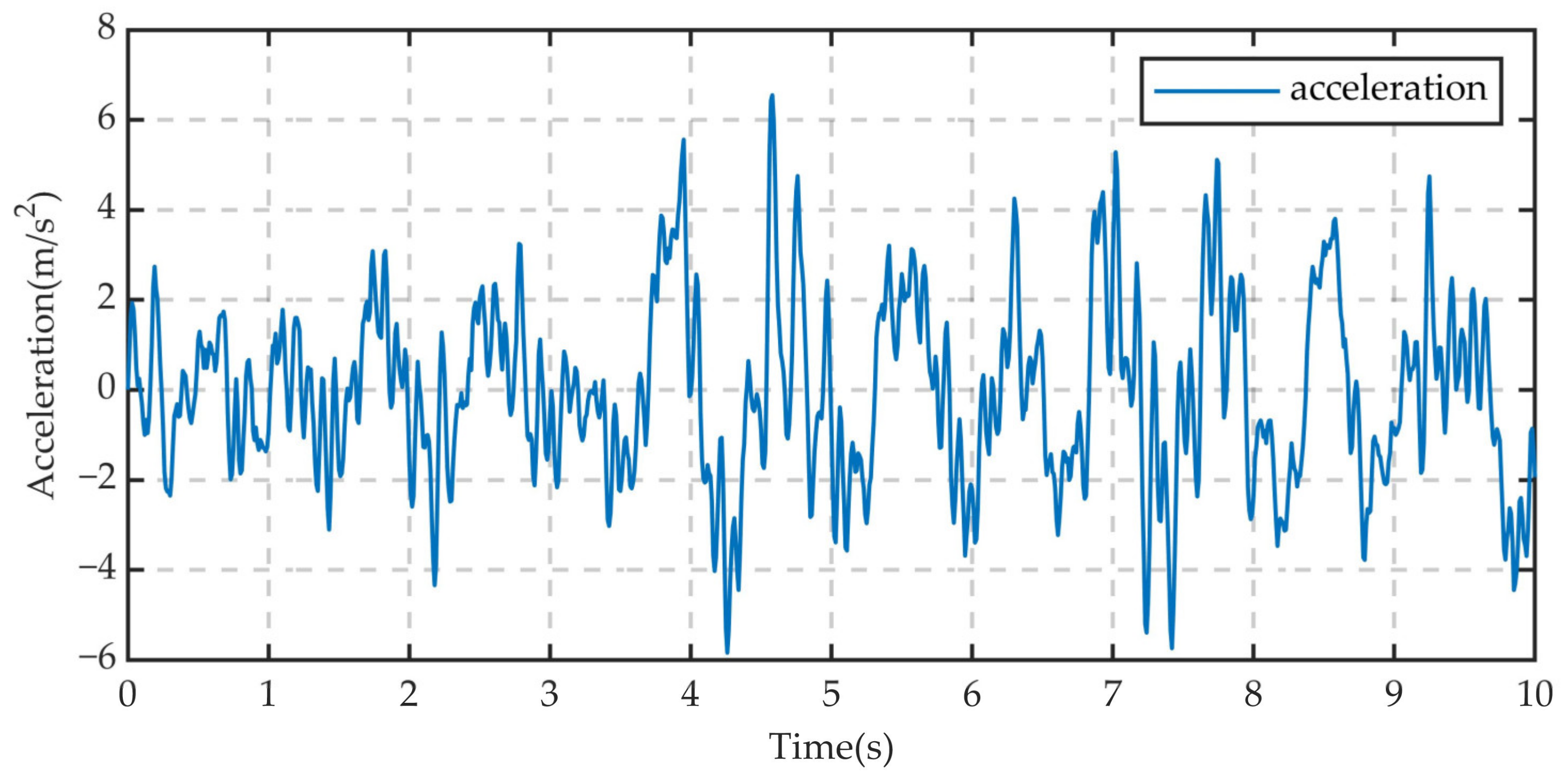
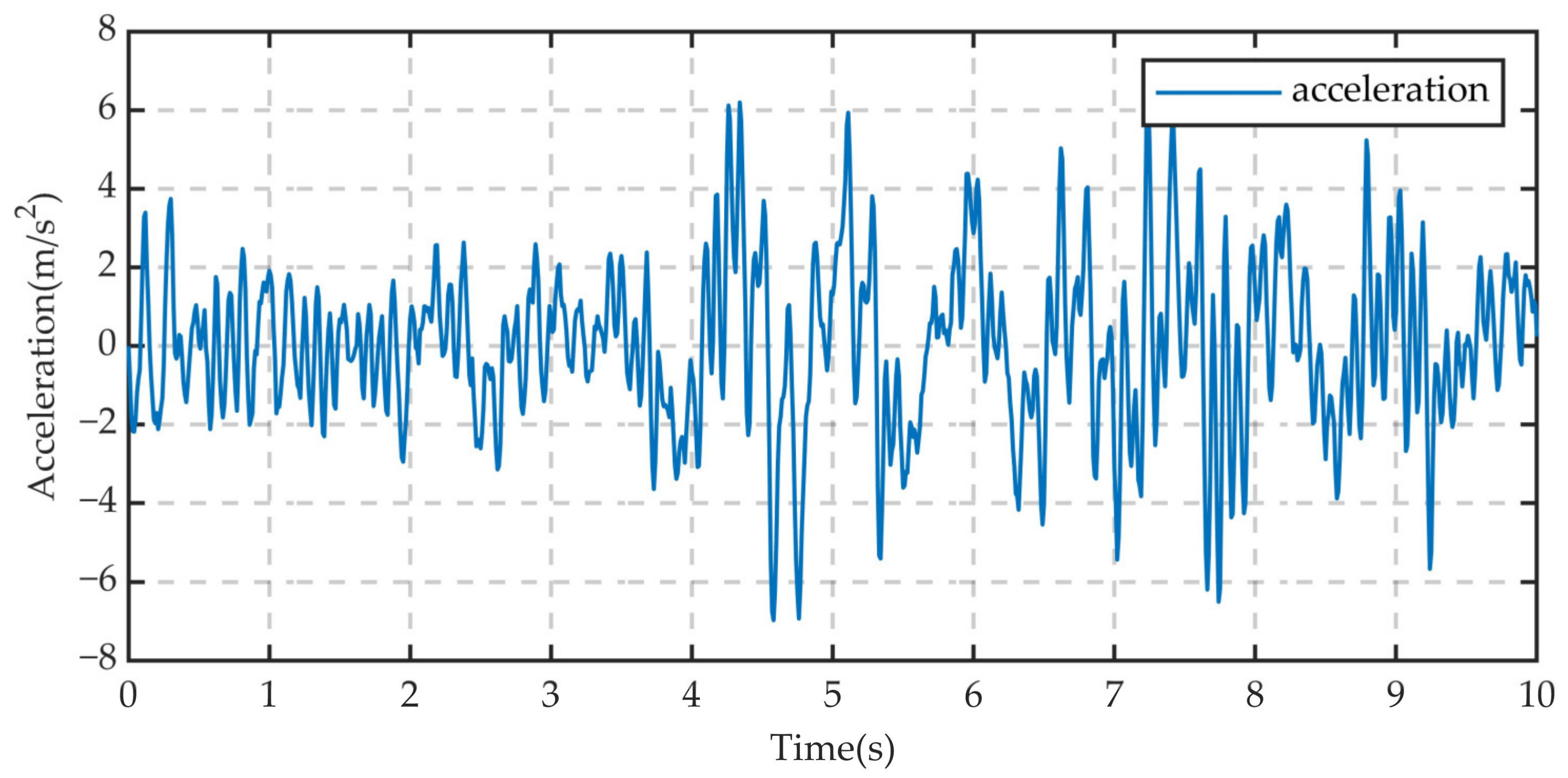
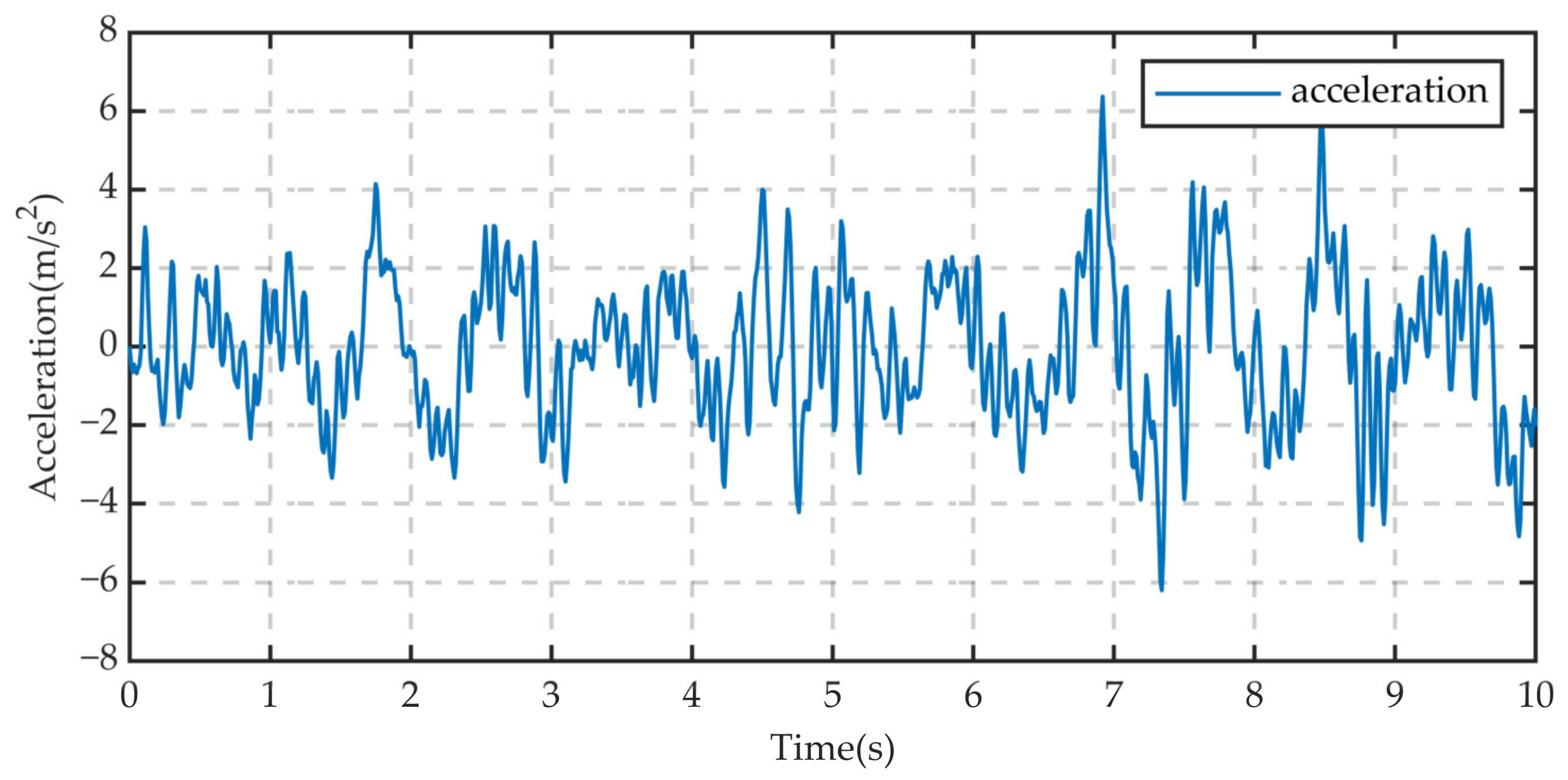
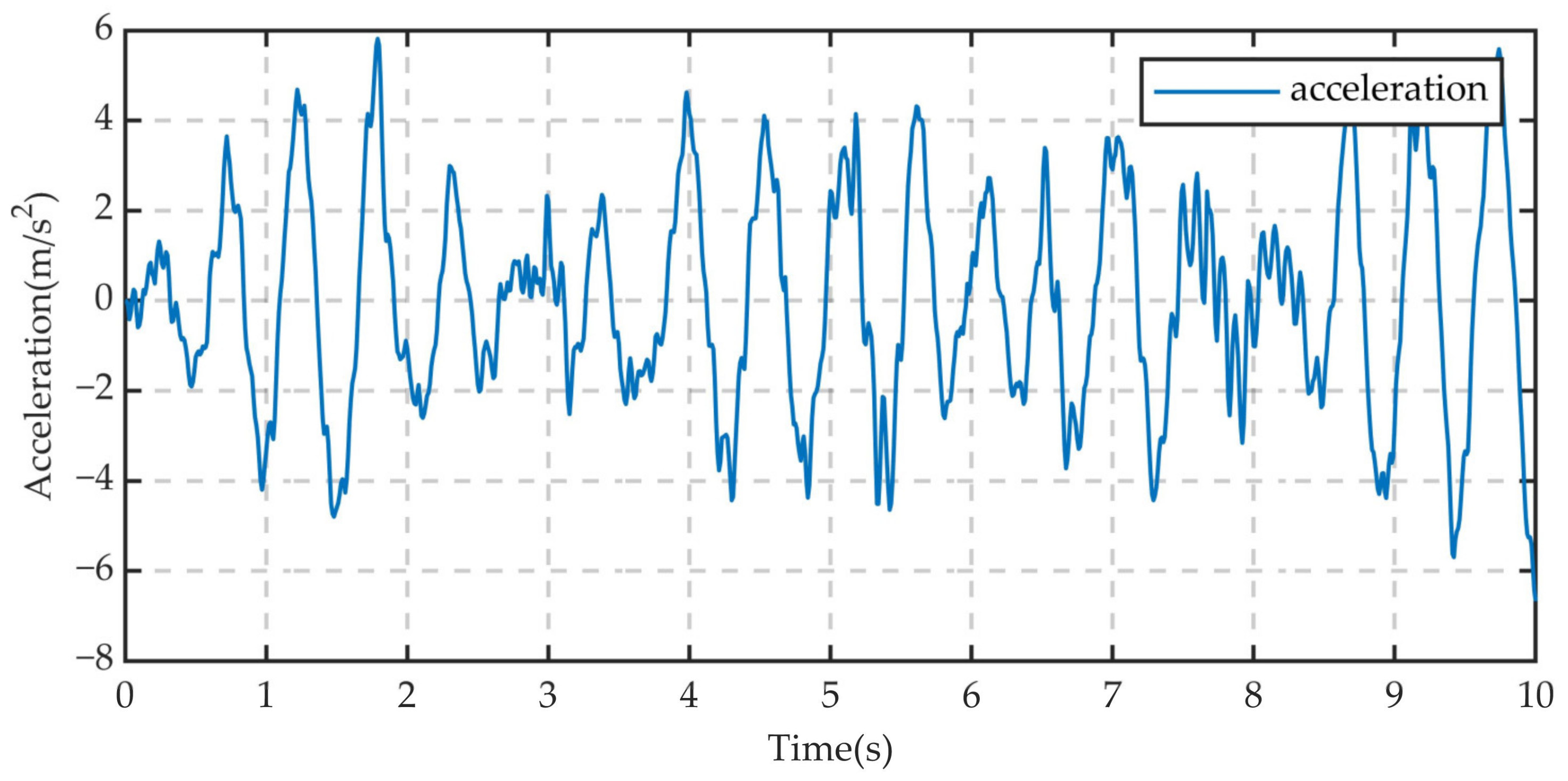
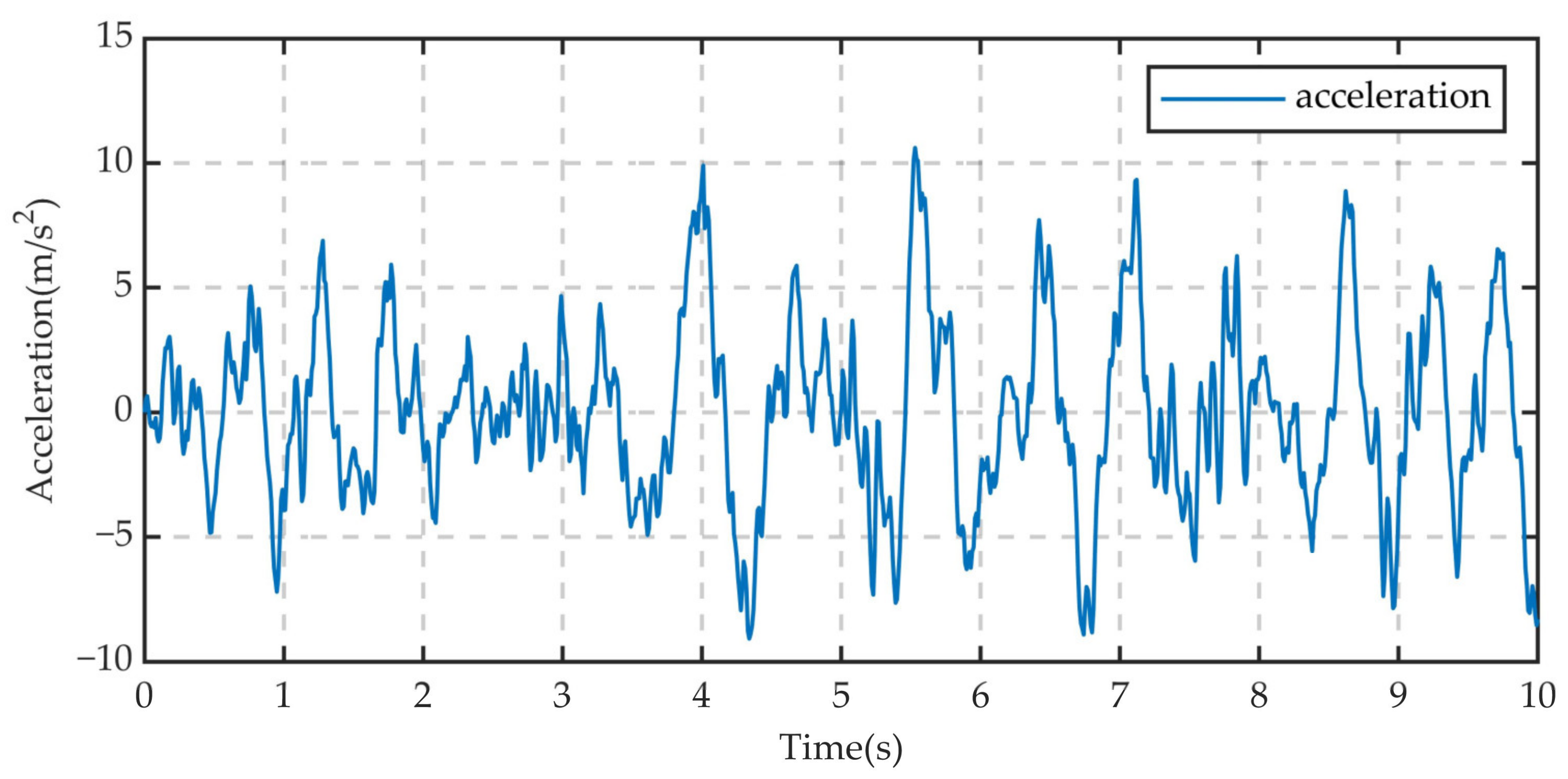
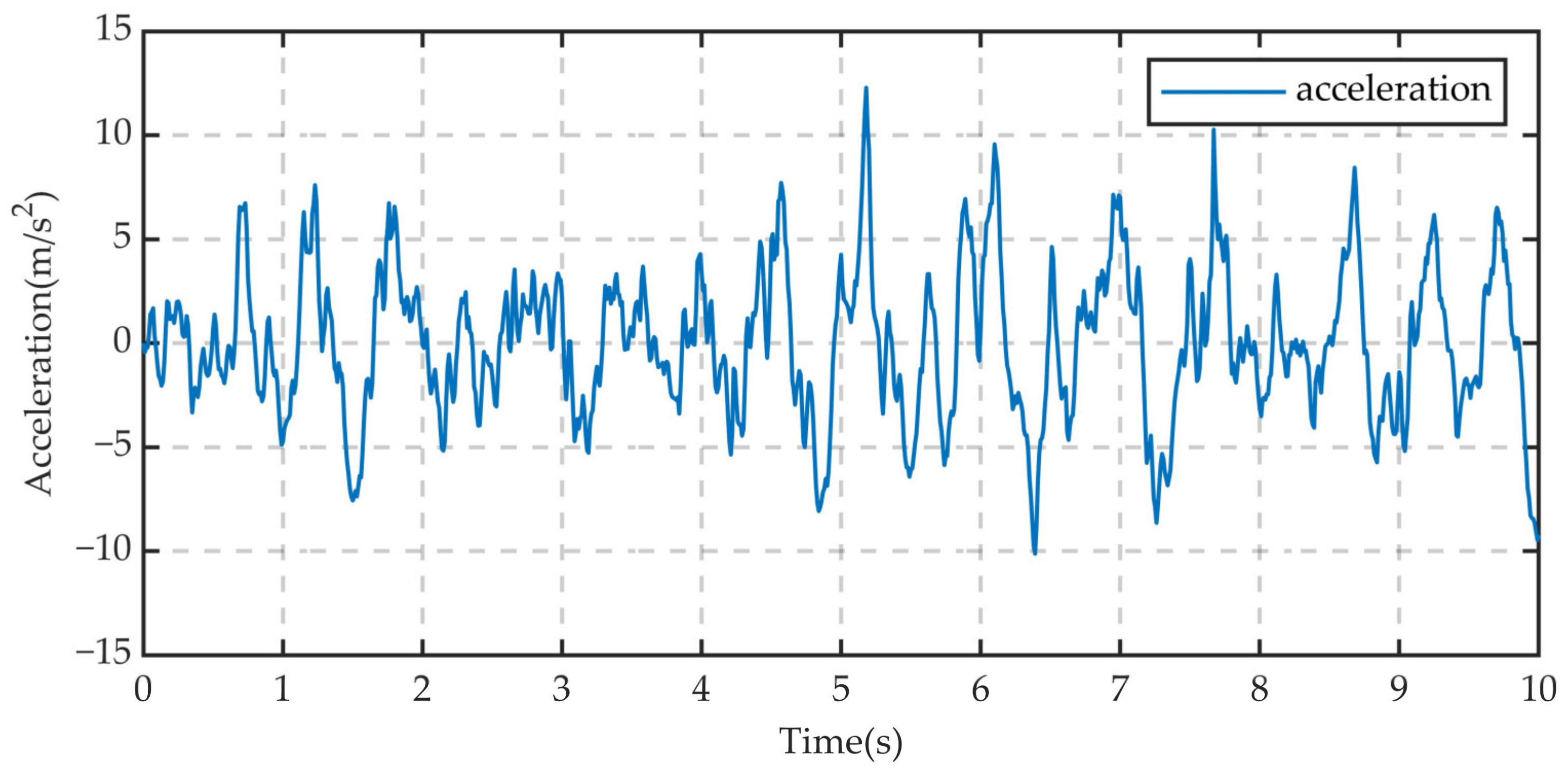
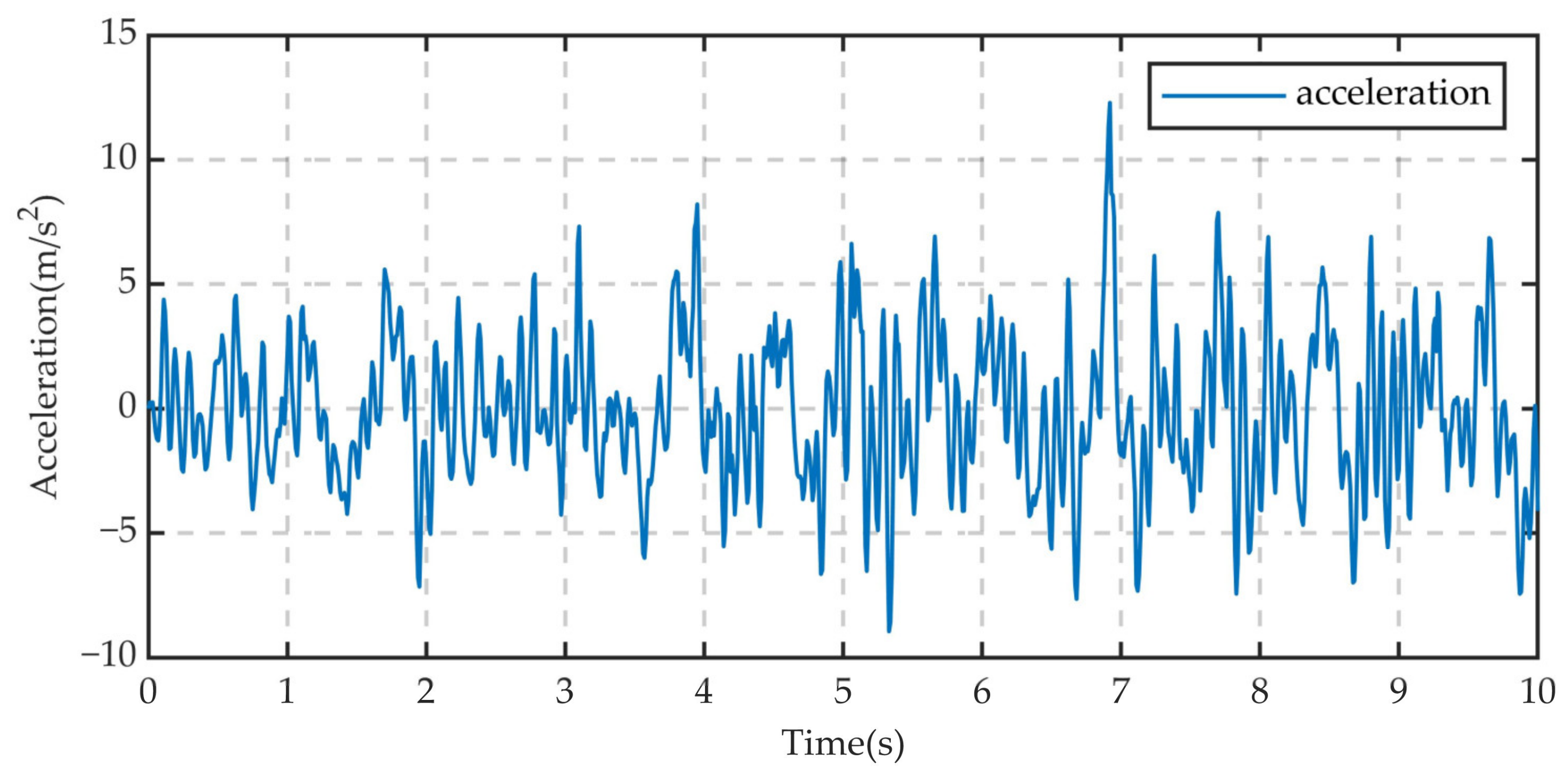
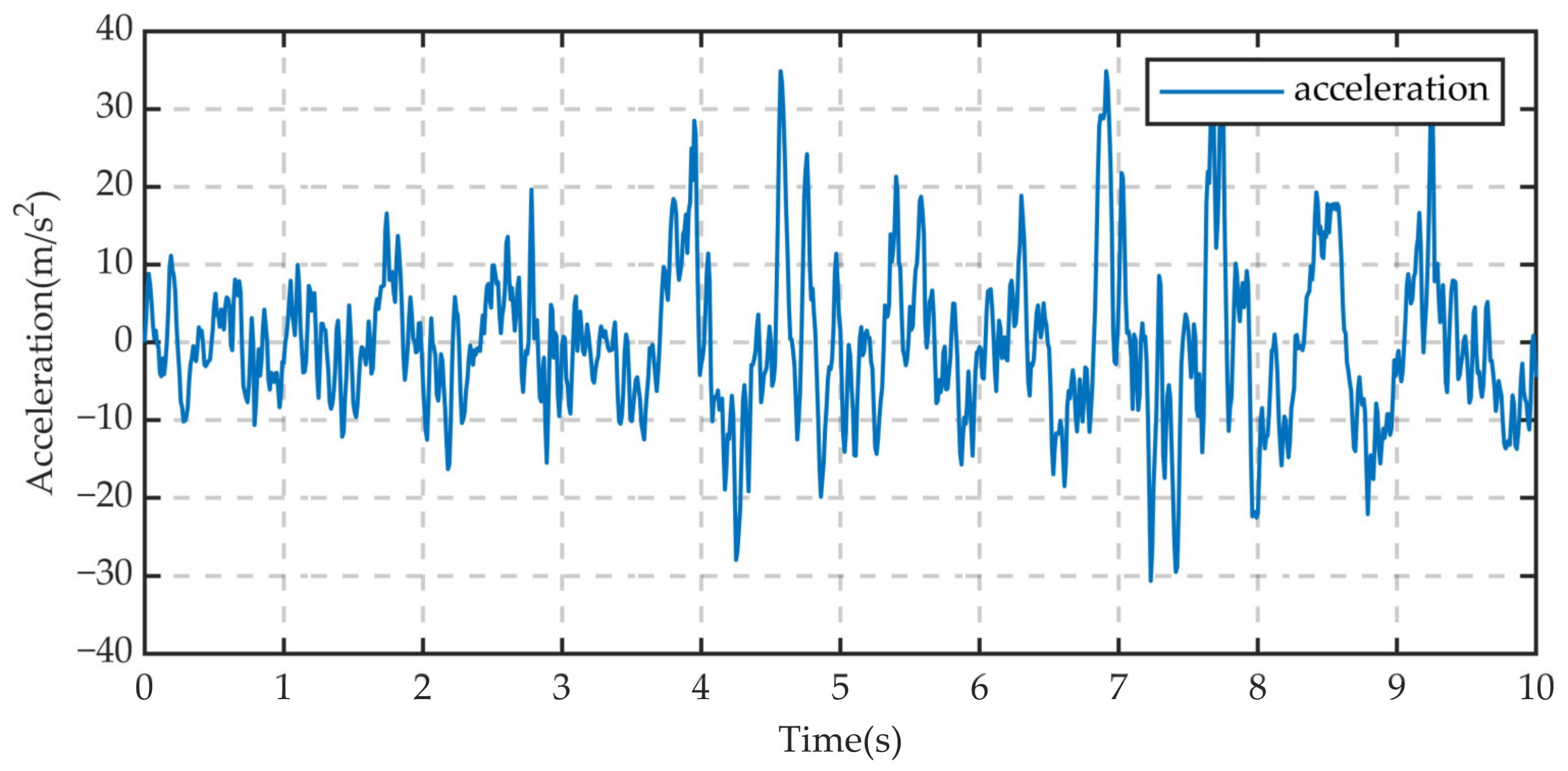
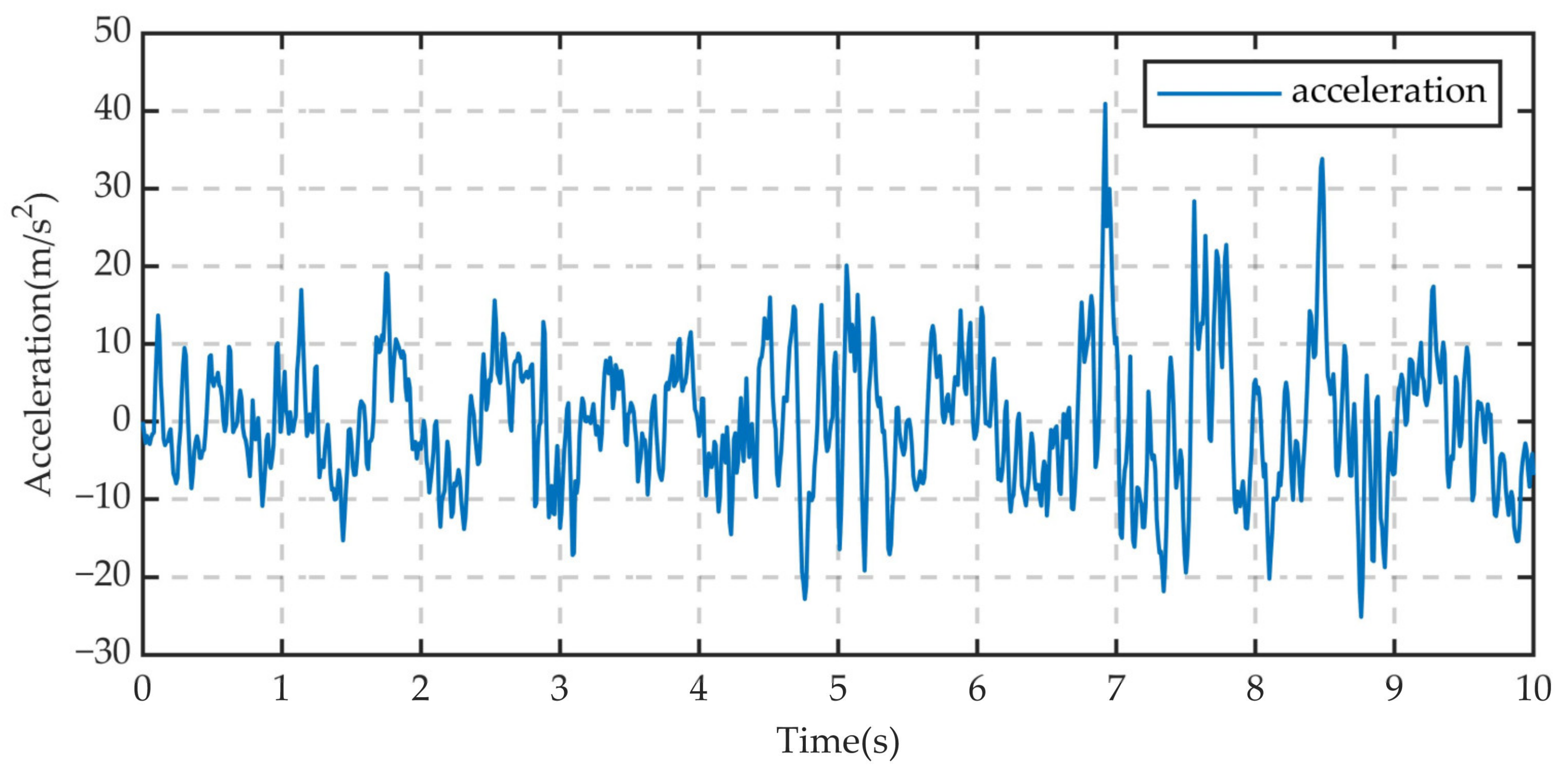
| No. | Road Class | Speed (m/s) | Position | Peak Acceleration (m/s2) | Acceleration RMS (m/s2) |
|---|---|---|---|---|---|
| 1 | C class | 10 | Centroid | 1.671 | 0.619 |
| 2 | 10 | RR | 6.180 | 1.750 | |
| 3 | 10 | RF | 6.550 | 1.995 | |
| 4 | 10 | LR | 6.977 | 2.075 | |
| 5 | 10 | LF | 6.369 | 1.837 | |
| 6 | 30 | Centroid | 6.673 | 2.399 | |
| 7 | 30 | RR | 11.082 | 3.781 | |
| 8 | 30 | RF | 10.612 | 3.641 | |
| 9 | 30 | LR | 12.103 | 4.113 | |
| 10 | 30 | LF | 12.286 | 3.539 | |
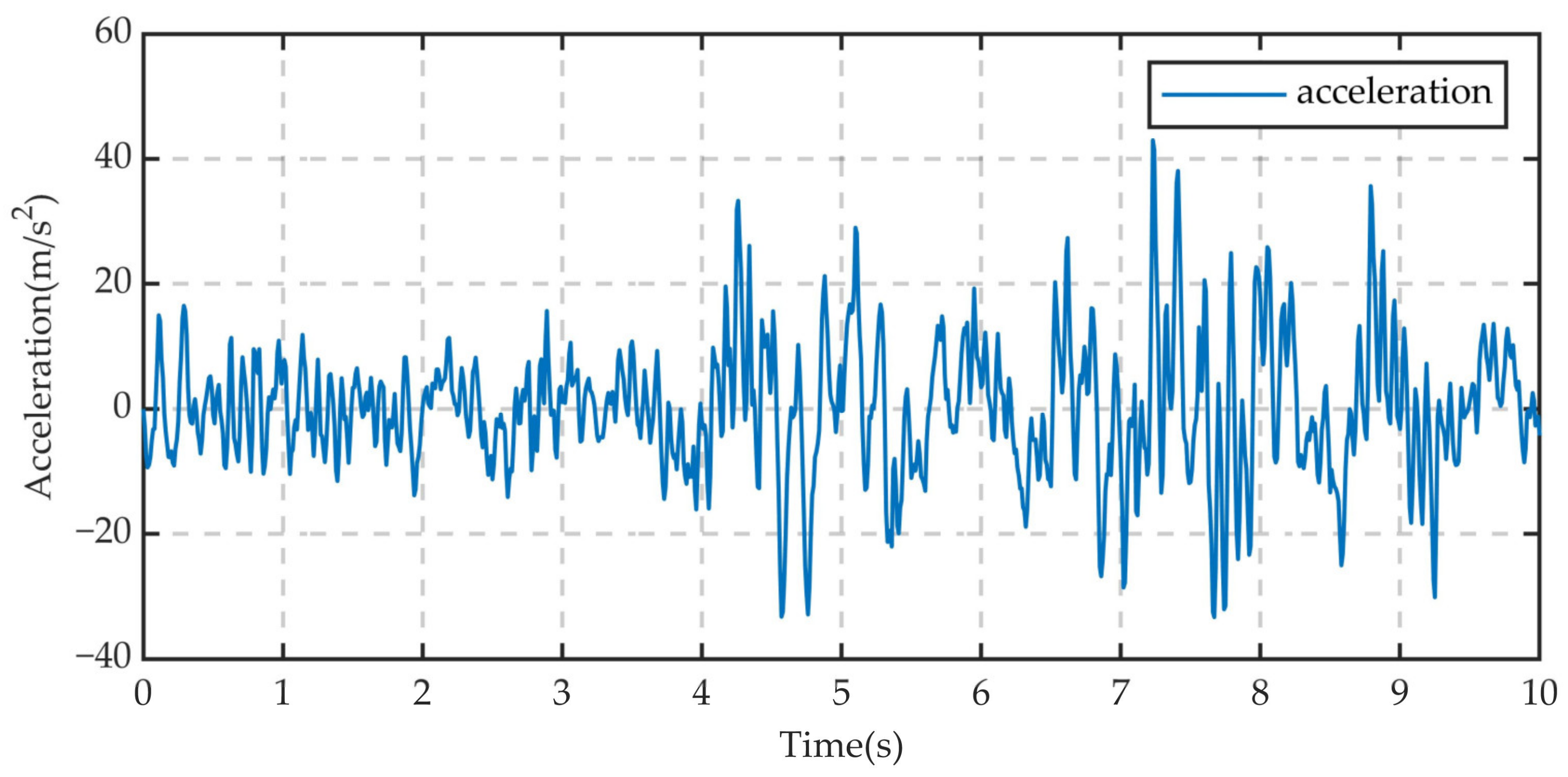
| 11 | E class | 10 | Centroid | 12.291 | 2.970 |
| 12 | 10 | RR | 33.973 | 8.802 | |
| 13 | 10 | RF | 34.871 | 9.917 | |
| 14 | 10 | LR | 42.979 | 10.463 | |
| 15 | 10 | LF | 40.914 | 8.729 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Che, J.; Wu, J.; Jiang, W.; Liu, R.; Zhao, Y. Integrated Dynamic Modeling and Simulation of Wheeled Vehicle with Outer-Rotor In-Wheel Motors and Key Units. Machines 2024, 12, 624. https://doi.org/10.3390/machines12090624
Liu X, Che J, Wu J, Jiang W, Liu R, Zhao Y. Integrated Dynamic Modeling and Simulation of Wheeled Vehicle with Outer-Rotor In-Wheel Motors and Key Units. Machines. 2024; 12(9):624. https://doi.org/10.3390/machines12090624
Chicago/Turabian StyleLiu, Xingyu, Jixing Che, Jiulin Wu, Wei Jiang, Rui Liu, and Yihui Zhao. 2024. "Integrated Dynamic Modeling and Simulation of Wheeled Vehicle with Outer-Rotor In-Wheel Motors and Key Units" Machines 12, no. 9: 624. https://doi.org/10.3390/machines12090624
APA StyleLiu, X., Che, J., Wu, J., Jiang, W., Liu, R., & Zhao, Y. (2024). Integrated Dynamic Modeling and Simulation of Wheeled Vehicle with Outer-Rotor In-Wheel Motors and Key Units. Machines, 12(9), 624. https://doi.org/10.3390/machines12090624






