An Investigation into the Optimal Dimple Geometry in a Single-Dimple Sliding Contact

Abstract

This study analyzes the influence of nine distinct texture geometries on a convergent oil film gap using a simulation model. The geometrical dimensions of the textures are characterized by the texture area density, $S_{tex.,A}$ and the ratio of the textured-to-untextured area ($A_{tex.}/A_0)$. The results show that different texture geometries optimize the tribological performance depending on the value of $S_{tex.,A}$. Rectangular textures with variable widths (85% of the texture length $a_{tex.}$) significantly enhance lifting and the drag force across a broad range of $S_{tex.,A}$. Furthermore, rectangular textures with a constant width (85% of the global width $b_0$) show the best improvement within this study. The investigation also reveals that a small texture pitch angle, ${\alpha }_{tex}$, further enhances tribological performance.

1. Introduction

In [1], it is presented that reducing the viscosity by 1 mPas at a temperature of 150 °C can lead to potential fuel savings ranging from 0.8% to 4%. The actual amount of savings will vary depending on the engine and test cycle. According to Woydt [1], Germany could save over 1.64 megatons of CO₂ per year by implementing a conservative fuel-saving potential of 1%. As a result, many researchers are focusing on the use of low-viscosity oils. In general, decreasing the viscosity also reduces the hydrodynamic pressure for constant oil film gap heights, which can be avoided by applying surface textures, as explained by Grützmacher et al. [2], who published that increasing the hydrodynamic pressure is one working principle of surface texturing. The concept of surface modifications has been under consideration for decades, particularly in the context of piston rings on cylinder liner contacts, as presented among others in [3], or for micro-grooved journal bearings [4]. The research effort, presented through the number of publications, for the application of surface textures strongly increased in the past 25 years [5,6,7,8]. The application of textures in hydrodynamic contacts can enhance the load-carrying capacity, as highlighted in [7,9]. To apply this beneficial behavior, various manufacturing processes are available for creating texture geometries, as summarized by Coblas et al. [10]:

• Adding material technologies;
• Removing material technologies;
• Material displacement technologies;
• Self-forming methods.

Typical examples of adding material technologies include the chemical and physical deposition processes, which are used in [11] to create micro-frustum-shaped dimples with a diameter of 50 µm to 75 µm on the base area. Laser surface texturing and mechanical processes, e.g., grinding and honing, are examples of removing material technologies. In [12], cylindrical-shaped dimples with a radius of up to 5 µm were created by a laser, and it was observed that the geometry of the texture was strongly influenced by the laser’s parameters. Pettersson et al. [13] developed a process for manufacturing embossing tools, which they used to produce pyramid- and rooftop-shaped textures. This method is an example of a material displacement technology. Self-forming texture dimples were numerically analyzed in [14], where the texture was created through elastic deformation caused by the applied load. Consequently, the shape of the texture depends on the load and the stiffness of the system.

The manufacturing process itself can limit the texture geometry. Nevertheless, the shape of the texture geometry varies in many publications, and in [15,16,17,18,19,20,21,22], the influence of the texture geometry is analyzed in detail. In [15,17,18,19,20], different texture shapes for a parallel oil film gap were evaluated using the Reynolds equation. Since the oil film gap is rarely parallel in technical applications, this study investigates the performance of different texture geometries for a convergent oil film gap. Regarding the simulation methodology, Dobrica et al. [23] published that the application of the Reynolds equation in full film lubrication is valid for large enough dimple aspect ratios and low Reynolds numbers. Simulating transient elastohydrodynamic contacts using the Reynolds equation results in small deviations compared to the simulating fluid dynamic models [24]. This study employs a full film lubrication model, incorporating Stokes flow in the simulation.

Wei et al. [21] analyzed different texture shapes on a convergent oil film gap, where the texture had specific dimensions. This led to different texture area densities $S_{tex.,A}=A_{tex.}/A_0$, as the texture area $A_{texture}$ depends on the texture shape (cf. Figure 1). Furthermore, they compared the performance of the different texture geometries by using a constant number of dimples; consequently, the texture area density $S_{tex.,A}$ for every textured surface is different [21]. Summarized, different texture area densities $S_{tex.,A}$ were examined.

In contrast to them, Uddin et al. [17] investigated different texture geometries at a constant texture area density $S_{tex,A}$. Additionally, they analyzed the influence of the bottom profile, which was flat, curved or coned [17]. In [18], five different texture densities $S_{tex.,A}$, in the range between 3% and 30%, were analyzed for a parallel sliding contact. Kumar et al. [19] analyzed eight different texture shapes and compared their load-carrying capacities over the texture area density $S_{tex.,A}$ for a thrust bearing. In [20], the dimensionless average pressure was analyzed for three different texture shapes, including the influence of the texture area density $S_{tex.,A}$. In contrast to these studies focusing on a parallel oil film gap, this study will discuss the influence of texture shape on a convergent oil film gap for specific texture area densities $S_{tex.,A}$.

As mentioned in [17], different bottom profiles influence the tribological performance, and it is found that a single wedge significantly enhances the tribological performance in full film lubrication. In [22,25], the performance of a wedge-shaped texture was analyzed in mixed lubrication and it could be observed that this texture improves tribological performance.

Based on the past paragraphs, this raises the question of the influence of the texture geometry at a constant $S_{tex.,A}$ and of the pitch angle ${\alpha }_{tex.}$. A pitch angle ${\alpha }_{tex.}$ equivalent to zero can be achieved with a constant texture height $h$, otherwise ${\alpha }_{tex.}$ is $>0°$.

2. Methodology

2.1. Simulation Methodology

Marian et al. [8] published that, in about 27% of all publications in the field of surface texturing between 1990 and 2020, a simulation model was investigated, and about 37% focused on hydrodynamic lubrication. In [15,17,18,19,20], the Reynolds equation is solved, which has strict limitations regarding the texture geometry and Reynolds number [23]. To avoid these problems in this current work, a Stokes flow is used. Cupillard et al. [26] discussed the influence of inertia effects in textured hydrodynamic contacts, mentioning that for low Reynolds numbers, these effects are neglectable. For the geometry used in this study, the maximal Reynolds number is approximately $Re\approx 1.6$ and, therefore, the inertia effects, which are described by the nonlinear term of the Navier–Stokes equation, are neglected. Based on these results, the application of the Stokes flow is acceptable. Equations (1) and (2) present the multiphase Stokes flow and the continuity equation, which is necessary to calculate the velocity field $\overrightarrow{u}$ and pressure field $p$. Here, $\nu$ is the kinematic viscosity, $\zeta$ is the second viscosity, $\mathit{I}$ is the identity matrix, $\rho$ is the density and $\overrightarrow{f}$ is the body force. This multiphase flow has to be solved if cavitation occurs; that means that the minimal pressure $p_{min}$ is lower than the vapor pressure $p_v$. Otherwise, the single-phase flow, presented by Equation (3), can be solved. In the case of cavitation, the viscosities $\nu$, $\zeta$ and density $\rho$ become scalar fields. The second viscosity $\zeta$ is set equal to the kinematic viscosity $\nu$, satisfying the inequality presented in [27]. In [28], this assumption was compared with an already existing solver for a multiphase flow.

$$-\nabla ·\left\{\nu \left[\nabla \overrightarrow{u}+{\left(\nabla \overrightarrow{u}\right)}^T-{\displaystyle \frac{2}{3}}\left(\nabla ·\overrightarrow{u}\right)I\right]+\zeta \left(\nabla ·\overrightarrow{u}\right)\mathit{I}\right\}+\nabla p=\rho \overrightarrow{f}$$

(1)

$$-\nabla ·\overrightarrow{u}=0$$

(2)

$$-\nu ∆\overrightarrow{u}+\nabla p=\rho \overrightarrow{f}$$

(3)

In [29], the Merkle [30] cavitation algorithm was used to simulate a journal bearing. This cavitation algorithm is described by Equations (4)–(9) and is based on a transport partial differential equation (cf. Equation (4)), where ${\alpha }_v$ represents the vapor volume fraction (cf. Equation (7)) and ${\dot{m}}^{+}$ and ${\dot{m}}^{-}$ are the source terms that describe the condensation and vaporization processes. The vapor volume fraction ${\alpha }_v$ represents the portion of vapor volume $V_v$ in the complete volume $V_v+V_l$. Therefore, the sum of the vapor volume fraction ${\alpha }_v$ and liquid volume fraction ${\alpha }_l$ is 1. The condensation term ${\dot{m}}^{+}$ depends on the condensation constant $Cc$, the density of the fluid ${\rho }_l$ and vapor ${\rho }_v$, the reference time $t_{\infty }$ and speed $U_{\infty }$ and the liquid volume fraction ${\alpha }_l$. The vaporization rate ${\dot{m}}^{-}$ depends on the parameter mentioned earlier and the vaporization constant $Cv$. The density $\rho$—and viscosity field $\nu$ are presented in the case of cavitation by multiplication, as shown in Equations (8) and (9).

$$\nabla ·\left(\overrightarrow{u}{\alpha }_v\right)={\dot{m}}^{+}-{\dot{m}}^{-}$$

(4)

$${\dot{m}}^{+}=Cc{\displaystyle \frac{\rho }{{\rho }_l{\rho }_v}}{\displaystyle \frac{(1-{\alpha }_l)}{0.5U_{\infty }^2{t}_{\infty }}}\mathrm{m}\mathrm{a}\mathrm{x}(p-p_v,0)$$

(5)

$${\dot{m}}^{-}=Cv{\displaystyle \frac{\rho }{{{\rho }_v}^2}}{\displaystyle \frac{{\alpha }_l}{0.5U_{\infty }^2{t}_{\infty }}}\mathrm{m}\mathrm{a}\mathrm{x}(p_v-p,0)$$

(6)

$${\alpha }_v={\displaystyle \frac{V_v}{V_v+V_l}}$$

(7)

$$\rho ={\rho }_v{\alpha }_v+{\rho }_l(1-{\alpha }_v)$$

(8)

$$\nu ={\nu }_v{\alpha }_v+{\nu }_l(1-{\alpha }_v)$$

(9)

To solve these equations numerically, the finite element method FEM is applied using a Python-based simulation package called Netgen/NGSolve [31]. For this study, the steady state is of interest, so the time derivatives for the transport and Stokes equation are not considered. For discretization of the geometries, tetrahedral-shaped elements with second-order shape functions are used. A maximal mesh size of 25 µm was defined to achieve sufficient accuracy. This mesh size was determined through a mesh study, where deviations of less than 0.5% for lifting and the drag force were observed.

Table 1. Simulation parameters.

Parameters
Density oil liquid ${\rho }_l$	860 kg/m3
Density oil vapor ${\rho }_v$	0.13 kg/m3
Dynamic viscosity liquid ${\eta }_l$	130 mPa s
Dynamic viscosity vapor ${\eta }_v$	0.02 mPa s
Condensation coefficient $C_C$	33.3
Vaporization coefficient $C_v$	0.00155
Vapor pressure $p_v$	165 Pa
Input velocity $U_{\infty }$	5 m/s
Reference time $t_{\infty }$	$l_0/U_{\infty }$

presents the simulation parameters for the oil and cavitation algorithm based on the work presented in [32,33].

In [28], this self-developed simulation methodology is compared with the results of the existing OpenFOAM IntherphaseChangeFOAM [34] solver, which is based on the full Navier–Stokes equation.

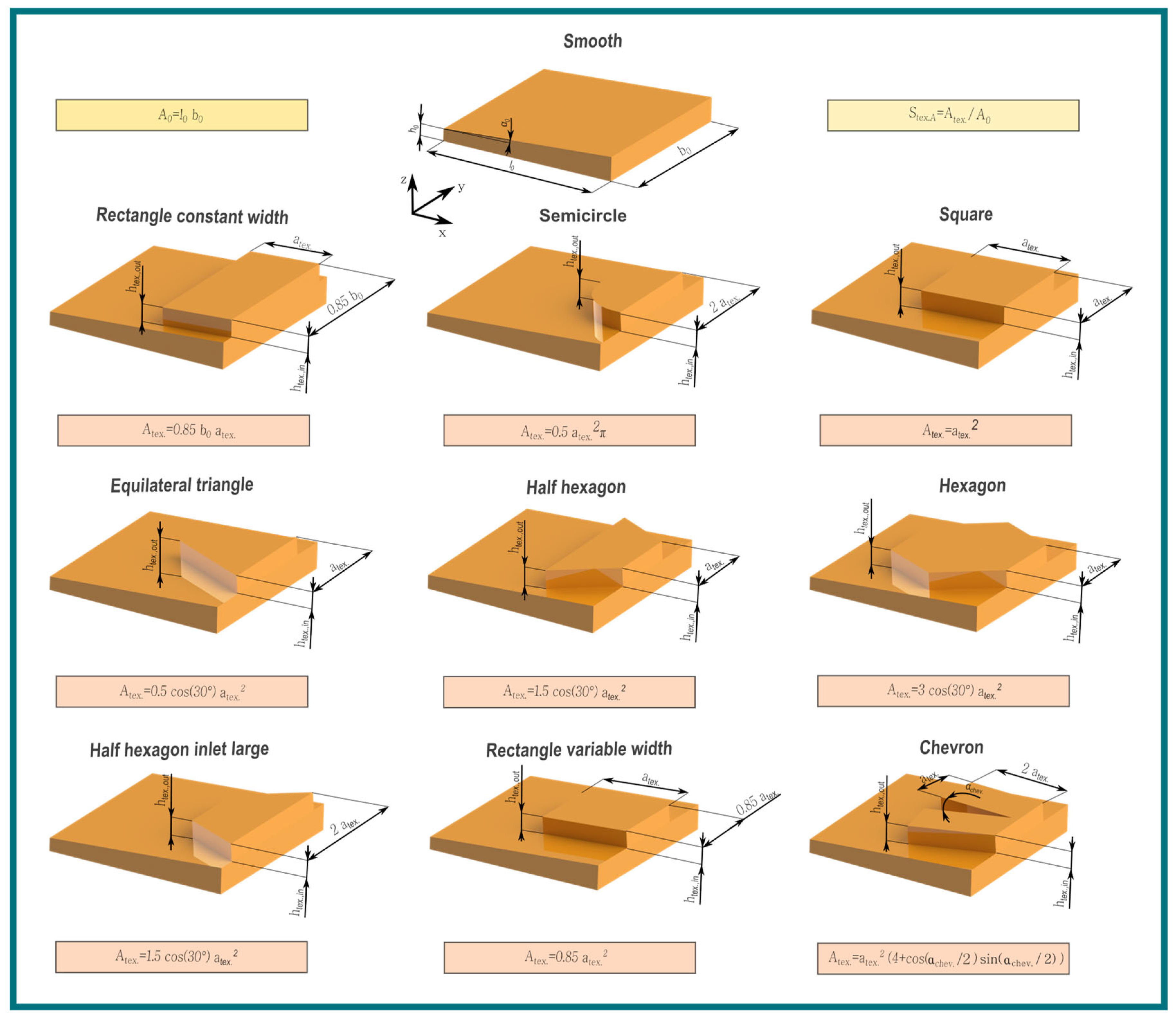
2.2. Texture Geometries and Simulation Parameters

The texture height at the inlet, $h_{tex.,in}$, was set to 30 µm and was kept constant in this work. Figure 1 shows the smooth convergent oil film gap and nine different texture geometries. The different dimple geometries were selected based on two points of view. On the one hand, as few as possible parameters should be varied, and on the other hand, these geometries should be quite simple so that a potential manufacturing process is applicable. To evaluate the performance of specific texture shapes, the texture area density $S_{tex,A}=A_{tex.}/A_0$ is used. This means that a specific texture area density $S_{tex,A}$ is defined, and with the help of the equations presented in Figure 1, the geometrical parameter $a_{tex.}$ is calculated. The parameters of the smooth wedge are $l_0=b_0=2 \mathrm{m}\mathrm{m}$, $h_0=15 \mathrm{\mu }\mathrm{m}$ and ${\alpha }_0=0.15°$. For the rectangle with a constant width, the texture width was defined as 85% of $l_0$. This 85% result is the best tribological performance in [28]. The angle ${\alpha }_{Chev.}$ is set to 20°. Initially, the tribological performance of the different texture geometries was analyzed for a constant texture height $h_{tex.in}=h_{tex.,out}=30 \mathrm{\mu }\mathrm{m}$, which corresponds to a pitch angle of ${\alpha }_{tex.}=0°$. For analyzing the influence of the pitch angle ${\alpha }_{tex.}$, the texture height at the outlet was varied between 0 and 30 µm with a s step size of 5 µm. This resulted in different pitch angles of the texture ${\alpha }_{tex.}$.

In Figure 2, the boundary conditions for an exemplary rectangle-shaped texture are depicted. The bottom surface of the oil film gap is moving with the velocity $\underset{\_}{u}$, while the top surface of the oil film gap and the surface of the texture are stationary. The lateral surface of the oil film has a relative pressure of $p=0\mathrm{P}\mathrm{a}$, resulting in a liquid volume fraction of ${\alpha }_l=1$. For all other boundary conditions not mentioned, a Neumann boundary condition, zero gradient, is applied. Furthermore, it is assumed that all surfaces are completely smooth.

For the numerical implementation of the simulation model, the sparse direct solver Unsymmetric Multi Frontal Package UMFPACK was used.

Solving the previously discussed equations leads to a pressure field $p$ and a velocity field $u$ for each geometry. In postprocessing, the lifting force ${\overrightarrow{F}}_{lift}$ is calculated by integrating the pressure field over the bottom surface (cf. Equation (10)). The drag force ${\overrightarrow{F}}_{drag}$ is calculated by integrating the shear stresses ${\tau }_x$ over the bottom surface.

$${\overrightarrow{F}}_{lift}.={\int }_A{p}_{\left(x,y,z=0\right)}·\overrightarrow{n}dA$$

(10)

Both forces, calculated on a smooth convergent oil film gap, were compared with the analytical solution according to [35], and similar results could be achieved.

In general, the texture should increase the lifting force ${\overrightarrow{F}}_{lift}$, decrease the drag force ${\overrightarrow{F}}_{drag}$ or combine both. However, to combine these two parameters, the performance enhancement ratio (PER), which is published in [36], is used. Sharma et al. [36] used the load-carrying capacity and friction coefficient as parameters. In this study, the ratio of the magnitudes of the lifting forces between textured $\left|\left.{\overrightarrow{F}}_{lift,textured}\right|\right.$ and untextured $\left|\left.{\overrightarrow{F}}_{lift,untextured}\right|\right.$ geometries is divided by the ratio of the magnitudes of their respective drag forces $\left|\left.{\overrightarrow{F}}_{drag,texured}\right|\right.$ and $\left|\left.{\overrightarrow{F}}_{drag,untextured}\right|\right.$ (cf. Equation (11)).

$$\mathrm{P}\mathrm{E}\mathrm{R}={\displaystyle \frac{\frac{\left|\left.{\overrightarrow{F}}_{lift,textured}\right|\right.}{\left|\left.{\overrightarrow{F}}_{lift,untextured}\right|\right.}}{\frac{\left|\left.{\overrightarrow{F}}_{drag,texured}\right|\right.}{\left|\left.{\overrightarrow{F}}_{drag,untextured}\right|\right.}}}$$

(11)

3. Results

3.1. Influence of Texture Geometry for Constant Width

In Figure 3, the performance enhancement ratio (PER) over the texture area density $S_{tex.,A}$ for each geometry is depicted. The maximal texture area density $S_{tex.,A}$ for every geometry is different, as the texture should not protrude the convergent oil film gap’s base area. In regions of low texture area density $S_{tex.,A}$ (less than 30%), the rectangle with a variable width and chevron-shaped texture led to the best tribological performance. In the region of a texture area density between 30% and 70%, the rectangle with a variable width causes the highest performance enhancement ratio (PER). With a further increasing texture area density, the performance of the rectangle with a constant width achieves the highest PER, in contrast to the regions with a low texture area density $S_{tex.,A}$, where this geometry has the worst tribological performance. As the texture area density $S_{tex.,A}$ increases, the difference between both half hexagons increases, followed by a continuous decrease. In the observed region, the half hexagon leads to better tribological performance compared to the half hexagon (inlet large), which is positioned so that the large area is located on the inlet side. Potentially, with increasing texture area density $S_{tex.,A}$ this effect can be reversed. Furthermore, it is depicted that in regions of texture area densities $S_{tex.,A}$ less than 40%, the square, the equilateral triangle and the hexagon exhibit similar tribological behaviors. The half hexagon (inlet large) and the semicircle led to tribological performance in a similar manner.

In Figure 4 and Figure 5, the magnitudes of the lifting force $\left|\left.{\overrightarrow{F}}_{lift}\right|\right.$ and drag force $\left|\left.{\overrightarrow{F}}_{drag}\right|\right.$ are depicted. It can be observed that all textures increase the hydrodynamic pressure $p$, which leads to a rising lifting force ${\overrightarrow{F}}_{lift}$. Additionally, the friction force ${\overrightarrow{|F}}_{drag}|$ decreases. However, the performance enhancement ratio (PER) of the chevron-shaped texture does not provide the highest values, although the magnitude of the drag force $\left|\left.{\overrightarrow{F}}_{drag}\right|\right.$ is the lowest. In contrast, the semicircle and half hexagon (inlet large) texture result in the highest drag force $\left|\left.{\overrightarrow{F}}_{drag}\right|\right.$. Generally, for the texture area densities $S_{tex.,A}$ less than 30%, the drag force $\left|\left.{\overrightarrow{F}}_{drag}\right|\right.$ does not differ much between the different geometries. The maximal lifting force $\left|\left.{\overrightarrow{F}}_{lift}\right|\right.$ is achieved before the maximal performance enhancement ratio (PER), as the influence of decreasing friction also positively affects tribological performance. However, with the further increasing texture area density $S_{tex.,A}$, the decreasing lifting forces $\left|\left.{\overrightarrow{F}}_{lift}\right|\right.$ dominate, leading to a decrease in the performance enhancement ratio (PER). For the triangle, half hexagon, hexagon and semicircle textures, this behavior is not visible, as the geometry dimension is limited by the assumption that the texture cannot protrude the convergent oil film gap.

3.2. Influence of Pitch Angle

Since the texture height is small compared to its horizontal and vertical extents, the pitch angle ${\alpha }_{tex.}$ is not used directly in this case. Instead, the texture height on the outlet side $h_{tex.,out}$ is used as a varying parameter.

In Figure 6, the texture area density $S_{tex.,A}$ is plotted over the texture height of the outlet $h_{tex.,out}$ for each geometry. The color of each point represents the performance enhancement ratio (PER) and is scaled from one to the maximal PER. For every geometry, it can be observed that a small step on the left side of the texture with a height of 5–15 µm leads to the best tribological performance. As previously discussed, the rectangle texture with a constant width also causes the highest performance enhancement ratio (PER). Generally, for this convergent oil film gap, it can be observed that with an increasing texture area density $S_{tex.,A}$, the performance enhancement increases, and if the expansion of the texture allows, a local maximum exists.

With the aid of the previously discussed data, the pitch angle ${\alpha }_{tex.}$ for the best-performing texture geometries is calculated (cf.

Table 2. Optimal pitch angle for each geometry.

Geometry	$\mathbf{Optimal}\mathbf{Pitch}\mathbf{Angle}{\mathit{\alpha }}_{\mathit{t}\mathit{e}\mathit{x}.}$ [°]
Rectangle constant width	0.66	Local maximum exists
Square	0.67
Rectangle variable width	0.52
Chevron	0.94
Equilateral triangle	0.87	No local maximum exists
Half hexagon	1.75
Hexagon	0.71
Half hexagon (inlet large)	1.75
Semicircle	1.52

). It can be observed that for textures where a local maximum of the PER exists, an optimal pitch angle ${\alpha }_{tex.}$ of about 0.52° to 0.67° exists, with the exception of the chevron-shaped one, which has an optimal pitch angle ${\alpha }_{tex.}$ of 0.94°.

To analyze the results of Figure 6 in detail, the performance enhancement ratio (PER) over the texture height on the outlet side $h_{tex.,out}$ and over the texture area density $S_{tex.,A}$ is plotted in Figure 7. In this figure, three horizontal axes are visible, where the blue axes are related to each other. The blue curves represent the influence of the texture area density $S_{tex.,A}$. The texture height at the outlet side is kept constant at the value of $h_{tex.,out}$, which achieved the highest performance enhancement ratio (PER). The purple curves visualize the dependency of $h_{tex.,out}$ for the best-performing texture at its optimal texture area density $S_{tex.,A}$. Compared with Figure 6, these graphs should quantitatively describe horizontal (blue curves) and vertical plots (purple curves) at the maximal PER for each geometry. For texture geometries with a pitch angle ${\alpha }_{tex}$ unequal to zero, where the texture area density $S_{tex.,A}$ and texture volume density $S_{tex.,V}=V_{tex.}/V_0$ differ, an additional x-axis is added to visualize this texture volume density $S_{tex.,V}$. For the different rectangles and the square-shaped texture, a local maximum at a texture area density $S_{tex.,A}$ of 69–75% exists. For the chevron-shaped geometry, the best tribological performance can be achieved at $S_{tex.,A}=53\mathrm{\%}$. All other geometries have the highest PERs at the highest texture area densities $S_{tex.,A}$. The blue curve of the equilateral triangle and the semicircle texture are quite similar. Additionally, it can be observed that the different orientation of the half hexagon influences the performance in the low region of $S_{tex.,A}$ and with an increasing density that both curves gradually approach. The purple curves in Figure 7 depict the influence of the texture height on the outlet side $h_{tex.,out}$, and it can be observed that for all visualizations, a local maximum exists. This means that a small step on the outlet side improves the tribological performance.

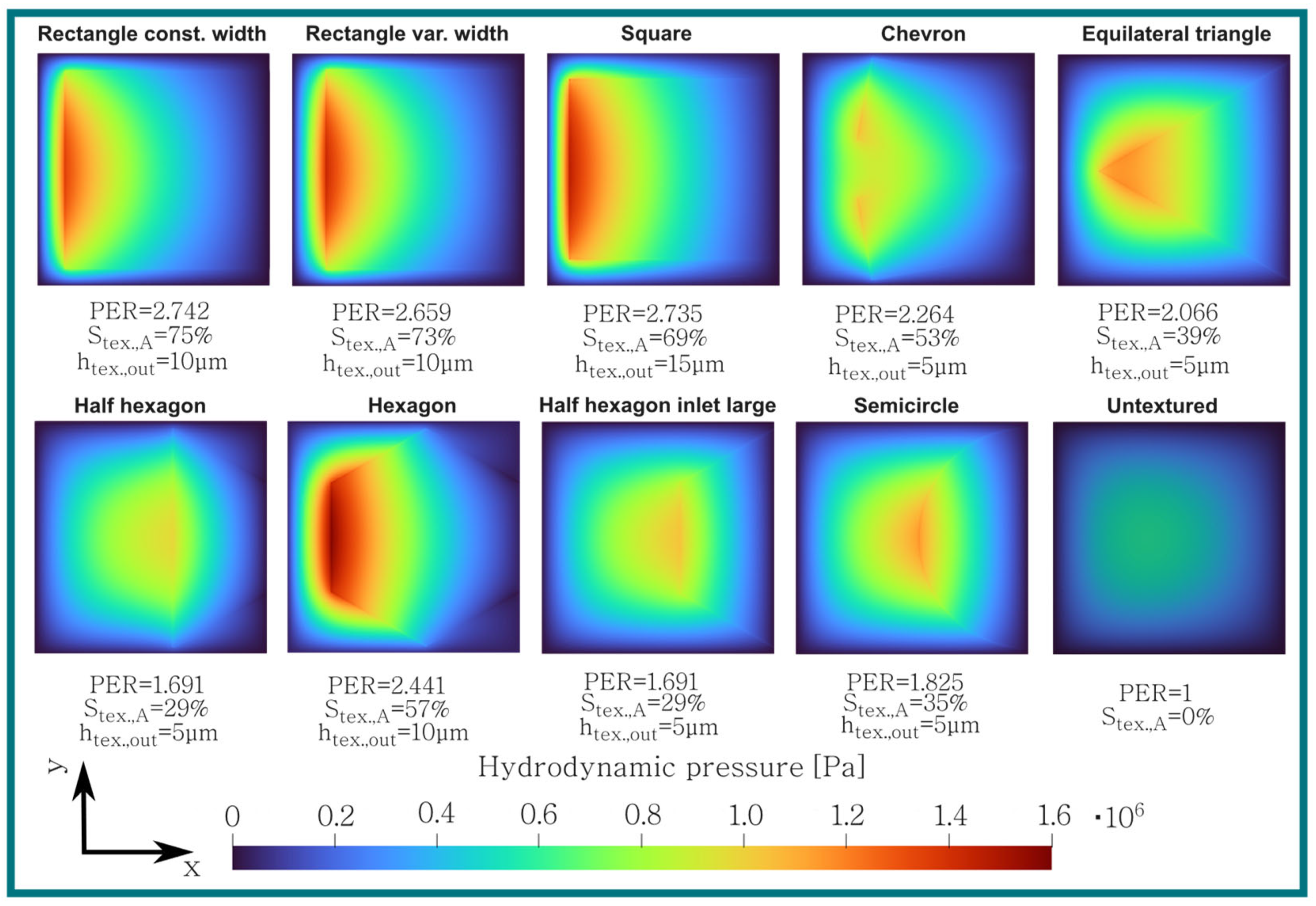
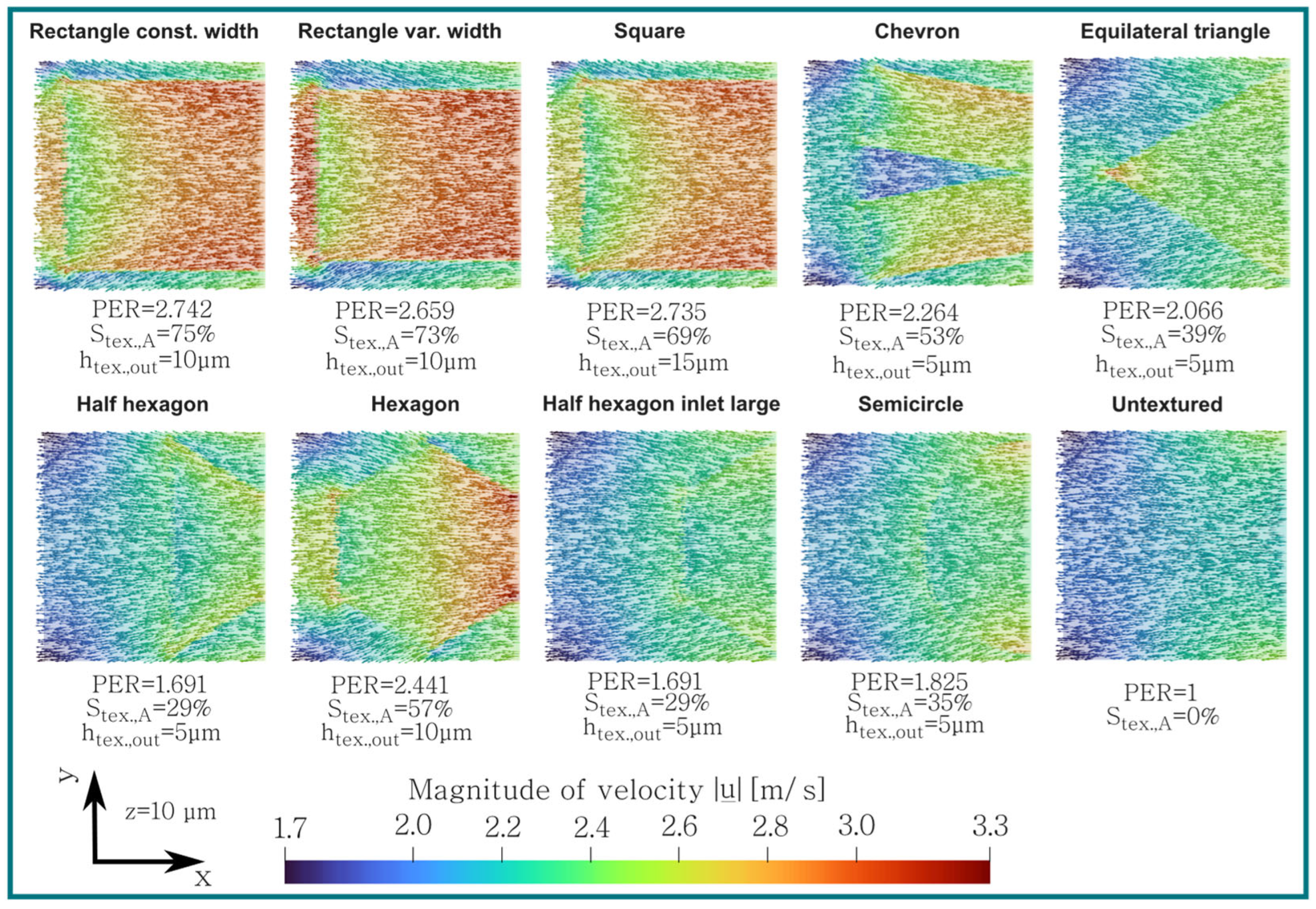
3.3. Pressure and Velocity Analyses of Best-Performing Geometries

In Figure 8, the pressure distribution of the best-performing geometries is visualized. The hydrodynamic pressure values are scaled to the same range. In contrast to the smooth geometry, the texture significantly increases the maximal pressure. The maximal pressure can be achieved with the hexagon-shaped geometry, but since this maximal pressure is concentrated on a smaller area compared to the rectangles and squares, the lifting force ${\overrightarrow{F}}_{lift}$ is lower than these geometries. On the inlet side of the hexagon-shaped texture, some regions with a pressure of less than 0 can be observed, indicating possible cavitation. It should be noted that as long as the relative pressure is not below the vapor pressure $p_v$, negative relative pressures are possible. For all other geometries presented in Figure 8, this could not be observed. In all geometries, it is noticeable that the region of maximal pressure is located at the outlet area of the texture, while for the untextured oil film gap, it is in the center.

The velocity field in the x–y direction is depicted in Figure 9. The slice at the position of $z=10\mu \mathrm{m}$ is used to calculate the glyphs in this x–y plane. All vectors are scaled to the same length, and the color represents the magnitude of the velocity $|\overrightarrow{u}|$. The gradient between the inlet and outlet sides of the geometry can be explained by the different heights, which lead to different shear rates and, consequently, to a different magnitude of velocity $|\overrightarrow{u}|$. In contrast to the smooth wedge, a significant increase in the flow out on the surfaces that are located perpendicular to the movement direction can be observed. At the textures’ end on the left side, an increase in the magnitude of the velocity $|\overrightarrow{u}|$ is visible. In these regions, a saltus of the height field exists, caused by the different heights in the texture at the outlet side $h_{tex.,out}$. This decreasing oil film gap height results in an increasing velocity regarding the shear rate.

To describe the previously mentioned results of Figure 9 quantitatively, the volume flow on each side’s surface is evaluated. In Figure 10, these results are presented for one specific texture height at the outlet side $h_{tex.,out}=10\mathrm{\mu }\mathrm{m}$. On the left side, the incoming volume flow $Q_{in}$, and on the right side, the volume flow that is perpendicular to the movement direction $Q_{side}$, are depicted. The volume flow on the left outlet side can be calculated by subtracting $Q_{side}$ two times from $Q_{in}$. In Figure 10a, it can be observed that the performance enhancement ratio (PER) increases with the increasing inflowing volume flow $Q_{in}$ until the local maximum of PER is achieved. This behavior is followed by a decreasing PER over $Q_{in}$. For geometries where no local maximum of the performance enhancement ratio (PER) exists, the PER increases with the increasing inflowing volume flow $Q_{in}$. These similar trends can also be detected for the volume flow perpendicular to the movement direction $Q_{side}$. For the rectangle-shaped textures, a special performance can be noticed. The volume flow that is perpendicular to the movement direction $Q_{side}$ increases to the maximal performance enhancement ratio (PER) and then decreases.

4. Discussion

In Figure 8, it can be observed that the highest performance enhancement ratio can be achieved with a rectangle-shaped texture with a texture length of $a_{tex.}=1.732 \mathrm{m}\mathrm{m}$ and a texture width of $b_{tex.}=1.700 \mathrm{m}\mathrm{m}$. The square-shaped surface modification with the dimensions $a_{tex.}=b_{tex.}=1.717 \mathrm{m}\mathrm{m}$ leads to nearly the same performance enhancement ratio. It should be noted that the geometry of the best-performing texture is also quite similar to a square. Gherca et al. [15] conducted simulations for rectangle-, triangle- and parabolic-shaped textures for a parallel lubricated contact and found that for textures with small inlet lengths, the rectangle textures provide the highest load-carrying capacity. In the current study, the texture is open at the inlet, corresponding to an inlet length of 0 mm, and similarly, the rectangle-shaped texture provides the highest performance enhancement ratio (PER). In [15], the texture area density $S_{tex.,A}$ is increased by adding an additional texture, but it was observed that with the increasing texture area density $S_{tex.,A}$, the friction force ${\overrightarrow{F}}_{drag}$ decreases, as shown in Figure 5. Uddin et al. [17] examined seven different texture geometries (circle, square, hexagon, octagon, triangle, ellipse and chevron) for a parallel slider and concluded that the square-shaped texture leads to the highest load-carrying capacity at a texture area density $S_{tex.,A}$ of 50%. In this work, the best performance can be achieved with a rectangle-shaped texture, but its width and length are almost the same, which concludes that the geometry is nearly a square. The best performance in this study is achieved at higher texture area densities $S_{tex.,A}$, compared to [17]. These differences could potentially be explained by different numerical models and simulation parameters, like the dimension of the parallel oil film gap ($l_0=b_0=100 \mathrm{\mu }\mathrm{m}$ and $h_0=1 \mathrm{\mu }\mathrm{m}$ in [17]) and different positions of the texture. In [17,18], the influence of the orientations of the chevron- and triangle-shaped elements are also discussed, and it was observed that for both textures, the highest load-carrying capacity can be achieved if the wide side is oriented at the inlet side, justifying the orientation of the textures used in this study for the chevron and rectangle.

In general, all textures look similar to a Rayleigh step, which is already known in literature. Rahmani et al. [37] optimized a Rayleigh step for a two-dimension parallel sliding bearing and concluded that the optimal length of the Rayleigh step is about $70\%l_0$. Within this study, the optimal texture length for a best-performing texture, at about $87\%l_0$, can be observed. It should be noted that, in this study, a finite convergent oil film gap is determined, compared to [37].

Yu et al. [18] analyzed the performances of circle-shaped, differently orientated triangle-shaped and ellipse-shaped textures. They found that as the texture area density $S_{tex.,A}$ increases, the dimensionless average pressure initially rises to a local maximum before decreasing [18]. For the best-oriented ellipse- and rectangle-shaped textures, no local maximum was observed, as the interval of the texture area density $S_{tex.,A}$ was defined between 3% and 30% [18]. The presence of a local maximum and a continuous increase in performance enhancement can also be seen in Figure 3 and Figure 4. However, in this study, higher texture area densities $S_{tex.,A}$ were examined, compared to the work of Yu et al. [18].

Ji et al. [20] focused on parabola-, rectangle- and triangle-shaped textures in their publication, where the parabola and triangle describe the geometry of the bottom profile. They discovered that the rectangle-shaped texture achieved the highest load-carrying capacity at a textured fraction $l_{tex.}/l_0$ of about 0.7 [20]. This value is close to the value (0.85) that yielded the best performance in this study.

However, the previously discussed publications analyzed the influence of different texture geometries for parallel sliding contact, in contrast to [21], where the performance of eight different textures for a convergent oil film gap was analyzed. Wei et al. [21] focused on dimples with a maximal dimension of 200 µm and used more dimples for their simulation model. The effect of the texture area density $S_{tex.,A}$ was only investigated for circle-shaped textures. The performance of the different texture geometries was analyzed for a constant number of equal dimples, causing different texture areas $A_{tex.}$ And, consequently, different $S_{tex.,A}$ [21]. Nevertheless, the highest load-carrying capacity can be achieved for a square-shaped texture with 91 dimples [21]. Additionally, in [21], the number of circle-shaped dimples varied between 15 and 91 dimples (which corresponds to a texture area density $S_{tex.,A}$ of between approximately 2% and 11.4%) and concluded that a linear regression between the dimple number and dimensionless pressure exists [21]. The comparison between this solution and the result of Figure 4 shows that in the region of low texture area density $S_{tex.,A}$, it seems that the lifting force ${\overrightarrow{F}}_{lift}$ is linearly dependent on the texture area density $S_{tex.,A}$. With the increasing texture area density $S_{tex.,A},$ this behavior definitely cannot be observed.

According to Grützmacher et al. [2], providing additional volume flow is one possible working principle of textures. In Figure 10a, it can be observed that this possible mechanism is also present in this study, as the performance enhancement ratio increases with the increasing inflowing volume flow $Q_{in}$. However, it is important to note that providing additional volume flow only at the inlet is not sufficient, as the performance enhancement ratio (PER) can also decrease with the increasing inflowing volume flow $Q_{in}$. Kumar et al. [19] found that for specific textures, there is a local maximum load-carrying capacity over the texture height $h_{tex.}$ and they also analyzed the flow rate, which increases with the increasing texture height $h_{tex.}$ Therefore, a similar performance to the one presented in this study could be observed by Kumar et al. [19].

In general, the lifting force ${\overrightarrow{F}}_{lift}$ of an infinite, expanded, convergent oil film gap, where no fluid is emitted on the surfaces perpendicular to the movement direction, is higher compared to a finite one [35]. Nevertheless, in Figure 10b, for a rectangle-shaped texture, it can be observed that the performance enhancement ratio (PER) increases with the increasing volume flow perpendicular to the movement direction. It appears that after achieving the highest performance enhancement ratio (PER), it then decreases.

Within this study, the tribological performance of open textures at the inlet was analyzed. Consequently, a modified chevron texture was used in this work. Figure 5 presented that in the region of the mid-texture area densities $S_{tex.,A},$ the drag force ${\overrightarrow{F}}_{drag}$ of the chevron-shaped texture was significantly lower compared to the other geometries, with a maximal relative reduction of approximately 18% in friction. Although Morris et al. [38] conducted simulations for a convergent oil film gap with multiple chevron textures, they published a maximal friction reduction of about 15%, which is similar to the value achieved in this study.

The influence of the bottom surface profile of a texture is discussed by Uddin et al. [17], and they showed that this profile significantly influences the load-carrying capacity. In contrast to this work, Uddin et al. [17] used bottom surface profiles, such as a constant height for a single or double wedge-shaped texture for the squared-shaped texture. This main conclusion is also observed in this study, where in Figure 6 and Figure 7, it is seen that a small step of the texture on the outlet side improves the tribological performance.

5. Conclusions

Within this study, a numerical model was implemented to investigate the influence of nine different texture geometries on different texture area densities $S_{tex.,A}$. In comparison to the existing studies, this work examines the performance of open textures at the inlet for a convergent oil film gap. Additionally, the influence of the pitch angle ${\alpha }_{tex.}$ was analyzed. The following conclusions are depicted in Figure 11 and can be summarized as follows:

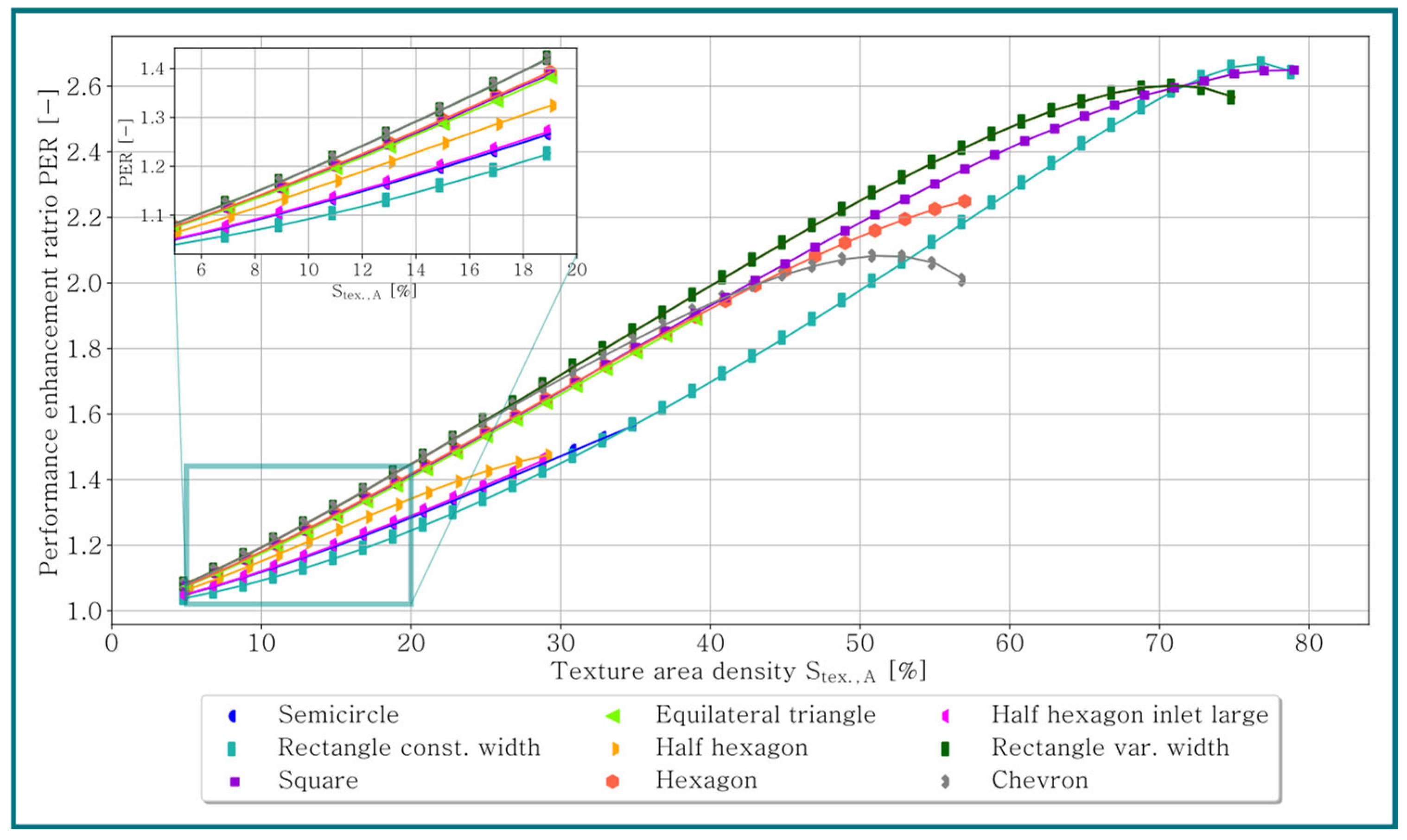
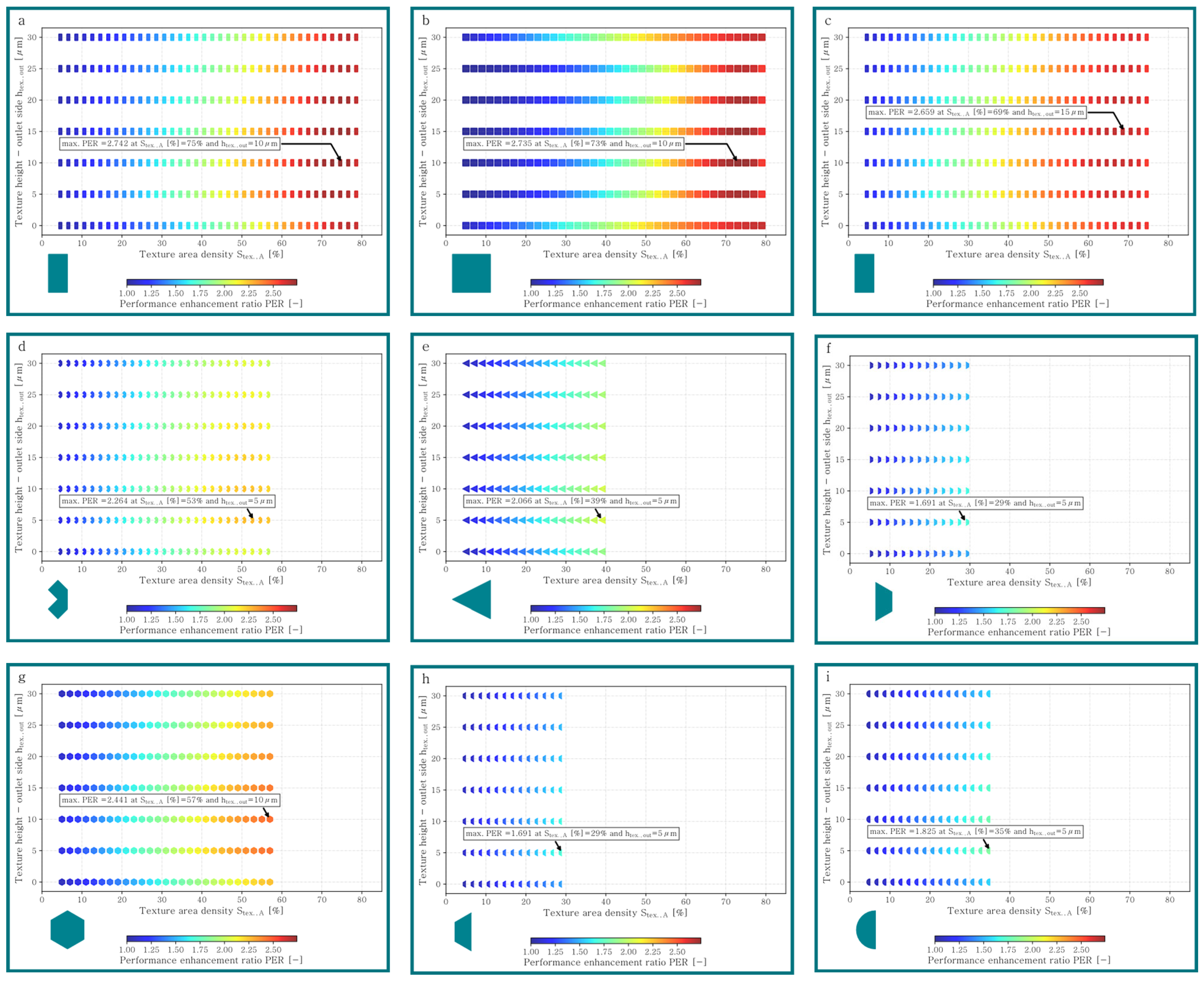
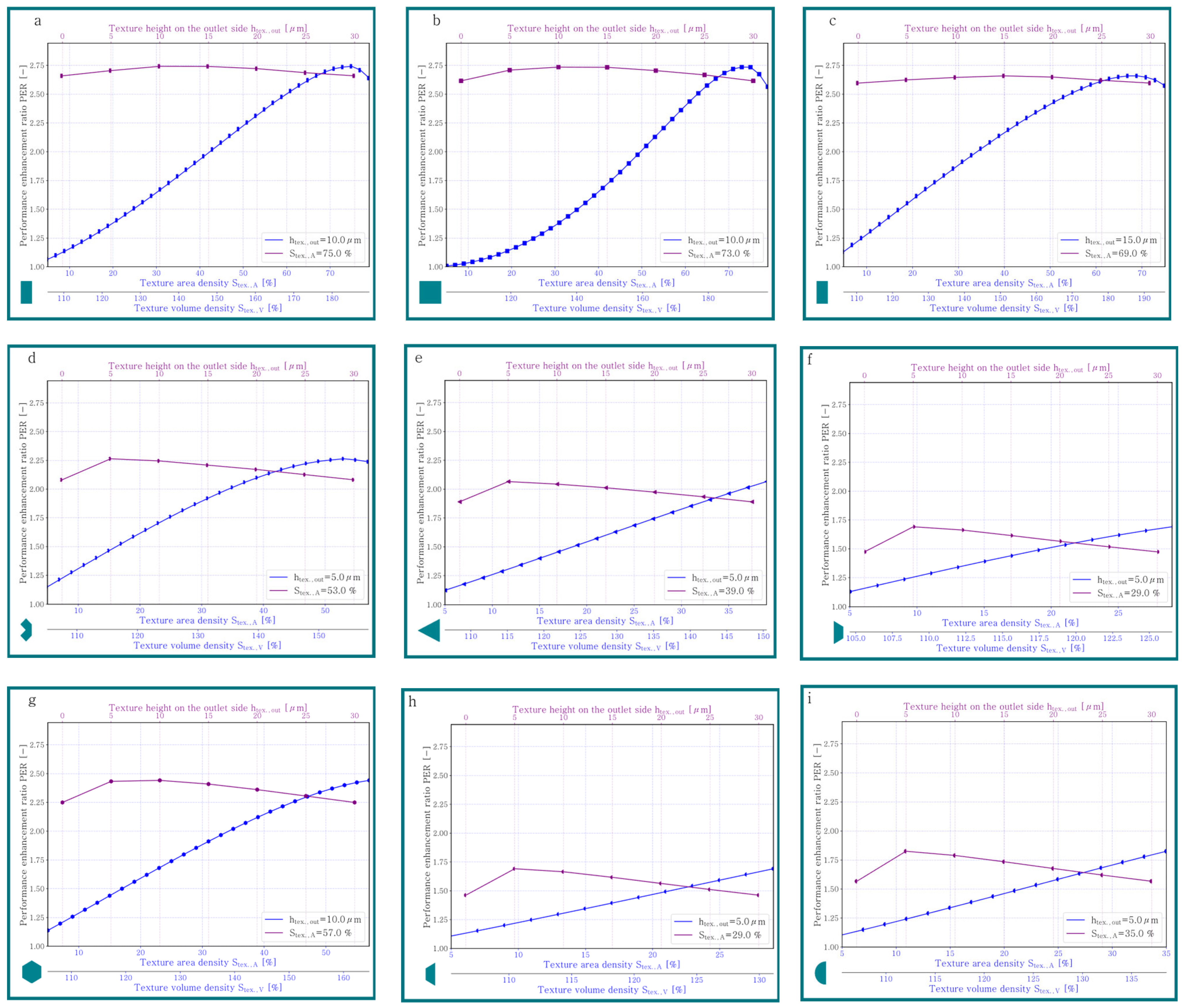
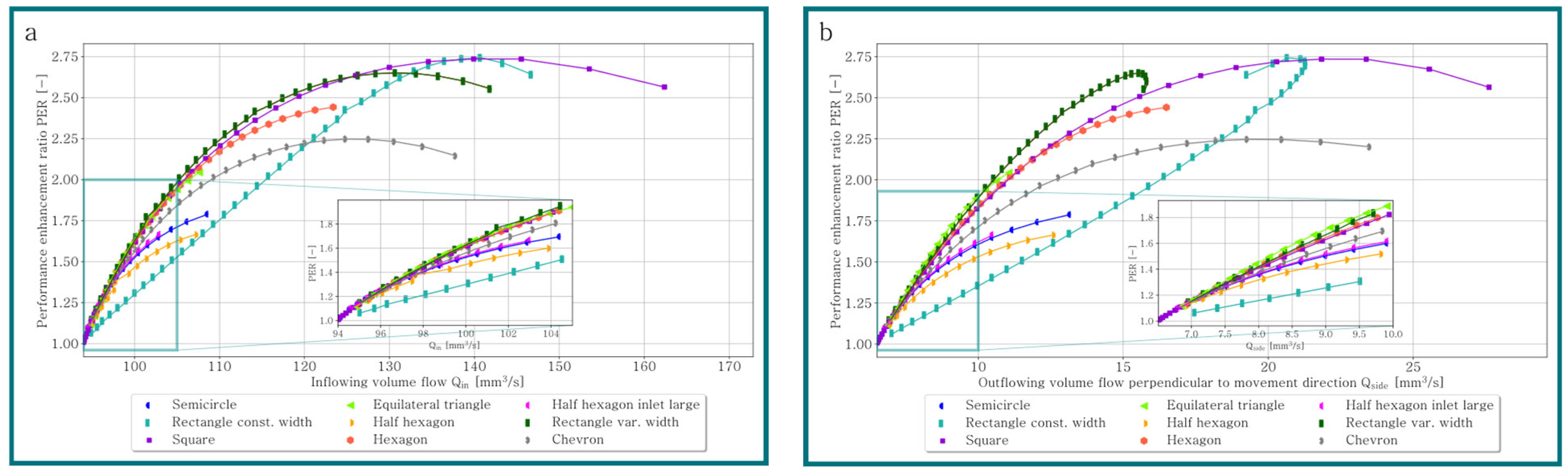
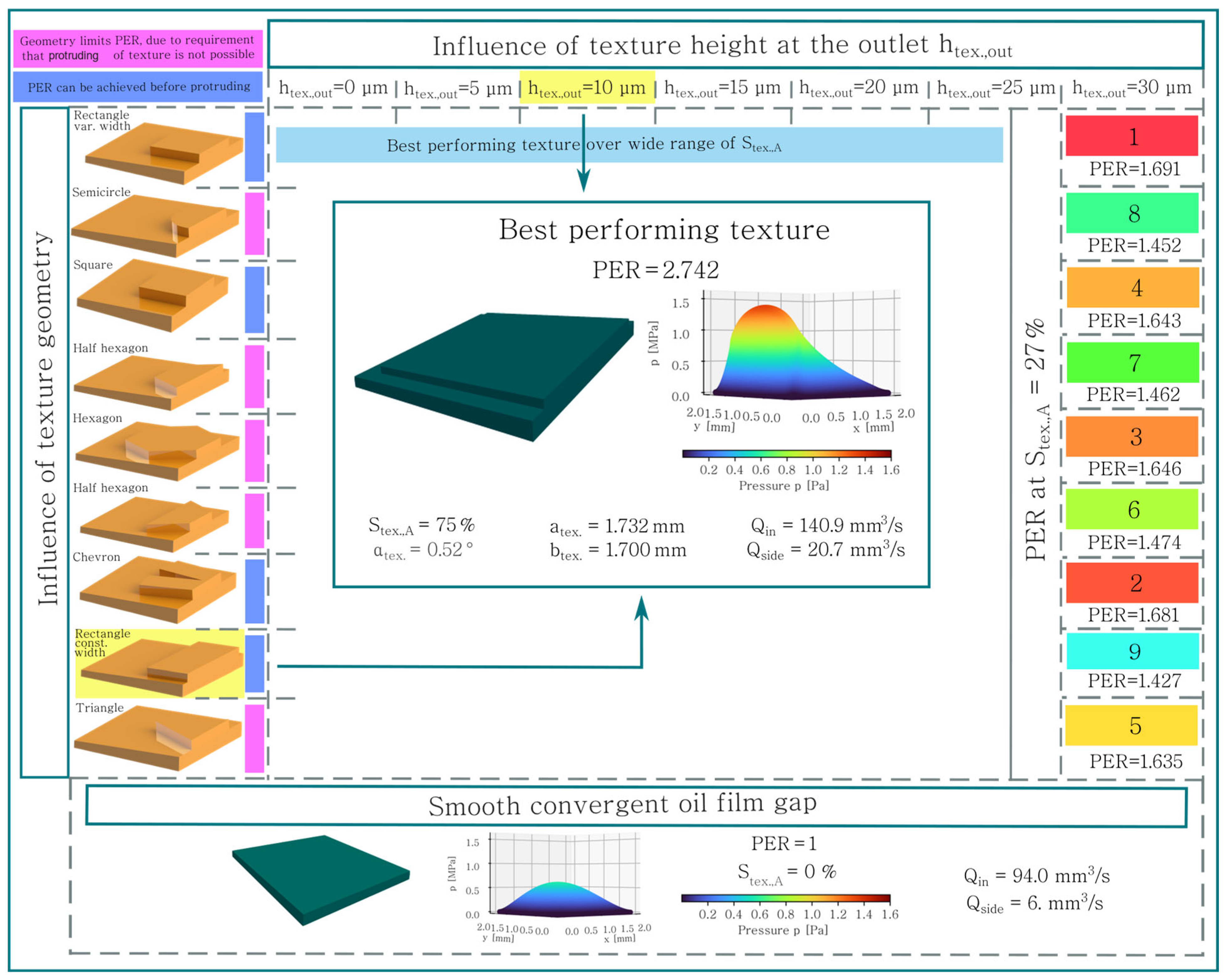
• Depending on the texture area density $S_{tex.,A},$ different texture geometries enhance the tribological performance the most (cf. Figure 11).
• The rectangle texture with a variable width enhances the tribological performance the most over a wide range of texture area densities $S_{tex.,A}$ (cf. example for $S_{tex.,A}=27\%$ and $h_{tex.,out}=30\mathrm{\mu }\mathrm{m}$ in Figure 11).
• The best performance can be achieved with a rectangle-shaped texture with a constant width (cf. Figure 11). The square-shaped texture also leads to almost the same performance (cf. Figure 11 for the best-performing texture).
• For rectangle-, square- and chevron-shaped elements, a local maximum of the performance enhancement ratio (PER) exists. For all other geometries, simulations had to be aborted before reaching a maximum due to the requirement that the texture geometry cannot protrude the convergent oil film gap (cf. Figure 11).
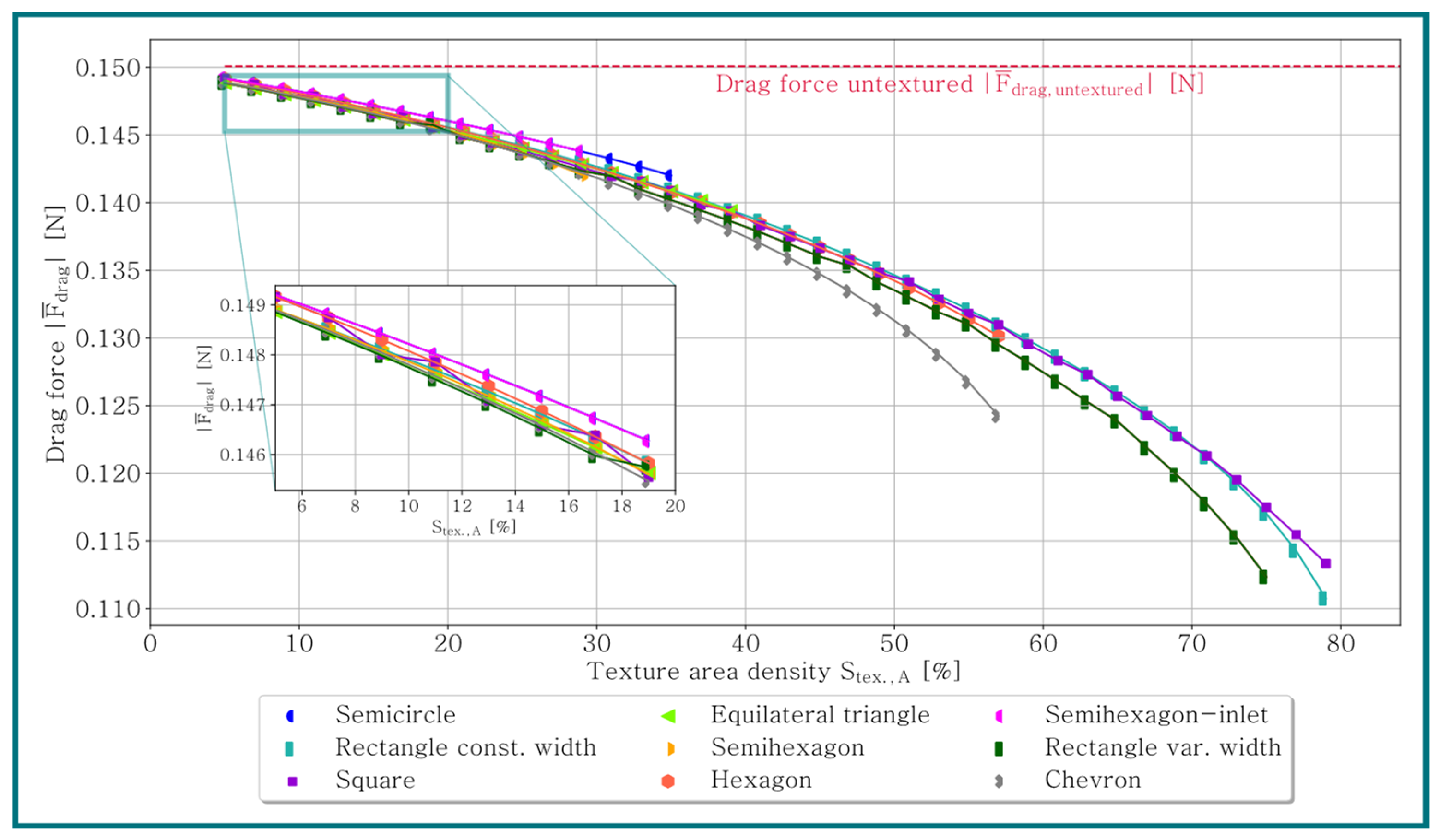
• The drag force ${\overrightarrow{F}}_{drag}$ decreases with the increasing texture area density $S_{tex.,A}$.
• A small step of the texture at the outlet side of the texture between 10 µm and 15 µm, corresponding to a pitch angle of the texture ${\alpha }_{tex.}$ between 0.5° and 1.8°, improves the tribological performance (cf. Figure 11).
• The hexagon-shaped texture leads to the highest pressure, but as it is located in a smaller region, compared to other texture geometries, the lifting forces ${\overrightarrow{F}}_{lift}$ of the rectangle- and square-shaped textures are higher.
• Providing an additional volume flow at the inlet $Q_{in}$ does not guarantee an improvement in tribological performance.
• Compared to a smooth convergent oil film gap, a significant increase in the volume flow can be observed (cf. Figure 11).