Abstract
To address the question of which posture trailing-arm vehicles (TAVs) should be adopted while driving, this study introduces an innovative active posture controller (APC) to improve both path-following and handling stability performance. Leveraging a nonlinear tire model that considers corner load variation and wheel camber, alongside the kinematics and double-track model of TAVs, the impact of vehicle body posture on handling performance has been investigated. To fully utilize the four-wheel independent drive and posture adjustable characteristics of the TAV mechanisms, an integrated nonlinear model predictive control (NMPC) combining APC and tire forces distribution is devised. Through simulations conducted using Simulink-Multibody (2023a), the effectiveness of the proposed controller is demonstrated, particularly when compared to the scheme that does not account for the unique posture adjustment mechanisms of TAVs.
1. Introduction
Vehicles equipped with trailing-arm suspension systems exhibit superior off-road capabilities compared to traditional suspension structures, allowing them to maintain a balanced posture across diverse terrains. This adaptability is notably advantageous in complex environments, including hazardous environment rescue operations [1,2], extraterrestrial exploration [3,4], and military field transportation [5,6].
The trailing-arm vehicle (TAV) integrates rocker arm and swing axle mechanisms, characterized by a uniform arrangement of links and joints, often mounting distributed drive in-wheel motors at the arm’s end [7,8]. Certain wheeled-legged mobile robots [9,10] also belong to this category. Leveraging its unique design, the TAV can dynamically adjust its wheelbases and modify its body posture during driving.
This mechanism offers potential benefits compared to traditional suspension structures. For instance, ref. [11] improves normal force distribution by adjusting each wheel to achieve average normal forces across all wheels. In [12], tire forces are regulated to maintain stable values, ensuring the vehicle’s posture stability when driving on uneven terrain. Additionally, refs. [3,13] propose a wheel-step locomotion strategy to enhance longitudinal locomotion by switching between dragging and driving wheels at the front and rear, coupled with active control of the trailing arm. The existing literature primarily focuses on the vehicle’s vertical and longitudinal performance. However, wheelbase configurations and posture adjustments can significantly impact the vehicle’s handling characteristics. Nevertheless, the intricate coupling between these factors necessitates further investigation.
Considering applications in unknown environments, achieving autonomous driving for unmanned vehicles relies heavily on effective path-following algorithms. Pure pursuit control (PPC) [14], in conjunction with geometry-based Ackermann steering kinematics, has been widely adopted by researchers due to its straightforward implementation. However, the reliability of PPC diminishes as vehicle speed increases [15]. To enhance PPC performance in the presence of wheel slip effects, ref. [16] modifies the PPC input using a vehicle model that accounts for slip. Additionally, in [17,18], the look-ahead distance of PPC is treated as a control input to balance trajectory smoothness and mitigate cutting error issues, especially in scenarios with dramatic desired path curvature rates.
For TAVs driving at low speeds, tire characteristics may be simplified, treating the tires as rigid wheels. This simplification facilitates applying a basic differential (speed) steering strategy to maintain the desired trajectory. Simultaneously, geometry-based steering policy ensures that the wheels remain aligned without opposing each other as depicted in Figure 1, where R represents the steering radius, with a positive value indicating a leftward steering direction and a negative value indicating a rightward steering direction. The point C depicted in Figure 1 serves as the steering center, corresponding to the steering radius R, and also represents the geometric center of the path of curvature of the PPC.
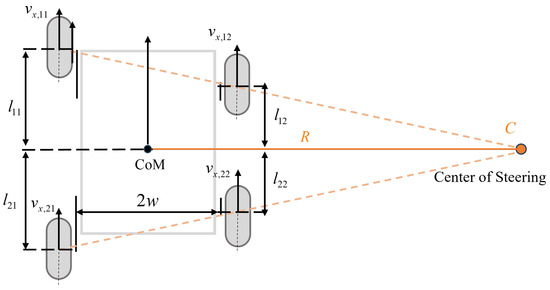
Figure 1.
Geometry-based steering policy of TAVs.
However, for TAVs driving at higher longitudinal velocities, the implementation of differential steering leads to a divergence in wheel speeds between the inner and outer sides. This disparity may induce vehicle sideslip and exacerbate the forces exerted on the outside tires, consequently accelerating tire wear [19]. It is important to note that defining C as the geometric center of the vehicle’s path of curvature becomes inaccurate in the presence of sideslip angles [20]. Therefore, careful consideration of the vehicle’s handling characteristics is essential during path-following tasks.
For the vehicles with distributed drive, direct yaw moment control (DYC) has been employed to precisely regulate the torque distributed to each wheel [21,22], thereby aligning with the driver’s intent for lateral motion control. In this context, DYC, implemented with judicious torque distribution among the wheels, has demonstrated efficacy in enhancing handling and stability, particularly in scenarios where the vehicle’s wheels rotate at similar speeds.
Modeling the vehicle executing the path-following task is key to designing the control algorithm. The linear single-track model, also known as the bicycle model, is a fundamental representation capable of capturing essential tire–road interaction forces necessary for path-following tasks. In [23], it is demonstrated that the linear quadratic regulator (LQR) yields significantly improved performance compared to kinematics-based pure pursuit controllers. Furthermore, ref. [24] introduces an online incorporation of linearized nonlinear vehicle dynamics into a model predictive control (MPC) framework. Addressing uncertainties associated with cornering stiffness and tire sliding effects, ref. [25] deploys an adaptive and robust LQR controller. Moreover, ref. [26] explores numerical linearization dynamics for path-tracking, achieving performance superior to that obtained with nonlinear controllers on flat terrains. Nonlinear model predictive control (NMPC) [27,28] offers a more accurate prediction of states and robust performance when confronted with nonlinearities beyond the linearizable region, such as tire saturation [29], substantial tire lateral slip [30], rollover [31], and acceleration effects [32], among others. In [33], the authors account for tire longitudinal slip within the bicycle model and apply NMPC to integrate steering and braking control. Additionally, ref. [34] utilizes NMPC to handle the nonlinear aspects of load transfer resulting from lateral acceleration and nonlinear adhesion limits.
While the active use of the vehicle body’s tilting has been extensively studied to enhance handling stability and steering safety in traditional active suspension systems [35,36,37], there is limited research that distinguishes the unique mechanical structure of TAVs from traditional vehicles. Specifically, the trailing-arm suspension allows for a broader range of posture adjustments and more significantly affects parameters related to handling. Although the single-track model remains adequate over a sufficiently large region around the equilibrium [26], it may lack the ability to capture the nonlinear effects introduced by the distinctive mechanisms of TAVs. More specifically, the distinctive mechanical characteristics of TAVs with active trailing-arm suspension manifest in their handling in the following ways:
- The swinging motion of each arm can directly change the length of the wheelbase. Through active allocation of the front and rear wheelbases, additional yaw resistance is generated.
- The varying wheelbases resulting from the swinging motion of the arms affect tire slip angles, thereby impacting the lateral forces exerted by the tires.
- Changes in the vehicle’s posture resulting from variable wheelbases affect the transfer of load within the sprung mass, thereby altering the left and right track widths.
- Consequently, these changes influence the vertical forces exerted by the tires, which in turn affect the lateral tire forces.
In this study, we will develop a TAV model that differentiates both the dynamics and kinematics from the vehicles with traditional suspension mechanisms. This distinction will facilitate the design of a posture-aware TAV controller.
Other main contributions of this paper are as follows: In this study, we redefine the path-following task of TAVs as a handling stability control problem aimed at improving path-following capabilities while ensuring vehicle handling performance. We propose an APC controller based on NPMC to determine the optimal posture for a TAV during driving. Subsequently, we introduce a path-following hierarchical control framework. The upper level is the NMPC-based APC controller, the middle level consists of the inverse kinematics mapper and longitudinal force calculator, and the lower level is responsible for the torque control of the motor actuators. Finally, we validate the proposed control framework in a simulation environment. Through actively adjusting the posture, the TAV acquires better handling stability and path-following performance than without.
The rest of this paper is organized as follows: the trajectory dynamics and the vehicle model considering trailing-arm suspension structure are presented in Section 2. The path-following control framework based on NMPC is developed in Section 3. Simulation results are provided in Section 4, followed by the conclusion in Section 5.
2. Modeling of Trajectory and TAV Dynamics
2.1. Path-Following Model
The primary objective of path-following is to minimize the lateral deviation between the TAV and the given path. A planar path-following model is depicted in Figure 2, where e represents the lateral offset defined as the distance between the vehicle’s center of mass (CoM) and the closest point on the desired path.
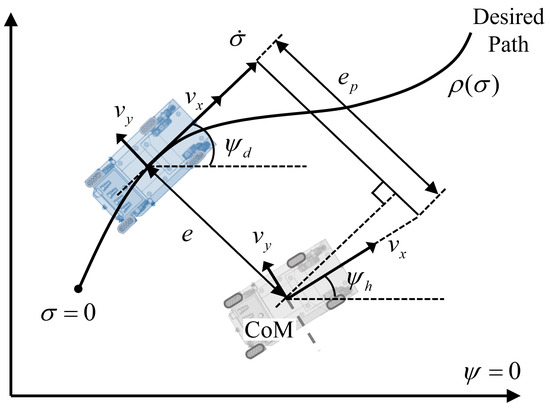
Figure 2.
Planer path-following model.
The dynamics of the trajectory, based on the curvilinear coordinate of the closest point along the path, are described by
where denotes the curvature of the target path. The term represents the heading error, where is the actual heading of the vehicle, and is the desired path heading. The path-following dynamics described by the Serret–Frenet equation in [38] are as follows:
where represents the yaw rate of the CoM of the vehicle body. It should be noted that in the path-tracking model shown in Figure 2, the “CoM” of the vehicle body is actually the projection of the CoM in the X-Y plane. Since this work takes the vehicle’s posture into account, the “CoM” will specifically refer to the mass center of the vehicle body in the X-Y-Z coordinate system when deducing the vehicle kinematics. However, for simplicity, we will not distinguish between the body’s CoM and its projection in the remainder of the context.
2.2. Inverse Kinematics of the TAV Body
In a TAV, where variations in tire radius under different vehicle postures and road undulations are disregarded, the length of wheelbases , as well as track width , with indicating the front and rear, and indicating left and right, are directly related to the the trailing-arm joint angle correspondingly: . Here, is the joint angles of each corner. Although the angles in the four corners primarily determine the vehicle’s pitch and significantly affect the length of the wheelbase, they do not directly impact the track width. However, they indirectly influence the track width through the vehicle’s inclination.
In this context, determining the roll angle and pitch angle specifies both the lengths of the wheelbases and the widths of the tracks at each corner through inverse kinematics. This interdependence between parameters poses challenges in directly optimizing the wheelbases and track widths, but it also provides opportunities to reduce system dimensions. To simplify the subsequent controller design, the coupled control variables of wheelbases and track widths will be mapped to the posture parameters and .
Temporarily disregarding the driving height h, we can utilize the inverse kinematics of the TAV body to map the posture position to the parameters required for TAV lateral dynamics to rewrite the wheelbases as . From Figure 3a, each wheelbase of the front and rear can be written as
with the height of each joint being
where is the length of the trailing arm.
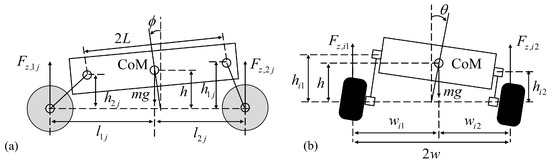
Figure 3.
Rolling and pitching geometry of the TAV. (a) Side view. (b) Rear view.
By a limited degree of linearization, the height of each joint can be represented by
The value of h impacts the rotational workspace of the TAV body, where the lower the height of the vehicle’s CoM to the ground, the greater the degree of the vehicle attitude change. However, it also creates more potential to collide with the ground. When given the equilibrium h, the (3) can be converted to
where is the equilibrium wheelbase for each corner decided by equilibrium h during the driving. is the equilibrium arm joint angles corresponding to , and every that is perpendicular to the vehicle body and downwards is at a zero scale.
On the contrary, due to the trailing-arm suspension construction, which has no extra-rolling DoF, leading the track widths of both sides equals , from the inverse kinematics read by . Specifically, from Figure 3b, the track widths of the left and right sides are given as
where is the track width at a zero body rolling angle.
2.3. Load Transfer Model
Assume that the vehicle’s longitudinal velocity remains constant, thereby minimizing the attention placed on load transfers resulting from CoM acceleration. Instead, our focus primarily lies on those induced by the TAV posture transformations. Due to the trailing-arm mechanism, even minor changes in roll and pitch angles can result in significant alterations in the wheelbase length, consequently impacting the distribution of vertical forces at each corner. Analytical solutions can be derived by solving the strain coordination equations, allowing us to represent the vertical tire force at each corner by
where represents the longitudinal coefficient, denotes the lateral coefficient, and f indicates the residual force. Consequently, the coordination equations can be expressed as
where the first equation is the balance condition of forces, the second pertains to the pitch torque, and the third concerns the roll torque balance. Notice that in (6), we have and . By substituting (7) into (8) and solving for the coefficients , and f, the vertical tire forces can be expressed as
with
The rotational inertia of the vehicle also changes with posture adjustments. For the path-following task, which primarily focuses on the X-Y plane, the vertical inertia is of particular importance compared to others. Utilizing the parallel-axis theorem, we can express as
where represents the original vertical inertia of the TAV when , denotes the mass of the arm–wheel assembly, which is equivalent to of the unsprung mass of the TAV, and represents the distance from the body’s CoM to each trailing-arm system’s CoM, following a similar representation to (5).
2.4. Tire Model
The tire model encompasses both longitudinal and lateral aspects. Given that the TAV wheel mechanism lacks steering degrees of freedom, the longitudinal and lateral directions align with the vehicle’s directions, respectively. Regarding the lateral characteristics of the tire, when the wheels’ sideslip angles are small, the lateral tire force falls within the linear region. Consequently, the cornering stiffness can be expressed as the relationship between the lateral tire force and the tire lateral slip angle :
For vehicles with traditional suspension structures, the cornering stiffness is commonly assumed to be constant. However, for TAVs, this assumption does not hold due to the more pronounced changes in the vehicle’s body posture and the wheel’s camber.
Assuming that tire pressure remains invariant over a short period, allowing us to neglect variation due to tire inflation effects, the nominal corner stiffness is given by
where and are the nominal tire load and current tire load, respectively. Since the rigid integration of the TAV with the body and wheel results in the body’s rolling directly impacting the camber angle of the wheel, we can approximate the camber as . Thus, the cornering stiffness when the whole vehicle is rolling can be calculated by
where , , and represent tire properties, indicating the maximum value of , the load at which reaches its maximum value, and the variation in with inclination, respectively.
While the lateral tire model is employed to represent the vehicle’s handling characteristics, the longitudinal force of each wheel serves as the sole control input for DYC to manage the interaction between the vehicle and the ground, given that the TAV lacks steering degrees of freedom. Additionally, it is used for designing the wheel speed controller.
The longitudinal tire model is fitted using the semi-empirical Magic Formula [39], which is expressed as
with
where is the longitudinal slip of the tire, is the wheel’s rotational speed, denotes the effective radius of the wheel, and and are the curve coefficients which decide the shape, peak value, and steady-state value of the curve, as well as the curvature at the peak value of the relationship between and .
The rotational dynamics of each wheel can be described by
where represents the wheel rolling inertia, and is the applied torque. It is important to note that in (15) is not a true actuation input; rather, it is a result of the slip between the tire and the road.
Equation (14) describes the relationship between the wheel’s rotational speed and the tire’s longitudinal force given the vehicle’s longitudinal velocity. It is worth noting two points: first, with the form of a lookup table, a specific longitudinal force may correspond to two different wheel speeds. In such cases, the smaller one is chosen as the desired wheel speed in the subsequent controller’s design, as a smaller longitudinal slip is preferred. Second, when both lateral and longitudinal slip occur simultaneously, known as combined slip condition, the model requires further modification to obtain the real tire forces [39]. However, since the vehicle’s lateral slip is typically small when the vehicle’s yaw angle is well controlled without drift, the impact from the lateral slip is negligible. Therefore, the longitudinal tire force attenuation is neglected in this work.
2.5. TAV Lateral Dynamics
The proposed double-track model for the TAV as depicted in Figure 4 accounts for the potential differences in wheelbases between the front and rear, as well as between the left and right sides. Assuming that the vehicle’s longitudinal velocity remains constant during steering maneuvers, the 2-DoF planar model of the vehicle can be expressed as
where represents the yaw inertia of the entire vehicle.
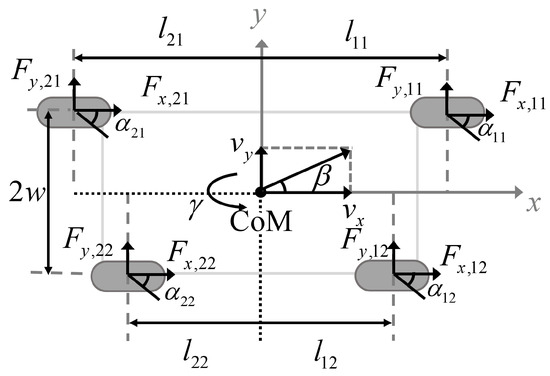
Figure 4.
Double-track TAV model.
Given that the tire type remains consistent across all corners, and the cornering stiffness of each tire is influenced by the vehicle’s posture, similar to Equation (13), the lateral tire force at each corner, in relation to the tire slip angle , can be expressed by substituting (13) into (11):
where is the cornering stiffness considering the posture impact of each tire.
The wheels’ sideslip angles are calculated by
By substituting (17) and (18) into (16), and incorporating the inverse kinematics of the TAV body (5), these equations can be expressed as a nonlinear state space equation in a concise form:
where is the CoM yaw rate and sideslip states to evaluate both path-following and handling stability performance, and are the input variables including the TAV posture and traction forces of each wheel.
3. Controllers Development
3.1. Overview
The objective of the path-following controller is to ensure the TAV accurately tracks a predefined path while regulating sideslip by utilizing four in-wheel motors to generate a combined yaw moment on the vehicle’s CoM, thereby guiding the TAV to an optimal posture. The overall architecture of the controller is illustrated in Figure 5.
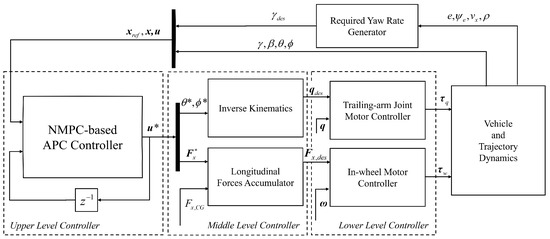
Figure 5.
Block diagram of overall controller structure.
The development of the controllers begins with deriving the required yaw rate generator. The desired yaw rate is obtained using the back-stepping method as previously outlined in our work [20], aiming for the global asymptotic stabilization of lateral offset e and heading error . This can be expressed as
where and are gains that satisfy .
Through the utilization of a required yaw rate generator, the path-following task is effectively transformed into a handling problem. Consequently, the proposed controller consists of a three-level hierarchy.
To track the desired CoM yaw rate while regulating sideslip , an NMPC-based APC controller is built as the upper-level controller. This controller optimizes the TAV posture and and generates the distributed steering traction forces . The middle-level controller comprises two components: inverse kinematics of the TAV and a longitudinal force accumulator. The former translates the optimized posture to the trailing-arm joints . The latter synthesizes the required tire forces with the total longitudinal force to each wheel located at the end of the trailing arm. At the lower level, the controller calculates the torque command for the motor actuation.
3.2. NMPC Formulation
Since the path-following problem has been converted to a vehicle handling problem, the primary objective of the NMPC controller is to track the desired yaw rate while regulating the CoM sideslip to zero. If , the discrete form of the NMPC controller can be constructed as
subject to
where , represents the discrete system state variables of at each step within the prediction horizon and the manipulated variables of at each step within control horizon . and are the weights of each cost. is the discretized nonlinear function of (19) by the Euler method. denotes the input increment. The NMPC with increment form facilitates the constraint on the rate of change of manipulated variables.
The selection of is related to the control preferences for weighting and tracking performance, which can improve path-following performance and handling performance, respectively. The choice of is designed to emphasize the ability to return the TAV to its equilibrium state when there is little tracking error. The parameter is chosen to ensure that the posture adjustment does not occur too quickly, considering the lower-level controller’s ability constraints.
Additionally, represent the inequality constraint function derived from three considerations: preventing the TAV from rollover, tire saturation, and the posture workspace limits.
The first part of the manipulated variable constraints, denoted by , ensures compliance with the rollover index (RI) to maintain it within an acceptable range [40]. This prevents radical changes in the roll angle and avoids vehicle rollover during turning. The RI is defined as
with
where and are the effective torsional stiffness and damping in the roll direction, respectively. These parameters will be obtained from the PD controller’s gains used in the lower level controller. , , , and are the masses and CoM heights of sprung and unsprung parts, in this context, the vehicle body and arm–wheel systems.
The second constraint denoted by is designed for the consideration of tire saturation. Assuming knowledge of the road–tire friction coefficient , the longitudinal tire forces of each corner should satisfy:
where represents the constant total traction force of the TAV since we assume that the longitudinal velocity is constant. The vertical forces, denoted as , are derived from the load transfer model given by (9).
Since we tend to optimize the posture parameters and , the last constraint denoted by , termed the posture cone (PC), is solely dependent on the posture parameters. The purpose of the PC is to ensure that the vehicle’s body remains within its workspace, as the CoM pitching and rolling are still confined by the limits of the trailing arms. An example of posture working spaces is depicted in Figure 6a.
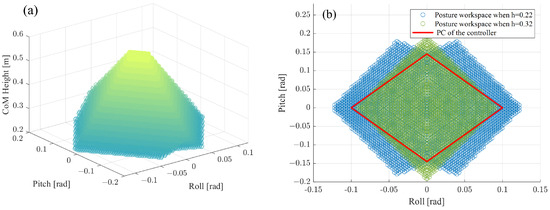
Figure 6.
The workspace of the TAV posture. (a) Posture cone. (b) The PC constraint used in the NMPC controller.
Due to the mechanical symmetry of the four trailing arms, the vehicle’s posture workspace takes on a pyramid-like shape as the center of mass’ driving height varies. Generally, the higher the desired CoM height, the smaller the posture workspace becomes, hence the origin of the term “Posture Cone”. Moreover, when the driving height is low, two diamonds overlap as depicted in Figure 6b. Typically, the pitching and rolling of the vehicle in a steady state exhibit an inversely proportional relationship. Hence, for a given driving height h, the PC is empirically simplified as a linear form, represented by
where and are the diagonal lengths of the PC.
At each sampling time k, the NMPC controller utilizes the measurements obtained from sensors to predict the future output of the system over a prediction horizon using the discretized model of the system and determines the input series from 0 to the number of control horizon . After the optimization process, only the first vector member of the obtained input series is applied to the system until the next sampling time.
The optimization problem presented in (21) and (22) constitutes a nonlinear programming (NLP) problem, which can be addressed analogously to linear MPC. In this work, the sequential quadratic programming (SQP) approach is employed for solving the NLP. During the solution process, the differential equations and the cost function are numerically integrated using the current guess of the input parameterization parameters of the optimizer.
3.3. Middle-Level Controller
The intermediate controller framework serves as a bridge, translating the inputs from the NMPC to the actuators of the TAV. As outlined in the previous Section 2.2, the inverse kinematics have been established for each joint motor. When the optimized posture parameters and are obtained, they are then substituted into (5)
Regarding each in-wheel motor, the optimized turning tire force and the vehicle’s longitudinal force can be converted to the longitudinal force exerted by each wheel by a simple uniform distribution law. The longitudinal force of each corner can be expressed as
This uniform distribution of the total longitudinal force is valid since the tire saturation limit has already been considered during optimization in (24).
3.4. Lower-Level Controller
Finally, the lower layer involves the actuation of the joints and in-wheel motors. The wheel speed controller in this work is implemented using simple feedback along with a feedforward term. The feedforward longitudinal force includes the previously distributed wheel force in (27) along with steady-state rolling friction and air resistance. The desired wheel speed can be determined using the force–slip relation in Equation (14). The torque command is then given by
where and represent the PD gains for the wheel traction controller, respectively. stands for the controller sample time, and represents a unit delay within one controller step.
The posture control problem can be converted to the trailing-arm joint control problem through inverse kinematics and gravity compensation. To achieve the posture control effect within an acceptable bandwidth, the torque command of each joint motor is given by
where denotes the current arm joint angle of each corner, is the desired joint angle after the first-order filter, stands for the time constant of the first-order filter, and is the gravity compensation of each corner after considering the posture changes as derived in (9). and are the PD gains of the joint motor, which is also the virtue stiffness and damping if treating the trailing arm as a passive suspension.
4. Simulation Results
The performance of the proposed path-following controller is assessed through multibody simulation. A simulation platform featuring a trailing-arm suspension is developed using Simscape Multibody (2023a) as depicted in Figure 7. Since the simulation’s primary objective is to validate the foundational principles, each rigid body element is assigned uniform mass distribution. The simulation step size is set to 0.001 s. The tire–road interaction is modeled using the PAC2002 approach [39]. The rest of the platform parameters can also be found in Table 1.
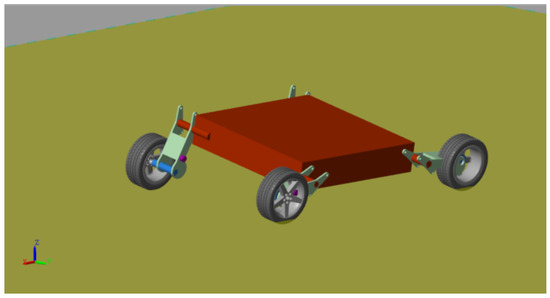
Figure 7.
A trailing-arm suspension platform in the Simscape Multibody environment.

Table 1.
Parameters used in the simulation.
A baseline MPC with a fixed TAV body posture is established for comparison, investigating the impact of integrating active posture adjustment into the path-following control framework. When the vehicle posture is not considered, when , the nonlinear double track model (19) can be simplified to linear bicycle model [41], where and . During this simplification, the varying tire cornering stiffness is assumed to be its nominal value . The comparison fixed-posture MPC employs a cost function similar to (21) and shares weights with the NMPC featuring posture control as well as the corresponding middle- and lower-level controllers. However, the MPC does not include the RI and PC constraints and only retains the tire saturation constraint (24). More specifically, the posture-fixed MPC is constructed as
subject to
The update step of both of the controllers is set as 200 ms. The state term weights are both . The manipulated variable weights , which emphasize the total quantity of each control effort, are set to for NMPC and for MPC, respectively. The manipulated variable rate weights , which emphasize the control effort increments, are set to for NMPC and for MPC. The control horizons and prediction horizons of both controllers are set as 5 and 10 steps, respectively.
Three sub-cases were designed to evaluate the controller’s response and path-following capabilities: the line-keeping condition and the S-turn (lane-changing) cases with different path curvatures. These sub-cases serve dual purposes: they assess the path-following performance within the proposed control framework and evaluate the vehicle’s handling ability during the task.
4.1. Lane-Keeping Results
For the lane-keeping condition, we set an initial lateral offset of 1.8 m from the left side of the target straight line and a forward velocity of 5 m/s. The lateral errors from the TAV CoM to the closest trajectories and the heading errors, representing the path-following performance, are depicted in Figure 8. After 5 s, both the posture-fixed MPC and posture-aware NMPC converge to the target straight lane. It can be observed that while NMPC shows no evident advantage over MPC in terms of lateral error, the NMPC exhibits less heading error from the beginning of the tracking process, specifically from 0 to 0.5 s.
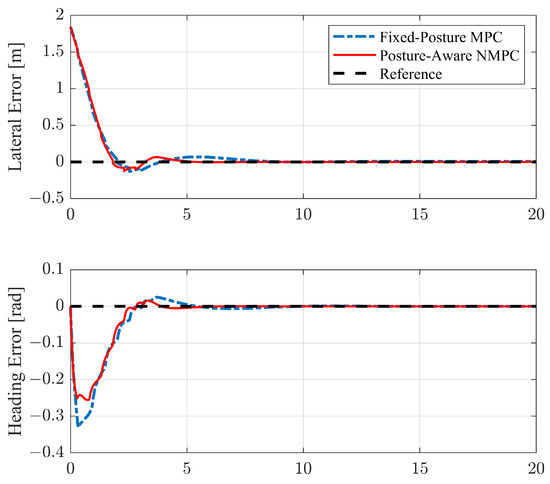
Figure 8.
Lateral and heading errors on lane-keeping condition.
The proposed path-following control framework has converted the path-following problem into a handling problem. Therefore, given that the target path is a straight line with zero curvature, the desired CoM yaw rate purely depends on the lateral offset and heading error. This dependence leads to a noticeable oscillation in the desired yaw rate, inherited from discrete path points and the error calculation method. Under these conditions, the yaw rates and sideslips of the vehicle body are depicted in Figure 9. During the lane-returning process, which occurs before 5 s, the posture-aware NMPC demonstrates superior performance compared to the fixed-posture MPC in controlling the desired yaw rates as evidenced by its smaller yaw rate error. Additionally, during the same lane-returning period, the MPC exhibits a larger CoM sideslip than the NMPC, indicating worse handling performance, as the goal is to minimize the sideslip to zero.
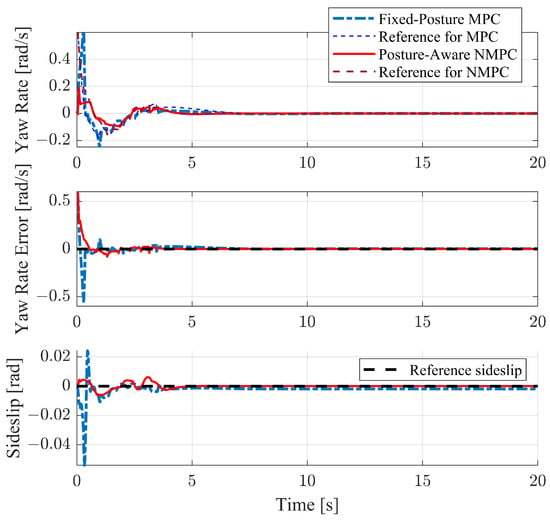
Figure 9.
Yaw rates and sideslips on lane-keeping condition.
Since the posture of the MPC is not controlled, and the vehicle’s roll and pitch angles are maintained at zero, only the posture of the vehicle using NMPC is analyzed in Figure 10. In this figure, the “optimized posture” refers to the desired roll and pitch angles optimized by the NMPC, while the “real posture” represents the run-time roll and pitch angles after being controlled by the middle and lower-level controllers. The consistent sign between the optimized roll angle and lateral error indicates that when the vehicle attempts to return to the target line by turning right, the APC actively controls the vehicle to lean to the right. Conversely, when it exceeds the straight line, the APC attempts to make the vehicle lean to the left. For the pitch angle, note that the lower-level trailing-arm controller is actually achieved by a PD control law, causing both the roll and pitch angles to show a delay from the desired values. Although this delay exists in posture adjustment which is difficult to avoid currently, the NMPC still outperforms the fixed-posture MPC in handling performance.
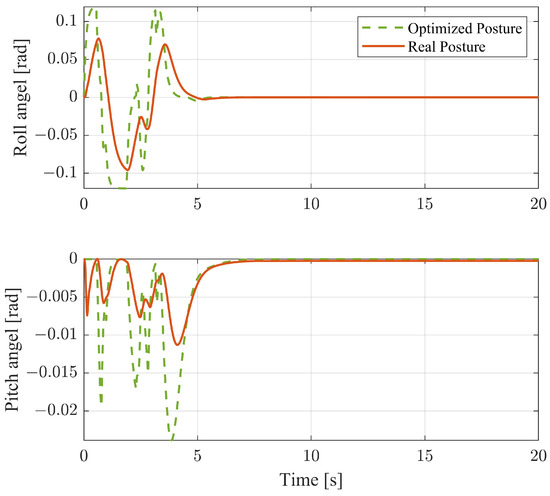
Figure 10.
Posture control on lane-keeping condition.
For the purpose of brevity, we introduce a CoM yaw moment instead of the longitudinal forces comparison of each tire across the controllers. The converted CoM yaw moments are depicted in Figure 11. Generally, the NMPC consumes less differential moment than the MPC. Observing the error performance, although the lateral errors of both controllers are positive at the beginning of the process (from 0 to 2 s), the yaw moments are initially positive and then become negative. This can be attributed to the internal look-ahead distance mechanism in (20) when designing the yaw rate generator. A more comprehensive understanding of this look-ahead mechanism can be found in [20].
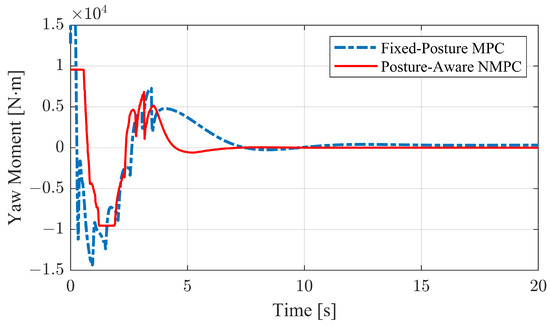
Figure 11.
Yaw moments of CoM on lane-keeping condition.
4.2. S-Turn Results: Smaller Curvature Case
The S-turn path, also known as lane changing condition, is characterized by a gradual change in curvature, ranging from a maximum value of ±0.05 to ±0.2 [1/m]. Beginning with the S-turn case with a smaller path curvature, the trajectories comparison between the MPC-based fixed-posture path-following controller and the NMPC-based posture-aware controller is presented in Figure 12. Overall, both controllers demonstrate similar performance. However, when examining the scaling around the maximum curvature, the fixed-posture MPC shows a larger deviation compared to the APC/NMPC.
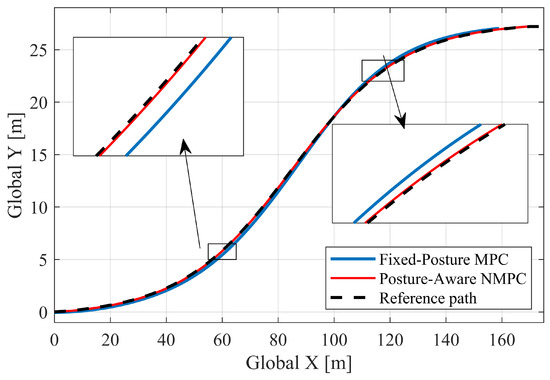
Figure 12.
Trajectories on S-turn with smaller path curvature case.
The path-following errors are depicted in Figure 13. The fixed-posture MPC shows less competitive performance in both lateral and heading errors compared to NMPC considering the TAV posture. Due to not closely adhering to the desired trajectory, the MPC requires more time to complete the entire task. The maximum deviations from the reference trajectories for both controllers occur around the path segment with the maximum curvature. While the NMPC achieves a more stable path-following performance in both lateral and heading errors, the MPC tends to correct the lateral error in the first half of the path, leading to a greater heading error in the latter half of the path.
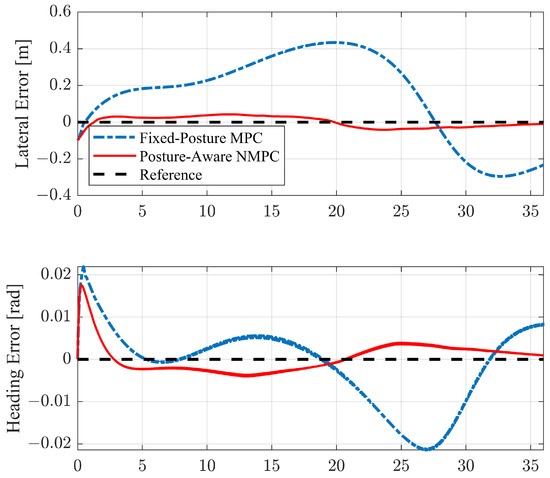
Figure 13.
Lateral and heading errors on S-turn with smaller path curvature case.
The run-time CoM yaw rate, yaw rate error, and sideslip which represent the handling performance are illustrated in Figure 14. Comparing the CoM yaw rate and yaw rate error can help explain the differences in their path-following performance. While both controllers achieve minimal CoM sideslip, the fixed-posture MPC seems less capable of tracking the desired yaw rate. Since our MPC and NMPC weights are similarly tuned for each control objective, improving the MPC path-following performance might involve adjusting the weights at the expense of handling.
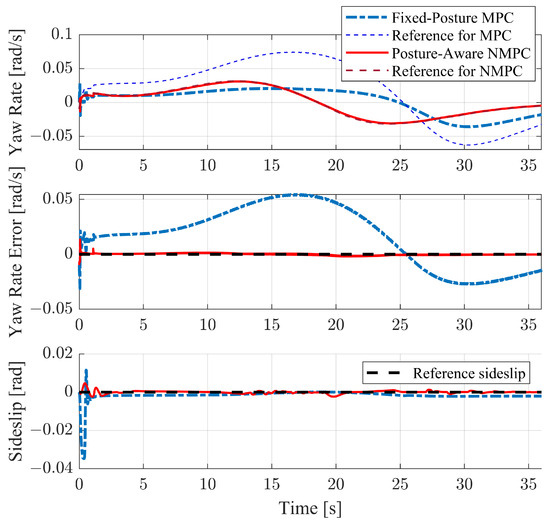
Figure 14.
Yaw rates and sideslips on S-turn with smaller path curvature case.
The posture of the TAV during the S-turn with a smaller path curvature case is depicted in Figure 15. Given the relatively small path curvature, the NMPC primarily adjusts the posture to enhance steering performance. Both signs of the desired rolling angle are consistent with the sign of turning, indicating rolling to the outside. This strategy aligns with steering geometry, where the inside wheelbase is smaller than the outside. As for the pitching angle, the vehicle tends to pitch backward as the desired CoM yaw rate increases, returning to 0 as it decreases.
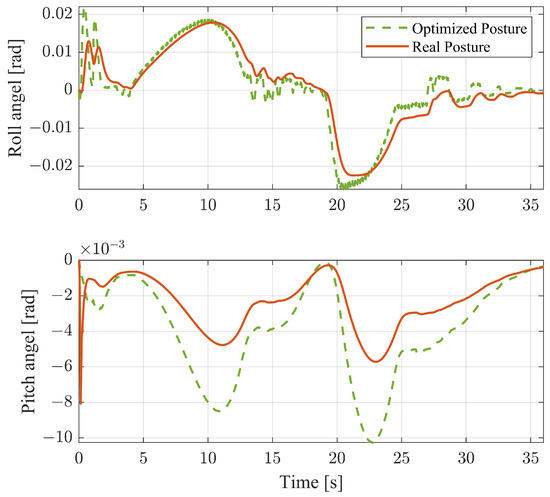
Figure 15.
Posture control on S-turn with smaller path curvature case.
As shown in Figure 16, the NMPC, which simultaneously controls the TAV posture and differential forces, requires less actuation compared to the MPC. Specifically, the maximum converted CoM yaw moment is 3416 N·m for the NMPC and 8026 N·m for the MPC in the first half, and a minimum of −3431 N·m and −6195 N·m in the last half of the path. This observation confirms that the APC controller can effectively reduce energy consumption.
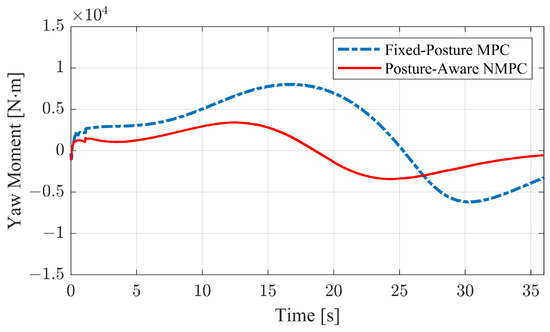
Figure 16.
Yaw moments of CoM on S-turn condition with smaller path curvature case.
4.3. S-Turn Results: Larger Curvature Case
In the case of larger curvature, the comparison of trajectories between the MPC-based fix-posture path-following controller and the NMPC-based posture-aware controller is illustrated in Figure 17. Overall, both controllers demonstrate comparable performance, with results that are even closer than in the smaller curvature case. The maximum deviations from the reference trajectories for both controllers occur around the path segment with the maximum curvature.
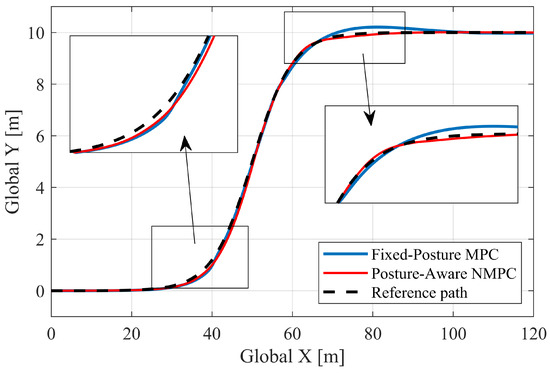
Figure 17.
Trajectories on S-turn condition with larger path curvature case.
The path-following performance is depicted in Figure 18. The NMPC exhibits a slight advantage in lateral error compared to the MPC. However, during certain periods, from 9 to 13 s, the NMPC exhibits larger lateral deviations than MPC. In terms of heading errors, the NMPC also seems not to outperform the MPC significantly. Particularly at 9 to 10 s, the MPC experiences sharp heading errors that far exceed those of the NMPC. Thus, both controllers, with or without posture consideration, achieve similar performance in terms of path-following. A deeper analysis will reveal differences in their handling aspects.
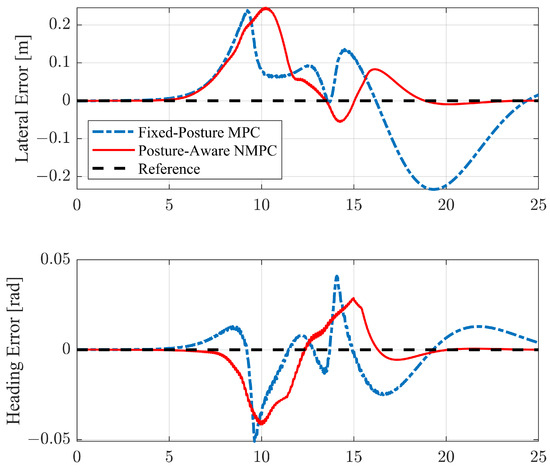
Figure 18.
Lateral and heading errors on S-turn with larger path curvature case.
The handling performance in the larger curvature case is depicted in Figure 19. Given that the reference yaw rate is determined by the lookahead path’s information, gradually increasing over time, the CoM yaw rate tracking performance with the NMPC outperforms that of the MPC. Examining the sideslip results, the MPC shows abrupt spikes at 8–9 and 13–14 s, corresponding to instances when the path reaches its maximum curvature. This behavior suggests that the TAV nears its limits and experiences drifting, leading to sudden changes in heading. While this eventually enhances path-following performance, it comes at the cost of stability loss. In contrast, the NMPC dynamically adjusts the TAV posture, leading to a more suitable tire load distribution and corresponding cornering stiffness. This expands the stability region for the differential steering of TAVs, enhancing overall stability and performance during path following.
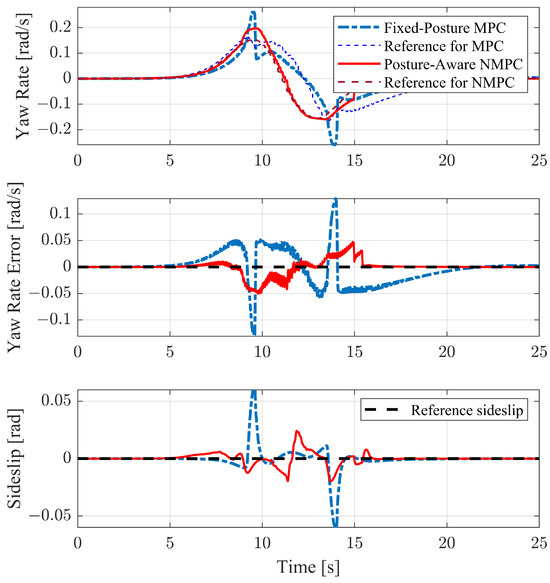
Figure 19.
Yaw rates and sideslips on S-turn with larger path curvature case.
Subsequently, Figure 20 depicts the TAV posture under NMPC control. Consistent with the previous smaller curvature case, the vehicle tends to roll outward during left turns. In the latter half of the path, during right turns, the NMPC initially anticipates outward rolling (before 12 s). However, it adjusts this rolling tendency as the path curvature increases. Observing the sideslip, this adjustment effectively alleviates the handling burden, especially since the latter half of the S-turn is more susceptible to stability loss than the first half. Concerning the pitching angle, the vehicle initially tends to pitch backward. As the sideslip tracking error increases, the NMPC shifts towards forward pitching rather than backward.
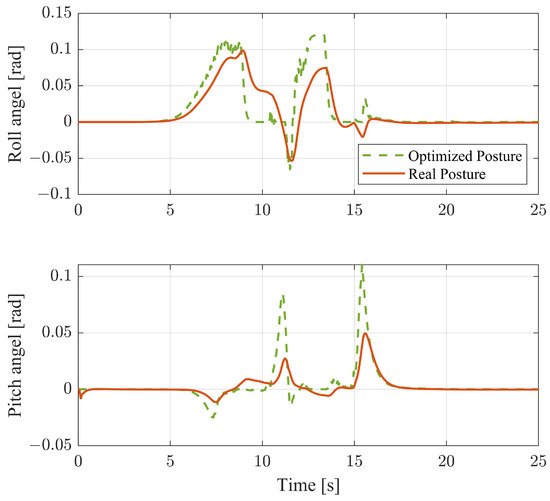
Figure 20.
Posture control on S-turn with larger path curvature case.
The comparison of yaw moments is depicted in Figure 21. Consistent with the findings from the step response case, the NMPC with APC effectively reduces the additional yaw moment demand. This reduction becomes more pronounced as the desired yaw rate increases, compared to the MPC. Notably, the converted yaw moment of the MPC experiences a sudden drop during drifting moments. However, even after the vehicle returns to stability, the yaw moment remains higher than that of the NMPC. This reveals the essential reason why NMPC maintains stability while MPC does not under the same working conditions: the lower differential forces in NMPC alleviate tire burdens, delaying it from approaching its limit.
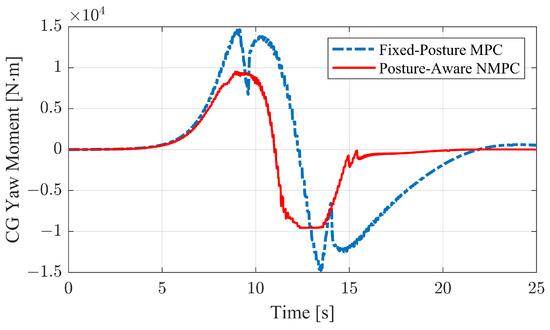
Figure 21.
Yaw moments of CoM on S-turn with larger path curvature case.
Therefore, in the S-turn path-following results, one can clearly observe that the objective of path-following, along with ensuring handling stability, is more satisfactorily achieved by the NMPC-based APC, which actively controls the trailing arm, adjusting wheelbases and body posture, compared to the MPC, which does not.
5. Conclusions
With the aim of enhancing the path-following capabilities and improving the handling ability of TAVs, an APC path-following control framework has been proposed. Consequently, a comprehensive investigation of these impacts has been conducted, considering nonlinear tire properties. The path-following problem is initially converted to the handling problem, specifically focusing on tracking the desired CoM yaw rate while regulating the sideslip. Subsequently, the APC controller, based on NMPC, has been developed to obtain optimal posture and longitudinal corner forces. Simulation results, based on a trailing-arm platform via Simscape Multibody, have been presented.
Compared with the fixed-posture MPC controller in lane keeping and S-turn sub-cases, the proposed controller demonstrates effectiveness in actively utilizing the TAV controllable posture to ensure stability while consuming less steering energy. It is noteworthy that the optimized posture results during steering also exhibit a counterintuitive contrary trend to the geometry-base steering policy, in which the former tends to roll inward while the latter rolls outward because the APC synthesizes the handling and path-following performance.
The proposed APC path-following control framework integrates nonlinear tire characteristics and wheel load coordination, which leads us to believe that it not only can benefit the other chassis structures but also has potential benefits for some wheel-legged robots. It is important to note that these results are obtained using pneumatic tires. Considering rigid wheels commonly used in the robotics field may yield different results, as well as vehicles with a hip DoF enabling the trailing arm to swing outward. These aspects will be investigated in our future studies. Lastly, this research relies on TAV inverse kinematics for posture control, which may lead to inferior transient performance and be impacted by uneven terrain. This could be improved by adjusting the posture before entering the path, particularly when the desired path and terrain topology are predictable.
Author Contributions
Conceptualization, Writing—Original Draft, Z.P.; Methodology, Writing—Review and Editing, B.L.; Conceptualization, Writing—Review and Editing, S.Z.; Software, Resources, S.L.; Investigation, Writing—Review and Editing, S.C.; Supervision, Funding acquisition, R.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the National Natural Science Foundation of China under project No. 51975358.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this work:
| APC | Active Posture Control |
| CoM | Center of Mass |
| DYC | Direct Yaw-moment Control |
| LQR | Linear Quadratic Regulator |
| TAV | Trailing-arm Vehicle |
| MPC | Model Predictive Control |
| NLP | Nonlinear Programming |
| NMPC | Nonlinear Model Predictive Control |
| PPC | Pure Pursuit Control |
| PC | Posture Cone |
| PD | Proportional–Derivative (Controller) |
| RI | Rollover Index |
| magic formula parameters | |
| rollover index gains | |
| lateral and heading errors | |
| total traction force | |
| longitudinal, lateral and vertical tire forces of each corner | |
| nominal tire vertical force | |
| h | height of body CoM |
| heights of sprung and unsprung masses | |
| prediction and control horizons | |
| index for front (1) and rear (2) | |
| index for left (1) and right (2) | |
| yaw inertia of vehicle | |
| nominal yaw inertia of vehicle | |
| yaw rate generator gains | |
| effective torsional stiffness and damping in roll direction | |
| nominal cornering stiffness | |
| cornering stiffness of each corner | |
| wheelbase of each corner | |
| L | bias from body CoM to hip (front or rear) |
| length of trailing arm | |
| sprung and unsprung masses | |
| tire cornering stiffness parameters | |
| nominal trailing-arm angle | |
| trailing-arm angle of each corner | |
| weights of NMPC | |
| effective wheel radius | |
| vehicle longitudinal and lateral speeds | |
| wheel speed of each corner | |
| w | track width when zero rolling |
| track width of each corner | |
| wheel slip of each corner | |
| sideslip of vehicle body | |
| vehicle yaw rate | |
| coefficients in load transfer model | |
| diagonal lengths of posture cone | |
| path curvature | |
| trailing-arm torque of each corner | |
| wheel torque of each corner | |
| rolling and pitching of vehicle body | |
| wheel longitudinal slip | |
| desired and actual heading | |
| wheel speed of each corner |
References
- Niu, J.; Wang, H.; Shi, H.; Pop, N.; Li, D.; Li, S.; Wu, S. Study on Structural Modeling and Kinematics Analysis of a Novel Wheel-Legged Rescue Robot. Int. J. Adv. Robot. Syst. 2018, 15, 172988141775275. [Google Scholar] [CrossRef]
- Klamt, T.; Rodriguez, D.; Baccelliere, L.; Chen, X.; Chiaradia, D.; Cichon, T.; Gabardi, M.; Guria, P.; Holmquist, K.; Kamedula, M.; et al. Flexible Disaster Response of Tomorrow: Final Presentation and Evaluation of the CENTAURO System. IEEE Robot. Autom. Mag. 2019, 26, 59–72. [Google Scholar] [CrossRef]
- Zheng, J.; Gao, H.; Yuan, B.; Liu, Z.; Yu, H.; Ding, L.; Deng, Z. Design and Terramechanics Analysis of a Mars Rover Utilising Active Suspension. Mech. Mach. Theory 2018, 128, 125–149. [Google Scholar] [CrossRef]
- Sravya, R.; Sreeja, S. Design and Simulation of Interplanetary Lunar Rover. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Banerjee, S.; Balamurugan, V.; Krishnakumar, R. Ride Comfort Analysis of Math Ride Dynamics Model of Full Tracked Vehicle with Trailing Arm Suspension. Procedia Eng. 2016, 144, 1110–1118. [Google Scholar] [CrossRef]
- Devesh, M.; Manigandan, R.; Banerjee, S.; Mailan, L.B. Development of Sprung Mass Non-Linear Mathematical Model of Pitch Dynamics with Trailing Arm Suspension. Vibroeng. Procedia 2021, 37, 1–6. [Google Scholar] [CrossRef]
- Kazemi, M.; Heydari Shirazi, K.; Ghanbarzadeh, A. Optimization of Semi-Trailing Arm Suspension for Improving Handling and Stability of Passenger Car. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2012, 226, 108–121. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, M.; Liang, H.; Xu, L. Simulation Research on PID Control of New Trailing Arm Active Suspension Based on Genetic Algorithm Optimization. In Proceedings of the 2022 IEEE 2nd International Conference on Data Science and Computer Application (ICDSCA), Dalian, China, 28–30 October 2022; pp. 1054–1058. [Google Scholar] [CrossRef]
- Ding, X.; Zheng, Y.; Xu, K. Wheel-Legged Hexapod Robots: A Multifunctional Mobile Manipulating Platform. Chin. J. Mech. Eng. 2017, 30, 3–6. [Google Scholar] [CrossRef]
- Sun, J.; Sun, Z.; Li, J.; Wang, C.; Jing, X.; Wei, Q.; Liu, B.; Yan, C. TeCVP: A Time-Efficient Control Method for a Hexapod Wheel-Legged Robot Based on Velocity Planning. Sensors 2023, 23, 4051. [Google Scholar] [CrossRef]
- Li, J.; He, J.; Xing, Y.; Gao, F. Towards Uniform Normal Force Distribution by Roll and Height Control for a Planetary Rover with Active Suspension. In Proceedings of the 2021 27th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Shanghai, China, 26–28 November 2021; pp. 275–280. [Google Scholar] [CrossRef]
- Pan, Z.; Li, B.; Zhou, S.; Liu, S.; Niu, Z.; Wang, R. Distributed MPC-based Posture Control for Knee-Wheeled Wheel-Legged Robots with Multi-Actuation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 09544070231198901. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, Z.; Gao, H.; Yu, H.; Deng, Z. A Novel Active Deform and Wheel-Legged Suspension of Mars Rover. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 7–12. [Google Scholar] [CrossRef]
- Samuel, M.; Hussein, M.; Mohamad, M.B. A Review of Some Pure-Pursuit Based Path Tracking Techniques for Control of Autonomous Vehicle. Int. J. Comput. Appl. 2016, 135, 35–38. [Google Scholar] [CrossRef]
- Ollero, A.; Heredia, G. Stability Analysis of Mobile Robot Path Tracking. In Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995; Volume 3, pp. 461–466. [Google Scholar] [CrossRef]
- Rajagopalan, V.; Mericli, C.; Kelly, A. Slip-Aware Model Predictive Optimal Control for Path Following. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4585–4590. [Google Scholar] [CrossRef]
- Ahn, J.; Shin, S.; Kim, M.; Park, J. Accurate Path Tracking by Adjusting Look-Ahead Point in Pure Pursuit Method. Int. J. Automot. Technol. 2021, 22, 119–129. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Han, K.; Choi, S.B. Vehicle Path Tracking Control Using Pure Pursuit With MPC-Based Look-Ahead Distance Optimization. IEEE Trans. Veh. Technol. 2024, 73, 53–66. [Google Scholar] [CrossRef]
- Veneri, M.; Massaro, M. The Effect of Ackermann Steering on the Performance of Race Cars. Veh. Syst. Dyn. 2021, 59, 907–927. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Yan, F.; Chen, N. Should the Desired Heading in Path Following of Autonomous Vehicles Be the Tangent Direction of the Desired Path? IEEE Trans. Intell. Transp. Syst. 2015, 16, 3084–3094. [Google Scholar] [CrossRef]
- Geng, C.; Mostefai, L.; Denai, M.; Hori, Y. Direct Yaw-Moment Control of an In-Wheel-Motored Electric Vehicle Based on Body Slip Angle Fuzzy Observer. IEEE Trans. Ind. Electron. 2009, 56, 1411–1419. [Google Scholar] [CrossRef]
- Asiabar, A.N.; Kazemi, R. A Direct Yaw Moment Controller for a Four In-Wheel Motor Drive Electric Vehicle Using Adaptive Sliding Mode Control. Proc. Inst. Mech. Eng. Part K: J. Multi-Body Dyn. 2019, 233, 549–567. [Google Scholar] [CrossRef]
- Snider, J.M. Automatic Steering Methods for Autonomous Automobile Path Tracking. Robotics Institute, Pittsburgh, PA, Tech. Rep. CMU-RITR-09-08. 2009. Available online: https://www.ri.cmu.edu/pub_files/2009/2/Automatic_Steering_Methods_for_Autonomous_Automobile_Path_Tracking.pdf (accessed on 3 February 2009).
- Falcone, P.; Borrelli, F.; Asgari, J.; Tseng, H.E.; Hrovat, D. Predictive Active Steering Control for Autonomous Vehicle Systems. IEEE Trans. Control Syst. Technol. 2007, 15, 566–580. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Yan, F.; Chen, N. Output Constraint Control on Path Following of Four-Wheel Independently Actuated Autonomous Ground Vehicles. IEEE Trans. Veh. Technol. 2016, 65, 4033–4043. [Google Scholar] [CrossRef]
- Peterson, M.T.; Goel, T.; Gerdes, J.C. Exploiting Linear Structure for Precision Control of Highly Nonlinear Vehicle Dynamics. IEEE Trans. Intell. Veh. 2023, 8, 1852–1862. [Google Scholar] [CrossRef]
- Allgöwer, F.; Findeisen, R.; Nagy, Z.K. Nonlinear Model Predictive Control: From Theory to Application. Nonlinear Model Predict. Control 2004, 35, 299–315. [Google Scholar]
- Johansen, T.A. Approximate Explicit Receding Horizon Control of Constrained Nonlinear Systems. Automatica 2004, 40, 293–300. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, H.; Wang, J.; Yan, F.; Chen, N. Robust Lateral Motion Control of Four-Wheel Independently Actuated Electric Vehicles with Tire Force Saturation Consideration. J. Frankl. Inst. 2015, 352, 645–668. [Google Scholar] [CrossRef]
- Gray, A.; Gao, Y.; Lin, T.; Hedrick, J.K.; Tseng, H.E.; Borrelli, F. Predictive Control for Agile Semi-Autonomous Ground Vehicles Using Motion Primitives. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 4239–4244. [Google Scholar] [CrossRef]
- Li, L.; Lu, Y.; Wang, R.; Chen, J. A Three-Dimensional Dynamics Control Framework of Vehicle Lateral Stability and Rollover Prevention via Active Braking With MPC. IEEE Trans. Ind. Electron. 2017, 64, 3389–3401. [Google Scholar] [CrossRef]
- Choi, C.; Kang, Y. Simultaneous Braking and Steering Control Method Based on Nonlinear Model Predictive Control for Emergency Driving Support. Int. J. Control Autom. Syst. 2017, 15, 345–353. [Google Scholar] [CrossRef]
- Falcone, P.; Eric Tseng, H.; Borrelli, F.; Asgari, J.; Hrovat, D. MPC-based Yaw and Lateral Stabilisation via Active Front Steering and Braking. Veh. Syst. Dyn. 2008, 46, 611–628. [Google Scholar] [CrossRef]
- Fu, T.; Zhou, H.; Liu, Z. NMPC-Based Path Tracking Control Strategy for Autonomous Vehicles with Stable Limit Handling. IEEE Trans. Veh. Technol. 2022, 71, 12499–12510. [Google Scholar] [CrossRef]
- Miège, A.J.P.; Cebon, D. Active Roll Control of an Experimental Articulated Vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2005, 219, 791–806. [Google Scholar] [CrossRef]
- Čorić, M.; Deur, J.; Xu, L.; Tseng, H.E.; Hrovat, D. Optimisation of Active Suspension Control Inputs for Improved Performance of Active Safety Systems. Veh. Syst. Dyn. 2018, 56, 1–26. [Google Scholar] [CrossRef]
- Liang, W.; Ahmac, E.; Khan, M.A.; Youn, I. Integration of Active Tilting Control and Full-Wheel Steering Control System on Vehicle Lateral Performance. Int. J. Automot. Technol. 2021, 22, 979–992. [Google Scholar] [CrossRef]
- Skjetne, R.; Fossen, T. Nonlinear Maneuvering and Control of Ships. In Proceedings of the MTS/IEEE Oceans 2001. An Ocean Odyssey. Conference Proceedings (IEEE Cat. No.01CH37295), Honolulu, HI, USA, 5–8 November 2001; Volume 3, pp. 1808–1815. [Google Scholar] [CrossRef]
- Pacejka, H. Tire and Vehicle Dynamics; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Ataei, M.; Khajepour, A.; Jeon, S. Model Predictive Rollover Prevention for Steer-by-Wire Vehicles with a New Rollover Index. Int. J. Control 2020, 93, 140–155. [Google Scholar] [CrossRef]
- Wang, R.; Hu, C.; Yan, F.; Chadli, M. Composite Nonlinear Feedback Control for Path Following of Four-Wheel Independently Actuated Autonomous Ground Vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2063–2074. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).