Numerical and Experimental Study on Dummy Blade with Underplatform Damper
Abstract
1. Introduction
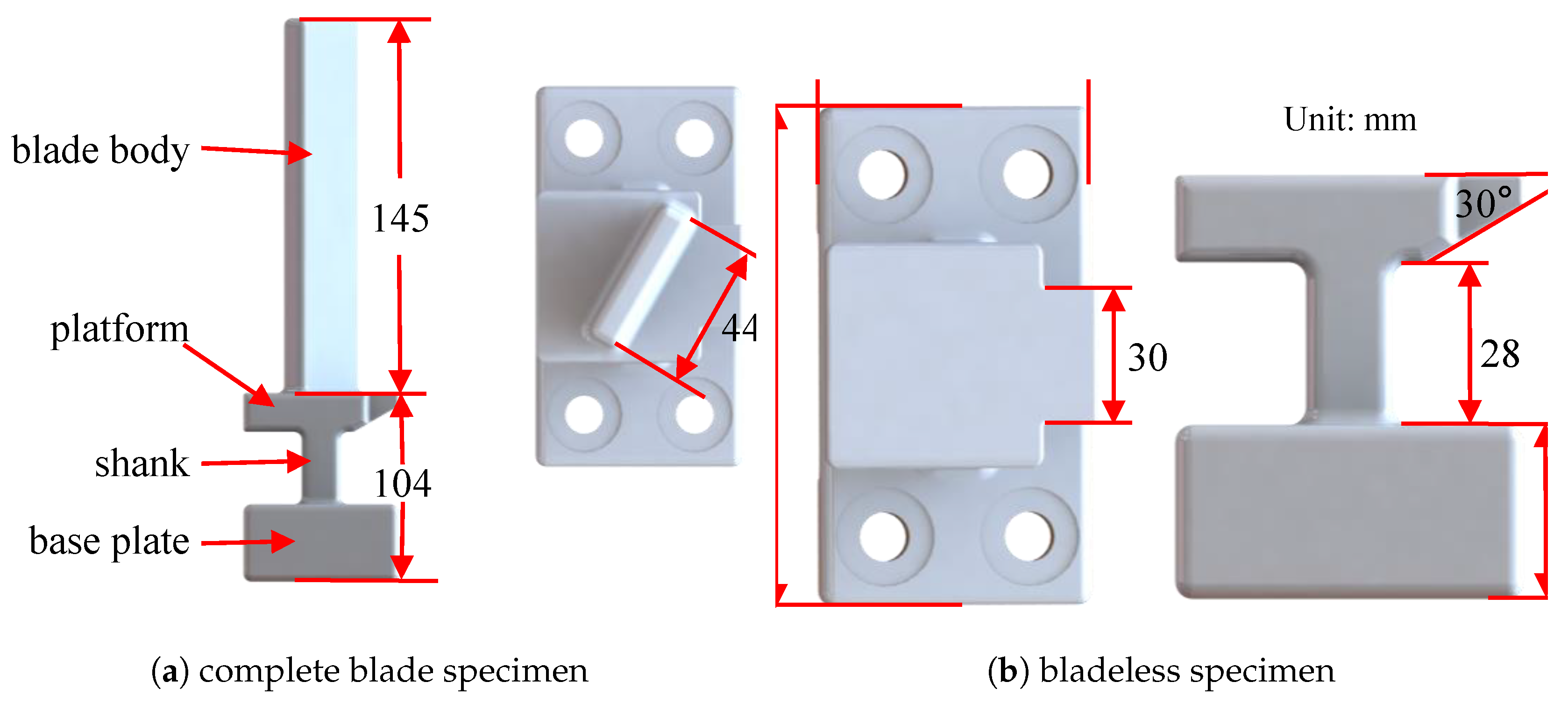
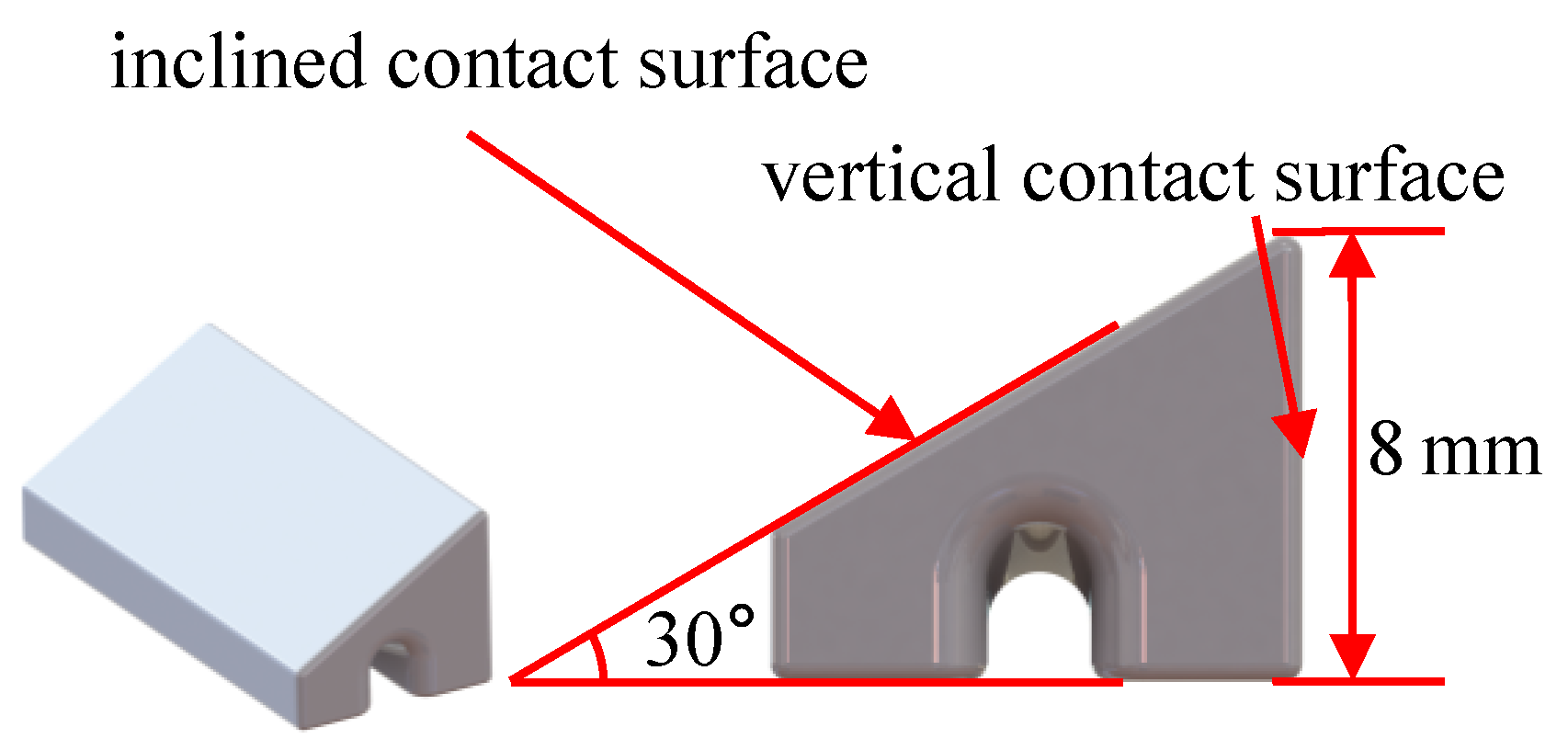
2. Test Rig Description
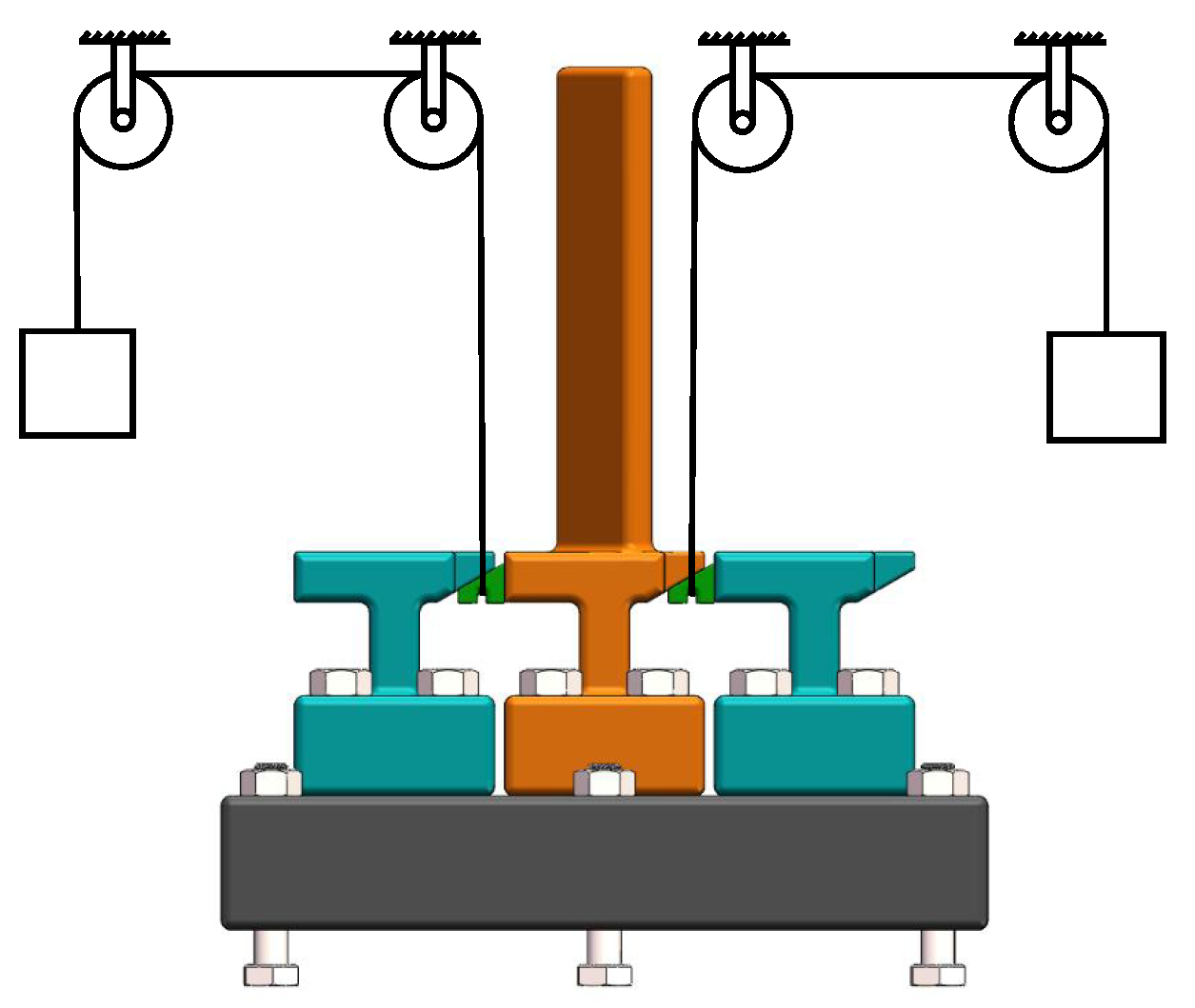
2.1. Test Rig
2.2. Experimental Principles
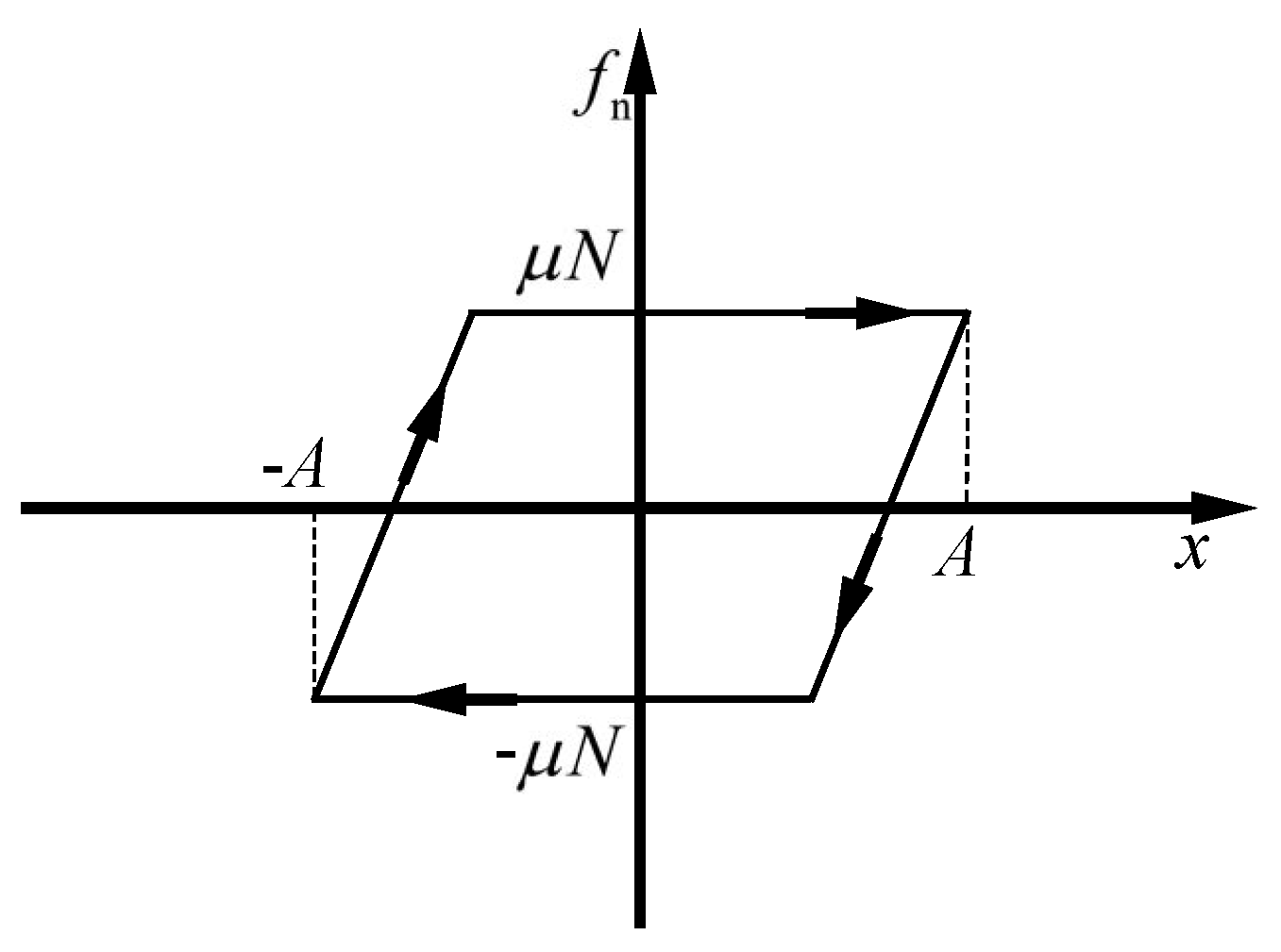
2.2.1. Exciter Excitation
2.2.2. Damping-Free Vibration
2.3. Experimental Method
2.3.1. Modal Testing
2.3.2. Shaker Excitation
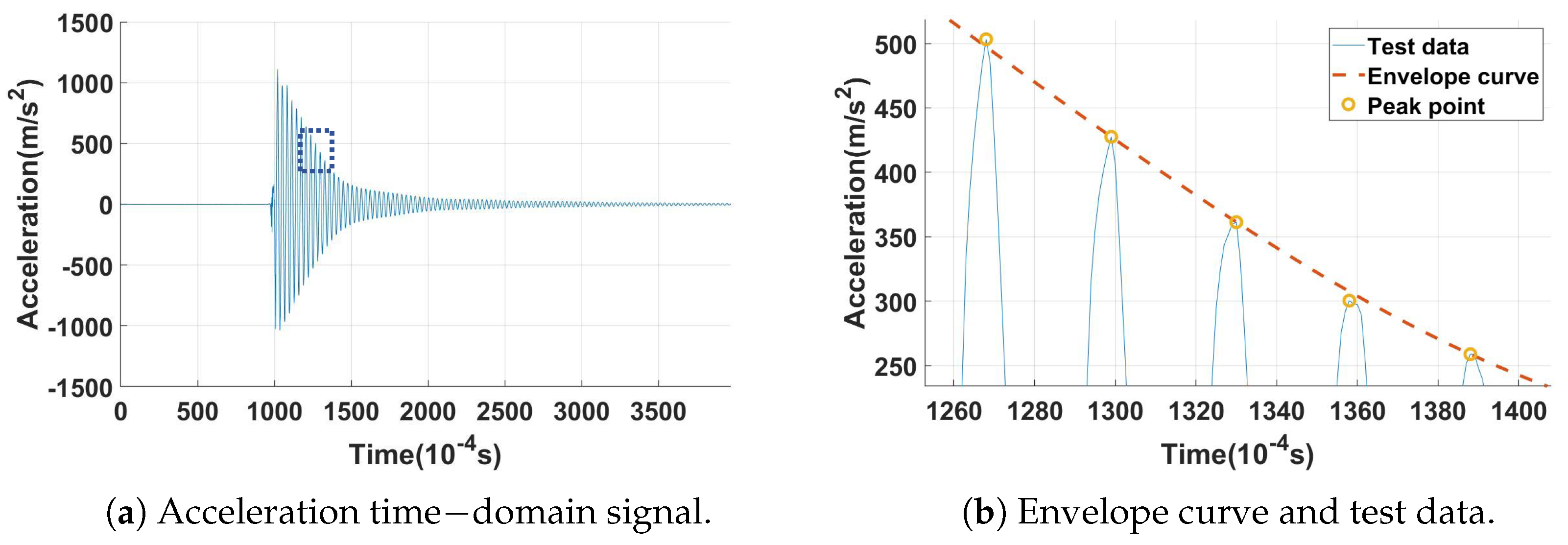
2.3.3. Damping-Free Vibration
3. Numerical Simulation Methods and Results
3.1. Computational Background
3.2. Results of Simulation
4. Test Results
4.1. Modal Testing
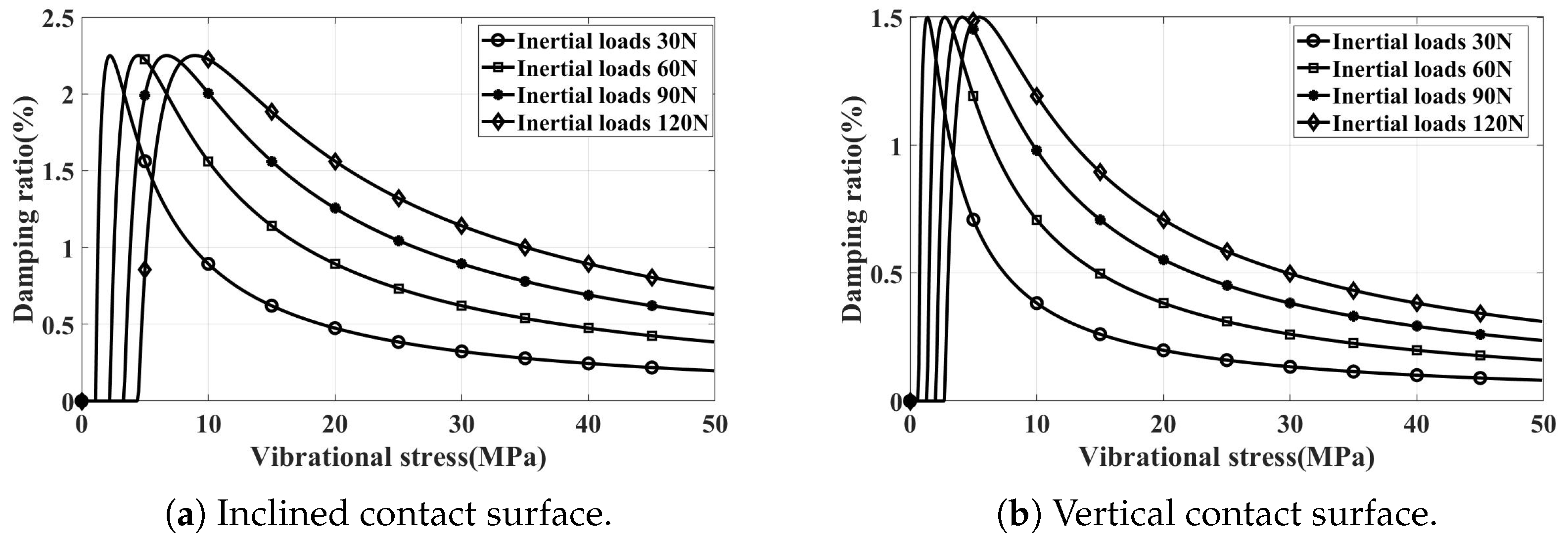
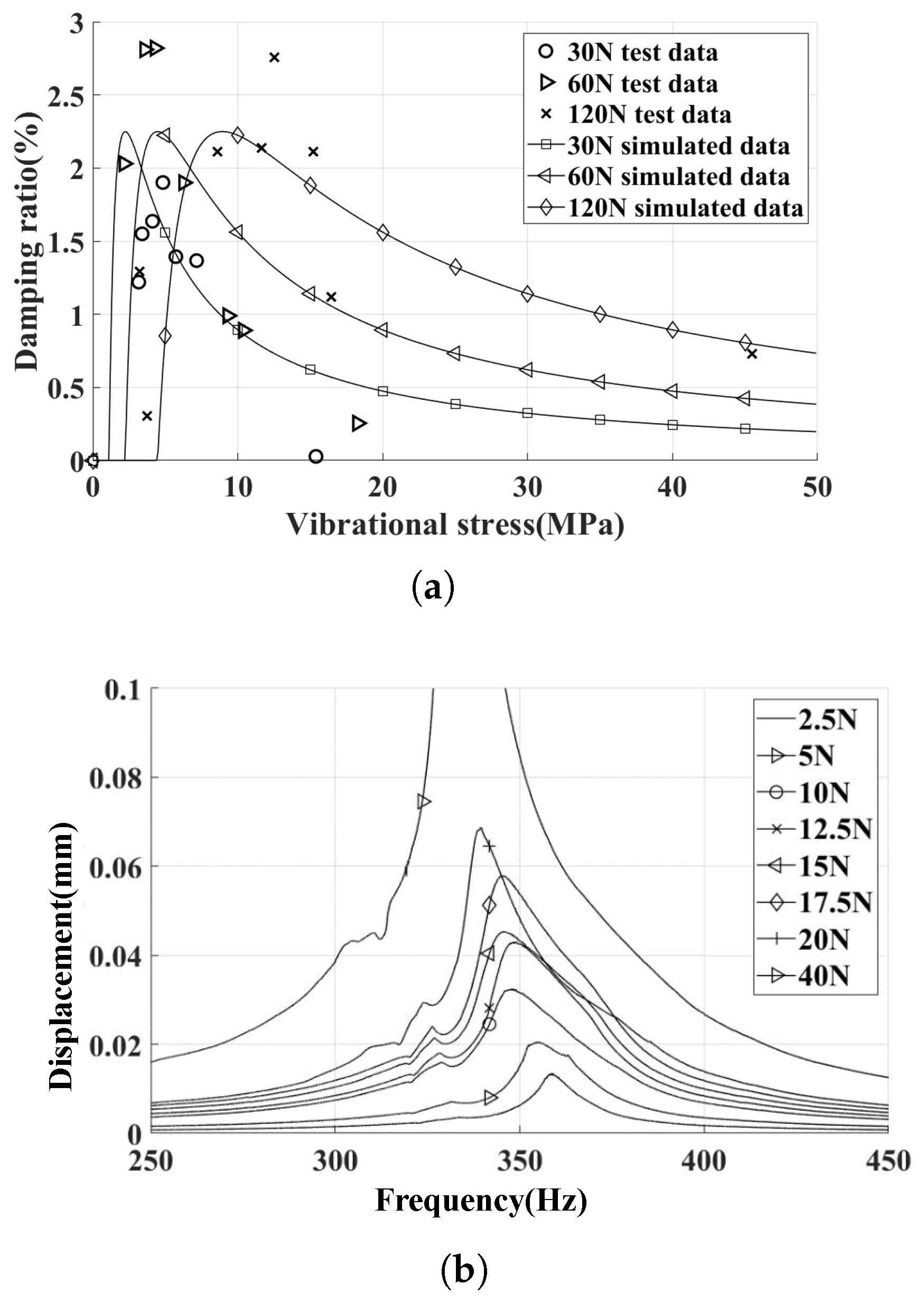
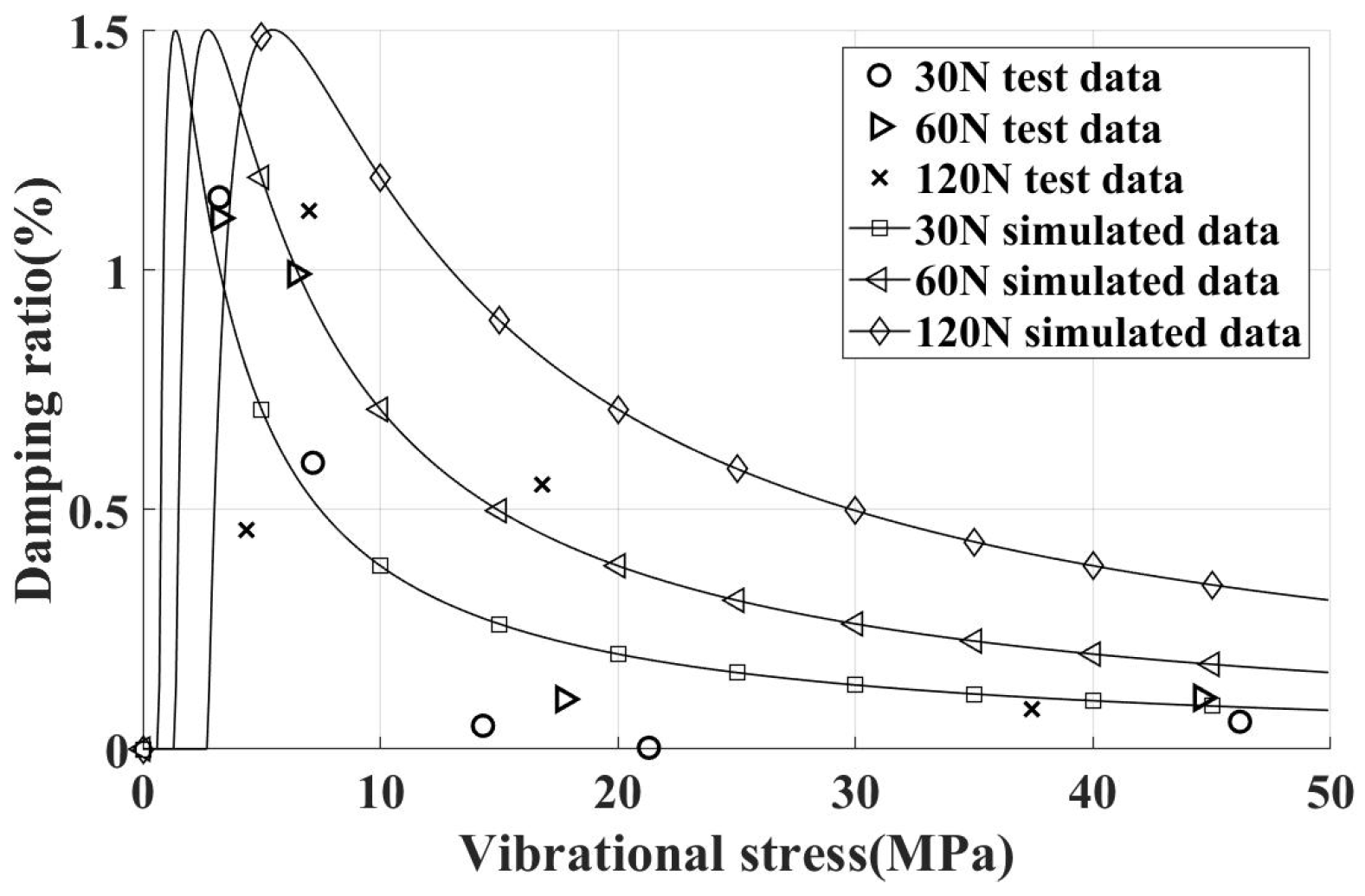
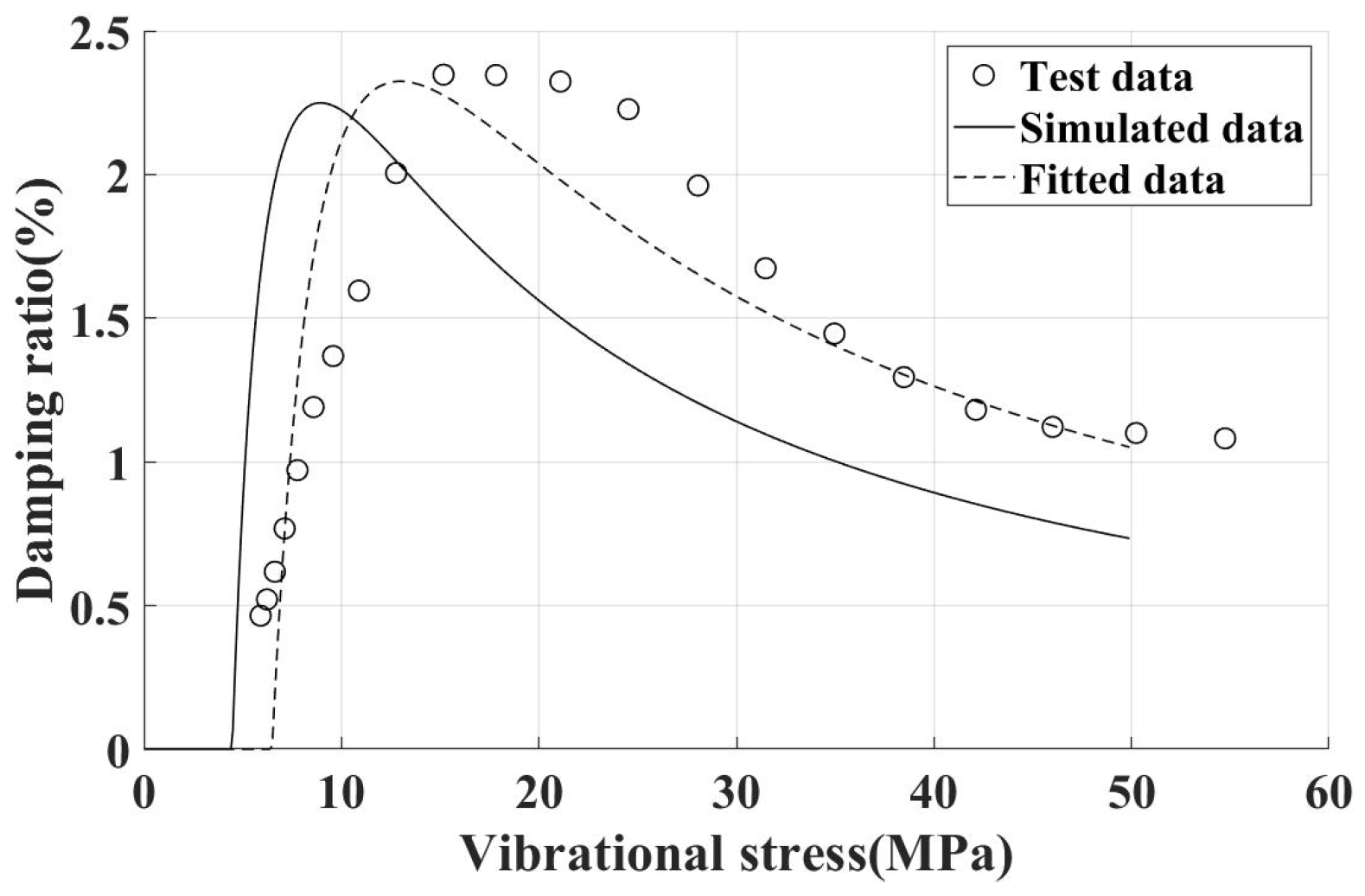
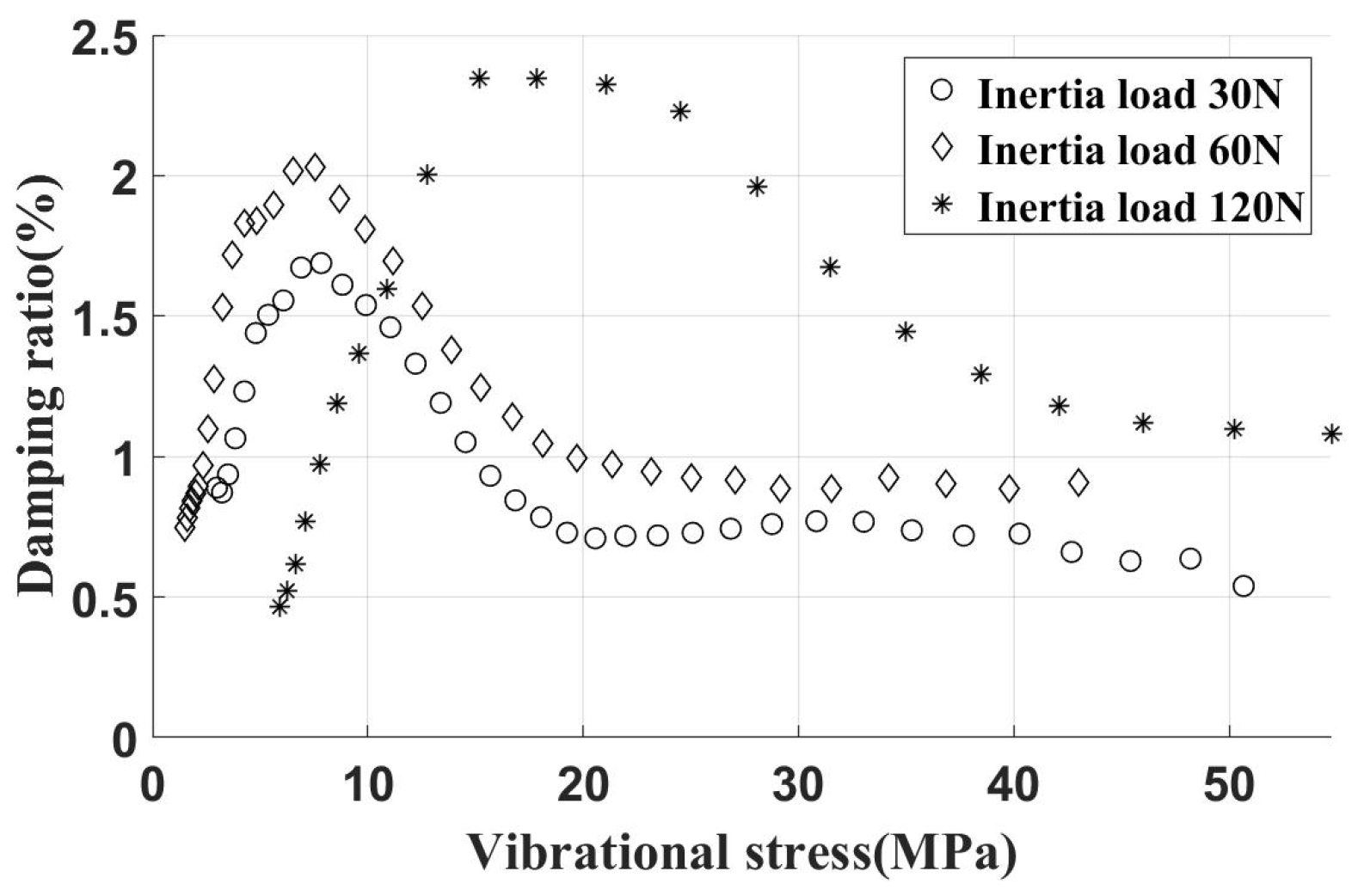
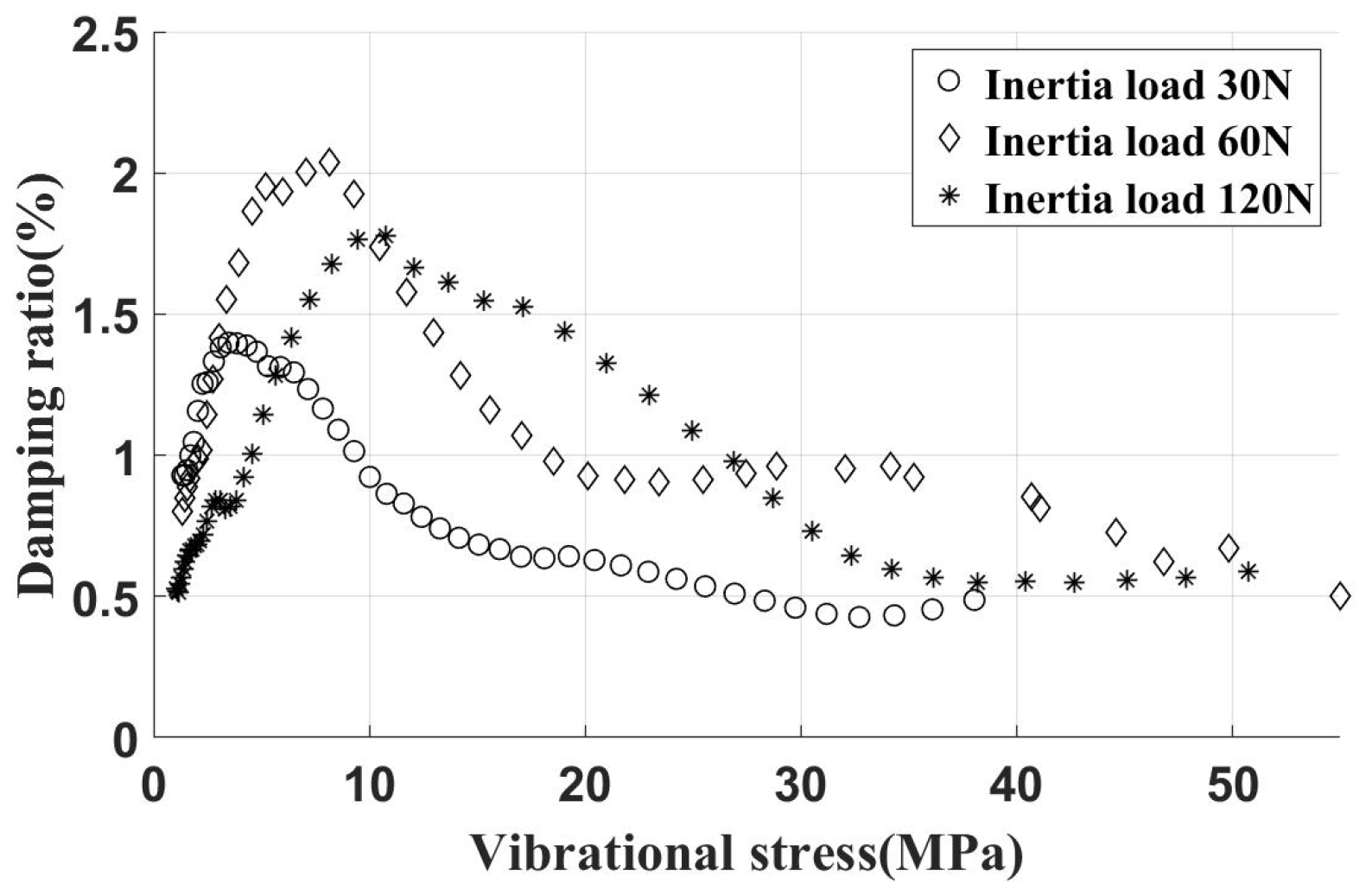
4.2. Sweep Frequency Vibration Test
- The inaccuracy of contact stiffness, especially for the experiments with an exciting force of 30 N.
- Our simulation method only considers the tangential displacement of one direction, and the displacement in the other direction can increase the relative displacement of the UPD and blade, which can make the UPD provide more damping.
- Only the damping of the contact surface of the complete blade specimen and UPD is considered in the simulation results; however, the contact surface of the bladeless specimen and UPD may provide damping as well, which may cause the maximum experimental damping ratio of the incline contact surface to be higher than the simulation results.
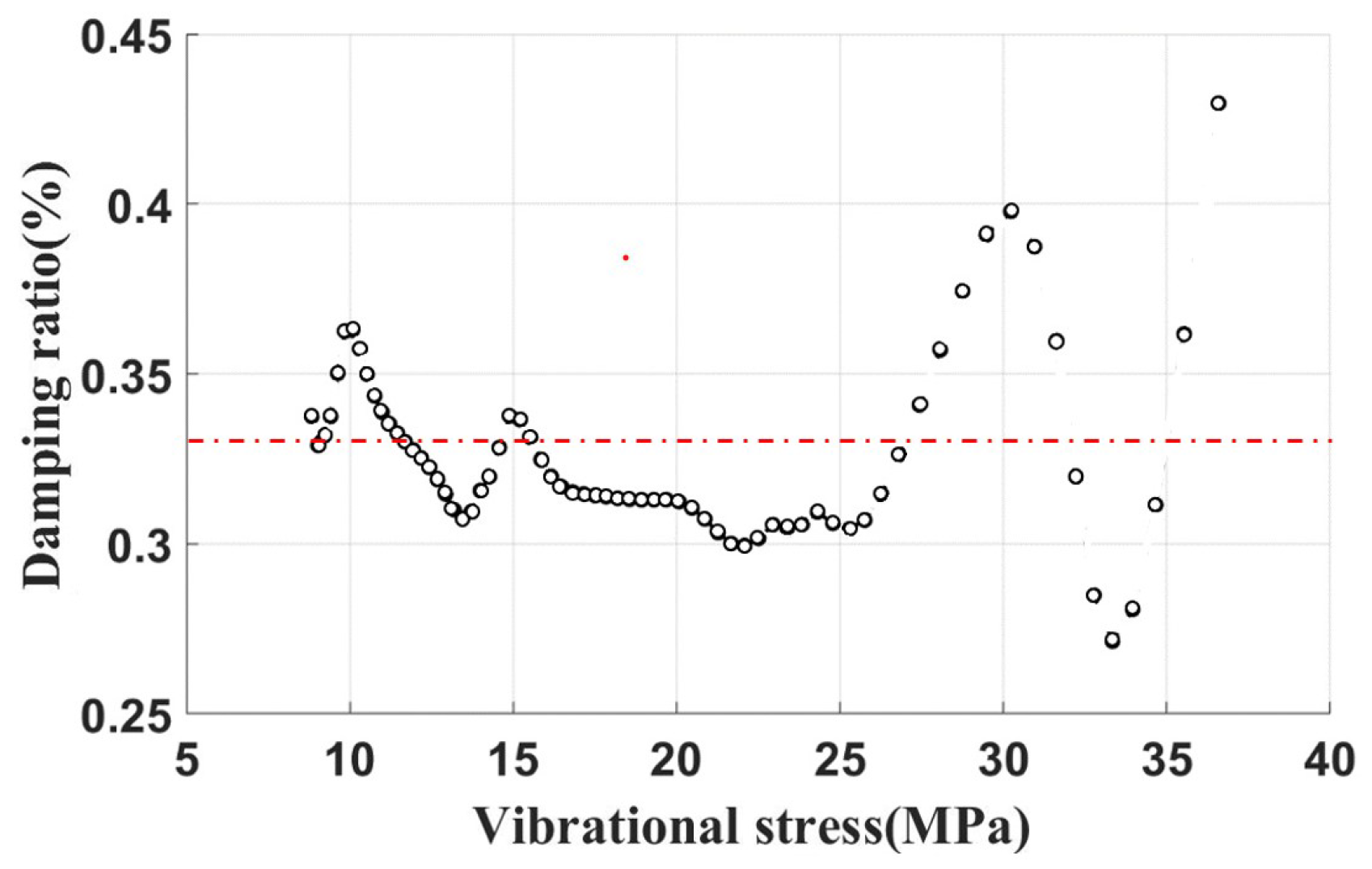
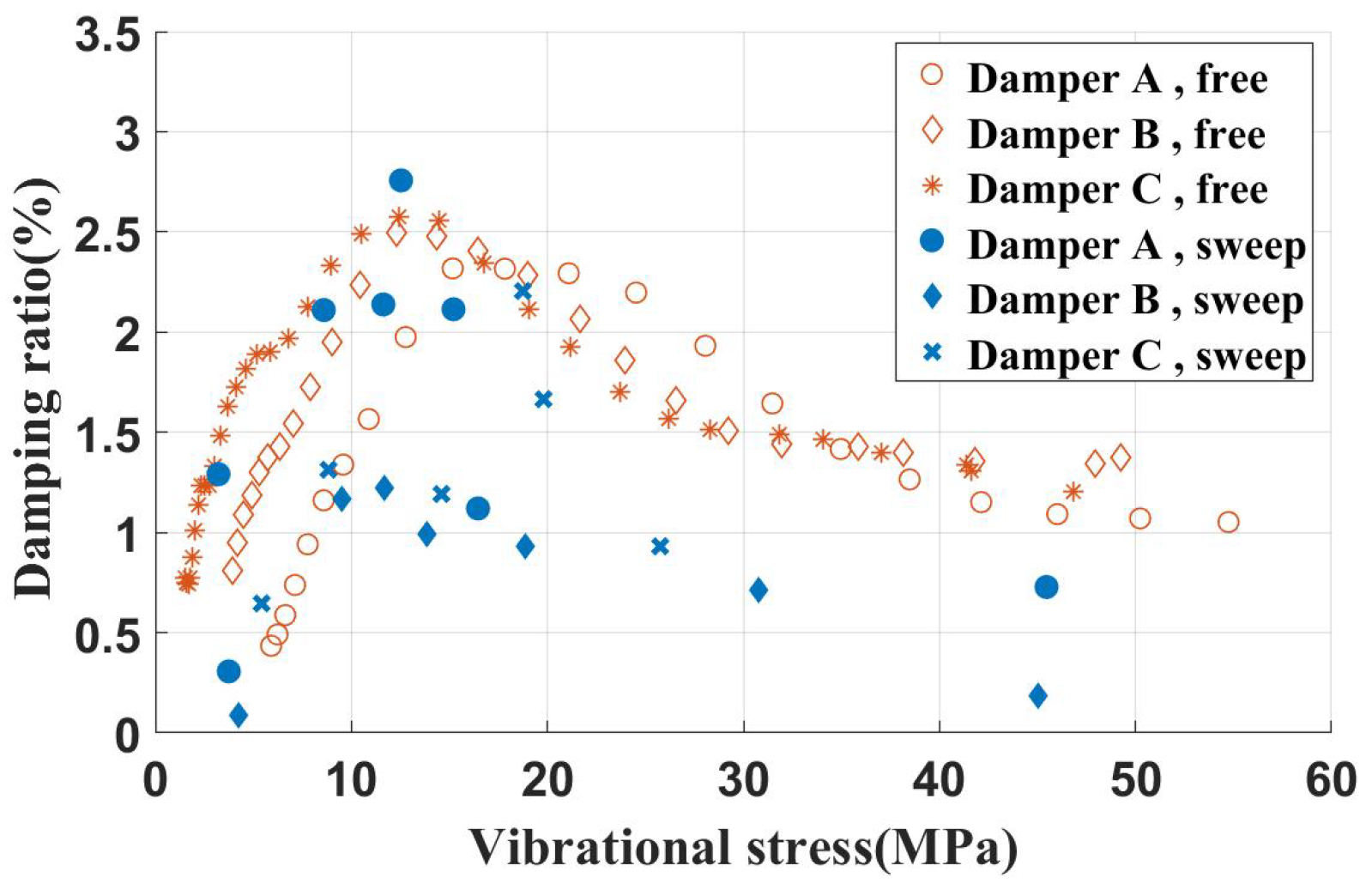
4.3. Free Vibration Test
4.4. The Influence of Contact Area and Root Extension Length
- The initial displacement of the free vibration experiment is not exactly the first bending mode, so the process of vibration is a mix of many modes.
- During the sweep frequency experiment, both the blade and shaker were vibrating.
- The exciting force is hard to maintain constant during the vibration.
- The process of the free vibration experiment is quite short and the wear of the contact surface is ignorable, but the sweep frequency experiments take a long time, so the wear may change the contact parameter.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, M.; Wang, Y. Efficient numerical prediction of blade forced response under inlet distortion. Aerosp. Sci. Technol. 2023, 142, 108612. [Google Scholar] [CrossRef]
- Fang, M.; Wang, Y. Intentional Mistuning Effect on the Blisk Vibration with Aerodynamic Damping. AIAA J. 2022, 60, 3884–3893. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, H.; Fan, Y.; Li, L. On the network of synchronized switch damping for blisks. Mech. Syst. Signal Process. 2023, 184, 109695. [Google Scholar] [CrossRef]
- Menq, C.H.; Chidamparam, P.; Griffin, J.H. Friction damping of two-dimensional motion and its application in vibration control. J. Sound Vib. 1991, 144, 427–447. [Google Scholar] [CrossRef]
- Sanliturk, K.Y.; Ewins, D.J. Modelling Two-Dimensional Friction Ccontact and its Application Using Harmonic Balance Method. J. Sound Vib. 1996, 193, 511–523. [Google Scholar] [CrossRef]
- Yang, B.D.; Menq, C.H. Modeling of Friction Contact and Its Application to the Design of Shroud Contact. J. Eng. Gas Turbines Power-Trans. ASME 1997, 119, 958–963. [Google Scholar] [CrossRef]
- Siewert, C.; Panning, L.; Wallaschek, J.; Richter, C. Multiharmonic Forced Response Analysis of a Turbine Blading Coupled by Nonlinear Contact Forces. J. Eng. Gas Turbines Power 2010, 132, 082501. [Google Scholar] [CrossRef]
- Gao, Q.; Fan, Y.; Wu, Y.; Liu, J.; Wang, J.; Li, L. A novel test apparatus to study the mechanism of harmonic normal force on fretting wear. Tribol. Int. 2024, 191, 109091. [Google Scholar] [CrossRef]
- Gao, Q.; Fan, Y.; Wu, Y.; Li, L. A harmonic balance-based method to predict nonlinear forced response and temperature rise of dry friction systems including frictional heat transfer. Nonlinear Dyn. 2023, 111, 14263–14291. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, D.; Wu, Y.; Shen, Q.; Hu, D. A semi-analytical multi-harmonic balance method on full-3D contact model for dynamic analysis of dry friction systems. Chin. J. Aeronaut. 2024, 37, 309–329. [Google Scholar] [CrossRef]
- Wu, Y.; Li, L.; Fan, Y.; Zucca, S.; Gastaldi, C.; Ma, H. Design of dry friction and piezoelectric hybrid ring dampers for integrally bladed disks based on complex nonlinear modes. Comput. Struct. 2020, 233, 106237. [Google Scholar] [CrossRef]
- Wu, Y.; Li, L.; Fan, Y.; Ma, H.; Wang, W.; Christen, J.L.; Ichchou, M. Design of semi-active dry friction dampers for steady-state vibration: Sensitivity analysis and experimental studies. J. Sound Vib. 2019, 459, 114850. [Google Scholar] [CrossRef]
- Ferhatoglu, E.; Zucca, S. Determination of periodic response limits among multiple solutions for mechanical systems with wedge dampers. J. Sound Vib. 2021, 494, 115900. [Google Scholar] [CrossRef]
- Denimal, E.; Wong, C.; Salles, L.; Pesaresi, L. On the Efficiency of a Conical Underplatform Damper for Turbines. J. Eng. Gas Turbines Power 2021, 143, 021020. [Google Scholar] [CrossRef]
- Gastaldi, C.; Berruti, T.M.; Gola, M.M. Best practices for underplatform damper designers. Proc. Inst. Mech. Eng. Part C. J. Mech. Eng. Sci. 2018, 232. [Google Scholar] [CrossRef]
- Gastaldi, C.; Berruti, T.M. Direct measurement of the damping and stiffening capabilities of cylindrical underplatform dampers. Mech. Syst. Signal Process. 2020, 139, 106632. [Google Scholar] [CrossRef]
- Gastaldi, C.; Berruti, T.M.; Gola, M.M. A novel test rig for friction parameters measurement on underplatform dampers. Int. J. Solids Struct. 2020, 185–186, 170–181. [Google Scholar] [CrossRef]
- Panning, L.; Popp, K.; Sextro, W.; Gotting, F.; Kayser, A.; Wolter, I. Asymmetrical Underplatform Dampers in Gas Turbine Bladings: Theory and Application. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004; Volume 6: Turbo Expo 2004, pp. 269–280. [Google Scholar] [CrossRef]
- Cigeroglu, E.; An, N.; Menq, C.H. A microslip friction model with normal load variation induced by normal motion. Nonlinear Dyn. 2007, 50, 609–626. [Google Scholar] [CrossRef]
- Salas, M.G.; Bladh, R.; Mårtensson, H.; Petrie-Repar, P.; Fransson, T.; Vogt, D.M. Forced Response Analysis of a Mistuned, Compressor Blisk Comparing Three Different Reduced Order Model Approaches. J. Eng. Gas Turbines Power 2017, 139, 062501. [Google Scholar] [CrossRef]
- Mehrdad Pourkiaee, S.; Zucca, S. A Reduced Order Model for Nonlinear Dynamics of Mistuned Bladed Disks with Shroud Friction Contacts. J. Eng. Gas Turbines Power 2018, 141, 011031. [Google Scholar] [CrossRef]
- Benfield, W.A.; Hruda, R.F. Vibration Analysis of Structures by Component Mode Substitution. Aiaa J. 1971, 9, 1255–1261. [Google Scholar] [CrossRef]
- Gola, M.M. A general geometrical theory of turbine blade underplatform asymmetric dampers. Mech. Syst. Signal Process. 2023, 191, 110167. [Google Scholar] [CrossRef]
- Rani, S. Parametric Evaluation and Dynamic Analysis of Turbine Blades–Damper Assembly Using Bond Graph Technique. J. Vib. Eng. Technol. 2023, 12, 681–693. [Google Scholar] [CrossRef]
- Pesaresi, L.; Salles, L.; Jones, A.; Green, J.; Schwingshackl, C. Modelling the nonlinear behaviour of an underplatform damper test rig for turbine applications. Mech. Syst. Signal Process. 2017, 85, 662–679. [Google Scholar] [CrossRef]
- Pesaresi, L.; Stender, M.; Ruffini, V.; Schwingshackl, C.W. DIC Measurement of the Kinematics of a Friction Damper for Turbine Applications. In Proceedings of the Dynamics of Coupled Structures; Allen, M.S., Mayes, R.L., Rixen, D.J., Eds.; Springer: Cham, Switzerland, 2017; Volume 4, pp. 93–101. [Google Scholar]
- Zhang, D.; Gao, B.; Hong, J.; Fu, J.; Ge, X. Experimental investigation on dynamic response of flat blades with underplatform dampers. Chin. J. Aeronaut. 2019, 32, 2667–2678. [Google Scholar] [CrossRef]
- Ferhatoglu, E.; Gastaldi, C.; Botto, D.; Zucca, S. An experimental and computational comparison of the dynamic response variability in a turbine blade with under-platform dampers. Mech. Syst. Signal Process. 2022, 172, 108987. [Google Scholar] [CrossRef]
- Ferhatoglu, E.; Zucca, S. On the non-uniqueness of friction forces and the systematic computation of dynamic response boundaries for turbine bladed disks with contacts. Mech. Syst. Signal Process. 2021, 160, 107917. [Google Scholar] [CrossRef]
- Hoffmann, T.; Panning-von Scheidt, L.; Wallaschek, J. Measured and Simulated Forced Response of a Rotating Turbine Disk With Asymmetric and Cylindrical Underplatform Dampers. J. Eng. Gas Turbines Power 2020, 142, 051002. [Google Scholar] [CrossRef]
- Gao, S.; Wang, Y.; Sun, Z. An Energy Method for Assessing the Damping of Turbine Blade Underplatform Damper and Forced Response Verification. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Virtual, 21–25 September 2020; Volume 11: Structures and Dynamics: Structural Mechanics, Vibration, and Damping; Supercritical CO2. p. V011T30A010. [Google Scholar] [CrossRef]
- Gao, S.; Wang, Y.; Sun, Z.; Chen, S. A Prediction Method with Altering Equivalent Stiffness for Damping Evaluation of Shrouded Bladed Disk Dynamic Systems. Symmetry 2021, 13, 413. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Y.; Wei, D.; Luo, Y.; Gao, S. Vibration Analysis and Methods of Dry Friction Damping of Tubed Vortex Reducer. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Virtual, 21–25 September 2020; Volume 11: Structures and Dynamics: Structural Mechanics, Vibration, and Damping; Supercritical CO2. p. V011T30A001. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear damping in large-amplitude vibrations: Modelling and experiments. Nonlinear Dyn. 2018, 93, 5–18. [Google Scholar] [CrossRef]
- Amabili, M. Derivation of nonlinear damping from viscoelasticity in case of nonlinear vibrations. Nonlinear Dyn. 2019, 97, 1785–1797. [Google Scholar] [CrossRef]
- Grosso, P.; Felice, A.D.; Sorrentino, S. A method for the experimental identification of equivalent viscoelastic models from vibration of thin plates. Mech. Syst. Signal Process. 2021, 153, 107527. [Google Scholar] [CrossRef]




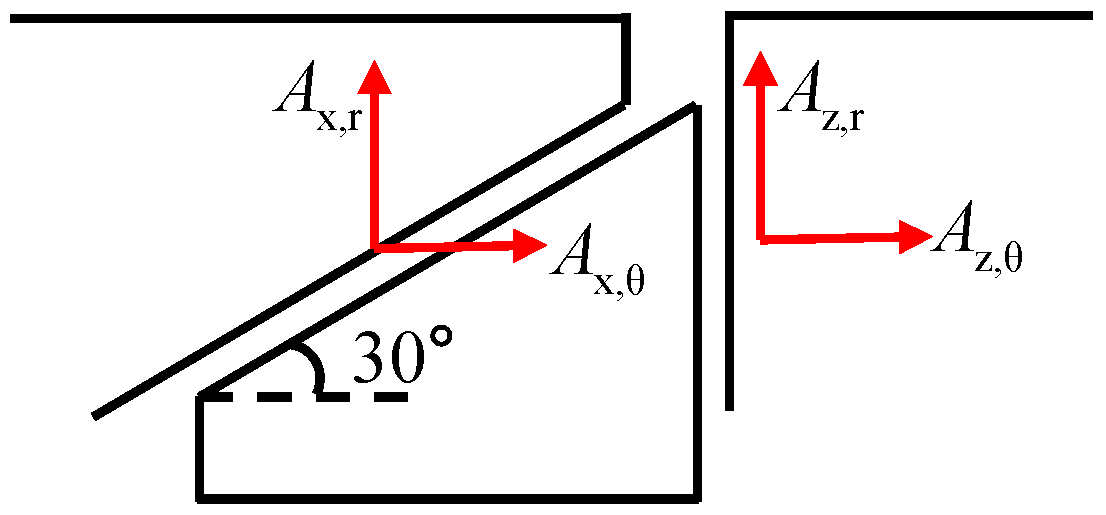

| Dense () | Poisson Ratio | Young’s Modulus (GPa) |
|---|---|---|
| 7810 | 0.269 | 201 |
| Parameters | Values |
|---|---|
| Frequency | 328.91 |
| Inclined contact surface radial modal displacement | 116 |
| Inclined contact surface tangential modal displacement | 97 |
| Vertical contact surface radial modal displacement | −116 |
| Vertical contact surface tangential modal displacement | 103 |
| Examination of modal equivalent stress at a nodal point | |
| Modal kinetic energy | |
| Frictional coefficient | 0.3 |
| Tangential contact stiffness | 30,000 |
| Inertial Load | Normal Pressure on Inclined Contact Surface | Normal Pressure on a Direct Contact Surface |
|---|---|---|
| 30 | 34.64 | 17.32 |
| 60 | 69.28 | 34.64 |
| 90 | 103.92 | 51.96 |
| 120 | 138.56 | 69.28 |
| Parameters | Values |
|---|---|
| Simulated frequency | 328.91 |
| Test frequency without dampers | 322.57 |
| Test frequency with 30 N inertial load | 327.15 |
| Test frequency with 120 N inertial load | 327.19 |
| Specimen Number | Contact Length | Contact Width |
|---|---|---|
| A | 33 | 16 |
| B | 22 | 16 |
| C | 11 | 16 |
| Specimen Number | Root Extension Length |
|---|---|
| I | 28 |
| II | 38 |
| III | 48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Du, C.; Li, H.; Meng, G. Numerical and Experimental Study on Dummy Blade with Underplatform Damper. Machines 2024, 12, 461. https://doi.org/10.3390/machines12070461
Li D, Du C, Li H, Meng G. Numerical and Experimental Study on Dummy Blade with Underplatform Damper. Machines. 2024; 12(7):461. https://doi.org/10.3390/machines12070461
Chicago/Turabian StyleLi, Di, Chenhong Du, Hongguang Li, and Guang Meng. 2024. "Numerical and Experimental Study on Dummy Blade with Underplatform Damper" Machines 12, no. 7: 461. https://doi.org/10.3390/machines12070461
APA StyleLi, D., Du, C., Li, H., & Meng, G. (2024). Numerical and Experimental Study on Dummy Blade with Underplatform Damper. Machines, 12(7), 461. https://doi.org/10.3390/machines12070461






