A Digital Twin-Based Adaptive Height Control for a Shearer
Abstract
1. Introduction
2. Digital Twin-Based Control Architecture for a Shearer
3. Digital Twin Model for Height Adjustment of a Shearer
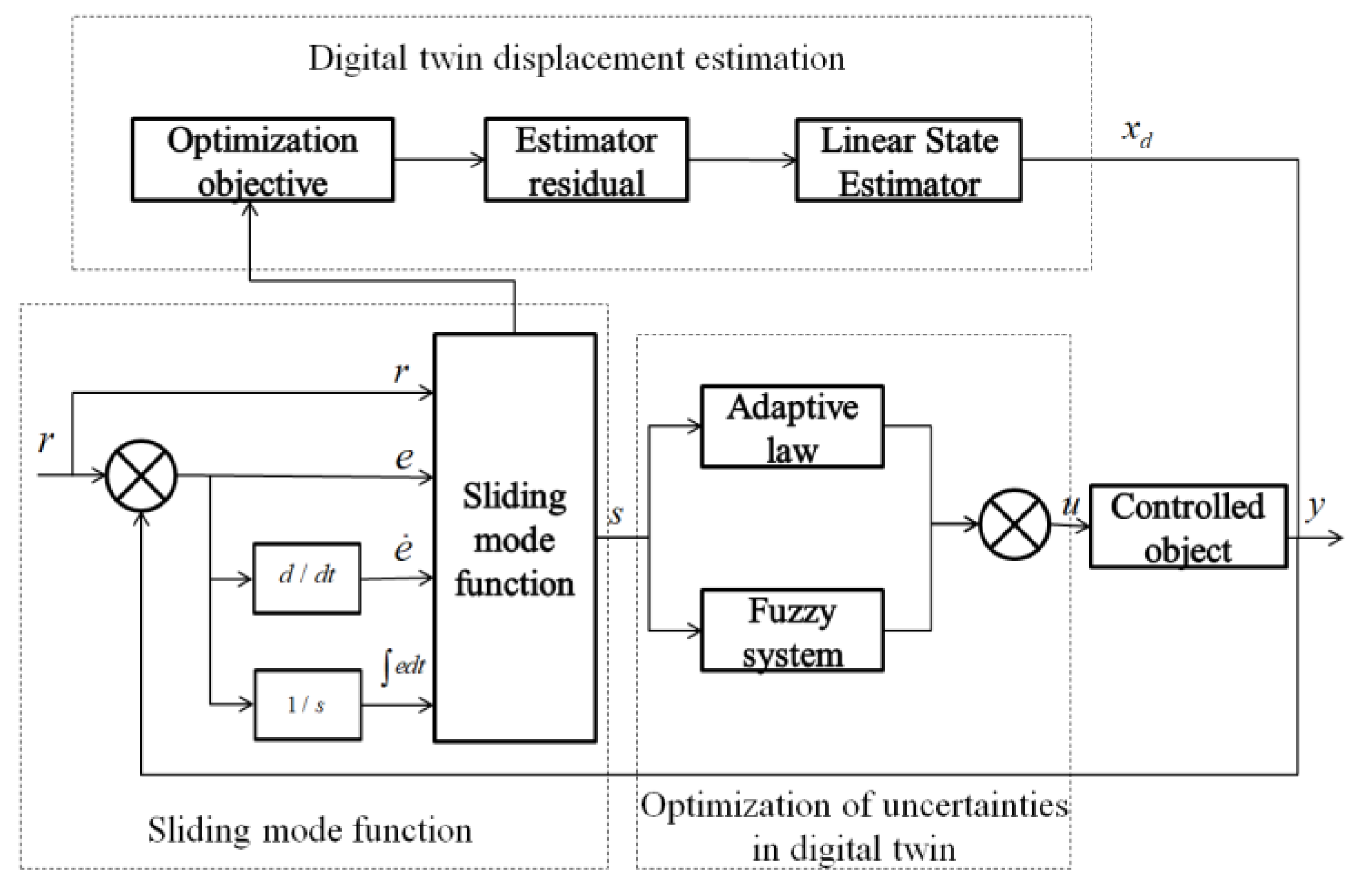
4. Digital Twin-Based Height Control System for Coal Mining Machine
4.1. Digital Twin-Based Displacement Estimation for Height Adjustment
4.2. Fuzzy System Design
4.3. Adaptive Fuzzy Sliding Mode Controller
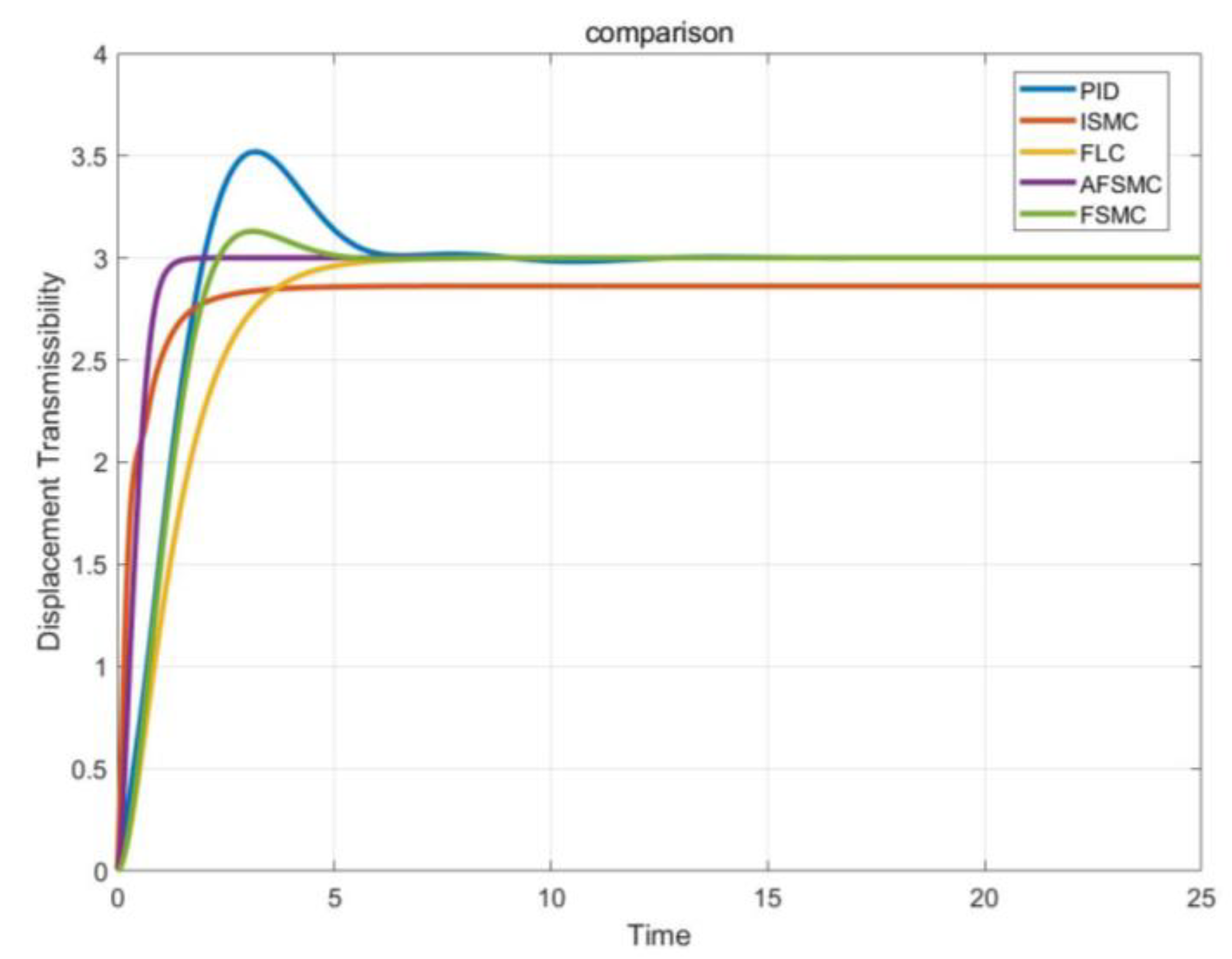
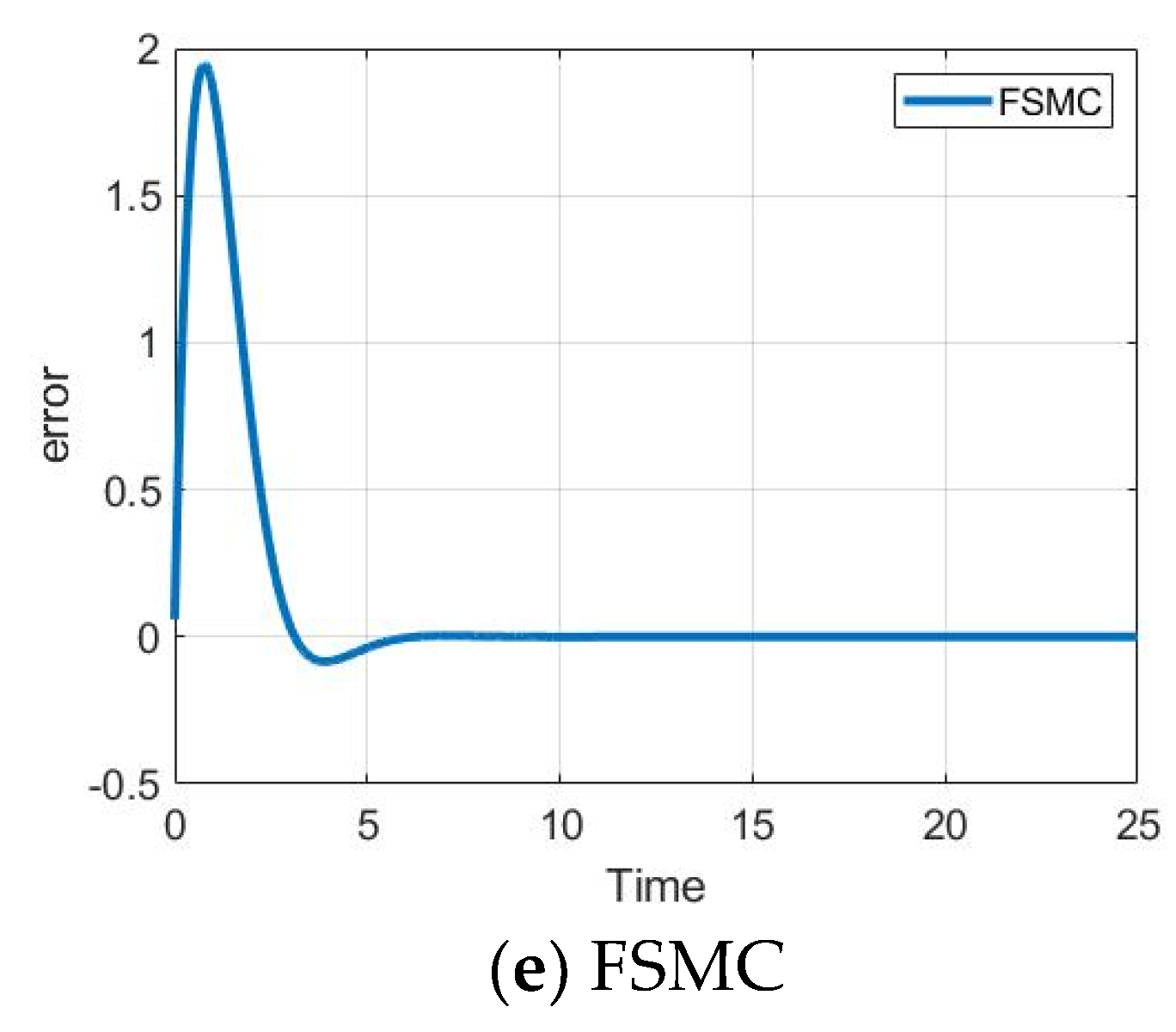
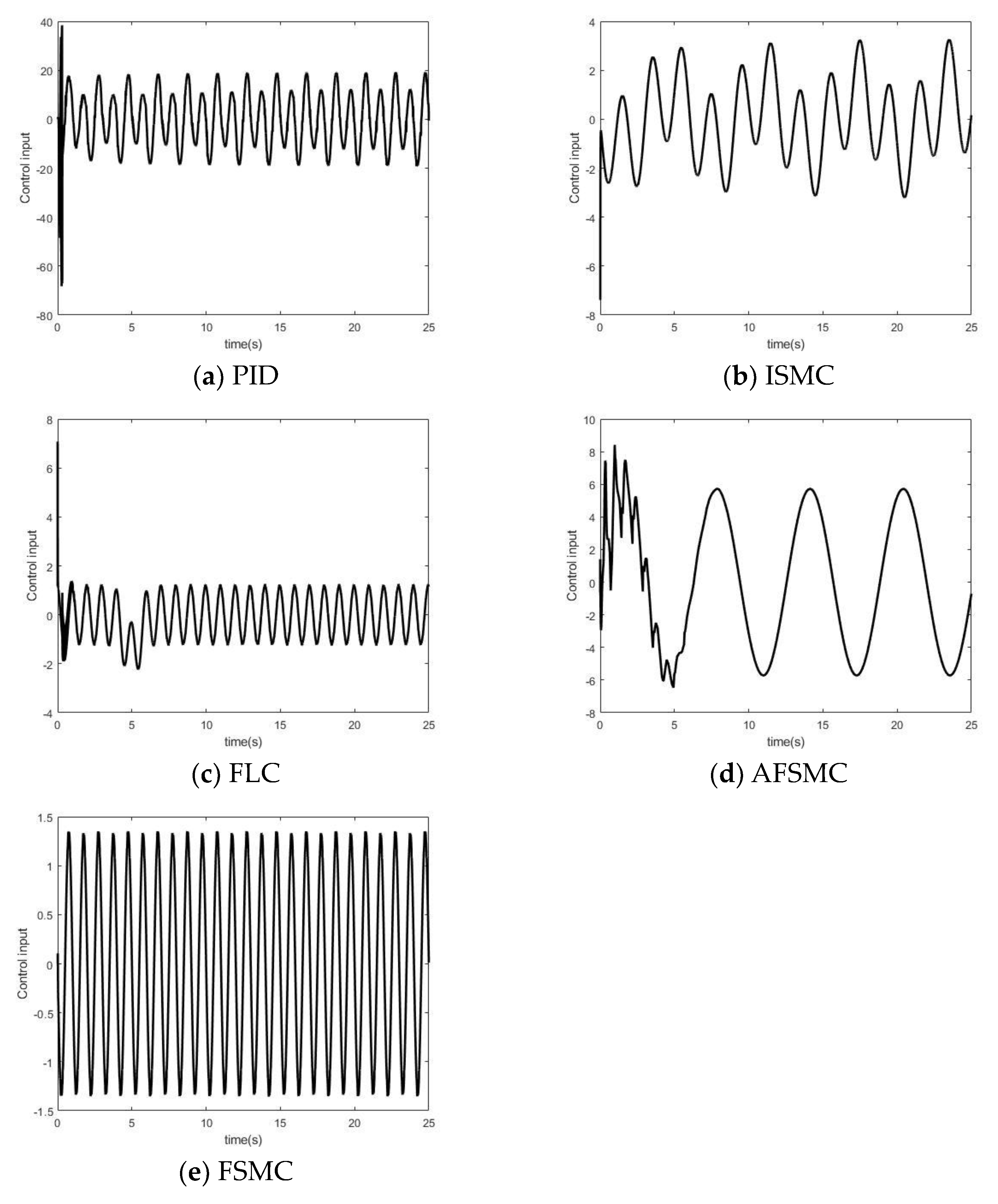
4.4. Simulation Analysis
- (1)
- PID controller
- (2)
- ISMC controller
- (3)
- FLC controller
- (4)
- FSMC controller
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ge, S.R.; Zhang, F.; Wang, S.B.; Wang, Z.B. Digital twin for smart coal mining workface: Technological frame and construction. J. China Coal Soc. 2020, 45, 1925–1936. [Google Scholar]
- Wang, G.F.; Liu, F.; Meng, X.J. Research and practice on intelligent coal mine construction (primary satge). Coal Sci. Technol. 2019, 47, 1–36. [Google Scholar]
- Zhang, C.; Wang, P.; Wang, E.; Chen, D.; Li, C. Characteristics of coal resources in China and statistical analysis and preventive measures for coal mine accidents. Int. J. Coal Sci. Technol. 2023, 10, 22. [Google Scholar] [CrossRef] [PubMed]
- Tao, F.; Zhang, M.; Liu, L.S.; Nee, N.Y.C. Digital twin driven prognostics and health management for complex equipment. Cirp Ann. 2018, 67, 169–172. [Google Scholar] [CrossRef]
- Xiang, F.; Zhou, S.; Zuo, Y.; Tao, F. Digital Twin Driven End-Face Defect Control Method for Hot-Rolled Coil With Cloud-Edge Collaboration. IEEE Trans. Ind. Inform. 2023, 19, 1674–1682. [Google Scholar] [CrossRef]
- Guo, Y.N.; Yang, F.; Ge, S.R.; Huang, Y.; You, X.S. Novel Knowledge-driven Active Management and Control Scheme of Smart Coal Mining Face with Digital Twin. J. China Coal Soc. 2023, 48, 334–344. [Google Scholar]
- Yang, T.M.; Xiong, S.B. Neural network based online self-learning adaptive PID control for automatic ranging cutting height of shearer. Proc. Int. Conf. Mach. Learn. Cybern. 2002, 2, 857–859. [Google Scholar]
- Liu, C.S.; Yang, Q.; Li, C.H. Simulation of shearer drum cutting with memory program controlling by fuzzy control. J. China Coal Soc. 2008, 7, 822–825. [Google Scholar]
- Ruan, J.X.; Liu, X.N.; Zhao, L.J. Study on the Height Adjusting Control System of Shearer Based on Virtual Simulation Technology. In Proceedings of the International Conference on Control Engineering and Automation, Chongqing, China, 29–30 November 2014. [Google Scholar]
- Li, W.; Fan, Q.G.; Wang, Y.Q. Adaptive height adjusting strategy research of shearer cutting drum. Acta Montan. Slovaca 2011, 16, 114–122. [Google Scholar]
- Wang, W.B.; Wang, S.Q.; Zhao, S.F.; Lu, Z.X.; He, H.T. Novel intelligent adjustment height method of Shearer drum based on adaptive fuzzy reasoning Petri net. J. Intell. Fuzzy Syst. 2022, 42, 1767–1781. [Google Scholar] [CrossRef]
- Wang, Y.D.; Zhao, L.J.; Zhang, M.C. Research on self-adaptive height adjustment control strategy of shearer. J. China Coal Soc. 2022, 47, 3505–3522. [Google Scholar]
- Zhang, Q.; Chen, H.; Zhu, Y.G.; Wang, J.Y.; Zhou, C.Z. Digital Twin Based on 3D Visualization and Computer Image Recognition Technology in Coal Preparation Plant. J. Phys. Conf. Ser. 2021, 2083, 042068. [Google Scholar] [CrossRef]
- Zhang, H.; Qi, Q.L.; Tao, F. A consistency evaluation method for digital twin models. J. Manuf. Syst. 2022, 65, 158–168. [Google Scholar] [CrossRef]
- Li, X.H.; Hu, Y.T.; Chi, Q.D.; Bai, S.W. Constant Power Speed-adjusting of Shearer Cutting Motor by Single Neuron Self-adaptive PID Controlling. Appl. Mech. Mater. 2012, 190, 856–859. [Google Scholar] [CrossRef]
- Ding, F.; Li, B.B.; Zhang, H.N. Cutting Constant Power Speed-Adjusting Control System of Electrical Haulage Shearer Based on Rbf Neural Network Pid Control; CNAI: Beijing, China, 2018. [Google Scholar]
- Tan, C.; Xu, R.; Wang, Z.B.; Si, L.; Liu, X.H. An Improved Genetic Fuzzy Logic Control Method to Reduce the Enlargement of Coal Floor Deformation in Shearer Memory Cutting Process. Comput. Intell. Neurosci. 2016, 2016, 3973627. [Google Scholar] [CrossRef]
- Liu, Y.G.; Hou, L.L.; Qin, D.T.; Zhang, Y. Self-adaptive control of shearer based on cutting resistance recognition. Int. J. Adv. Manuf. Technol. 2018, 94, 3553–3561. [Google Scholar] [CrossRef]
- Rezvani, S.; Kim, C.-J.; Park, S.S.; Lee, J. Simultaneous Clamping and Cutting Force Measurements with Built-In Sensors. Sensors 2020, 20, 3736. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, Y.N.; Gong, D.W.; Zhu, S. Hybrid extended state observer-based integral sliding mode control of the propulsion for a hydraulic roofbolter. Control Eng. Pract. 2022, 126, 105260. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Y.; Tian, Y.; Christov, N. Fuzzy sliding mode based active disturbance rejection control for active suspension system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 449–457. [Google Scholar] [CrossRef]
- Yoav, V.; Stephen, J.E. The use of digital twins to remotely update feedback controllers for the motion control of nonlinear dynamic systems. Mech. Syst. Signal Process. 2023, 185, 109770. [Google Scholar]
- Yang, Y.; Fan, H.; Ma, P. Research on dynamic characteristics for longwall shearer cutting transmission system with varying cutting speed. Int. J. Precis. Eng. Manuf. 2017, 18, 1131–1138. [Google Scholar] [CrossRef]

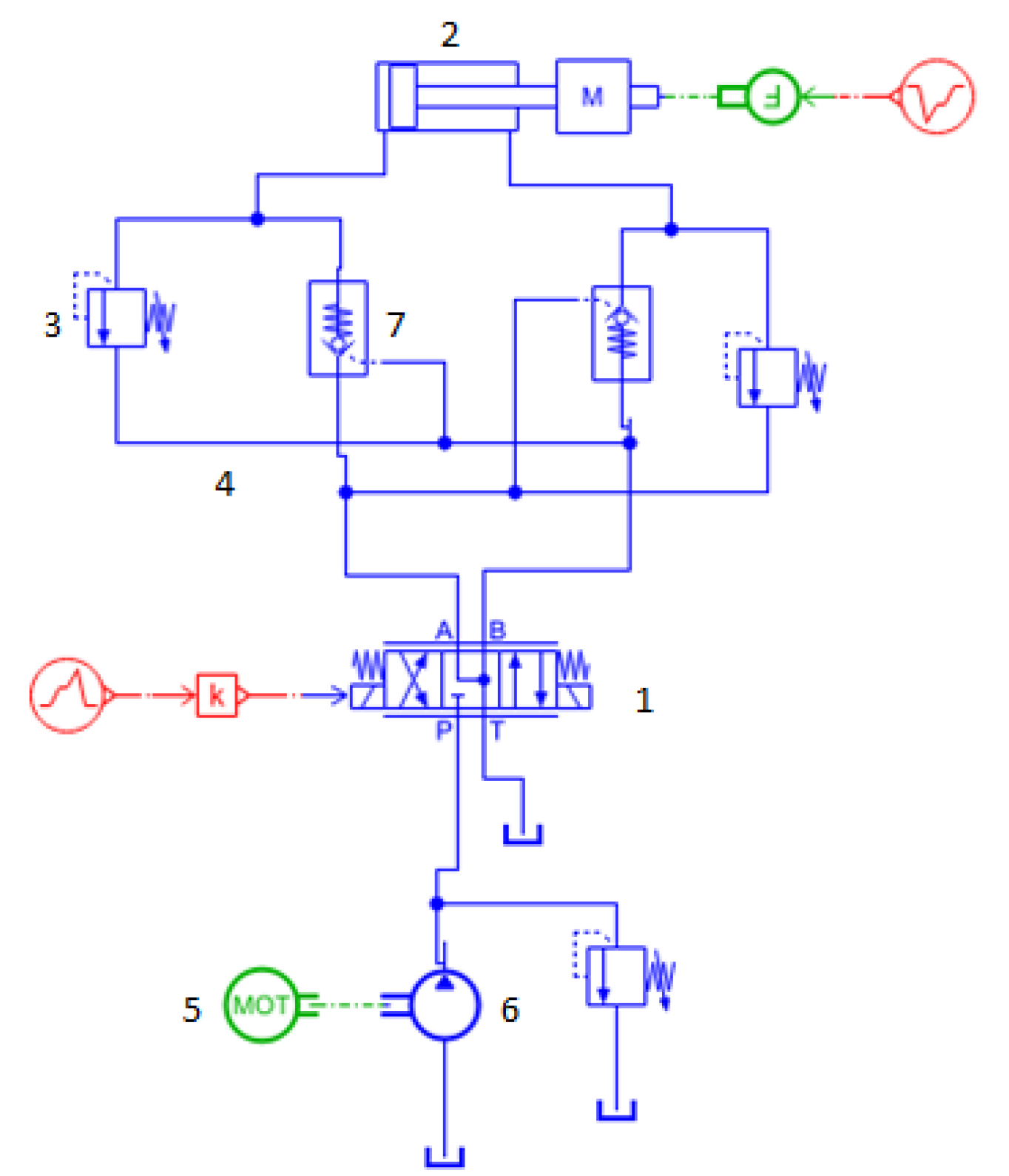
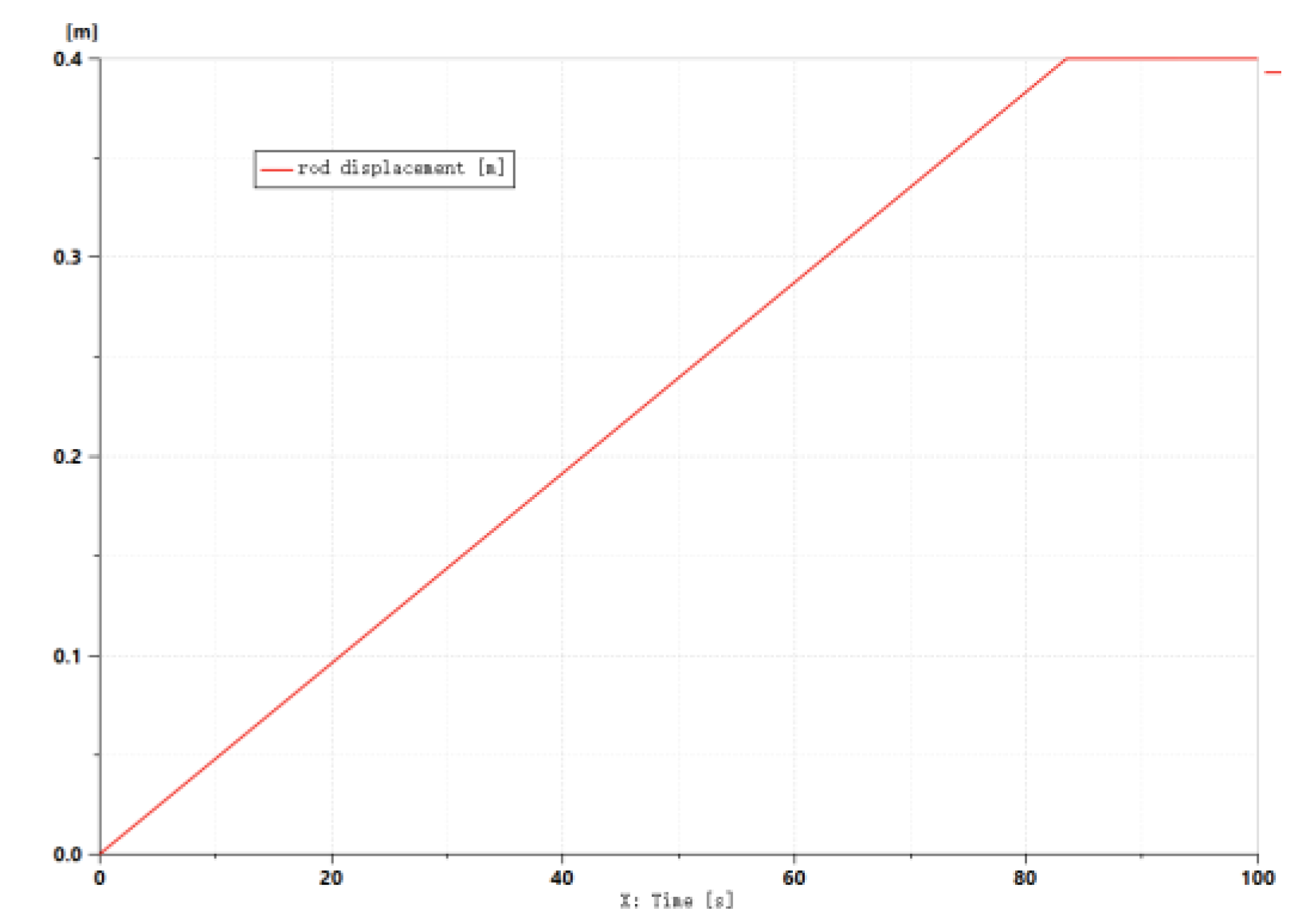
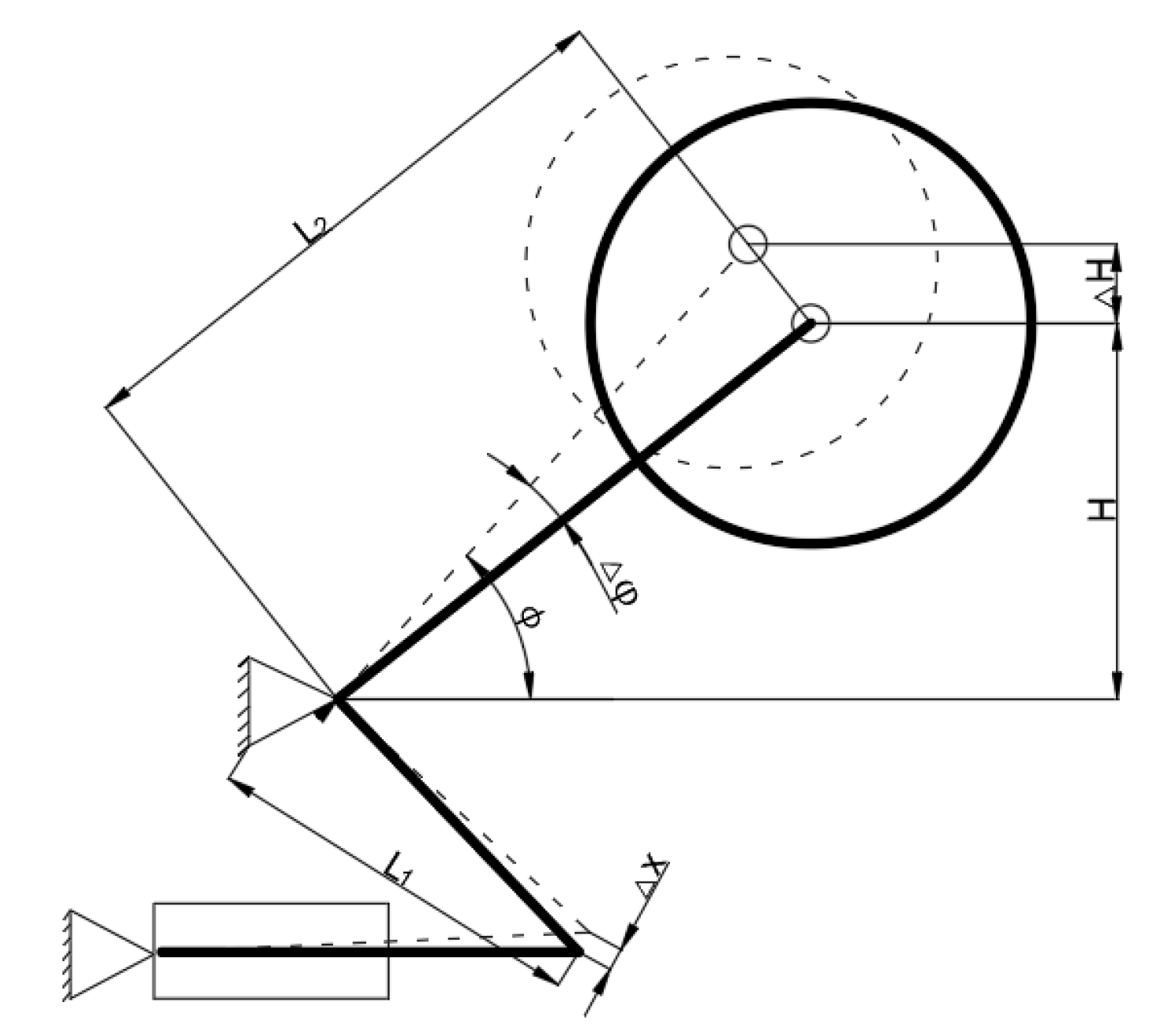
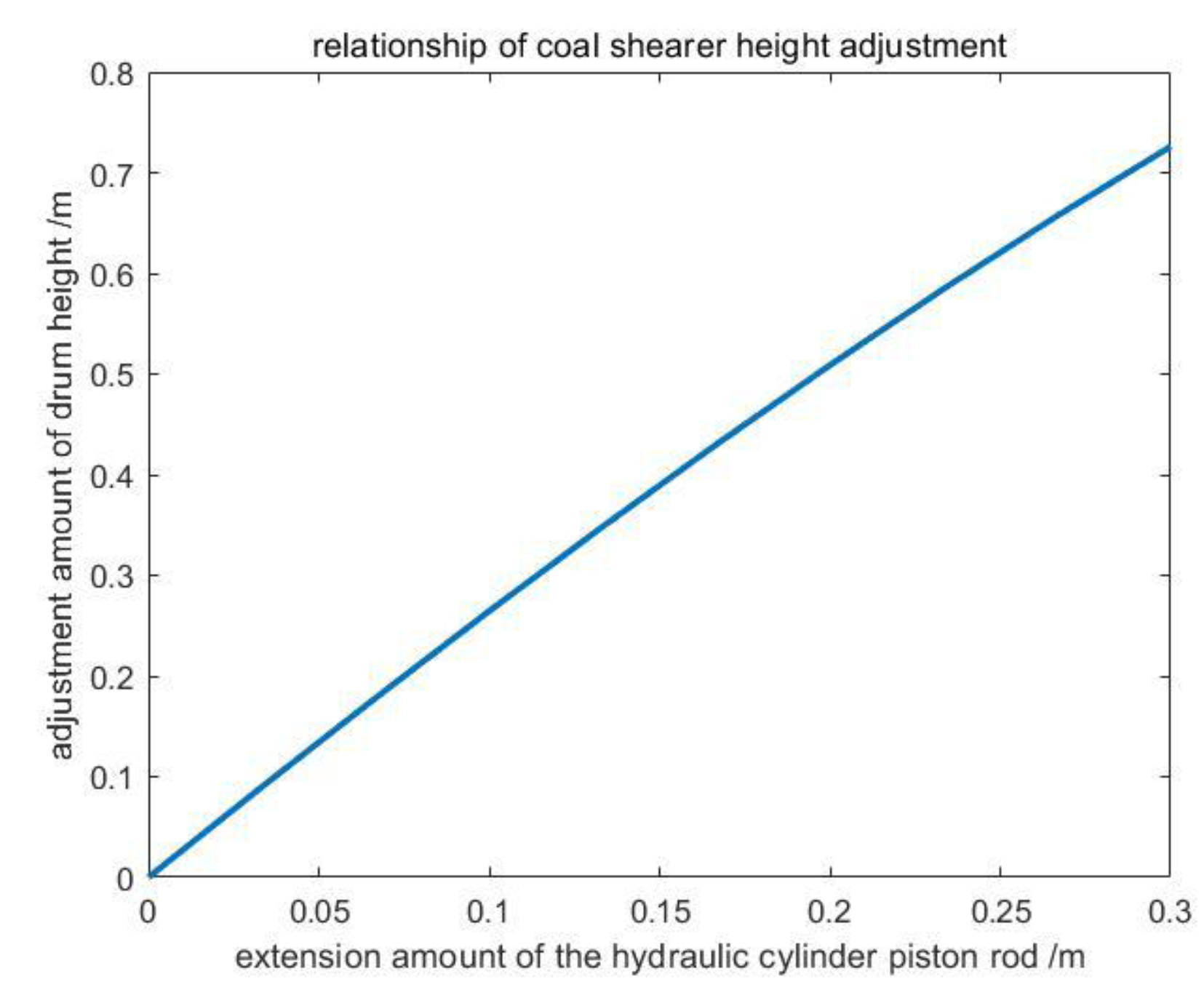


| Parameters | Label | Parameters | Label |
|---|---|---|---|
| Flow rate of the rodless chamber | Q1 | Flow rate of the rod chamber | Q2 |
| Effective working area of the rodless chamber | A1 | Effective working area of the rod chamber | A2 |
| Total fluid volume of the rodless chamber | V1 | Total fluid volume of the rod chamber | V2 |
| Comprehensive internal leakage coefficient | C1 | External leakage coefficient | C2 |
| Pressure in the rodless chamber | P1 | Pressure in the rod chamber | P2 |
| Piston displacement of | x | Bulk modulus of elasticity of the working fluid | |
| Mass | m | Viscosity coefficient of moving parts | B |
| External disturbance force acting | Fz | Oil pressure | Ps |
| Flow coefficient | Cd | Area of the electro-hydraulic proportional directional valve | W |
| Density of hydraulic oil | Hydraulic pump pressure | Pf |
| Parameter (Unit) | Value | Parameter (Unit) | Value |
|---|---|---|---|
| M (kg) | 2.2 | (N/m2) | |
| (m2) | 0.003 | C1 | 0.2 |
| B | 0.6 | Cd | 0.7 |
| W (m2) | pf | 0.35 | |
| (kg/m3) | 860 | (mm2/s) | 32 |
| I (m) | 1.2 | Kb (m2/s) |
| Control Methods | Steady-State Error | Settling Time/s | Maximum Absolute Control Input |
|---|---|---|---|
| PID | 0.161 | 6.12 | 39.14 |
| ISMC | 0.256 | 3.49 | 3.57 |
| FLC | 0.026 | 6.31 | 1.87 |
| AFSMC | 0.024 | 1.74 | 8.43 |
| FSMC | 0.029 | 5.07 | 1.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, X.; Guo, Y.; Miao, B.; Ge, S. A Digital Twin-Based Adaptive Height Control for a Shearer. Machines 2024, 12, 460. https://doi.org/10.3390/machines12070460
You X, Guo Y, Miao B, Ge S. A Digital Twin-Based Adaptive Height Control for a Shearer. Machines. 2024; 12(7):460. https://doi.org/10.3390/machines12070460
Chicago/Turabian StyleYou, Xiusong, Yinan Guo, Bing Miao, and Shirong Ge. 2024. "A Digital Twin-Based Adaptive Height Control for a Shearer" Machines 12, no. 7: 460. https://doi.org/10.3390/machines12070460
APA StyleYou, X., Guo, Y., Miao, B., & Ge, S. (2024). A Digital Twin-Based Adaptive Height Control for a Shearer. Machines, 12(7), 460. https://doi.org/10.3390/machines12070460






