Fault-Tolerant Control Study of Four-Wheel Independent Drive Electric Vehicles Based on Drive Actuator Faults
Abstract
1. Introduction
2. Vehicle Dynamic Model
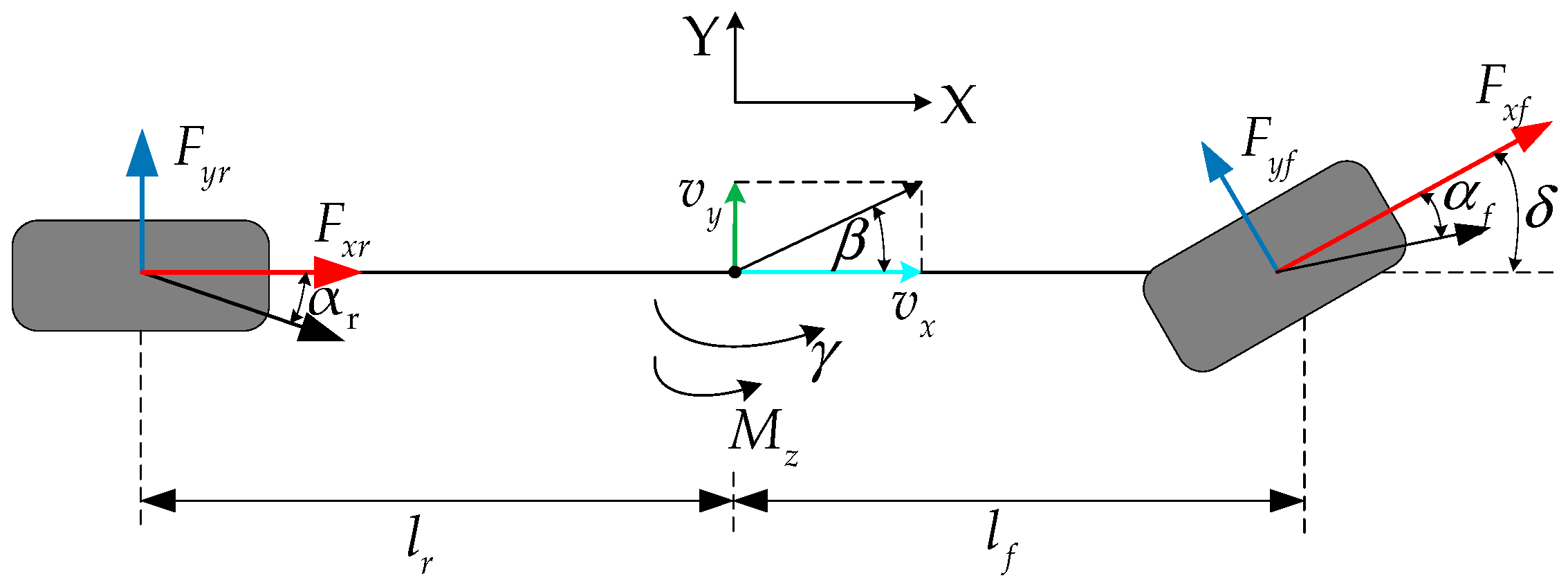
2.1. Two-Degree-of-Freedom Vehicle Dynamics Model
2.2. Tracking Model
2.3. Vehicle Expected Yaw Speed Reference Model
2.4. Vertical Load Dynamics Model of the Wheel
3. Drive Actuator Fault Model
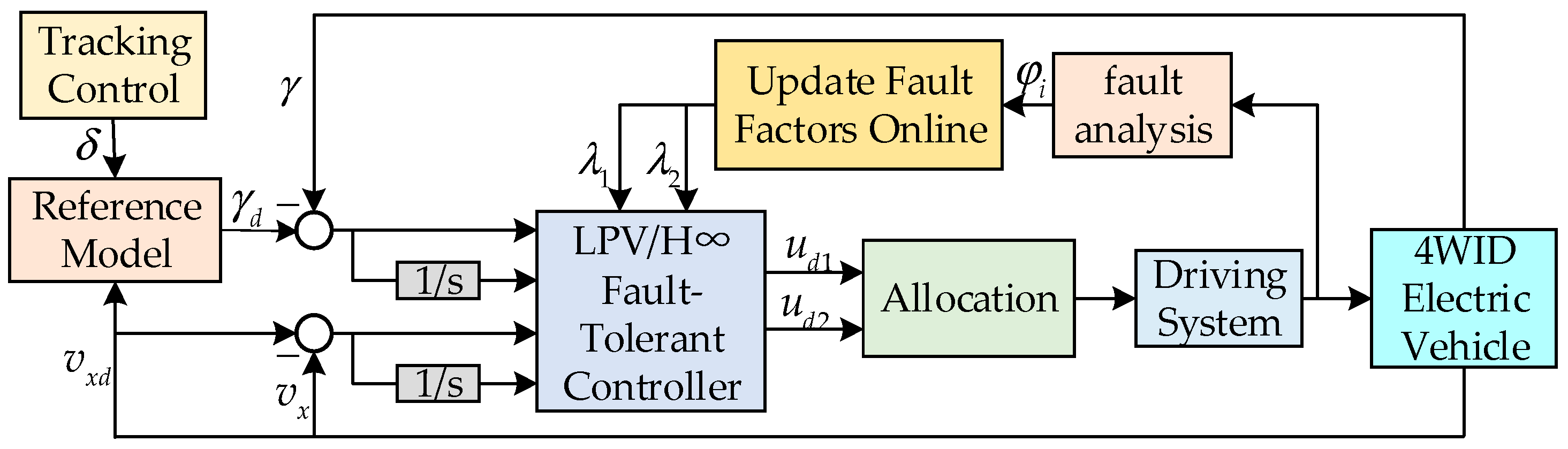
4. Fault-Tolerant Controller Design
4.1. LPV Model
4.2. LPV/H∞ Output Feedback Fault-Tolerant Controller Design
4.3. Control Rate Solving
4.4. Driver Distribution Scheme
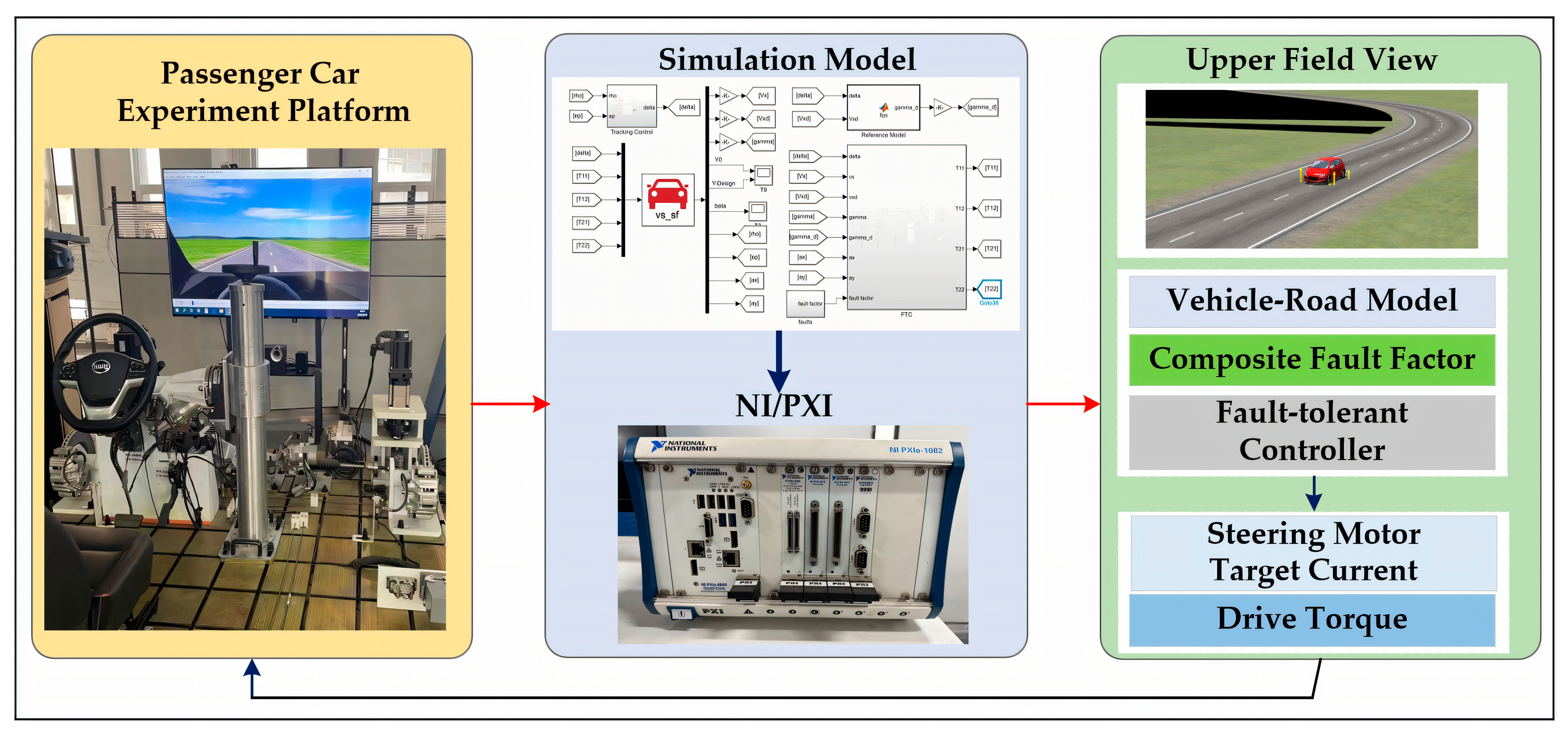
5. Co-Simulation and HIL Experiments
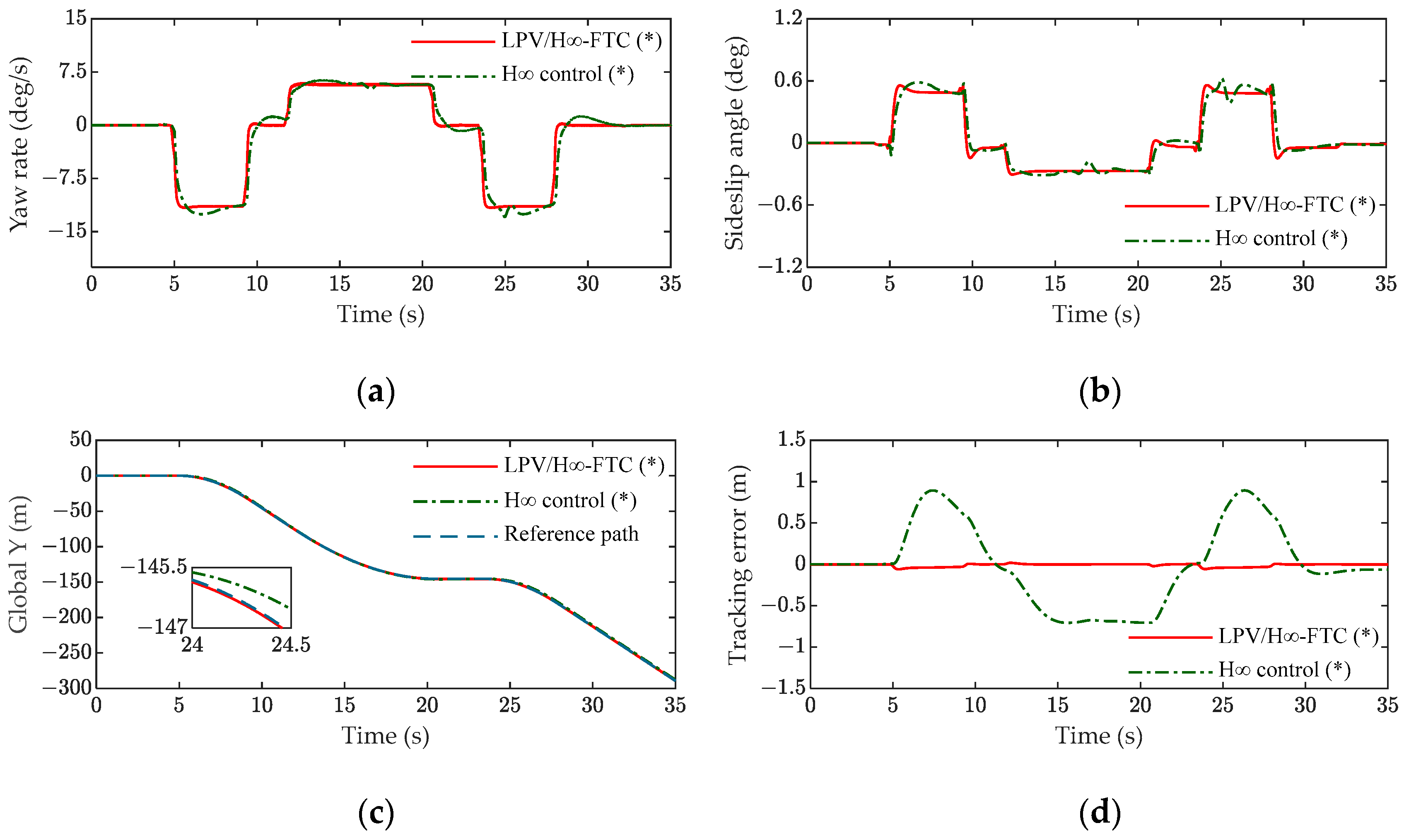
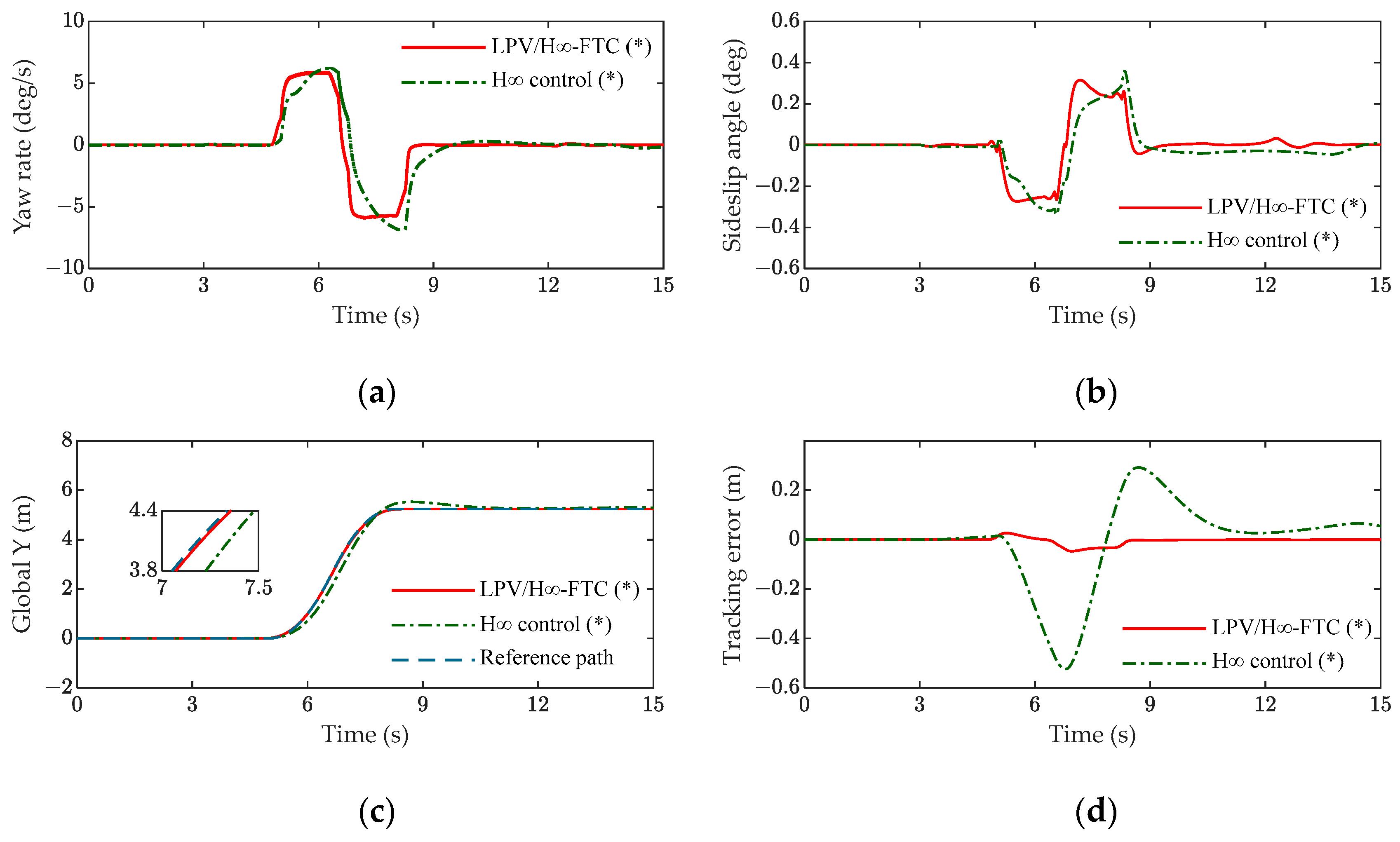
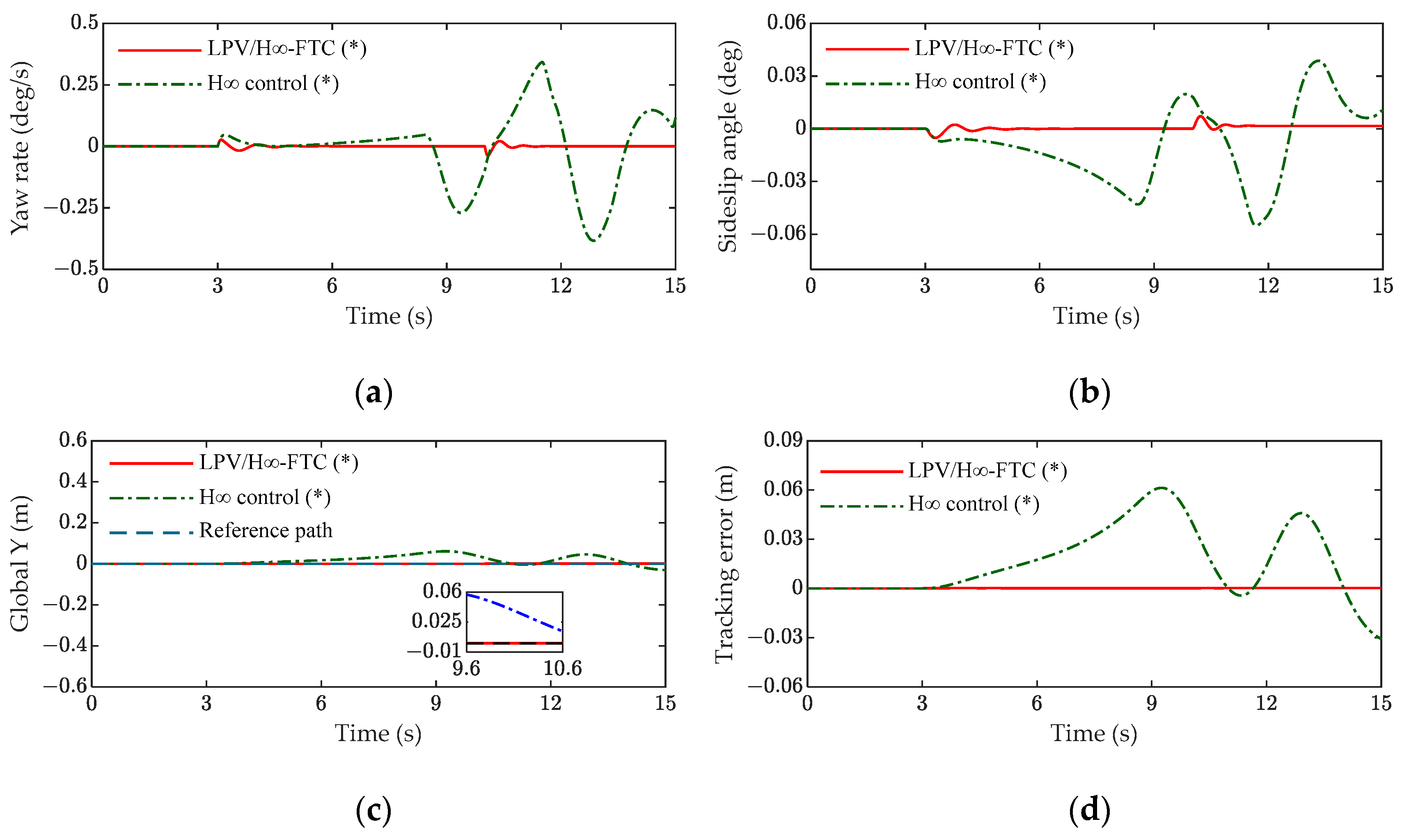
5.1. Analysis of Simulation Results
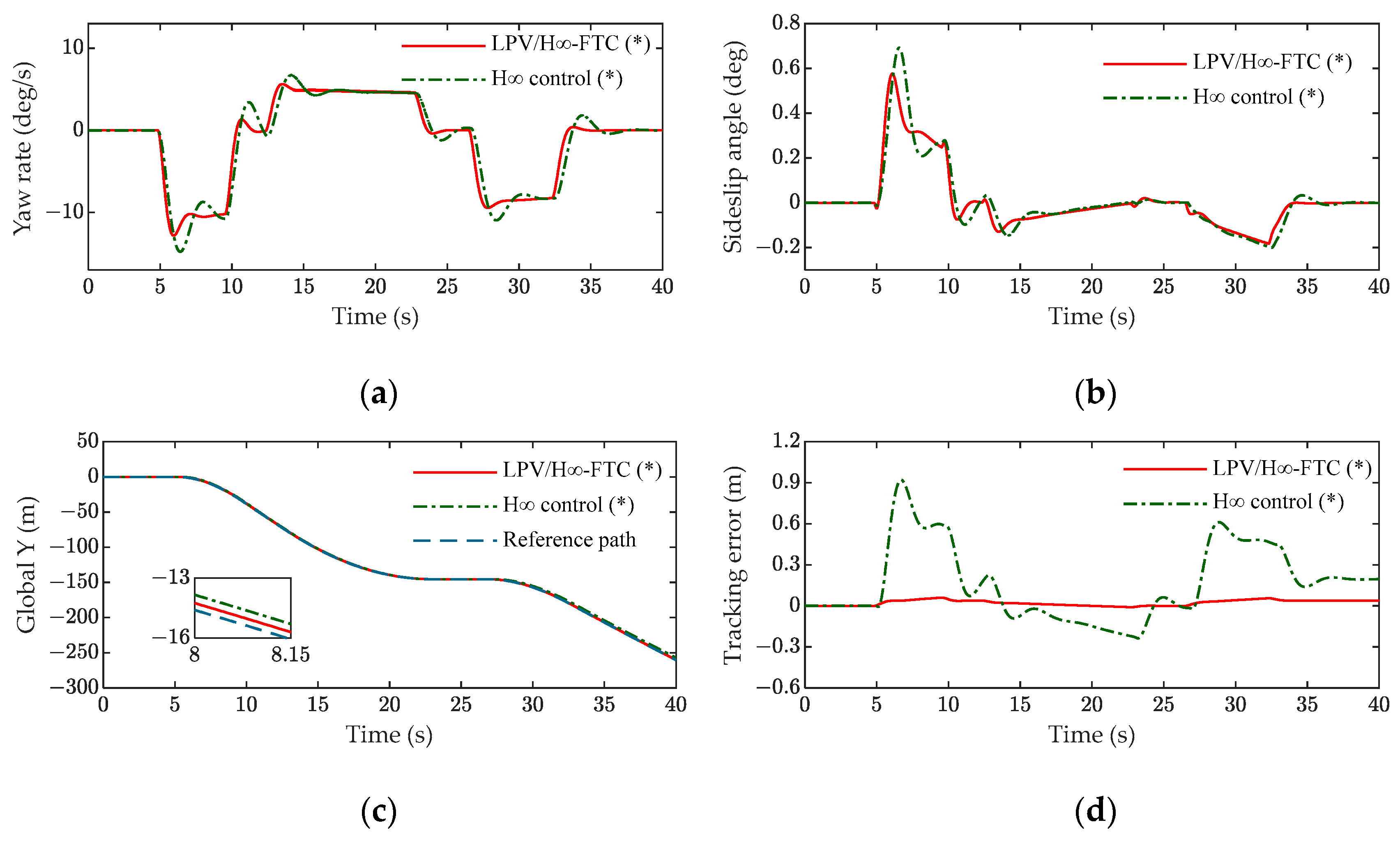
5.2. Analysis of HIL Experiment Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barari, A.; Afshari, S.S.; Liang, X. Coordinated control for path-following of an autonomous four in-wheel motor drive electric vehicle. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 6335–6346. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Li, C.; Jing, H.; An, W.; Qin, J. Integrated control for path tracking and stability based on the model predictive control for four-wheel independently driven electric vehicles. Machines 2022, 10, 859. [Google Scholar] [CrossRef]
- Li, Z.; Jiao, X.; Zhang, T. Robust H∞ Output Feedback Trajectory Tracking Control for Steer-by-Wire Four-Wheel Independent Actuated Electric Vehicles. World Electr. Veh. J. 2023, 14, 147. [Google Scholar] [CrossRef]
- Baldini, A.; Felicetti, R.; Freddi, A.; Longhi, S.; Monteriù, A. Actuator fault-tolerant control architecture for multirotor vehicles in presence of disturbances. J. Intell. Robot. Syst. 2020, 99, 859–874. [Google Scholar] [CrossRef]
- You, Z. Fault Tolerant Control Method of Power System of Tram Based on PLC. Jordan J. Mech. Ind. Eng. 2021, 15, 133–142. [Google Scholar]
- Zhu, S.; Li, H.; Wang, G.; Kuang, C.; Chen, H.; Gao, J.; Xie, W. Research on Fault-Tolerant Control of Distributed-Drive Electric Vehicles Based on Fuzzy Fault Diagnosis. Actuators 2023, 12, 246. [Google Scholar] [CrossRef]
- Zhang, B.; Lu, S. Fault-tolerant control for four-wheel independent actuated electric vehicle using feedback linearization and cooperative game theory. Control Eng. Pract. 2020, 101, 104510. [Google Scholar] [CrossRef]
- Liu, Y.; Zong, C.; Zhang, D.; Zheng, H.; Han, X.; Sun, M. Fault-tolerant control approach based on constraint control allocation for 4WIS/4WID vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2281–2295. [Google Scholar] [CrossRef]
- Wu, C.; Sehab, R.; Akrad, A.; Morel, C. Fault diagnosis methods and Fault tolerant control strategies for the electric vehicle powertrains. Energies 2022, 15, 4840. [Google Scholar] [CrossRef]
- Li, H.; Zhang, N.; Wu, G.; Li, Z.; Ding, H.; Jiang, C. Active Fault-Tolerant Control of a Four-Wheel Independent Steering System Based on the Multi-Agent Approach. Electronics 2024, 13, 748. [Google Scholar] [CrossRef]
- Hu, C.; Wei, X.; Ren, Y. Passive fault-tolerant control based on weighted LPV tube-MPC for air-breathing hypersonic vehicles. Int. J. Control Autom. Syst. 2019, 17, 1957–1970. [Google Scholar] [CrossRef]
- El-Bakkouri, J.; Ouadi, H.; Giri, F.; Saad, A. Optimal control for anti-lock braking system: Output feedback adaptive controller design and processor in the loop validation test. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 237, 3465–3477. [Google Scholar] [CrossRef]
- Aljarbouh, A.; Fayaz, M.; Qureshi, M.S.; Boujoudar, Y. Hybrid sliding mode control of full-car semi-active suspension systems. Symmetry 2021, 13, 2442. [Google Scholar] [CrossRef]
- Girovský, P.; Žilková, J.; Kaňuch, J. Optimization of vehicle braking distance using a fuzzy controller. Energies 2020, 13, 3022. [Google Scholar] [CrossRef]
- Liang, J.; Tian, Q.; Feng, J.; Pi, D.; Yin, G. A polytopic model-based robust predictive control scheme for path tracking of autonomous vehicles. IEEE Trans. Intell. Veh. 2023, 9, 3928–3939. [Google Scholar] [CrossRef]
- He, X.; Huang, W.; Lv, C. Trustworthy autonomous driving via defense-aware robust reinforcement learning against worst-case observational perturbations. Transp. Res. Part C Emerg. Technol. 2024, 163, 104632. [Google Scholar] [CrossRef]
- He, X.; Huang, W.; Lv, C. Toward trustworthy decision-making for autonomous vehicles: A robust reinforcement learning approach with safety guarantees. Engineering 2024, 33, 77–89. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhu, J.; Li, Y. Robust control of vehicle multi-target adaptive cruise based on model prediction. Cogn. Comput. Syst. 2020, 2, 254–261. [Google Scholar] [CrossRef]
- Kou, F.; Chen, C.; Xiao, W.; Hu, K. Study on Adaptive Sliding Mode Fault-tolerant Control of 1/4 Vehicle Electromagnetic Suspension. J. Phys.: Conf. Ser. 2023, 2528, 012025. [Google Scholar]
- Zhang, B.; Lu, S.; Zhao, L.; Xiao, K. Fault-tolerant control based on 2D game for independent driving electric vehicle suffering actuator failures. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 3011–3025. [Google Scholar] [CrossRef]
- Yang, K.; Tang, X.; Qin, Y.; Huang, Y.; Wang, H.; Pu, H. Comparative study of trajectory tracking control for automated vehicles via model predictive control and robust H-infinity state feedback control. Chin. J. Mech. Eng. 2021, 34, 1–14. [Google Scholar] [CrossRef]
- Liang, J.; Wang, F.; Feng, J.; Zhao, M.; Fang, R.; Pi, D.; Yin, G. A Hierarchical Control of Independently Driven Electric Vehicles Considering Handling Stability and Energy Conservation. IEEE Trans. Intell. Veh. 2023, 9, 738–751. [Google Scholar] [CrossRef]
- Li, P.; Nguyen, A.T.; Du, H.; Wang, Y.; Zhang, H. Polytopic LPV approaches for intelligent automotive systems: State of the art and future challenges. Mech. Syst. Signal Process. 2021, 161, 107931. [Google Scholar] [CrossRef]
- Long, Y.; Feng, J.; Zhang, R.; Wei, T. H∞ Robust Fault-Tolerant Control for Lateral Stability of Four-wheel independent driving EV. Mech. Sci. Technol. Aerosp. Eng. 2023, 42, 92–98. [Google Scholar]
- Nguyen, M.Q.; Sename, O.; Dugard, L. An LPV fault tolerant control for semi-active suspension-scheduled by fault estimation. IFAC-PapersOnLine 2015, 48, 42–47. [Google Scholar] [CrossRef]
- Tayari, R.; Ben Brahim, A.; Ben Hmida, F.; Sallami, A. Active fault tolerant control design for lpv systems with simultaneous actuator and sensor faults. Math. Probl. Eng. 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Wang, H.; Cui, W.; Lin, S.; Tan, D.; Chen, W. Stability control of in-wheel motor drive vehicle with motor fault. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 3147–3164. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, W.; Wang, Z.; Ding, X. Fault tolerant control based on multi-methods switching for four-wheel-independently-actuated electric vehicles. J. Mech. Eng. 2020, 56, 227–239. [Google Scholar]
- Lee, K.; Lee, M. Fault-tolerant stability control for independent four-wheel drive electric vehicle under actuator fault conditions. IEEE Access 2020, 8, 91368–91378. [Google Scholar] [CrossRef]
- Luo, Y.; Cao, K.; Xie, L.; Li, K. Coordinated fault tolerant control of over-actuated electric vehicles based on optimal tyre force distribution. Int. J. Veh. Des. 2017, 75, 47–74. [Google Scholar] [CrossRef]
- Luo, Y.; Hu, Y.; Jiang, F.; Chen, R.; Wang, Y. Active fault-tolerant control based on multiple input multiple output-model free adaptive control for four wheel independently driven electric vehicle drive system. Appl. Sci. 2019, 9, 276. [Google Scholar] [CrossRef]
- Yao, Y.; Li, E.; Peng, C. Research on the Distribution Strategy of Longitudinal Driving Force of Vehicle Driven by 8× 8 In-wheel Motors. J. Phys. Conf. Ser. 2022, 2181, 012017. [Google Scholar] [CrossRef]
- Huang, X.; Zha, Y.; Lv, X.; Quan, X. Torque Fault-Tolerant Hierarchical Control of 4WID Electric Vehicles Based on Improved MPC and SMC. IEEE Access 2023, 11, 132718–132734. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.; Ding, X.; Li, S.; Wang, Z. Fault-tolerant control for intelligent electrified vehicles against front wheel steering angle sensor faults during trajectory tracking. IEEE Access 2021, 9, 65174–65186. [Google Scholar] [CrossRef]
- Liu, X.; Pang, H.; Shang, Y.; Wu, W. Optimal design of fault-tolerant controller for an electric power steering system with sensor failures using genetic algorithm. Shock Vib. 2018, 2018, 1801589. [Google Scholar] [CrossRef]
- Khaneghah, M.Z.; Alzayed, M.; Chaoui, H. Fault detection and diagnosis of the electric motor drive and battery system of electric vehicles. Machines 2023, 11, 713. [Google Scholar] [CrossRef]
- Şimşir, M.; Bayır, R.; Uyaroğlu, Y. Real-time monitoring and fault diagnosis of a low power hub motor using feedforward neural network. Comput. Intell. Neurosci. 2015, 2016, 36. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Liang, X.; Wang, Q.; Zhao, L.; Wang, X. Extension coordinated control of four wheel independent drive electric vehicles by AFS and DYC. Control Eng. Pract. 2020, 101, 104504. [Google Scholar] [CrossRef]
- Liang, J.; Feng, J.; Fang, Z.; Lu, Y.; Yin, G.; Mao, X.; Wu, J.; Wang, F. An energy-oriented torque-vector control framework for distributed drive electric vehicles. IEEE Trans. Transp. Electrif. 2023, 9, 4014–4031. [Google Scholar] [CrossRef]
- Nah, J.; Yim, S. Vehicle stability control with four-wheel independent braking, drive and steering on in-wheel motor-driven electric vehicles. Electronics 2020, 9, 1934. [Google Scholar] [CrossRef]
- He, X.; Liu, Y.; Yang, K.; Wu, J.; Ji, X. Robust coordination control of AFS and ARS for autonomous vehicle path tracking and stability. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation, Changchun, China, 5–8 August 2018; pp. 924–929. [Google Scholar]
- Lin, J.; Zou, T.; Su, L.; Zhang, F.; Zhang, Y. Optimal Coordinated Control of Active Front Steering and Direct Yaw Moment for Distributed Drive Electric Bus. Machines 2023, 11, 640. [Google Scholar] [CrossRef]
- Apkarian, P.; Gahinet, P.; Becker, G. Self-scheduled H∞ control of linear parameter-varying systems: A design example. Automatica 1995, 31, 1251–1261. [Google Scholar] [CrossRef]
- Scherer, C.; Gahinet, P.; Chilali, M. Multiobjective output-feedback control via LMI optimization. IEEE Trans. Autom. Control 1997, 42, 896–911. [Google Scholar] [CrossRef]


| Parameter | Value | Units | Parameter | Value | Units |
|---|---|---|---|---|---|
| m | 1274 | kg | 1.523 | m | |
| Ca | 0.3 | Null | 0.375 | m | |
| 120,000 | N/rad | 1.739 | m | ||
| 100,000 | N/rad | 0.303 | m | ||
| 1.016 | m | 1523 | kg·m2 |
| Experimental Scene | Control Strategy | Fault Status | Performance Comparison | ||
|---|---|---|---|---|---|
| S-turn | Status 2, 4 | 12.8166 deg/s | 0.5765° | 0.0603 m | |
| Control | Status 2, 4 | 14.7888 deg/s | 0.6926° | 0.9205 m | |
| Change lanes | Status 3 4 | 5.9135 deg/s | 0.3150° | 0.0471 m | |
| Control | Status 3, 4 | 6.8536 deg/s | 0.3585° | 0.5239 m | |
| Straight line | Status 3 | 0.0372 deg/s | 0.0071° | 0.0002 m | |
| Control | Status 3 | 0.3837 deg/s | 0.0553° | 0.0613 m | |
| Experimental Scene | Control Strategy | Fault Status | Performance Comparison | ||
|---|---|---|---|---|---|
| S-turn | Status 2, 4 | 11.6386 deg/s | 0.5594° | 0.0589 m | |
| Control | Status 2, 4 | 12.9392 deg/s | 0.6256° | 0.8937 m | |
| Change lanes | Status 3 4 | 6.9521 deg/s | 0.2748° | 0.1663 m | |
| Control | Status 3 4 | 9.5229 deg/s | 0.3414° | 0.5013 m | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Bao, C.; Cao, Q.; Xu, F.; Miao, X.; Wu, J. Fault-Tolerant Control Study of Four-Wheel Independent Drive Electric Vehicles Based on Drive Actuator Faults. Machines 2024, 12, 450. https://doi.org/10.3390/machines12070450
Guo M, Bao C, Cao Q, Xu F, Miao X, Wu J. Fault-Tolerant Control Study of Four-Wheel Independent Drive Electric Vehicles Based on Drive Actuator Faults. Machines. 2024; 12(7):450. https://doi.org/10.3390/machines12070450
Chicago/Turabian StyleGuo, Mingjie, Chunjiang Bao, Qinghua Cao, Fuxing Xu, Xinhong Miao, and Jian Wu. 2024. "Fault-Tolerant Control Study of Four-Wheel Independent Drive Electric Vehicles Based on Drive Actuator Faults" Machines 12, no. 7: 450. https://doi.org/10.3390/machines12070450
APA StyleGuo, M., Bao, C., Cao, Q., Xu, F., Miao, X., & Wu, J. (2024). Fault-Tolerant Control Study of Four-Wheel Independent Drive Electric Vehicles Based on Drive Actuator Faults. Machines, 12(7), 450. https://doi.org/10.3390/machines12070450






