S-Graph-Based Reactive Scheduling with Unexpected Arrivals of New Orders

Abstract

Manufacturing processes are often disrupted by unexpected events, such as machine breakdowns, raw material shortages, and the arrival of new orders. Effectively managing these uncertainties is crucial for maintaining the feasibility and optimality of the production system. The efficiency of a manufacturing system is heavily dependent on the optimality of its scheduling plan. In this study, we present a reactive scheduling approach based on the S-graph framework. The proposed method is specifically designed to handle the arrival of new jobs and generate schedules with the shortest makespan, i.e., the minimum total completion time. Whenever a new order is received, the method dynamically adjusts the production plan through rescheduling. Three distinct scheduling policies are identified that determine which tasks require scheduling or rescheduling and which tasks should remain unchanged in their schedules. To evaluate the effectiveness of the algorithm, we solve several examples from the literature and analyze the results. The findings demonstrate the efficiency and efficacy of the proposed approach. The ability to accommodate new job arrivals and generate schedules with a minimized makespan highlights the practical relevance and benefits of the S-graph-based reactive scheduling method.

1. Introduction

The source of the idea for this study originates from the waste recycling industry, where unexpected new orders to be processed can disrupt the existing processing schedule. The research aims to develop a solution that enables efficient reactive scheduling, allowing the facility to adapt to new orders without significantly altering the original plan. By optimizing the processing sequence and minimizing the impact of new orders on the overall processing time, this study can help waste recycling facilities to improve their responsiveness to changing demands and enhance their overall efficiency.

Scheduling problems are ubiquitous in various sectors, including public transportation, CPU time allocation, and manufacturing, where they play a crucial role in optimizing resource allocation and time management. In the context of a circular economy and the fourth industrial revolution, production scheduling takes on a new significance, as it enables the efficient use of resources, reduction in waste, and adaptation to changing market demands.

The primary objective of production scheduling is to allocate available production resources, such as raw materials, equipment units, facilities, and personnel, to tasks and define their sequential and timing parameters. This allocation process is critical in minimizing waste, reducing energy consumption, and promoting the reuse and recycling of materials, all of which are essential principles of a circular economy [1].

Traditionally, scheduling problems were deterministic, assuming that all parameters were known in advance and remained unchanged. However, the increasing complexity of modern manufacturing systems and the need for adaptability in a circular economy necessitate the development of dynamic scheduling methods that can respond to uncertainties and changes in real time [2].

The first scheduling problem to incorporate uncertainty was published in 1957 [3], introducing the concepts of static and dynamic scheduling. Static scheduling, where all data are fixed and unchanging, is insufficient for industrial applications, as it cannot accommodate the various uncertainties that arise in production, such as machine breakdowns, changes in raw material availability, or the arrival of new orders.

Dynamic scheduling, on the other hand, allows for the modification of schedules in response to unexpected events, enabling manufacturers to adapt to changing circumstances [4,5]. Uncertain events can be classified into workpiece-related, machine-related, process-related, and other events [6,7]. This paper focuses on the unexpected arrivals of new orders, a critical aspect of workpiece-related events, and proposes a dynamic scheduling approach that can effectively manage these uncertainties in a circular economy and Industry 4.0 context.

Numerous methods have emerged to tackle batch process scheduling, each differing in various aspects and capable of addressing diverse industrial problems [8]. Many of these methods utilize mixed integer linear programming (MILP) formulations, which offer solutions to a broad range of scheduling problems. In contrast, graph-based methods have been introduced specifically for a special class of batch scheduling problems. These approaches successfully circumvent the modeling complexities associated with MILP formulations and provide the assurance of global optimality while maintaining favorable computational requirements. Furthermore, MILP-based approaches strive to reduce model size and enhance formalizations, whereas graph-theoretical approaches continue to expand their applicability to a broader range of scheduling problems [9,10].

In this study, we addressed dynamic scheduling challenges utilizing the S-graph framework [11], originally devised for static problem resolution. The branch-and-bound algorithm integrated within the S-graph framework facilitates the derivation of optimal solutions for these scheduling dilemmas. Given the NP-completeness inherent in scheduling quandaries, substantial computational resources are necessitated, prompting the development of various acceleration techniques over recent decades [12,13]. The efficacy of this approach has been substantiated through its successful application in addressing significant industrial scheduling challenges, such as paint production scheduling [14]. Consequently, the potential of the S-graph framework in addressing dynamic scheduling problems in a circular economy and Industry 4.0 context warrants further investigation. The reactive approach can significantly contribute to the circular economy and Industry 4.0 by integrating the principles of a circular economy with the technological advancements of Industry 4.0 [15]. By leveraging real-time data, data analytics, and adaptability, Industry 4.0 technologies can support the circular economy by enhancing its responsiveness to unexpected events [16,17]. This integration enables the circular economy to effectively address disruptions by dynamically adjusting current scheduling plans without altering existing plans and decisions.

1.1. Literature Review

The transition to a circular economy and the adoption of Industry 4.0 technologies face several challenges. One key challenge is the lack of data on waste, such as its location, volume, and composition, which hinders the substitution of primary materials with secondary ones [18,19]. Another challenge is the need for digitalization and semantic interoperability, which possess high driving power and low dependence, requiring keen attention to improve resource efficiency and sustainability. Additionally, the lack of cyber–physical system standards and specifications, sensor technology, and design challenges are also influential Industry 4.0 barriers for achieving circular economy [20]. Overcoming these challenges requires rethinking and redesigning business models and current routines [21], as well as integrating Industry 4.0 technologies into manufacturing and business strategies to lead to a cleaner and more productive industrial sector [22,23].

Within the broad areas of the circular economy and Industry 4.0, addressing uncertain scheduling issues is crucial for maintaining the feasibility and optimality of production systems. Several approaches have been developed to provide suitable solutions depending on the needs, considerations, and types of uncertainties [24]. These methods can be classified into four basic classes:

• Proactive approach: By modeling emerging unexpected events and uncertainties [25,26], different scenarios are solved [27]. This method can be seen as a form of capacity shortage scheduling, where robustness is sought to be maintained. In a circular economy, proactive approaches help to anticipate and mitigate disruptions, ensuring the efficient use of resources and minimizing waste.
• Reactive approach: During production, the schedule is changed in response to unexpected events. It is characterized by simple rules; therefore, the need for computation is low. Due to the use of local information, the new schedule may not provide a globally optimal solution. Reactive approaches in Industry 4.0 enable real-time adaptation to changing circumstances, allowing manufacturers to quickly respond to disruptions and maintain production efficiency.
• Proactive–reactive approach: As a first step, a timetable is created that takes into account future disruptions. In addition, reactive steps are used, but fewer modifications are required due to the robustness of the schedule. This hybrid approach combines the benefits of proactive planning and reactive adaptation, providing a balance between resource efficiency and responsiveness in a circular economy.
• Predictive–reactive approach: This method can be divided into two parts. First, an optimal schedule is generated through iterative search processes, typically using a static scheduling method. Second, the schedule changes during execution as a result of unexpected events [28]. For reactive scheduling, most approaches revise only a portion of the original schedule without rescheduling all necessary tasks [29,30]. Predictive–reactive approaches in Industry 4.0 leverage data analytics and machine learning to anticipate disruptions and proactively adapt schedules, while still maintaining the flexibility to react to unforeseen events.

The integration of predictive, predictive–reactive, and reactive mechanisms in scheduling decisions is crucial for achieving energy efficiency in manufacturing systems [31]. These mechanisms enable the calculation of optimal production schedules based on the availability of renewable energy and other factors, while also allowing for real-time adjustments to be made in response to changing circumstances. Predictive mechanisms involve the creation of schedules that are designed to remain unchanged during execution or incorporate slack times to enhance schedule robustness against disruptions. This approach can provide potentially optimal solutions but may be limited by the complexity involved and the inability to fully consider disturbances that cannot be perfectly predicted. Reactive mechanisms, on the other hand, involve making real-time scheduling decisions based on the current system state, without pre-scheduling. This approach can provide quick responses to disturbances, but may be limited by its myopic perspective, which only allows for local optimization. The combination of predictive and reactive mechanisms, known as predictive–reactive approaches, offers a proactive scheduling strategy that can dynamically adjust to disruptions and effectively meet customer requirements. This approach can be particularly beneficial in the context of a circular economy and Industry 4.0, where the efficient use of resources and the minimization of waste are crucial for maintaining sustainability and competitiveness.

The predictive schedule serves as a foundation for efficient production planning, but it is not immune to disruptions [2]. When a disruption occurs, a reactive approach is necessary to adapt the schedule to the new circumstances. Rescheduling is a crucial component of this reactive approach, as it enables the optimal production schedule to be adjusted dynamically and stochastically. This adaptability is essential in the context of a circular economy and Industry 4.0, where disruptions can lead to inefficient resource utilization, increased waste, and delays in meeting customer demands [32]. By incorporating rescheduling into the reactive approach, manufacturers can ensure that their production systems remain agile and responsive to changing circumstances, ultimately enhancing operational efficiency and sustainability.

The adoption of reactive scheduling strategies in circular economy manufacturing systems has been shown to provide significant benefits. Numerical analyses have indicated that reactive scheduling approaches tend to achieve higher profitability for manufacturers compared to anticipatory strategies [33]. The relative advantage of the reactive strategy is influenced by the product return rate and the consumers’ consumption share of remanufactured goods. In circular economy models, where the reuse and recycling of materials are crucial, the ability to effectively manage product returns is a key determinant of operational efficiency and financial performance. Furthermore, the preferability of a scheduling strategy is critically dependent on its impact on product modularity and consumers’ willingness to pay. Reactive scheduling approaches, with their focus on responsiveness and adaptability, have been found to be more beneficial than anticipatory strategies in situations where the product return rate exceeds a certain threshold. This is because companies employing reactive scheduling are better equipped to deal with uncertainties surrounding product returns, enabling them to rapidly adjust their production plans and minimize waste. This agility is a key requirement in circular economy manufacturing, where the efficient use of resources and the minimization of waste are essential for maintaining sustainability and competitiveness.

The selection of the most suitable approach depends on the specific requirements of the manufacturing system, the nature of uncertainties, and the desired balance between robustness and adaptability in a circular economy context. In this regard, each scheduling method has its own advantages and disadvantages that must be carefully considered.

Scheduling in a disruptive environment has a major impact not only on production but also on logistics performance [34]. In the context of a circular economy and Industry 4.0, this impact is amplified, as disruptions can lead to inefficient resource utilization, increased waste, and delays in meeting customer demands. Compliance with customer-specific delivery times is a crucial factor that should be prioritized due to its importance in maintaining customer satisfaction and operational efficiency [35]. For this reason, great emphasis needs to be placed on robust performance.

Robustness, defined as the ability of a schedule to achieve its intended performance despite dynamic disturbances, plays a vital role in ensuring the resilience of manufacturing systems in the face of unexpected events [36]. While predictive scheduling offers potentially optimal solutions, the complexity involved can lead to significant computational demands, limiting its practicality in real-time decision making within dynamic environments. Additionally, disturbances that cannot be perfectly predicted pose challenges in fully incorporating them into predictive scheduling strategies [34].

On the other hand, reactive scheduling provides the advantage of quick responses to disturbances, enabling timely adjustments to the schedule. However, its myopic perspective may limit the optimization to local levels, potentially overlooking broader system-wide efficiencies and opportunities for improvement. Considering the challenges of a circular economy and Industry 4.0, balancing the benefits of predictive and reactive scheduling approaches is crucial for enhancing operational agility, resource efficiency, and sustainability in manufacturing processes [37,38].

The classification of dynamic scheduling approaches into predictive, predictive–reactive, and purely reactive methods is essential for optimizing resource allocation and enhancing operational efficiency [39]. Predictive approaches aim to create schedules that remain unchanged during execution or incorporate slack times to enhance schedule robustness against disruptions. On the other hand, purely reactive approaches make real-time scheduling decisions based on the current system state, without pre-scheduling. However, these two traditional approaches may not fully meet the specific and evolving needs of customers in a rapidly changing manufacturing landscape [40]. In contrast, predictive–reactive approaches offer a proactive scheduling strategy that can dynamically adjust to disruptions and effectively meet customer requirements, aligning with the principles of adaptability and efficiency in circular economy and Industry 4.0 initiatives.

A fundamental requirement for reactive scheduling is an initial schedule that undergoes modification and optimization in response to unexpected events or uncertain parameters. The rescheduling process can occur periodically, either at fixed or variable intervals, or in an event-triggered manner, where adjustments are made in reaction to specific events [41]. Hybrid solutions that combine both periodic and event-driven rescheduling approaches are also being explored to enhance scheduling adaptability and efficiency in dynamic manufacturing environments [42]. Reactive scheduling strategies can be either partial or full, with the latter posing challenges in terms of time and frequency constraints. Heuristic methods, such as genetic algorithms [43,44], particle swarm optimization [45], and proprietary heuristic algorithms [46,47], are widely favored for addressing reactive scheduling challenges. Additionally, mathematical model-based solutions offer alternative approaches to optimizing reactive scheduling processes in the context of sustainable manufacturing practices and advanced industrial technologies [48,49].

Stochastic scheduling, as defined in the scholarly literature, encompasses the management of scheduling problems characterized by inherent uncertainty or the utilization of solution methods tailored to address such uncertainties. A stochastic scheduling model represents an adaptation of deterministic methods, integrating stochastic variables to effectively manage uncertainties. This method quantifies uncertainties using probabilities and is particularly applicable when information regarding uncertainties or their occurrences is accessible. Notably, two prominent types of stochastic models are recognized: the two-stage (multi-stage) stochastic programming (e.q., [50,51,52]) and the chance-constrained programming-based approach (e.g., [53,54]). Stochastic programming stands out as a widely adopted and effective method for resolving scheduling challenges in the presence of uncertainties.

When historical data regarding uncertainty are unavailable and the probability distributions are not known, fuzzy programming offers a viable solution by employing fuzzy numbers in lieu of stochastic variables [55]. These models necessitate intricate integration techniques for continuous probability models while minimizing the need for an extensive array of scenarios. In the realm of fuzzy sets, membership functions are characterized by interval-based values rather than binary, with higher values indicating a greater degree of membership [56]. Fuzzy numbers serve to represent uncertain variables through intervals, and membership functions may deviate from certain constraints, allowing for the quantification of constraint satisfaction. Objective functions are managed through constraints, enabling the definition of expectations. Type-1 fuzzy sets are distinguished by their membership functions based on fuzzy numbers. Additionally, type-2 fuzzy sets incorporate fuzzy membership functions, offering a means to model uncertainties [57]. The resolution of fuzzy models typically involves the application of heuristic methods such as genetic algorithms [58,59,60], particle swarm optimization [61,62], and tabu search [63,64].

Incorporating uncertainty into the model describing the schedule is a primary objective of robust scheduling. This approach aims to mitigate the sensitivity of the schedule to perturbations by minimizing the impact of distributions on performance. Robust optimization encompasses two key aspects: solution robustness and quality robustness [65]. Solution robustness examines the effect of changes in input data, while quality robustness focuses on reducing the deterioration of the objective function due to uncertainty. During the optimization process, not only is the value of the objective function considered, but also the discrepancy between the expected value and the actual value, depending on the environmental conditions.

While numerous studies have focused on the simplified static environment of scheduling problems [66,67], it is essential to address the dynamic aspects that frequently occur in real-world scenarios. These dynamic factors include the arrival of new jobs [68,69], machine breakdowns [70], and rush orders [71]. In the current era of mass customization, factories often experience a continuous influx of new orders, which introduces significant complexity to the scheduling process due to dynamic changes and various resource constraints.

New orders refer to the arrival of new jobs or products that need to be manufactured and delivered. These orders can arrive at any time and their quantities are typically unknown in advance. New orders can be a significant challenge for manufacturing systems because they require the production schedule to be adjusted dynamically to accommodate the new orders while ensuring that existing orders are completed on time [72]. Rush orders, on the other hand, are special orders that require expedited production and delivery [73]. These orders typically have a shorter deadline than regular orders and may require additional resources or overtime to meet the deadline. Rush orders can be particularly challenging for manufacturing systems because they require immediate attention and may disrupt the existing production schedule [74].

When considering new orders, three crucial questions arise: the feasibility of accepting a new order with given due date constraints of existing orders; the prioritization of the completion of new orders as quickly as possible; and the maximization of the number of accepted orders to optimize revenue. The uncertainties surrounding job types, quantities, arrival times, and due dates pose substantial challenges, significantly increasing the complexity of the scheduling problem [68,75].

This dynamic nature of order arrivals is also observed in warehouse environments, where online order batching problems arise [76,77,78]. In these scenarios, new orders arrive frequently and stochastically, requiring immediate scheduling or rescheduling upon their arrival.

1.2. Problem Definition

Scheduling problems can be classified into various categories based on their characteristics. In shop-scheduling problems, a set of jobs is given where each job consists of a set of operations. The problem involves assigning operations to machines from a set of available machines. Different problem types can be defined based on the job topology.

• Single machine: Only one machine is available and each job consists of a single operation.
• Parallel machines: Multiple machines are available and each job consists of a single operation.
• Flow shop: Jobs have the same number of operations and the order of machine usage is consistent for all jobs.
• Flexible flow shop: Similar to the flow shop problem but multiple machines are available for each stage.
• Job shop: Jobs can have different numbers and types of operations and the order of operations can vary between jobs.
• Flexible job shop: An extension of the job shop problem with multiple machines available for performing operations.
• Open shop: The order of operations for a job is not predefined.

This study focuses on a flexible job shop scheduling environment where each operation can be performed on multiple machines with different processing times, and the S-graph framework is used to model and optimize the production process in the presence of unexpected new order arrivals. The primary focus of this study is to investigate the impact of unexpected new order arrivals on manufacturing systems and to develop effective reactive scheduling policies that can dynamically accommodate these new orders while minimizing disruptions to the existing production schedule.

The examined reactive scheduling problems are defined as follows. The finite set of potential products to be produced is denoted by P. $I_p$ denotes the set of tasks of product $p\in P$ and $I_i^{-}$ denotes the set of tasks, which are the prerequisites of task $i\in I_p$. The set of all tasks is denoted by $I={\bigcup }_{p\in P}{I}_p$. Following the standards of the literature, the set of units is denoted by J, the set of applicable units for task $i\in I$ is $J_i$, and the set of tasks that can be performed by unit $j\in J$ is $I_j$. The processing time of task i performed by unit j is denoted by $p{t}_{i,j}$.

The output of the original deterministic problem is a schedule that can be represented by a set of 4-tuples in the following form: $(i,j,t^s,t^f)$, where j is the unit assigned to task i in the time interval $[t^s,t^f]$. This set (schedule) is denoted by S. Obviously, each 4-tuples has to satisfy the constraints of the recipe, e.g., $j\in J_i$ and $t^f-t^s\ge p{t}_{i,j}$.

In real life, during the operation of a factory, the number of products to be scheduled and produced is not always given at the beginning. Over time, multiple orders will arrive, $o_1,o_2,\dots ,o_n\in O$, where order $o_k$ can be represented by a pair $(I_k,t_k)$, where $I_k$ is the set of new tasks ($I_k\subseteq I$, $I={\bigcup }_k{I}_k$), which has to be performed, and $t_k$ is the arrival time of order $o_k$. O is an ordered set, where order $o_{k_1}$ precedes $o_{k_2}$ ($o_{k_1},o_{k_2}\in O,k_1\ne k_2$) if and only if $t_{k_1}<t_{k_2}$, assuming that two orders cannot arrive at the same time.

If set O is singular, then it represents a deterministic scheduling problem. Order $o_1\in O$ represents the first/initial order of the stochastic problem, which has no preceding order because $t_1<t_k$ for all $o_k\in O,k\ne 1$. Without losing generality, we can assume that $t_1=0$. The set of tasks that has to be performed to produce orders $o_1,\dots ,o_k$ is denoted by $I_k^{*}$ ($={\bigcup }_{k^{\prime }\le k}{I}_{k^{\prime }}$) and a feasible schedule of orders $o_1,\dots ,o_k$ is denoted by $S_k$.

The schedule of the first order, $o_1$, is a deterministic scheduling problem; therefore, it can be solved by the traditional S-graph method. Let us assume that we are at the time point $t_{k+1}$, where order $o_{k+1}\in O$ has arrived. As previous orders, $o_1,\dots ,o_k$, arrived earlier, the execution of some tasks has already been started (${\underline{I}}_k^{*}$) and there can be tasks that have not been started; yet, (${\overline{I}}_k^{*}$). Note that ${\underline{I}}_k^{*}\cup {\overline{I}}_k^{*}=I_k^{*}$ and ${\underline{I}}_k^{*}\cap {\overline{I}}_k^{*}=\varnothing$. The schedule of tasks, which have already begun or even finished at time $t_{k+1}$ consistently, cannot be changed. The part of the schedule that cannot be changed is denoted by ${\underline{S}}_k=S_k\setminus {\bigcup }_{(i,j,t^s,t^f)\in S_k,t^s\ge t_{k+1}}\left\{(i,j,t^s,t^f)\right\}$ and the modifiable part is denoted by ${\overline{S}}_k=S_k\setminus {\bigcup }_{(i,j,t^s,t^f)\in S_k,t^s<t_{k+1}}\left\{(i,j,t^s,t^f)\right\}$.

The goal of the optimization problem is to provide a schedule $S_{k+1}$ such as the following:

• $S_{k+1}$ is a feasible solution for the already received orders and the new order, i.e., for orders $o_1,\dots ,o_k,o_{k+1}$.
• ${\underline{S}}_k\subseteq S_{k+1}$, i.e., the assignments in $S_k$ already started before $t_{k+1}$ cannot be altered.
• $t^s\ge t_{k+1}$ must hold for all $(i,j,t^s,t^f)\in S_{k+1}\setminus {\underline{S}}_k$, i.e., no new assignment can be placed before time $t_{k+1}$.
• $S_{k+1}$ has the minimal makespan among all schedules satisfying the above three conditions.

2. Methodology

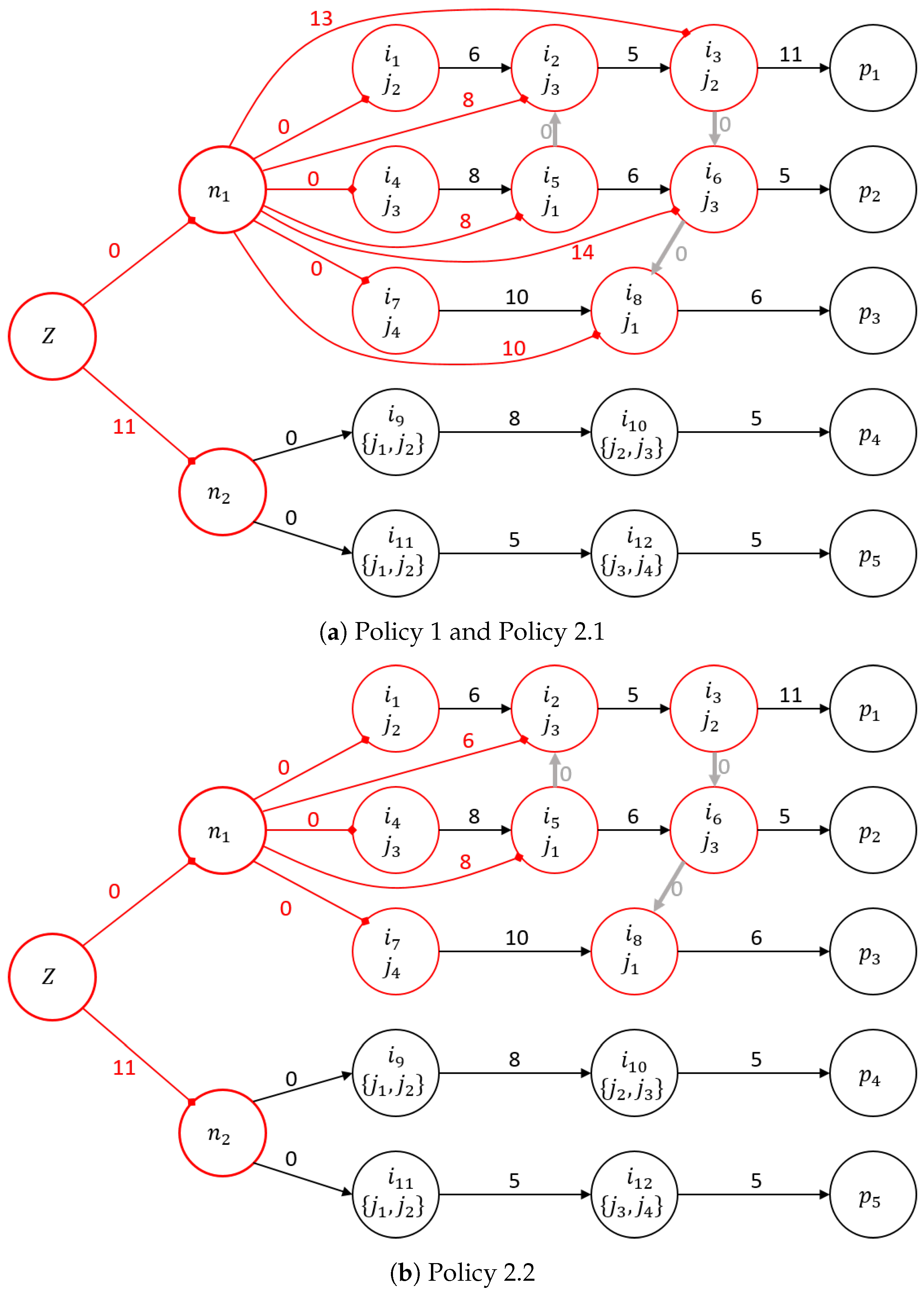
2.1. S-Graph Framework

The S-graph framework [11] is a mathematical model and an algorithmic approach for production scheduling that uses a directed acyclic graph supplemented by arc weights to model complete or partial schedules. It consists of two fundamental components: the S-graph representation, which provides the model of the process, and the associated algorithms. Nodes, N, represent the beginning of the tasks (task-nodes, $N^t\subset N$) and the completion of the products (product-nodes, $N^p\subset N$), where $N^t\cap N^p=\varnothing$ and $N^t\cup N^p=N$. For better understanding, the expressions task and task-node are used as interchangeable expressions because exactly one node belongs to each task ($\left|I\right|=|N^t|$); moreover, the node representing task i is also denoted by i. Similarly, exactly one node belongs to each product ($\left|P\right|=|N^p|$); therefore, the node representing product p is denoted by p.

In an S-graph, two types of arcs are present: recipe-arcs, which capture production-related constraints, and schedule-arcs, representing sequencing decisions made by optimization algorithms. Recipe-arcs establish precedence relationships within the recipe and their set is denoted by $A_1$. If task i is followed by $i^{\prime }$, a recipe-arc $(i,i^{\prime })$ is created in the S-graph. The weight of arc $(i,i^{\prime })\in A_1$ is the minimum processing time of task i using any unit $j\in J_i$, denoted by $c(i,i^{\prime })$, i.e., $c(i,i^{\prime })={min}_{j\in J_i}p{t}_{i,j}$. This weight may be adjusted during optimization after selecting a unit for task i. The resulting recipe-graph, $G(N,A_1,\varnothing )$, serves as input for the scheduling algorithm.

The recipe-graph is a significant S-graph type that represents the network of tasks to be executed. Figure 1 illustrates a production sequence involving three products ($p_1,p_2,p_3$), where the first two productions comprise three consecutive steps and the third production involves two consecutive steps. Product-nodes ($p_1,p_2,p_3$) and task-nodes ($i_1,\dots ,i_8$) represent the products and tasks, respectively. The arcs between task-nodes indicate the production order, while the arcs from task-nodes to product-nodes indicate the completion of respective products. Each arc, referred to as a recipe-arc, signifies a timing constraint between the start times of connected tasks or between the start time of a task and the completion time of the corresponding product. The sets displayed in each task-node represent the units capable of performing the task, e.g., task $i_1$ can be executed by either unit $j_1$ or $j_2$. It should be noted that the processing time of the equipment units available for task i may vary.

On the other hand, a schedule-graph represents a fully scheduled solution of a scheduling problem. Figure 2 depicts two schedule-graphs illustrating the schedules derived from the recipe-graph shown in Figure 1. Schedule-graphs differ from recipe-graphs in two aspects:

• The sets of units have been replaced by the specific unit chosen by the algorithm to perform each task.
• Additional grey arcs expressing the activity order of units are included in the graph.

All these additional arcs are schedule-arcs, and their insertion into the graph depends on the availability of storage for intermediate materials in the manufacturing plant [79]. In the absence of intermediate storage (NIS), the equipment units are subject to additional constraints imposed by the NIS policy. Specifically, an equipment unit cannot be freed up for the next task until the material processed in the current task has been transferred to the equipment unit assigned to the subsequent task in the recipe. This tight coupling between task assignments and material flow is represented by arcs in the schedule-graph, ensuring that the schedule adheres to the requirement of sequential material transfer between consecutive tasks without any intermediate storage. In contrast, when unlimited intermediate storage (UIS) is available, the sequence of tasks to be processed can be represented using a graph-based formulation. In this graph representation, the task sequence for each equipment unit is defined by a set of conjunctive arcs that connect the tasks assigned to the same equipment unit. This graph-based approach allows for the explicit modeling of the timing constraints and the sequencing of tasks assigned to the same equipment unit, which is a key characteristic of the UIS scenario. The use of conjunctive arcs to represent the task sequence within each equipment unit enables the scheduling algorithm to consider the flexibility in task ordering, as opposed to the more restrictive sequential task execution required in the NIS case.

During the NIS scenario, the zero-weighted schedule-arcs must originate from consecutive nodes following the source node in the recipe-graph, as shown in Figure 2a. For example, the sequencing of unit $j_1$ is represented by the zero-weighted schedule-arc between $i_6$ and $i_8$, indicating that $j_1$ performs task $i_5$, transfers the result of task $i_5$ to its next unit $j_3$, and then the $j_1$ unit proceeds to work on task $i_8$. In the UIS case, the schedule-arcs are inserted between tasks assigned to the same unit, and the weight of the arc corresponds to the processing time. This scenario is depicted in Figure 2b. For instance, unit $j_1$ performs task $i_5$ first and then starts working on task $i_8$, where the processing time of task $i_5$ is assigned to the schedule-arc between $i_5$ and $i_8$. It is essential to note that the weight of the schedule-arc must be increased by the changeover time if necessary in both NIS and UIS cases.

In the Gantt diagram, the width of a rectangle represents the processing time of the task using the corresponding unit. However, in the case of NIS, the processing time on the Gantt diagram may differ from the time indicated on the schedule-graph. For instance, in Figure 2a, task $i_7$ is assigned to unit $j_4$, which is expected to take 10 time based on the schedule-graph. However, unit $j_1$ is still performing task $i_5$ at time 10, which delays the start of task $i_8$. Until that, unit $j_4$ is used to store the output material of task $j_7$, as there is no intermediate storage unit available. In the following examples in this paper, storage is assumed to not be available; thus, NIS schedule-arcs will be used. It is worth noting that the solutions can differ but the proposed method is not affected by the storage policy.

Every schedule-graph of a recipe-graph contains the same nodes and recipe-arcs as the recipe-graph. The weight of the recipe-arcs can be increased according to the unit assignments as mentioned before. The schedule-graph of the recipe-graph $G(N,A_1,\varnothing )$ is denoted by $G(N,A_1,A_2)$, where $A_2$ is the set of schedule-arcs.

It is worth noting that if two nodes, i and $i^{\prime }$, have been connected by a recipe- or a schedule-arc $(i,i^{\prime })$, then it defines a precedence constraint between them, where $i^{\prime }$ has to start at least $c(i,i^{\prime })$ times later than i. Formally, if $t_i$ denotes the starting time of task i, then $\forall (i,i^{\prime })\in A_1\cup A_2$, $t_i+c(i,i^{\prime })\le t_{i^{\prime }}$.

In the followings, we will use so-called zero-wait arcs as well, which represent that no delay is allowed between the two connected tasks [80]. From the mathematical point of view, the starting time of the second task must be equal to the completion time of the first task, i.e., $t_i+c(i,i^{\prime })=t_{i^{\prime }}$ for all zero-wait arcs $(i,i^{\prime })$. For easy comprehension, a different graphical representation is introduced for zero-wait arcs. They are marked with diamond heads instead of arrowheads.

A recipe-graph $G(N,A_1,\varnothing )$ represents the recipe of a scheduling problem and schedule-graphs $G(N,A_1,A_2)$ represent its solutions, i.e., it is a fully scheduled S-graph. To generate schedule-graphs, the recipe-graph has to be extended with schedule-arcs. A partially scheduled S-graph $G^{\prime }(N,A_1,A_2^{\prime })$ contains schedule-arcs but not all decisions have been made. The solution method is a branch-and-bound (B&B)-based approach where every node in the B&B tree corresponds to a subproblem that can be represented by an S-graph. The recipe-graph belongs to the root of the search tree, schedule-graphs belong to the leaves of the tree, and a partially scheduled S-graph belongs to each intermediate node.

The branch-and-bound procedure makes the necessary assignments and sequencing decisions by introducing new arcs to the S-graph. For makespan minimization, the longest path of the graph provides a lower bound for a partial schedule or the objective value for a solution. If the S-graph contains a cycle, then it means that the subproblem is infeasible; therefore, it can be pruned.

There are two branching S-graph strategies published for making assignment and sequencing decisions expressed by the schedule-arcs. In the case of the original algorithm [11], an equipment unit is selected in each branching step and different tasks are added to the end of the current production sequence at each child node. In the case of the newer proposed algorithm [81,82], an unscheduled task is selected in the branching steps and, in the child nodes, the task is added to different positions in the production sequence of the corresponding suitable unit. The approaches are named equipment-based and task-based algorithms based on the branching step principle. The branching methods have different efficiencies for different examples but both of them can generate the optimal solution.

2.2. Equipment-Based and Task-Based Method

The recipe-graph of a scheduling problem is a fundamental component that serves as a subgraph of its corresponding schedule-graphs. Each schedule-graph contains arcs that are not present in the recipe-graph, which are referred to as schedule-arcs. All feasible schedule-graphs can be generated by extending the recipe-graph with arcs in all possible directions, subject to constraints on task assignments. This process can be efficiently performed using a branch-and-bound (B&B) algorithm, where each branching step involves assigning an equipment unit to a task and determining its order.

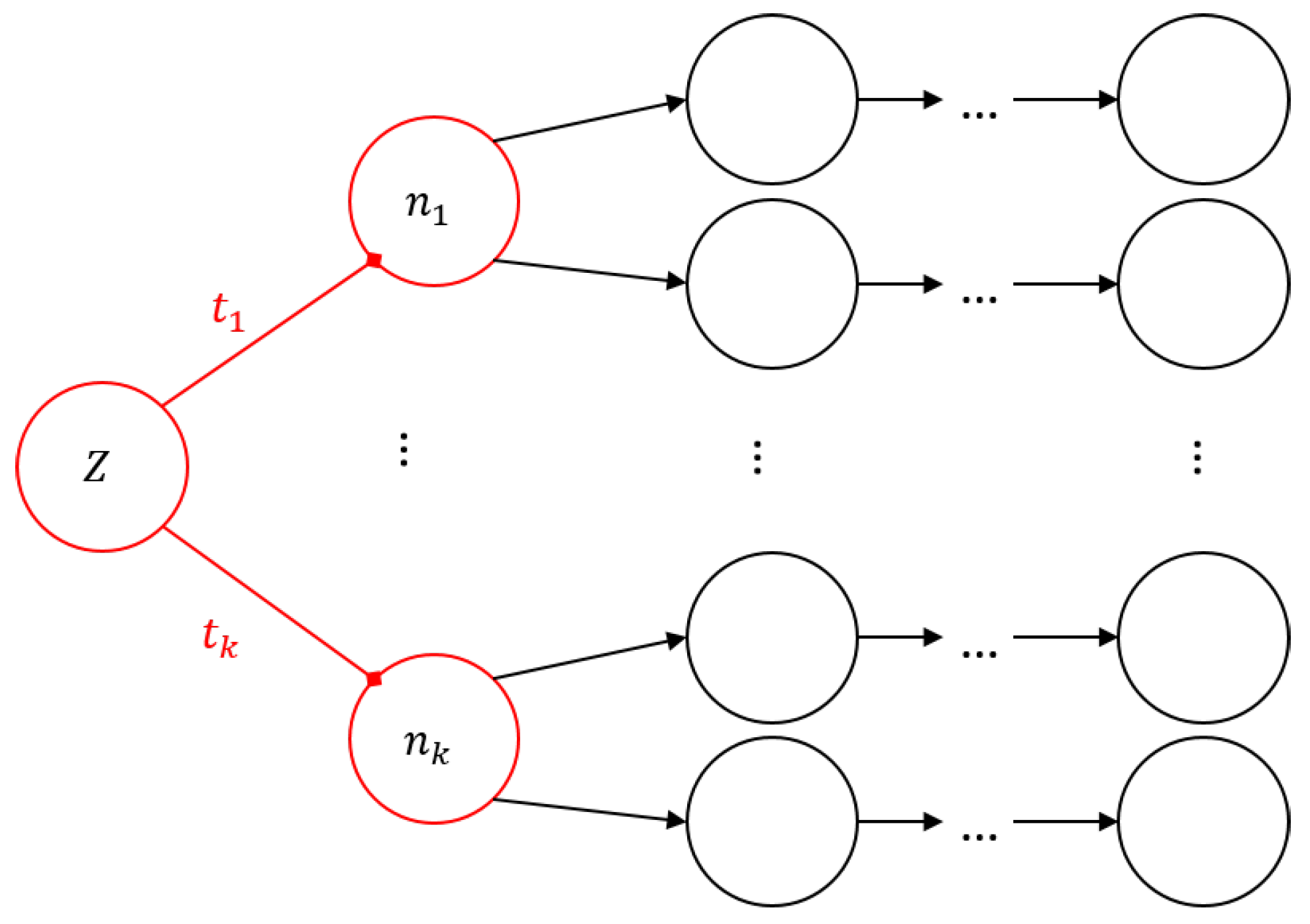
• Branching: During the generation of schedule-graphs in the B&B procedure, an S-graph and a partial assignment belong to a subproblem, i.e., to a node in the enumeration tree. The recipe-graph with no assignments serves as the root of the tree. At each partial problem, the equipment-based approach selects one equipment unit and generates child partial problems by considering all possible assignments of this equipment unit to unscheduled tasks. In contrast, the task-based approach selects one unscheduled task and generates all child partial problems by considering the possible equipment assignments to this task. In both cases, the processing time of a task may depend on the assigned equipment unit, which can modify the weight of the recipe-arcs starting from the node representing the task. The equipment-based approach ensures that if an assignment has already been made, the next assignment can only be made to the end of the sequence of tasks on the equipment, whereas the task-based approach allows for the sequence to change.
• Bounding: The bounding procedure evaluates the feasibility of a partial problem by testing whether it can be extended to a feasible schedule. If the test is positive, the algorithm determines a lower bound for the makespan of all solutions that can be derived from this partial problem. The feasibility of a partial problem is tested using a cycle search algorithm, which ensures that the schedule graph remains acyclic.

2.3. Reactive Method

Rescheduling is a critical process in dynamic scheduling that involves modifying an existing schedule in response to changes in the system or unexpected events. This can include re-optimizing the production plan to accommodate new orders, changes in processing times, or other disruptions. Rescheduling is a fundamental component of reactive scheduling as it allows the system to adapt to changing circumstances and maintain feasibility and optimality. Reactive scheduling is a broader concept that encompasses various strategies for handling unexpected events or changes in the system. It involves making real-time scheduling decisions based on the current system state, without pre-scheduling. Reactive scheduling can be either partial or full, with the latter posing challenges in terms of time and frequency constraints. In the context of manufacturing systems, reactive scheduling is particularly important for handling unexpected events such as the arrival of new orders. Effective reactive scheduling strategies can help to maintain the feasibility and optimality of the production system by dynamically adjusting the production plan in response to these events. In summary, rescheduling is a specific process within reactive scheduling that involves modifying an existing schedule in response to changes in the system. Reactive scheduling is a broader concept that encompasses various strategies for handling unexpected events or changes in the system, with rescheduling being a critical component of this process.

When considering the practical implementation of reactive scheduling, if there is only one order, then it is a deterministic scheduling problem. The predictive–reactive scheduling approach commences by generating an initial schedule, which is the schedule of the first order $o_1$. This initial schedule can be generated by the traditional S-graph framework or other traditional methods. If an uncertain event occurs, i.e., new order $o_{k+1}$ arrives, a reactive scheduler has to be applied. For this scheduler, an S-graph representation of the actual state of the manufacturing process is needed and the scheduling algorithm has to be modified to handle this input.

As has been written above, the schedule of tasks of ${\underline{I}}_k^{*}$ cannot be modified. There are three different policies for how the tasks of ${\overline{I}}_k^{*}$, which are scheduled in $S_k$ to start after $t_{k+1}$, can be handled. These three policies differ in their representations and solution methods.

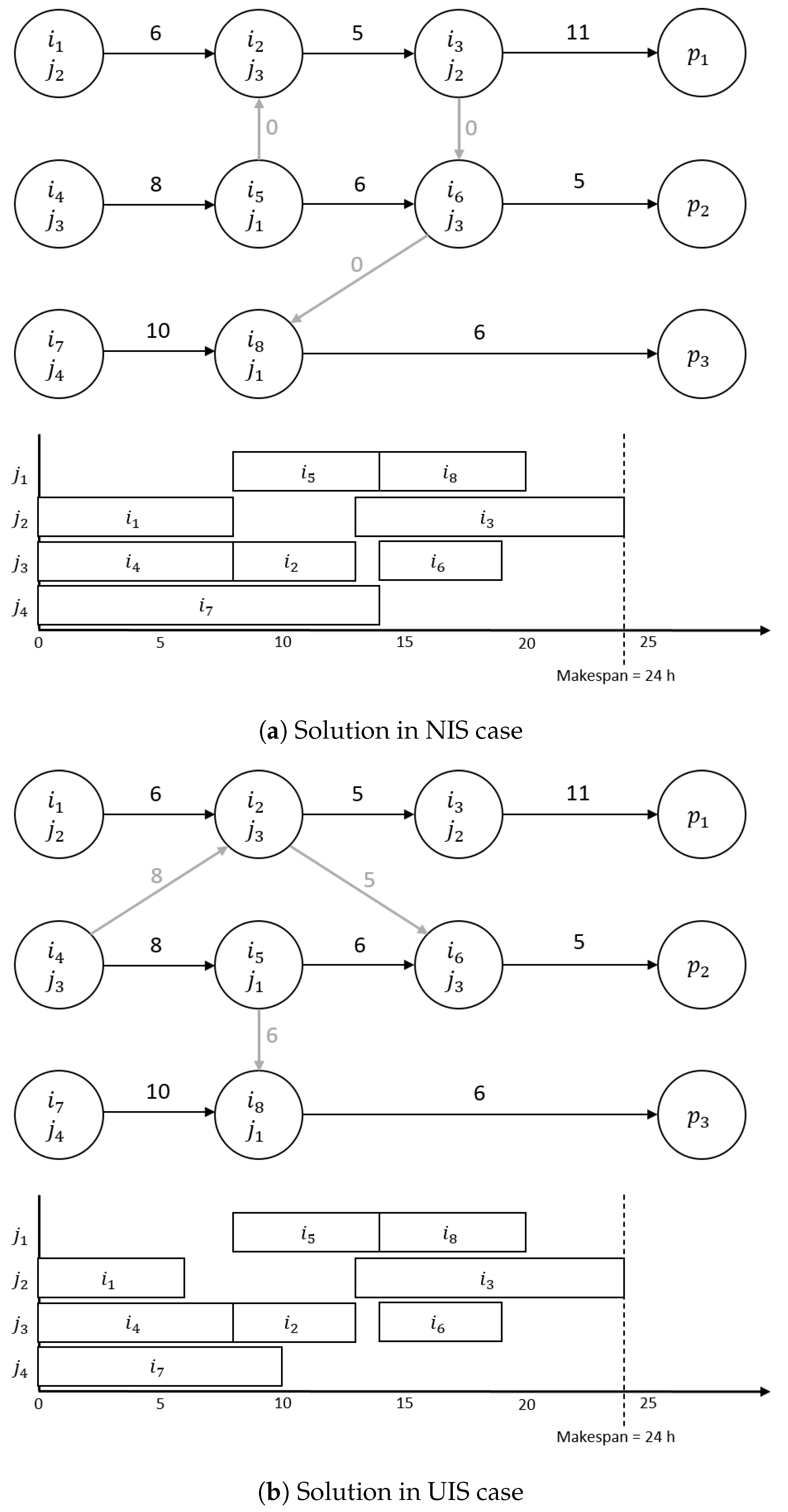
• Policy 1: None of the schedules of these tasks is allowed to be modified. It implies that the tasks of the new order $o_{k+1}$ can only be put to the end of the schedule.
• Policy 2: The sequence of tasks ${\overline{I}}_k^{*}$ has to remain as defined in $S_k$ but the tasks of $o_{k+1}$ can be inserted between them. We can define a strict and a less strict sub-policy.

  –

  Policy 2.1: The timing of the older tasks cannot be changed, i.e., $S_k\subseteq S_{k+1}$ and free-time gaps are needed for inserting the new tasks.

  –

  Policy 2.2: The timing of the older tasks can be changed but their sequence and unit-task assignments must remain unchanged, i.e., they can only be delayed.

  In the followings, statements referring to Policy 2 are true for both Policy 2.1 and 2.2.
• Policy 3: All tasks of ${\overline{I}}_k^{*}$ are free to reschedule.

It often occurs in the industry that a time interval is given when the tasks cannot be modified after a new order arrives. For example, the schedule of the actual and the next shifts cannot be modified. The proposed approach can handle this case by increasing the arriving time $t_k$ to the appropriate value and using Policy 3. In this case, $t_k$ means not the arriving time of order $o_k$ but the time when the schedule cannot be modified.

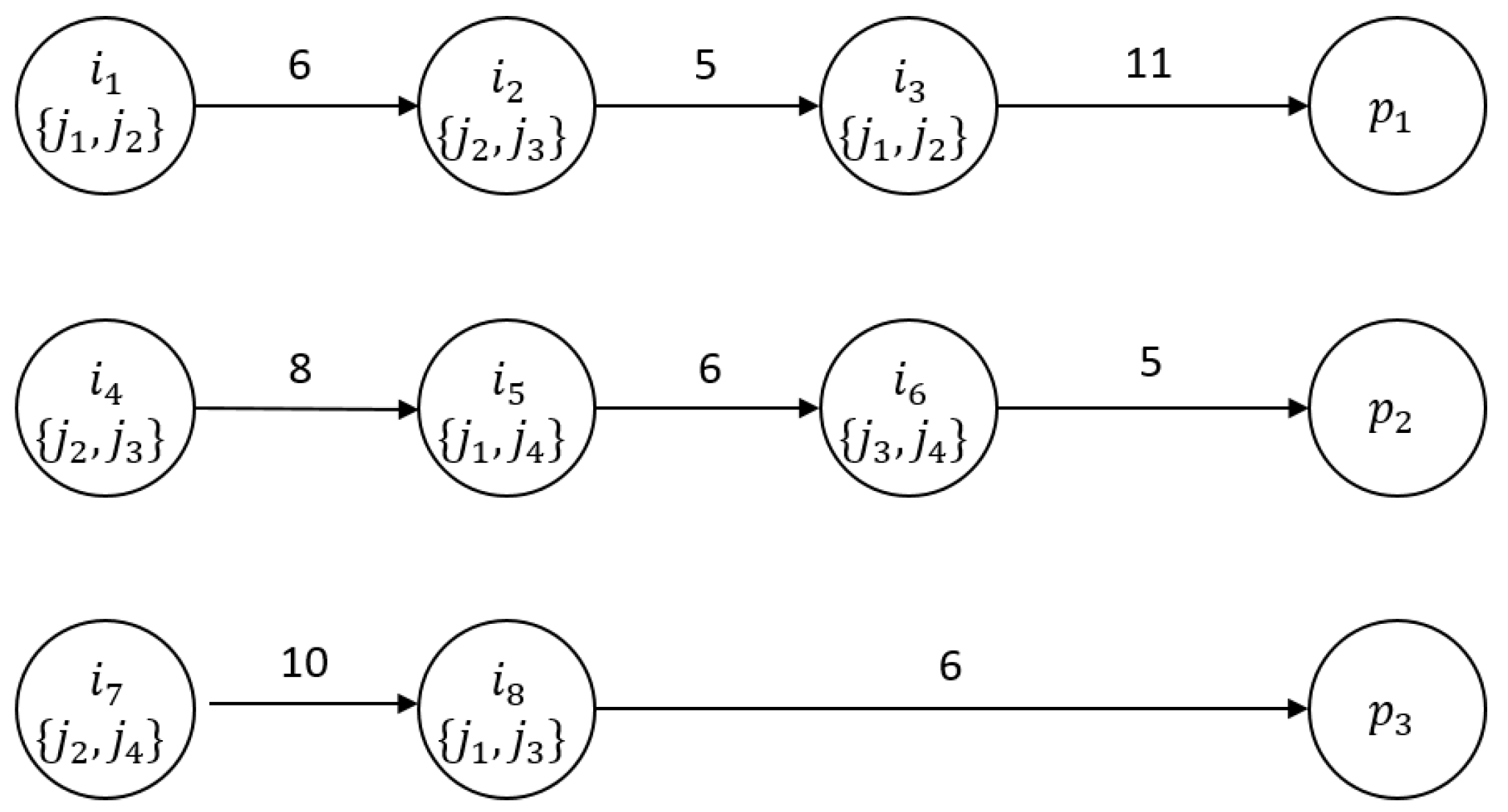
2.4. S-Graph Representation of the Current State of the Manufacturing Process

Order $o_k$ can be represented by a recipe-graph $G_k(N_k,A_{1k},\varnothing )$ because each order can be considered as a deterministic scheduling problem. To represent the arrival of order $o_k$, an additional node $n_k\in N_k$ is established. A zero-weighted arc points from node $n_k$ to those nodes that represent the first task of each product of order $o_k$, i.e., to nodes $i\in N_k$, where $I_i^{-}=\varnothing$. These arcs ensure that no task can start earlier than the arrival of order $o_k$.

A recipe-graph of order $o_k$ is not usable alone (except for the first/initial order $o_1$) and has to be combined with the recipe-graphs of orders $o_1,\dots ,o_{k-1}$. To represent the timing between orders, a new node Z (zero-node) is established and a zero-wait arc is drawn from Z to each $n_k$ weighted by $t_k$. Because each arc in an S-graph represents a constraint of the starting time of two connected nodes/tasks, none of the tasks of order $o_k$ can start earlier than $t_k$. Using a zero-wait arc from node Z to node $n_k$ ensures that the arrival happens exactly at time $t_k$ in the model. The resulting recipe-graph should be used for a deterministic method, where a lower bound is given to start the manufacturing of products, e.g., in the case where the arrival of raw materials is known in advance.

Figure 3 shows a schematic S-graph recipe of the reactive scheme. From the zero node, zero-wait arcs point to the starting nodes, $n_1,\dots ,n_k$, of the orders, where the weight of the arc is the arrival time of the corresponding order.

In a predictive–reactive scheduling approach, the schedule has to be modified responding to an event, where an event is the arrival of a new order. Let us suppose that we are at time $t_{k+1}$, which means that

• Orders $o_1,\dots ,o_k$ have arrived;
• Their tasks ($I_k^{*}=I_1\cup \cdots \cup I_k$) have been scheduled, i.e., $S_k$ has been generated;
• Schedule $S_k$ is under execution;
• Order $o_{k+1}$ has just arrived.

This implies that there are two constraints.

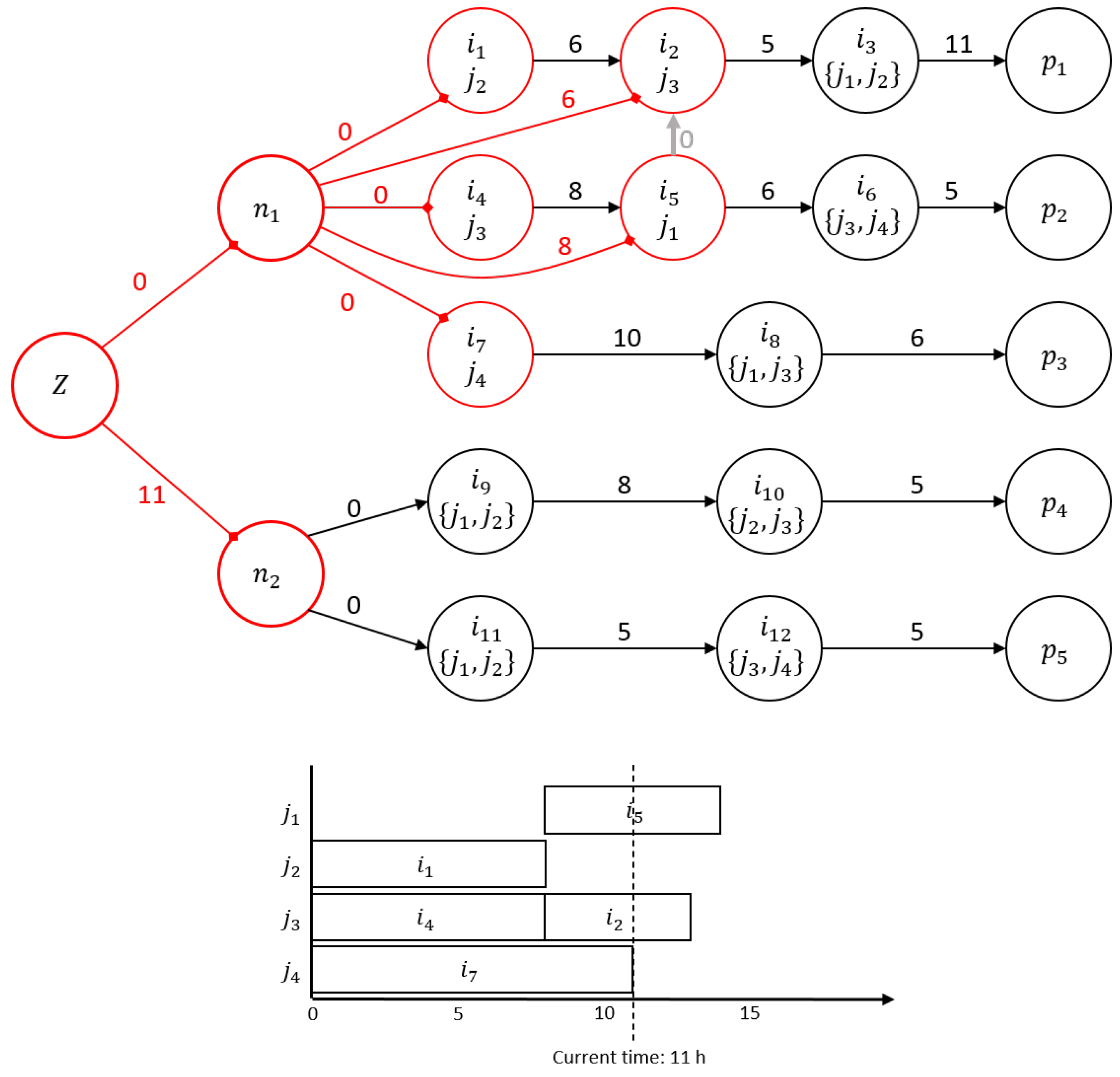
• The tasks of the new order, $I_{k+1}$, cannot be scheduled to start earlier than $t_{k+1}$, i.e., $t_s\ge t_{k+1}$, $\forall (i,j,t^s,t^f)\in S_{k+1}$, $i\in I_{k+1}$.
• Some tasks of previous orders have already started, ${\underline{I}}_k^{*}$, which means that their schedule cannot be modified, i.e., $(i,j,t^s,t^f)\in S_{k+1},\forall (i,j,t^s,t^f)\in S_k,t^s\le t_{k+1}$.

The first constraint stands because of the structure of the recipe-graph. To satisfy the second constraint, the starting time of tasks in ${\underline{I}}_k^{*}$ has to be fixed. It can be solved by adding zero-wait arcs, which represent equality constraints between the starting time of the two connected nodes. For example, if $(i,j,t^s,t^f)\in {\underline{S}}_k$, then the weight of the zero-wait arc $(n_k,i)$ is $t^s-t_k$. The zero-wait arcs should start from node Z with weight $t^s$, as well.

As mentioned at the beginning of the section, there is an arc established from nodes $n_i$ ($i=1,\dots ,k)$ to the first tasks of each corresponding product. Moreover, if any of these tasks have already started, a zero-wait arc has to be established as well. The zero-wait arc means a stricter constraint than an ordinary arc; therefore, parallel ordinary arcs can be neglected. Thus, only the zero-wait arcs will be presented in the figures instead of two parallel arcs.

Let us suppose that the first order $o_1$ is given in Figure 1, a schedule $S_1$ is generated (Figure 2a), it is under execution, and a new order $o_2$ arrives at time $t_2=11$. Order $o_2$ contains two products ($p_4,p_5$) with two consecutive tasks for each. The S-graph in Figure 4 represents the current state of the manufacturing system with the arcs preventing the modification of the ’past’. Moreover, the figure also contains the Gantt chart of this time period. The fixed tasks are $i_1$, $i_2$, $i_4$, $i_5$, and $i_7$, which are the members of ${\underline{I}}_1^{*}$ and denoted by red nodes. The unmodifiable part of the schedule is ${\underline{S}}_1=\{(i_1,j_2,0,6)$, $(i_4,j_3,0,8)$, $(i_7,j_4,0,10)$, $(i_2,j_3,8,13)$, $(i_5,j_1,8,14)\}$.

The S-graph described above is presenting the current state of the manufacturing system concentrating on tasks $\underline{I_k^{*}}$. This representation is valid for Policy 3 and needs some extension for Policies 1 and 2. If all schedule-arcs of the schedule-graph of the solution $S_k$ are inserted into the S-graph, then the sequence of the tasks cannot be changed in the algorithm. These schedule-arcs only define the sequence but do not fix the time; therefore, this modification covers Policy 2.2. To fix the timing of the solution $S_k$, additional zero-wait arcs are needed similarly to ${\underline{I}}_k^{*}$ nodes. Using both schedule-arcs and zero-wait arcs, Policy 2.1 and Policy 1 can be handled appropriately, but different methods will be used for scheduling.

Figure 5 shows the S-graph of the current state of the manufacturing system in cases of Policy 1 and Policy 2 approaches. In the case of Policy 1 and 2.1 (Figure 5a), the red nodes represent the already assigned tasks ($I_k^{*}$), which cannot be changed, and ZW-arcs determine the start time of these tasks precisely, not allowing for any changes. In Policy 2.2 (Figure 5b), red node marking with incoming ZW-arcs used only for the tasks (${\underline{I}}_k^{*}$) already began before the arrival of order $o_2$ to determine their start times, which cannot be modified. Red nodes without ZW-arcs indicate the assignments, which allow only for the modification of the starting time of these tasks. The grey arcs ensure that the order of these tasks cannot be changed but that tasks can be inserted between them.

2.5. Solution Methods

Scheduling the first/initial order, $o_1$, can be performed by a traditional S-graph method using either an equipment-based or a task-based branching strategy. When a new order arrives, a reactive scheduling algorithm has to be used, but the three policies need different approaches.

Table 1. Reactive S-graph approaches for order $o_{k+1}$.

Policy	Tasks with ZW-arc	Tasks to Schedule	EQ-Based Branching	Task-Based Branching
Policy 1	$I_k^{*}$	$I_{k+1}$	✓	stricted
Policy 2.1	$I_k^{*}$	$I_{k+1}$	extended	stricted
Policy 2.2	${\underline{I}}_k^{*}$	$I_{k+1}$	extended	✓
Policy 3	${\underline{I}}_k^{*}$	$I_{k+1}\cup {\overline{I}}_k^{*}$	✓	✓

summarizes the different policies and their characteristics, e.g., which set of tasks needs ZW arcs to be introduced, the set of tasks that it needs to be scheduled or rescheduled, and how the algorithms should be initialized. Checkmarks in the table indicate that the original branching methods of the algorithms do not require any modifications to be applied in the reactive method for the given policy.

2.5.1. Initialization

The first step of the reactive algorithm is the initialization according to schedule $S_k$. The initialization includes the establishment of zero-wait arcs, the specification of ‘unscheduled’ tasks, and other necessary settings. The establishment of zero-wait arcs has been discussed in the previous section; in this section, we concentrate on the other part of initialization.

Using the reactive method, a static schedule of the initial order or a reactive schedule of all previous orders is available. During a reactive schedule, the original schedule is converted to a subproblem of a branch and bound algorithm and this subproblem becomes the root of the B&B tree.

A subproblem contains all the details of the partial schedule, including task-equipment assignments and start and end times of tasks. Therefore, each subproblem has to store the set of unscheduled nodes and the previously made decisions, which are different for different branching strategies.

The equipment-based S-graph algorithm maintains a set of pairs, which represent the last assigned task to each unit if the unit has been assigned to any task. In the deterministic case, this set is initialized to be an empty set; however, in the reactive case, it must contain the last assignments of each unit that happened in the ‘past’. Using the task-based algorithm, a list of tasks has to be stored for each unit, which represents the activity order of the corresponding unit. For deterministic problems, the lists are initialized as empty lists, and for reactive problems, they contain the activities of the ‘past’.

• For Policy 1, the previous schedule cannot be modified, so each task of $I_k^{*}$ is in the ‘past’; therefore, only the tasks of order $o_{k+1}$ have to be scheduled, i.e., all tasks of $I_{k+1}$. Using equipment-based branching, the initial set should contain the last assignment of each unit from schedule $S_k$. Using task-based branching, the initial activity lists contain all tasks of $I_k^{*}$ according to schedule $S_k$.
• For Policy 2, tasks that have already started before the arrival of order $o_{k+1}$ at time $t_{k+1}$ are considered as part of the ’past’ and cannot be modified. The initial set for equipment-based branching should include the last assignment of each unit from the past schedule ${\underline{S}}_k$. However, the original equipment-based approach lacks the capability to insert tasks into the activity list. To address this limitation, a modification is necessary to the approach to enable the insertion of new tasks between tasks that have not yet been started from previous orders ${\overline{I}}_k^{*}$. This modification allows the approach to insert new tasks without rescheduling the tasks that have not yet been started, thereby reducing the search space. The task-unit assignments for tasks ${\overline{I}}_k^{*}$ have to remain as defined in schedule $S_k$. The schedule-arcs of schedule $S_k$ ensure that the order of these tasks cannot change. As a result, only the new tasks ($I_{k+1}$) have to be scheduled. Using task-based branching, the initial activity lists contain all tasks of $I_k^{*}$ according to schedule $S_k$. Because task-based branching can insert a task into an existing activity list, only the new tasks ($I_{k+1}$) have to be scheduled. Policy 2.1 is characterized by a stricter approach, as it permits task insertion only if a sufficient free time gap is available. Specifically, this policy ensures that the necessary completion time for the inserted task is available, thereby maintaining the integrity of the existing schedule. Policy 2.2 exhibits a more lenient characteristic as it does not enforce the availability of free time gaps. Consequently, task insertion is permitted between all tasks in the set ${\overline{I}}_k^{*}$.
• For Policy 3, all tasks, which have not started before $t_{k+1}$, can be modified; therefore, all tasks of $I_{k+1}\cup {\overline{I}}_k^{*}$ have to be scheduled. Using equipment-based branching, the initial set should contain the last assignment of each unit, which has already started (${\underline{I}}_k^{*}$). Using task-based branching, the initial activity lists contain tasks that have started according to schedule $S_k$.

2.5.2. Algorithms

Both equipment-based and task-based branching strategies can be used for all policies, but, in certain cases, they need some modifications.

• Policy 1 can be solved by the original equipment-based method after the proper initialization (see the previous section). The algorithm needs only to schedule the newly arrived tasks ($I_{k+1}$), putting them after the previously scheduled tasks ($I_k^{*}$).
• Policy 1 cannot be solved by the original task-based algorithm because this method cannot handle the constraint that the insertion between tasks of the original order is not allowed. Therefore, the algorithm has to be modified in such a way that, during the construction of the B&B tree, all branches where such an insertion would occur must be restricted.
• Equipment-based branching can only put tasks at the end of the activity lists of units, but Policy 2 allows tasks to be inserted into the lists. The equipment-based approach can be employed to solve Policy 2, but requires proper initialization and a necessary modification of the method, as discussed in the previous section. The initialization distinguishes the tasks of ${\overline{I}}_k^{*}$ in the activity list, and using the schedule-arcs ensures that the order of these tasks remains as it was in the original list. The equipment-based approach generates branches that differ from the original method for tasks ${\overline{I}}_k^{*}$, ensuring that their order remains unchanged while allowing for the insertion of new tasks between them.
• Policy 2 can be solved by the original task-based algorithm because this approach allows for direct insertion between tasks, unlike in the case of the original equipment-based method. Therefore, the search space is smaller using the task-based method compared to using the equipment-based method.
• Policy 3 can be solved by the original equipment-based method after the initialization. The algorithm needs to schedule the newly arrived tasks ($I_{k+1}$) and reschedule all tasks, which have not started yet (${\overline{I}}_k^{*}$), by adding them to the end of the activity lists.
• Policy 3 can be solved by the original task-based algorithm. However, this method inserts the tasks into the activity lists, and the structure of the S-graph (node $n_{k+1}$, zero-wait arcs) ensures that none of the tasks, which have to be scheduled or rescheduled ($I_{k+1}\cup {\overline{I}}_k^{*}$), can start earlier than the already started tasks. Therefore, no modification of the task-based algorithm is necessary.

Among the three policies, Policy 1 has the most restrictions on scheduling decisions; therefore, it has the smallest search space. Policy 3 has the fewest constraints; therefore, it has the biggest search space. It means that Policy 1 can be solved the fastest but Policy 3 can provide a better solution. Policy 2 is between Policy 1 and Policy 3 regarding the size of the search space, the computational needs, and the quality of the solution.

However, the size of the S-graph does not have a large impact on the computational requirements because there is no need to reschedule the tasks of the past and the size of the S-graph should be decreased over time. If all tasks of order $o_k$ were performed in the past, then all of its task-nodes, product-nodes, node $n_k$, and the connected arcs can be removed from the S-graph.

3. Results

The reactive S-graph method has been implemented in C++, which was run on a computer with a 2.9 GHz CPU and 16 GB memory under Windows 11. To evaluate the performance of the proposed algorithm, we solved literary examples. We did not find any example in the literature that perfectly fits the examined problem class; therefore, slightly modified examples are used. Two of them are presented in detail and we provide a summary for the others. For uniformity, we use the notations introduced in Section 1.2 instead of the original notations of the examples.

3.1. Example 1

This example was proposed by Rahmani and Heydari [83]. The plant consists of two equipment units, $j_1$ and $j_2$, where five products have to be produced, and each of them consists of two consecutive tasks. The first task of each product must be processed by unit $j_1$ and the second task by unit $j_2$, i.e., it is a two-machine flow shop problem. In this example, the initial order ($o_1$) is not directly defined but an initial schedule ($S_1$) is given.

In the original example, the processing times of the tasks are uncertain, and are defined by three scenarios. We use the second scenario because, in the paper, they assume that ’the second scenario has occurred in the system really’. Moreover, the objective of the original example is not makespan minimization but the minimization of the so-called MSR, which is a weighted function of makespan, stability, and robustness. According to the makespan, the published initial schedule is not optimal because of the different objectives; moreover, it has been generated according to the three scenarios. We use the same initial schedule for the S-graph algorithm, which is used in this paper to compare the solutions. Since computational results have not been published for this example, no efficiency comparison is made.

The Gantt chart of the initial schedule is shown in Figure 6. As the figure shows, the example uses UIS policy because $j_1$ starts its work on product 1 before the material of product 2 fills into machine $j_2$. Therefore, UIS-arcs are used in the S-graphs approach. Moreover, a new order ($o_2$) arrives during the execution of the schedule; the arriving new order consists of one product with two tasks and the arrival time is $t_2=8$.

In the Gantt chart, each task is identified by the product number and the used machine, i.e., both tasks of a product have the same product number. In the mathematical formalism, we have to distinguish the tasks; therefore, the tasks of product p will be denoted by $i_1^p$ and $i_2^p$ for machines $j_1$ and $j_2$, respectively. The initial schedule can be denoted as follows.

The status of the schedule at arriving time, $t_2=8$, is ${\underline{S}}_1=$$\{(i_1^1,j_1,5,9)$, $(i_1^2,j_1,3,5)$, $(i_2^2,j_2,6,7)$, $(i_1^3,j_1,0,3)$, $(i_2^3,j_2,3,6)\}$, where tasks $i_1^3$, $i_2^3$, $i_1^2$, and $i_2^2$ are already finished and task $i_1^1$ is being processed on $j_1$. The comparison of the literature examples and the proposed methods is presented in Figure 7 and Figure 8, respectively. In these figures, the arrival time of new orders is represented by dashed lines, and the new tasks are denoted by yellow bars.

Figure 7a shows the solution to the problem based on a heuristic FIFO (first-input–first-output) method from the literature, where the tasks are processed based on their arrival times; therefore, an earlier job is processed earlier. Based on this, the new tasks, namely $i_1^6$ and $i_2^6$, are scheduled in the last position. Figure 8 shows the solution of the proposed methods. The reactive S-graph method provides the same solution for Policy 1 (Figure 8a) as the literature example using the FIFO method. Due to the continuous operation of unit $j_1$, there is no free time gap for task $i_1^6$; therefore, Policy 2.1 provides the same result as Policy 1. Figure 8b shows the solution of the problem with the method of Policy 2.2. The solution is not the same but equivalent with the MSR solution (Figure 7b). Solving the problem with the Policy 3 reactive S-graph method (Figure 8c), the makespan is better, namely 19. The improvement in makespan achieved by Policy 3 can be attributed to the distinct objective function used in the original example (MSR) and the capability of Policy 3 to reschedule tasks that have not yet started at the time of arrival.

3.2. Example 2

In the second example, a two-stage artificial bee colony (TABC) algorithm is proposed for the scheduling and rescheduling problem in remanufacturing engineering with new job(s) insertion [84]. The objective is makespan minimization. The TABC algorithm is coded in C++ and the execution has been made on an Intel Core 2 Duo CPU P8600 2.40 GHz computer with 4 GB of RAM.

This paper presents an instance set, which includes eight instances of the example. From the eight example instances, instance two was used to illustrate the new job insertion. The initial order $\left(o_1\right)$ arrives at $t_1=0$ and its published initial schedule is shown in Figure 9. According to the initial schedule, all existing jobs will be completed at time 36. The products belonging to the order are denoted by numbers. A task of a product is denoted by two numbers: the number of the product and the number of the task in the production sequence. For example, $i_1^2$ denotes the first task of the second product. The UIS policy is used in the schedule, e.g., task $i_1^3$ ends at time 8 and task $i_2^3$ starts at time 10. To compare the reactive approaches, this solution is used as the initial schedule $S_1$.

Three re-scheduling strategies were presented in the literature example.

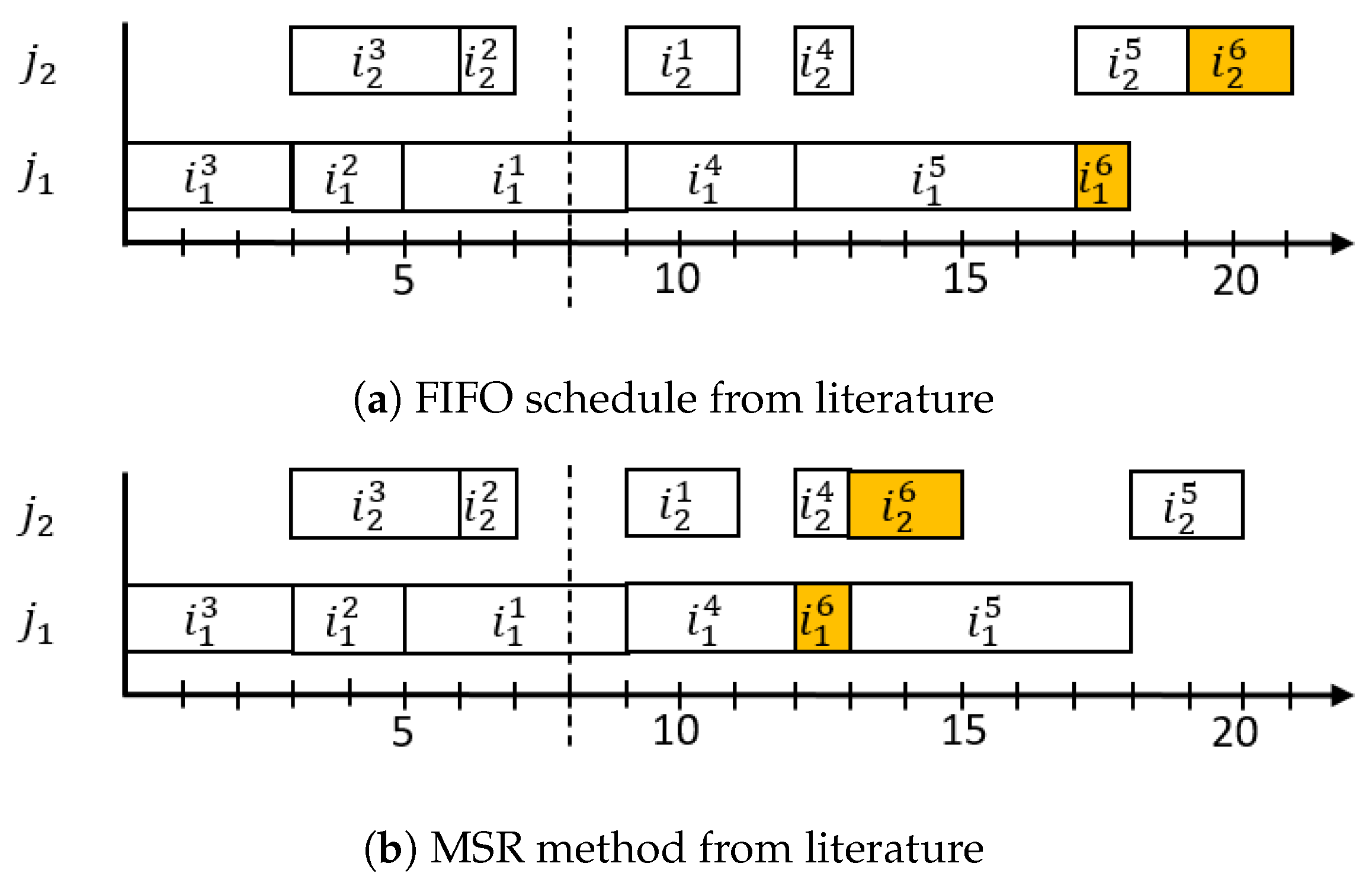
• In Strategy I, the tasks of the new order are rescheduled, while the already existing scheduling scheme remains constant. Machines are available after all assigned operations have been completed. This strategy is identical to the Policy 1 approach.
• The aim of Strategy II is to re-schedule new tasks and those that have not started yet. Therefore, the operations of existing tasks can be revised. The principle of Strategy II is identical to the proposed Policy 3 reactive approach.
• Strategy III includes an available-time block re-scheduling-based policy on the existing scheduling scheme. New tasks are scheduled on time gaps of all machines if it is possible. Therefore, if one machine is available and it has a free-time gap on the initial schedule, the machine can be employed with a new task. Finally, if all available time blocks on each machine are considered, the Strategy I scheduling scheme is employed for the remaining new tasks. Strategy III is equivalent to Policy 2.1.

The new order $\left(o_2\right)$ arrives at $t_2=12$, which contains one product. Product 9 (job 9) consists of eight consecutive tasks. Figure 10 shows the solutions of the proposed reactive S-graph approaches. Moreover,

Table 2. Comparison of the results for Example 3 (Strategy I, II, and III are equivalent to Policy 1, 3, and 2.1, respectively, and Strategy III is similar to Policy 2.2 and equivalent to Policy 2.1).

Algorithm	Strategy	CPU Time [s]	Makespan
TABC algorithm [84]	Strategy I	0.235	63
	Strategy II	2.343	44
	Strategy III	0.419	53
Task-based	Policy 1	0.013	62
	Policy 2.1	0.083	53
	Policy 2.2	0.073	44
	Policy 3	487.253	44
Equipment-based	Policy 1	0.005	62
	Policy 2.1	0.156	53
	Policy 2.2	2.307	44
	Policy 3	2.270	44

shows differences between the literature example and the proposed reactive approaches.

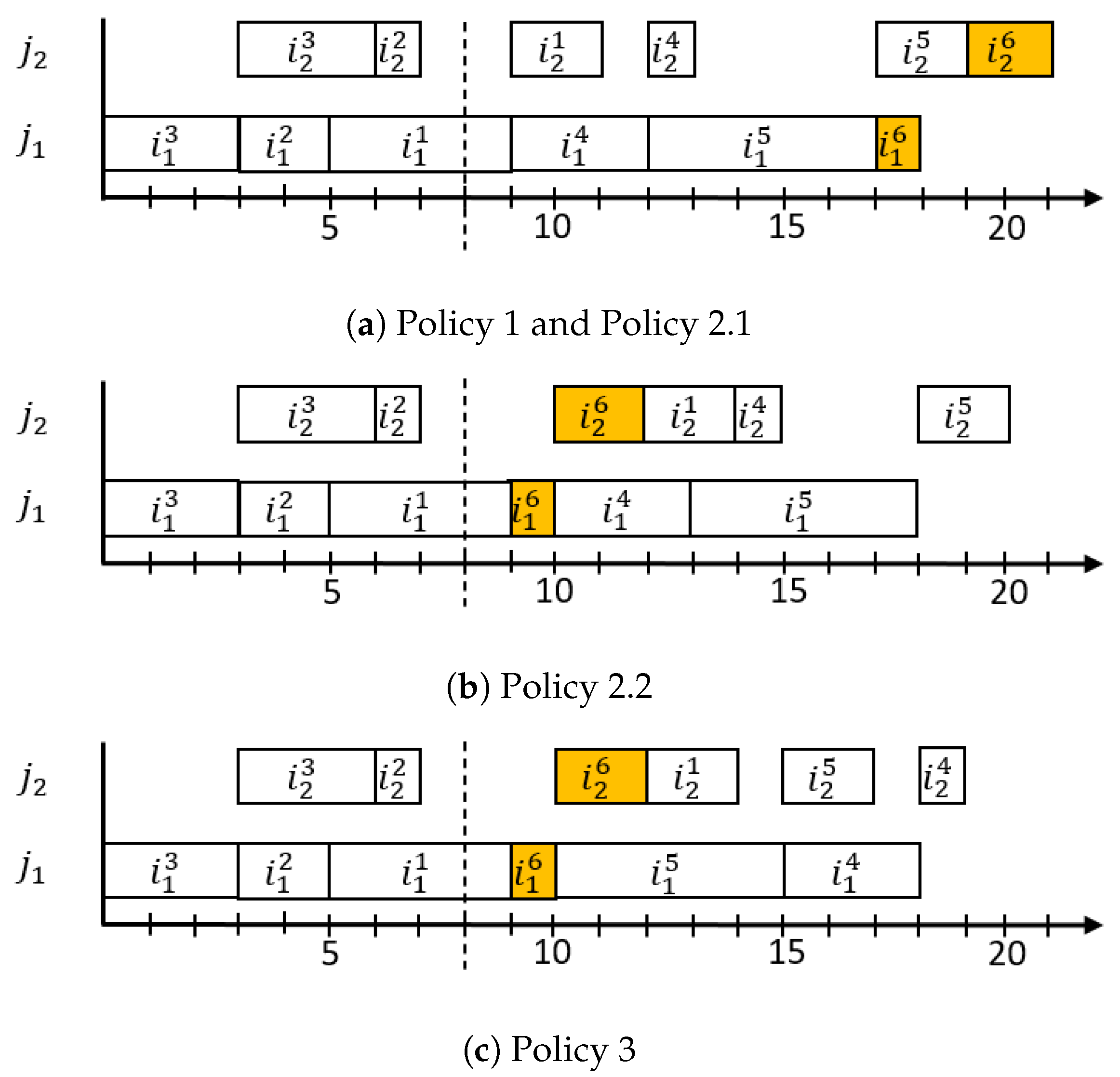
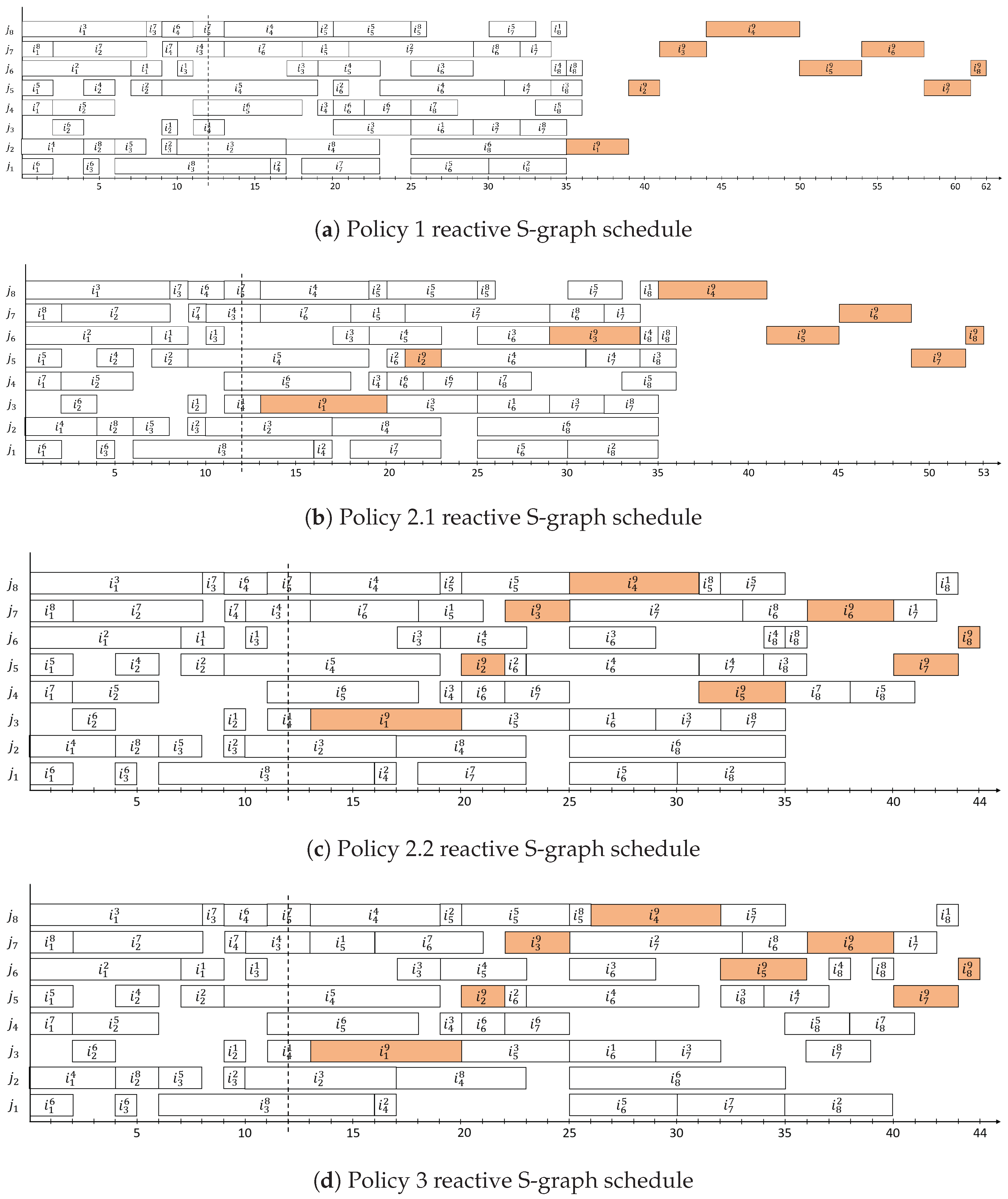
• The proposed Policy 1 approach provides a slightly better result (Figure 10a) than Strategy I, namely that the makespans are 63 and 62 for Strategy I and Policy 1, respectively. In our case, the production of product 9 starts when machine $j_2$ finishes its work ($t=35$). In the published solution, it starts at the end of the whole initial schedule ($t=36$); however, Strategy I should allow for an earlier start.
• For Policy 3, both equipment-based and task-based approaches have a makespan of 44. Compared with Strategy II, the same result is achieved, which can be explained by the consistency of the approaches. The significantly larger execution time for the task-based approach is caused by the complexity of the example (compared with the equipment-based approach) and the heuristic nature of the TABC algorithm. The Policy 3 solution is shown in Figure 10d.
• Comparing Policy 2 approaches with Strategy III, several differences can be discovered. The result of Policy 2.1, shown in Figure 10b, is equivalent to Strategy II. Using the Policy 2.2 approach, a better solution can be generated (Figure 10c) because the existing tasks can be delayed, i.e., the time gaps can be increased for longer tasks. Since there are more possibilities for Policy 2.2 than for Policy 2.1, it needs more CPU time, which can be seen clearly in the case of the equipment-based approach.

3.3. Additional Examples

This chapter presents additional literature examples in a condensed form. The problems do not entirely fit the classes of problems that we have examined (see the details later). Most of the examples are multi-objective optimization problems; therefore, they only serve as the foundation for the initial schedule used in each case. Furthermore, multiple types of events were taken into account, e.g., new order arrivals, machine breakdowns, changes in due dates, rush order arrivals, or order cancellations. Because the events occurred at different times in the examples, only the new job arrivals were considered. A summary of the results can be seen in

Table 3. Results of literature examples.

	Example			S-Graph Reactive Method
Paper	Approach	Objectives	Makespan	Policy	Makespan
[85]	Greedy randomized adaptive search	mean tardiness, instability, makespan, mean flow time	19	Policy 1	24
				Policy 2.1	24
				Policy 2.2	19
				Policy 3	19
[86]	Swarm algorithm	makespan	22	Policy 1	28
				Policy 2.1	28
				Policy 2.2	27
				Policy 3	22
[87]	Genetic algorithm	effectiveness, stability	Strategy 1: 28	Policy 1	23
			Strategy 2: 23	Policy 2.1	22
			Strategy 3: 19	Policy 2.2	20
			Strategy 4: 19	Policy 3	19
[88]	Evolutionary algorithm	makespan, disruption	117	Policy 1	113
				Policy 2.1	113
				Policy 2.2	113
				Policy 3	113
[89]	Genetic algorithm	energy consumption, makespan		Policy 1	40.1
			Strategy 1: 40.1	Policy 2.1	40.1
				Policy 2.2	40.1
			Strategy 2: 37.6	Policy 3	37.6
[90]	MIP model	overall idle time, makespan		Policy 1	25
			FPFS: 24	Policy 2.1	23.5
				Policy 2.2	23.5
			FPRS: 24	Policy 3	23.5
[91]	Clonal selection principle	completion time	Strategy i: 24	Policy 1	24
			Strategy ii: 25	Policy 2.1	24
			Strategy iii: 24	Policy 2.2	20
			Strategy iv: 22	Policy 3	20
[92]	Backtracking search algorithm	makespan, energy consumption, instability	52	Policy 1	57
				Policy 2.1	54
				Policy 2.2	50
				Policy 3	50

. The makespans of the examples only indicate that the proposed S-graph method can generate solutions that are not worse than the formerly published ones.

A greedy randomized adaptive search for dynamic rescheduling is presented in [85]. They solved flexible job shop problems (FJSPs) and dynamic flexible job shop problems (DFJSPs) with machine capacity limitations and a sequence-dependent setup time. A lexicographic method was used for the four objectives, minimizing the mean tardiness, minimizing the instability, minimizing the makespan, and minimizing the mean flow time.

Duan and Wang [86] used a robust optimization technique with dynamic events, such as machine failures and arrival of new jobs, using makespan minimization as the objective function. The paper contains multiple examples; we used the DFJSP example for comparison. Full rescheduling (Policy 3) with the S-graph method was able to obtain the same result.

A multi-objective mathematical model for DFJSPs was published by Fattahi and Fallahi [87]. The effectiveness and the stability of the schedules are taken into account as two goals. However, the published method can handle multiple objective functions; the authors present an example where they only minimized the makespan. We have chosen this example for comparison. Four strategies (Strategy 1, 2, 3, and 4) were presented in the paper to solve the problem.

• The new jobs are scheduled after the existing schedule is finished in the case of Strategy 1. Strategy 1 is more strict than Policy 1 because, despite the free capacity of machines, the new jobs cannot start before finishing the whole initial schedule.
• Using Strategy 2, each machine must complete all operations in the initial schedule before executing the new jobs. Strategy 2 is equivalent to Policy 1.
• The third strategy means simultaneously rescheduling the new jobs and the ongoing operations based on a single objective. Strategy 3 is equivalent to Policy 3.
• Strategy 4 is the same as Strategy 3 but it is based on the bi-criteria model.

Focusing on job shop rescheduling problems in a dynamic environment with random job arrivals and machine breakdowns, Hao and Lin [88] provided a rescheduling solution utilizing mathematical modeling, as well as an interactive adaptive-weight evolutionary algorithm. Three jobs and three machines make up the proposed problem. Because the original example has two objectives, the S-graph generated makespan is better than the published one.

Li et al. [89] proposed an energy-conscious optimization method for flexible machining job shop problems taking into account dynamic events. Actual machining and machine idling/stand-by are taken into account by the method when calculating machine tool energy consumption. The non-dominated sorting genetic algorithm II (NSGA-II) approach is used to obtain a solution that takes into account the overall energy consumption and the makespan. The presented test case differs from the previous ones because the recipe is not sequential, i.e., an operation can have multiple preceding operations. In the paper, two strategies were created. Strategy 1 prevents changing the original assignment and sequence of the unprocessed operations (equivalent to Policy 2.1), and Strategy 2 allows for changing the original schedule (equivalent to Policy 3). The solutions for the two strategies are equivalent to the solutions of the S-graph approach.

Moghaddam and Saitou [90] proposed a mixed integer programming model with rescheduling based on the concept of dynamic pegging in multi-level production for new order arrival. The information about how jobs are assigned to orders is known as pegging. Pegging is generated at the start of a planning cycle and is fixed until the start of a new planning cycle, i.e., fixed pegging. On the other hand, in dynamic pegging, the job order assignment may change due to interruptions, like the arrival of new orders during the planning horizon. Products are assumed to have multi-level structures that are represented by product structure trees. The objective is to minimize the machines’ overall idle time costs and the total makespan. Both fixed pegging–rescheduling (FPRS) and fixed pegging–fixed schedule (FPFS) are used. A new schedule for all orders (original and new) is created in FPRS based on the pegging of the original schedule upon the arrival of a new order. In FPFS, a new schedule is made specifically for a new order upon its arrival using the idle time of the machines in the initial schedule.

Muhamad et al. [91] discussed a clonal selection principle-based rescheduling method for job shop and flexible job shop scheduling problems. Machine breakdown and the arrival of new jobs were the two causes that necessitated rescheduling. Four strategies were introduced in the paper, with example data for new job arrivals.

• Scheduling the new jobs after the current jobs are finished (Policy 1).
• Scheduling the new jobs immediately and continuing with current jobs after new jobs are finished (rush orders).
• Inserting the new jobs into idle time while the current jobs are being finished (Policy 2.1).
• Scheduling the new jobs immediately and inserting the current jobs into idle time during completion of current jobs (rush order combined with Policy 2.2).

The S-graph reactive method can produce equivalent results for the same policies.

Caldeira et al. [92] proposed a slack-based insertion rescheduling strategy to handle new job arrivals while minimizing makespan, energy consumption, and instability. Every idle time of the initial schedule is considered during rescheduling, including the idle time, partial slack, and total slack of each operation. The partial slack time of an operation is the time window when the operation can start without delaying other operations. The total slack time of an operation is the time window when the operation can start without increasing the makespan. The authors’ proposed rescheduling strategy is equivalent to Policy 2.2.

4. Discussion

This study focuses on a flexible job shop scheduling environment where each operation can be performed on multiple machines with different processing times, and the S-graph framework is used to model and optimize the production process in the presence of unexpected new order arrivals. The proposed S-graph-based reactive scheduling approach offers a robust and efficient solution for handling unexpected arrivals of new orders in dynamic manufacturing systems. The key contributions of this work are the development of several reactive scheduling policies and their implementation using the S-graph framework.

Real-world manufacturing systems, including waste recycling facilities, are subject to various unforeseen events, such as machine failures, addition of new machines, arrival of new jobs, job cancellations, changes in processing times, rush orders, rework or quality issues, and date changes. The most frequent event is the arrival of new orders or jobs. These orders can arrive at any time, and their quantities are typically unknown in advance. Simply appending new orders to the end of the scheduling plan often fails to yield an optimal solution, necessitating modifications to the schedule whenever a new order arrives. The source of the idea for this study originates from the waste recycling industry, where unexpected new orders to be processed can disrupt the existing processing schedule. The research aims to develop a solution that enables efficient reactive scheduling, allowing the facility to adapt to new orders without significantly altering the original plan. By optimizing the processing sequence and minimizing the impact of new orders on the overall processing time, this study can help waste recycling facilities to improve their responsiveness to changing demands and enhance their overall efficiency.

Within the framework of a circular economy and Industry 4.0, the efficient management of manufacturing systems is crucial for maintaining feasibility and optimality in the face of unforeseen events. This study proposes an S-graph-based predictive–reactive approach to address the challenges posed by the arrival of new orders in dynamic scheduling. The approach involves initially preparing a schedule based on available information and executing the production accordingly. Subsequently, when an unexpected new order arrives during the execution of the initial schedule, an appropriate reactive strategy is employed based on the proposed approach.

The approach does not require the initial schedule to be generated using the S-graph framework. Instead, it can work with any arbitrary initial schedule as long as the details of this initial schedule are available. This flexibility is an important feature of the proposed approach, allowing manufacturers to utilize their existing scheduling methods to generate the initial production plan and then leverage the reactive S-graph algorithm to dynamically adjust this schedule when new orders arrive.

The reactive S-graph method takes the current state of the manufacturing process, represented by an S-graph, and the details of the initial schedule, and then applies one of the three proposed reactive scheduling policies (Policy 1, Policy 2, or Policy 3) to efficiently reschedule the tasks and accommodate the new order. The comparison of the proposed policies highlights the trade-offs between the level of flexibility, computational requirements, and solution quality. Policy 1, which schedules new tasks after the completion of the existing schedule, provides a simple and efficient approach but has limited flexibility. Policy 2 ensures that tasks already in progress are not modified while allowing the insertion of new tasks between tasks that have not yet started from the previous schedule. This approach provides a balance between flexibility and computational requirements. Policy 3 takes the flexibility a step further by allowing for the rescheduling of all tasks that have not started before the arrival of the new order, providing the greatest flexibility but requiring more computational resources.

The S-graph framework provides a structured way to model the manufacturing process. This allows the scheduling algorithms to consider the feasibility and optimality of the schedule, ensuring that the final solution adheres to the process requirements.

The key contribution of this study lies in the realization of reactive scheduling using the S-graph framework, which has demonstrated its efficiency in solving large-scale industrial problems and delivering optimal solutions [14]. The proposed algorithms have been implemented in C++ and extensively tested using several literature examples, validating the effectiveness of the methods and policies. Comparative analysis of existing examples within the literature reveals that the proposed S-graph reactive method performs at the same level as other published methods. Furthermore, the proposed policies can accommodate diverse industrial requirements while still providing optimal solutions to the scheduling problem.

For future research, there are two clear directions for extending the scope of solvable scheduling problems. One avenue involves improving the efficiency of the algorithms, handling more complex scenarios, extending to additional unexpected events (e.g., machine breakdown), and integrating the approach with other Industry 4.0 technologies. The other direction involves modifying the objective function, such as introducing a cost function that incorporates storage costs and deadline penalties to optimize for robust scheduling. Additionally, further studies are needed to validate the approach in different manufacturing settings and to address the challenges and limitations identified in this study.

The proposed approach offers a comprehensive framework for addressing the challenges posed by the arrival of new orders in dynamic scheduling, providing a valuable contribution to the field of the circular economy and Industry 4.0.