Experimental Evaluation of Mechanical Compression Properties of Aluminum Alloy Lattice Trusses for Anti-Ice System Applications
Abstract
1. Introduction
2. Materials and Methods
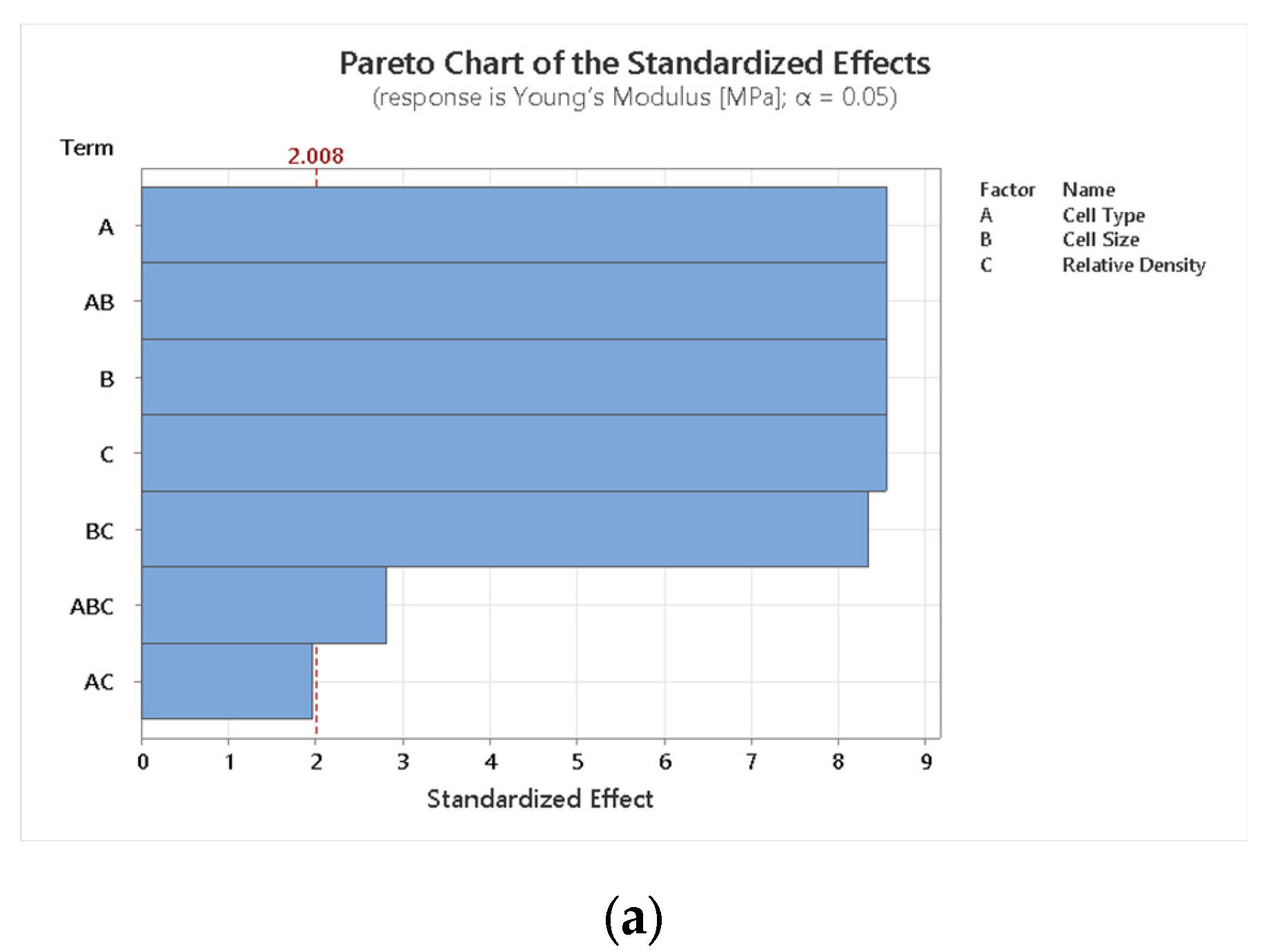
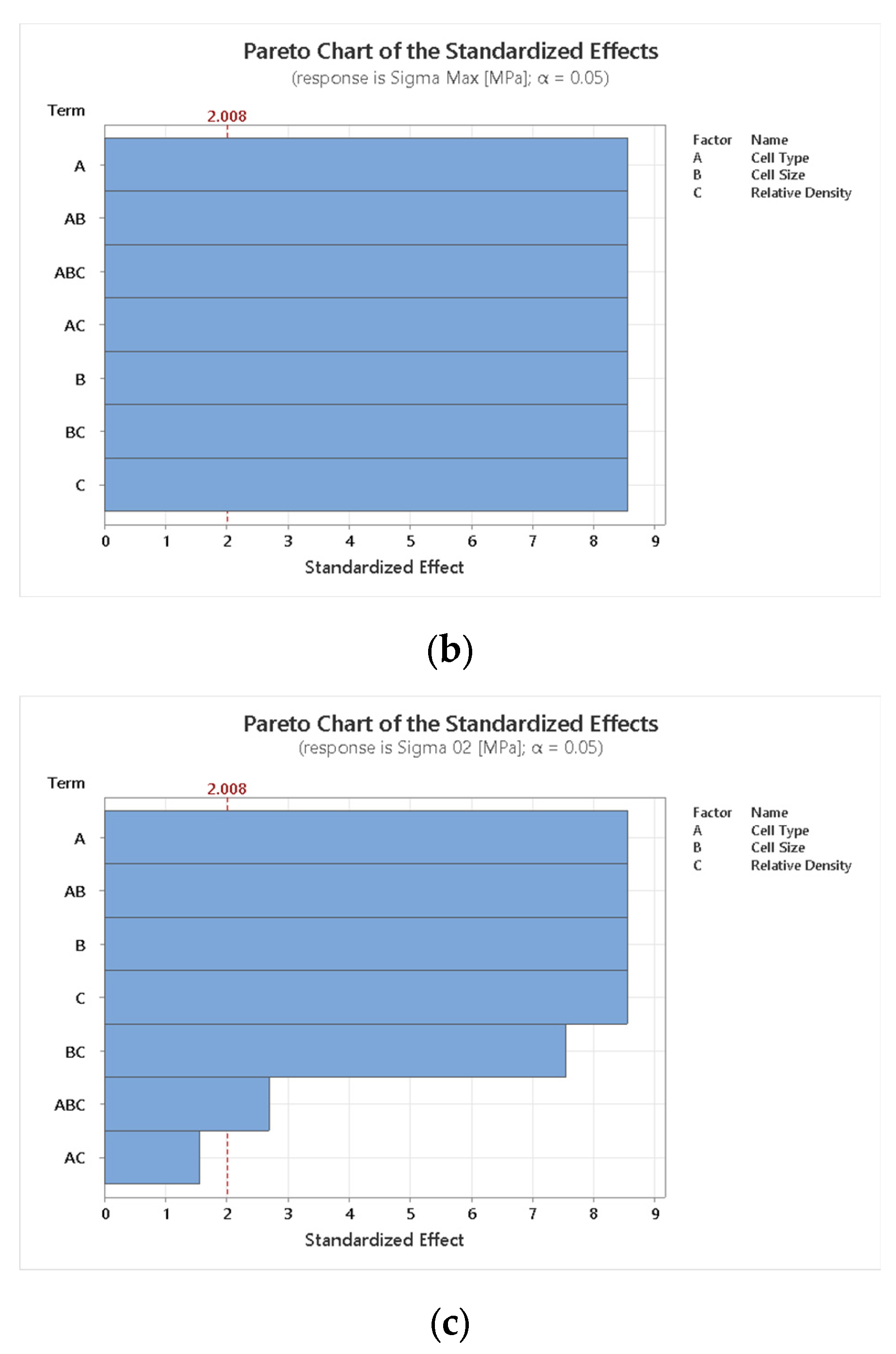
- Lattice equivalent Young’s Modulus (E), calculated from the slope of the stress–strain curve obtained by the compression of the lattices within the linear elastic region;
- Maximum Stress (σmax), representing the highest point on the curve compression/deformation of the lattices;
- Yield Stress (σ0.2), defined as the lattice stress value corresponding to a permanent plastic deformation of 0.2%.
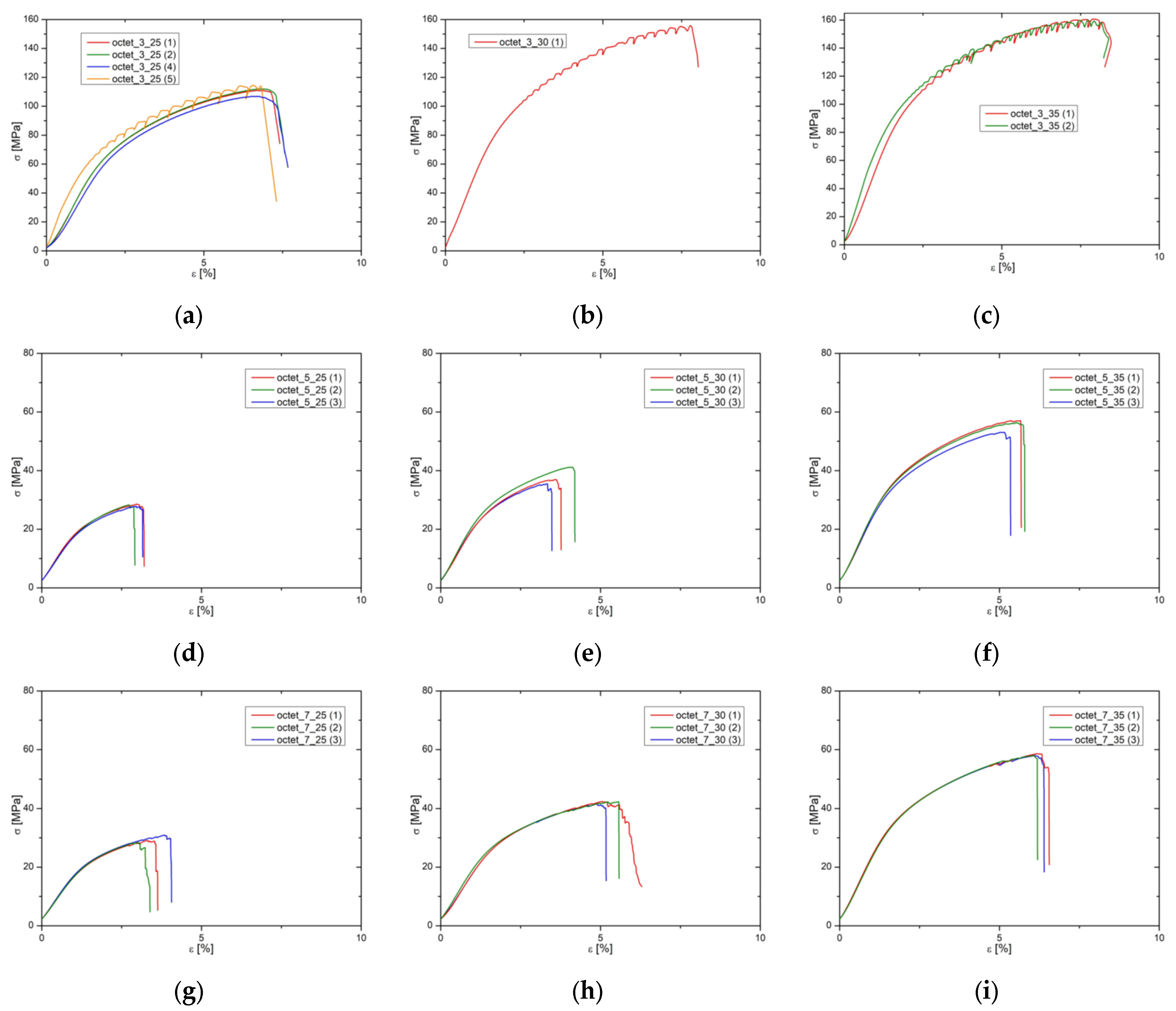
3. Results
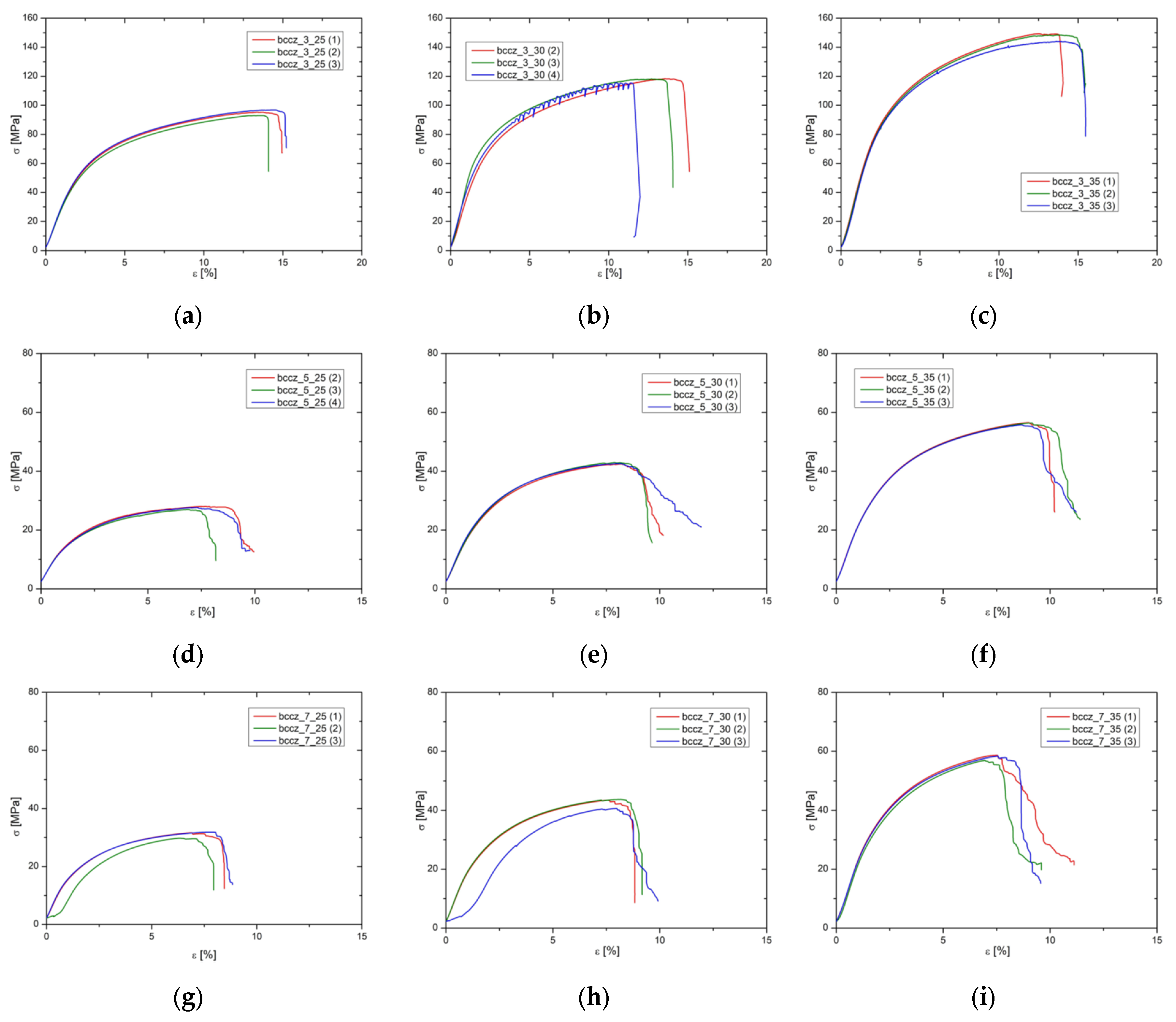
3.1. Bccz Specimens
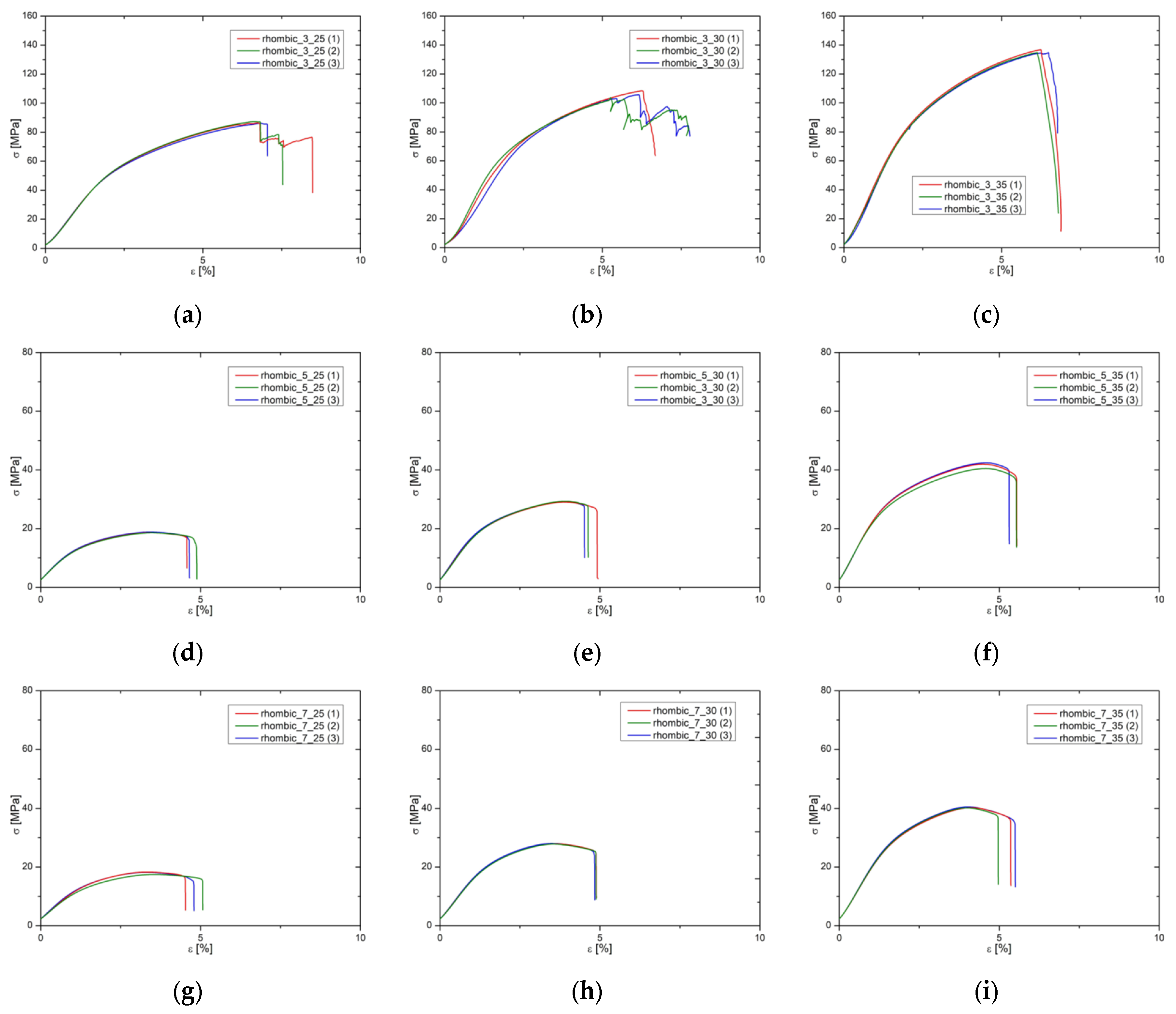
3.2. Rhombic Dodecahedron Specimens
3.3. Octet-Truss Specimens
4. Discussion
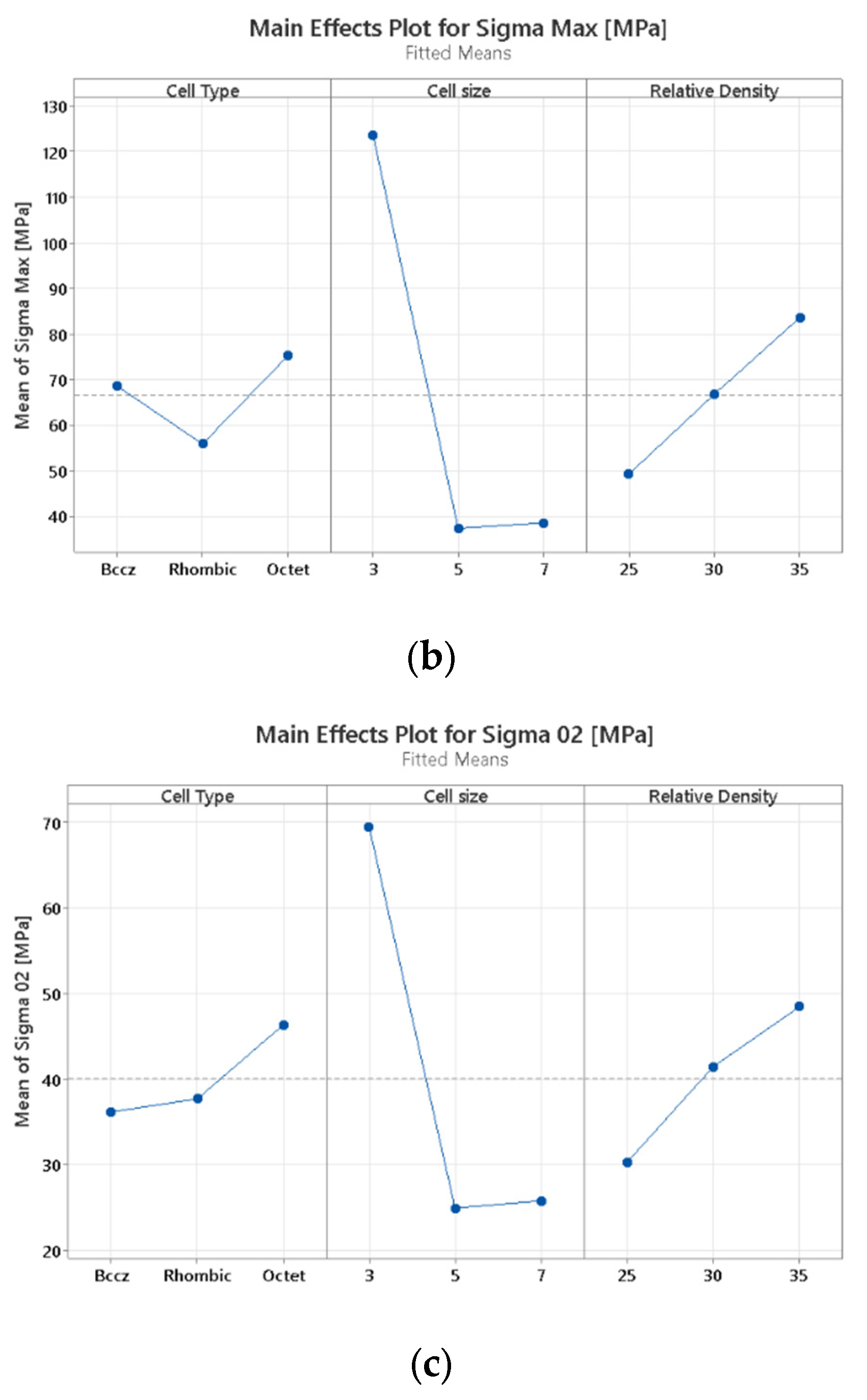
4.1. DOE Analysis
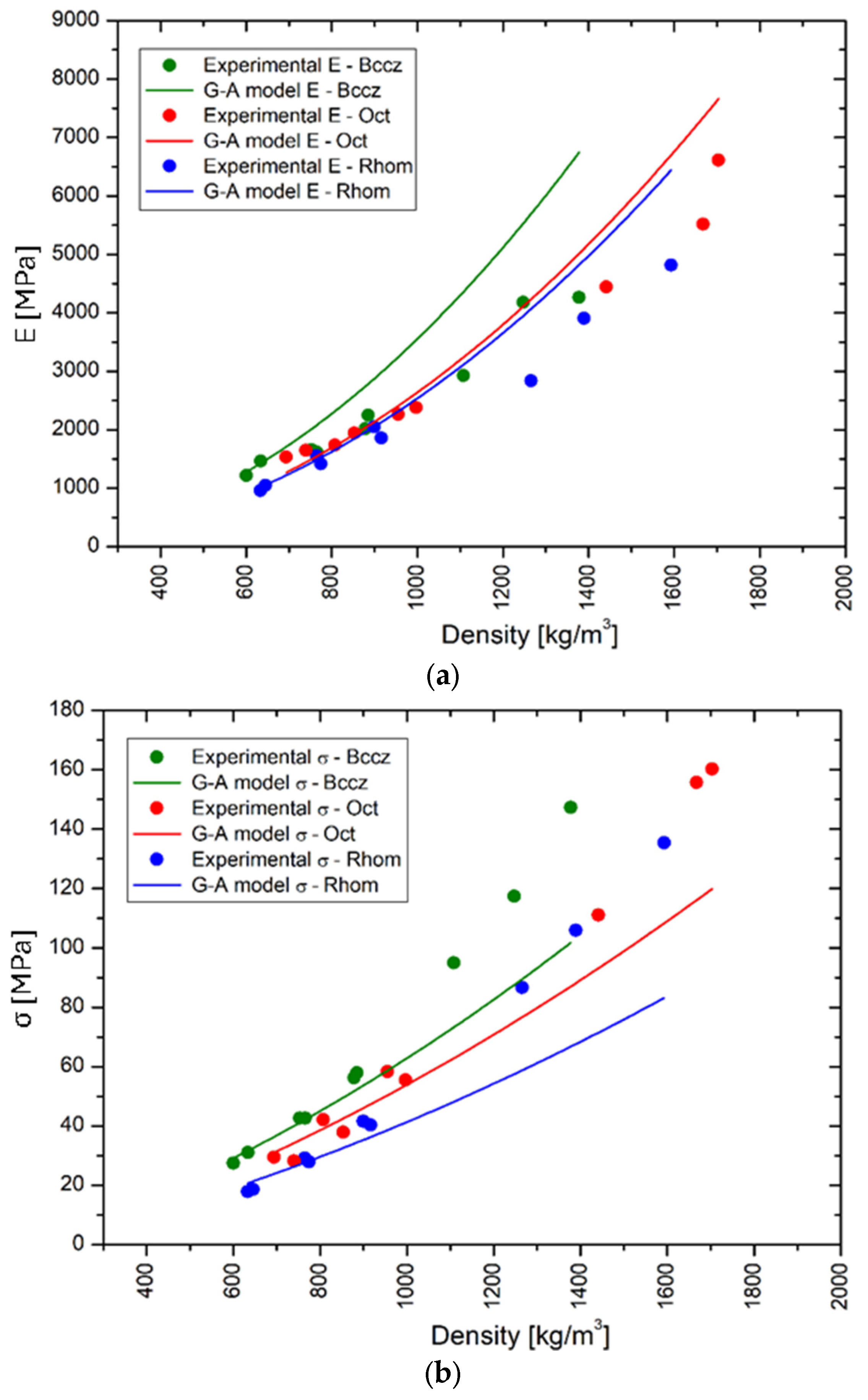
4.2. Comparison with Gibson–Ashby Model
5. Conclusions
- Cell size and type: Smaller cell sizes (3 mm) and octet-truss structures exhibit superior Young’s modulus compared to larger cell sizes (5 and 7 mm) and other cell geometries (BCCZ and rhombic dodecahedron). The octet truss, characterized by shorter beam lengths, outperforms other structures due to its efficient load distribution.
- Relative density: There is a linear relationship between relative density and all measured mechanical properties, with higher densities enhancing Young’s modulus, maximum stress, and yield stress. This correlation is consistent with the Gibson–Ashby model for low-density foams, though deviations are observed at higher densities due to manufacturing and design complexities.
- Failure mechanisms: The failure mechanisms vary with cell geometry, with stretching-dominated structures (BCCZ) showing distinct failure patterns compared to bending-dominated structures (rhombic dodecahedron and octet truss). These differences highlight the importance of considering cell geometry in design optimization.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
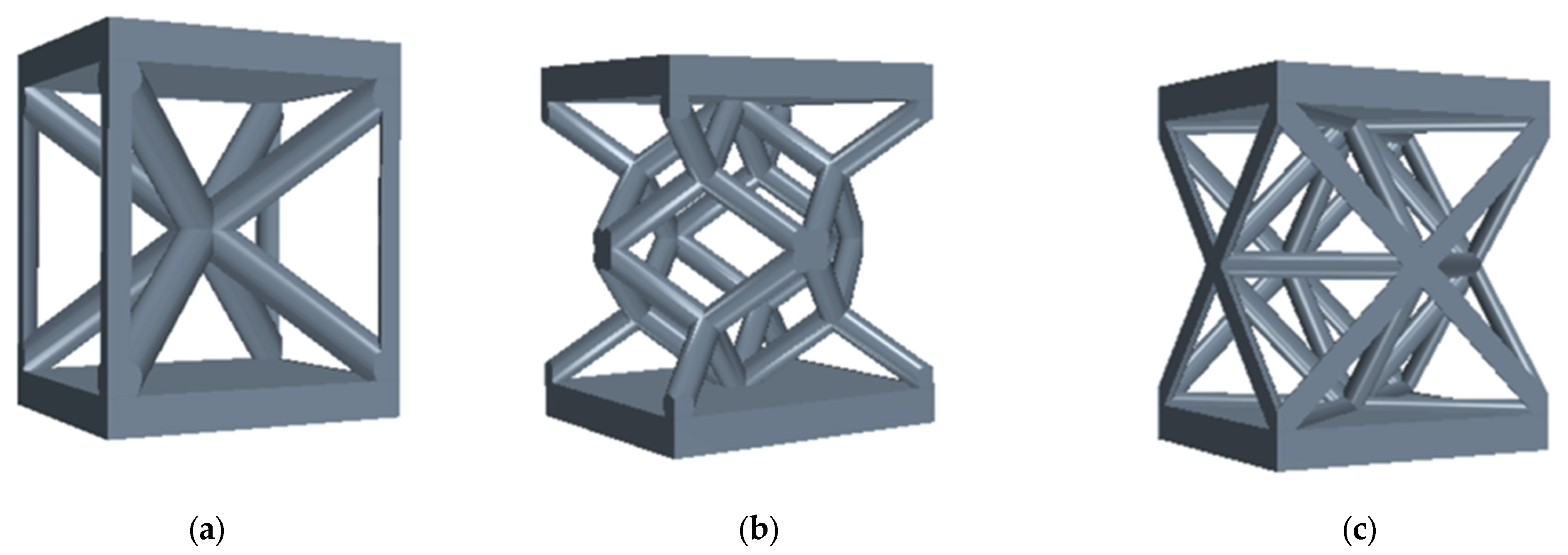
Appendix A. Elementary Unit Cells Drawing
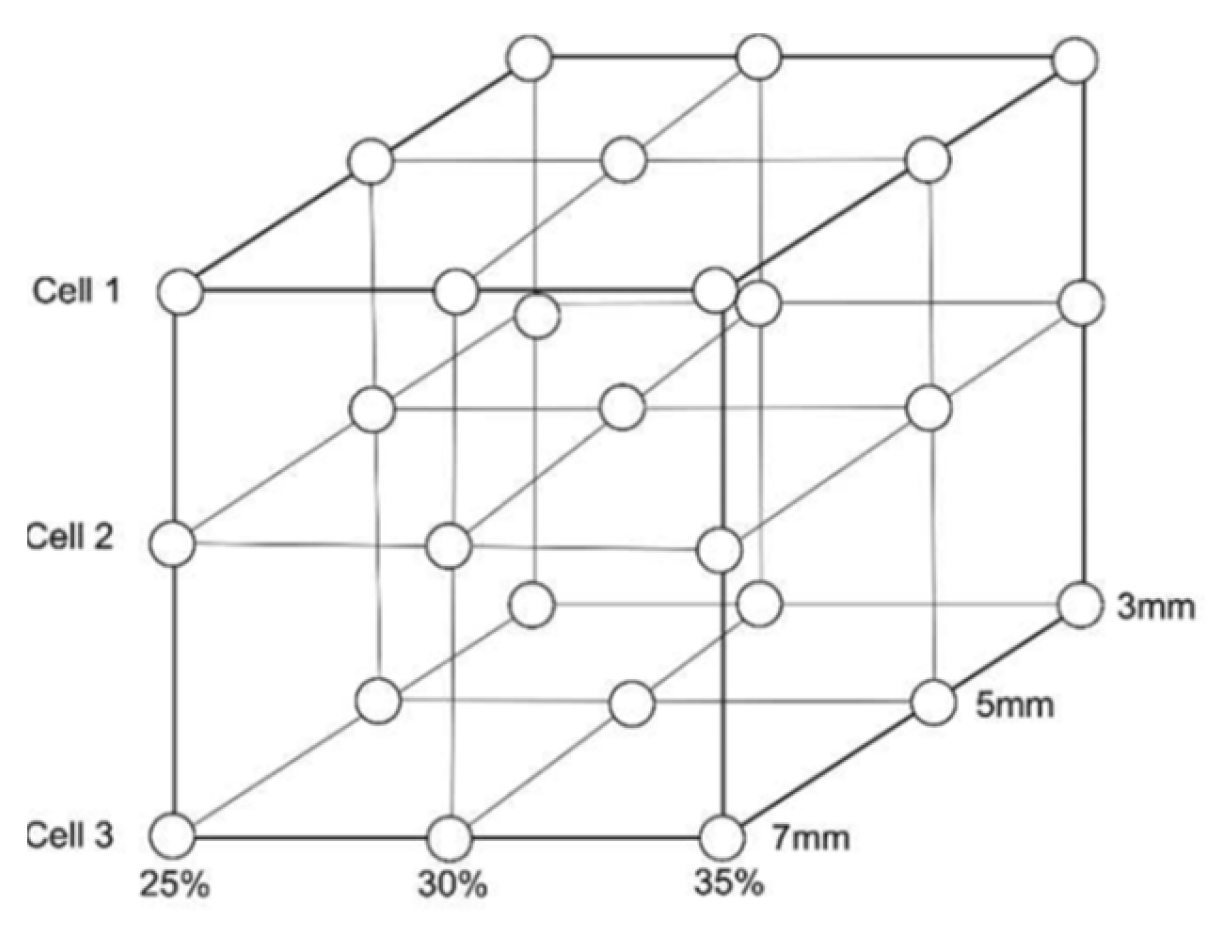
Appendix B. Experimental Collected Results
| Cell Type | Cell Size | Relative Density | Sigma Max [MPa] | Sigma 02 [MPa] | Young’s Modulus [MPa] |
|---|---|---|---|---|---|
| Bccz | 3 | 25 | 95 | 48 | 2954 |
| Bccz | 3 | 30 | 116 | 59 | 3927 |
| Bccz | 3 | 35 | 149 | 77 | 4315 |
| Bccz | 5 | 25 | 25 | 15 | 1322 |
| Bccz | 5 | 30 | 42 | 25 | 1579 |
| Bccz | 5 | 35 | 57 | 31 | 2011 |
| Bccz | 7 | 25 | 32 | 18 | 1491 |
| Bccz | 7 | 30 | 44 | 24 | 1822 |
| Bccz | 7 | 35 | 59 | 32 | 2273 |
| Rhombic | 3 | 25 | 86 | 50 | 2847 |
| Rhombic | 3 | 30 | 108 | 72 | 4009 |
| Rhombic | 3 | 35 | 137 | 76 | 4840 |
| Rhombic | 5 | 25 | 19 | 15 | 1046 |
| Rhombic | 5 | 30 | 29 | 21 | 1522 |
| Rhombic | 5 | 35 | 42 | 30 | 2059 |
| Rhombic | 7 | 25 | 18 | 15 | 955 |
| Rhombic | 7 | 30 | 28 | 22 | 1403 |
| Rhombic | 7 | 35 | 40 | 30 | 1845 |
| Octet | 3 | 25 | 111 | 61 | 4070 |
| Octet | 3 | 30 | 156 | 89 | 5520 |
| Octet | 3 | 35 | 161 | 91 | 5902 |
| Octet | 5 | 25 | 28 | 24 | 1610 |
| Octet | 5 | 30 | 37 | 27 | 1906 |
| Octet | 5 | 35 | 57 | 36 | 2426 |
| Octet | 7 | 25 | 29 | 23 | 1502 |
| Octet | 7 | 30 | 42 | 29 | 1732 |
| Octet | 7 | 35 | 59 | 36 | 2289 |
| Bccz | 3 | 25 | 93 | 44 | 2837 |
| Bccz | 3 | 30 | 118 | 55 | 3804 |
| Bccz | 3 | 35 | 149 | 70 | 4264 |
| Bccz | 5 | 25 | 28 | 17 | 1224 |
| Bccz | 5 | 30 | 43 | 26 | 1565 |
| Bccz | 5 | 35 | 56 | 30 | 2020 |
| Bccz | 7 | 25 | 30 | 20 | 1282 |
| Bccz | 7 | 30 | 44 | 25 | 1826 |
| Bccz | 7 | 35 | 57 | 28 | 2251 |
| Rhombic | 3 | 25 | 87 | 51 | 2823 |
| Rhombic | 3 | 30 | 104 | 68 | 4254 |
| Rhombic | 3 | 35 | 135 | 80 | 4641 |
| Rhombic | 5 | 25 | 19 | 15 | 1001 |
| Rhombic | 5 | 30 | 29 | 22 | 1526 |
| Rhombic | 5 | 35 | 40 | 29 | 2006 |
| Rhombic | 7 | 25 | 17 | 14 | 908 |
| Rhombic | 7 | 30 | 28 | 22 | 1405 |
| Rhombic | 7 | 35 | 40 | 31 | 1840 |
| Octet | 3 | 25 | 112 | 62 | 4057 |
| Octet | 3 | 30 | * | * | * |
| Octet | 3 | 35 | 160 | 84 | 7321 |
| Octet | 5 | 25 | 28 | 23 | 1599 |
| Octet | 5 | 30 | 41 | 30 | 2011 |
| Octet | 5 | 35 | 56 | 36 | 2396 |
| Octet | 7 | 25 | 28 | 23 | 1507 |
| Octet | 7 | 30 | 42 | 28 | 1787 |
| Octet | 7 | 35 | 58 | 36 | 2240 |
| Bccz | 3 | 25 | 97 | 47 | 3000 |
| Bccz | 3 | 30 | 118 | 61 | 4821 |
| Bccz | 3 | 35 | 144 | 71 | 4224 |
| Bccz | 5 | 25 | 27 | 16 | 1233 |
| Bccz | 5 | 30 | 43 | 25 | 1707 |
| Bccz | 5 | 35 | 56 | 30 | 2018 |
| Bccz | 7 | 25 | 32 | 18 | 1626 |
| Bccz | 7 | 30 | 41 | 32 | 1337 |
| Bccz | 7 | 35 | 58 | 33 | 2219 |
| Rhombic | 3 | 25 | 86 | 52 | 2853 |
| Rhombic | 3 | 30 | 106 | 78 | 3464 |
| Rhombic | 3 | 35 | 135 | 89 | 4973 |
| Rhombic | 5 | 25 | 19 | 15 | 1096 |
| Rhombic | 5 | 30 | 29 | 22 | 1610 |
| Rhombic | 5 | 35 | 42 | 30 | 2090 |
| Rhombic | 7 | 25 | 18 | 15 | 1008 |
| Rhombic | 7 | 30 | 28 | 23 | 1440 |
| Rhombic | 7 | 35 | 41 | 31 | 1899 |
| Octet | 3 | 25 | 107 | 72 | 3747 |
| Octet | 3 | 30 | * | * | * |
| Octet | 3 | 35 | * | * | * |
| Octet | 5 | 25 | 29 | 22 | 1741 |
| Octet | 5 | 30 | 36 | 27 | 1922 |
| Octet | 5 | 35 | 53 | 35 | 2321 |
| Octet | 7 | 25 | 31 | 23 | 1595 |
| Octet | 7 | 30 | 42 | 29 | 1691 |
| Octet | 7 | 35 | 58 | 37 | 2260 |
References
- Masiol, M.; Harrison, R.M. Aircraft engine exhaust emissions and other airport-related contributions to ambient air pollution: A review. Atmos. Environ. 2014, 95, 409–455. [Google Scholar] [CrossRef] [PubMed]
- Baxter, G. Assessing the Carbon Footprint and Carbon Mitigation Measures of a Major Full-Service Network Airline: A Case Study of Singapore Airlines. Int. J. Environ. Agric. Biotechnol. 2022, 7, 81–107. [Google Scholar] [CrossRef]
- Kloewer, M.; Allen, M.R.; Lee, D.S.; Proud, S.R.; Gallagher, L.; Skowron, A. Quantifying aviation’s contribution to global warming. Environ. Res. Lett. 2021, 16, 104027. [Google Scholar] [CrossRef]
- Ryley, T.; Baumeister, S.; Coulter, L. Climate change influences on aviation: A literature review. Transp. Policy 2020, 92, 55–64. [Google Scholar] [CrossRef]
- Afonso, F.; Sohst, M.; Diogo, C.M.; Rodrigues, S.S.; Ferreira, A.; Ribeiro, I.; Marques, R.; Rego, F.F.; Sohouli, A.; Portugal-Pereira, J.; et al. Strategies towards a more sustainable aviation: A systematic review. Prog. Aerosp. Sci. 2023, 137, 100878. [Google Scholar] [CrossRef]
- Dessens, O.; Köhler, M.O.; Rogers, H.L.; Jones, R.L.; Pyle, J.A. Aviation and climate change. Transp. Policy 2014, 34, 14–20. [Google Scholar] [CrossRef]
- Gössling, S.; Humpe, A. The global scale, distribution and growth of aviation: Implications for climate change. Glob. Environ. Chang. 2020, 65, 102194. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Liang, E. Metal additive manufacturing in aircraft: Current application, opportunities and challenges. IOP Conf. Ser. Mater. Sci. Eng. 2019, 493, 012032. [Google Scholar] [CrossRef]
- Ferro, C.; Grassi, R.; Seclì, C.; Maggiore, P. Additive Manufacturing Offers New Opportunities in UAV Research. Procedia CIRP 2016, 41, 1004–1010. [Google Scholar] [CrossRef]
- Petrovic, V.; Haro, J.V.; Jordá, O.; Delgado, J.; Blasco, J.R.; Portolés, L. Additive Layer Manufacturing: State of the art in industrial applications through case studies. Int. J. Prod. Res. 2011, 49, 1061–1079. [Google Scholar] [CrossRef]
- Noronha, J.; Qian, M.; Leary, M.; Kyriakou, E.; Brandt, M. Hollow-walled lattice materials by additive manufacturing: Design, manufacture, properties, applications and challenges. Curr. Opin. Solid State Mater. Sci. 2021, 25, 5. [Google Scholar] [CrossRef]
- Deckers, J. Additive manufacturing of ceramics: A review. J. Ceram. Sci. Technol. 2014, 2014, 245–260. [Google Scholar] [CrossRef]
- Blakey-Milner, B.; Gradl, P.; Snedden, G.; Brooks, M.; Pitot, J.; Lopez, E.; Leary, M.; Berto, F.; du Plessis, A. Metal additive manufacturing in aerospace: A review. Mater. Des. 2021, 209, 110008. [Google Scholar] [CrossRef]
- Udroiu, R. Applications of Additive Manufacturing Technologies for Aerodynamic Tests. Acad. J. Manuf. Eng. 2010, 8, 3. [Google Scholar]
- Hao, L.; Raymont, D.; Yan, C.; Hussein, A.; Young, P. Design and additive manufacturing of cellular lattice structures. Innov. Dev. Virtual Phys. Prototyp. 2011, 2016, 249–254. [Google Scholar] [CrossRef]
- Mclaren, D. Thermal Anti-Icing System for Aircraft. US Patent 5011098, 30 December 1988. [Google Scholar]
- Ferro, C.; Varetti, S.; Maggiore, P.; Lombardi, M.; Biamino, S.; Manfredi, D.; Calignano, F. Design and characterization of trabecular structures for an anti-icing sandwich panel produced by additive manufacturing. J. Sandw. Struct. Mater. 2018, 22, 1111–1131. [Google Scholar] [CrossRef]
- Ferro, C.G.; Varetti, S.; De Pasquale, G.; Maggiore, P. Lattice structured impact absorber with embedded anti-icing system for aircraft wings fabricated with additive SLM process. Mater. Today Commun. 2018, 15, 185–189. [Google Scholar] [CrossRef]
- Vacca, A.P. 180 Main Wing Anti-Ice System: Analysis and Improvements. 2013. Available online: http://www.dicat.unige.it/bottaro/Presentation%20group/Tesi_Vacca.pdf (accessed on 30 May 2024).
- Maggiore, P.; Ferro, C.G.; Varetti, S.; Vitti, F. Thermal Anti Ice System Integrated in the Structure and Method for Its Fabrication. 102016000098196. 2016. Available online: https://patents.google.com/patent/US20200031479A1/en (accessed on 30 May 2024).
- Ferro, C.G. Multidisciplinary Analysis of a Novel Anti-Icing System for a Fixed Wing UAV. 2019. Available online: https://iris.polito.it/handle/11583/2742536 (accessed on 30 May 2024).
- Bici, M.; Brischetto, S.; Campana, F.; Ferro, C.G.; Seclì, C.; Varetti, S.; Maggiore, P.; Mazza, A. Development of a multifunctional panel for aerospace use through SLM additive manufacturing. Procedia CIRP 2018, 67, 215–220. [Google Scholar] [CrossRef]
- Ferro, C.G.; Varetti, S.; Maggiore, P. Experimental Evaluation on Fatigue Strength of Lattice Structures of AlSi10Mg Fabricated by AM for an Innovative Aerospace Anti-Ice System. Aerospace 2023, 10, 400. [Google Scholar] [CrossRef]
- Ferro, C.G.; Pietrangelo, F.; Maggiore, P. Heat exchange performance evaluation inside a lattice panel using CFD analysis for an innovative aerospace anti-icing system. Aerosp. Sci. Technol. 2023, 141, 108565. [Google Scholar] [CrossRef]
- Mahmoud, D.; Elbestawi, M.A. Lattice structures and functionally graded materials applications in additive manufacturing of orthopedic implants: A review. J. Manuf. Mater. Process. 2017, 1, 13. [Google Scholar] [CrossRef]
- Chen, L.-Y.; Liang, S.-X.; Liu, Y.; Zhang, L.-C. Additive manufacturing of metallic lattice structures: Unconstrained design, accurate fabrication, fascinated performances, and challenges. Mater. Sci. Eng. R. Rep. 2021, 146, 100648. [Google Scholar] [CrossRef]
- Hasib, H.; Rennie, A.; Burns, N.; Geekie, L. Non-stochastic lattice structures for novel filter applications fabricated via additive manufacturing. In Proceedings of the Conference: The Filtration Society 50th Anniversary International Conference and Exhibition, Chester, UK, 13–14 November 2014. [Google Scholar]
- Seharing, A.; Azman, A.H.; Abdullah, S. A review on integration of lightweight gradient lattice structures in additive manufacturing parts. Adv. Mech. Eng. 2020, 12, 168781402091695. [Google Scholar] [CrossRef]
- Zargarian, A.; Esfahanian, M.; Kadkhodapour, J.; Ziaei-Rad, S. Numerical simulation of the fatigue behavior of additive manufactured titanium porous lattice structures. Mater. Sci. Eng. C 2016, 60, 339–347. [Google Scholar] [CrossRef] [PubMed]
- Dong, G.; Tang, Y.; Zhao, Y.F. A survey of modeling of lattice structures fabricated by additive manufacturing. J. Mech. Des. Trans. ASME 2017, 139, 100906. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Spierings, A.B.; Mohr, D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- Mantovani, S.; Giacalone, M.; Merulla, A.; Bassoli, E.; Defanti, S. Effective Mechanical Properties of AlSi7Mg Additively Manufactured Cubic Lattice Structures. 3D Print. Addit. Manuf. 2022, 9, 326–336. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Xu, X.; Feng, G.; Li, S.; Song, W.; Jiang, Z. Compressive performance and energy absorption of additively manufactured metallic hybrid lattice structures. Int. J. Mech. Sci. 2022, 219, 107093. [Google Scholar] [CrossRef]
- Li, D.; Qin, R.; Chen, B.; Zhou, J. Analysis of mechanical properties of lattice structures with stochastic geometric defects in additive manufacturing. Mater. Sci. Eng. A 2021, 822, 141666. [Google Scholar] [CrossRef]
- Ueno, A.; Guo, H.; Moritoyo, R.; Takezawa, A.; Kitamura, M. Lemperature distribution design of functionally graded structure based on lattice volume fraction distribution optimization and metal additive manufacturing. Seimitsu Kogaku Kaishi/J. Jpn. Soc. Precis. Eng. 2021, 87, 827–833. [Google Scholar] [CrossRef]
- Raž, K.; Chval, Z.; Santos, R. Development of a Computational Model of Lattice Structure. MATEC Web Conf. 2022, 357, 02012. [Google Scholar] [CrossRef]
- Lozanovski, B.; Leary, M.; Tran, P.; Shidid, D.; Qian, M.; Choong, P.; Brandt, M. Computational modelling of strut defects in SLM manufactured lattice structures. Mater. Des. 2019, 171, 107671. [Google Scholar] [CrossRef]
- Arabnejad, S.; Pasini, D. Mechanical properties of lattice materials via asymptotic homogenization and comparison with alternative homogenization methods. Int. J. Mech. Sci. 2013, 77, 249–262. [Google Scholar] [CrossRef]
- Herrnböck, L.; Steinmann, P. Homogenization of fully nonlinear rod lattice structures: On the size of the RVE and micro structural instabilities. Comput. Mech. 2022, 69, 947–964. [Google Scholar] [CrossRef]
- PBarclay, L.; Zhang, D.Z. A combined ensemble-volume average homogenization method for lattice structures with defects under dynamic and static loading. Comput. Mater. Sci. 2023, 228, 112357. [Google Scholar] [CrossRef]
- Liu, H.; Long, L. Equivalent homogenization design method for stretching-bending hybrid lattice structures. J. Mech. Sci. Technol. 2023, 37, 4169–4178. [Google Scholar] [CrossRef]
- Huang, L.; Yuan, H.; Zhao, H. An FEM-based homogenization method for orthogonal lattice metamaterials within micropolar elasticity. Int. J. Mech. Sci. 2023, 238, 107836. [Google Scholar] [CrossRef]
- Somnic, J.; Jo, B.W. Status and Challenges in Homogenization Methods for Lattice Materials. Materials 2022, 15, 605. [Google Scholar] [CrossRef]
- Somnic, J.; Jo, B.W. Homogenization Methods of Lattice Materials. Encyclopedia 2022, 2, 72. [Google Scholar] [CrossRef]
- Beaver, R.J. Design and Analysis of Experiments-Montgomery, DC. International Biometric SOC 808 17th ST NW SUITE 200, Washington, DC 20006-3910. 1977. Available online: https://www.researchgate.net/profile/Farshad-Fattahi/post/Need-the-procedure-for-critical-limit-fixation/attachment/59d6459179197b80779a0aa7/AS%3A453901993418752%401485230076186/download/Douglas-C.-Montgomery-Design-and-Analysis-of-Experiments-Wiley-2012.pdf (accessed on 30 May 2024).
- Montgomery, D.C. Design and Analysis of Experiments; Jojn Wiley & Sons, Inc.: Tucson, AZ, USA, 2017; p. 684. [Google Scholar]
- SLM Solutions Group AG. SLM®500. The High Power Machine for Metal Additive Manufacturing. Available online: https://www.slm-solutions.com/en/products-and-solutions/machines/slm-500/ (accessed on 30 May 2024).
- Latture, R.M.; Rodriguez, R.X.; Holmes, L.R.; Zok, F.W. Effects of nodal fillets and external boundaries on compressive response of an octet truss. Acta Mater. 2018, 149, 78–87. [Google Scholar] [CrossRef]
- EOS GmbH—Electro Optical Systems. Material Data Sheet: EOS Aluminium AlSi10Mg; EOS GmbH: Temple, TX, USA, 2014; Volume 49, pp. 1–5. [Google Scholar]







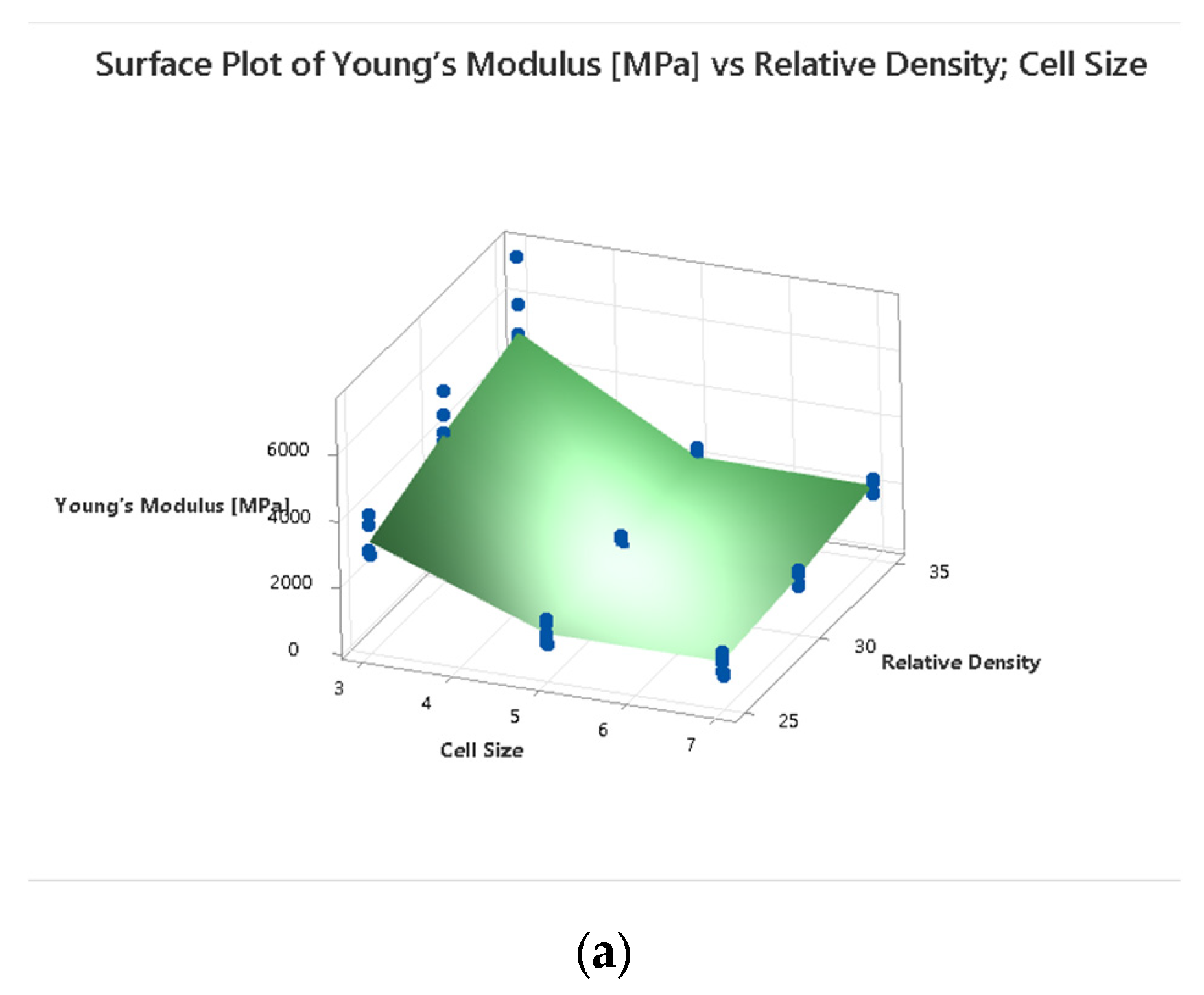




| Cell Type | Cell Size [mm] | Volume Fraction [%] |
|---|---|---|
| Bccz | 3 | 30 |
| Bccz | 5 | 25 |
| Bccz | 7 | 35 |
| Rhombic | 3 | 25 |
| Rhombic | 5 | 35 |
| Rhombic | 7 | 30 |
| Octet | 3 | 35 |
| Octet | 5 | 30 |
| Octet | 7 | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferro, C.G.; Varetti, S.; Maggiore, P. Experimental Evaluation of Mechanical Compression Properties of Aluminum Alloy Lattice Trusses for Anti-Ice System Applications. Machines 2024, 12, 404. https://doi.org/10.3390/machines12060404
Ferro CG, Varetti S, Maggiore P. Experimental Evaluation of Mechanical Compression Properties of Aluminum Alloy Lattice Trusses for Anti-Ice System Applications. Machines. 2024; 12(6):404. https://doi.org/10.3390/machines12060404
Chicago/Turabian StyleFerro, Carlo Giovanni, Sara Varetti, and Paolo Maggiore. 2024. "Experimental Evaluation of Mechanical Compression Properties of Aluminum Alloy Lattice Trusses for Anti-Ice System Applications" Machines 12, no. 6: 404. https://doi.org/10.3390/machines12060404
APA StyleFerro, C. G., Varetti, S., & Maggiore, P. (2024). Experimental Evaluation of Mechanical Compression Properties of Aluminum Alloy Lattice Trusses for Anti-Ice System Applications. Machines, 12(6), 404. https://doi.org/10.3390/machines12060404







