Abstract
Scarfing is a type of flame treatment used to improve the quality of metal generated during steelmaking. It employs the principles of gas cutting to remove impurities and defects. Due to the high-temperature conditions and the need for uniform metal treatment, mechanical scarfing performed via a frame is preferred over manual hand scarfing. To achieve stable mechanical scarfing, a properly designed frame is essential. Generally, while using more material can create stable equipment, it also increases costs. Therefore, this study proposed a design method that selects an acceleration profile to minimize the shock on the frame during scarfing equipment operation while using a multi-objective genetic algorithm to minimize weight and maximize rigidity. Because modifying existing scarfing equipment based on the optimization results would incur additional costs and time, pre-optimizing through simulation before equipment fabrication is crucial. Optimization was achieved via the dimensional optimization of the existing frame equipment. As a result, the weight of each part and the deformation decreased by an average of 17.05 kg and 3.93%, respectively.
1. Introduction
The metal production process generally proceeds in the order of smelting, steelmaking, casting, and rolling. In the steelmaking phase, impurities such as carbon, phosphorus, and sulfur are removed from the metal. However, this process can lead to defects, such as decarburization layers, micro-cracks, rust, and other impurities on the surfaces of slabs and billets [1,2]. Such surface defects can be predicted through thermal transfer analysis [3,4,5]. Moreover, these surface defects on steel ingots or plates can significantly impact product quality. Therefore, it is essential to minimize the possible defects that may arise during the steelmaking process to produce high-grade products such as automotive steel plates [6,7,8].
Scarfing is a type of flame treatment that utilizes the principles of gas cutting to remove defects by melting a wide, shallow area of the steel surface. It is used to remove surface defects such as pits, cracks, non-metallic inclusions, or decarburization layers on steel ingots or plates [9]. By performing scarfing, defects on the steel surface are eliminated, enhancing the stability of the steel [10,11,12,13]. The basic principle of this technology involves the chemical reaction between iron and oxygen, as shown in Figure 1. First, the preheat zone is heated to the ignition temperature of oxygen. Then, a strong blast of pure oxygen is applied, leading to intense combustion in the preheated area and the formation of iron oxide. Because the generated iron oxide has a lower melting point than the base material, it melts due to the heat generated by the combustion. Simultaneously, it is removed by the flow of oxygen, completing the scarfing process.

Figure 1.
Scarfing schematic.
The types of scarfing methods include mechanical scarfing, which uses gas torches to mechanically remove surface defects from the front and back of slabs; hand scarfing, where an operator manually removes defects; grinding scarfing, which uses abrasive stones to eliminate surface defects; and hard scarfing, which employs gases (e.g., acetylene and propane) to melt imperfections. Among these, mechanical scarfing is widely used due to its excellent productivity, which reduces costs. The reduced working time due to the design used for this technique allows for the simultaneous scarfing of the top, bottom, and sides of the slabs and consequently produces a high-quality scarfing surface. Additionally, mechanical scarfing substantially reduces fuel consumption compared to hand scarfing, lowering CO2 emissions. However, due to its functional limitations, a post-process in which workers manually perform hand scarfing to adjust and improve the working material is inevitably required after mechanical scarfing. In the case of hand scarfing, quality differences can arise depending on the skill level of the worker, and hazardous situations may occur due to poor working conditions [14]. Moreover, there is the drawback of excessive energy consumption when workers visually assess the slab shape to perform the task, resulting in increased carbon emissions. To address these issues, there is growing attention toward the development of energy-efficient, low-pressure spray scarfing equipment tailored to the slab conditions [15].
When conducting mechanical scarfing, the scarfing unit is mounted on a frame, and stability is ensured as the operation occurs at high temperatures. However, during the manufacture of frame equipment, excessive focus on stability can lead to the use of unnecessary materials and components, which can incur additional costs [16,17,18]. When restarting scarfing equipment after a stop, different shocks are applied to the structure depending on the acceleration profile [19,20,21]. Therefore, an acceleration profile that minimizes the shock should be used. In this study, as shown in Figure 2, we utilize a multi-objective genetic algorithm (MOGA) to adjust the dimensions of up to three parts of each component in the scarfing equipment, aiming to minimize weight and maximize rigidity. We discern that the acceleration profile minimizes shock while satisfying the maximum transfer speed per second. The extent of this effect is verified through the maximum stress values applied to the frame.
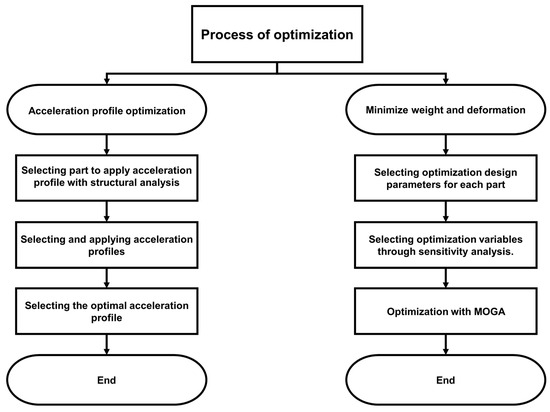
Figure 2.
Flowchart of optimization process.
Optimization is carried out after generating a response surface model that represents the relationship between the results and design variables [22]. Here, the response surface model can be obtained using different experimental design methods that calculate the outcomes for candidate variables. Experimental design enumerates the possible combinations of candidate variables to achieve the desired outcomes, and the methods for setting up the experimental design include central composite design and Box–Behnken design. Both methods define the possible combinations of candidate variables at three levels, but the Box–Behnken design can yield optimal results with fewer experiments compared to the central composite design [23,24,25,26,27,28,29,30,31]. Therefore, in this study, Box–Behnken design is employed to set up the experimental design, and the response surface model is generated based on the derived results.
After obtaining the response surface, design variables are optimized based on a MOGA. Dao [32] and Hashemian [33] used genetic algorithms to optimize the structure. However, their optimization was a single-objective function optimization rather than a multi-objective function, and they did not consider the acceleration profile of the machine as it moved. There are a variety of optimization methods that can be used to optimize a single-objective function, such as least-squares, genetic algorithms, and artificial neural networks [34]. However, the problem with multiple objectives is that it is difficult to optimize each objective at the same time, similar to how excessive materials are used in machine designs which focus on minimizing strain regardless of increasing the weight of the machine. To address this problem, a MOGA has been used. There are various genetic algorithms such as Vector Evaluated Genetic Algorithm (VEGA) and MOGA. Both VEGA and MOGA have the advantage of being simple to build, but VEGA has the disadvantage of converging to the extremes of each objective. MOGA assigns fitness through Pareto ranking. A fitness value is assigned to each solution based on the population’s ranking, assuming that all objectives are minimized. Figure 3 below explains the MOGA process. As mentioned above, the fitness value is evaluated after assigning a fitness rank to each solution. The process is repeated to identify the Pareto solutions and find the optimal solution that satisfies the objective function [35,36,37,38,39,40,41,42,43,44]. Figure 3 shows a diagram of the structure of MOGA. As shown in Figure 3, MOGA consists of initialization, evaluation, selection, crossover, and mutation. First, the initial population is randomly generated in the initialization step, and then the fitness is calculated for each individual according to the objective function in the evaluation stage. Pareto ranking is used to rank solutions by assigning a fitness value to each solution. Then, the parent generation is selected from the current population based on the fitness. In the crossover phase, offspring are created by combining genetic materials from pairs of parents, and in the mutation procedure, random changes are introduced in the offspring to maintain genetic diversity. The algorithm then terminates when a predefined number of generations is reached or the population converges to a satisfactory solution, otherwise it repeats the algorithm again. An additional advantage of MOGAs is that they can be optimized without the need for complex physical or mathematical analysis. In this study, the objective functions are defined as minimizing mass and deformation to achieve both weight reduction and increased rigidity in the frame equipment.

Figure 3.
Block diagram of the multi-objective genetic algorithm.
2. Geometry
Frame for the Scarfing Process
The model and structure of the scarfing equipment frame are shown in Figure 4. The frame structure consists of four major parts, each named based on the axis along which the equipment is aligned: x-axis part, y-axis part, z-axis part, and head part. Except for the head part, each part is equipped with motors and rack gears suitable for transferring the scarfing equipment along the x-, y-, and z-axes. The x-axis part is anchored to the ground with anchor bolts and supports the other three parts via a saddle plate, enabling movement along the x-axis. The y-axis part is double-ended and supports the head part in the center, allowing for y-axis movement. It is connected to the z-axis part via an LM guide, enabling movement along the z-axis. The z-axis part is directly connected to the x-axis part and supports both the y-axis and head parts, allowing for z-axis movement.
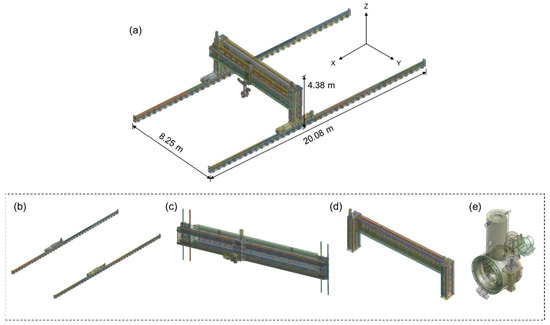
Figure 4.
Schematic of scarfing machine: (a) scarfing model, (b) x-axis part, (c) y-axis part, (d) z-axis part, and (e) head part.
Structural analysis was performed on each part of the scarfing machine to determine which parts of the machine to apply the acceleration profile before selecting the optimal acceleration profile. The scarfing machine is stressed even before it is driven due to its own weight. When the machine is driven, it is impacted further by the acceleration. This leads to increased stress concentration, which in turn leads to the deformation of the machine. Therefore, different acceleration profiles were applied to the most stressed parts in the structural analysis to select the optimal acceleration profile that minimizes deformation when the machine is driven. In addition, three variables were selected, including the stress concentration of each part and the structural stress concentration of the scarfing machine, and optimized as an objective function to minimize the weight and deformation of the machine. The boundary conditions for the structural analysis of each part can be found in Table 1. The load condition is the self-weight of each part. As shown in Figure 5, fixed support conditions were applied to the surface where the anchor bolts are connected for the x-axis part, and fixed support conditions were applied to the surface that is in contact with other parts. The material used was structural steel, which is provided as a default option in the ANSYS 2022 R1 software. The structural analysis results are shown in Figure 5a–d, which display the x-axis, y-axis, z-axis, and head parts, respectively. The highest stress was recorded in the y-axis part. This elevated stress in the y-axis part is due to its unique positioning. Compared with the other parts, it is elevated from the ground and fixed to the z-axis part, resulting in concentrated stress at the connection point with the z-axis part. Therefore, considering the direction in which the y-axis part is transferred, we proposed an acceleration profile that minimizes deformation due to shock, and selected design variables for optimization based on a sensitivity analysis of the dimensions that constitute each part.

Table 1.
Boundary conditions of structural analysis.

Figure 5.
Structural analysis: (a) x-axis, (b) y-axis, (c) z-axis, and (d) head parts.
3. Optimization Method
3.1. Selection of Acceleration Profile
The shock exerted on the frame of the scarfing equipment varies with the control method used during its transfer. The control method involves sketching an acceleration profile and applying it to the frame equipment. Rapid acceleration or deceleration of the stationary scarfing equipment can result in shocks to the equipment. If such shocks repeatedly occur, deformation or fracturing may occur, causing the equipment to fail. Minimizing shocks during operation is crucial because this directly impacts the lifespan of the scarfing equipment. Furthermore, if mechanical scarfing is followed by a lot of post-processing by hand scarfing due to a deformation of the scarfing equipment, the quality of the product after scarfing depends on the skill level of the operator, and worker safety accidents may occur. In addition, the advantages of mechanical scarfing, such as reduced fuel consumption, working time, and CO2 emissions, are lost when hand scarfing is required. To mitigate this issue, this study aims to propose an optimal acceleration profile by comparing three different acceleration profiles. In terms of force, it is the product of acceleration and mass. In selecting the acceleration profile, Figure 6a shows the acceleration profiles of a quadratic, triangle, and trapezoid, with 0, 1, and 2 points, where the force changes dramatically. Each acceleration profile was made to reach 25 minutes-per-minute (mpm), the driving speed of the scarifying machine, after 1 s, and the initial velocities were both 0 mpm. In the case of the triangle profile shown in Figure 6a, a target speed of 25 mpm must be reached and maintained within 1 s. Therefore, the acceleration increases for 0.5 s and then decreases for the next 0.5 s, ultimately maintaining a speed of 25 mpm. For the quadratic profile, a speed of 25 mpm must also be reached and maintained after 1 s, following to set the acceleration. For the trapezoid profile, the acceleration increases for 0.25 s, remains constant from 0.25 to 0.75 s, and then decreases. The speed is stabilized at 25 mpm by the time it reaches 1 s. Figure 6b shows the area of maximum deformation in the y-axis part when the triangle acceleration profile is applied to operate the scarfing equipment. Figure 6c shows the results of the application of the quadratic acceleration profile, and Figure 6d presents the results of the application of the trapezoid acceleration profile. For the y-axis part, which has a fixed-end support shape, the largest deformation occurred at the bottom center under all acceleration profiles. The maximum stress occurred at the point of connection with the z-axis part. The application of the acceleration profiles showed that the smallest deformations occurred when accelerating along the quadratic profile, which has no points where the force changes abruptly. This confirms that applying acceleration in the form of a quadratic profile when stopping or starting the scarfing machine has less of an impact on the scarfing machine. This is due to the quadratic profile having less-abrupt force changes compared to the other two profiles.

Figure 6.
Acceleration profiles and the respective results: (a) acceleration profile, (b) triangle profile, (c) quadratic profile, and (d) trapezoid profile.
3.2. Design of Experiment
Generally, various techniques, such as response surface analysis, interaction plots, and sensitivity analysis, are carried out to understand the relationship between design factors and objective functions. For such analyses, the design of experiments is conducted, and the objective functions are calculated for multiple cases based on the values of the design variables. In most systems, the input and output variables are not linear; therefore, to accommodate this non-linearity, the independent and dependent variables are represented by the quadratic regression below (Equation (4)), where , and are the independent variables and is the dependent variable. Also, is a constant, and , and are the regression coefficients.
Popular methods for constructing the design of experiments include central composite design and Box–Behnken design. The central composite design sets up the experimental plan based on the vertices, axial points, and center points of design variables, as shown in Figure 7a. The Box–Behnken design sets up the experimental plan within the safety range without axial points, as shown in Figure 7b. The Box–Behnken design requires three levels for each factor, and the number of experiments required () is defined as , where is the number of design variables and is the number of center points. In this article, we set the number of design variables to 3 and the number of center points to 1; therefore, the number of experiments required for the Box–Behnken design is 13, as shown in Table 2. In contrast, the central composite design requires five levels for each factor, and the number of experiments is defined as . Accordingly, a total of 15 experiments are required. The advantage of a Box–Behnken design is that the predicted variance is reasonably distributed across the experimental design area. It also has the advantage of requiring fewer experiments than the central composite design to evaluate multiple variables and their interactions, and is more practical and efficient than central composite design with the same number of factors. In addition, Box–Behnken design has the advantage of reducing the number of experiments performed under extreme conditions that are prone to unsatisfactory results because it does not include combinations where all factors are at their highest and lowest levels at the same time [24]. Considering these advantages, in this article, the design of experiments was created using Box–Behnken design, and based on the results, a sensitivity analysis was performed to select only the two most sensitive factors per part for optimization.
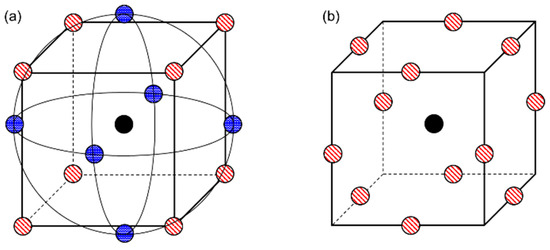
Figure 7.
Design of experiment: (a) central composite design and (b) Box–Behnken design.

Table 2.
Box–Behnken design.
When constructing the experimental design for the structural analysis of the x-axis part, the three dimensions were selected as input variables (Figure 8), and the maximum deformation and mass were chosen as the output variables. The names of each design variable were defined as saddle plate thickness, top rail plate width, and bottom rail plate width, and the dimensions for these existing design variables are shown in Table 3. These factors were selected to ensure that dimensional changes in each part would not interfere with the other parts and would not disrupt machine operation. The results of the experimental plan based on the Box–Behnken design revealed that the thickness of the saddle plate and the width of the top rail plate are sensitive factors affecting maximum deformation (Figure 9a), and in the case of the response surface, they showed near-linear changes (Figure 9b). Additionally, there was no interaction between the two factors, as shown in Figure 9c.

Figure 8.
Schematic of scarfing machine: (a) x-axis part model, (b) saddle plate, (c) top rail plate, and (d) bottom rail plate.

Table 3.
Dimensions of each design parameter.

Figure 9.
The x-axis part: (a) analysis of sensitivity, (b) response surface, and (c) intersection plot.
When constructing the experimental design for the structural analysis of the y-axis part, the input variables were selected as three dimensions (Figure 10), and the output variables were chosen as the maximum deformation and mass. The names of each design variable were defined as front beam thickness, behind beam width, and plate height, and the dimensions for these existing design variables are shown in Table 3. The results of the experimental plan based on the Box–Behnken design showed that the thickness of the front beam and width of the behind beam are sensitive factors to maximum deformation, as shown in Figure 11a. In the case of the response surface, the deformation reached its minimum value when the front beam thickness is 30 mm, as shown in Figure 11b. Additionally, the two factors were independent of each other, as shown in Figure 11c.
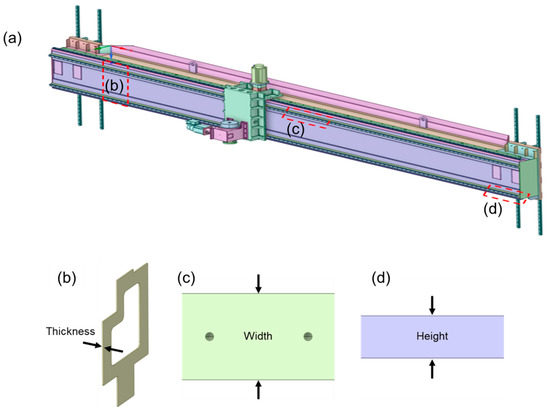
Figure 10.
Schematic of scarfing machine: (a) y-axis part model, (b) front beam, (c) behind beam, and (d) rail plate.
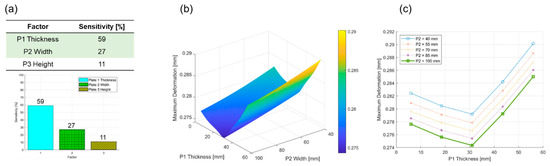
Figure 11.
The y-axis part: (a) analysis of sensitivity, (b) response surface, and (c) intersection plot.
When constructing the experimental design for the structural analysis of the z-axis part, input variables were selected as three dimensions (Figure 12), and output variables were chosen as the maximum deformation and mass. The names of each design variable were defined as the horizontal beam plate thickness, vertical beam plate thickness, and rail length, and Table 3 lists the dimensions for these existing design variables. The results of the experimental design based on the Box–Behnken design revealed that the thickness of the horizontal beam plate and the width of the vertical beam plate are sensitive factors affecting maximum deformation, as shown in Figure 13a. In the case of the response surface, they showed near-linear changes, as shown in Figure 13b. Additionally, there was no interaction between the two factors, as shown in Figure 13c.
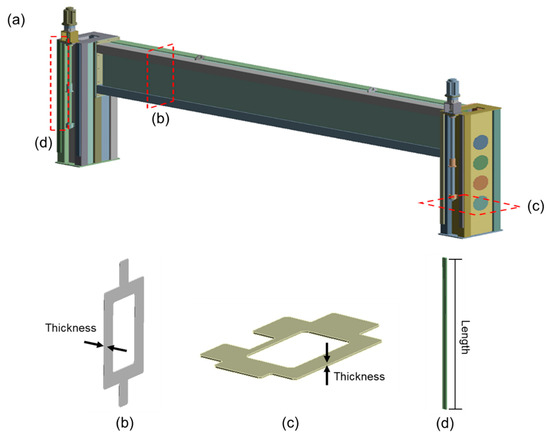
Figure 12.
Schematic of scarfing machine: (a) z-axis part model, (b) horizontal beam plate, (c) vertical beam plate, and (d) rail.

Figure 13.
The z-axis part: (a) analysis of sensitivity, (b) response surface, and (c) intersection plot.
When constructing the experimental design for the structural analysis of the head part, input variables were selected as three dimensions (Figure 14), and output variables were chosen as the maximum deformation and mass. The names of each design variable were defined as the servo motor base thickness, servo motor base height, and handling head body thickness. Table 3 lists the dimensions for these existing design variables. The results of the experimental design based on the Box–Behnken design revealed that the servo motor base thickness and servo motor base height are sensitive factors to maximum deformation, as shown in Figure 15a. In the case of the response surface, they showed near-linear changes, as shown in Figure 15b. Additionally, there was no interaction between the two factors, as shown in Figure 15c.

Figure 14.
Schematic of scarfing machine: (a) head part model, (b) servo motor base thickness, (c) handling head body thickness, and (d) servo motor base height.

Figure 15.
Head part: (a) analysis of sensitivity, (b) response surface, and (c) intersection plot.
Table 4 lists the optimization results obtained through MOGA, which sets the minimization of deformation and weight as objective functions based on the sensitivity analysis for each part. The parameters of MOGA are “Number of initial samples” and “Number of samples per iteration” set to 100. “Maximum allowable Pareto percentage” is set to 70%, and the “Maximum number of iterations” is set to 20. Therefore, the optimization process is terminated when the resulting MOGA edge contains 70 points, which is 70% of the number of samples per iteration of 100, or when the maximum number of iterations is reached [45,46]. In the case of the x-axis part, structural analysis revealed that the maximum stress occurs in the saddle plate, which connects with the other parts. To improve the equipment’s stability, this component was optimized by increasing its thickness from 10 to 35.95 mm. Additionally, to reduce the weight, the width of the top rail plate, which is the connection point between the ground-fixed rail and the scarfing equipment’s transporting rail, decreased from 150 to 101.84 mm. As a result of the optimization, the weight of the x-axis part and the deformation decreased by 11.3 kg and 3.31%, respectively.

Table 4.
Optimization results of each part.
For the y-axis part, the head part is attached, concentrating the load on the front beam. Thus, to reduce deformation, the thickness of the front beam was optimized, increasing from 6 to 30.03 mm. However, if the thickness exceeds 30.03 mm, the weight of the front beam becomes considerably large, increasing the deformation. Additionally, the width of the behind beam, which receives a relatively smaller load, was optimized from 70 to 44.72 mm, satisfying the weight minimization objective. As a result, the weight of the y-axis part and the deformation were reduced by 27.8 kg and 1.18%, respectively, confirming an improvement in rigidity.
For the z-axis part, the y-axis and head parts are attached to the horizontal beam. This load is supported by the vertical beam, resulting in maximum stress occurring in the vertical beam. The thickness of the vertical beam plate was increased from 6 to 7.96 mm to minimize the deformation in the vertical beam. Conversely, the thickness of the horizontal beam plate, which receives a relatively lower load from the y-axis part, was reduced from 6 to 4.05 mm, achieving weight minimization. As a result, the weight of the z-axis part was reduced by a total of 23 kg, and the deformation also decreased by 1.94%.
For the head part, the maximum stress was identified in the servo motor base, which received a substantial load due to motor support. To minimize deformation, the thickness of the servo motor base was increased from 7.6 to 11.6 mm. The thickness of the handling head body, which receives a relatively smaller load, was reduced from 20 to 16.8 mm as the thickness of the servo motor base increased, leading to a total weight reduction of 6.1 kg for the head part. Additionally, the deformation decreased by 9.28%, achieving the highest rigidity maximization among all components.
4. Conclusions
This study proposed a MOGA for optimizing scarfing equipment and an acceleration profile to minimize shock during equipment operation. Additionally, the deformation rate occurring during equipment operation was predicted using this acceleration profile. For the optimization of the scarfing equipment, design variables that could be changed in the design drawings were selected, and their initial ranges were determined in a manner that did not induce deformation in other parts. Subsequently, Box–Behnken design was employed to generate combinations of variables, and sensitivity analysis was conducted to identify two design variables for each part. An optimization process was carried out using the selected variables with the MOGA.
As a result of optimization, the thickness or width of components where maximum stress occurs increased, enhancing the stability of the scarfing equipment. Conversely, dimensions of components subjected to relatively lower stress were reduced, making the equipment more lightweight. The weight reduction for each part amounted to 11.3, 27.8, 23, and 6.1 kg, for a total decrease of 68.2 kg, and the rigidity increased by an average of approximately 3.93% compared to that of the original equipment.
Minimizing the deformation during operation is critical because scarfing equipment is both heavy and bulky. Focusing solely on minimizing deformation during production could lead to the use of unnecessary materials and components, thereby wasting production costs and potentially increasing the equipment’s weight. This could amplify the shock due to inertia during operation.
Based on these simulation results, performing appropriate simulations and optimizations in the early stages of equipment production is highly rational considering the additional costs and time associated with the replacement of the actual equipment. Moreover, this study provides practical guidelines for the design and operation of scarfing equipment. The approach utilized in this study is applicable to other industrial sectors and will help lay the foundation for future research and development.
Author Contributions
Conceptualization, C.L., S.L., Y.L. and B.P.; methodology, C.L. and S.L.; software, S.L., Y.L. and B.P.; validation, C.L., S.L. and Y.L.; formal analysis, S.L.; investigation, S.L.; data curation, S.L., Y.L. and B.P.; writing—original draft preparation, S.L.; writing—review and editing, C.L.; visualization, S.L.; supervision, C.L.; project administration, C.L.; funding acquisition, C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Industrial Fundamental Technology Development Program (No. 20018041, “Development of Energy-saving Low Pressure Injection type Scarfing machine for High-Quality Rolled Steel materials”) funded by the Ministry of Trade, Industry and Energy (MOTIE) of Korea and Korea Institute for Advancement of Technology (KIAT) grant funded by the Korea Government (MOTIE) (P0012770).
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Knap, M.; Bradaškja, B. Determination of the Influence of Steelmaking Parameters on Surface Defects in Quarto Plates. Metals 2023, 13, 536. [Google Scholar] [CrossRef]
- Sychkov, A.B.; Zhigarev, M.A.; Perchatkin, A.V.; Mazanov, S.N.; Zenin, V.S. The transformation of defects in continuous-cast semifinished products into surface defects on rolled products. Metallurgist 2006, 50, 83–90. [Google Scholar] [CrossRef]
- Upadhya, G.K.; Das, S.; Chandra, U.; Paul, A.J. Modelling the Investment Casting Process: A Novel Approach for View Factor Calculations and Defect Prediction. Appl. Math. Model. 1995, 19, 354–362. [Google Scholar] [CrossRef]
- Jeon, H.; Noh, J.; Kim, M.; Jo, M.; Nam, S.; Jo, J.; Lee, C. Control Methodology for Tensioned Web Considering Thermal Behavior in Roll-to-Roll Manufacturing Systems. Eng. Sci. Technol. Int. J. 2023, 46, 101508. [Google Scholar] [CrossRef]
- Noh, J.; Jo, M.; Jeon, H.; Kim, M.; Jo, J.; Lee, C. Web Wrinkle Defects Due to Temperature Profile in Roll-to-Roll Manufacturing Systems. Polymers 2023, 15, 15020457. [Google Scholar] [CrossRef]
- Erlbacher, E.A.; Godwin, L.E. Automated Scarfing and Surface Finishing Apparatus for Curved Composite Structures. In Proceedings of the ASME 1997 International Mechanical Engineering Congress and Exposition, Dallas, TX, USA, 16–21 November 1997; Volume 1, pp. 309–316. [Google Scholar] [CrossRef]
- Straka, Ľ.; Čorný, I. Prediction and Multiparametric Optimization of the Machined Surface Quality of Tool Steels in Precise Wire Electrical Discharge Machining. Machines 2024, 12, 248. [Google Scholar] [CrossRef]
- Gordon, T.; Xu, X.; Kawashita, L.; Wisnom, M.R.; Hallett, S.R.; Kim, B.C. Delamination Suppression in Tapered Unidirectional Laminates with Multiple Ply Drops Using a Tape Scarfing Technique. Compos. Part. A Appl. Sci. Manuf. 2021, 150, 106627. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.; Yue, X.; Li, Z.; Li, B. Experimental and Numerical Analysis on Noise Characteristics of Parallel Multiple Jets Obliquely Impinging on a Flat Surface in the Steel Slab Scarfing. Steel Res. Int. 2020, 91, 2000125. [Google Scholar] [CrossRef]
- Gordon, T.; Xu, X.; Wisnom, M.R.; Hallett, S.R.; Kim, B. Improved Impact Damage Resistance of Tapered Composite Laminates Using a Ply Scarfing Technique. Compos. Part. A Appl. Sci. Manuf. 2023, 166, 107391. [Google Scholar] [CrossRef]
- Sui, L.; Zhidong, G.; Xia, G.; Jianhua, C.; Guofen, X.; Jing, C. Tensile Behavior of Hybrid Plain Woven Fabric Laminate Repaired by Scarfing Method. Polym. Poly Compos. 2013, 21, 599–606. [Google Scholar] [CrossRef]
- Contuzzi, N.; Mortello, M.; Casalino, G. On the Laser Scarfing of Epoxy Resin Matrix Composite with Copper Reinforcement. Manuf. Lett. 2021, 27, 1–3. [Google Scholar] [CrossRef]
- Contuzzi, N.; Casalino, G. Statistical Modelling and Optimization of Nanosecond Nd:YAG Q-Switched Laser Scarfing of Carbon Fiber Reinforced Polymer. Opt. Laser Technol. 2022, 147, 107599. [Google Scholar] [CrossRef]
- Setyanto, N.W.; Efranto, R.; Lukodono, R.P.; Dirawidya, A. Ergonomics Analysis in the Scarfing Process by OWAS, NIOSH and Nordic Body Map’s Method at Slab Steel Plant’s Division. Int. J. Innov. Res. Sci. Eng. Technol. 2015, 2006, 1086–1093. [Google Scholar] [CrossRef]
- Holzhüter, D.; Pototzky, A.; Hühne, C.; Sinapius, M. Automated scarfing process for bonded composite repairs. In Adaptive, Tolerant and Efficient Composite Structures; Springer: Berlin/Heidelberg, Germany, 2013; pp. 297–307. [Google Scholar] [CrossRef]
- Masoudi, N.; Fadel, G. An Optimization Framework for the Design of Cable Harness Layouts in Planar Interconnected Systems. ASME J. Mech. Des. 2021, 144, 011701. [Google Scholar] [CrossRef]
- Biswas, A.; Fuentes, C.; Hoyle, C. A Multi-Objective Bayesian Optimization Approach Using the Weighted Tchebycheff Method. ASME J. Mech. Des. 2022, 144, 1–14. [Google Scholar] [CrossRef]
- Jo, M.; Noh, J.; Cho, G.; Lee, T.M.; Oh, B.; Nam, S.; Lee, C. Strain Optimization of Tensioned Web through Computational Fluid Dynamics in the Roll-to-Roll Drying Process. Polymers 2022, 14, 2515. [Google Scholar] [CrossRef] [PubMed]
- Lewin, C. Mathematics of Motion Control Profiles; Performance Motion Devices Inc.: Lincoln, MA, USA, 2007; pp. 1–5. [Google Scholar]
- Rew, K.; Ha, C.; Kim, K. A Practically Efficient Method for Motion Control Based on Asymmetric Velocity Profile. Int. J. Mach. Tools Manuf. 2009, 49, 678–682. [Google Scholar] [CrossRef]
- Jo, M.; Kim, S.; Cho, G.; Lee, T.; Lee, J.; Lee, C. Achieving specified geometric quality in a fully printed flexible functional layer using process parameters in roll-to-roll printed electronics. Flex. Print. Electron. 2022, 7, 014007. [Google Scholar] [CrossRef]
- Abbaszadeh, K.; Alam, F.R.; Saied, S.A. Cogging Torque Optimization in Surface-Mounted Permanent-Magnet Motors by Using Design of Experiment. Energy Convers. Manag. 2011, 52, 3075–3082. [Google Scholar] [CrossRef]
- Xiong, J.; Sun, Y.; Zheng, J.; Dong, D.; Bai, L. Design and Experiment of a SMA-Based Continuous-Stiffness-Adjustment Torsional Elastic Component for Variable Stiffness Actuators. Smart Mater. Struct. 2021, 30, 105021. [Google Scholar] [CrossRef]
- Ferreira, S.C.; Bruns, R.E.; Ferreira, H.S.; Matos, G.D.; David, J.M.; Brandão, G.C.; da Silva, E.P.; Portugal, L.A.; Dos Reis, P.S.; Souza, A.S.; et al. Box-Behnken Design: An Alternative for the Optimization of Analytical Methods. Anal. Chim. Acta 2007, 597, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Loutas, T.H.; Sotiriadis, G.; Tsonos, E.; Psarras, S.; Kostopoulos, V. Investigation of a Pulsed Laser Ablation Process for Bonded Repair Purposes of CFRP Composites via Peel Testing and a Design-of-Experiments Approach. Int. J. Adhes. Adhes. 2019, 95, 102407. [Google Scholar] [CrossRef]
- Mahdavi, R.; Talesh, S.S.A. Effects of Amine (APTES) and Thiol (MPTMS) Silanes-Functionalized ZnO NPs on the Structural, Morphological and, Selective Sonophotocatalysis of Mixed Pollutants: Box–Behnken Design (BBD). J. Alloys Compd. 2022, 896, 163121. [Google Scholar] [CrossRef]
- Patnaik, L.; Maity, S.R.; Kumar, S. Modeling of Wear Parameters and Multi-Criteria Optimization by Box-Behnken Design of AlCrN Thin Film against Gamma-Irradiated Ti6Al4V Counterbody. Ceram. Int. 2021, 47, 20494–204511. [Google Scholar] [CrossRef]
- Polat, S.; Sayan, P. Application of Response Surface Methodology with a Box–Behnken Design for Struvite Precipitation. Adv. Powder Technol. 2019, 30, 2396–2407. [Google Scholar] [CrossRef]
- Wu, L.; Yick, K.L.; Ng, S.P.; Yip, J. Application of the Box-Behnken Design to the Optimization of Process Parameters in Foam Cup Molding. Expert. Syst. Appl. 2012, 39, 8059–8065. [Google Scholar] [CrossRef]
- Nam, S.; Cho, H.; Han, J.; Her, N.; Yoon, J. Photocatalytic Degradation of Acesulfame K: Optimization Using the Box–Behnken Design (BBD). Process Saf. Environ. Prot. 2018, 113, 10–21. [Google Scholar] [CrossRef]
- Tak, B.; Tak, B.; Kim, Y.; Park, Y.; Yoon, Y.; Min, G. Optimization of Color and COD Removal from Livestock Wastewater by Electrocoagulation Process: Application of Box-Behnken Design (BBD). J. Ind. Eng. Chem. 2015, 28, 307–315. [Google Scholar] [CrossRef]
- Dao, S.D.; Abhary, K.; Marian, R. An innovative framework for designing genetic algorithm structures. Expert Syst. Appl. 2017, 90, 196–208. [Google Scholar] [CrossRef]
- Hashemian, A.H.; Kargarnovin, M.H.; Jam, J.E. Optimization of geometric parameters of latticed structures using genetic algorithm. Aircr. Eng. Aerosp. Technol. 2011, 83, 59–68. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Nojima, Y.; Doi, T. Comparison between Single-Objective and Multi-Objective Genetic Algorithms: Performance Comparison and Performance Measures. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; Volume 2006, pp. 1143–1150. [Google Scholar] [CrossRef]
- Wu, D.; Sotnikov, D.; Wang, G.G.; Coatanea, E.; Lyly, M.; Salmi, T.A. Dimension Selection-Based Constrained Multi-Objective Optimization Algorithm Using a Combination of Artificial Intelligence Methods. ASME J. Mech. Des. 2023, 145, 1–15. [Google Scholar] [CrossRef]
- Li, R.; Wang, Z.; Yan, J. Multi-Objective Optimization of the Process Parameters of a Grinding Robot Using LSTM-MLP-NSGAII. Machines 2023, 11, 882. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Yildiz, A.R. Comparison of Evolutionary-Based Optimization Algorithms for Structural Design Optimization. Eng. Appl. Artif. Intell. 2013, 26, 327–333. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-Objective Optimization Using Genetic Algorithms: A Tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Elhadidy, A.A.; Elbeltagi, E.E.; Ammar, M.A. Optimum Analysis of Pavement Maintenance Using Multi-Objective Genetic Algorithms. HBRC J. 2015, 11, 107–113. [Google Scholar] [CrossRef]
- Ghorbani-Menghari, H.; Mohammadhosseinzadeh, M.; Sarband, A.S.; Wahabzadeh, A.H.; Kahhal, P.; Kim, J.H. Investigation of the Effects of Process Parameters on Hydrodynamic Deep Drawing of AL-1050 Sheet with Indentations Using Genetic Algorithm–Based Optimization. Int. J. Adv. Manuf. Technol. 2023, 129, 3949–3964. [Google Scholar] [CrossRef]
- Lu, X.; Luan, Y.; Qiao, J.; Yang, B.; Zhang, W.; Liang, S.Y. Optimization of Process Parameters in Friction Stir Welding of 2219 Aluminum Alloy Thick Plate. Int. J. Adv. Manuf. Technol. 2023, 129, 4201–4215. [Google Scholar] [CrossRef]
- Li, C.; Zhao, G.; Meng, F.; Yu, S.; Yao, B.; Liu, H. Multi-objective optimization of machining parameters in complete peripheral milling process with variable curvature workpieces. J. Manuf. Process 2024, 117, 95–110. [Google Scholar] [CrossRef]
- Yu, H.; Han, J.; Li, S.; Han, X.; Liu, Y.; Wang, J.; Lin, J. Multi-objective optimization design and performance evaluation of a novel flexure-based tri-axial servo cutting system. J. Manuf. Process 2022, 84, 1133–1149. [Google Scholar] [CrossRef]
- Moghimi, M.A.; Craig, K.J.; Meyer, J.P. Optimization of a trapezoidal cavity absorber for the Linear Fresnel Reflector. Sol. Energy 2015, 119, 343–361. [Google Scholar] [CrossRef]
- Ndiogou, B.A.; Thiam, A.; Mbow, C.; Adjibade, M.I.S.; Sambou, V. Modeling and optimization method of an indirectly irradiated solar receiver. MethodsX 2019, 6, 43–55. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).