Design and Test of a 2-DOF Compliant Positioning Stage with Antagonistic Piezoelectric Actuation
Abstract
1. Introduction
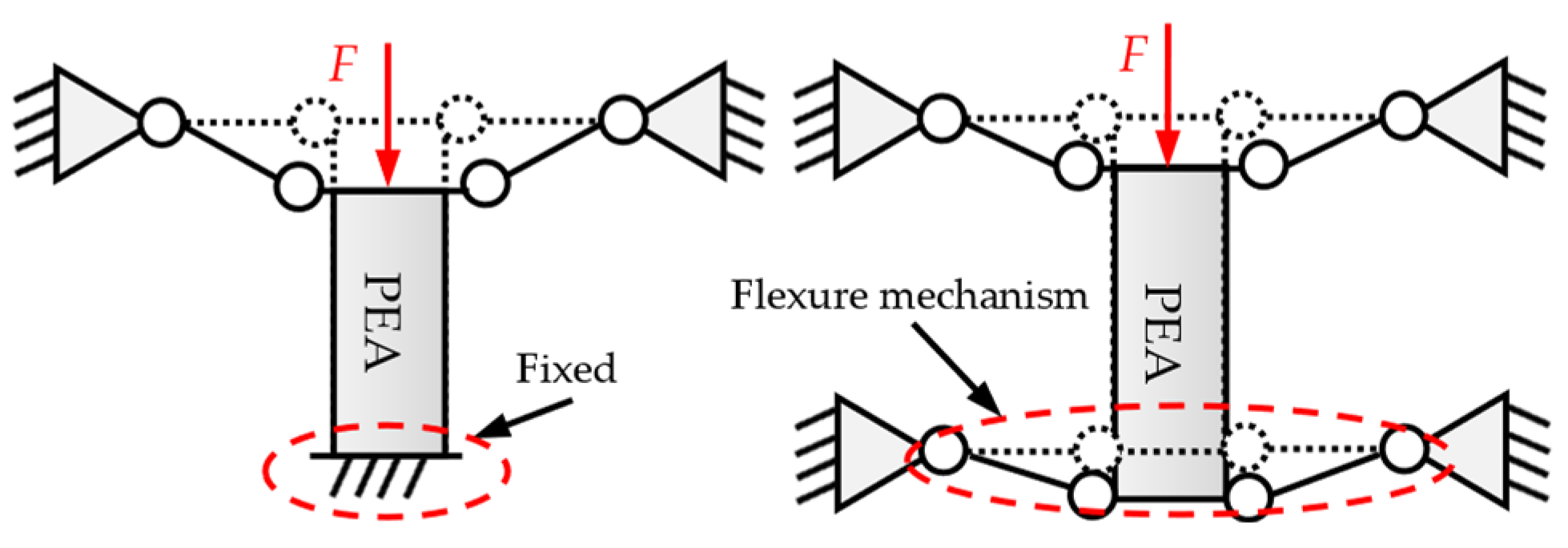
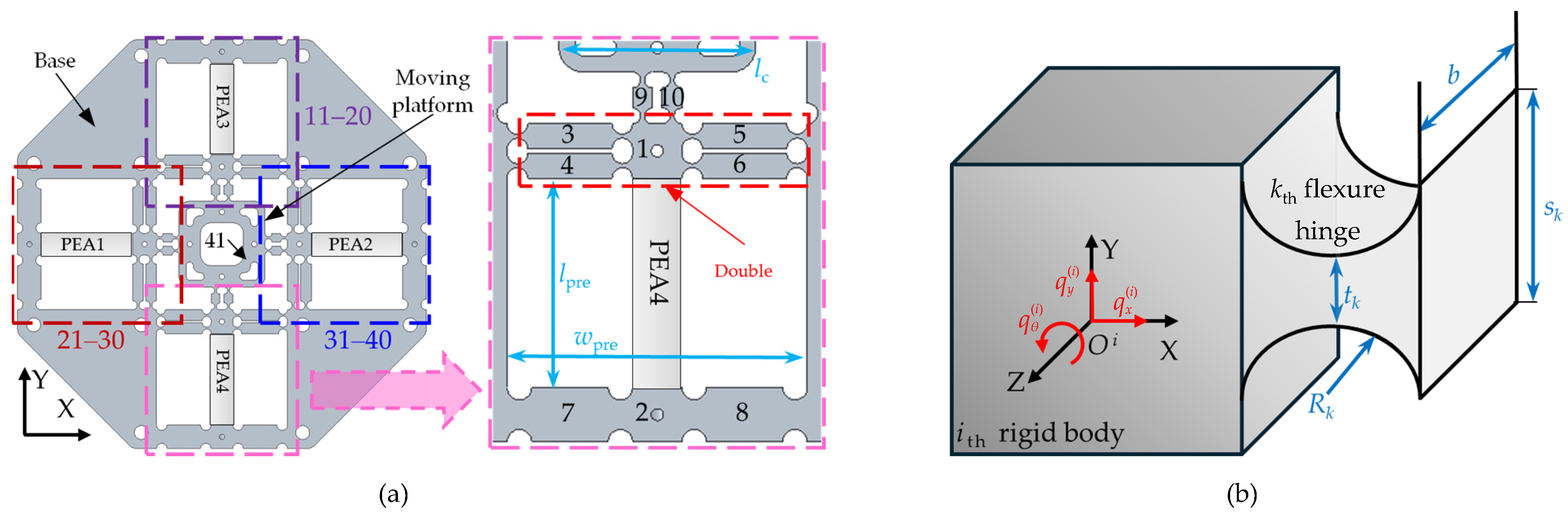
2. Mechanical Design
- (1).
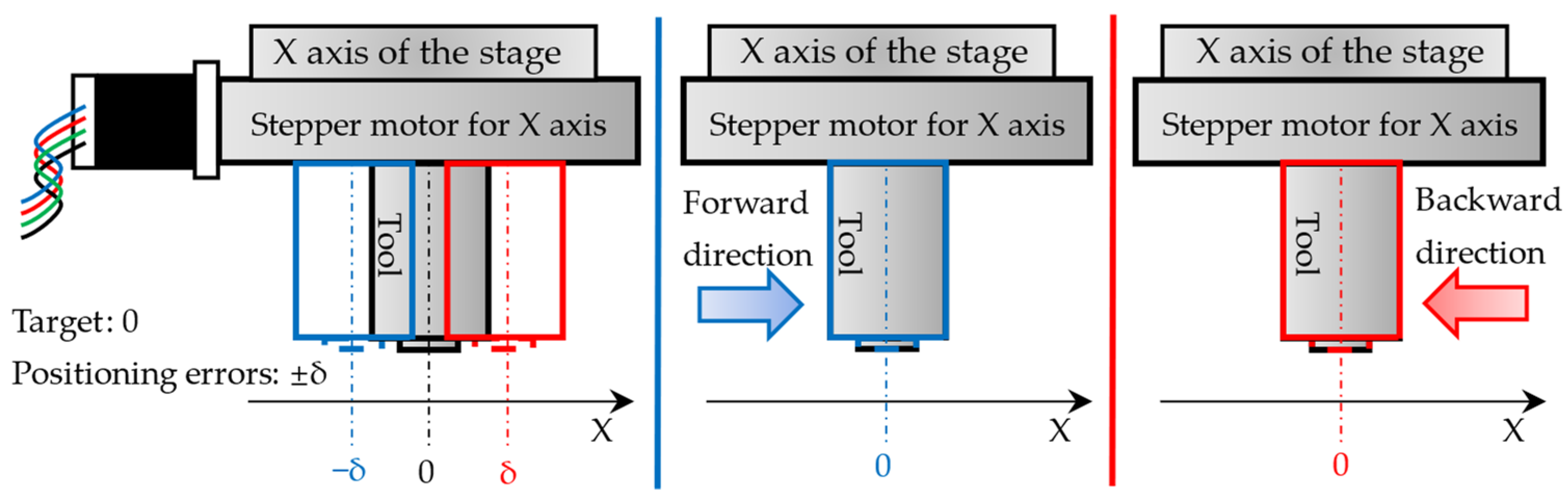
- Single PEA actuation. In this case, a single PEA is used to drive the moving platform. The PEA is unidirectional in nature because only non-negative voltages are allowed for PEAs. To realize bidirectional actuation, half of the maximum voltage is adopted as a bias to the control voltage. This is equivalent to manually translating the origin of the PEA from 0% to 50% of the stroke. To compensate for the positioning error of ±δ μm, the stroke of the PEA should be larger than 2δ μm. This method has been widely adopted, whereas it will keep the PEA energized all the time. This might cause undesired heating to the PEA and reduce the lifetime of the PEA.
- (2).
- Dual PEAs in antagonistic actuation. In this case, two PEAs are placed in an antagonistic configuration and energized alternately to realize bidirectional actuation. Different from the first method, in antagonistic actuation, neither PEA has to be initialized to half of the maximum voltage, and the stroke of the PEA only needs to be larger than δ μm.
3. Parameter Optimization and FEA Verification
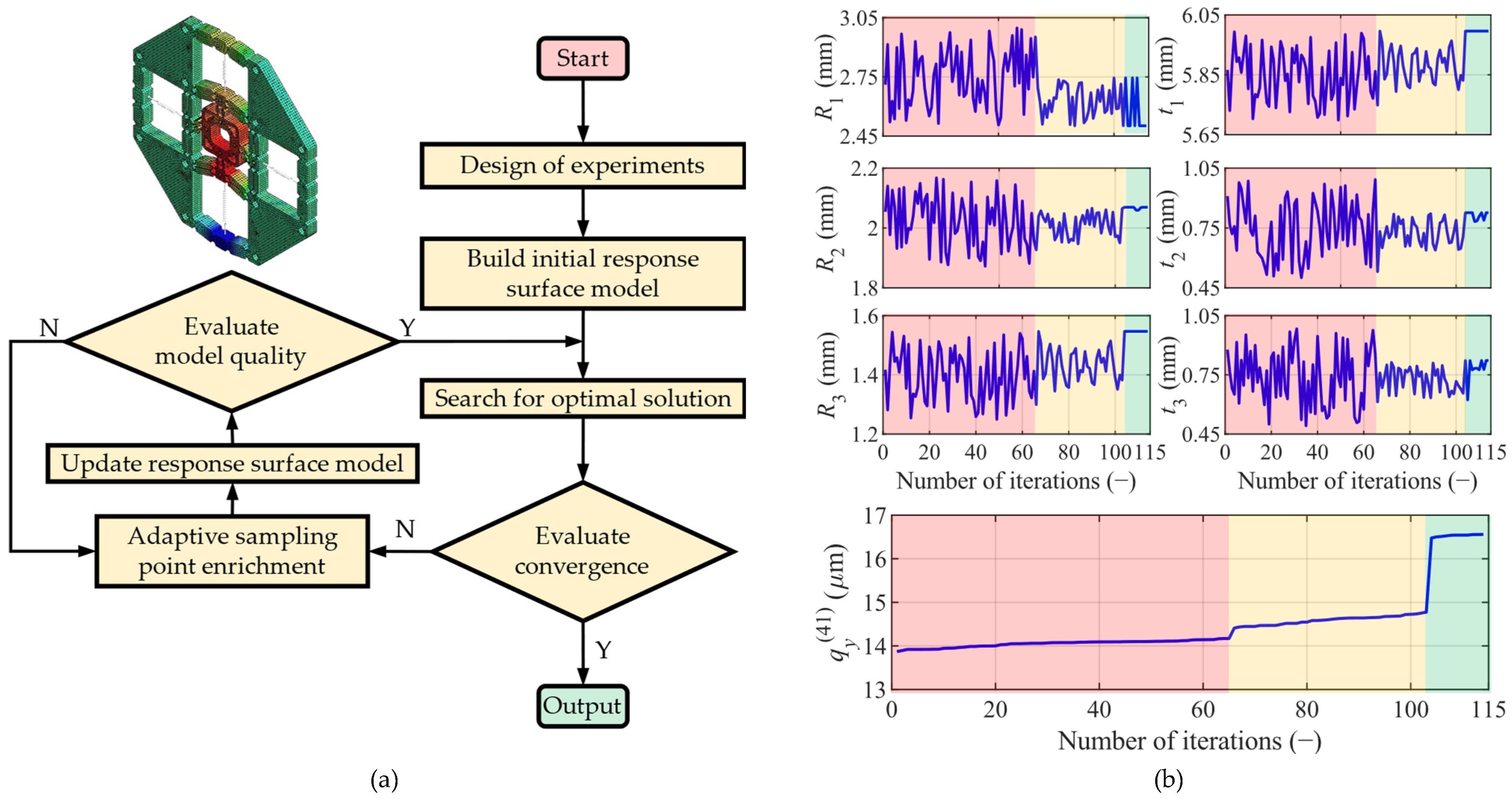
3.1. Parameter Optimization
- (1).
- Stochastic vibration status (the red background): This is the status where the optimization algorithm explores the parameter space extensively. The vibration phenomenon indicates that the algorithm is trying different parameter combinations, attempting to escape local optimums and find the global optimum. Vibrations at this stage are normal and indicate that the algorithm has not prematurely converged.
- (2).
- Decreasing vibration interval status (the yellow background): In this status, the vibration interval gradually decreases, indicating that the algorithm is searching around one or a few potentially optimal solution regions. This is the transition process of the algorithm from extensive exploration to fine-tuned search.
- (3).
- Convergence trend status (the green background): The value of the optimization objective function gradually stabilizes at this stage, indicating that the algorithm has approached the optimal solution. The convergence trend indicates that the optimization process has achieved a certain level of success, and the optimized values obtained can be used as a reference for the final design.
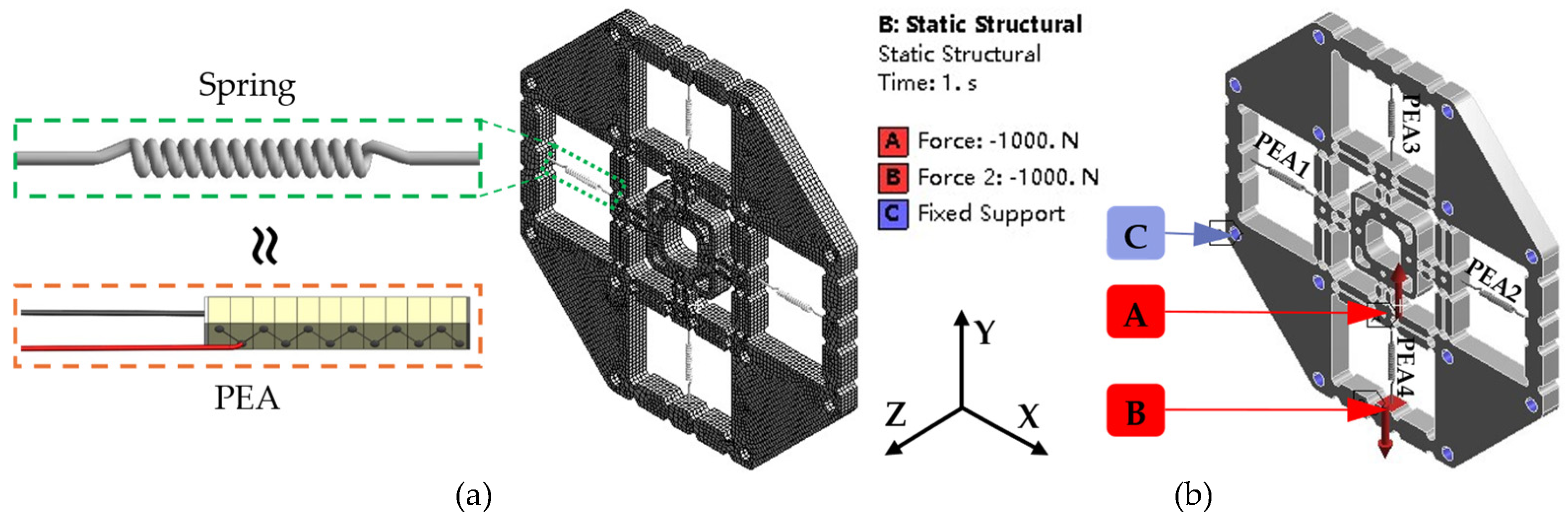
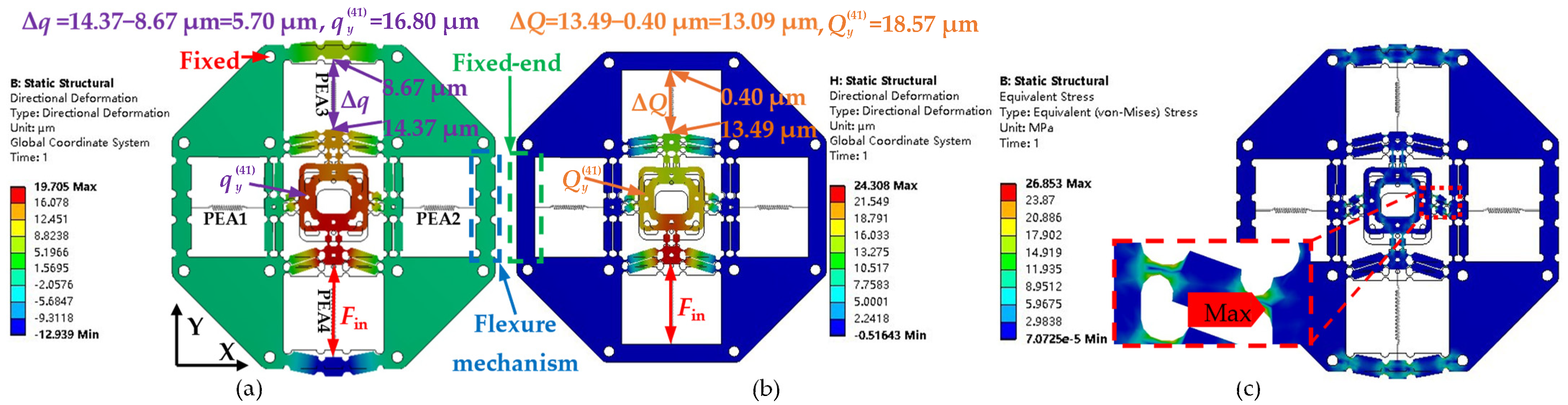
3.2. Static Analysis and Comparison
3.3. Dynamic Analysis Results
4. Experimental Verification
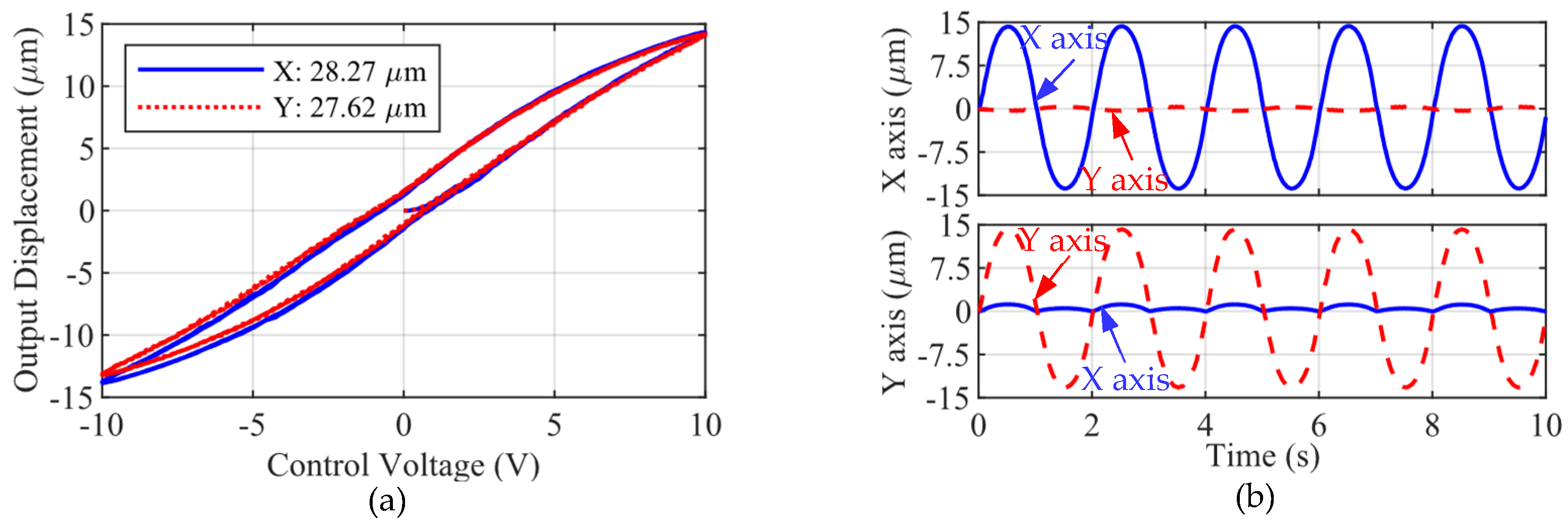
4.1. Stroke and Coupling Performance Testing
4.2. Natural Frequency Testing
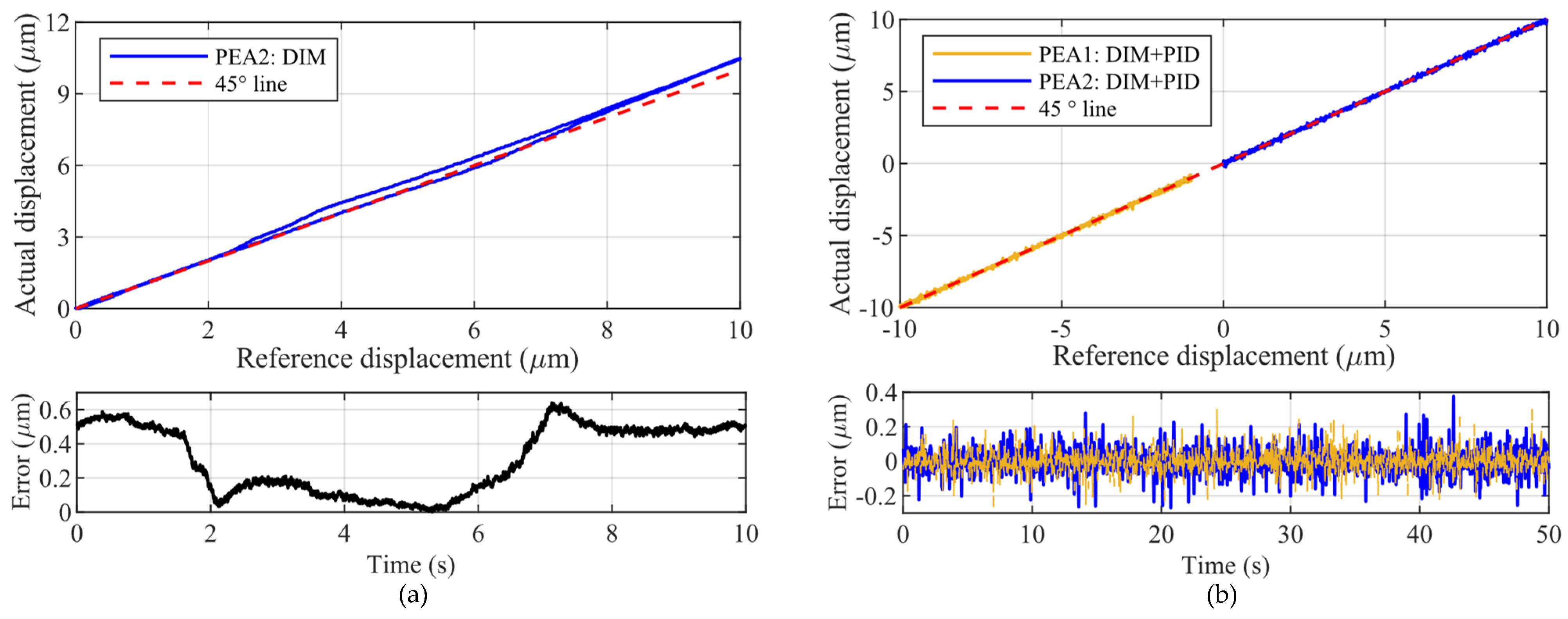
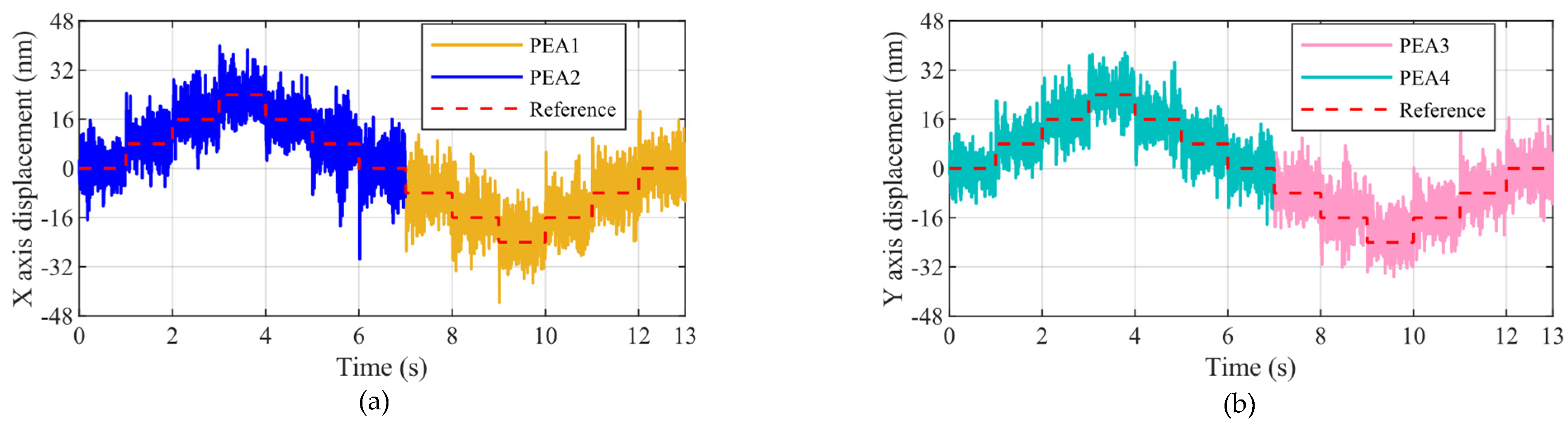
4.3. Hysteresis Compensation and Resolution Testing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, H.; Li, H.; To, S.; Yu, K.-M.; He, Y.; Gao, J.; Chen, X.; Li, J. Design and control of a new 3-PUU fast tool servo for complex microstructure machining. Int. J. Adv. Manuf. Technol. 2017, 94, 3503–3517. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Liu, Y.; Li, K.; Feng, Y. Development of a resonant piezoelectric micro-jet for high-viscosity liquid using a longitudinal transducer. Mech. Syst. Signal Proc. 2021, 146, 107012. [Google Scholar] [CrossRef]
- Yun, H.; Liu, L.; Li, Q.; Yang, H. Investigation on two-stage vibration suppression and precision pointing for space optical payloads. Aerosp. Sci. Technol. 2020, 96, 105543. [Google Scholar] [CrossRef]
- Fan, Y.; He, Y.; Tan, U.X. Real-time compensation system via gyroscope and fast steering mirror for wide-bandwidth multiple-frequency vehicle disturbance. IEEE-ASME Trans. Mechatron. 2020, 25, 650–660. [Google Scholar] [CrossRef]
- Qin, Y.; Soundararajan, R.; Jia, R.; Huang, S.-L. Direct inverse linearization of piezoelectric actuator’s initial loading curve and its applications in full-field optical coherence tomography (FF-OCT). Mech. Syst. Signal Proc. 2021, 148, 107147. [Google Scholar] [CrossRef]
- Ling, M.; Yuan, L.; Zhang, X. Bionic design of a curvature-adjustable flexure hinge inspired by red blood cells. Precis. Eng.—J. Int. Soc. Precis. Eng. Nanotechnol. 2023, 81, 124–134. [Google Scholar] [CrossRef]
- Wei, Y.; Xu, Q. A survey of force-assisted robotic cell microinjection technologies. IEEE Trans. Autom. Sci. Eng. 2019, 16, 931–945. [Google Scholar] [CrossRef]
- Deng, J.; Liu, Y.; Li, J.; Zhang, S.; Li, K. Displacement linearity improving method of stepping piezoelectric platform based on leg wagging mechanism. IEEE Trans. Ind. Electron. 2022, 69, 6429–6432. [Google Scholar] [CrossRef]
- Mohith, S.; Upadhya, A.R.; Navin, K.P.; Kulkarni, S.M.; Rao, M. Recent trends in piezoelectric actuators for precision motion and their applications: A review. Smart Mater. Struct. 2020, 30, 013002. [Google Scholar] [CrossRef]
- Sabarianand, D.V.; Karthikeyan, P.; Muthuramalingam, T. A review on control strategies for compensation of hysteresis and creep on piezoelectric actuators based micro systems. Mech. Syst. Signal Proc. 2020, 140, 106634. [Google Scholar] [CrossRef]
- Yu, H.; Deng, J.; Liu, Y.; Wang, Y. Piezoelectric hybrid actuation mode to improve speeds in cross-scale micromanipulations. Int. J. Mech. Sci. 2023, 240, 107943. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Deng, J.; Zhang, S.; Li, J.; Wang, W.; Liu, J.; Chen, W.; Quan, Q.; Liu, G.; et al. Miniature amphibious robot actuated by rigid-flexible hybrid vibration modules. Adv. Sci. 2022, 9, 2203054. [Google Scholar] [CrossRef]
- Morkvenaite-Vilkonciene, I.; Bucinskas, V.; Subaciute-Zemaitiene, J.; Sutinys, E.; Virzonis, D.; Dzedzickis, A. Development of electrostatic microactuators: 5-year progress in modeling, design, and applications. Micromachines 2022, 13, 1256. [Google Scholar] [CrossRef]
- Tang, Y.; Li, J.; Xu, L.; Lee, J.-B.; Xie, H. Review of electrothermal micromirrors. Micromachines 2022, 13, 429. [Google Scholar] [CrossRef]
- Mirvakili, S.M.; Hunter, I.W. Artificial muscles: Mechanisms, applications, and challenges. Adv. Mater. 2017, 30, 1704407. [Google Scholar] [CrossRef]
- Xu, Q.; Gao, X.; Zhao, S.; Liu, Y.N.; Zhang, D.; Zhou, K.; Khanbareh, H.; Chen, W.; Zhang, Y.; Bowen, C. Construction of bio-piezoelectric platforms: From structures and synthesis to applications. Adv. Mater. 2021, 33, 2008452. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Tjiptoprodjo, R.C.; Zhang, W.J.; Yang, G.S. Micro-motion devices technology: The state of arts review. Int. J. Adv. Manuf. Technol. 2007, 38, 463–478. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Zhang, W.J.; Gupta, M.M. A new compliant mechanical amplifier based on a symmetric five-bar topology. J. Mech. Des. 2008, 130, 104501. [Google Scholar] [CrossRef]
- Pinskier, J.; Shirinzadeh, B.; Al-Jodah, A. Design and evaluation of a dual-stage, compensated stick-slip actuator for long-range, precision compliant mechanisms. Sens. Actuator A—Phys. 2021, 331, 113007. [Google Scholar] [CrossRef]
- Tian, Y.; Huo, Z.; Wang, F.; Shi, B. Precision tracking of a 2-DOF stick-slip positioner using modeling-free inversion-based iterative control and modified inverse hysteresis compensator. Sens. Actuator A—Phys. 2021, 331, 112959. [Google Scholar] [CrossRef]
- Wang, J.; Huang, H.; Zhao, H. Model-based optimization for structure dimension and driving signal of a stick-slip piezoelectric actuator. Mech. Syst. Signal Proc. 2022, 164, 108191. [Google Scholar] [CrossRef]
- An, Y.; Ji, S.; Zhao, J. Achieving significant burst motion based on epicycloid induction principle for stick–slip piezoelectric actuator. IEEE Trans. Ind. Electron. 2023, 70, 9301–9311. [Google Scholar] [CrossRef]
- Tian, X.; Chen, W.; Zhang, B.; Liu, Y. Restraining the backward motion of a piezoelectric stick-slip actuator with a passive damping foot. IEEE Trans. Ind. Electron. 2022, 69, 10396–10406. [Google Scholar] [CrossRef]
- Qiao, G.; Ning, P.; Xia, X.; Yu, Y.; Lu, X.; Cheng, T. Achieving smooth motion for piezoelectric stick–slip actuator with the inertial block structure. IEEE Trans. Ind. Electron. 2022, 69, 3948–3958. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, X.; Huo, Z.; Shi, B.; Tian, Y.; Zhang, D. A novel large stepping-stroke actuator based on the bridge-type mechanism with asymmetric stiffness. Mech. Syst. Signal Proc. 2022, 179, 109317. [Google Scholar] [CrossRef]
- Xu, Z.; Huang, H.; Dong, J. A stick-slip piezoelectric actuator with measurable contact force. Mech. Syst. Signal Proc. 2020, 144, 106881. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.J.; Hesselbach, J.; Kerle, H. Development of a two-degree-of-freedom piezoelectric rotary-linear actuator with high driving force and unlimited linear movement. Rev. Sci. Instrum. 2006, 77, 035112. [Google Scholar] [CrossRef]
- Bani Melhem, M.K.; Simic, M.; Lai, C.Y.; Feng, Y.; Ding, S. Fuzzy control of the dual-stage feeding system consisting of a piezoelectric actuator and a linear motor for electrical discharge machining. Proc. Inst. Mech. Eng. Part B—J. Eng. Manuf. 2019, 234, 945–955. [Google Scholar] [CrossRef]
- Salton, A.T.; Chen, Z.; Zheng, J.; Fu, M. Constrained optimal preview control of dual-stage actuators. IEEE-ASME Trans. Mechatron. 2016, 21, 1179–1184. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, J.; Chen, X.; Tang, H.; Chen, Y.; He, Y.; Yang, Z. A rapid vibration reduction method for macro–micro composite precision positioning stage. IEEE Trans. Ind. Electron. 2017, 64, 401–411. [Google Scholar] [CrossRef]
- Zhu, H.; Pang, C.K.; Teo, T.J. A flexure-based parallel actuation dual-stage system for large-stroke nanopositioning. IEEE Trans. Ind. Electron. 2017, 64, 5553–5563. [Google Scholar] [CrossRef]
- Torralba, M.; Valenzuela, M.; Yagüe-Fabra, J.A.; Albajez, J.A.; Aguilar, J.J. Large range nanopositioning stage design: A three-layer and two-stage platform. Measurement 2016, 89, 55–71. [Google Scholar] [CrossRef]
- Ling, M.; He, X.; Wu, M.; Cao, L. Dynamic design of a novel high-speed piezoelectric flow control valve based on compliant mechanism. IEEE-ASME Trans. Mechatron. 2022, 27, 4942–4950. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, K.; Wang, F.; Zhou, C.; Ma, Y.; Jing, X.; Yang, C.; Zhang, D. A spatial deployable three-DOF compliant nano-positioner with a three-stage motion amplification mechanism. IEEE-ASME Trans. Mechatron. 2020, 25, 1322–1334. [Google Scholar] [CrossRef]
- Wei, Y.; Xu, Q. Design and testing of a new force-sensing cell microinjector based on small-stiffness compliant mechanism. IEEE-ASME Trans. Mechatron. 2021, 26, 818–829. [Google Scholar] [CrossRef]
- Xun, M.; Yu, H.; Liu, Y.; Deng, J.; Zhang, S.; Li, K. A precise rotary piezoelectric actuator based on the spatial screw compliant mechanism. IEEE-ASME Trans. Mechatron. 2023, 28, 223–232. [Google Scholar] [CrossRef]
- Mynderse, J.A.; Chiu, G.T.C. Modeling of a dynamic mirror with antagonistic piezoelectric stack actuation. J. Dyn. Syst. Meas. Control-Trans. ASME 2014, 136, 024501. [Google Scholar] [CrossRef]
- Jiao, C.; Wang, Z.; Lv, B.; Wang, G.; Yue, W. Design and analysis of a novel flexure-based XY micropositioning stage. Appl. Sci. 2020, 10, 8336. [Google Scholar] [CrossRef]
- Wang, S.; Rong, W.; Wang, L.; Xie, H.; Sun, L.; Mills, J.K. A novel linear-rotary piezoelectric positioning stage based on surface’s rectangular trajectory driving. Precis. Eng.—J. Int. Soc. Precis. Eng. Nanotechnol. 2019, 55, 376–380. [Google Scholar] [CrossRef]
- Liao, C.; Xu, M.; Xiao, R.; Han, W. Integrated design of piezo-actuated 2-DOF submillimeter-range super-resolution platform with self-sensing unit. Mech. Syst. Signal Proc. 2020, 139, 106569. [Google Scholar] [CrossRef]
- Xie, Y.; Li, Y.; Cheung, C.F.; Zhu, Z.; Chen, X. Design and analysis of a novel compact XYZ parallel precision positioning stage. Microsyst. Technol. 2020, 27, 1925–1932. [Google Scholar] [CrossRef]
- Yang, Y.; Wen, J.; Zhang, Y. Development of a novel XZ workpiece vibration generator for cooperative vibration cutting of hierarchical grating structures. Mech. Syst. Signal Proc. 2023, 198, 110422. [Google Scholar] [CrossRef]
- Huang, W.-W.; Li, L.; Zhu, Z.; Zhu, L.-M. Modeling, design and control of normal-stressed electromagnetic actuated fast tool servos. Mech. Syst. Signal Proc. 2022, 178, 109304. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, J.; Peng, Y.; Pu, H.; Yang, Y. A novel amplification ratio model of a decoupled XY precision positioning stage combined with elastic beam theory and castigliano’s second theorem considering the exact loading force. Mech. Syst. Signal Proc. 2020, 136, 106473. [Google Scholar] [CrossRef]
- Qin, Y.; Tian, Y.; Zhang, D.; Shirinzadeh, B.; Fatikow, S. A novel direct inverse modeling approach for hysteresis compensation of piezoelectric actuator in feedforward applications. IEEE-ASME Trans. Mechatron. 2013, 18, 981–989. [Google Scholar] [CrossRef]


| Optimization Settings | Optimization Status | ||
|---|---|---|---|
| Property | Value | Property | Value |
| Estimated number of design points | 220 | Number of design points | 142 |
| Number of initial samples | 66 | Number of domain reductions | 1 |
| Maximum number of evaluations | 220 | Number of failures | 53 |
| Convergence tolerance | 1 × 10−6 | Size of generated sample set | 114 |
| Parameter | Value (mm) | Parameter | Value (mm) |
|---|---|---|---|
| R1 | 2.5020→2.50 | t1 | 5.9960→6.00 |
| R2 | 2.0688→2.10 | t2 | 0.8624→0.80 |
| R3 | 1.5886→1.60 | t3 | 0.8228→0.80 |
| d1 | 15.492→15.5 | d3 | 4.1456→4.10 |
| d2 | 17.224→17.1 |
| FEA (Hz) | Exp. (Hz) | |||
|---|---|---|---|---|
| X Axis | Y Axis | X Axis | Y Axis | |
| Without PEA | 1457.4 | 1450.7 | 1323.0 | 1327.0 |
| With PEA | 2064.0 | 2070.5 | 2018.0 | 2024.0 |
| With PEA and load mass | 595.60 | 596.00 | 598.00 | 610.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Tang, H.; Qin, Y. Design and Test of a 2-DOF Compliant Positioning Stage with Antagonistic Piezoelectric Actuation. Machines 2024, 12, 420. https://doi.org/10.3390/machines12060420
Wu H, Tang H, Qin Y. Design and Test of a 2-DOF Compliant Positioning Stage with Antagonistic Piezoelectric Actuation. Machines. 2024; 12(6):420. https://doi.org/10.3390/machines12060420
Chicago/Turabian StyleWu, Haitao, Hui Tang, and Yanding Qin. 2024. "Design and Test of a 2-DOF Compliant Positioning Stage with Antagonistic Piezoelectric Actuation" Machines 12, no. 6: 420. https://doi.org/10.3390/machines12060420
APA StyleWu, H., Tang, H., & Qin, Y. (2024). Design and Test of a 2-DOF Compliant Positioning Stage with Antagonistic Piezoelectric Actuation. Machines, 12(6), 420. https://doi.org/10.3390/machines12060420






