Abstract
This article deals with the consensus tracking problem for multi-agent systems (MAS) under the influence of unknown time-varying delays. Each agent of the MAS is a quadrotor unmanned aerial vehicle (UAV) represented as a linear continuous-time system. The main objective of this paper is the stabilization of multi-agent systems where the control input is affected by unknown time-varying delays, which are assumed to be upper-bounded, and where these bounds are not required to be known. The proposed observer-based control scheme guarantees the consensus tracking of multi-UAV systems with the desired performance, which adds a further level of mitigation of unknown delays present in MAS systems by minimizing the norm, which measures the maximum gain from the disturbance to the controlled output of the system. For each UAV agent, an unknown input observer is employed to isolate the unknown time-varying delays in the state estimation process. With the use of an unknown input observer-based consensus tracking control, sufficient conditions are derived to ensure that all follower UAVs can reach a consensus with the leader, despite the presence of distinct unknown time-varying delays. The stability of the proposed scheme is proven using Lyapunov theory for the leader and follower agents. Finally, numerical examples are provided to illustrate the effectiveness of the proposed method.
1. Introduction
In recent years, the study of multiple unmanned aerial vehicles (UAVs) in formation has attracted attention, because of their diverse applications in target enclosure and tracking, search and rescue, surveillance, and heavy payload transportation, among others [1,2,3,4]. Compared with a single UAV, as in [5], using multiple UAVs working cooperatively has advantages, such as greater thrust force, high efficiency, wide coverage area, and increased versatility.
A multiple UAV system can be conceptualized as a multi-agent system (MAS). MAS formation and tracking control is considered a fundamental problem, in which agents are required to produce a desired trajectory. This topic has been extensively studied in the literature [6,7,8]. One of the most commonly proposed approaches for formation control in MASs is consensus protocols [9,10,11,12]. Consensus means that a team of agents reaches an agreement about a particular variable of interest by interacting with each other via a communication network. Some studies [13,14,15,16,17,18,19,20,21,22] suggested that consensus protocols in multi-agent systems provide benefits such as achieving agreement in various conditions (antagonistic interactions, noisy environments, and heterogeneous systems), enabling distributed and adaptive solutions, and ensuring stability and finite settling times.
Consensus protocols can be affected by the presence of time-varying delays, which can lead to reduced performance, instability, or prevent the desired agreement. Certain protocol designs can compensate for these delays, ensuring proper system performance and achieving consensus under specific conditions such as network topologies [23,24] and design parameters [25]. Other authors have explored different approaches, such as consensus protocols based on observation. For example, the authors in [26,27] addressed this problem by designing a leader–follower consensus control strategy based on predictive control, where an observer is used for estimation of the state of the agents when communication constraints exist. The authors in [28] presented a predictive extended state observer (ESO) to estimate the consensus tracking error when having time-varying input/output delays and mismatched disturbances in a linear MAS, and the ESO was used for designing the controller. In addition, ref. [29] developed a distributed extended state observer and a leader–follower consensus control based on the relative estimated states between each agent and its neighbors in the presence of unknown external disturbances.
Moreover, the authors in [30,31] focused on the problem of fault detection for a MAS in continuous time, where they used consensus protocols and unknown input observer (UIO) schemes to deal with disturbances, failures, and time-varying delays, a where numerical example demonstrated the effectiveness and feasibility of the proposed approach. The authors in [32] implemented a fault diagnosis strategy based on the stages of detection, isolation, and estimation for satellites in formation. In the isolation stage, a bank of robust and non-linear UIOs were designed to isolate the faulty actuator, allowing the unknown input disturbances to be decoupled and their effects attenuated. In addition, UIOs can effectively track state errors in multi-agent systems with directed switching topologies, enabling consensus tracking, even with external inputs affecting the leader [33]. For example, the authors in [34] used a UIO to estimate an unknown state affected by simultaneous connectivity-mixed attacks, actuator/sensor faults, and disturbances, and developed a leader–follower consensus control for a MAS. In summary, research indicates that consensus in multi-agent systems can be achieved despite unknown input delays or faults. Protocols that utilize UIOs to detect, isolate, or estimate these elements have been developed, ensuring that the systems can reach consensus.
In general, time-varying delays are unavoidable in complex systems such as UAVs. Time-varying delays in UAVs are primarily caused by factors related to communication and computation, such as wireless communication issues, satellite communication transport delays, or problems with vision-based navigation systems. In UAV systems, time-delays can reduce the effectiveness of control performance, affecting the stability and making the system vulnerable to an actuator, sensor, or process fault. These problems become more critical in multiple-UAV systems in formation schemes. Therefore, developing formation control schemes for multiple UAVs subject to delays has attracted the attention of academia and industry. For example, the authors of [35] investigated the robust control problem of time-varying formation flight for multiple-UAV systems with external disturbances and time delay. However, ref. [35] only considered a model based on fixed-wing vehicles. Moreover, the authors in [36] proposed an algorithm for leader–following consensus control of multiple fixed-wing UAVs with time-varying delays and unknown external disturbances but limited their study to the dynamic model of the attitude (aircraft orientation).
The time-varying delay problem for a single quadrotor was addressed in [37], where a Lyapunov barrier was used to ensure that the tracking error was limited within a range, and a Pade approximation was applied to compensate for the effect of input delay.
In the literature, many works have addressed the problem of observer-based consensus formation control for different cases of multi-agent systems with time-varying delay. However, few studies have addressed this problem in the specific case of multi-UAV systems. Therefore, the main contribution of this work is a new methodology to obtain mitigation of an unknown input delay in a tracking control in the formation of multiple-UAV systems under consensus protocols, where the stability of the proposed scheme is proved in the leader and followers, despite unknown time-varying delays. It is essential to mention that unknown delays are assumed to be upper-bounded, and these bounds are not required to be known. In addition, the proposed observer-based control scheme guarantees the consensus tracking of multi-UAV systems with the desired performance, which adds a further level of mitigation to unknown delays present in an MAS system by minimizing the norm, which measures the maximum gain from the disturbance to the controlled output of the system. In other words, in the proposed method, we address the problem related to a distinct unknown delay of the input of cooperative control, where consensus tracking control for the translation dynamics based on an unknown input observer is proposed. Thus, the designed consensus control between the leader and followers is guaranteed, and this scheme can be applied to solve the cooperative control problem of multiple UAVs in the presence of distinct unknown delays.
The paper is organized as follows. Section 2 is related to the dynamic model of the considered quadrotors and the problem formulation. Section 3 is dedicated to the control strategy design, which involves the inner attitude control and the consensus tracking control for translation. Section 3 analyzes the observer-based control strategy for the tracking control of the leader and follower agents, which involves observers used to isolate the unknown time-varying delays in the state estimation process; in addition, in this section, consensus tracking control under unknown time-varying delays is presented. Section 4 presents the results of numerical simulations, to show the effectiveness of the observer-based consensus control applied to multiple UAVs subject to distinct unknown time-varying delays. Finally, Section 5 ends the document with the conclusions.
2. System Dynamic Model
In this article, the MAS consists of a group of quadrotors under a leader—follower scheme. Each of the quadrotors in the MAS is a system with six degrees of freedom that consists of the translation coordinates ; and three rotations, one in each of the axes called roll, pitch, and yaw, respectively. The MAS can be described with respect to an inertial reference I, where the UAVs are considered mass points. The translational and rotational dynamics of the vehicles are defined by the second law of Newton and the external torque equation as follows [38]:
where g, m, and are the gravitational acceleration, mass, and lineal acceleration; and are the angular velocity and angular acceleration of the vehicle, respectively. In addition, is the total thrust of the vehicle and . The term is a constant, and is the angular velocity of each rotor. The terms represent the orientation relative to I, and is the inertia tensor of the body:
where the shorthand notations and represent the sine and cosine of the angle , respectively; are the torques defined as , , ; L is the distance between the rotors and the center of mass, is the reaction torque and is a constant. In addition, , , and have the following definitions:
The Equations (1) and (2) are the nonlinear dynamic model of the quadrotor multi-agent system. We use the Taylor series and obtain the following expressions:
Thus, the linear representation of the quadrotor multi-agent system is defined as:
where is the desired yaw angle of each UAV.
3. Control Strategy
We consider a leader–follower strategy for the formation control of the MAS. The system has the scheme shown in Figure 1, in which it is considered that the quadrotors are underactuated systems. For all agents, the coordinates , , , and can be controlled directly and individually, without sharing information between the vehicles. At the same time, the translational movement is conducted in a coordinated way.
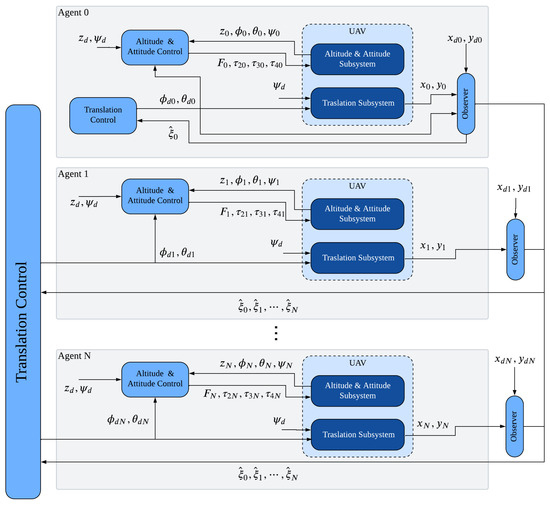
Figure 1.
Control scheme for the multi-UAV system.
For the translational subsystem, it is considered that the coordinate can be controlled indirectly by the coordinate, and the coordinate is controlled indirectly using the coordinate . In this work, we address the problem of a possible actuator time-varying delay affecting the motion in the plane. Therefore, the coordinates and are controlled by schemes based on state estimation to isolate the time-varying delay. Specifically, a coordinated control of the translational movement based on a leader–follower scheme is considered. Thus, a consensus tracking control based on an unknown input observation is proposed, for the follower agents to maintain formation flight, with the leader agent’s estimated translational position as the reference. In contrast, a disturbance observer-based control is formulated for the leader agent, to follow a desired trajectory despite the presence of time-varying delays.
3.1. Altitude and Attitude Control
This section proposes using simple linear control laws for the altitude and attitude subsystems, to ensure the stability of the flying attitude of the quadrotor multi-agent system. Thus, the control inputs , , , for each of the agents are denoted as
where
The control inputs are substituted in the equations of the linear multi-agent system (5); thus, the following closed-loop expressions are obtained:
3.2. Translation Subsystem
From the linear quadrotor multi-agent system (5), the translation movement of the quadcopter can be obtained:
Now, since all orientation errors of the quadrotor multi-agent system tend to be zero, it can be assumed that , . Moreover, if is considered a constant equal to zero, the dynamics corresponding to the and coordinates are described in the following form:
Then, one can define the following state vector for each agent, where
Thus, the x and y coordinate errors are defined as follows:
Considering and as constants, the elements of the derivative are represented as follows:
Therefore, the translation movement x-y of the quadcopter multi-agent dynamics can be expressed in the following state-space form:
where matrix and
A practical problem in the position tracking and formation control of quadrotor multi-agent systems is related to the time difference between the translation sensor as a global positioning system (GPS) that detects a position measurement and the force input that applies torque to each motor (input signal) of the aerial vehicle. This time difference is due to the communication or synchronization time between each servo controller, which entails UAVs not receiving the proper real-time input, meaning the system has an inherent input delay. Therefore, it is necessary to address the effect of variable time-varying delay in the input application on the UAV tracking control design. Thus, an observer-based consensus control is proposed, to ensure that all UAV agents can reach consensus with the leader, despite the presence of distinct unknown time-varying delays.
Considering the previous problem, the lineal multi-agent system of the position tracking error dynamics (13) has inherent input delays. Therefore, the following delayed lineal multi-agent system is formulated:
where is the unknown control input under the effect of unknown time-varying delay , which is present in every agent i, with . The delay problem in multi-agent systems is focused on the unknown time-varying delay , where each unknown delay is assumed to be continuous and bounded; i.e., , ; is the maximum delay of the i-th agent, which is assumed to be upper bounded, and this bound is not required to be known; the assumptions about the control input and the unknown time-varying delay are given in [39,40]. Thus, it is essential to note that each agent has its own inherent unknown delay, unlike other approaches proposed in the literature; e.g., in [31], a single random time-varying delay is present in the whole multi-agent system.
Thus, considering the unknown delayed input in the translation movement of each agent, the delayed linear multi-agent system in (14) is modified as follows:
where is the unknown input signal of each agent, which is given by , as in [39].
3.3. Translation Control
According to Equation (5), the control inputs are computed to determine the desired roll and pitch angles for all agents. These angles are functions of the tracking errors in the and coordinates, respectively. Specifically, in the leader–follower scheme, a disturbance observer-based control is implemented on the leader agent to enable it to track the desired trajectory within the plane. Consequently, an observer-based consensus control is formulated for the follower agents to maintain formation flight, with the leader agent as the reference. Addressing the challenge of an unknown delayed input in Equation (15), control schemes are developed based on estimating the state vectors for all agents.
- Leader agent control
Thus, for the leader agent, the control inputs are as follows:
where and are the estimations of and . The terms and are the gain feedback matrices. Then, the signal can be expressed as
where
Therefore, the dynamics of the leader agent are given by
where is the unknown input of the leader agent, which is affected by the time-varying delay .
Now, the following unknown input observer is proposed for the translation movement of the leader agent under an unknown time-varying delay:
where and are the states of the observer, and the estimations of the system states . The constant matrices and E are chosen to make converge to in the delay-free case.
Now, the following lemma is used in the design of the unknown input observer.
Lemma 1.
Given any matrices C and B, equation has a solution if and only if .
Then, the following theorem provides sufficient conditions that guarantee the convergence of the observation error .
Theorem 1.
The unknown input of the leader agent system (18) can be decoupled form the state estimation under the unknown input observer (19) if the following conditions are satisfied:
where N is a Hurwitz matrix used to achieve exponential convergence of the observation error . This means the observer is not subject to an unknown time-varying delay .
Proof.
Now, the observation error is ; then, the dynamics of the estimation error is
Now, in order to obtain E and H matrices, from Lemma 1, one can deduce that the general solution of E is as follows:
where X is an arbitrary matrix. Thus, is selected for ease of calculation, and one obtains .
From the matrix E, H is obtained as follows: . Now, this denotes that ; thus, Equation (20) can be rewritten as
Then,
where . Now, is a Hurwitz matrix used to ensure convergence of the observation error. Thus, the matrix should be placed anywhere in the complex s-plane by a suitable selection of matrix L, where must be observable. Subsequently, it is possible to find J, computed as . Then, the unknown input observer provides an easy-to-implement algorithm that eliminates the influence of the unknown delayed input in the state estimation process.
Based on the above, if these conditions are fulfilled, the following dynamics of the error of observation can be obtained:
where N should be a Hurwitz matrix for achieving exponential convergence of the observation error. This means the observer is not subject to an unknown delayed input . This ends the proof. □
Now, it is possible to design an observer-based control strategy to stabilize the leader agent system (18), where the following observer-based control for the leader agent is considered:
Then, the closed-loop dynamics of the leader are
Now, it is evident that there is an influence of the unknown signal on the closed-loop system (29). Therefore, the stability of the closed-loop system must be guaranteed.
Theorem 2.
Consider the disturbance observer-based control (28) of the leader agent system (18), which is exponentially stable if there exists a such that the following inequation holds for :
where the control gain is . Thus, the system’s stability is guaranteed, even in the presence of the unknown time-varying delay .
Proof.
Considering the quadratic function , one obtains the following dynamics:
The following proposition provides a criterion that guarantees the exponential stability of the disturbance system (18).
Proposition 1.
From Proposition 1, one can rewrite (31) as follows:
Therefore, the following inequality must hold
Now, the above equation is a bilinear matrix inequality; thus, a non-singular transformation, such as , must be introduced:
Defining , this yields
Thus, the following LMI is obtained,
where .
- Follower agent control
For the follower agents, the consensus control for formation is based on the estimation of the states of each agent, which are error states in the and coordinates. In the consensus protocols, the communication between agents in a MAS can be described by the graph . Let , where is a nonempty finite node set and is an edge set. The edge in the edge set denotes that agent can obtain information from agent , but not vice versa. The adjacency matrix associated to the graph is defined such that and for . The Laplacian matrix of the graph is defined as and , . In leader–follower schemes, can be partitioned as , where and . In addition, the constant formation structure of the agents in the graph in a reference coordinate frame is denoted by , where is the formation variable corresponding to agent i.
Assuming that each agent has access to its own state and the states of its neighbors, the agents achieve consensus in the sense of . Thus, the following law of observer-based consensus control for the coordinates x and y is considered:
The terms and are the feedback gain matrices, which will be defined later; is the -th element of the adjacency matrix associated with , and , , , and are the state estimations of , , , and . Moreover, , , and are constant vectors that describe the formation structure in coordinates x and y.
Considering the vectors , and , the consensus control law based on state estimation can be formulated as a single control input for each agent:
where
Then, the follower agent dynamics are given:
where is the unknown input of the follower agent, which is affected by time-varying delay .
Substitute the observer-based control law (40) into the follower agent system (41) of agent i. By making use of the properties of the Kronecker product, one can rewrite this in the following form:
where , and denotes the follower agent’s state estimation. This yields the following follower agent system:
with , , , .
Now, the same estimation approach is used in the follower agent system; thus, unknown input observers are applied to isolate the external disturbances with the unknown boundary , where the unknown delayed input of each agent is present . For isolation of each delayed control input, an observer like a nonlinear unknown input observer on agent i is constructed as follows:
where and are the states of the observer, and the estimations of the system states for each agent i. The constant matrices and are chosen to make converge to in a delay-free case.
Now, based on the properties of the Kronecker product, one can formulate the following unknown input observer on the agent:
where , , , .
Now, the following theorem is provided to ensure convergence of the proposed observer:
Theorem 3.
The unknown inputs of the follower agent system (41) can be decoupled from the state estimation under the unknown input observer (45) if the following conditions are satisfied:
where is a Hurwitz matrix to achieve an exponential convergence of the observation error . This means the follower observers are not subject to the unknown time-varying delay .
Proof.
Now, the observation error is , and using Equations (43) and (45), one obtains the following dynamics:
Then,
where . Since , using Lemma 1, one can easily obtain the matrix . In addition, the following assumption must be satisfied:
where and the matrix . It is worth recalling that the matrix depends on the gain matrix of the consensus control, which will be further detailed below. Therefore, to guarantee the convergence of the observation error , one should satisfy that is a Hurwitz matrix, to ensure convergence of the observation error. Therefore, should be placed anywhere in the complex s-plane by a suitable selection of matrix .
Based on the above, the dynamics of the observation error is given by , where the Hurwitz matrix achieves exponential convergence of the observation error. This means that the followers’ observers will be not subject to the unknown time-varying delays . □
Now, it is possible to design an observer-based control strategy to stabilize the follower agents’ system, where the following observer-based control is considered:
Since all estimation errors and tend to zero, the control law can be simplified as
For the follower agents, let
According to Equations (29), (41) and (51), for , we have
Considering the new variables and , where is a stable matrix according to the solution of the LMI in Theorem 2. Then, is now defined as follows:
It is important to note that the achievable formation structures must satisfy the constraints . Therefore, the closed-loop dynamic of the followers is
where and . Now, as happened with the leader agent, it is evident that the dynamics of the followers are influenced by the unknown signal . Therefore, the stability of the closed-loop system must also be guaranteed.
Theorem 4.
For a direct communications graph , the agents (41) reach the formation under the protocol (52) if there exists a such that the following inequation holds for :
where the control gain is , and it satisfies that . Thus, the observer-based control (40) of the follower agent system (41) is exponentially stable, even in the presence of unknown time-varying delays . Then, the formation described by can be accomplished for the leader–follower system (41) via the protocol (40).
Proof.
Considering the quadratic function , one obtains the following dynamics:
Then, Equation (56) can be expressed in matrix form as
Proceeding as in the stability analysis of the leader system, one can use Proposition 1, and making use of a non-singular transformation, one obtains the following LMI:
where the control gain is and the positive constants guarantee the above LMI, which can ensure the exponential stability and the performance of the follower system in the presence of the unknown inputs, being affected by the unknown time-varying delays . □
4. Simulation Results
A numerical simulation was performed to validate the performance of the control scheme based on an unknown input observer for the formation flight of three UAVs. For this formation, consider the communication graph in Figure 2, where node 0 is associated with the leader agent and the other nodes are associated with the follower agents. Then, the Laplacian matrix of the graph is defined as follows:
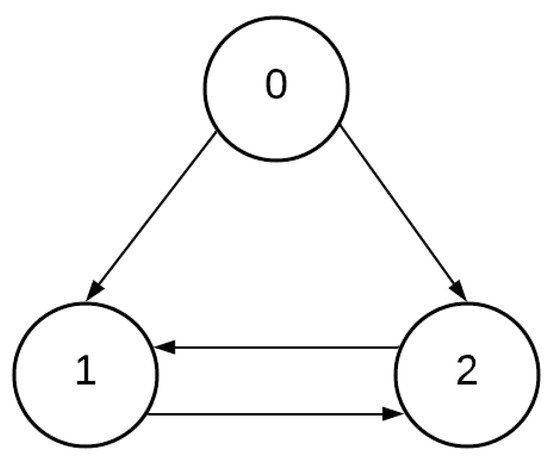
Figure 2.
Communication graph .
The formation structure is shown in Figure 3, where the followers (gray) have a distance of m in the y coordinate from the leader (red). Therefore, because the leader is the origin of the formation, the vector . For the follower agents, constant vectors that describe the formation structure are .
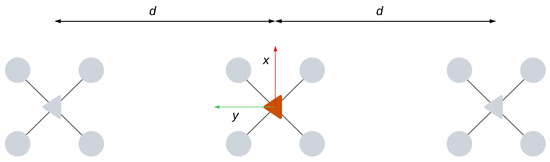
Figure 3.
Formation structure of the UAVs.
Furthermore, the linear dynamic model of altitude and attitude is given by (5), and the control scheme was implemented according to (6)–(9). The parameters used in the simulation are presented in Table 1. The translation movement is described by Equation (15) with input delays as shown in Table 2. The observer-based consensus control for the coordinates x and y was designed according to Equations (40) and (44), the feedback gain matrices were obtained through Theorem 4 with and . In addition, the observer gain selected was as follows:

Table 1.
Parameters employed in the simulations for each agent.

Table 2.
Signal of input delays created for each agent.
Moreover, the control law based on an unknown input observer for the leader agent was designed using Equations (17) and (19), the gain matrices were selected according to Theorem 2 with and . In this agent, the observer gain is the same as in Equation (60).
The desired trajectory , the initial conditions of the agents, and the unknown input observer were as follows:
Figure 4 shows the trajectories of all agents under the formation structure and Figure 5 shows the time-varying delays trajectories affecting the system. Note that, in this simulation, the linear control law provided good tracking in altitude of all UAVs, as shown in Figure 6, where the errors in z and coordinates are close to zero. These results were because the control scheme was independent of the translational movements.
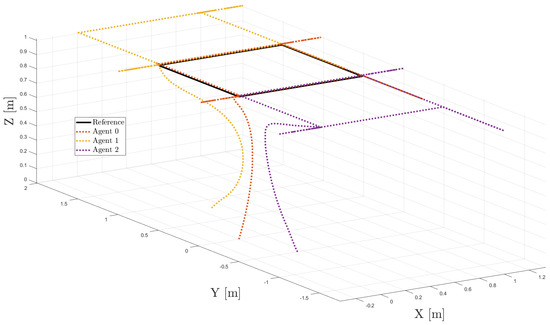
Figure 4.
Trajectories of all agents in formation.
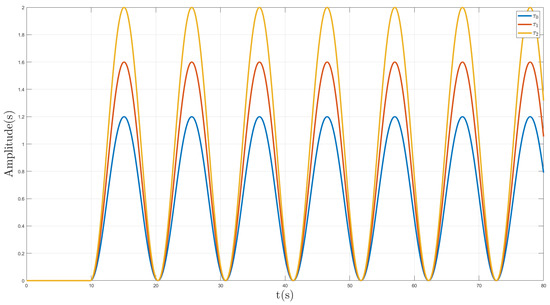
Figure 5.
Time-varying delay trajectories.
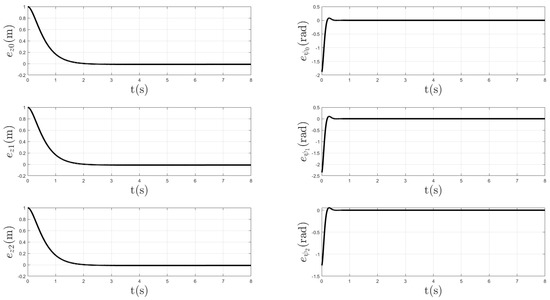
Figure 6.
Tracking error of all agents in z and coordinates.
Tracking errors in x, y, and coordinates are shown in Figure 7. It is appreciated that there are peaks in the errors due to the reference changes and the presence of time-varying delays. However, the proposed scheme caused the error to converge to zero, despite the presence of distinct unknown delays.
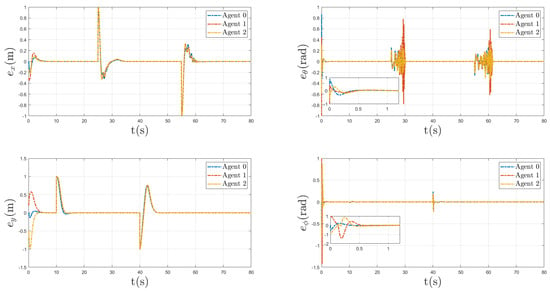
Figure 7.
Tracking error of all agents in x, y, , and coordinates.
Figure 8 illustrates the evolution of the x, y, , and coordinates of the leader vehicle, where it is shown that the tracking performance is quite satisfactory. We can note that when the desired x position changed at s and s, and the desired y position at s and s, the effects of the input time-varying delay were visible and caused a small tracking error in both the translation and rotation of the leader vehicle.
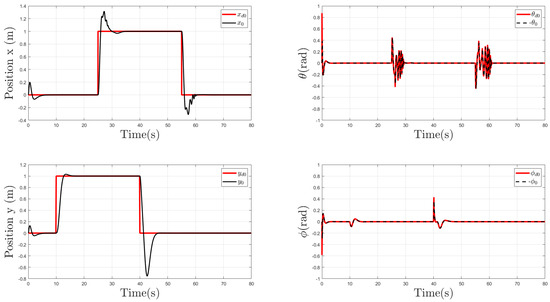
Figure 8.
Trajectories of Agent 0 (Leader) in x, y, and coordinates.
Figure 9 shows the behavior of follower Agent 1. We can observe that it is evident that the input time-varying delay impacted the follower more significantly than the leader. The trajectories of x, y, , and remained unaffected, except when the desired position changed. Moreover, the x coordinate was more affected by time-varying delays than the y coordinate; the reason for this behavior was that, during the time intervals when the x coordinate changed position, the functions , and had periods of greater amplitude, as shown in Figure 5, thus resulting in a more significant delay in the control input.
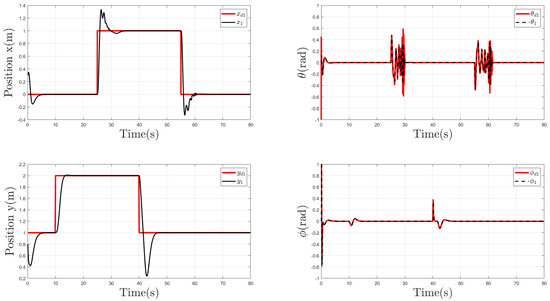
Figure 9.
Trajectories of Agent 1 in x, y, and coordinates.
Figure 10 illustrates the results of follower Agent 2. Notably, the behavior closely mirrored that of Agent 1, except for the initial part of the simulation, due to the initial conditions. This is characteristic of such control schemes, wherein any signal delay in the leader agent’s state inevitably ripples through the entire agent system.

Figure 10.
Trajectories of Agent 2 in x, y, and coordinates.
In Figure 11, the estimation errors between and of all agents are depicted. It is evident that the error approached zero, indicating the convergence of to . Finally, Figure 12 shows the estimation errors between and of all agents, we can see that the proposed algorithm caused the error to converge to zero; thus, the effectiveness of the designed control schemes based on state estimation was verified by isolating these errors in all agents, despite the presence of distinct unknown delays.
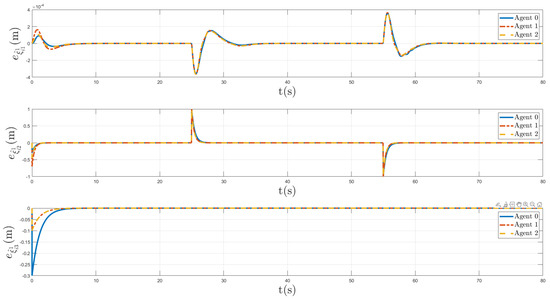
Figure 11.
Error estimation between and of all agents.
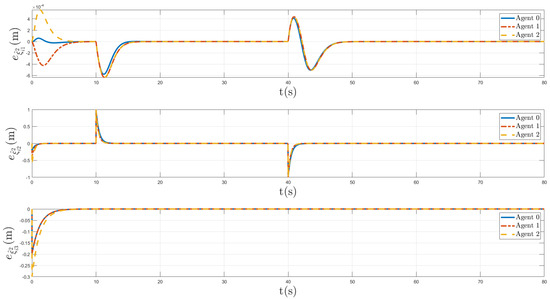
Figure 12.
Error estimation between and of all agents.
5. Conclusions
This paper addressed an observer-based consensus tracking control algorithm for multiple quadrotor unmanned aerial vehicles under the presence of unknown time-varying delays. The state estimation, consensus, and tracking errors of the closed-loop system converged to small values, and the stability of the proposed strategy was guaranteed using Lyapunov theory for the leader and followers, despite a distinct unknown time-varying delay. Future work includes extending the scheme to a multi-quadrotor nonlinear dynamic model and control, and considering external disturbances, measurement noise, and parametric uncertainty, as well as the case of fault isolation.
Author Contributions
Conceptualization, S.-N.C.-M. and O.H.-G.; methodology, G.V.-P. and F.-R.L.-E.; software, M.-E.G.-S.; validation, S.-N.C.-M.; formal analysis, O.H.-G.; investigation, M.-E.G.-S.; writing—original draft preparation, G.V.-P., B.T. and F.-R.L.-E.; writing—review and editing, S.-N.C.-M.; visualization, O.H.-G.; supervision, M.-E.G.-S.; project administration, O.H.-G.; funding acquisition, G.V.-P., B.T. and F.-R.L.-E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Tecnológico Nacional de México under the program Proyectos de Investigación Científica y Desarrollo Tecnológico e Innovación and the international network Red Internacional de Control y Cómputo Aplicado. Additional support was provided by Conahcyt under the program Investigadoras e Investigadores por México Project 88 and the work of S.-N. Campos-Martínez through a Doctoral Fellowship Assignment.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hou, Z.; Wang, W.; Zhang, G.; Han, C. A survey on the formation control of multiple quadrotors. In Proceedings of the 2017 14th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Jeju, Republic of Korea, 28 June–1 July 2017; pp. 219–225. [Google Scholar]
- Mishra, B.; Garg, D.; Narang, P.; Mishra, V. Drone-surveillance for search and rescue in natural disaster. Comput. Commun. 2020, 156, 1–10. [Google Scholar] [CrossRef]
- Farrera, B.; López-Estrada, F.R.; Chadli, M.; Valencia-Palomo, G.; Gómez-Peñate, S. Distributed fault estimation of multi–agent systems using a proportional–integral observer: A leader–following application. Int. J. Appl. Math. Comput. Sci. 2020, 30, 551–560. [Google Scholar]
- Trejo, J.A.V.; Ponsart, J.C.; Adam-Medina, M.; Valencia-Palomo, G.; Theilliol, D. Distributed Observer-based Leader-following Consensus Control for LPV Multi-agent Systems: Application to multiple VTOL-UAVs Formation Control. In Proceedings of the 2023 International Conference on Unmanned Aircraft Systems (ICUAS), Warsaw, Poland, 6–9 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1316–1323. [Google Scholar]
- Hernández-González, O.; Targui, B.; Valencia-Palomo, G.; Guerrero-Sánchez, M. Robust cascade observer for a disturbance unmanned aerial vehicle carrying a load under multiple time-varying delays and uncertainties. Int. J. Syst. Sci. 2024, 55, 1056–1072. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Wang, Z. Formation control: A review and a new consideration. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 3181–3186. [Google Scholar]
- Dong, X.; Yu, B.; Shi, Z.; Zhong, Y. Time-Varying Formation Control for Unmanned Aerial Vehicles: Theories and Applications. IEEE Trans. Control Syst. Technol. 2015, 23, 340–348. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, Y.; Jin, Y.; Wang, T.; Nie, X.; Yan, T. A Survey of An Intelligent Multi-Agent Formation Control. Appl. Sci. 2023, 13, 5934. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z.; Huang, L. Leader-follower consensus of multi-agent systems. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3256–3261. [Google Scholar]
- Gao, Y.; Wang, L. Sampled-Data Based Consensus of Continuous-Time Multi-Agent Systems with Time-Varying Topology. IEEE Trans. Autom. Control 2011, 56, 1226–1231. [Google Scholar] [CrossRef]
- Liu, W.; Huang, J. Leader-Following Consensus for Linear Multiagent Systems via Asynchronous Sampled-Data Control. IEEE Trans. Autom. Control 2020, 65, 3215–3222. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.L.; Zuo, Z.; Ding, L.; Lu, Q.; Ge, X. Fixed-Time and Prescribed-Time Consensus Control of Multiagent Systems and Its Applications: A Survey of Recent Trends and Methodologies. IEEE Trans. Ind. Inform. 2023, 19, 1121–1135. [Google Scholar] [CrossRef]
- Ren, W. On Consensus Algorithms for Double-Integrator Dynamics. IEEE Trans. Autom. Control 2008, 53, 1503–1509. [Google Scholar] [CrossRef]
- Li, Z.; Ren, W.; Liu, X.; Fu, M. Consensus of Multi-Agent Systems with General Linear and Lipschitz Nonlinear Dynamics Using Distributed Adaptive Protocols. arXiv 2011, arXiv:1109.3799. [Google Scholar] [CrossRef]
- Cheng, L.; Hou, Z.G.; Tan, M.; Wang, X. Necessary and Sufficient Conditions for Consensus of Double-Integrator Multi-Agent Systems with Measurement Noises. IEEE Trans. Autom. Control 2011, 56, 1958–1963. [Google Scholar] [CrossRef]
- Altafini, C. Consensus Problems on Networks with Antagonistic Interactions. IEEE Trans. Autom. Control 2013, 58, 935–946. [Google Scholar] [CrossRef]
- Li, Z.; Wen, G.; Duan, Z.; Ren, W. Designing Fully Distributed Consensus Protocols for Linear Multi-Agent Systems with Directed Graphs. IEEE Trans. Autom. Control 2015, 60, 1152–1157. [Google Scholar] [CrossRef]
- Meng, D.; Jia, Y.; Du, J. Finite-Time Consensus for Multiagent Systems with Cooperative and Antagonistic Interactions. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 762–770. [Google Scholar] [CrossRef] [PubMed]
- Meng, D.; Zou, Z. Signed-average consensus for networks of agents: A nonlinear fixed-time convergence protocol. Nonlinear Dyn. 2016, 85, 155–165. [Google Scholar] [CrossRef]
- Li, H.; Chen, G.; Liao, X.; Huang, T. Leader-Following Consensus of Discrete-Time Multiagent Systems with Encoding–Decoding. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 401–405. [Google Scholar] [CrossRef]
- Li, Y.; Tang, K.; Yan, F. A Consensus Control Algorithm of High-order Multi-agent Systems with Time Delay. In Proceedings of the 2019 3rd International Symposium on Autonomous Systems (ISAS), Shanghai, China, 29–31 May 2019; pp. 502–507. [Google Scholar]
- Geng, H.; Wu, H.; Miao, J.; Hou, S.; Chen, Z. Consensus of Heterogeneous Multi-Agent Systems Under Directed Topology. IEEE Access 2022, 10, 5936–5943. [Google Scholar] [CrossRef]
- Xiao, F.; Chen, T.; Gao, H. Synchronous Hybrid Event- and Time-Driven Consensus in Multiagent Networks with Time Delays. IEEE Trans. Cybern. 2016, 46, 1165–1174. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, K.; Xie, W.C. Consensus of multi-agent systems via hybrid impulsive protocols with time-delay. Nonlinear Anal. Hybrid Syst. 2018, 30, 134–146. [Google Scholar] [CrossRef]
- Qi, T.; Lu, R.; Chen, J. Consensus of Continuous-Time Multiagent Systems via Delayed Output Feedback: Delay Versus Connectivity. IEEE Trans. Autom. Control 2021, 66, 1329–1336. [Google Scholar] [CrossRef]
- Cao, L.; Liu, G.P.; Zhang, D.W. A leader-follower consensus control of networked multi-agent systems under communication delays and switching topologies. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 4378–4383. [Google Scholar]
- Tan, C.; Dong, X.; Li, Y.; Liu, G.P. Leader–following consensus problem of networked multi-agent systems under switching topologies and communication constraints. IET Control Theory Appl. 2020, 14, 3686–3696. [Google Scholar] [CrossRef]
- Jiang, W.; Charalambous, T. Distributed Consensus Tracking of Multi-Agent Systems with Time-varying Input/Output Delays and Mismatched Disturbances. IFAC-PapersOnLine 2021, 54, 787–794. [Google Scholar] [CrossRef]
- Cao, W.; Zhang, J.; Ren, W. Leader–follower consensus of linear multi-agent systems with unknown external disturbances. Syst. Control Lett. 2015, 82, 64–70. [Google Scholar] [CrossRef]
- Zhu, J.W.; Yang, G.H.; Zhang, W.A.; Yu, L. Cooperative Fault Tolerant Tracking Control for Multiagent Systems: An Intermediate Estimator-Based Approach. IEEE Trans. Cybern. 2018, 48, 2972–2980. [Google Scholar] [CrossRef]
- Zhao, S.; Yu, J.; Wang, Z.; Gao, D. Unknown input observer based distributed fault detection for nonlinear multi-agent systems with probabilistic time delay. J. Frankl. Inst. 2023, 360, 1058–1076. [Google Scholar] [CrossRef]
- Nemati, F.; Safavi Hamami, S.; Zemouche, A. A nonlinear observer-based approach to fault detection, isolation and estimation for satellite formation flight application. Automatica 2019, 107, 474–482. [Google Scholar] [CrossRef]
- Zhu, F.; Tan, C. Consensus Control of Linear Parameter-Varying Multi-Agent Systems with Unknown Inputs. Sensors 2023, 23, 5125. [Google Scholar] [CrossRef]
- Liu, C.; Shi, Y.; Meng, Y.; Wang, Y. Leader-following consensus of multi-agent systems with connectivity-mixed attacks and actuator/sensor faults. J. Frankl. Inst. 2023, 360, 3592–3617. [Google Scholar] [CrossRef]
- Li, P.; Qin, K.; Pu, H. Distributed robust time-varying formation control for multiple unmanned aerial vehicles systems with time-delay. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 1539–1544. [Google Scholar] [CrossRef]
- Tang, Y.; Xue, Z.; Liu, X.; Han, Q.; Tuo, X. Leader-Following Consensus Control for Multiple Fixed-Wing UAVs’ Attitude System with Time Delays and External Disturbances. IEEE Access 2019, 7, 169773–169781. [Google Scholar] [CrossRef]
- Li, S.; Duan, N.; Xu, Z.; Liu, X.Y. Tracking Control of Quadrotor UAV with Input Delay. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 646–649. [Google Scholar] [CrossRef]
- Pedro, C.; Rogelio, L.; Alejandro, D. Modelling and Control of Mini-Flying Machines; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Nguyen, C.M.; Tan, C.P.; Trinh, H. State and delay reconstruction for nonlinear systems with input delays. Appl. Math. Comput. 2021, 390, 125609. [Google Scholar] [CrossRef]
- Nguyen, C.M.; Zemouche, A.; Trinh, H. Observer-Based Control Design for Nonlinear Systems with Unknown Delays. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1327–1331. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).