Natural Characteristics of a Marine Two-Stage Tandem Hybrid Planetary System
Abstract
1. Introduction
2. Dynamic Model of the Transmission System
3. Mode Analysis
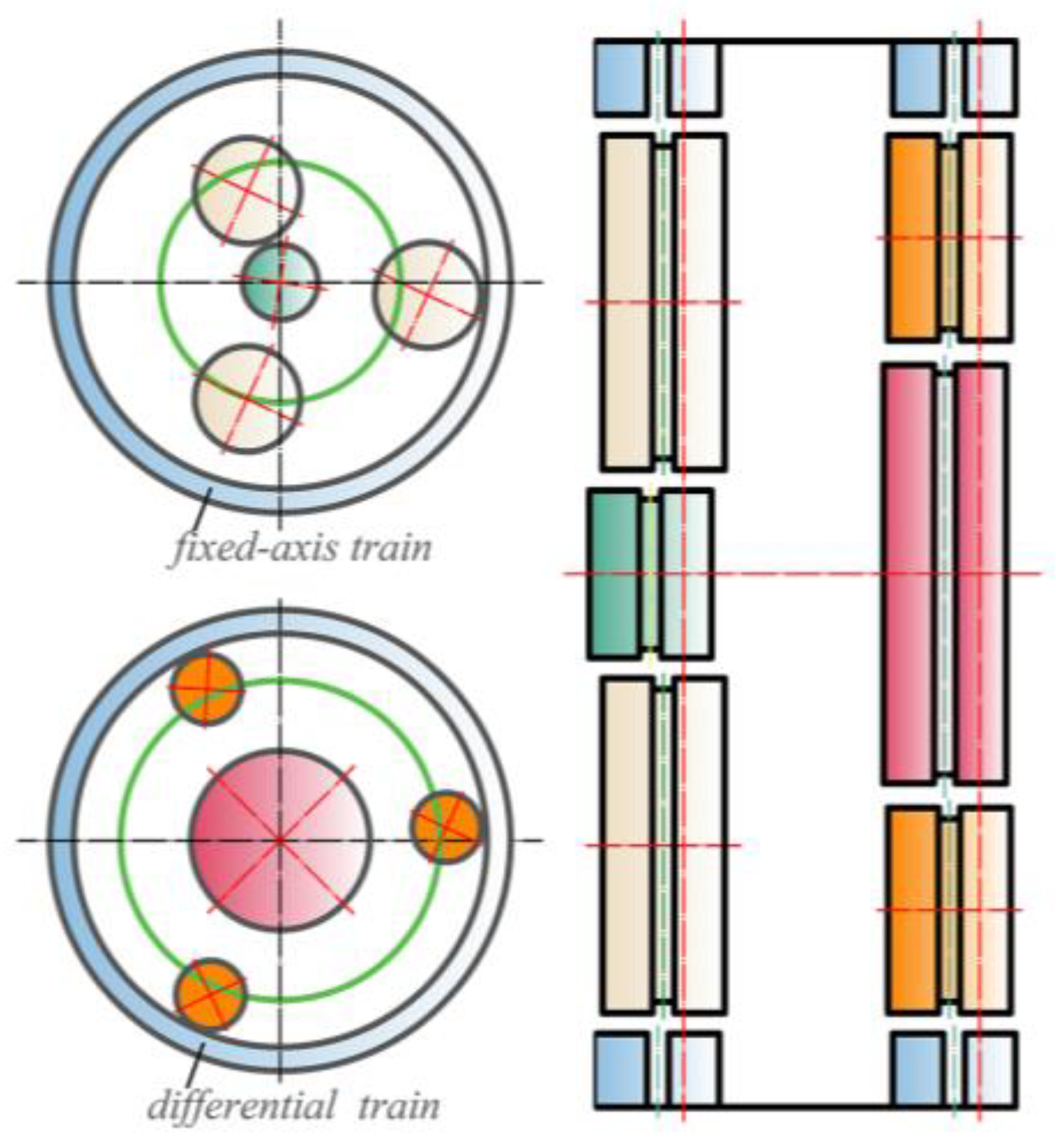
3.1. Fixed-Axis Train Vibration Mode
3.2. Differential Train Vibration Mode
3.3. Coupled Vibration Mode
3.4. Verification of the Mathematical Model Using the Finite Element Method
4. Sensitivity Analysis of Natural Frequency
4.1. Unequally Spaced Planets
4.2. Mesh Stiffness
4.2.1. Mesh Stiffness Sensitivity Analysis
4.2.2. Mode Transition Criterion
4.2.3. Sensitivity and Modal Transition Verification
4.3. Planet Mass
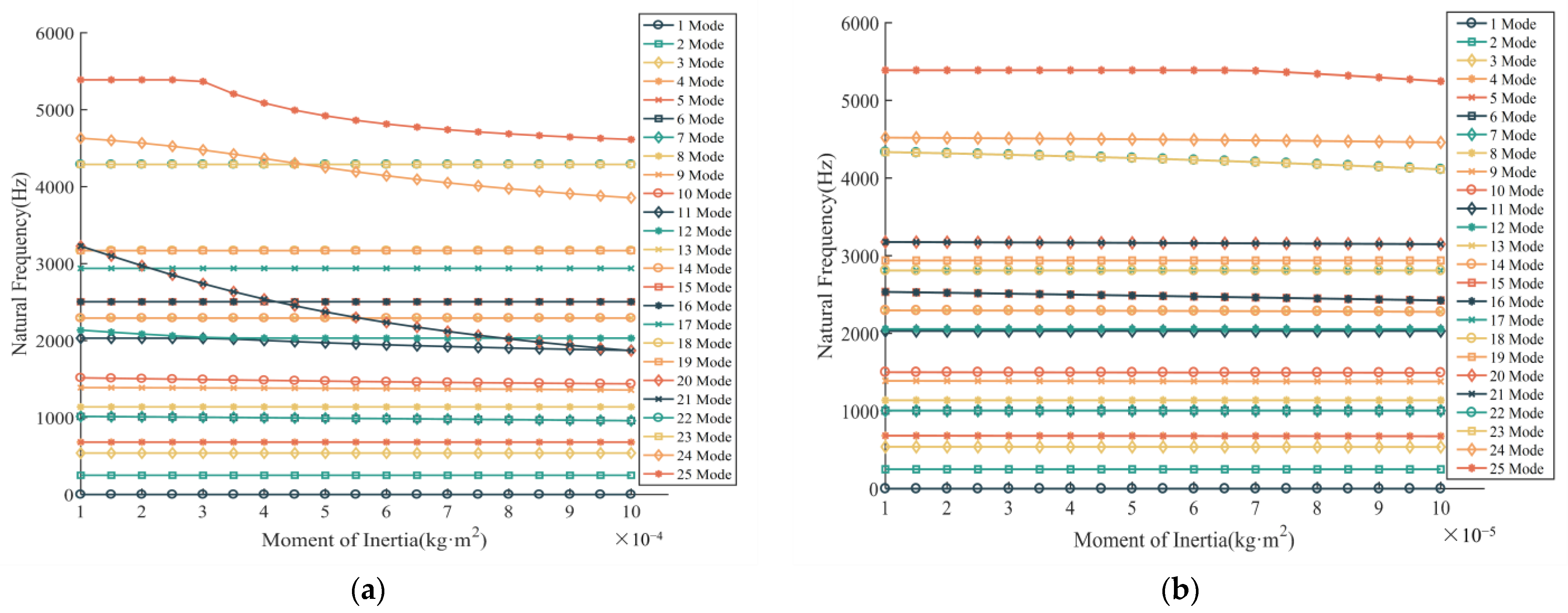
4.4. Planet Rotational Inertia
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ambarisha, V.K.; Parker, R.G. Nonlinear dynamics of planetary gears using analytical and finite element models. J. Sound Vib. 2007, 302, 577–595. [Google Scholar] [CrossRef]
- Kahraman, A.; Blankenship, G.W. Interactions between commensurate parametric and forcing excitations in a system with clearance. J. Sound Vib. 1996, 194, 317–336. [Google Scholar] [CrossRef]
- Zhao, R.Z.; Liu, H.; Zheng, Y.Q. Parameter sensitivity for the torsional vibration of wind turbine drive train system. In Proceedings of the International Conference on Information Science and Intelligent Control, Shanghai, China, 24–25 April 2015; pp. 71–76. [Google Scholar]
- Zhang, L.; Wang, Y.; Wu, K.; Sheng, R.; Huang, Q. Dynamic modeling and vibration characteristics of a two-stage closed-form planetary gear train. Mech. Mach. Theory 2016, 97, 12–28. [Google Scholar] [CrossRef]
- Wu, X.; Parker, R.G. Mode characteristics of planetary gears with an elastic continuum ring gear. J. Appl. Mech. 2008, 75, 031014. [Google Scholar] [CrossRef]
- Sondkar, P.; Kahraman, A. A dynamic model of a double-helical planetary gear set. Mech. Mach. Theory 2013, 70, 157–174. [Google Scholar] [CrossRef]
- Hao, D.; Zhi, L.; Jian, Z. Inherent characteristic analysis of a dual power split gear train. IOP Conf. Ser. Earth Environ. Sci. 2019, 233, 032007. [Google Scholar] [CrossRef]
- Cui, T.; Li, Y.; Zan, C.; Chen, Y. Dynamic modeling and analysis of nonlinear compound planetary system. Machines 2022, 10, 31. [Google Scholar] [CrossRef]
- Shuai, M.; Ting, Z.; Guo-Guang, J.; Xiao-Lin, C.; Han-Jun, G. Analytical investigation on load sharing characteristics of her-ringbone planetary gear train with flexible support and floating sun gear. Mech. Mach. Theory 2020, 144, 103670. [Google Scholar] [CrossRef]
- Mbarek, A.; Hammami, A.; Del Rincon, A.F.; Chaari, F.; Rueda, F.V.; Haddar, M. Effect of load and mesh stiffness variation on mode characteristics of planetary gear. Appl. Acoust. 2019, 147, 32–43. [Google Scholar] [CrossRef]
- Cooley, C.G.; Parker, R.G. Vibration properties of high-speed planetary gears with gyroscopic effects. J. Vib. Acoust. 2012, 134, 061014. [Google Scholar] [CrossRef]
- Qiu, W.; Yang, F.; Wang, D.; Jiang, X. Design and free vibration characteristics of linkage planetary gear trains. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 58. [Google Scholar] [CrossRef]
- Liu, H.; Zhan, Z. Modal properties of a two-stage planetary gear system with a Timoshenko beam as the intermediate shaft model. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 353–365. [Google Scholar] [CrossRef]
- Hu, Z.; Tang, J.; Wang, Q.; Chen, S.; Qian, L. Investigation of nonlinear dynamics and load sharing characteristics of a two-path split torque transmission system. Mech. Mach. Theory 2020, 152, 103955. [Google Scholar] [CrossRef]
- Huang, C.; Huang, B.; Zhang, Y.; Xiao, K. Modal analysis and experimental research on a planetary reducer with small tooth number difference. Trans. Can. Soc. Mech. Eng. 2019, 44, 202–212. [Google Scholar] [CrossRef]
- Hu, C.; Geng, G.; Liu, X.; Yang, S.; Tang, X. Dynamic Characteristics of the Multistage Planetary Gear Transmission System Based on a Stochastic Load. Int. J. Precis. Eng. Manuf. 2023, 24, 657–669. [Google Scholar] [CrossRef]
- Tatar, A.; Schwingshackl, C.W.; Friswell, M.I. Dynamic behaviour of three-dimensional planetary geared rotor systems. Mech. Mach. Theory 2019, 134, 39–56. [Google Scholar] [CrossRef]
- Tatar, A.; Schwingshackl, C.W.; Friswell, M.I. Modal sensitivity of three-dimensional planetary geared rotor systems to planet gear parameters. Appl. Math. Model. 2023, 113, 309–332. [Google Scholar] [CrossRef]
- Guo, Y.; Parker, R.G. Sensitivity of general compound planetary gear natural frequencies and vibration modes to model parameters. J. Vib. Acoust. 2010, 132, 11006. [Google Scholar] [CrossRef]
- Parker, R.G.; Wu, X. Vibration modes of planetary gears with unequally spaced planets and an elastic ring gear. J. Sound Vib. 2010, 329, 2265–2275. [Google Scholar] [CrossRef]
- Cooley, C.G.; Parker, R.G. Eigenvalue sensitivity and veering in gyroscopic systems with application to high-speed planetary gears. Eur. J. Mech.-A/Solids 2018, 67, 123–136. [Google Scholar] [CrossRef]
- Qian, P.-Y.; Zhang, Y.-L.; Cheng, G.; Ge, S.-R.; Zhou, C.-F. Model analysis and verification of 2K-H planetary gear system. J. Vib. Control 2015, 21, 1946–1957. [Google Scholar] [CrossRef]
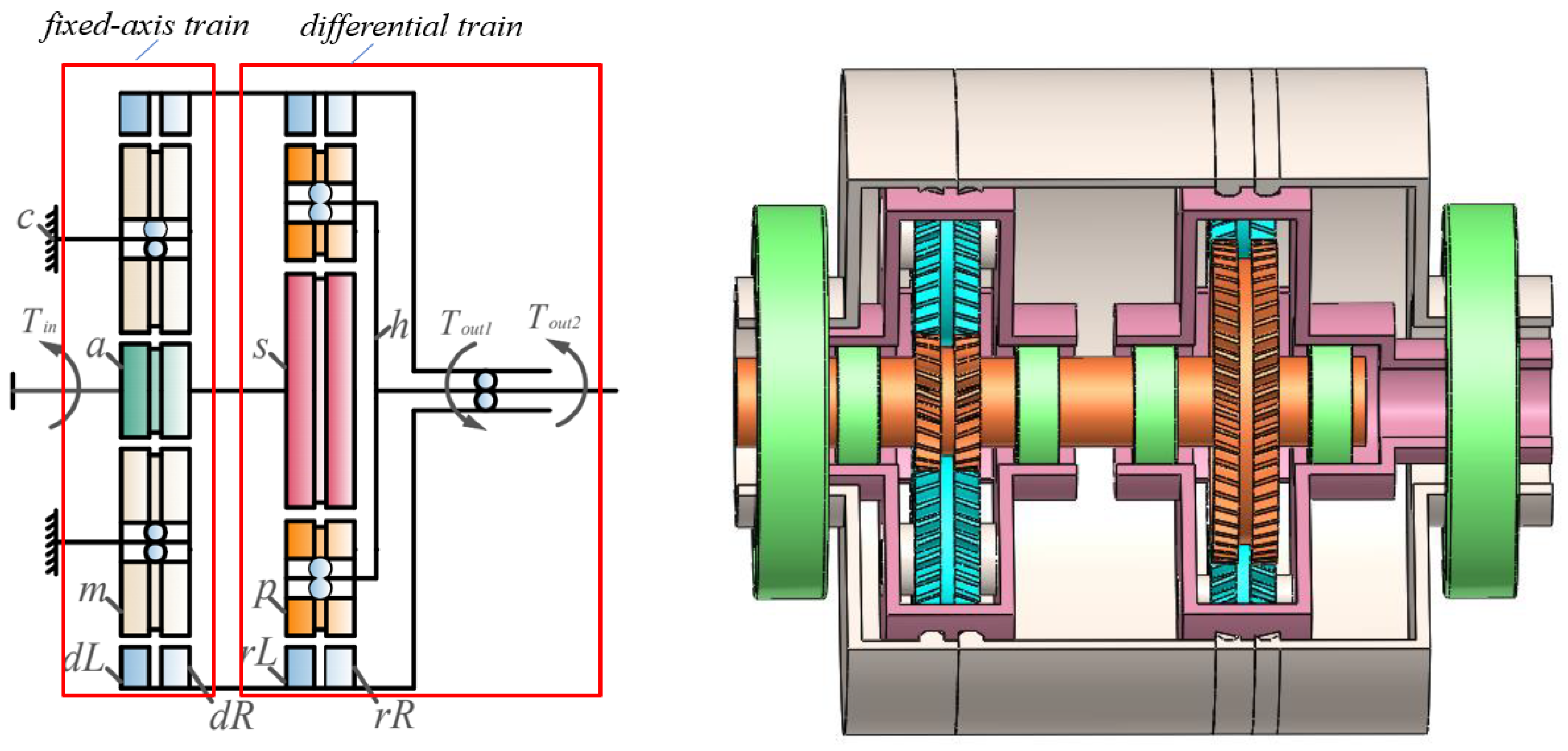
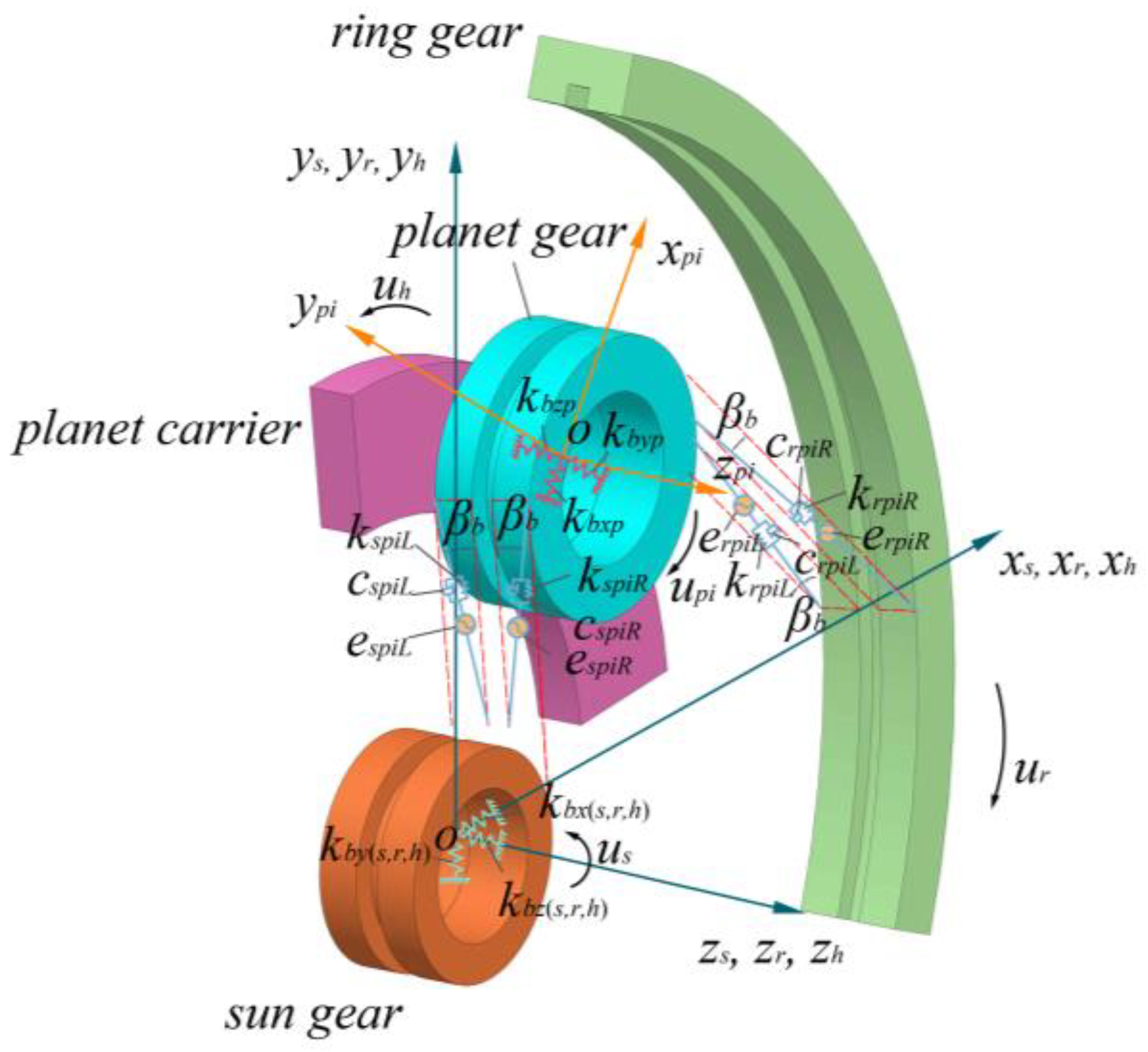
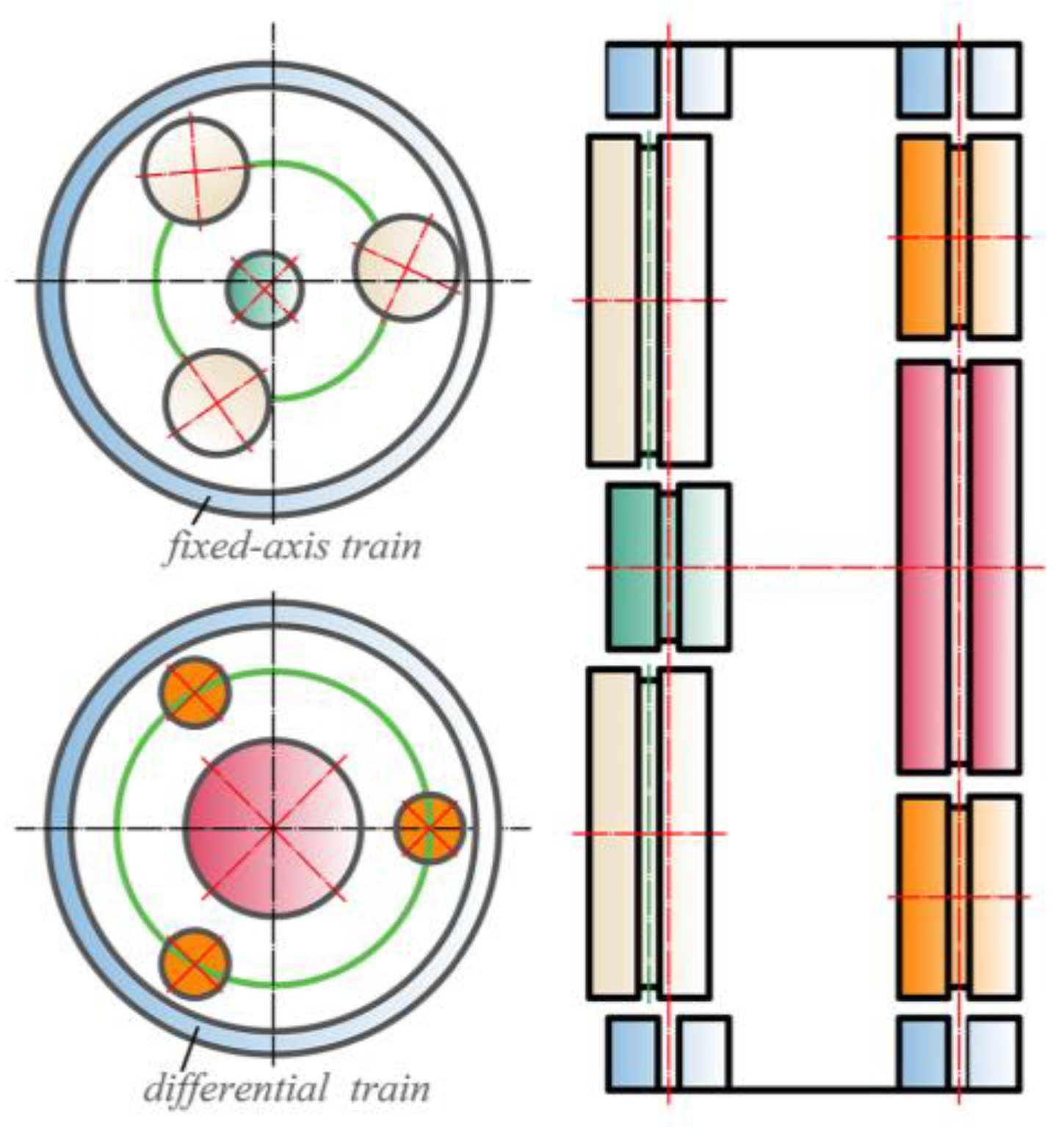
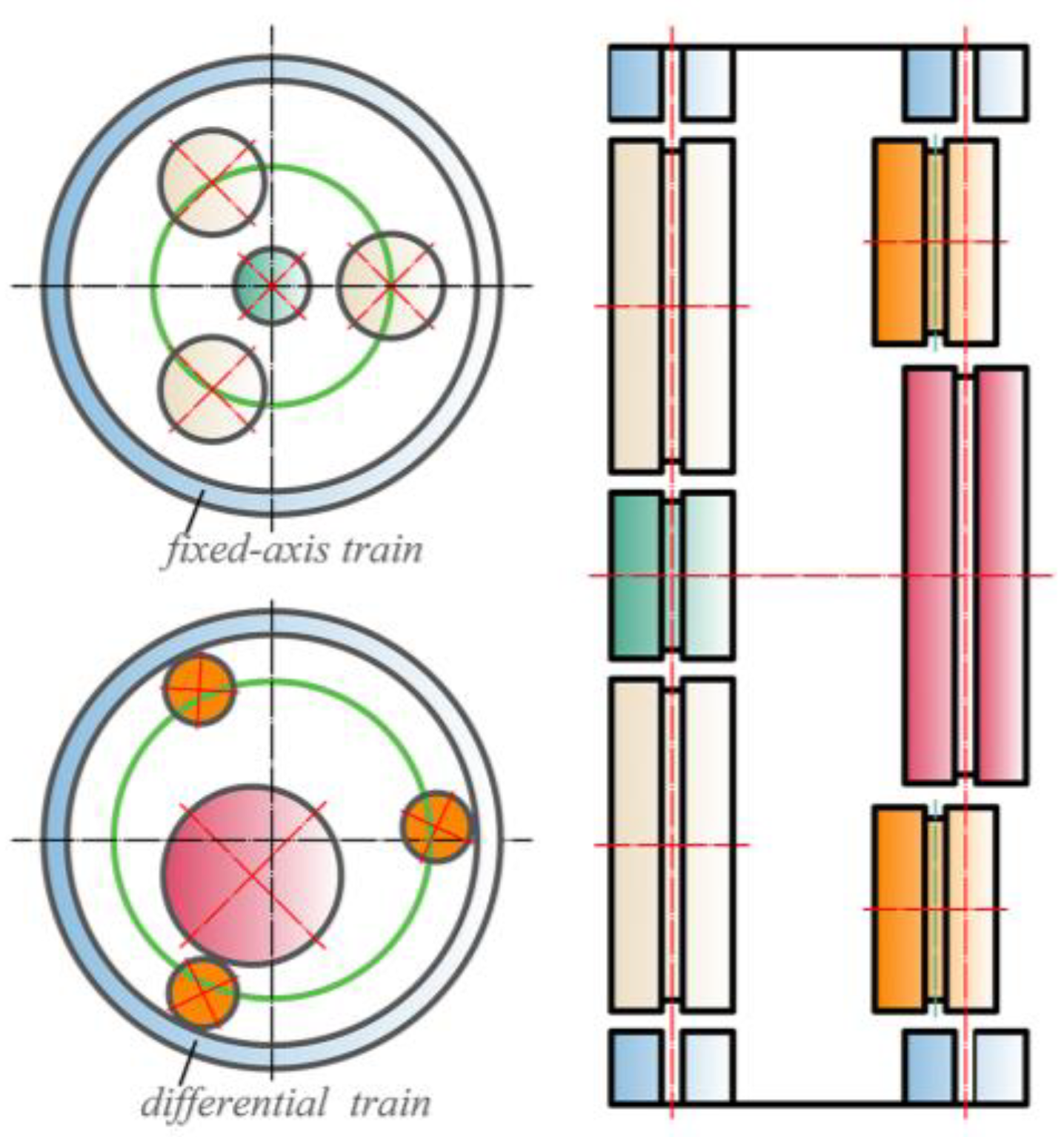



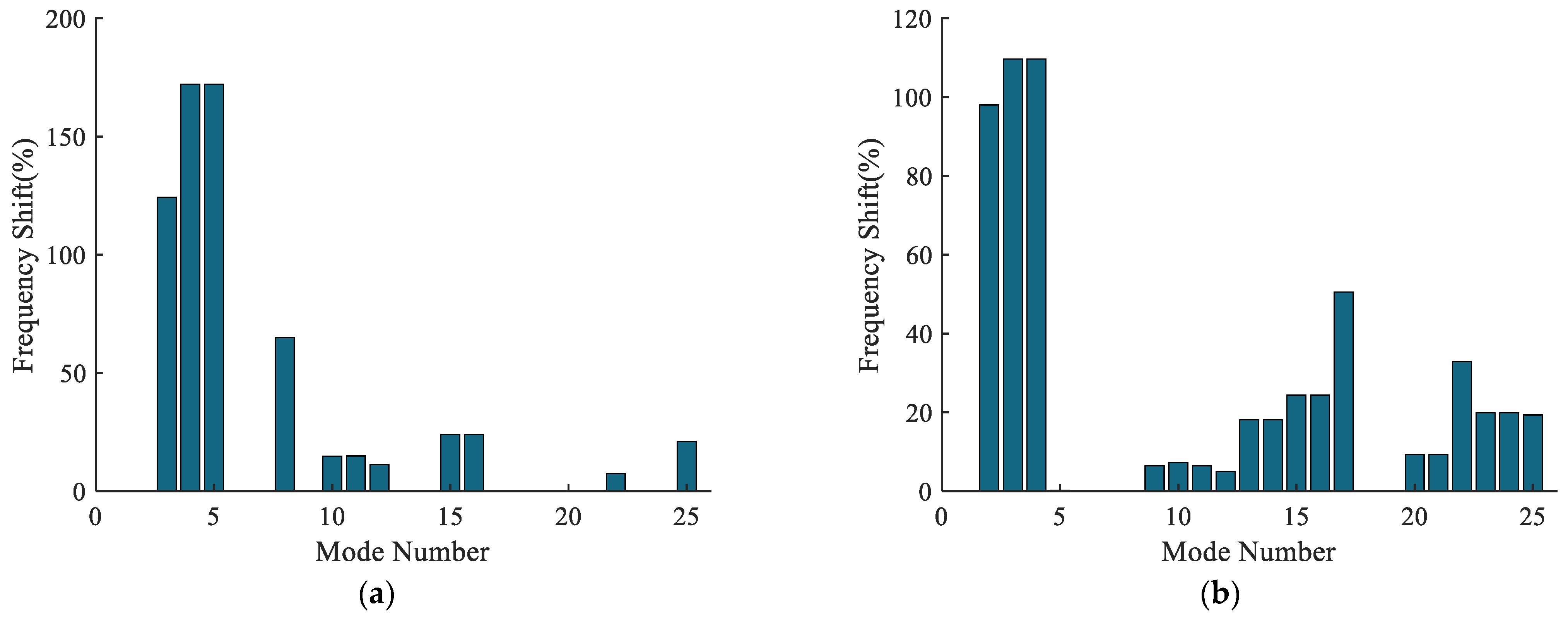

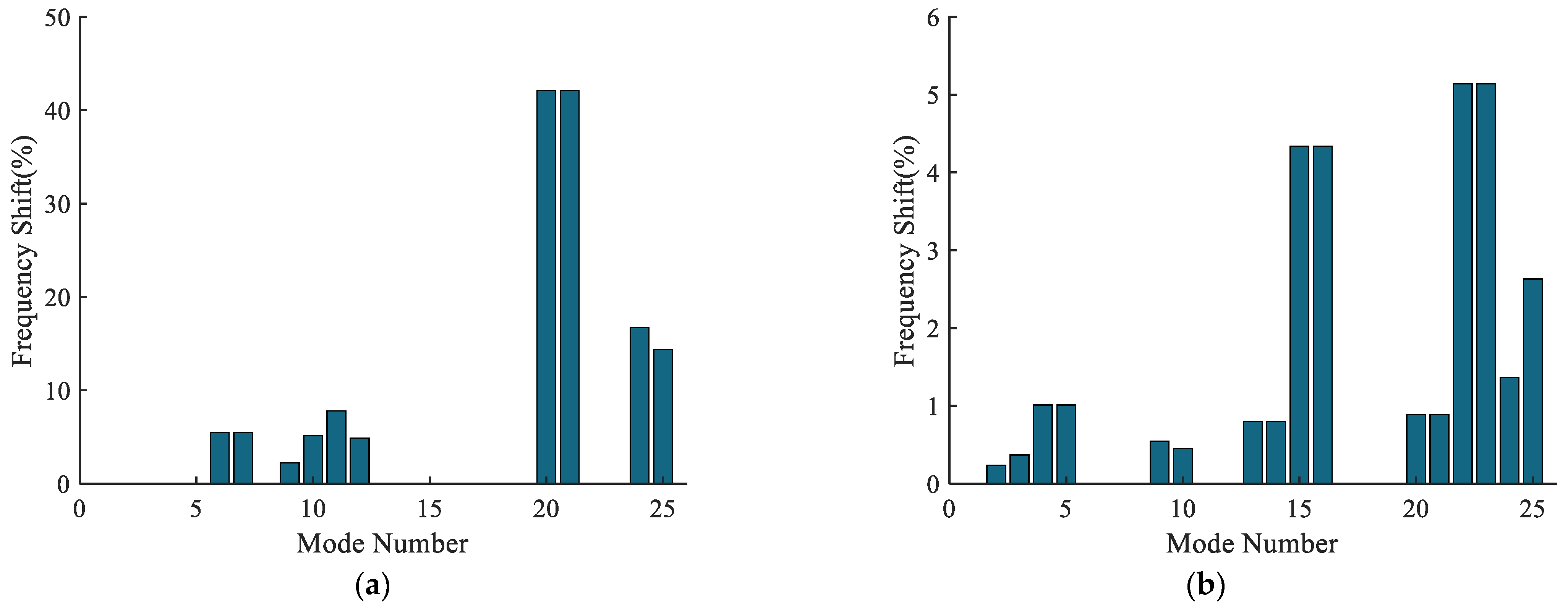
| Item | Number of Teeth | Angle of Helix (°) | Normal Pressure Angle (°) | Module | Mass (kg) | Rotational Inertia (kg·mm2) |
|---|---|---|---|---|---|---|
| Sun gear a | 22 | 20 | 20 | 1.5 | 0.092 | 17.664 |
| Planet gear m | 44 | 20 | 20 | 1.5 | 0.327 | 268.521 |
| Ring gear dL | 110 | 20 | 20 | 1.5 | 0.163 | 1325.860 |
| Ring gear dR | 110 | 20 | 20 | 1.5 | 0.163 | 1325.860 |
| Sun gear s | 55 | 20 | 20 | 1.5 | 0.488 | 525.752 |
| Planet gear p | 27 | 20 | 20 | 1.5 | 0.108 | 35.531 |
| Ring gear rL | 110 | 20 | 20 | 1.5 | 0.163 | 1325.860 |
| Ring gear rR | 110 | 20 | 20 | 1.5 | 0.163 | 1325.860 |
| Planet carrier h | / | / | / | / | 1.648 | 4946.014 |
| Mode | Mathematical Model Nat. Freq. (Hz) | Finite Element Model Nat. Freq. (Hz) | Difference (%) | Mod Type |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | / |
| 2 | 249.96 | 255.71 | 2.3 | couple |
| 3 | 538.75 | 564.61 | 4.8 | couple |
| 4 | 680.52 | 656.02 | −3.6 | differential train |
| 5 | 680.52 | 656.02 | −3.6 | differential train |
| 6 | 1005.47 | 1031.6 | 2.6 | fixed-axis train |
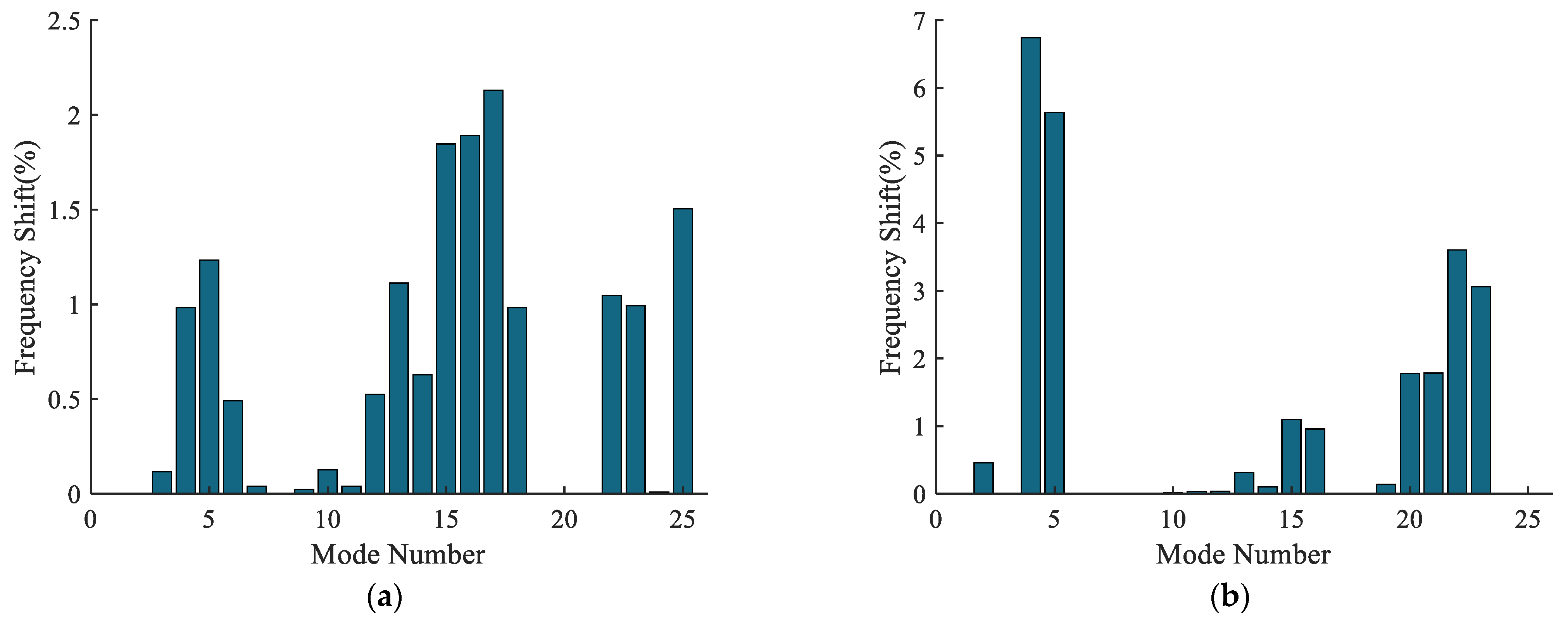
| Mode | Dev. Ang. = 0° Nat. Freq. (Hz) | Dev. Ang. = 0° Mod Type | Fixed-Axis Train | Differential Train | ||||
|---|---|---|---|---|---|---|---|---|
| Dev. Ang. = 15° Nat. Freq. (Hz) | Dev. Ang. = 15° Mod Type | Freq. Shift(%) | Dev. Ang. = 15° Nat. Freq. (Hz) | Dev. Ang. = 15° Mod Type | Freq. Shift (%) | |||
| 1 | 0 | couple | 0 | global | 0 | 0 | couple–global | 0 |
| 2 | 249.96 | couple | 249.96 | global | 0 | 248.81 | couple–global | 0.46 |
| 3 | 538.75 | couple | 538.12 | global | 0.12 | 538.74 | couple–global | 0 |
| 4 | 680.52 | differential train | 673.84 | global | 0.98 | 634.64 | couple–global | 6.74 |
| 5 | 680.52 | differential train | 688.91 | global | 1.23 | 718.85 | couple–global | 5.63 |
| 6 | 1005.47 | fixed-axis train | 1000.53 | global | 0.49 | 1005.47 | fixed-axis train | 0 |
| 7 | 1005.47 | fixed-axis train | 1005.87 | global | 0.04 | 1005.47 | fixed-axis train | 0 |
| 8 | 1138.42 | planet carrier | 1138.42 | planet carrier | 0 | 1138.42 | planet carrier | 0 |
| 9 | 1385.93 | couple | 1385.6 | global | 0.02 | 1385.85 | couple–global | 0.01 |
| 10 | 1497.41 | couple | 1495.52 | global | 0.13 | 1497.12 | couple–global | 0.02 |
| 11 | 2030.67 | couple | 2029.86 | global | 0.04 | 2030.03 | couple–global | 0.03 |
| 12 | 2054.77 | couple | 2044 | global | 0.52 | 2053.98 | couple–global | 0.04 |
| 13 | 2292.34 | differential train | 2266.85 | global | 1.11 | 2285.13 | couple–global | 0.31 |
| 14 | 2292.34 | differential train | 2306.73 | global | 0.63 | 2294.74 | couple–global | 0.1 |
| 15 | 2504.67 | differential train | 2458.41 | global | 1.85 | 2477.16 | couple–global | 1.1 |
| 16 | 2504.67 | differential train | 2552.05 | global | 1.89 | 2528.65 | couple–global | 0.96 |
| 17 | 2809.75 | fixed-axis train | 2749.92 | global | 2.13 | 2809.75 | fixed-axis train | 0 |
| 18 | 2809.75 | fixed-axis train | 2837.37 | global | 0.98 | 2809.75 | fixed-axis train | 0 |
| 19 | 2938.39 | couple | 2938.39 | global | 0 | 2934.2 | couple–global | 0.14 |
| 20 | 3169.47 | differential train | 3169.39 | global | 0 | 3113.13 | couple–global | 1.78 |
| 21 | 3169.47 | differential train | 3169.55 | global | 0 | 3225.96 | couple–global | 1.78 |
| 22 | 4288.77 | differential train | 4243.9 | global | 1.05 | 4134.17 | couple–global | 3.6 |
| 23 | 4288.77 | differential train | 4331.34 | global | 0.99 | 4420.11 | couple–global | 3.06 |
| 24 | 4507.93 | couple | 4508.32 | global | 0.01 | 4508.21 | couple–global | 0.01 |
| 25 | 5388.32 | couple | 5307.26 | global | 1.5 | 5388.33 | couple–global | 0 |
| Vibration Mode | Meshing Stiffness kam Mode Transition Criterion | Meshing Stiffness ksp Mode Transition Criterion | |
|---|---|---|---|
| Case1 | All vibration modes are fixed-axis train vibration modes | transition | unchange |
| Case2 | All vibration modes are differential train vibration modes | unchange | transition |
| Case3 | All vibration modes are coupled vibration modes | transition | transition |
| Case4 | Vibration modes are coupled vibration mode and fixed-axis train vibration mode | intersect | intersect |
| Case5 | Vibration modes are coupled vibration mode and differential train vibration mode | intersect | intersect |
| Case6 | Vibration modes are fixed-axis train vibration mode and differential train vibration mode | intersect | intersect |
| Mode | Fixed-Axis Train | Differential Train | ||||||
|---|---|---|---|---|---|---|---|---|
| kam = 107 N/m Nat. Freq. (Hz) | kam =108 N/m Nat. Freq. (Hz) | Mod Type | Freq. Shift (%) | ksp =107 N/m Nat. Freq. (Hz) | ksp =108 N/m Nat. Freq. (Hz) | Mod Type | Freq. Shift (%) | |
| 1 | 0 | 0 | couple | 0 | 0 | 0 | couple | 0 |
| 2 | 249.74 | 249.97 | couple | 0.09 | 142.13 | 281.43 | couple | 98.01 |
| 3 | 280.62 | 629.29 | couple | 124.25 | 375.67 | 787.68 | differential train | 109.67 |
| 4 | 479.39 | 1304.38 | fixed-axis train | 172.09 | 375.67 | 787.68 | differential train | 109.67 |
| 5 | 479.39 | 1304.38 | fixed-axis train | 172.09 | 537.79 | 538.86 | couple | 0.2 |
| 6 | 680.52 | 680.52 | differential train | 0 | 1005.47 | 1005.47 | differential train | 0 |
| 7 | 680.52 | 680.52 | differential train | 0 | 1005.47 | 1005.47 | differential train | 0 |
| 8 | 845.65 | 1394.85 | couple | 64.94 | 1138.42 | 1138.42 | planet carrier | 0 |
| 9 | 1138.42 | 1138.42 | planet carrier | 0 | 1311.12 | 1395.07 | couple | 6.4 |
| 10 | 1403.53 | 1611.29 | couple | 14.8 | 1405.05 | 1508.04 | couple | 7.33 |
| 11 | 1768.45 | 2031.44 | couple | 14.87 | 1916.28 | 2040.61 | couple | 6.49 |
| 12 | 2031.58 | 2259.49 | couple | 11.22 | 1972.24 | 2071.08 | couple | 5.01 |
| 13 | 2292.34 | 2292.34 | differential train | 0 | 2049.22 | 2420.15 | differential train | 18.1 |
| 14 | 2292.34 | 2292.34 | differential train | 0 | 2049.22 | 2420.15 | differential train | 18.1 |
| 15 | 2399.26 | 2973.19 | fixed-axis train | 23.92 | 2129.58 | 2648.16 | differential train | 24.35 |
| 16 | 2399.26 | 2973.19 | fixed-axis train | 23.92 | 2129.58 | 2648.16 | differential train | 24.35 |
| 17 | 2504.67 | 2504.67 | differential train | 0 | 2322.19 | 3495.13 | couple | 50.51 |
| 18 | 2504.67 | 2504.67 | differential train | 0 | 2809.75 | 2809.75 | differential train | 0 |
| 19 | 2938.38 | 2938.39 | couple | 0 | 2809.75 | 2809.75 | differential train | 0 |
| 20 | 3169.47 | 3169.47 | differential train | 0 | 3057.45 | 3341.41 | differential train | 9.29 |
| 21 | 3169.47 | 3169.47 | differential train | 0 | 3057.45 | 3341.41 | differential train | 9.29 |
| 22 | 4265.82 | 4581.29 | couple | 7.4 | 3392.91 | 4509.21 | couple | 32.9 |
| 23 | 4288.77 | 4288.77 | differential train | 0 | 3756.92 | 4503.96 | differential train | 19.88 |
| 24 | 4288.77 | 4288.77 | differential train | 0 | 3756.92 | 4503.96 | differential train | 19.88 |
| 25 | 4593.9 | 5557.98 | couple | 20.99 | 4514.16 | 5388.37 | couple | 19.37 |
| Mode | Fixed-Axis Train | Differential Train | ||||||
|---|---|---|---|---|---|---|---|---|
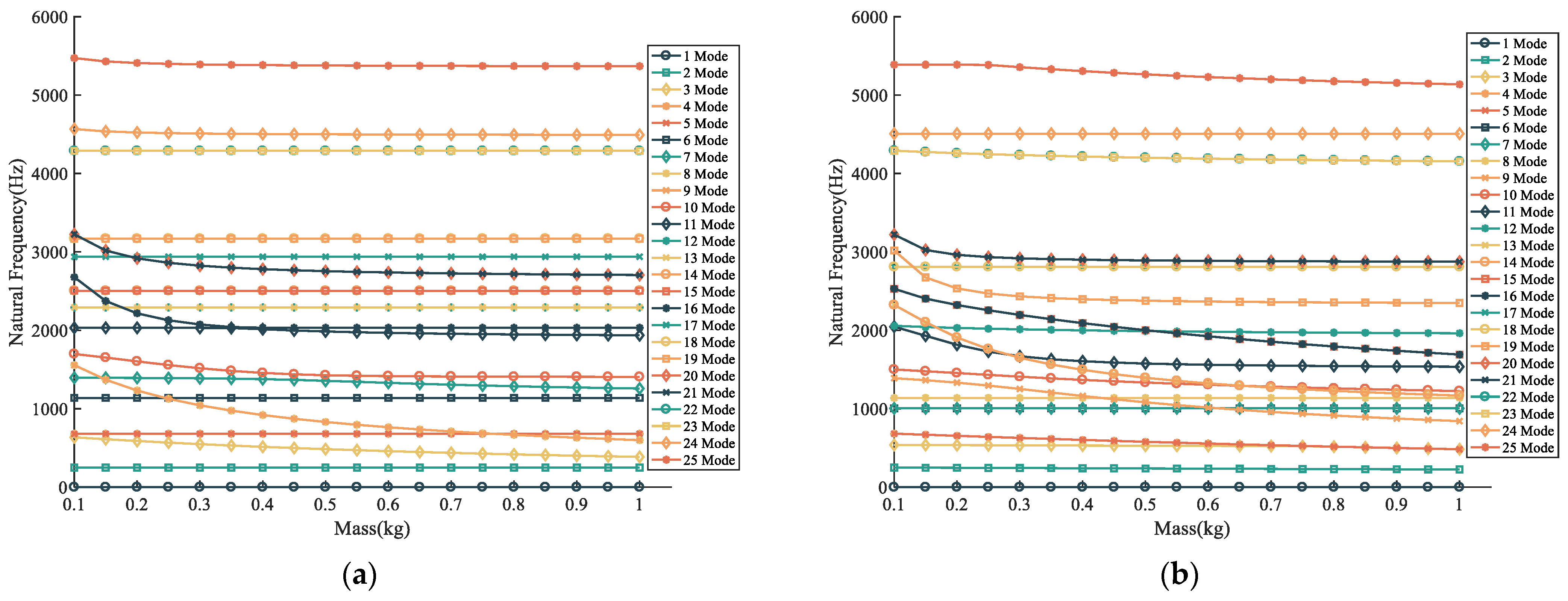
| Mm = 0.1 kg Nat. Freq. (Hz) | Mm = 1 kg Nat. Freq. (Hz) | Mod Type | Freq. Shift (%) | Mp = 0.1 kg Nat. Freq. (Hz) | Mp = 1 kg Nat. Freq. (Hz) | Mod Type | Freq. Shift (%) | |
| 1 | 0 | 0 | couple | 0 | 0 | 0 | couple | 0 |
| 2 | 249.96 | 249.96 | couple | 0 | 250.2 | 225.68 | couple | 9.8 |
| 3 | 635.37 | 385.58 | couple | 39.31 | 538.98 | 483.77 | couple | 10.24 |
| 4 | 680.52 | 680.52 | differential train | 0 | 682.74 | 483.77 | differential train | 29.14 |
| 5 | 680.52 | 680.52 | differential train | 0 | 682.74 | 483.77 | differential train | 29.14 |
| 6 | 1138.42 | 1138.42 | planet carrier | 0 | 1005.47 | 1005.47 | fixed-axis train | 0 |
| 7 | 1395.16 | 1257.79 | couple | 9.85 | 1005.47 | 1005.47 | fixed-axis train | 0 |
| 8 | 1556.41 | 599.63 | fixed-axis train | 61.47 | 1138.42 | 1138.42 | planet carrier | 0 |
| 9 | 1556.41 | 599.63 | fixed-axis train | 61.47 | 1389.59 | 842.26 | couple | 39.39 |
| 10 | 1698.55 | 1406.46 | couple | 17.2 | 1500.94 | 1225.51 | couple | 18.35 |
| 11 | 2031.74 | 1936.78 | couple | 4.67 | 2047.01 | 1536.29 | couple | 24.95 |
| 12 | 2292.34 | 2292.34 | differential train | 0 | 2058.29 | 1962.92 | couple | 4.63 |
| 13 | 2292.34 | 2292.34 | differential train | 0 | 2324.64 | 1168.2 | differential train | 49.75 |
| 14 | 2504.67 | 2504.67 | differential train | 0 | 2324.64 | 1168.2 | differential train | 49.75 |
| 15 | 2504.67 | 2504.67 | differential train | 0 | 2529.83 | 1691.2 | differential train | 33.15 |
| 16 | 2678.12 | 2031.99 | couple | 24.13 | 2529.83 | 1691.2 | differential train | 33.15 |
| 17 | 2938.39 | 2938.39 | couple | 0 | 2809.75 | 2809.75 | fixed-axis train | 0 |
| 18 | 3169.47 | 3169.47 | differential train | 0 | 2809.75 | 2809.75 | fixed-axis train | 0 |
| 19 | 3169.47 | 3169.47 | differential train | 0 | 3017.75 | 2348.77 | couple | 22.17 |
| 20 | 3224.87 | 2705.55 | fixed-axis train | 16.1 | 3221.6 | 2875.26 | differential train | 10.75 |
| 21 | 3224.87 | 2705.55 | fixed-axis train | 16.1 | 3221.6 | 2875.26 | differential train | 10.75 |
| 22 | 4288.77 | 4288.77 | differential train | 0 | 4291.78 | 4154.75 | differential train | 3.19 |
| 23 | 4288.77 | 4288.77 | differential train | 0 | 4291.78 | 4154.75 | differential train | 3.19 |
| 24 | 4567.2 | 4492.48 | couple | 1.64 | 4507.93 | 4507.88 | couple | 0 |
| 25 | 5472.18 | 5368.31 | couple | 1.9 | 5388.33 | 5137.52 | couple | 4.65 |
| Mode | Fixed-Axis Train | Differential Train | ||||||
|---|---|---|---|---|---|---|---|---|
| Jm = 0.1 kg Nat. Freq. (Hz) | Jm = 1 kg Nat. Freq. (Hz) | Mod Type | Freq. Shift (%) | Jp = 0.1 kg Nat. Freq. (Hz) | Jp = 1 kg Nat. Freq. (Hz) | Mod Type | Freq. Shift (%) | |
| 1 | 0 | 0 | couple | 0 | 0 | 0 | couple | 0 |
| 2 | 249.97 | 249.94 | couple | 0.01 | 250.18 | 249.59 | couple | 0.24 |
| 3 | 538.76 | 538.73 | couple | 0.01 | 539.47 | 537.49 | couple | 0.37 |
| 4 | 680.52 | 680.52 | differential train | 0 | 682.46 | 675.56 | differential train | 1.01 |
| 5 | 680.52 | 680.52 | differential train | 0 | 682.46 | 675.56 | differential train | 1.01 |
| 6 | 1014.34 | 959.12 | fixed-axis train | 5.44 | 1005.47 | 1005.47 | fixed-axis train | 0 |
| 7 | 1014.34 | 959.12 | fixed-axis train | 5.44 | 1005.47 | 1005.47 | fixed-axis train | 0 |
| 8 | 1138.42 | 1138.42 | planet carrier | 0 | 1138.42 | 1138.42 | couple | 0 |
| 9 | 1389.05 | 1358.09 | couple | 2.23 | 1388.53 | 1380.97 | couple | 0.54 |
| 10 | 1516.17 | 1438.54 | couple | 5.12 | 1499.92 | 1493.13 | couple | 0.45 |
| 11 | 2031.35 | 1872.99 | couple | 7.8 | 2030.7 | 2030.61 | couple | 0 |
| 12 | 2135.99 | 2031.66 | couple | 4.88 | 2054.82 | 2054.66 | couple | 0.01 |
| 13 | 2292.34 | 2292.34 | differential train | 0 | 2295.32 | 2276.9 | differential train | 0.8 |
| 14 | 2292.34 | 2292.34 | differential train | 0 | 2295.32 | 2276.9 | differential train | 0.8 |
| 15 | 2504.67 | 2504.67 | differential train | 0 | 2534.01 | 2424.1 | differential train | 4.34 |
| 16 | 2504.67 | 2504.67 | differential train | 0 | 2534.01 | 2424.1 | differential train | 4.34 |
| 17 | 2938.39 | 2938.39 | couple | 0 | 2809.75 | 2809.75 | fixed-axis train | 0 |
| 18 | 3169.47 | 3169.47 | differential train | 0 | 2809.75 | 2809.75 | fixed-axis train | 0 |
| 19 | 3169.47 | 3169.47 | differential train | 0 | 2938.39 | 2938.39 | couple | 0 |
| 20 | 3227.44 | 1868.08 | fixed-axis train | 42.12 | 3176.61 | 3148.44 | differential train | 0.89 |
| 21 | 3227.44 | 1868.08 | fixed-axis train | 42.12 | 3176.61 | 3148.44 | differential train | 0.89 |
| 22 | 4288.77 | 4288.77 | differential train | 0 | 4334.67 | 4111.9 | differential train | 5.14 |
| 23 | 4288.77 | 4288.77 | differential train | 0 | 4334.67 | 4111.9 | differential train | 5.14 |
| 24 | 4630.25 | 3855.18 | couple | 16.74 | 4520.8 | 4459.12 | couple | 1.36 |
| 25 | 5388.48 | 4613.61 | couple | 14.38 | 5388.38 | 5246.58 | couple | 2.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Yue, Z.; Qu, J.; Dzianis, M.; Wang, Y. Natural Characteristics of a Marine Two-Stage Tandem Hybrid Planetary System. Machines 2024, 12, 338. https://doi.org/10.3390/machines12050338
Zhao X, Yue Z, Qu J, Dzianis M, Wang Y. Natural Characteristics of a Marine Two-Stage Tandem Hybrid Planetary System. Machines. 2024; 12(5):338. https://doi.org/10.3390/machines12050338
Chicago/Turabian StyleZhao, Xingfu, Zongxiang Yue, Jianjun Qu, Marmysh Dzianis, and Yanzhong Wang. 2024. "Natural Characteristics of a Marine Two-Stage Tandem Hybrid Planetary System" Machines 12, no. 5: 338. https://doi.org/10.3390/machines12050338
APA StyleZhao, X., Yue, Z., Qu, J., Dzianis, M., & Wang, Y. (2024). Natural Characteristics of a Marine Two-Stage Tandem Hybrid Planetary System. Machines, 12(5), 338. https://doi.org/10.3390/machines12050338






