Study on the Parameter Influences of Gear Tooth Profile Modification and Transmission Error Analysis

Abstract

Gear transmission systems are widely used to transfer energy and motion and to guarantee the accuracy of the entire machine system. The modification technique is a common method that improves the gear profile and reduces the transmission error. Based on the parametric model, a modified gear can be established for the evaluation of static and dynamic characteristics. The influences of profile modification parameters and gear parameters are investigated while changing the rules of different kinds of factors. Based on sensitive parameters, a two-stage profile modification curve is proposed to improve the performance of gear pairs. Thus, considering the time-varying mesh stiffness and backlash, a novel, dynamic modified gear model is established to analyze the dynamic performance, such as the dynamic transmission error. Based on the proposed curve, the range and amplitude of the transmission error can be decreased. Additionally, the vibration displacement and noise can be reduced to improve the running characteristics.

1. Introduction

As the most widely used form of mechanical transmission, gear transmission systems play an important role in machine tools, and the accuracy of gear drives largely guarantees the accuracy of the entire machine system. It has been shown that gear tooth modification is effective for reducing the transmission error and improving the dynamic performance. The tooth modification method has always attracted different researchers’ attention with regard to gear trains. The curve of a parabola [1] was taken as the modified curve to improve the tooth surface of the pinion in a transmission system. A gear model with tooth profile modification was analyzed with different parameters, and the effects of the tooth profile modification on mesh stiffness were investigated [2]. Considering the coupling flexibility of the gear body, tip relief modification [3] was investigated to optimize the tooth profile by an analytical model. Based on alignment errors, an effective axial modification method of straight bevel gears was proposed to reduce the contact force and bending stress [4]. A theoretical model and the Monte Carlo method were investigated in terms of gear modification and the transmission process considering various machining errors [5,6]. Considering tooth profile modifications in sun–planet and ring–planet meshes, tooth profile modification was utilized to decrease the spur planetary gear vibration [7]. A comprehensive modification method [8] was proposed to improve the transmission process of different gears, and the mesh behavior of the gear surface was analyzed. The finite element analysis (FEA) method was utilized to establish a precise tooth profile modification approach for gear pairs [9]. The type and amount of the modified value were accurately determined by the static-contact FEA results. A finite element model with tip relief modification was developed to obtain the static transmission error for several angular configurations at different torques [10]. Based on the lateral–torsional–pendulum coupling nonlinear dynamic model, a gear transmission system and the corresponding dynamic optimization modification technology [11] were investigated to improve the tooth profile and the load factor of a driving wheel. An experimental study was utilized to optimize the geometrical features of spur gear pair teeth to minimize the system vibration [12,13]. The analytical method, finite element analysis, and an experimental study were utilized to establish the modified curve for different modes of tooth profiles in gear transmission systems.

According to the modification curve, the effects of the modified parameters and structural parameters were investigated. Parametric influences were analyzed for a modified gear on the basis of a novel two-part gear tribo-dynamic model considering tooth profile modification [14]. Different factors have been considered to address the influences between parameters and operating characteristics. The severity of vibration and noise under different operating conditions has been measured by different metrics, namely, dynamic mesh force, dynamic tooth force, and bearing force along the line-of-action direction [15]. The variation in (spur gear pair) teeth meshing stiffness due to tooth profile modification has been introduced for different amounts of transmitted torque [16]. The mesh stiffness [17], load sharing [18], and transmission error [19] of a modified gear have been investigated, and the peak-to-peak amplitude was calculated based on the analytical model [20]. Additionally, the sensitivity of tooth modification parameters was presented to reduce the transmission error fluctuations of a gear train in a wind turbine gearbox [21]. The effect of weight-reduction holes was investigated, and a polygonal approximation method was developed for mesh stiffness. Additionally, the tooth modification method was utilized to reduce the vibration [22]. Structural parameters and modified parameters have both been investigated to determine the effects of modification curves. Hence, different parameters should be considered to select a suitable parameter or optimize the curve.

Transmission error is commonly utilized to evaluate the characteristics of gear trains in different industries. The multi-tooth contact analysis of a gear train using the finite element method was used to calculate static transmission errors, which were caused by mesh stiffness, manufacturing errors, and geometric errors [23]. Static transmission errors between a standard gear and a modified gear with linear tip relief were compared to determine the effects of modification at a low velocity [24]. Additionally, a novel approach for calculating static transmission errors based on measured discrete tooth surfaces was proposed with profile modifications [25]. Novel analytical gear mesh stiffness was established to analyze the static transmission error in a gear pair [26,27]. Moreover, factors such as the variation in the contact ratio, manufacturing errors, and installation errors always result in vibration and noise that seriously affect the dynamic performance of a gear train. Both static transmission errors and dynamic transmission errors [28] are considered to influence tooth modification, which are influenced by backlash, time-varying stiffness, and damping force [29]. Hence, transmission error excitation has been investigated via the gear modification method to decrease noise. A higher-order transmission error was adopted to depict nonlinear vibration [30]. The dynamic transmission error was regarded as an important index for evaluating the system characteristics with stochastic excitations [31,32]. Additionally, time-varying factors [33] and economic factors [34] were considered to analyze the parameters’ effects on system characteristics. Based on dynamic transmission errors, a vibration-based scheme was proposed for gear wear prediction to be updated [35]. Considering static and dynamic characteristics, transmission errors should be investigated to evaluate the system performance of modified gear trains. Therefore, improving the performance of a modified gear drive is significant for improving the performance and reliability of an entire machine tool.

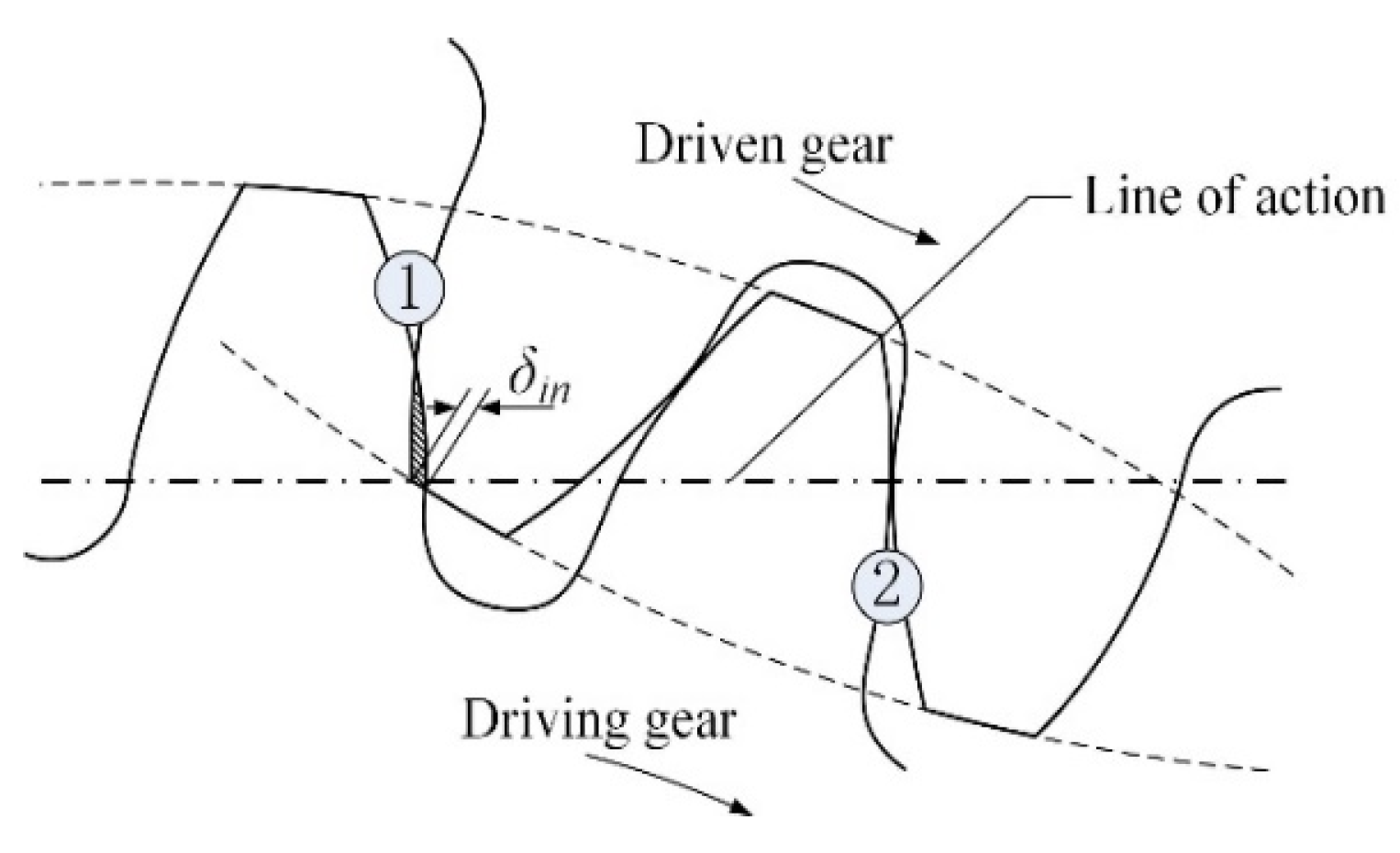
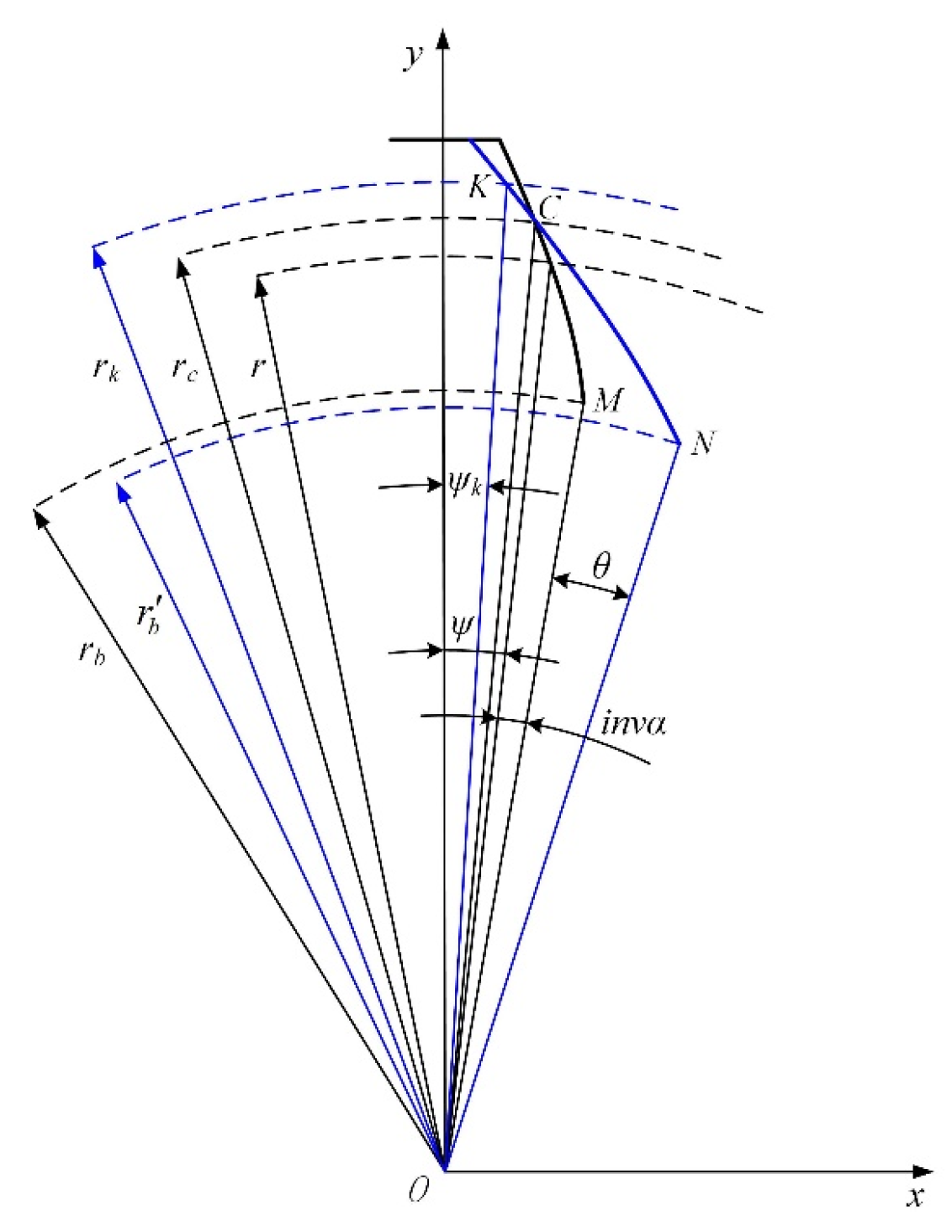
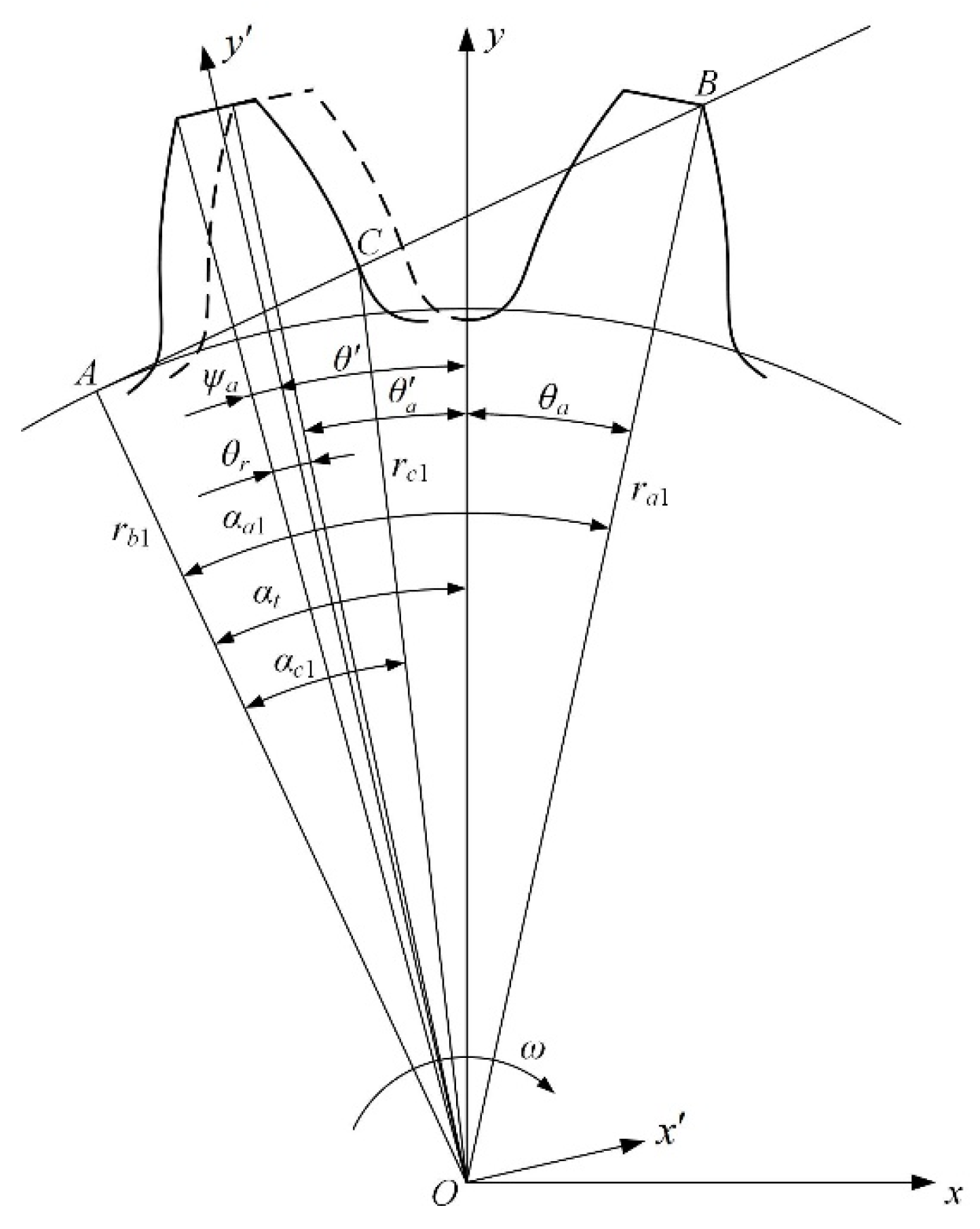
Tooth profile modification and its parametric influences have been investigated to improve transmission characteristics and reduce vibration and noise. In Section 2, gear modification theory is introduced, and three elements of gear modification theory are analyzed. The parametric model for the modified gear is investigated in Section 3. The finite element method is utilized to investigate the static transmission error of modified gears with different parameters. The influences of the profile modification parameters and gear parameters on the transmission error are analyzed in Section 4 and Section 5, respectively. Additionally, an optimized profile modification curve is proposed in Section 6. The dynamic model of the modified gear is established in Section 7. The corresponding dynamic transmission error and the parametric influences are investigated to reduce the gear vibration and system noise. The results indicate that only a targeted modification design under certain load conditions can lead to a satisfying modification effect and improve the transmission performance of the gear drive.

2. Gear Modification Theory

The scraping process not only causes the gear tooth to engage and produce sharp noise but also destroys the lubricating oil film and accelerates adhesive failure. To eliminate the influence of elastic deformation on the gear tooth, some parts of the gear along the direction of the tooth height are artificially removed to offset the elastic deformation, that is, the tooth profile modification. The condition of tooth interference between the driving gear and driven gear is shown in Figure 1. Parameter δ is the maximum interference value along the line of engagement, which is utilized to determine the maximum value.

Considering gear addendum and gear dedendum, complete tooth profile modification is always utilized to optimize the load characteristics, as shown in Figure 2. Line AD is the actual length of the meshing line. AB and CD belong to the double-tooth engagement zone, and BC is the single-tooth engagement area.

The linear modification in Equation (3) can be expressed as $\Delta ={\Delta }_{\max }x/L$, in which Parameters x and L are the relative coordinates of the meshing position and modified length, respectively. Parameters Δ_max and Δ represent the maximum modified value and the modified value corresponding to position x, respectively. Additionally, Walker [5] recommends the following equation: $\Delta ={\Delta }_{\max }{\left(x/L\right)}^{1.5}$. Yoshio and Kazuteru [8] proposed a modification equation with a different parameter, $\Delta ={\Delta }_{\max }{\left(x/L\right)}^{1.2}$. Instead of Δ and Δ_max, Ca and Ca_max are utilized for a general formula of modification equations, as follows:

$$Ca=C{a}_{\max }{\left(x/L\right)}^{\beta }$$

(1)

where parameter β is the modified index, which is a number greater than 1. Based on Equation (1), the modified gear can eliminate the mutant load caused by the alternation of single and double teeth. The load of gear teeth can be changed smoothly during the whole meshing process.

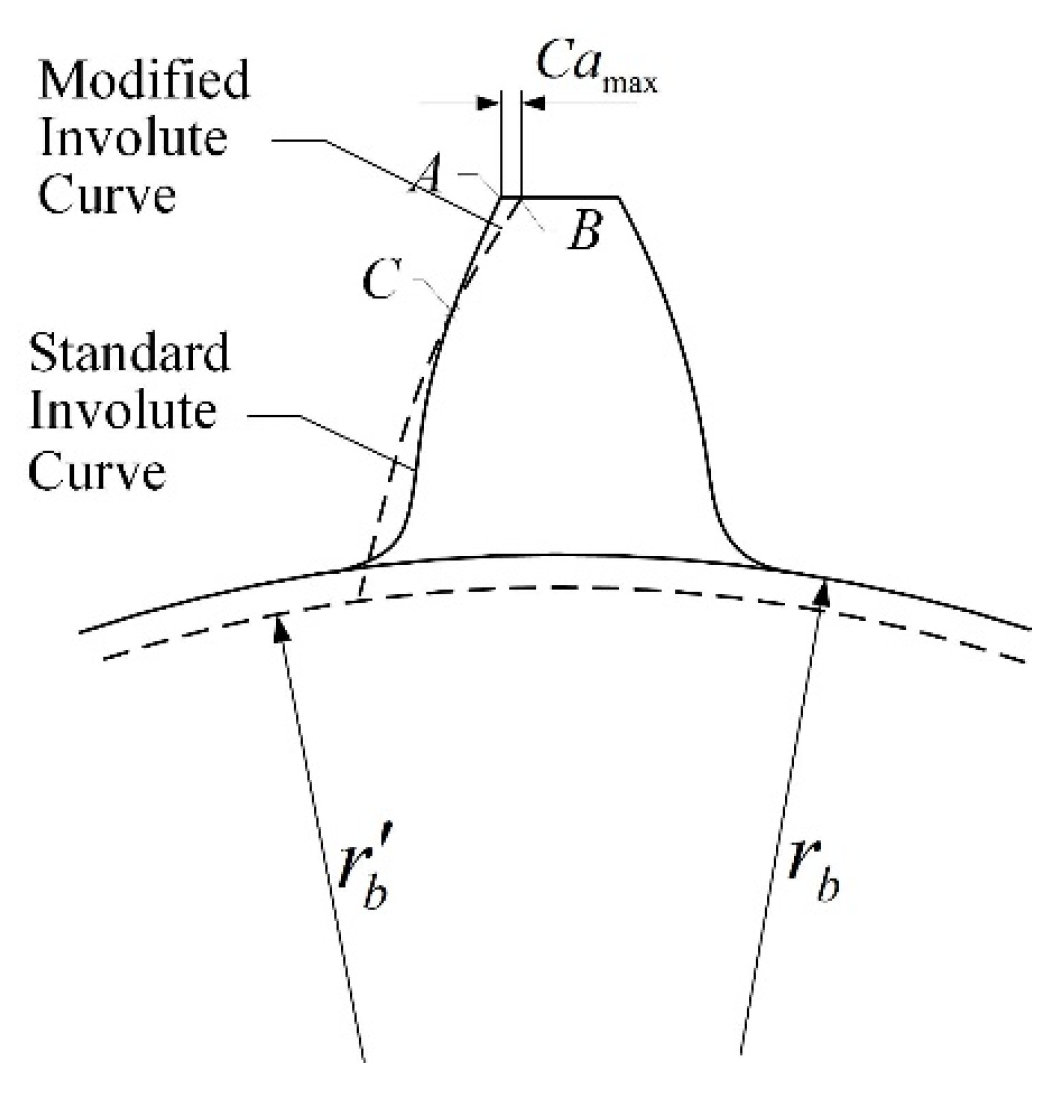
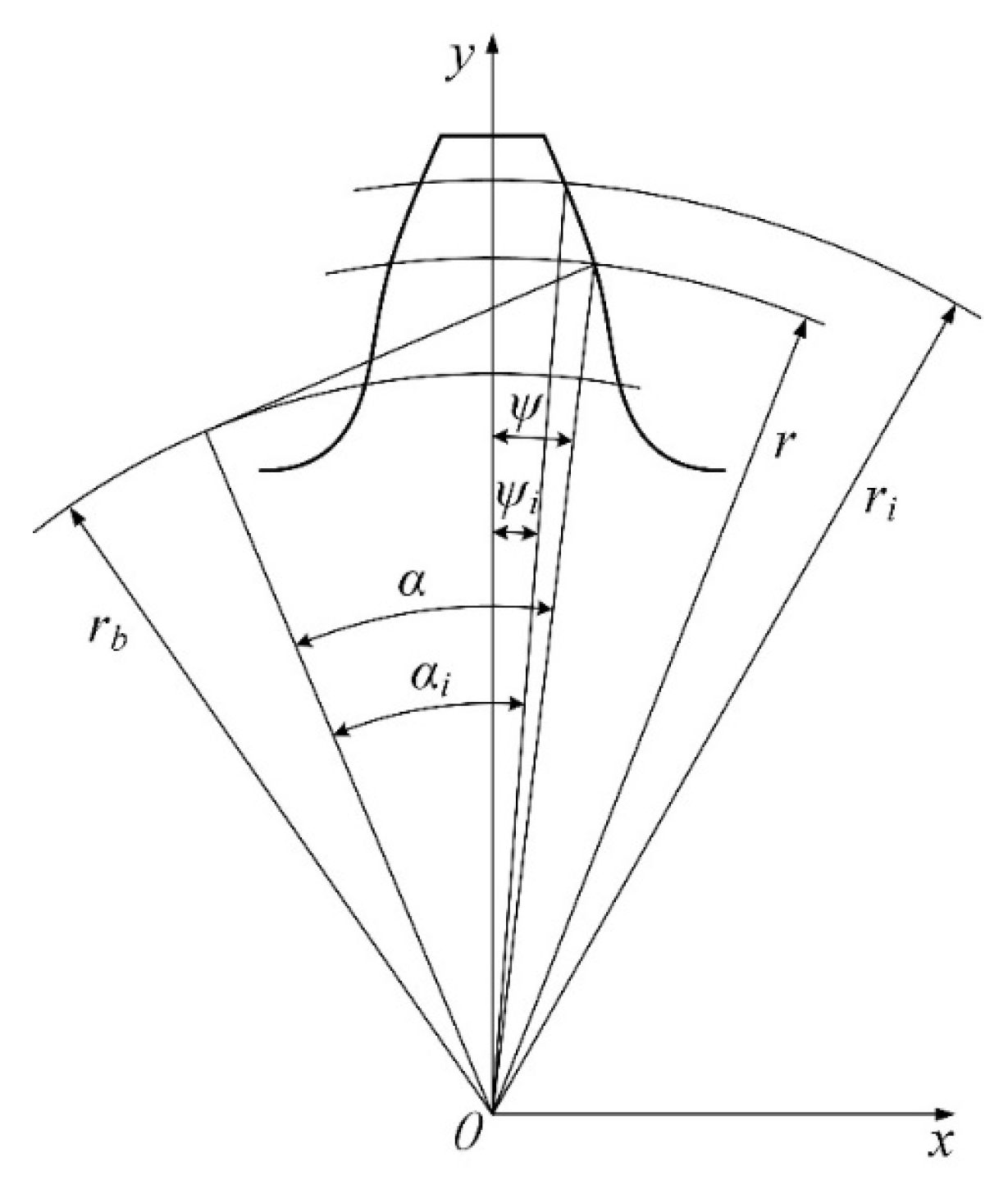
3. Parametric Model for Modified Gear

Considering the tip relief, the modified curve is still an involute curve, whose base radius is smaller than that of the unmodified involute curve. In Figure 3, Point C is the starting point of the modified curve in the tooth top. After the modification, the involute curve BC replaces the unmodified involute curve AC. The redundant part between AC and BC needs to be removed. The relationship between the base radius of the modified involute curve and the maximum modified value Ca_max can be expressed as follows:

$$\{\begin{array}{c}{r^{\prime }}_b=r_b-\Delta r_b\\ \Delta r_b=\frac{C{a}_{\max }}{\frac{\tan {\alpha }_a}{\cos {\alpha }_a}-\frac{r_a}{r_c}\left(\frac{\tan {\alpha }_c}{\cos {\alpha }_c}\right)}\end{array}$$

(2)

where parameters r_b and ${r^{\prime }}_b$ are the base radii of the standard and modified involute curves, respectively. r_c and r_a are the radius of the starting point in the modified involute curve and the radius of the addendum circle, respectively. Additionally, α_a and α_c are the pressure angles of the standard and modified involute curve.

The involute equation can be expressed as follows:

$$\{\begin{array}{l}x=r_i\sin ({\psi }_i)\hfill \\ y=r_i\cos ({\psi }_i)\hfill \\ {\psi }_i=\psi -(inv{\alpha }_i-inv\alpha )\hfill \\ \psi =\mathsf{\pi }/z\hfill \end{array}$$

(3)

The parameters in Equation (3) are listed in Figure 4. Hence, the involute curve of the modified gear can be explained by the following:

$$\{\begin{array}{l}{\psi }_k=\psi +inv\alpha +\theta -inv{\alpha }_k\\ \theta =inv{{\alpha }^{\prime }}_c-inv{\alpha }_c\\ \psi =\mathsf{\pi }/z\end{array}$$

(4)

The parameters in Equation (4) are listed in Figure 5. Parameters z, r, and α represent the number of teeth, the reference circle, and the pressure angle of the reference circle, respectively. Point K represents any point located in the modified involute profile. Parameters r_k and α_k are the distance between Point K and Center O and the pressure angle in the modified gear, respectively. Additionally, ${\alpha }_c^{\prime }$ is the pressure angle of the starting point in the modified involute curve.

The modified involute profile can be depicted by the involute profile of the standard gear with different starting points. In Equation (4), Parameter α_k ranges in the interval [${\alpha }_c^{\prime }$, ${\alpha }_a^{\prime }$], and ${\alpha }_a^{\prime }$ is the pressure angle of the tip circle in the modified gear. Hence, points in the modified gear can be gained by Equations (3) and (4) to transmit smoothly. Taking Point K as an example, the modified value can be defined by Figure 6. Lines ED and KE correspond to Parameters L and x in Equation (1). The geometrical relationship in Figure 6 can be depicted by the following:

$$\{\begin{array}{l}\overline{EK}=\overline{AK}-\overline{AE}=r_{b1}\tan ({\alpha }_k)-\overline{AE}\\ \overline{DE}=\overline{AD}-\overline{AE}=r_{b1}\tan ({\alpha }_{a1})-\overline{AE}\\ \overline{AE}=\overline{AC}+\overline{CE}=\overline{AC}+p_b\\ \overline{AC}=\overline{AB}-\overline{BC}=(r_{b1}+r_{b2})\tan ({\alpha }_t)-r_{b2}\tan ({\alpha }_{a2})\end{array}$$

(5)

Hence, the modified value of Point K can be calculated by the following:

$$Ca=C{a}_{\max }{\left(\frac{r_{b1}\tan ({\alpha }_k)-((r_{b1}+r_{b2})\tan ({\alpha }_t)-r_{b2}\tan ({\alpha }_{a2})+p_b)}{r_{b1}\tan ({\alpha }_{a1})-((r_{b1}+r_{b2})\tan ({\alpha }_t)-r_{b2}\tan ({\alpha }_{a2})+p_b)}\right)}^{\beta }$$

(6)

where the base pitch p_b can be computed by $p_b=\pi m\cos (\alpha )$. Based on the property of the involute curve, the K coordinate (x_k, y_k) is rotated around the center of the base circle at an angle λ = Ca/r_b1. Point K can be computed by the following:

$$({x^{\prime }}_k,{y^{\prime }}_k)=(x_k,x_y)\left(\begin{array}{cc}\cos (\lambda )& \sin (\lambda )\\ -\sin (\lambda )& \cos (\lambda )\end{array}\right)$$

(7)

The parametric model for the modified gear can be established. According to Equations (6) and (7), the coordinates of all points can be depicted for the modification. The approach can be used to analyze the system characteristics of the modified gear.

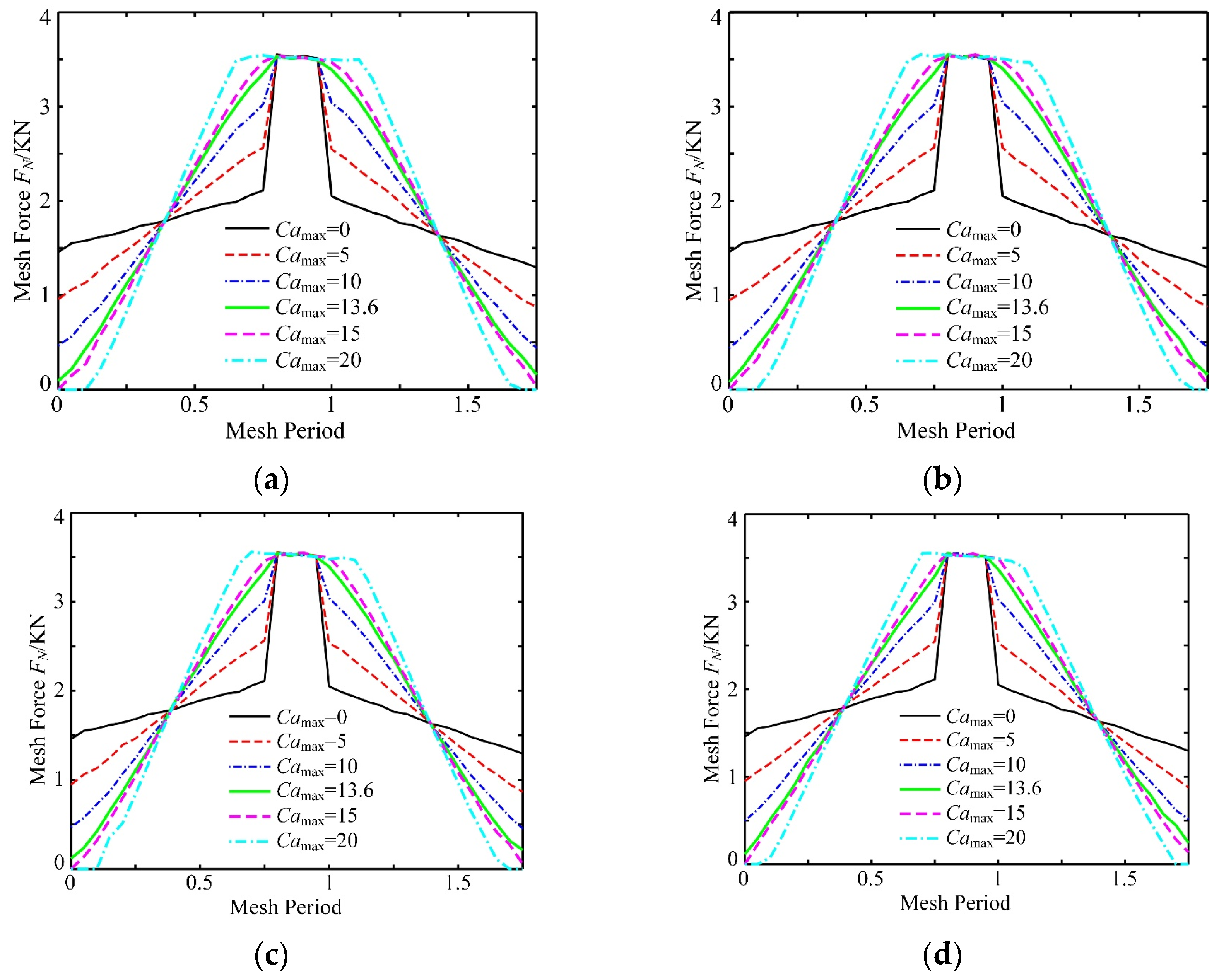
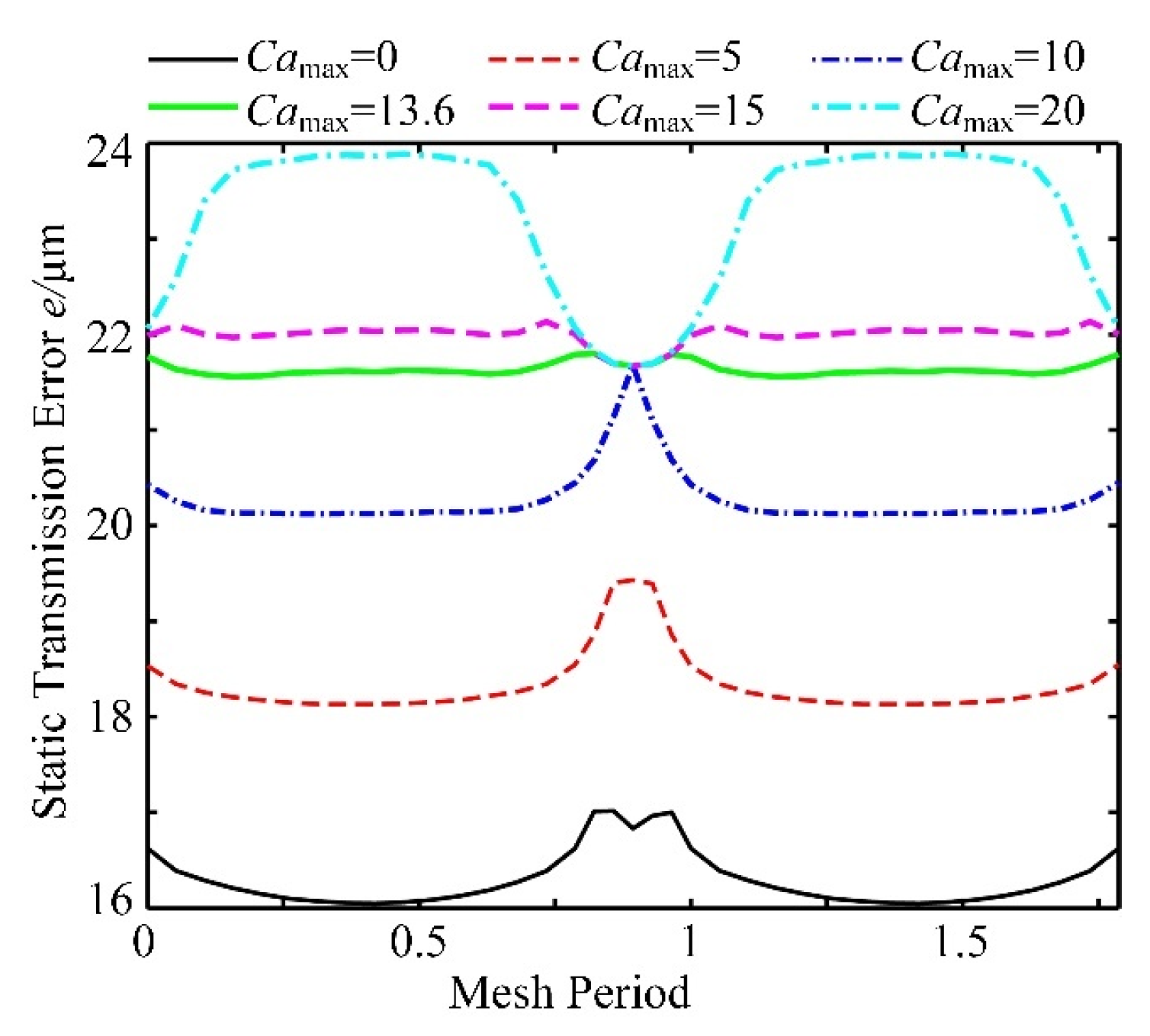
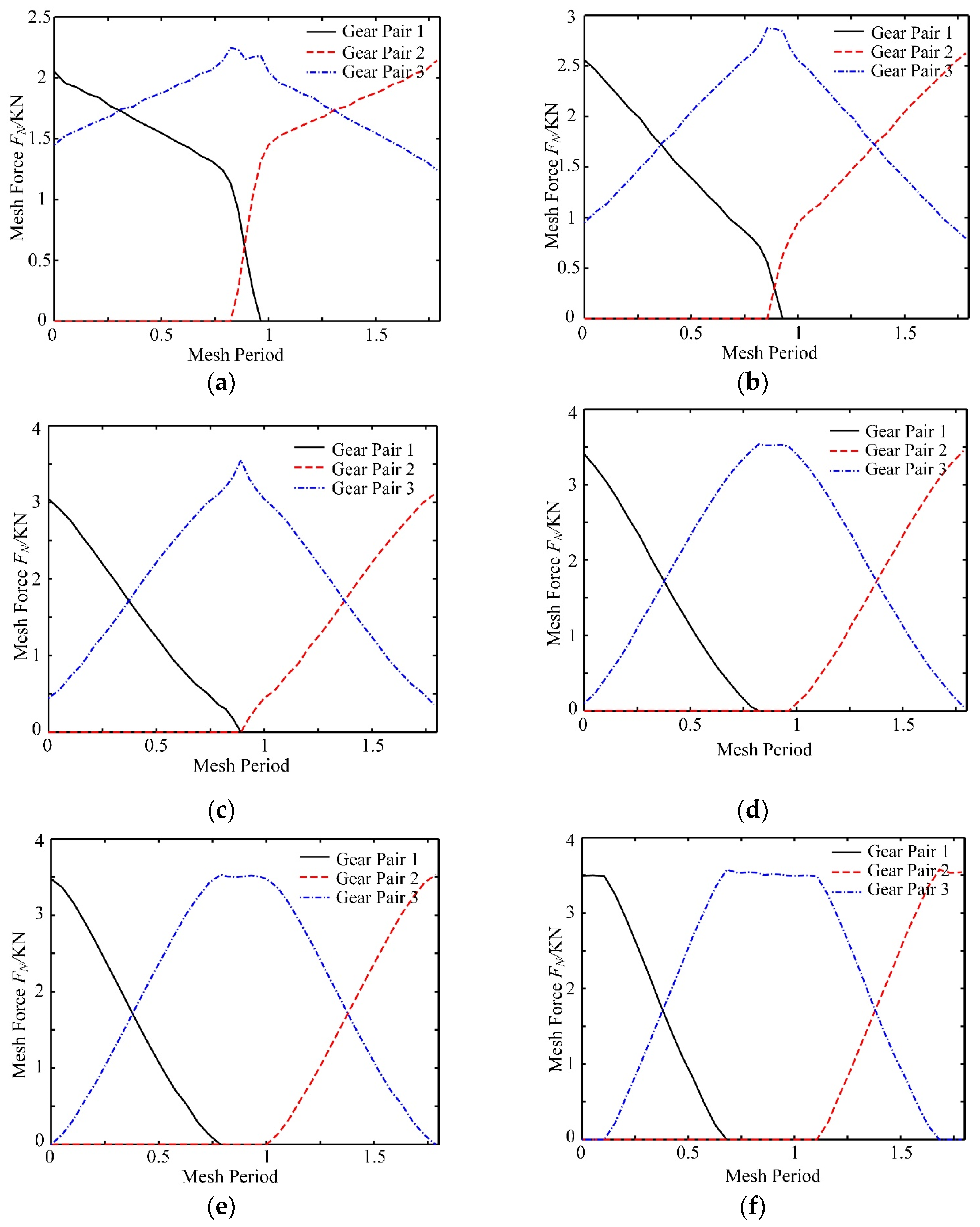
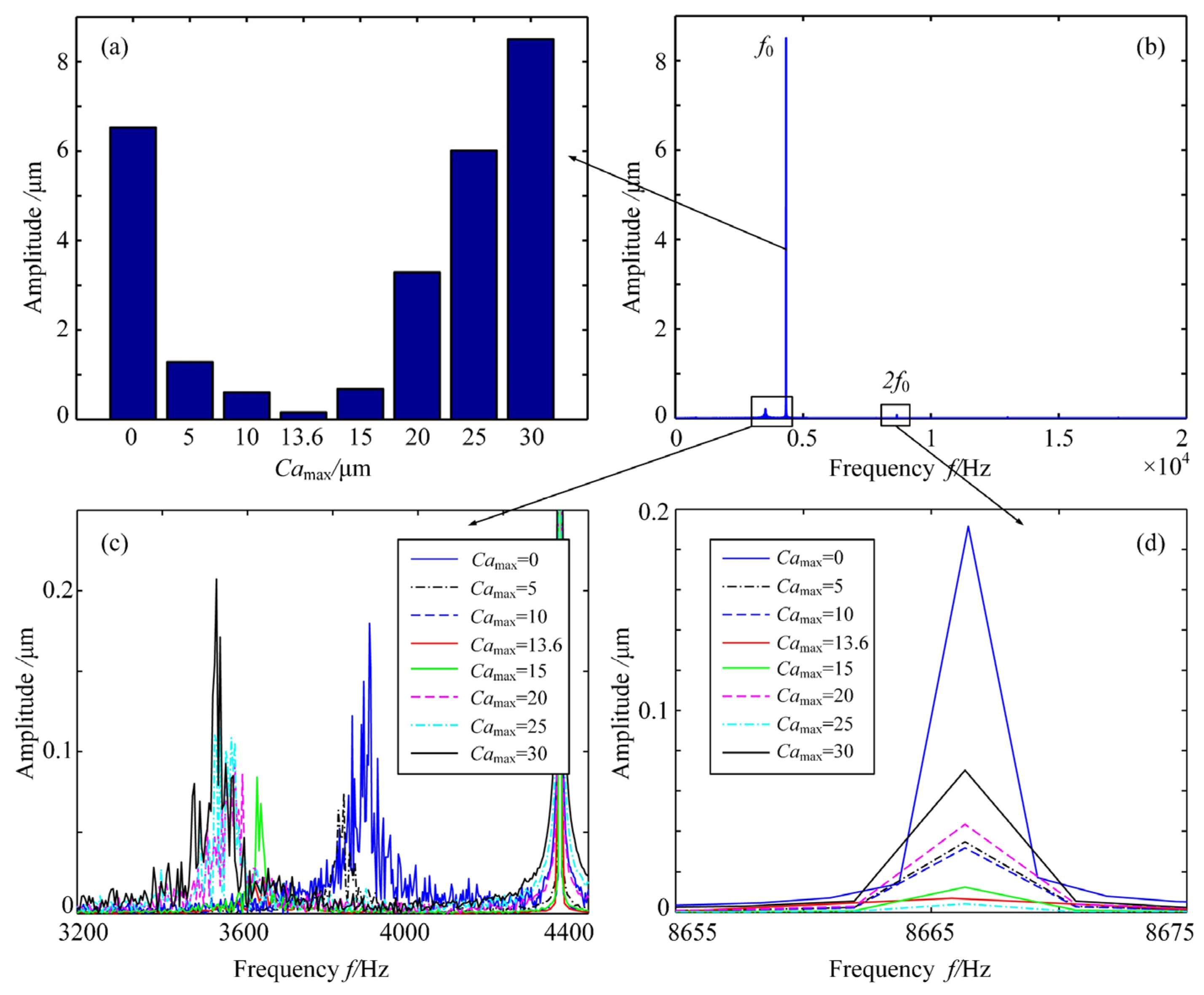
4. Influences of the Profile Modification Parameters

According to Section 3, ANSYS can be utilized to establish the model of the modified gear. Pinion Gear 1 is the driving gear, and Gear 2 is the driven gear in Figure 7. The transmission error is the difference between the actual position of the output gear and the theoretical position of the output gear, in which the tooth profile is an ideal involute and the tooth is not deformed. The transmission error is calculated and measured along the direction of the line of engagement in ANSYS.

In Figure 7, a two-dimensional plane strain unit is utilized to establish the model. Several teeth are ignored for the computation cost. Also, the symmetric contact pair in ANSYS is used to depict the gear contact. All nodes of the gear hole form a rigid surface with the center node of the gear, which are the fixed constraint. Considering the torque, the deformation of the driven gear can be regarded as the static transmission error. The tooth numbers of the driving gear and driven gear are 52 and 72, respectively. Also, the modulus of each gear is 1.75. The algorithm of transmission error is shown in Algorithm 1.

Algorithm 1: Static transmission error for the modified gear by ANSYS
Input: Number of teeth z, Modulus m, Load T, Pressure angle α. Output: Static transmission error e.
1:	Based on input data, parameters of the corresponding standard gear can be calculated by (3), such as ri, αi, rb and ψi.
2:	For Camax = 0, 5,…,20 do
3:		The base radius of modified involute curve can be computed by (2).
4:		The angle ψk of any point K (xk, yk) in the modified involute profile can be depicted by (4).
		For β = 1, 1.2, 1.5, 2.0 do
5:			The modified value of Point K can be calculated by (6). The coordinates (xk’, yk’) of points can be depicted for the modification.
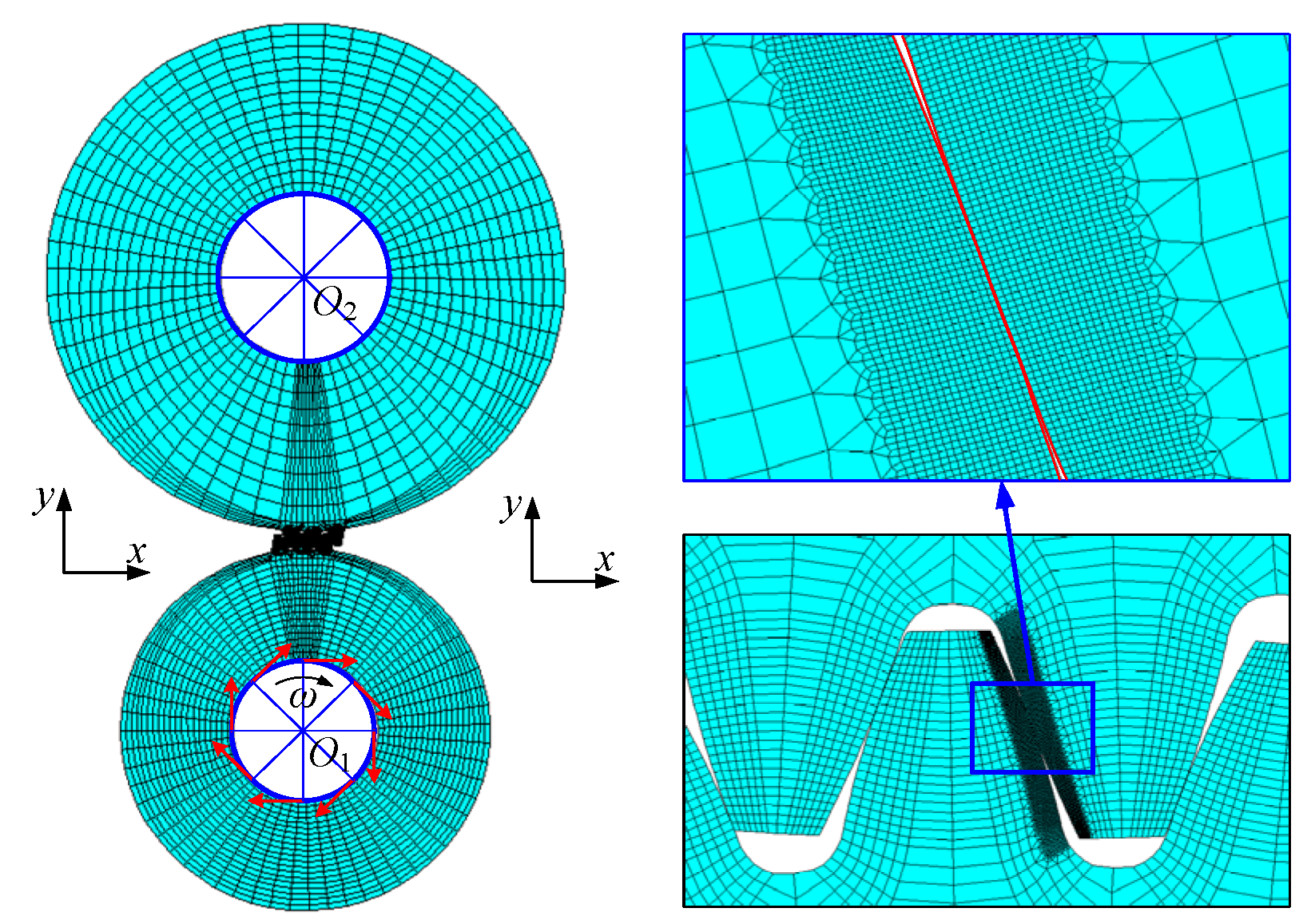
6:			Based on coordinates, establish the finite element model of the modified spur gear by ANSYS.
7:			Solve the static transmission error e based on load T. Mesh force FN can extracted by ANSYS.
8:		End
9:	End

Different factors, such as external and internal factors, are investigated for tooth profile modification. According to Equation (1), the effects of Parameters β and Ca_max are investigated to analyze the relationship among modified gears in Figure 8. The static transmission error represents the transmission performance, which contains the elastic deformation and the comprehensive meshing error.

The convexity and concavity of the static transmission error are different under different modification values. Because prolonged meshing is not considered, the static transmission error of a single-tooth meshing zone is nearly the same under different modification curves. With the increase in the maximum modification Ca_max, the static transmission error in the double-tooth meshing region gradually increases. If Ca_max increases to a certain extent, the static transmission error in the double-tooth meshing region is equal to or even exceeds the static transmission error in the single-tooth meshing region. In the case of β = 1, the static transmission error curve basically presents an upward convex trend in the meshing zone of the double tooth, and the upward convex trend becomes more obvious with the increase in the amount of modification. However, the static transmission error shows a downward trend in the cases of β = 1.5 and 2. The static transmission error curve is basically horizontal in the whole gear meshing cycle with β = 1.2 and Ca_max = 13.6 μm, which can cause the gear to drive more smoothly.

The frequency characteristics of the static transmission error curve with different Ca_max and β values are investigated, as shown in Figure 9. With increasing Ca_max, the amplitude of the transmission error first decreases and then increases. The amplitude reaches the minimum value in the case of Ca_max = 13.6 μm. The smaller β is, the more sensitive the amplitude A is to the change in Ca_max. The first four frequencies of the static transmission error spectrum are the smallest in the case of β = 1.2 and Ca_max = 13.6 μm. These parameters have the best effect.

The meshing process of a single tooth is investigated, as shown in Figure 10, with different Ca_max and β values. Single and double teeth are engaged alternately, from double-tooth meshing to single-tooth meshing and then to double-tooth meshing. A high mesh force F_N is generated in the single-tooth meshing. There is an abrupt change between single-tooth meshing and double-tooth meshing under the condition of Ca_max = 0. However, the modified gear can reduce the abrupt change in the mesh force F_N. Additionally, a suitable parameter β can smooth the turning point in the transmission process of the modified gear.

The influences of the parameters are investigated depending on the modified gear system. Based on Equation (1), Ca_max = 13.6 μm and β = 1.2 are recommended to improve the static transmission error.

5. Influences of the Modification Gear on the Transmission Error

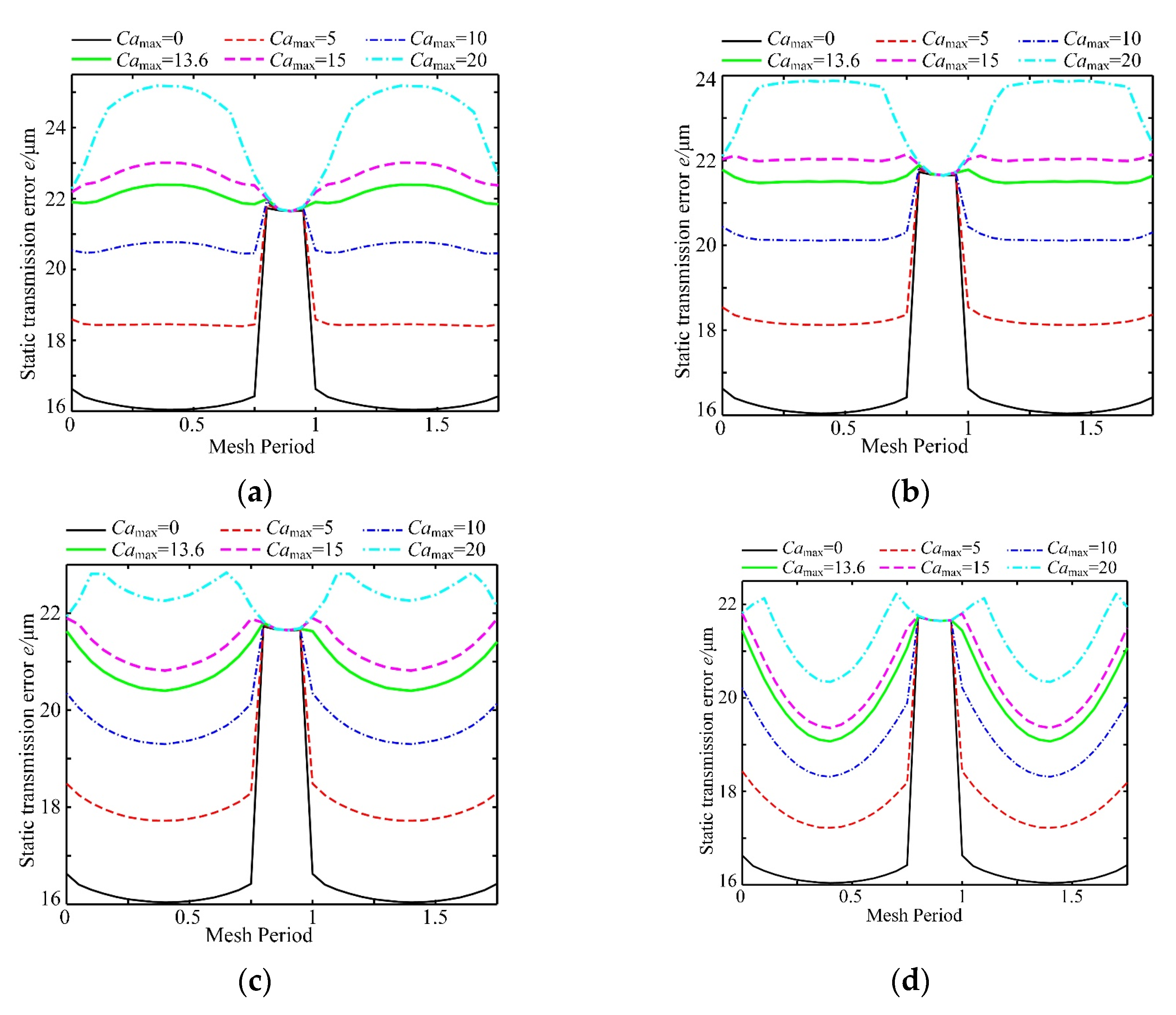
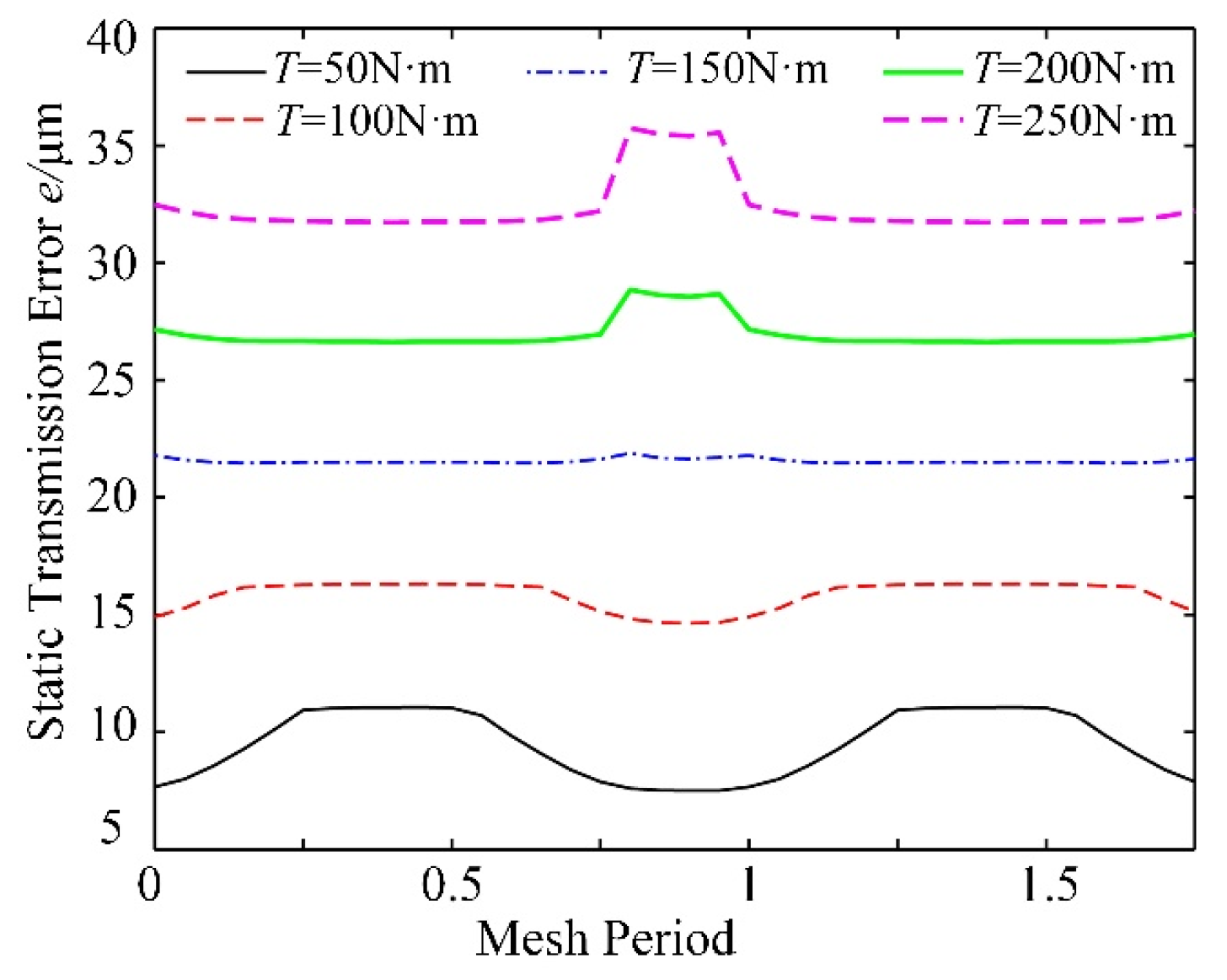
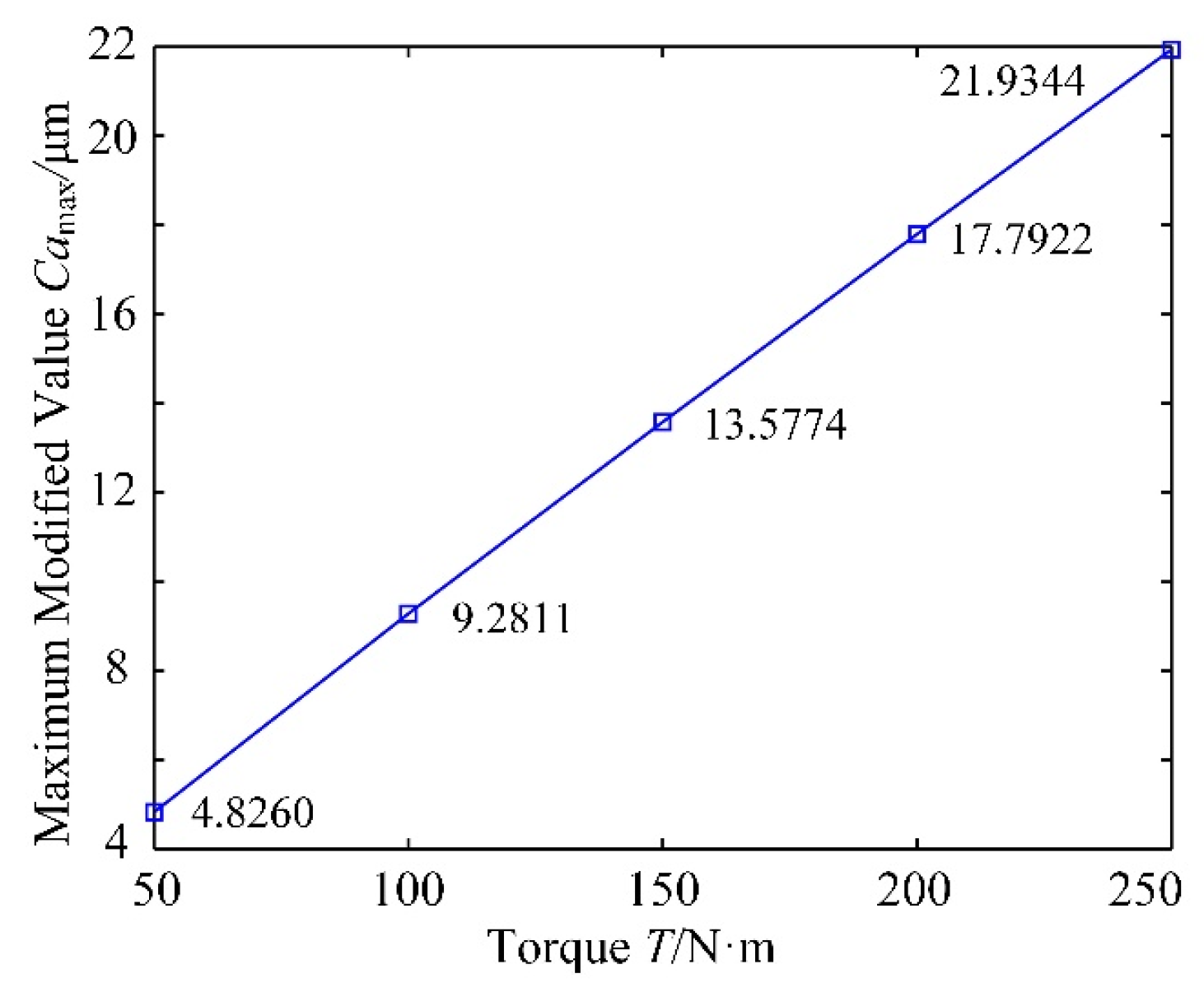
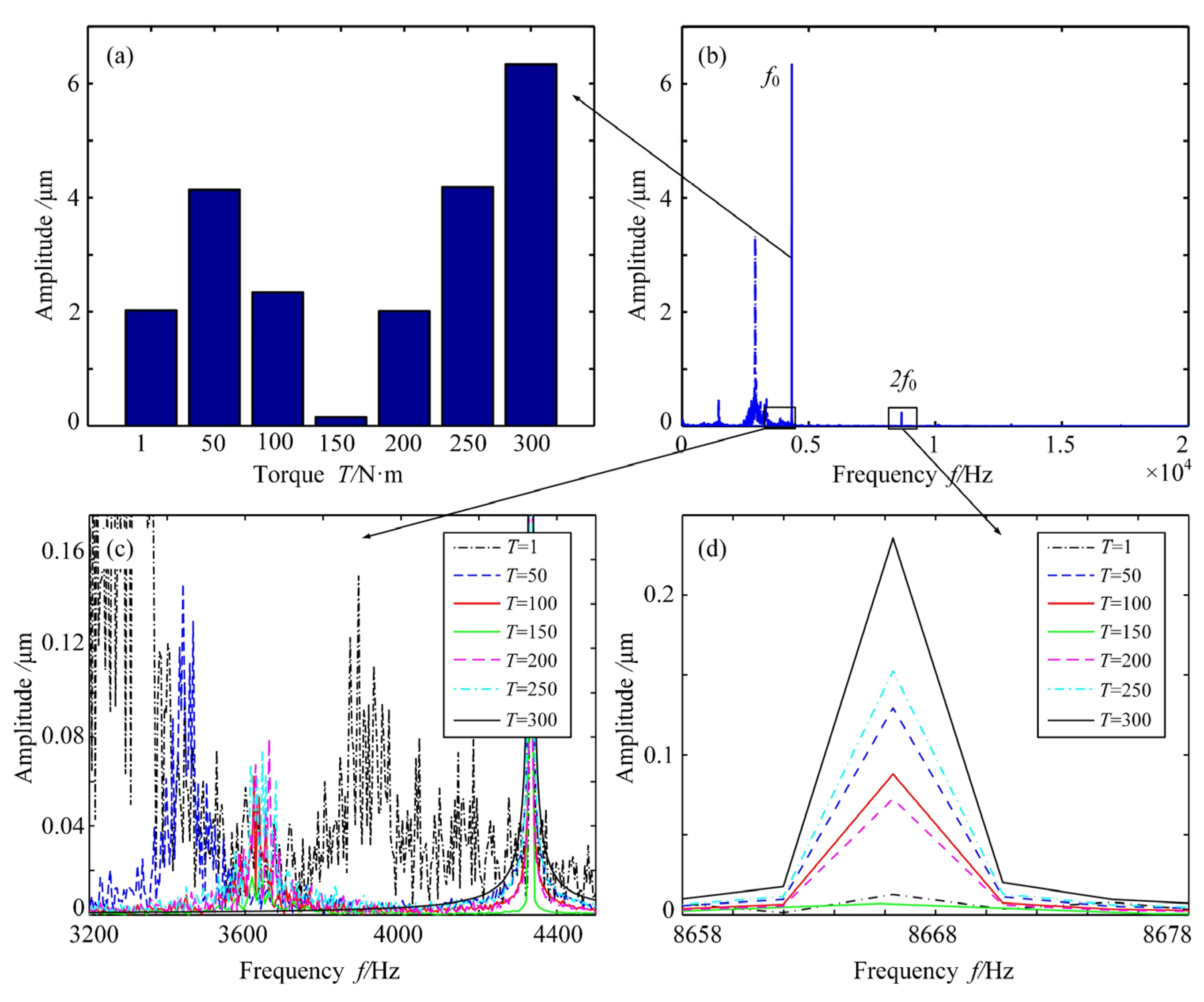
5.1. Effect of the Load

Structural parameters and load parameters are investigated to analyze the transmission error of the modified gear on the condition of Ca_max = 13.6 μm and β = 1.2. Considering different load torques T, the static transmission error is investigated, as shown in Figure 11. In the case of T < 150 N·m, the static transmission error is increased during double-tooth meshing. However, the error is decreased during double-tooth meshing in the case of T > 150 N·m. For the modified gear, different load torques can cause different changing rules of the transmission error.

Additionally, the relation between the maximum modification value and load torque is expressed as shown in Figure 12. The maximum modified value is almost linear to the load torque, which can be utilized to determine the modified value on the condition of different torques.

5.2. Effect of Prolonged Meshing

Prolonged meshing is due to the elastic deformation of the gear tooth under the load torque, which makes the last pair of gear teeth enter meshing in advance before the theoretical meshing point. Prolonged meshing is impacted by the modification value and load. Considering different cases of Ca_max and β = 1.2, the static transmission error is calculated to present the performance of gear teeth in Figure 13.

In the case of Ca_max < 13.6 μm, double- or even triple-tooth meshing occurs, which is caused by prolonged meshing. The early meshing and delayed meshing of different gear teeth can appear in Ca_max = 0. Additionally, the error is approximately stable in the case of Ca_max = 13.6 μm, which is beneficial for the gear transmission. The results of the meshing process are listed in Figure 14 with different modification values of Ca_max. A suitable modification value can prevent the performance of triple-gear-tooth meshing from decreasing the fluctuation of the mesh force.

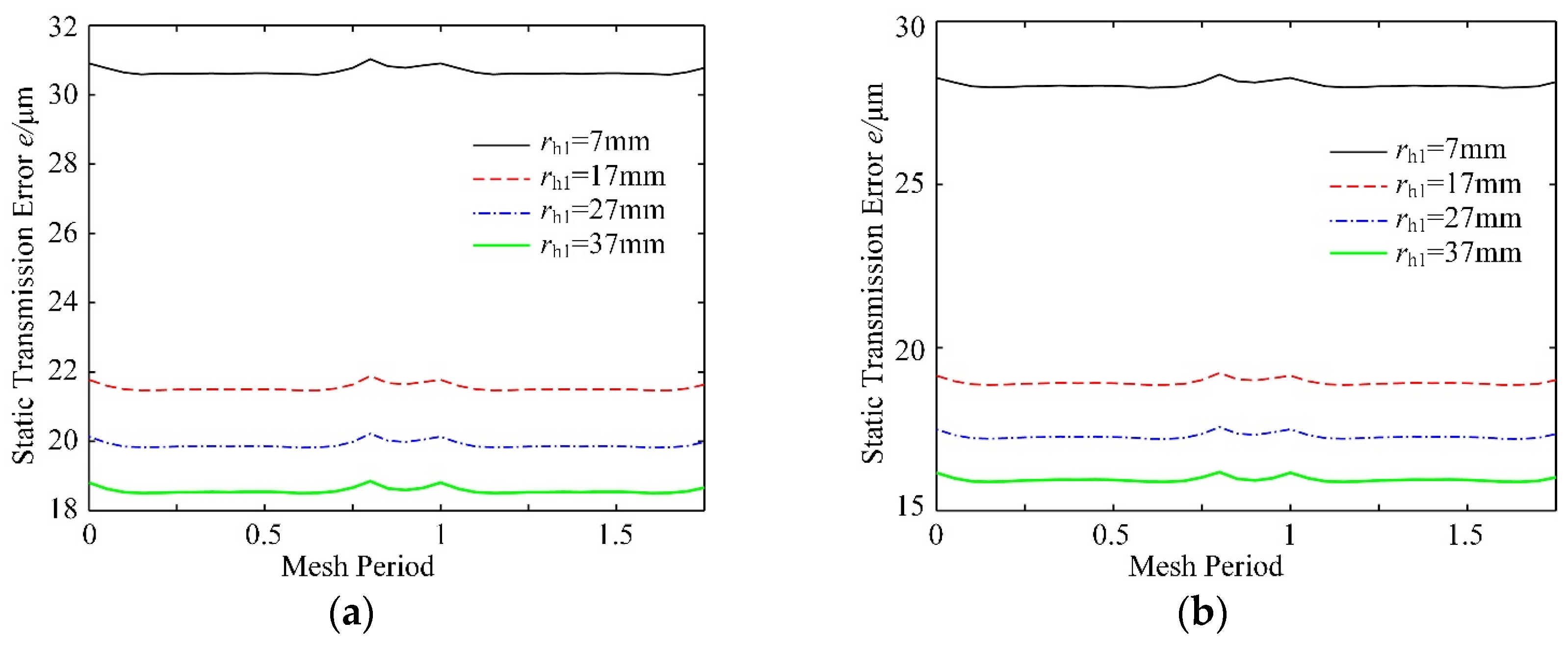
5.3. Effect of the Gear Hole Radii

In engineering, gears with the same basic parameters may be matched with different shafts that have different diameters. The radius of the gear hole also changes accordingly. Different radii of the gear hole can change the stiffness of the gear body and then affect the elastic deformation of the gear pair under load. Additionally, the gear transmission error is directly related to the elastic deformation of the gear body. Considering different radii of the gear holes r_h1 and r_h2, the relationship between the static transmission error and modification values, Ca_max = 13.6 μm and β = 1.2, are analyzed, as shown in Figure 15.

The static transmission error under different gear hole radii basically does not change, except for a slight fluctuation in the alternating position of single and double teeth. This is because the aim of the modification is mainly to eliminate the interference caused by the elastic deformation of gear teeth, which can reduce and eliminate the impact of meshing in and meshing out. However, the change in the hole radius does not affect the elastic deformation of gear teeth or the interference value of gear teeth. The static transmission error decreases with the increasing radius of the gear hole, and the change rate of the gear with the small hole is larger than that of the large hole. If the gear basic parameters are determined, only the fluctuation degree of the static transmission error curve is considered in the modification design. However, the effects of the radius of the gear hole can be ignored.

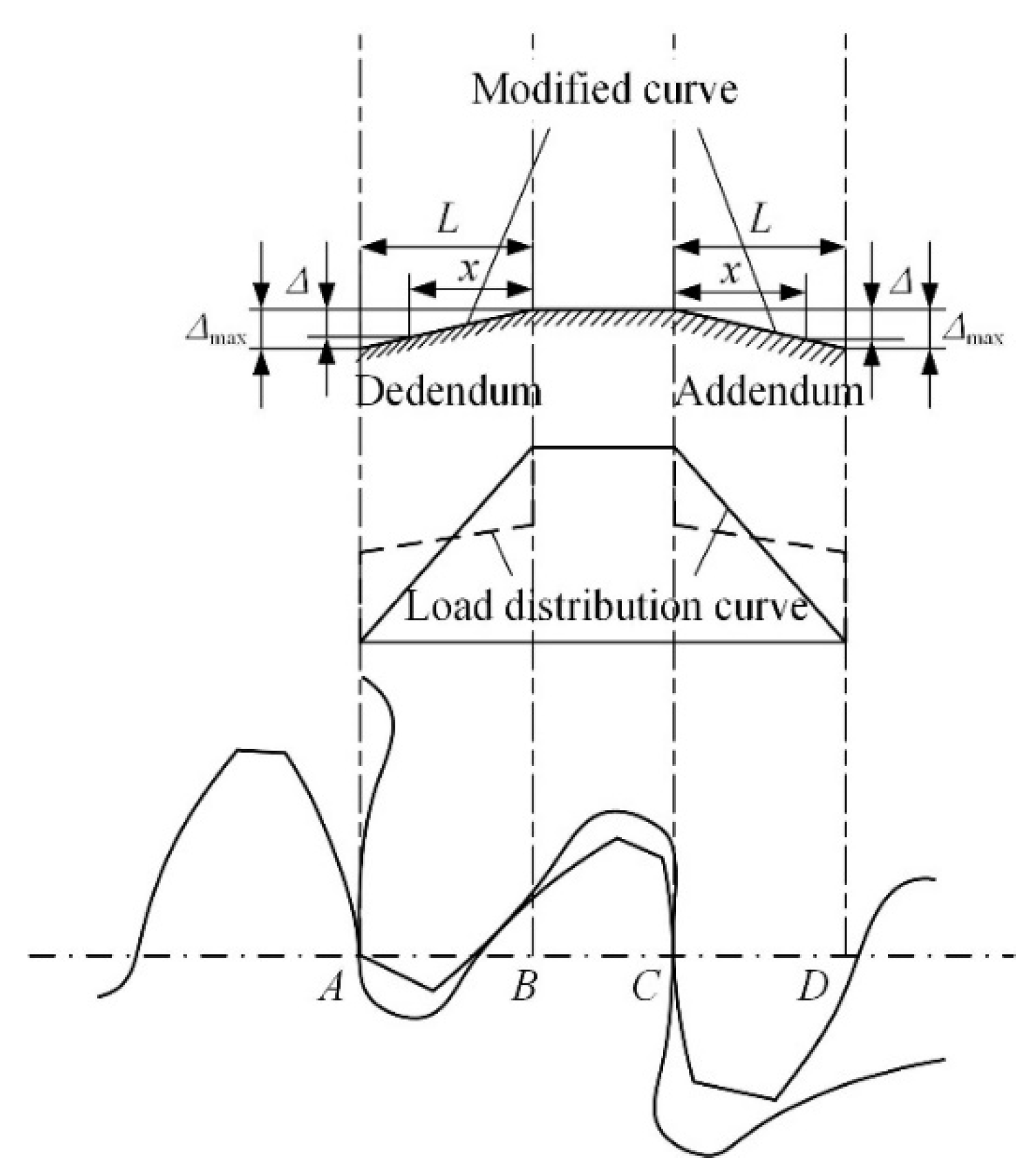
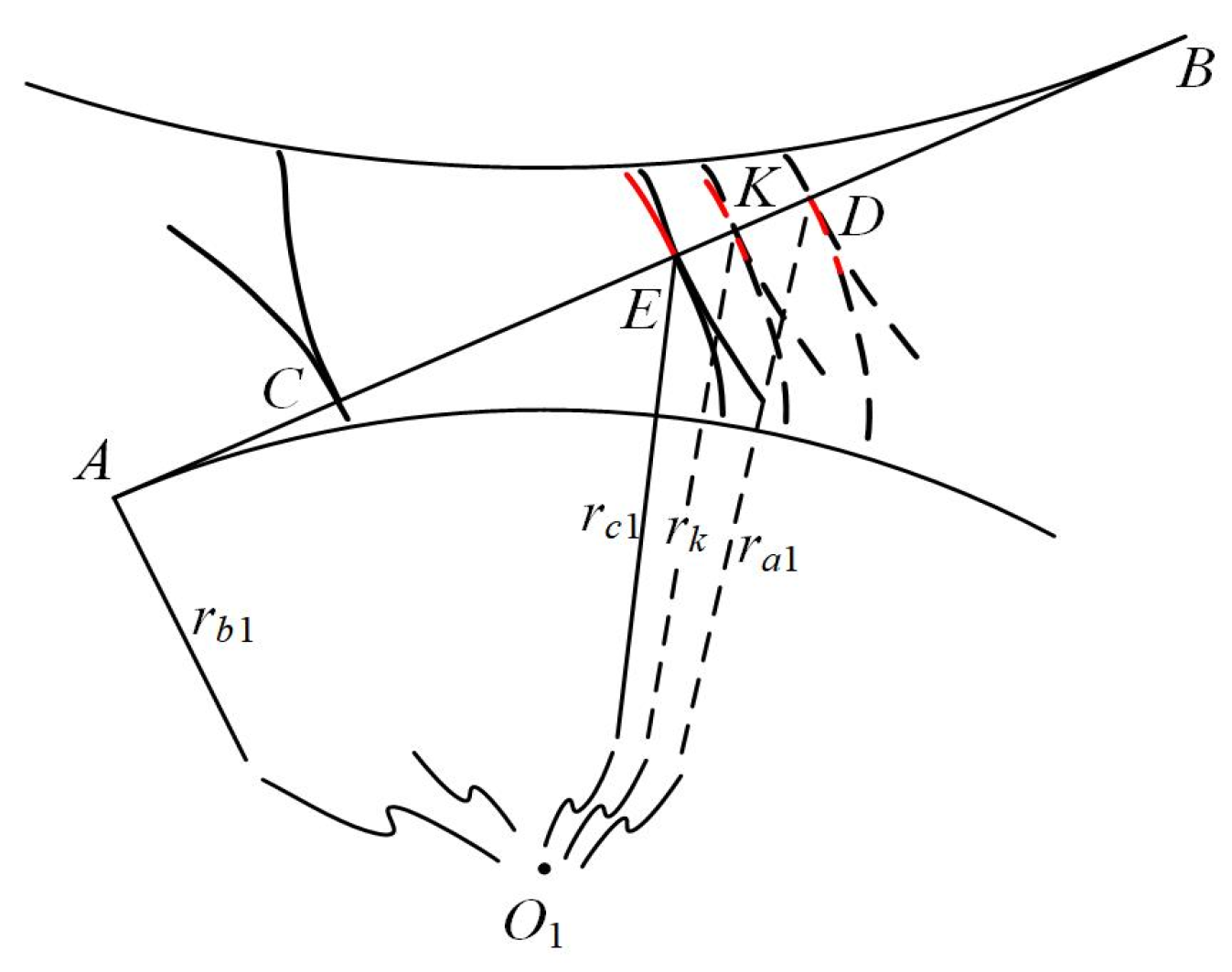
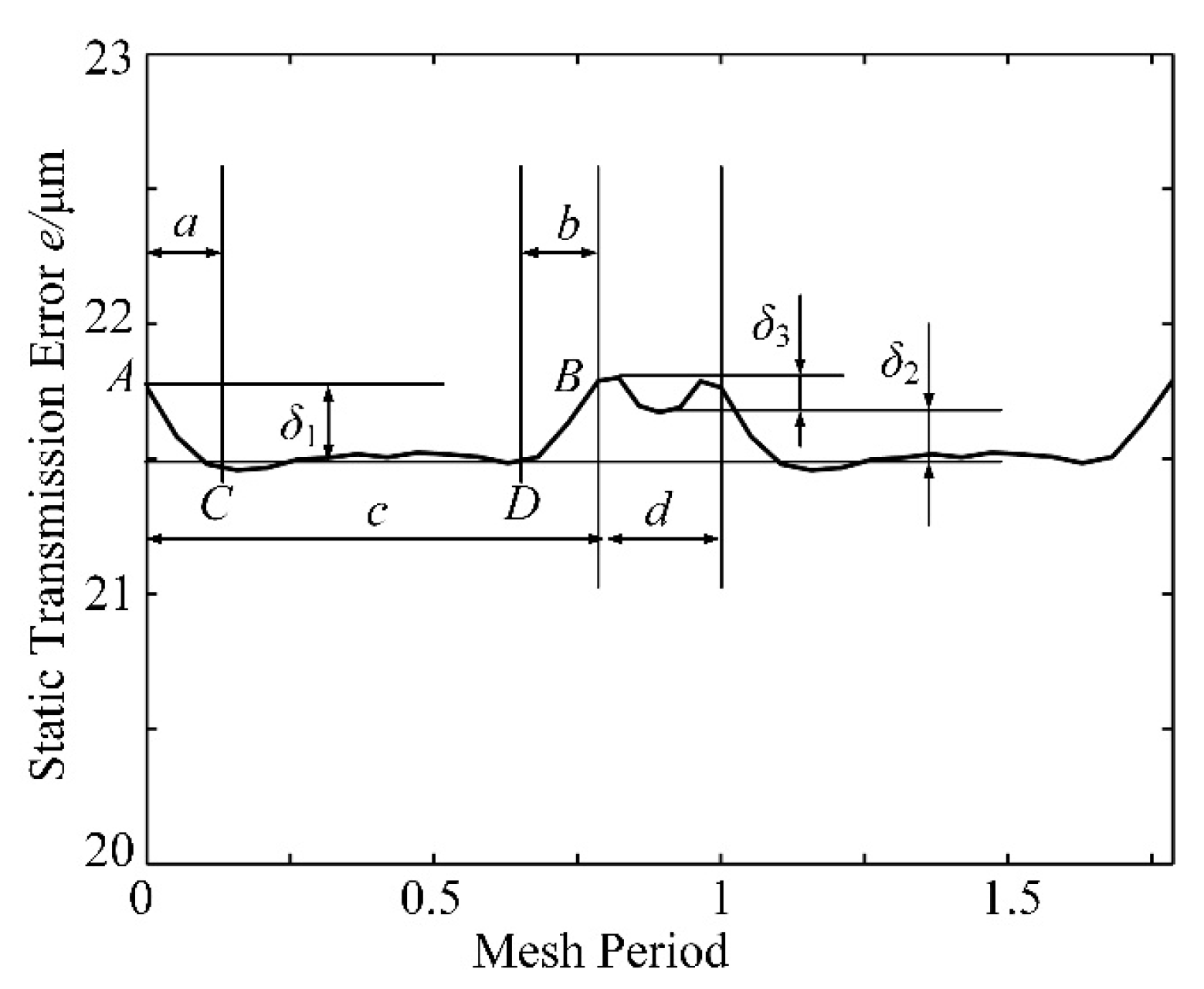
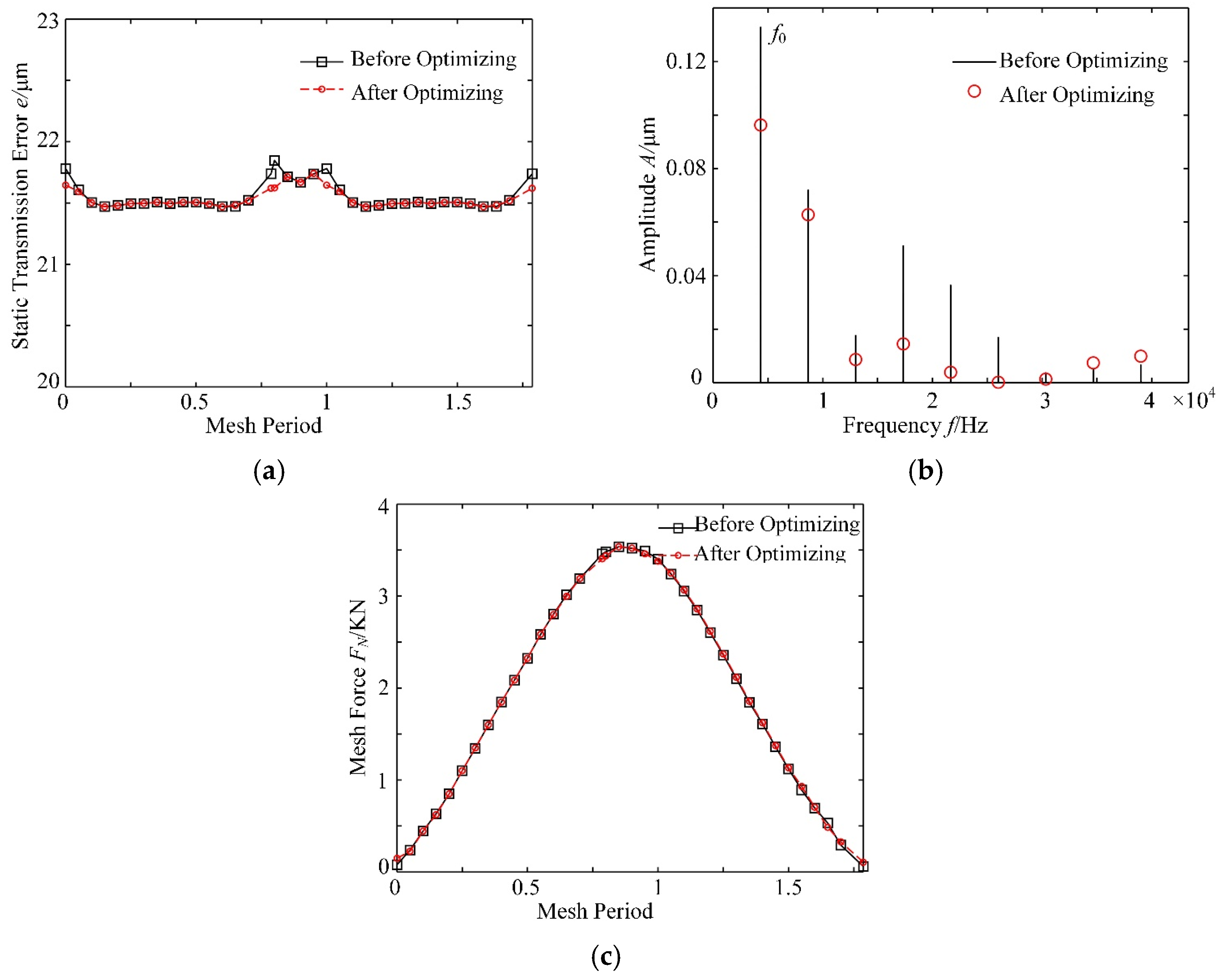
6. A Two-Stage Profile Modification Curve

The modified parameters, Ca_max = 13.6 μm and β = 1.2, can reduce the mean value and fluctuation of the static transmission error. However, the fluctuation cannot be ignored in Figure 16, such as in AC and BD. The optimization design of the profile modification curve should be investigated to decrease the fluctuation.

Parameters δ1, δ2, and δ3 can be optimized for the static transmission error in Figure 16. Parameter δ3 is utilized to depict the meshing process of the single gear tooth, which causes an increase in the transmission error. Prolonged meshing can increase the double-tooth meshing and mesh stiffness. The transmission error can be decreased. Hence, a suitable Parameter Ca_max can generate prolonged meshing with a stable transmission error. According to Section 4, Parameters Ca_max and β can decrease the values a and b and Parameters δ1 and δ2 in Figure 16. A suitable modification curve can increase the mesh stiffness and decrease the static transmission error. Point D is taken as a changing point. The modification curve is divided into two curves. Parameter β of the modified curve near the top of the tooth is changed from 1.2 to 1. An optimized modification curve is proposed as follows:

$$Ca=\{\begin{array}{cc}C{a}_{\max }{\left(\frac{x}{L}\right)}^{1.2}& 0\le x<\alpha L\\ C{a}_{\max }{\left(\frac{\alpha }{L}\right)}^{1.2}+\gamma C{a}_{\max }\left(\frac{(x-\alpha L)}{(1-\alpha )L}\right)& \alpha L\le x<L\end{array}$$

(8)

where α = 0.9 and γ = 0.07. The other parameters are the same as those in Equation (1). Considering Ca_max = 13.6 μm, the effects of Equation (1) and Equation (8) are compared. The gears before and after optimization are investigated, as shown in Figure 17.

Parameters δ1, δ2, and δ3 decrease between the single-tooth meshing and double-tooth meshing in Figure 17a. Moreover, the difference between the maximum transmission error and the minimum transmission error decreases from 0.3760 to 0.2721, and it can be defined as ep. The peak value and the range of fluctuation of the static transmission error are both reduced. Additionally, the amplitude of each frequency and the maximum mesh force are decreased in Figure 17b,c, respectively. The optimized profile modification curve in Equation (8) can reduce the static transmission error and improve the meshing process of the gear transmission. Moreover, Equation (8) is utilized to modify different gears, as shown in

Table 1. Parameters of the gears.

Parameter		Number of Teeth z	Modulus m	Load T (N·m)
A	Driving gear	72	1.75	150
	Driven gear	72	1.75
B	Driving gear	26	3.5	150
	Driven gear	26	3.5
C	Driving gear	52	1.75	75
	Driven gear	52	1.75
D	Driving gear	20	4	300
	Driven gear	20	4

, to evaluate the effects. The different gears with different parameters in Table 1 are considered to verify the applicability of the proposed curve of Equation (8). The results are listed in

Table 2. Static transmission error of the peak-to-peak value.

	Before Optimizing	After Optimizing	Amplitude
A	0.2417	0.1916	20.7%
B	0.2853	0.1691	40.7%
C	0.1408	0.0671	52.3%
D	1.0288	0.5192	49.5%

.

In Table 1, Parameter ep is utilized to evaluate the modification effect. The modified gear can decrease the transmission error by at least 20.7%. The difference between the maximum transmission error and the minimum transmission error can be reduced, which is beneficial for the transmission process.

Hence, the optimized modification curve in Equation (8), which is a two-stage curve, can be utilized to modify the driving and driven gears. Additionally, the mesh force and static transmission error can be reduced in modified gears.

7. Dynamic Analysis of the Modified Gear System

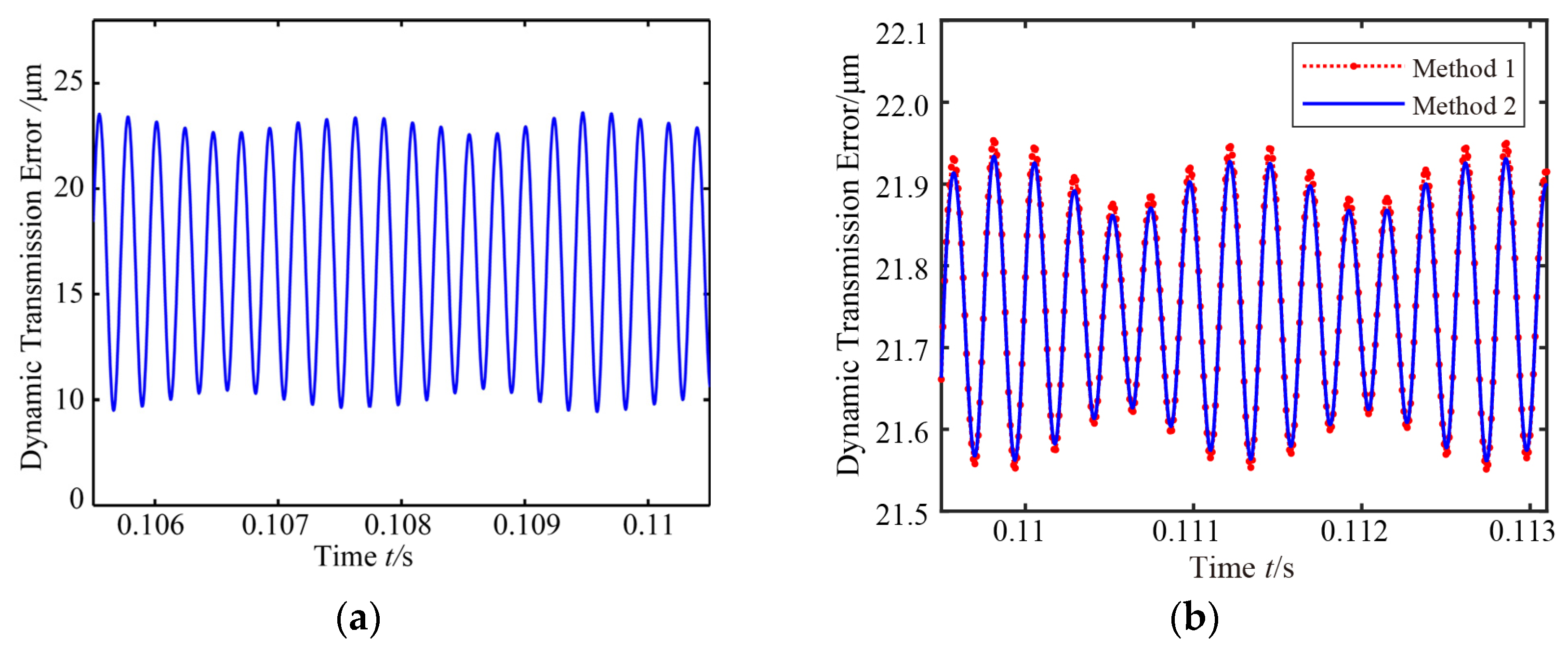
7.1. Dynamic Responses of the Modified Gear System

The dynamic performance of the gear transmission system is investigated to determine the influence of the modified gear. Because of the modification value, the mesh stiffness k(t) and time-varying backlash b(t) are different from those of the standard gears. The dynamic model of the modified gear drive is established as shown in Figure 18. Parameters k₁(t), b₁(t) and k₂(t), b₂(t) are influenced by the modification value, which is considered as different values in forward and backward gear meshing [36].

Additionally, the dynamic equation can be expressed as follows:

$$\begin{array}{l}{I}_1{\ddot{\theta }}_1+c_m{r}_{b1}(r_{b1}{\dot{\theta }}_1-r_{b2}{\dot{\theta }}_2)+r_{b1}k(t)f(r_{b1}{\theta }_1-r_{b2}{\theta }_2)=T_1\\ I_2{\ddot{\theta }}_2-c_m{r}_{b2}(r_{b1}{\dot{\theta }}_1-r_{b2}{\dot{\theta }}_2)-r_{b2}k(t)f(r_{b1}{\theta }_1-r_{b2}{\theta }_2)=-T_2\end{array}$$

(9)

In which I_i, T_i, k(t), c_m, θ_i, and r_bi (i = 1, 2) represent the moment of inertia, torque, mesh stiffness, mesh damping, torsional displacement, and base radius of the modified gear, respectively, as shown in Figure 18. The dynamic transmission error can be expressed as $x=r_{b1}{\theta }_1-r_{b2}{\theta }_2$. In Figure 18, the nonlinear backlash function can be expressed as follows:

$$f(x)=\{\begin{array}{cc}x-b_1(t)& x>b_1(t)\\ 0& -b_2(t)\le x\le b_1(t)\\ x+b_2(t)& x<-b_2(t)\end{array}$$

(10)

According to Figure 6 and Equation (6), the relation between Parameter b₁(θ(t)) and angle θ(t) of the driving gear can be presented by the following:

$$b_1(\theta (t))=\{\begin{array}{c}C{a}_{\max }{((r_{b1}\tan (\arctan (\tan {\alpha }_{st}+\theta (t)))-L_{st})/L)}^{1.2}\\ \mathrm{if} 0\le \theta (t)<{\psi }_0/2\\ C{a}_{\max }{((r_{b1}\tan (\arctan (\tan {\alpha }_{st}+({\psi }_0-\theta (t))))-L_{st})/L)}^{1.2}\\ \mathrm{if} {\psi }_0/2\le \theta (t)\le {\psi }_0\\ 0 \mathrm{if} {\psi }_0<\theta (t)\le 2\psi \end{array}$$

(11)

In which $\psi =\mathsf{\pi }/z$. In Equation (11), Parameters α_st, L_st, L, ψ₀, and ω represent the pressure angle at the starting point of modification, the corresponding radius AE in Figure 6, the modified length DE in Figure 6, the angle of the driving gear in the double-tooth meshing, and the rotating angular speed, respectively. Backlash is influenced by forward and backward meshing. In Figure 19, the solid profile and the dashed profile represent the forward meshing position of the driven gear and the exit position of backward meshing.

According to Figure 19, the relation of angles can be expressed as follows:

$$\begin{array}{l}{{\theta }^{\prime }}_a={\theta }_a={\alpha }_{a1}-{\alpha }_t\\ {\theta }_r={\psi }_a+{\theta }^{\prime }-{{\theta }^{\prime }}_a\end{array}$$

(12)

where ${\psi }_a=\psi -(inv{\alpha }_{a1}-inv\alpha )$ and ${{\theta }^{\prime }}_r={\theta }_r-(2\psi -{\psi }_0)$. The nonlinear backlash, b₁(t) and b₂(t), can be depicted for the meshing process. Additionally, the meshing process can be divided into different sections to depict the forward and backward meshing in Figure 20.

Based on Figure 7, the time-varying stiffness of forward meshing is depicted as k₁(θ(t)), and the corresponding stiffness of backward meshing can be expressed as follows:

$$k_2(\theta (t))=\{\begin{array}{ll}{k}_1({{\theta }^{\prime }}_r-\theta (t))\hfill & 0\le \theta (t)<{{\theta }^{\prime }}_r\hfill \\ k_1({{\theta }^{\prime }}_r+2\psi -\theta (t))\hfill & {{\theta }^{\prime }}_r<\theta (t)\le 2\psi \hfill \end{array}$$

(13)

In contrast to standard gears, modified gears can lead to different backlash and mesh stiffnesses, which directly influence the dynamic transmission process. The algorithm of dynamic transmission error of modified gear is listed in Algorithm 2.

Algorithm 2: Dynamic transmission error for the modified gear by the dynamic model
Input: Number of teeth z, Modulus m, Load T, Base radius rb, Moment of inertia I. Output: Dynamic transmission error e.
1:	Establish the nonlinear backlash function by (10).
2:	For Camax = 0, 5,…,20 do
3:		Establish the relationship between backlash and angle by (11).
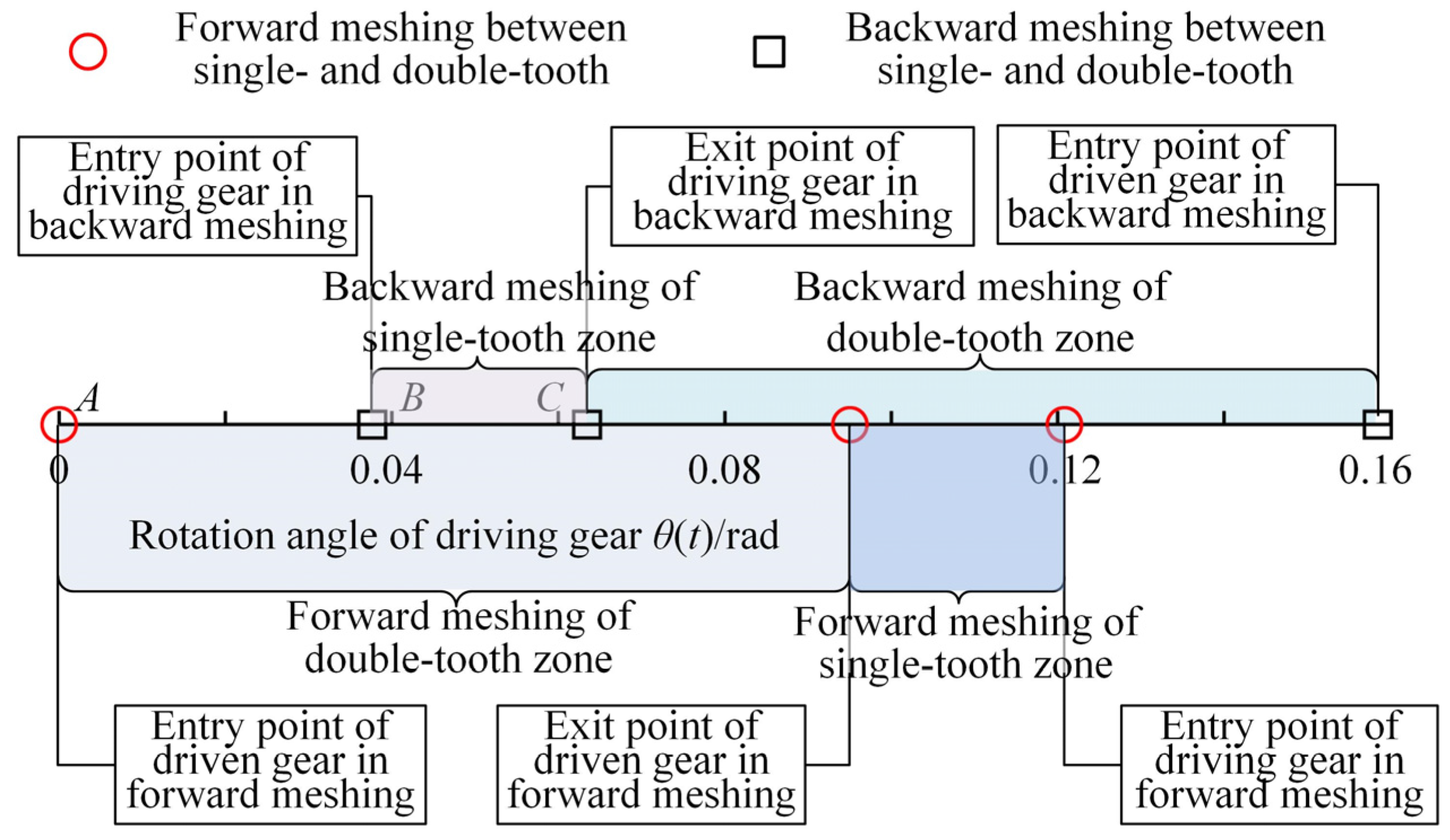
4:		Depict the transition location of single and double-teeth meshing by Figure 20 in the dynamic model.
5:		Mesh stiffness can be calculated by (12) and (13).
6:		Calculate the dynamic equation of gear pair by (9).
7:		Compute θ1 and θ2. Dynamic transmission error can be calculated by {rb1θ1–rb2θ2} based on Figure 18.
6:	End

Considering Team C in Table 1 and n = 5000 r/min, the dynamic transmission error is investigated with regard to the modified gears with the proposed method. In Figure 21, the dynamic transmission error decreases rapidly and reaches the steady state, which is shown in Figure 22. The negative value in Figure 21a indicates backward meshing, which can be eliminated by the modified gears. Compared to Figure 22a,b, the mean values are close to each other. However, the modified gear can decrease the range of the dynamic transmission error in Figure 22. Also, the dynamic performance of the proposed modified method in Equation (8) is better than the modified method in Equation (1). The amplitude of the transmission error can also be reduced by the proposed modified method in Figure 23. Also, the mesh force can be decreased, as shown as Figure 24.

The root mean square value of the acceleration of the dynamic transmission error can be utilized to evaluate the intensity of the vibration and noise, which can be expressed as follows:

$$\overline{a}=\sqrt{{\displaystyle \sum _{i=1}^N{\ddot{x}}_i{(t)}^2/N}}$$

(14)

where N and ${\ddot{x}}_i(t)$ are the number of samples and the acceleration of the dynamic transmission error, respectively. The $\overline{a}$ values of the modified gear and standard gear are 76.375 m/s⁻² and 3321 m/s⁻², respectively. Hence, the modification technique can lower the meshing noise of the gear system.

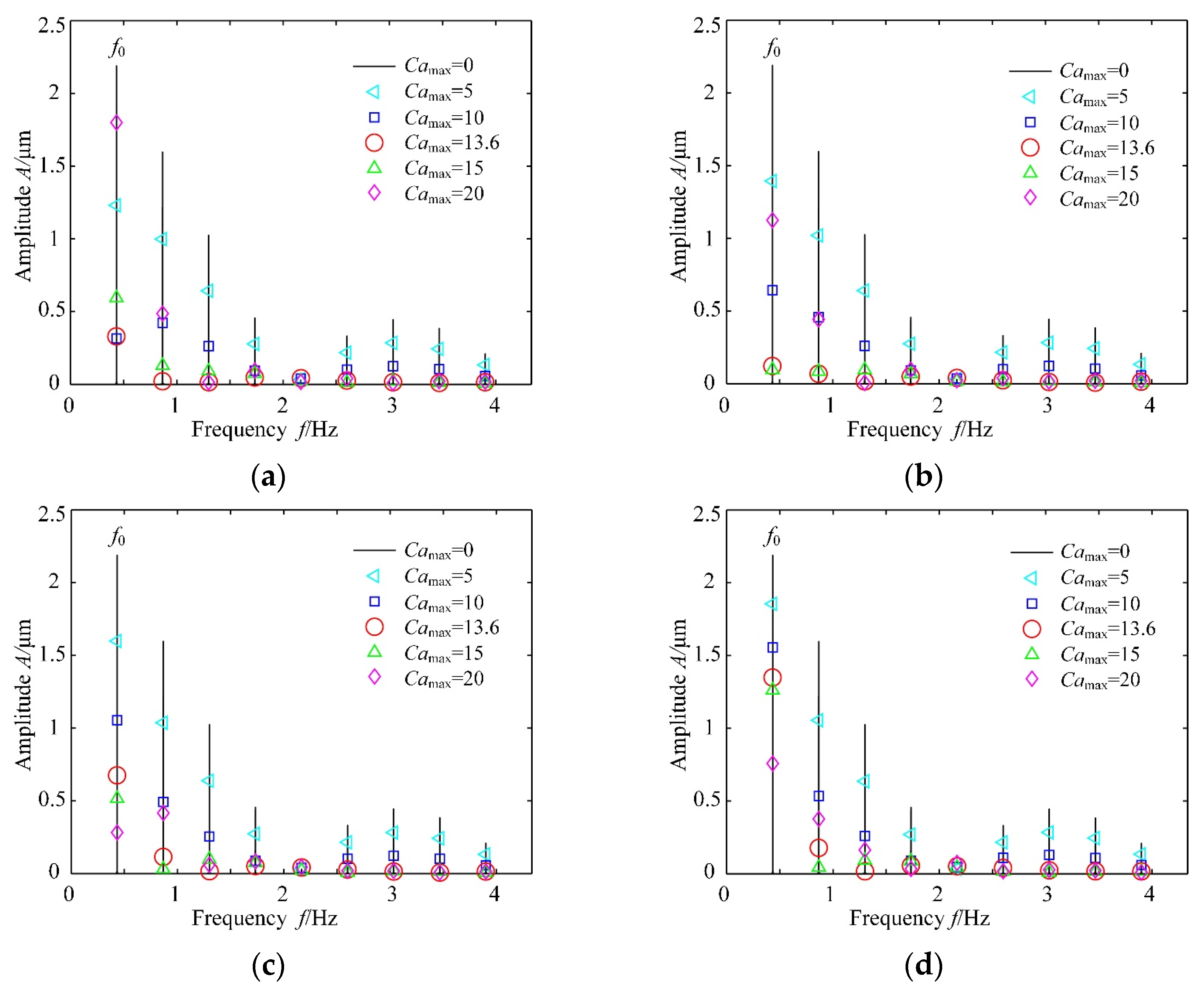
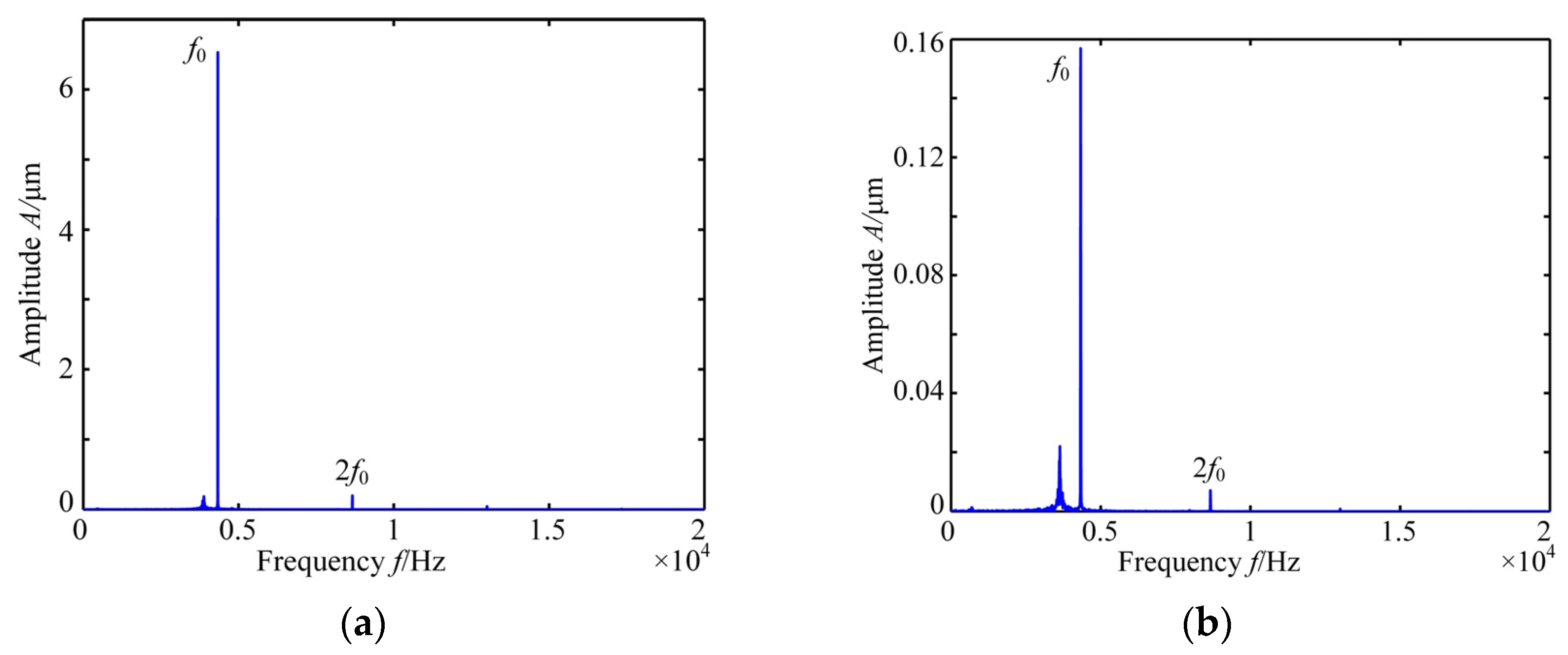
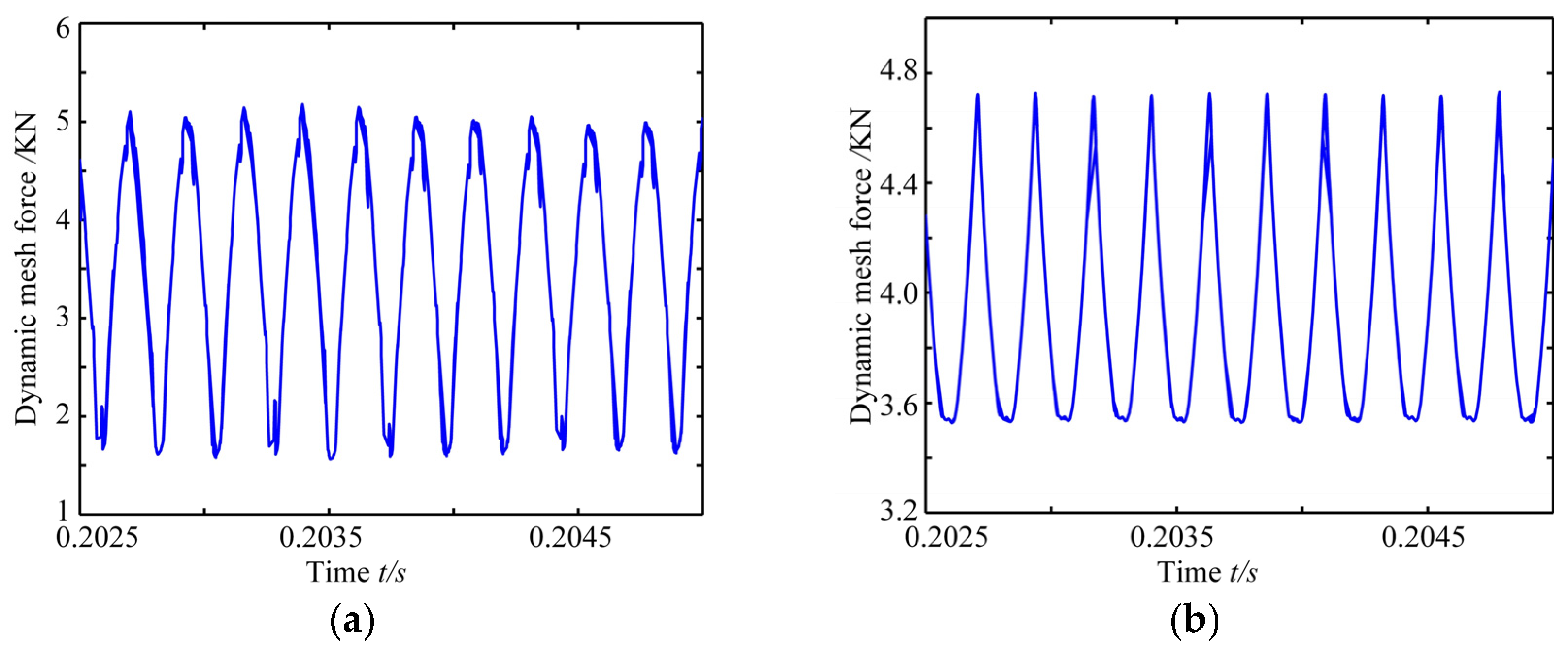
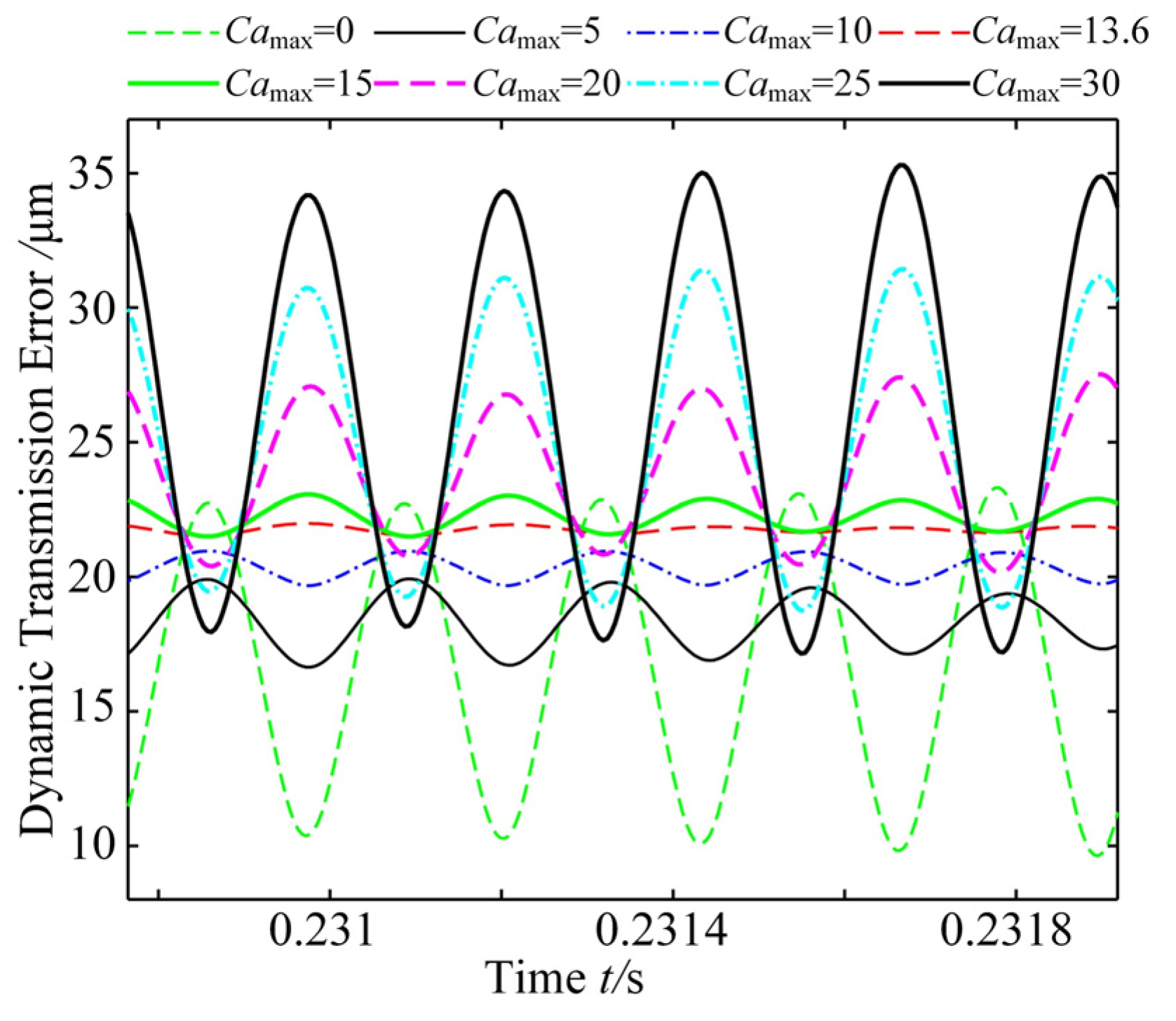
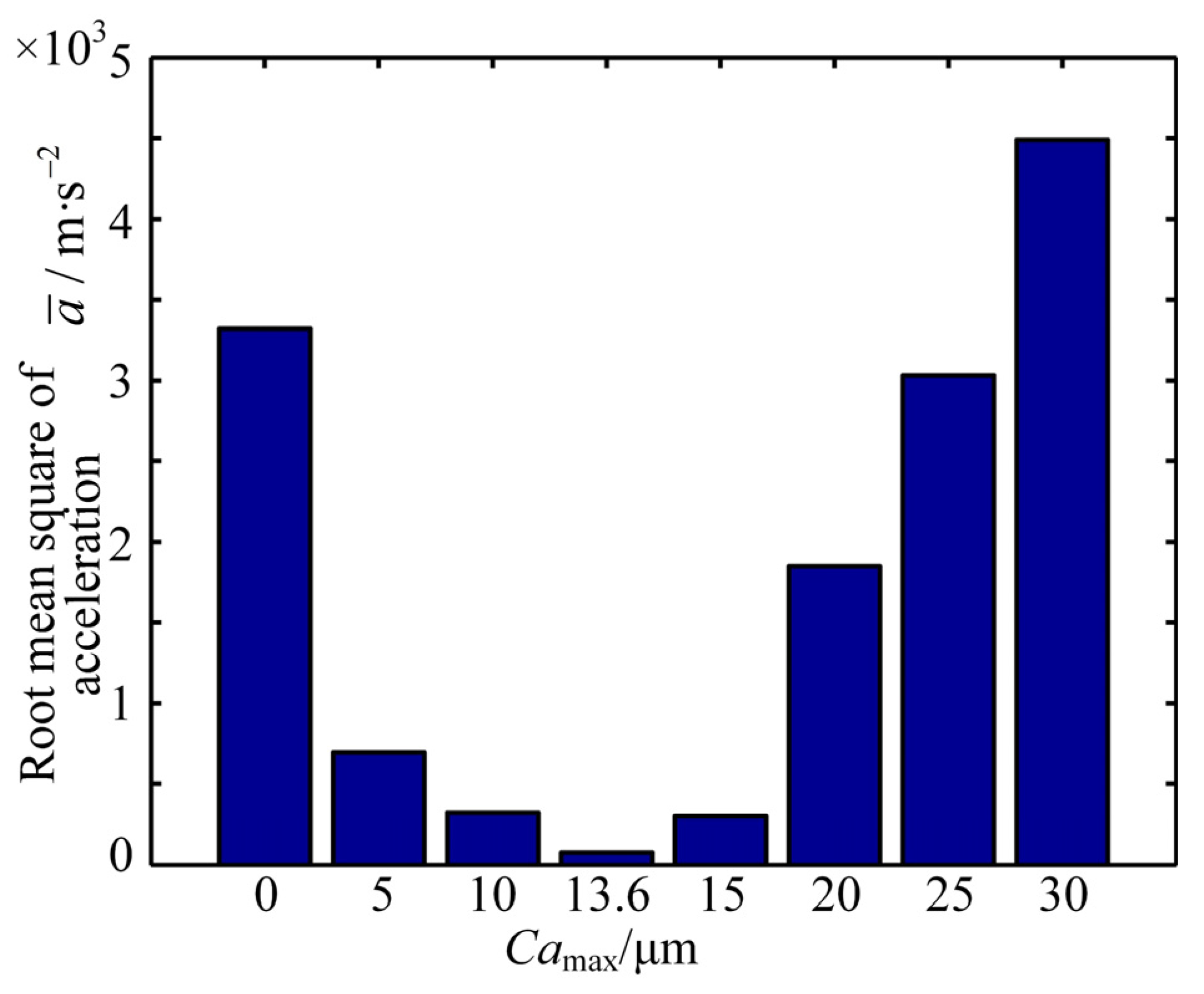
7.2. Parametric Effects on the Dynamic Responses

According to the dynamic model of the modified gear, the dynamic transmission error is investigated under the condition of different modification values of Ca_max. Considering Ca_max = 13.6, a good effect can be achieved to reduce the dynamic transmission error, as shown in Figure 25. Additionally, the root mean square of acceleration can be decreased, which reduces the influence of noise, as shown in Figure 26.

The spectrum of the dynamic transmission error with different Ca_max values is expressed as shown in Figure 27. The whole frequency of the transmission error is presented in Figure 27b. Ca_max = 13.6 can reduce the amplitude of the main frequency f₀, as shown in Figure 27a. The amplitudes of other frequencies are expressed in Figure 27c,d. With increasing Ca_max, the amplitude of the dynamic transmission error first decreases and subsequently increases.

The relation between the torque T and dynamic transmission error is investigated in Figure 28. The suitable torque, T = 150 N·m, can reduce the root mean square of acceleration, as shown in Figure 29. Lower and higher torques can cause higher dynamic transmission errors, which are influenced by backward and forward meshing between single and double teeth. Hence, the suitable torque needs to be found for smooth meshing.

The spectrum of the dynamic transmission error with different T values is expressed as shown in Figure 30.

The whole frequency of transmission error is presented in Figure 30b. With increasing T, the amplitude of the dynamic transmission error first decreases and subsequently increases. Hence, a suitable modification value and torque can reduce the meshing noise and the transmission error. Considering forward meshing and backward meshing, a dynamic model with backlash and time-varying stiffness is investigated to depict the dynamic performance of the modified gear. Additionally, the influences of Parameters Ca_max and T are investigated to present the relationship between each parameter and the transmission error.

8. Conclusions

The modification technique can improve the transmission characteristics of any gear system, which reduces the static transmission error and dynamic transmission error. The parametric model of the modified gear is set up. The influences of the load, radius of the gear hole and prolonged meshing on the static transmission error are investigated. The radius of the gear hole only affects the overall level of static transmission error but does not affect its fluctuation. Depending on the maximum interference value, the modification values, β = 1.2 and Ca_max = 13.6 μm, can be defined to avoid prolonged meshing.

Based on the calculated values β = 1.2 and Ca_max = 13.6 μm, a two-stage modification curve is proposed to optimize the gear pair. The range and amplitude of the static transmission error is decreased, which can improve the performance of the spur gear system. Moreover, a dynamic transmission model is analyzed for the dynamic characteristics, considering the time-varying stiffness and backlash of the modified gear. The proposed modification curve can decrease the vibration displacement and noise. Additionally, the amplitudes of different frequencies can be reduced, which is beneficial for dynamic transmission. Considering different working conditions, both static transmission error and dynamic transmission error are considered to evaluate the proposed modified method, which can be utilized for spur gear drives. The avoidance of the interference of the modified gear and the use of a modified method for dynamic transmission errors can be investigated in the future.