Adaptive Terminal Sliding Mode Trajectory Tracking Control for Autonomous Vehicles Considering Completely Unknown Parameters and Unknown Perturbation Conditions
Abstract
1. Introduction
- (1)
- A non-singular terminal sliding model control protocol is proposed to track the ideal trajectory and guarantee the preview error converging to zero in a finite time. The chattering issue encountered by the conventional sliding mode controller is effectively addressed by the proposed method.
- (2)
- The proposed controller is integrated with the adaptive algorithm, eliminating the need for prior knowledge of vehicle parameters and perturbation bounds. This ensures a more flexible and robust system capable of dynamically adjusting to varying conditions.
- (3)
- To illustrate the effectiveness of the proposed method, the CarSim–Matlab joint simulations and real-world experimental studies are conducted. The proposed method is compared with the conventional controllers and verified under various driving conditions.
2. Modeling and Problem Description
2.1. Modeling of Vehicle Three-Degrees-of-Freedom Dynamics
2.2. Problem Formulation
3. Trajectory Tracking Controller Design
3.1. Controller with the Known Vehicle Parameters
3.2. Controller with the Unknown Vehicle Parameters
4. Simulation Analysis
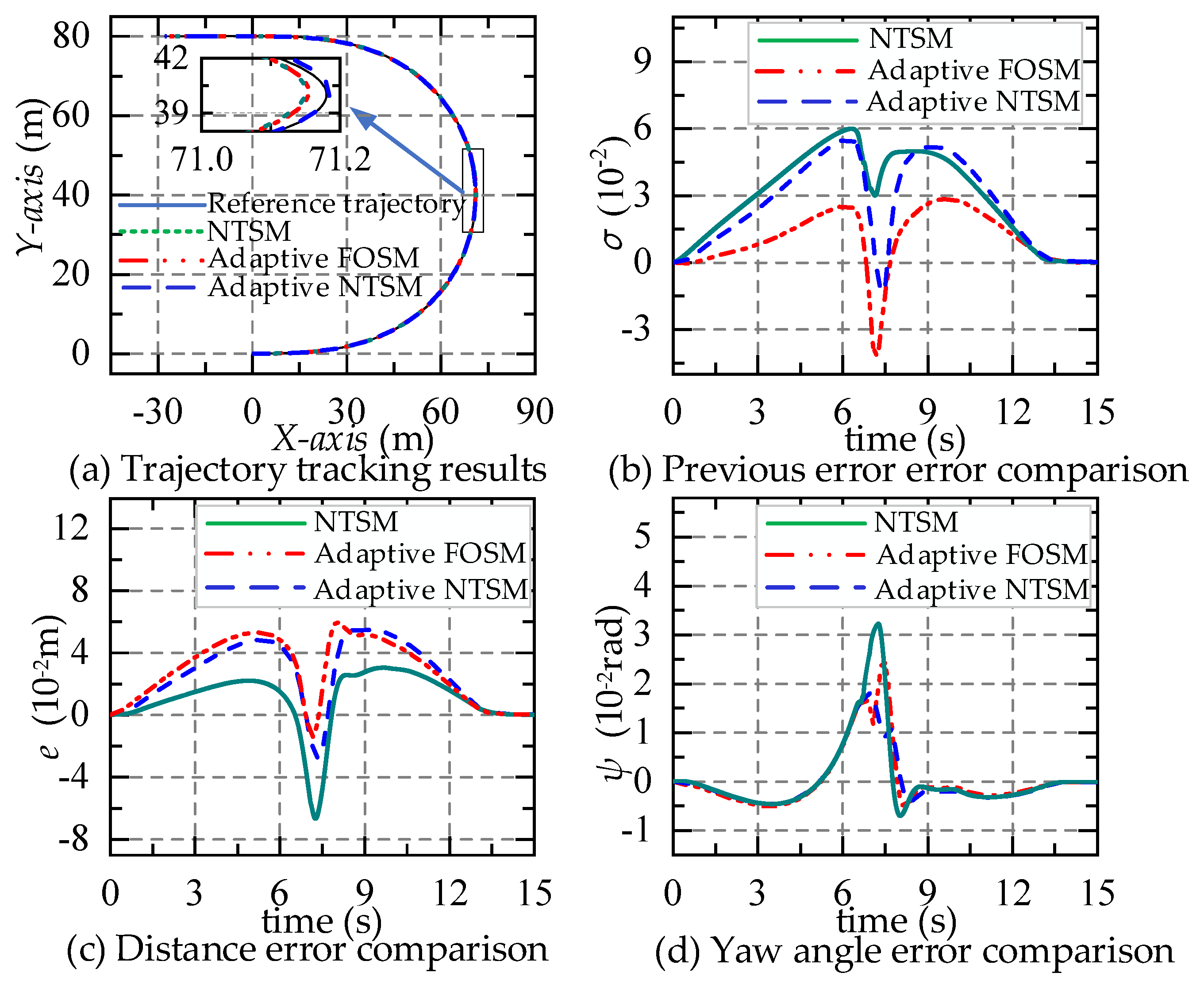
4.1. Simulation Results of Three Sliding Mode Controllers
4.2. Robustness of Non-Singular Terminal Sliding Mode with Parameter Adaptation
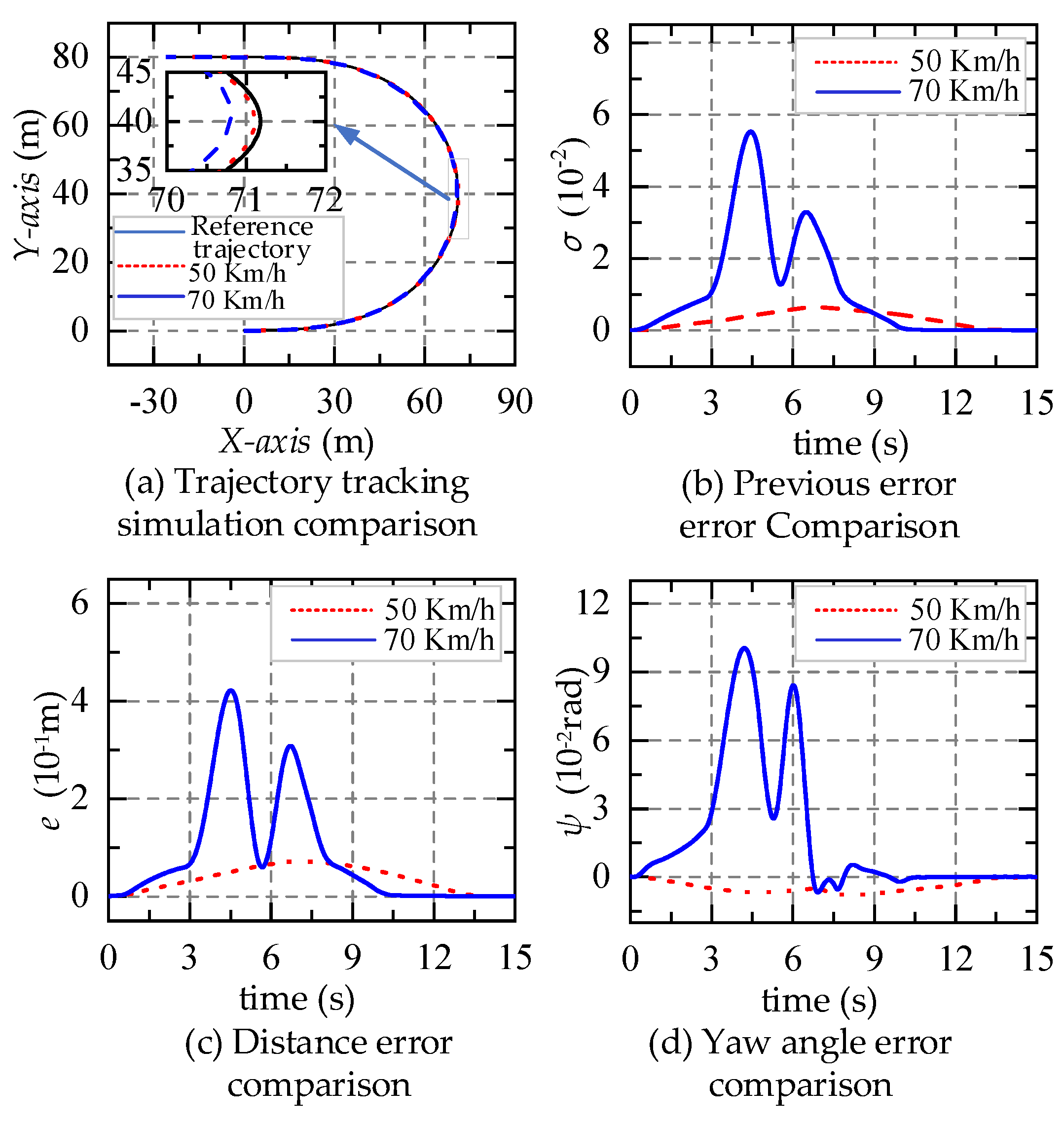
4.2.1. Robustness to Vehicle Speed
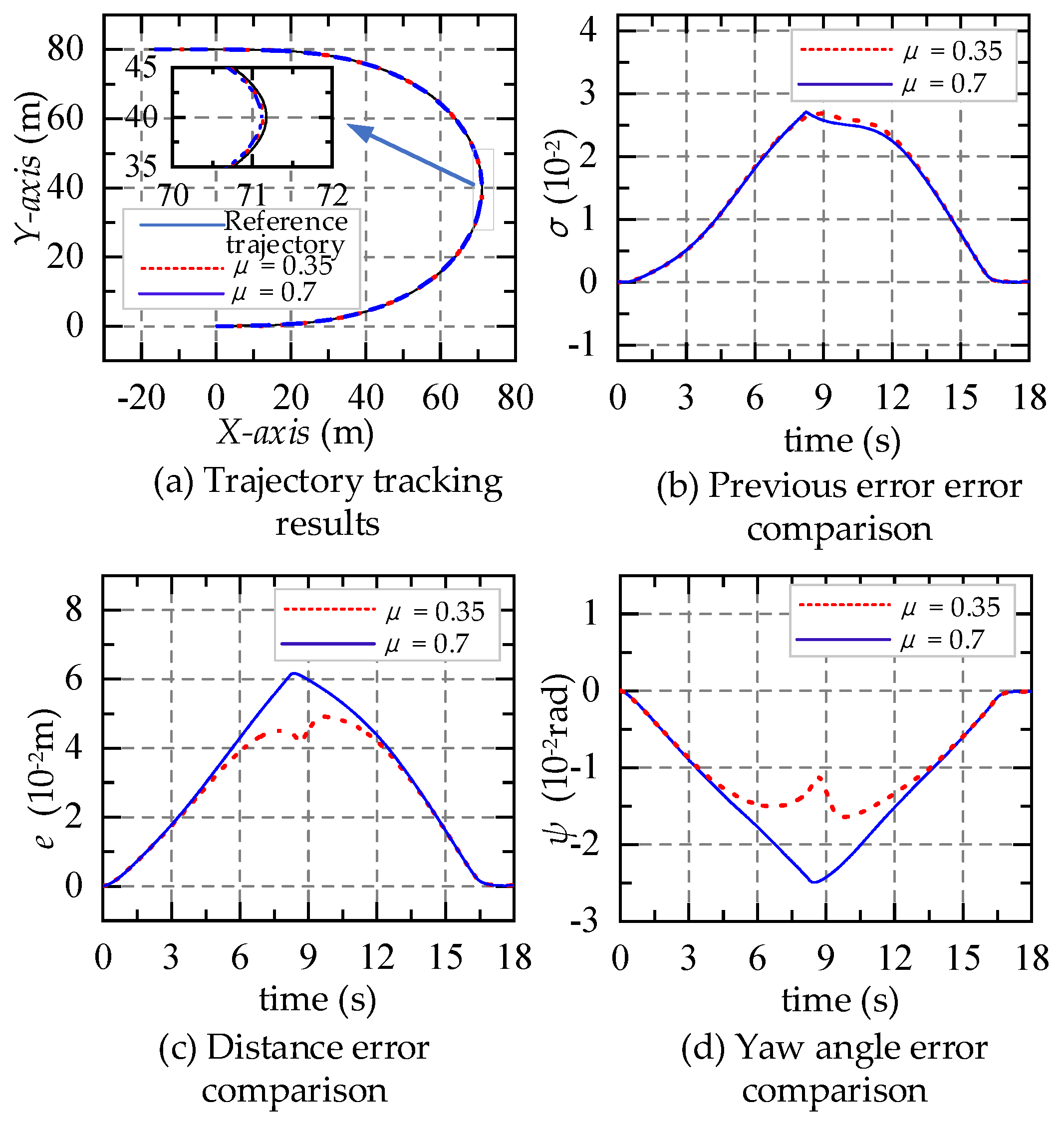
4.2.2. Robustness to Road Adhesion Coefficients
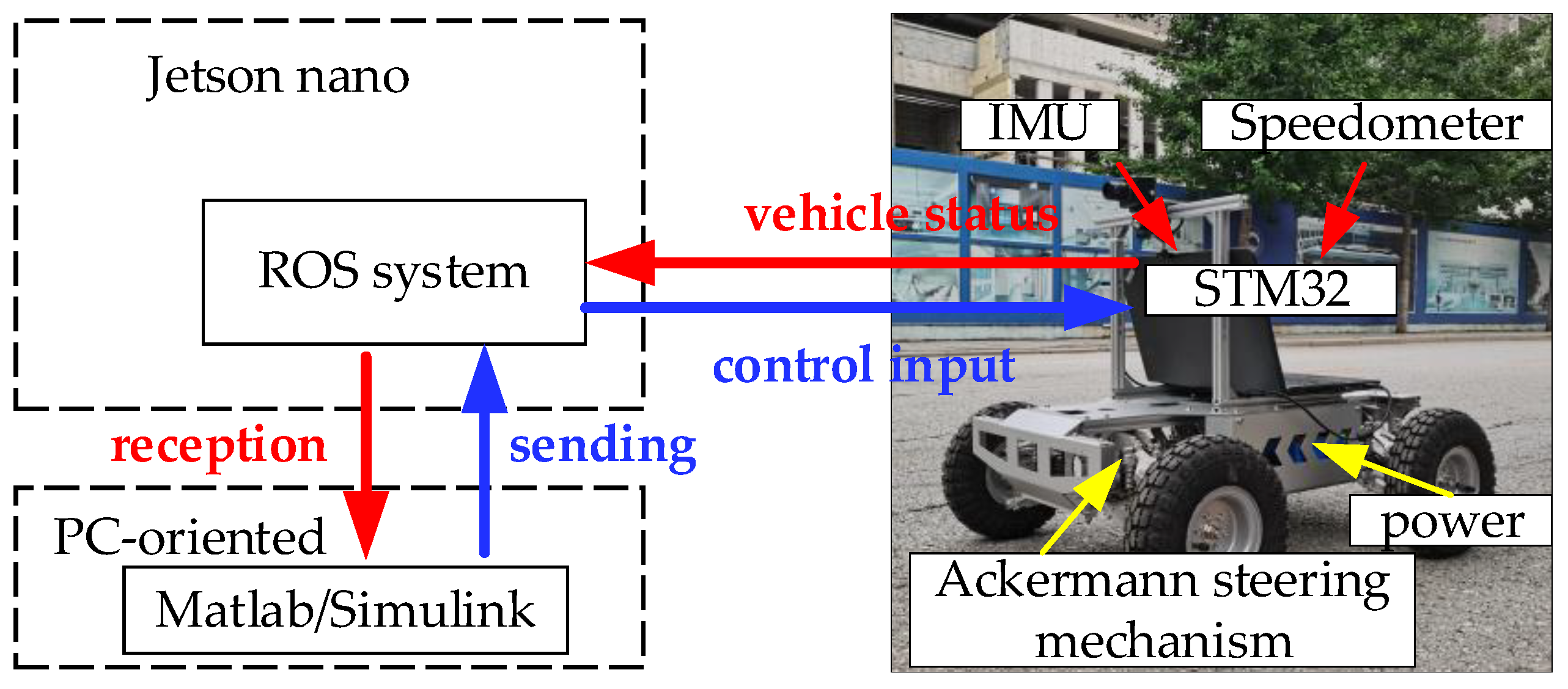
5. Experimental Verification of Trajectory Tracking Controller
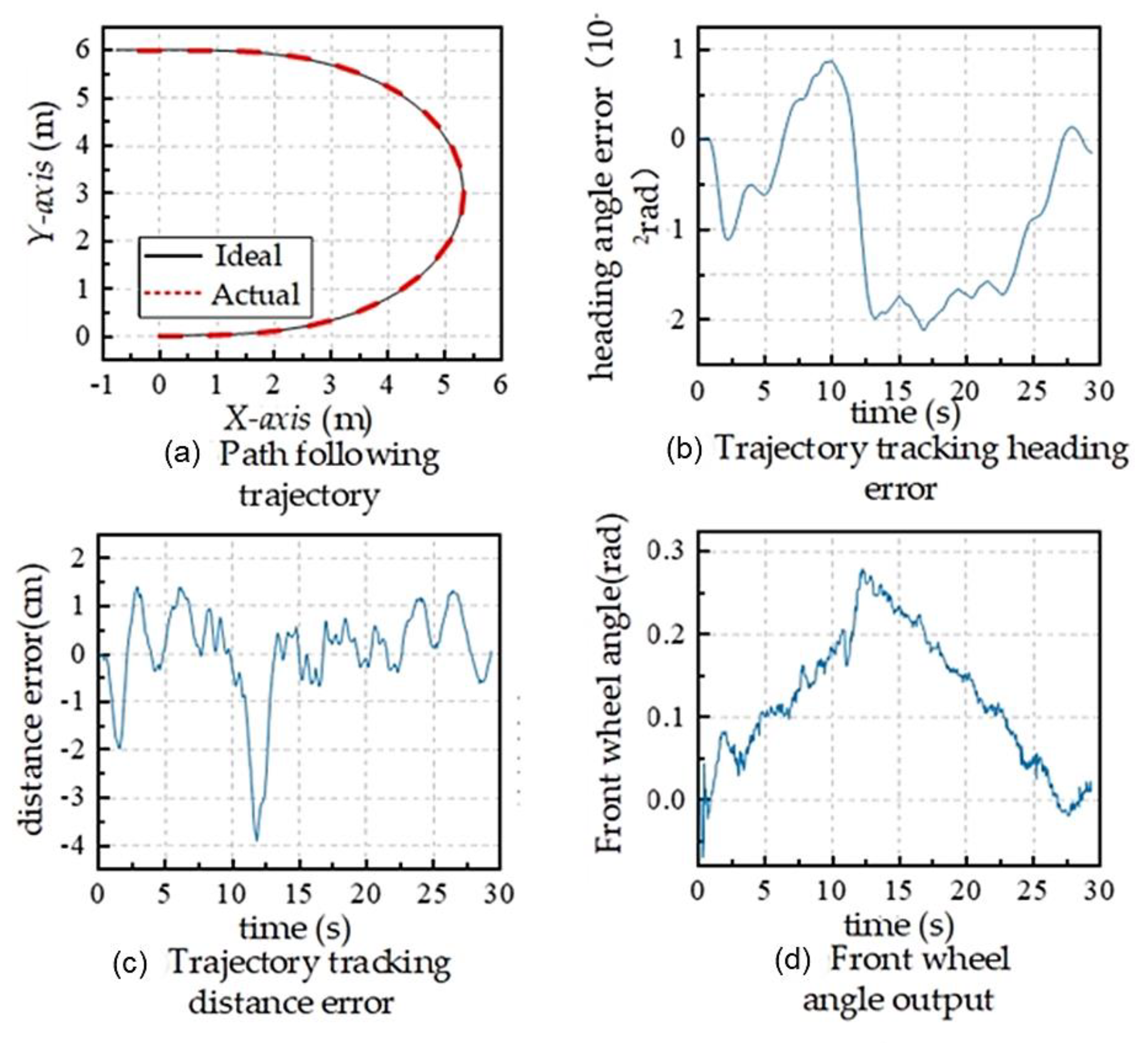
Algorithm Experimental Validation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xavier, N.; Bandyopadhyay, B. Practical Sliding Mode Using State Depended Intermittent Control. IEEE Trans. Circuits Syst. II: Express Briefs 2021, 68, 341–345. [Google Scholar] [CrossRef]
- Liang, Z.; Zhao, J.; Dong, Z.; Wang, Y.; Ding, Z. Torque Vectoring and Rear-Wheel-Steering Control for Vehicle’s Uncertain Slips on Soft and Slope Terrain Using Sliding Mode Algorithm. IEEE Trans. Veh. Technol. 2020, 69, 3805–3815. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Oh, H.; Moon, J. Continuous Nonsingular Terminal Sliding-Mode Control With Integral-Type Sliding Surface for Disturbed Systems: Application to Attitude Control for Quadrotor UAVs Under External Disturbances. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5635–5660. [Google Scholar] [CrossRef]
- Guo, S.; Orosz, G.; Molnar, T.G. Connected Cruise and Traffic Control for Pairs of Connected Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 12648–12658. [Google Scholar] [CrossRef]
- Chen, X.; Xu, B.; Qin, X.; Bian, Y.; Hu, M.; Sun, N. Non-Signalized Intersection Network Management With Connected and Automated Vehicles. IEEE Access 2020, 8, 122065–122077. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, L.; Fan, J.; Xu, B.; Hu, M.; Chen, X. An Improved Real-Time Slip Model Identification Method for Autonomous Tracked Vehicles Using Forward Trajectory Prediction Compensation. IEEE Trans. Instrum. Meas. 2021, 70, 7501012. [Google Scholar] [CrossRef]
- Subroto, R.K.; Wang, C.Z.; Lian, K.L. Four-Wheel Independent Drive Electric Vehicle Stability Control Using Novel Adaptive Sliding Mode Control. IEEE Trans. Ind. Appl. 2020, 56, 5995–6006. [Google Scholar] [CrossRef]
- Wen, S.; Guo, G. Distributed Trajectory Optimization and Sliding Mode Control of Heterogenous Vehicular Platoons. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7096–7111. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.-L.; Wu, Q.; Zhang, X.-M. Resilient and Safe Platooning Control of Connected Automated Vehicles Against Intermittent Denial-of-Service Attacks. IEEE/CAA J. Autom. Sin. 2023, 10, 1234–1251. [Google Scholar] [CrossRef]
- Wang, B.; Su, R. A Distributed Platoon Control Framework for Connected Automated Vehicles in an Urban Traffic Network. IEEE Trans. Control Netw. Syst. 2022, 9, 1717–1730. [Google Scholar] [CrossRef]
- Scheffe, P.; Henneken, T.M.; Kloock, M.; Alrifaee, B. Sequential Convex Programming Methods for Real-Time Optimal Trajectory Planning in Autonomous Vehicle Racing. IEEE Trans. Intell. Veh. 2023, 8, 661–672. [Google Scholar] [CrossRef]
- Ju, Z.; Zhang, H.; Li, X.; Chen, X.; Han, J.; Yang, M. A Survey on Attack Detection and Resilience for Connected and Automated Vehicles: From Vehicle Dynamics and Control Perspective. IEEE Trans. Intell. Veh. 2022, 7, 815–837. [Google Scholar] [CrossRef]
- Tang, L.; Yan, F.; Zou, B.; Wang, K.; Lv, C. An Improved Kinematic Model Predictive Control for High-Speed Path Tracking of Autonomous Vehicles. IEEE Access 2020, 8, 51400–51413. [Google Scholar] [CrossRef]
- Wang, H.; Liu, B. Path Planning and Path Tracking for Collision Avoidance of Autonomous Ground Vehicles. IEEE Syst. J. 2022, 16, 3658–3667. [Google Scholar] [CrossRef]
- Hu, C.; Chen, Y.; Wang, J. Fuzzy Observer-Based Transitional Path-Tracking Control for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3078–3088. [Google Scholar] [CrossRef]
- Guan, Y.; Ren, Y.; Li, S.E.; Sun, Q.; Luo, L.; Li, K. Centralized Cooperation for Connected and Automated Vehicles at Intersections by Proximal Policy Optimization. in IEEE Trans. Veh. Technol. 2020, 69, 12597–12608. [Google Scholar] [CrossRef]
- Bai, W.; Xu, B.; Liu, H.; Qin, Y.; Xiang, C. Robust Longitudinal Distributed Model Predictive Control of Connected and Automated Vehicles With Coupled Safety Constraints. IEEE Trans. Veh. Technol. 2023, 72, 2960–2973. [Google Scholar] [CrossRef]
- Xu, H.; Xiao, W.; Cassandras, C.G.; Zhang, Y.; Li, L. A General Framework for Decentralized Safe Optimal Control of Connected and Automated Vehicles in Multi-Lane Signal-Free Intersections. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17382–17396. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, B.; Wang, X.; Li, L.; Cheng, S.; Chen, Z.; Li, G.; Zhang, L. Dynamic Lane-Changing Trajectory Planning for Autonomous Vehicles Based on Discrete Global Trajectory. IEEE Trans. Intell. Transp. Syst. 2022, 23, 8513–8527. [Google Scholar] [CrossRef]
- Mohamed, M.; Rabik, S.; Vasanth, T. Muthuramalingam. Implementation of LQR based SOD control in diode laser beam machining on leather specimens, Optics & Laser Technology. Automatica 2024, 170, 110328. [Google Scholar]
- Li, Q.; Ding, B. Design of Backstepping Sliding Mode Control for a Polishing Robot Pneumatic System Based on the Extended State Observer. Machines 2023, 11, 904. [Google Scholar] [CrossRef]
- Ye, Y.; Wang, Y.; Wang, L.; Wang, X. A modified predictive PID controller for dynamic positioning of vessels with autoregressive model. Ocean Eng. 2023, 284, 115176. [Google Scholar] [CrossRef]
- Fu, Q.; Wu, J.; Yu, C.; Feng, T.; Zhang, N.; Zhang, J. Linear Quadratic Optimal Control with the Finite State for Suspension System. Machines 2023, 11, 127. [Google Scholar] [CrossRef]
- Gao, Z.; Wu, Z.; Hao, W.; Long, K.; Byon, Y.-J.; Long, K. Optimal Trajectory Planning of Connected and Automated Vehicles at On-Ramp Merging Area. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12675–12687. [Google Scholar] [CrossRef]
- Chen, N.; van Arem, B.; Alkim, T.; Wang, M. A Hierarchical Model-Based Optimization Control Approach for Cooperative Merging by Connected Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7712–7725. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Han, K.; Choi, S.B. Vehicle Path Tracking Control Using Pure Pursuit With MPC-Based Look-Ahead Distance Optimization. IEEE Trans. Veh. Technol. 2024, 73, 53–66. [Google Scholar] [CrossRef]
- Liang, Z.; Zhao, J.; Liu, B.; Wang, Y.; Ding, Z. Velocity-Based Path Following Control for Autonomous Vehicles to Avoid Exceeding Road Friction Limits Using Sliding Mode Method. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1947–1958. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, L.; Zhang, J.; Li, F. Path Following Control of Autonomous Ground Vehicle Based on Nonsingular Terminal Sliding Mode and Active Disturbance Rejection Control. IEEE Trans. Veh. Technol. 2019, 68, 6379–6390. [Google Scholar] [CrossRef]
- Labbadi, M.; Djemai, M.; Boubaker, S. A novel non-singular terminal sliding mode control combined with integral sliding surface for perturbed quadrotor. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2022, 236, 999–1009. [Google Scholar] [CrossRef]
- Lei, Q.; Zhang, W. Adaptive non-singular integral terminal sliding mode tracking control for autonomous underwater vehicles. IET Control Theory Appl. 2017, 11, 1293–1306. [Google Scholar]
- Shen, H.; Pan, Y.J.; Ahmad, U.; He, B. Pose Synchronization of Multiple Networked Manipulators Using Nonsingular Terminal Sliding Mode Control. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 12. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Li, K. An Adaptive Hierarchical Trajectory Following Control Approach of Autonomous Four-Wheel Independent Drive Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2482–2492. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, Z.; Zhao, J.; Wong, P.K.; Yang, Z.; Ding, Z. Fixed-Time Prescribed Performance Path-Following Control for Autonomous Vehicle With Complete Unknown Parameters. IEEE Trans. Ind. Electron. 2023, 70, 8426–8436. [Google Scholar] [CrossRef]
- Liang, Z.; Shen, M.; Li, Z.; Yang, J. Model-Free Output Feedback Path Following Control for Autonomous Vehicle With Prescribed Performance Independent of Initial Conditions. IEEE/ASME Trans. Mechatron. 2023, 10, 1–12. [Google Scholar] [CrossRef]
- Ghasemi, M.; Nersesov, S.G. Finite-time coordination in multiagent systems using sliding mode control approach. Automatica 2014, 50, 1209–1216. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Zhao, L. Finite-time command filtered backstepping control for a class of nonlinear systems. Automatica 2018, 92, 173–180. [Google Scholar] [CrossRef]
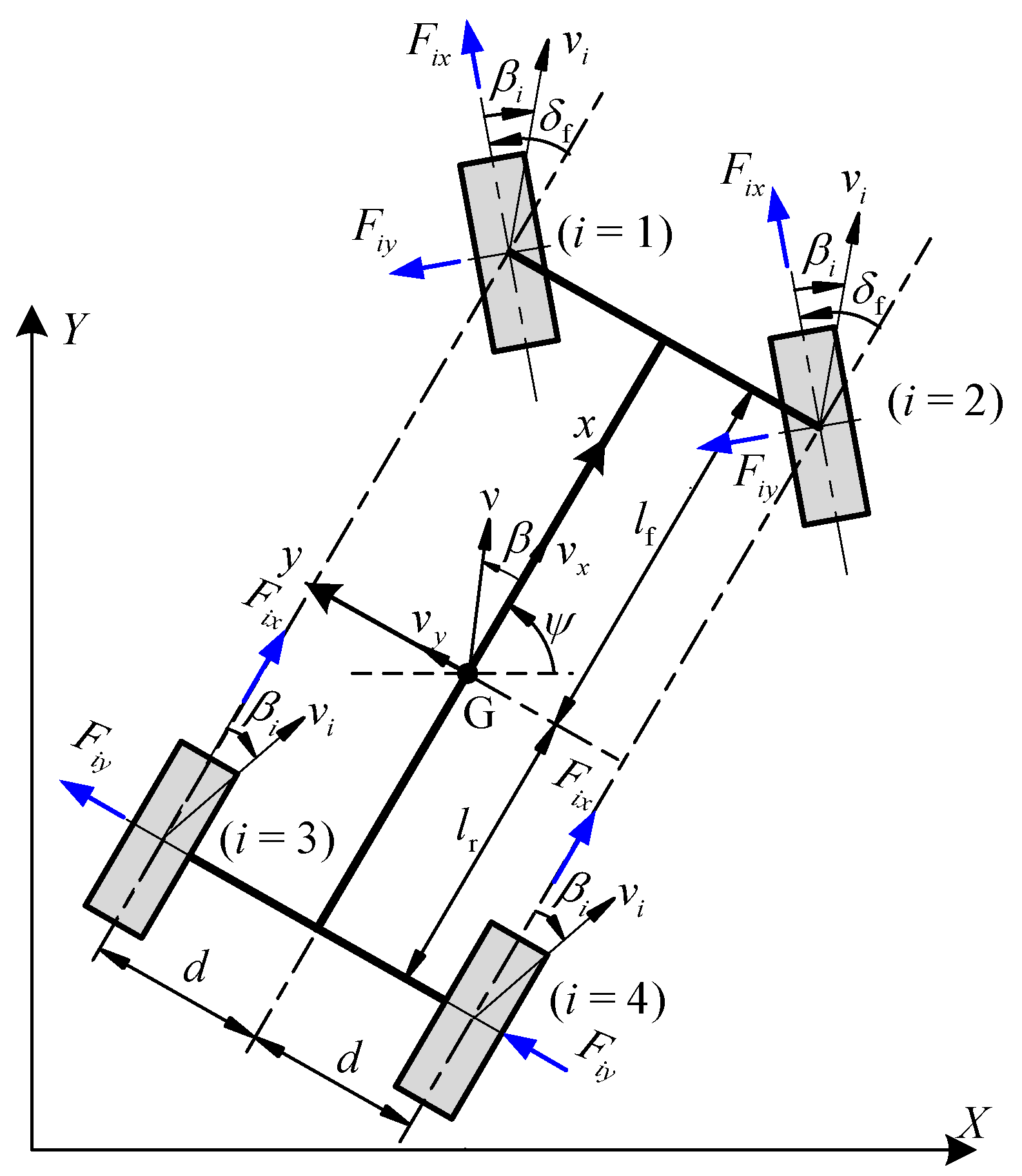
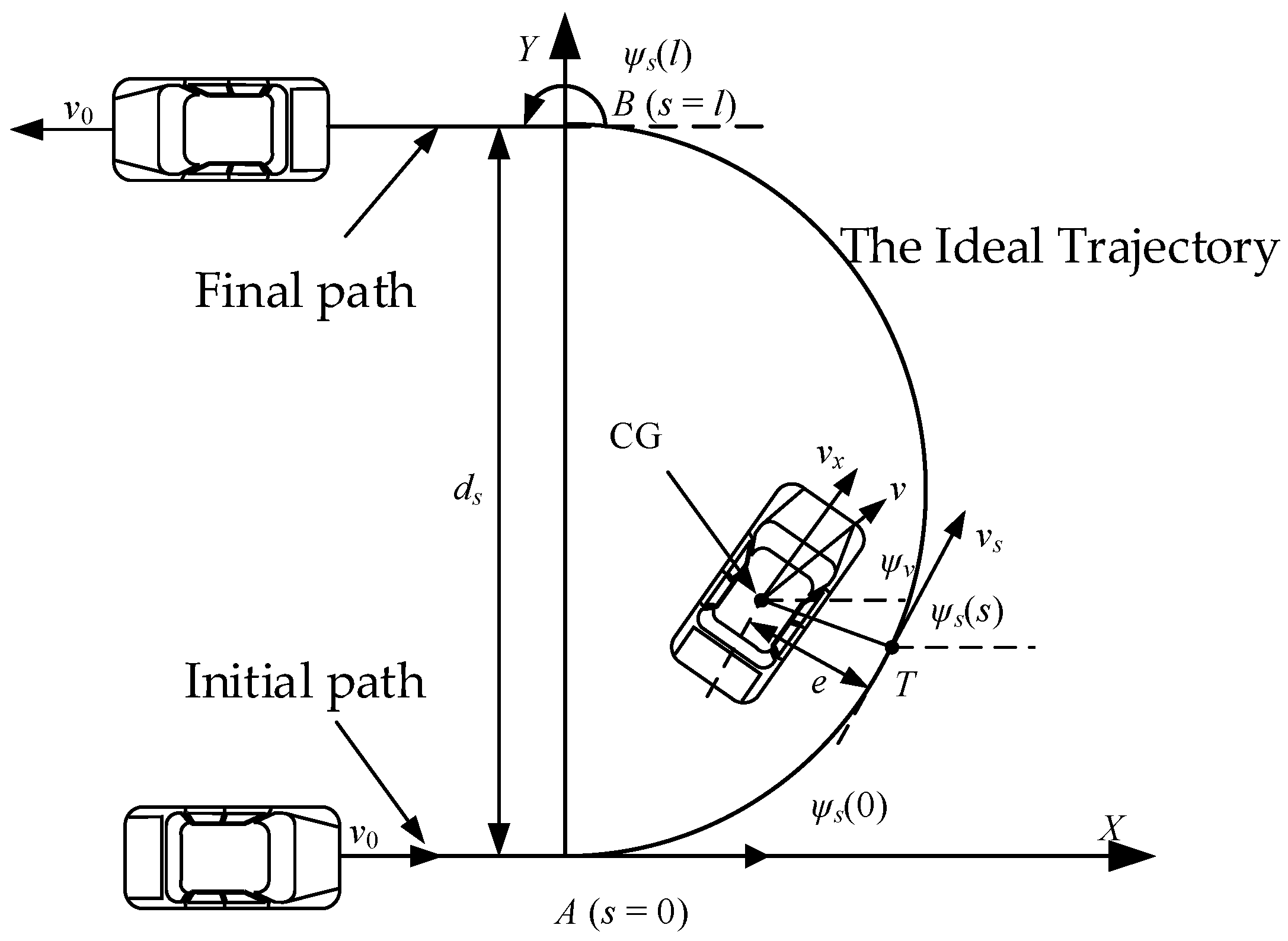

| Symbolic | Unit | Description |
|---|---|---|
| m | kg | Vehicle mass |
| lf | m | Distance from center of gravity (CG) to front axle |
| lr | m | Distance from CG to rear axle |
| δf | rad | Steering angle of front wheels |
| d | m | Distance from CG to left/right wheel |
| i | Wheel ID, and i = 1, 2, 3, 4 | |
| Iz | kg·m2 | Yaw moment of inertia of vehicle |
| γ | rad/s | Yaw rate of vehicle |
| β | rad | Sideslip angle of vehicle |
| βi | rad | Sideslip angle of wheel i |
| v | m/s | Total velocity of CG |
| vi | m/s | Speed of wheel i |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m | 1230 kg | IZ | 1343 kg·m2 |
| lf | 1.04 m | cf | 96,300 N/rad |
| lr | 1.56 m | cr | 64,200 N/rad |
| d | 1.48 m | g | 9.8 m/s2 |
| R | 0.3 m | vd | 50 km/h |
| Controllers | Parameter |
|---|---|
| Sliding mold surface (22) | ξ = 0.4, p = 7, q = 5 |
| Adaptive control laws, (40) | η1 = 0.4, η11 = 0.08, η2 = [0.5 1], η22 = [1 0.5], η3 = 5, η33 = 2 |
| NTSM controllers, (39) | ηd = 5, L = 1.4, ksat = 8 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m | 35.16 kg | IZ | 2.188 kg·m2 |
| lf | 0.25 m | cf | 1130 N/rad |
| lr | 0.25 m | cr | 1130 N/rad |
| d | 0.6 m | g | 9.8 m/s2 |
| R | 0.128 m | vd | 1.8 km/h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, C.; Shen, M.; Wang, Z.; Wu, H.; Liang, Z.; Liang, Z. Adaptive Terminal Sliding Mode Trajectory Tracking Control for Autonomous Vehicles Considering Completely Unknown Parameters and Unknown Perturbation Conditions. Machines 2024, 12, 237. https://doi.org/10.3390/machines12040237
Feng C, Shen M, Wang Z, Wu H, Liang Z, Liang Z. Adaptive Terminal Sliding Mode Trajectory Tracking Control for Autonomous Vehicles Considering Completely Unknown Parameters and Unknown Perturbation Conditions. Machines. 2024; 12(4):237. https://doi.org/10.3390/machines12040237
Chicago/Turabian StyleFeng, Chengyang, Mingyu Shen, Zhongnan Wang, Hao Wu, Zenghui Liang, and Zhongchao Liang. 2024. "Adaptive Terminal Sliding Mode Trajectory Tracking Control for Autonomous Vehicles Considering Completely Unknown Parameters and Unknown Perturbation Conditions" Machines 12, no. 4: 237. https://doi.org/10.3390/machines12040237
APA StyleFeng, C., Shen, M., Wang, Z., Wu, H., Liang, Z., & Liang, Z. (2024). Adaptive Terminal Sliding Mode Trajectory Tracking Control for Autonomous Vehicles Considering Completely Unknown Parameters and Unknown Perturbation Conditions. Machines, 12(4), 237. https://doi.org/10.3390/machines12040237







