Experimental Investigation and Control of Driveline Torsional Vibrations during Clutch-to-Clutch Shifts of Electrified Vehicles
Abstract
1. Introduction
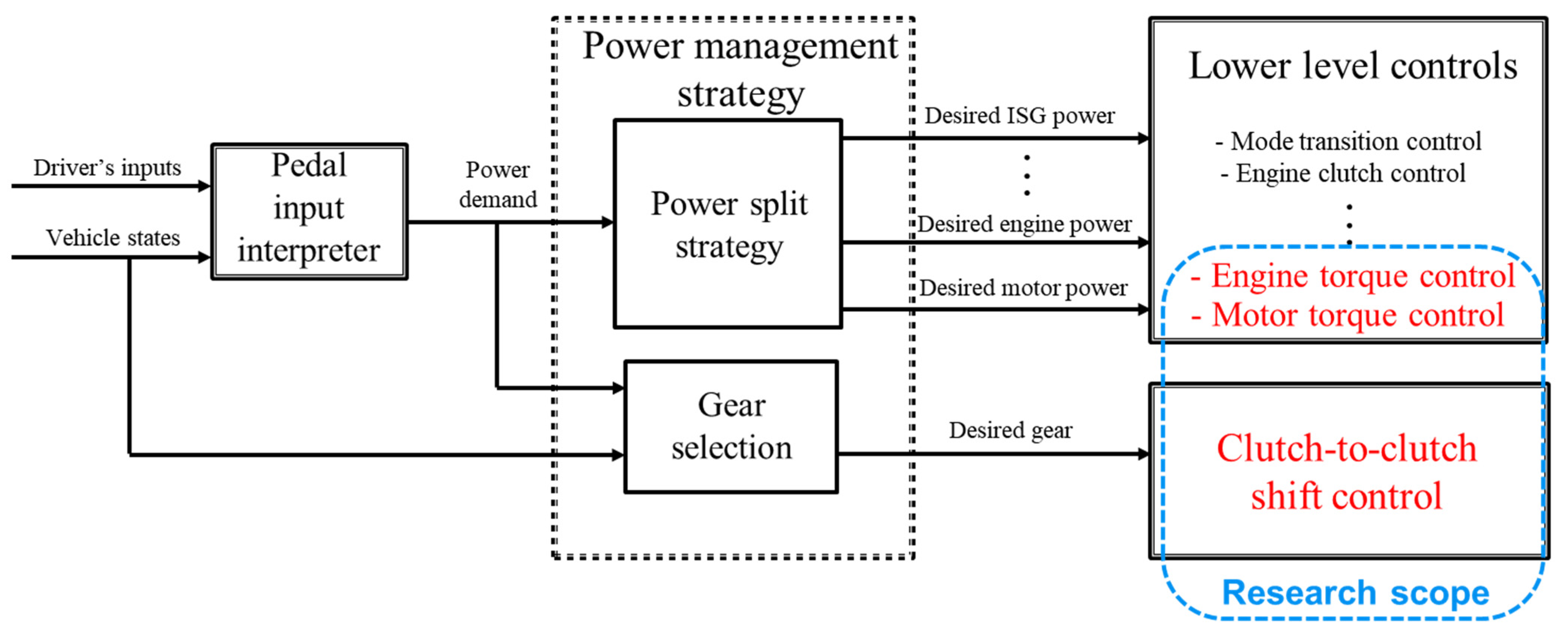
2. Investigation of Clutch-to-Clutch Shifts
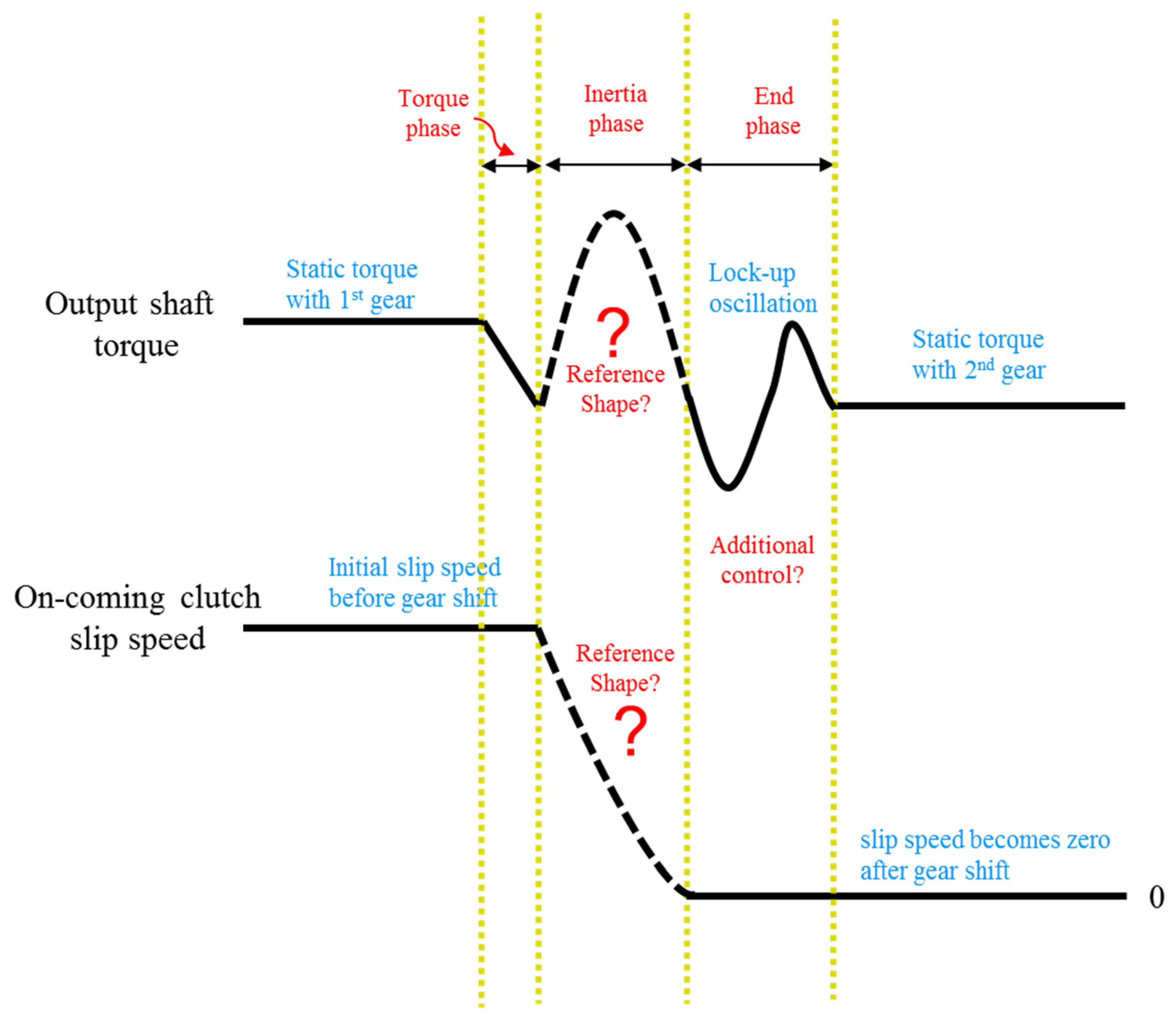
2.1. Clutch-to-Clutch Shift Process
2.2. Model-Based Analysis
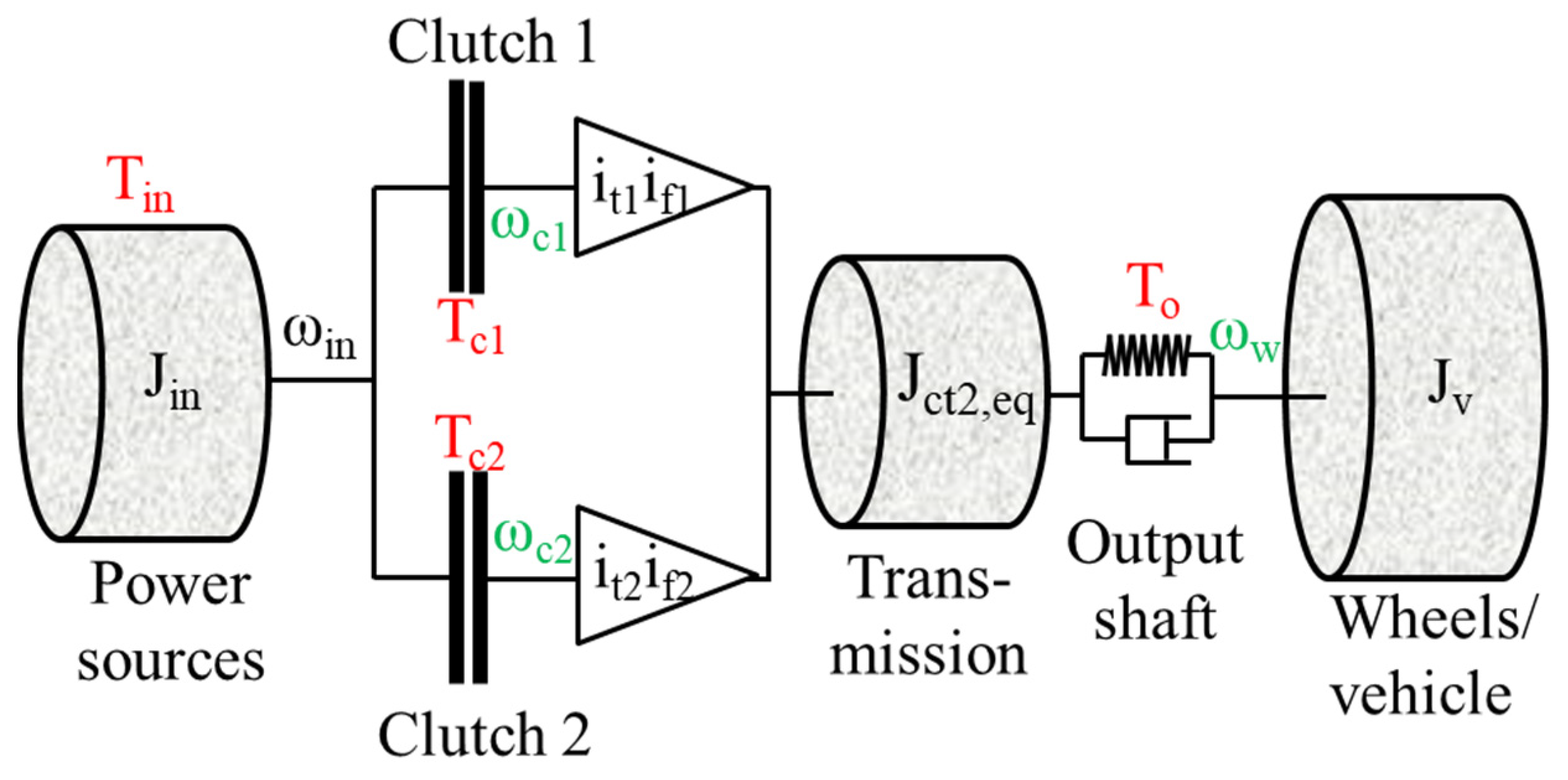
2.2.1. Driveline Model
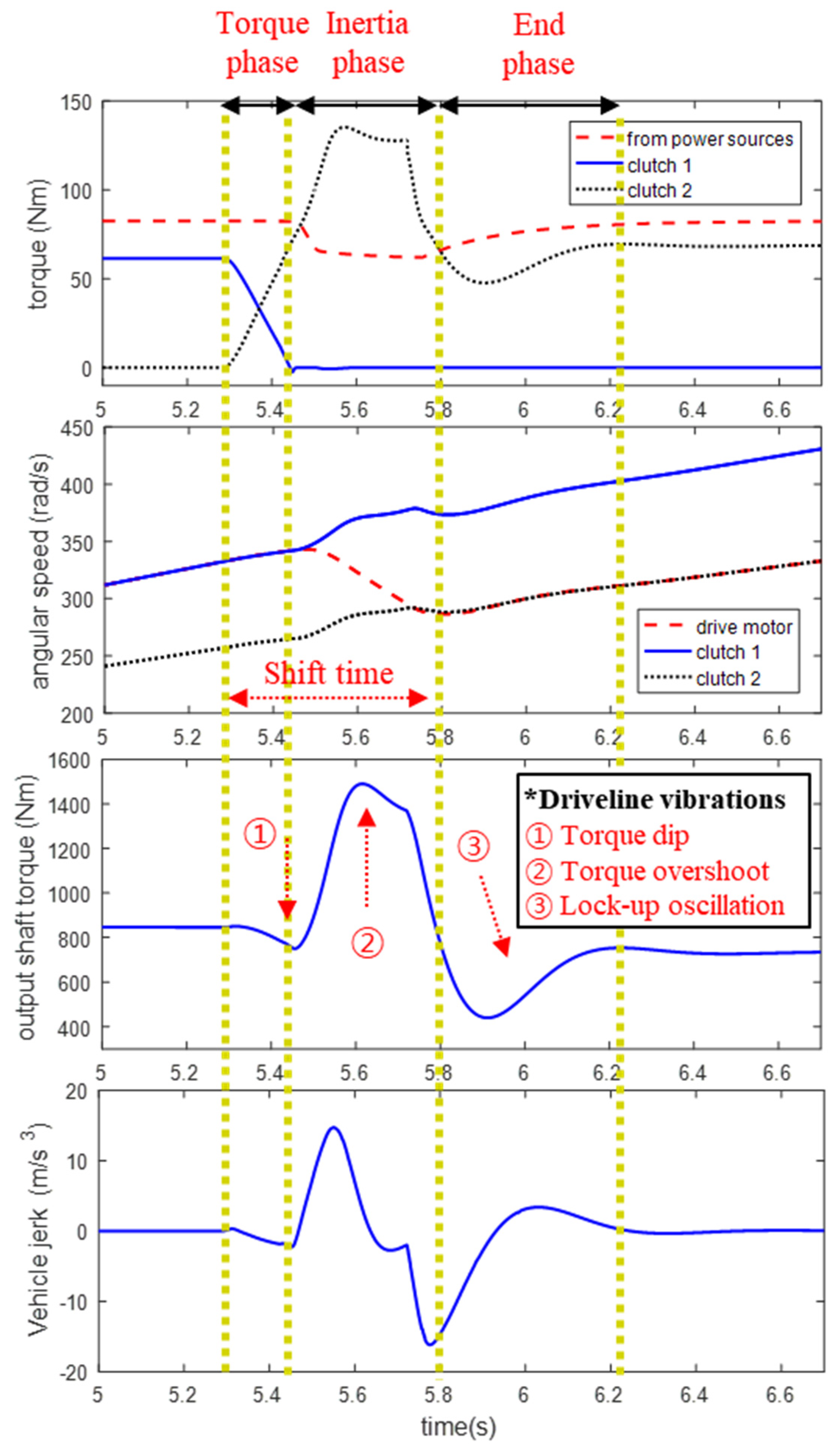
2.2.2. Investigation of Driveline Vibrations
2.3. Experimental Analysis
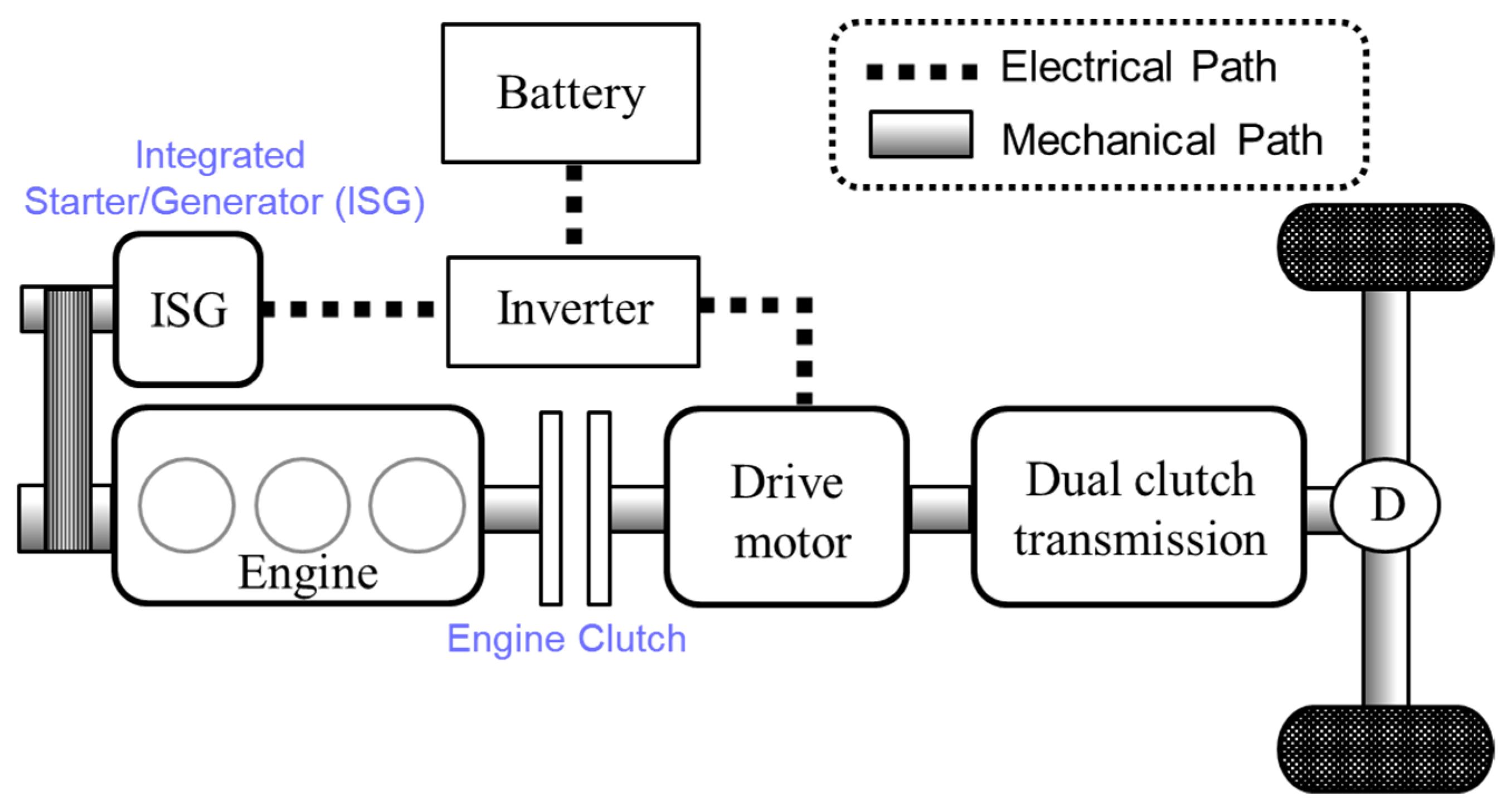
2.3.1. Experimental Setup
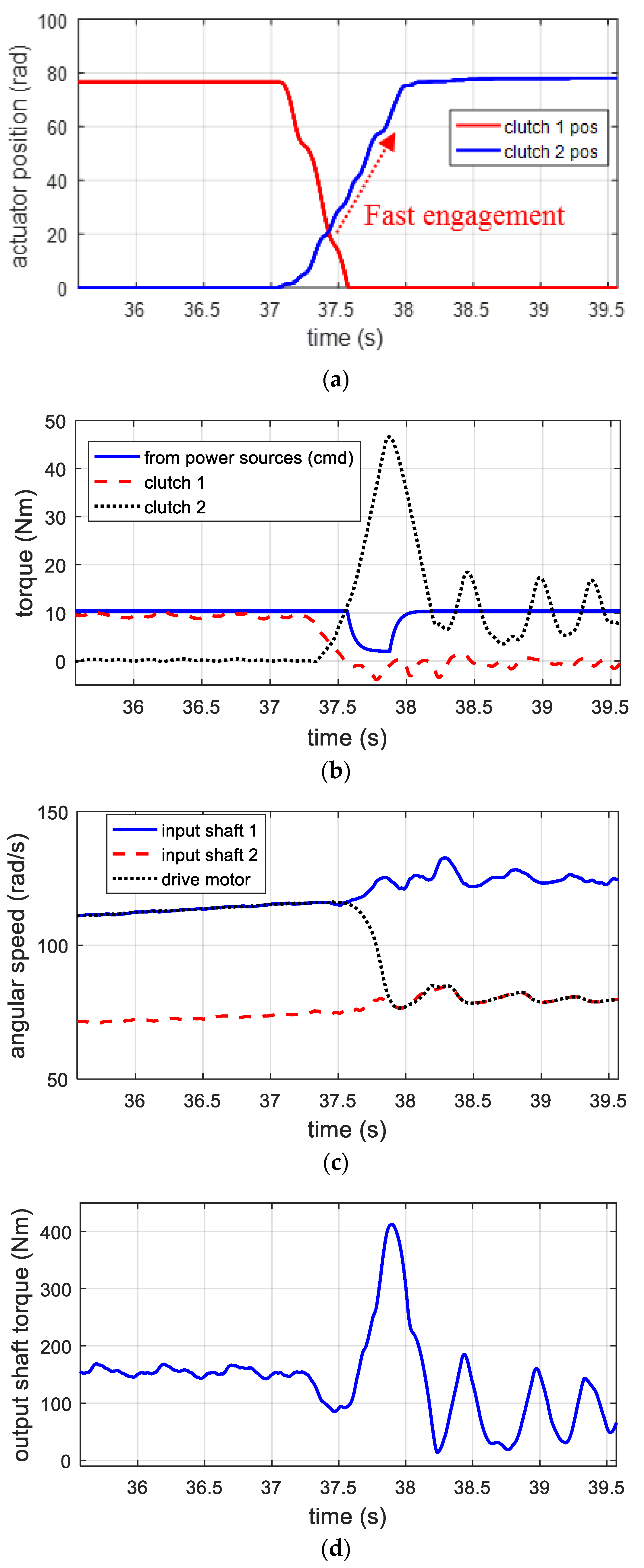
2.3.2. Experiments: Open-Loop Control
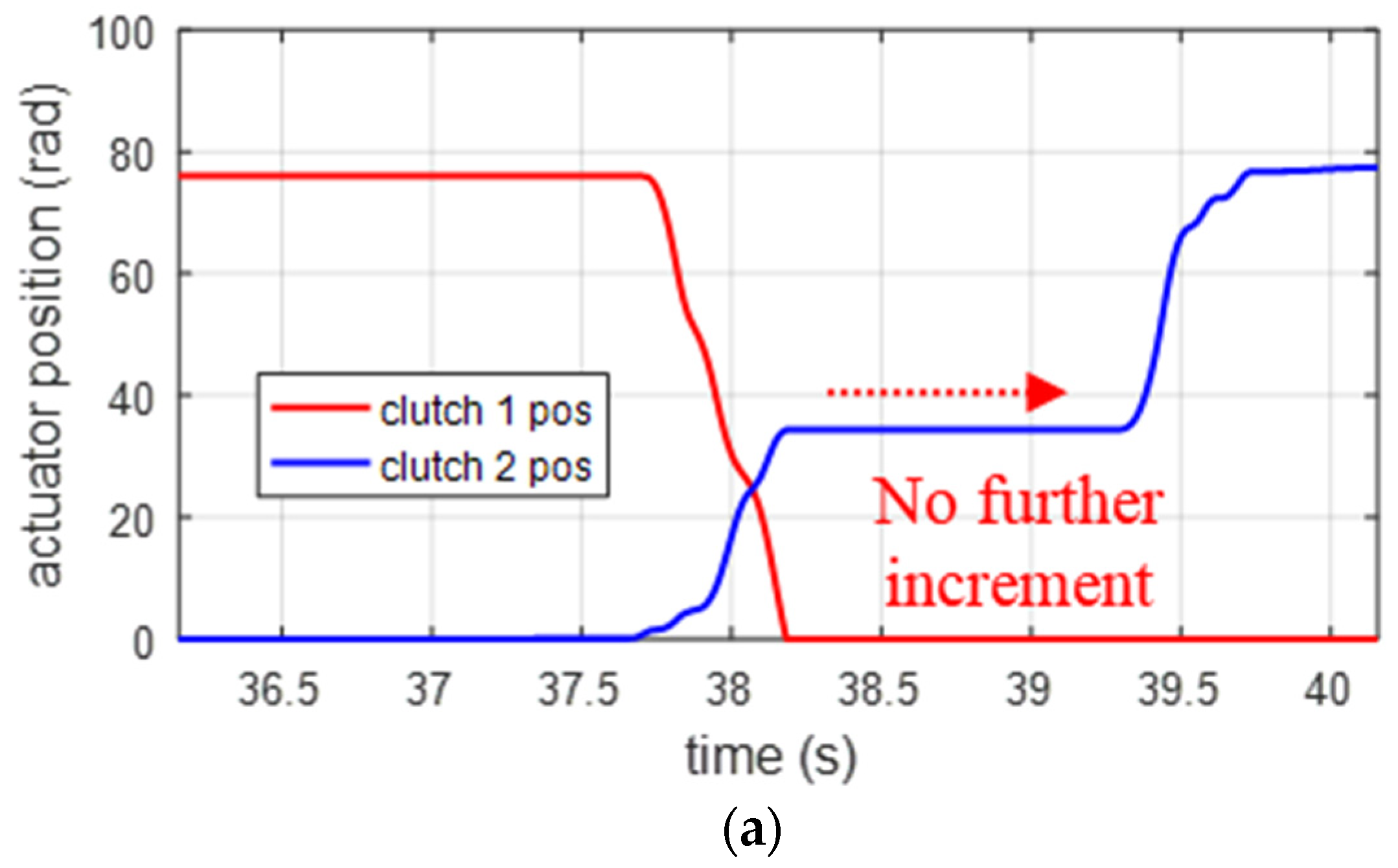
2.4. Improving Tradeoff between Shift Time and Smoothness
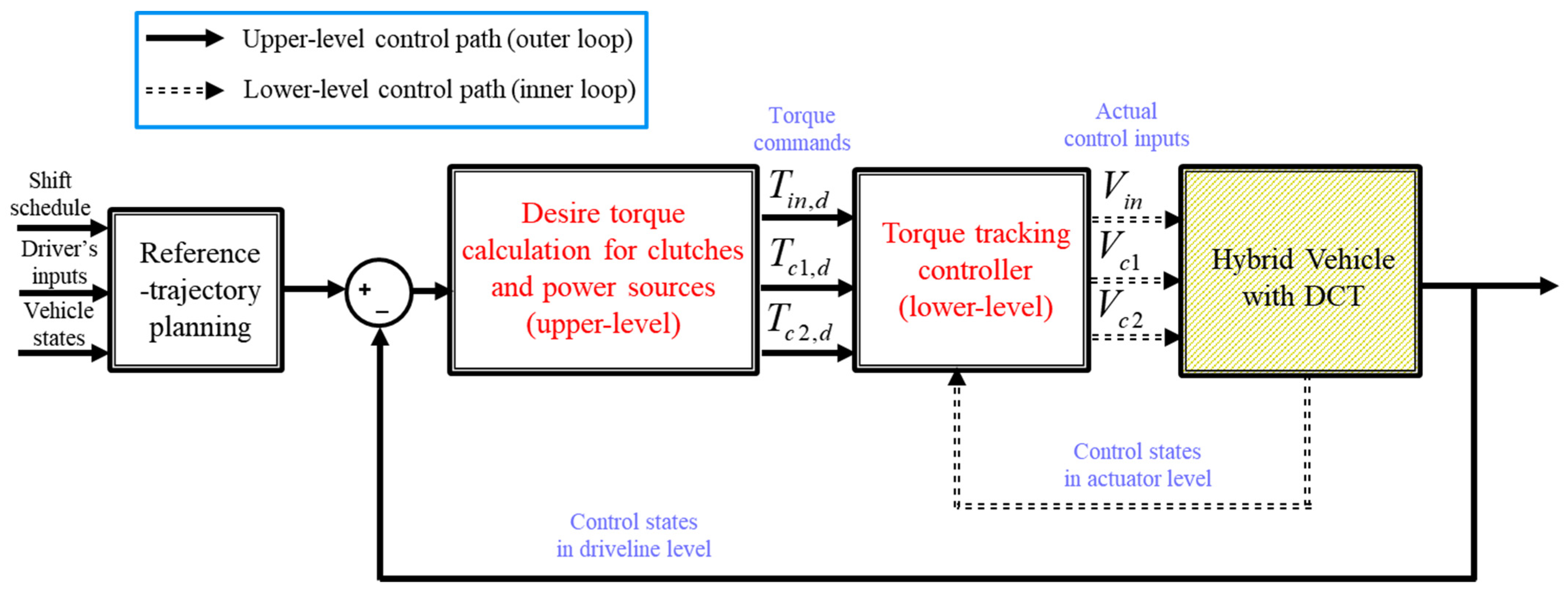
3. Shift Control Strategy for Driveline Vibration Minimization
- The ISG is inactive during gear shifts, implying that .
- To prevent excessive torsional distortion in the driveline, the reduction in torque from the power sources is constrained by the inequality: .
- The drive motor is solely responsible for adjusting torque during the inertia phase control within the constraints of motor power.
3.1. Control Strategy and Analysis for Inertia Phase
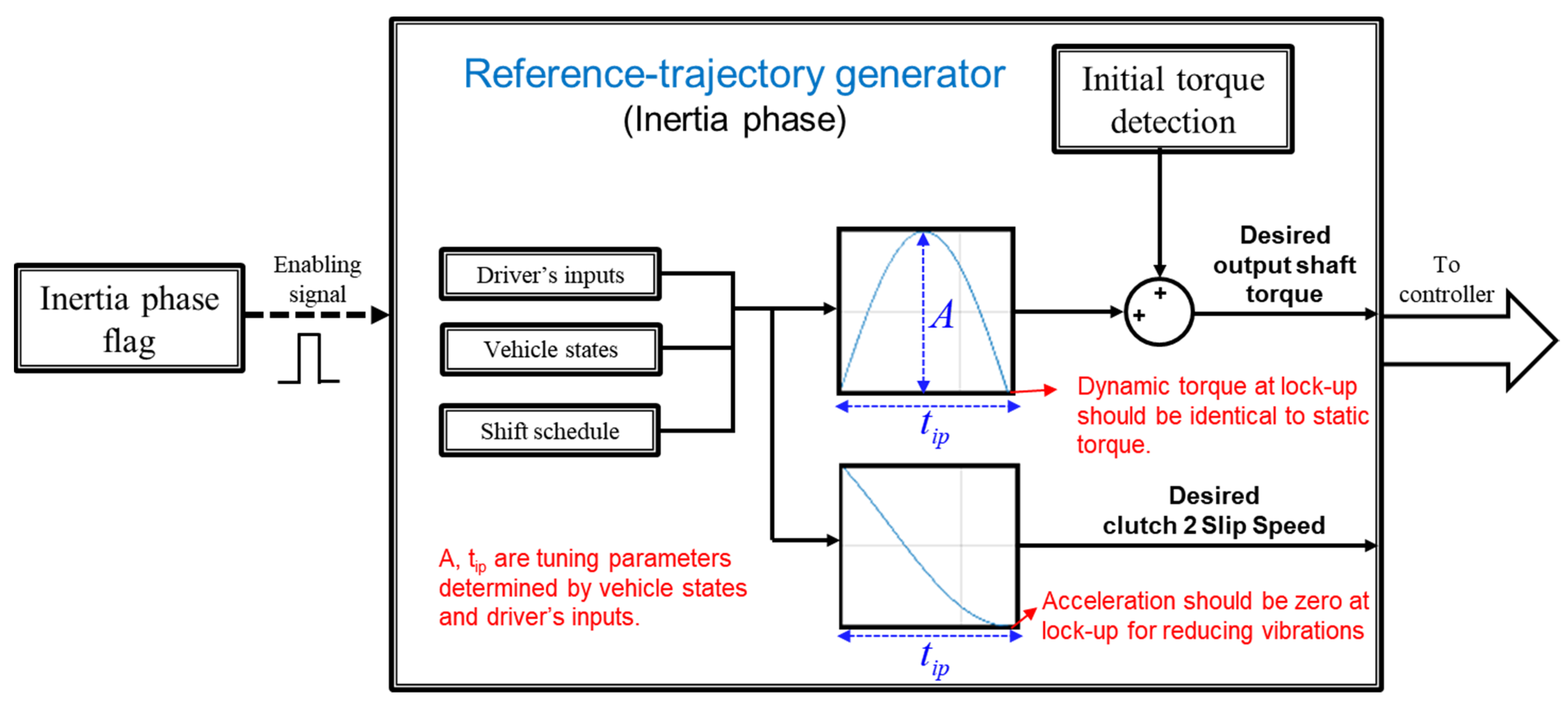
3.1.1. Reference-Trajectory Planning
3.1.2. Reference Tracking Controllers
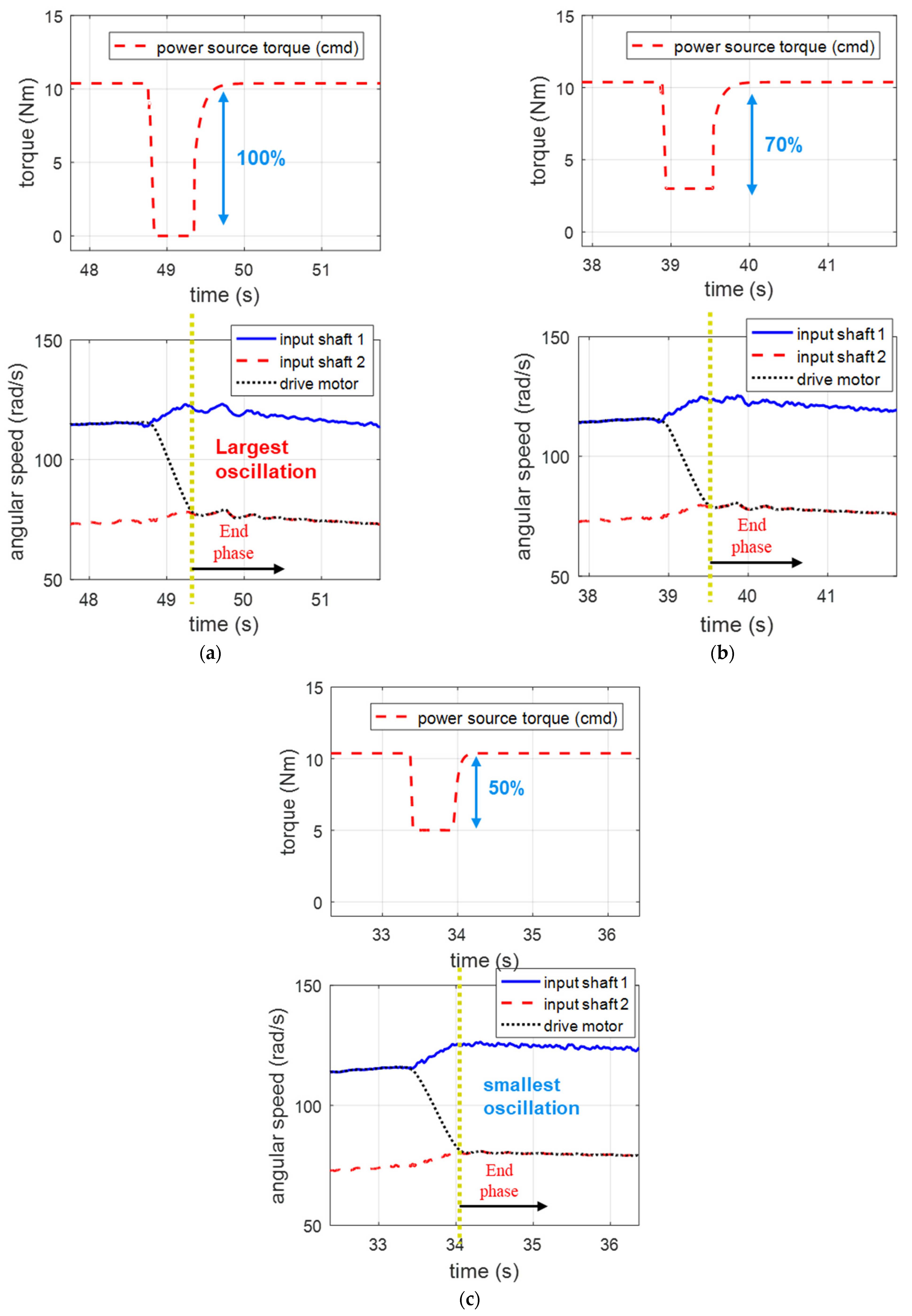
3.1.3. Influences of Inaccurate Power-Source Control
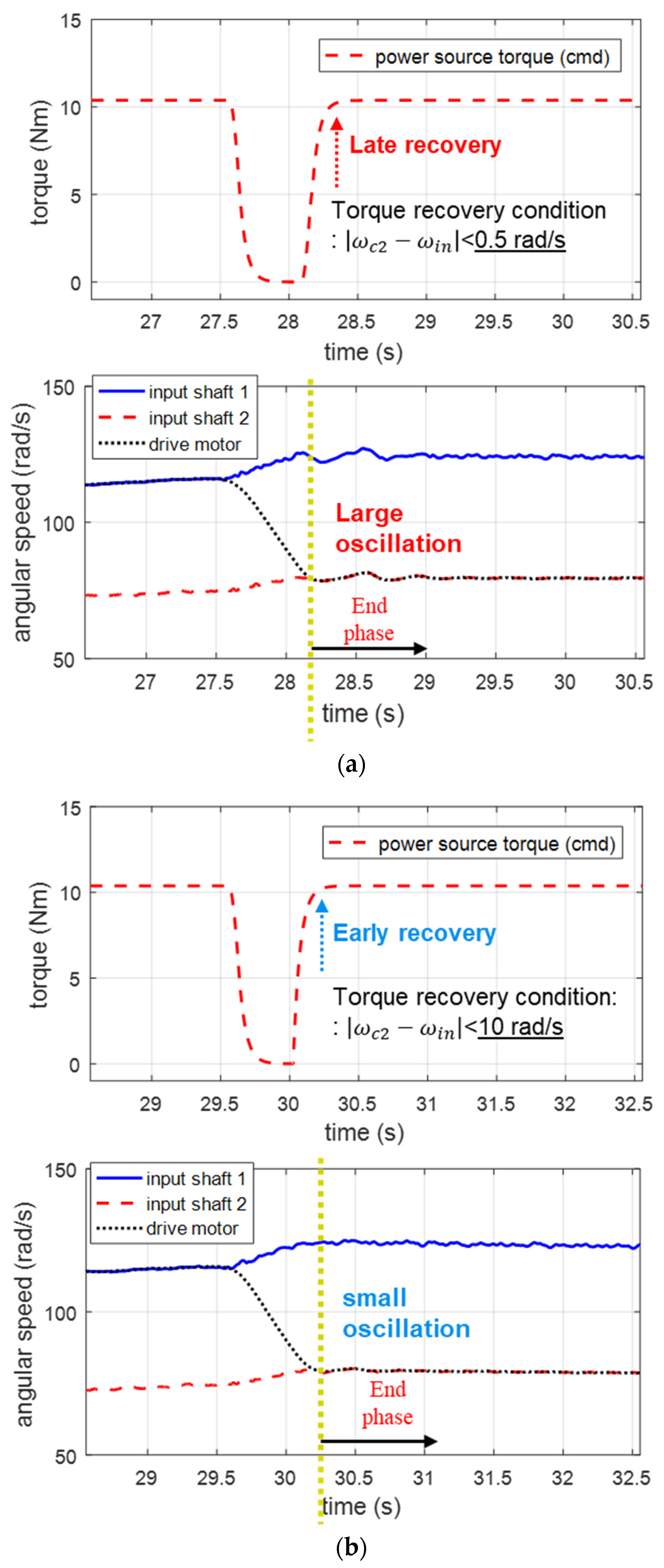
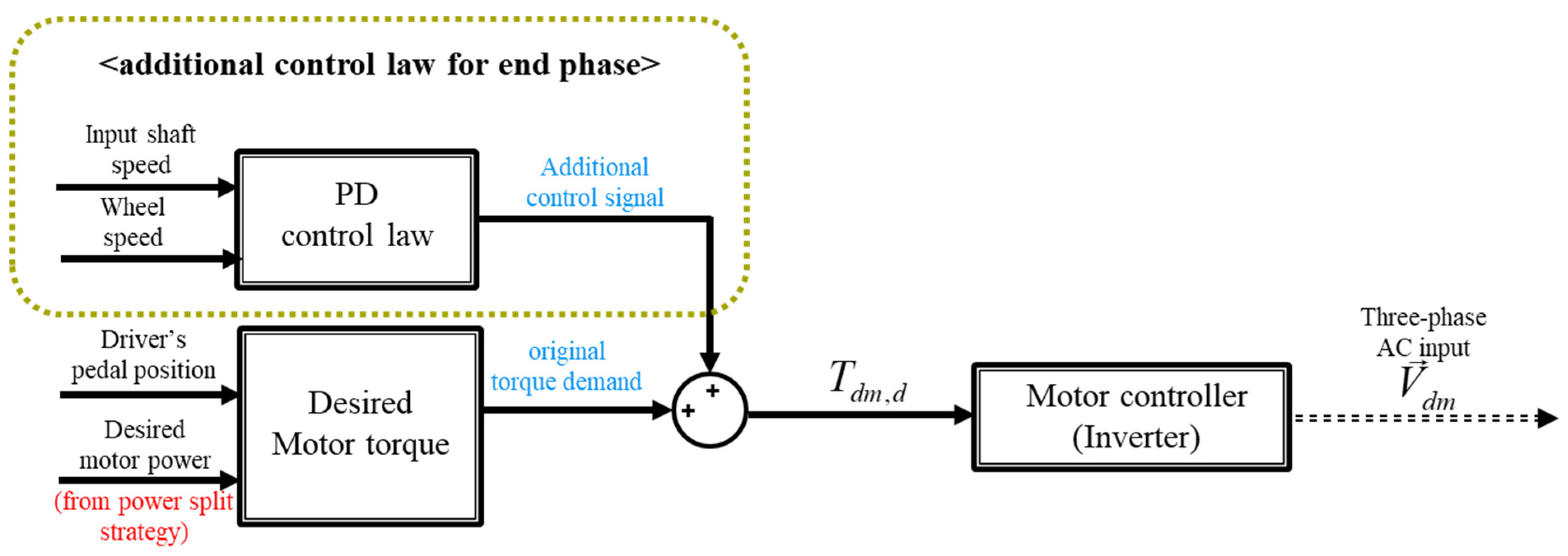
3.2. Additional End-Phase Control
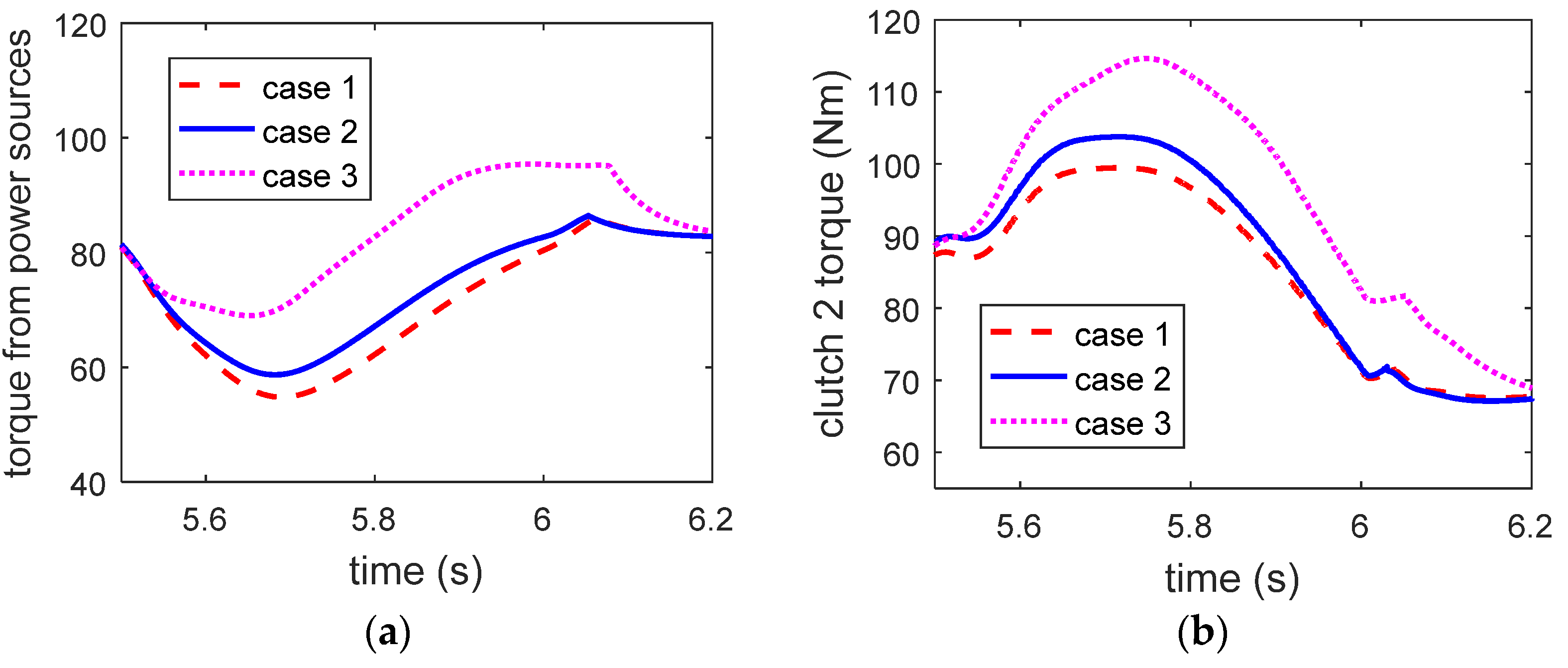
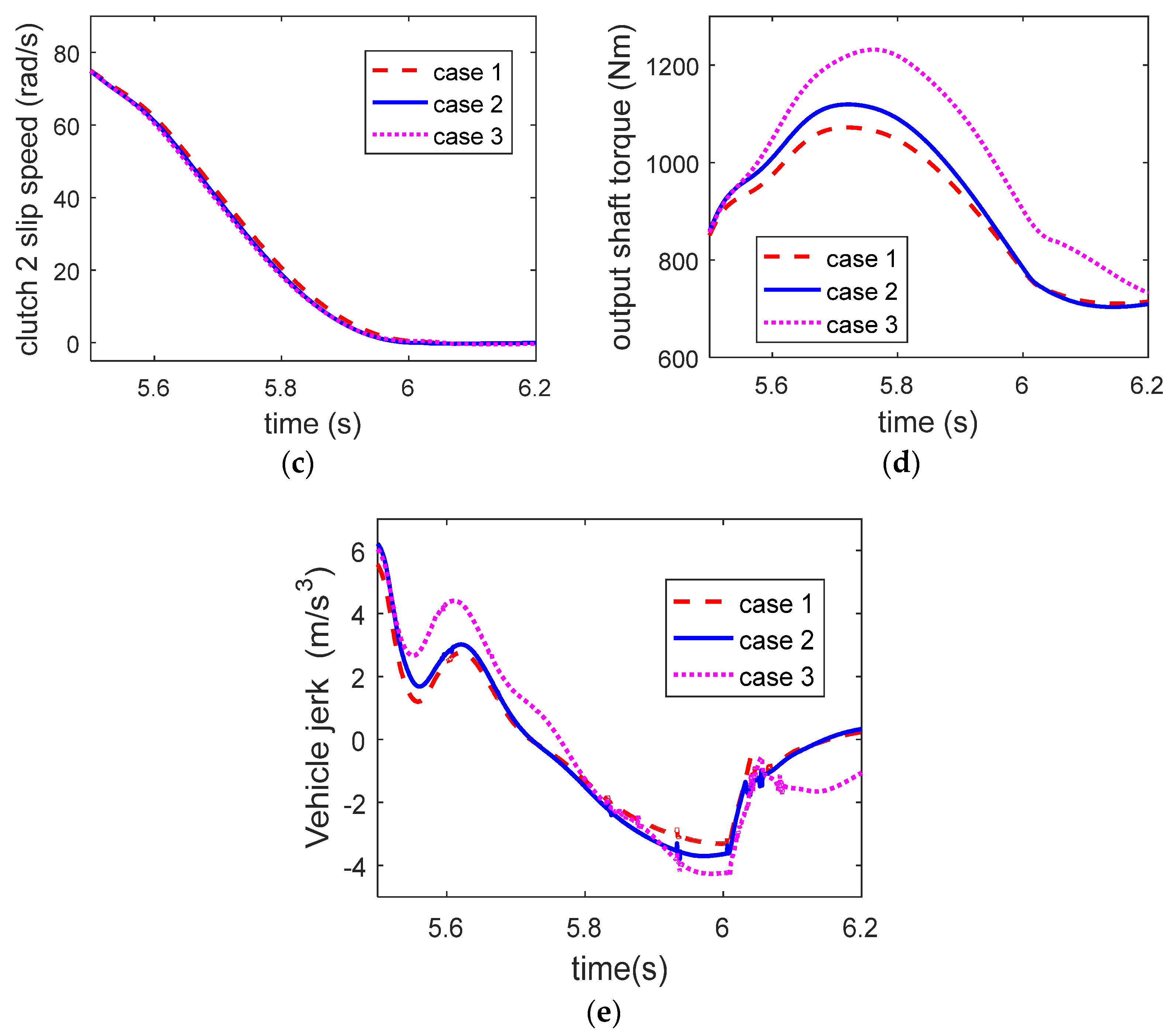
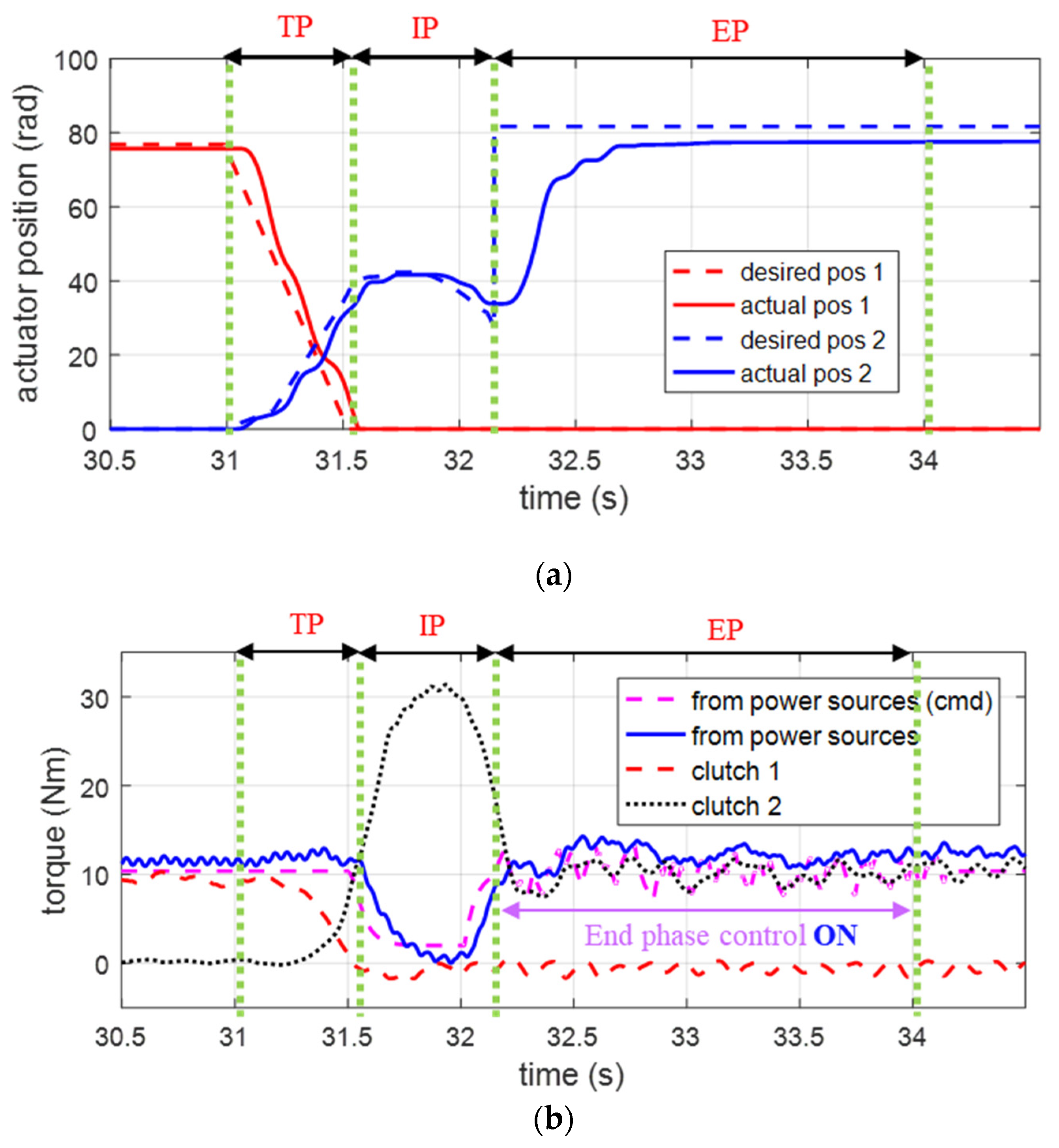
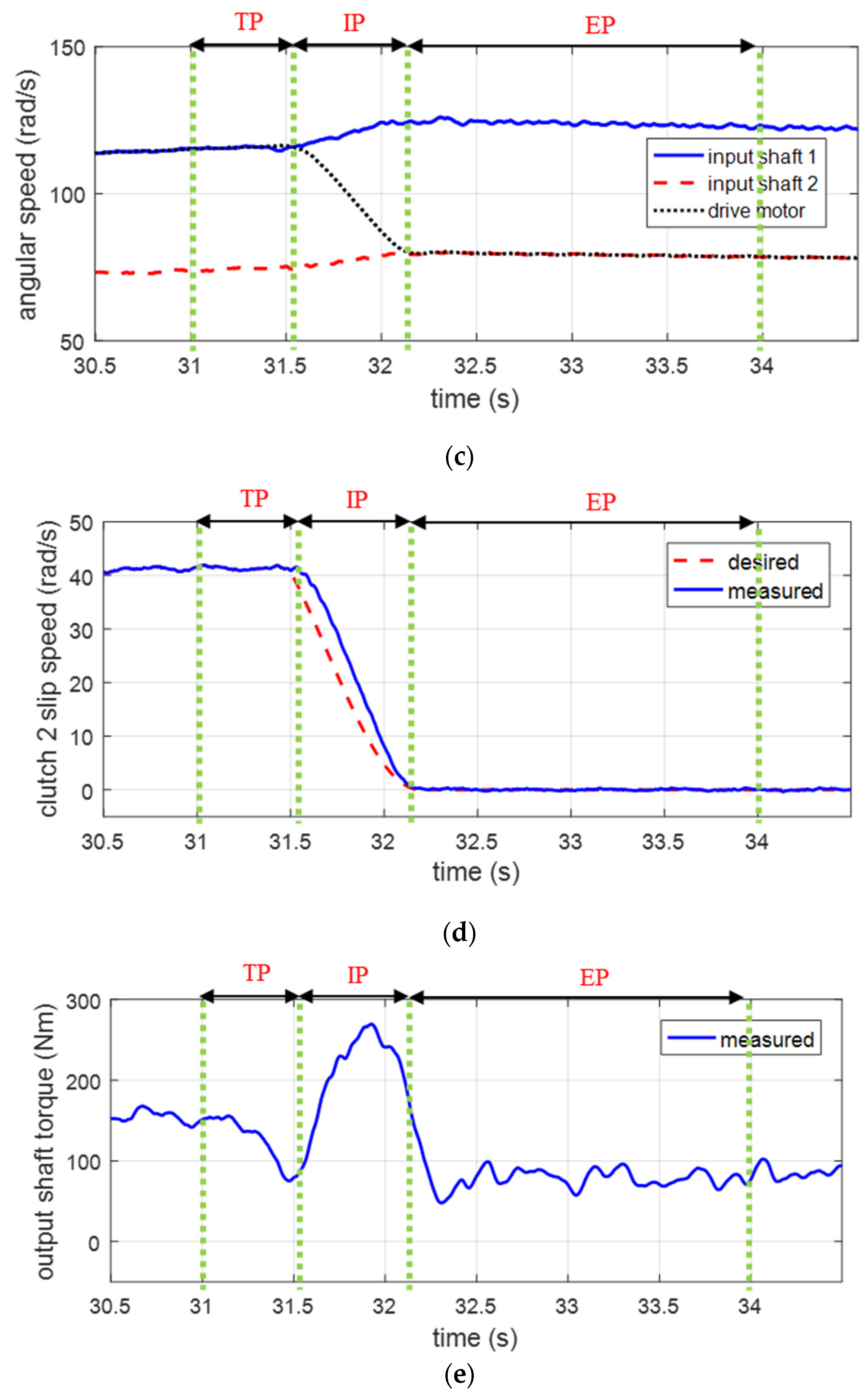
3.3. Experimental Validation
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pisu, P.; Rizzoni, G. A comparative study of supervisory control strategies for hybrid electric vehicles. IEEE Trans. Control Syst. Technol. 2007, 15, 506–518. [Google Scholar] [CrossRef]
- Lin, C.; Peng, H.; Grizzle, J.W.; Kang, J. Power management strategy for a parallel hybrid electric truck. IEEE Trans. Control Syst. Technol. 2003, 11, 839–849. [Google Scholar]
- Zeng, X.; Wang, J. Optimizing the energy management strategy for plug-in hybrid electric vehicles with multiple frequent routes. IEEE Trans. Control Syst. Technol. 2017, 27, 394–400. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Zhang, X.; Tobler, W.; Jiang, H. Dynamic modeling of a dual-clutch automated lay-shaft transmission. J. Mech. Des. 2005, 127, 302–307. [Google Scholar] [CrossRef]
- Walker, P.D.; Zhang, N. Active damping of transient vibration in dual clutch transmission equipped powertrains: A comparison of conventional and hybrid electric vehicles. Mech. Mach. Theory 2014, 77, 1–12. [Google Scholar] [CrossRef]
- Walker, P.; Zhu, B.; Zhang, N. Powertrain dynamics and control of a two speed dual clutch transmission for electric vehicles. Mech. Syst. Signal Process. 2017, 85, 1–15. [Google Scholar] [CrossRef]
- Kim, S.; Choi, S.B. Cooperative control of drive motor and clutch for gear shift of hybrid electric vehicles with dual-clutch transmission. IEEE/ASME Trans. Mechatron. 2020, 25, 1578–1588. [Google Scholar] [CrossRef]
- Galvagno, E.; Velardocchia, M.; Vigliani, A. Dynamic and kinematic model of a dual clutch transmission. Mech. Mach. Theory 2011, 46, 794–805. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, D.; Jiang, H.; Zhang, Y. Shift control strategy and experimental validation for dry dual clutch transmissions. Mech. Mach. Theory 2014, 75, 41–53. [Google Scholar] [CrossRef]
- Van Berkel, K.; Hofman, T.; Serrarens, A.; Steinbuch, M. Fast and smooth clutch engagement control for dual-clutch transmissions. Control Eng. Pract. 2014, 22, 57–68. [Google Scholar] [CrossRef]
- Gao, B.; Chen, H.; Li, J.; Tian, L.; Sanada, K. Observer-based feedback control during torque phase of clutch-to-clutch shift process. Int. J. Veh. Des. 2012, 58, 93–108. [Google Scholar] [CrossRef]
- Kim, D.; Peng, H.; Bai, S.; Maguire, J.M. Control of integrated powertrain with electronic throttle and automatic transmission. IEEE Trans. Control Syst. Technol. 2007, 15, 474–482. [Google Scholar] [CrossRef]
- Pettersson, M.; Nielsen, L. Gear shifting by engine control. IEEE Trans. Control Syst. Technol. 2000, 8, 495–507. [Google Scholar] [CrossRef]
- Goetz, M.; Levesley, M.C.; Crolla, D.A. Dynamics and control of gearshifts on twin-clutch transmissions. Proc. Inst. Mech. Eng. Pt. D J. Automob. Eng. 2005, 219, 951–963. [Google Scholar] [CrossRef]
- Walker, P.D.; Zhang, N.; Tamba, R. Control of gear shifts in dual clutch transmission powertrains. Mech. Syst. Signal Process. 2011, 25, 1923–1936. [Google Scholar] [CrossRef]
- Li, M.; Khonsari, M.; Yang, R. Dynamics analysis of torsional vibration induced by clutch and gear set in automatic transmission. Int. J. Automot. Technol. 2018, 19, 473–488. [Google Scholar] [CrossRef]
- Qu, J.; Shi, W.; Wang, J.; Chen, Z. Modeling and analysis of clutch nonlinear behavior in an automotive driveline for suppressing torsional vibration. Machines 2022, 10, 819. [Google Scholar] [CrossRef]
- Guo, D.; Ning, Q.; Ge, S.; Zhou, Y.; Luo, R. Dynamic analysis of gear rattling of a certain type of dual-clutch transmission. Machines 2022, 10, 805. [Google Scholar] [CrossRef]
- Brancati, R.; Pagano, S.; Rocca, E. Dynamic behaviour of an automotive dual clutch transmission during gear shift maneuvers. Appl. Sci. 2023, 13, 4828. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, D.; Jiang, H.; Zhang, Y. A systematic model for dynamics and control of dual clutch transmissions. J. Mech. Des. 2009, 131, 061012. [Google Scholar] [CrossRef]
- Kim, S.; Choi, S. Control-oriented modeling and torque estimations for vehicle driveline with dual-clutch transmission. Mech. Mach. Theory 2018, 121, 633–649. [Google Scholar] [CrossRef]
- Oh, J.; Choi, S.B.; Chang, Y.J.; Eo, J.S. Engine clutch torque estimation for parallel-type hybrid electric vehicles. Int. J. Automot. Technol. 2017, 18, 125–135. [Google Scholar] [CrossRef]
- Crowther, A.; Zhang, N.; Liu, D.K.; Jeyakumaran, J.K. Analysis and simulation of clutch engagement judder and stick-slip in automotive powertrain systems. Proc. Inst. Mech. Eng. Pt. D J. Automob. Eng. 2004, 218, 1427–1446. [Google Scholar] [CrossRef]
- Kim, S.; Oh, J.; Choi, S. Gear shift control of a dual-clutch transmission using optimal control allocation. Mech. Mach. Theory 2017, 113, 109–125. [Google Scholar] [CrossRef]
- Li, G.; Görges, D. Optimal control of the gear shifting process for shift smoothness in dual-clutch transmissions. Mech. Syst. Signal Process. 2018, 103, 23–38. [Google Scholar] [CrossRef]
- Flash, T.; Hogan, N. The coordination of arm movements: An experimentally confirmed mathematical model. J. Neurosci. 1985, 5, 1688–1703. [Google Scholar] [CrossRef]
- Garofalo, F.; Glielmo, L.; Iannelli, L.; Vasca, F. Smooth Engagement for Automotive Dry Clutch. In Proceedings of the 40th IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 529–534. [Google Scholar]
- McFarlane, D.; Glover, K. A loop-shaping design procedure using H/sub infinity/synthesis. IEEE Trans. Automat. Contr. 1992, 37, 759–769. [Google Scholar] [CrossRef]
- Kim, S.; Oh, J.J.; Choi, S.B. Driveline torque estimations for a ground vehicle with dual-clutch transmission. IEEE Trans. Veh. Technol. 2017, 67, 1977–1989. [Google Scholar] [CrossRef]





| Test-Bench Parameters | |
|---|---|
Units are SI-derived. (kg, N, m, rad, s) | |
| Fast Shift Control (Scenario 1) | Smooth Shift Control (Scenario 2) | |
|---|---|---|
| Shift time (s) | 0.892 | 1.64 |
| Integral of squared jerk | 48.28 | 2.99 |
| Amount of Torque Reduction | Average Inertia-Phase Time (s) | Integral of Squared Jerk |
|---|---|---|
| 100% | 0.60 | 7.65 |
| 70% | 0.67 | 6.24 |
| 50% | 0.74 | 3.40 |
| Torque Recovery Time | Average Inertia-Phase Time (s) | Integral of Squared Jerk |
|---|---|---|
| Late | 0.61 | 6.68 |
| Early | 0.66 | 2.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S. Experimental Investigation and Control of Driveline Torsional Vibrations during Clutch-to-Clutch Shifts of Electrified Vehicles. Machines 2024, 12, 239. https://doi.org/10.3390/machines12040239
Kim S. Experimental Investigation and Control of Driveline Torsional Vibrations during Clutch-to-Clutch Shifts of Electrified Vehicles. Machines. 2024; 12(4):239. https://doi.org/10.3390/machines12040239
Chicago/Turabian StyleKim, Sooyoung. 2024. "Experimental Investigation and Control of Driveline Torsional Vibrations during Clutch-to-Clutch Shifts of Electrified Vehicles" Machines 12, no. 4: 239. https://doi.org/10.3390/machines12040239
APA StyleKim, S. (2024). Experimental Investigation and Control of Driveline Torsional Vibrations during Clutch-to-Clutch Shifts of Electrified Vehicles. Machines, 12(4), 239. https://doi.org/10.3390/machines12040239






