Design and Control Performance Optimization of Variable Structure Hydrostatic Drive Systems for Wheel Loaders
Abstract
1. Introduction
- A new variable-structure hydrostatic drive system is proposed to meet the driving requirements of wheel loaders, and its operating principles, structural layout, and basic control methods are analyzed.
- The mathematical model of the variable-structure hydrostatic drive is established, and the parameter relationships of the system’s main components are analyzed. The theoretical performance of the proposed drive system is analyzed through the establishment of a simulation model of the system.
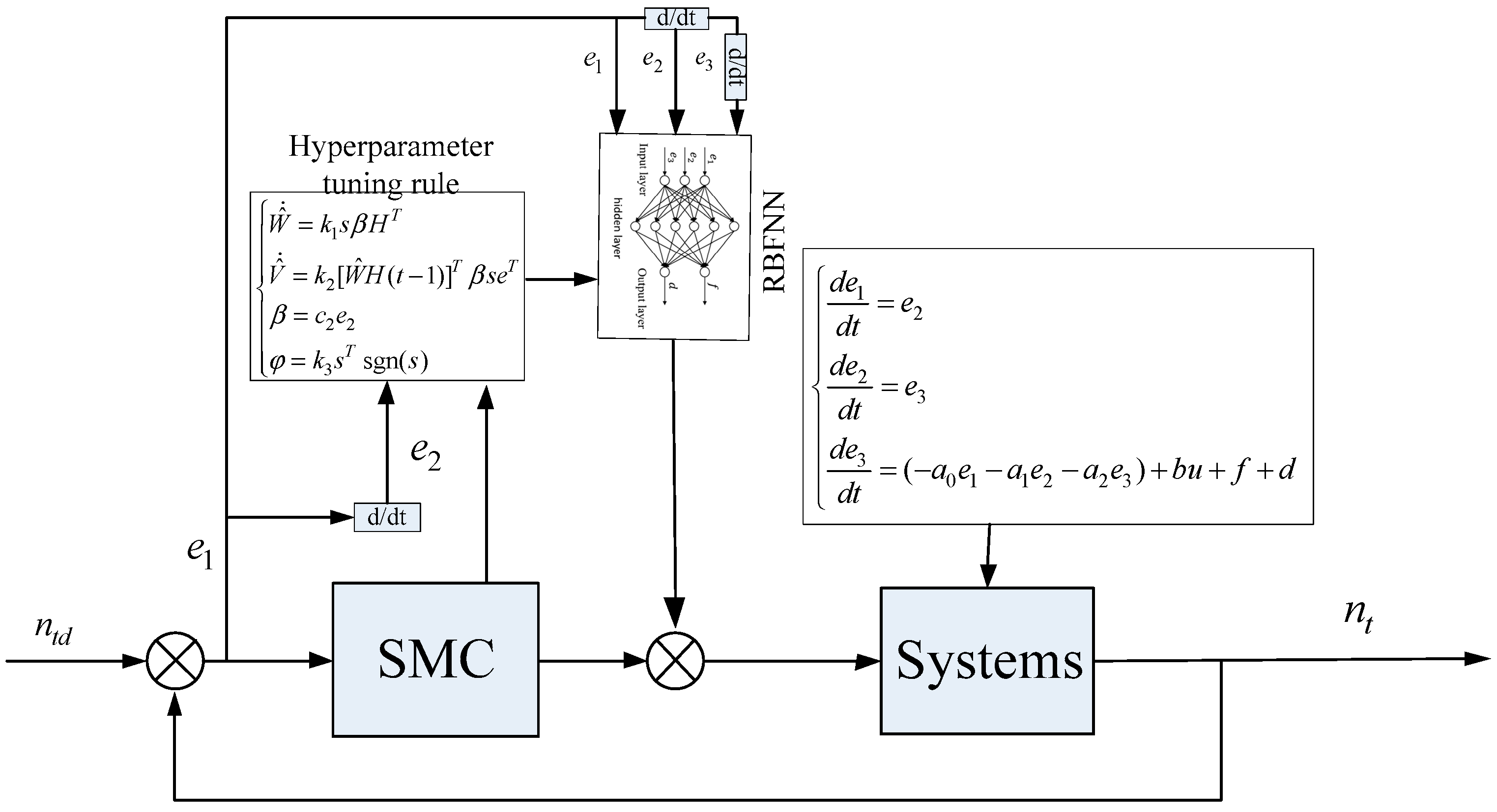
- An HST adaptive SMC strategy based on RBFNN optimization is proposed to address the displacement matching problem during the control process. The adaptive mechanism updates the RBFNN hyperparameters, improving the system’s tracking capability and robustness.
- The variable-structure hydrostatic drive system is successfully applied to actual loader products and put into commercial production.
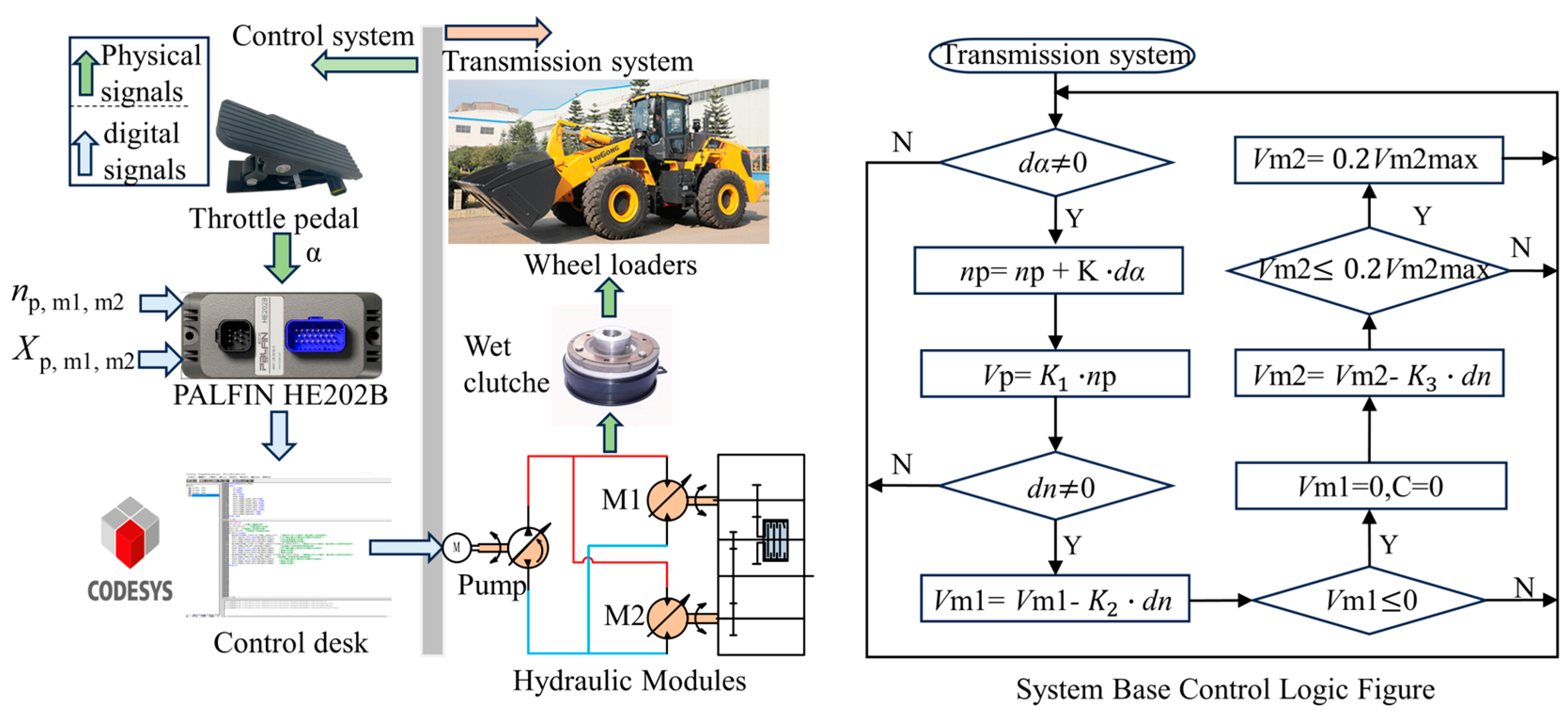
2. Working Principle and Mathematical Model
2.1. Variable Structure Hydrostatic Drive System
2.2. Analysis of Control Principles for Variable Structure Hydrostatic Drive Systems
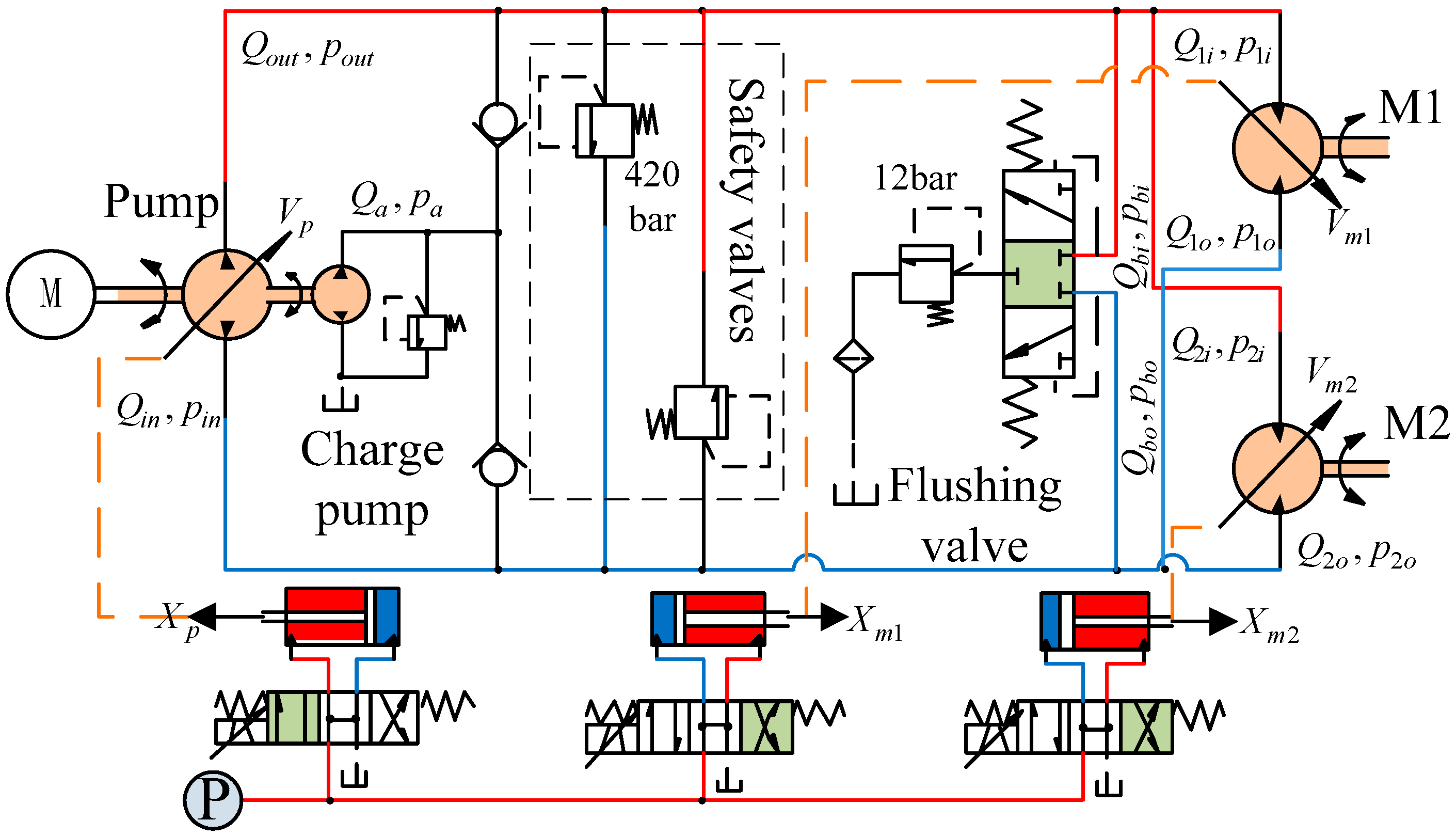
2.3. Analysis of the Variable Structure Hydrostatic Drive System and its Components
2.3.1. Variable Displacement Control Valve Group
2.3.2. Flushing Valve Group
2.3.3. Dual Motor Coordination Relationship
2.3.4. Charge Pump
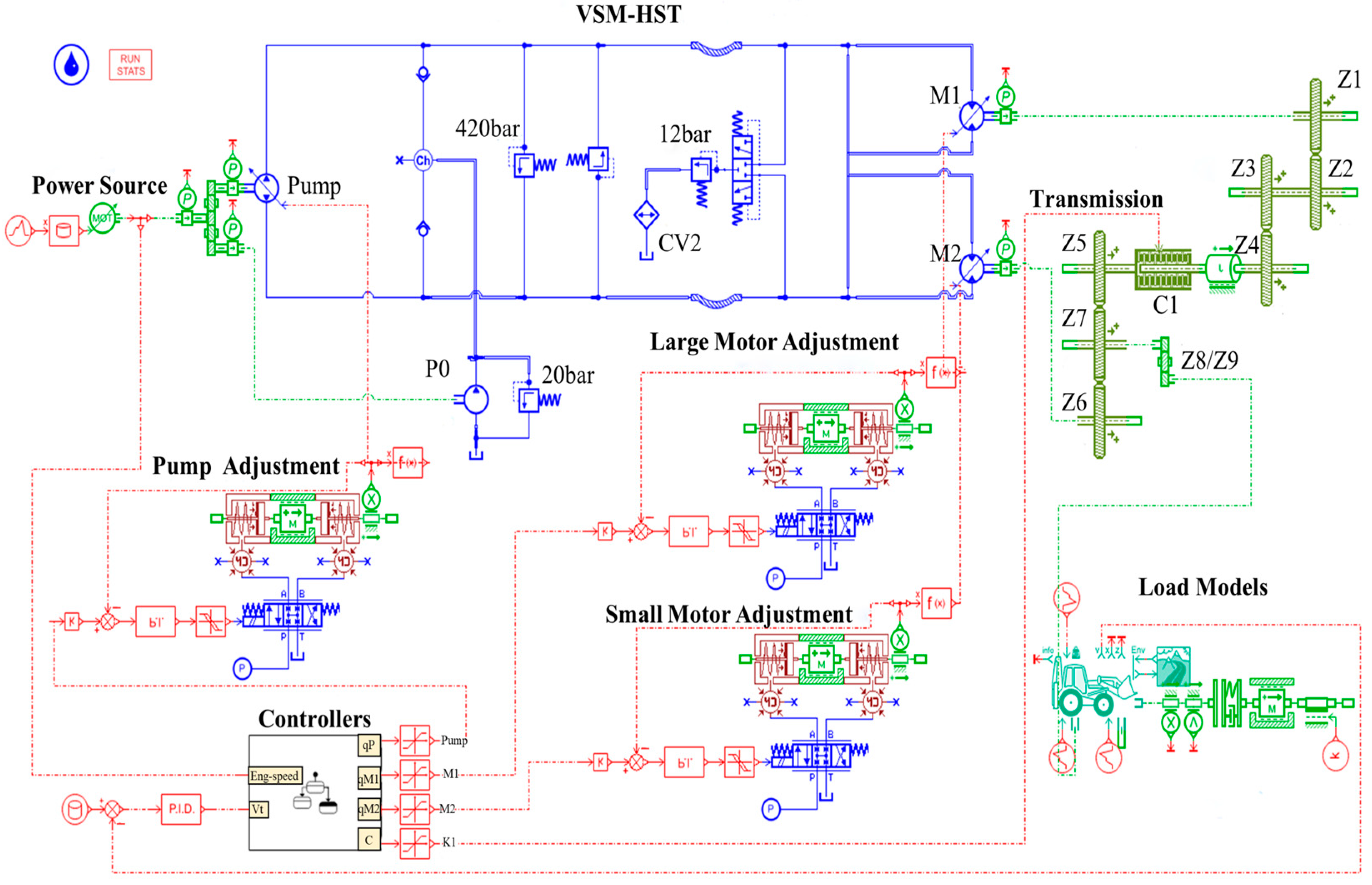
3. Simulation Methods and Control Strategies
3.1. Simulation Method
3.2. Simulation Model Validation
3.3. Displacement Matching Control Strategy
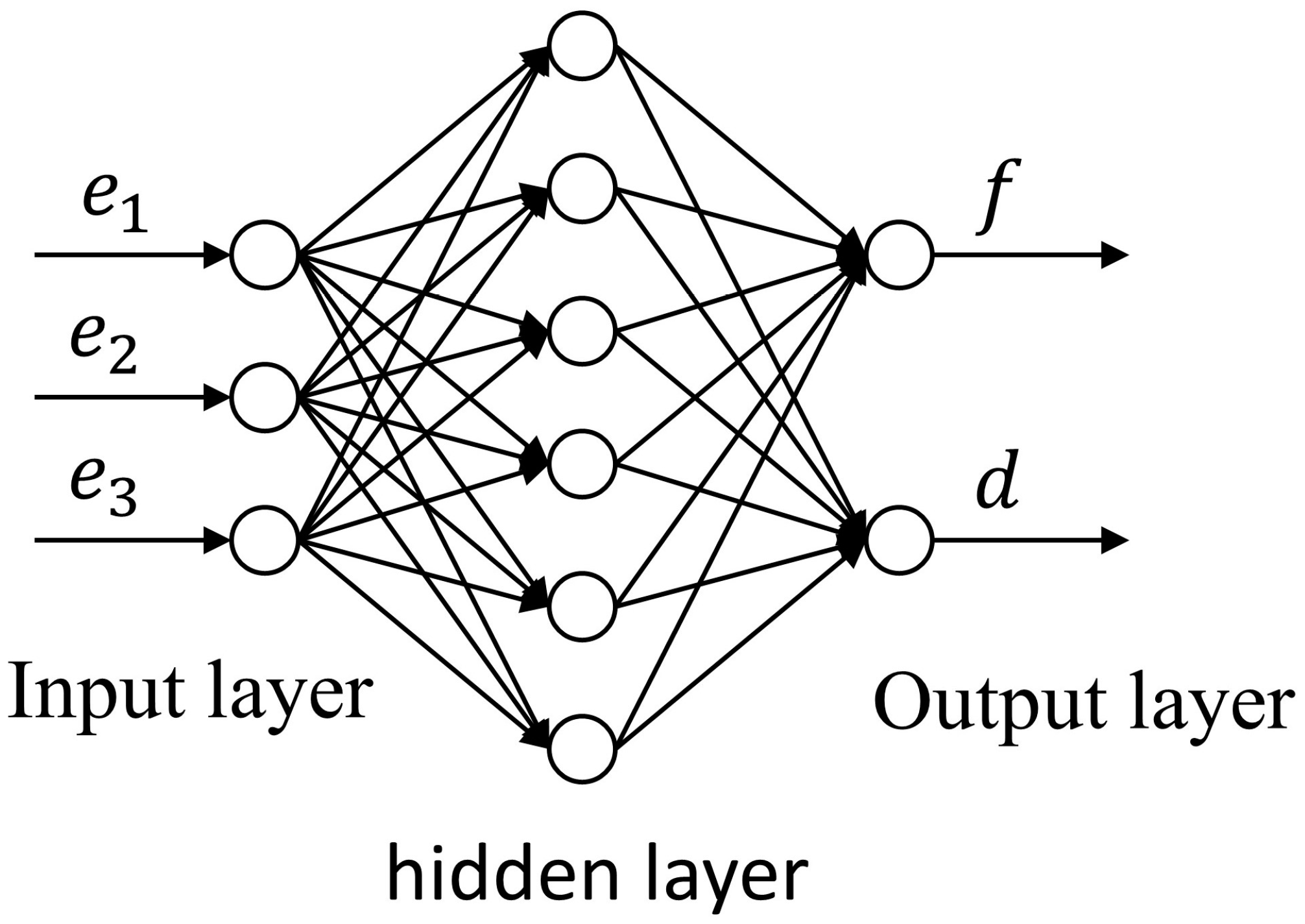
3.3.1. The Design of the RBFNN Algorithm
3.3.2. SMC Algorithm Design
3.3.3. Stability Verification and Adaptive Adjustment
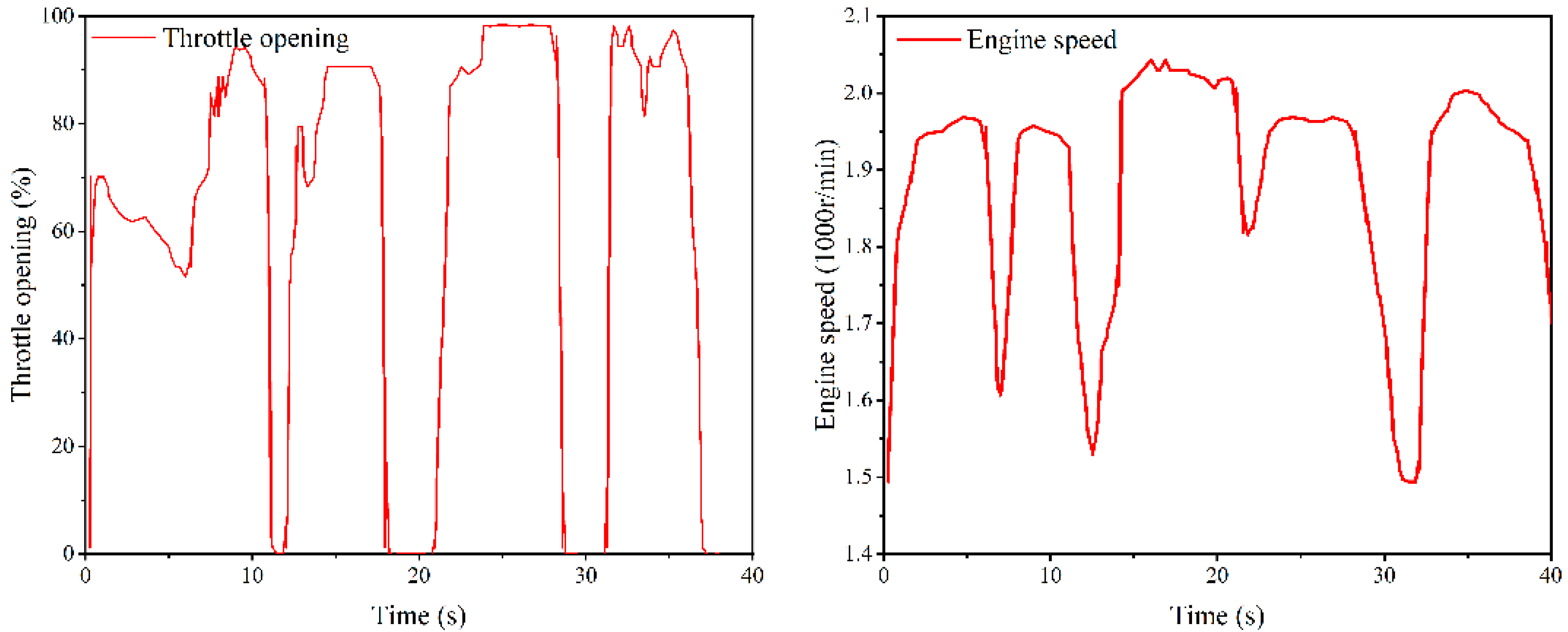
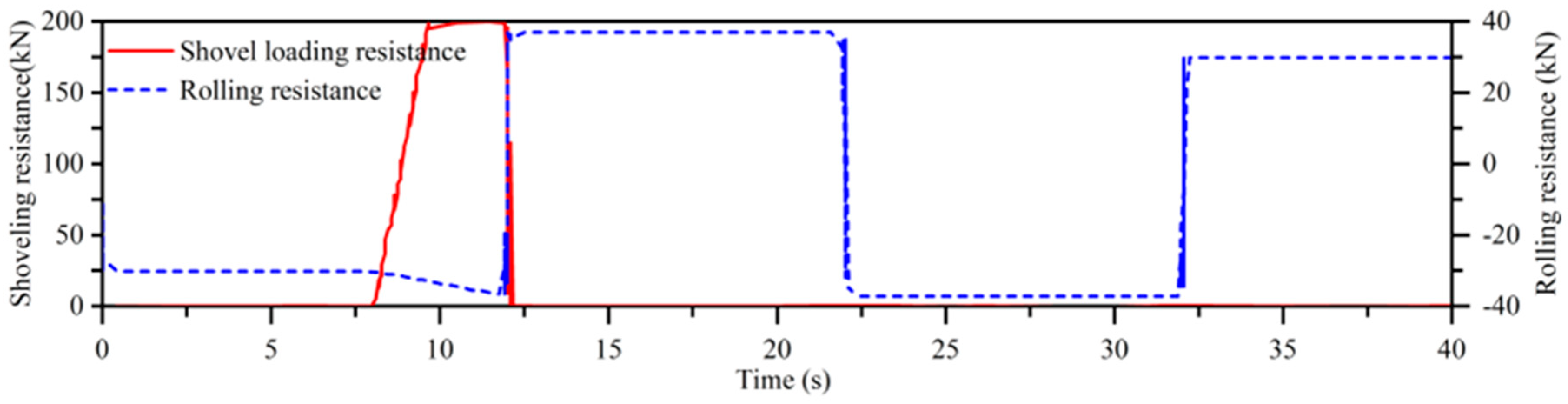
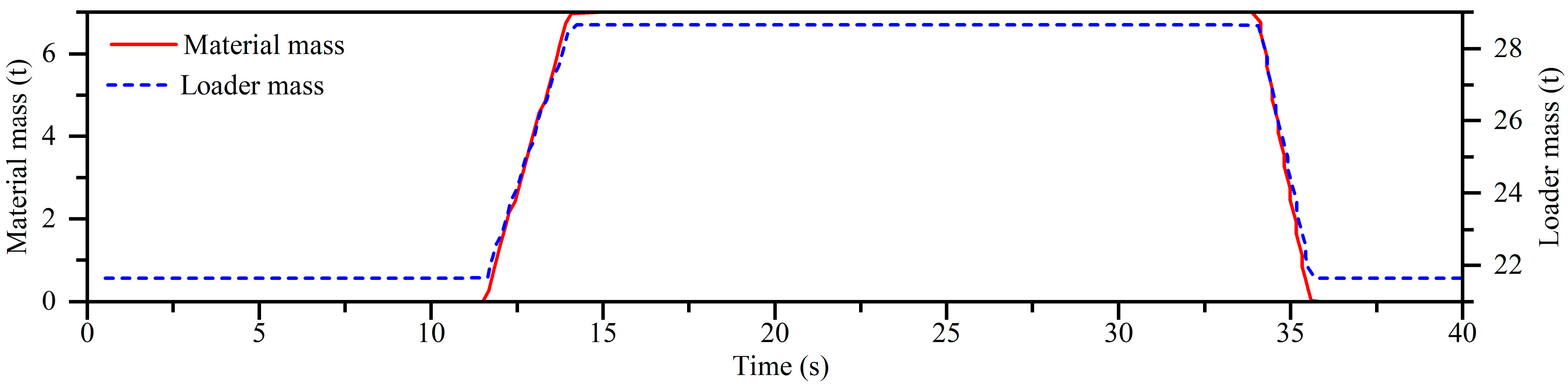
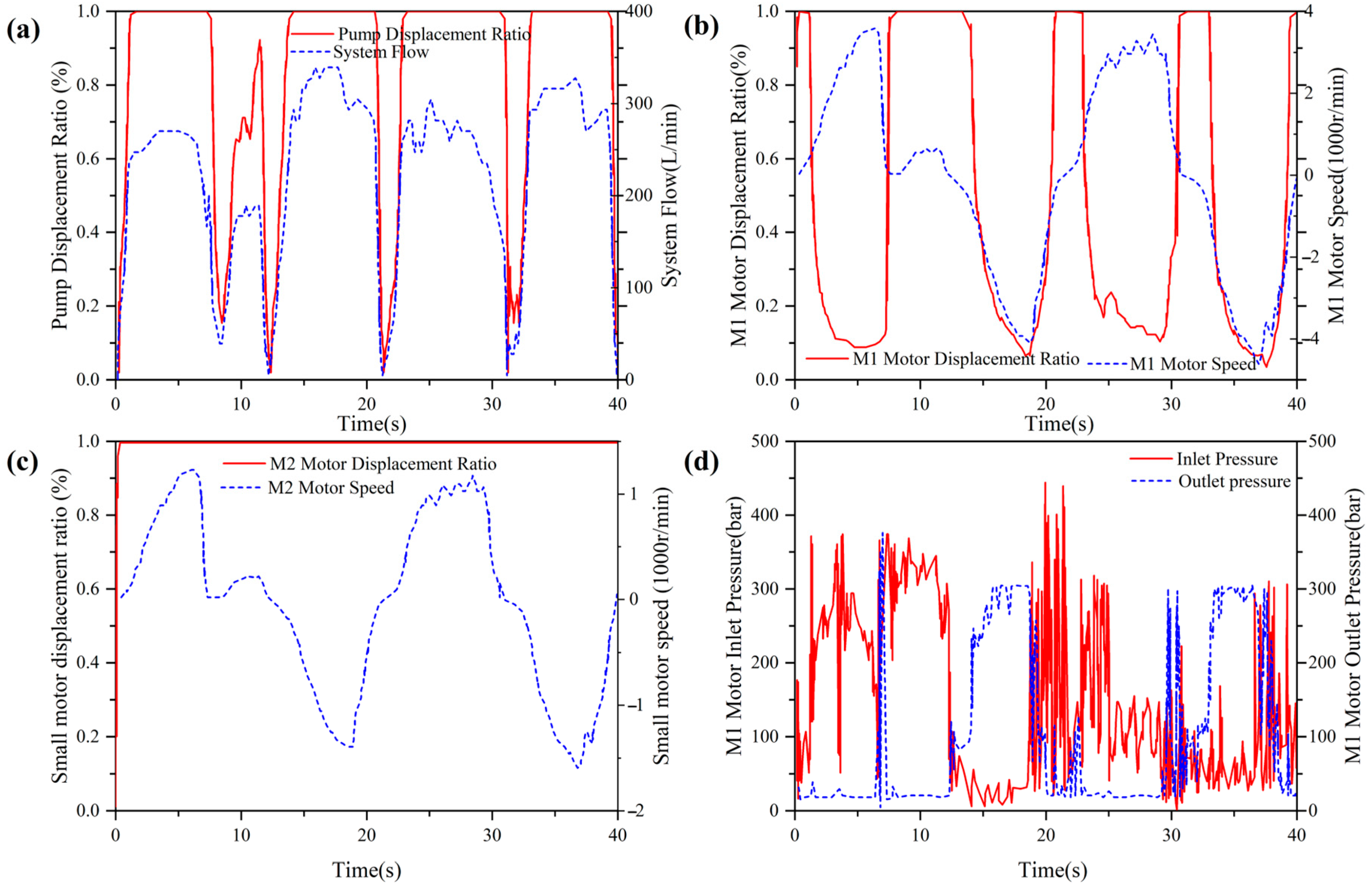
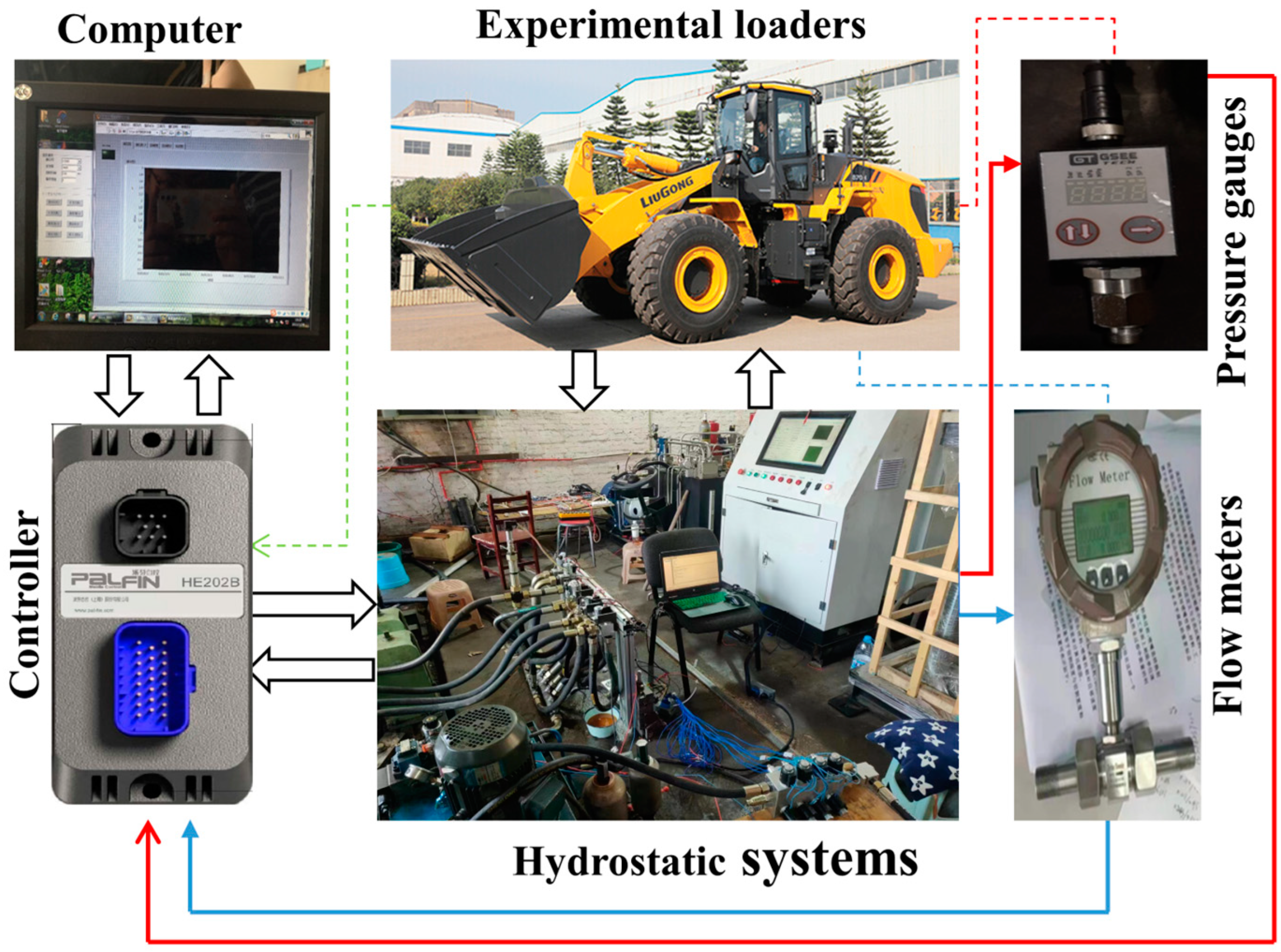
4. Field Experiment
4.1. Test System
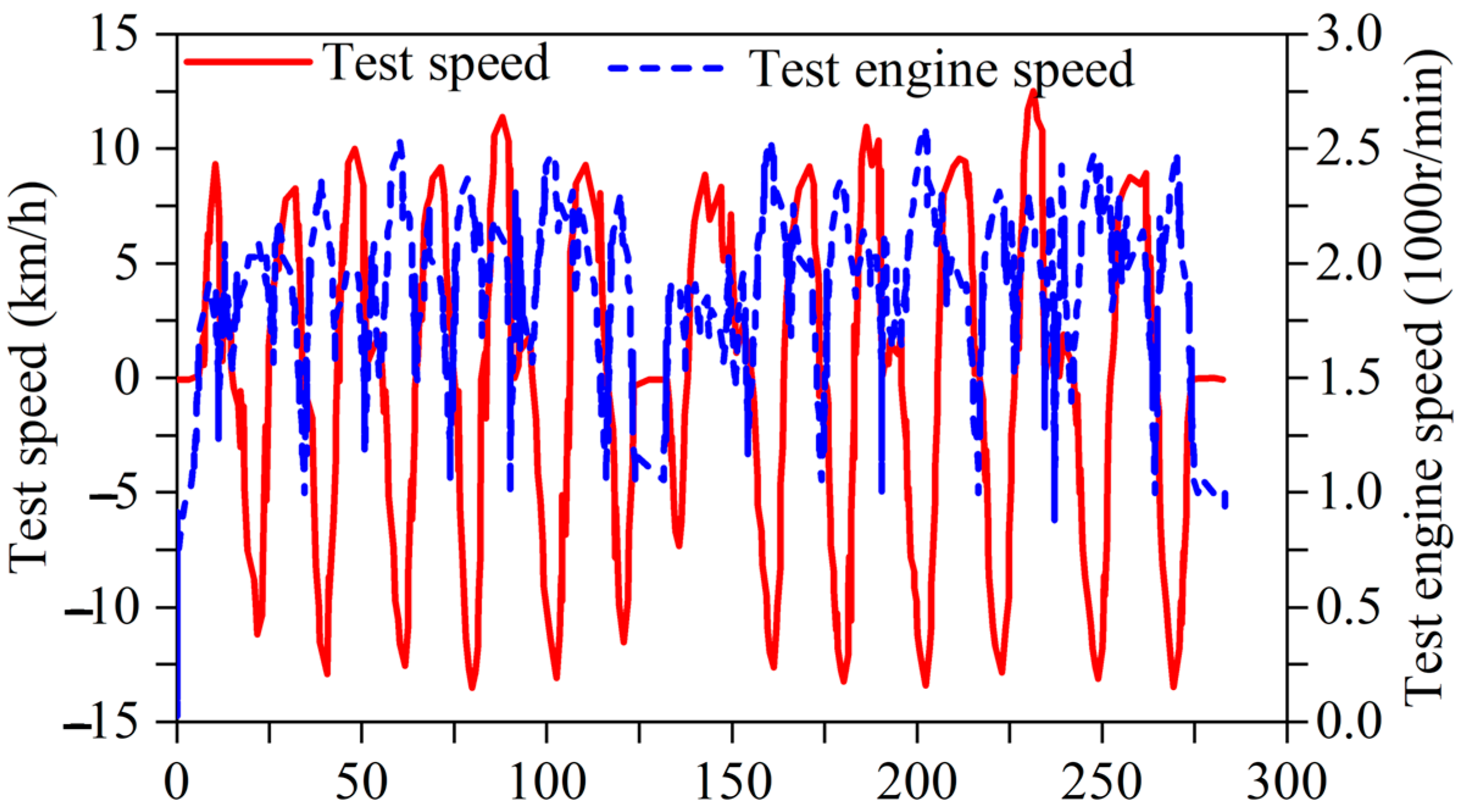
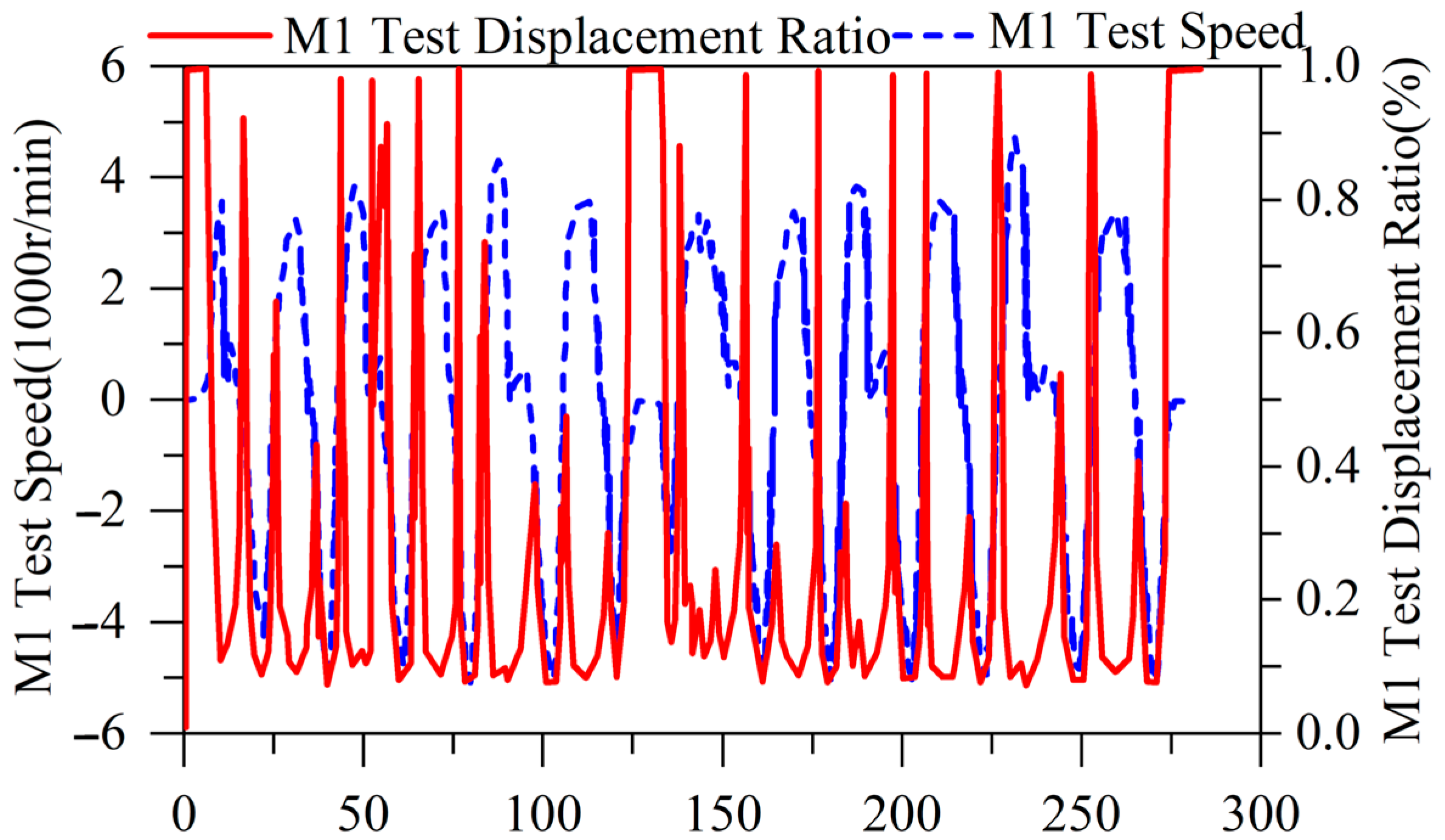
4.2. Experiment Results
5. Conclusions
- Through simulation and field tests, it has been demonstrated that the proposed variable-structure hydrostatic drive system for loaders can meet the driving requirements of loaders in V-type working mode. The speed regulation process is smooth, and speed switching is seamless compared to traditional automatic speed regulation.
- The mathematical model established through principle analysis, structural analysis, and component analysis of the variable-structure hydrostatic drive system, along with simulation experiments, has proven to accurately predict and simulate the designed drive system.
- Addressing the displacement matching issue of the designed drive system, the proposed HST adaptive SMC strategy based on RBFNN compensation has been verified through experiments to effectively control and compensate the system. This ensures smooth speed fluctuation in situations such as climbing, rapid gear shifting, and sudden load changes, achieving automatic smooth gear shifting and improving the driving comfort and work efficiency of the operators.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Frank, B.; Kleinert, J.; Filla, R. Optimal control of wheel loader actuators in gravel applications. Autom. Constr. 2018, 91, 1–14. [Google Scholar] [CrossRef]
- Wang, F.; Hong, J.; Ding, R.; Xu, B.; Fiebig, W.J. A Torque Conversion Solution to the Powertrain of Mobile Machine and Its Control Strategy. IEEE Trans. Veh. Technol. 2022, 71, 10361–10373. [Google Scholar] [CrossRef]
- Oh, K.; Yun, S.; Ko, K.; Kim, P.; Seo, J.; Yi, K. An investigation of energy efficiency of a wheel loader with automated manual transmission. J. Mech. Sci. Technol. 2016, 30, 2933–2940. [Google Scholar] [CrossRef]
- You, Y.; Sun, D.; Qin, D. Shift strategy of a new continuously variable transmission based wheel loader. Mech. Mach. Theory 2018, 130, 313–329. [Google Scholar] [CrossRef]
- He, X.; Jiang, Y. Review of hybrid electric systems for construction machinery. Autom. Constr. 2018, 92, 286–296. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Du, S.; Ma, H.; Zhao, W.; Li, H. Energy Management Strategies for Hybrid Construction Machinery: Evolution, Classification, Comparison and Future Trends. Energies 2019, 12, 2024. [Google Scholar] [CrossRef]
- Lin, T.; Wang, L.; Huang, W.; Ren, H.; Fu, S.; Chen, Q. Performance analysis of an automatic idle speed control system with a hydraulic accumulator for pure electric construction machinery. Autom. Constr. 2017, 84, 184–194. [Google Scholar] [CrossRef]
- Wang, F.; Lin, Z.; Xu, B.; Fiebig, W. An Electric-Hydrostatic Energy Storage System for Hydraulic Hybrid Wheel Loader. IEEE Trans. Veh. Technol. 2022, 71, 7044–7056. [Google Scholar] [CrossRef]
- Liu, F.; Wu, W.; Hu, J.; Yuan, S. Design of multi-range hydro-mechanical transmission using modular method. Mech. Syst. Signal Process. 2019, 126, 1–20. [Google Scholar] [CrossRef]
- Wang, F.; Chen, J.; Xu, B.; Stelson, K.A. Improving the reliability and energy production of large wind turbine with a digital hydrostatic drivetrain. Appl. Energy 2019, 251, 113309. [Google Scholar] [CrossRef]
- Han, X.; Su, W.; Zhao, H.; Zheng, Y.; Hu, Q.; Wang, C. Research of the hydrostatic transmission for deep-sea current energy converter. Energy Convers. Manag. 2020, 207, 112544. [Google Scholar] [CrossRef]
- Comellas, M.; Pijuan, J.; Nogués, M.; Roca, J. Efficiency analysis of a multiple axle vehicle with hydrostatic transmission overcoming obstacles. Veh. Syst. Dyn. 2018, 56, 55–77. [Google Scholar] [CrossRef]
- Rabbo, S.A.; Tutunji, T. Identification and analysis of hydrostatic transmission system. Int. J. Adv. Manuf. Technol. 2008, 37, 221–229. [Google Scholar] [CrossRef]
- Zhou, S.; Walker, P.; Wu, J.; Zhang, N. Power on gear shift control strategy design for a parallel hydraulic hybrid vehicle. Mech. Syst. Signal Process. 2021, 159, 107798. [Google Scholar] [CrossRef]
- Backas, J.; Ghabcheloo, R.; Huhtala, K. Gain scheduled state feedback velocity control of hydrostatic drive transmissions. Control. Eng. Pract. 2017, 58, 214–224. [Google Scholar] [CrossRef]
- Fu, S.; Ren, H.; Lin, T.; Zhou, S.; Chen, Q.; Li, Z. SM-PI Control Strategy of Electric Motor-Pump for Pure Electric Construction Machinery. IEEE Access 2020, 8, 100241–100250. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.; Yang, R.; Fu, Y.; Zhu, D. A Sliding Mode Control Strategy for an ElectroHydrostatic Actuator with Damping Variable Sliding Surface. Actuators 2021, 10, 3. [Google Scholar] [CrossRef]
- Kim, J.; Jin, M.; Choi, W.; Lee, J. Discrete time delay control for hydraulic excavator motion control with terminal sliding mode control. Mechatronics 2019, 60, 15–25. [Google Scholar] [CrossRef]
- Li, H.; Chen, B.; Ma, B.; Zhang, H. Fuzzy adaptive PID synchronization control of hydrostatic transmission for high-speed overlay vehicles. J. Agric. Mach. 2010, 41, 16–19. [Google Scholar]
- Huo, D.; Chen, J.; Zhang, H.; Shi, Y.; Wang, T. Intelligent prediction for digging load of hydraulic excavators based on RBF neural network. Measurement 2023, 206, 112210. [Google Scholar] [CrossRef]
- Deng, P.; Zeng, L.; Liu, Y. RBF Neural Network Backstepping Sliding Mode Adaptive Control for Dynamic Pressure Cylinder Electrohydraulic Servo Pressure System. Complexity 2018, 2018, 4159639. [Google Scholar] [CrossRef]
- Li, X.; Gao, H.; Xiong, L.; Zhang, H.; Li, B. A Novel Adaptive Sliding Mode Control of Robot Manipulator Based on RBF Neural Network and Exponential Convergence Observer. Neural Process. Lett. 2023, 55, 10037–10052. [Google Scholar] [CrossRef]
- Fu, Y.; Zhou, X.; Wan, B.; Yang, X. Decoupled adaptive terminal sliding mode control strategy for a 6-DOF electro-hydraulic suspension test rig with RBF coupling force compensator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 4339–4357. [Google Scholar] [CrossRef]
- Ma, W.; Xie, D.; Wang, Z.; Ran, Z.; Liu, C.; Wang, S. Modeling, calculation, and analysis of torsional vibration characteristics of the hydrodynamic transmission system in engineering vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 1824–1839. [Google Scholar] [CrossRef]
- Feng, H.; Song, Q.; Ma, S.; Ma, W.; Yin, C.; Cao, D.; Yu, H. A new adaptive sliding mode controller based on the RBF neural network for an electro-hydraulic servo system. ISA Trans. 2022, 129, 472–484. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Wen, G.; Gan, J.; Zheng, W.; Lei, C. Self-paced Learning for K-means Clustering Algorithm. Pattern Recognit. Lett. 2020, 132, 69–75. [Google Scholar] [CrossRef]
- Cerman, O.; Hušek, P. Adaptive fuzzy sliding mode control for electro-hydraulic servo mechanism. Expert Syst. Appl. 2012, 39, 10269–10277. [Google Scholar] [CrossRef]
- Chiang, M.-H.; Lee, L.-W.; Liu, H.-H. Adaptive fuzzy controller with self-tuning fuzzy sliding-mode compensation for position control of an electro-hydraulic displacement-controlled system. J. Intell. Fuzzy Syst. 2014, 26, 815–830. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, D.; Shen, G.; Sun, Z.; Xia, Y. Corrigendum to “Disturbance observer based adaptive fuzzy sliding mode control: A dynamic sliding mode surface approach” [Automatic 129 (2021) 109606]. Automatic 2022, 142, 110413. [Google Scholar] [CrossRef]
- Singh, V. A note on Routh’s criterion and Lyapunov’s direct method of stability. Proc. IEEE 1973, 61, 503. [Google Scholar] [CrossRef]



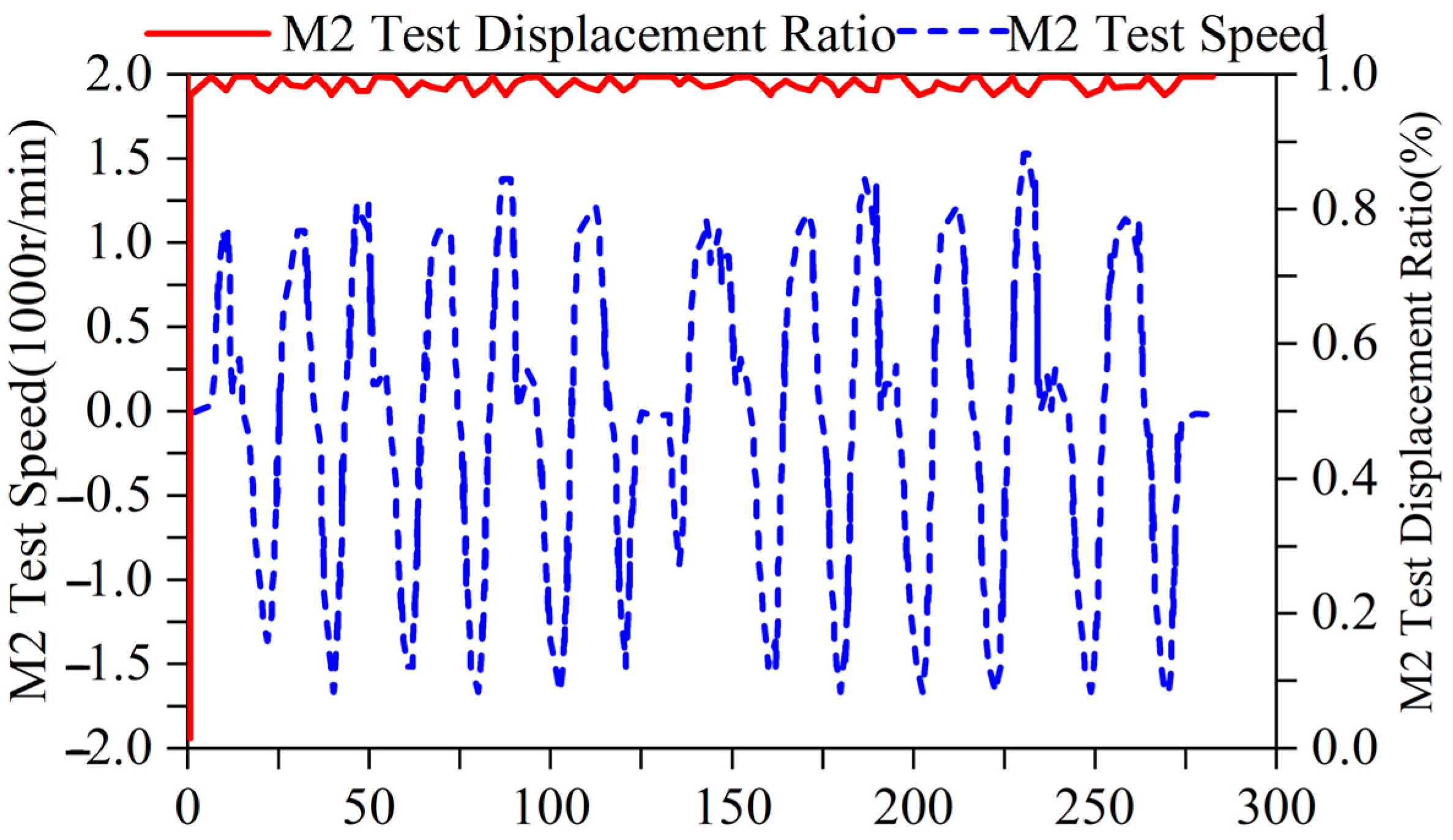
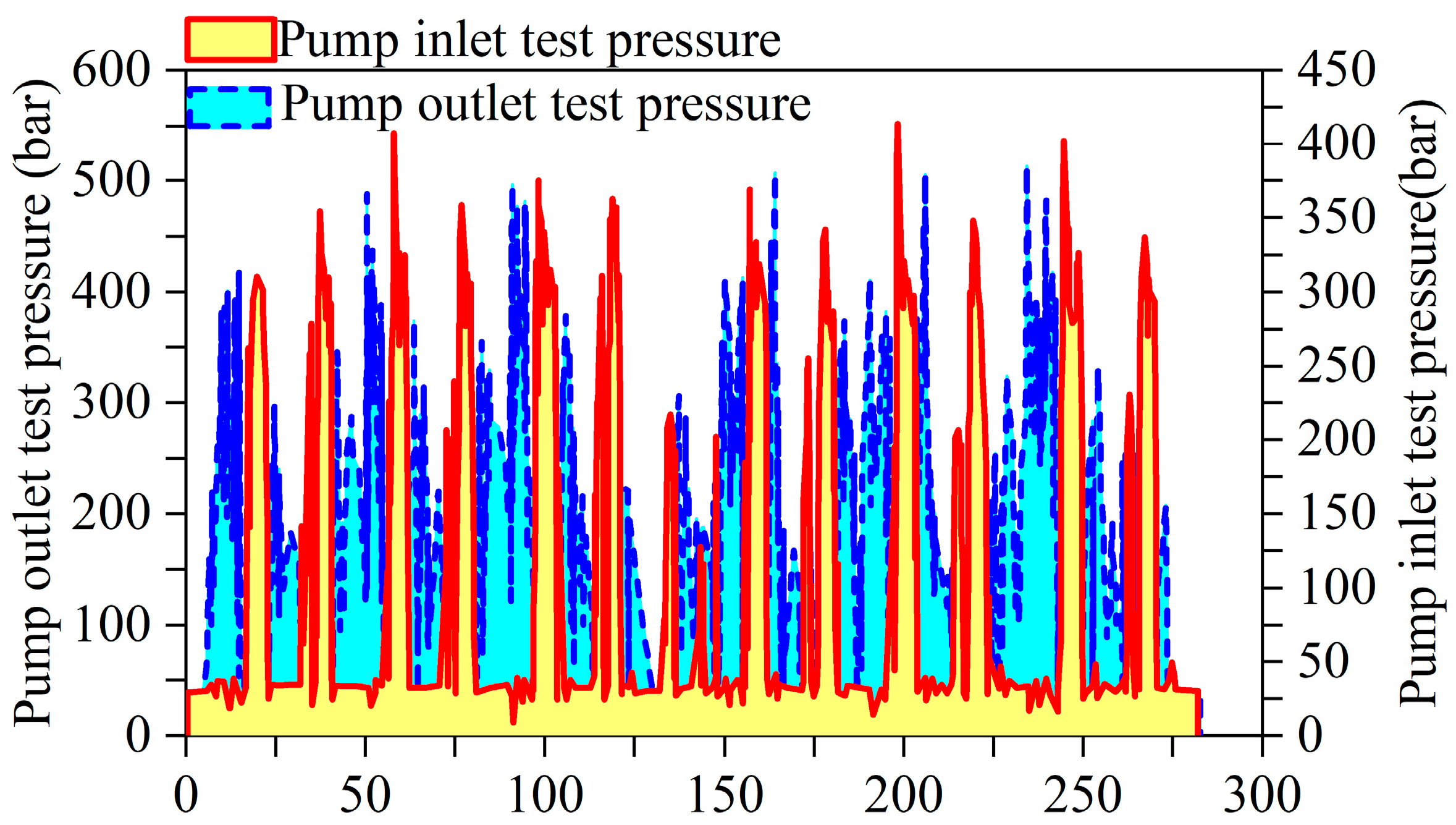

| Name | Value | Unit |
|---|---|---|
| Pump displacement | 175.4 | mL/r |
| Pump volumetric efficiency | 96 | % |
| Pump mechanical efficiency | 94 | % |
| Small motor displacement | 164.2 | mL/r |
| Small motor volumetric efficiency | 92 | % |
| Small motor mechanical efficiency | 95 | % |
| Large motor displacement | 170.6 | mL/r |
| Large motor volumetric efficiency | 92 | % |
| Large motor mechanical efficiency | 92 | % |
| Charge pump displacement | 24.5 | mL/r |
| Charge pump overflow pressure | 2.5 | MPa |
| Relief valve setting pressure | 42 | MPa |
| Flush valve setting pressure | 2 | MPa |
| Flush valve setting flow rate | 20 | L/min |
| Engine standard power | 180 | kW |
| Engine rated speed | 2000 | r/min |
| Maximum engine output torque | 1187 | Nm |
| Engine nominal fuel consumption | 235 | g/kWh |
| Lowest engine fuel consumption at full load | 230 | g/kWh |
| Drive axle transmission ratio (Z9/Z8) | 24.67 | |
| Large motor transmission ratio [(Z2Z4Z7)/(Z1Z3Z5)] | 3.23 | |
| Small motor transmission ratio (Z7/Z6) | 1.44 | |
| Transmission mechanical efficiency | 92 | % |
| Name | Value | Unit |
|---|---|---|
| Overall vehicle mass | 21,650 | kg |
| Loading mass | 7000 | kg |
| Asphalt road resistance factor | 0.010–0.018 | |
| Potholes road resistance factor | 0.035–0.050 | |
| Gravel road resistance factor | 0.020–0.025 | |
| Compression road resistance factor | 0.050–0.150 | |
| Muddy road resistance factor | 0.100–0.250 | |
| Iced road resistance factor | 0.015–0.030 | |
| Dry sand road resistance factor | 0.100–0.300 | |
| Wheel radius | 0.75 | m |
| Windward area | 5 | m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, Z.; Wang, S.; Cai, W.; Wu, Q.; Ma, W. Design and Control Performance Optimization of Variable Structure Hydrostatic Drive Systems for Wheel Loaders. Machines 2024, 12, 238. https://doi.org/10.3390/machines12040238
Wang X, Wang Z, Wang S, Cai W, Wu Q, Ma W. Design and Control Performance Optimization of Variable Structure Hydrostatic Drive Systems for Wheel Loaders. Machines. 2024; 12(4):238. https://doi.org/10.3390/machines12040238
Chicago/Turabian StyleWang, Xin, Zhongyu Wang, Songlin Wang, Wei Cai, Qingjie Wu, and Wenxing Ma. 2024. "Design and Control Performance Optimization of Variable Structure Hydrostatic Drive Systems for Wheel Loaders" Machines 12, no. 4: 238. https://doi.org/10.3390/machines12040238
APA StyleWang, X., Wang, Z., Wang, S., Cai, W., Wu, Q., & Ma, W. (2024). Design and Control Performance Optimization of Variable Structure Hydrostatic Drive Systems for Wheel Loaders. Machines, 12(4), 238. https://doi.org/10.3390/machines12040238







