Design, Control, and Analysis of a 3-Degree-of-Freedom Kinematic–Biologically Matched Hip Joint Structure for Lower Limb Exoskeleton †
Abstract
1. Introduction
2. Materials and Methods
2.1. Mechanical Design
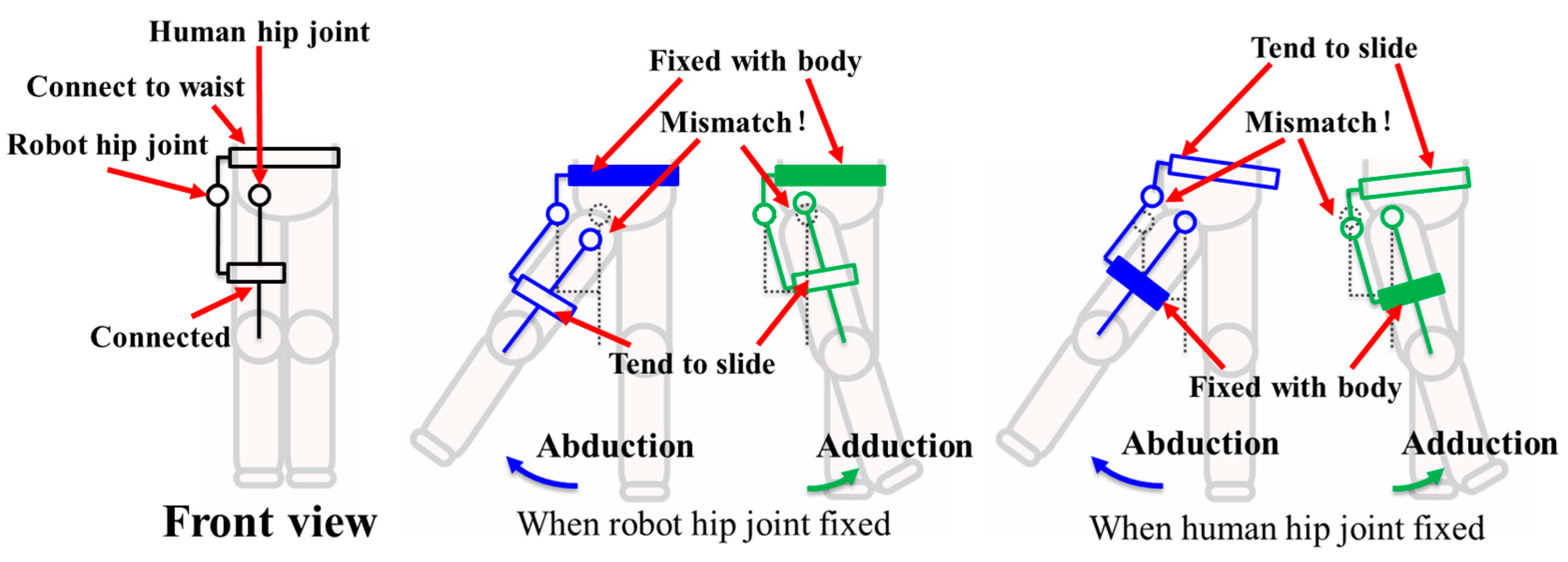
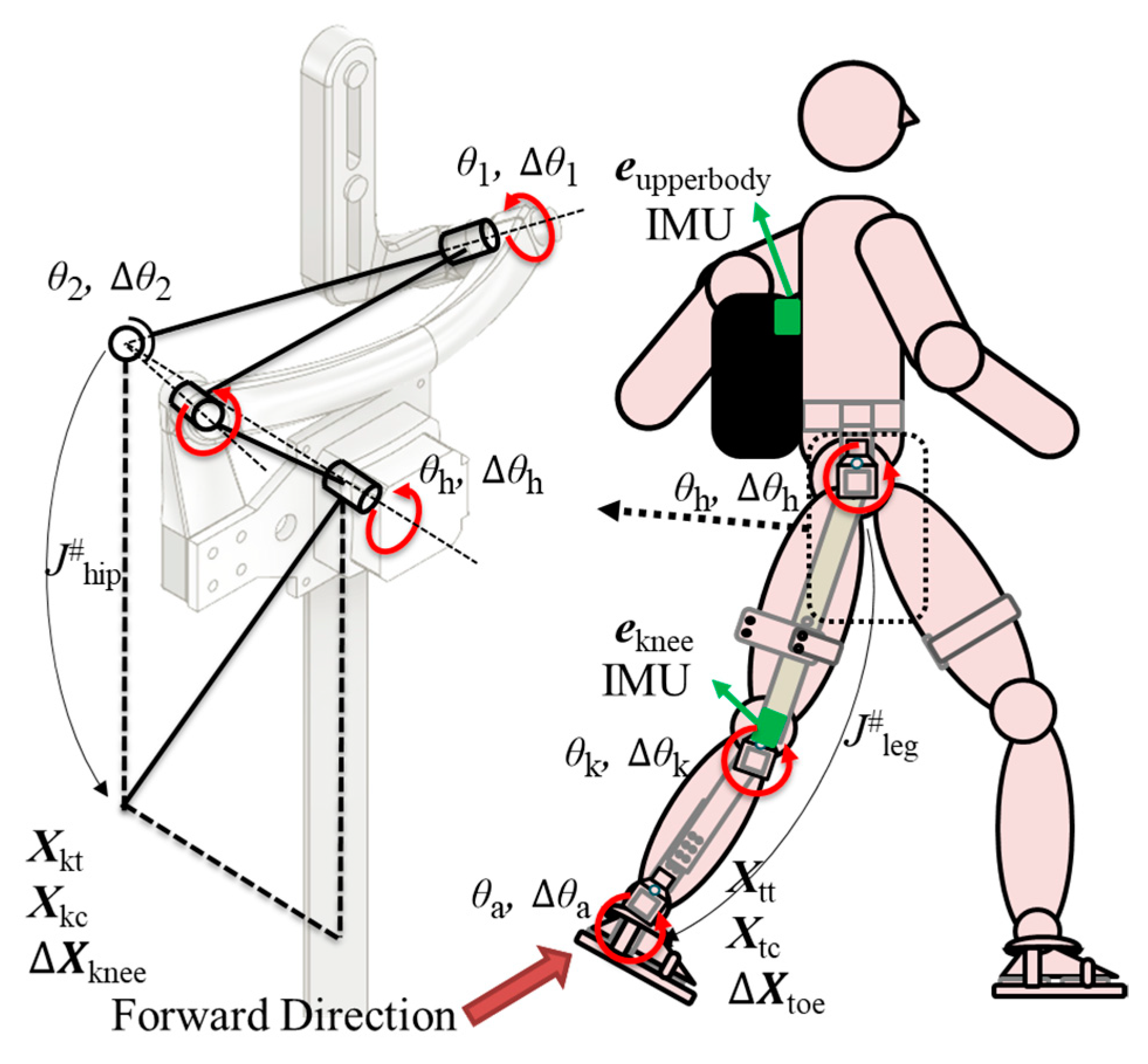
2.1.1. 3-DOF Hip Joint Structure for Lower Limb Exoskeleton
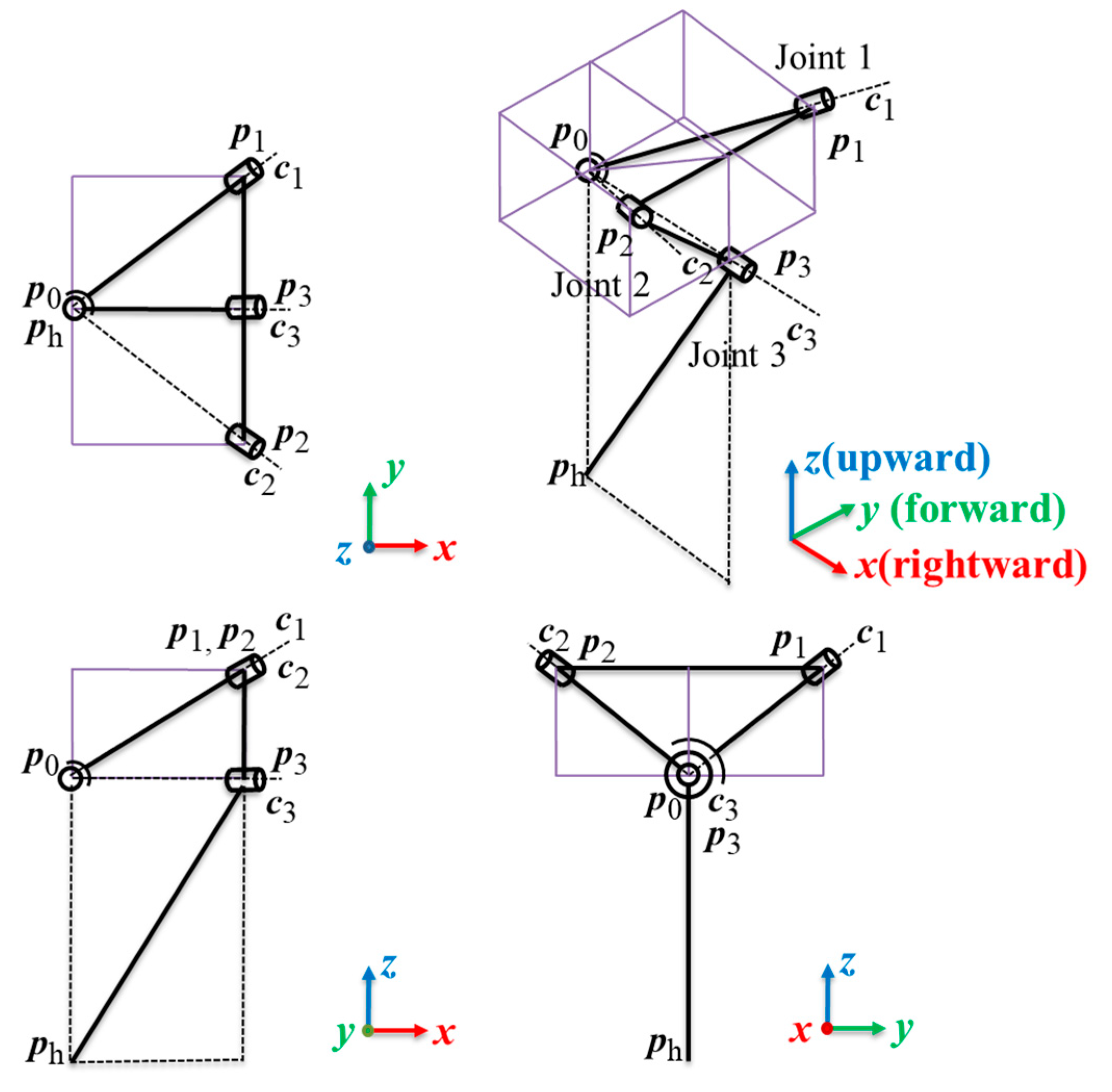
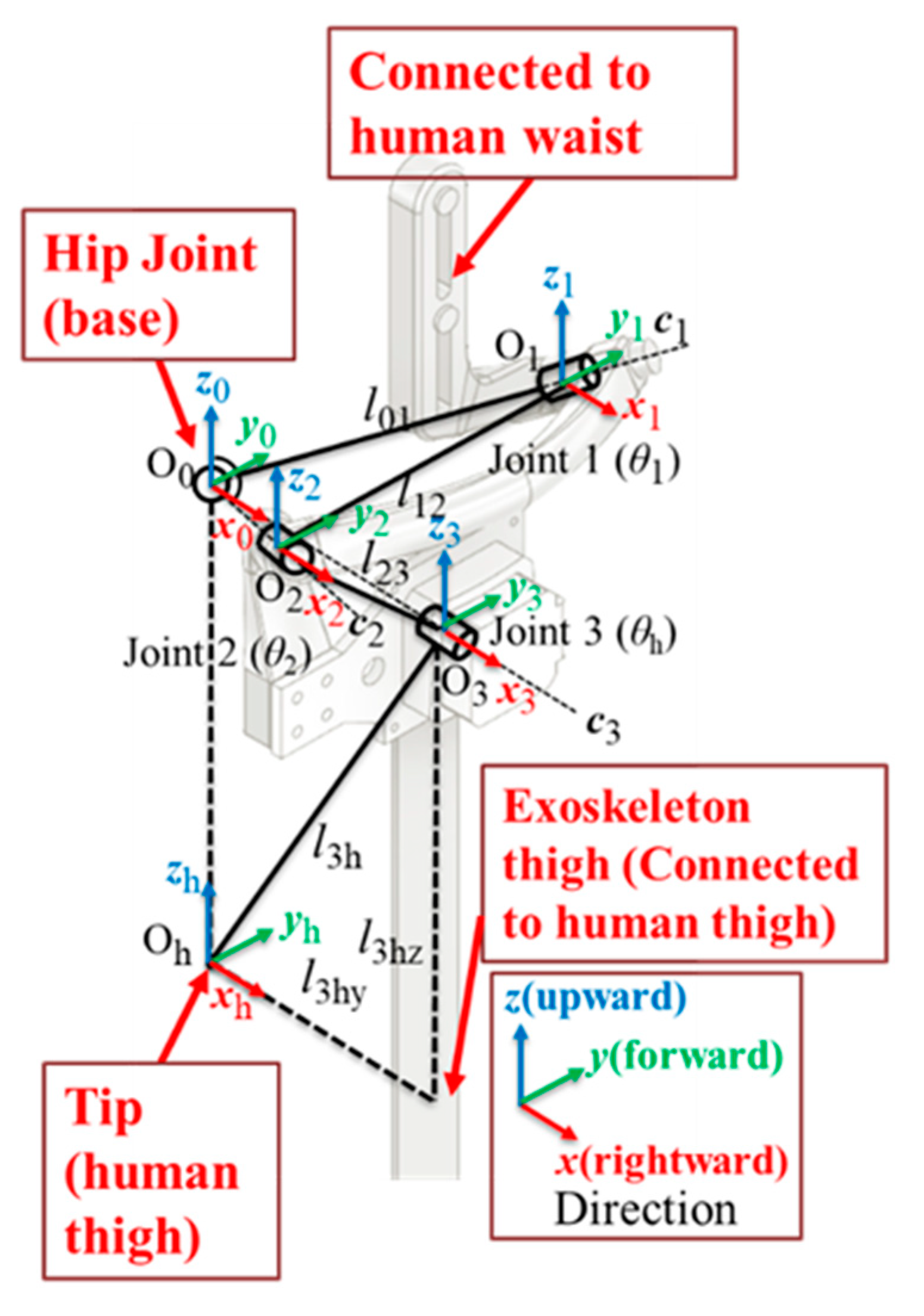
2.1.2. Kinematics of the Structure
2.1.3. Simulation and Shape Design
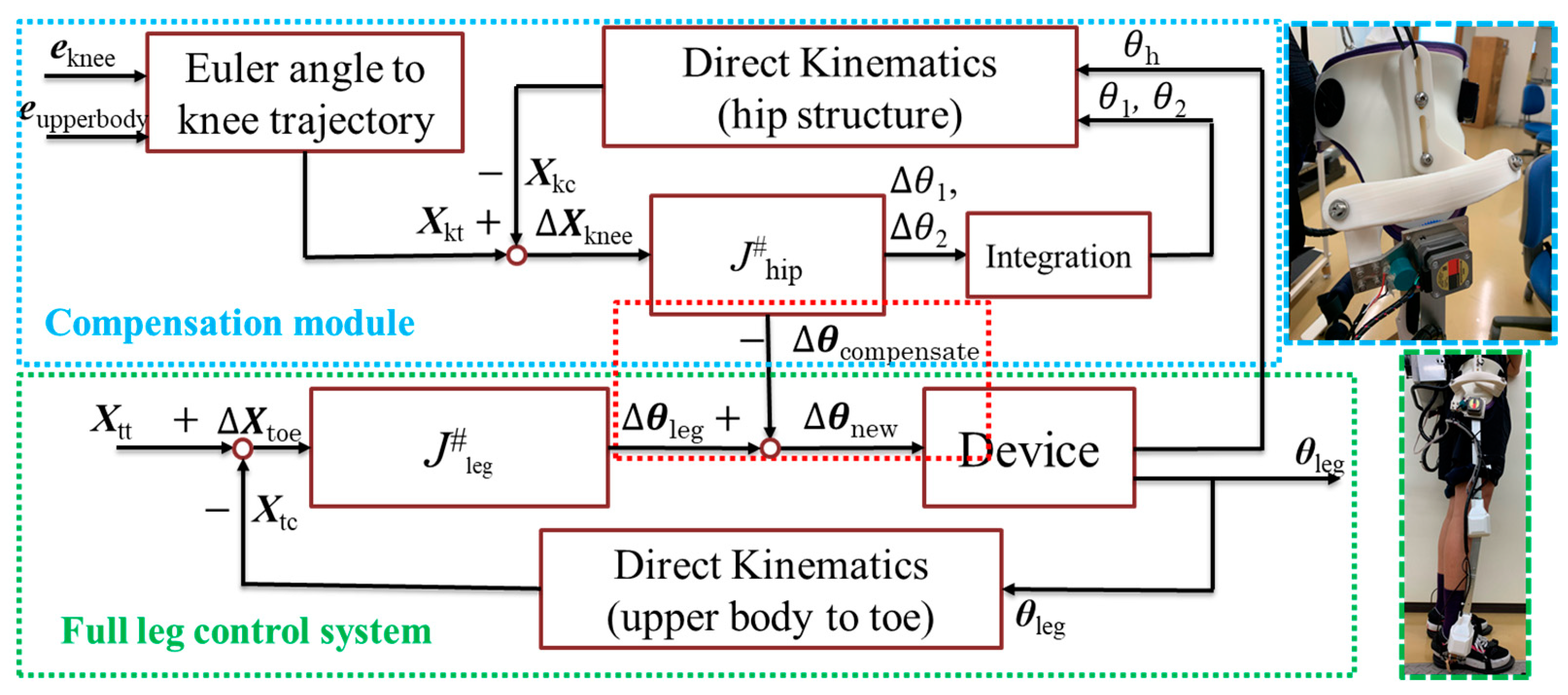
2.2. Control Method
2.2.1. Process of IMUs’ Data
2.2.2. Control Method of Walking Assistance
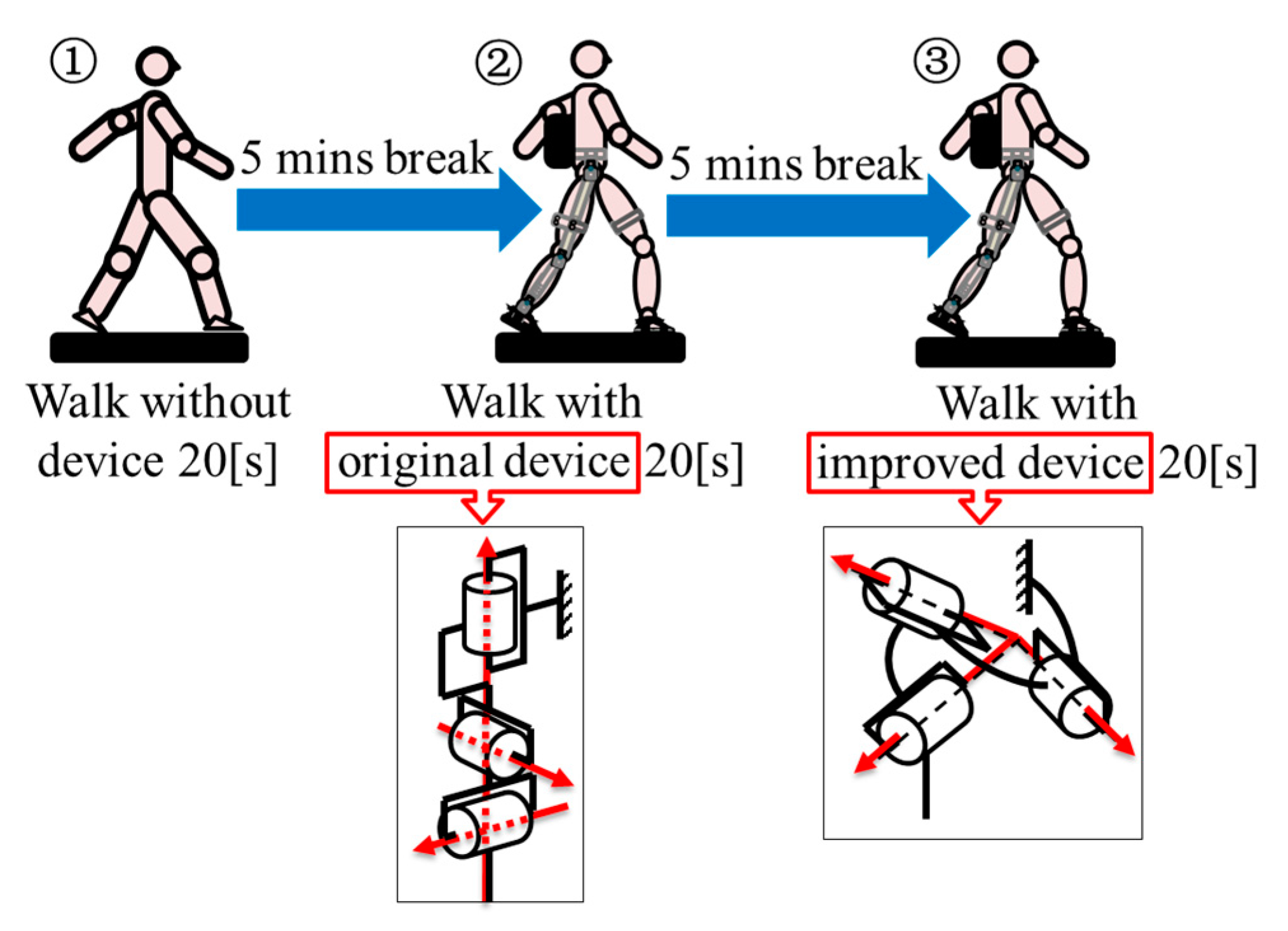
2.3. Experiment Method
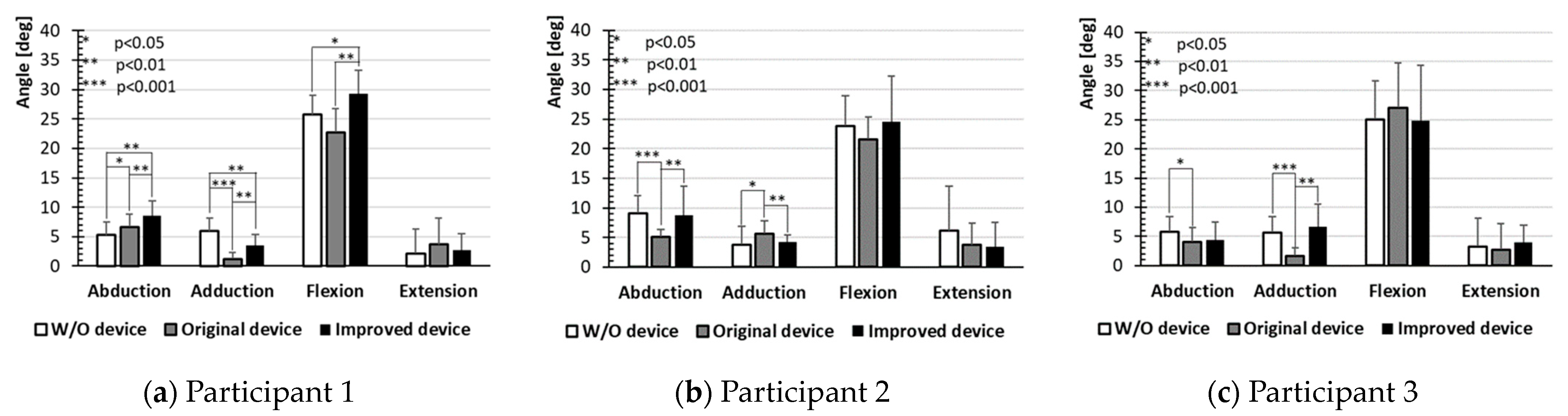
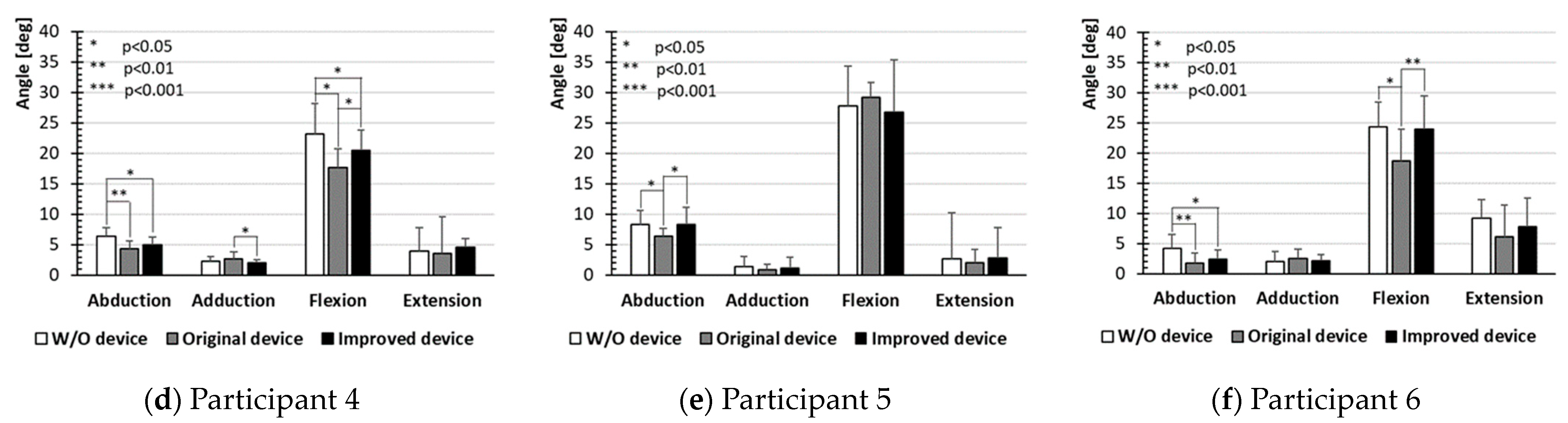
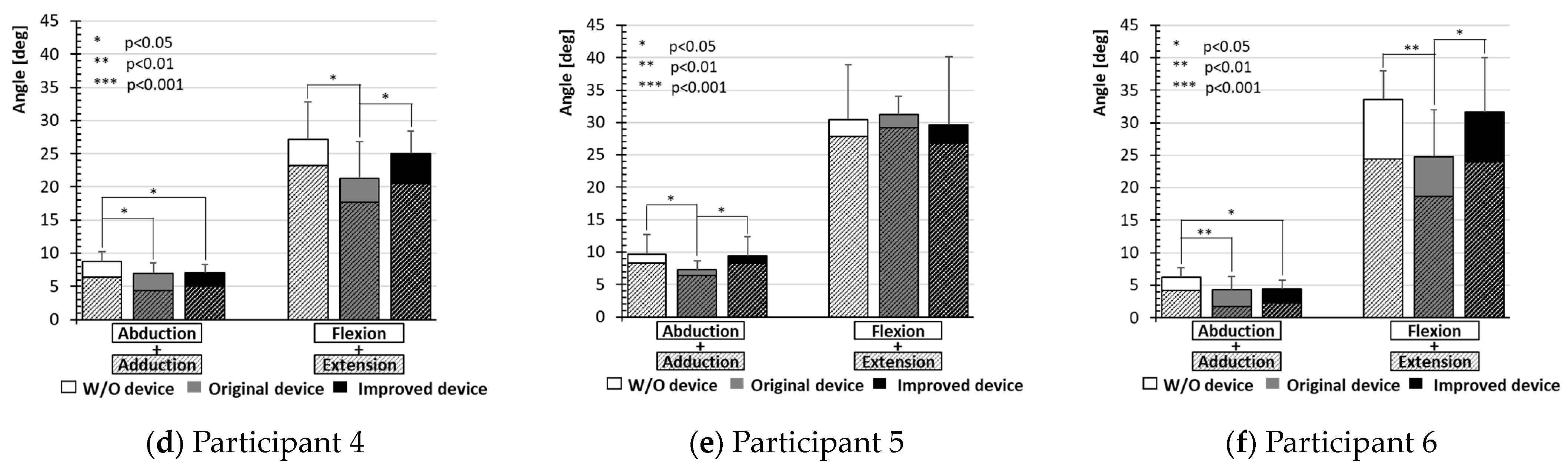
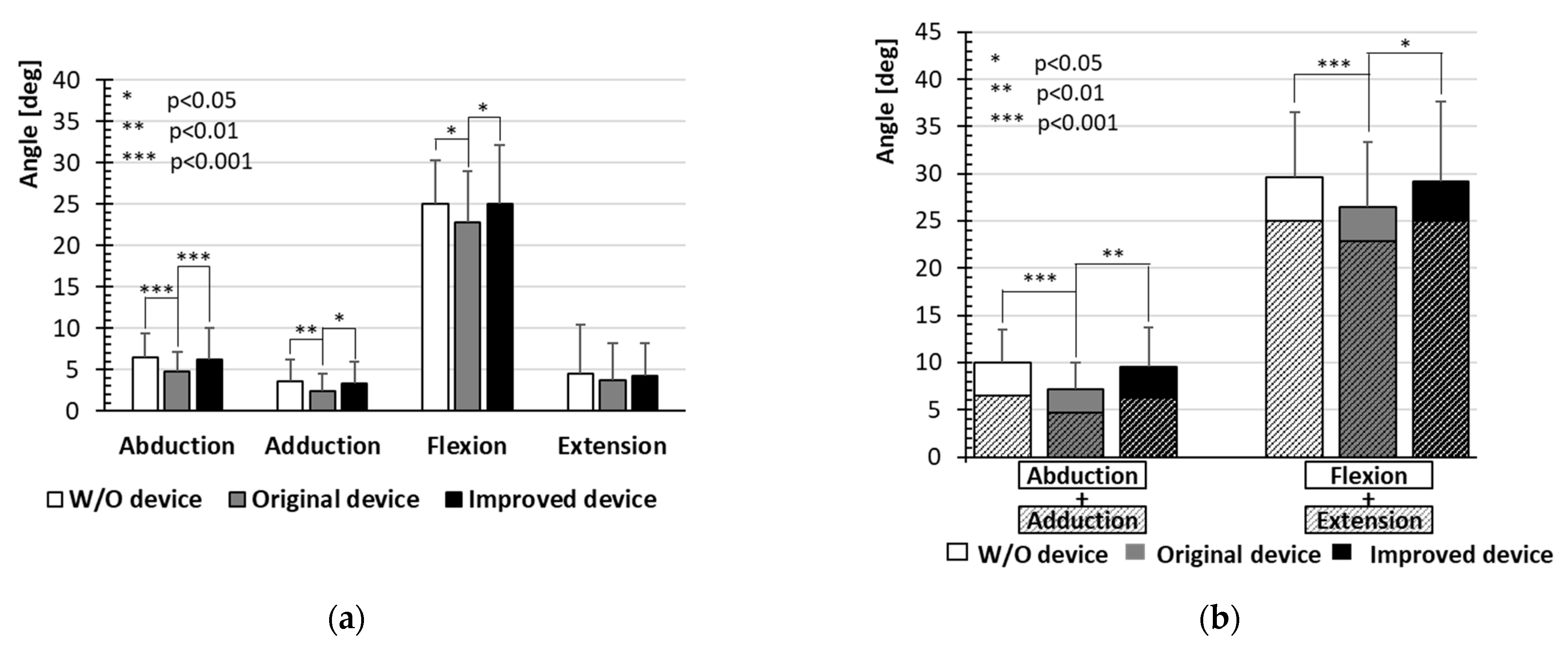
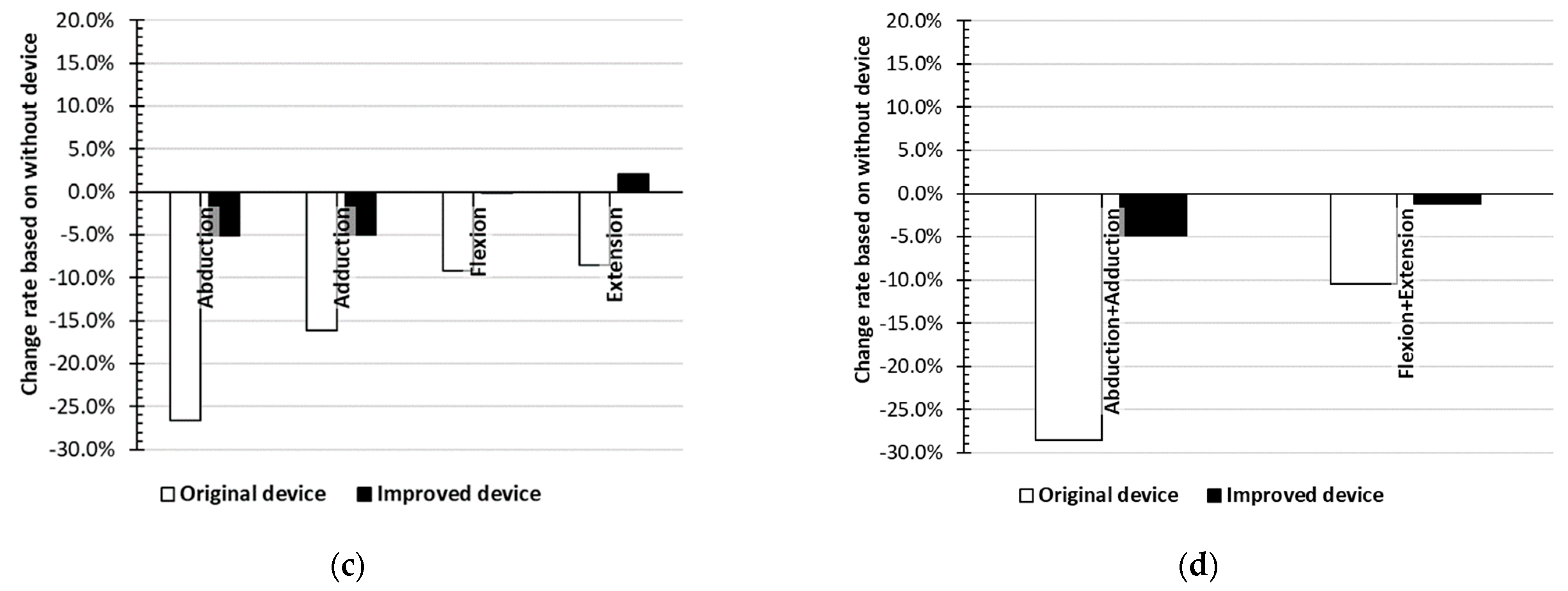
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wall, A.; Borg, J.; Vreede, K.; Palmcrantz, S. A randomized controlled study incorporating an electromechanical gait machine, the Hybrid Assistive Limb, in gait training of patients with severe limitations in walking in the subacute phase after stroke. PLoS ONE 2020, 15, e0229707. [Google Scholar] [CrossRef] [PubMed]
- Esquenazi, A.; Talaty, M.; Packel, A.; Saulino, M. The Rewalk powered exoskeleton to restore ambulatory function to individuals with thoracic-level motor-complete spinal cord injury. Am. J. Phys. Med. Rehabil. 2012, 91, 911–921. [Google Scholar] [CrossRef]
- Wu, J.; Gao, J.; Song, R.; Li, R.; Li, Y.; Jiang, L. The design and control of a 3DOF lower limb rehabilitation robot. Mechatronics 2016, 33, 13–22. [Google Scholar] [CrossRef]
- Rose, L.; Bazzocchi, M.C.F.; de Souza, C.; Vaughan-Graham, J.; Patterson, K.; Nejat, G. A framework for mapping and controlling exoskeleton gait patterns in both simulation and real-world. In Proceedings of the 2020 Design of Medical Devices Conference, (DMD2020), DMD2020-9009, Minneapolis, MN, USA, 6–9 April 2020. [Google Scholar]
- Sarajchi, M.; Sirlantzis, K. Pediatric Robotic Lower-Limb Exoskeleton: An Innovative Design and Kinematic Analysis. IEEE Access 2023, 11, 115219–115230. [Google Scholar] [CrossRef]
- Zhang, T.; Tran, M.; Huang, H.H. NREL-Exo: A 4-DoFs wearable hip exoskeleton for walking and balance assistance in locomotion. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS2017), Vancouver, BC, Canada, 24–28 September 2017; pp. 508–513. [Google Scholar]
- Guzmán-Valdivia, C.H.; Blanco-Ortega, A.; Oliver-Salazar, M.A.; Gómez-Becerra, F.A.; Carrera-Escobedo, J.L. HipBot—The design, development and control of a therapeutic robot for hip rehabilitation. Mechatronics 2015, 30, 55–64. [Google Scholar] [CrossRef]
- Yasuhara, K.; Shimada, K.; Koyama, T.; Ido, T.; Kikuchi, K.; Endo, Y. Walking Assist Device with Stride Management System. Honda R&D Tech. Rev. 2009, 21, 57–66. [Google Scholar]
- Sadeqi, S.; Bourgeois, S.P.; Park, E.J.; Arzanpour, S. Design and performance analysis of a 3-RRR spherical parallel manipulator for hip exoskeleton applications. J. Rehabil. Assist. Technol. Eng. 2017, 4, 1–11. [Google Scholar] [CrossRef]
- Yusa, H.; Tanaka, E.; Ikehara, T.; Ito, K.; Saegusa, S.; Hashimoto, K.; Sato, Y.; Yuge, L. Development of a walking assistance apparatus using a spatial parallel link mechanism and evaluation of muscle activity. In Proceedings of the 19th IEEE International Symposium in Robot and Human Interactive Communication (IEEE Ro-Man 2010), Viareggio, Italy, 13–15 September 2010; pp. 151–158. [Google Scholar]
- Tanaka, E.; Saegusa, S.; Yuge, L. Development of a Whole Body Motion Support Type Mobile Suit and Evaluation of Cerebral Activity Corresponding to the Cortical Motor Areas. J. Adv. Mech. Des. Syst. Manuf. 2013, 7, 82–94. [Google Scholar] [CrossRef]
- Yang, B.R.; Lee, H.H.; Tanaka, E. Posture compensation of a walking assistive device using zero-moment point to stabilize motions on stairs. J. Adv. Mech. Des. Syst. Manuf. 2020, 14, 1–18. [Google Scholar] [CrossRef]
- Yang, B.R.; Zhang, Y.C.; Wang, H.T.; Yu, S.H.; Lee, H.H.; Tanaka, E. Automatic walking pattern transformation method of an assistive device during stair-ground transition. J. Adv. Mech. Des. Syst. Manuf. 2021, 15, 1–20. [Google Scholar] [CrossRef]
- Fang, Y.; Hou, B.; Wu, X.; Wang, Y.; Osawa, K.; Tanaka, E. A Stepper Motor-Powered Lower Limb Exoskeleton with Multiple Assistance Functions for Daily Use by the Elderly. J. Robot. Mechatron. 2023, 35, 601–611. [Google Scholar] [CrossRef]
- Tanaka, E.; Suzuki, T.; Saegusa, S.; Yuge, L. Walking assistance apparatus able to select the control method according to the purpose of the user. In Proceedings of the World Automation Congress, Waikoloa, HI, USA, 3–7 August 2014; pp. 537–542. [Google Scholar]
- Wang, Y.; Fang, Y.; Wu, X.; Osawa, K.; Tanaka, E. Development of a 3-DOF Kinematic-Biological Matched Hip Joint Structure for Lower Limb Exoskeleton. In Proceedings of the ICMDT2023, ThE1-1, Jeju Island, Republic of Korea, 8–11 March 2023; p. 65. [Google Scholar]
- Wang, Y.; Wu, X.; Fang, Y.; Osawa, K.; Nakagawa, K.; Yamasaki, S.; Eiichiro, T. Mechanical Design of a 3-DOF Kinematic-Biological matched Hip Joint Structure for Lower Limb Exoskeleton, Mechanism Design for Robotics. In MEDER 2024. Mechanisms and Machine Science; Springer: Cham, Switzerland, 2024; Volume 166. [Google Scholar]
- Wang, Y.; Wu, X.; Fang, Y.; Osawa, K.; Nakagawa, K.; Tanaka, E. Development of the Control Method of a 3-DOF KinematicBiological Matched Hip Joint Structure for Lower Limb Exoskeleton. In Proceedings of the ICARM 2024, Tokyo, Japan, 6–8 July 2024; pp. 13–18. [Google Scholar]
- Ehara, Y.; Yamamoto, S. Introduction to Body-Dynamics—Analysis of Gait and Gait Initiation; Ishiyaku Publishers, Inc.: Tokyo, Japan, 2002; p. 137. (In Japanese) [Google Scholar]
- Ehara, Y. Introduction to Body-Dynamics—Analysis of Standing up Movement; Ishiyaku Publishers, Inc.: Tokyo, Japan, 2001; p. 67. (In Japanese) [Google Scholar]
- Nakamura, R.; Saito, H.; Nagasaki, H. Fundamental Kinesiology; Ishiyaku Publishers, Inc.: Tokyo, Japan, 2003; pp. 403–405. (In Japanese) [Google Scholar]
- Rodríguez-Panes, A.; Claver, J.; Camacho, A.M. The influence of manufacturing parameters on the mechanical behavior of PLA and ABS pieces manufactured by FDM: A comparative analysis. Materials 2018, 11, 1333. [Google Scholar] [CrossRef] [PubMed]
- Hamill, J.; Knutzen, K.M.; Derrick, T.R. Biomechanical Basis of Human Movement, 5th ed.; Wolters Kluwer: Alphen aan den Rijn, The Netherlands, 2022; p. 184. [Google Scholar]



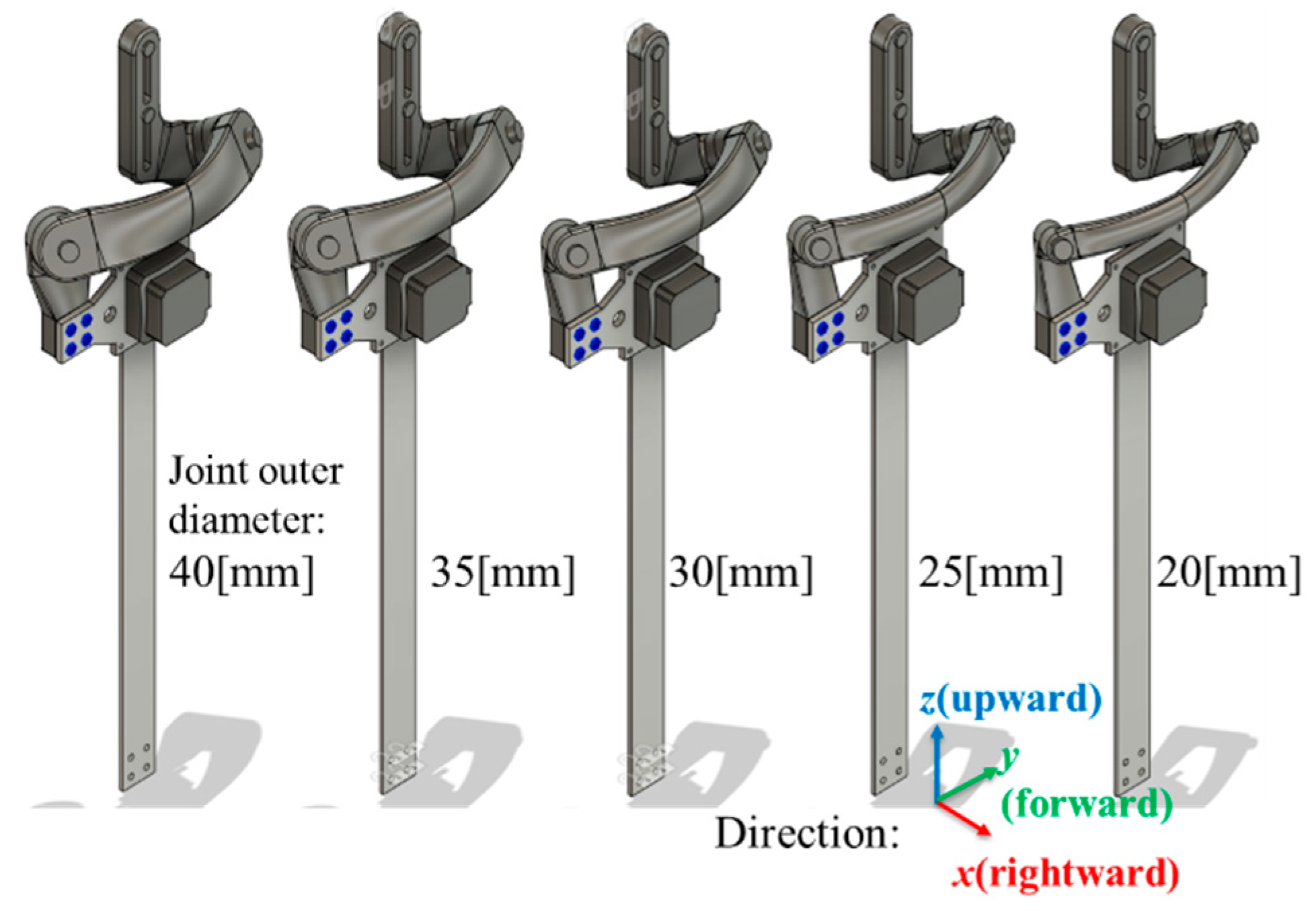
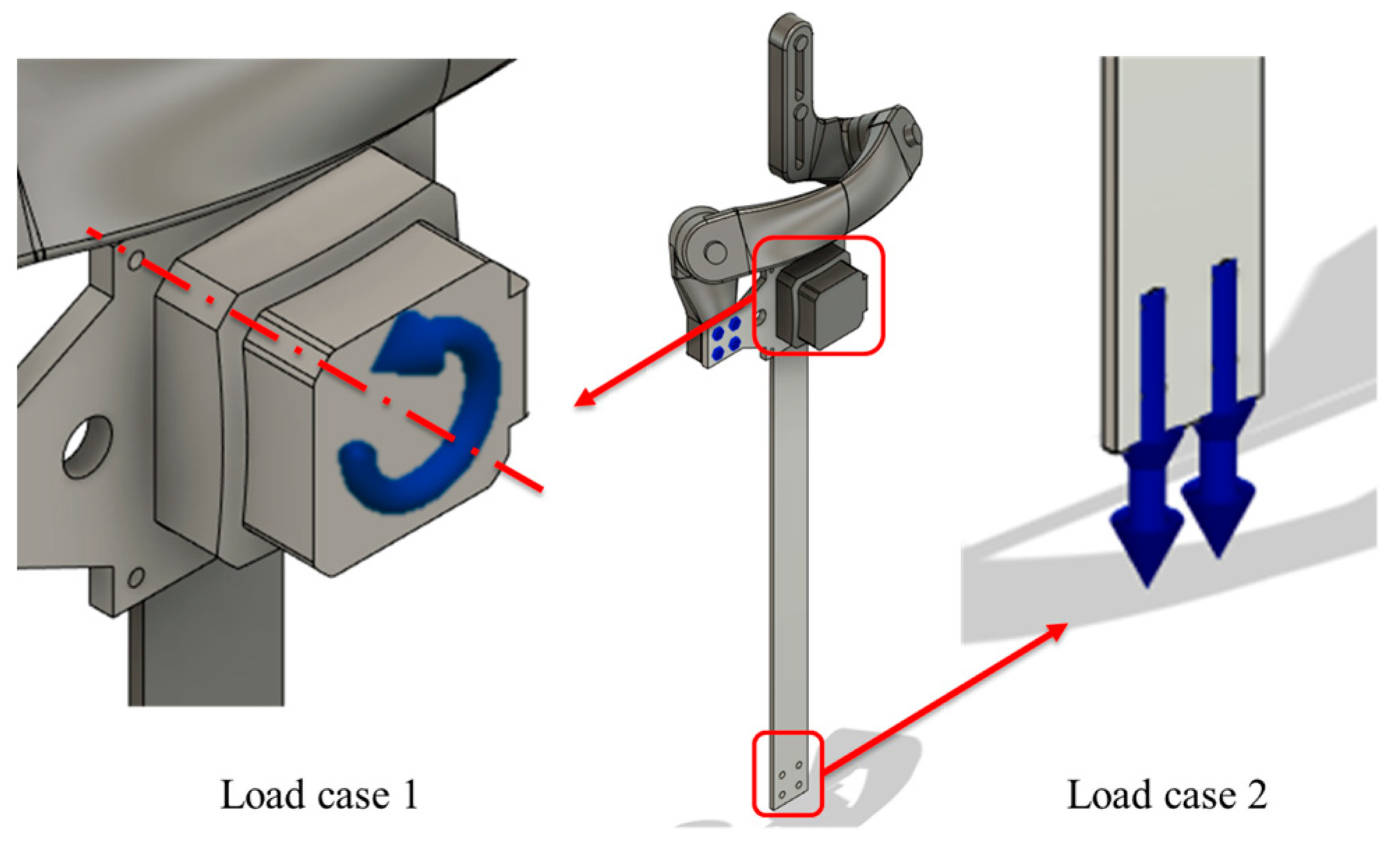
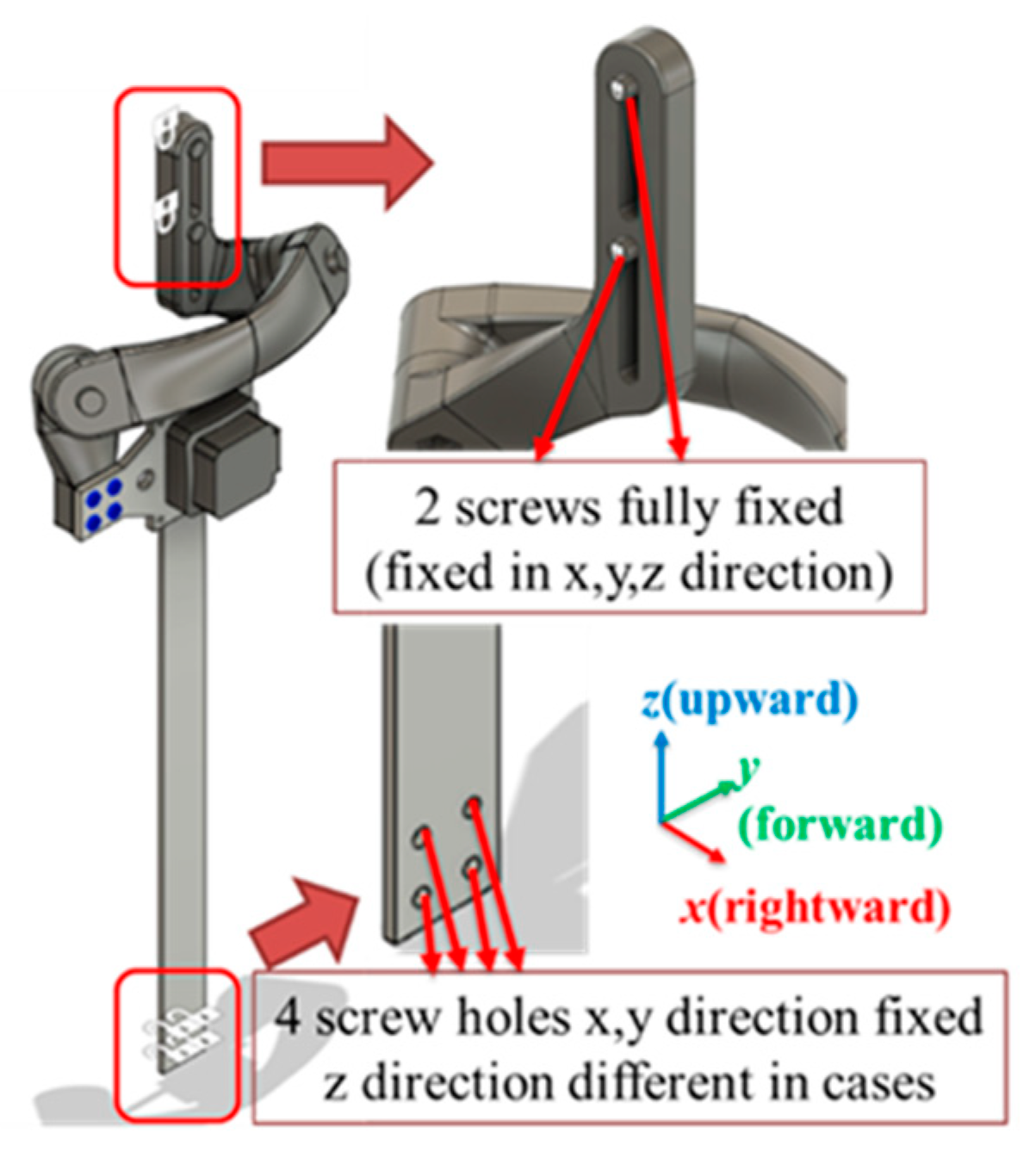
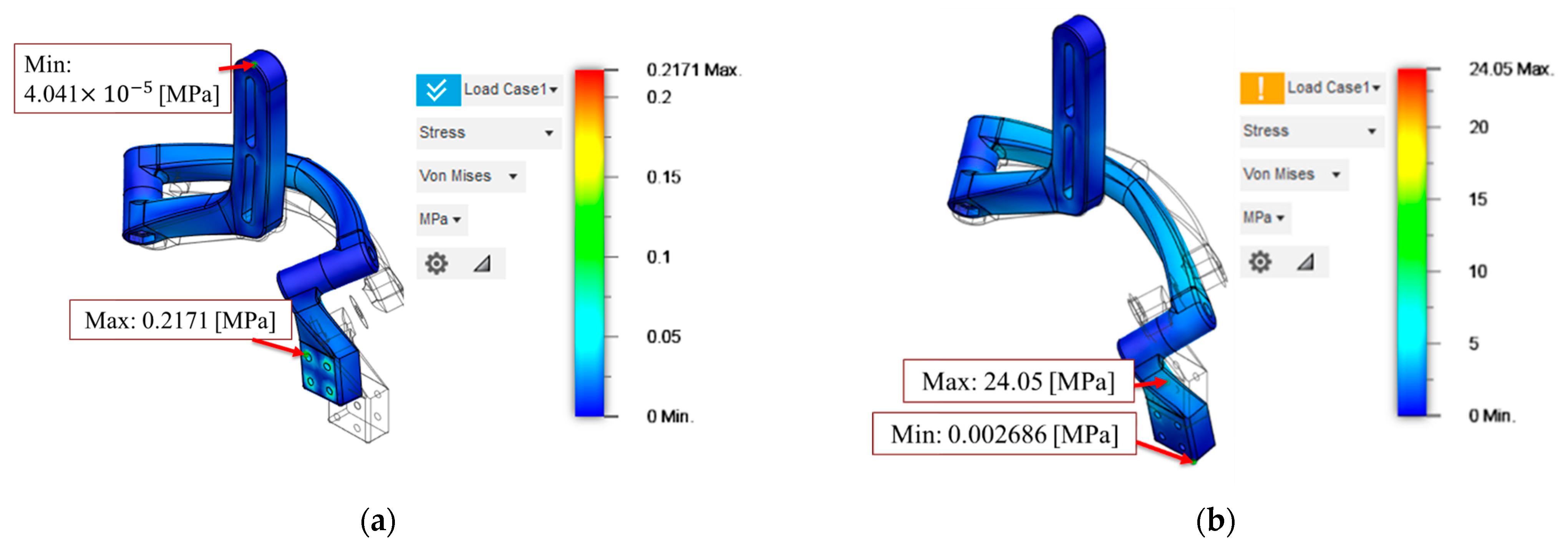

| Diameter | 20 [mm] | 25 [mm] | 30 [mm] | 35 [mm] | 40 [mm] | |
|---|---|---|---|---|---|---|
| Study 1 | Max stress | 0.217 [MPa] | 0.205 [MPa] | 0.192 [MPa] | 0.110 [MPa] | 0.105 [MPa] |
| Safety factor | >10 | >10 | >10 | >10 | >10 | |
| Study 2 | Max stress | 24.05 [MPa] | 13.32 [MPa] | 12.89 [MPa] | 8.99 [MPa] | 8.762 [MPa] |
| Safety factor | 1.93 | 3.49 | 3.61 | 5.18 | 5.31 | |
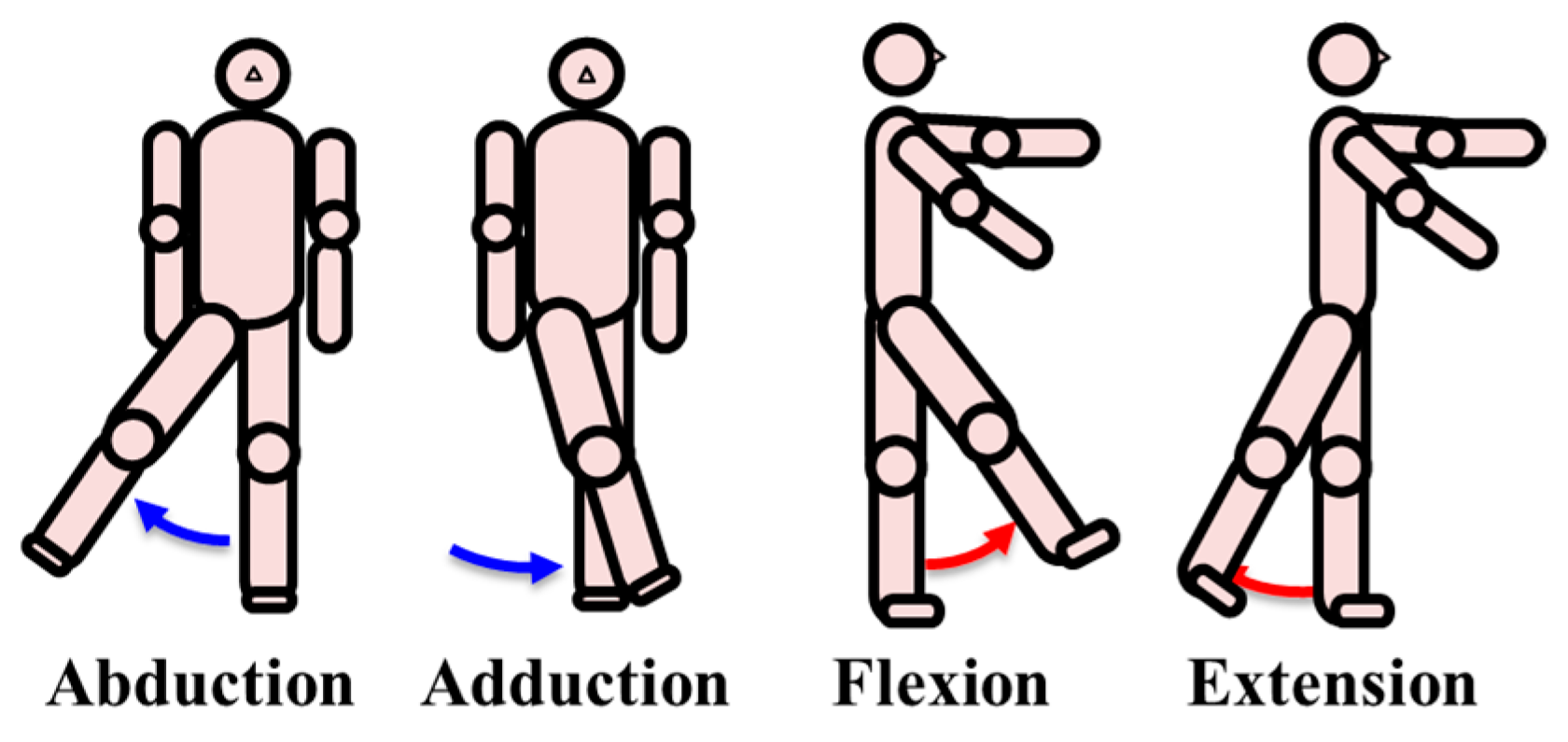
| Range of Motion [deg] | |||
|---|---|---|---|
| Flexion/ Extension | Abduction/ Adduction | ||
| Diameter [mm] | 20 | +115.06/−60.07 | +14.55/−54.16 |
| 25 | +113.83/−60.07 | +13.74/−54.16 | |
| 30 | +112.28/−60.07 | +12.88/−54.16 | |
| 35 | +109.86/−60.07 | +12.14/−54.16 | |
| 40 | +108.08/−60.07 | +10.94/−54.16 | |
| Human walking [23] | +40/−15 | +12/−12 | |
| Vector | Elements | Meaning |
|---|---|---|
| Xtt | {xtt ytt ztt θxtt θytt θztt}T | toe’s target trajectory |
| Xtc | {xtc ytc ztc θxtc θytc θztc}T | toe’s current trajectory |
| Xkt | {xkt ykt zkt θxkt θykt θzkt}T | knee’s target trajectory |
| Xkc | {xkc ykc zkc θxkc θykc θzkc}T | knee’s current trajectory |
| ΔXtoe | {Δxtoe Δytoe Δztoe Δθxtoe Δθytoe Δθztoe}T | derivation of toe’s trajectory |
| ΔXknee | {Δxknee Δyknee Δzknee Δθxknee Δθyknee Δθzknee}T | derivation of knee’s trajectory |
| θleg | {θh θk θa}T | hip/knee/ankle joint’s rotation angle |
| Δθleg | {Δθh Δθk Δθa}T | hip/knee/ankle joint’s rotation speed |
| θhip | {θ1 θ2 θh}T | hip structure joint’s rotation angle |
| Δθhip | {Δθ1 Δθ2 Δθh}T | hip structure joint’s rotation speed |
| eupperbody | {Ψu ϴu Φu}T | Euler angle read by upper IMU |
| eknee | {Ψk ϴk Φk}T | Euler angle read by lower IMU |
| Participant | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Height [cm] | 173 | 170 | 177 | 180 | 180 | 178 |
| Weight [kg] | 58 | 60 | 77 | 63 | 100 | 70 |
| Age [years] | 25 | 25 | 24 | 24 | 23 | 23 |
| Body condition | Able-bodied | Able-bodied | Able-bodied | Able-bodied | Able-bodied | Able-bodied |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wu, X.; Fang, Y.; Osawa, K.; Nakagawa, K.; Yamasaki, S.; Tanaka, E. Design, Control, and Analysis of a 3-Degree-of-Freedom Kinematic–Biologically Matched Hip Joint Structure for Lower Limb Exoskeleton. Machines 2024, 12, 924. https://doi.org/10.3390/machines12120924
Wang Y, Wu X, Fang Y, Osawa K, Nakagawa K, Yamasaki S, Tanaka E. Design, Control, and Analysis of a 3-Degree-of-Freedom Kinematic–Biologically Matched Hip Joint Structure for Lower Limb Exoskeleton. Machines. 2024; 12(12):924. https://doi.org/10.3390/machines12120924
Chicago/Turabian StyleWang, Yuntian, Xiuyuan Wu, Yifan Fang, Keisuke Osawa, Kei Nakagawa, Shintaro Yamasaki, and Eiichiro Tanaka. 2024. "Design, Control, and Analysis of a 3-Degree-of-Freedom Kinematic–Biologically Matched Hip Joint Structure for Lower Limb Exoskeleton" Machines 12, no. 12: 924. https://doi.org/10.3390/machines12120924
APA StyleWang, Y., Wu, X., Fang, Y., Osawa, K., Nakagawa, K., Yamasaki, S., & Tanaka, E. (2024). Design, Control, and Analysis of a 3-Degree-of-Freedom Kinematic–Biologically Matched Hip Joint Structure for Lower Limb Exoskeleton. Machines, 12(12), 924. https://doi.org/10.3390/machines12120924






