Fault Feature Extraction Based on Variational Modal Decomposition and Lifting Wavelet Transform: Application in Gear of Mine Scraper Conveyor Gearbox
Abstract
1. Introduction
2. Materials and Methods
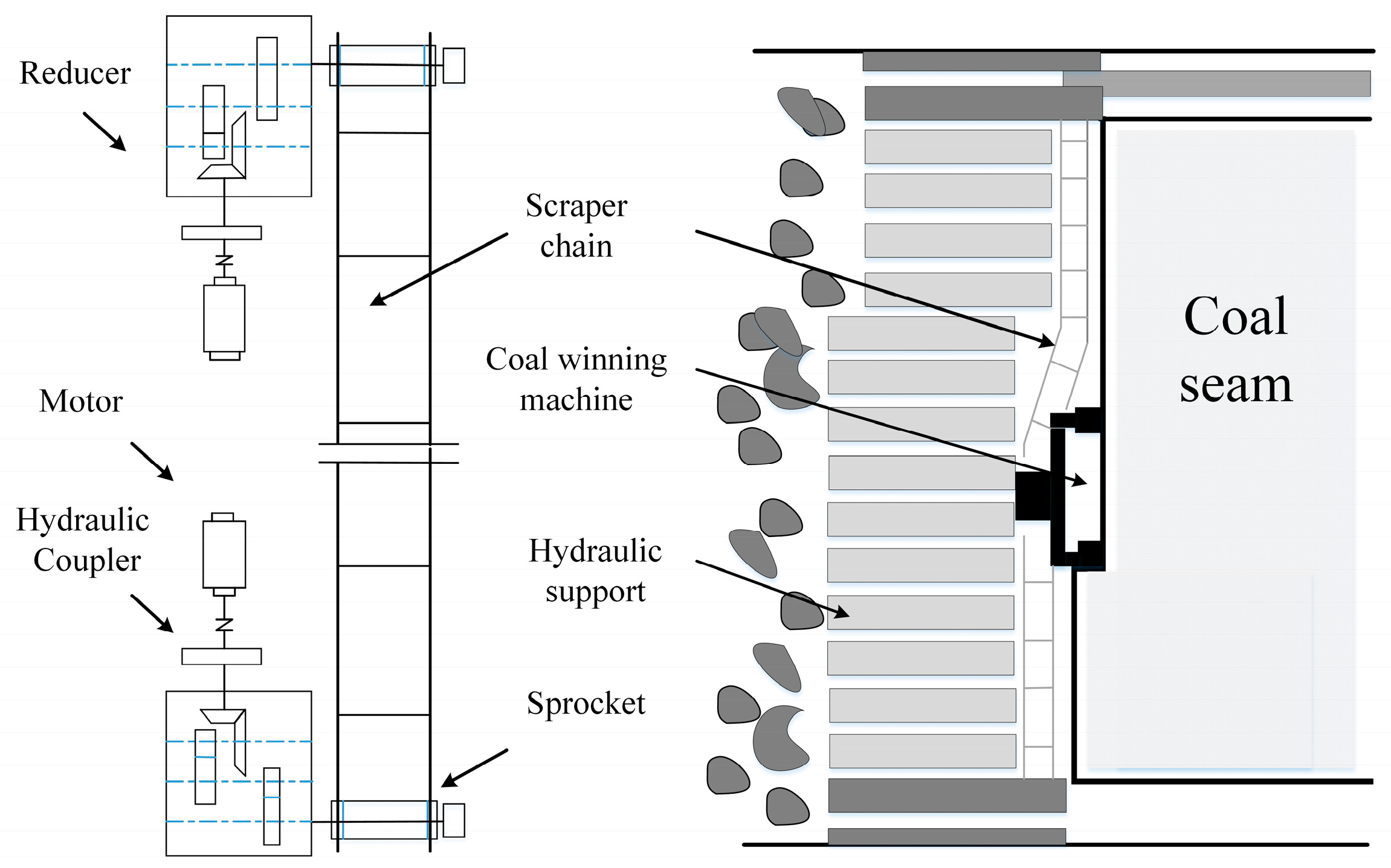
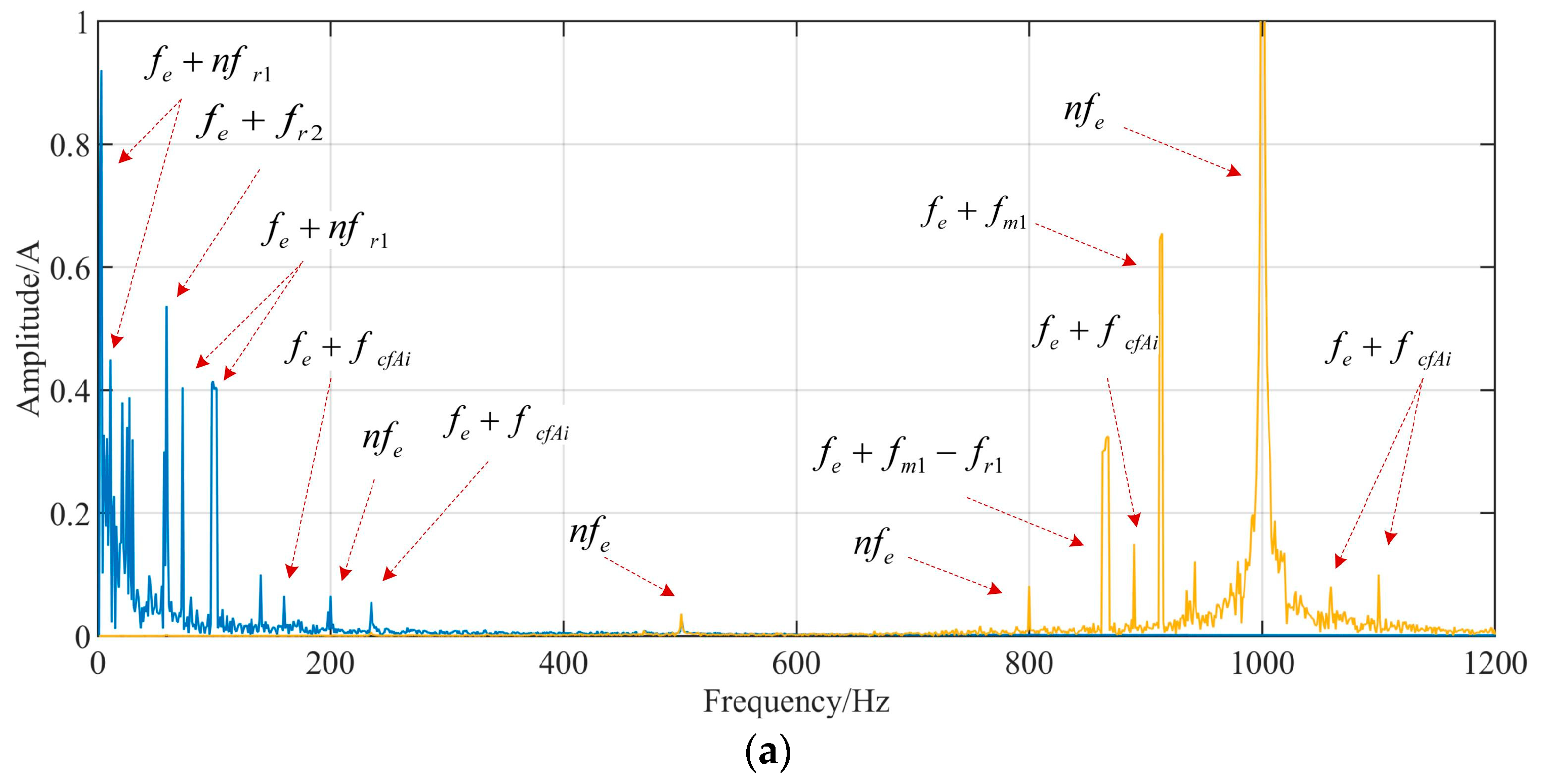
2.1. Current Signal Characteristics of Scraper Conveyor Under Load Impact
2.2. VMD-Related Theories
2.2.1. Construction of Variational Problems
2.2.2. Solution of Variational Problems
2.3. Optimization of VMD Parameters by Genetic Algorithm
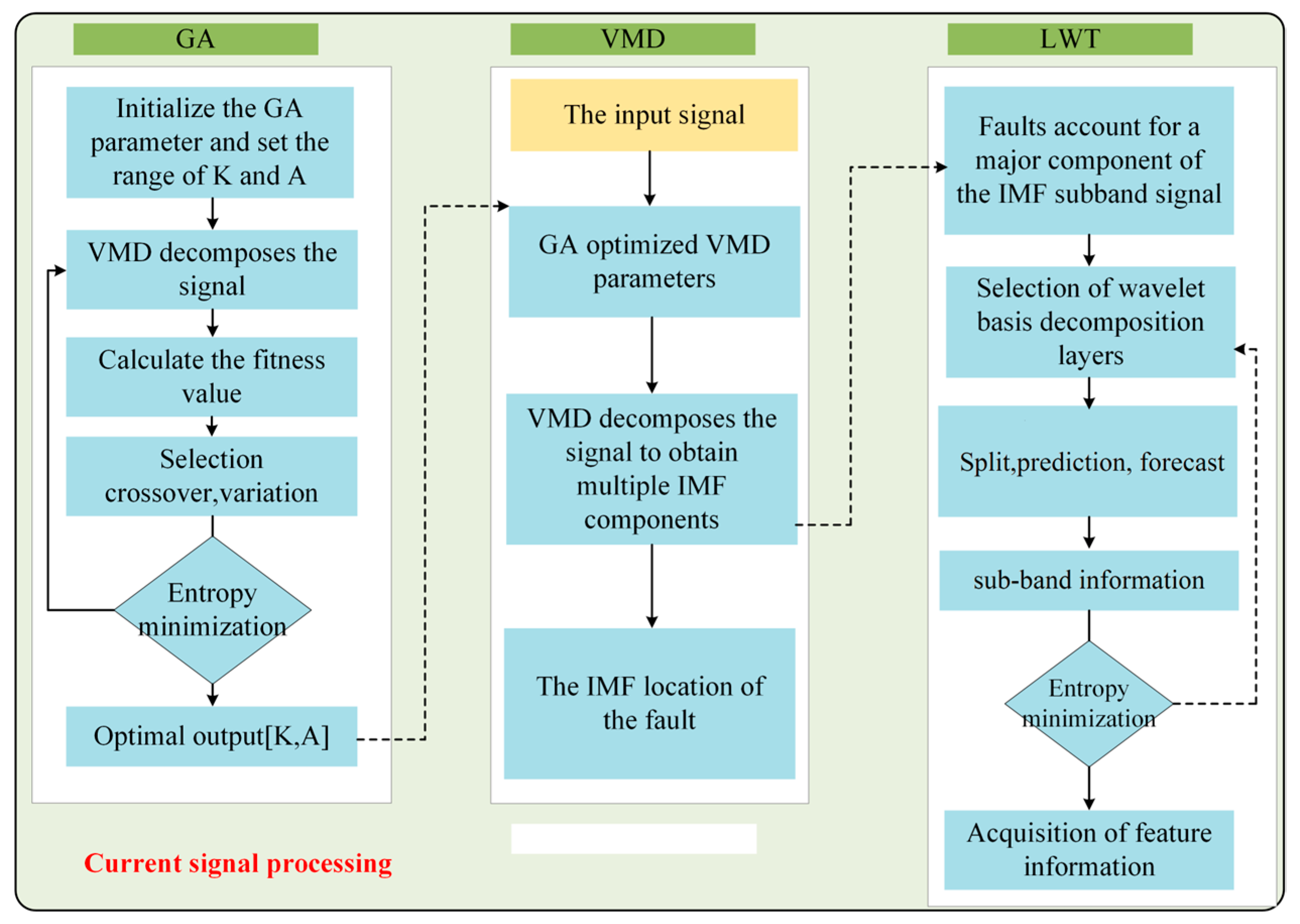
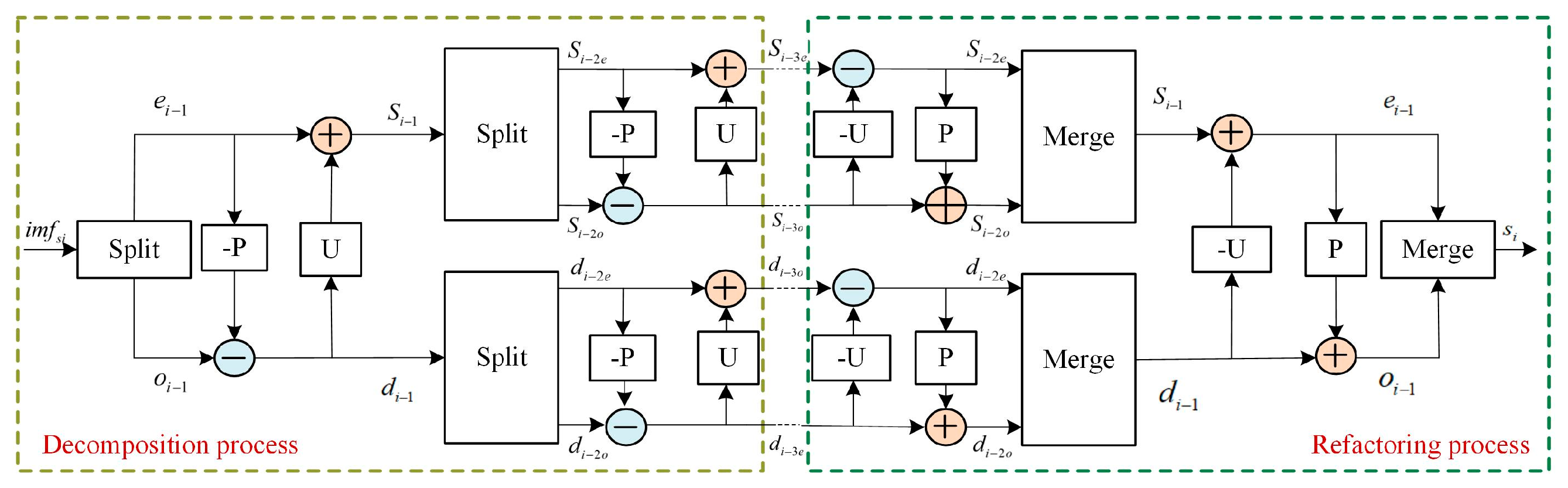
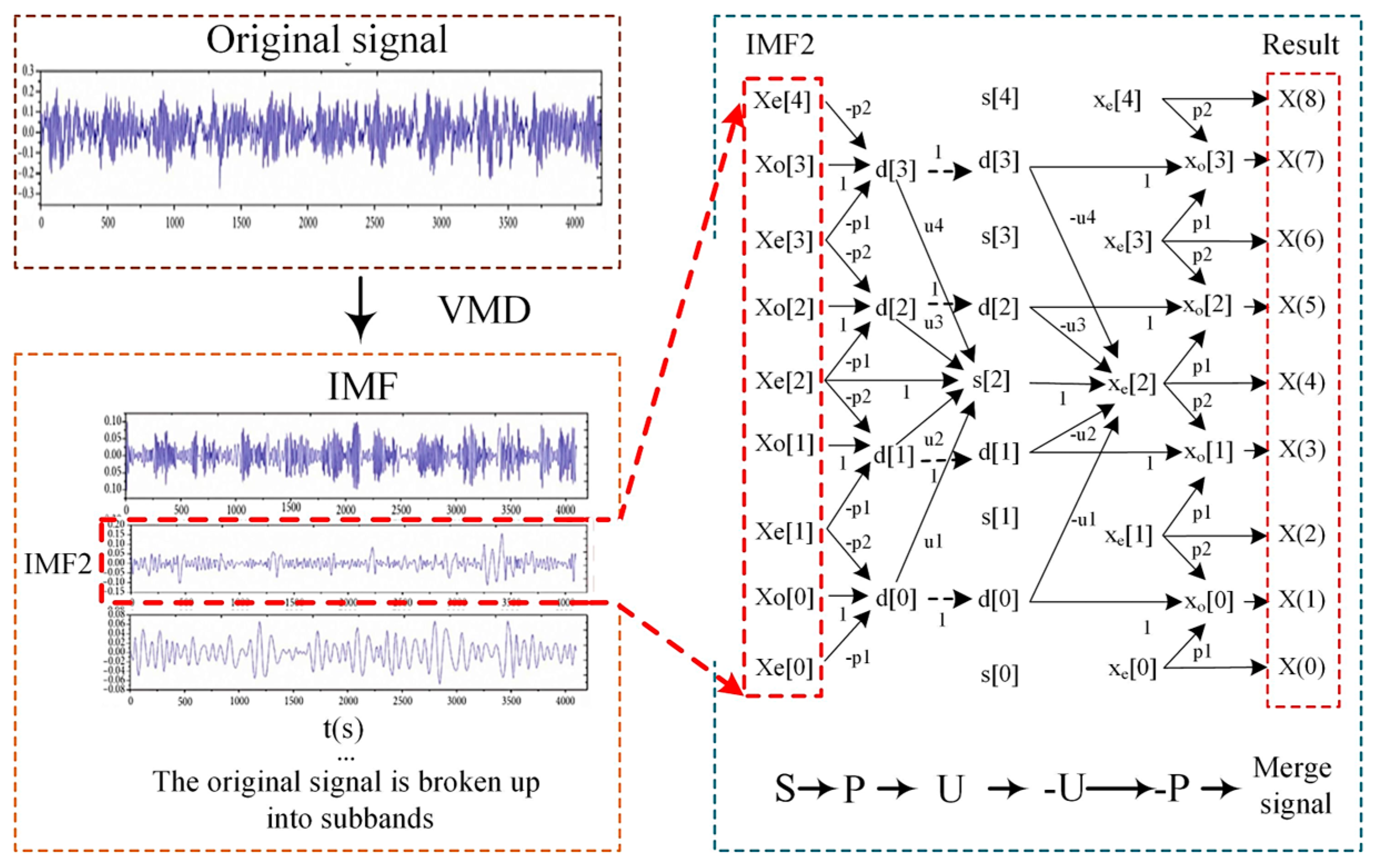
2.4. Fault Feature Extraction Strategy Based on VMD and LWT
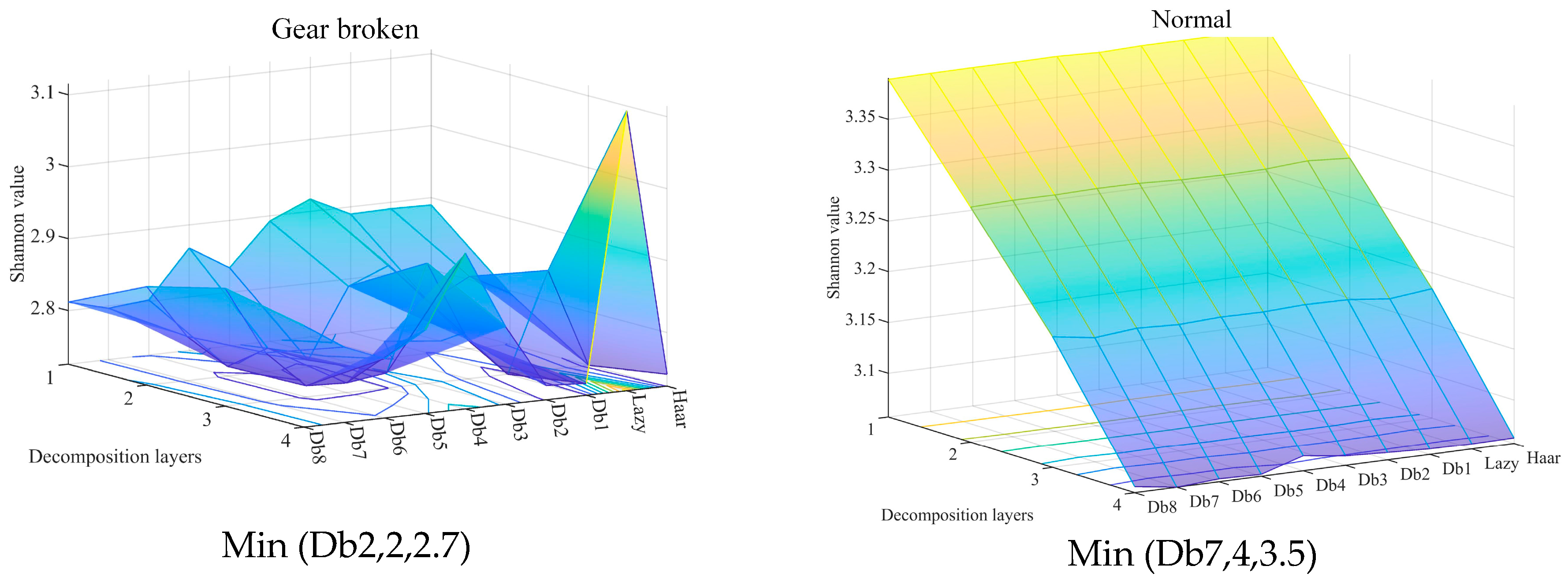
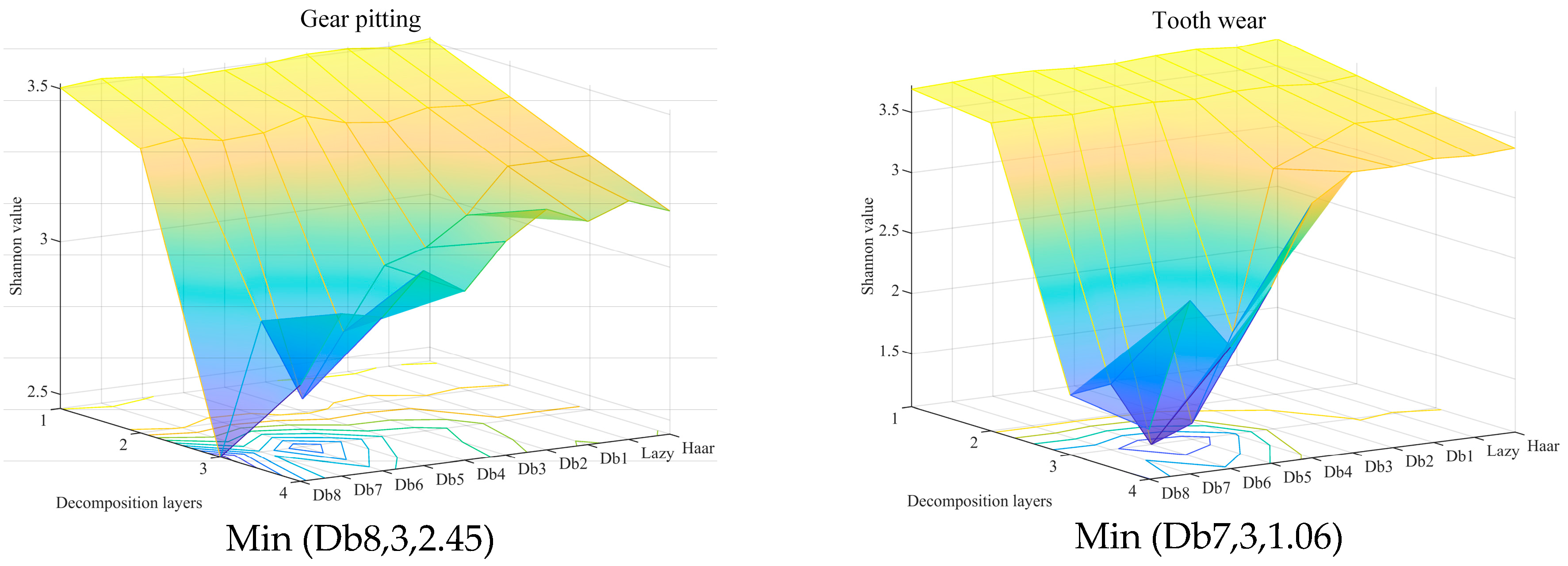
2.5. Determination Criterion of Sensitive Parameters of VMD-LWT Based on Entropy
2.6. The Proposed Method
3. Experimental Validation
3.1. Current Data Acquisition
3.2. Frequency Band Division Based on VMD-GA
3.3. Feature Enhancement Based on VMD-LWT Algorithm
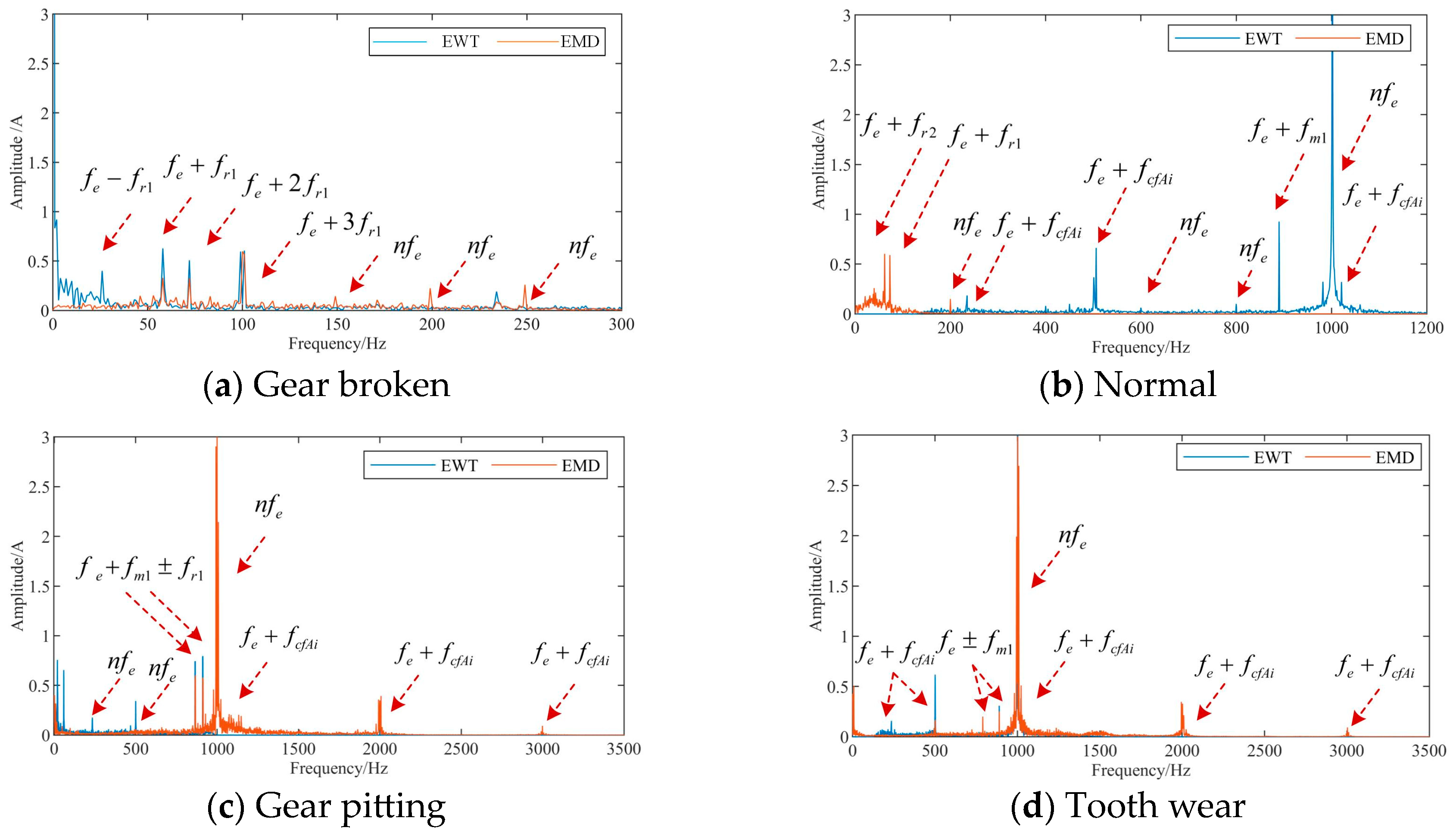
4. Comparative Test Under Load Interference
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, Y.L.; Cai, T.T.; Zhang, X.Q. A multifactor coupling prediction model for the failure depth of floor rocks in fully mechanized caving mining: A numerical and in situ study. R. Soc. Open Sci. 2019, 6, 190528. [Google Scholar] [CrossRef] [PubMed]
- Fedorko, G.; Nečas, J.; Zegzulka, J.; Gelnar, D.; Molnár, V.; Tomašková, M. Measurement of Amount for Steel Abrasive Material Transported by Special Scraper Conveyor. Appl. Sci. 2021, 11, 1852. [Google Scholar] [CrossRef]
- Liang, X.H.; Zuo, M.J.; Feng, Z.P. Dynamic modeling of gearbox faults: A review. Mech. Syst. Signal Process. 2018, 98, 852–876. [Google Scholar] [CrossRef]
- Ding, H.; Liu, Y.; Liu, J. Volumetric tooth wear measurement of scraper conveyor sprocket using shape from focus-based method. Appl. Sci. 2019, 9, 1084. [Google Scholar] [CrossRef]
- Zhao, S.F.; Zhao, J.J.; Lu, Z.X.; He, H.T.; Zhang, C.W.; Miao, Y.; Xing, Z.Z. Data-Driven Cooperative Control Model of Shearer-Scraper Conveyor Based on Rough Set Theory. Front. Energy Res. 2022, 10, 811648. [Google Scholar] [CrossRef]
- Gómez, M.J.; Marklund, P.; Strombergsson, D.; Castejón, C.; Prada, J.C.G. Analysis of vibration signals of drivetrain failures in wind turbines for condition monitoring. Exp. Tech. 2020, 45, 1–12. [Google Scholar] [CrossRef]
- Yin, A.; Yan, Y.; Zhang, Z.; Li, C.; Sánchez, R.-V. Fault diagnosis of wind turbine gearbox based on the optimized LSTM neural network with cosine loss. Sensors 2020, 20, 2339. [Google Scholar] [CrossRef] [PubMed]
- Hao, H.; Fuzhou, F.; Feng, J.; Jiang, X.; Zhou, J.Z.; Zhu, J.X.; Jiang, P.C.; Li, Y.Z.; Qian, Y.C.; Sun, G.H.; et al. Gear Fault Detection in a Planetary Gearbox Using Deep Belief Network. Math. Probl. Eng. 2022, 9, 9908074. [Google Scholar] [CrossRef]
- Kia, S.H.; Henao, H.; Capolino, G.A. Gear tooth surface damage fault detection using induction machine stator current space vector analysis. IEEE Trans. Ind. Electron. 2015, 62, 1866–1878. [Google Scholar] [CrossRef]
- Chaves, D.S.A.P.; Sena, D. Fuzzy diagnostics for gearbox failures based on induction motor current and wavelet entropy. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 265. [Google Scholar]
- Blodt, M.; Chabert, M.; Regnier, J. Mechanical load fault detection in induction motors by stator current time-frequency analysis. IEEE Trans. Ind. Appl. 2006, 42, 1454–1463. [Google Scholar] [CrossRef]
- Blodt, M.; Bonacci, D.; Regnier, J.; Chabert, M.; Faucher, J. On-line monitoring of mechanical faults in variable-speed induction motor drives using the Wigner distribution. IEEE Trans. Ind. Electron. 2008, 55, 522–533. [Google Scholar] [CrossRef]
- Feng, Z.; Chen, X.; Zuo, M.J. Induction motor stator current AM-FM model and demodulation analysis for planetary gearbox fault diagnosis. IEEE Trans. Ind. Inform. 2018, 15, 2386–2394. [Google Scholar] [CrossRef]
- Izaz, R.; Hyewon, L.; Soo, K.H. Mechanical fault detection based on machine learning for robotic RV reducer using electrical current signature analysis: A data-driven approach. J. Comput. Des. Eng. 2022, 9, 417–433. [Google Scholar]
- Raouf, I.; Lee, H.; Noh, Y.R.; Youn, B.D.; Kim, H.S. Prognostic health management of the robotic strain wave gear reducer based on variable speed of operation: A data-driven via deep learning approach. J. Comput. Des. Eng. 2022, 9, 1775–1788. [Google Scholar] [CrossRef]
- Marzebali, M.H.; Kia, S.H.; Henao, H.; Capolino, G.A.; Faiz, J. Planetary gearbox torsional vibration effects on wound-rotor induction generator electrical signatures. IEEE Trans. Ind. Appl. 2016, 52, 4770–4780. [Google Scholar] [CrossRef]
- Li, F.; Pang, X.; Yang, Z. Motor current signal analysis using deep neural networks for planetary gear fault diagnosis. Measurement 2019, 145, 45–54. [Google Scholar] [CrossRef]
- Gültekin, Ö.; Cinar, E.; Özkan, K.; Yazıcı, A. Multisensory data fusion-based deep learning approach for fault diagnosis of an industrial autonomous transfer vehicle. Expert Syst. Appl. 2022, 200, 117055. [Google Scholar] [CrossRef]
- Chen, X.; Feng, Z. Induction motor stator current analysis for planetary gearbox fault diagnosis under time-varying speed conditions. Mech. Syst. Signal Process. 2020, 140, 106691. [Google Scholar] [CrossRef]
- Cheng, F.; Qu, L.; Qiao, W.; Wei, C.; Hao, L.W. Fault diagnosis of wind turbine gearboxes based on DFIG stator current envelope analysis. IEEE Trans. Sustain. Energy 2018, 10, 1044–1053. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Mahgoun, H.; Chaari, F.; Felkaoui, A. Detection of gear faults in variable rotating speed using variational mode decomposition (VMD). Mech. Ind. 2016, 17, 207. [Google Scholar] [CrossRef]
- Fan, H.; Yang, Y.; Ma, H.; Zhang, X.H.; Wan, X.; Cao, X.G.; Mao, Q.H.; Zhang, C.; Liu, Q. Root Crack Identification of Sun Gear in Planetary Gear System Combining Fault Dynamics with VMD Algorithm. Shock Vibr. 2021, 2021, 5561417. [Google Scholar] [CrossRef]
- Zhang, J.; Zhong, M.; Yao, L.G. A GOA-MSVM based strategy to achieve high fault identification accuracy for rotating machinery under different load conditions. Measurement 2020, 163, 108067. [Google Scholar] [CrossRef]
- An, X.; Yang, J. Denoising of hydropower unit vibration signal based on variational mode decomposition and approximate entropy. Trans. Inst. Meas. Control 2016, 38, 282–292. [Google Scholar] [CrossRef]
- Liu, C.; Cheng, G.; Chen, X.H.; Pang, Y.S. Planetary gears feature extraction and fault diagnosis method based on VMD and CNN. Sensor 2018, 18, 1523. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, W.; Ding, Q. Understanding and improving deep learning-based rolling bearing fault diagnosis with attention mechanism. Signal Process. 2019, 161, 136–154. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Wang, S.; Yang, Z.J.; Cai, L. The transporting efficiency and mechanical behavior analysis of scraper conveyor. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 3315–3324. [Google Scholar] [CrossRef]
- Xing, Z.Z.; Zhao, S.F.; Guo, W.; Guo, X.J.; Wang, S.Q.; Li, M.Y.; Wang, Y.; He, H.T. Analyzing point cloud of coal mining process in much dust environment based on dynamic graph convolution neural network. Environ. Sci. Pollut. Res. 2022, 30, 4044–4061. [Google Scholar] [CrossRef] [PubMed]
- Kia, S.H.; Henao, H.; Capolino, G.A. Analytical and experimental study of gearbox mechanical effect on the induction machine stator current signature. IEEE Trans. Ind. Appl. 2009, 45, 1405–1415. [Google Scholar] [CrossRef]
- Yacamini, R.; Smith, K.S.; Ran, L. Monitoring torsional vibrations of electro-mechanical systems using stator currents. J. Vib. Acoust. 1998, 120, 72–79. [Google Scholar] [CrossRef]
- Yang, B.S.; Oh, M.S.; Tan, A.C.C. Fault diagnosis of induction motor based on decision trees and adaptive neuro-fuzzy inference. Expert Syst. Appl. 2009, 36, 1840–1849. [Google Scholar]
- Zhang, R.; Gu, F.; Mansaf, H. Gear wear monitoring by modulation signal bispectrum based on motor current signal analysis. Mech. Syst. Signal Process. 2017, 94, 202–213. [Google Scholar] [CrossRef]
- Sun, S.G.; Pang, Y.; Wang, J.Q.; Zhang, C.; Du, T.H.; Yu, H. EEMD harmonic detection method based on the new wavelet threshold denoising pretreatment. Power Syst. Prot. Control 2016, 44, 42–48. [Google Scholar]
- Guijarro, F.; Martínez-Gómez, M.; Visbal-Cadavid, D. A model for sector restructuring through genetic algorithm and inverse DEA. Expert Syst. Appl. 2020, 154, 113422. [Google Scholar] [CrossRef]
- Chen, Q.Z.; Zhang, C.R.; Hu, T.L.; Zhou, Y.; Ni, H.P.; Wang, T. Online chatter detection in robotic machining based on adaptive variational mode decomposition. Int. J. Adv. Manuf. Technol. 2021, 117, 555–577. [Google Scholar] [CrossRef]
- Sun, H.; Zi, Y.Y.; He, Z.J.; Yuan, Y.; Wang, X.D. Customized multiwavelets for planetary gearbox fault detection based on vibration sensor signals. Sensors 2013, 13, 1183–1209. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Cao, S.; Ren, G.X.; Su, F.X.; Jiang, H.; Zhao, Q. LW-Net: An interpretable network with smart lifting wavelet kernel for mechanical feature extraction and fault diagnosis. Neural Comput. Appl. 2022, 34, 15661–15672. [Google Scholar] [CrossRef]
- Wang, Y.K.; Li, H.R.; Wang, B.; Xu, B.H. Spatial information entropy and its application in the degradation state identification of hydraulic pump. Math. Probl. Eng. 2015, 2015, 532684. [Google Scholar] [CrossRef]
- Wang, W.B.; Guo, S.; Zhao, S.F.; Lu, Z.X.; Xing, Z.Z.; Jing, Z.; Wei, Z.; Wang, Y. Intelligent Fault Diagnosis Method Based on VMD-Hilbert Spectrum and ShuffleNet-V2: Application to the Gears in a Mine Scraper Conveyor Gearbox. Sensors 2023, 23, 4951. [Google Scholar] [CrossRef] [PubMed]
- Marta, W.; Adam, K. Application of Continuous Wavelet Transform and Artificial Naural Network for Automatic Radar Signal Recognition. Sensors 2022, 22, 7434. [Google Scholar] [CrossRef]
- Fu, Z.; Chang, L.; Yang, J.W.; Wang, S. An Improved MobileNet Network with Wavelet Energy and Global Average Pooling for Rotating Machinery Fault Diagnosis. Sensors 2022, 22, 4427. [Google Scholar] [CrossRef]
- Yu, G.; Gao, M.; Jia, C. A fast filtering method based on adaptive impulsive wavelet for the gear fault diagnosis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 1994–2008. [Google Scholar] [CrossRef]
- Qin, Y. A new family of model-based impulsive wavelets and their sparse representation for rolling bearing fault diagnosis. IEEE Trans. Ind. Electron. 2017, 65, 2716–2726. [Google Scholar] [CrossRef]


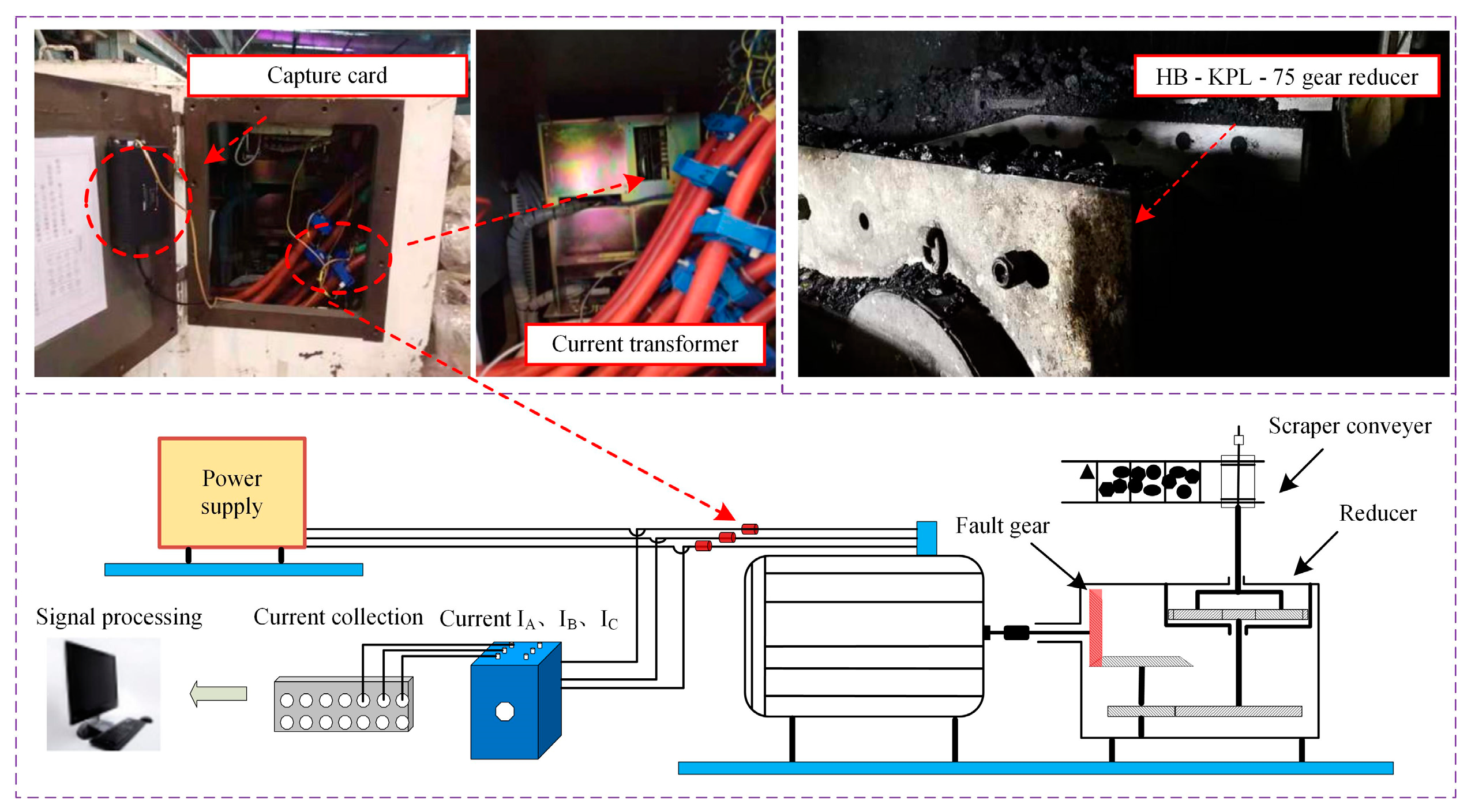




| Gear Name | Number of Teeth | Rotation Frequency (Hz) | Gear Mesh Frequency (Hz) |
|---|---|---|---|
| Bevel gear | 36 | 23.3 | |
| Bevel gear | 70 | ||
| Helical gear | 36 | ||
| Helical gear | 83 | ||
| Sun wheel | 17 | ||
| Planetary gear | 21 | ||
| Internal gear ring | 71 |
| Parameter | Setting |
|---|---|
| Penalty factor | 1000–4500 |
| Decomposition layers | 3–8 |
| Generations | 10 |
| Population size | 20 |
| Mutation probability | 0.18 |
| Crossover probability | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Li, L.; Zhang, C.; Zhao, S.; Gong, L. Fault Feature Extraction Based on Variational Modal Decomposition and Lifting Wavelet Transform: Application in Gear of Mine Scraper Conveyor Gearbox. Machines 2024, 12, 871. https://doi.org/10.3390/machines12120871
Lu Z, Li L, Zhang C, Zhao S, Gong L. Fault Feature Extraction Based on Variational Modal Decomposition and Lifting Wavelet Transform: Application in Gear of Mine Scraper Conveyor Gearbox. Machines. 2024; 12(12):871. https://doi.org/10.3390/machines12120871
Chicago/Turabian StyleLu, Zhengxiong, Linyue Li, Chuanwei Zhang, Shuanfeng Zhao, and Lingxiao Gong. 2024. "Fault Feature Extraction Based on Variational Modal Decomposition and Lifting Wavelet Transform: Application in Gear of Mine Scraper Conveyor Gearbox" Machines 12, no. 12: 871. https://doi.org/10.3390/machines12120871
APA StyleLu, Z., Li, L., Zhang, C., Zhao, S., & Gong, L. (2024). Fault Feature Extraction Based on Variational Modal Decomposition and Lifting Wavelet Transform: Application in Gear of Mine Scraper Conveyor Gearbox. Machines, 12(12), 871. https://doi.org/10.3390/machines12120871






