Unbalanced Position Recognition of Rotor Systems Based on Long and Short-Term Memory Neural Networks

Abstract

Rotor unbalance stands as one of the primary causes of vibration and noise in rotating equipment. Accurate identification of unbalanced positions enables targeted measures for balance correction, thereby reducing vibration and noise levels and enhancing the operational efficiency and stability of the equipment. However, the complexity of rotor structures may lead to a diversity of vibration transmission paths, which complicates the identification of unbalanced positions. In this paper, an experimental platform for rotor systems is established to analyze the change patterns of vibration displacement in rotor systems at four unbalanced positions. Additionally, a rotor dynamics model is developed based on the finite element method and verified through experiments. Furthermore, an unbalanced rotor position identification method based on Long Short-Term Memory (LSTM) neural networks is proposed. This method utilizes multiple sets of measured response data and simulated data from unbalanced rotor positions to train the LSTM network, achieving precise identification of unbalanced positions at various rotational speeds. The research results indicate that under subcritical, critical, and supercritical speeds, the identification accuracy based on measured data reaches 95.5%, while the accuracy based on simulated data remains at a high level of 90.5%. These results fully validate the effectiveness and accuracy of the proposed model and identification method, providing new insights and technical means for identifying unbalanced rotor positions.

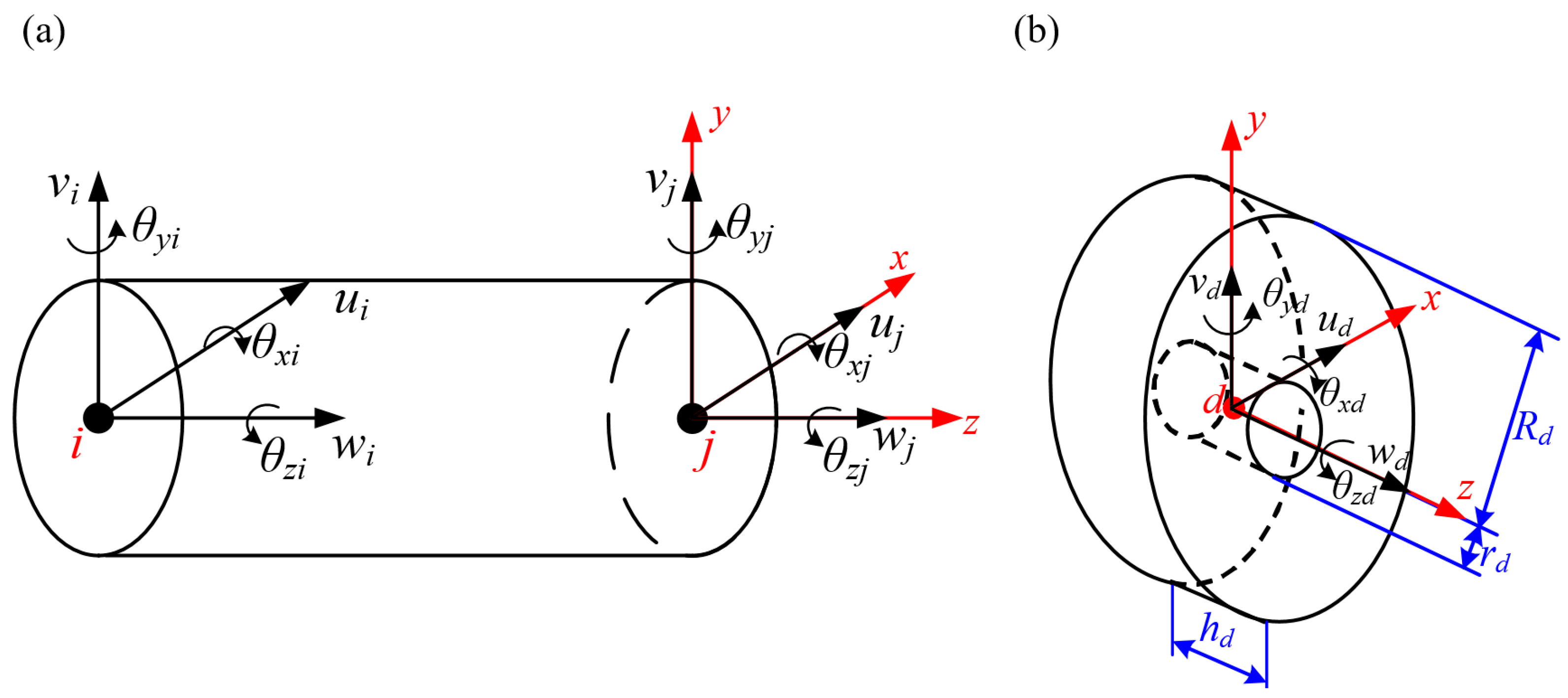
1. Introduction

The rotor system serves as a fundamental component of an aero-engine, primarily consisting of crucial parts such as the high-pressure compressor rotor and high-pressure turbine rotor, which are assembled into a unified whole through coupling devices. Before being reassembled and interconnected, both the compressor and turbine rotors undergo individual dynamic balancing. However, unbalanced faults in the rotors frequently lead to excessive vibration of the entire aero-engine [1]. Especially in extreme operating conditions, characterized by high temperatures, high pressures, and high speeds, unbalanced conditions are significantly amplified, exceeding controllable limits and potentially causing severe faults such as blade rubbing, which poses a severe threat to the longevity of the aero-engine [2]. Therefore, the accurate identification of unbalanced positions within the rotor system, followed by effective prediction, monitoring, and control of unbalance vibrations, has emerged as a critical technical challenge that demands immediate attention and innovative solutions.

Investigating the dynamic characteristics of rotor systems and constructing corresponding dynamic models can reveal the motion laws and vibration characteristics of rotors under complex operating conditions, thereby providing theoretical support for the identification and diagnosis of unbalance faults. In terms of dynamic modeling of rotor systems, the primary methods encompass the analytical method [3,4,5], the lumped parameter method [6,7,8], the transfer matrix method [9], and the finite element method [10,11,12,13]. Zhao et al. [3] established an analytical model for a flexible shaft-disk-drum rotor, examining the influence patterns of uncertain parameters on the vibration response of rotor systems with elastic supports. Miao et al. [4] built a rotor dynamic model considering the coupling of the coupling shaft based on the analytical method and subsequently explored the nonlinear vibration characteristics of the system on this basis, analyzing the characteristics of friction faults. Luo et al. [6] adopted the lumped mass method to establish a coupling model for rotor systems, taking into account angular misalignment and analyzed the influence of structural parameters of squeeze film dampers on the nonlinear vibration characteristics of the system. Li et al. [7] further established a lumped mass model for bolted-disk joints, deeply discussing the significant impact of tangential stiffness and bending stiffness at bolted connections on the vibration response of the system. Gupta et al. [9] utilized the extended transfer matrix method to establish a dynamic model for dual-rotor systems, studying the effects of rotational inertia and gyroscopic moments on the dynamic characteristics of the system and conducting a stability analysis of the system. Qin et al. [10] derived an analytical model for the bending stiffness of disk-drum connection structures and introduced it into the finite element model of rotor systems, solving the dynamic equations of rotor systems using the harmonic balance method. Lu et al. [11] established a finite element model for dual-rotor systems with breathing cracks and analyzed the dynamic response of these systems using the harmonic balance method. Chen et al. [12] considered spatial crack faults to establish a finite element model for gear-rotor systems, analyzing the impact of gear mesh stiffness and cracks on mesh stiffness and the vibration response of the system.

Rotor unbalance can induce severe vibrations in aero-engines, with the majority of mechanical failures in such engines being vibration-induced or vibration-related [14,15,16,17,18,19]. Therefore, an in-depth analysis of the influence patterns of rotor unbalance on system vibration characteristics is particularly significant. Numerous scholars have conducted extensive research on this issue. Yu et al. [14] performed dynamic modeling of a dual-rotor system in an aero-engine and found that, during the operation of turbofan engines, rotor blades not only introduce sudden unbalances and inertial asymmetries but also impose significant impact loads, leading to friction between the rotor and stator. Wang et al. [15] established a dynamic model that considered the nonlinear force coupling effects of squeeze film dampers and intermediate bearings in a dual-rotor system under multiple unbalanced forces. Through simulations, they observed that the rotor system exhibits quasi-periodic motion with four cycles near the critical speed. Yang et al. [16] addressed the issue of fixed-point friction in aero-engines by developing a mechanical vibration model for a dual-rotor system under the coupling effects of two unbalanced rotors and fixed-point friction. Chen et al. [20,21] proposed an assembly optimization method for multi-stage rotors in a specific type of aero-engine, using coaxiality and unbalance parameters as dual objective functions and employing genetic algorithms to solve for the optimal assembly angles of rotors at various stages. Song et al. [22] established a prediction model for unbalance in multi-stage assembled rotors, accurately forecasting bilateral unbalances and their acting phases in multi-stage rotors. In summary, the influence of rotor unbalance on the vibration characteristics of aero-engine is a complex and important issue. By conducting in-depth research on this issue, not only can the operational stability and reliability of aero-engines be improved, but valuable support can also be provided for the design and optimization of aero-engines.

Rotor unbalance can exacerbate vibrations in aero-engines, adversely impacting their operational stability and service life. In response to this challenge, numerous scholars have conducted in-depth research. Jiang et al. [23] proposed a method for dynamic unbalance compensation by generating control signals based on the real-time position of the rotor’s unbalanced mass. They analyzed the control performance under different unbalance phases, optimization step sizes, and noise levels. Ma et al. [24] delved into the impact of unbalanced rotor vibration coupling, vibration transmission, and sensitivity on overall machine vibration and dynamic balance, revealing the intricate mechanisms through which unbalanced location, magnitude, and phase influence rotor vibration response. Wang et al. [25] further explored the influence of rotational speed and rotor unbalance on the deviation between static and dynamic balance positions of the rotor. They discovered that, under the influence of rotational unbalanced forces, there is a significant deviation between the rotor’s dynamic and static balance positions, and this deviation approximates a linear relationship with rotational speed. Therefore, accurately identifying the unbalanced rotor position is crucial for precise fault diagnosis and rapid response. However, traditional methods for identifying unbalanced rotor positions often rely on empirical judgments and extensive test data, making it challenging to accurately capture subtle changes in unbalanced vibrations. With the advancement of signal processing technology and machine learning algorithms, in-depth analysis of vibration data can be conducted to achieve real-time monitoring and precise identification of unbalanced states, providing strong support for preventive maintenance and health management of engines. Han et al. [26,27] proposed a transfer learning method for unbalanced rotor fault localization that combines finite element models of rotor dynamics with experimental data. Although it achieves unbalanced rotor position identification to a certain extent, its accuracy and efficiency still require further enhancement.

In the research of rotor unbalance issues, Artificial Neural Networks (ANNs) have demonstrated immense potential in assisting the dynamic balancing process. Compared to traditional dynamic balancing methods, which often rely on experience and manual adjustments, ANNs can automatically adjust the rotor’s balance state by deeply learning and simulating critical data such as vibration signals, thereby enhancing the precision and efficiency of rotor balancing. Santos et al. [28] established an analytical model for rotor systems supported by sliding bearings, utilizing plane separation techniques and ANNs to predict the position and magnitude of the balance correction masses for rotor systems. This method provides an effective pathway for continuous monitoring of dynamic balancing in rotating machinery. Walker et al. [29] further employed a data-driven approach, utilizing ANNs to achieve automatic localization of rotor unbalance and incorporating friction and misalignment faults into their research to validate the system’s stability and reliability. Yan et al. [30] proposed an unbalanced rotor fault diagnosis method based on the Deep Belief Network (DBN), which can automatically learn typical features of rotor unbalance faults and accurately identify unbalance fault states. Zhong et al. [31,32] introduced a rotor balancing method based on unsupervised deep learning, capable of efficiently determining the magnitude and position of unbalance in two correction planes. Xing et al. [33] utilized Convolutional Neural Networks (CNNs) to detect the magnitude and position of dynamic unbalance in wind turbine rotors, with the natural modal functions of nacelle vibrations as the input variables, successfully discerning weak unbalance signals. Long Short-Term Memory (LSTM) networks, a variant of Recurrent Neural Networks (RNNs) designed for processing sequential data [34,35], have exhibited exceptional performance in many application scenarios due to their ability to learn and remember long-term dependencies. In the research of unbalanced rotor issues, LSTM networks also have broad application prospects and are anticipated to provide innovative solutions for the intellectualization and automation of rotor balancing processes.

This paper is organized as follows: In Section 2, the dynamic model of the rotor system is established using the finite element method, comprehensively considering the shaft, disks, support elements, and couplings. Following the establishment of the model, a rotor test tig is constructed, and preliminary modal validation is conducted to ensure the accuracy and reliability of the model. This validation step is crucial as it provides a solid foundation for subsequent experiments and analyses. In Section 3, vibration response experiments and simulation studies are carried out on the rotor system. These experiments are designed to assess the system’s behavior at four different unbalanced positions and under various rotational speeds. The results obtained from these experiments further confirm the accuracy and reliability of the established dynamic model, reinforcing our confidence in its predictive capabilities. Additionally, an LSTM neural network structure is constructed, and deep training and intelligent analysis are performed on rotor vibration data. This advanced analysis enables us to effectively identify the rotor’s unbalanced positions, which is a critical step in fault diagnosis and predictive maintenance. In Section 4, the identification results are analyzed and discussed. Section 5 summarizes the research conclusions of this paper. The innovation of this paper lies in the first application of the LSTM neural network to identify the unbalanced position of an aero-engine turbine rotor. LSTM networks are particularly suitable for processing time-varying vibration signal sequence data, which makes them ideal for dealing with unbalanced position identification problems. By training the LSTM model on a comprehensive dataset containing experimental and simulation data at different speeds, it is able to learn complex relationships between vibration patterns and unbalanced positions.

2. Rotor System Dynamics Modeling and Verification

During the operation of an aero-engine rotor system, its working rotational speed often exceeds the range of two critical speeds. Under such high-speed conditions, even minute unbalances on flexible shafts can trigger significant vibrations, thereby exacerbating the unbalanced vibration response of the rotor. Therefore, conducting in-depth research on the vibration characteristics of aero-engine rotor systems is particularly crucial, with the establishment of an accurate dynamic model crucial for accurately describing and predicting the system’s vibration behavior. This section will mainly focus on the following three aspects: First, simplifying the model to eliminate unnecessary complexity while preserving the system’s primary dynamic characteristics; Second, establishing differential equations of motion based on the simplified model to mathematically describe the system’s vibration behavior; Finally, validating the model to ensure that it accurately reflects the vibration characteristics of the actual system.

2.1. Rotor Dynamics Modeling

The finite element method (FEM) is utilized for dynamic modeling of aero-engine rotor systems in this paper. The core principle of FEM involves dividing the entire system into multiple elements with specific shapes and degrees of freedom. These elements are interconnected through physical relationships at nodes to construct the dynamic equations of the entire system. The aero-engine rotor system constitutes a complex coupled system comprising components such as rotor shafts, disks, bearings, and couplings arranged in a specific quantity and sequence.

2.1.1. Rotating Shaft Model

The rotor shaft of an aero-engine is divided into several axial segments, and in this paper, Timoshenko beam elements are used for equivalence. Each beam element is comprised of two nodes, with each node possessing six degrees of freedom. A schematic diagram of the beam element is shown in Figure 1a. In the coordinate system oxyz, u, v, and w represent the displacements of the node in the x, y, and z axes, respectively, while θ_x, θ_y, and θ_z represent the angular displacements of the node in the x, y, and z axes, respectively. Therefore, the node displacement vector for the beam element is as follows:

$${\mathit{q}}^{\mathrm{e}}={[u_i,v_i,w_i,{\theta }_{xi},{\theta }_{yi},{\theta }_{zi},u_j,v_j,w_j,{\theta }_{xj},{\theta }_{yj},{\theta }_{zj}]}^{\mathrm{T}}$$

(1)

According to Hamilton’s principle, the expressions of the beam element’s mass matrix ${\mathit{M}}^{\mathrm{e}}$, stiffness matrix ${\mathit{K}}^{\mathrm{e}}$, and gyroscopic matrix ${\mathit{G}}^{\mathrm{e}}$ are as follows:

$$\left\{\begin{array}{ll}{\mathit{M}}^{\mathrm{e}}=& {\displaystyle {\int }_L\rho A({\mathit{N}}_u^{\mathrm{T}}{\mathit{N}}_u+{\mathit{N}}_v^{\mathrm{T}}{\mathit{N}}_v+{\mathit{N}}_w^{\mathrm{T}}{\mathit{N}}_w)+\rho (I_x{\mathit{N}}_u^{\mathrm{T}}{\mathit{N}}_u+I_y{\mathit{N}}_v^{\mathrm{T}}{\mathit{N}}_v+I_z{\mathit{N}}_w^{\mathrm{T}}{\mathit{N}}_w)\mathrm{d}x}\\ {\mathit{K}}^{\mathrm{e}}=& {\int }_{L}EA{{\mathit{N}}^{\prime }}_u^{\mathrm{T}}{\mathit{N}}_u^{\prime }+{\kappa }_{y}GA{{\mathit{N}}^{\prime }}_v^{\mathrm{T}}({\mathit{N}}_v^{\prime }-{\mathit{N}}_{\phi })+{\kappa }_{z}GA{{\mathit{N}}^{\prime }}_w^{\mathrm{T}}({\mathit{N}}_w^{\prime }+{\mathit{N}}_{\phi })+GJ{{\mathit{N}}^{\prime }}_{{\theta }_x}^{\mathrm{T}}{\mathit{N}}_{{\theta }_x}^{\prime }\\ & +E{I}_y{{\mathit{N}}^{\prime }}_{{\theta }_y}^{\mathrm{T}}{\mathit{N}}_{{\theta }_y}^{\prime }+EI{{\mathit{N}}^{\prime }}_{{\theta }_z}^{\mathrm{T}}{\mathit{N}}_{{\theta }_z}^{\prime }+{\kappa }_{z}GA{{\mathit{N}}^{\prime }}_{{\theta }_y}^{\mathrm{T}}({\mathit{N}}_w^{\prime }+{\mathit{N}}_{{\theta }_y})-{\kappa }_{y}GA{\mathit{N}}_{{\theta }_z}^{\mathrm{T}}({\mathit{N}}_v^{\prime }-{\mathit{N}}_{{\theta }_z})\mathrm{d}x\\ {\mathit{G}}^{\mathrm{e}}=& {\displaystyle {\int }_L\Omega \rho I_x({\mathit{N}}_{{\theta }_y}^{\mathrm{T}}{\mathit{N}}_{{\theta }_z}-{\mathit{N}}_{{\theta }_z}^{\mathrm{T}}{\mathit{N}}_{{\theta }_y})\mathrm{d}x}\end{array}\right.$$

(2)

where N_n (n = u, v, w, θ_x, θ_y, θ_z) represents the element-shaped function, ρ is the material density, and A is the cross-sectional area of the element. I_x, I_y, and I_z represent the moment of inertia of the section with respect to the x, y, and z axes, respectively. J is the torsion moment of inertia, $\Omega$ is the angular velocity of rotation, and κ_y and κ_z represent the shear coefficient with respect to the y and z axes, respectively. Since the cross-section is circular, the expressions for the shear coefficients κ_y, κ_z, and the torsional inertia J are given as follows:

$${\kappa }_y={\kappa }_z={\displaystyle \frac{6\left(1+\upsilon \right)}{\left(7+6\upsilon \right)}}$$

(3)

$$J=\mathsf{\pi }{d}_{\mathrm{s}}^4/32$$

(4)

where d_s is the diameter of the shaft section, and υ is Poisson’s ratio.

2.1.2. Disk Model

In this paper, a lumped mass model is employed for the disk [36], equating them to mass points fixed at the nodes of the rotor shaft with specific mass and rotational inertia. It is assumed that the unbalanced forces of the rotor only act on the two nodes corresponding to the disks. The expressions for the element mass matrix ${\mathit{M}}_{\mathrm{d}}^{\mathrm{e}}$ and the element gyroscopic moment matrix ${\mathit{G}}_{\mathrm{d}}^{\mathrm{e}}$ of the disk are as follows:

$${\mathit{M}}_{\mathrm{d}}^{\mathrm{e}}=\mathrm{diag}\left(m_{\mathrm{d}},m_{\mathrm{d}},m_{\mathrm{d}},J_{\mathrm{d}},J_{\mathrm{d}},J_{\mathrm{p}}\right)$$

(5)

$${\mathit{G}}_{\mathrm{d}}^{\mathrm{e}}=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& J_{\mathrm{p}}& 0\\ 0& 0& 0& -J_{\mathrm{p}}& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$$

(6)

where the mass, diameter moment of inertia, and polar moment of inertia of the disk are m_d, J_d, and J_p, respectively, as shown in Figure 1b:

$$m_{\mathrm{d}}=\pi \rho h_{\mathrm{d}}{\left(R_{\mathrm{d}}-r_{\mathrm{d}}\right)}^2, J_{\mathrm{d}}={\displaystyle \frac{\pi \rho h_{\mathrm{d}}{\left(R_{\mathrm{d}}-r_{\mathrm{d}}\right)}^4}{4}}, J_{\mathrm{p}}={\displaystyle \frac{\pi \rho h_{\mathrm{d}}{\left(R_{\mathrm{d}}-r_{\mathrm{d}}\right)}^4}{2}}$$

(7)

where r_d is the inner radius of the disk, R_d is the outer radius of the disk, and h_d is the thickness of the disk.

2.1.3. Support Element Model

Bearings and supports are integrated to provide support for the rotor system. In this paper, a linear spring-damping model [37] is adopted for equivalent treatment of the support elements of the rotor system. Subsequently, the stiffness matrix ${\mathit{K}}_{\mathrm{b}}^{\mathrm{e}}$ and damping matrix ${\mathit{C}}_{\mathrm{b}}^{\mathrm{e}}$ of the support element can be expressed as follows:

$${\mathit{K}}_{\mathrm{b}}^{\mathrm{e}}=\mathrm{diag}\left(k_{\mathrm{b}u},k_{\mathrm{b}v},k_{\mathrm{b}w},k_{\mathrm{b}\theta x},k_{\mathrm{b}\theta y},k_{\mathrm{b}\theta z}\right)$$

(8)

$${\mathit{C}}_{\mathrm{b}}^{\mathrm{e}}=\mathrm{diag}\left(c_{\mathrm{b}u},c_{\mathrm{b}v},c_{\mathrm{b}w},c_{\mathrm{b}\theta x},c_{\mathrm{b}\theta y},c_{\mathrm{b}\theta z}\right)$$

(9)

where k_bn (n = u, v, w, θ_x, θ_y, θ_z) represents the support stiffness in the n-direction, and c_bn (n = u, v, w, θ_x, θ_y, θ_z) is the support damping in the n-direction.

2.1.4. Coupling Model

The bearing is equipped with a coupling to connect the a node of shaft 1 and the b node of shaft 2. The two halves of the coupling adopt a clearance fit, and the matching clearance is uniformly denoted as ${\delta }_{ab}$, as shown in Figure 2. The nonlinear bearing forces of the coupling in all directions $F_{cn}$(n = u, v, w, θ_x, θ_y, θ_z) can be expressed as follows:

$$F_{\mathrm{c}n}=\left\{\begin{array}{l}{k}_{\mathrm{c}n}\left(n_a-n_b\right)+c_{\mathrm{c}n}\left({\dot{n}}_a-{\dot{n}}_b\right),\left|n_a-n_b\right|>{\delta }_{ab}\\ 0,\left|n_a-n_b\right|\le {\delta }_{ab}\end{array}\right.$$

(10)

where $k_{\mathrm{c}n}$ and $c_{\mathrm{c}n}$ are the stiffness and damping of the coupling in each direction, respectively.

Therefore, the dynamic equation of the rotor system under unbalanced excitation is as follows:

$$\mathit{M}\ddot{\mathit{q}}+(\mathit{C}+\omega \mathit{G})\dot{\mathit{q}}+\mathit{K}\mathit{q}={\mathit{F}}_{\mathrm{b}}-{\mathit{G}}_{\mathrm{s}}$$

(11)

where q represents the generalized displacement vector of the rotor system, and ω denotes the rotor speed. M is the mass matrix of the rotor system, which is obtained by the mass matrix of the shaft segment element ${\mathit{M}}^{\mathrm{e}}$ and the mass matrix of the disk element ${\mathit{M}}_{\mathrm{d}}^{\mathrm{e}}$. K is the stiffness matrix of the rotor system, which can be obtained by the combination of the axial segment element stiffness matrix ${\mathit{K}}^{\mathrm{e}}$ and the supporting element stiffness matrix ${\mathit{K}}_{\mathrm{b}}^{\mathrm{e}}$. G is the gyro matrix of the rotor system, which can be obtained by grouping the axis segment element gyro matrix ${\mathit{G}}^{\mathrm{e}}$, the disk element gyro matrix ${\mathit{G}}_{\mathrm{d}}^{\mathrm{e}}$, and the damping matrix of the supporting element ${\mathit{C}}_{\mathrm{b}}^{\mathrm{e}}$. The rotor damping matrix C is simulated by proportional damping, which can be expressed as follows:

$$\mathit{C}={\alpha }_0\mathit{M}+{\beta }_0\mathit{K}$$

(12)

where the expressions of α₀ and β₀ are shown in Ref. [38].

G_s is the gravity vector, and F_b is the unbalanced rotor force vector. The unbalanced force vector and gravity vector at node i can be expressed in the following form:

$${\mathit{F}}_{\mathrm{b}}^i={\left[\begin{array}{cccccc}{F}_{\mathrm{b}ui}& F_{\mathrm{b}vi}& 0& M_{\mathrm{b}ui}& M_{\mathrm{b}vi}& 0\end{array}\right]}^{\mathrm{T}}$$

(13)

$${\mathit{G}}_{\mathrm{s}}^i={\left[\begin{array}{cccccc}0& m_{i}g& 0& 0& 0& 0\end{array}\right]}^{\mathrm{T}}$$

(14)

where g represents the acceleration of gravity, which is 9.8 m/s² in this paper. F_bui, F_bvi, M_bui, and M_bvi are the unbalanced rotor forces and moments located at node i, which can be expressed as follows:

$$\left\{\begin{array}{c}{F}_{\mathrm{b}ui}\\ F_{\mathrm{b}vi}\\ M_{\mathrm{b}ui}\\ M_{\mathrm{b}vi}\end{array}\right\}=m_i{e}_{1i}{\omega }^2\left\{\begin{array}{c}\begin{array}{l}\cos (\omega t+{\phi }_i)\\ \sin (\omega t+{\phi }_i)\end{array}\\ \begin{array}{l}-e_{2i}\sin (\omega t+{\phi }_i)\\ e_{2i}\cos (\omega t+{\phi }_i)\end{array}\end{array}\right\}$$

(15)

where φ_i is the initial phase of the unbalance, m_i is the unbalanced mass, and e_1i and e_2i are the radial and axial eccentricity, respectively. Therefore, the vibration response of the rotor system is not only related to the unbalanced amplitude and position but also to the initial phase of the unbalance.

2.2. Model Verification

To validate the effectiveness of the established rotor dynamics model, a turbine rotor system test rig is designed and constructed in this paper, with its experimental setup illustrated in Figure 3. The test rig primarily comprises four core components: the high and low-pressure turbine rotor structures, the experimental platform, the drive motor, and the lubrication system. Among these, the low-pressure turbine section utilizes a hollow, flexible, slender shaft as the main transmission component, which is fixed and supported by bearings, elastic supports, and supporting structures. The power input end is connected to the drive motor through a short shaft, and the power is then transmitted to the hollow, flexible, slender shaft through a spline connection. In contrast, the high-pressure turbine structure is more complex, consisting of various components such as a power stub shaft, two-stage high-pressure turbines, end tooth coupling structures, bearings, damping devices, and supporting structures. Power is inputted through the hollow, flexible, slender shaft and transmitted via a spline connection.

During the modeling process, a linear spring-damper model is adopted to equivalently represent the bearings and support structures within the rotor system. The rotor shaft elements are connected through nodes, while the turbine disks are treated as rigid bodies, simplified as lumped masses with gyroscopic effects. Based on the above assumptions and simplifications, the geometric model of the turbine rotor system is established, as shown in Figure 4. With the known elastic modulus of the rotor shaft E = 2.1 × 10¹¹ Pa, density ρ = 7800 kg/m³, and Poisson’s ratio ν = 0.3, the moment of inertia of the disk diameter is 0.12 kg·m² and the moment of inertia of the disk is 0.13 kg·m², the parameters of the shafts are shown in

Table 1. Comparisons of natural frequency between simulation and experiment.

Shaft Number	Length (mm)	Diameter (mm)
Shaft 1	95	32
Shaft 2	156.5	40
Shaft 3	104	70
Shaft 4	66	36
Shaft 5	162	34.8
Shaft 6	130	33.6

. The rotor dynamics model is constructed according to the generalized modeling method presented in Section 2.1.

The simulated rotor test rig designed in this paper employs a high-performance electric spindle motor as its driving component. This motor is securely connected to the transmission shaft via a coupling to ensure stable power transmission. The transmission shaft is further linked to the slender shaft through a precise spline connection, thereby effectively transmitting torque and driving the entire simulated rotor system to operate efficiently. To accurately measure the vibration displacement signals of the rotor system, four high-sensitivity eddy current sensors (Type: RP6600XL, Precision: <0.1%, Kaihang, Huanggang Hubei, China) and two acceleration sensors (Type: PCB-356A01, PCB, Buffalo, New York, NY, USA) are utilized to capture the vibration displacement signals at the measurement points, ensuring data accuracy and reliability. The test system selects an LMS acquisition instrument (LMS SCADAS Mobile) for data collection, and the experimental setup layout is shown in Figure 5. During the experiment, precise control of the driving motor is achieved through a frequency converter, enabling speed-up and speed-down tests on the rotor system to verify its inherent characteristics. The sampling frequency is 5120 Hz, and the sampling time is 10 s.

A natural characteristic analysis is conducted on the rotor system dynamics model established using the finite element method. To validate the effectiveness of the model, detailed comparisons between the simulations and the experiments are performed, as presented in

Table 2. Comparisons of natural frequency between simulation and experiment.

Frequency Order	fn1	fn2
Experiment (Hz)	121	236
Simulation (Hz)	115.8	227.3
Error (%)	4.3	3.7

. In the table, the maximum error between the simulation results and the experimental results is only 4.3%, which fully demonstrates the high accuracy and validity of the constructed dynamics model. This finding not only provides a solid theoretical foundation for subsequent rotor dynamics research but also offers powerful technical support for rotor system design in practical engineering applications.

3. Rotor Vibration Response and Unbalance Position Identification

In the previous section, the accuracy of the established dynamic model has been preliminarily verified by analyzing the inherent characteristics of the rotor system. To thoroughly validate the accuracy of the constructed dynamic model, a constant-speed test is conducted on the built test rig. During the testing process, vibration response data of the rotor system at various rotational speeds are meticulously recorded. A comprehensive comparison between these experimental data and the unbalanced vibration responses predicted by the finite element model is performed, further confirming the high accuracy and reliability of the established dynamic model. On this basis, through the construction of neural network architecture, the vibration signal data based on the measured data and the simulation data are deeply trained and intelligent analysis so as to identify the unbalanced position of the rotor, which provides a new method and method for improving the accuracy and reliability of the rotor balance.

3.1. Vibration Response Analysis of Rotor System at Different Speed

Based on Section 2.2, the first-order critical speed of the experimental system in this paper is determined to be 7260 rpm. To comprehensively evaluate the dynamic response of the rotor under different rotational speeds, constant-speed tests are conducted at subcritical (5600 rpm), critical (7260 rpm), and supercritical (8400 rpm) speeds. In the test, we set an unbalance of approximately 15 gmm millimeters (gmm) using a balance chuck to induce an observable unbalance response. This setting is designed to simulate the imbalances that may be encountered in actual operation and to assess their impact on system performance. Unbalance response analysis is an important part of rotating machinery fault diagnosis, through which we can understand the effects of unbalance on vibration, noise, and service life of the system. To verify the accuracy of the model, the signals collected by the eddy current sensor at measurement point 3 are selected for detailed analysis and comparison. The eddy current sensor is a non-contact measuring tool that accurately captures small vibration changes during the operation of rotating machinery. By comparing the measured signal with the simulation results, we can assess the predictive power of the model and identify potential sources of error.

It is noteworthy that the actual rotor test bench possesses a relatively complex structure, incorporating various friction coupling elements such as bearings and bolted connections, which may introduce nonlinear phenomena within the system. Consequently, the measured signals often exhibit greater complexity compared to simulated signals. Theoretically, unbalance solely induces rotational frequency components. However, in practical scenarios, other nonlinear frequency components may also influence the signals. To more accurately analyze the unbalanced response, band-pass filtering technology is used to eliminate the impact of other nonlinear frequencies, retaining only the rotational frequency components of the measured signals. This processing step is crucial for precisely identifying unbalanced responses.

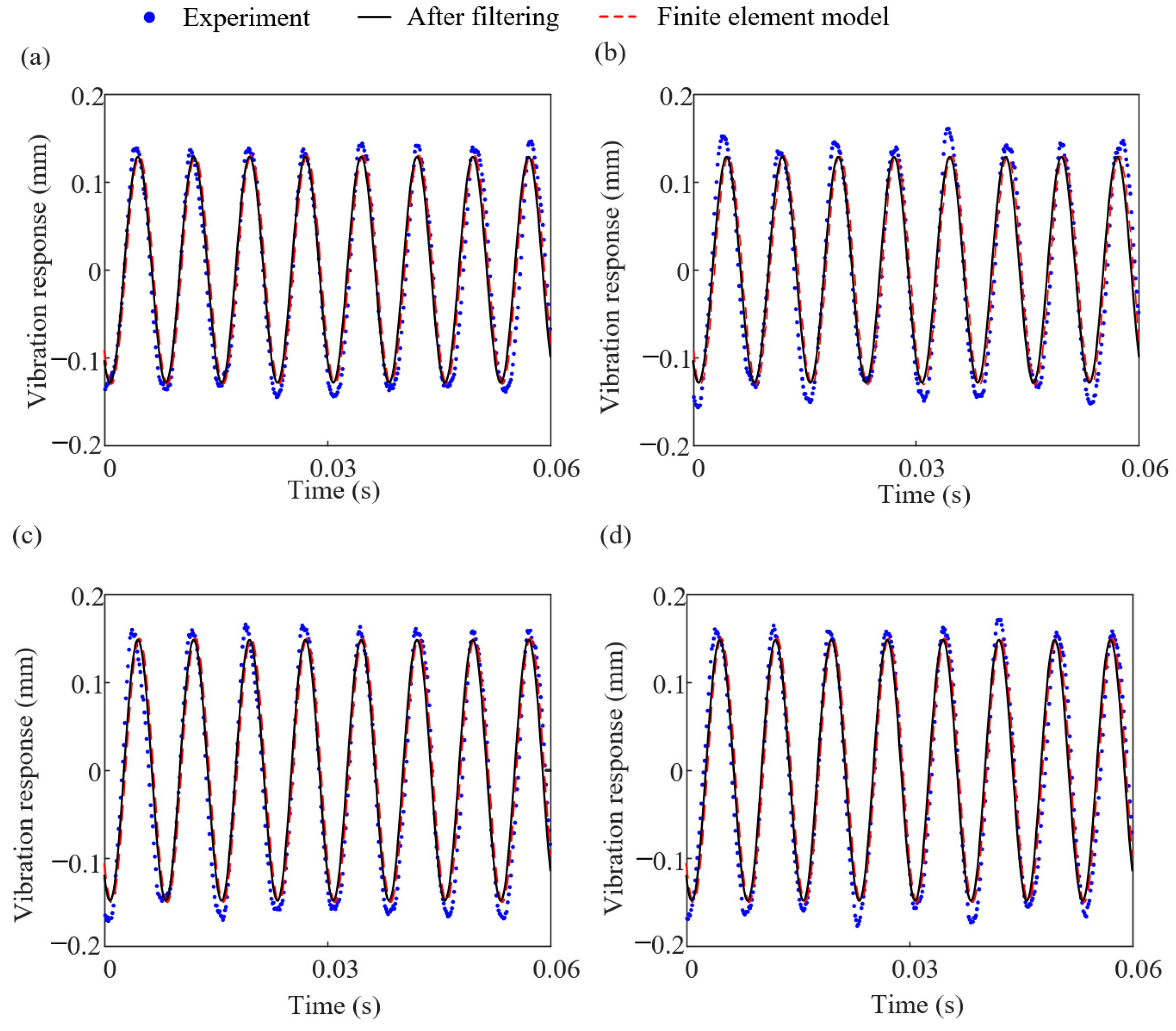
In summary, vibration experiments are conducted at four different unbalanced positions under subcritical (5600 rpm), critical (7260 rpm), and supercritical (8400 rpm) conditions. At the same time, based on the established rotor finite element model, the unbalance is added to the corresponding position of the experiment to calculate the system vibration response. The experimental results are then compared with the simulation results. The comparison results are illustrated in Figure 6, Figure 7 and Figure 8.

Through in-depth analysis of the experimental data, we can observe that, under the condition of exceeding the critical speed, the filtered experimental results of the rotor system exhibit a high degree of consistency with the simulation results. This comparison, to a certain extent, validates the rationality and accuracy of the established dynamic model. Specifically, the experimental waveform aligns well with the simulation waveform in terms of shape, amplitude, and phase. However, under subcritical and critical speed conditions, the time-domain waveform of the rotor system shows certain discrepancies. These discrepancies may primarily arise from the complexity of the test bench system. Specifically, the interfacial contact friction of components such as bearings and bolts within the test bench may more readily induce nonlinear behavior in the system. These nonlinear factors may include but are not limited to, variations in friction force, minute deformations at the contact interfaces, and the additional vibrations resulting from these. These factors collectively contribute to a certain deviation between the experimental waveform and the simulation waveform. To gain a deeper understanding of these discrepancies and further improve the accuracy of the model, future research should strengthen the study of nonlinear behavior in the test bench system, including the establishment of more precise nonlinear dynamic models.

3.2. Long Short-Term Memory Neural Network

In the research of high-speed dynamic balancing of flexible rotors, the identification of unbalanced rotor positions has always been a challenging problem. Especially for slender rotors, the axial location of unbalance has a significant impact on the high-speed dynamic balancing of the rotor. In recent years, deep learning, as a powerful machine learning technique, has achieved remarkable results in fields such as image recognition and speech recognition. In the area of unbalanced rotor position identification, deep learning techniques based on limited labeled data have also demonstrated great potential. By training deep neural networks, effective feature information can be extracted from the limited labeled data, thereby enabling accurate identification of unbalanced positions.

The LSTM (Long Short-Term Memory) network significantly enhances the neural network’s capability in processing time-series data by introducing memory cells and control units such as input gates, forget gates, and output gates. The core of its working mechanism lies in the self-looping and feedback mechanism of the internal state of the memory cells. This mechanism, combined with sophisticated gating strategies, regulates the inflow and outflow of information streams, achieving effective truncation of error signals. This ensures the stability and integrity of errors during the backward propagation process, thereby avoiding common issues in traditional recurrent neural networks, such as gradient vanishing or gradient exploding. Figure 9 provides a detailed illustration of the structural composition of the LSTM unit.

The computational process of LSTM can be divided into three stages based on its three gate structures: the forget stage, the input stage, and the output stage. During the forget stage, the forget gate assesses the significance of the information in the cell state at time (t − 1) and selects whether to retain or discard it. The important information that is retained is then passed on to the input stage:

$$f_{t1}=\sigma ({\mathit{W}}_f\left[S_{t-1},X_t\right]+{\mathit{b}}_f)$$

(16)

where ${\mathit{W}}_f$ and ${\mathit{b}}_f$ are the weight matrix and bias vector of the forgetting gate, respectively, $\sigma$ is the Sigmoid activation function, $S_{t-1}$ represents the output value of the network hidden layer at time (t − 1) and $X_t$ is the input parameter of the structure at time t. In addition, when $f_{t1}=0$, it represents the cell state of (t − 1) at the moment of complete abandonment, while when $f_{t1}=1$, it represents the cell state of complete retention of (t − 1).

The input stage mainly stores the input data at time (t − 1) and the important information in the hidden state at time t in the cell state through the relevant calculation of the input gate:

$$U_t=\sigma \left({\mathit{W}}_u\left[S_{t-1},X_t\right]+{\mathit{b}}_u\right)$$

(17)

$$U_t=\sigma \left({\mathit{W}}_u\left[S_{t-1},X_t\right]+{\mathit{b}}_u\right)$$

(18)

$$f_{t2}=U_t\otimes P_t$$

(19)

where W_u and W_p are the weight matrices of input gate and loop cell states, respectively, b_u and b_p are the bias vectors of the input gate and the loop unit, respectively, and $\otimes$ represents the element-by-element product operation between vectors.

The output phase mainly determines the output of the LSTM unit at time t through the output gate:

$$o_t=sigmoid\left({\mathit{W}}_o\left[S_{t-1}, X_t\right]+{\mathit{b}}_o\right)$$

(20)

$$C_t=C_{t-1}\otimes f_{t1}\oplus f_{t2}$$

(21)

$$S_t=o_t\otimes \mathit{tanh}\left(C_t\right)$$

(22)

where C_t and C_t−1 are the output of the memory unit at time t and (t − 1), respectively. W_o and b_o are the weight matrix and bias vector of the output stage, respectively. For a single-output network, the output of the output layer is represented as follows:

$$Y_t=sigmoid\left({\mathit{W}}_Y{S}_t+{\mathit{b}}_Y\right)$$

(23)

where Y_t is the corresponding matrix of X_t at time t, and W_Y and b_Y are the weight matrix and bias vector of the output gate.

3.3. Unbalanced Position Identification of Rotor Based on LSTM

In flexible rotor systems, unbalance is one of the primary causes of vibration and noise. For slender rotors, due to their long axial extension, the occurrence of unbalance at different locations will directly affect the dynamic characteristics and stability of the rotor. Therefore, accurately identifying the axial location of unbalance is of great significance for achieving high-speed dynamic balancing of the rotor and improving the overall performance of rotating machinery.

3.3.1. Data Preprocessing

Initially, four unbalanced positions, A, B, C, and D, are selected on the constructed rotor test bench, with their specific layout illustrated in Figure 5. At each of these positions, an unbalanced mass of 15 gmm with a phase of 30° is manually added to obtain the measured vibration response of the rotor at each unbalanced position. To ensure the accuracy and reliability of the data, preprocessing steps are taken to eliminate noise and outliers from the raw data. Furthermore, dynamic simulations are performed with consistent parameter settings to calculate the vibration displacement of the nodes. Based on this, both filtered measured vibration data and dynamic model simulation data are collected, covering vibration responses under different unbalanced positions (A, B, C, D). This provides a reliable data foundation for subsequent model training and validation. Given the significant advantages of LSTM models in processing sequential data, the vibration data are arranged in time series to form input sequences. To facilitate the recognition and classification of unbalanced positions by the LSTM model, the unbalanced positions (A, B, C, D) are converted into corresponding numerical labels for model recognition and classification.

3.3.2. Optimization Model Construction

In designing the LSTM neural network for rotor imbalance position recognition, careful consideration is given to the choice of network structure. Since an unbalanced distribution state corresponds to the vibration data composed of four measurement points of the rotor, the number of nodes in the input layer of the designed neural network is 4. Hidden Layer determines the ability of neural networks to learn features, and the number of hidden layers and nodes determines the complexity of the network to process data and the mapping ability of complex functions. In general, the formula for calculating the number of hidden layer nodes is as follows:

$$n_m=\sqrt{n_x+n_y}+a$$

(24)

where n_m indicates the number of hidden layer nodes, n_x is the number of nodes in the input layer, n_y is the number of nodes in the output layer, and a is the constant between the intervals [1, 10].

In addition, the choice of activation function is crucial for the performance of neural networks. In this case, the Sigmoid function is selected for the hidden layers compared to other activation functions like ReLU; the Sigmoid function has a smoother gradient that can help mitigate issues with gradient vanishing, especially in deeper networks. Additionally, its output range is well-suited for representing probabilities, although this is not directly leveraged in the output layer, which instead uses the Softmax function for classification. The Sigmoid function’s properties made it a suitable choice for enhancing the network’s nonlinear processing capabilities and improving its generalization performance on the rotor imbalance position recognition task. Following the LSTM layers, fully connected layers are added for feature extraction and classification. The output layer employed the Softmax function, which converted the outputs of the fully connected layer into a probability distribution, indicating the likelihood of each possible rotor imbalance position. Overall, the constructed multi-layer regression LSTM neural network model, as illustrated in Figure 10, is designed to strike an optimal balance between network complexity and convergence speed, making it well-suited for the task of rotor imbalance position recognition.

3.3.3. Model Training

The preprocessed data is divided into training, validation, and test sets, which are respectively utilized for model training, validation, and evaluation. For the purpose of model training and optimization, the cross-entropy loss function and Adam optimizer are selected. The training set data is input into the LSTM model for multiple iterations of training, continuing until the model’s performance on the validation set stabilizes or begins to decline. It is noteworthy that the loss function serves as a crucial metric in neural network training, quantifying the error between the network’s output and the desired output. A lower loss function value indicates better network performance. During the training process, the loss function value for all samples in the training set is calculated in each iteration, and the weights and biases of the neural network are updated according to the optimizer settings to minimize the loss function value. Simultaneously, the validation set is used to evaluate the network’s performance and generalization ability, ensuring that the model does not suffer from overfitting. The loss curve during the training process at a subcritical rotational speed of 5600 rpm, as shown in Figure 11, demonstrates that the model exhibits good performance on both the training and validation data.

4. Discussion

At present, researchers have explored various techniques for unbalanced identification in rotating machinery. Traditional methods often involve vibration analysis using Fast Fourier Transform (FFT) or other signal processing techniques to detect harmonic components indicative of unbalance. However, these methods can be limited in their ability to accurately pinpoint the exact location of the unbalance, especially in complex systems like aero engines. More advanced approaches, such as those utilizing machine learning algorithms, have emerged in recent years. While these methods have shown promise, they may struggle with the temporal dependencies inherent in vibration data, which can be crucial for accurate identification.

To solve the difficult problem of unbalanced position identification of an aero-engine rotor, a method of unbalanced position identification of an aero-engine power turbine rotor based on the LSTM is proposed. This method addresses this limitation by capturing the long-term dependencies in the vibration signals. LSTM networks are particularly well-suited for sequential data analysis, making them ideal for processing vibration signals recorded over time. By training the LSTM model on a comprehensive dataset that includes both experimental and simulation data from different rotational speeds, the method is able to learn the complex relationships between vibration patterns and unbalanced positions. The unbalanced position is identified by the neural network model trained by experimental data and simulation data at different rotational speeds. The results are as follows:

(1) At a subcritical rotational speed of 5600 rpm, the measured unbalanced rotor vibration response data from the test bench and the vibration response data obtained through simulation are input into the LSTM model for training, with the aim of identifying the unbalanced rotor position. The results of unbalanced rotor position identification based on the LSTM model are presented in Figure 12. Figure 12a shows that the accuracy of identification results based on measured data can be controlled above 97.5%, with an impressive 100% accuracy when unbalanced masses are present at positions B and D. Figure 12b demonstrates that the accuracy of identification results based on simulated data can be maintained above 91.2%, achieving a perfect 100% accuracy specifically when an unbalanced mass is at position B. These results validate the effectiveness of the proposed method in identifying unbalanced positions at subcritical speeds.

(2) According to the experimental test results, the first-order critical speed of the rotor system is 7260 rpm. Therefore, by varying four unbalanced positions at the critical speed, the unbalanced vibration response data measured on the test bench and the vibration response data calculated through simulations are input into the LSTM model for training in order to identify the unbalanced position of the rotor at the critical speed, as shown in Figure 13. Figure 13a indicates that the accuracy of identification results based on measured data can be maintained above 95.5%, with an impressive 100% accuracy, specifically when unbalanced masses are present at positions A and B. Figure 13b demonstrates that the accuracy of identification results based on simulated data can be controlled above 93.1%, achieving a perfect 100% accuracy when an unbalanced mass is at position A. These results validate the effectiveness of the proposed method in identifying unbalanced positions at the critical speed.

(3) When varying four unbalanced positions at supercritical speed (8400 rpm), the unbalanced vibration response data measured on the test bench and the vibration response data calculated through simulations are input into the LSTM model for training in order to identify the unbalanced position of the rotor at supercritical speed, as shown in Figure 14. Figure 14a indicates that the accuracy of identification results based on measured data can be maintained above 97.8%, with an impressive 100% accuracy, specifically when unbalanced masses are present at positions A and B. Meanwhile, Figure 14b demonstrates that the accuracy of identification results based on simulated data can be controlled above 90.5%, achieving a perfect 100% accuracy when an unbalanced mass is at position A. These results validate the effectiveness of the proposed method in identifying unbalanced positions at supercritical speed.

In summary, the LSTM-based approach offers superior performance in identifying unbalanced positions with high accuracy. Preliminary results, as presented earlier, indicate that the method can achieve accuracies above 90.5% for experimental data and above 95.5% for simulated data, with specific cases reaching perfect accuracy. By leveraging the strengths of LSTM networks and incorporating both experimental and simulation data, the method demonstrates the potential to overcome the limitations of traditional and other machine learning-based approaches, thereby enhancing the reliability and efficiency of aero engine maintenance and operation.

5. Conclusions

This paper focuses on the study of turbo-rotor systems in aero-engines, addressing critical issues such as excessive high-speed dynamic balance vibrations and the challenges associated with achieving dynamic balance. The main contributions of this paper include the following:

(1) A rotor system dynamics model is proposed based on the finite element method. In this paper, the finite element method is utilized to construct a dynamics model for the turbo-rotor system. This model can more accurately describe the dynamic behavior of the rotor system, providing a solid foundation for subsequent vibration analysis and research on unbalanced responses;

(2) A turbo-rotor vibration test bench is designed and validated. To verify the accuracy and effectiveness of the established model, this paper designed a turbo-rotor vibration test bench and, through comparison with measured data, validated that the prediction error of the model’s natural frequencies is controlled within 5%, demonstrating the model’s high precision and practicality;

(3) Unbalanced responses at different rotational speeds are studied. This paper conducted an in-depth analysis of unbalanced responses of the rotor at subcritical, critical, and supercritical speeds. By comparing experimental and simulation results, it verified the good consistency and minimal errors between them, providing important references for vibration control and optimal design of the rotor system.

(4) A method for identifying unbalanced positions based on LSTM neural networks is proposed. This paper innovatively proposed a method for identifying unbalanced positions in aero-engine turbo-rotors using Long Short-Term Memory (LSTM) neural networks. The recognition accuracy of this method reached 95.5% and 90.5% on experimental and simulation data, respectively, providing new ideas and technical means for intelligent detection and processing of rotor imbalance issues.

The innovation of this paper lies in the first application of LSTM neural networks to identify unbalanced positions in aero-engine turbo-rotors. Traditional methods for identifying unbalanced positions may rely on human experience and complex calculation processes. However, the method based on LSTM neural networks achieves intelligent recognition, is capable of automatically processing and analyzing data, reduces dependence on human experience, and improves the efficiency and accuracy of identification. By training and optimizing the LSTM neural networks, high accuracy in unbalanced position recognition is achieved on both experimental and simulation data, providing new ideas and technical means for vibration control and optimal design of aero-engine rotor systems.