Optimization of Motor Rotor Punch Wear Parameters Based on Response Surface Method
Abstract
1. Introduction
2. Finite Element Simulation Analysis
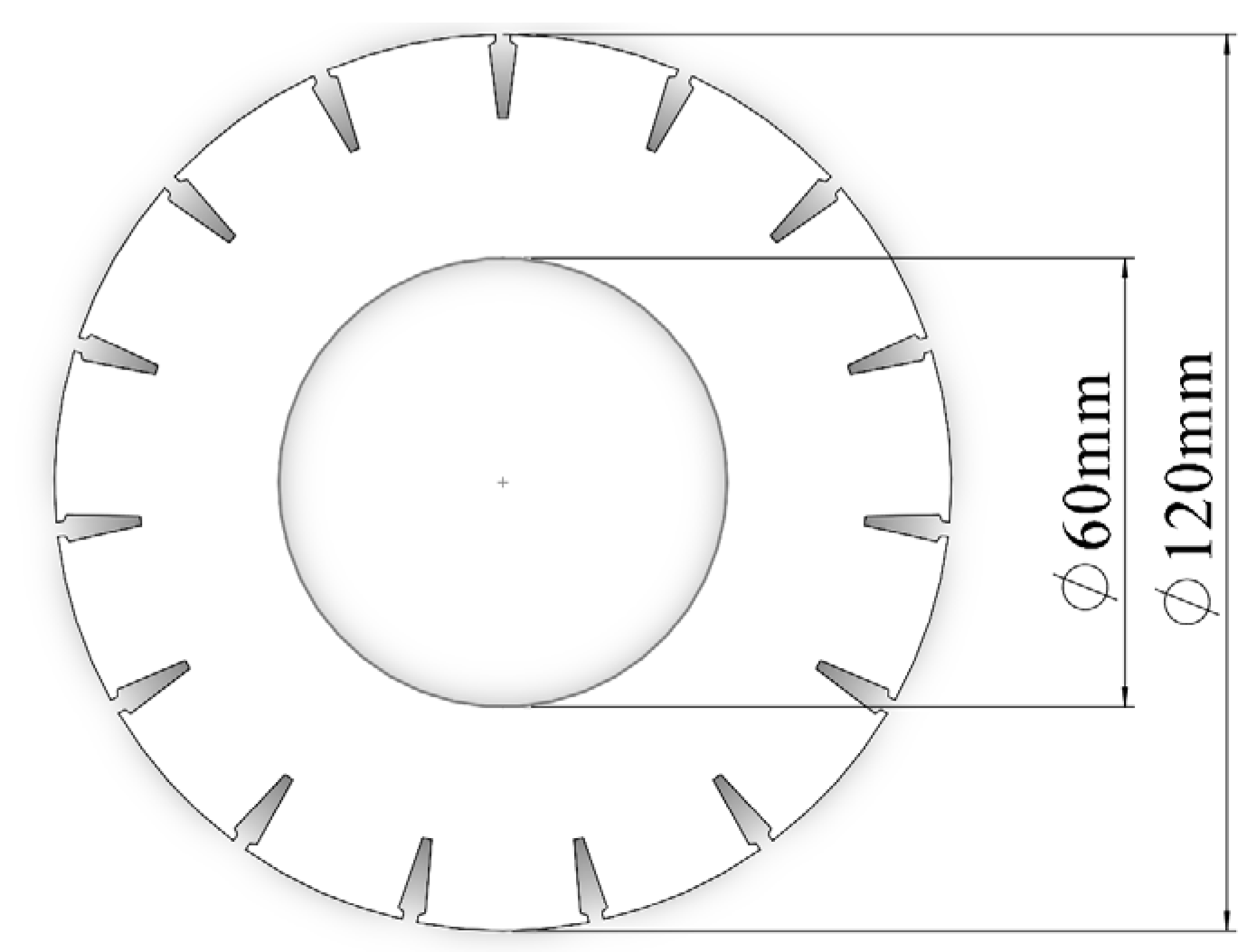
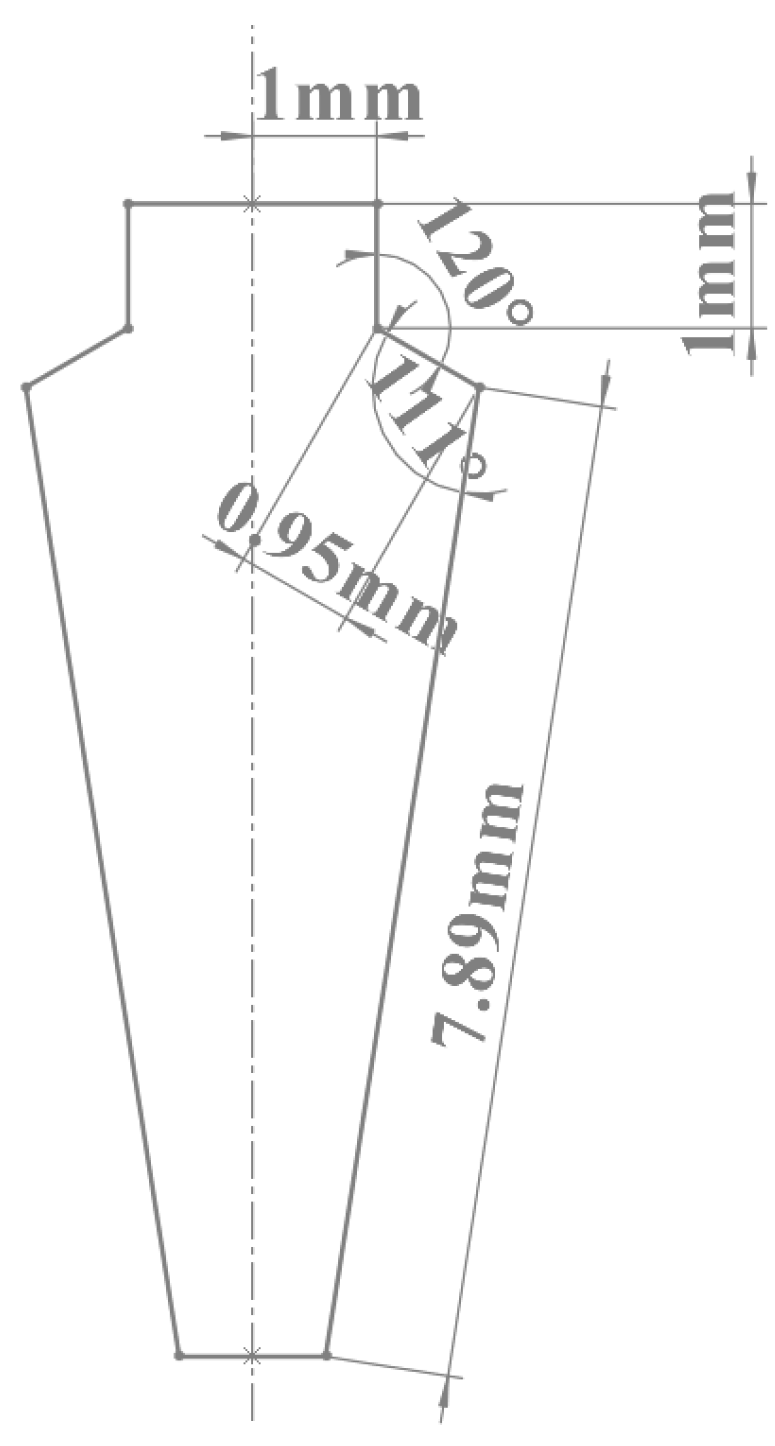
2.1. Model Establishment
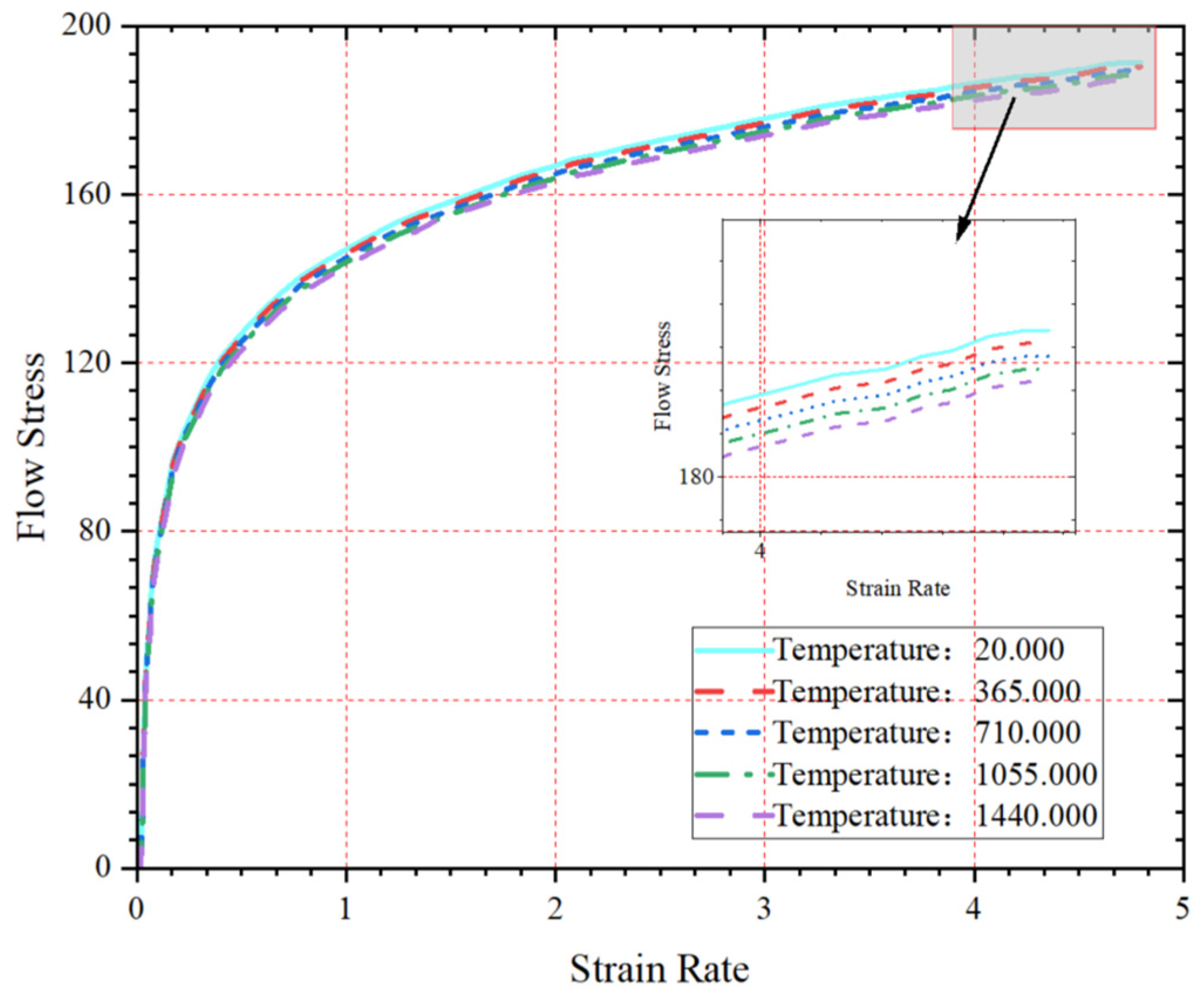
2.2. Constitutive Model Establishment
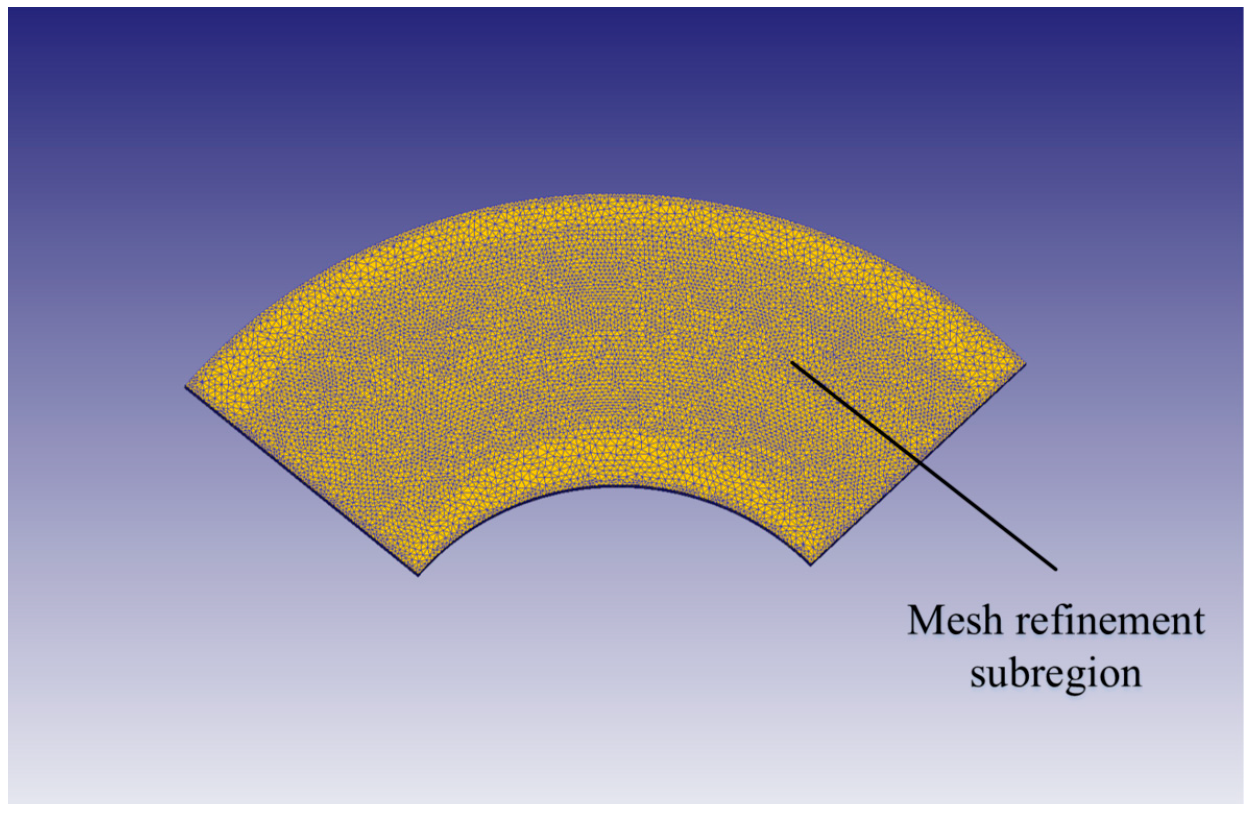
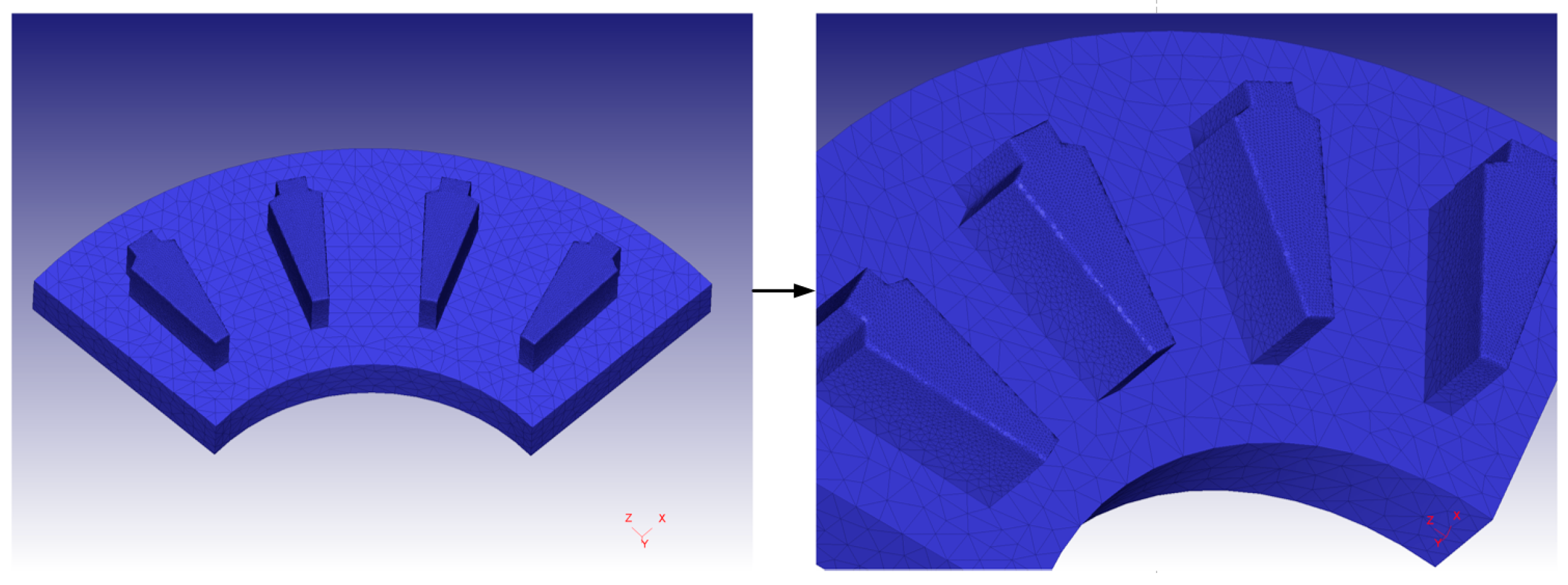
2.3. Grid Division
3. Mold Wear Analysis
3.1. Archard Model Theory
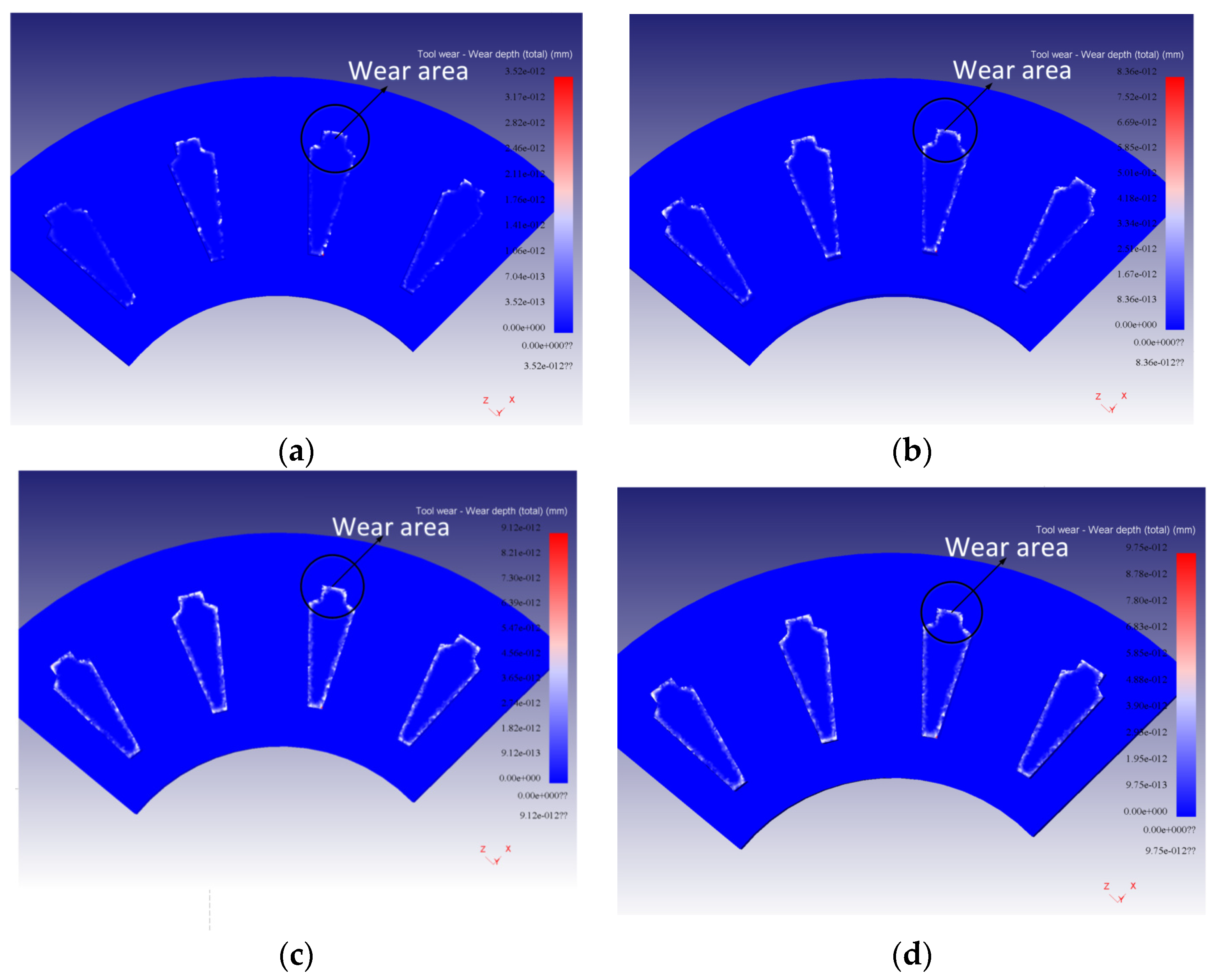
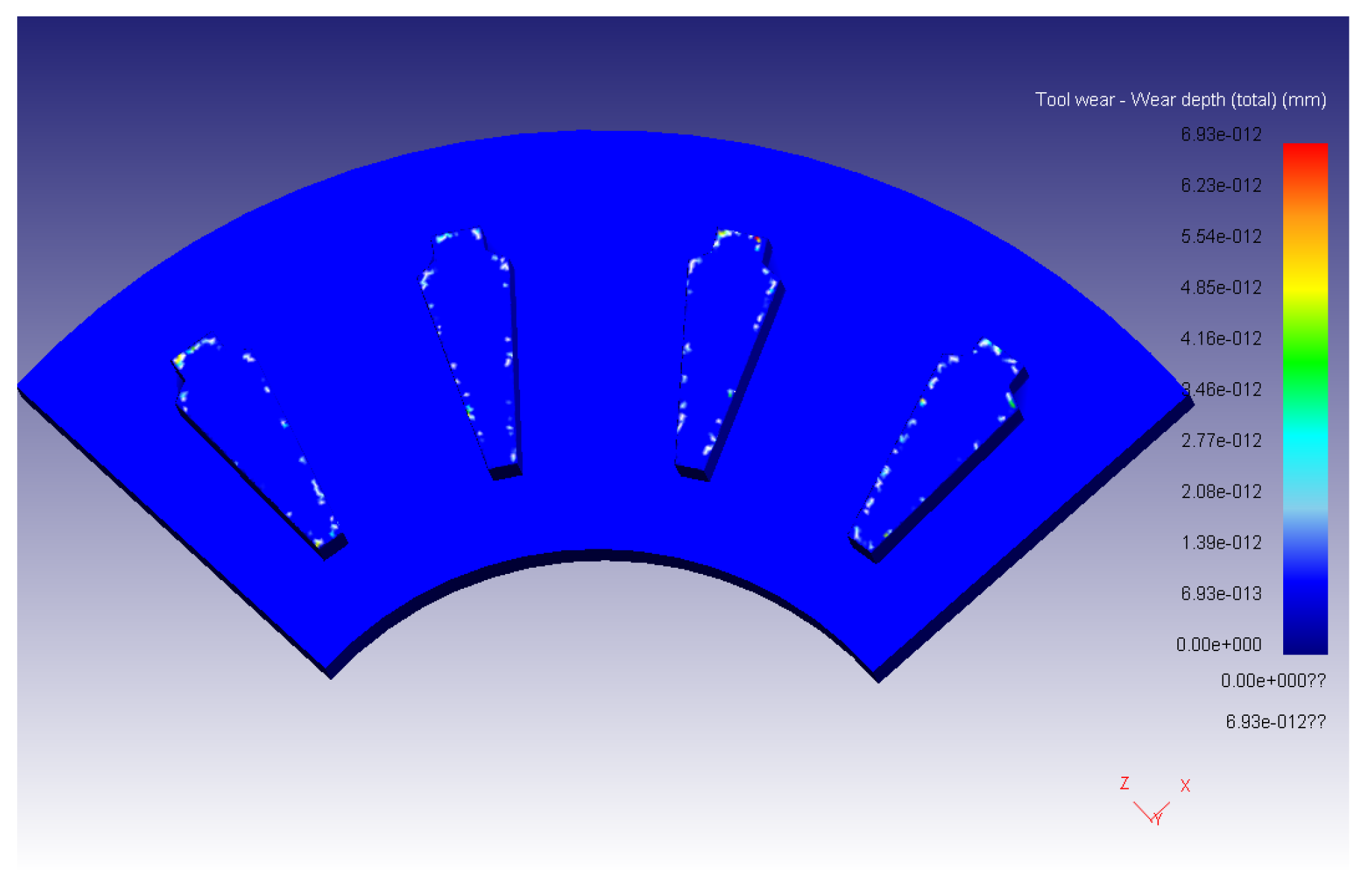
3.2. Punch Wear Change Process
4. Blanking Punch Wear Optimization Based on Response Surface Method
4.1. Response Surface Experiment Design
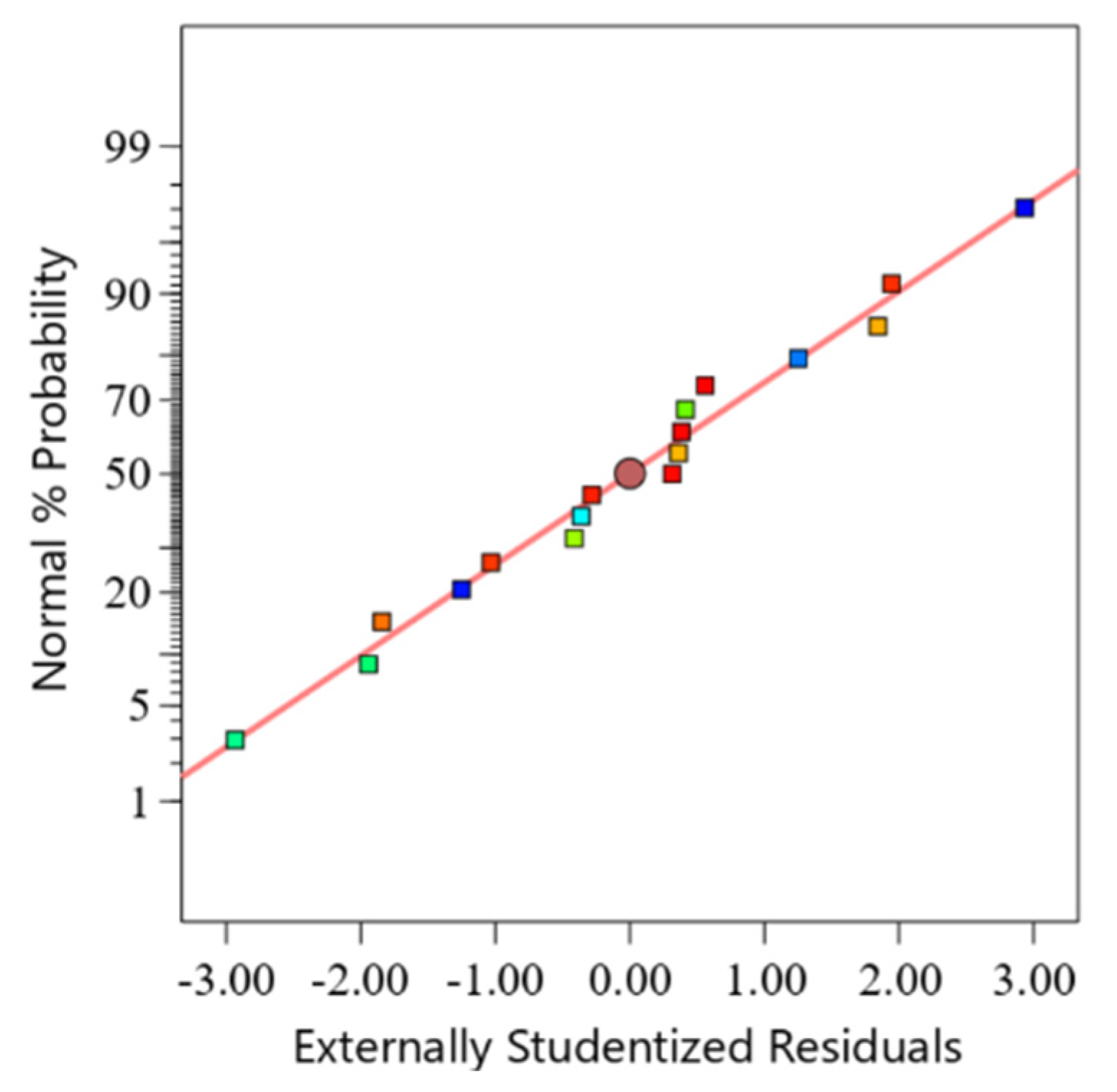
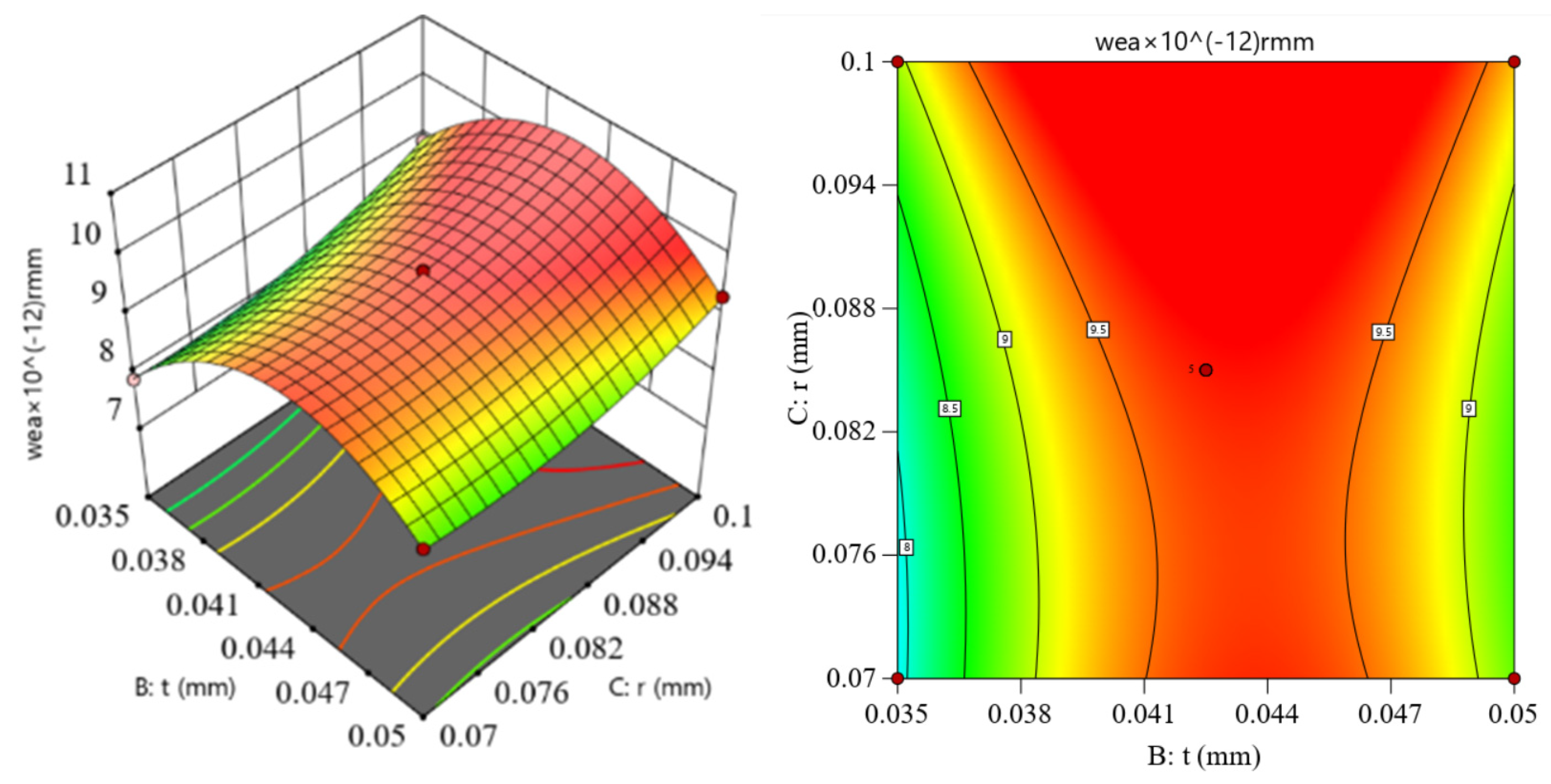
4.2. Analysis of Response Surface Test Design Results
− 0.9397A2 − 1.40B2 + 0.4040C2
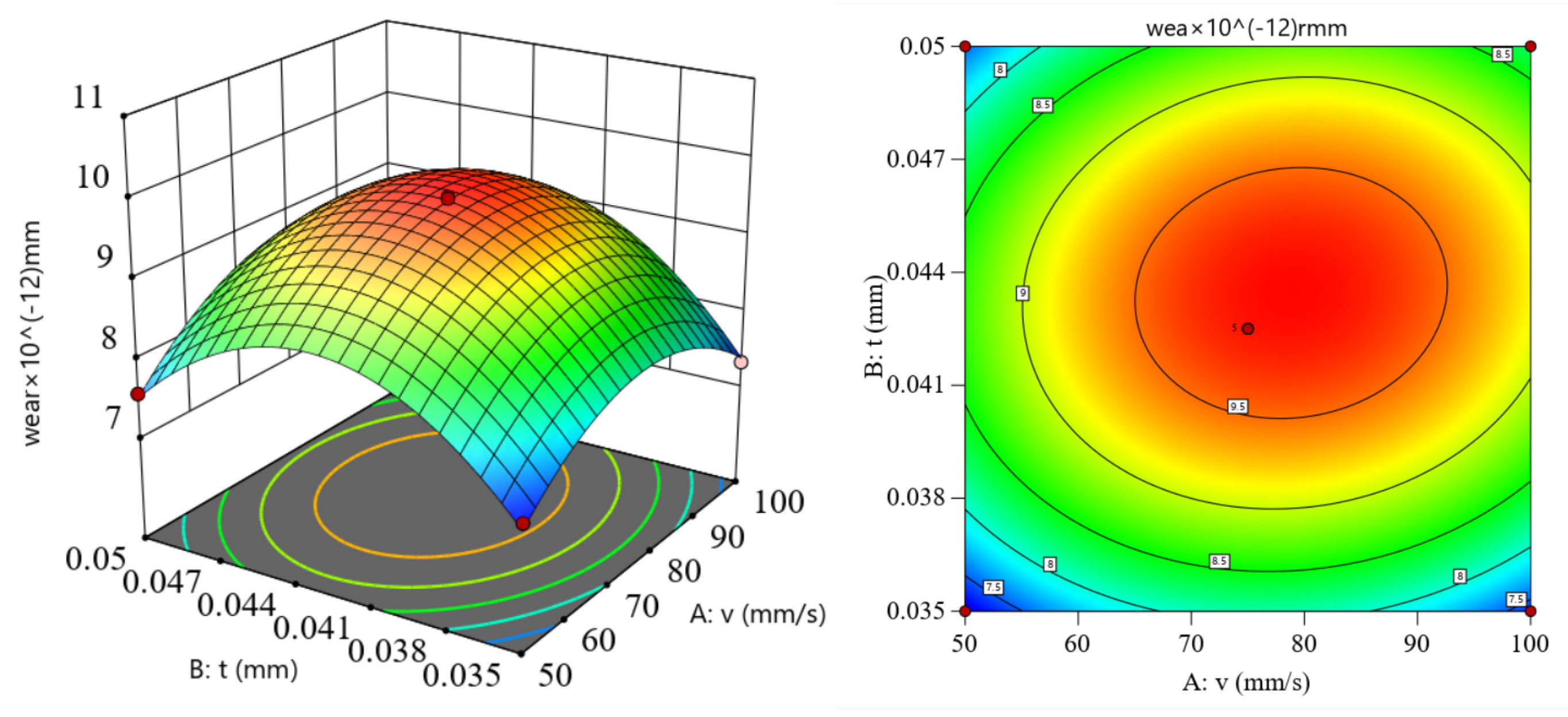
4.3. Blanking Process Parameters Optimization and Verification
5. Conclusions
- (1)
- Based on the response method and Deform-3D, the finite element model of punch wear in the punching process of the motor rotor is analyzed, and it is found that the punch wear is mainly concentrated in the cutting-edge area directly in contact with the sheet metal.
- (2)
- Through the response surface Box–Behnken test design, the influence rule of each punching parameter on punch wear is obtained from the variance analysis of the response surface model. The influence magnitude of each factor is as follows: punch cutting edge rounded Angle C > punch clearance B > punch speed A. The order of the interactive influence of punch wear is as follows: punch speed and punch edge fillet AC > punch speed and punch clearance AB > punch clearance and punch edge fillet BC.
- (3)
- Optimized by the response surface method, the optimal parameter combination with the smallest wear depth of the rotor punching punch is as follows: The blanking speed is 50 mm/s, the blanking clearance is 0.036 mm, and the die cutting edge is 0.076 mm. The predicted response surface value is 6.95 × 10−12 mm, with a simulated test value of 6.93 × 10−12 mm. The relative error between them is 0.2%, which verifies the effectiveness of the response surface method for optimizing the rotor blanking punch wear. It lowers punch wear and establishes a theoretical foundation for assessing and minimizing wear in rotor blanking production.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Wang, Y.; Liu, X.; Gao, Y. Topology Optimization of Rotor Punch Structure of Permanent Magnet Synchronous Motor for Commercial Vehicles. China Automob. 2024, 3, 38–41. [Google Scholar]
- Cui, Y. Analysis of Rotor Strength and Fatigue Characteristics of Permanent Magnet Synchronous Motor for Vehicles. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, 2023. [Google Scholar]
- Trzepiecinski, T.; Lemu, G.H. FEM-based assessment of wear of stamping die. IOP Conf. Ser. Mater. Sci. Eng. 2019, 526, 012002. [Google Scholar] [CrossRef]
- Hernández, J.J.; Franco, P.; Estrems, M.; Faura, F. Modelling and experimental analysis of the effects of tool wear on form errors in stainless steel blanking. J. Mater. Process. Technol. 2006, 180, 143–150. [Google Scholar] [CrossRef]
- Hambli, R. Blanking tool wear modeling using the finite element method. Int. J. Mach. Tools Manuf. 2001, 41, 1815–1829. [Google Scholar] [CrossRef]
- Hambli, R. Design of experiment-based analysis for sheet metal blanking processes optimization. Int. J. Adv. Manuf. Technol. 2002, 19, 403–410. [Google Scholar] [CrossRef]
- Mo, J.; Liu, J.; Li, X.; Zheng, Q.-E. Wear Analysis and Process Parameter Optimization of Hexagonal Punch Based on Orthogonal Test. Forg. Stamp. Technol. 2022, 47, 1–6. [Google Scholar]
- Mucha, J.; Jaworski, J. The tool surface wear during the silicon steel sheets blanking process. Eksploat. I Niezawodn.—Maint. Reliab. 2016, 18, 332–342. [Google Scholar] [CrossRef]
- Luo, S.Y. Effect of geometry and the surface of treatment of punching tool on the tool life and wear conditions in the piercing of thick sheet plate. J. Mater. Process. Technol. 1999, 88, 122–133. [Google Scholar] [CrossRef]
- Mucha, J. An experimental analysis of effects of various material tool’s wear on burr during generator sheets blanking. Int. J. Adv. Manuf. Technol. 2010, 50, 495–507. [Google Scholar] [CrossRef]
- Ruan, G. Based on the response surface method of high strength steel stamping DP800 springback process parameters optimization. J. Forg. Technol. 2015, 40, 40–44. [Google Scholar]
- Feng, C.X.; Wang, X. Development of empirical models for surface roughness prediction in finish turning. Int. J. Adv. Manuf. Technol. 2002, 20, 348–356. [Google Scholar]
- Pereira, M.P.; Yan, W.; Rolfe, B.F. Contact pressure evolution and its relation to wear in sheet metal forming. Wear 2008, 265, 1687–1699. [Google Scholar] [CrossRef]
- Pereira, M.P.; Yan, W.; Rolfe, B.F. Sliding distance, contact pressure and wear in sheet metal stamping. Wear 2010, 268, 1275–1284. [Google Scholar] [CrossRef]
- Pereira, M.P.; Weiss, M.; Rolfe, B.F.; Hilditch, T.B. The effect of the die radius profile accuracy on wear in sheet metal stamping. Int. J. Mach. Tools Manuf. 2013, 66, 44–53. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, S.; Mu, Z.; Wang, W.; Yan, H.; Ma, S.; Zhang, Y. Research on Numerical Simulation of Die Wear of Automobile Covering Based on Dynamic Wear Model. China Mech. Eng. 2024, 35, 515–523. [Google Scholar]
- Zhang, W.; Wang, S.; Chen, J.; Cheng, C.; Zhang, L. Experimental and continuous stamping simulation study on surface wear of hardened steel mold. Int. J. Interact. Des. Manuf. (IJIDeM) 2018, 12, 1481–1494. [Google Scholar] [CrossRef]
- Mei, R.; Bao, L.; Li, C.; Liu, X. Constitutive Equation of mid-temperature deformation of Fe-6.5%Si Steel. J. Northeast. Univ. (Nat. Sci. Ed.) 2019, 40, 43–47. [Google Scholar]
- Sellars, C.M.; Mctegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136. [Google Scholar] [CrossRef]
- Mei, R.; Bao, L.; Du, Y.; Zhang, X.; Li, C.; Liu, X. Constitutive Equation of high temperature deformation of Fe-6.5%Si Steel. Iron Steel 2018, 53, 98–102. [Google Scholar]
- Li, Y.; Lv, Y.; Ni, M. Analysis of Influence of Die Design Parameters on Die Wear of Aircraft Blade. Mater. Sci. Technol. 2019, 27, 79–84. (In Chinese) [Google Scholar]
- Cao, H. Influence of Blanking Parameters on Blanking Quality of Non-Oriented Silicon Steel. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2016. [Google Scholar]
- Liu, K.-W.; Bian, W. Optimization of blanking process Parameters of C75S Spring Steel based on Response Surface Method. Forg. Stamp. Technol. 2016, 41, 32–36. [Google Scholar]
- Liu, J.; Zhang, M.; Chen, H. Optimization of Punching process Parameters for Stepped Punch based on Response Surface Method. J. Plast. Eng. 2016, 23, 52–57+67. [Google Scholar]
- Jiang, T.-L.; Gong, H.-Y.; Shi, W.-Z.; Zhao, X.-Y. Optimization of U-shaped Bending Forming Process Parameters Based on Response Surface Method. J. Shanghai Univ. Eng. Technol. 2019, 33, 278–282. [Google Scholar]
- Liang, H.Y. Finite Element Simulation and Life Analysis of Die Wear in Heavy Plate Punching. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2017. [Google Scholar]




| Parameter Name | Material Parameter Value | |
|---|---|---|
| Work Material | Punch Material | |
| Thermal conductivity (W/m·K) | 18.9 | 24 |
| Coefficient of thermal expansion (μm/m·K) | ||
| Hardness (HV) | 395 | 690 |
| Young’s modulus (Gpa) | 190 | 206 |
| Poisson’s ratio | 0.28 | 0.3 |
| Density (g/cm3) | 7.85 | 7.85 |
| Name | Numerical Value |
|---|---|
| Constant (A) | 0.0433 |
| Constant (α) | 0.0136 |
| Deformation activation Energy (Q) | 342.2 |
| Stress index (n) | 2.4593 |
| Gas constant (R) | 8.314 |
| Factor | Process Parameter | Level | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| A | Blanking speed | 50 | 75 | 100 |
| B | Blanking clearance | 0.035 | 0.0425 | 0.05 |
| C | Rounded edge | 0.07 | 0.085 | 0.1 |
| Test Number | A | B | C | Punch Wear |
|---|---|---|---|---|
| 1 | 100 | 0.05 | 0.085 | 8.173 |
| 2 | 100 | 0.035 | 0.085 | 7.318 |
| 3 | 50 | 0.0425 | 0.1 | 9.489 |
| 4 | 75 | 0.0425 | 0.085 | 9.751 |
| 5 | 75 | 0.035 | 0.07 | 7.889 |
| 6 | 75 | 0.0425 | 0.085 | 9.692 |
| 7 | 75 | 0.0425 | 0.085 | 9.745 |
| 8 | 50 | 0.05 | 0.085 | 7.566 |
| 9 | 100 | 0.0425 | 0.1 | 9.564 |
| 10 | 100 | 0.0425 | 0.07 | 9.338 |
| 11 | 75 | 0.0425 | 0.085 | 9.632 |
| 12 | 75 | 0.035 | 0.1 | 8.906 |
| 13 | 75 | 0.05 | 0.07 | 8.785 |
| 14 | 50 | 0.0425 | 0.07 | 8.245 |
| 15 | 50 | 0.035 | 0.085 | 7.266 |
| 16 | 75 | 0.0425 | 0.085 | 9.766 |
| 17 | 75 | 0.05 | 0.1 | 9.318 |
| Source of Variance | Sum of Squares | Degree of Freedom | Mean Variance | F Value | p Value | Significance |
|---|---|---|---|---|---|---|
| Model | 13.48 | 9 | 1.50 | 174.85 | <0.0001 | significant |
| A-punch speed | 0.4594 | 1 | 0.4594 | 53.61 | 0.0002 | |
| B-punch clearance | 0.7583 | 1 | 0.7583 | 88.50 | <0.0001 | |
| C-punch edge fillet | 1.21 | 1 | 1.21 | 141.10 | <0.0001 | |
| AB | 0.0770 | 1 | 0.0770 | 8.99 | 0.0200 | |
| AC | 0.2153 | 1 | 0.2153 | 25.13 | 0.0015 | |
| BC | 0.0586 | 1 | 0.0586 | 6.83 | 0.0347 | |
| A2 | 2.97 | 1 | 2.97 | 346.50 | <0.0001 | |
| B2 | 7.08 | 1 | 7.08 | 826.28 | <0.0001 | |
| C2 | 0.3892 | 1 | 0.3892 | 45.42 | 0.0003 | |
| Residual | 0.0600 | 7 | 0.0086 | |||
| Lack of Fit | 0.0478 | 3 | 0.0159 | 5.23 | 0.0720 | not significant |
| Pure Error | 0.0122 | 4 | 0.0030 | |||
| Cor Total | 13.54 | 16 | ||||
| R-Squared = 0.9956 | Adj R-Squared = 0.9899 | Pred R-Squared = 0.9421 | ||||
| Blanking Parameter | The Optimal Parameter Value |
|---|---|
| Blanking speed | 50 mm/s |
| Blanking clearance | 0.036 mm |
| Punch edge rounded corners | 0.076 mm |
| Punch wear value (forecast) | 6.95 × 10−12 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, S.; She, R.; Zhao, Z.; Gong, Y. Optimization of Motor Rotor Punch Wear Parameters Based on Response Surface Method. Machines 2024, 12, 671. https://doi.org/10.3390/machines12100671
Wen S, She R, Zhao Z, Gong Y. Optimization of Motor Rotor Punch Wear Parameters Based on Response Surface Method. Machines. 2024; 12(10):671. https://doi.org/10.3390/machines12100671
Chicago/Turabian StyleWen, Shaobo, Ran She, Zhendong Zhao, and Yipeng Gong. 2024. "Optimization of Motor Rotor Punch Wear Parameters Based on Response Surface Method" Machines 12, no. 10: 671. https://doi.org/10.3390/machines12100671
APA StyleWen, S., She, R., Zhao, Z., & Gong, Y. (2024). Optimization of Motor Rotor Punch Wear Parameters Based on Response Surface Method. Machines, 12(10), 671. https://doi.org/10.3390/machines12100671







