Double-Sided Surface Structures with Undercuts on Cold-Rolled Steel Sheets for Interlocking in Hybrid Components
Abstract
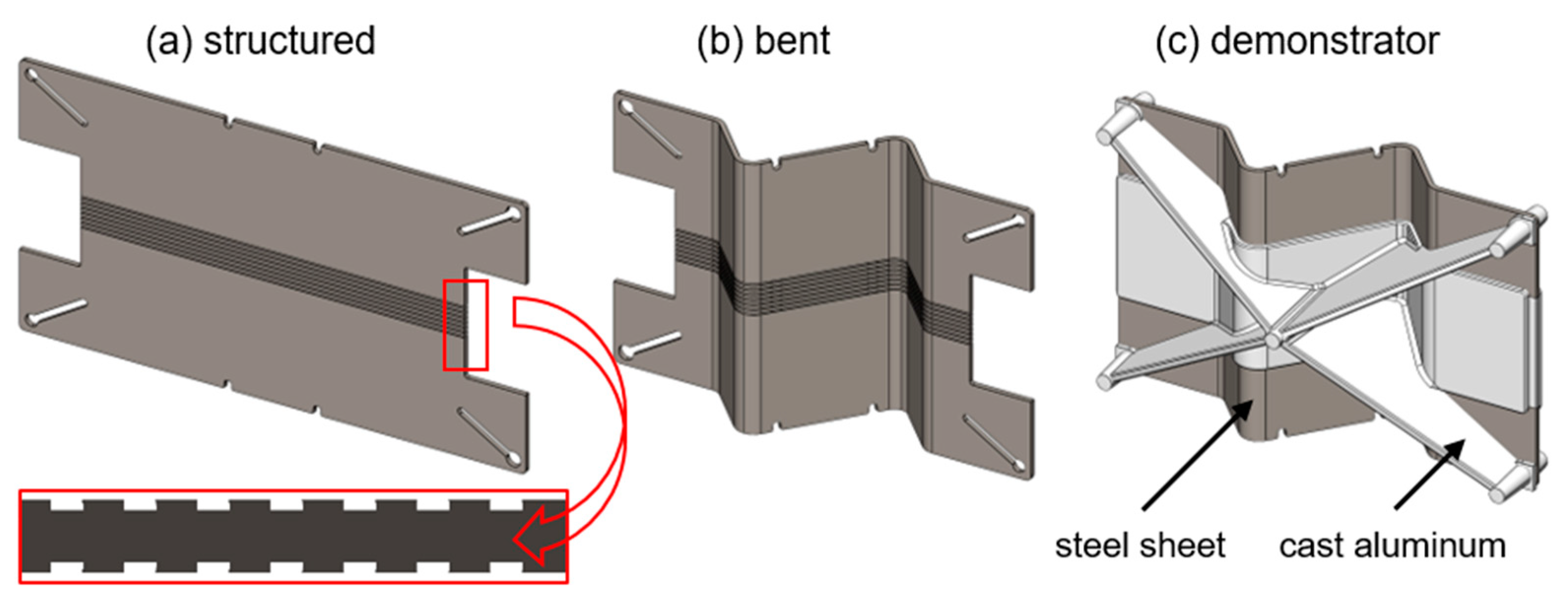
1. Introduction
2. Materials and Methods
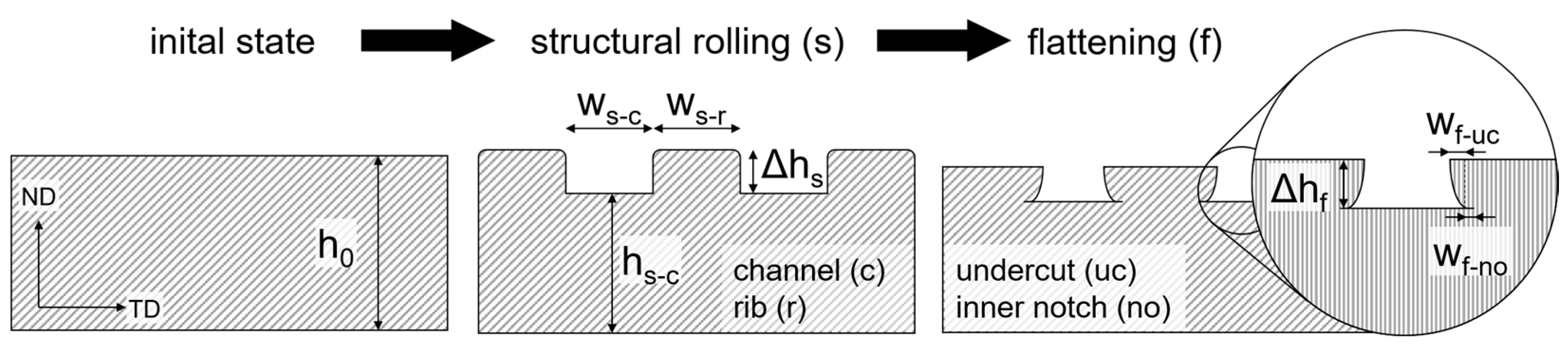
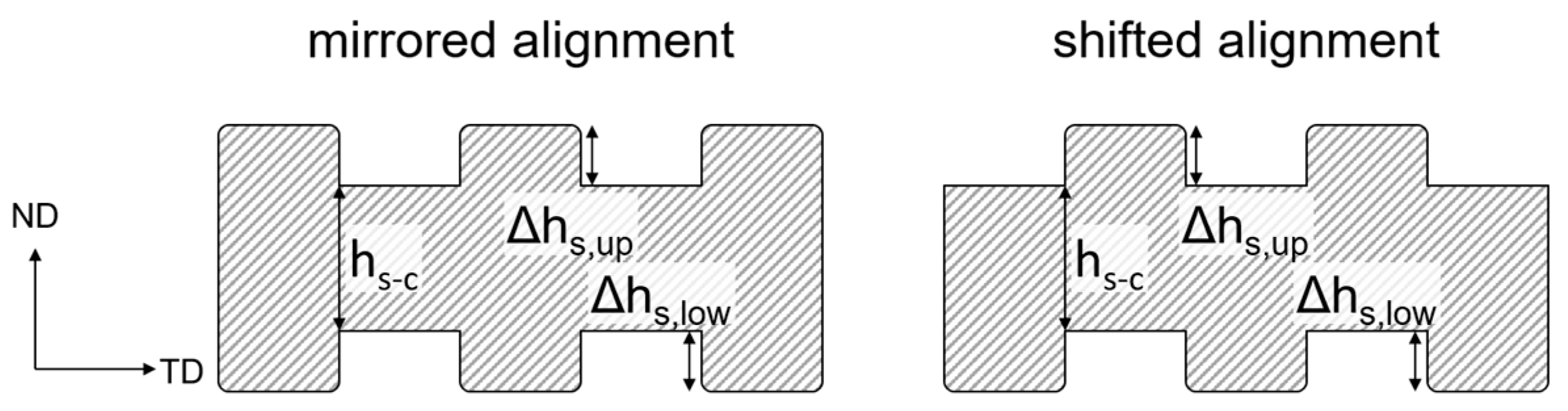
2.1. FE-Simulation of the Structural Rolling Process
2.2. Experimental Validation of Structural Cold-Rolling
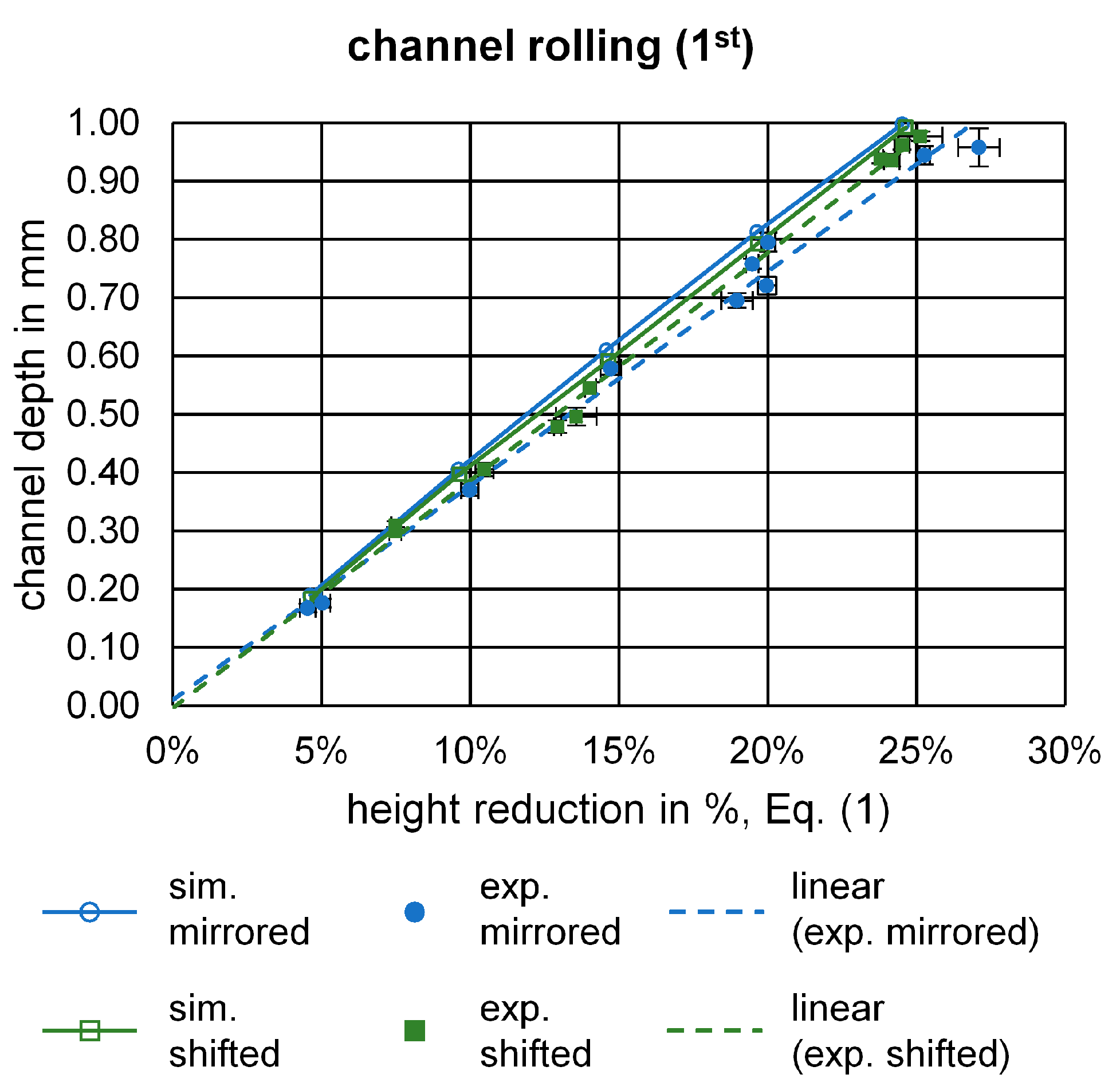
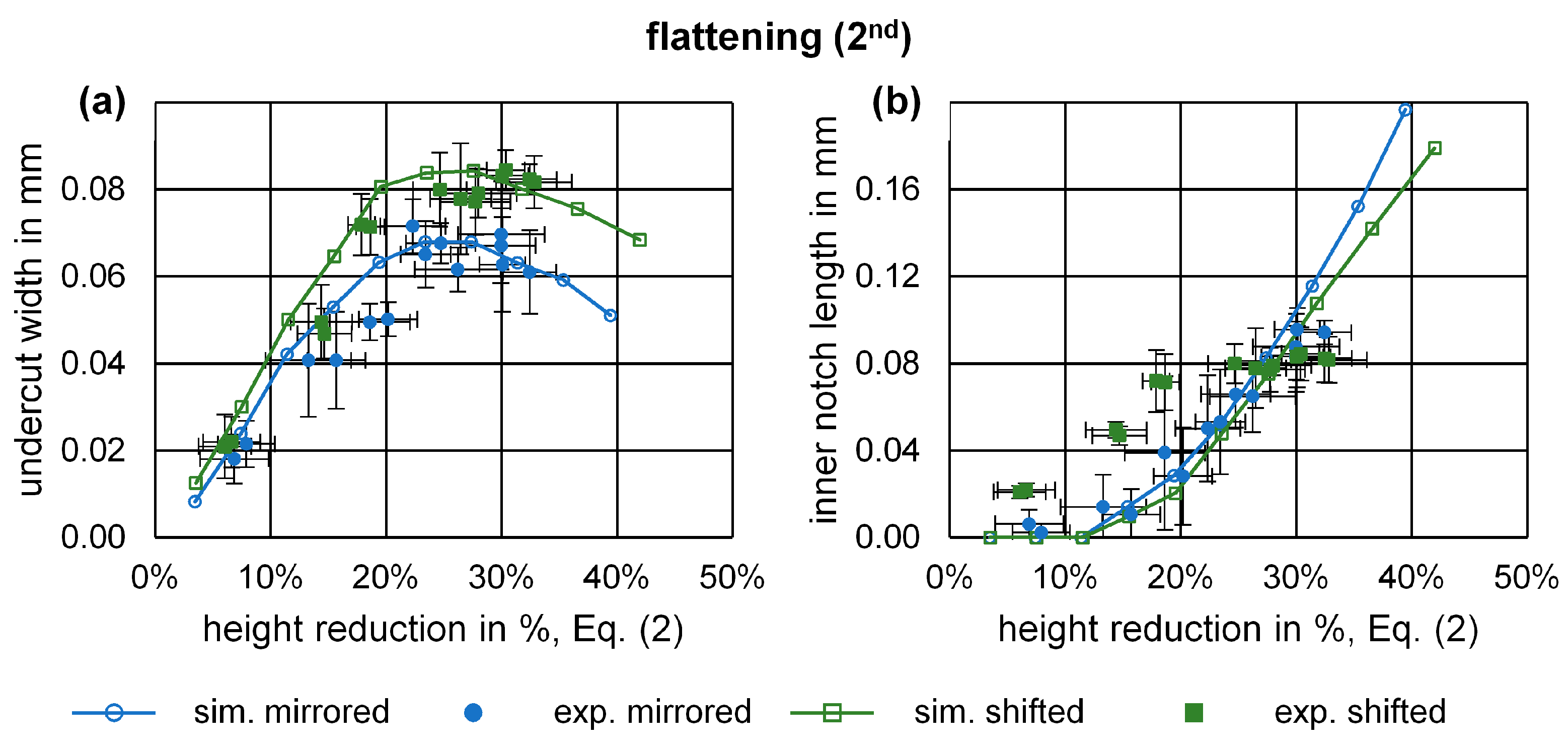
3. Results and Discussion
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, H.C.; Wallington, T.J. Life-cycle energy and greenhouse gas emission benefits of lightweighting in automobiles: Review and harmonization. Environ. Sci. Technol. 2013, 47, 6089–6097. [Google Scholar] [CrossRef] [PubMed]
- Cecchel, S. Materials and Technologies for Lightweighting of Structural Parts for Automotive Applications: A Review. SAE Int. J. Mater. Manf. 2021, 14, 81–97. [Google Scholar] [CrossRef]
- Mori, K.; Abe, Y. A review on mechanical joining of aluminium and high strength steel sheets by plastic deformation. Int. J. Lightweight Mater. Manuf. 2018, 1, 1–11. [Google Scholar] [CrossRef]
- Meschut, G.; Janzen, V.; Olfermann, T. Innovative and Highly Productive Joining Technologies for Multi-Material Lightweight Car Body Structures. J. Mater. Eng. Perform. 2014, 23, 1515–1523. [Google Scholar] [CrossRef]
- Mori, K.; Bay, N.; Fratini, L.; Micari, F.; Tekkaya, A.E. Joining by plastic deformation. CIRP Ann. Manuf. Technol. 2013, 62, 673–694. [Google Scholar] [CrossRef]
- Salamati, M.; Soltanpour, M.; Fazli, A.; Zajkani, A. Processing and tooling considerations in joining by forming technologies; part A—Mechanical joining. Int. J. Adv. Manuf. Technol. 2019, 101, 261–315. [Google Scholar] [CrossRef]
- Feistauer, E.E.; dos Santos, J.F.; Amancio-Filho, S.T. A review on direct assembly of through-the-thickness reinforced metal–polymer composite hybrid structures. Polym. Eng. Sci. 2019, 59, 661–674. [Google Scholar] [CrossRef]
- Noguchi, T.; Asano, K.; Hiratsuka, S.; Miyahara, H. Trends of composite casting technology and joining technology for castings in Japan. Int. J. Cast Met. Res. 2008, 21, 219–225. [Google Scholar] [CrossRef]
- Fang, X.; Gundlach, J.; Schipperges, J.-J.; Jiang, X. On the Steel–Aluminum Hybrid Casting by Sand Casting. J. Mater. Eng. Perform. 2018, 27, 6415–6425. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, G.; Cao, S.; Huo, Z.; Han, J.; Ma, S.; Huang, Z. A Review of Advances in Fabrication Methods and Assistive Technologies of Micro-Structured Surfaces. Processes 2023, 11, 1337. [Google Scholar] [CrossRef]
- Müller, S.; Brand, M.; Dröder, K.; Meiners, D. Increasing the Structural Integrity of Hybrid Plastics-Metal Parts by an Innovative Mechanical Interlocking Effect. Mater. Sci. Forum 2015, 825–826, 417–424. [Google Scholar] [CrossRef]
- Buxton, A.L.; Ferhati, A.; Glen, R.J.; Dance, B.G.I.; Mullen, D.; Karayiiannis, T. EB Surface Engineering for High Performance Heat Exchangers. In Proceedings of the First International Electron Beam Welding Conference, Chicago, Illinois, USA, 17–18 November 2009. [Google Scholar]
- Ucsnik, S.; Gradinger, R.; Becirovic, A.; Waldhör, A. Enhanced Performance of Steel-Aluminium Cast Nodes through Cold Metal Transfer. Mater. Sci. Forum 2013, 765, 736–740. [Google Scholar] [CrossRef]
- Abe, H.; Chung, J.C.; Mori, T.; Hosoi, A.; Jespersen, K.M.; Kawada, H. The effect of nanospike structures on direct bonding strength properties between aluminum and carbon fiber reinforced thermoplastics. Compos. Part B Eng. 2019, 172, 26–32. [Google Scholar] [CrossRef]
- Senge, S.; Brachmann, J.; Hirt, G.; Bührig-Polaczek, A. Interlocking Multi-Material Components made of Structured Steel Sheets and High-Pressure Die Cast Aluminium. In Proceedings of the 20th International ESAFORM Conference on Material Forming, Dublin, Ireland, 26–28 April 2017; p. 190007. [Google Scholar]
- Senge, S.; Brachmann, J.; Hirt, G.; Bührig-Polaczek, A. Evaluation of interlocking bond strength between structured 1.0338 steel sheets and high pressure die cast AlMg5Si2. In Proceedings of the 21st International ESAFORM Conference on Material Forming, Palermo, Italy, 23–25 April 2018; p. 40019. [Google Scholar]
- Ringel, A.; Lohmar, J. Optimization of the Surface Geometry in Structured Cold Rolling for Interlocking of Formed and Die-Cast Metal Components. Defect Diffus. Forum 2022, 414, 89–94. [Google Scholar] [CrossRef]
- Jakumeit, J.; Behnken, H.; Laqua, R.; Eiken, J.; Brachmann, J. Multi-scale simulation of hybrid light metal structures produced by high pressure die casting. IOP Conf. Ser. Mater. Sci. Eng. 2020, 861, 12035. [Google Scholar] [CrossRef]
- Joop, D. Präzisionsbestimmende Faktoren bei der Herstellung blechverstärkter Hybridstrukturen im Druckguss: Grenzflächenanalyse und Verzugsoptimierung. Doctoral Thesis, Gießerei-Institut, RWTH Aachen University, Aachen, Germany, 2018. [Google Scholar]
- Ringel, A.; Hirt, G. Bending behavior of structured steel sheets with undercuts for interlocking with Al die-cast metal. Int. J. Mater. Form. 2024, 17, 2. [Google Scholar] [CrossRef]
- Bruckmeier, L.; Ringel, A.; Vroomen, U.; Bailly, D.; Bührig-Polaczek, A. Influence of High-Pressure Die Casting Process Parameters on the Compound Strength of Hybrid Components with Undercut Sheet Metal. Metals 2023, 13, 1717. [Google Scholar] [CrossRef]
- Tieu, A.; Liu, Y. Friction variation in the cold-rolling process. Tribol. Int. 2004, 37, 177–183. [Google Scholar] [CrossRef]
- Clausmeyer, T.; Schowtjak, A.; Wang, S.; Gitschel, R.; Hering, O.; Pavliuchenko, P.; Lohmar, J.; Ostwald, R.; Hirt, G.; Tekkaya, A.E. Prediction of Ductile Damage in the Process Chain of Caliber Rolling and Forward Rod Extrusion. Procedia Manuf. 2020, 47, 649–655. [Google Scholar] [CrossRef]


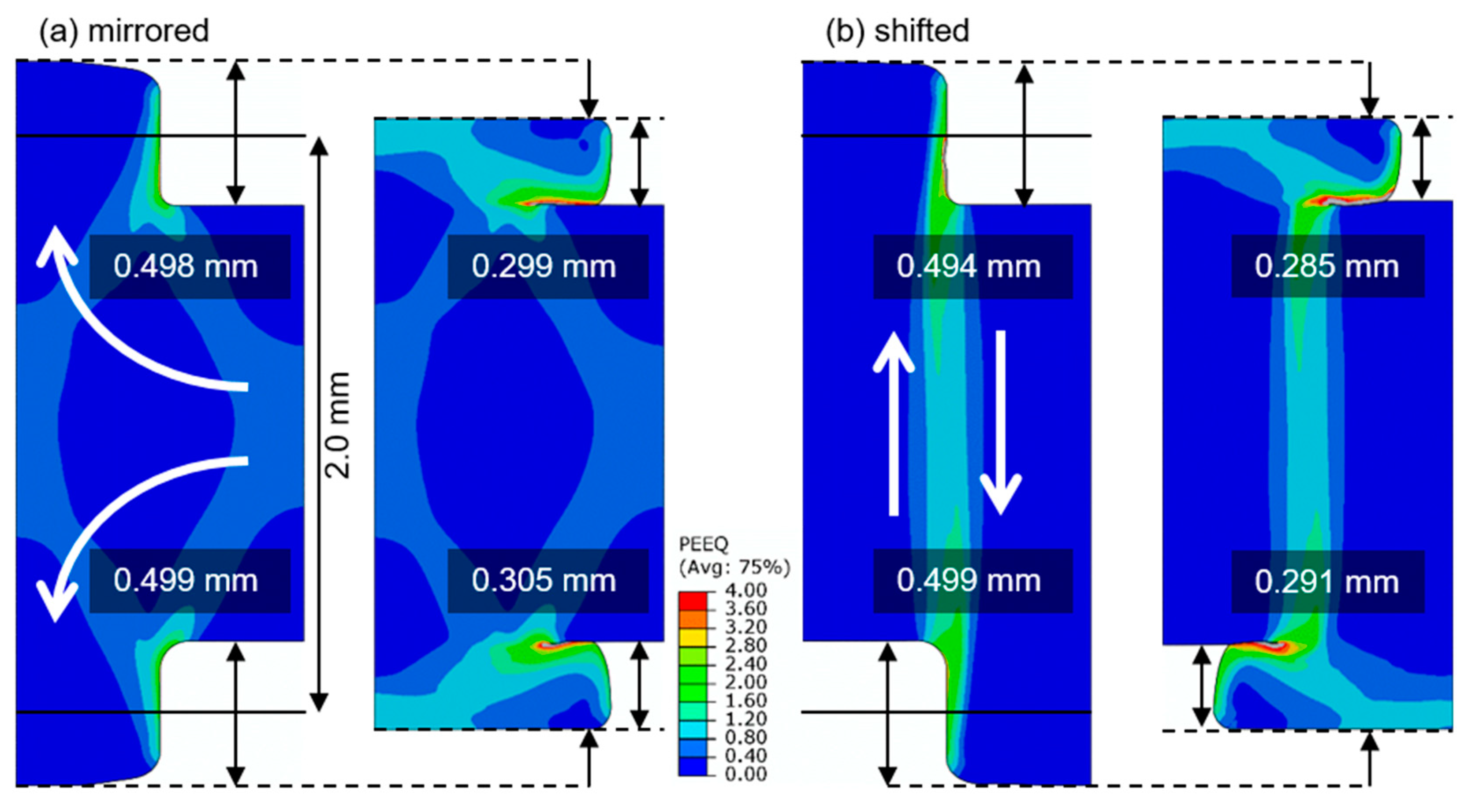


| in % | Single [17] | Mirrored | Shifted |
|---|---|---|---|
| Ideal case | 12.50 | ||
| Simulation | 12.04 (−3.7% *) | 12.05 (−3.6% *) | 12.37 (−1.0% *) |
| Experiment | 19.66 (+57.3% *) | 14.18 (+13.4% *) | 13.01 (+4.1% *) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ringel, A.; Shayan, S.; Bailly, D. Double-Sided Surface Structures with Undercuts on Cold-Rolled Steel Sheets for Interlocking in Hybrid Components. Machines 2024, 12, 562. https://doi.org/10.3390/machines12080562
Ringel A, Shayan S, Bailly D. Double-Sided Surface Structures with Undercuts on Cold-Rolled Steel Sheets for Interlocking in Hybrid Components. Machines. 2024; 12(8):562. https://doi.org/10.3390/machines12080562
Chicago/Turabian StyleRingel, Aron, Sindokht Shayan, and David Bailly. 2024. "Double-Sided Surface Structures with Undercuts on Cold-Rolled Steel Sheets for Interlocking in Hybrid Components" Machines 12, no. 8: 562. https://doi.org/10.3390/machines12080562
APA StyleRingel, A., Shayan, S., & Bailly, D. (2024). Double-Sided Surface Structures with Undercuts on Cold-Rolled Steel Sheets for Interlocking in Hybrid Components. Machines, 12(8), 562. https://doi.org/10.3390/machines12080562






