A Denoising Algorithm for Wear Debris Images Based on Discrete Wavelet Multi-Band Sparse Representation
Abstract
1. Introduction
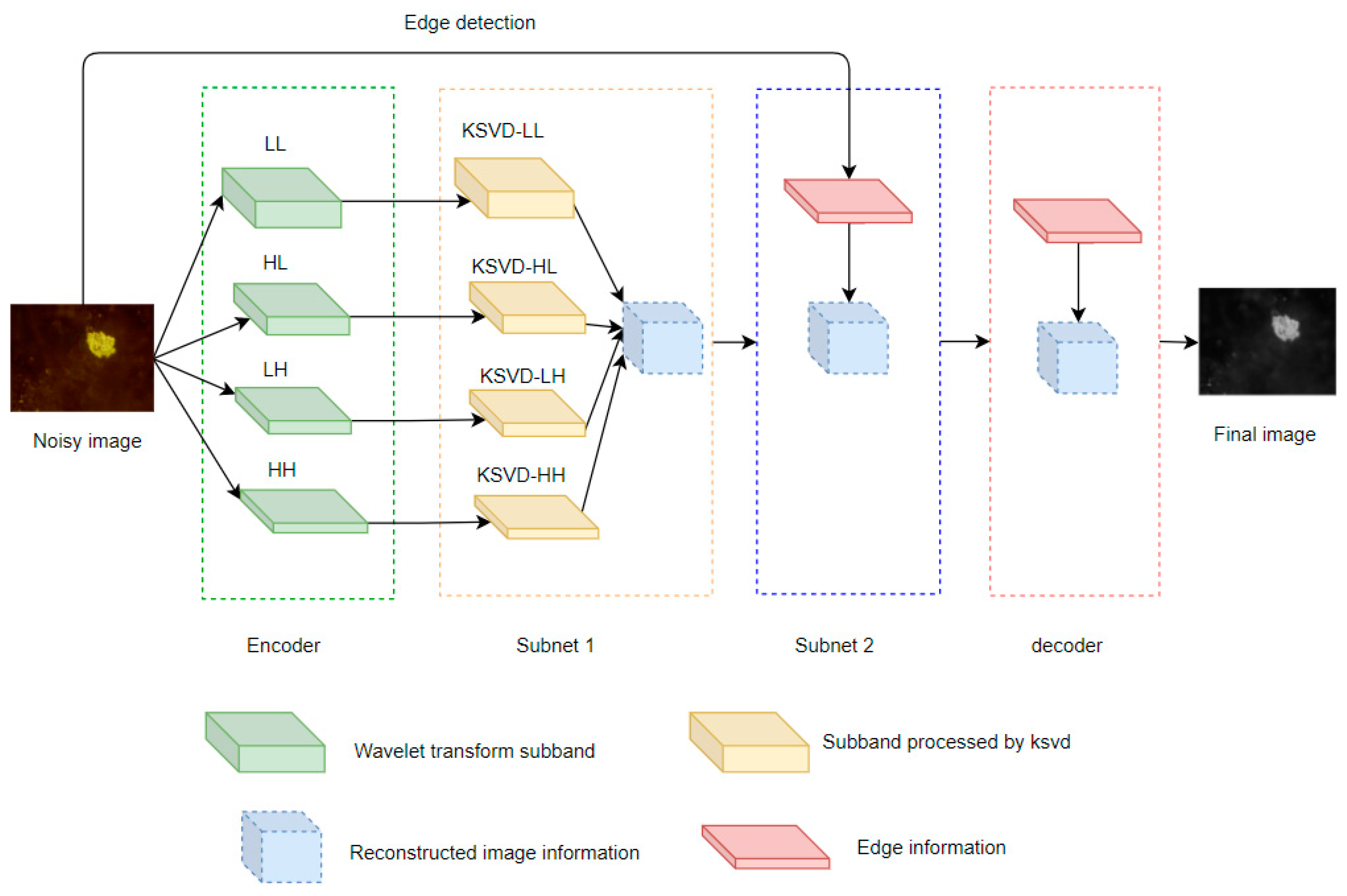
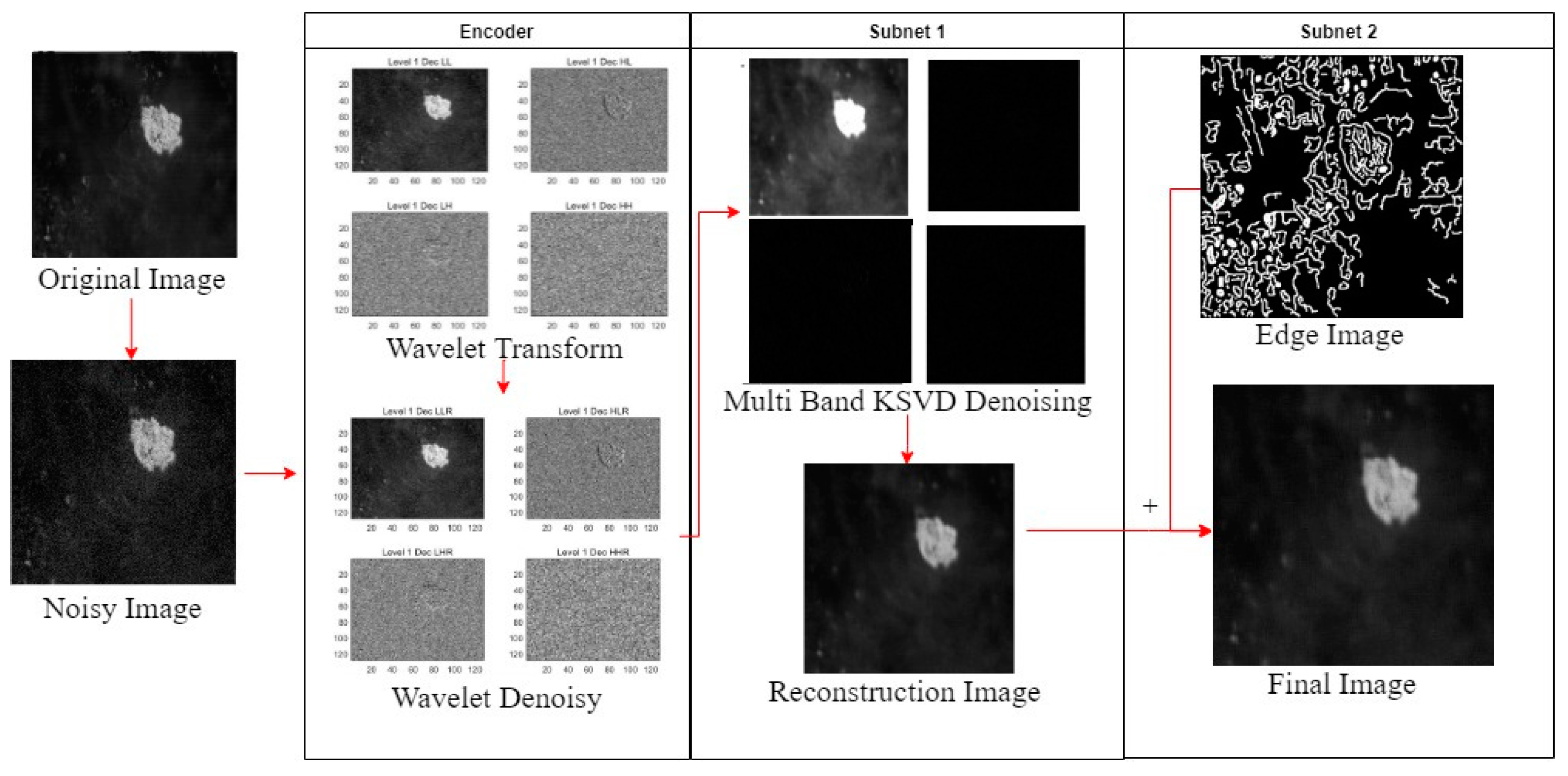
2. Principle of W-KSVD-EDGE Algorithm
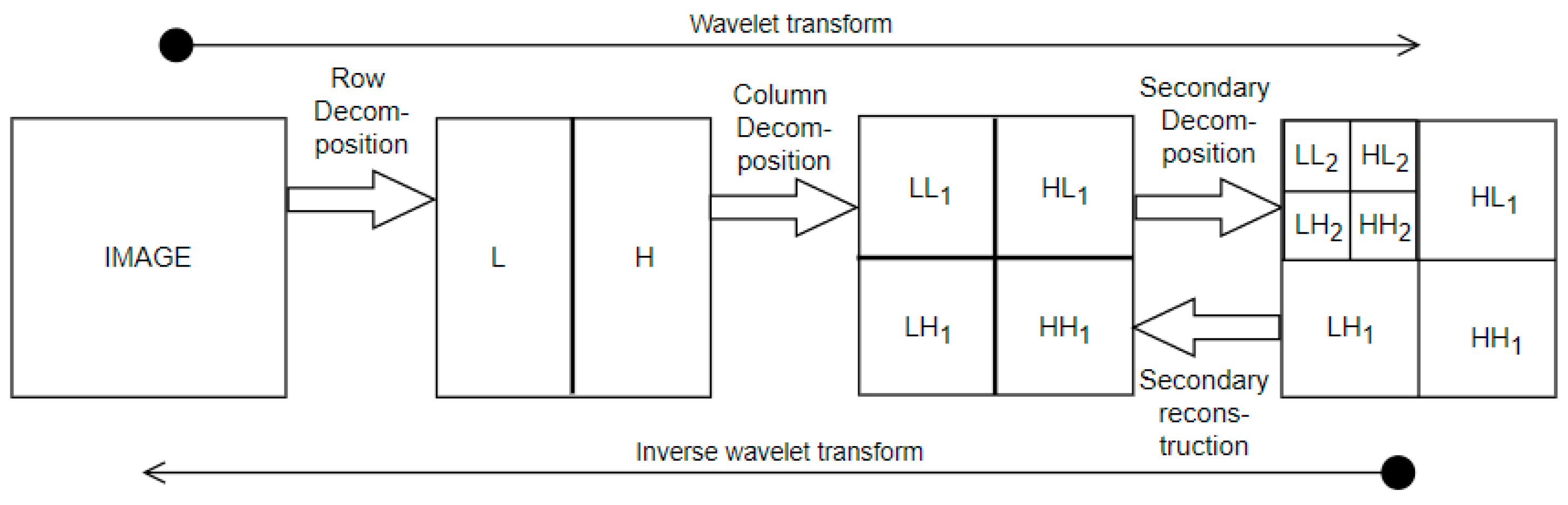
2.1. Multi-Scale Decomposition of Wavelet Transform
2.2. Multi-Band KSVD Denoising Algorithm
2.3. Enhancement of Edge Information
3. Experiment
3.1. Image Denoising Performance Evaluation Metrics
3.1.1. Visual Comparison Methods
3.1.2. Objective Evaluation Methods
- 1.
- PSNR.
- 2.
- SSIM.
- 3.
- Edge preservation index (EPI) [33].
3.2. Experimental Details Information
3.3. Visual Comparison of Image Denoising Effectiveness
3.4. Objective Evaluation
4. Conclusions
4.1. Summary of Conclusions
4.2. Future Research Directions and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhattacharya, A.; Dan, P.K. Recent trend in condition monitoring for equipment fault diagnosis. Int. J. Syst. Assur. Eng. Manag. 2014, 5, 230–244. [Google Scholar] [CrossRef]
- Peng, P.; Chen, L.; Wang, J.; Chen, F. A Review on Detection Technology of Mechanical Wear. Lubr. Eng. 2018, 43, 115–124. [Google Scholar]
- Scott, D.; Seifert, W.W.; Westcott, V.C. Ferrography-an advanced design aid for the 80’s. Wear 1975, 34, 251–260. [Google Scholar] [CrossRef]
- Wu, H.; Li, R.; Kwok, N.M.; Peng, Y.; Wu, T.; Peng, Z. Restoration of low-informative image for robust debris shape measurement in on-line wear debris monitoring. Mech. Syst. Signal Process. 2019, 114, 539–555. [Google Scholar] [CrossRef]
- More, P.P.; Jaybhaye, M.D. Wear Pattern and Debris Analysis in Gearbox System. J. Fail. Anal. Prev. 2021, 21, 1697–1703. [Google Scholar] [CrossRef]
- Dai, X.; Wang, Y.; Yu, S. Ferrographic analysis of pivot jewel bearing in oil-bath lubrication. Wear 2017, 376–377, 843–850. [Google Scholar] [CrossRef]
- Hong, H.; Liang, M. A fractional calculus technique for on-line detection of oil debris. Meas. Sci. Technol. 2008, 19, 055703. [Google Scholar] [CrossRef]
- Zhi, Z.; Wang, S.; Wei, H.; Tomovic, M. Aliasing signal separation of oil debris monitoring. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Li, Y.; Zhang, P.; Xu, C.; Zhang, Y.; Li, L. An improved online de-noising method for Ultrasonic echo signal of wear debris in oil. In Proceedings of the International Conference on Information Technology and Management Innovation 2014, Singapore, 23–25 September 2014. [Google Scholar]
- Hubel, D.H.; Wiesel, T.N. Receptive fields of single neurones in the cat’s striate cortex. J. Physiol. 1959, 148, 574–591. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Tropp, A.; Wright, S.J. Computational methods for sparse solution of linear inverse problems. Proc. IEEE 2010, 98, 948–958. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Farouk, R.M.; Elsayed, M.; Aly, M. Medical Image Denoising based on Log-Gabor Wavelet Dictionary and K-SVD Algorithm. Int. J. Comput. Appl. 2016, 141, 27–32. [Google Scholar] [CrossRef]
- Chen, R.; Pu, D.; Tong, Y.; Wu, M. Image-denoising algorithm based on improved K-singular value decomposition and atom optimization. CAAI Trans. Intell. Technol. 2021, 7, 117–127. [Google Scholar] [CrossRef]
- Shensa, M.J. The discrete wavelet transform: Wedding the a trous and Mallat algorithms. IEEE Trans Signal Process. 1992, 40, 2464–2482. [Google Scholar] [CrossRef]
- Wang, L.; Li, X.; Qin, J. Cascade discrete wavelet multi-band decomposition attention image denoising method. Appl. Res. Comput. 2024, 41, 288–295. [Google Scholar]
- Khmag, A.; Ramli, A.R.; Al-Haddad, S.A.R.; Hashim, S.J.; Noh, Z.M.; Najih, A.A.M. Design of Natural Image Denoising Filter Based on Second-Generation Wavelet Transformation and Principle Component Analysis. J. Med. Imaging Health Inform. 2015, 5, 1261–1266. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, H.; Nie, F.; Wang, R.; Yang, C.; Jia, X.; Li, X. Double-attentive principle component analysis. IEEE Signal Process. Lett. 2020, 27, 1814–1818. [Google Scholar] [CrossRef]
- Guhathakurta, R. Denoising of image: A wavelet based approach. In Proceedings of the 2017 8th Annual Industrial Automation and Electromechanical Engineering Conference (IEMECON), Bangkok, Thailand, 16–18 August 2017; pp. 194–197. [Google Scholar]
- Duan, Y.; Liu, F.; Jiao, L.; Zhao, P.; Zhang, L. SAR image segmentation based on convolutional-wavelet neural network and Markov random field. Pattern Recognit. 2017, 64, 255–267. [Google Scholar] [CrossRef]
- Cao, W.; Yan, J.; Jin, Z.; Han, Z.; Zhang, H.; Qu, J.; Zhang, M. Image denoising and feature extraction of wear debris for online monitoring of planetary gearboxes. IEEE Access 2021, 9, 168937–168952. [Google Scholar] [CrossRef]
- Neshatavar, R.; Yavartanoo, M.; Son, S.; Lee, K.M. CVF-SID: Cyclic multi-Variate Function for Self-Supervised Image Denoising by Disentangling Noise from Image. arXiv 2022. [Google Scholar] [CrossRef]
- Chen, H.; Gu, J.; Liu, Y.; Magid, S.A.; Dong, C.; Wang, Q.; Pfister, H.; Zhu, L. Masked Image Training for Generalizable Deep Image Denoising. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023. [Google Scholar] [CrossRef]
- Han, L.; Zhao, Y.; Lv, H.; Zhang, Y.; Liu, H.; Bi, G. Remote sensing image denoising based on deep and shallow feature fusion and attention mechanism. Remote Sens. 2022, 14, 1243. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Anwar, S.; Ji, P.; Kim, D.; Caldwell, S.; Gedeon, T. Invertible Denoising Network: A Light Solution for Real Noise Removal. arXiv 2021. [Google Scholar] [CrossRef]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H.; Shao, L. Learning enriched features for fast image restoration and enhancement. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 1934–1948. [Google Scholar] [CrossRef] [PubMed]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Ma-Chine Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Zhu, X.; Tang, M.; Zhang, K.; Wang, Q. Image detection method based on improved Canny algorithm. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 7033–7039. [Google Scholar]
- Pang, T.; Zheng, H.; Quan, Y.; Ji, H. Recorrupted-to-recorrupted: Unsupervised deep learning for image denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Schmid-Schickhardt, D. Adaptive Canny Edge Detection: Hysteresis Thresholds with Deep Learning. Bachelor’s Thesis, Radboud University, Nijmegen, Germany, 2021. [Google Scholar]
- Choi, K.H.; Ha, J.E. An adaptive threshold for the Canny edge with actor-critic algorithm. IEEE Access 2023, 11, 67058–67069. [Google Scholar] [CrossRef]
- Chumning, H.; Huadong, G.; Changlin, W. Edge preservation evaluation of digital speckle filters. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium IEEE 2002, Toronto, ON, Canada, 24–28 June 2002. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Two-Dimensional Variational Mode Decomposition. In Energy Minimization Methods in Computer Vision and Pattern Recognition; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising with block-matching and 3D filtering//Image Processing: Algorithms and Systems, Neural Networks, and Machine Learning. Int. Soc. Opt. Photonics 2006, 6064, 354–365. [Google Scholar] [CrossRef]
- Zhao, W.; Lv, Y.; Liu, Q.; Qin, B. Detail-Preserving Image Denoising via Adaptive Clustering and Progressive PCA Thresholding. IEEE Access 2018, 6, 6303–6315. [Google Scholar] [CrossRef]
- Hou, Y.; Xu, J.; Liu, M.; Liu, G.; Liu, L.; Zhu, F.; Shao, L. Nlh: A blind pixel-level non-local method for real-world image denoising. IEEE Trans. Image Process. 2020, 29, 5121–5135. [Google Scholar] [CrossRef]








| Project | Parameter |
|---|---|
| Oil sample usage | 3 mL |
| Solvent dosage | 2 mL |
| Immersion range of oil sample water area | Completely submerged |
| Using solvents | Tetrachloroethylene |
| Oil velocity | 30 mL/h |
| Oil delivery time | 600 s |
| Cleaning solution speed | 10 mL/h |
| Cleaning solution cleaning time | 480 s |
| Spectral tilt angle | 1° |
| Magnetic field intensity | >1.5 T |
| Field Gradient | >5.0 T/cm |
| Spectral specifications | 60 mm × 24 mm × 0.17 mm |
| Test tube specifications | 10 mm × 100 mm |
| Oil pipeline specifications | 2.4 mm × 2.0 mm × 400 mm |
| Noisy | Algorithm | Evaluating Indicator | ||
|---|---|---|---|---|
| PSNR | SSIM | EPI | ||
| Wavelet | 30.6178 | 0.9791 | 0.4073 | |
| Wavelet | 30.6187 | 0.9791 | 0.4073 | |
| 2DVMD | 30.5740 | 0.4356 | 0.2235 | |
| BM3D | 31.5566 | 0.4830 | 0.2728 | |
| ACPT | 14.3799 | 0.4639 | 0.3938 | |
| NLH | 26.4130 | 0.3893 | 0.1996 | |
| WVBOD | 29.7972 | 0.4474 | 0.3384 | |
| W-KSVD-EDGE | 30.8558 | 0.9801 | 0.4116 | |
| Wavelet | 28.9542 | 0.3447 | 0.3805 | |
| Wavelet | 28.9542 | 0.3447 | 0.3805 | |
| 2DVMD | 20.0244 | 0.1469 | 0.2034 | |
| BM3D | 31.0612 | 0.4363 | 0.2943 | |
| ACPT | 14.4087 | 0.4578 | 0.4335 | |
| NLH | 24.2461 | 0.3636 | 0.1910 | |
| WVBOD | 28.3035 | 0.3820 | 0.3283 | |
| W-KSVD-EDGE | 28.3436 | 0.9639 | 0.3819 | |
| Wavelet | 25.1490 | 0.2171 | 0.2122 | |
| Wavelet | 25.1490 | 0.2171 | 0.2122 | |
| 2DVMD | 13.9084 | 0.0536 | 0.1695 | |
| BM3D | 24.8182 | 0.1898 | 0.0237 | |
| ACPT | 1.9900 | 0.0995 | 0.0127 | |
| NLH | 23.4012 | 0.2902 | 0.1429 | |
| WVBOD | 24.6660 | 0.2618 | 0.1581 | |
| W-KSVD-EDGE | 25.6201 | 0.9338 | 0.1672 | |
| Noisy | Algorithm | Evaluating Indicator | ||
|---|---|---|---|---|
| PSNR | SSIM | EPI | ||
| Wavelet | 26.2071 | 0.3098 | 0.3400 | |
| Wavelet | 26.2071 | 0.3098 | 0.3400 | |
| 2DVMD | 26.2718 | 0.3211 | 0.2097 | |
| BM3D | 29.4446 | 0.4135 | 0.4991 | |
| ACPT | 17.1517 | 0.4339 | 0.5203 | |
| NLH | 24.6530 | 0.4804 | 0.3716 | |
| WVBOD | 22.1156 | 0.2484 | 0.2508 | |
| W-KSVD-EDGE | 29.7305 | 0.9913 | 0.5638 | |
| Wavelet | 25.1859 | 0.2678 | 0.2934 | |
| Wavelet | 25.1859 | 0.2678 | 0.2934 | |
| 2DVMD | 20.1330 | 0.2893 | 0.2020 | |
| BM3D | 29.0227 | 0.4183 | 0.4895 | |
| ACPT | 17.4524 | 0.5148 | 0.5612 | |
| NLH | 24.0563 | 0.4487 | 0.3554 | |
| WVBOD | 21.9298 | 0.2116 | 0.2431 | |
| W-KSVD-EDGE | 27.1489 | 0.9840 | 0.4616 | |
| Wavelet | 23.0312 | 0.2136 | 0.1653 | |
| Wavelet | 23.0312 | 0.2136 | 0.1653 | |
| 2DVMD | 13.8484 | 0.1308 | 0.1427 | |
| BM3D | 23.9127 | 0.3135 | 0.0731 | |
| ACPT | 6.5382 | 0.2105 | 0.0137 | |
| NLH | 22.6154 | 0.3717 | 0.2776 | |
| WVBOD | 21.5036 | 0.1631 | 0.2141 | |
| W-KSVD-EDGE | 24.6771 | 0.9719 | 0.2347 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Xian, C.; Kim, Y.-C. A Denoising Algorithm for Wear Debris Images Based on Discrete Wavelet Multi-Band Sparse Representation. Machines 2024, 12, 672. https://doi.org/10.3390/machines12100672
Zhang H, Xian C, Kim Y-C. A Denoising Algorithm for Wear Debris Images Based on Discrete Wavelet Multi-Band Sparse Representation. Machines. 2024; 12(10):672. https://doi.org/10.3390/machines12100672
Chicago/Turabian StyleZhang, Han, Chen Xian, and Young-Chul Kim. 2024. "A Denoising Algorithm for Wear Debris Images Based on Discrete Wavelet Multi-Band Sparse Representation" Machines 12, no. 10: 672. https://doi.org/10.3390/machines12100672
APA StyleZhang, H., Xian, C., & Kim, Y.-C. (2024). A Denoising Algorithm for Wear Debris Images Based on Discrete Wavelet Multi-Band Sparse Representation. Machines, 12(10), 672. https://doi.org/10.3390/machines12100672





