Influence of Seal Structure on the Motion Characteristics and Stability of a Steam Turbine Rotor

Abstract

Sealing aerodynamic characteristics are affected by the seal structure, and thus the stability of the rotor system is affected too. A 1.5-stage, three-dimensional, full-cycle model of the high-pressure cylinder of a 1000 MW steam turbine was established. The high eccentricity whirl of the rotor was realized using mesh deformation technology and the multi-frequency whirl model. The nonlinear steam-flow-exciting force of different sealing structures was obtained using CFD/FLUENT, and the motion equations with a nonlinear steam-exciting force were solved using the Runge–Kutta method. The motion characteristics and stability of the rotor system with different sealing structures were obtained. The results show that there are “inverted bifurcation” and “double bifurcation” phenomena in the bifurcation diagrams of different tooth numbers, boss numbers, and tooth lengths, and a 1/2 power frequency of different sealing structures goes through the process of weakening, disappearing, reproducing, and evolving into a 1/3 power frequency and a 2/3 power frequency. With the increasing load, the steam-flow-exciting force becomes stronger, and the multi-frequency vibration and dense frequency phenomena are significant. Under some load conditions, the change curves of three kinds of teeth in 1/3 and 2/3 power frequency vibrations are highly similar, and the tooth number has little influence on the system stability. Under the high load condition, with the boss number increasing, the chaos phenomenon is weakened. Increasing the tooth length is beneficial to the stability of the rotor.

1. Introduction

Steam flow excitation vibration was an important factor affecting the safe, stable, and economic operation of the unit, and the sealing structure has a great influence on steam flow excitation vibration. Since the phenomenon of steam flow excitation was discovered by GE in 1940, scholars have gradually carried out different studies and put forward single-control body, double-control body, and multi-control body models for sealing and steam flow excitation. The mechanism of steam flow excitation vibration was summarized, including the tip clearance steam flow excitation vibration, the steam seal flow excitation vibration, and the asymmetric steam flow excitation vibration [1]. Based on the catastrophe theory, the nonlinear vibration theory, and fluid dynamics, the steam flow excitation vibration in the governing stage of a steam turbine was studied, and the influence factors of the system vibration catastrophe were obtained [2]. By coupling the thermal dynamic load, the Riccati transfer matrix method was used to study its influence on the anisotropic mode of the steam turbine rotor [3]. By comparing the dynamic performance of two statistical models, a new fractal method for the design of gas face seals was suggested [4]. With the development of computational fluid dynamics (CFD), the influence of unsteady steam flow excitation vibration on the dynamic characteristic coefficient of the rotor was given under three different inlet pre-swirls of a typical tip labyrinth seal using ANSYS CFX [5]. The dynamic characteristic coefficients of rotors were analyzed with different tooth numbers, boss numbers, and tooth lengths using FLUENT [6]. The effects of the swirling radius, swirling speed, swirling frequency, and inlet and outlet pressure ratio on the rotor dynamic characteristic coefficient were explored, and the quadratic orthogonal regression test was carried out on the influence of the labyrinth seal structural parameters on leakage [7,8]. Then, a new type of shroud seal was designed, and the influence of this seal on leakage was numerically simulated [9]. A finite element analysis of temperature and pressure on the sealing performance was carried out [10]. It was found that the seal geometry influenced the seal leakage of high-pressure turbines [11]. A seal structure with inclined fins was proposed to improve the aerodynamics, and the results showed that the flow coefficient was reduced by 40% [12]. According to the influence of seal leakage on steam flow excitation vibration, the structure of the seal was improved, and the seal gas bearing effect was one of the most important factors affecting the steam flow excitation force of the seal [13,14,15].

In addition, some scholars have studied the influence of steam flow excitation vibration on the rotor system. Cui Ying et al. [16] applied the nonlinear steam-flow-exciting force on the rotor-bearing seal system of a large steam turbine and studied the effects of seal clearance, rotor damping, and sealing axial velocity on the system instability caused by steam flow excitation vibration. Weng Lei et al. [17] pointed out the influence of steam flow excitation vibration on the motion characteristics of cracked rotor-bearing systems. Xi Wenkui et al. [18] concluded that the seal is the main factor affecting shafting stability in 1000 MW units. Zhang Enjie et al. [19] showed the influence of seal structure on the seal leakage and the axial average velocity and obtained the effects of rotor speed, eccentricity, teeth number, and teeth width on the nonlinear dynamic characteristics of the system.

In light of the analyses mentioned above, it was found that the influence of different seal structures on the motion characteristics and stability of the rotor-bearing seal system needs to be further investigated. In addition, the traditional steam-flow-exciting force model cannot meet the actual situation of significant eccentricity, strong nonlinearity, and a continuous time domain vortex. Therefore, in this paper, a 1.5-stage, three-dimensional, full-cycle model of a high-pressure cylinder of a 1000 MW ultra-supercritical steam turbine is established, and the multi-frequency whirl is used to consider the influence of revolution and rotation on the rotor. The nonlinear steam-flow-exciting forces of different seal structures are calculated using CFD/FLUENT. The motion equations with nonlinear steam-flow-exciting forces are derived and solved using the Runge–Kutta method. Then, the motion characteristics of the rotor-bearing seal system under different steam-flow-exciting forces corresponding to different tooth numbers, boss numbers, and tooth lengths are studied. The stability of the system is analyzed using the largest Lyapunov exponent diagram. The overall flowchart is shown in Figure 1.

2. Rotor-Bearing Seal System

The rotor-bearing seal system of a steam turbine was established based on the Jeffcott rotor model, as shown in Figure 2. The second stage of the high-pressure cylinder in a 1000 MW steam turbine is simplified to a single disk with concentrated mass, which is supported on the symmetrical bearing at both ends. The shaft is a massless elastic shaft, the axial vibrations and torsional effects of the shaft are ignored, and only the transverse vibrations are considered. The m₁ and m₂ are the equivalent concentrated mass of the bearing and disc, respectively. The O₁ and O₂ are the centroid of the bearing and disc, and O₃ is the centroid of the disk. Fx and Fy are the components of the oil film force at the bearing, respectively, in the x and y directions. Fax and Fay are the components of the sealing nonlinear steam-flow-exciting force at the disk, respectively, in the x and y directions.

2.1. Nonlinear Steam-Flow-Exciting Force Model

A 1.5-stage model of the second stage of the high-pressure cylinder of a 1000 MW steam turbine was established, as shown in Figure 3.

The blade tip clearance steam-flow-exciting force, the static blade ring seal steam-flow-exciting force, and the moving blade passage steam-flow-exciting force were considered to calculate the nonlinear steam-flow-exciting force. Taking a 1.5 stage as a whole, the corresponding nonlinear steam-flow-exciting force was obtained by changing the sealing structure, and the influence on the motion characteristics and stability of the rotor system was studied. Among them, the tooth thickness of the tip seal and the stator ring seal is 0.6 mm, the spacing between the seal teeth is 8.5 mm, and the height of the boss is 7.6 mm and 5.6 mm, respectively. The calculation arrangement of the main sealing structure is shown in

Table 1. Calculation arrangement of the sealing structure.

Parameter	Value
Teeth number	5	7	9	7	7	7	7	7	7
Boss number	0	0	0	0	1	2	2	2	2
Teeth length/mm	4.6	4.6	4.6	4.6	4.6/2.2	4.6/2.2	4.4/2.0	4.6/2.2	4.8/2.4

.

According to the structural parameters of the actual units, a three-dimensional full-cycle model is established as shown in Figure 4. The structured grid was divided by ANSYS ICEM, and the unsteady flow field was calculated by CFD/FLUENT.

The calculated boundary conditions were set as the steam parameters under different loads according to the off-design calculation method. The boundary conditions at the 100%THA (Turbine Heat Acceptance) are shown in

Table 2. Boundary conditions of 100%THA.

Inlet Pressure /MPa	Outlet Pressure /MPa	Inlet Temperature /°C	Outlet Temperature /°C
18.96	16.46	544.2	518.38

. The SST k-ω model [20] of CFX and the SIMPLE algorithm were used to solve the flow field.

In the process of numerical simulation, the control equations of the seal fluid are solved to obtain approximate values of the calculated variables. All problems involving fluid flow adhere strictly to the three fundamental conservation laws of mass conservation, momentum conservation, and energy conservation. Their mathematical formulations are outlined as follows:

Equation of mass conservation:

$${\displaystyle \frac{\mathsf{\partial }\rho }{\mathsf{\partial }t}}+\mathrm{div}(\rho \mathit{u})=0$$

(1)

where ρ is the fluid density, kg/m³. t is time, s. u is the velocity vector, m/s.

Momentum conservation equations:

$${\displaystyle \frac{\mathsf{\partial }(\rho u)}{\mathsf{\partial }t}}+\mathrm{div}(\rho u\mathit{u})=\mathrm{div}(\mu \mathrm{grad}u)-{\displaystyle \frac{\mathsf{\partial }\rho }{\mathsf{\partial }x}}+S_u$$

(2)

$${\displaystyle \frac{\mathsf{\partial }(\rho v)}{\mathsf{\partial }t}}+\mathrm{div}(\rho v\mathit{u})=\mathrm{div}(\mu \mathrm{grad}v)-{\displaystyle \frac{\mathsf{\partial }\rho }{\mathsf{\partial }y}}+S_v$$

(3)

$${\displaystyle \frac{\mathsf{\partial }(\rho w)}{\mathsf{\partial }t}}+\mathrm{div}(\rho w\mathit{u})=\mathrm{div}(\mu \mathrm{grad}w)-{\displaystyle \frac{\mathsf{\partial }\rho }{\mathsf{\partial }z}}+S_w$$

(4)

where μ is dynamic viscosity, N·s/m². u, v and w are the components of the velocity vector in x, y and z directions. S_u, S_v and S_w are generalized source terms in the momentum conservation equation.

Energy conservation equation:

$${\displaystyle \frac{\mathsf{\partial }(\rho T)}{\mathsf{\partial }t}}+\mathrm{div}(\rho \mathit{u}T)=\mathrm{div}\left({\displaystyle \frac{C_k}{{\mathrm{c}}_p}}\mathrm{grad}T\right)+S_T$$

(5)

where T is temperature, K. C_k is heat transfer coefficient of fluid, W/(m²·K). c_p is the specific heat capacity of fluid, J/(kg·K). S_T is a viscous dissipation term.

The SST k-ω model equation of CFX is as follows:

$${\displaystyle \frac{\mathsf{\partial }(\rho k)}{\mathsf{\partial }t}}+{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}}(\rho k{u}_i)={\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}}\left({\Gamma }_k{\displaystyle \frac{\mathsf{\partial }k}{\mathsf{\partial }{x}_j}}\right)+G_k-Y_k+S_k$$

(6)

$${\displaystyle \frac{\mathsf{\partial }(\rho \omega )}{\mathsf{\partial }t}}+{\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}}(\rho k{u}_j)={\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }{x}_j}}\left({\Gamma }_{\omega }{\displaystyle \frac{\mathsf{\partial }\omega }{\mathsf{\partial }{x}_j}}\right)+G_{\omega }-Y_{\omega }+D_{\omega }+S_{\omega }$$

(7)

where G_k is the turbulent kinetic energy, J. G_ω is the turbulence ratio dissipation rate. Г_k and Г_ω are the effective diffusion terms of k and ω. Y_k and Y_ω are divergence terms of k and ω. D_ω is the orthogonal divergence term. S_k and S_ω are the user customizations.

The relative value of shaft power is used to verify the grid independence. The calculation expression of shaft power is as follows:

$$W_a=T_a\omega$$

(8)

where T_a is the torque at each position of the rotating surface, N·m. The subscript a represents the axis. ω is the angular velocity of rotation, rad/s.

The tip clearance was set to 0.5 mm, and the corresponding shaft power was calculated, when the numbers of grids were 1.02 million, 2.56 million, 3.13 million, 4.25 million and 4.86 million, respectively. When the calculated total number of grids was 3.13 million, the shaft power no longer changed with the number of grids. Since the CPU and memory usage of the computer need to be considered, the total number of grids was set at about 4.25 million.

In addition, considering the grid domain change caused by the rotor whirl, the dynamic grid technology was adopted. The rotor trajectory was defined by the user-defined function UDF (user-defined function), and the grids were updated by re-meshing. In order to better simulate the swirl of the rotor, the whirling frequencies are 5–60 Hz for a total of 12 frequency points.

The appropriate whirling radius and whirling frequency are selected for numerical simulation, and the simulated nonlinear steam-flow-exciting force is fitted using polynomial the fitting method in MATLAB. The fitting results are shown in Figure 5. The nonlinear steam-flow-exciting force calculation formulas F_ax and F_ay under different sealing structures are obtained. This formula is a polynomial of whirling frequency Ω and whirling radius C_r.

$$\left\{\begin{array}{c}{F}_{ax}=f\left(\Omega ,C_r\right)\\ F_{ay}=f\left(\Omega ,C_r\right)\end{array}\right.$$

(9)

The specific expression is as follows:

$$\begin{array}{ll}{F}_{ax}\hfill & =p1+p2\times C_r+p3\times omega+p4\times C_r^2+\hfill \\ & p5\times C_r\times omega+p6\times omeg{a}^2+p7\times C_r^3+\hfill \\ & p8\times C_r^2\times omega+p9\ast C_r\times omeg{a}^2+\hfill \\ & p10\times omeg{a}^3+p11\times C_r^4+p12\times C_r^3\times omega+\hfill \\ & p13\times C_r^2\times omeg{a}^2+p14\times C_r\times omeg{a}^3+\hfill \\ & p15\times omeg{a}^4+p16\times C_r^5+p17\times C_r^4\times omega+\hfill \\ & p18\times C_r^3\times omeg{a}^2+p19\times C_r^2\times omeg{a}^3+\hfill \\ & p20\times C_r\times omeg{a}^4+p21\times omeg{a}^5;\hfill \end{array}$$

(10)

$$\begin{array}{ll}{F}_{ay}\hfill & =p22+p23\times C_r+p24\times omega+\hfill \\ & p25\times C_r^2+p26\times C_r\times omega+p27\times omeg{a}^2+\hfill \\ & p28\times C_r^3+p29\times C_r^2\times omega+p30\times C_r\times omeg{a}^2+\hfill \\ & p31\times omeg{a}^3+p32\times C_r^4+p33\times C_r^3\times omega+\hfill \\ & p34\times C_r^2\times omeg{a}^2+p35\times C_r\times omeg{a}^3+\hfill \\ & p36\times omeg{a}^4+p37\times C_r^5+p38\times C_r^4\times omega+\hfill \\ & p39\times C_r^3\times omeg{a}^2+p40\times C_r^2\times omeg{a}^3+\hfill \\ & p41\times C_r\times omeg{a}^4+p42\times omeg{a}^5;\hfill \end{array}$$

(11)

where F_ax and F_ay represent the nonlinear steam-exciting force in x and y directions, N. C_r is the eccentricity, mm. omega is the whirling frequency, Hz. p1,…, p42 are the coefficients.

2.2. Nonlinear Oil Film Forces Model

The dimensionless oil film forces in the x and y directions are [21] as follows

$$\left\{\begin{array}{c}{f}_x\\ f_y\end{array}\right\}=-{\displaystyle \frac{{\left[{\left(x-2y^{\prime }\right)}^2+{\left(y+2x^{\prime }\right)}^2\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{1-x^2-y^2}}\times \left\{\begin{array}{c}\begin{array}{l}3x\cdot V\left(x,y,\alpha \right)-sin\alpha \cdot G\left(x,y,\alpha \right)\\ -2cos\alpha \cdot S\left(x,y,\alpha \right)\end{array}\\ \begin{array}{l}3y\cdot V\left(x,y,\alpha \right)+cos\alpha \cdot G\left(x,y,\alpha \right)\\ -2sin\alpha \cdot S\left(x,y,\alpha \right)\end{array}\end{array}\right\}$$

(12)

in the formula

$$V\left(x,y,\alpha \right)={\displaystyle \frac{2+\left(ycos\alpha -xsin\alpha \right)G\left(x,y,\alpha \right)}{1-x^2-y^2}}$$

$$S\left(x,y,\alpha \right)={\displaystyle \frac{xcos\alpha +ysin\alpha }{1-{\left(xcos\alpha +ysin\alpha \right)}^2}}$$

$$G\left(x,y,\alpha \right)={\displaystyle \frac{2}{{\left(1-x^2-y^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}\times \left[{\displaystyle \frac{\pi }{2}}+arctg{\displaystyle \frac{ycos\alpha -xsin\alpha }{{\left(1-x^2-y^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}}\right]$$

$$\mathsf{\alpha }=\mathrm{arctg}{\displaystyle \frac{y+2x^{\prime }}{x-2y^{\prime }}}-{\displaystyle \frac{\pi }{2}}sign\left({\displaystyle \frac{y+2x^{\prime }}{x-2y^{\prime }}}\right)-{\displaystyle \frac{\pi }{2}}sign\left(y+2x^{\prime }\right)$$

$$f_x={\displaystyle \frac{F_x}{sP}} ,f_y={\displaystyle \frac{F_y}{sP}}$$

(13)

$$s=\mu \omega RL{\left({\displaystyle \frac{R}{b}}\right)}^2{\left({\displaystyle \frac{L}{2R}}\right)}^2$$

(14)

where x, y, $x^{\prime }$, and $y^{\prime }$ are the dimensionless displacement and velocity of the bearing. s is the Sommerfeld correction coefficient. P is the half of the rotor mass, kg. μ is the viscosity of lubricating oil, Pa·s. b is the bearing radius clearance, mm. R is the bearing radius, mm. L is the bearing length, mm.

2.3. Motion Equations of a Rotor-Bearing Seal System

$$\left\{\begin{array}{l}{m}_1{\ddot{x}}_1+c_1{\dot{x}}_1+{\displaystyle \frac{1}{2}}k(x_1-x_2)=F_x\\ m_1{\ddot{y}}_1+c_1{\dot{y}}_1+{\displaystyle \frac{1}{2}}k(y_1-y_2)=F_y-m_{1}g\\ m_2{\ddot{x}}_2+c_2{\dot{x}}_2+k(x_2-x_1)=F_{ax}+m_{2}e{\omega }^2\cos \omega t\\ m_2{\ddot{y}}_2+c_2{\dot{y}}_2+k(y_2-y_1)=F_{ay}+m_{2}e{\omega }^2\sin \omega t-m_{2}g\end{array}\right.$$

(15)

$$\begin{array}{l}{X}_1=x_1/b, Y_1=y_1/b\\ X_2=x_2/c, Y_2=y_2/c\\ {\dot{X}}_1={\dot{x}}_1/b\omega , {\dot{Y}}_1={\dot{y}}_1/b\omega \\ {\dot{X}}_2={\dot{x}}_2/c\omega , {\dot{Y}}_2={\dot{y}}_2/c\omega \\ {\ddot{X}}_1={\ddot{x}}_1/b{\omega }^2,{\ddot{Y}}_1={\ddot{y}}_1/b{\omega }^2\\ {\ddot{X}}_2={\ddot{x}}_2/c{\omega }^2, {\ddot{Y}}_2={\ddot{y}}_2/c{\omega }^2 \end{array}$$

The dimensionless motion differential equations of the system are obtained as follows:

$$\left\{\begin{array}{c}{\ddot{X}}_1=-{\displaystyle \frac{c_1}{m_1\omega }}{\dot{X}}_1-{\displaystyle \frac{k}{2m_1{\omega }^2}}{X}_1+{\displaystyle \frac{kc{X}_2}{2m_1{\omega }^{2}b}}+{\displaystyle \frac{F_x}{m_{1}b{\omega }^2}}\hfill \\ {\ddot{Y}}_1=-\frac{c_1}{m_1\omega }{\dot{Y}}_1-\frac{k}{2m_1{\omega }^2}{Y}_1+\frac{kc{Y}_2}{2m_1{\omega }^{2}b}+\frac{F_y}{m_{1}b{\omega }^2}-\frac{g}{b{\omega }^2}\hfill \\ {\ddot{X}}_2=-\frac{c_2}{m_2\omega }{\dot{X}}_2-\frac{k}{m_2{\omega }^2}{X}_2+\frac{kb{X}_1}{m_1{\omega }^{2}c}+\frac{F_{ax}}{m_{1}c{\omega }^2}+\frac{e}{c}\cos \omega t\hfill \\ {\ddot{Y}}_2=-\frac{c_2}{m_2\omega }{\dot{Y}}_2-\frac{k}{m_2{\omega }^2}{Y}_2+\frac{kb{Y}_1}{m_1{\omega }^{2}c}+\frac{F_{ay}}{m_{1}c{\omega }^2}+\frac{e}{c}\sin \omega t-\frac{g}{c{\omega }^2}\hfill \end{array}\right.$$

(16)

where c₁ and c₂ are the damping of bearing and rotor, respectively, N·s/m. k is the shaft stiffness, N/m. c is the sealing gap, mm. g is the acceleration of gravity, m/s². e is the mass eccentricity, mm. t is the time, s.

The experimental data from reference [22] are adopted to verify the selected SST k-ω model, as shown in Figure 6. The variation trends of the non-dimensional blade height with the static pressure coefficient under different models are shown. Below the 80% blade height, the calculation results of the four turbulence models are close to the experimental values. At a 90% blade height, the results obtained by the SST k-ω model are close to the experimental values. Above the 95% blade height, however, the experimental value deviates greatly from the simulated value. This is because the width of the extension section of the sealing section is insufficient, which makes the flow direction of the tip leakage flow deviate from the flow direction in the simulation. Based on the four simulation results, the SST k-ω model was used to solve the three-dimensional flow field.

The nonlinear steam-flow-exciting force equation fitted in the paper is verified, and the relative error is obtained by comparing the calculation results of the equation with the simulation results, as shown in

Table 3. Verification of the nonlinear steam-flow-exciting force equation fitted.

Verification Point	Modeling Results/N	Relative Error/%
Fay (20, 0.06)	10.199	6.5
Fay (25, 0.08)	9.977	6.3
Fay (30, 0.10)	15.499	5.8
Fay (35, 0.12)	18.029	5.4
Fay (40, 0.20)	9.001	4.7
Fay (45, 0.40)	24.484	4.2

. It can be seen from the table that the nonlinear steam-flow-exciting force obtained by the fitting equation is accurate and reliable, and can be further simulated based on the data of the equation.

3. Result Analysis

In this paper, the Runge–Kutta method was used to solve the system of second-order differential equations in MATLAB 2021. The main parameters of the system are shown in

Table 4. Main parameters of the rotor system.

Parameter	Value
m1/kg	298
m2/kg	806
R/mm	125
L/mm	180
μ/Pa·s	0.018
e/mm	0.05
c/mm	1.2
b/mm	0.19
c1/N·s/m	2.6 × 106
c2/N·s/m	7.5 × 104
k/N/m	2.5 × 107

.

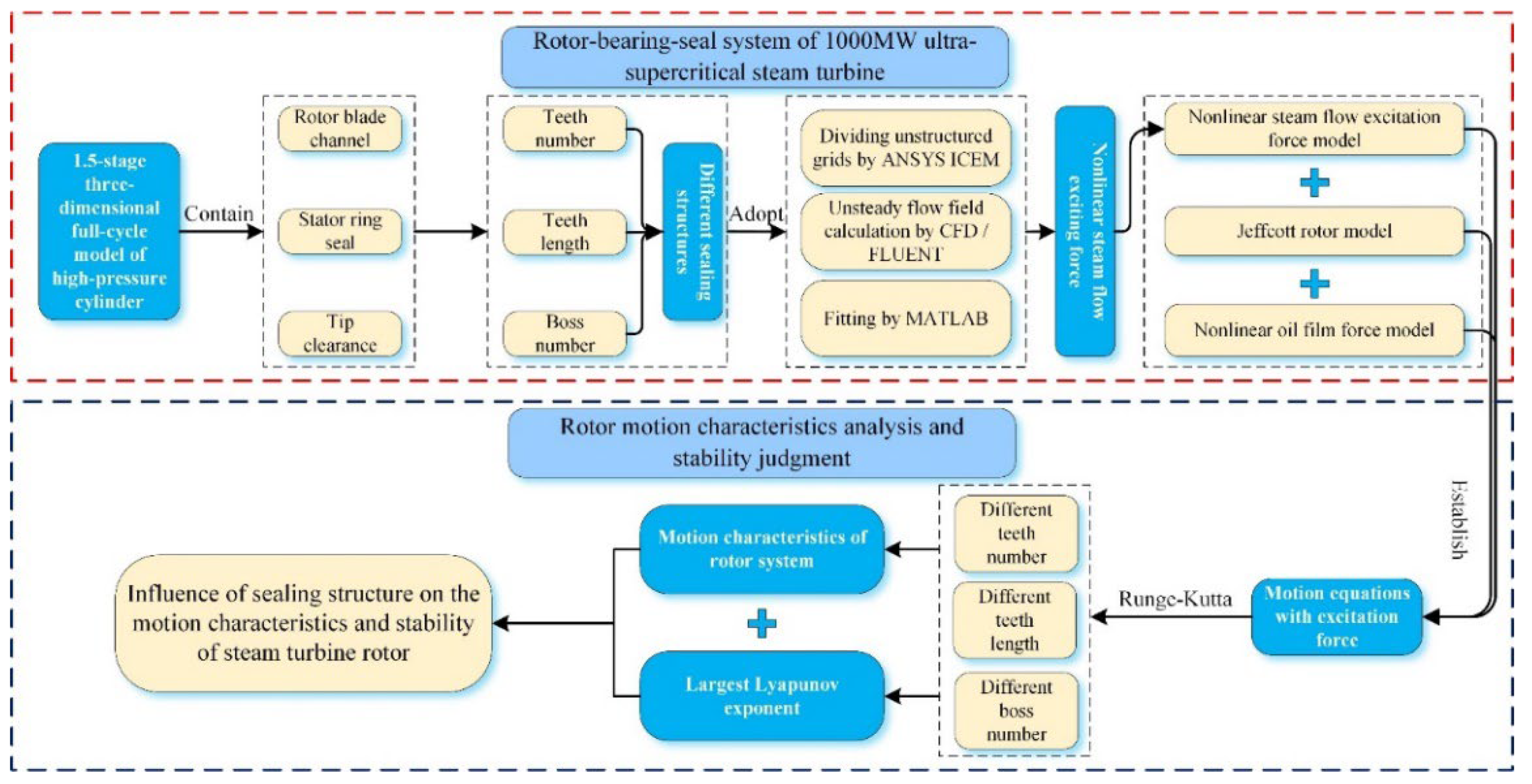
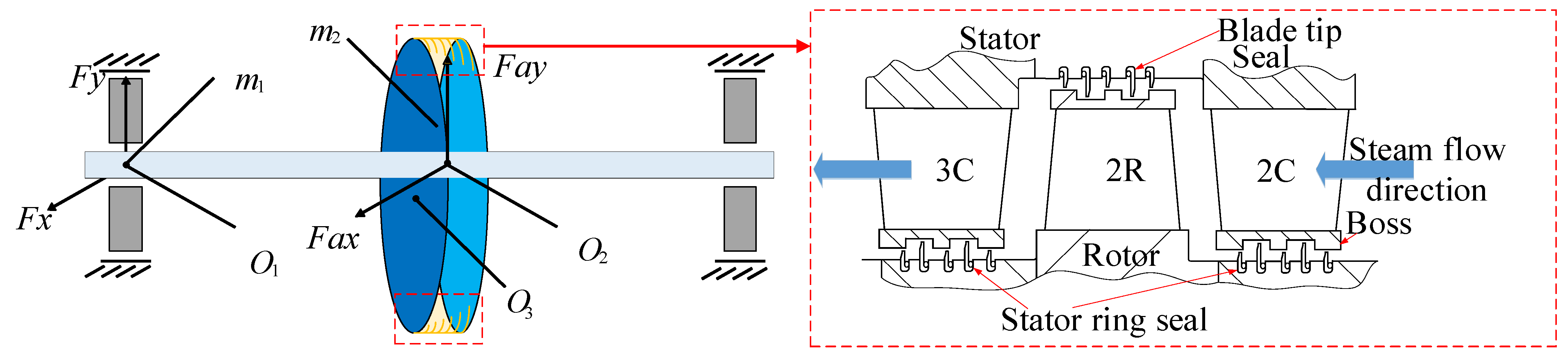
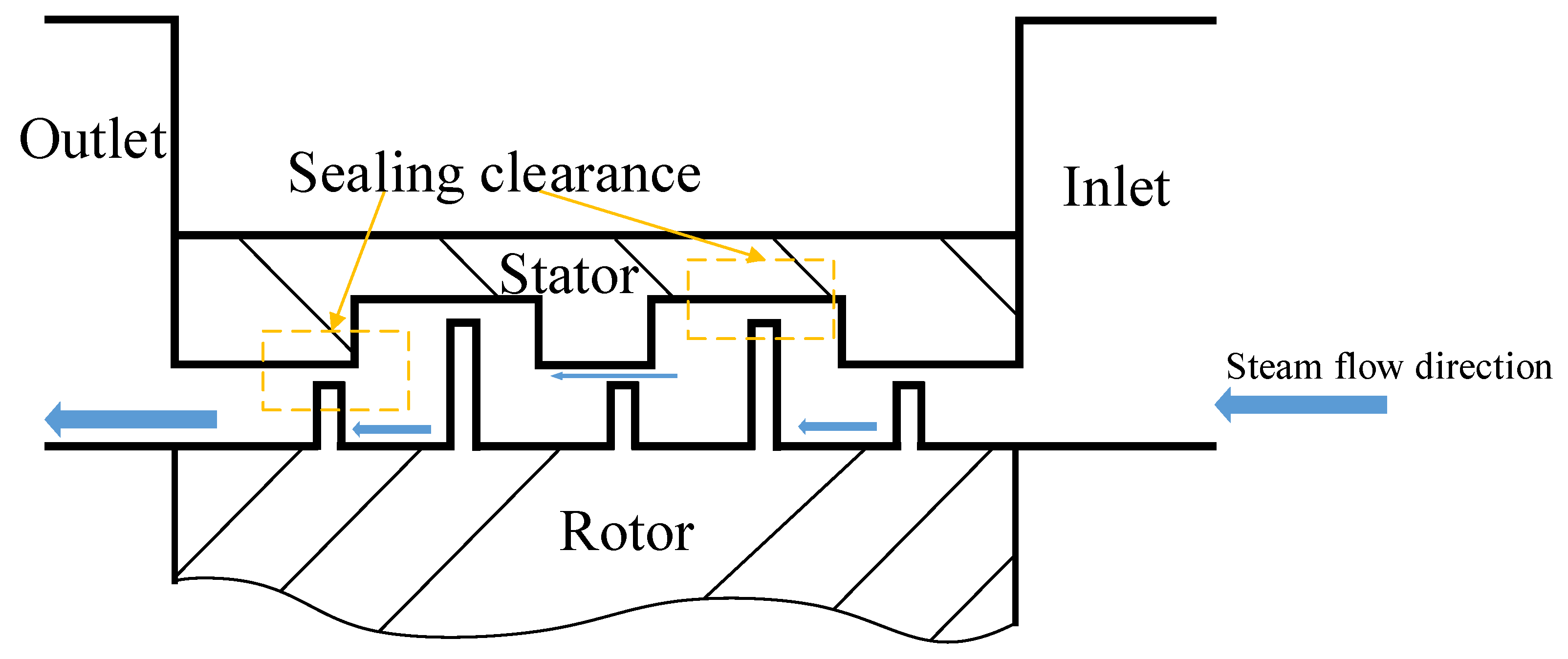
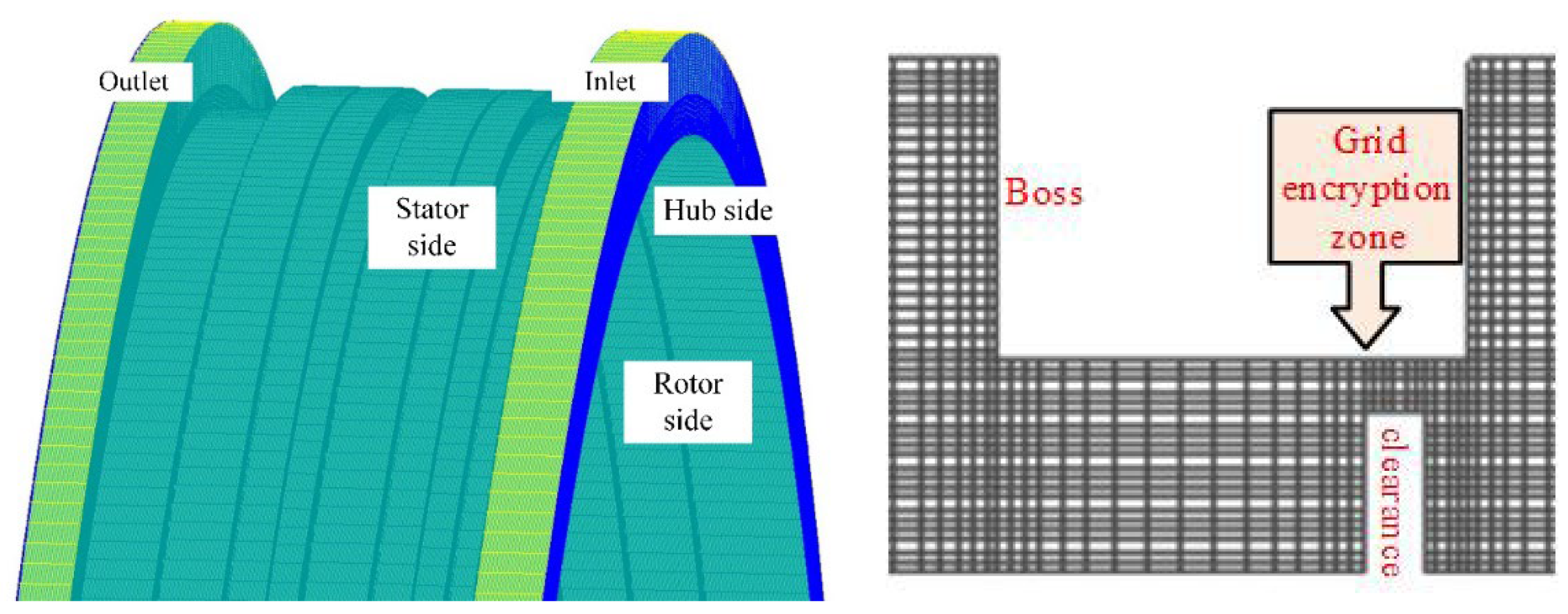
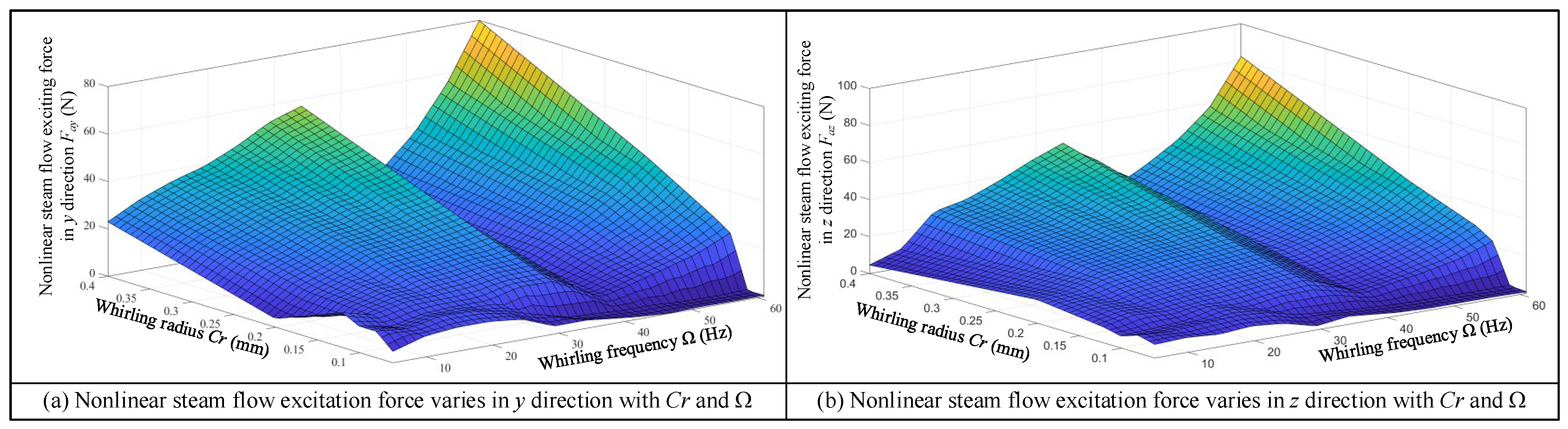
3.1. Influence of Seal Tooth Numbers on Motion Characteristics of System

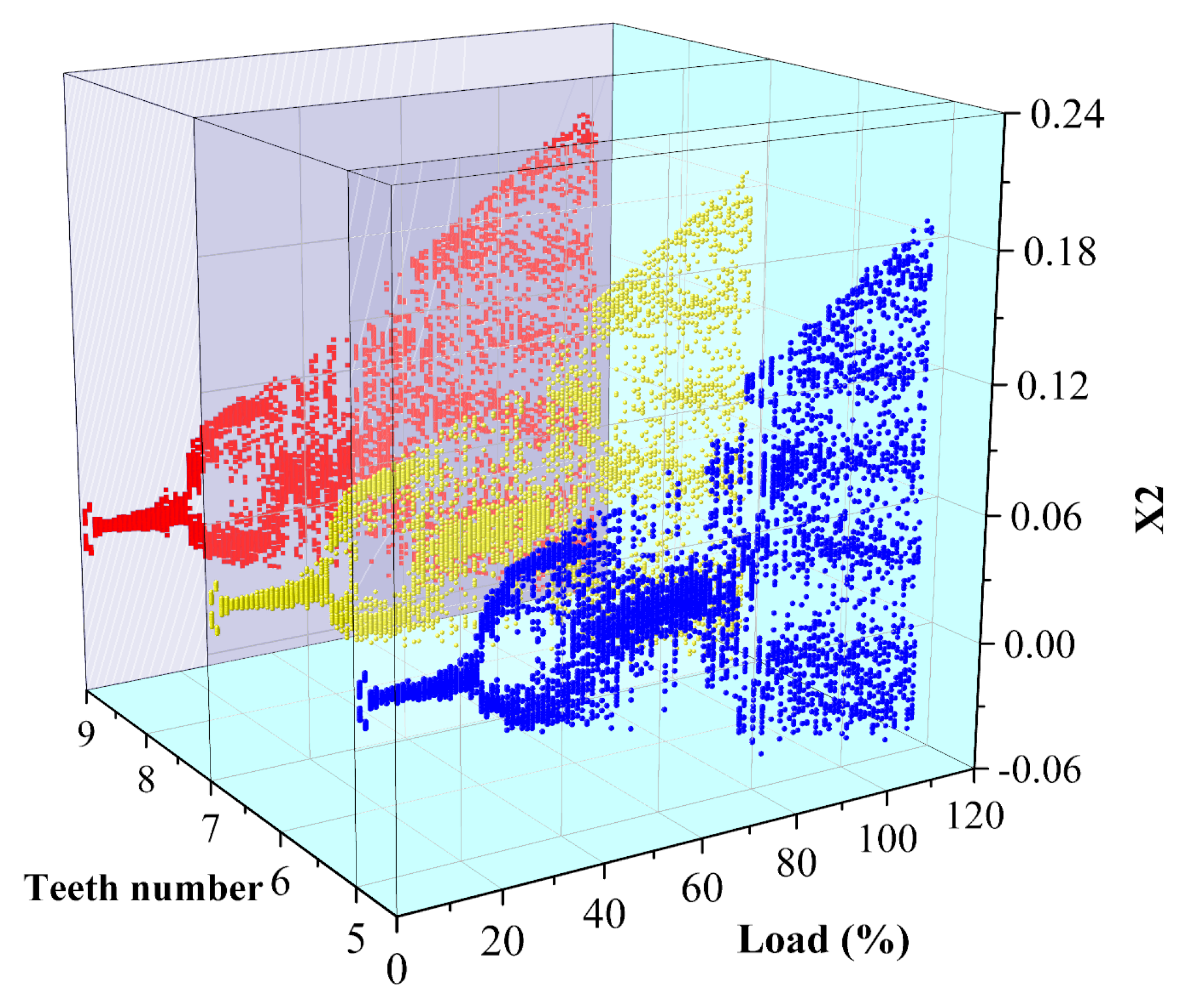
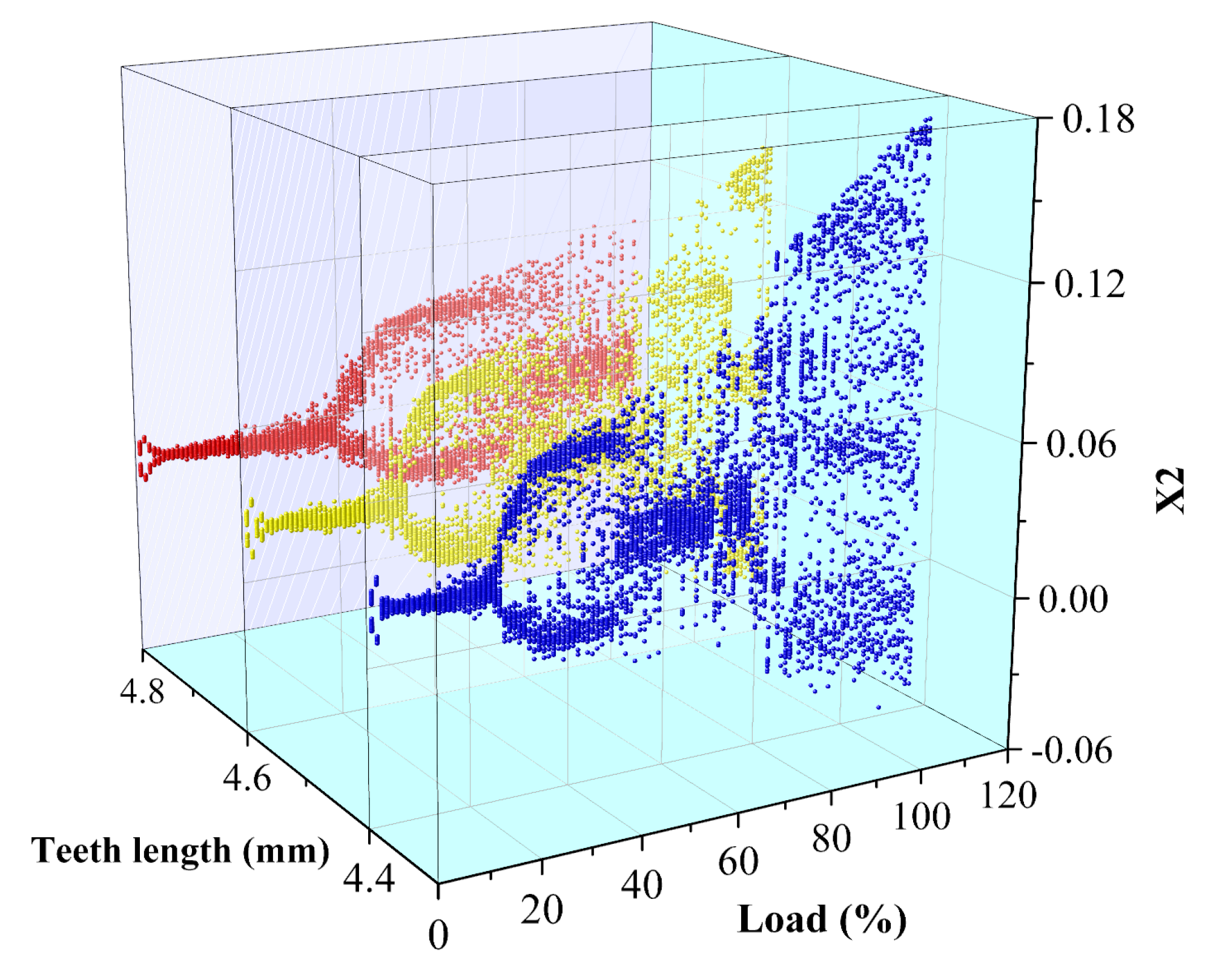
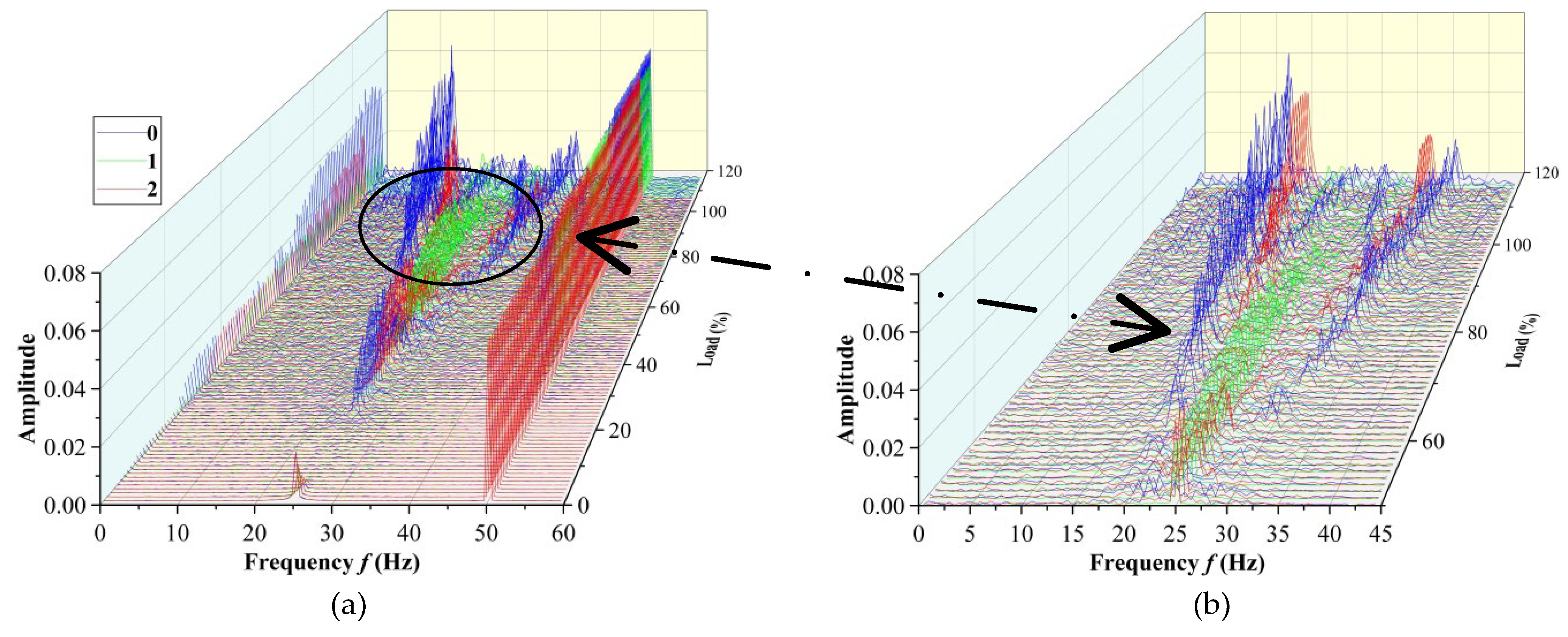
Figure 7 shows the bifurcation diagram corresponding to different numbers of seal teeth. It can be seen from the diagram that at the initial load, the corresponding systems of five teeth, seven teeth and nine teeth all experience the process of “inverted bifurcation” from a two-phase motion with a chaotic tendency toward a chaotic one-cycle motion. Blue corresponds to five teeth, yellow corresponds to seven teeth, and red corresponds to nine teeth. In the paper, THA is used to describe the load. Under the 20–40%THA condition, the motion law of the system changes obviously with the increase in load, during which the system experiences “chaotic two-period” motion, and the phenomenon of “double bifurcation” appears in the bifurcation diagram. The system response points are relatively concentrated in the bifurcation diagram under the 40–100%THA condition. With the increase in the number of teeth, the response points of the system become more dispersed. After 100%THA, the vibration area of the system increases and the amplitude increases. The response points in the bifurcation diagram spread to both ends, and there are five relatively concentrated regions. So, the change in the number of seal teeth has little effect on the system in this condition, and the motion state of the system does not change obviously.

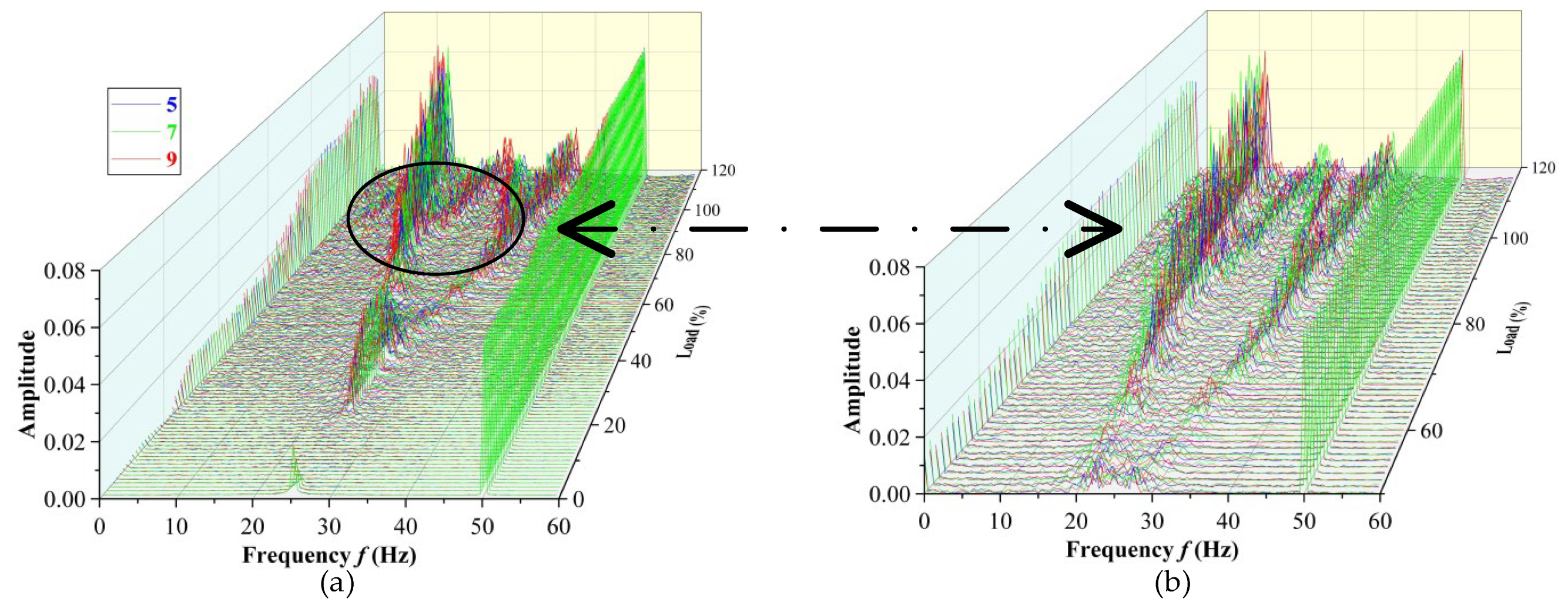
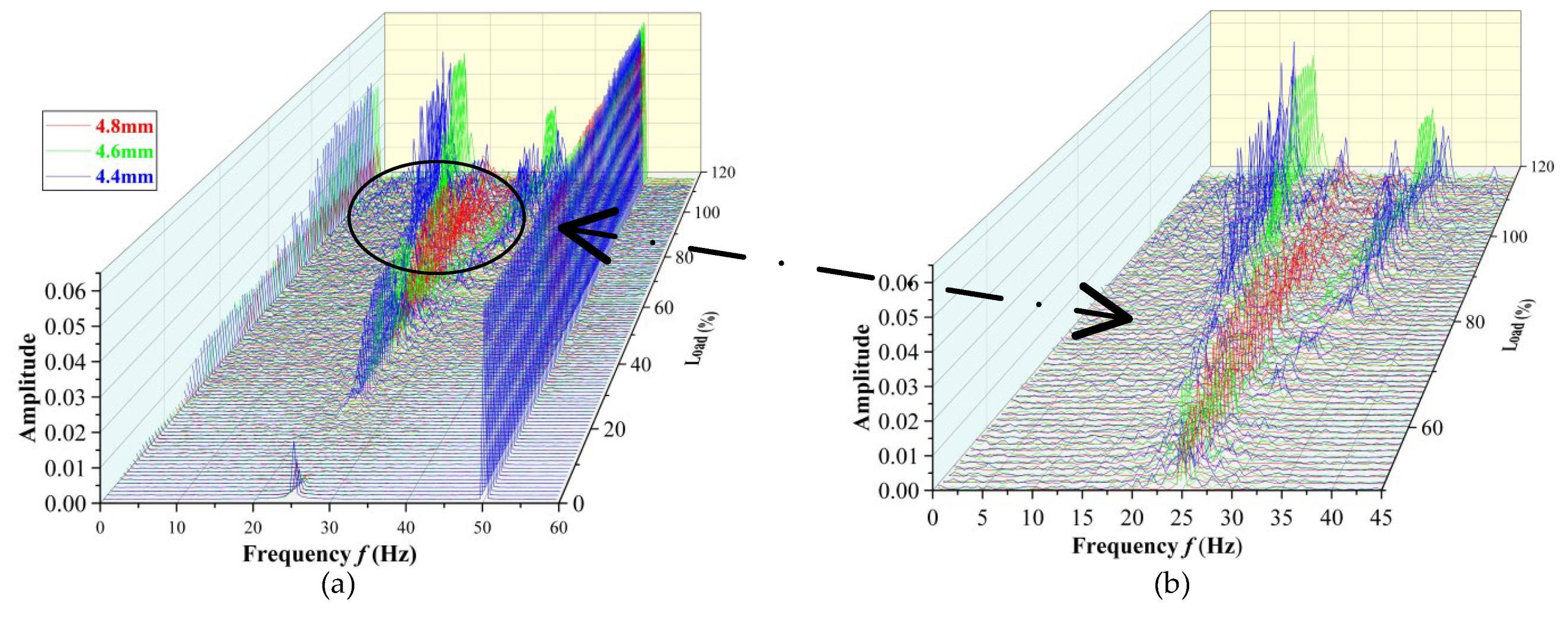
Figure 8 shows the three-dimensional waterfall diagram and a partially enlarged diagram corresponding to different numbers of teeth. Before 20%THA, five teeth, seven teeth and nine teeth appear to have a transient semi-power frequency vibration with the increase in load. Under the 20–60%THA condition, the amplitude fluctuation law of the frequency spectrum corresponding to the three kinds of tooth numbers is similar. The amplitude of a 1/2 power frequency vibration of the three tooth numbers increased steadily to about 0.02 and decreased gradually after 40% THA, and there is a tendency to differentiate between the 1/3 and 2/3 power frequency vibrations. From 60% THA to 100% THA, as shown in the partially enlarged diagram, the amplitudes corresponding to a 1/3 power frequency and a 2/3 power frequency of the three tooth numbers increase. After 100% THA, there is an obvious dense frequency phenomenon, and the three teeth numbers all form 1/3 and 2/3 power frequency vibrations. Although the change curves are highly similar, the corresponding amplitudes are different. The amplitude of a 2/3 power frequency vibration is 1/3 that of a 1/3 power frequency. At the same time, a 1/2 power frequency vibration gradually increases after 100%THA, but the amplitude is lower than a 1/3 power frequency and a 2/3 power frequency. As the load increases, the dense frequency phenomenon became more and more obvious and serious, reflecting that the higher the load, the more disordered the flow field in the seal, the greater the steam-flow-exciting force, and the more the other frequency vibrations in the multi-frequency whirl begin to show.

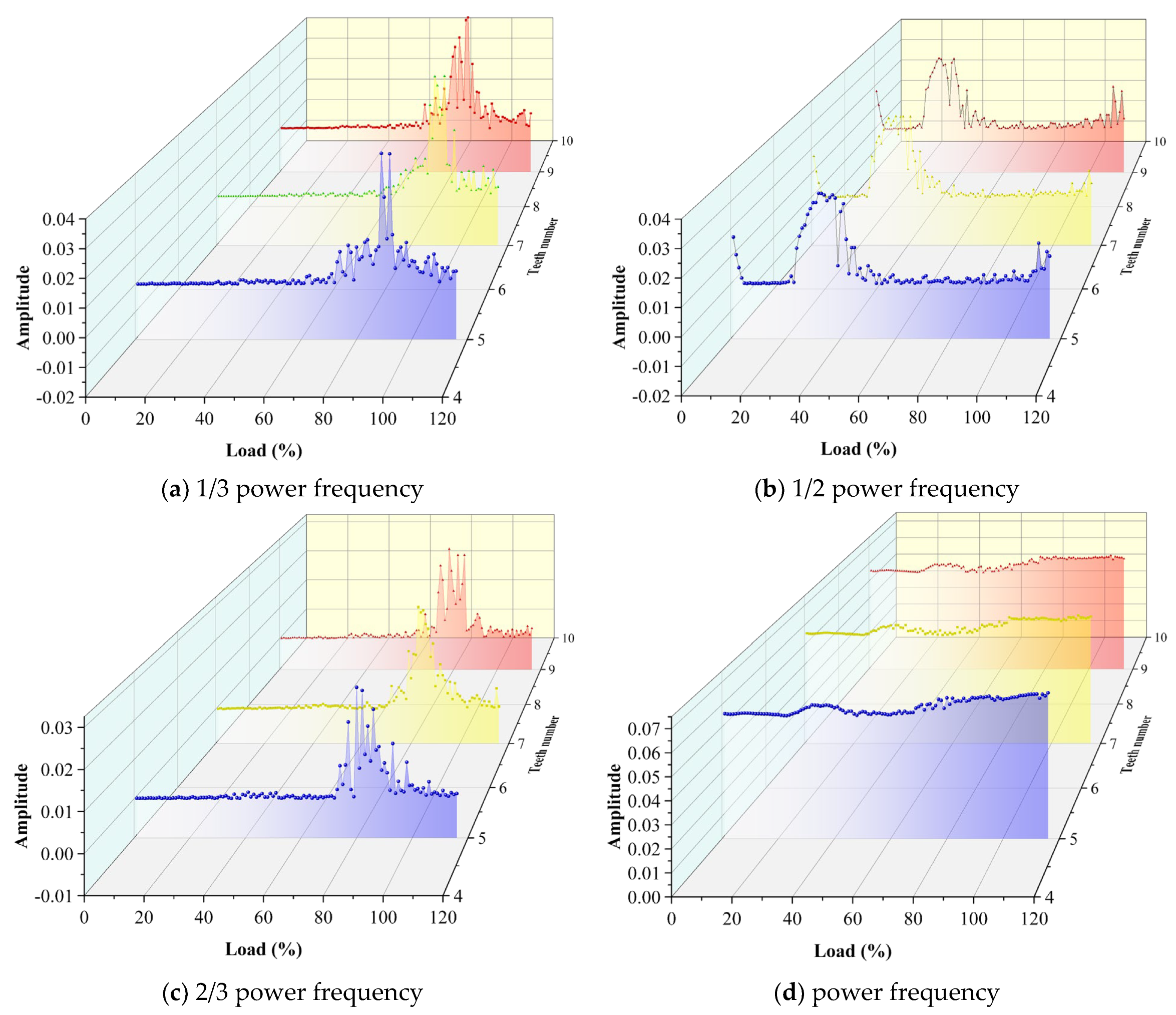
Figure 9 is a dimensionless amplitude diagram of the main frequencies of different seal tooth numbers. Blue corresponds to five teeth, yellow corresponds to seven teeth, and red corresponds to nine teeth. Before 30%THA, the amplitudes corresponding to the main frequencies of three teeth are roughly the same, indicating that the influence of the teeth number on the steam flow excitation at low load can be ignored, and the system is relatively stable. With the increase in load, the influence of steam excitation begins to appear. Beginning with the 30%THA, a 1/2 power frequency vibration begins to evolve into the 1/3 and 2/3 power frequency vibration. As the amplitude corresponding to a 1/2 power frequency gradually decreases, the amplitude corresponding to a 1/3 power frequency and a 2/3 power frequency begins to fluctuate slightly. Due to the nonlinear characteristics of steam-exciting force, the amplitude of different teeth is different. Figure 9a–c show the change in the dimensionless amplitude of three tooth numbers at a 1/3, 1/2 and a 2/3 power frequency under different loads. The overall trends of the 1/3 power frequency and 2/3 power frequency amplitudes corresponding to three teeth are the same, which is that the fluctuation rises to the highest level and then gradually decreases, but the amplitude deviates. The amplitude corresponding to a 1/2 power frequency fluctuates steadily and tends to increase after 100%THA. This is because the influence of oil film force, unbalanced mass force, gravity and steam-flow-exciting force on the motion characteristics of the rotor is considered comprehensively. At the low load, the steam-flow-exciting force is relatively small, the oil film force and unbalanced mass force are the main forces, so the vibration caused is mainly 1/2 power frequency. With the increase in load, the influence of steam-flow-exciting force is enhanced. After 60%THA, the effect of steam-flow-exciting force is enhanced, and the 1/2 power frequency vibration gradually evolves into the 1/3 and 2/3 power frequency vibration. The steam-flow-exciting force excites the vibrations at low frequencies and critical frequencies. Under the 90–100%THA condition, the vibration direction of these two frequencies is consistent. The frequency amplitude change is the same, but the low-frequency steam-flow-exciting force is strong, so the amplitude value of a 1/3 power frequency is relatively larger. Figure 9d is the amplitude diagram of power frequency. The amplitude change is not nonlinear, and it begins to stabilize after 100%THA.

3.2. Influence of Seal Tooth Lengths on System Motion Characteristics

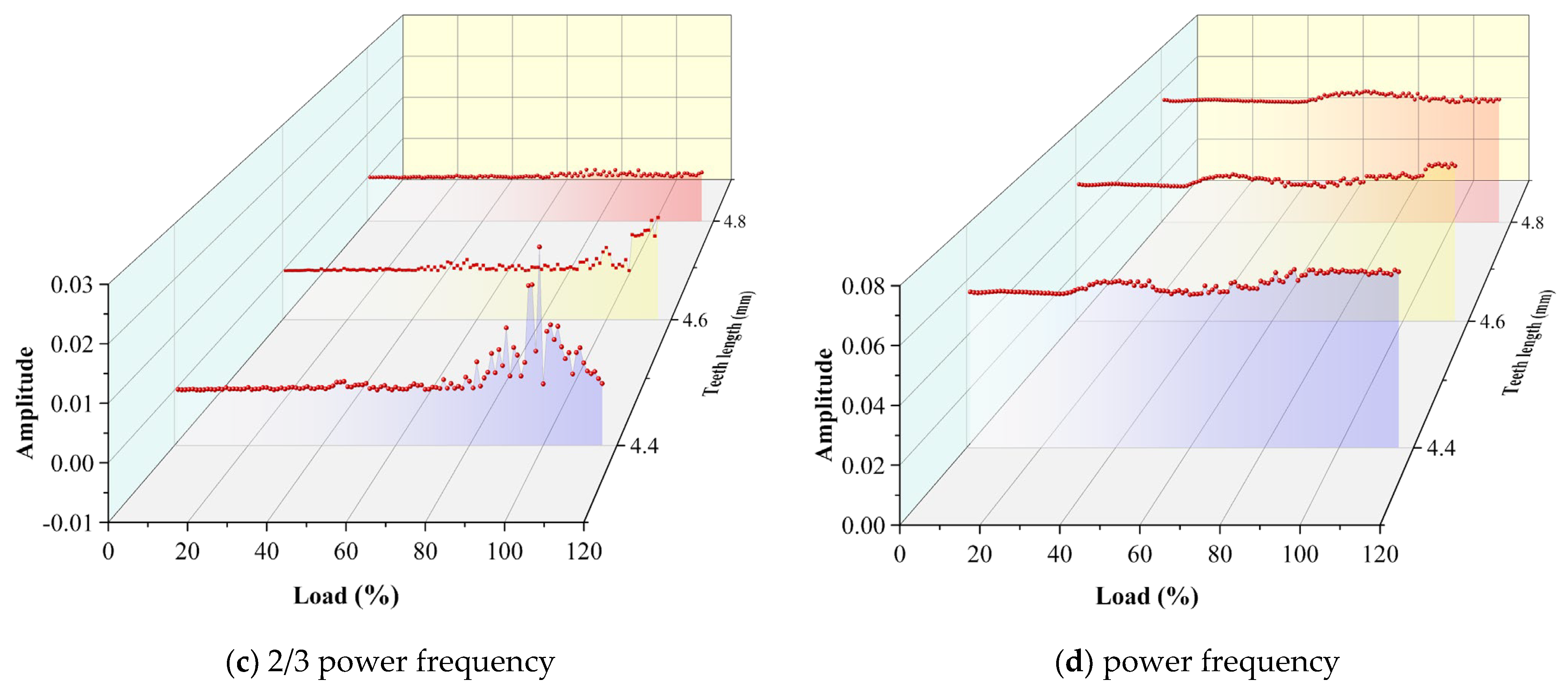
Figure 10 shows the three-dimensional bifurcation diagram of the corresponding system with different teeth lengths. Blue corresponds to 4.4 mm, yellow corresponds to 4.6 mm, and red corresponds to 4.8 mm. The systems corresponding to different teeth length also undergo the process of “inverted bifurcation” at the initial load. Under the 20-40%THA condition, the motion state of the system corresponding to the teeth length of 4.4 mm changes, and the system goes through the “chaotic two-periodic” motion. After 40%THA, the system enters chaotic motion, but the amplitude has an obvious concentrated area. When the tooth length increases to 4.6 mm, the system experiences the “chaotic two-period” motion under 30–50%THA condition, and the motion state of the system changes, and then it also enters the chaotic motion. When the tooth length increases to 4.8 mm, the “chaotic two-period” motion occurs under 40–80%THA condition. After 80%THA, the system undergoes chaotic motion. The increase in tooth length will delay the change in the motion state of the system and maintain the stability of the system. After 80%THA, the system experiences chaotic motion, but with the increase in tooth length, the amplitude distribution range of the system decreases gradually. The reason is that with the increase in tooth length, the throttling effect of sealing tooth increases, the carrying effect of rotor surface becomes stronger, the axial speed decreases, and the carrying effect of the rotor surface becomes stronger. At the same time, with the increasing load, the steam pressure and flow rate of sealing inlet increase, and the effect of long tooth is more significant.

Figure 11 shows the three-dimensional spectrum corresponding to different seal teeth lengths. As shown in the figure, the system experienced a short half-frequency vibration during the initial load. At the beginning of 20%THA, a 1/2 power frequency begins to appear in the spectrum corresponding to the system with a tooth length of 4.4 mm, and with the increasing load, the corresponding amplitude increases slowly. At about 40%THA, the amplitude corresponding to a 1/2 power frequency decreased and differentiated to both ends, resulting in the 1/3 and 2/3 power frequencies. As the teeth length increases, the load corresponding to the 1/2 power frequency of the system increases. When the tooth length increases to 4.8 mm, the 1/2 power frequency appears at 40%THA and gradually decreases at 80%THA, but there are no obvious 1/3 and 2/3 power frequencies. After 80%THA, there is a load range where the dense frequency phenomena are concentrated. In this range, as the tooth length increases, the dense frequency phenomenon decreases. This is because as the tooth length increases, the tip clearance becomes smaller, the throttling effect is enhanced, the sealing leakage resistance becomes better, the steam pressure in the sealing chamber decreases, and the steam-flow-exciting force becomes smaller; therefore, the frequency division vibration in the multi-frequency whirl is weakened.

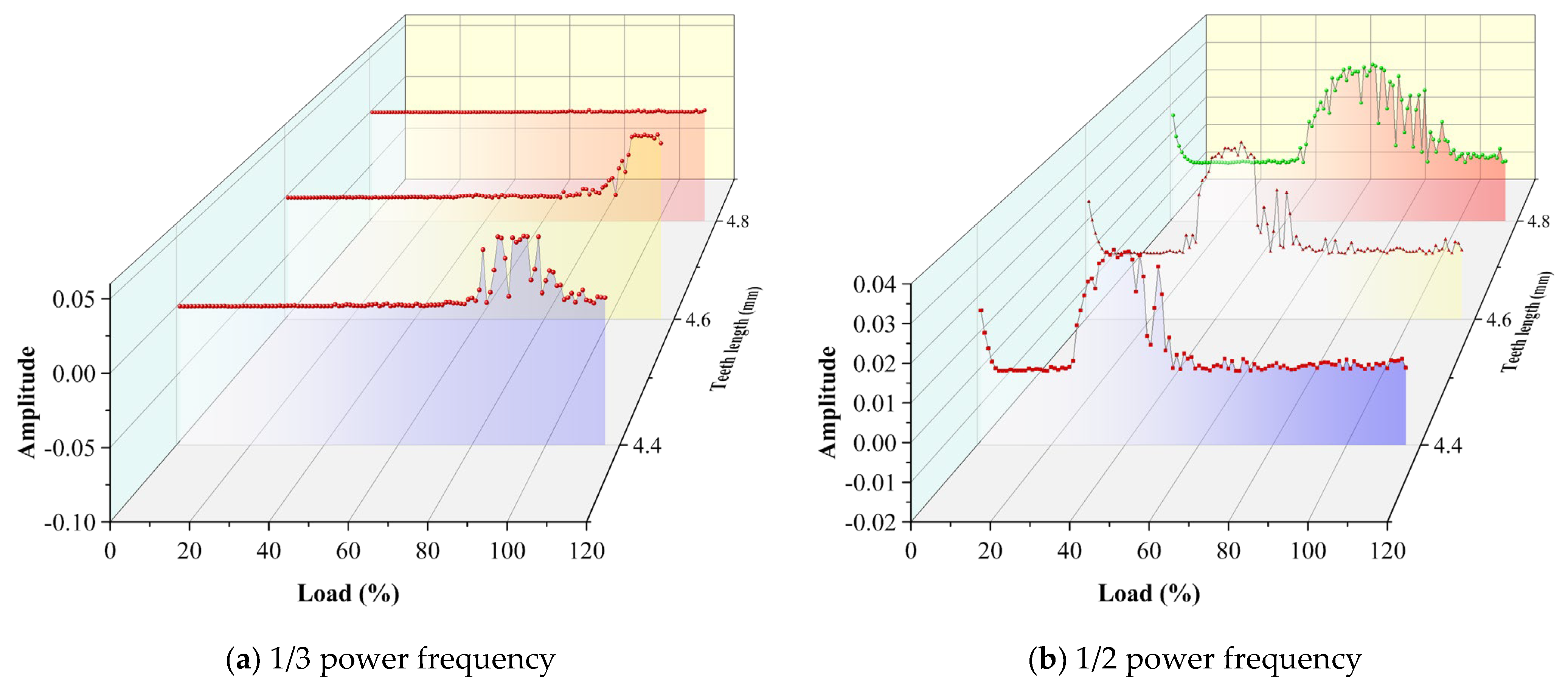
Figure 12 shows the amplitude diagram of the main frequency of the system corresponding to different seal tooth lengths. Blue corresponds to 4.4 mm, yellow corresponds to 4.6 mm, and red corresponds to 4.8 mm. The system corresponding to the tooth length of 4.4 mm, a 1/3 power frequency, a 1/2 power frequency and a 2/3 power frequency appear earliest in the same load range, and the corresponding amplitude is the largest. The system corresponding to the tooth length of 4.8 mm does not show the obvious 1/3 power frequency and 2/3 power frequency corresponding to the smaller amplitude. However, after 100%THA, the 4.4 mm tooth length has a sharp decrease in the amplitude of the local load at a 1/3 power frequency, which reflects the strong nonlinearity of the steam-exciting force. The 4.8 mm tooth length has a good suppression effect on the steam excitation after 100%THA. Under the general law, there will still be a phenomenon that the amplitude of the short tooth length decreases sharply and rebounds.

3.3. Influence of Boss Numbers on Motion Characteristics of System

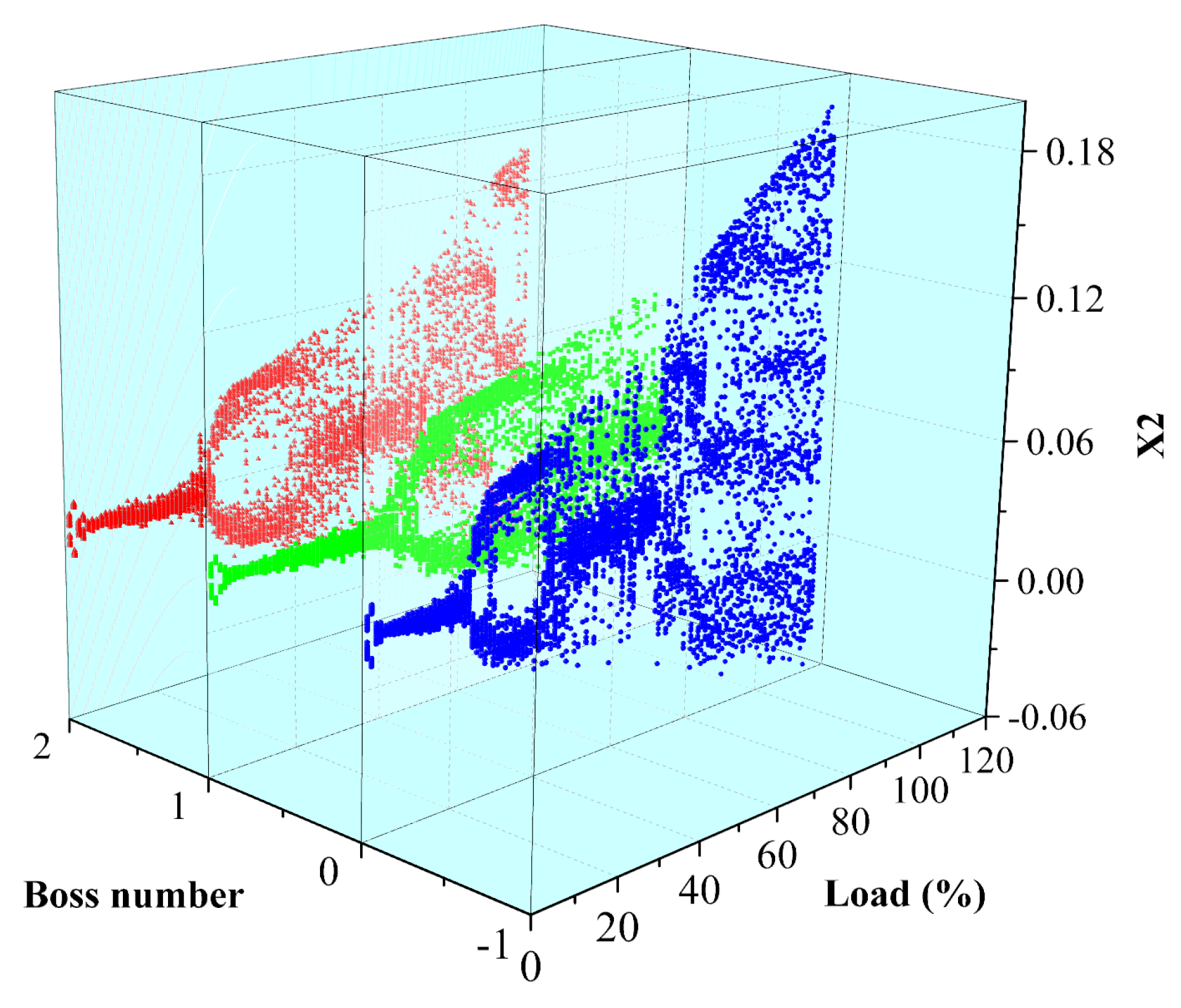
Figure 13 shows the bifurcation diagram of the system corresponding to the different numbers of the bosses. Blue corresponds to the number of boss 0, yellow corresponds to the number of boss 1, and red corresponds to the number of boss 2. The phenomena of “inverted bifurcation” also appear in the bifurcation diagram of the system corresponding to different numbers of bosses at the initial load, because the steam flow excitation has little influence on the system. So, the motion law of the system is roughly similar. Under the 20–80%THA condition, the system with the number of boss 0 first changes from chaotic motion to “chaotic two-period” motion. But the systems with the numbers of boss 1 and 2 are more stable, and the motion state changes later. Under the 80–100%THA condition, with the increase in the number of bosses, the response points of the system gradually converge, especially when the numbers of bosses are 0 and 1, the aggregation phenomena are the most obvious, the chaos of rotor motion is weakened, and the number of the boss plays a role in restraining chaos. But when the number of the boss increases to 2, the response points in the system bifurcation diagram are more discrete relative to the number of the boss, and the degree of discretization is less than that for the boss 0. Three obvious concentrated regions gradually form after 100%THA, which means that the system goes through a “chaotic three-period” motion. The chaotic trend of the boss 0 platform is more obvious, and the covering load is greater because there is no bump blocking, the steam leakage is large, the axial flow is smooth and fast, and the pressure is large but the fluctuation of the pressure is small, and the stable steam-flow-exciting force is aroused, forming obvious chaotic motion.

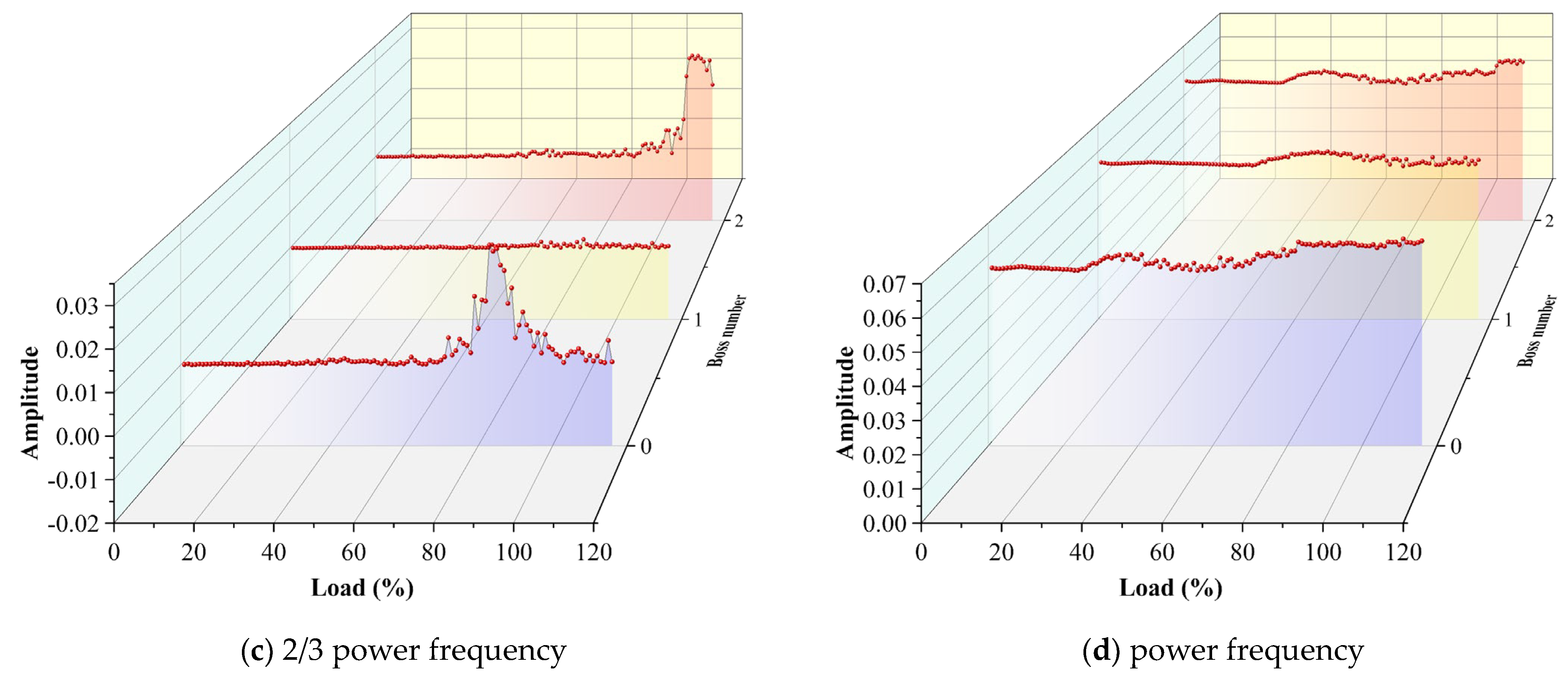
Figure 14 is the three-dimensional spectrum diagram and partially enlarged diagram of the system corresponding to different bosses. As shown in the diagram, the system with boss 0 first appears as a 1/2 power frequency component under the 20–80%THA condition. At the beginning of 30%THA, a 1/2 power frequency component gradually begins to decrease and the 1/3 and 2/3 power frequencies appear, but the amplitude change is small. After 80%THA, it can be seen from Figure 14b that the amplitude corresponding to the 1/3 and 2/3 power frequencies corresponding to boss 0 increases significantly. When the number of bosses increases to 1, the 80%THA in the spectrum of the corresponding system is dominated by the power frequency component of 1/2, and the corresponding amplitude is large. As the load continues to increase, the amplitude corresponding to a 1/2 power frequency gradually decreases, and other power frequency components with lower amplitude are derived. However, as the number of bosses increases to 2, at about 60%THA, the amplitude corresponding to a 1/2 power frequency of the system almost disappears, and the 1/3 power frequency and 2/3 power frequency components begin to appear, but the corresponding amplitude is low. With the increase in load, it remains relatively stable. However, the amplitude corresponding to the 1/3 and 2/3 power frequencies increases significantly at 100%THA. After 80%THA, the dense frequency phenomena appear in the spectrum diagram, and the dense frequency phenomena are the most serious in the spectrum diagram of the system corresponding to boss 0.

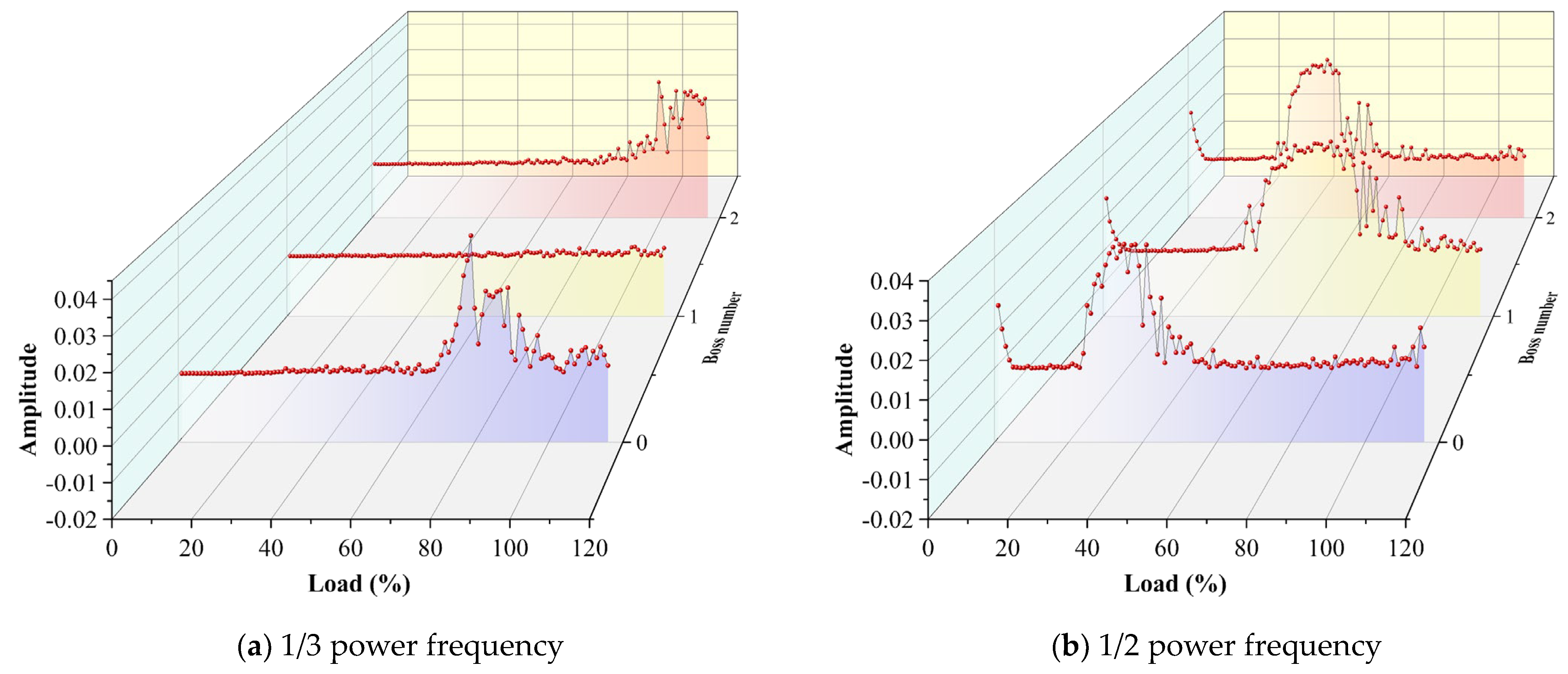
Figure 15 is the amplitude diagram of the main frequencies corresponding to the different numbers of the bosses. Blue corresponds to the number of boss 0, yellow corresponds to the number of boss 1, and red corresponds to the number of boss 2. From Figure 15b, it can be seen that the system corresponding to the boss 0 first appears at the 1/2 power frequency and then approximately disappears after 60%THA. Combined with Figure 15a,cc, after 60%THA, the 1/3 and 2/3 power frequencies begin to appear and gradually decrease after the largest amplitude of 70%THA. When the number of the boss increases to 1, the corresponding power frequency of 1/2 appears the latest, and the amplitude of the corresponding power frequencies of 1/3 and 2/3 is the smallest. Although there is little difference between the load of the 1/2 power frequency vibration corresponding to the number of boss 2 and the number of boss 1, the amplitudes of the power frequencies corresponding to 1/3 and 2/3 increase sharply after 100%THA. This is due to the fact that with the increase in the number of bosses, the throttling effect in the sealing cavity increases and the leakage decreases, so that the influence of steam-flow-induced vibration weakens. At this time, the influence of the system should be mainly a nonlinear oil film force and the unbalanced response of the rotor. This leads to a relatively strong 1/2 power frequency vibration. However, the increase in the number of bosses will cause the instability of the flow field and the nonlinearity of steam-induced vibration, which will also have a certain impact on the stability of the system with the increase in load.

3.4. Stability Analysis of Rotor System under Different Sealing Structures

The largest Lyapunov exponent is an important quantitative index to evaluate the stability of a rotor dynamic system, which represents the average exponential rate of convergence or divergence between adjacent orbits in phase space. If the exponent is positive, it shows that the system is chaotic and the stability is poor. If it is negative, it shows that the system is in periodic deterministic motion and has good stability. Chaos refers to the uncertain or unpredictable random phenomenon of a certain macroscopic nonlinear system under certain conditions, and it is also a phenomenon of the integration of certainty and uncertainty, regularity and irregularity or orderliness and disorder. 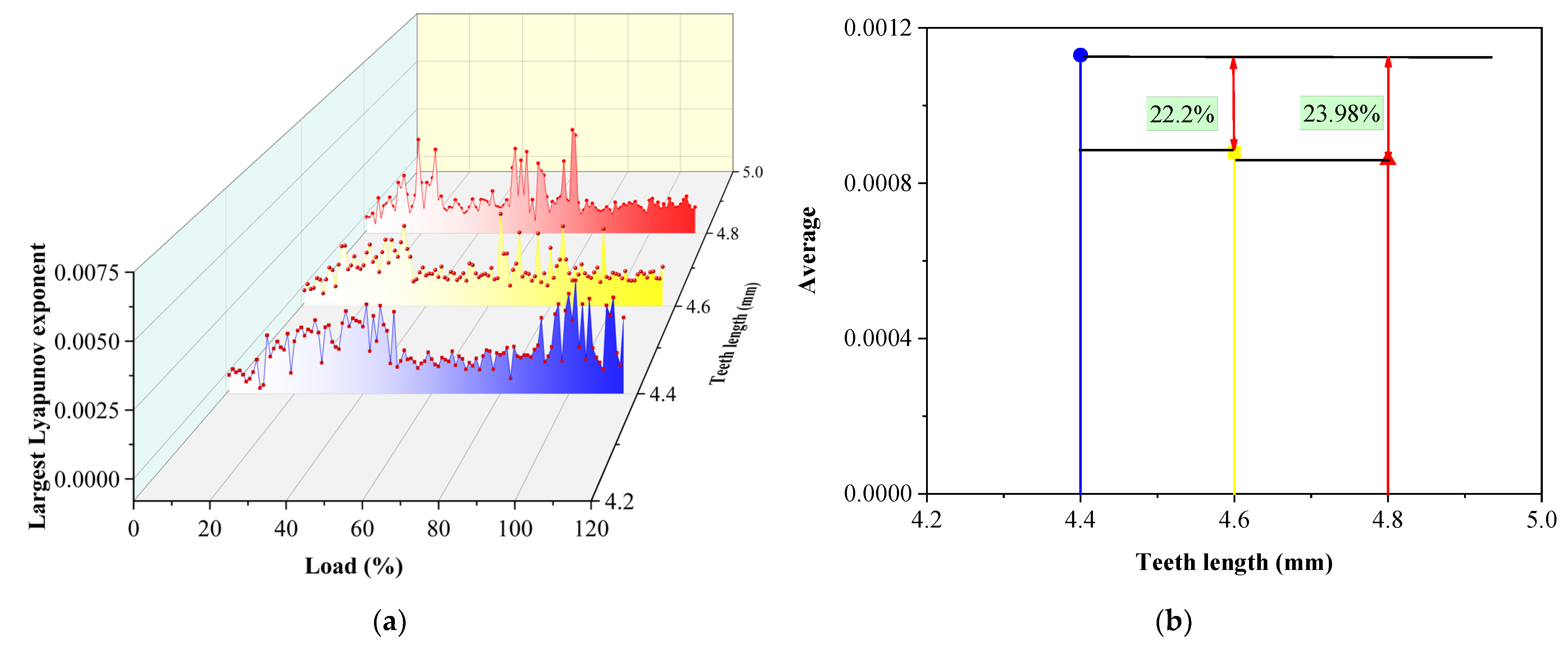Figure 16a shows the largest Lyapunov exponent corresponding to different teeth lengths. Blue corresponds to 4.4 mm, yellow corresponds to 4.6 mm, and red corresponds to 4.8 mm in Figure 16a,b. When the tooth length is 4.4 mm, at the initial load, the largest Lyapunov exponent increases from “touching zero point”, and the exponent value fluctuates greatly and tends to be flat at 50%THA. When the load increases to 90%THA, due to the influence of steam flow excitation, vibration is enhanced; the chaos of the system is enhanced too, and the fluctuation of exponential value is more intense. When the tooth length increases to 4.6 mm, although the chaotic characteristic of the same system is strong at the initial load, after 40%THA, the system begins to stabilize and the exponential value fluctuates gently. Beginning with 60%THA, the exponential value fluctuates strongly because of the nonlinear enhancement of steam-flow-induced vibration. With the continuous increase in load, the effect of teeth length on steam-induced vibration appears initially, the exponential value returns to stable, and the system is relatively stable too. When the tooth length is 4.8 mm, the exponent value fluctuates smoothly in advance, and in the high load area, the inhibitory effect of teeth length on steam-flow-induced vibration is enhanced and the system remains stable. Combined with the analysis of Figure 16b, when the tooth length increases to 4.6, the average exponent value decreases by 22.2%. When the tooth length increases to 4.8 mm, the average exponent value decreases by 23.98%. The law reflected is more practical in this paper because CFD is used to simulate the three-dimensional multi-frequency whirl of the rotor.

With the increase in teeth length, the carrying capacity of the rotor is enhanced, the circumferential velocity of the steam increases, the axial speed decreases, the anti-leakage effect increases, and the stability of the rotor becomes better.

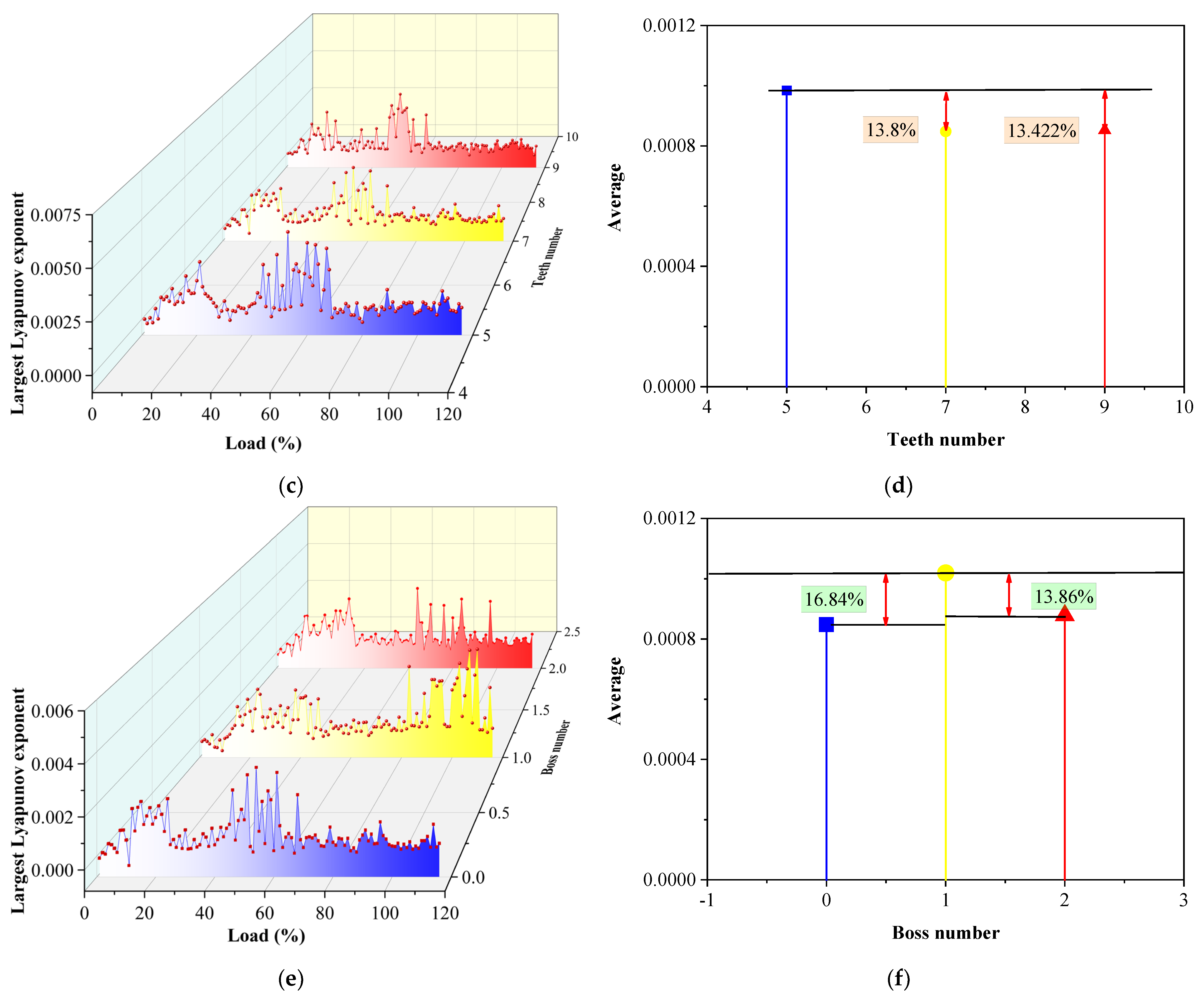
Figure 16c shows the largest Lyapunov exponent chart corresponding to different numbers of teeth. Blue corresponds to five teeth, yellow corresponds to seven teeth, and red corresponds to nine teeth in Figure 16c,d. The change in the number of teeth has little effect on the stability of the system, and the law of the largest Lyapunov exponent is basically unchanged. Combined with Figure 16d, when the number of teeth increases to seven teeth and nine teeth, the average exponent value decreases by 13.8% and 13.422%, respectively. This is because the change in the number of teeth does not affect the tooth tip clearance, and the ability of the rotor to carry steam in the circumferential direction remains unchanged, which has little effect on the axial speed, so it has little influence on the stability of the system.

Figure 16e shows the largest Lyapunov exponent corresponding to the different numbers of the bosses. Blue corresponds to the number of boss 0, yellow corresponds to the number of boss 1, and red corresponds to the number of boss 2 in Figure 16e,f. When the number of the boss is 0, the exponent has a strong jump before 80%THA, indicating that the chaos of the system is strong during this period, especially during the period from 40%THA to 70%THA. Then, with the increase in load, the exponent value fluctuates smoothly and the system is stable. When the number of the boss is 1, the stability of the system is poor and the exponential value fluctuates greatly under a low load. Under 40–90%THA condition, the exponent value fluctuates gently and the chaos of the system is weakened. However, after 90%THA, the exponential value fluctuates sharply, indicating that the stability of the system is weak. When the number of the boss increases to 2, the exponent value fluctuates greatly before 30%THA, and with the continuous increase in load, although a few exponent values jump under 60–90%THA condition, the overall value is relatively flat. Combined with Figure 16f, when the number of the boss increases to 1, the average exponent increases by 16.84%, and when the number of the boss increases to 2, the average exponent decreases by 13.86% relative to that of the boss number 1. The reason is when there is no boss, the lengths of the sealing tooth are the same, so it becomes a flat-toothed seal, the flow field is stable, there is no complex vortex system, and the steam flow excitation vibration is stable. But boss 0 can lead to steam leakage increasing, which reduces power.

In summary, the change in the number of seal teeth has a relatively small impact on the system state, and the motion state of the system does not change obviously. As the system load increases, the internal flow field of the seal becomes more chaotic, and the steam-flow-exciting force also increases accordingly. The increase in seal tooth lengths and the decrease in blade tip clearance enhance the throttling effect, reduce the steam pressure inside the chamber, and decrease the steam-flow-exciting force. As the load increases, the pressure and flow rate at the sealing inlet increase, and the impact on the long teeth becomes more significant. The system with a tooth length of 4.8 mm has a good suppression effect on steam excitation after 100% THA. The number of the boss increases, the leakage decreases, the steam excitation effect weakens, and the chaotic state of rotor motion weakens. When boss 0 is used, the internal coverage load of the seal is high, and the steam leakage is large. However, it makes the axial flow inside the seal smooth, the pressure fluctuation small, and the steam excitation stable. When the number of the boss increases to 2, the degree of discretization is less than that of boss 0, indicating that the boss plays a role in uniform chaos.

4. Conclusions

In this paper, a 1.5-stage three-dimensional full-cycle model of the high-pressure cylinder of a 1000 MW ultra-supercritical steam turbine is established. The effects of rotor revolution and rotation are considered through the use of a multi-frequency swirl. The nonlinear steam-flow-exciting forces under different sealing structures are calculated using CFD/FLUENT, and the motion equations of a steam turbine rotor-bearing seal system are solved by the Runge–Kutta method. The effects of seal teeth number, boss number and teeth length on the motion characteristics and stability of the system are analyzed. The specific conclusions are as follows:

(1)

The bifurcation diagrams with different tooth numbers, boss numbers and tooth lengths all have the phenomenon of “inverted bifurcation” and “period-doubling bifurcation”. With the increase in load, a 1/2 frequency division gradually decreases to disappear, then appears again, and gradually evolves into the 1/3 power frequency and 2/3 power frequency. The power frequency vibration fluctuates at a high position and a small amplitude. With the increase in load, the phenomena of dense frequency become more and more obvious and serious, and other frequency vibrations in multi-frequency vorticity begin to appear. At the low load, the influence of teeth number, boss number and teeth length on rotor motion can be ignored.

(2)

Compared with other influencing factors, the change in tooth number has little influence on the stability of the rotor system. The motion law of the rotor system in the bifurcation diagram and the variation curves of different tooth numbers in the 1/3 and 2/3 power frequency vibrations are highly similar, but the amplitudes are different. With the increase in the number of teeth, the average exponent value decreases. The number of teeth increases from five teeth to nine teeth, and the average exponent value decreases by 13.442%. But the chaos of the system changes little according to the largest Lyapunov exponent.

(3)

The change in the numbers of the bosses has a significant influence on the stability of the rotor system. With the increase in the numbers of the bosses, the change in the motion law of the system is delayed, and the appearance of the power frequencies of 1/3 and 2/3 is delayed. Combined with the largest Lyapunov exponent diagram and the average exponent diagram, with the increase in load, the fluctuation of boss 0’s exponent is small, and its average exponent is lower, but the steam leakage is larger. In a comparison of boss 1 and boss 2, the corresponding average exponent of boss 2 is smaller, and the chaos of the system is weak.

(4)

Under the higher load condition, with the increase in the tooth length, the scatter becomes more concentrated and the jump range of the scatter becomes increasingly smaller. With the increase in the tooth length, it can effectively delay or restrain the emergence of the power frequencies of 1/3 and 2/3, the fluctuation of the largest Lyapunov exponent decreases and the average exponent decreases too. The effect of 4.8 mm tooth length on suppressing steam-flow-induced vibration is more obvious after 80%THA. Due to the strong nonlinear characteristics of steam-flow-exciting force, the amplitude of short tooth length will decrease sharply.