New Method for Precise Measurement of Clamping Plate Deformations on Forming Presses
Abstract
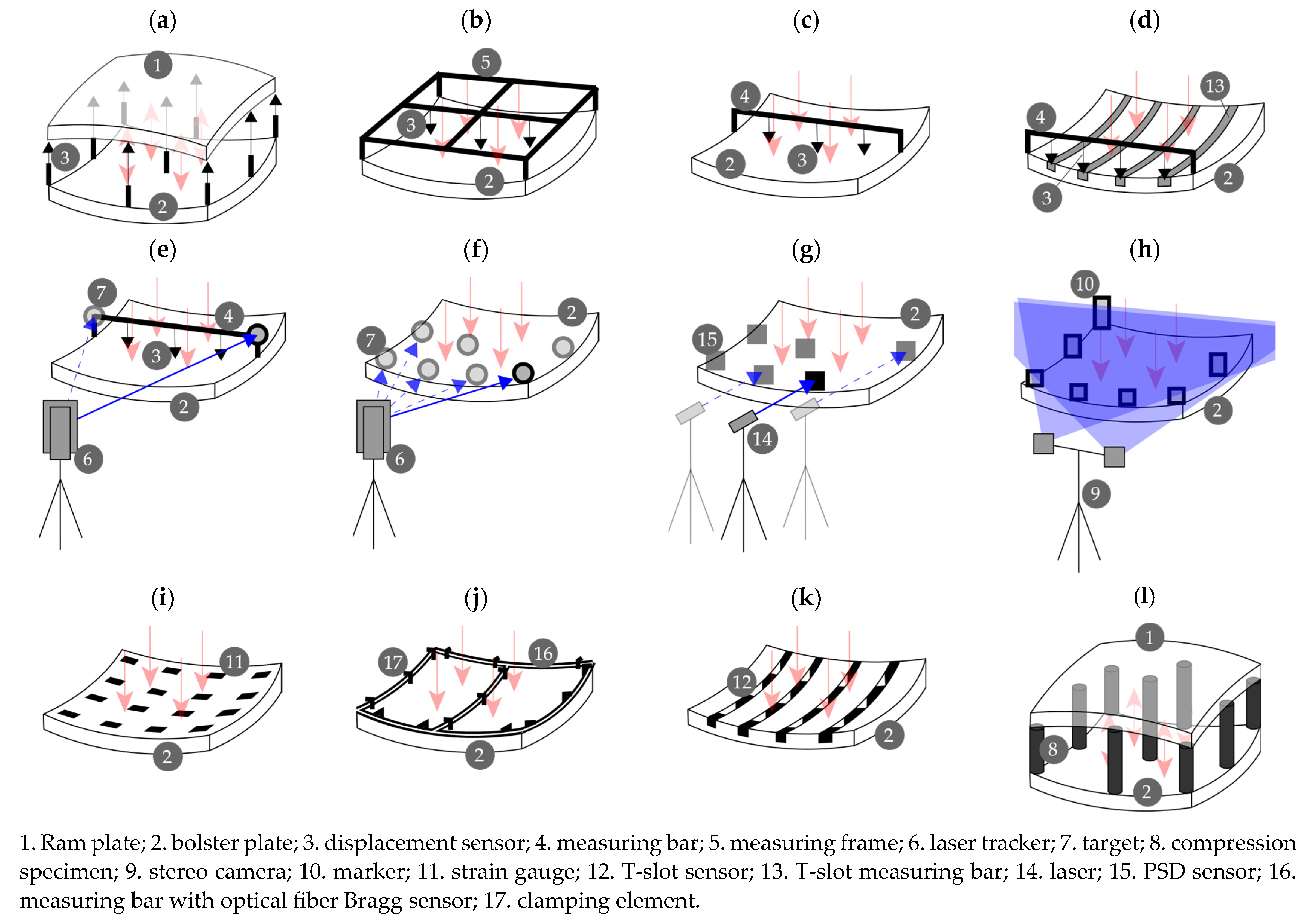
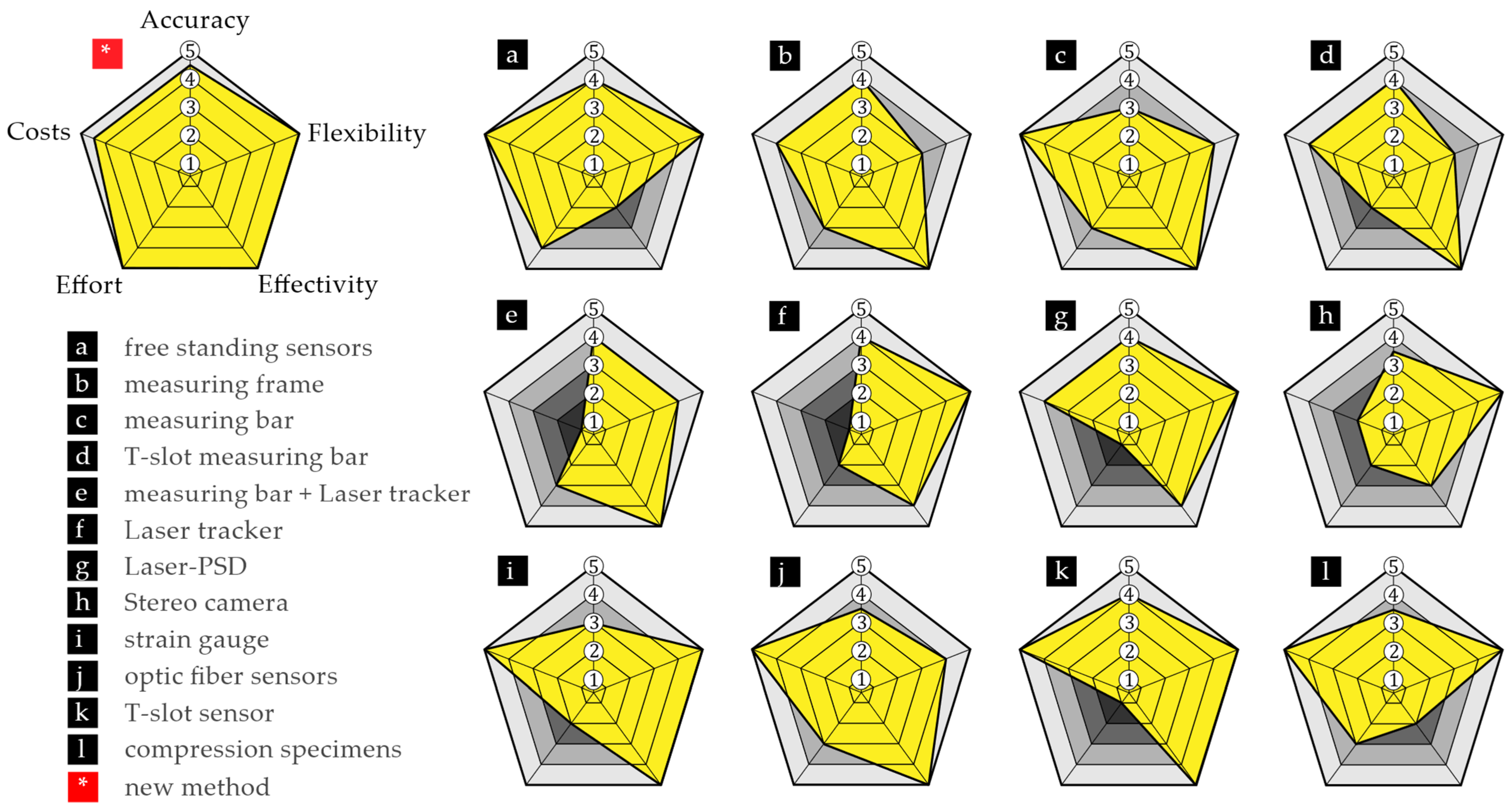
1. Introduction
- Accuracy: low resolution/coarse results;
- Flexibility: inflexibility for varying machine dimensions;
- Effectivity: only overall deformations; limited visibility of the clamping plate;
- Effort: time-consuming setup, many measurements, and calibration measurement;
- Costs: expensive equipment; execution only by highly qualified staff.
2. Development and Testing of an Inclination-Based Deformation Measuring Method
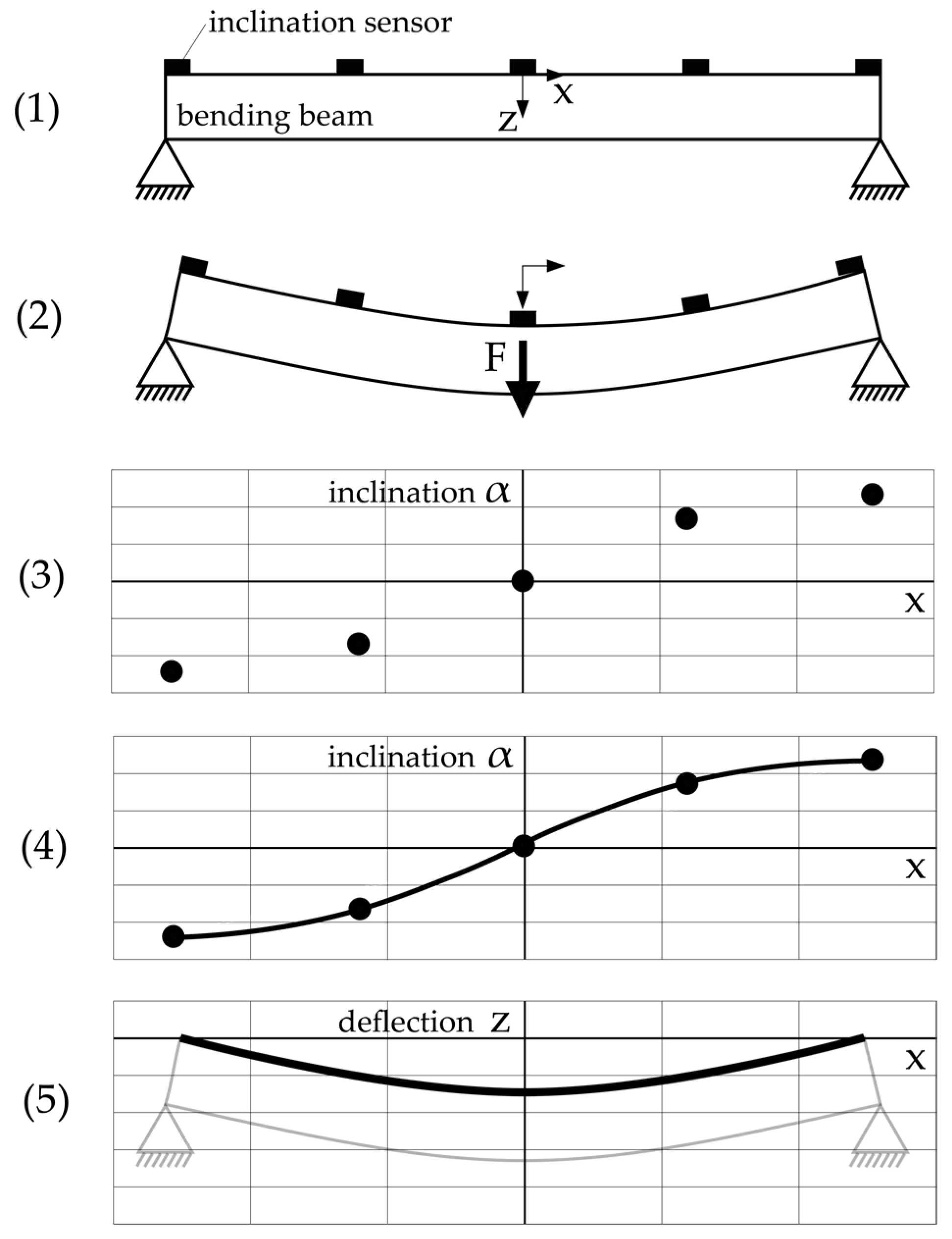
2.1. Development and Theoretical Testing
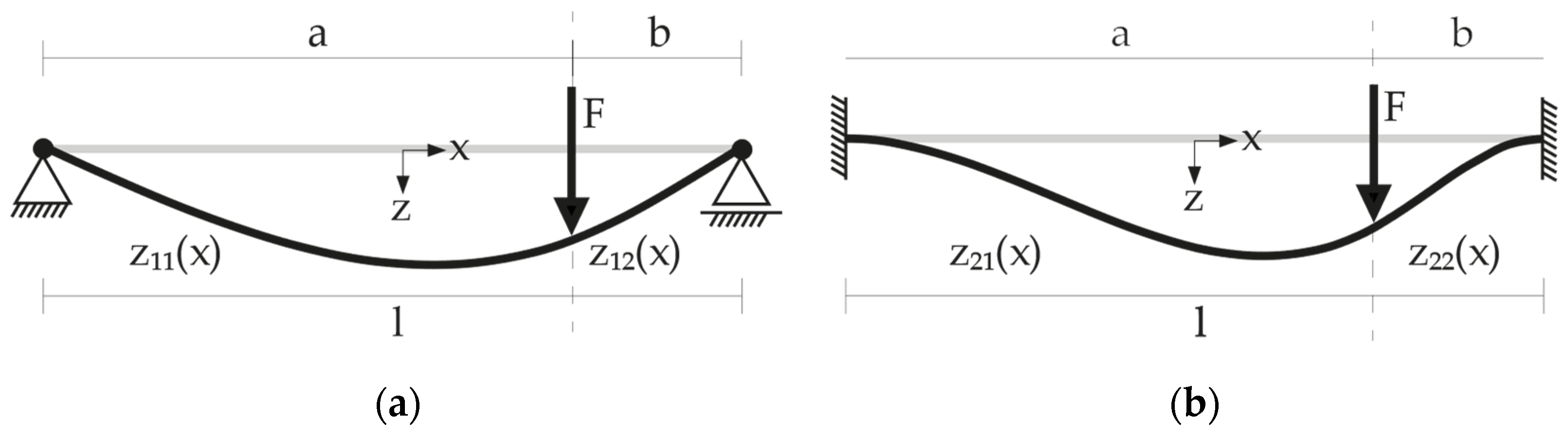
2.1.1. Approach for Two-Dimensional Measurements
2.1.2. Theoretical Analysis of the Example of a Two-Dimensional Bending Beam
2.1.3. Approach for Three-Dimensional Measurements
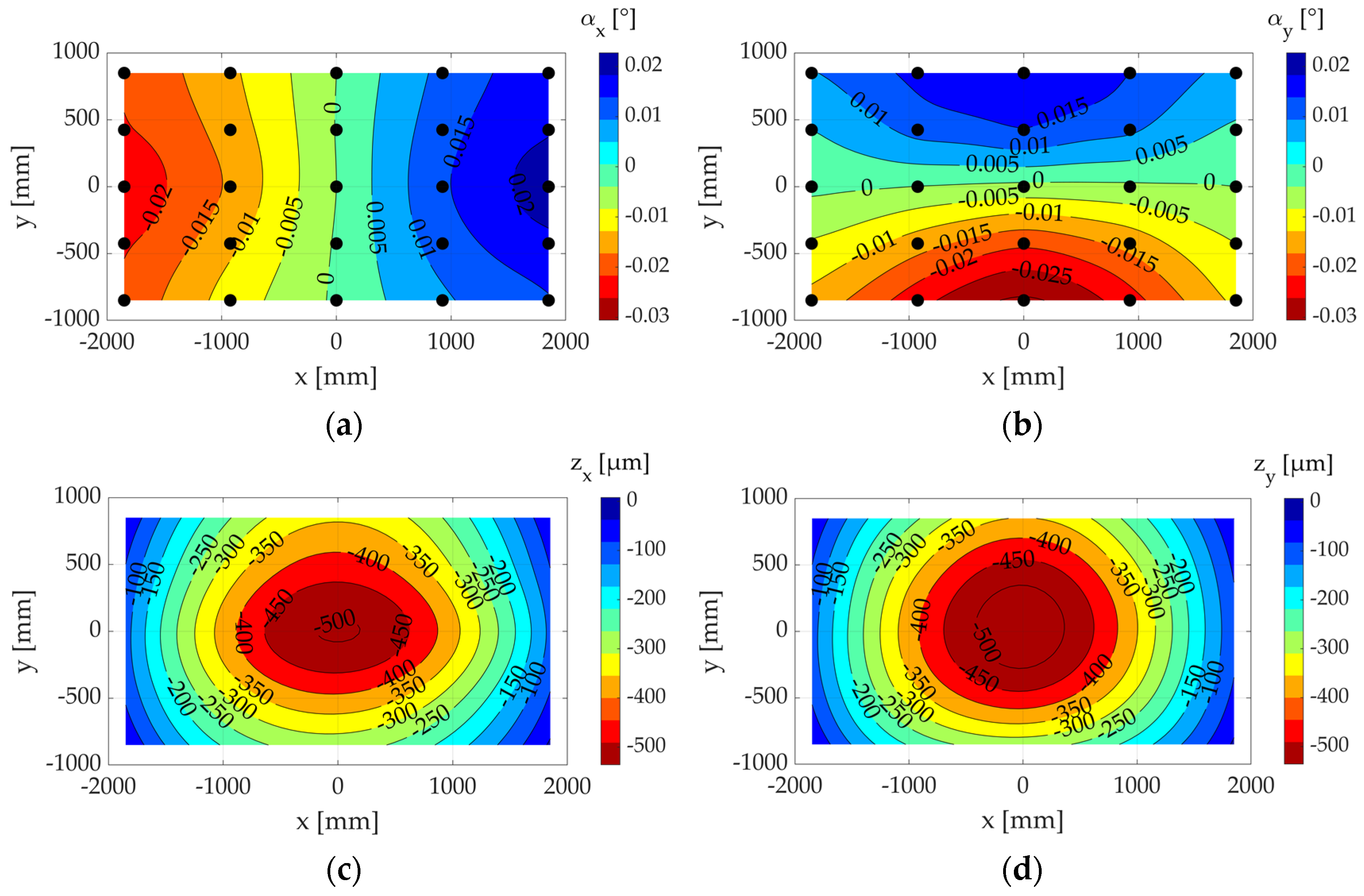
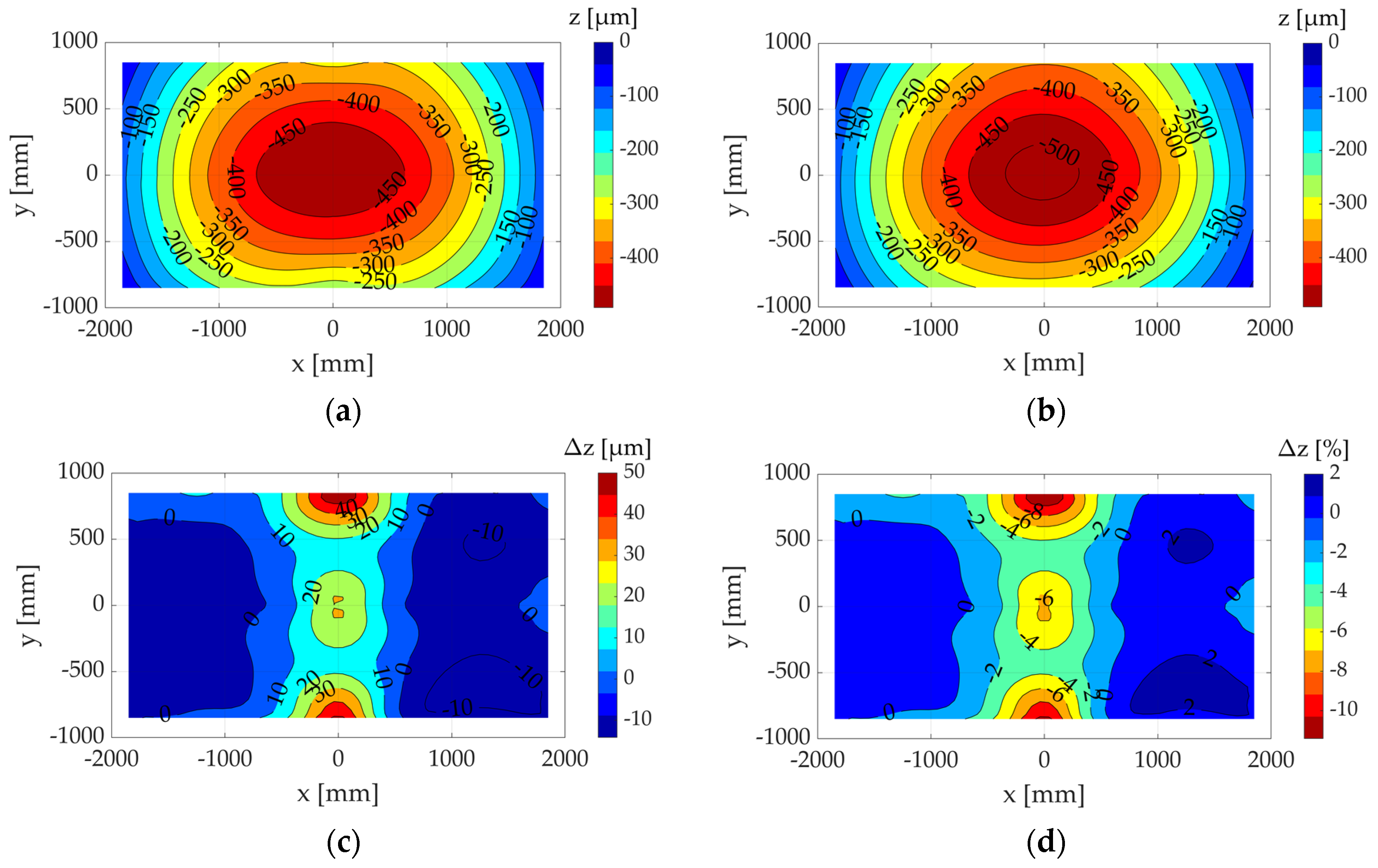
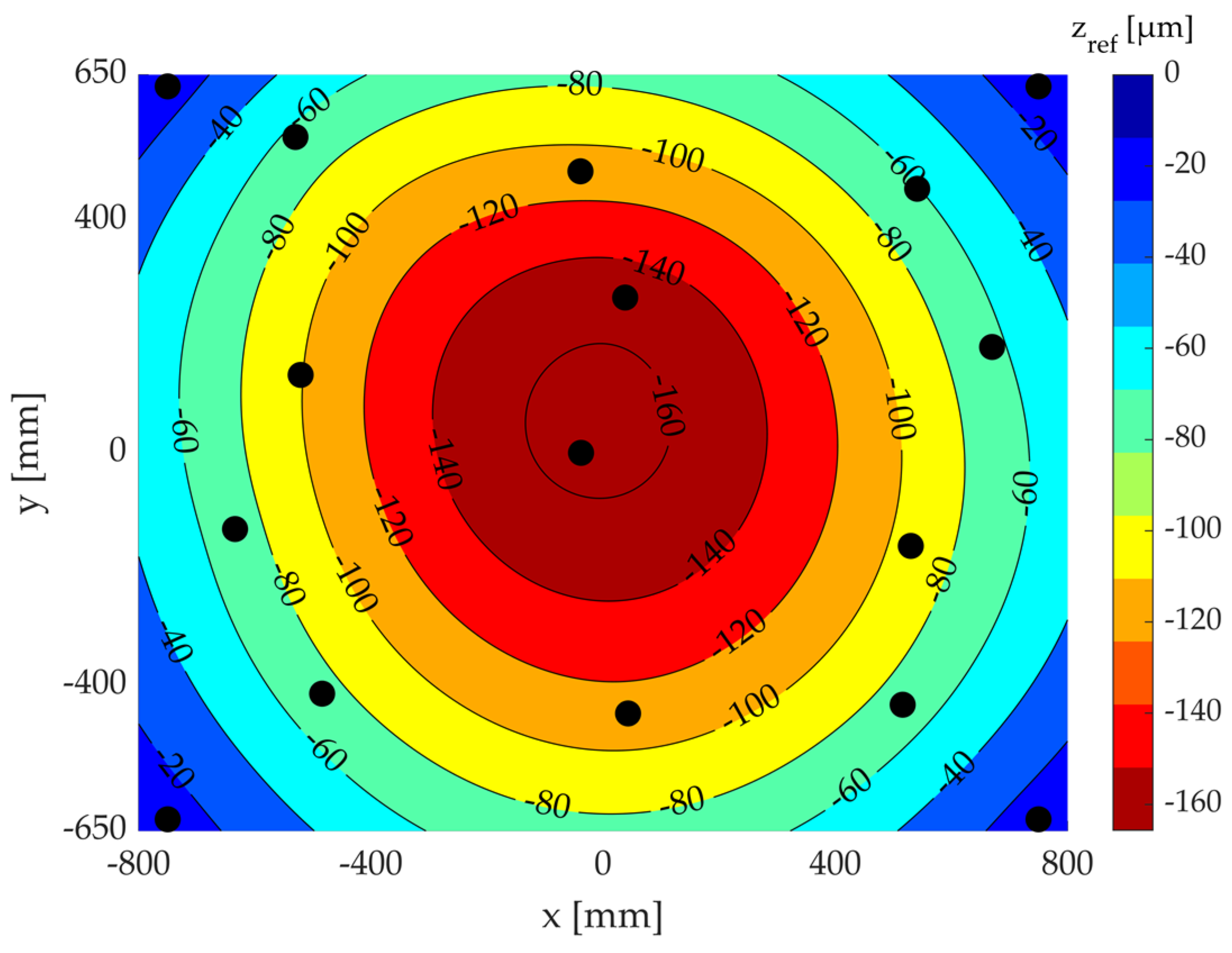
2.1.4. Theoretical Analysis of the Example of Three-Dimensional Deformation Data
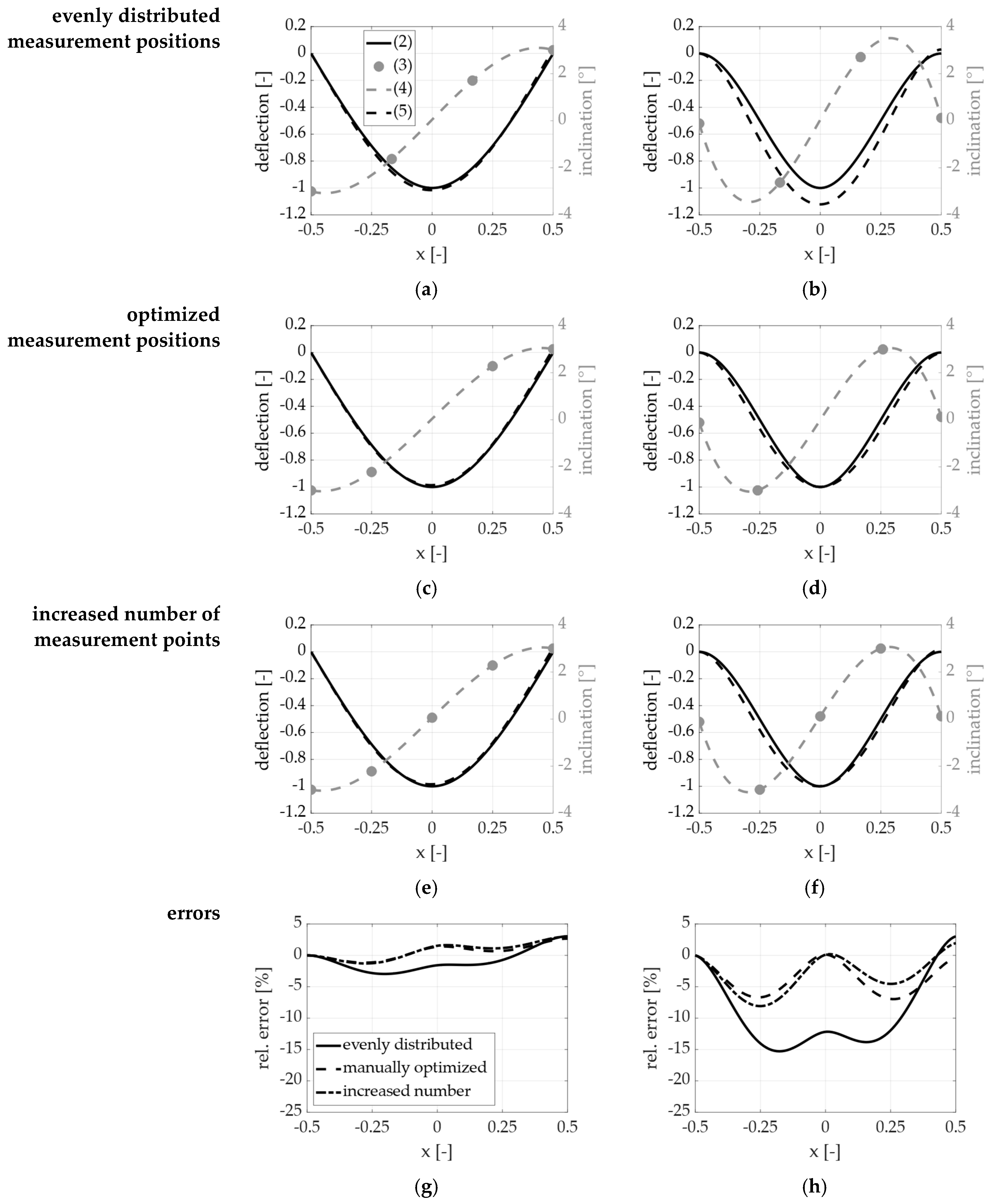
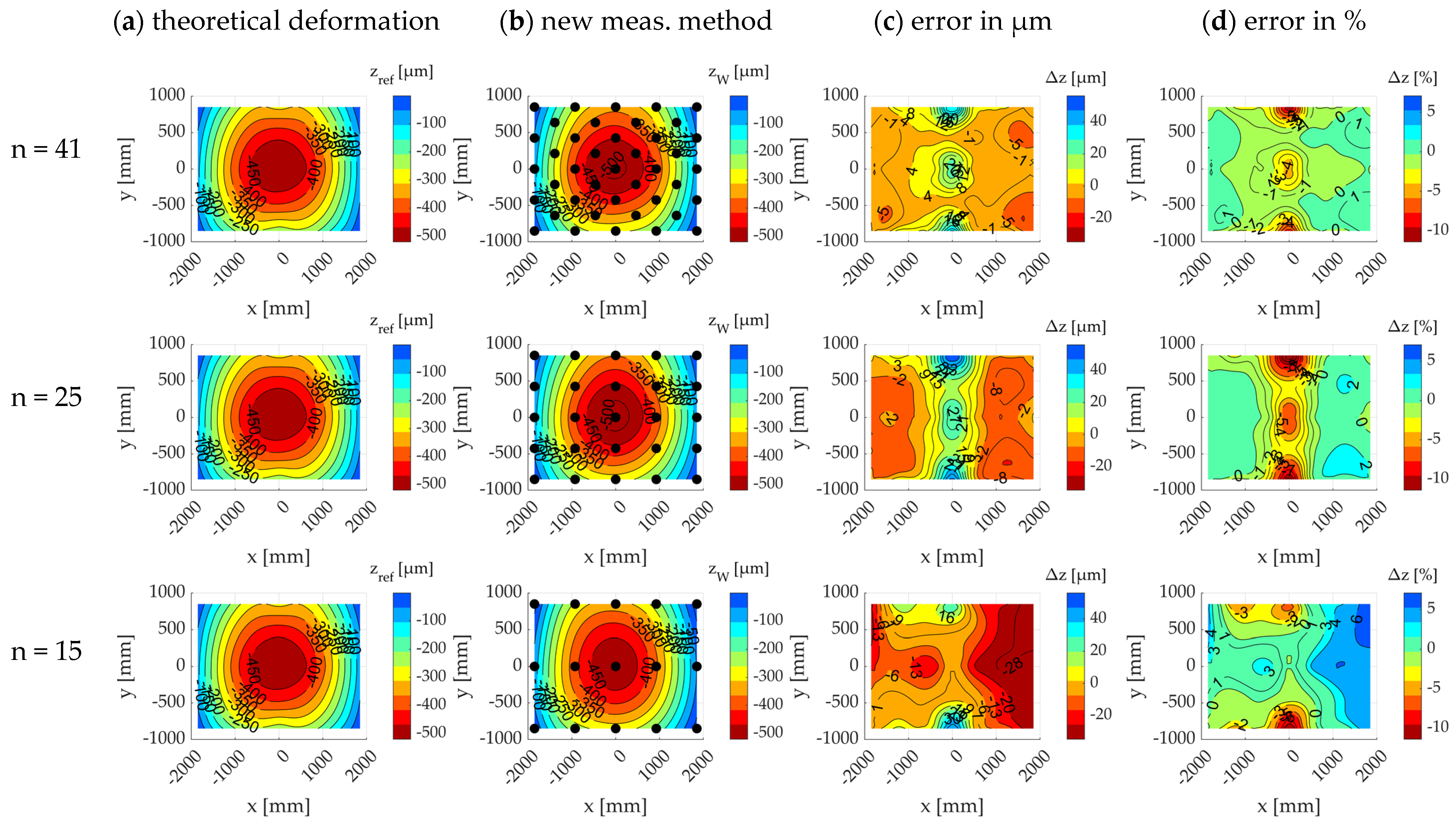
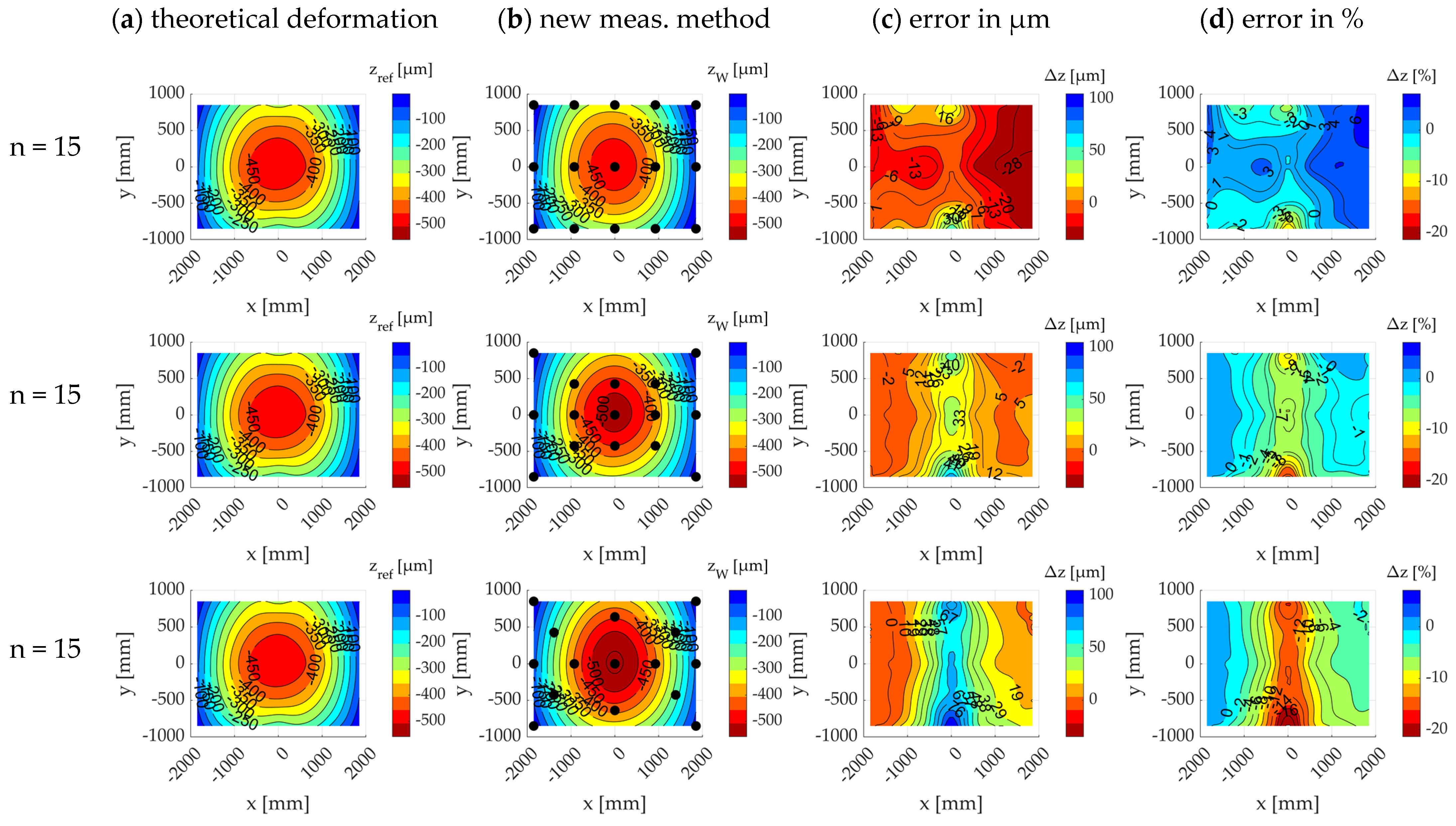
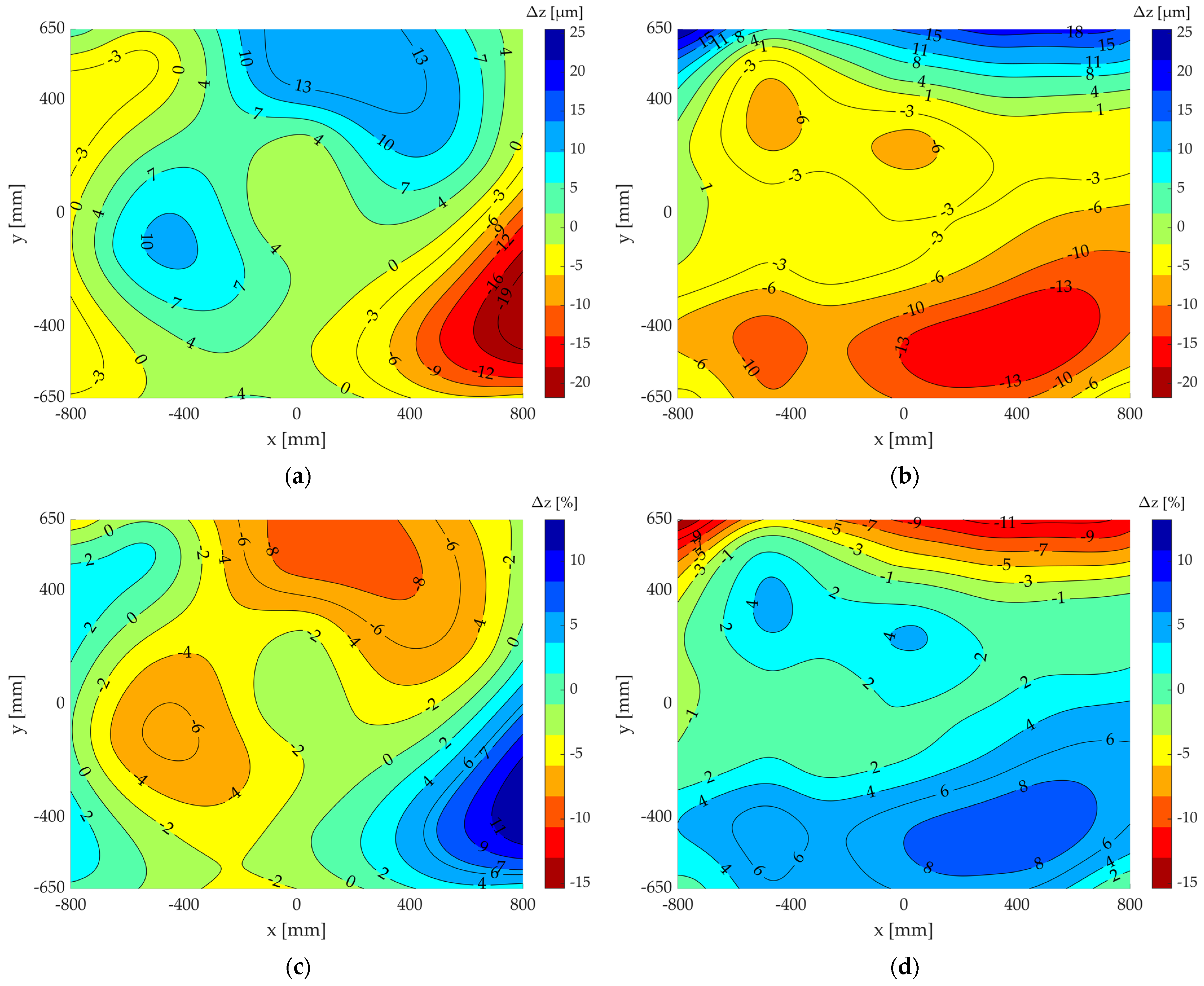
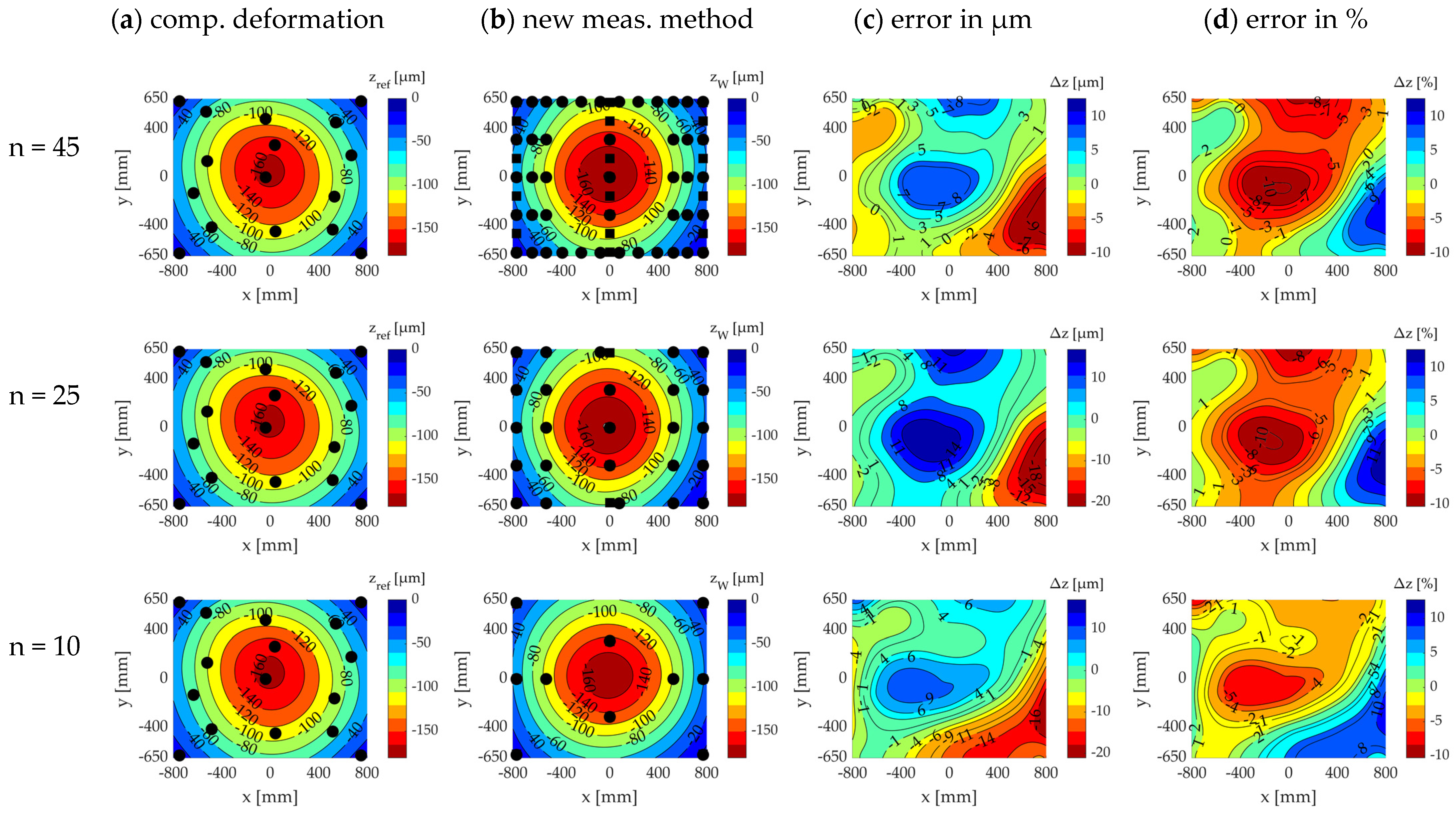
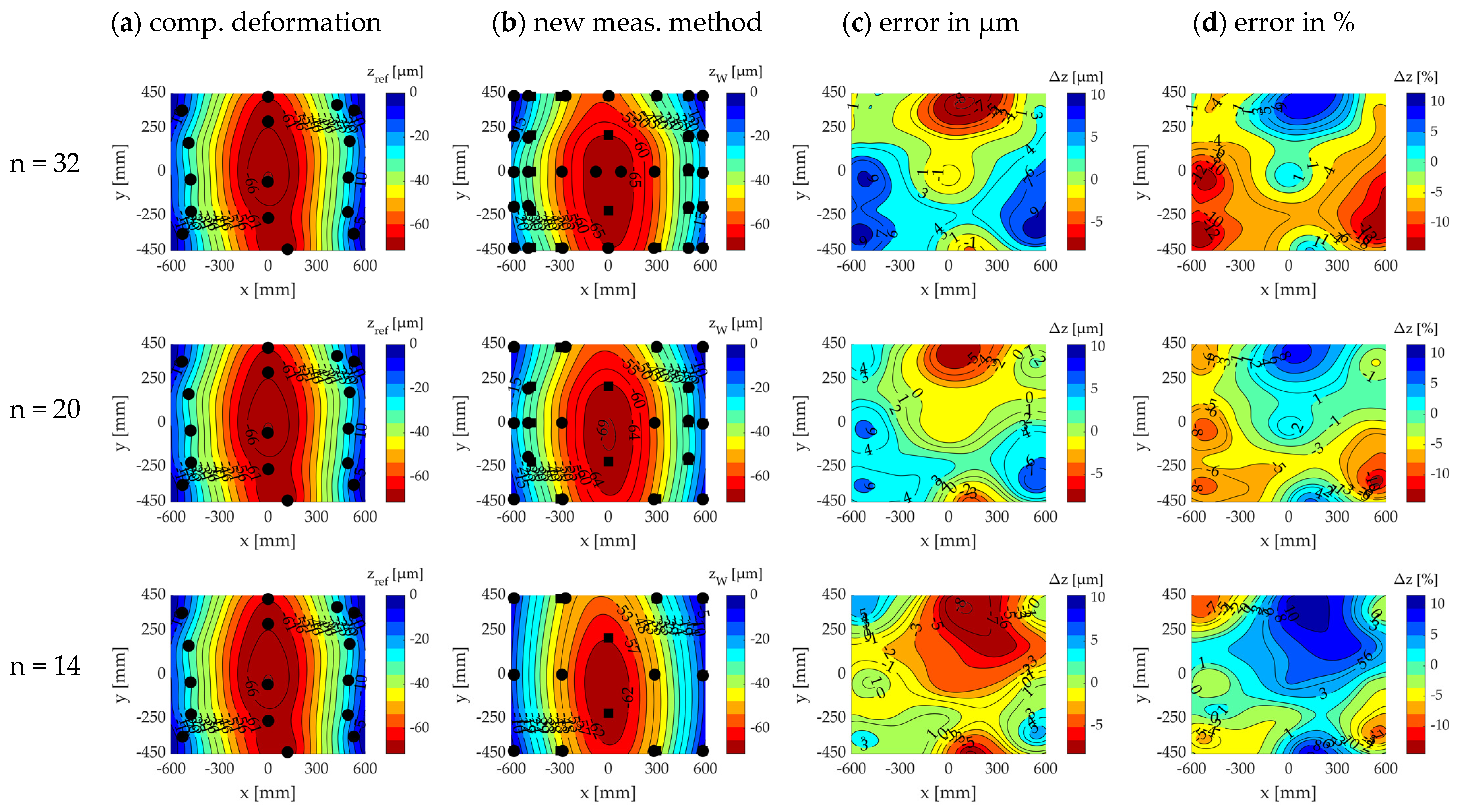
2.1.5. Sensitivity Analysis of the Theoretical Measurement Point Quantity and Position
2.2. Experimental Verification of Deformation Measurement of Press Bolster Plates
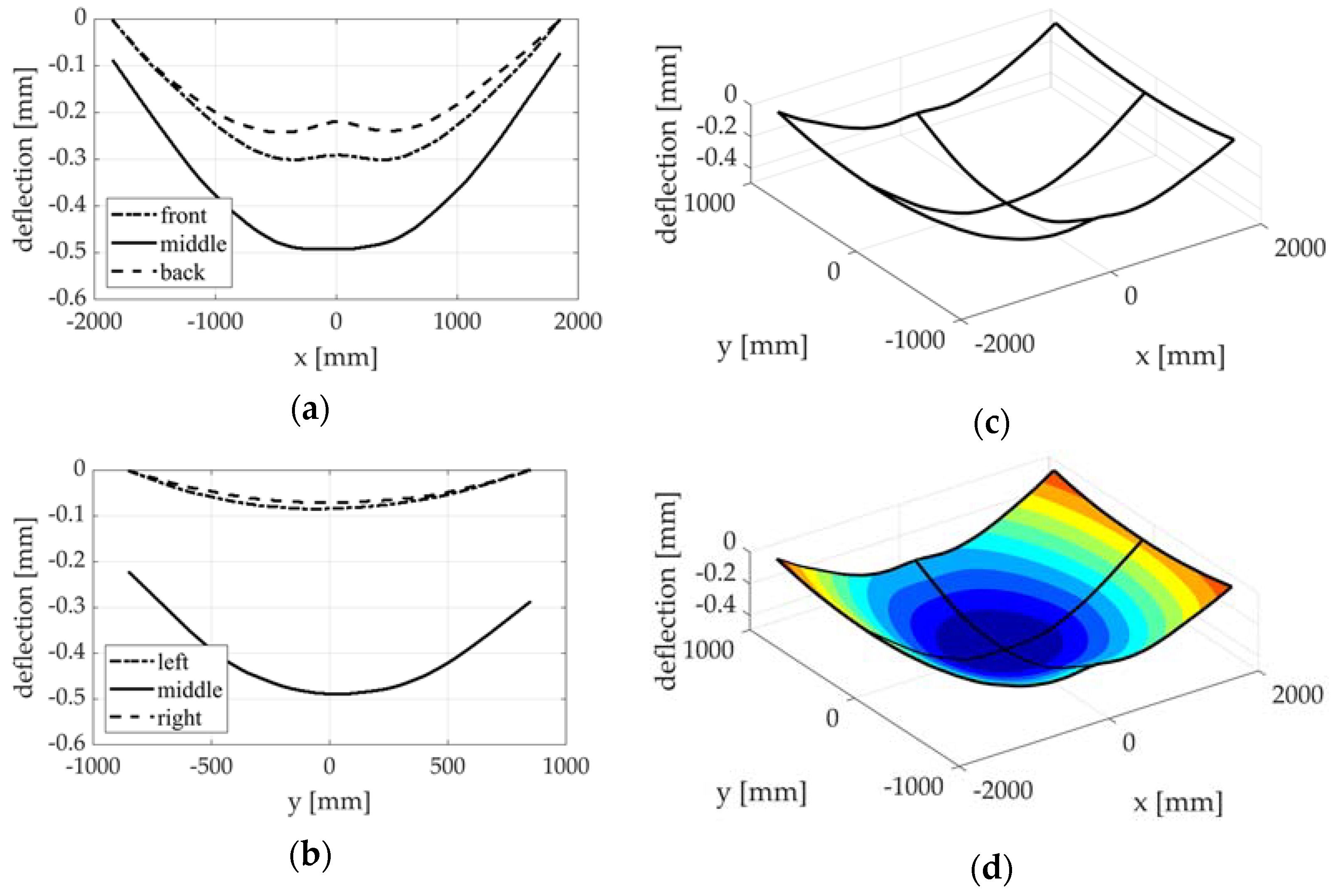
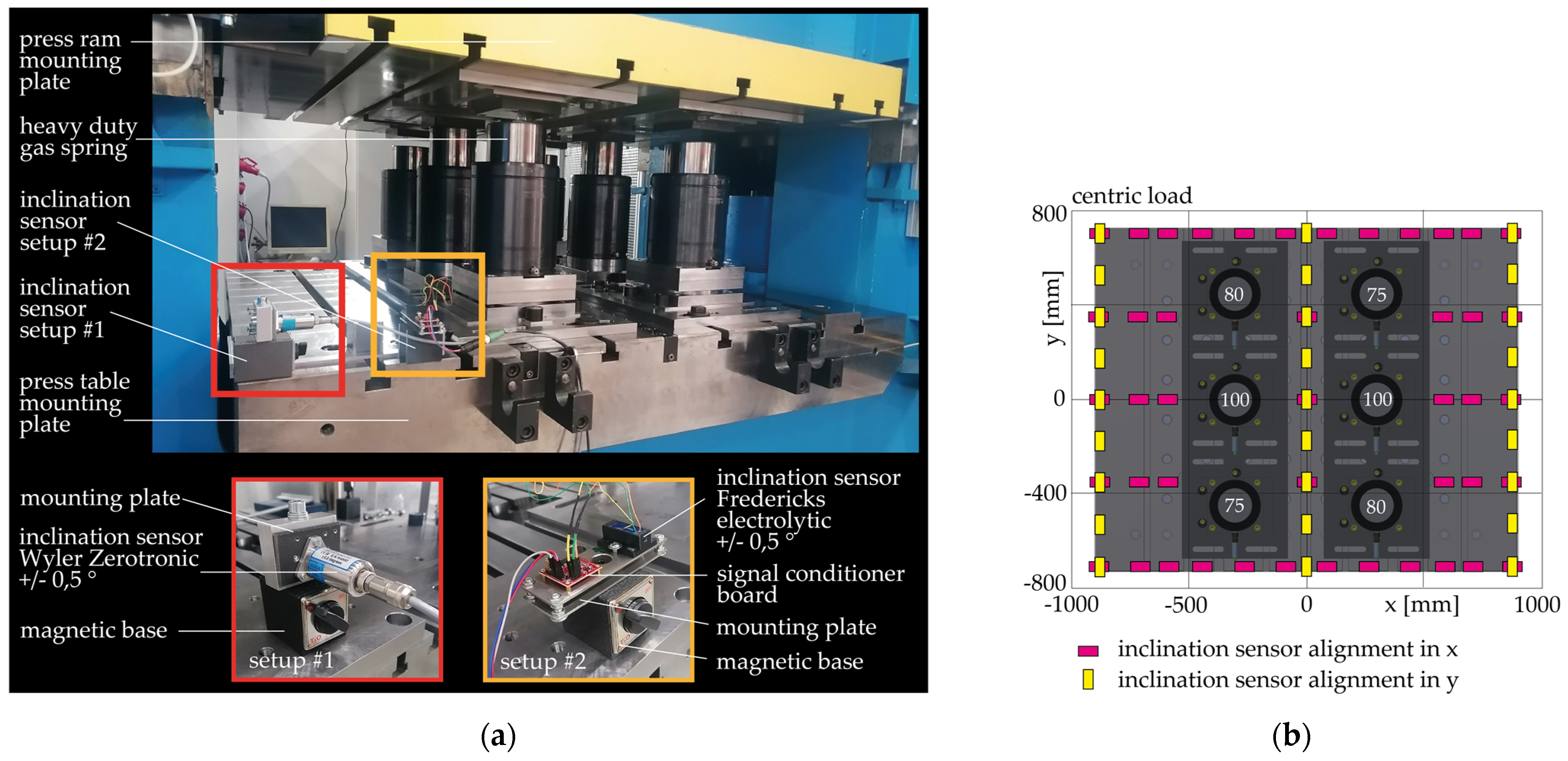
2.2.1. Basic Experimental Testing under Laboratory Conditions
2.2.2. Testing as Part of a Press Commissioning at a Press Manufacturer
3. Discussion
3.1. Sensitivity Analysis of Measurement Point Quantity
3.2. Sensitivity Analysis of Measurement Point Position
3.3. Error Considerations of the Conducted Measurements
- Deviations in the load application between the inclination-based deformation measurement and the comparative measurement due to temperature differences in the gas pressure springs and minimal leakage at the spring valves;
- Deviations in the load application due to control deviations in the force or stroke controls of the test object and the machine;
- Inaccuracies in the manual evaluation of the non-synchronized raw measurement data of the individual inclination measurements;
- Inaccuracies in the manual alignment of the sensor setups on the bolster plates;
- Angular errors due to deviations from perpendicularity during the setup of the sensors on the simplified sensor setups;
- Angular errors due to deviations from perpendicularity during the alignment of the sensor setups on the bolster plates of the test machines;
- Temperature drifts of the inclination sensors during the recording of a measurement series (lasting several hours);
- Minimal adjustment of the sensor alignment on the recording plates of the simplified sensor setups;
- Insufficient holding time at maximum load at BDC.
4. Conclusions
5. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations/Nomenclature
| Term | Explanation |
| bolster plate | clamping plate for tool fixture in forming presses |
| press commissioning | setup and initiation process, including testing and making the press operational |
| press ram | movable part of a press that applies pressure to the material being processed |
| press table | flat surface or platform on a press where the material or workpiece is positioned and processed |
| press working space/area | area between the table and the ram of a forming press |
| T-slot | groove in press table or ram for tool fixation |
| BDC | Bottom Dead Center |
| DIC | Digital Image Correlation |
| ICM | ICM—Institut Chemnitzer Maschinen- und Anlagenbau e.V. |
| PSD | Position Sensitive Detector |
| TPS | Thin plate smoothing spline |
| 2D | Two dimensional |
| 3D | Three dimensional |
References
- Behrens, B.-A.; Werbs, M.; Brecher, C.; Hork, M. Entwicklung und Erweiterung Standardisierter Messverfahren zur Statischen und Dynamischen Pressenvermessung; EFB-Forschungsbericht: Hanover, Germany, 2006; p. 250. [Google Scholar]
- Behrens, B.-A.; Brecher, C.; Hork, M.; Werbs, M. New standardized procedure for the measurement of the static and dynamic properties of forming machines. Prod. Eng. Res. Dev. 2007, 1, 31–36. [Google Scholar] [CrossRef]
- Abbasi, F.; Sarasua, A.; Trinidad, J.; Otegi, N.; Saenz de Argandoña, E.; Galdos, L. Substitutive Press-Bolster and Press-Ram Models for the Virtual Estimation of Stamping-Tool Cambering. Materials 2022, 15, 279. [Google Scholar] [CrossRef]
- Roth, T. Ermittlung von Kennwerten von Einfachwirkenden Umformmaschinen für die Zustandsorientierte Instandhaltung und die Qualifizierung des Werkzeugentstehungsprozesses. Ph.D. Thesis, Chemnitz University of Technology, Chemnitz, Germany, 2015. [Google Scholar]
- Struck, R. Berücksichtigung von Werkzeug- und Pressenelastizitäten in der Umformsimulation zur verbesserten Vorhersage des Pressenkraftbedarfes. VDI-Berichte 2008, 2031, 185–199. [Google Scholar]
- Struck, R. Bestimmung der Minimal Notwendigen Pressenkraft zur Herstellung von Karosseriestrukturbauteilen im Automobilbau. Ph.D. Thesis, Leibniz University Hannover, Hannover, Germany, 2010. [Google Scholar]
- Wagener, H.-W.; Weikert, J. Messung der Tisch- und Stößeldurchbiegung an Torgestellpressen. Blech Rohre Profile 1997, 5, 46–52. [Google Scholar]
- Tehel, R.; Päßler, T.; Kurth, R.; Nagel, M.; Reichert, W.; Ihlenfeldt, S. Virtual Tryout: Case Study on Simulation-Based Design and Die Spotting of Forming Tools. Eng. Proc. 2022, 26, 9. [Google Scholar] [CrossRef]
- Pilthammar, J.; Skåre, T.; Galdos, L.; Fröjdh, K.; Ottosson, P.; Wiklund, D.; Carlholmer, J.; Sigvant, M.; Ohlsson, M.; Sáenz de Argandoña, E.; et al. New press deflection measuring methods for the creation of substitutive models for efficient die cambering. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1157, 012076. [Google Scholar] [CrossRef]
- Wiedenmann, X. Dynamische Prozesse in Pressen erkennen—Der digitale Fingerabdruck. In Proceedings of the Conference Mehr Effizienz im Presswerk 2023, Würzburg, Germany, 15 June 2023. [Google Scholar]
- Zgoll, F. Methodik zur Maschinenoptimalen Werkzeugeinarbeitung Durch Virtuelle Kompensation der Werkzeug- und Pressendurchbiegung. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2021. [Google Scholar]
- Kurth, R.; Bergmann, M.; Tehel, R.; Dix, M.; Putz, M. Cognitive clamping geometries for monitoring elastic deformation in forming machines and processes. CIRP Ann. 2021, 70, 235–238. [Google Scholar] [CrossRef]
- Schapp, L.O. Gekoppelte Simulation von Maschine und Prozess in der Massivumformung. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2008. [Google Scholar]
- Tehel, R.; Päßler, T.; Mihm, M. Modeling elastic behavior of forming machine components to reduce tool manufacturing time. Procedia Manuf. 2019, 27, 177–184. [Google Scholar] [CrossRef]
- Tehel, R.; Päßler, T.; Bergmann, M. Effective FE models for simulating the elasto-mechanical characteristics of forming machines. Int. J. Adv. Manuf. Technol. 2020, 58, 9–12, 588. [Google Scholar] [CrossRef]
- Wagener, H.-W.; Wiedner, M. Analyse des statischen und dynamischen Genauigkeitsverhaltens einer 5000 kN-Vierpunkt-Exzenterpresse mit Hilfe der Lasermesstechnik. UTF Sci. 2001, 1, 9–14. [Google Scholar]
- GOM Gesellschaft für Optische Messtechnik. Application Note: 3D Motion Analysis—Optical Measuring Technology for Dynamic Analysis of Press Machines. Available online: https://mailassets.gom.com/user_upload/industries/forming_machine_EN.pdf (accessed on 30 December 2023).
- Müller, P. Analyse Elastischer Wechselwirkungen an Servo-Spindelpressen. Ph.D. Thesis, Chemnitz University of Technology, Chemnitz, Germany, 2018. [Google Scholar]
- Müller, P.; Kriechenbauer, S.; Drossel, W.-G. Experimental analysis of the elastic boundary conditions of press machines for modelling the deep-drawing process. Int. J. Adv. Manuf. Technol. 2019, 101, 579–592. [Google Scholar] [CrossRef]
- Pilthammar, J.; Sigvant, M.; Hansson, M.; Pálsson, E.; Rutgersson, W. Characterizing the Elastic Behaviour of a Press Table through Topology Optimization. J. Phys. Conf. Ser. 2017, 896, 12068. [Google Scholar] [CrossRef]
- Pilthammar, J. Elastic Press and Die Deformations in Sheet Metal Forming Simulations. Ph.D. Thesis, Blekinge Institute of Technology, Karlskrona, Germany, 2017. [Google Scholar]
- Zgoll, F.; Götze, T.; Volk, W. Building a substitute model of a bolster based on experimentally determined deflection. J. Phys. Conf. Ser. 2017, 896, 012044. [Google Scholar] [CrossRef]
- Zgoll, F.; Götze, T.; Volk, W. Influence of the elastic behaviour of a moving bolster on the active surface of a punch: A numerical investigation. In Proceedings of the Forming Technology Forum 2017, Enschede, The Netherlands, 12–13 October 2017. [Google Scholar]
- Zgoll, F.; Kuruva, S.; Götze1, T.; Volk, W. Virtual die spotting: Compensation of elastic behavior of forming presses. IOP Conf. Ser. Mater. Sci. Eng. 2019, 651, 012021. [Google Scholar] [CrossRef]
- Pan, B. Digital image correlation for surface deformation measurement: Historical developments, recent advances and future goals. Meas. Sci. Technol. 2018, 29, 082001. [Google Scholar] [CrossRef]
- Amirpour, M.; Bickerton, S.; Calius, E.; Das, R.; Mace, B. Numerical and experimental study on deformation of 3D-printed polymeric functionally graded plates: 3D-Digital Image Correlation approach. Compos. Struct. 2019, 211, 481–489. [Google Scholar] [CrossRef]
- Almazán-Lázaro, A.-J.; López-Alba, E.; Rubio-García, L.; Díaz-Garrido, F.-A. Indentation Measurement in Thin Plates under Bending Using 3D Digital Image Correlation. Appl. Sci. 2021, 11, 2706. [Google Scholar] [CrossRef]
- Pupurs, A.; Loukil, M.; Varna, J. Digital Image Correlation (DIC) Validation of Engineering Approaches for Bending Stiffness Determination of Damaged Laminates. Appl. Compos. Mater. 2022, 29, 1937–1958. [Google Scholar] [CrossRef]
- Xu, W.; Li, J.; Zhang, B.; Yang, L. A new approach to reduce springback in sheet metal bending using digital image correlation. Int. J. Mater. Res. 2019, 110, 726–733. [Google Scholar] [CrossRef]
- Gothivarekar, S.; Coppieters, S.; Van de Velde, A.; Debruyne, D. Advanced FE model validation of cold-forming process using DIC: Air bending of high strength steel. Int. J. Mater. Form. 2020, 13, 409–421. [Google Scholar] [CrossRef]
- Sun, W.; Xu, Z.; Li, X.; Chen, Z.; Tang, X. Three-Dimensional Shape and Deformation Measurements Based on Fringe Projection Profilometry and Fluorescent Digital Image Correlation via a 3 Charge Coupled Device Camera. Sensors 2023, 23, 6663. [Google Scholar] [CrossRef] [PubMed]
- Salfeld, V. Experimentelle und numerische Untersuchungen zur Verlagerung des Pressenstößels infolge einer Horizontalkraft. Ph.D. Thesis, Leibniz University Hannover, Hannover, Germany, 2015. [Google Scholar]
- Ottosson, P.; Pilthammar, J.; Wiklund, D.; Skåre, T.; Sigvant, M. Substitutive models of press deflections for efficient numerical die cambering. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1284, 012060. [Google Scholar] [CrossRef]
- Kurth, R.; Alaluss, M.; Wagner, M.; Tehel, R.; Riemer, M.; Ihlenfeldt, S. Process Monitoring using Digital Twin-Based Sensors integrated in Tool Clamping Surfaces. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1284, 012016. [Google Scholar] [CrossRef]
- Alaluss, M.; Kurth, R.; Tehel, R.; Wagner, M.; Wagner, N.; Ihlenfeldt, S. Potential of Tool Clamping Surfaces in Forming Machines for Cognitive Production. J. Mach. Eng. 2022, 22, 116–131. [Google Scholar] [CrossRef]
- Kurth, R.; Tehel, R.; Päßler, T.; Putz, M.; Wehmeyer, K.; Kraft, C.; Schwarze, H. Forming 4.0: Smart machine components applied as a hybrid plain bearing and a tool clamping system. Procedia Manuf. 2019, 27, 65–71. [Google Scholar] [CrossRef]
- Tehel, R. Smart Machine Components. Fundamental Part of Cognitive Forming Machines. 21; Werkzeugmasch.-Fachsemin: Dresden, Germany, 2019. [Google Scholar] [CrossRef]
- Gao, N.H.; Zhao, M.; Li, S.Z. Displacement Monitoring Method Based on Inclination Measurement. Adv. Mater. Res. 2011, 368–373, 2280–2285. [Google Scholar]
- Guidi, V.; Mazzolari, A.; Salvador, D.; Carnera, A. Silicon crystal for channelling of negatively charged particles. J. Phys. D Appl. Phys. 2009, 42, 182005. [Google Scholar] [CrossRef]
- Hou, X.; Yang, X.; Huang, Q. Using Inclinometers to Measure Bridge Deflection. J. Bridge Eng. 2005, 10, 564–569. [Google Scholar] [CrossRef]
- Sousa, H.; Cavadas, F.; Henriques, A.; Bento, J.; Figueiras, J. Bridge deflection evaluation using strain and rotation measurements. Smart Struct. Syst. 2013, 11, 365–386. [Google Scholar] [CrossRef]
- Yu, H.; Chen, X.; Ren, M.; Yin, L.; Wu, Q.; Zhan, J.; Liu, Q. A coupled bend-twist deformation monitoring method based on inclination measurement and rational cubic spline fitting. Mech. Syst. Signal Process. 2021, 147, 107084. [Google Scholar] [CrossRef]
- Roskam, R. In-Prozess-Überwachung von Pressen der Blechverarbeitung. Ph.D. Thesis, Leibniz University Hannover, Hannover, Germany, 1999. [Google Scholar]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanov, G.; Burkhardt, T.; Penter, L.; Ihlenfeldt, S. New Method for Precise Measurement of Clamping Plate Deformations on Forming Presses. Machines 2024, 12, 40. https://doi.org/10.3390/machines12010040
Ivanov G, Burkhardt T, Penter L, Ihlenfeldt S. New Method for Precise Measurement of Clamping Plate Deformations on Forming Presses. Machines. 2024; 12(1):40. https://doi.org/10.3390/machines12010040
Chicago/Turabian StyleIvanov, Georg, Thomas Burkhardt, Lars Penter, and Steffen Ihlenfeldt. 2024. "New Method for Precise Measurement of Clamping Plate Deformations on Forming Presses" Machines 12, no. 1: 40. https://doi.org/10.3390/machines12010040
APA StyleIvanov, G., Burkhardt, T., Penter, L., & Ihlenfeldt, S. (2024). New Method for Precise Measurement of Clamping Plate Deformations on Forming Presses. Machines, 12(1), 40. https://doi.org/10.3390/machines12010040






