Abstract
This paper presents a range control approach for implementing hard geofencing for unmanned air vehicles (UAVs), and especially remotely piloted versions (RPVs), via a proposed anticipatory range calculator. The approach employs turning circle intersection tests that anticipate the fence perimeter on approach. This ensures the vehicle turns before penetrating the geofence and remains inside the allowable operational airspace by accounting for the vehicles’ turning dynamics. Allowance is made for general geozone shapes and locations, including those located at the problematic poles and meridians where nonlinear angle mapping is dealt with, concave geozones, narrow corners with acute internal angles, and transient turn dynamics. The algorithm is shown to prevent any excursions using a high-fidelity simulation of a small remotely piloted vehicle. The algorithm relies on a single tuning parameter which can be determined from the closed-loop rise time in the aircraft’s roll command tracking.
1. Introduction
Geofencing is an approach to automatically constrict the operating airspace of unmanned air vehicles (UAVs). This terminology includes remotely piloted vehicles (RPVs) and autonomous unmanned systems; both are colloquially referred to as ‘drones’. This has become a particularly important concept in recent years following the rapid proliferation of consumer-grade RPVs and the ignorance, or wilful defiance, of the rules of air law by those who operate them.
In a broader sense, geofencing involves the positional management of any particular object relative to a virtual barrier. It has applications in a variety of telematic areas including location-based business services where information on individuals entering the fenced zone can be collected/interacted with. For example, tracking vehicles in relation to geographical areas and points of interest (POI) has monitoring, organizational, and customer service applications for fleet management in transport and logistics services [1]. Geofencing requires the position of the object to be known; thus, for aerospace applications, global navigation satellite system (GNSS) data are predominately used. Other localizing methods, such as radio frequency identification (RFID), are limited to a single degree of freedom, and hence simpler, circular geofences. Indoor fencing is also possible using a sensor fusion of optics inertial and altitude data [2]. Such a complimentary sensor approach is likely to be necessary for guaranteeing containment for certification of larger vehicles and for operations in GPS-denied environments [3].
A geofence may identify the area that the vehicle must operate within, or alternatively, an area the vehicle must remain outside of. Employing geofences as ‘no-fly’ zones can have applications to trajectory optimization and collision avoidance (see, for example, [4,5,6]). The problem is still essentially a multiconstraint trajectory optimization problem. There is a wealth of existing research on path planning and trajectory optimization that is not discussed here.
Work by Gurriet and Ciarletta [7] used quadratic programming techniques to determine the most appropriate modification to the vehicle’s velocity in a seamless manner with the pilot’s original flight path in order to avoid entering certain areas, or ‘geozones’. This would be quite attractive when navigating through fields of small obstacles for fully autonomous vehicles, but it introduces an element of uncertainty for the pilot of RPVs with large no-fly zones unless it is clear to them they have full or partial control of the vehicle.
Comprehensive geofencing solutions will play an important part in future traffic management in urban environments and in the provision of autonomous advanced air mobility (AAM). There is much research ongoing on traffic planning [8,9,10], risk management [11] and collision avoidance [12,13] in this area.
Following concerns of collisions between scheduled airport traffic and privately operated RPVs, geofencing has been established as a means to prevent private RPV flights in areas such as airports, stadiums, government buildings and facilities, and other restricted areas where security is a requirement or the risk of an in-air collision is sufficiently high. These geofences can be set up to either contain the vehicle or define ‘no-fly’ zones. Many civilian drone manufacturers now provide some form of geofencing functionality on their products, though it may be relatively simple in operation. Geofencing can also provide a useful failsafe capability for remote or semiautonomous operations in environments where the loss of line-of-sight (LOS) may make it difficult to recover the vehicle, e.g., arctic exploration or volcanic inspection. It may also be an effective technique in establishing cut-down boundaries for the failsafe operation of experimental aircraft, those that wander uncontrolled, or for creating emergency safety flight paths [14].
In the basic geofencing detection and control algorithms presented in the literature, some form of point-in-polygon (PIP) test is conducted to determine if corrective flight control is needed to bring the vehicle back into the allowable airspace. The process of most simple geofencing algorithms for RPVs is illustrated in Algorithm 1. The desired action (typically, for an RPV, this is a return to base (RTB) command) happens only when the vehicle has crossed the geofence. The border to the geofence is usually a ’hard’ one, and some due consideration needs to be given to the placement of the fences. For rotorcraft, a ‘hard’ fence is normally acceptable due to the slower flight speeds and greater maneuverability. Sometimes, demarcated safety zones will be created to ensure excursions are prevented before corrective control is engaged. However, zone inclusion tests will still be used. If strict compliance is required, then a predictive system utilizing some form of control would be needed to anticipate the approach and act accordingly [15]. Zhang et al. [16] used model predictive control in this way to create virtual ‘soft’ fences and develop a ‘braking’ controller for a quadcopter. The soft geozones were restricted to circular shapes and scaled based on the UAVs’ speed. Cavanini et al. [17] proposed a similar solution but again focusing on multirotor vehicles. For fixed-wing aircraft, this is a more challenging problem, as the higher flight speeds, poorer maneuverability, and requirement to turn means the vehicle will exceed the fence by some considerable distance before turning back towards the allowable airspace. If the return command is instigated upon crossing the fence then, depending on the current velocity and maximum turn rate, the additional range of penetration can be considerable. Seiferth et al. [18] generate ‘safety zones’ within the allowable airspace using Voronoi diagrams. The size of this safety zone is determined by the vehicle’s allowable bank angle and airspeed, thus ensuring the vehicle turns before crossing the geofence. This is also considered by Thiele et al. [19], who note that a turn follows a varying curvature, which is often treated as a constant by assuming the roll rate is instantaneous. In that paper only convex geozones were considered. Furthermore, to prevent further egress, manual control should only be returned once the vehicle is inside the geozone, but this return should be instigated by the pilot for safety. Stevens et al. [2,20] propose that the geofencing system should be independent of the flight control system of the UAV, as opposed to most current commercial systems that are integrated into the standard autopilot control loops. Such a system has already been developed and tested by NASA [21]. This would provide improved redundancy and resilience to onboard hardware and software failures, but it would be difficult to optimize overall system performance for specific airframes and would require additional communication systems. Consideration of vehicle performance constraints, namely turn performance, is necessary to provide improved range management. Considering the effect wind has on the vehicles’ trajectory has also led to strategies to scale the size of the ’soft’ boundaries around the geofence [22,23,24].
| Algorithm 1 Return to Base |
| Require: C: Database of n geopost positions for where .
Require: : Base coordinates. Require: : Current geodetic coordinates.
|
Despite the progress in the development and implementation of geofencing control for rotary-wing UAVs [25,26], the problem for fixed-wing UAVs has received less attention, and in total, geofencing remains an open problem [5]. The approach in this paper is similar to the methods described above in that a prediction of the aircraft’s flight towards the geofence is computed and includes the transient dynamics of the turn so that the allowable flight region can be maximized while ensuring excursions do not occur. The work in this paper focuses on a combined, general geofencing approach that provides predictive monitoring and scaling of the soft geozone (or safety zone) based on the aircraft’s current behavior, includes consideration of noninstantaneous turn dynamics, and can handle arbitrary geozone shapes, including concave geozones with fences with acute internal angles. Subsequently, this paper proposes an anticipatory range control algorithm for proactive control override of the RPV or UAV before it crosses the geofence boundary. It is derived using elementary geometry and takes into account the transient nature of the turn dynamics. The approach in this paper is specifically developed for fixed-wing UAVs; however, it can easily support rotorcraft or lighter-than-air RPVs and UAVs. The approach in this paper is used for standard ‘fly-in’ geozones, and successful operation is demonstrated using a high-fidelity six-degree-of-freedom simulation of a fixed-wing RPV at the end of the paper. This method can easily be configured to operate with no-fly zones, which can then be used to enable collision avoidance during encounters with irregularly shaped obstacles.
2. Mathematical Framework
2.1. Geozones
Consider a line mapped to an orthodromic length around the surface of Earth between two nodes, so-called ‘geonodes’, that can be located by geographical points on Earth. When a number of these lines are connected, they form a closed polygon, defining an enclosed area—a ‘geozone’. The perimeter of the geozone is referred to as the geofence. A minimum of three nodes are required to specify a valid geozone, unless the desired zone is elliptical. In this special case, a single node can specify the center of the geozone, and an equation defines the lay of the geofence.
An altitude may be associated with the geozone to implement a flight ceiling (effectively creating an aerodrome). Traditionally there is only one altitude limit set, especially for simple localized flying. Considering full three-dimensional positional constraints is of increasing interest in urban environments and the expansion of urban air mobility systems [27,28]. Furthermore, the complexity of such environments would likely require more orchestrated planning of the turning trajectories in three-dimensional space [24] and flight corridor control [29,30].
2.2. Determining Geozone Inclusion: Point-in-Polygon (PIP) Algorithms
The geofencing problem can be thought of as a version of the PIP test. Given an arbitrary polygon C with n vertices , resulting in edges, and a point of interest p, the task is to determine whether p is enclosed by C. This is a fundamental test in computer graphics (of particular interest in graphical user interface design) but has applications in other fields requiring computational geometry, including robotics, acoustics, and geoscience. A number of different algorithms have been developed to solve the PIP problem and Haines [31] provides a concise summary of these. They can be broadly categorized into two types: (1) those that perform an iterative examination of p (or some representation of it) relative to each polygon vertex and (2) those that use preprocessing to obtain a simpler representation of the polygon for faster intersection tests. The former types are generally more flexible, while the latter benefit from reduced computational overhead for large and fixed polygons. Substantially better computational speed is possible with convex polygons due to their geometric properties.
The two most commonly used methods are subtly different forms of the first type of PIP algorithm and are general enough to work for most complex convex polygons. These so-called crossing test methods involve the identification of the number of crossings made by the polygon over a reference axis (or ray). The earliest demonstration of this for nonconvex polygons is commonly attributed to Shimrat in 1962 [32] (though his algorithm was later corrected by Hacker [33]) and is often called the even–odd or parity rule. Given a rectilinear line (or ray) starting from infinity and ending at p (alternatively, the ray may start from p and extend to infinity, but the difference is trivial), if the line passes the edges of the polygon an odd number of times, then p is located inside C, and conversely, outside C if the edges are crossed an even number of times. This can be proved with the Jordan Curve Theorem. This PIP algorithm is intuitively easy to understand though there are problems with special cases such as self-intersecting polygons (where the Jordan Curve Theorem is no longer valid), when p lies on the vertices or the edges, or when the ray is parallel to one of the edges, as well as tolerances associated with numerical finite precision. Various solutions have been proposed to address these issues [31] and involve the use of strict additional modifications (or ‘rules’) to the base algorithm.
The other commonly used crossing test is often referred to as the winding number test and is only subtly different from the parity test in concept [34]. It involves determining the direction and frequency of crossings over the ray when looping once along the edges of C. The winding number test is of the same computational complexity as the parity test, , and both give the same result, except when C is self-intersecting, wherein the parity algorithm will give an erroneous result. Thus, the winding number method is the safer algorithm for arbitrary polygons. For the problem of the ray axis crossing an edge or vertex, either modifying the placement of the ray [31] or using half-increments when summing w [35] provide viable solutions. These algorithms also extend easily to three dimensions.
The concept of the winding number is also used with what is called the angle summation method. Given vertices, let be the i-th angle that the polygon edge subtends with p. Then,
Note that when p is located on one of the edges or vertices, (1) becomes undefined but can be accommodated with programming logic. The angle summation method appeared as early as 1974 when illustrated by Sutherland et al. [36]. This method is generally not favored due to the need to solve the time-consuming arccosine function for each vertex. It is, however, backwards stable [37].
The second type of algorithms include ray–triangle intersection [38,39,40], constructive solid geometry (CSG) representation [41,42], and wedge inclusion [43], among others. These are generally faster than the first type of algorithm, especially for polygons with a large number of vertices, as the initial preprocessing cost is amortized by the faster intersection testing. However, these methods are dependent on available memory to store the processed polygons. Perhaps the fastest but most memory-intensive method involves the spatial discretization of the polygon into a grid, wherein each cell can be readily categorized as fully inside, fully outside, or indeterminate. The intersection of p is then quickly determined by a look-up grid. If p is located in an indeterminate cell, then line segment intersection [44,45,46] can be used to determine its inclusivity.
The spherical nature of Earth means that the polygon C should be mapped to the spherical surface of Earth. However, for small areas, a planar approximation of Earth’s surface is often sufficient. The spherical nature of Earth’s surface also makes representing lines or areas difficult over the poles and the antimeridian when using geodetic coordinates. The latitudinal direction of movement over the poles is indeterminant unless the longitude is taken into account (since the sign of the latitude remains constant—positive at the North pole and negative at the South pole). However, the longitude will change abruptly by . Similarly, across the antimeridian, the longitude jumps between . It then becomes convoluted to project the correct variation in geodetic position across the poles or antimeridian onto a Cartesian coordinate space and, hence, makes the use of crossing tests difficult for polygons located at such locations. In many applications, this problem is rarely encountered, as the flight is relatively small-scale and, if away from these singularity regions, allows the latitude, , and longitude, , to be approximated as planar coordinates that can be used to determine the intersection of lines through Euclidean geometry (see Pratyusha and Naida [47] for an example). However, this approach would present a problem for search and rescue or survey missions, for example, at the poles and across the antimeridian.
The problem is avoided by using the angle summation rule at a given point on the spheroid surface, rather than using a crossing test. If is the forward azimuth from p to each geopost then (1) can be used, with exchanged for . The suitability of this approach, in terms of computational speed, will depend on the size of n. Additionally, this approach will become undetermined for the case when p is coincident with the poles but can be resolved with some conditional logic, since the intersection of these points with C should be evident upon the construction of the polygon.
2.3. Anticipatory Range Controller
The proposed anticipatory range controller (ARC) algorithm is conceptually straightforward:
- Compute the range to the geofence on the UAV’s current heading.
- Taking into account additional distance covered due to the transient dynamics of the vehicle (based on the current speed), if the distance of the vehicle or any of its turning circles from the fence is less than this modified turn radius, then instruct the vehicle to turn.
With reference to Figure 1, let and be the geodetic coordinates of two points on a spherical Earth with radius . The angle that is subtended by the two lines that extend from the origin through each point is . The orthodromic (i.e., great circle) arc distance between the two points is then
Given the irregularities in (nonspherical) Earth, more accurate values for the central angle, , can be determined with a number of formulas that balance computational processing with accuracy and generality. Additionally, a vector-based approach is far simpler and less convoluted than spherical trigonometry expressions, especially when having to deal with polar singularities. Let the n-vectors, defined as
for the two geodetic points be , , and the angle subtended by the two points is then
Here, × denotes the cross product and the Euclidean norm. The operator · denotes the dot product. The great circle plane that contains both and is then
or, in terms of the geodetic coordinates for point 1 and the azimuth from point 1 to point 2 (which is ),
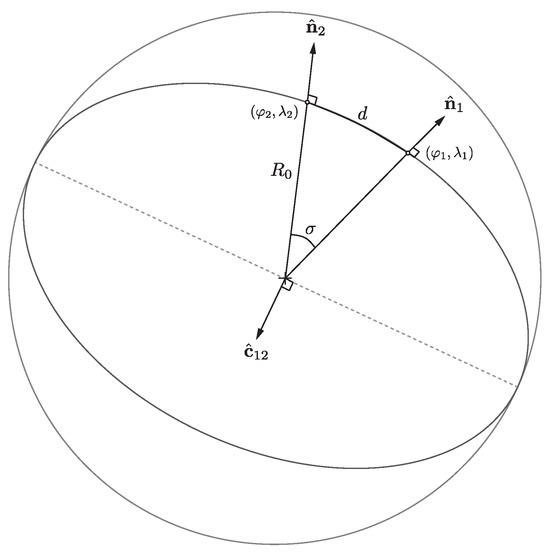
Figure 1.
N-vectors and great circle plane of two geodetic points on the surface of a sphere.
At small distances, geodesics may not be required, and simple planar geometry could be used. Solutions using calculations in a local tangent plane still give workable accuracies for geozones of kilometers in size. However, this is a fundamentally limiting issue for a general solution, so the algorithm is presented in spherical geometry. As mentioned before, the use of vector algebra can be more compact and concise. A solution given in spherical geometry is still prone to error at large distances due to the ellipsoidal nature of Earth, but the error is less than a flat plane approximation.
3. The ARC Algorithm for Flight within a Polygonal Geozone
Most uses of UAV geofencing are to keep the vehicle operating inside a specified geozone. While it is quite straightforward to determine the inclusion of a point within a circular geozone (namely if the distance of the point from the origin of the zone is less than or equal to the circular radius), it is more difficult to determine the range from an arbitrary point p and heading to the geofence compared with the polygonal case. In contrast, the polygonal case is more straightforward, and since it is more general, it is dealt with exclusively.
3.1. Determining the Range to the Geofence
Let p denote the current position of the vehicle, comprising the current geodetic location of the vehicle, , and having a heading, . Its n-vector is then . For all geoposts having known coordinates and, hence, known n-vectors, , the distance between any post and the vehicle, , can be obtained via (2). The forward azimuth to each post from the vehicle is
where and . is the n-vector for the datum—the northern pole: . The term is used to determine the direction of the angle with respect to the datum. However, since the inverse cosine function becomes ill-conditioned at small distances and for at 0 or , it is preferable to use the alternative formulation:
If , then the smaller the value of , the closer the bearing of the vehicle is to that post. indicates the vehicle is bearing directly towards post i, and computing the distance to the fence is trivial since both points are known. Provided that , for all i, then the fence edge that the vehicle is bearing to is deducible from when . If the geozone is convex, then there should only be one such edge detectable. Otherwise, multiple edges could satisfy this condition.
In order to determine the range of the vehicle to the geofence on its current heading the location of the two posts on either side of the current heading is required. Then, the intersection of the two great circle planes (one given by the position and heading of the vehicle, the other the plane containing both geoposts) will give the location of a point on the geofence the vehicle is heading towards. If defines the great circle containing the two geoposts, and , that straddle the vehicle’s heading, and defines the great circle containing the point where it intersects and the current position of the vehicle, p, then two possible antipodal intersection points exist: and . Which of these is the correct intersection for the geofence can be deduced by considering the angle between the heading and intersection n-vectors. With reference to Figure 2, if , then the heading vector, , points immediately towards . This amounts to . Conversely, (or ) indicates is pointing immediately towards . Therefore, the intersection vector can be written as
Then, the range to the geofence, , is the distance from to , solved with (2). For the case of a concave geozone, where multiple fence edge intersections exist, s is calculated for each intersecting point, i.e.,
and the smallest value determines the range to the nearest fence edge.
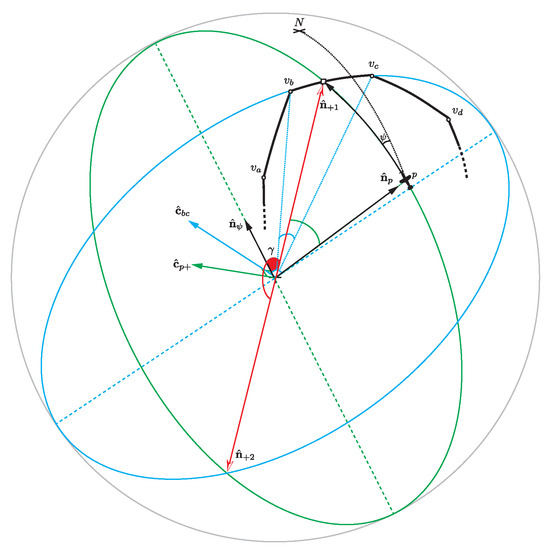
Figure 2.
Intersection of great circles defining the fence edge currently being approached, , and the intersection of the fence and vehicle trajectory, .
3.2. Calculating Minimum Turn Distance
Once is known, it can be compared with the minimum turn distance, . Figure 3 illustrates the computation of . Let and be the angle the vehicle is bearing towards the point (or ), relative to the geofence edge (i.e., is with respect to the edge segment (or ), while is the smallest magnitude of the two possible values with respect to ). If the vehicle is bearing perpendicularly towards the fence (i.e., deg), then is simply r, the minimum turn radius of the vehicle. For any other angle of , the minimum turn distance required can be reduced depending on the angle to which the vehicle is heading toward the geofence. Then, by assuming the resulting vertices of the spherical triangle can be treated as coplanar (a simplification not too erroneous since from this range to the fence the triangles are quite small),
The angle , and hence , can be obtained using (8) where, in this case, the datum plane is with intersecting plane and focal point . If , the vehicle must begin turning to avoid crossing the geofence. Since the turn radius is affected by the airspeed using its current value, V, provides the current minimum turn radius for the vehicle:
Here, is fixed at a value, limited by the characteristics of the vehicle, leaving r simply proportional to the square of the airspeed through the constant G.
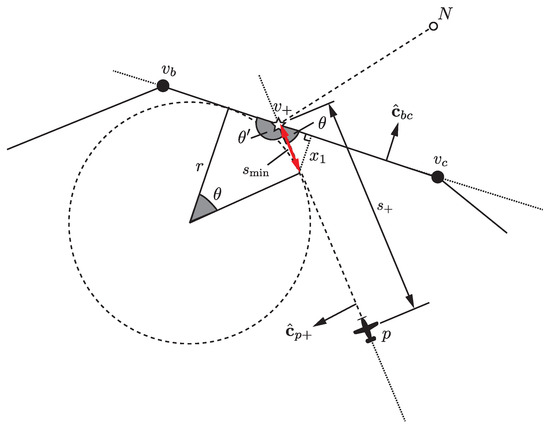
Figure 3.
Geometry for computing based on the minimum turn radius r and the approach angle .
In practice, (11) will not be sufficient to prevent the vehicle from crossing the geofence, as it fails to account for the initial dynamics of the vehicle on starting a turn. Therefore, the value of , taking into account the turn dynamics, is calculated via
with being an additional term to cover the distance required for the transient behavior on initiating a turn (i.e., the rise time delay). The transience will be dictated by the maneuverability of the specific vehicle and the heading flight controller and so must be tailored for each vehicle. Determining a suitable value for is discussed later in Section 4.3.
3.3. Determining the Direction of Turn
Ideally, the turn should be made away from the fence such that its heading rotates through the closest matching orientation of the fence: the port turn in Figure 3, for example. The turn is initiated by overriding manual control with an automatic heading controller. This heading could be set to match the orientation of the fence, but this tends to result in the vehicle ‘scraping’ the geofence and causing a small excursion. A more effective solution is to set a heading command that instructs a constant turn in the desired direction for as long as : , where k is a signed integer having the value or 1 to instruct the desire direction of turn (port or starboard, respectively). The value of k can be determined by considering the sign of : .
3.4. Acute Internal Angles
The approach so far is satisfactory when all of the internal angles of the geofence are reflex or obtuse. A problem arises when the angle between two fences is acute. In this scenario, as illustrated in Figure 4, such that the vehicle will be driven towards the vertex of the two fences at post b and eventually penetrate the fence. Furthermore, if the turn is initiated when , then the vehicle will be unable to complete a full turn, as the turning circle extends out of the geozone. In order to avoid this event, consideration of the two fences on either side of the one currently being approached is needed, along with the minimum turning circle. If the vehicle approaches an acute vertex, it must initiate a turn sufficiently soon enough to not lead to an excursion (turning circle in Figure 4).
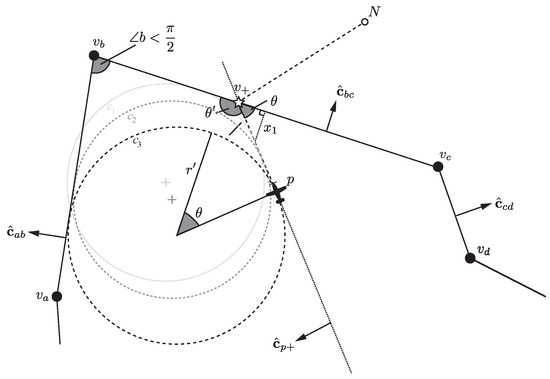
Figure 4.
Scenario involving an acute fence corner at .
The strategy to achieve this is to investigate the minimum turning circles on either side of the vehicle’s current position and heading. The centers of the port (left) and starboard (right) turning circles ( and , respectively) are determined by considering the radius of the circle, along with the extra ground distance required for the initial transient behavior. This radius is (turning circle in Figure 4). The n-vectors of the turning circle centers are then obtained through vector summation:
We then seek the perpendicular distances of these turning circle centers from the approaching geofence and, importantly, the two adjacent fences. If one turning circle extends past the fence, then the aircraft must be prevented from turning in that direction. If the second turning then circle reaches the fence while the first is still beyond the fence boundary, then the aircraft must be instructed to turn.
The approaching geofence sits on the great circle , so let the two adjacent fences be identified by the great circle planes and . The minimum (perpendicular) distance from a point to a great circle plane is
Depending on the orientation of the computed value is either positive or negative (indicating the hemisphere that is located in). Since this is not needed, the absolute value of the angle is taken. Equation (14) is evaluated for the three fences, for both turning circle centers. These distances are then compared to to determine which turning circles have penetrated the great circles corresponding to each fence. This is the first test (i) for determining the turning circle intersection.
Since these great circles extend beyond the actual length of each fence edge, the location of this penetration must be determined, as it is possible for the turning circle to overlap a great circle but still be inside the geozone. This is performed by examining the angle of the perpendicular distance from each fence edge (i.e., a great circle that intersects perpendicularly the great circle of the fence), , to the angles of the two posts comprising each fence ( and ). These angles are relative to the vehicle’s trajectory along , having their apex at the turning circle centers. If the angle of the great circle from the turning center to the fence is between the angles of both posts, then the turning circle center (and, hence, the vehicle) is adjacent to that fence. This is the second test (ii). The angles of the posts should be unwrapped to avoid computational wrapping errors.
If a turning circle center has a distance to a plane less than (test i), and if the fence posts straddle the turning circle center (test ii), then it may be concluded the turning circle has intersected that fence edge. Figure 5 illustrates computing , , and for (in this case the fence ) for the port (left) turning circle. Similar computations are also made for the other two fences. In this scenario, the starboard turning circle has already extended past the geofence, so , and it remains to determine if the port turning circle has reached the geofence. It can be seen that and that , so neither criteria is satisfied against the fence . , but , so the port turning circle has not penetrated the fence . However, and , so the turning circle has reached the fence , and so the vehicle is required to turn to a heading .
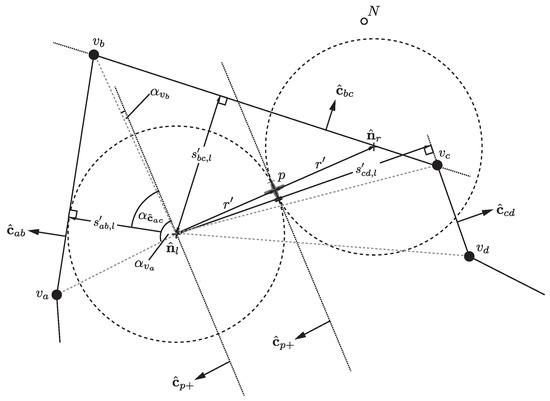
Figure 5.
Illustration of evaluating tests (i) and (ii) for (in this case the fence ) for the port (left) turning circle.
It is possible that condition (ii) not be satisfied despite the turning circle clearly intersecting with the fence (Figure 6). In this example, condition (i) is satisfied for both fences but not condition (ii). The fact that condition (i) is satisfied for two connected fences is indication enough that the turning circle intersects the fence. A further test can be used to account for such cases, (iii), checking the distance from each turning circle center to each post, i.e., evaluating to see if
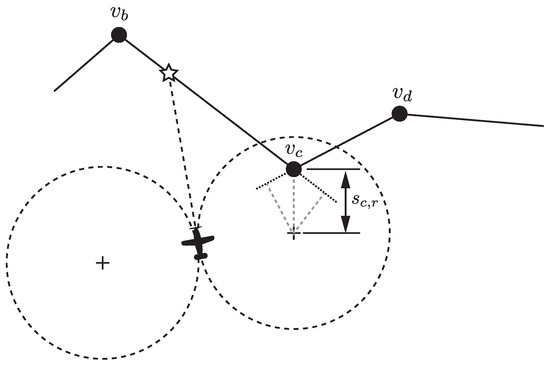
Figure 6.
Illustration of evaluation test (iii).
The final criterion is then (i) and (ii) or (iii) for any j. This criterion needs to be assessed and satisfied for each fence and for each turning circle to establish whether that turning circle has left the geozone. If the criteria are satisfied for any one fence, then the turning circle is considered to have penetrated the geofence. When the first turning circle has achieved this, k (the parameter used to indicate the direction of the turn) can be set and held, ensuring any new heading commands given to the vehicle turn it about the opposite turning circle. This approach to determining k replaces the previous one. If the same turning circle no longer satisfies the two criteria, then k can be set to zero. If, while , the criteria for the other turning circle is met, then the vehicle heading is set to turn the vehicle. As before, a simple way to ensure the vehicle turns to a sufficient amount to avoid the geofence is to set a heading command of (i.e., always turn an additional 90 degrees to the current heading), where the sign of k will ensure the turn is in the correct direction to avoid the vehicle crossing the geofence.
In the case illustrated in Figure 5, the distance to the approaching fence , despite the fact the turn should be initiated to avoid an excursion. Hence, both approaches in Section 3.2 and Section 3.4 should be evaluated. If approaching the geofence with sufficient clearance on either side, the criterion on the last turning circle inside the geozone amounts to a similar criterion as . The main difference is that the transient turn dynamics is now incorporated into the turning radius ( is used instead of r), whereas in the approach in Section 3.2, the transient turn dynamics are incorporated in the computation of . Of course, if the geofence corners are closely packed together and are particularly acute, an excursion may be unavoidable due to the maneuvering limitations of the vehicle. A judicious design of the geozone would therefore be sensible to avoid problematic corners.
3.5. Manual Control
The heading autopilot remains active until the current value of exceeds the current value of and at least one turning circle is located inside the geozone. As it is potentially dangerous to return manual control to a pilot without warning, an intermediary flight controller retains control of the vehicle (in straight and level flight) until the system is instructed by the pilot to hand control back. During this time, the ARC is still functional and runs the same as in manual mode. It will only allow manual control to be handed back when or and and for at least one turning circle for all j fences and posts around the intersection point.
3.6. Excursions
Provided the turn dynamics have been accounted for, the vehicle should not penetrate the geofence at any point when the ARC is active. In the event that it does, a sensible action is to set the heading command to be the base coordinates, as per a normal RTB algorithm. The aircraft will then navigate towards the designated point inside the geozone until it re-enters. For convex geozones, this will suffice, since the base is typically located in the central region of the geozone and the heading towards that point will result in a turn away from the geofence. However, this can be problematic in concave geozones, as illustrated in Figure 7. Turning and flying towards the base coordinate would result in an extended excursion. Some consideration of the local shape of the geozone therefore needs to be incorporated. This is performed by creating a local base coordinate, or anchor point, to orientate the vehicle to instead of the main base coordinates.
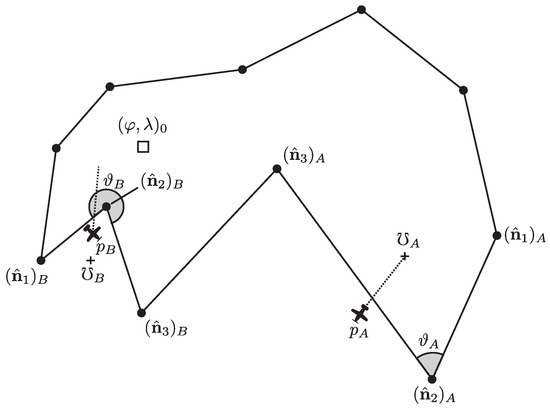
Figure 7.
Illustration of computing the anchor point ℧.
Consider the scenario in Figure 7, where the vehicle at has left the geozone. The closest post is given by the n-vector, , determined by the smallest value of . The posts on either side of this are given by and , and the three vertices form a spherical triangle. A point inside this triangle will serve as a useful point to orient that vehicle towards in the event of crossing the fence. The lengths of all three sides are known, so the centroid is easily computed:
The geodetic coordinates of this point, if required, are
The heading angle to the anchor point, , can then computed using (8)
It is worth noting that this approach has no penalty when approaching obtuse or acute fence corners and will work in most cases. This will result in the vehicle returning to the geozone more quickly than if it were to fly towards the base location, denoted by □ in Figure 7. However, it can be seen that this approach will not work when the internal angle, , is reflexive, such as in the case of example B in Figure 7. The closest post to the vehicle is , which has a reflex internal angle . As a result, the spherical triangle formed from the three nearest posts and, hence, the anchor point is outside the geozone. This can be easily solved by rotating by 180 degrees for such cases (the resulting trajectory is shown by the dotted line in Figure 7).
The vehicle’s inclusion in the geozone can be determined with any of the PIP techniques discussed in Section 2.2. However, since the forward azimuth angles from p to all v are calculated in order to determine the intersecting fence edge, the same data can be used to obtain the winding number through the angle summation method. Hence,
and the condition for activating the RETURN algorithm is . Computational inaccuracies for small distances between p and v may mean the computed value of w should be rounded to ensure logical operators work as intended. The ARC algorithm described above is succinctly given in Algorithms 2–6.
| Algorithm 2 Anticipatory range controller |
| Require: g: Gravitational acceleration
Require: R: Radius of Earth. ▹ or, more generally, R Require: C: Database of n geopost positions for . Require: : N-vector for datum (North). ▹ Require: : User-specified base coordinates. Require: : Maximum bank angle. Require: : Transient effect on turn distance. Require: : Current geodetic coordinates. Require: : Current heading. Require: V: Current speed. ▹ Ideally ground speed Output: |
| Algorithm 3 FENCE: Determine fence intersection |
| Algorithm 4 INTERSECT: Determine intersection of turning circles |
|
| Algorithm 5 TURN: Test the turn criteria |
|
| Algorithm 6 RETURN: Set the anchor point for return |
4. Simulation
The ARC algorithm discussed in the previous sections is demonstrated in a simulated environment written in MATLAB/Simulink. Figure 8 outlines the structure of the simulation model. The vehicle model is generated from aerodynamic stability and control derivatives that compute the aerodynamic forces and moments acting on the vehicle. A propulsion subsystem models a combustion engine with a propeller. Inputs to these are the control surface deflections and throttle inputs. The forces and moments from both the aerodynamic and propulsion models are combined to determine the forces and moments acting about the c.g., which is used to solve the equations of motion. The motion states are used to further influence the aerodynamics, propulsion, and atmospheric model (for air density). Motion states are fed into the flight controller for the flight control system (FCS) as well as the ARC. For these specific simulations, a fixed-step Runge–Kutta integration solver is used with a time-step of 0.01 s.
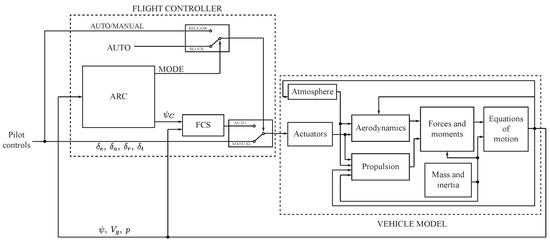
Figure 8.
Diagram of the simulation model.
The output from the vehicle model provides the three state variables necessary for the ARC algorithm: the vehicle heading , the ground speed , and the current geodetic position, p. The ARC algorithm outputs the control mode flag (BLOCK or RELEASE) and the heading command . When the mode flag is set to AUTO, the manual commands are bypassed and a flight control algorithm (comprising Proportional–Integral–Derivative (PID) controllers in this simulation) in the FCS provides control surface deflections for the vehicle. In AUTO mode, the pilot is unable to disengage this control loop. When the mode flag is set to RELEASE, the PID controllers are still in control of the vehicle but the pilot is able to disengage them and regain manual control. Although the heading command in RELEASE mode is set to the same as the current heading, the other controllers in the FCS ensure the vehicle wings remain level and at a steady pitch angle in the hold state.
4.1. Vehicle Model
The vehicle model represents a small, 4 kg remotely operated vehicle with a high wing trainer-like configuration and conventional control surfaces. The model was developed to represent a modified off-the-shelf radio-controlled scale model aircraft of the type shown in Figure 9. A set of nonlinear, decoupled six-degrees-of-freedom rigid-body equations of motion was then derived from the vehicle’s geometric, inertial, and performance data [48]. An explanation for the symbols used in the following equations is given in Table 1.

Figure 9.
Scale model aircraft of a Piper Cub J-3.

Table 1.
Nomenclature of symbols used in the aircraft simulation.
The propulsion system is modeled after a four-stroke internal combustion engine, implemented as a database containing the engine power as functions of throttle setting and engine speed for a single-piston internal combustion engine. The power produced by the engine is used to calculate the engine torque that drives a fixed-pitch propeller in producing the thrust.
The combined aerodynamic and propulsive forces and moments are used in the solution of the equations of motion in the typical way to obtain the acceleration, speed, and position of the body center. In order to avoid the singularities at the poles, it is necessary to formulate these equations with respect to the Earth-Centered, Earth-Fixed (ECEF) coordinate system:
In (18), is the vector of orthogonal velocities at the body center, along each of the three body axes, and are the three angular velocities about these axes. The aircraft’s mass is represented by m, is its inertia tensor, and is the aircraft’s position in the ECEF coordinates. The angular rate of the earth is given by , where rad/s. The matrix is the rotation matrix from the ECEF axes to the body axes, defined by the vehicle’s orientation in quaternion form.
4.2. Geodetic Position
After solving for from (18), the ECEF location is given by
The geodetic latitude, , is then calculated using Bowring’s method [49], which involves iterative solutions (though in practice very few are needed to obtain a sufficiently high accuracy) to the following equations:
where
Here, is the equatorial radius, and f is Earth’s flattening (). The geodetic longitude is given by
To complete the geodetic triad, the altitude of the vehicle is
where is the vertical prime radius of curvature.
4.3. Vehicle Turn Dynamics
For this particular aircraft, when control of the vehicle is removed from the pilot, PID (Proportional–Integral–Derivative) controllers control the altitude, airspeed, and heading of the vehicle through control of the throttle, elevator , and ailerons , respectively. A sideslip regulator uses the rudder, , to eliminate sideslip during turns. In the case of the heading control, an inner loop roll controller is fed commands from the outer loop heading controller. Actuator limits are imposed, and antiwindup algorithms are subsequently used on the integrator feedback tracks, though the actuators did not reach their limits in the simulations.
The dynamics of the vehicle and flight controller during a turn are shown in Figure 10. The roll response is reasonably modeled with a first-order response with a time constant, , of 0.8 s (the dashed trace in the top subplot). The time to reach 99% of the maximum bank angle is then
Given the airspeed V, let in (12) equal . In effect, after seconds, the vehicle reaches (extremely close to) the maximum bank angle and is able to complete the turn with radius r. Clearly, (23) gives a trivial solution for (), so a value sufficiently close to (i.e., 99%) needs to be chosen.
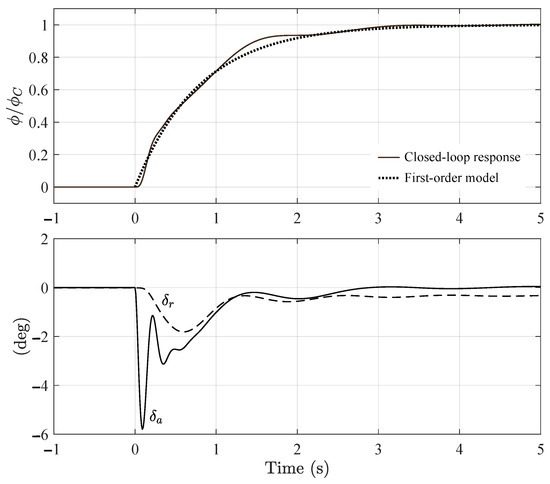
Figure 10.
Turn dynamics of the vehicle following a step input in roll command, , with aileron, , and rudder, , inputs.
4.4. Simulation Results
By way of example, a polygonal geofence is established with seven geoposts surrounding the northern pole, as shown in Figure 11. If is a geodetic coordinate triad, then the vehicle’s start position is . The base location for the vehicle to turn towards following activation of the flight controller is . The vehicle’s starting airspeed, altitude, and heading are set at 12 m/s (23 knots), 100 m (328 ft), and 90, respectively.
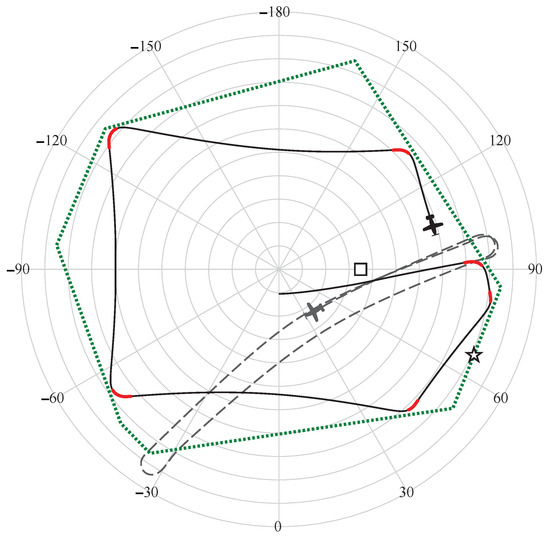
Figure 11.
Simulated constraint inside a geozone (denoted by the outer dotted line) with ARC, centered on the northern pole. □ indicates the location of ‘home’. The star indicates the current flight path intercept with the geofence for the ARC algorithm. Parts of the trace in red indicate where the ARC had control.
The behavior of the vehicle in a simulation around the northern pole is shown in Figure 11. The dashed black trace shows a conventional RTB algorithm acting only when the vehicle leaves the geozone. The solid black trace shows the vehicle’s trajectory for s, where the parts in red indicate where the ARC has control over the aircraft’s flight. The star shows the location on the geofence the vehicle is currently bearing to (only shown for the simulation with ARC), while □ indicates the location of ‘home’. The center of the plot is the northern pole, and the concentric circles represent decrements in latitude of . The angles of longitude are shown on the outer latitude ring. Simulation time is 320 s.
Upon starting the simulation, the vehicle is instructed to maintain straight-wing-level flight, leading to it approaching the geofence approximately near the 90-longitude line. The ARC takes control of the vehicle and instructs it to turn to starboard, resulting in it flying slightly inwards away from the fence. The hold controller maintains control of the vehicle in straight-wing-level flight until it approaches the portion of the fence directly below. The ARC then instructs the vehicle to perform another turn to keep the vehicle inside the geozone. This behavior is maintained indefinitely, with the pilot able to retake control only when the hold controller is active (the solid black parts of the trace). This behavior contrasts with the response from a simple RTB algorithm (indicated by the dashed trace), which shows the vehicle passing the geofence before it is returned by following a heading towards the base, located with the □ symbol. Implementing the ARC ensures the vehicle does not leave the geozone.
The algorithm is further demonstrated in the other problematic area: over the antimeridian (see Figure 12). In this case, a more constrictive geofence is used, though the algorithm is still capable of ensuring the vehicle does not exceed the fence boundary. Figure 12 also shows the effect different values of will have on the ability of the algorithm to maintain the vehicle inside the geozone. Using a lower value below the minimum value computed in (23) results in the vehicle deviating from the geozone. However, since the turn was initiated before the vehicle left, the deviation is much less compared with a wholly reactive RTB approach. The deviations can be eliminated by increasing the value of and, hence, in (12), effectively increasing the responsiveness of the ARC to the approaching fence. In (23), s corresponds with , and in (23), s corresponds with , whereas s corresponds with . Increasing (through increasing ) provides more secure flight around the fence, creating a larger buffer zone around the zone edge. The disadvantage to the pilot is a reduced working field for which manual flight is allowed. Increasing progressively creates a larger buffer between the second-stage trajectory and the geofence and, hence, is a convenient way of adding robustness to the system.
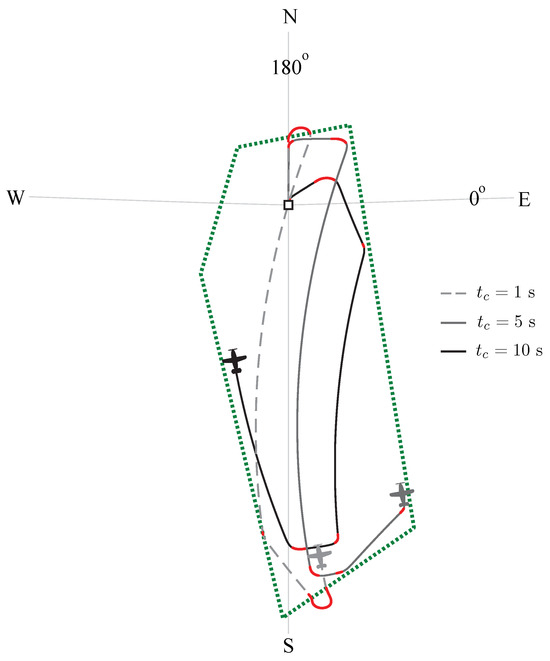
Figure 12.
Simulated constraint inside a geozone with ARC over the antimeridian on the equator. □ indicates the location of ‘home’. Parts of the trace in red indicate where the ARC had control.
Figure 13 illustrates the requirement of assessing the turning circle criterion to ensure the vehicle remains inside the geozone if dealing with fences that have acute internal angles, as well as the effectiveness of using the anchor points instead of the home point when dealing with excursions. The dashed gray trace shows the ARC algorithm without consideration of test condition (ii), leading to the vehicle being driven down into the bottom right geozone vertex. As a result. it leaves the geozone and follows a heading toward the home location (denoted by the symbol □). This results in a considerable time outside the geozone before it re-enters at the other end of the geozone. Alternatively, the solid gray trace shows the behavior of the vehicle using the local anchor point as the target coordinates during an excursion. The vehicle is seen to quickly turn back towards the centroid of the bottom triangle of the geozone and re-enter the geozone sooner. Lastly, the solid black trace indicates the desired performance by considering the inclusion of the turning circles within the geozone (test condition ii). As a result, the vehicle turns before it reaches the bottom fence vertex and subsequently remains inside the geozone at all times. As with Figure 11 and Figure 12, the parts highlighted in red indicate when the ARC has control over the vehicles’ trajectory.
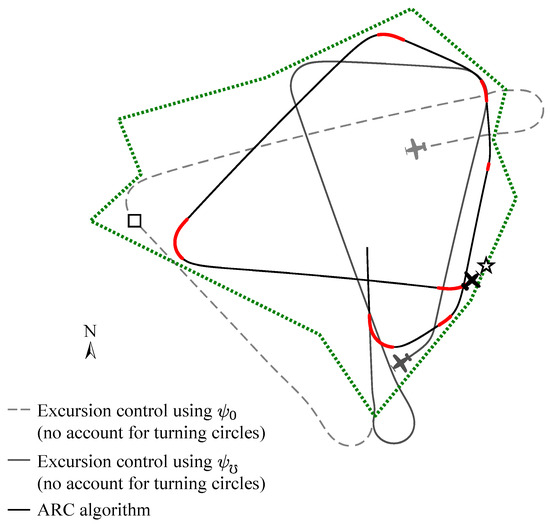
Figure 13.
Simulation illustrating the effect of using either the home coordinate (dashed gray trace) or the local anchor point (solid gray trace) to deal with excursions. □ indicates the location of ‘home’. Parts of the trace in red indicate where the ARC had control.
5. Remarks
5.1. Algorithm Complexity
It was previously mentioned that, for geozones of reasonably small size, it is sufficient to approximate the distances between points on the surface of the earth as those projected onto a flat plane. This greatly simplifies the algebra, as the geodetic coordinates can be mapped to linear distances and simpler planar geometry can be used to assess the criterion for initiating the turns. The ARC algorithm can be readily implemented in planar geometry. However, the accuracy of certain mapping algorithms differs at different latitudes, so the most appropriate one for the operating location would need to be chosen to ensure reasonably accurate estimates. The use of geodesics, along with vector algebra, provides a general and more concise implementation at any coordinates on (the spherical model of) Earth. The downside is the larger computational cost, mainly from the dot product operations. However, the implementation is still fast enough for real-time operation. Further improved range accuracy, and completely generalizing the current implementation, would need to take into account the local radius of Earth rather than the average spherical Earth radius used. However, this is largely an issue at latitudes near the Equator. Such further accuracy is not needed for most geofencing applications, though the same argument could be made for using geodesics instead of planar approximations in the first place.
The use of the tuning parameter effectively controls the size of the soft geozone—the allowable area for manual control before the ARC takes control from the pilot. The concept of a soft geozone, or safety zone, is common in the literature, e.g., [15,16,17,18,19]. The algorithm in this paper provides the handling of arbitrary geozone shapes (including concave zones with acute angles) and also a scalable soft geozone based on the aircraft’s current flight behavior to maximize the flight region of manual control. Algorithmically, the various test conditions make the ARC algorithm complex. It has a cyclomatic complexity [50] of 37, which is towards the higher side of a complex structured code (≤10 being simple, 20 to 50 being highly complex, and >50 generally being considered untestable). A breakdown of the complexity for each of the subalgorithms is shown in Table 2. Testing for the turning circle intersections and dealing with potential acute angles (contained in Algorithm 4: INTERSECT) is shown to introduce a substantial amount of complexity. The turn test criteria used here are similar in concept and function to those developed in [18] and achieve the same performance when dealing with acute geofence corners. The algorithm used here achieves this without the need for the preliminary creation of defined safety areas. However, there are benefits to that approach in terms of checking the validity of the proposed geozone.

Table 2.
Cyclomatic complexities. The arrows indicate sub-algorithms of the whole ARC algorithm.
The algorithm in this paper does not incorporate altitude fencing, but the problem is somewhat easier to deal with. Multiple altitude limits could be dealt with via look-up tables based on the current geodetic coordinates of the vehicle. The same anticipatory range approach can be used by comparing the current altitude of the vehicle with the altitude of the fence. The current climb rate and pitch response dynamics may also be used to provide anticipation control for the approach to the altitude limit.
5.2. Uncertainty Handling
The presence of wind and turbulence would be expected to deteriorate the performance of the algorithm, but two aspects would support limiting this effect. First, by using the ground speed rather than the airspeed in computing the anticipatory range and turning circle radii, the turn should be initiated depending on any variations in atmospheric wind. Secondly, the timing parameter can also be increased to improve the buffer zone around the geofence. This would amount to effectively altering the size of the soft geozone to account for the uncertainty in the atmospheric conditions. This amounts to adding an additional safety, or ‘slack’ parameter, as used in [19] to define the boundaries of the soft geozone. However, a sideslip of considerable speed would still potentially push the vehicle outside of the geozone. Additional modeling of the dynamics of the aircraft would be needed to eliminate this, which could be achieved with additional measurements of wind speeds and the use of more predictive control (e.g., [51,52]) to achieve robust management of more extreme approaches to the geofence.
5.3. Enhancements
The ARC algorithm could also be modified to work as no-fly zones (i.e., keeping the vehicle outside a geozone), which could be made dynamic by updating the geopost coordinates (see, for example, [53,54]). In this way, the algorithm could provide real-time obstacle avoidance of moving objects. Examples of where such online updates of geofencing would be useful are in effective traffic rerouting following abnormally busy traffic or emergency flights.
5.4. Experimental Validation
This paper demonstrated the viability of the algorithm in a comprehensive software simulation environment. It remains to demonstrate the operation of this system with hardware in either a hardware-in-the-loop scenario and/or an actual fight test. The complexity analysis of the code showed it to be reasonably traceable, and the calculations are not onerously complex to expect the algorithm to be easily run on modern embedded platforms. Integration with open-source flight control and management software, such as ArduPilot [55] and Mission Planner [56], is a sensible progression for this work.
6. Conclusions
This paper detailed and demonstrated the concept of an anticipatory range controller (ARC) for implementing geofencing, primarily for fixed-wing aircraft. Due to the flight behavior of such craft compared with multicopter UAVs, there is a greater need to compensate for the reduced mobility and speed of these aircraft to avoid them penetrating a geofence. Furthermore, techniques to deal with the concave and internal acute angles on the geofence were presented and demonstrated. Simulations showed the improved range management of this system compared with a standard return to a base geofencing system, as well as compared with using a locally calculated anchor point to determine a re-entry trajectory following an excursion. By using a tuning parameter, , linked to the rise-time performance of the vehicle’s roll command tracking, the ‘hard’ geofence can be maintained based on the dynamic characteristics of the specific vehicle. The tuning parameter also allows for variation in the buffer zone around the geofence where the ARC overrides manual (or normal) control to improve the robustness of the hard border to deal with vehicle performance uncertainty or atmospheric turbulence.
Author Contributions
Conceptualization, P.R.T. and P.S.; methodology, P.R.T.; software, P.R.T.; formal analysis, P.R.T.; investigation, P.R.T.; data curation, P.R.T.; writing—original draft preparation, P.R.T.; writing—review and editing, P.S.; visualization, P.R.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
The following symbols are used in this manuscript:
| C | Geozone |
| Vector for a plane | |
| g | Acceleration due to gravity |
| h | Altitude |
| Inertia tensor | |
| L | Rolling moment |
| M | Pitching moment |
| m | Mass |
| N | Yawing moment |
| n-vector | |
| n-vector for the intersection point on the geofence | |
| Position vector in ECEF reference frame | |
| p | Position |
| Transformation matrix for angular velocities from ECEF to body axes | |
| Average radius of the Earth | |
| Vertical prime radius curvature of Earth | |
| r | Turn radius |
| s | Distance |
| Minimum distance required to complete a turn | |
| Distance covered to start the turn (i.e., rise-time delay) | |
| Distance to the intersection point with the geofence | |
| t | Time |
| Rise time of the transient roll response | |
| Velocity vector | |
| V | Velocity |
| v | Geopost location |
| w | Winding number |
| X | Axial force |
| Y | Side (or lateral) force |
| Z | Normal force |
| Geometry reference angles | |
| Aileron deflection | |
| Elevator deflection | |
| Rudder deflection | |
| Longitude | |
| Geometric angle | |
| Roll angle | |
| Maximum (commanded) bank angle during a turn | |
| Geodetic latitude | |
| Heading | |
| Heading command | |
| Time constant | |
| Subtended central angle | |
| ℧ | Excursion anchor point |
| Angular velocity vector | |
| AAM | Advanced air mobility |
| ARC | Anticipatory range controller |
| ECEF | Earth-Centered, Earth-Fixed |
| GPS | Global positioning system |
| PID | Proportional-Intergal-Derivative (control) |
| RPV | Remotely piloted vehicle |
| RTB | Return to base |
| UAV | Unmanned air vehicle |
References
- Reclus, F.; Drouard, K. Geofencing for fleet & Freight Management. In Proceedings of the 9th International Conference on Intelligent Transport Systems Telecommunications (ITST), Lille, France, 20–22 October 2009; pp. 353–356. [Google Scholar]
- Stevens, M.N.; Coloe, B.T.; Atkins, E.M. Platform-Independent Geofencing for Low Altitude UAS Operations. In Proceedings of the 15th AIAA Aviation Technology, Integration, and Operations Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Hayhurst, K.J.; Maddalon, J.M.; Neogi, N.A.; Verstynen, H.A. A Case Study for Assured Containment. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 260–269. [Google Scholar]
- Liu, Y.; Lv, R.; Guan, X.; Zeng, J. Path Planning for Unmanned Aerial Vehicle under Geo-Fencing and Minimum Safe Separation Constraints. In Proceedings of the 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016. [Google Scholar]
- Hosseinzadeh, M. UAV geofencing: Navigation of UVAs in constrained environments. In Unmanned Aerial Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 567–594. [Google Scholar]
- Lee, H.I.; Shin, H.S.; Tsourdos, A. A Probabilistic–Geometric Approach for UAV Detection and Avoidance Systems. Sensors 2022, 22, 9230. [Google Scholar] [CrossRef] [PubMed]
- Gurriet, T.; Ciarletta, L. Towards a generic and modular geofencing strategy for civilian UAVs. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 540–549. [Google Scholar]
- Alarcón, V.; Garcia, M.; Alarcón, F.; Viguria, A.; Martinez, A.; Janisch, D.; Acevedo, J.J.; Maza, I.; Ollero, A. Procedures for the Integration of Drones into the Airspace Based on U-Space Services. Aerospace 2020, 7, 128. [Google Scholar] [CrossRef]
- Nagrare, S.R.; Tony, L.A.; Ratnoo, A.; Ghose, D. Multi-Lane UAV Traffic Management with Path and Intersection Planning. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Kedarisetty, S.; Ratnoo, A. Cooperative Loiter Lane Diversion Guidance Planning for Fixed-Wing UAV Corridors. In Proceedings of the AIAA Scitech 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Altun, A.T.; Xu, Y.; Inalhan, G.; Hardt, M.W. Comprehensive Risk Assessment and Utilization for Contingency Management of Future AAM System. In Proceedings of the AIAA Aviation Forum, San Diego, CA, USA, 12–16 June 2023. [Google Scholar]
- Zhang, N.; Liu, H.; Low, K.H. UAV Collision Risk Assessment in Terminal Restricted Area by Heatmap Representation. In Proceedings of the AIAA Scitech 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Janson, V.; Ahlbrecht, A.; Durak, U. Architectural Challenges in Developing an AI-based Collision Avoidance System. In Proceedings of the EEE/AIAA 42nd Digital Avionics Systems Conference (DASC), Barcelona, Spain, 1–5 October 2023. [Google Scholar]
- Grüter, B.; Seiferth, D.; Bittner, M.; Holzapfel, F. Emergency Flight Planning using Voronoi Diagrams. In Proceedings of the AIAA SciTech Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Stevens, M.N.; Atkins, E.M. Layered Geofences in Complex Airspace Environments. In Proceedings of the AIAA Aviation Forum, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Zhang, S.; Wei, D.; Huynh, M.Q.; Quek, J.X.; Ma, X.; Xie, L. Model Predictive Control Based Dynamic Geofence System for Unmanned Aerial Vehicles. In Proceedings of the AIAA Information Systems-AIAA Infotech @ Aerospace, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Cavanini, L.; Ferracuti, F.; Ippoliti, G.; Orlando, G. Model Predictive Control for UAV Geofencing. In Proceedings of the 9th International Conference on Control, Decision and Information Technologies, Rome, Italy, 3–6 July 2023. [Google Scholar]
- Seiferth, D.; Gruter, B.; Heller, M.; Holzapfel, F. Fully-Automatic Geofencing Module for Unmanned Air Systems In Two Dimensional Space. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Theile, M.; Yu, S.; Dankster, O.D.; Caccamo, M. Trajectory estimation for geo-fencing applications on small-size fixed-wing UAVs. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019. [Google Scholar]
- Stevens, M.N.; Atkins, E.M. Multi-Mode Guidance for an Independent Multicopter Geofencing System. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 12–16 July 2016. [Google Scholar]
- Dill, E.T.; Young, S.D.; Hayhurst, K.J. SAFEGUARD: An assured safety net technology for UAS. In Proceedings of the 2016 IEEE/AIAA 35th Digital Avionics Systems Conference (DASC), Sacramento, CA, USA, 25–29 September 2016. [Google Scholar]
- D’Souza, S.; Ishihara, A.; Nikaido, B. Feasibility of Varying Geo-Fence around an Unmanned Aircraft Operation based on Vehicle Performance and Wind. In Proceedings of the 2016 IEEE/AIAA 35th Digital Avionics Systems Conference (DASC), Sacramento, CA, USA, 25–29 September 2016. [Google Scholar]
- Stevens, M.N.; Atkins, E.M. Generating Airspace Geofence Boundary Layers in Wind. J. Aerosp. Inf. Syst. 2019, 17, 113–124. [Google Scholar] [CrossRef]
- Seiferth, D.; Holzapfel, F.; Heller, M. Evasive Maneuvers of Optionally Piloted Air Vehicles For Three-Dimensional Geofencing. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Ghaffari, A. Analytical Design and Experimental Verification of Geofencing Control for Aerial Applications. IEEE/ASME Trans. Mechatron. 2021, 26, 1106–1117. [Google Scholar] [CrossRef]
- Vagal, V.; Markantonakis, K.; Shepherd, C. A New Approach to Complex Dynamic Geofencing for Unmanned Aerial Vehicles. In Proceedings of the IEEE/AIAA 40th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 3–7 October 2021; pp. 1–7. [Google Scholar]
- Kim, J.; Mathur, A.; Liberko, N.; Atkins, E. Operational Volumization and Inverse Volumization for Low-Altitude Airspace Geofencing. In Proceedings of the AIAA Aviation Forum, Virtual Event, 2–6 August 2021. [Google Scholar]
- Kim, J.; Atkins, E. Airspace Geofencing and Flight Planning for Low-Altitude, Urban, Small Unmanned Aircraft Systems. Appl. Sci. 2022, 12, 576. [Google Scholar] [CrossRef]
- Bhise, A.A.; Garg, S.; Ratnoo, A.; Ghose, D. Signed Distance Function based Geofencing for UAV Corridors. In Proceedings of the AIAA Scitech Forum, Virtual, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Nagrare, S.R.; Ratnoo, A.; Ghose, D. Multi-intersection planning with durational speed scheduling for drone corridors. In Proceedings of the AIAA Scitech 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar]
- Haines, E. Point in Polygon Strategies. In Graphics Gems IV; Heckbert, P.S., Ed.; Academic Press: Cambridge, MA, USA, 1994; pp. 24–46. [Google Scholar]
- Shimrat, M. Algorithm 112: Position of point relative to polygon. Commun. ACM 1962, 5, 434. [Google Scholar] [CrossRef]
- Hacker, R. Certification of Algorithm 112: Position of point relative to polygon. Commun. ACM 1962, 5, 606. [Google Scholar] [CrossRef]
- Hormann, K.; Agathos, A. The point in polygon problem for arbitrary polygons. Comput. Geom. 2001, 20, 131–144. [Google Scholar] [CrossRef]
- Alciatore, D.G.; Miranda, R. A Winding Number and Point-In-Polygon Algorithm; Colorado State University: Fort Collins, CO, USA, 1995. [Google Scholar]
- Sutherland, I.E.; Sproull, R.F.; Schumacker, R.A. A Characterization of Ten Hidden-Surface Algorithms. ACM Comput. Surv. 1974, 6, 1–55. [Google Scholar] [CrossRef]
- Gatilov, S. Efficient Angle Summation Algorithm for Point Inclusion Test and Its Robustness. Reliab. Comput. 2013, 19, 1–25. [Google Scholar]
- Badouel, D. An Efficient Ray-Polygon Intersection. In Graphics Gems; Glassner, A.S., Ed.; Academic Press: Cambridge, MA, USA, 1990; pp. 390–393. [Google Scholar]
- Fieto, F.R.; Torres, J.C. Inclusion Test for General Polyhedra. Comput. Graph. 1997, 21, 23–30. [Google Scholar] [CrossRef]
- Moeller, T.; Trumbore, B. Fast, minimum storage ray triangle intersection. J. Graph. Tools 1997, 2, 21–28. [Google Scholar] [CrossRef]
- Dobkin, D.; Guibas, L.; Hershberger, J.; Snoeyink, J. An efficient algorithm for finding the CSG representation of a simple polygon. In Proceedings of the 15th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 1–5 August 1988; Dill, J., Ed.; ACM Press: New York, NY, USA, 1988; Volume 22, pp. 31–40. [Google Scholar]
- Walker, R.J.; Snoeyink, J. Practical point-in-polygon tests using CSG representations of polygons. In Proceedings of the Algorithm Engineering and Experimentation Meeting, Baltimore, MD, USA, 15–16 January 1999; Goodrich, M.T., McGeoch, C.C., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1619, pp. 114–128. [Google Scholar]
- Preparata, F.P.; Shamos, M.I. Computational Geometry: An Introduction; Springer: New Your, NY, USA, 1985; pp. 41–67. [Google Scholar]
- Bentley, J.L. Algorithms for Reporting and Counting Geometric Intersections. IEEE Trans. Comput. 1979, C-28, 643–647. [Google Scholar] [CrossRef]
- Prasad, M. Intersection of line segments. In Graphics Gems II; Arvo, J., Ed.; Academic Press: Cambridge, MA, USA, 1991; pp. 7–9. [Google Scholar]
- Antonio, F. Faster Line Segment Intersection. In Graphics Gems III; Kirk, D., Ed.; Academic Press: Cambridge, MA, USA, 1991; pp. 199–202. [Google Scholar]
- Pratyusha, P.L.; Naidu, V.P.S. Geo-Fencing for Unmanned Aerial Vehicle. In Proceedings of the National Conference “Electronics, Signals, Communication and Optimization” (NCESCO), Mysuru, Karnataka, 9 September 2015; pp. 1–7. [Google Scholar]
- Thomas, P.R.; Richardson, T.S.; Cooke, A.K. Estimation of Stability and Control Derivatives for a Piper Cub J-3 Remotely Piloted Vehicle. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Minneapolis, MN, USA, 13–16 August 2012; pp. 1–26. [Google Scholar]
- Bowring, B.R. Transformation from spatial to geographical coordinates. Surv. Rev. 1976, 23, 323–327. [Google Scholar] [CrossRef]
- Watson, A.H.; McCabe, T.J. Structured Testing: A Testing Methodology Using the Cyclomatic Complexity Metric; NIST Special Publication 500-235; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1996.
- Gros, S.; Quirynen, R.; Diehl, M. Aircraft control based on fast non-linear MPC & multiple-shooting. In Proceedings of the 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012. [Google Scholar]
- Stastny, T.; Dash, A.; Siegwart, R. Nonlinear MPC for Fixed-wing UAV Trajectory Tracking: Implementation and Flight Experiments. In Proceedings of the AIAA Scitech Forum, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Zhu, G.; Wei, P. Low-Altitude UAS Traffic Coordination with Dynamic Geofencing. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washinton, DC, USA, 13–17 June 2016. [Google Scholar]
- Kuenz, A.; Lieb, J.; Rudolph, M.; Volkert, A.; Geister, D.; Ammann, N.; Zhukov, D.; Feurich, P.; Gonschorek, J.; Gessner, M.; et al. Live Trials of Dynamic Geo-Fencing for the Tactical Avoidance of Hazard Areas. IEEE Aerosp. Electron. Syst. Mag. 2023, 38, 60–71. [Google Scholar] [CrossRef]
- Ardupilot Project. Available online: https://ardupilot.org (accessed on 1 June 2023).
- Oborne, M. Mission Planner, v1.3.81. Available online: https://ardupilot.org/planner/ (accessed on 1 June 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).