Abstract
Starting from the current need for the safety of energy systems, in which power transformers play a key role, the study of the health of power transformers in service is a difficult and complex task, since the assessment consists of identifying indicators that can provide accurate data on the extent of degradation of transformer components and subcomponents, in order to establish a model for predicting the remaining life of transformers. Therefore, this paper proposes a model for assessing the remaining service life by diagnosing the condition of the transformer based on the health index (HI) obtained from a multi-parameter analysis. To determine the condition of power transformers, a number of methods are presented based on the combination of the combined Duval pentagon (PDC) method and ethylene concentration (C2H4) to determine the fault condition, the combination of the degree of polymerisation (DP) and moisture to determine the condition of the cellulose insulation and the use of the oil quality index (OQIN) to determine the condition of the oil. For each of the classification methods presented, applications based on machine learning (ML), in particular support vector machine (SVM), have been implemented for automatic classification using the Matlab development environment. The global algorithmic approach presented in this paper subscribes to the idea of event-based maintenance. Two case studies are also presented to validate SVM-based classification methods and algorithms.
1. Introduction
Today, electricity is an important part of human life, industry and agriculture and has a major impact on the economy of any country. The energy sector is therefore a fundamental strategic infrastructure for any country’s economy and a public service with a strong social impact. The quality of energy and increased energy efficiency is an important national and international objective and can be achieved by applying preventive and corrective management of energy equipment, of which the transformer is the most important component in the transmission and distribution of electricity.
The safe operation of high-power transformers is a particular problem because their failure in most cases leads to explosions followed by fires with very serious consequences for the substations, the national energy system (SEN) and, not least, the environment. In this case, a good maintenance strategy, by detecting any anomaly before it causes damage, will ensure availability and reliability throughout their lifetime at minimum cost.
Early assessment of the condition of the transformer in service, the severity of the problem, its location and the determination of an appropriate remedial action will prevent serious events that are costly to both electricity suppliers and consumers. This reduces downtime and repair costs and even extends the life of the equipment [].
The study of the health of in-service power transformers is a difficult and complex task, as the assessment consists of identifying indicators that can provide accurate data on the extent of degradation of transformer components and subcomponents, in order to establish a model for predicting the remaining life of the transformer [].
Transformers are generally designed to operate for 35–40 years. This can be as long as 60 years if the transformer is properly maintained. However, years of operation and transformer failures can quickly shorten the design life. For this reason, estimating the remaining life of the transformer is of paramount importance.
The main focus in assessing the remaining life of the power transformer is its mixed paper–oil insulation system. The end of life of transformers is therefore not determined by the design life but by the end of life of the insulation system [].
Over the years, previous studies and research have evaluated the life of power transformers through the prism of the solid insulation condition, as this condition is considered irreversible. The article [] points out that a low DP does not necessarily mean the end of the transformer’s life, as long as the integrity of the overall insulation system is maintained. However, a few researchers have proposed to determine the remaining life by multi-parameter assessment [,,,].
In recent decades, the paper–oil insulation system has been a common key component in the development of monitoring techniques used to diagnose the health and estimate the useful life of power transformers [,,].
Several papers have been published to explain the ageing mechanism of the paper–oil insulation system of power transformers, and their health and service life have been assessed using various parameters of the insulation system. Electrical and physico-chemical tests are generally used to determine the health of the transformer [,,,,,].
To determine and monitor transformer condition, many users rely solely on dissolved gas analysis [], so a number of standards have been reviewed [,] and diagnostic methods using artificial intelligence-based programmes have been developed [,].
Several studies have shown that the transformer HI is a factor that uses information from operational studies, field inspections and laboratory tests to provide a reliable decision for the user [,,,,].
Therefore, this paper proposes a model to assess the remaining functional life (RFL) by diagnosing the transformer condition based on the HI obtained from a multi-parameter analysis. Therefore, methods for assessing the remaining life of power transformers based on their health status through multi-parameter analysis of the transformer’s paper–oil insulation system have been described.
A first method described in this paper for assessing the remaining life of power transformers is the use of the PDC [] and ethylene to determine fault location in thermal fault situations with paper carbonisation [,]. The second method described is the determination of the condition of the cellulose insulation based on furan compounds, low molecular weight alcohols and the moisture content of the paper–oil insulation system. The third method described is the condition of the transformer according to the condition of the insulating oil, as determined by the oil quality index [,,].
The methods presented above have been implemented to classify the operating states of power transformers using ML algorithms, namely SVM. Based on the results obtained by using SVM algorithms, the HI of the transformer is obtained, which can be used to determine its RFL.
The main contributions of this article are as follows:
- Development of a method to determine the fault condition of power transformers by combining the PDC method and C2H4 concentration;
- Development of a method to determine the condition of cellulose insulation based on DP and moisture;
- Development of a method to determine the state of oil quality;
- Implementation of an SVM algorithm to classify the fault condition of power transformers by combining the PDC method and C2H4 concentration;
- Implementation of an SVM algorithm to classify the condition of cellulose insulation based on DP and moisture;
- Implementation of an SVM algorithm for oil quality classification;
- Determination of the HI based on the methods and algorithms described above.
The rest of the article is structured as follows: methods for assessing the RFL of power transformers are presented in Section 2, and the Matlab implementation of SVM algorithms for determining the operating state of power transformers is presented in Section 3. The validation of SVM-based classification methods and algorithms is presented in Section 4 using two case studies. Some conclusions and perspectives are presented in the final section.
2. Methods for Assessing the Remaining Functional Life of Power Transformers
This section presents the methods used to implement a system for assessing the RFL of the power transformers. The system uses multi-classification to determine the remaining functional life based on the assessment of the transformer condition and the overall health index. Its health is determined by multi-parameter analysis of the transformer’s paper–oil insulation system.
The general block diagram of the proposed assessment system is shown in Figure 1. Also in Figure 1, with HIF is noted the health index according to the fault state, with HIP is noted the health index according to the condition of the cellulose insulation, with HIO is noted the health index according to the condition of the oil, and with HIT is noted the overall health index of the transformer.
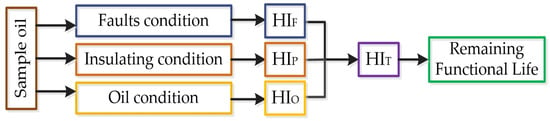
Figure 1.
General block diagram of the proposed assessment system.
As shown in the previous figure, the proposed RFL assessment system consists of three subsystems for diagnosing the operating condition of the transformer and determining its HI.
The methods for implementing the overall system for assessing the RFL are presented below.
2.1. Methods for Determining the Fault Diagnostic Subsystem
Figure 2 shows the general block diagram for determining the fault condition where GC represent gas chromatography used to determine the concentration of dissolved gases.

Figure 2.
Block diagram of fault condition diagnosis.
2.1.1. Combined Duval Pentagon Method
The PDC is an important analysis tool obtained by overlapping Duval pentagons 1 and 2 and has been developed to easily and maximally exploit the properties of the original pentagons to identify defects in mineral-oil-filled transformers using specialised software Matlab/Simulink version 2021b [,].
This method shows fewer fault zones than using both pentagons (10 fault zones for PDC and 14 zones for Duval pentagons 1 and 2). Figure 3 shows the PDC with the ten fault zones and Table 1 shows what these zones represent [].
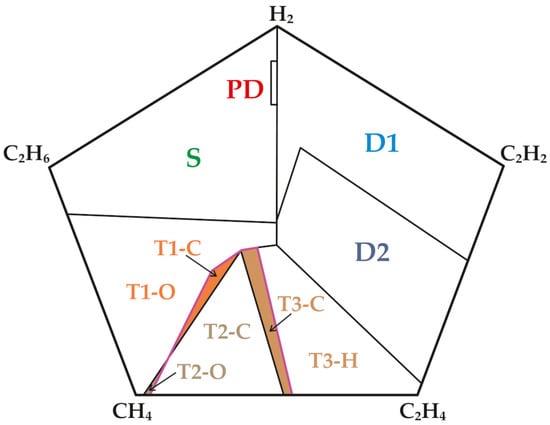
Figure 3.
Combined Duval pentagon and ten fault zones [].

Table 1.
Significance of the fault zones in the combined Duval pentagon.
The PDC method classifies the main defect types and provides decisions for several subtypes, such as O (overheating < 250 °C) and C (thermal defects with paper charring), making it useful for easier identification of defect combinations. In addition, this method does not replace the diagnosis carried out using the two Duval pentagons, but it simplifies the calculations by using a single geometry to represent both pentagons.
2.1.2. Ethylene Concentration
When identifying thermal faults that may involve cellulose insulation, it is important to determine the exact location of the fault, as in these cases the warning levels of ethylene concentration (the main gas formed in this case) are very different and lead to different actions on the transformer [].
Acoustic testing can also be used to locate faults involving carbonisation of the cellulose insulation, but this is expensive and can only be applied to a small number of transformers.
Thermal failures involving the carbonisation of the solid insulation are dangerous because they are the main cause of arcing faults in the cellulose insulation and can lead to short circuits that severely reduce the life of the transformer.
The CIGRE 771 [] technical leaflet describes the most dangerous paper carbonisation faults that can occur in transformers, namely:
- in the turns of the windings or inside the windings where the voltage is higher (these are the most dangerous);
- in the cables in or out of the windings or loosely screwed to the connection rods;
- on the outside of the windings due to abnormal circulating currents.
IEC, IEEE and CIGRE specialists calculated typical gas concentration values of 90%, but only CIGRE specialists calculated gas concentration values before the fault. Typical and pre-defect ethylene (C2H4) concentration values for different types of thermal defects involving paper carbonisation are shown in Table 2 []. The codes to be used in the proposed evaluation system are also given in this table.

Table 2.
The C2H4 concentration levels for thermal faults involving paper carbonisation and the associated codes.
The identification of thermal faults involving carbonisation of the solid insulation and their location is particularly helpful to transformer operators in their maintenance schedules, i.e., it helps them to determine whether the transformer requires urgent action (removal from service and inspection for repair) or whether it can continue to operate but with increased frequency of oil sampling for dissolved gas analysis (DGA) testing.
The flowchart used to determine the fault condition and implemented in the proposed evaluation system is shown in Figure 4.
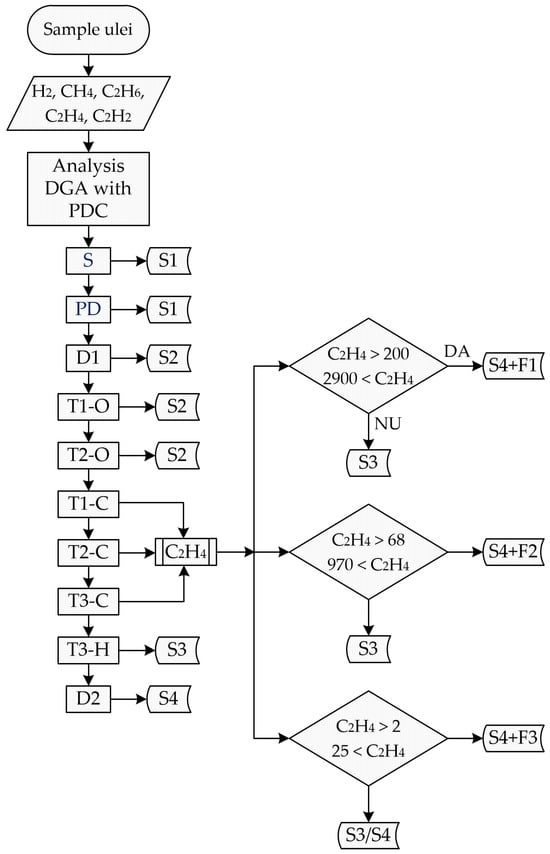
Figure 4.
Flow chart for determining the fault condition.
The fault conditions shown in the above diagram are as follows:
S1—normal state—normal operation of the transformers. The frequency of DGA testing must be once a year.
S2—acceptable state—normal transformer operation. In this case, it is good practice to monitor and determine the gas generation rate and perform DGA tests every six months.
S3—caution/warning—monitor transformer operation by checking load, gas generation status, cooling system status. It is good practice to carry out DGA testing on a quarterly or even monthly basis.
S4—critical condition—in this case, special attention should be paid to the operation of the transformer by performing monthly or even weekly DGA tests, checking the gas generation rate, performing electrical tests for confirmation and even considering decommissioning for further evaluation.
Since, as mentioned above, thermal defects involving carbonisation of the paper are the most dangerous, it is good practice to identify not only the type of defect but also its location. Thus, as can be seen from the flowchart in Figure 4, if the DGA reveals a T1-C, T2-C or T3-C type thermal failure, the programme checks the C2H4 concentration and, depending on its value, determines the location of the defects indicating carbonisation of the paper. That is, whether the thermal fault detected is accompanied by paper carbonisation in the conductors (F1), on the outside of the windings (F2) or inside the windings or between the turns of the windings (F3).
2.1.3. Single Gas Ratio Method
The IEC 60599:2022 and IEEE C57.104-2019 standards [,] have introduced three unique gas ratios (CO2/CO, O2/N2 and C2H2/H2) in DGA as complementary methods for fault diagnosis in transformers.
(a) CO2/CO ratio
In addition to determining the involvement of cellulose insulation in a diagnosed transformer failure, carbon oxides (CO—carbon monoxide and CO2—carbon dioxide) have been used until recently but have been shown not to be a direct result of solid insulation degradation. These gases are also produced by the thermal degradation of other components in the transformer, such as oil, paints, varnishes and phenolic resins and by the ingress of atmospheric air into free-breathing transformers or by leakage.
Therefore, the new views on the interpretation of carbon oxides and CO2/CO ratio are extensively presented in the IEC 60599:2022 and IEEE Std.C57.104-2019 standards [,].
Therefore, the involvement of cellulose insulation in a failure or the determination of the degree of solid insulation degradation will be based not only on the analysis of carbon oxides and their ratio but also on other oil analyses (e.g., analysis of furan compounds, methanol).
(b) O2/N2 ratio
Oxygen (O2) and nitrogen (N2) dissolved in oil are detected by contact with atmospheric air in the conservator of free-breathing transformers or by air ingress through leaks in sealed equipment. In a state of equilibrium with air, the O2/N2 ratio is ~0.5, and the normal value of this ratio is influenced by the type of transformer, loading and conservation system used.
The influence of the O2/N2 ratio on typical gas values and the occurrence of defects is presented in the technical brochure CIGRE 771 []. The values of this ratio have also been calculated and determined for free-breathing (>0.2) and sealed (<0.2) transformers.
(c) C2H2/H2 ratio
In power transformers equipped with on-load tap-changers (OLTCs), C2H2/H2 ratio values between 2 and 3 indicate contamination of the oil in the main tank with oil or gas from the OLTC. In this case, the interpretation of the DGA results obtained in the main tank should be made by reducing the contamination from the OLTC or be considered inconclusive.
The design of modern OLTCs eliminates the possibility of oil contamination in the main transformer tank.
2.2. Methods for Determining the Cellulose Insulation Condition Diagnostic Subsystem
Figure 5 shows the block diagram of the diagnostic subsystem for determining the condition of the cellulose insulation. This diagram also shows the methods used to determine the concentration of furan (HPLC—high-pressure liquid chromatography), low molecular weight alcohols (GC/MS—gas chromatography/mass spectrometry) and moisture (K.F.T.—Karl Fischer titration) in insulating oil.
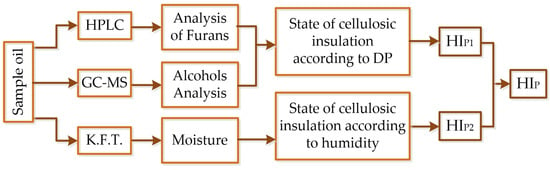
Figure 5.
Cellulose insulation condition diagnostic block diagram.
2.2.1. Analysis of Furan Compounds
Some of the specific markers of cellulose insulation degradation are furan compounds and play an important role in determining the state of ageing of the solid insulation of power transformers in service and thus in assessing their service life. They are a family of chemical compounds that are found dissolved in transformer oil and can be measured by HPLC. The names of the furan compounds and the most common causes of their occurrence, as determined through in-service experience, are listed in Table 3 [].

Table 3.
Names and possible causes of furan compounds.
The most important furan compound and the most commonly used parameter to determine the DP of cellulose insulation is 2-FAL. Depending on its concentration, an interpretation of the state of cellulose insulation as a function of the DP for the paper has been established [,].
The papers [,,] present the characteristics of furan compounds, their application, the factors that have a significant influence on the composition of 2-FAL in transformer oil and the difficulties associated with their correlation with DP. It was also found that 5-HMF and then 2-FAL are produced in the process of solid insulation degradation, and that the concentration of 5-HMF increases with age. At an early stage of cellulose insulation ageing (DP > 600) or at low temperatures (100–160 °C), 5-HMF shows better stability than 2-FAL and its rate of generation is higher than that of 2-FAL. We can therefore say that 5-HMF is the main product in the early stages of cellulose insulation degradation and can be a good indicator in assessing the condition of insulation in the early stages of ageing.
2.2.2. Analysis of Low Molecular Weight Alcohols
Low molecular weight alcohols dissolved in oil, such as methanol (MeOH/CH3OH) and ethanol (EtOH/CH3CH2OH), are increasingly used to diagnose the condition of the transformer, i.e., the ageing of the cellulose insulation [,,].
Several methods have been described in the literature for the determination of methanol and ethanol concentrations in oil, of which the head space/gas chromatography/mass spectrometry (HS/GC/MS) method has proven to be the most effective. The method consists of the following steps: HS allows the molecules to be evaporated, then GC separates the different molecules and finally MS is used to analyse and quantify these molecules.
The technical brochure CIGRE 779 [] presents the origin, stability and kinetic studies of solid insulation ageing accompanied by methanol and ethanol generation and concludes that methanol can be considered as an important marker for monitoring paper depolymerisation and can be useful for diagnosing the condition of transformer solid insulation because this marker has the following advantages:
- it is generated in the first stage of the degradation of cellulose insulation (DP > 900);
- it does not chemically interact with oil stabilisers, so it can be used in different types of mineral oils (uninhibited and inhibited);
- it is generated by all types of cellulose-based paper, including paper with improved thermal properties even at low temperatures, unlike 2-FAL;
- methanol production is proportional to the cleavage of glycosidic bonds in the cellulose chain;
- varying the methanol concentration allows the ageing of the insulation to be phased from a rapid initial degradation rate followed by a slow progression to a steady rate in both standard and thermally enhanced kraft papers;
- the correlation between PD and methanol generation is directly proportional and well established, but it should be noted that the prior detection of methanol in relation to 2-FAL is very important to establish an effective technique for monitoring and assessing the state of degradation of the solid insulation in the transformer;
- as it has a higher adsorption capacity on insulating paper than carbon oxides, it tends to return to equilibrium after an oil change;
- MeOH recovery time after a given transformer oil process is half the time required for 2-FAL recovery.
Ethanol has been found to behave particularly well at temperatures >250 °C and, when levoglucosan is produced from the decomposition of cellulose, it continues to decompose, producing large amounts of ethanol, greater than methanol. Therefore, ethanol can be used as a chemical hot-spot marker for cellulose insulation and as an indicator for diagnosing thermal failure of transformer insulation.
Such behaviour of low molecular weight alcohols dissolved in oil allows us to distinguish between normal and abnormal ageing of cellulose insulation and thus to distinguish the area of moderate ageing from a small area of accelerated ageing of solid insulation.
We can conclude that the concentrations of methanol, ethanol and furan compounds, especially 2-FAL, can be used to monitor the health of the cellulose insulation in the transformer at any stage, from the initial ageing state to the final stage [].
CIGRE specialists [] propose the following kinetic equation to determine the DP of cellulose as a function of methanol concentration:
where: MeOH is the concentration of methanol in ppb, correlated at 20 °C. Based on this model, thresholds have been set similar to those for 2-FAL (see Table 4).

Table 4.
Transformer condition as a function of methanol content [].
Several models and systems used to assess the remaining life of transformers have shown that it is not possible to accurately determine the remaining life of a transformer on the basis of 2-FAL or MeOH content alone, but by correlating several techniques (e.g., DGA, oil and paper moisture, acid index, interfacial tension, etc.).
Table 5 and Table 6 show the condition of the cellulose insulation according to DP, the causes of degradation markers (furan compounds and alcohols) and their corresponding codes used in the proposed evaluation system [].

Table 5.
State of cellulose insulation according to DP and corresponding code.

Table 6.
Causes of occurrence of degradation markers and associated codes.
2.2.3. Moisture Content
The moisture content in the oil–paper insulation system plays a fundamental role in the service life and reliability of the transformer. Due to the high hygroscopicity of the cellulose material, the solid insulation in the transformer absorbs almost all the moisture (99%) from the transformer. High humidity leads to accelerated ageing of the cellulose insulation, initiation of partial discharges and even explosions inside the transformer.
From the research carried out by several scientists on the moisture content of the transformer paper–oil insulation system, we can state the following [,,]:
- The degradation rate of cellulose insulation is proportional to moisture content, so a 0.5% increase in the moisture concentration of the paper–oil insulation system will halve the mechanical strength of the cellulose insulation and double its thermal ageing rate;
- During the life of the transformer, the moisture content in the cellulose insulation increases from 0.5% (factory value) to 4–8% (in the advanced degradation phase).
Oil moisture content is expressed as relative saturation (RS) values or parts per million by weight (ppm), while the recommended moisture content of solid insulation is generally expressed in percent by weight.
The maintenance guides IEC 60422:2013 and IEEE C57.106:2015 [,] give the condition of cellulose insulation as a function of the percentage of water saturation of the insulating oil as a guideline, and the papers [,] have established ranges of moisture content in cellulose insulation for different conditions of cellulose insulation (from new insulation to very wet insulation with imminent risk of failure/explosion) as they are presented in Table 7.

Table 7.
Condition of cellulose insulation according to moisture content and associated code.
In view of the damaging effects of moisture on the transformer insulation system, its level should be closely monitored so that, when it reaches certain thresholds, measures can be taken to eliminate excessive moisture levels using on-line drying methods such as cartridges with adsorbent materials or zeolite molecular sieves to extend the life of the transformer.
2.3. Methods for Determining the Diagnostic Subsystem of Insulating Oil Quality
According to IEC 60422:2013 [], in-service oils are classified as good, suitable and unsuitable based on an assessment of their significant insulating properties and ability to recover their previous properties. The dielectric characteristics of the oil are therefore regularly tested when evaluating the transformer. These characteristics consist of many parameters related to the oil properties such as: breakdown voltage, water, colour, interfacial tension, acidity index, etc. Recommended conditions and limits for transformers in service are given in Table 8.

Table 8.
Dielectric properties according to IEC 60422:2013 [].
The breakdown voltage is one of the indicators used to evaluate the dielectric properties of the oil and its value must be high enough to ensure that the insulating oil does not break down under the effect of the electrical voltage. Low breakdown voltage values indicate the presence of moisture and other conductive substances in the oil.
As mentioned above, the presence of water in transformer oil is undesirable because it has a strong and negative effect on the dielectric properties of the transformer, reducing the breakdown voltage, and also accelerates the degradation process of the entire insulation system (oil–paper). The water content of the oil is determined according to IEC 60814:1997 [] and the accepted limits are specified in IEC 60422:2013 [] (see Table 8).
Colour, a physical property of oil, is a visual and complementary indicator of other parameters in determining the state of degradation of oil. For oils in service, a high or increasing colour number is an indicator of contamination, degradation or both.
In addition, the colour and appearance of cloudy or sedimented oil may indicate the presence of free water, sludge or other insoluble contaminants. The colour scale can be determined according to ISO 2049:1996 [] or ASTM D1500-12(2017) [].
The acid index and interfacial tension were found to have the best correlation with transformer life. Thus, in the proposed evaluation system, the block diagram in Figure 6 is used to determine the condition of the insulating oil.
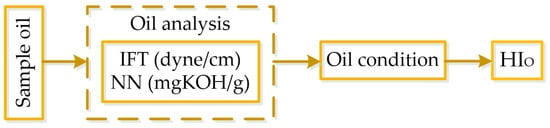
Figure 6.
Oil condition diagnosis block diagram.
2.3.1. Acidity/Acidity Index
During transformer operation, the insulation system ages and more degradation by-products are generated. Acids are some of these products and result from the oxidation of the insulating oil and the degradation process of the cellulose insulation.
Oil oxidation produces several types of acids (high and low molecular weight), but only some (low molecular weight) are involved in the process of cellulose insulation degradation by acid hydrolysis. Therefore, oil acidity can be used as an indicator to define the state of degradation of cellulose insulation.
The acidity of the insulating oil increases with the operating time of the transformer, and the accumulation of acids in the oil leads to the formation of insoluble sludge-like deposits. It reduces the dielectric strength of the oil and reduces heat transfer when deposited on the cellulose insulation and inside the radiator tubes, leading to catastrophic power transformer failure. Acids are also involved in the corrosion process of metal parts in a transformer.
The acid number is the mass of potassium hydroxide (KOH) required to neutralise the acids in the oil sample and is expressed in mg KOH/g. To eliminate the problems caused by sludge formation and deposition, it is recommended to treat (regenerate) transformer oil when the acid index is between 0.20 and 0.40 mg KOH/g [,]. Normal and critical values of the acid index are also specified in IEC 60422:2015, IEEE Std. C57.106:2015 and IEEE Std.C57.637-2015 [,,].
2.3.2. Interfacial Tension
Interfacial tension is the tension at the interface between two immiscible liquids and is expressed in mN/m or dyne/cm.
In the case of oil-immersed transformers, the interfacial tension of the insulating oil is an effective diagnostic indicator of its degree of degradation. The interfacial tension provides a reliable indication of the amount of polar contaminants and degradation by-products dissolved in the transformer oil.
During transformer operation, the dielectric oil ages, i.e., it undergoes oxidative degradation, which leads to a decrease in the interfacial tension value. The greater the ageing of the transformer, the lower the interfacial tension value.
A good, clean oil will have an interfacial tension of between 40 and 50 dyne/cm, whereas a heavily degraded oil will have an interfacial tension of around 14 dyne/cm. The maintenance guides for transformer oils recommend that they should be treated (reconditioned or regenerated) when the interfacial tension drops to 25 dyne/cm, because below this value (around 22 dyne/cm) sludge starts to form which, by depositing on the windings, in the cooling equipment, etc., affects the cellulose insulation and causes loading and cooling problems.
The drop in interfacial tension may also indicate an incompatibility between the oil and other materials used in the transformer, such as varnishes, paints and seals, or it may indicate accidental contamination when the transformer was filled with oil.
Interfacial tension can therefore be considered as a precursor of oxidation by-products. As studies in the literature have shown, there is a strong correlation between the interfacial tension and the acidity index []. A decrease in the interfacial tension normally represents an increase in the acidity index.
It has been shown that there are also some unusual situations where the interfacial tension and acidity index values are lower, due to contamination from solid insulation materials, leakage compounds at the ends of bushings or from a source outside the transformer []. Also, a decrease in interfacial tension does not necessarily mean an increase in acidity, as there may be other non-acidic contaminants present in the oil that only cause a decrease in interfacial tension. Such a situation can be explained in the case of a free-breathing transformer located in an area close to salt water. The formation of saltwater mist can enter the transformer unit, affecting the dielectric strength and interfacial tension of the oil but not the acidity index. IEEE Std.C57.106-2015 gives some guidelines for interfacial tension values, depending on the type of oil and the equipment in which it is used.
A relationship has been established between the values of the interfacial tension and the acidity index, given by Equation (2) and called the Myers index number or OQIN, whose value can be used as an indicator in diagnosing the condition of the oil. Thus, new oil has an OQIN = 1500 and an oil to be treated or replaced has an OQIN of about 100 [].
The paper [] presents indicative criteria and preventive measures based on interfacial tension, acidity index, oil colour and OQIN values. In Table 9, the condition of the oil is specified with the related codes depending on the interfacial tension, acidity index and oil quality index.

Table 9.
Condition of insulating oil and associated codes.
2.4. Determination of the Health Index and Service Life of the Transformer
The relationships used to determine the total transformer health index HIT and RFL are as follows [,,]:
where: HIF is the health index according to the fault state, and SF and WF are the score and weight, respectively, for each transformer state according to the fault state.
where: HIP is the health index according to the condition of the cellulose insulation and SP1, SP2, WP1 and WP2 are the scores and weights for each condition of the cellulose insulation according to DP and moisture, respectively.
where: HIO is the health index according to the condition of the oil, and SO and WO are the score and weight, respectively, for each oil condition.
where: HIT is the total health index of the transformer.
The remaining functional life of the power transformer is calculated in this paper based on the overall health index of the transformer using the following relationship (7):
where RFL is the remaining functional life (in years), HIT is the current HI value and Rd is the typical health index decline rate (HIT/year).
The approach is based on the weights associated with the health subindices. HI average represents the case of equal weights and is characterised by a uniformity of defect states, while the weakest element method is characterised by the fact that the weakest element will be given the highest weight, thus generating the presumption that the RFL will be at least equal to that indicated by the calculation.
3. SVM Algorithms’ Matlab Implementation for Determining the Operating Condition of Power transformers
Based on the proposed methods and evaluation system for determining the RFL of power transformers, this section presents the Matlab implementation of SVM classification algorithms. SVM algorithms were implemented to classify the following: the fault condition of power transformers by combining the PDC method and C2H4 concentration, the condition of cellulose insulation based on DP and moisture and oil quality classification.
The rate for each key gas concentration used in the relationships for determining the coordinates of a point in the PDC is given by the following relationships [,]:
The coordinates of the point are calculated as follows:
- for point 1:
;
;
- for point 2:
;
;
- for point 3:
;
;
- for point 4:
;
;
- for point 5:
;
.
The formulas for determining the centroid of the polygon defined by the five points are as follows []:
from which the following relationship can be written for the area of the polygon:
The coordinate of the point on the Ox axis can be written as follows:
which can be explained as:
The coordinate of the point on the Oy axis can be written as follows:
which can be explained as:
3.1. Description of the SVM Algorithms
SVM is a classifier type of learning machine and is one of the most widely used types of classifier. The operation of an SVM can be characterised by the fact that it aims to draw decision boundaries between data points in order to obtain a decision boundary that best divides the data points into classes or that can be regarded as the most general decision boundary. The aim is to make the decision boundary between given points as large as possible, so that the distance between a given point and the boundary is maximised. Note that the hyperplane must practically balance the distance between the classes of points obtained. A suggestive graphical representation is given in Figure 7 [].
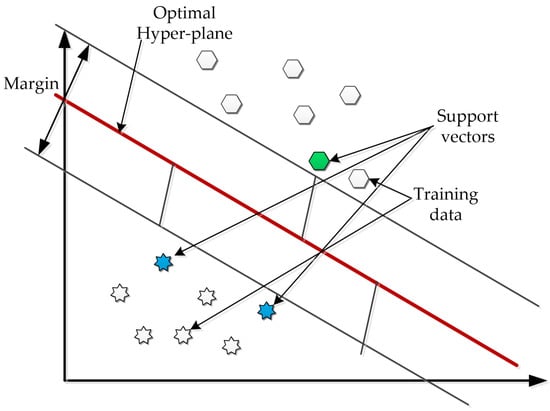
Figure 7.
Graphical representation for the separation of 2 classes using SVM.
From an analytical point of view, given a data set , where is the input vector, is the corresponding output vector and m is the number of data patterns, we can write the regression function of the SVM in relation (14) [,]:
In relation (14), b is the bias term and w is the weight vector. The separating hyperplane can be obtained from the following constraints:
Using the Lagrangian multiplier method, we write:
where Lagrangian multipliers are denoted by . The optimality conditions are obtained by cancelling the partial derivatives with respect to w and b. This results in the equations:
that give the following system of equations:
To solve this, we consider the dual problem of Equations (21) and (23) and obtain the system (24):
We define the manifold of support vectors vs. as any vector that satisfies the relation (25).
This relationship can be written in condensed form as in the relationship (26).
Accordingly, we define the function as follows []:
Note that if , then x is in class −1, otherwise it is in class 1. In the general non-linear case, the system to be solved becomes:
where C is a parameter characterising the margin in Figure 7.
The kernel function is expressed as []:
As can be seen, the SVM uses training based on inputs called samples, and the choice of kernel function is very important to obtain the classification. The following are the most commonly used kernel functions in the relationships from (30) to (33):
is a linear kernel function.
is a polynomial kernel function.
is a Gaussian radial basis kernel function.
is a sigmoid kernel function.
3.2. Numerical Implementation of the SVM Algorithms
Equations (13)–(18) are used to generate a sufficient number of points to cover all the characteristic surfaces of the PDC shown in Figure 3, in order to further train an SVM-based ML model for subsequent classification of real samples. To check whether a point, whose coordinates are generated by Equations (13)–(18), belongs to a surface in the PDC characterised by its vertex coordinates, the Matlab “inpolygon” command is used in the specially created software application. In this way, specific training sets are obtained for the points that belong to the corresponding surfaces, creating the conditions for good training on the entire surface of the PDC. The Classification Learner of the Matlab Statistics and Machine Learning Toolbox was used [].
Table 10 shows the accuracy and training time for the SVM-type algorithms used for the classification of the transformer condition based on the faults detected using PDC and specified in Table 1. It can be seen that the best accuracy is obtained with the Cubic SVM algorithm.

Table 10.
Efficiency of SVM algorithms in the training stage for transformer condition classification based on faults detected using PDC.
For the SVM algorithm with Cubic Kernel function, Figure 8 shows the validation confusion matrix. Figure 8 shows that the training was performed with good accuracy.
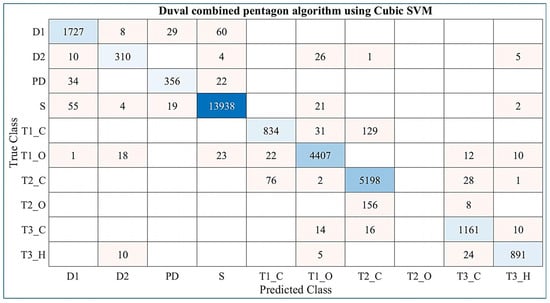
Figure 8.
Validation of the confusion matrix of the SVM algorithm with Cubic Kernel function for determining the condition of the transformer based on faults detected using PDC.
With i1 (H2), i2 (C2H6), i3 (CH4), i4 (C2H4), i5 (C2H2) as the gas percentage values of the PDC peaks, Figure 9 shows a prediction of the separation of the classes defined in Table 1 according to the inputs i1 (H2) and i3 (CH4) in the case of the SVM algorithm with Cubic Kernel function for determining the condition of the transformer based on the faults detected using PDC.
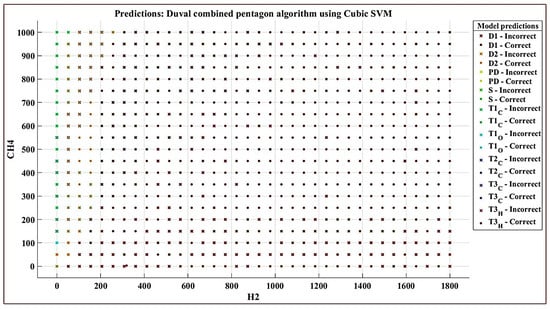
Figure 9.
Separation of classes in the case of the SVM algorithm with Cubic Kernel function for determining the condition of the transformer on the basis of the faults detected using the PDC as a function of the inputs i1 and i3.
Figure 10 shows the study of the predictors that perform the correct separation into the 10 defined classes used in the SVM algorithm with Cubic Kernel function for determining the condition of the transformer based on the faults detected using the PDC.
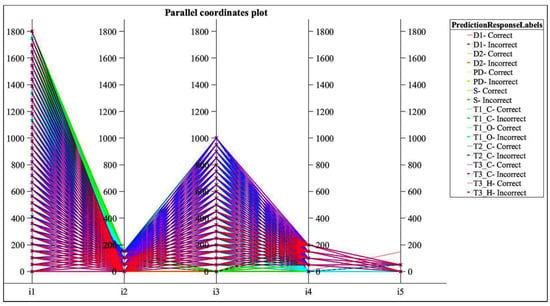
Figure 10.
Parallel coordinate plot of the predictors used in the SVM algorithm with Cubic Kernel function for determining the condition of the transformer based on the faults detected using the PDC.
Figure 11 shows the classification efficiency in terms of receiver operating characteristic (ROC) curves of the SVM algorithm with Cubic Kernel function for determining the condition of the transformer based on the faults detected using the PDC in the case of the T3-C class, i.e., true positive rate versus false positive rate.
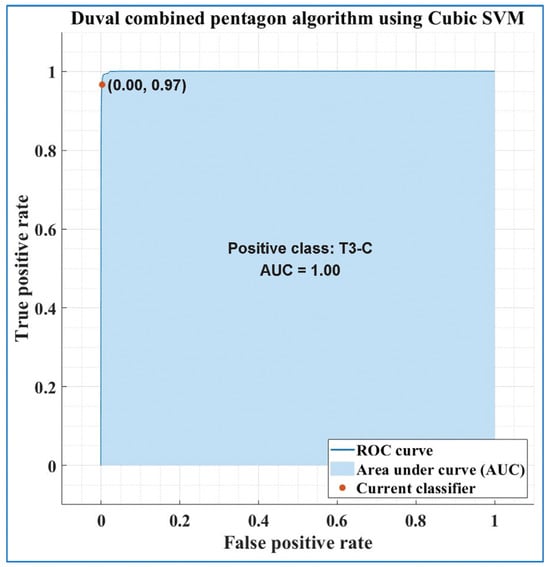
Figure 11.
ROC curves for the T3-C class of the SVM algorithm with Cubic Kernel function for determining the condition of the transformer based on the faults detected using the PDC.
SVM algorithms are used to classify the condition of the cellulose insulation as a function of the DP according to the data presented in Table 5, where it is noted that the input values are the concentrations of the chemical markers 2-FAL and MeOH, as well as the DP of the cellulose insulation, and the output values represent the states of degradation of the cellulose insulation. Thus, Table 11 shows the accuracy and training time for the SVM algorithms used to classify the condition of cellulose insulation as a function of DP. It can be seen that the best accuracy is obtained for the Quadratic SVM-type algorithm.

Table 11.
Efficiency of SVM algorithms in the training stage for classifying the condition of cellulose insulation as a function of DP.
Figure 12 shows the validation confusion matrix for the SVM algorithm with Quadratic Kernel function used to classify the cellulose insulation condition as a function of DP. Figure 12 shows that the training was performed with good accuracy.
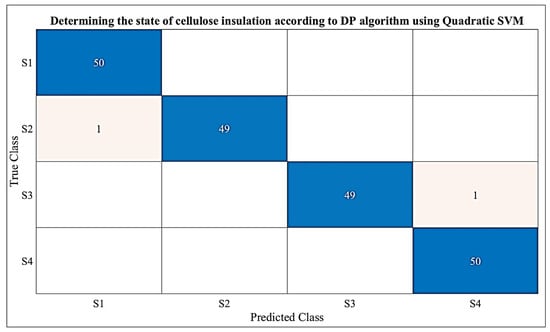
Figure 12.
Validation of the confusion matrix of the SVM algorithm with Quadratic Kernel function for determining the condition of cellulose insulation as a function of DP.
In the case of the SVM algorithm with Quadratic Kernel function for determining the condition of the cellulose insulation as a function of DP, Figure 13 shows a prediction of the separation of the classes defined in Table 5 as a function of the 2-FAL and DP value inputs.
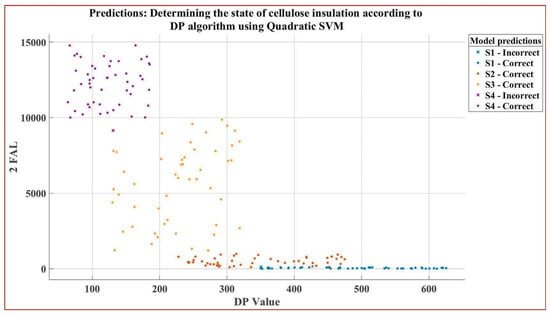
Figure 13.
Separation of S1, S2, S3 and S4 classes in the SVM algorithm with Quadratic Kernel function for determining the condition of the cellulose insulation as a function of DP according to 2-FAL and DP value inputs.
Figure 14 shows the study of the predictors that perform the correct separation into the four defined classes used in the SVM algorithm with Quadratic Kernel function for determining the condition of the cellulose insulation as a function of DP.
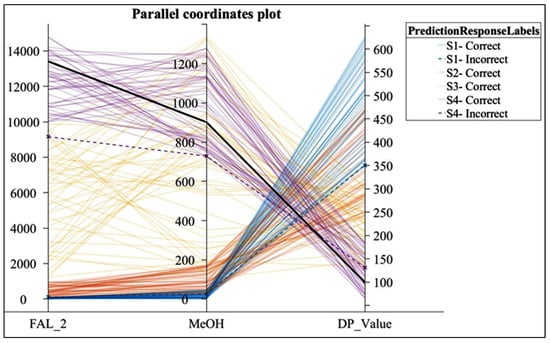
Figure 14.
Parallel coordinate plot of the predictors used in the SVM algorithm with Quadratic Kernel function for determining the condition of the cellulose insulation as a function of the DP.
Figure 15 shows the classification efficiency in the form of receiver operating characteristic (ROC) curves in terms of the true positive rate versus false positive rate for the SVM algorithm with Quadratic Kernel function for determining the condition of the cellulose insulation as a function of the DP.
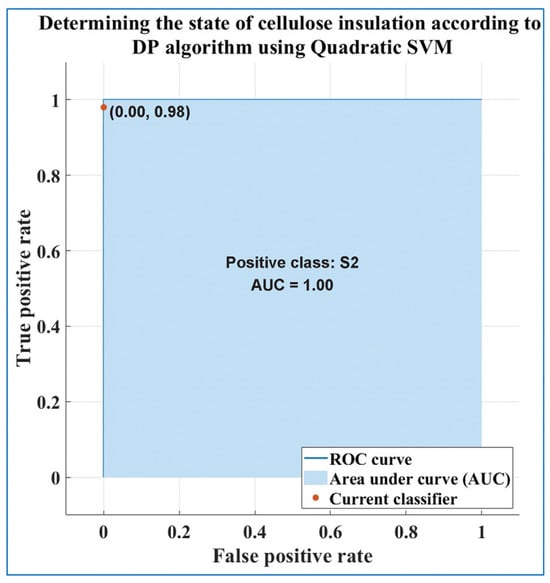
Figure 15.
ROC curves for the S2 class of the SVM algorithm with Quadratic Kernel function for determining the condition of the cellulose insulation as a function of the DP.
SVM algorithms are used to classify the condition of the cellulose insulation as a function of moisture content, according to the data presented in Table 7, where it is noted that the input values are the relative saturation of moisture in the oil and the concentration of moisture in the cellulose insulation, and the output values represent the condition of the cellulose insulation and the risk of failure. Thus, Table 12 shows the accuracy and training time for the SVM algorithms used to classify the condition of cellulose insulation as a function of moisture. It can be seen that the best accuracy is obtained for the Cubic SVM-type algorithm.

Table 12.
Efficiency of SVM algorithms in the training stage for classifying the condition of cellulose insulation as a function of moisture.
Figure 16 shows the validation confusion matrix for the SVM algorithm with Cubic Kernel function used to classify the cellulose insulation condition as a function of moisture. Figure 15 shows that the training was performed with good accuracy.
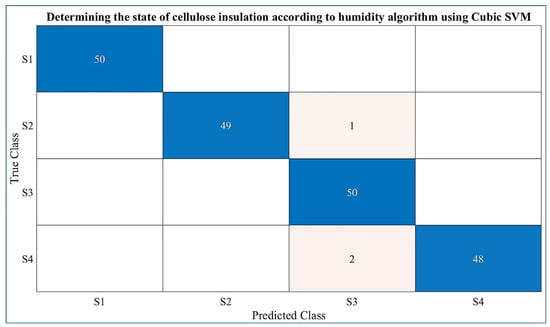
Figure 16.
Validation of the confusion matrix of the SVM algorithm with Cubic Kernel function for determining the condition of cellulose insulation as a function of moisture.
In the case of the SVM algorithm with Cubic Kernel function for determining the condition of the cellulose insulation as a function of moisture, Figure 17 shows a prediction of the separation of the classes defined in Table 7 (S1, S2, S3 and S4) as a function of RS and Cw input values.
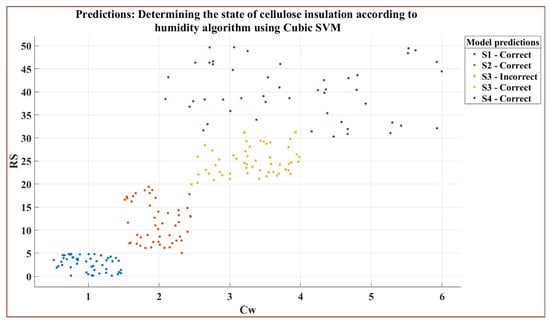
Figure 17.
Identification of a predictor that separates S1, S2, S3 and S4 value classes in the case of the SVM algorithm with Cubic Kernel function for determining the condition of the cellulose insulation as a function of moisture according to RS and Cw input values.
Figure 18 shows the study of the predictors that perform the correct separation into the four defined classes used in the SVM algorithm with Cubic Kernel function for determining the condition of the cellulose insulation as a function of moisture.
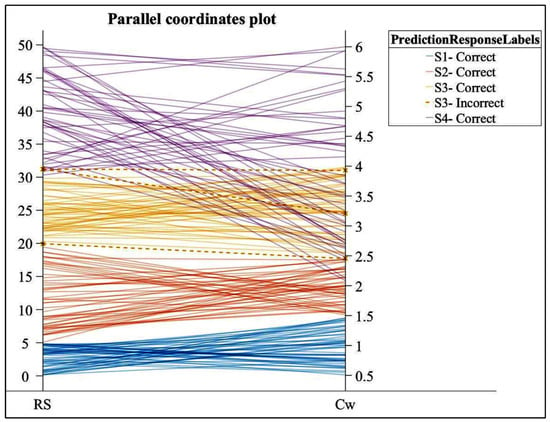
Figure 18.
Parallel coordinate plot of the predictors used in the SVM algorithm with Cubic Kernel function for determining the condition of the cellulose insulation as a function of moisture.
Figure 19 shows the classification efficiency in the form of receiver operating characteristic (ROC) curves in terms of the true positive rate versus false positive rate for the SVM algorithm with Cubic Kernel function for determining the condition of the cellulose insulation as a function of moisture.
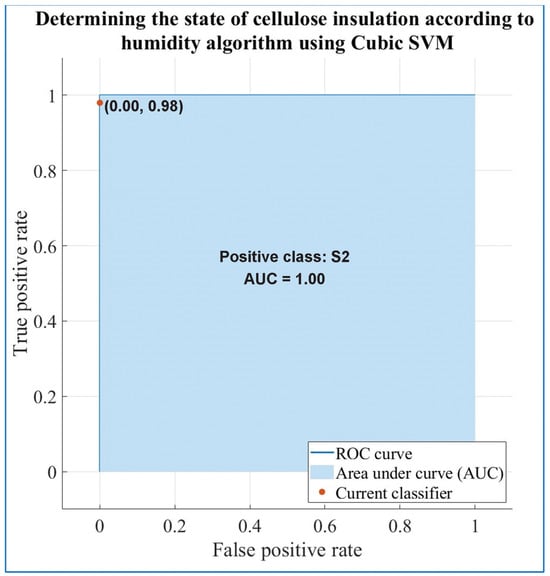
Figure 19.
ROC curves for the S1 class of the SVM algorithm with Cubic Kernel function for determining the condition of the cellulose insulation as a function of moisture.
SVM algorithms are used to classify the oil quality according to the data presented in Table 9, where it is noted that the input values are the interfacial tension, the acidity index and the oil quality index, respectively, and the output values represent the oil quality. Thus, Table 13 shows the accuracy and training time for the SVM algorithms used to classify the oil quality. It can be seen that the best accuracy is obtained for the Quadratic SVM-type algorithm.

Table 13.
Efficiency of SVM algorithms in the training stage for oil quality classification.
Figure 20 shows the validation confusion matrix for the SVM algorithm with Quadratic Kernel function used to classify the oil quality. Figure 20 shows that the training was performed with good accuracy.
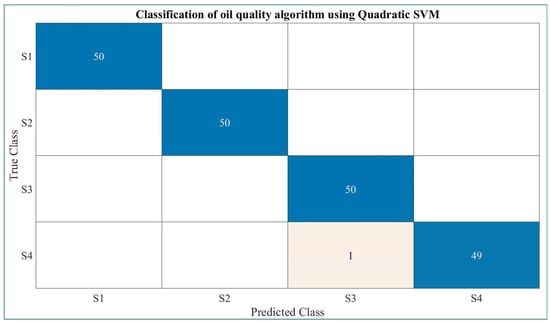
Figure 20.
Validation of the confusion matrix of the SVM algorithm with Quadratic Kernel function for determining the oil quality.
In the case of the SVM algorithm with Quadratic Kernel function for determining the oil quality, Figure 21 shows a prediction of the separation of the classes defined in Table 9 (S1, S2, S3 and S4) as a function of IFT and OQIN input values.
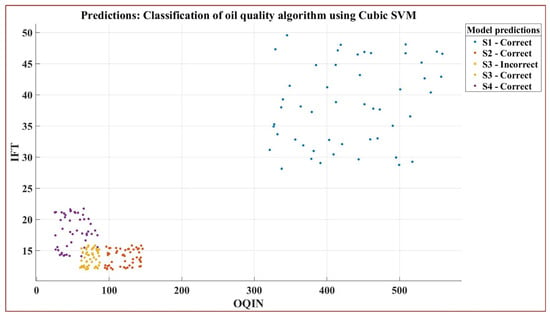
Figure 21.
Identification of a predictor that separates S1, S2, S3 and S4 value classes in the case of the SVM algorithm with Quadratic Kernel function for determining the oil quality as a function of RS and Cw input values.
Figure 22 shows the study of the predictors that perform the correct separation into the four defined classes used in the SVM algorithm with Quadratic Kernel function for determining the oil quality.
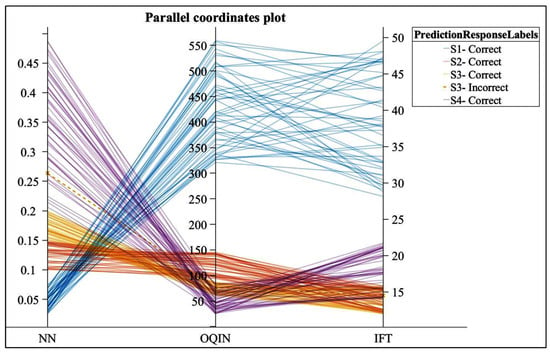
Figure 22.
Parallel coordinate plot of the predictors used in the SVM algorithm with Quadratic Kernel function for determining the oil quality.
Figure 23 shows the classification efficiency in the form of receiver operating characteristic (ROC) curves in terms of the true positive rate versus false positive rate for the SVM algorithm with Quadratic Kernel function for determining the oil quality.
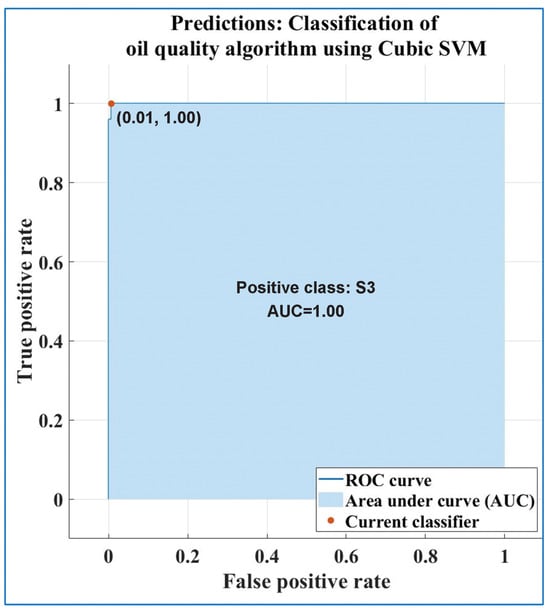
Figure 23.
ROC curves for the S3 class of the SVM algorithm with Quadratic Kernel function for determining the oil quality.
4. Case Studies
The validation of the proposed system was also carried out by comparing the results obtained with real cases where refurbishment and repairs were carried out.
The following are two case studies carried out on three-phase power transformers serving a cement factory and a chemical plant with the following characteristics: 25 MVA, 35/6.3 kV, free-breathing, uninhibited mineral oil and kraft paper.
Table 14 shows the values determined based on the complete (electrical and physico-chemical) analysis of the oil. Thus, an oil quantity of 1.3 L/transformer was used.

Table 14.
Values determined based on the complete oil analysis for the two transformers studied.
Case 1—Transformer T1
For the data in Table 14 for transformer T1, the methods presented in Section 2 and the classification corresponding to the four SVM-based algorithms for classifying the transformer condition based on the faults detected using the PDC, for classifying the cellulose insulation condition as a function of the DP, for classifying the cellulose insulation condition as a function of moisture and for classifying the oil quality were applied.
Figure 24 shows the results obtained in terms of conditions characterising each method.
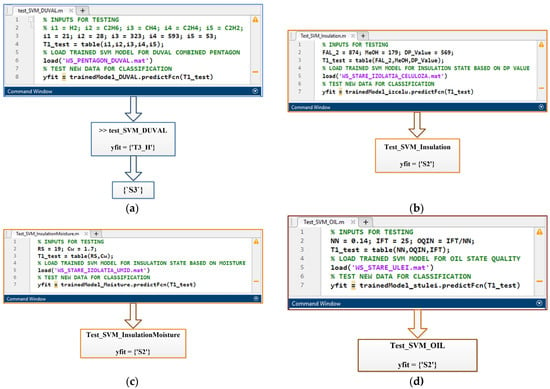
Figure 24.
Case 1—Testing of SVM classification algorithms for: (a) transformer condition based on faults detected using the PDC; (b) cellulose insulation condition as a function of PD; (c) cellulose insulation condition as a function of moisture; (d) oil quality.
Figure 25 also shows the determination of the DP value used by the SVM algorithm to classify the cellulose insulation condition as a function of DP, based on classification software realised in Matlab/Simulink version 2021b using neural networks developed by the authors [].
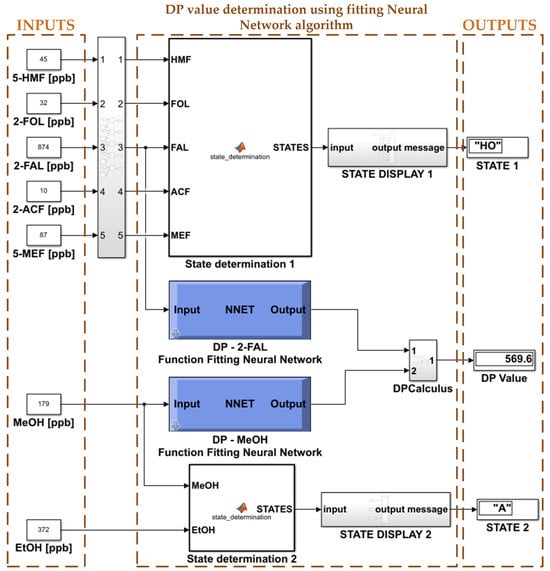
Figure 25.
Determination of PD value using fitting neural networks—Case 1.
The analysis carried out using the remaining life assessment system revealed the following:
- The analysis of the fault condition identified a T3-H fault, i.e., the presence of a fault in oil only, resulting in an S3—caution (see Figure 4). It was also noted that the acetylene concentration values were above the acceptable values specified in the standards and that the ratio C2H2/H2 = 2.52, which is in the range [2, 3). According to IEC 60599:2022, the oil in the main tank was contaminated with oil from the on-load tap-changer.
- The analysis of furan compounds and alcohols showed that the condition of the cellulose insulation is S2, i.e., there is a moderate degradation of the insulation due to oxidation of the paper and local overheating (5-MEF > 5-HMF and EtOH > MeOH, respectively).
- It should also be noted that in terms of oil quality, the IFT and NN values give a quality index of 171, which means that the condition of the oil is S2—satisfactory oil. As can be seen, the properties of the oil are affected, leading to a reduction in the cooling function and the presence of sludge in the oil.
- The total health index of this transformer is 81 and the remaining service life is 17 years, representing accelerated ageing or significant deterioration of some components.
The results showed that there are problems with the OLTC that need to be repaired. So, the transformer was disconnected from the grid and the tank was removed. As shown in Figure 26, the OLTC switch insulation is contaminated with oil degradation products and has an aged paper appearance, and the OLTC tank is leaking. The problems found have been rectified: the OLTC switch has been cleaned, the connections on the switch’s contact plates have been checked for tightness and the leaks have been repaired. The oil has also undergone a regeneration treatment.

Figure 26.
OLTC switch.
Case 2—Transformer T2
For the data in Table 14 for transformer T2, the methods presented in Section 2 and the classification corresponding to the four SVM-based algorithms for classifying the transformer condition based on the faults detected using the PDC, for classifying the cellulose insulation condition as a function of the DP, for classifying the cellulose insulation condition as a function of moisture and for classifying the oil quality were applied. Figure 27 shows the results obtained in terms of conditions characterising each method.
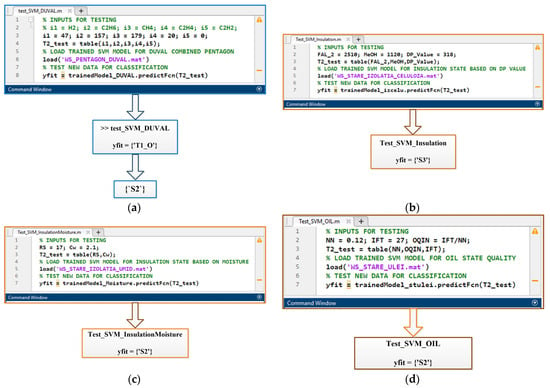
Figure 27.
Case 2—Testing of SVM classification algorithms for: (a) transformer condition based on faults detected using the PDC; (b) cellulose insulation condition as a function of PD; (c) cellulose insulation condition as a function of moisture; (d) oil quality.
The neural-network-based classification software shown above in Figure 28 shows the determination of the DP value used by the SVM-type algorithm to classify the condition of the cellulose insulation as a function of DP.
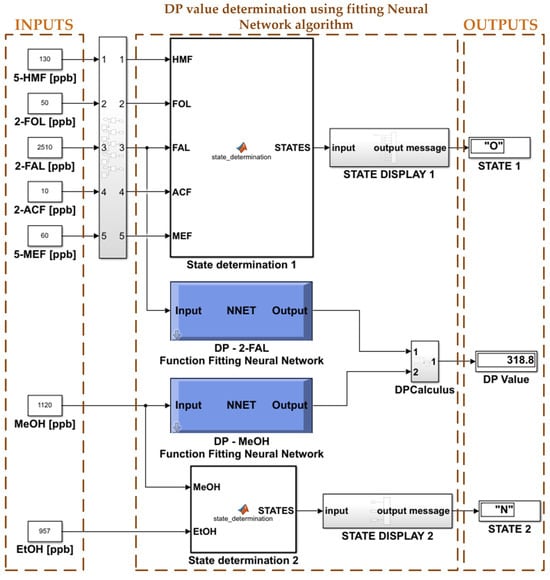
Figure 28.
Determination of PD value using fitting neural networks—Case 2.
After applying the proposed remaining life assessment system to this transformer, the following results were obtained:
- The analysis of the fault condition identified a T3-H fault, i.e., the presence of thermal faults with values below 300 °C, resulting in an S2—acceptable condition (see Figure 4).
- The analysis of furan compounds and alcohols showed that the condition of the cellulose insulation is S3, i.e., the cellulose insulation shows extensive degradation with a risk of failure due to general overheating, which may be caused by a fault in the windings or insufficient cooling.
- In terms of oil quality, the IFT and NN values give a quality index of 225 < 300, which means that the condition of the oil is S2—satisfactory oil. As can be seen, the properties of the oil are affected, leading to a reduction in the cooling function and the presence of sludge in the oil.
- The total health index of this transformer is 73 and the remaining functional life is 15 years. The transformer undergoes accelerated ageing which requires increased attention.
In view of the results, it was decided to repeat the DGA and furan and alcohol measurements one month later. This repeat test showed an increase in carbon dioxide but very little increase in other gases. At the same time, the concentrations of furan compounds and especially of 2-FAL increased (2-FAL = 3.17 ppm; 5HMF = 0.15; 2FOL = 0.07; 2ACF = 0.01 and 5MEF = 0.08), confirming the previously observed condition.
Several tests were carried out and the cooling system was found to be faulty. The cooling system was repaired and temperature sensors were installed in the oil path at the inlet and outlet of the cooling system (radiators) in order to effectively monitor the operating status of the cooling system.
5. Conclusions
The elements presented in this article focus on the description of combined methods for diagnosing the operating condition of power transformers and their implementation in the form of automatic classification programmes. Therefore, a number of methods for diagnosing the condition of power transformers have been presented using: the combination of the PDC method and ethylene C2H4 concentration to determine the fault condition, the combination of DP and humidity to determine the condition of the cellulose insulation and the use of the OQIN to determine the condition of the oil.
For each of the classification methods presented above, SVM-based applications have been implemented for automatic classification using the Matlab development environment. In order to validate the SVM-based classification methods and algorithms, two case studies were presented in which health indices and neural-network-based classification applications developed by the authors in previous work were used to determine the RFL of power transformers.
Future work will consider the optimisation of the classification methods presented in this paper using both statistically derived weights and combined ML algorithms.
Author Contributions
Conceptualisation, A.-M.A., M.-C.N., C.-I.N. and M.N.; methodology, A.-M.A. and M.-C.N.; software, C.-I.N. and M.N.; validation, A.-M.A., C.-I.N. and M.N.; formal analysis, A.-M.A.; investigation, A.-M.A. and M.-C.N.; resources, A.-M.A. and M.-C.N.; data curation, A.-M.A. and M.-C.N.; writing—original draft preparation, A.-M.A.; writing—review and editing, A.-M.A., M.-C.N., C.-I.N. and M.N.; visualisation, C.-I.N. and M.N.; supervision, A.-M.A. and M.-C.N.; project administration, M.-C.N.; funding acquisition, M.-C.N. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was elaborated as part of the NUCLEU Program within the framework of the National Research, Development, and Innovation Plan for 2022–2027, developed with the support of the Ministry of Research, Innovation, and Digitization, Project No. PN 23 33 02 03.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| HI | Health Index |
| IFT | Interfacial Tension |
| NN | Acidity Index |
| RS | Relative Moisture Saturation in Oil |
| Cw | Moisture Content of Cellulose Insulation |
| PDC | Combined Duval Pentagon |
| OQIN | Oil Quality Index |
| DGA | Dissolved Gas Analysis |
| OLTC | On-Load Tap-Changers |
| HPLC | High-Pressure Liquid Chromatography |
| RFL | Remaining Functional Life |
| SEN | National Energy System |
| GC | Gas Chromatography |
| MS | Mass Spectrometry |
| K.F.T. | Karl Fischer Titration |
| HS | Head Space |
| ML | Machine Learning |
| SVM | Support Vector Machine |
| ROC | Receiver Operating Characteristic |
References
- CIGRÉ. Life Extension of Oil Filled Transformers and Shunt Reactors; W.G. A2.55; Technical Brochure No. 887; CIGRÉ: Paris, France, 2022. [Google Scholar]
- CIGRÉ. Condition Assessment of Power Transformers; WG A2.49; Technical Brochure No. 761; CIGRÉ: Paris, France, 2019. [Google Scholar]
- Prasojo, R.A.; Setiawan, A.; Suwarno, A.; Maulidevi, N.U.; Soedjarno, B.A. Development of Power Transformer Remaining Life Model Using Multi-Parameters. In Proceedings of the 13th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Johor Bahru, Malaysia, 12–14 July 2021; pp. 99–102. [Google Scholar] [CrossRef]
- Duval, M.; De Pablo, A.; Atanasova-Hoehlein, I.; Grisaru, M. Significance and detection of very low degree of polymerization of paper in transformers. IEEE Electr. Insul. Mag. 2017, 33, 31–38. [Google Scholar] [CrossRef]
- Mharakurwa, E.T.; Goboza, R. Multiparameter-Based Fuzzy Logic Health Index Assessment for Oil-Immersed Power Transformers. Hindawi Adv. Fuzzy Sys. 2019, 2019, 2647157. [Google Scholar] [CrossRef]
- Ghoneim, S.S.M. Identification of Power Transformer Insulating Paper’s State Based on Principal Component Analysis. International Journal Elec. Eng. Inf. 2022, 14, 770–781. [Google Scholar] [CrossRef]
- Forouhari, S.; Abu-Siada, A. Integrated Life Estimation and Asset Management Decision Model for Power Transformers Using ANFIS; Department of Electrical and Computer Engineering, Curtin University: Perth, Australia, 2016; pp. 1–7. Available online: https://espace.curtin.edu.au/bitstream/handle/20.500.11937/70187/267681.pdf?sequence=2 (accessed on 9 November 2023).
- Diwyacitta, K.; Prasojo, R.A.; Suwarno. Study on Correlation Among Oil Dielectric Characteristics, Dissolved Gases, and Operating Life of 150 kV Power Transformer. Int. J. Elec. Eng. Inf. 2017, 9, 585–602. [Google Scholar] [CrossRef]
- García, J.J.M.; Drake, S.A.D.; del Castillo Serpa, A.M. Avances en evaluación del estado y la vida remanente de transformadores de fuerza. Ing. Energética 2019, 40, 245–256. [Google Scholar]
- Zhang, M.; Liu, J.; Liao, L.; Chen, Q.; Qi, P.; Chen, X. Method for predicting the remaining life of oil–paper insulation system based on stochastic degradation process. IET Sci. Measure. Tech. 2019, 13, 478–485. [Google Scholar] [CrossRef]
- Zhang, E.; Liu, J.; Zhang, C.; Zheng, P.; Nakanishi, Y.; Wu, T. State-of-Art Review on Chemical Indicators for Monitoring the Aging Status of Oil-Immersed Transformer Paper Insulation. Energies 2023, 16, 1396. [Google Scholar] [CrossRef]
- Zhang, E.; Zheng, H.; Zhang, Y.; Liu, J.; Zhang, C.; Shao, G.; Li, Y.; Zhang, C.; Fan, X. Feasibility Study on Evaluating Degree of Polymerization of Insulating Paper by Ethanol Content Dissolved in Transformer Oil. In Proceedings of the IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Richland, WA, USA, 20–23 October 2019; pp. 271–274. [Google Scholar] [CrossRef]
- Zhang, E.; Zheng, H.; Zhang, C.; Wang, J.; Shi, K.; Guo, J.; Schwarz, H.; Zhang, C. Aging state assessment of transformer cellulosic paper insulation using multivariate chemical indicators. Cellulose 2021, 28, 2445–2460. [Google Scholar] [CrossRef]
- Mihajlovic, D.; Ivancevic, V.; Vasovic, V.; Lukic, J. Cellulose Degradation and Transformer Fault Detection by the Application of Integrated Analyses of Gases and Low Molecular Weight Alcohols Dissolved in Mineral Oil. Energies 2022, 15, 5669. [Google Scholar] [CrossRef]
- Soni, R.; Chakrabarti, P.; Leonowicz, Z.; Jasiński, M.; Wieczorek, K.; Bolshev, V. Estimation of Life Cycle of Distribution Transformer in Context to Furan Content Formation, Pollution Index, and Dielectric Strength. IEEE Access 2021, 9, 37456–37465. [Google Scholar] [CrossRef]
- Thango, B.A.; Jordaan, J.A.; Nnachi, A.F. Assessment of Transformer Cellulose Insulation Life Expectancy Based on Oil Furan Analysis (Case Study: South African Transformers). ASTESJ-Adv. Sci. Tech. Eng. Sys. J. 2021, 6, 29–33. [Google Scholar] [CrossRef]
- Walker, C.; Al Rashdan, A.; Agarwal, V. Transformer Health Monitoring Using Dissolved Gas Analysis: A Technical Brief. Int. J. Prog. Health Manag. 2022, 13, 1–8. [Google Scholar] [CrossRef]
- IEC 60599:2022; Mineral Oil-Impregnated Electrical Equipment in Service—Guide to the Interpretation of Dissolved and Free Gas Analysis. International Electrotechnical Commission: Geneva, Switzerland, 2022.
- IEEE C57.104-2019; Guide for the Interpretation of Gases Generated in Mineral Oil-Immersed Transformers. Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2019.
- Prasojo, R.A.; Gumilang, H.; Suwarno; Maulidevi, N.U.; Soedjarno, B.A. A Fuzzy Logic Model for Power Transformer Faults’ Severity Determination Based on Gas Level, Gas Rate, and Dissolved Gas Analysis Interpretation. Energies 2020, 13, 1009. [Google Scholar] [CrossRef]
- Siregar, Y.; Lumbanraja, T.J.H. Analysis of interference methods on transformers based on the results of dissolved gas analysis tests. Int. J. Electr. Comp. Eng. (IJECE) 2023, 13, 3672–3685. [Google Scholar] [CrossRef]
- Rediansyah, D.; Prasojo, R.A.; Suwarno and Abu-Siada, A. Artificial Intelligence-Based Power Transformer Health Index for Handling Data Uncertainty. IEEE Access 2021, 9, 150637–150648. [Google Scholar] [CrossRef]
- Alqudsi, A.; El-Hag, A. Application of Machine Learning in Transformer Health Index Prediction. Energies 2019, 12, 2694. [Google Scholar] [CrossRef]
- Zaldivar, D.A.; Romero, A.A.; Rivera, S.R. Risk Assessment Algorithm for Power Transformer Fleets Based on Condition and Strategic Importance. Algorithms 2021, 14, 319. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Cui, Y.; Li, H. Review of Transformer Health Index from the Perspective of Survivability and Condition Assessment. Electronics 2023, 12, 2407. [Google Scholar] [CrossRef]
- Chitnavis, K.; Bhasme, N.R. Modeling and Simulation for Critical Analysis of Power Transformer for Life Estimation in Matlab. Int. J. Electr. Eng. Tech. (IJEET) 2017, 8, 1–10. Available online: http://www.iaeme.com/IJEET/issues.asp?JType=IJEET&VType=8&IType=4 (accessed on 2 October 2023).
- Cheim, L.; Duval, M.; Haider, S. Combined Duval Pentagons: A Simplified Approach. Energies 2020, 13, 2859. [Google Scholar] [CrossRef]
- CIGRÉ. Advances in DGA Interpretation; JWG D1/A2.47; Technical Brochure No. 771; CIGRÉ: Paris, France, 2019. [Google Scholar]
- Duval, M.; Buchacz, J. Detection of Carbonization of Paper in Transformers Using Duval Pentagon 2 and Triangle 5. IEEE Transact. Dielectr. Electr. Insul. 2023, 30, 1534–1539. [Google Scholar] [CrossRef]
- Hadjadj, Y.; Fofana, I.; Jalbert, J. Insulating oil decaying assessment by FTIR and UV-Vis spectrophotometry measurements. In Proceedings of the Annual Report IEEE Conference on Electrical Insulation and Dielectric Phenomena, Chenzhen, China, 20–23 October 2013; pp. 1310–1313. [Google Scholar] [CrossRef]
- I.A.R. GRAY. A Guide to Transformer Oil Analysis. Available online: http://www.satcs.co.za/Transformer_Oil_Analysis.pdf (accessed on 11 October 2023).
- Bryakin, I.V.; Bochkarev, I.V.; Khramshin, V.R.; Gasiyarov, V.R.; Liubimov, I.V. Power Transformer Condition Monitoring Based on Evaluating Oil Properties. Machines 2022, 10, 630. [Google Scholar] [CrossRef]
- Aciu, A.-M.; Nicola, C.-I.; Nicola, M.; Nițu, M.-C. Complementary Analysis for DGA Based on Duval Methods and Furan Compounds Using Artificial Neural Networks. Energies 2021, 14, 588. [Google Scholar] [CrossRef]
- CIGRÉ. Field Experience with Transformer Solid Insulation Ageing Markers; JWG A2/D1.46; Technical Brochure No. 779; CIGRÉ: Paris, France, 2019. [Google Scholar]
- Aciu, A.-M.; Nițu, M.C.; Nicola, M.; Nicola, C.-I.; Lăzărescu, F. Complementary Analysis of the Degree of Polymerization Based on Chemical Markers 2-Furaldehyde and Methanol Using the Fuzzy Logic. In Proceedings of the 21st International Symposium on Electrical Apparatus and Technologies (SIELA), Burgas, Bulgaria, 3–6 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Aciu, A.-M.; Nițu, M.-C.; Nicola, M.; Nicola, C.-I. Determination of the Condition of Solid Insulation in High-Power Transformers Based on 2-Furfuraldehyde and Methanol Markers Using Neural Networks. In Proceedings of the IEEE International Conference on Electromechanical and Energy Systems (SIELMEN), Iași, România, 6–8 October 2021; pp. 175–180. [Google Scholar] [CrossRef]
- Arshad, M.; Islam, S.M. Significance of cellulose power transformer condition assessment. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1591–1598. [Google Scholar] [CrossRef]
- Liu, J.; Fan, X.; Zhang, C.; Lai, C.; Zhang, Y.; Zheng, H.; Lai, L.; Zhang, E. Moisture Diagnosis of Transformer Oil-Immersed Insulation with Intelligent Technique and Frequency-Domain Spectroscopy. IEEE Trans. Ind. Inform. 2021, 17, 4624–4634. [Google Scholar] [CrossRef]
- IEC 60422:2013; Mineral Insulating Oils in Electrical Equipment—Supervision and Maintenance Guidance. International Electrotechnical Commission: Geneva, Switzerland, 2013.
- IEEE C57.106-2015; Guide for Acceptance and Maintenance of Insulating Mineral Oil in Electrical Equipment. Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2015.
- IEC 60814:1997; Insulating liquids - Oil-impregnated paper and pressboard - Determination of water by automatic coulometricKarl Fischer titration. International Electrotechnical Commission: Geneva, Switzerland, 1997.
- ISO 2049:1996; Petroleum Products - Determination Of Colour (ASTM Scale). International Organization for Standardization: Geneva, Switzerland, 1996.
- ASTM D1500-12(2017); Standard Test Method for ASTM Color of Petroleum Products (ASTM Color Scale). ASTM International: West Conshohocken, PA, USA, 2017.
- IEEE C57. 637-2015; Guide for the Reclamation of Mineral Insulating Oil and Criteria for Its Use. Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2015.
- Forouhari, S.; Abu-Siada, A. Remnant life estimation of power transformer based on IFT and acidity number of transformer oil. In Proceedings of the 11th International Conference on the Properties and Applications of Dielectric Materials (ICPADM), Sydney, Australia, 19–22 July 2015; pp. 552–555. [Google Scholar] [CrossRef]
- MathWorks—Statistics and Machine Learning Toolbox. Available online: https://www.mathworks.com/products/statistics.html (accessed on 14 May 2023).
- Bacha, K.; Souahlia, S. Power Transformer fault diagnosis based on dissolved gas analysis by support vector machine. Electr. Power Syst. Res. 2012, 83, 73–79. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).