A Three-State Space Modeling Method for Aircraft System Reliability Design
Abstract
:1. Introduction
2. Theoretical Basis of Aircraft System Reliability Analysis
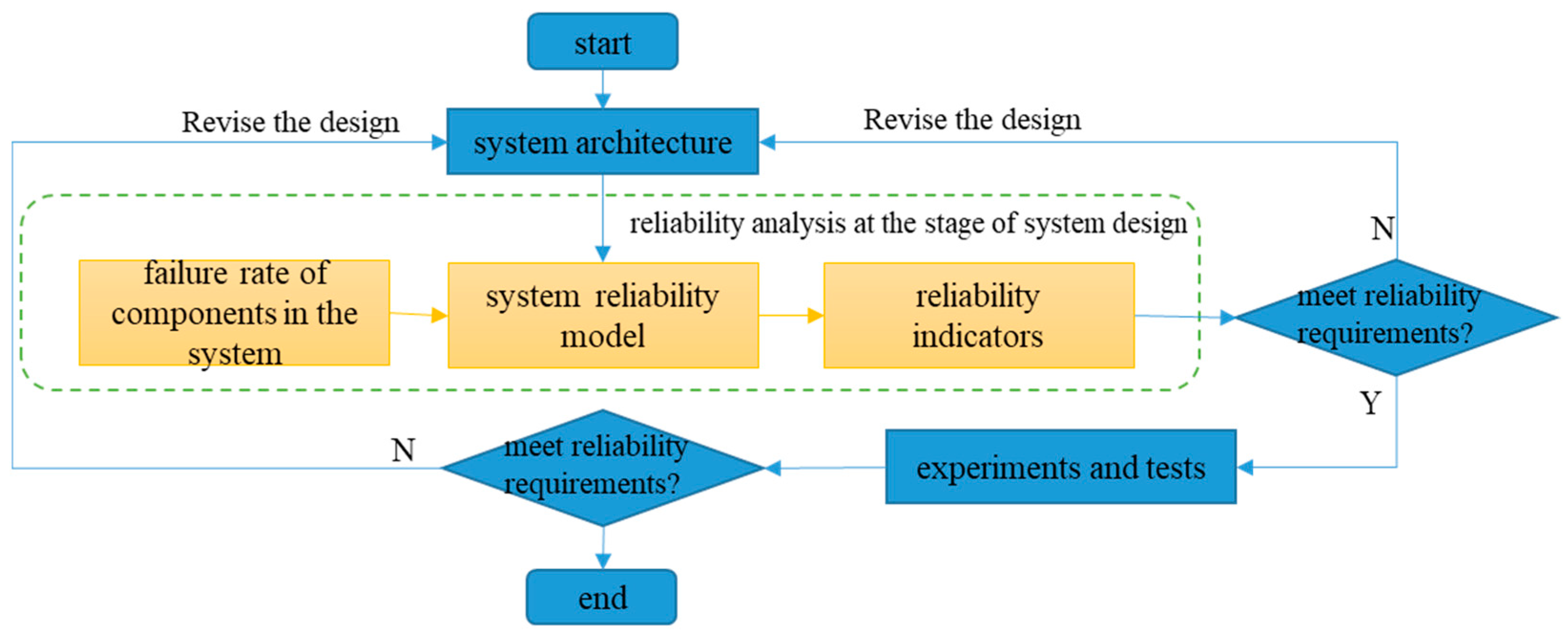
2.1. System Reliability Optimization Process
2.2. Basis of Aircraft System Reliability Modeling
3. The Proposed Three-State Space Modeling Method
3.1. Non-Physical Failure State Identified from the Traditional Failure State
3.2. Principles of the Proposed three-State Space Modeling Method
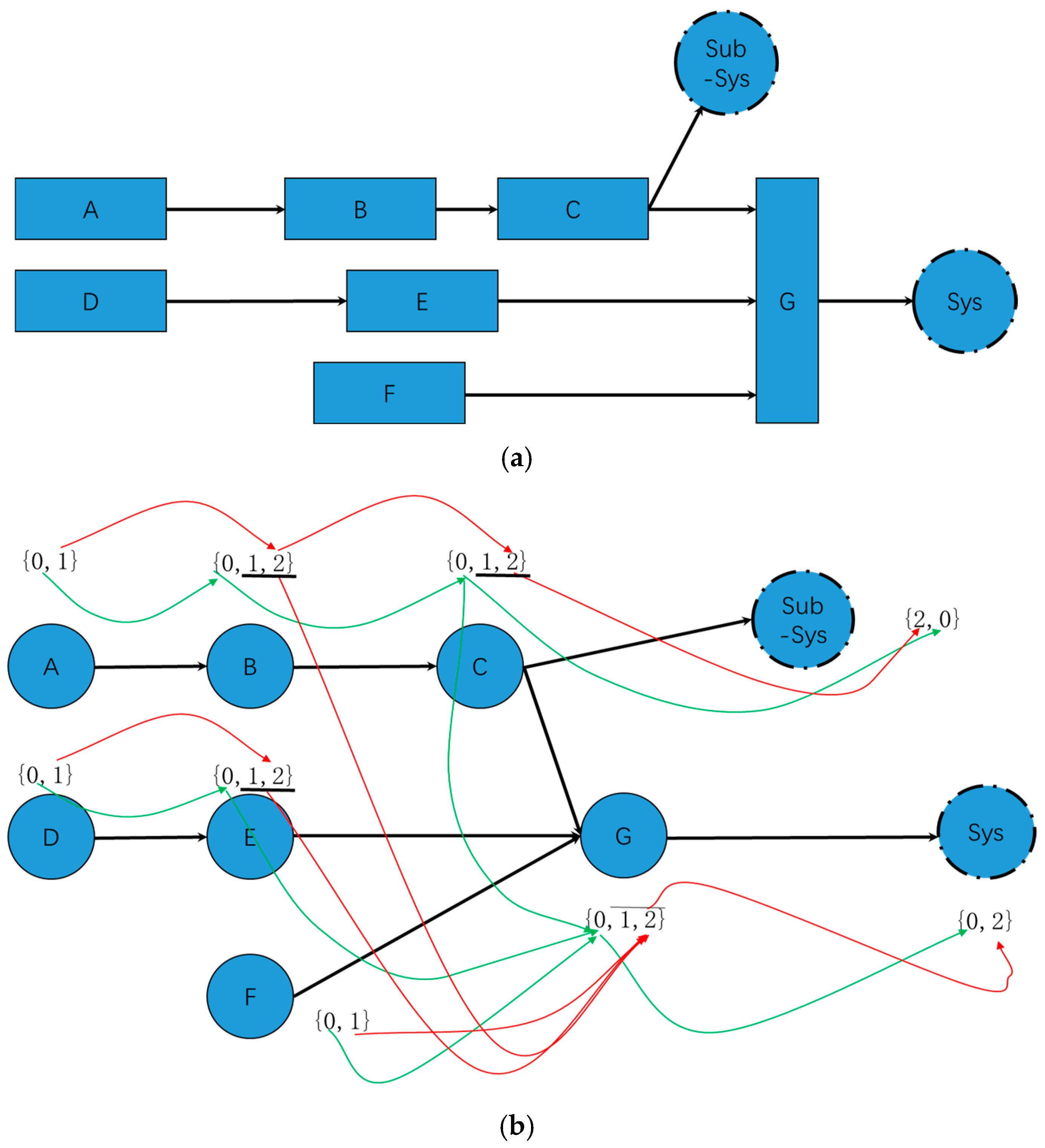
3.3. Steps of Building the Proposed Three-State Space Model
- List the functions of the system, subsystems, and components the system architecture involves.
- For each component in the architecture, sort out the function flow in the system function architecture from the following two perspectives.
- Firstly, suppose that the component itself has no physical failure;
- Then list the function logic between the component and its upstream components. Generally, the logic among components in the architecture is not drawn in the architecture directly, so the logic should be added to the architecture through logic gates in a clear way.
- Without changing the basic topological structure of the system function architecture, transform the sorted function flow into fault propagation paths in two ways to complete the transformation from the function space to the fault space:
- Transform component in the non-physical failure state in the function flow of the architecture to the node with physical failure state, that is, the type I node, which is represented as the root node in the topological structure of the system reliability model.
- According to the converting process from Figure 7b,c, convert nodes representing components’ normal states into nodes representing function loss states. Additionally, convert nodes representing non-physical failure states into nodes representing physical failure states. In this way, type II nodes of the system reliability model are obtained. Additionally, each logic gate expressed from a functional perspective should be converted into its equivalent logic gate with physical meaning from a fault perspective. When a type II node represents a system’s function loss state, it serves as a leaf node in the reliability model and an intermediate node if it represents a component’s function loss.
- Although the modeling method proposed in this paper has one more state than traditional two-state models, modelers still only need to provide failure probabilities or rates of components in the system as inputs for the system reliability model and do not require any additional parameters for the introduced third state of function loss.
- The modeling method proposed in this paper is not limited to a specific modeling language, so it can be used to construct three-state space models with Petri nets, Bayesian networks, and other modeling languages.
4. Case Studies
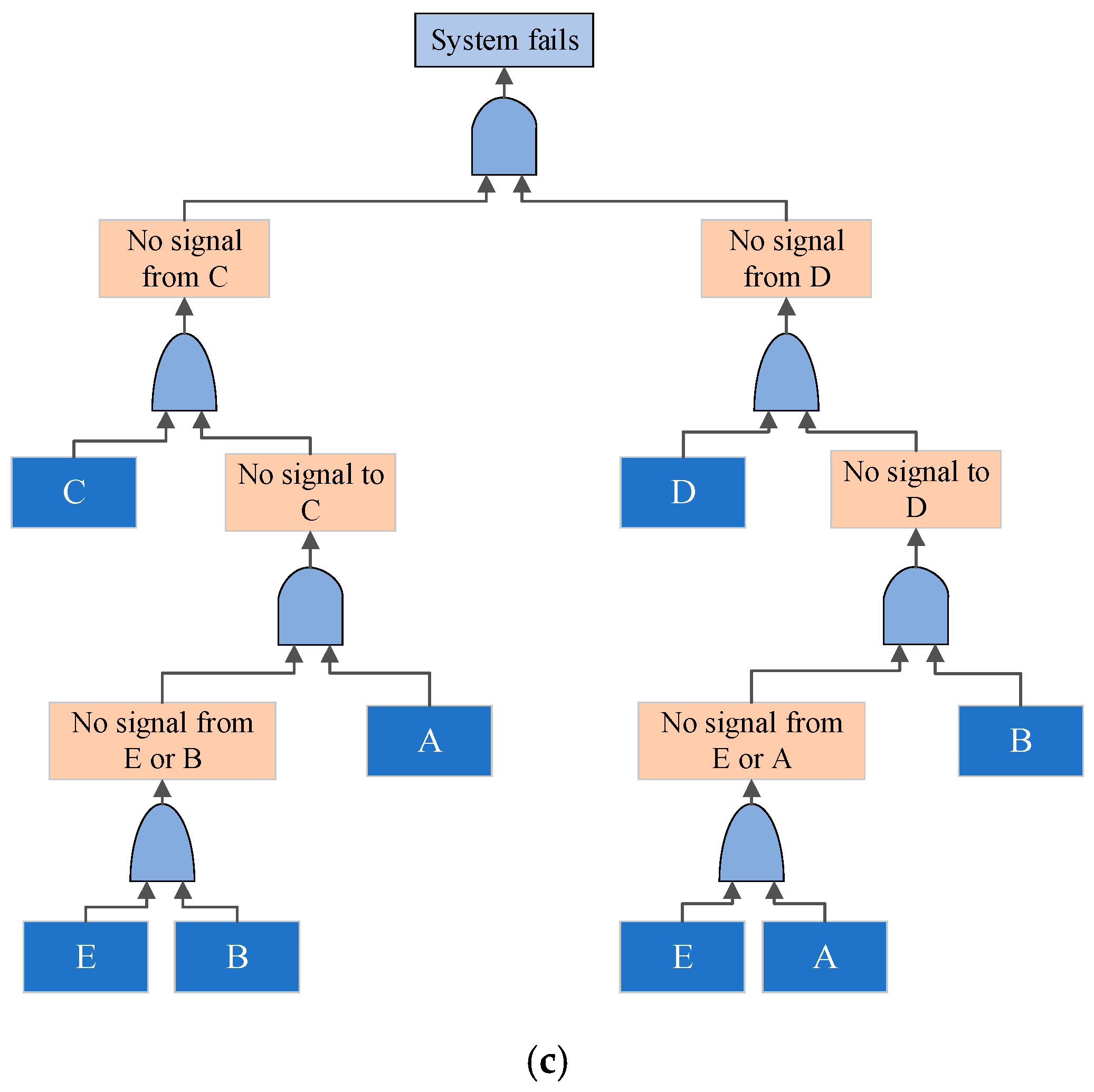
4.1. Reliability Analysis of a Rudder Control System
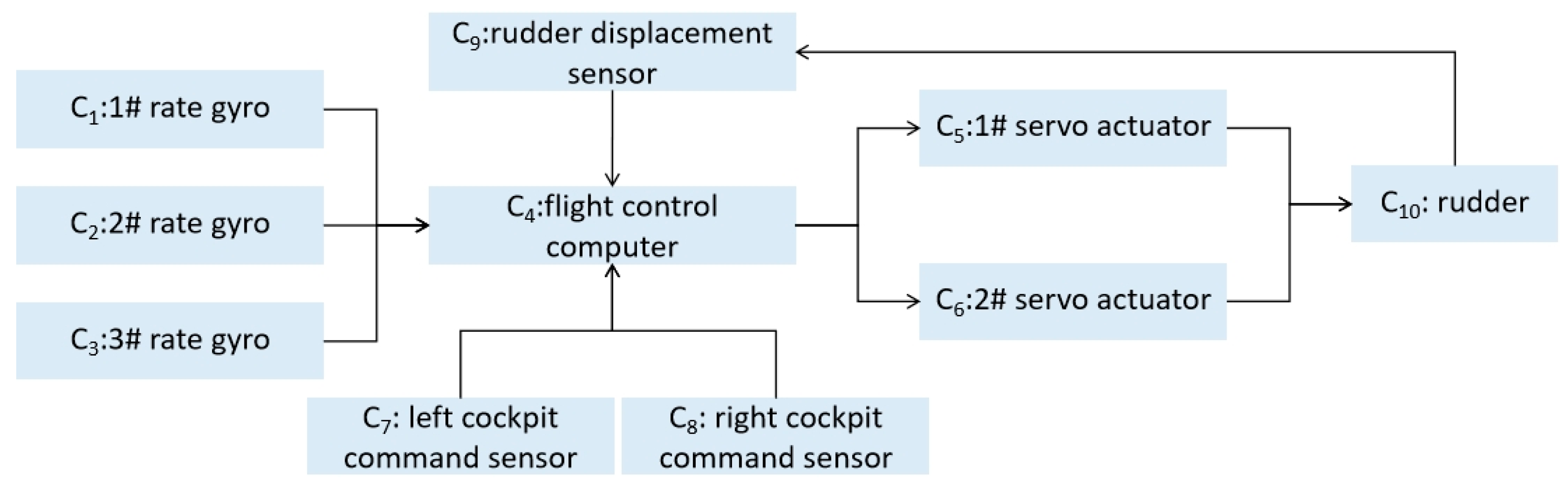
4.1.1. A Brief Introduction to the Rudder Control System
4.1.2. Reliability Model Construction for the Rudder Control System
- (1)
- The physical failure in the parent node must lead to the function loss of node Y, after which holds; according to the principle of probability normalization, the equation also holds.
- (2)
- When there is no physical failure in the parent node, the probability of working normally of Y is 1.0, namely ; according to the principle of probability normalization, the equation also holds.
4.1.3. Reliability Calculation and Discussion for the Rudder Control System
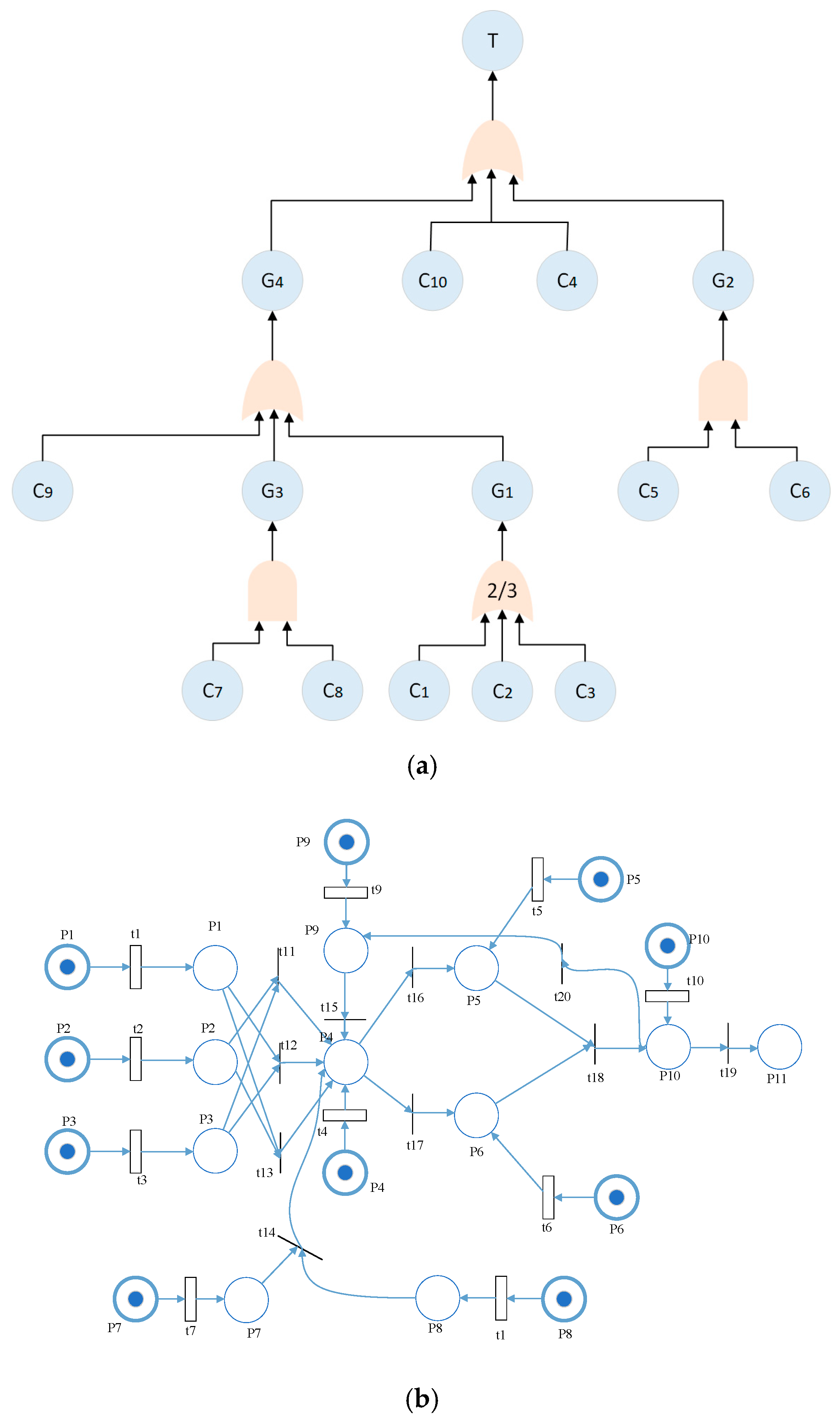
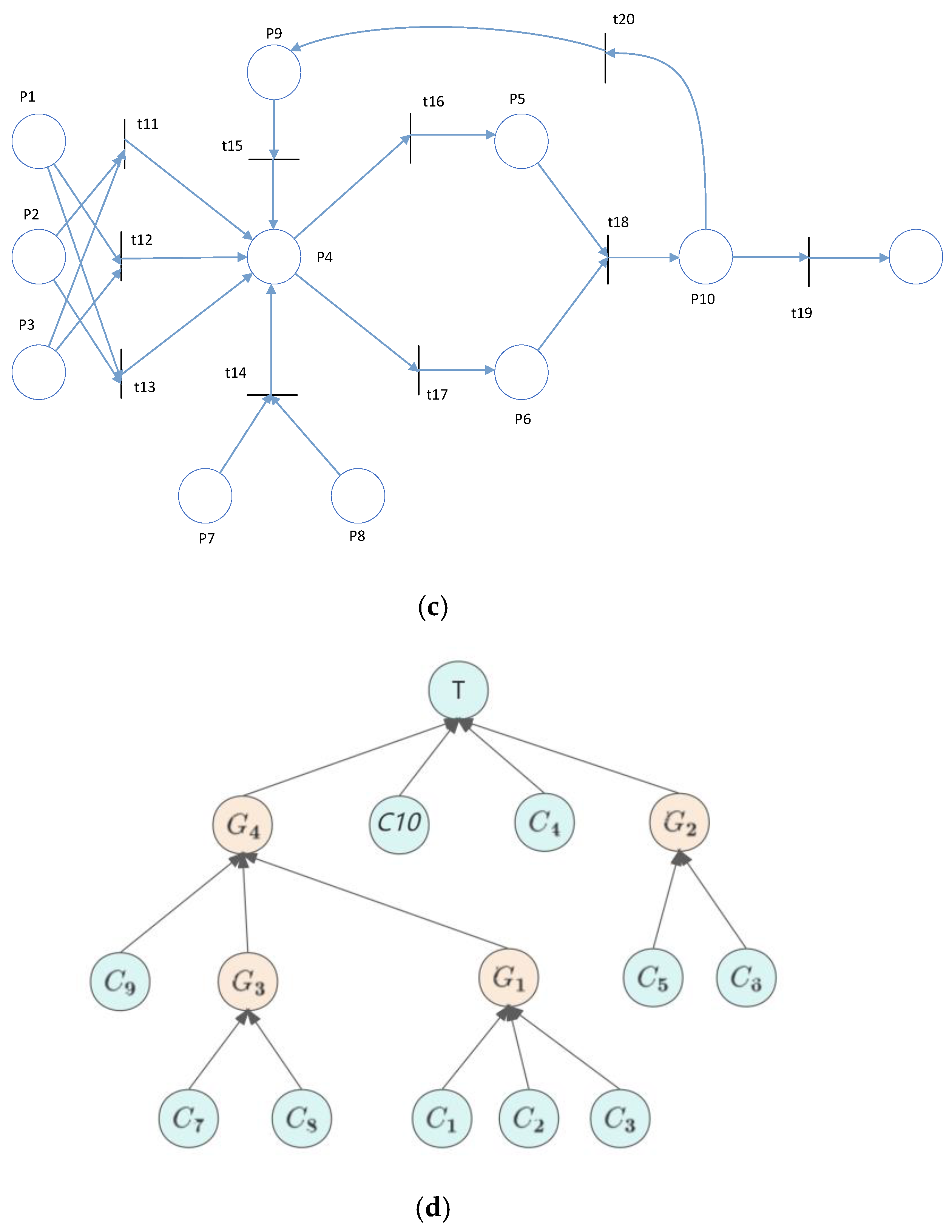
4.2. Reliability Analysis of Aircraft Fly-by-Wire Control System
4.2.1. A Brief Introduction to the Fly-by-Wire Control System
4.2.2. Reliability Model Construction for the Fly-by-Wire Control System
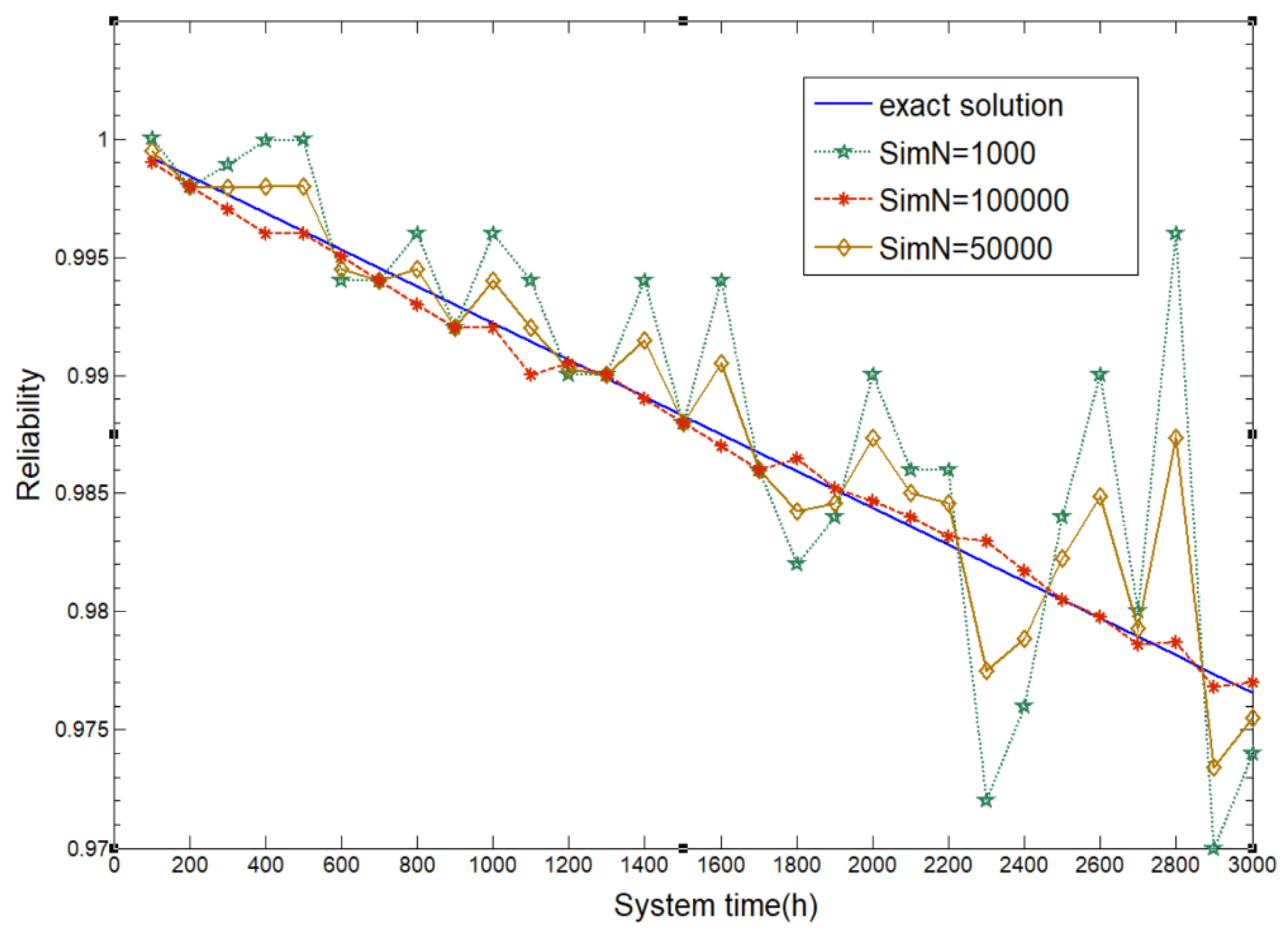
4.2.3. Reliability Calculation and Discussion for the Fly-by-Wire Control System
5. Conclusions
6. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moir, I.; Seabridge, A. Aircraft Systems: Mechanical, Electrical, and Avionics Subsystems Integration; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Guo, W. Analysis of Maintenance Cost of B737NG Aircraft. Available online: https://www.sohu.com/a/358383293_651535 (accessed on 12 October 2023).
- Society of Automotive Engineers Aerospace. Guidelines for Development of Civil Aircraft and Systems; SAE: Warrendale, PA, USA, 2010. [Google Scholar]
- Tiassou, K.; Kanoun, K.; Kaâniche, M.; Seguin, C.; Papadopoulos, C. Aircraft operational reliability—A model-based approach and a case study. Reliab. Eng. Syst. Saf. 2013, 120, 163–176. [Google Scholar] [CrossRef]
- Blatnický, M.; Dižo, J.; Sága, M.; Molnár, D.; Slíva, A. Utilizing Dynamic Analysis in the Complex Design of an Unconventional Three-Wheeled Vehicle with Enhancing Cornering Safety. Machines 2023, 11, 842. [Google Scholar] [CrossRef]
- Song, L.K.; Bai, G.C.; Fei, C.W.; Tang, W.Z. Multi-failure probabilistic design for turbine bladed disks using neural network regression with distributed collaborative strategy, Aerosp. Sci. Technol. 2019, 92, 464–477. [Google Scholar]
- Zio, E.; Fan, M.; Zeng, Z.; Kang, R. Application of reliability technologies in civil aviation: Lessons learnt and perspectives. Chin. J. Aeronaut. 2019, 32, 143–158. [Google Scholar] [CrossRef]
- Coit, D.W.; Zio, E. The evolution of system reliability optimization. Reliab. Eng. Syst. Saf. 2019, 192, 106259. [Google Scholar] [CrossRef]
- Zhou, C.; Chang, Q.; Zhao, H.; Ji, M.; Shi, Z. Fault tree analysis with interval uncertainty: A case study of the aircraft flap mechanism. IEEE T. Reliab. 2020, 70, 944–956. [Google Scholar] [CrossRef]
- Kornecki, A.; Liu, M. Fault Tree Analysis for Safety/Security Verification in Aviation Software. Electronics 2013, 2, 41–56. [Google Scholar] [CrossRef]
- Xu, Q.; Xu, Y.; Tu, P.; Zhao, T.; Wang, P. Systematic Reliability Modeling and Evaluation for On-Board Power Systems of More Electric Aircrafts. IEEE T. Power Syst. 2019, 34, 3264–3273. [Google Scholar] [CrossRef]
- Xiong, L.; Fan, Y.; Liu, Y.; Yang, Z.; Zeng, Z. Reliability analysis of service routing for a power system communication network based on MCS-RBD. IEEJ T. Electr. ELectr. 2018, 13, 1642–1648. [Google Scholar] [CrossRef]
- Anes, V.; Morgado, T.; Abreu, A.; Calado, J.; Reis, L. Updating the FMEA Approach with Mitigation Assessment Capabilities—A Case Study of Aircraft Maintenance Repairs. Appl. Sci. 2022, 12, 11407. [Google Scholar] [CrossRef]
- Ivančan, J.; Lisjak, D.; Pavletić, D.; Kolar, D. Improvement of Failure Mode and Effects Analysis Using Fuzzy and Adaptive Neuro-Fuzzy Inference System. Machines 2023, 11, 739. [Google Scholar] [CrossRef]
- Shiao, M.; Chen, T.K. Probabilistic Risk Assessment Tool AMETA (Aircraft Maintenance Event Tree Analysis) for Aircraft Structural Integrity and Fatigue Maintenance. In Proceedings of the AIAA SciTech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Lawhorn, D.; Rallabandi, V.; Ionel, D.M. Scalable graph theory approach for electric aircraft power system optimization. In Proceedings of the 2019 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Indianapolis, IN, USA, 22–24 August 2019. [Google Scholar]
- Kumar, T.B.; Sekhar, O.C.; Ramamoorty, M. Composite power system reliability evaluation using modified minimal cut set approach. Alex. Eng. J. 2018, 57, 2521–2528. [Google Scholar] [CrossRef]
- Nobakhti, A.; Raissi, S.; Damghani, K.K.; Soltani, R. Dynamic reliability assessment of a complex recovery system using fault tree, fuzzy inference and discrete event simulation. Eksploat. Niezawodn. 2021, 4, 593–604. [Google Scholar] [CrossRef]
- Mueller, S.; Gerndt, A.; Noll, T. Synthesizing Failure Detection, Isolation, and Recovery Strategies from Nondeterministic Dynamic Fault Trees. J. Aeros. Comp. Inf. Com. 2019, 16, 52–60. [Google Scholar] [CrossRef]
- Swanke, J.A.; Jahns, T.M. Reliability Analysis of a Fault-Tolerant Integrated Modular Motor Drive for an Urban Air Mobility Aircraft Using Markov Chains. IEEE T. Transp. Electr. 2022, 8, 4523–4533. [Google Scholar] [CrossRef]
- Bayrak, G.; Acar, E. Reliability Estimation Using Markov Chain Monte Carlo–Based Tail Modeling. AIAA J. 2017, 56, 1211–1224. [Google Scholar] [CrossRef]
- Zhao, Y.; Che, Y.; Lin, T.; Wang, C.; Liu, J.; Xu, J.; Zhou, J. Minimal cut sets-based reliability evaluation of the more electric aircraft power system. Math. Probl. Eng. 2018, 2018, 9461823. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, L.; Rong, H.; Gu, Q.; Zhang, R. A Dynamic Fault Tree Analysis Method Based on Discrete-time Bayesian Network for the Core Processing System of IMA. In Proceedings of the 2020 IEEE 11th International Conference on Software Engineering and Service Science (ICSESS), Cairo, Egypt, 16–18 October 2020. [Google Scholar]
- Wang, Y.; Yang, M.; Miao, Z.; Dong, X. A Reliability Modelling Method for Aircraft Electrical Power System Based on Probability Network. In Proceedings of the International Conference on Mathematics and Computers in Sciences and Industry (MCSI), Corfu, Greece, 25–27 August 2018. [Google Scholar]
- Guo, P. Research on the reliability analysis method of the complex aircraft system based on the Petri nets. Adv. Aeronaut. Sci. Eng. 2016, 7, 174–180. (In Chinese) [Google Scholar]
- Menu, J.; Nicolai, M.; Zeller, M. Designing fail-safe architectures for aircraft electrical power systems. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Cincinnati, OH, USA, 12–14 July 2018. [Google Scholar]
- Hoz, C.; Bussemaker, J.H.; Fioriti, M.; Boggero, L.; Nagel, B. Environmental and Flight Control System Architecture Optimization from a Family Concept Design Perspective. In Proceedings of the AIAA Aviation Forum, Virtual, 15–19 June 2020. [Google Scholar]
- Zio, E. Reliability engineering: Old problems and new challenges. Reliab. Eng. Syst. Saf. 2009, 94, 125–141. [Google Scholar] [CrossRef]
- Zhang, Y.; Kurtoglu, T.; Tumer, I.Y.; O’Halloran, B. System-Level Reliability Analysis for Conceptual Design of Electrical Power Systems. In Proceedings of the Conference on Systems Engineering Research (CSER), Redondo Beach, CA, USA, 15–16 April 2011. [Google Scholar]
- Joshi, A.; Heimdahl, M.P.E.; Miller, S.P.; Whalen, M.W. Model-Based Safety Analysis; No. NASA/CR-2006-213953; National Aeronautics and Space Administration, Langley Research Center: Hampton, VA, USA, 2006. [Google Scholar]
- Barker, T.; Parnell, G.S.; Pohl, E.; Specking, E.; Goerger, S.R.; Buchanan, R.K. Impact of Reliability in Conceptual Design—An Illustrative Trade-Off Analysis. Systems 2022, 10, 227. [Google Scholar] [CrossRef]
- Diatte, K.; O’Halloran, B.; Van Bossuyt, D.L. The Integration of Reliability, Availability, and Maintainability into Model-Based Systems Engineering. Systems 2022, 10, 101. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, X.; Cai, Y.; Yang, M.; Li, S.; Li, Y. Reliability evaluation for aviation electric power system in consideration of uncertainty. Energies 2020, 13, 1175. [Google Scholar] [CrossRef]
- Kritzinger, D. Aircraft System Safety: Military and Civil Aeronautical Application; Woodhead Publishing: Cambridge, UK, 2006. [Google Scholar]
- Modarres, M.; Kaminskiy, M.P.; Krivtsov, V. Reliability Engineering and Risk Analysis: A Practical Guide, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Elsayed, E.A. Reliability Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Khakzad, N.; Khan, F.; Amyotte, P. Safety analysis in process facilities: Comparison of fault tree and Bayesian network approaches. Reliab. Eng. Syst. Saf. 2011, 96, 925–932. [Google Scholar] [CrossRef]
- Kim, M.C. Reliability block diagram with general gates and its application to system reliability analysis. Ann. Nucl. Energy 2011, 38, 2456–2461. [Google Scholar] [CrossRef]
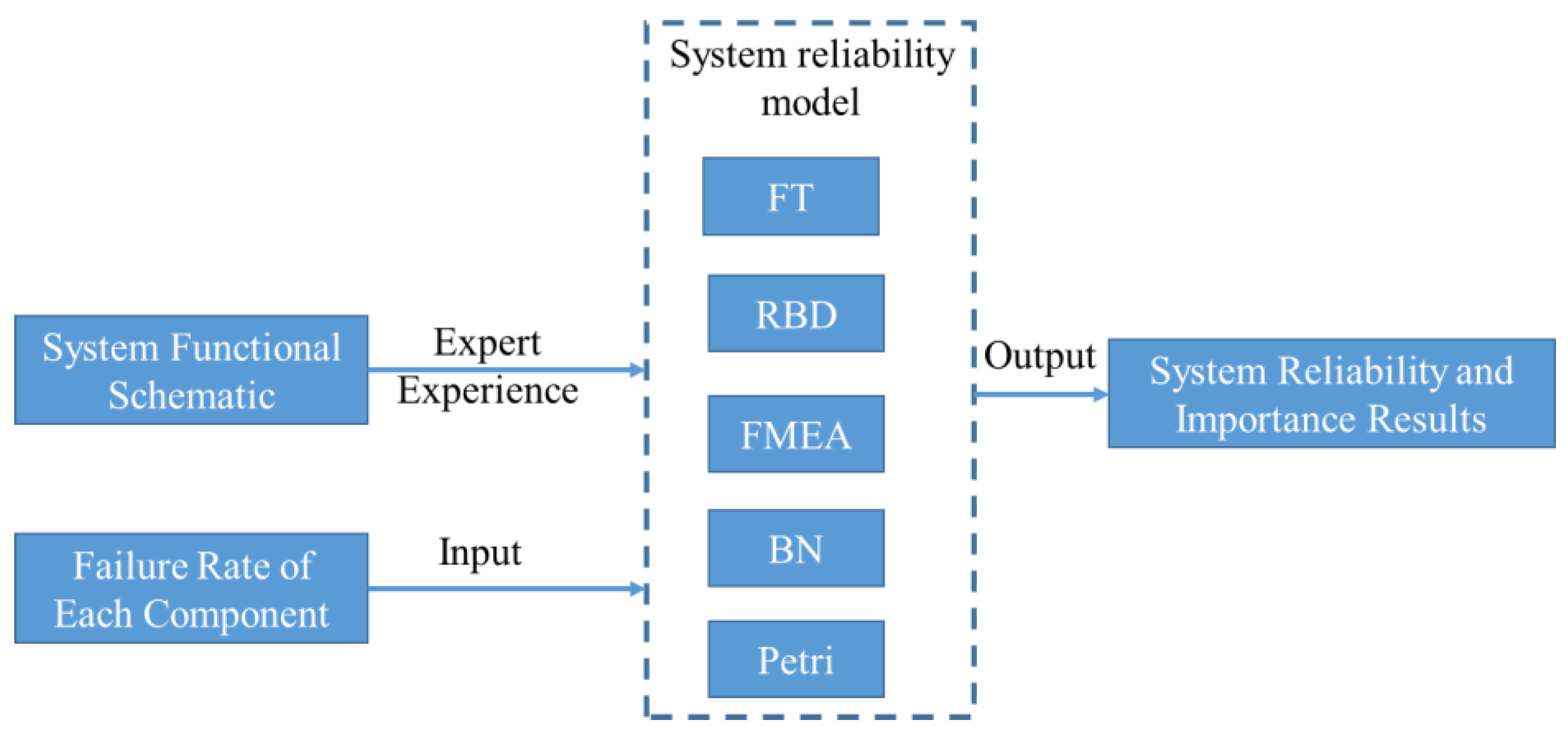







| System Models | Model Structure | Input Parameters of the Model | The Output of the Model | The Way of Modeling | Computing Ability |
|---|---|---|---|---|---|
| FTA | Tree structure consisting of basic events, intermediate events, and top events | Fixed failure rates of components | System reliability, structural importance, probabilistic importance, etc. | Relying on expert experience | Involving Boolean disjoint operations and combinatoric explosion problems |
| RBD | Composite for series, parallel, etc. | System reliability | Relying on expert experience | Involving Boolean disjoint operations and combinatoric explosion problems | |
| ET | Branch structure | System reliability, consequences of component failure | Relying on expert experience | Involving Boolean disjoint operations | |
| FMEA | The form of a table | Severity level of failure modes | Relying on expert experience | Unable to perform quantitative calculations | |
| BN | Directed acyclic graph with multiple nodes | System reliability, structural importance, probabilistic importance, Bayesian importance, etc. | Transformed from FTA, RBD, FEMA | Boolean disjoint operations are avoided and have a superior computational ability than FTA and RBD | |
| Petri net | A graph consisting of places, tokens, directed flows, and transitions | System reliability | Transformed from FTA, RBD, FMEA | Having the ability of visualization of fault propagation with the help of Monte Carlo simulation |
| Y′ Y | Pr(Y|Y′) |
|---|---|
| 0 0 | 1.0 |
| 0 1 | 0.0 |
| 1 0 | 0.0 |
| 1 1 | 1.0 |
| RBD Analysis Method | FTA Method | BN Reasoning Technique | |||
|---|---|---|---|---|---|
| RBD Model | FTA Model | BN Converted from RBD | BN Converted from FTA | The Proposed Three-State Space Model | |
| Pr(Sys = 0) | 0.989893 | 0.989893 | 0.989893 | 0.989893 | 0.989893 |
| Pr(A1 = 1|Sys = 1) | ⁄ | ⁄ | 0.019697 | 0.019697 | 0.019697 |
| Pr(A2 = 1|Sys = 1) | ⁄ | ⁄ | 0.019697 | 0.019697 | 0.019697 |
| Pr(A3 = 1|Sys = 1) | ⁄ | ⁄ | 0.010288 | 0.010288 | 0.010288 |
| Pr(A4 = 1|Sys = 1) | ⁄ | ⁄ | 0.010288 | 0.010288 | 0.010288 |
| Pr(A5 = 1|Sys = 1) | ⁄ | ⁄ | 0.010288 | 0.010288 | 0.010288 |
| Pr(A6 = 1|Sys = 1) | ⁄ | ⁄ | 0.010288 | 0.010288 | 0.010288 |
| Pr(A7 = 1|Sys = 1) | ⁄ | ⁄ | 0.010288 | 0.010288 | 0.010288 |
| Pr(A8 = 1|Sys = 1) | ⁄ | ⁄ | 0.010288 | 0.010288 | 0.010288 |
| Pr(A9 = 1|Sys = 1) | ⁄ | ⁄ | 0.010288 | 0.010288 | 0.010288 |
| Pr(A10 = 1|Sys = 1) | ⁄ | ⁄ | 0.010288 | 0.010288 | 0.010288 |
| Pr(A11 = 1|Sys = 1) | ⁄ | ⁄ | 0.989427 | 0.989427 | 0.989427 |
| Pr(Sys = 1|A1 = 1) | 0.019908 | 0.019908 | 0.019908 | 0.019908 | 0.019908 |
| Pr(Sys = 1| A2 = 1) | 0.019908 | 0.019908 | 0.019908 | 0.019908 | 0.019908 |
| Pr(Sys = 1|A3 = 1) | 0.010398 | 0.010398 | 0.010398 | 0.010398 | 0.010398 |
| Pr(Sys = 1|A4 = 1) | 0.010398 | 0.010398 | 0.010398 | 0.010398 | 0.010398 |
| Pr(Sys = 1|A5 = 1) | 0.010398 | 0.010398 | 0.010398 | 0.010398 | 0.010398 |
| Pr(Sys = 1|A6 = 1) | 0.010398 | 0.010398 | 0.010398 | 0.010398 | 0.010398 |
| Pr(Sys = 1|A7 = 1) | 0.010398 | 0.010398 | 0.010398 | 0.010398 | 0.010398 |
| Pr(Sys = 1|A8 = 1) | 0.010398 | 0.010398 | 0.010398 | 0.010398 | 0.010398 |
| Pr(Sys = 1|A9 = 1) | 0.010398 | 0.010398 | 0.010398 | 0.010398 | 0.010398 |
| Pr(Sys = 1|A10 = 1) | 0.010398 | 0.010398 | 0.010398 | 0.010398 | 0.010398 |
| Pr(Sys = 1|A11 = 1) | 1 | 1 | 1 | 1 | 1 |
| System Time | FTA Method | BN Converted from FTA | Three-State Space Method in GSPN Language simN = 1000 | Three-State Space Method in GSPN Language simN = 50,000 | Three-State Space Method in GSPN Language simN = 100,000 |
|---|---|---|---|---|---|
| 200 | 0.998440 | 0.998440 | 0.998000 | 0.998000 | 0.998000 |
| 400 | 0.996880 | 0.996880 | 0.999950 | 0.997675 | 0.996000 |
| 600 | 0.995320 | 0.995320 | 0.994000 | 0.995500 | 0.995000 |
| 800 | 0.993759 | 0.993759 | 0.996000 | 0.996500 | 0.993000 |
| 1000 | 0.992199 | 0.992199 | 0.996000 | 0.993900 | 0.992000 |
| 1200 | 0.990639 | 0.990639 | 0.990000 | 0.990240 | 0.990500 |
| 1400 | 0.989079 | 0.989079 | 0.994000 | 0.991600 | 0.989000 |
| 1600 | 0.987519 | 0.987519 | 0.994000 | 0.990600 | 0.987000 |
| 1800 | 0.985958 | 0.985958 | 0.982000 | 0.984240 | 0.986500 |
| 2000 | 0.984398 | 0.984398 | 0.990000 | 0.987340 | 0.984700 |
| 2200 | 0.982838 | 0.982838 | 0.986000 | 0.984700 | 0.983200 |
| 2400 | 0.981278 | 0.981278 | 0.976000 | 0.978840 | 0.981700 |
| 2600 | 0.979718 | 0.979718 | 0.990000 | 0.985000 | 0.979800 |
| 2800 | 0.978158 | 0.978158 | 0.996000 | 0.987360 | 0.978700 |
| 3000 | 0.976599 | 0.976599 | 0.974000 | 0.975200 | 0.977000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, F.; Feng, Y.; Cao, S. A Three-State Space Modeling Method for Aircraft System Reliability Design. Machines 2024, 12, 13. https://doi.org/10.3390/machines12010013
Wang Y, Wang F, Feng Y, Cao S. A Three-State Space Modeling Method for Aircraft System Reliability Design. Machines. 2024; 12(1):13. https://doi.org/10.3390/machines12010013
Chicago/Turabian StyleWang, Yao, Fengtao Wang, Yue Feng, and Shancheng Cao. 2024. "A Three-State Space Modeling Method for Aircraft System Reliability Design" Machines 12, no. 1: 13. https://doi.org/10.3390/machines12010013
APA StyleWang, Y., Wang, F., Feng, Y., & Cao, S. (2024). A Three-State Space Modeling Method for Aircraft System Reliability Design. Machines, 12(1), 13. https://doi.org/10.3390/machines12010013







