Abstract
A new multirotor aerial vehicle with two rotor arms formed in a V-shape configuration is introduced in this paper. To figure out the aerodynamic interference effects between rotors as an implication of the control method, this paper discusses the aerodynamic performance of the V8 Octorotor MAV with different rotor spacing using both experiments and simulations. A hovering experiment platform is applied to obtain the thrust, power consumption and rotational speed. PL (power loading) is promoted to characterize the aerodynamic performance of the V8 Octorotor MAV. The velocity vector, streamline and turbulent vortices’ distribution of the V8 Octorotor MAV are presented as the simulation results, which indicates that turbulence intensity generated by the MAV dissipates faster in a large rotor spacing. Therefore, rotor vibration is reduced with an increased hovering stability, and the power loading is much improved at G3 (1.2D–1.4D–1.6D–1.8D) with a better aerodynamic performance both with a thrust increment and power decrement.
1. Introduction
Currently, MAVs (Multirotor Aerial Vehicle) are widely used in various service missions, including field exploration, agricultural irrigation and aerial photography [1,2,3,4], because of the VTOL (vertical take-off and landing) abilities and efficient propulsion system [5,6]. Traditional configurations of multirotor vehicles such as coaxial rotors, quadrotors and Hex-rotors are arranged as a circle, X or star shape. In particular, the MAVs with coaxial rotors are inclined with strong interference between the upper and lower rotor which obtains only about 80% efficiency. Generally, the camera is installed concentric to the CG (Centre of Gravity) to maintain mass balance [7]. Thus, a tilt angle in the direction of forward motion for accelerating is desired. In this case, flight view of the vehicle is limited, as showed in the Figure 1a. This paper introduces a new MAV with two rotor arms formed in a V-shape configuration, and there are four rotors equipped on each rotor arm. We call it the V8 Octorotor MAV, which is more convenient for camera installation without any extra manipulation for the MAV (see Figure 1b). Compared to traditional configurations of MAVs, the most significant character of the V8 Octorotor MAV is the non-centrosymmetric-distributed combination of rotors. The V8 Octorotor MAV has more rotors to provide efficient thrust for flight, which also makes it possible to carry larger payloads. Especially, for the forward flight, fuselage of the V8 Octorotor MAV tilts towards the acceleration direction where the flight view is much wider, with a proper rotor spacing compared to that of traditional configurations. Therefore, V8 Octorotor MAV is a popular choice in aerial photography.
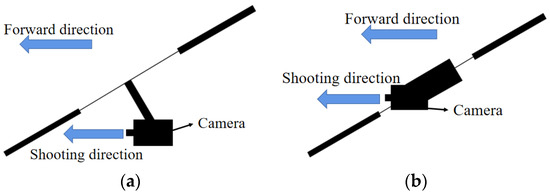
Figure 1.
Camera installation for forward flight. (a)Traditional MAV; (b) V8 Octorotor MAV.
Current studies are focused on the control strategies of the MAVs, withfew of them concentrated on the improved aerodynamics either in experiments or numerical simulations. Sina Rezazadeh et al. [7] applied the laboratory data and genetic optimization algorithm on a dynamic model to estimate the performance of the MAV. Cole, J.A. et al. [8] investigated an integrated propeller-wing system and found that the power of the propeller required trimming, for the vehicle was sensitive to the vertical location of the propeller. Yuhui Huang et al. [9] studied the aerodynamic performance of a small Octorotor MAV with different rotor spacing in hover; they found that the optimal ratio of rotor spacing will improve the aerodynamic efficiency with thrust increment. Zou, Xiaohua et al. [10] also found that the aerodynamic performance of the micro-motor in a quadrotor increased with the Reynolds number for a given range. These studies are only based on the numerical method with flow field analysis. Additionally, Salazar, S. et al. [11] introduced an original configuration of an Octorotor, and they developed a new type of dynamic model for the Octorotor using the Euler–Lagrange approach and verified its abilities. Osmic, Nedim et al. [12] derived the detail model of the specific Octorotor system, and designed a stabilization control for the Octorotor system. Haddadi, S. Jamal et al. [13] discussed a full procedure of mechanical design and the system of a new Octorotor configuration that includes four coaxial rotors, and achieved automatic control of the motor with the PID control method. Additionally, Sadeghi, Parichehr Shahidi et al. [14] used the Euler–Lagrange method to realize a dynamic model of the V8 Octorotor MAV to stabilize Octorotor altitude angles.
The studies mentioned above do not consider or just simplify aerodynamic interference effects between rotors or fuselage drag, and hence, as an implication for the control method. Since the V8 Octorotor MAV is promoted as the novel configuration in this paper, it is noted that the overall aerodynamics are clearly more complex than traditional MAVs where the rotor interference are likely to be larger and nonlinear. To avoid a number of simplifying assumptions on the further control strategies with the effect of the rotor wakes, this paper studied the aerodynamic performance of the V8 Octorotor MAV. Additionally, results presented in this paper can be the implication of these works to complete control strategies. Hence, this work seeks to answer the following questions: (1) How does a change in rotor spacing between the two rotor arms affect propulsive efficiency at the extremes? (2) Where does the higher thrust come from, compared to the isolated rotor without interference? (3) How do the interferences change into a benefit for the thrust increment, or power decrement, or even the flight duration?
2. Aerodynamic Model of V8 Octorotor MAV
2.1. V8 Configuration
A sketch of the V8 Octorotor MAV is showed in Figure 2, where ‘D’ represents the rotor diameter of 400 mm, ‘L’ is the rotor spacing of two rotor arm, ‘n’ is the rotor spacing of adjacent rotors on the same rotor arm, ‘T’ the thrust generated by each rotor and ‘ω’ is the rotational speed of each rotor. Each rotor is labelled from ‘1’ to ‘8’, and arrows are the rotation direction which means adjacent rotors are clockwise and counterclockwise. Clearly, rotor interference mainly comes from: (1) the interaction between the adjacent rotors on the same rotor arm where the spacing is limited to n and the inflow concentrates on the rotor disks, which results in the interaction of the downstream and variation of the induced velocity; and (2) interference from the adjacent rotors between the two rotor arms where the spacing L is considered as a variable to characterize the strength of the interference. Eventually, the aerodynamic performance of the V8 Octorotor MAV is determined by rotor spacing L, and the stability and flight efficiency of MAV in hover are affected as a whole. Figure 2b shows the aerodynamic interference between the rotors ‘1’ and ‘5’ as an example. Adjacent rotors are counterrotating with the same level of velocity to offset torque generated by each rotor, which is aiming to avoid yaw drift [15]. T1 and T5 represent thrust generated by rotors ‘1’ and ‘5’, respectively. Thus, the vertical movement is achieved by increasing or decreasing the thrust of the whole vehicle [16]. For optimal tasks, the engineering requirement for this V8 Octorotor MAV is to design the propulsion group for maximum thrust/power ratio with better hover efficiency. In the meantime, the structural mass is also assumed to be minimized. Hence, there has to be a suitable tradeoff between improved efficiency to provide sufficient thrust with lower power or reduced payload with increased weight. Furthermore, the complex aerodynamic environment with rotor interference also imposes difficulties to obtain the best rotor configuration of the V8 Octorotor MAV. For example, the stronger rotor interferences with vortices movement in the outflow also needs to be considered. Additionally, the strict design requirement for the hover efficiency is also affected by several variables besides the adjacent rotor spacing L. To promote a propulsion system with the greatest degree of capacity and aerodynamic performance, it is important to obtain the optimal rotor arrangement for our further flight tests and some particular applications.
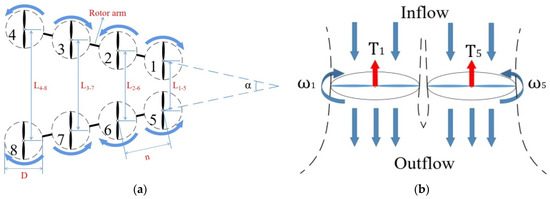
Figure 2.
Sketch of V8 Octorotor MAV. (a) Geometry and forces which each rotor is labelled from 1 to 8, and arrows are the rotation direction which means adjacent rotors are clockwise and counterclockwise.; (b) Flow field with aerodynamic interference for rotors 1 and 5, for instance.
2.2. Theoretical Analyze
2.2.1. Aerodynamic performance
The hover efficiency of the V8 Octorotor MAV is characterized by its power loading (PL). The specific calculation formula is as follows.
T and vh indicate thrust and induced flow velocity; the relation of T and vh can be expressed as [17]:
where the A is the area of rotor disk, V is the total velocity and ρ is the air density of 1.225 kg/m3. According to Equation (2), it is easy to get the theoretical induced power consumption of each rotor Pi, and it can be defined as follows [18]:
Power loading is defined as PL which is the ratio of the thrust to the power consumption; PL increases with the thrust increment or the power decrement, which is [19]:
where DL is the disk loading and can be defined as:
Additionally, the hover efficiency is:
Clearly, the hover efficiency is achieved by not only the increased thrust but also the reduced power consumption. When designing a MAV, it is wanted to maximize the hover efficiency such that energy requirements are minimized. This will give the whole vehicle the best endurance or payload capabilities possible.
2.2.2. Turbulence Analysis
Generally, the increased pressure difference between the upper and lower surfaces of the rotor leads to the increase of vortex movement with a higher thrust. Specifically, vortices on the rotor tip could easily cause rotor vibration with increased power consumption [20,21,22]. Since the flow around the blade tips is more chaotic with higher turbulence intensity, it will affect the aerodynamic performance of the rotor due to interaction with the vortices caused by the other blades, and lead to less lift generation or additional energy loss, and thus decreases the hover efficiency of the whole MAV.
The turbulence flow contains vortices with different sizes and scales. The large vortex in airflow will be broken into small vortices, which will constantly be consumed by viscosity. Turbulence intensity is defined as the change of flow velocity over time and space. The formula for calculating turbulence intensity is as follows [23]:
where I is turbulence intensity, U is the average velocity, u′ represents the mean square root of turbulence velocity pulsation and k is turbulent kinetic energy.
Turbulent kinetic energy is presented to obtain the turbulence intensity and represents the degree of turbulence velocity pulsation. Generally, the turbulent kinetic energy is low in the area of uniform flow. Its calculation formula is as follows:
where k represents the turbulent kinetic energy, and u′, v′ and w′ represent the pulsation velocity of turbulence in X, Y and Z directions. Generally, the areas with high speed pulsation may lead to the rotor vibration.
3. Technique Approach
3.1. Experiment
A hovering test platform was built to obtain the thrust, power consumption and rotational speed of the V8 Octorotor MAV. Sensor information is showed in Table 1. All data obtained from experiment are transferred to the data acquisition system. The main sources of error in these experiments are the standard deviations of the rotational speed and the mean voltages from the thrust sensors. Typical values of the standard deviations of thrust are about 1% of the mean values. Rotational speed error is related to the finite number of magnets that excite the tachometer. To determine accuracy of the test measurements, an uncertainty analysis of all the key parameters was performed. The values of uncertainty that are presented in this study are all calculated for 95% confidence levels.

Table 1.
Sensors.
The V8 Octorotor MAV is located at 1.5 m to avoid any ground effect and the experimental setup is showed in Figure 3.
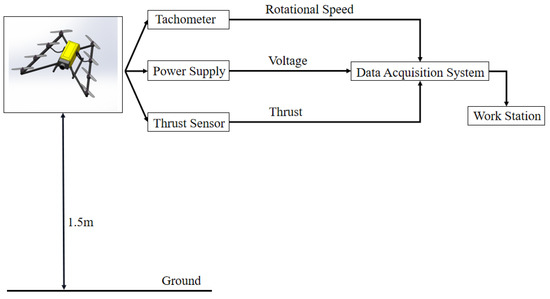
Figure 3.
Sketch of the experimental setup.
To avoid an oversize of the MAV, the rotor spacing on the same rotor arm, n, is considered as a constant. There are four different rotor spacings between the two rotor arms which will be considered as one group to study the aerodynamic performance of the V8 Octorotor MAV. In this paper, seven groups of the rotor spacings to avoid rotor crash or oversize of the vehicle are listed in Table 2, where D is the rotor diameter and L is rotor spacing between two rotor arms. Clearly, the rotors ‘1’ and ‘5’ obtain the strongest aerodynamic interference with a small rotor spacing.

Table 2.
Rotor spacing groups for V8 Octorotor MAV.
The Reynolds number is approximately 0.59 × 105~0.99 × 105, and density of air and viscosity of air are set as 1.225 kg/m3 and 1.7894 × 10−5 kg/(m·s) respectively. The rotor model is displayed in Figure 4.

Figure 4.
Propeller model. (a) Top view; (b) Front view.
The rotational speed is ranged from 1600 rpm to 2300 rpm including all the speed in hover flight. Rotors are made of carbon-fibre-reinforced composite, and the rotor diameter is 400 mm with an average chord length of 35 mm and a pitch of 157 mm. Detailed parameters of the rotor are listed in Table 3.

Table 3.
Parameters of the propeller. RPM: Revolutions per Minute.
3.2. Numerical Simulation
The whole computational domain, as showed in Figure 5, is divided into nine regions including one cylinder stationary region (10 times of the rotor diameter) and eight cylinder rotating regions (to capture the flow detail of four rotors with refined mesh), which has a total size of 25 million cells. The MAV is located the upper region of the domain to obtain the detail of the downwash flow of the MAV. The element sizing of an isolated rotation region is 2 mm. The max element metrics is below 0.8, which is enough to capture the flow detail of the rotor tip and the interfaces between stationary and rotating regions. Additionally, the mesh on the rotor tip is refined to reach the independence state. The cylinder is set as a pressure outlet. Transient flow solver, combining two algorithms, Pressure-Implicit with Splitting of Operators (PISO) and Semi-Implicit Method for Pressure-Linked Equations (SIMPLE), is used in simulations. The adjustable time step, based on the dimensionless Courant–Friedrichs–Lewy condition (CFL) number of less than one, is used for all simulations. The second order discretization schemes are utilized for the time discretization and also for convection and diffusion terms, which are more accurate than standard since interpolation errors and pressure gradient assumptions on the boundaries are avoided. Furthermore, a central differencing scheme is selected to achieve a low numerical diffusion. The bounded central differencing scheme is a composite scheme that consists of a pure central differencing, a blended scheme of central differencing and second-order upwind scheme. The bounded central differencing scheme is performed for the final simulations to prevent any unnecessary fluctuations in the solution fields. Additionally, a formal grid independence study was conducted to show that the results are already reaching the grid independence state.
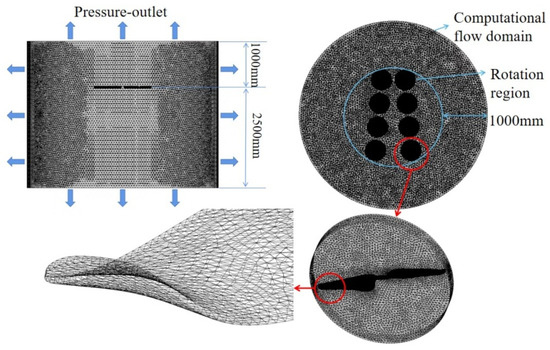
Figure 5.
Computational domain.
4. Results
4.1. Experiment Results
The rotational speeds of 1600 rpm, 1800 rpm, 2000 rpm and 2200 rpm are selected as four specific rotational speed cases in hover. ‘G’ is short for Group in the following figures. The variation of thrust with increased rotor spacing at 1600 rpm, 1800 rpm, 2000 rpm and 2200 rpm are shown in Figure 6. Eight single rotors without interference are also introduced as comparison to obtain the effect of the interference. As shown in the figure, the maximum thrust of the V8 Octorotor MAV is 3362.801 g which increased 4.05% compared with isolated rotors without interference. There is a sudden change at G3 and G5, and there is also a moderate thrust increment from G1 to G3, and huge increment from G5 to G7. Thus, it is very interesting to note the thrust increment, which indicated an improved aerodynamic performance with a higher manipulation.
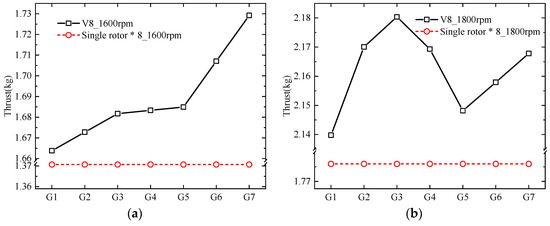
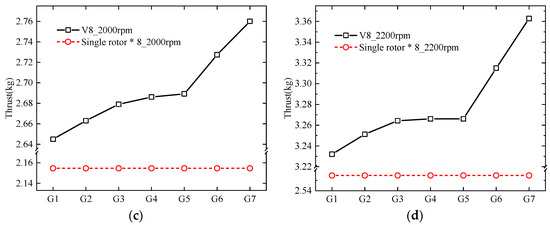
Figure 6.
Thrust variation. (a) 1600 rpm; (b) 1800 rpm; (c) 2000 rpm; (d) 2200 rpm.
The variation of power consumption with increased rotor spacing at 1600 rpm, 1800 rpm, 2000 rpm and 2200 rpm are shown in Figure 7. Power consumption of V8 Octorotor MAV is lower than that of the isolated rotors at 1600 rpm and 1800 rpm, which indicates that this kind of MAV achieved a higher flight duration, especially for a lower rotor speed. The hovering power consumption for G1 and G2 is higher than that of eight single rotors which may be caused the strong interference for a smaller rotor spacing. Additionally, there is clear sudden change at G3 where the lowest power consumption is about 125.743 w. Thereafter, the power increased with the rotor speed. This may be caused by the increasing rotor interference between the adjacent rotors on the same rotor arm with the fixed rotor spacing while the rotor interference is intended to decrease from G5 to G7 with the increasing rotor spacing.
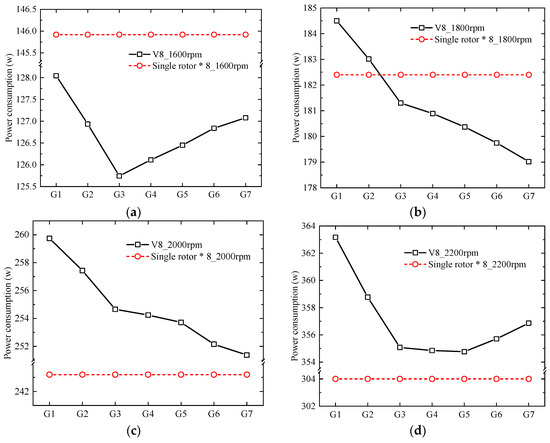
Figure 7.
Power variation. (a) 1600 rpm; (b) 1800 rpm; (c) 2000 rpm; (d) 2200 rpm.
PL variation with rotor spacing is shown in Figure 8. It can be seen that the PL decreased with the rotor speed and achieved the maximum at 1800 rpm. However, the hover efficiency is much improved with the increasing rotor speed, which may be caused by the higher thrust increment for the higher rotor speed.
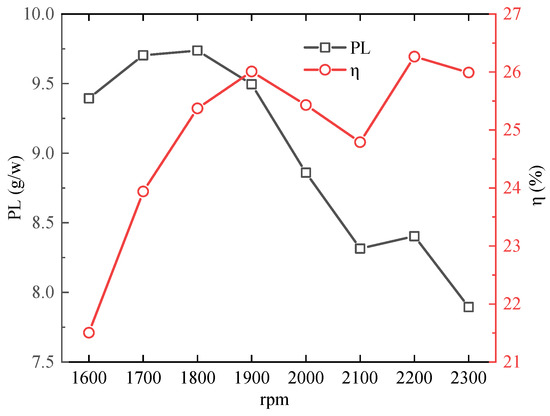
Figure 8.
PL variation.
4.2. Numerical Simulations Results
Validation of the simulations with experimental results is showed in Figure 9. The thrust coefficient CT exported from the simulations and calculated with the experimental data is promoted as the comparison. Results showed that the relative error between the experiments and simulations is less than 5% and they were generally in good agreement.
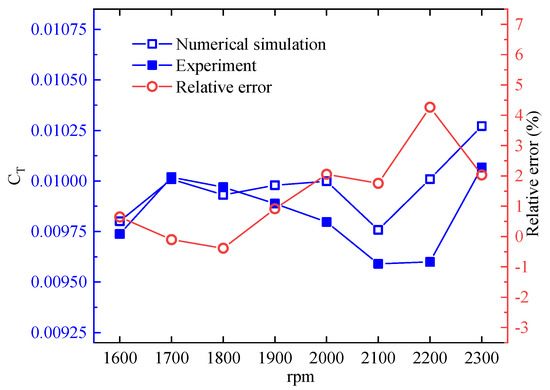
Figure 9.
Comparison of thrust coefficient CT.
4.2.1. Velocity and Streamline Distribution
Cross sections of V8 Octorotor MAV to present the variation of the velocity and streamline are shown in Figure 10, where Z is the distance between the cross profile and the XY plane, and R is rotor radius.
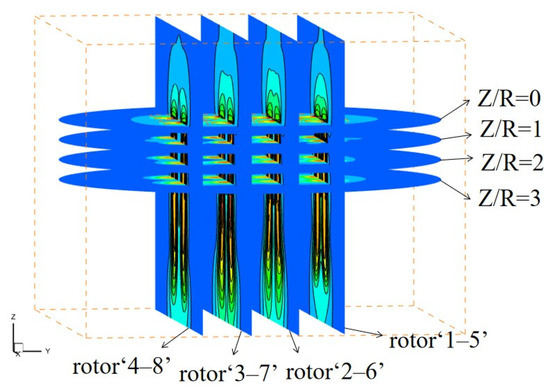
Figure 10.
Cross sections of V8 Octorotor MAV.
Figure 11 shows the velocity and streamline distribution of the V8 Octorotor MAV on the planes ‘1–5’, ‘2–6’, ‘3–7’, and ‘4–8’ for 2000 rpm in hover. The rotor spacing on each plane is 480 mm, 560 mm, 640 mm and 720 mm respectively. As showed in the figure, two distinct vortices are generated on each side of the downwash, and the inflow between the two adjacent rotors increases with the increase of rotor spacing. With the increase of rotor spacing, the inflow at the gap between the two rotors will also increase. Velocity of airflow over the rotor is about 3.22 m/s. The induced velocity increases when the airflow passes through the rotor disk, and the maximum downwash velocity, can reach up to 5.15 m/s. Additionally, the high-speed area ranged from 3.125 m/s to 5.15 m/s at the bottom of rotor ‘1–5’ generally contracted to the gap between two rotors. The downwash generated by the two rotors was prone to overlap, which maintains relatively strong aerodynamic interference. Additionally, the gap increased with the increase of rotor spacing for the planes of ‘2–6’, ‘3–7’ and ‘4–8’, which indicated the downwash is inclined to separate with less rotor interference.
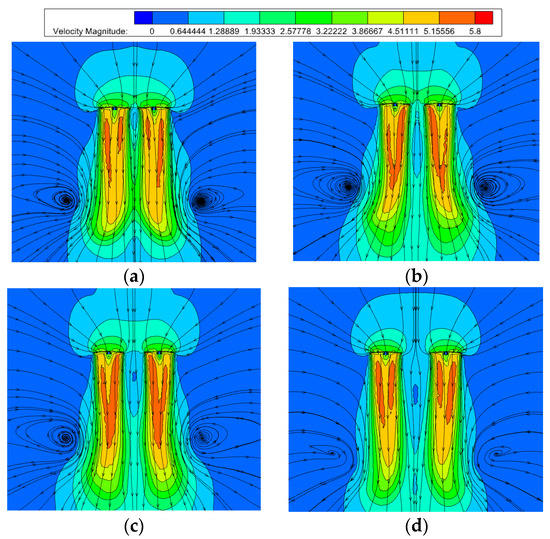
Figure 11.
Velocity distribution. (a) rotor ‘1–5’; (b) rotor ‘2–6’; (c) rotor ‘3–7’; (d) rotor ‘4–8’.
Figure 12 shows the velocity distribution of the V8 Octorotor MAV in cross profiles at 0R, 1R, 2R and 3R from the XY plane for Group 1, Group 3, Group 5 and Group 7. The inflow is coupled easily between adjacent rotors with small rotor spacing, especially between four rotors on the same rotor arm. At plane of Z/R = 0 for Group 1, the velocity of the concentrated airflow is higher than the external airflow velocity, especially for the rotor ‘1–5’ and ‘2–6’. In this case, the mutual induction of downwash tends to attract each other, which will lead to thrust increment. However, this increment is weakened between the rotor ‘4–8’ for the increase of rotor spacing, especially at Group 7. The airflow velocity decreases where the improved performance may come from the further decreased power consumption, and the interference of the downwash is also weakened.
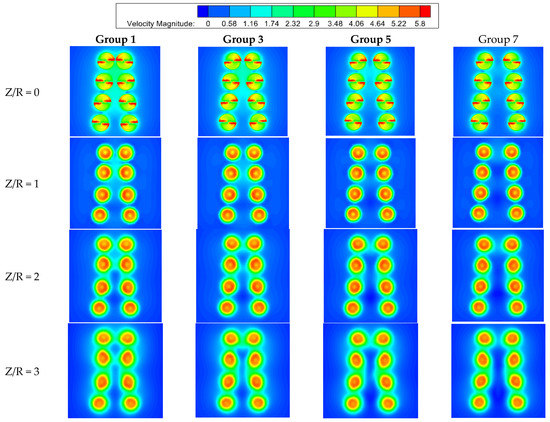
Figure 12.
Velocity distribution.
4.2.2. Turbulent Kinetic Energy Distribution
Figure 13 shows turbulent kinetic energy and velocity distribution of the V8 Octorotor MAV at Group 3 (1.2D–1.4D–1.6D–1.8D) where both the thrust and the power consumption presented a sudden change for this case. As showed in the figure, the higher turbulent kinetic energy is mainly distributed on the blade tip for each rotor of the V8 Octorotor MAV, which indicates that this part maintains a higher velocity pulsation of airflow. Obviously, there is turbulence coupling between adjacent rotors on the same rotor arms with a fixed rotor spacing, and the turbulence kinetic energy generated by turbulence coupling at this part of the position is relatively higher. On the contrary, the turbulent kinetic energy of the airflow of the adjacent rotors on the two rotor arms with the increasing rotor speed caused the turbulent kinetic energy is lower at the centre of the V8 Octorotor MAV system, which indicates that the pulsation degree of the airflow velocity is also low. For velocity distribution, the high-speed area is mainly distributed near the surface of each rotor. On the contrary, the airflow velocity at gaps between adjacent rotors is relatively lower.
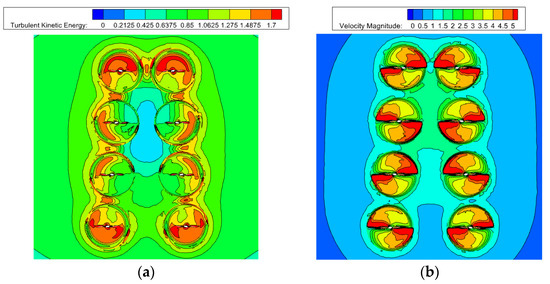
Figure 13.
Turbulent kinetic energy and velocity distribution at G3. (a) Turbulent kinetic energy; (b) Velocity.
According to Formula (9) and the mentioned numerical simulation results, the turbulence intensity between adjacent rotors with small spacing is relatively high. In this case, the energy loss in the adjacent rotor gap is higher, which increases the power consumption of the V8 Octorotor MAV. Figure 14 shows the turbulent kinetic energy distribution at 2000 rpm for Group 1, Group 3, Group 5 and Group 7. The range of turbulent kinetic energy of the external airflow around the V8 Octorotor MAV is about 0.756 m2/s2~1.322 m2/s2. As showed in the Figure 14, the turbulent kinetic energy at the rotor tip of ‘1’, ‘4’, ‘5’ and ‘8’ is significantly lower than that of the other rotors. However, the turbulent kinetic energy at the rotor tip will gradually increase with the rotor spacing. In addition, for a smaller spacing, such as for rotors ‘1’ and ‘5’, the turbulent kinetic energy is weakened significantly. Considering that the rotor spacing on the same rotor arm is fixed as a constant, the turbulent kinetic energy on the same arm is almost the same.
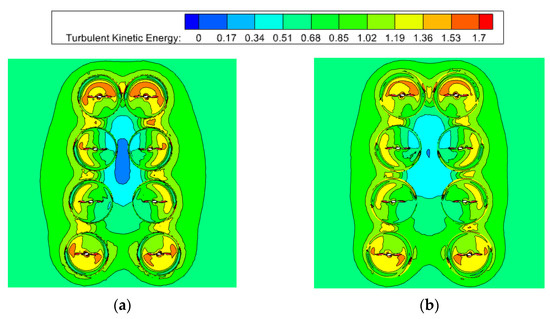
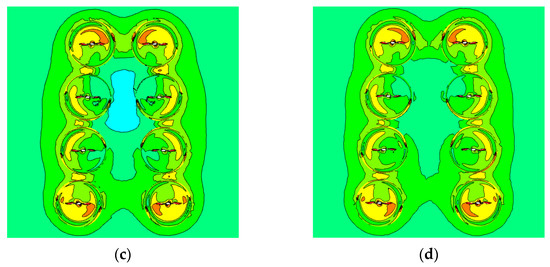
Figure 14.
Turbulent kinetic energy distribution. (a) Group 1; (b) Group 3; (c) Group 5; (d) Group 7.
5. Conclusions
This paper introduced a V8 Octorotor MAV with arms in a V shape, and it is focused on the aerodynamic performance of the V8 Octorotor MAV in hover, which is characterized by PL and hover efficiency, using both experiments and numerical simulations. Conclusions are as followed:
- (1)
- The aerodynamic performance of the V8 Octorotor MAV is much improved compared to traditional MAVs. The thrust increased with the rotor spacing and it is also higher than the sum of the eight single rotors, which indicates that the rotor interference is inclined to increase the thrust as an improvement of the V8 Octorotor MAV. Additionally, the power consumption is also decreased, especially for the lower rotor spacing. It is interesting to note that the aerodynamic performance characterized with power loading and flight efficiency is much improved in this case.
- (2)
- Numerical simulations showed that the improved performance comes from the collapse of the suction forces on the tip and the increase in turbulent kinetic energy caused by the flow separation. The outflow is relatively unsteady at some rotor spacing, and the rotor is apt to have somewhat greater interaction with its own wake. This highlighted interaction may lead to the decrease of PL. For higher rotor spacing, the vortex deformation related to the power consumption also results from the movement of the vortices and the symmetric of the vortices, which may cause vibration or extra power consumption, or even offset the rotor interference with a small extra induced power.
- (3)
- The V8 Octorotor MAV of Group 3 (1.2D–1.4D–1.6D–1.8D) is the optimal rotor configuration in hover where the downwash interference is relatively stable for all the rotor speed and the turbulent kinetic energy is also concentrated at the blade tip. In this case, the V8 Octorotor MAV is advantageous for obtaining extra thrust with decreasing power for higher flight duration and hover efficiency. Further studies will involve the advanced control strategies with the rotor interference and more field flight tests.
Author Contributions
Y.L. carried out experiments; Z.F. wrote the manuscript with assistant of Y.L. and C.M. performed the data analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This project was supported by the National Natural Science Foundation of China (Grant No. 52275095).
Data Availability Statement
All data are already included in the manuscript.
Acknowledgments
The authors thank the Key Laboratory of Fluid Power and Intelligent Electro-Hydraulic Control (Fuzhou University) for applying the experimental field.
Conflicts of Interest
The authors declare that there are no conflict of interest regarding the publication of this paper.
References
- Atmaca, M.; Cetin, B.; Yilmaz, E. CFD Analysis of Unmanned Aerial Vehicles (UAV) Moving in Flocks. Acta Phys. Pol. A 2019, 135, 694–696. [Google Scholar] [CrossRef]
- Otsuka, H.; Nagatani, K. Thrust Loss Saving Design of Overlapping Rotor Arrangement on Small Multirotor Unmanned Aerial Vehicles. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3242–3248. [Google Scholar]
- Teng, H.; Ahmad, I.; Alamgir, M.S.M.; Chang, K. 3D Optimal Surveillance Trajectory Planning for Multiple UAVs by Using Particle Swarm Optimization With Surveillance Area Priority. IEEE Access 2020, 8, 86316–86327. [Google Scholar] [CrossRef]
- Ni, X.; Yin, Q.; Wei, X.; Zhong, P.; Nie, H. Research on Landing Stability of Four-Legged Adaptive Landing Gear for Multirotor UAVs. Aerospace 2022, 9, 776. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, G.P.; Xia, C. Analysis of fixed-wing VTOL aircraft with gas-driven fan propulsion system. Aerosp. Sci. Technol. 2020, 104, 105984. [Google Scholar] [CrossRef]
- Bogue, R. The role of robots in the green economy. Ind. Robot. Int. J. Robot. Res. Appl. 2022, 49, 6–10. [Google Scholar] [CrossRef]
- Rezazadeh, S.; Shahri, A.M.; Farrokhi, M. Dynamical Modeling and Experimental Validation of a Novel V8 Octorotor Flying Robot. In Proceedings of the 2016 4th International Conference on Control, Instrumentation, and Automation (ICCIA), Qazvin, Iran, 27–28 January 2016; pp. 366–371. [Google Scholar]
- Cole, J.A.; Krebs, T.; Barcelos, D.; Bramesfeld, G. Influence of Propeller Location, Diameter, and Rotation Direction on Aerodynamic Efficiency. J. Aircr. 2021, 58, 63–71. [Google Scholar] [CrossRef]
- Lei, Y.; Huang, Y.; Wang, H. Aerodynamic Performance of an Octorotor SUAV with Different Rotor Spacing in Hover. Processes 2020, 8, 1364. [Google Scholar] [CrossRef]
- Zou, X.; Ling, M.; Zhai, W. Aerodynamic and Vibration Characteristics of the Micro-Octocopter at Low Reynolds Number. Mob. Inf. Syst. 2021, 2021, 3691559. [Google Scholar] [CrossRef]
- Salazar, S.; Romero, H.; Lozano, R.; Castillo, P. Modeling and Real-Time Stabilization of an Aircraft Having Eight Rotors. J. Intell. Robot. Syst. 2009, 54, 455–470. [Google Scholar] [CrossRef]
- Osmic, N.; Kuric, M.; Petrovic, I. Detailed octorotor modeling and PD control. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 2182–2189. [Google Scholar]
- Haddadi, S.J.; Zarafshan, P. Design and Fabrication of an Autonomous Octorotor Flying Robot. In Proceedings of the 3rd RSI/ISM International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 7–9 October 2015; pp. 702–707. [Google Scholar]
- Sadeghi, P.S.; Shahri, A.M.; Ardestani, M.A. LQG-I Control for Attitude Stabilization of V8 Octorotor Flying Robot. In Proceedings of the 6th Conference on Artificial Intelligence and Robotics (IRANOPEN), Qazvin, Iran, 9 April 2016; pp. 151–157. [Google Scholar]
- Castillo, P.; Lozano, R.; Dzul, A. Stabilization of a mini rotorcraft with four rotors. IEEE Control. Syst. Mag. 2005, 25, 45–55. [Google Scholar]
- Tayebi, A.; Mcgilvray, S. Attitude stabilization of a four-rotor aerial robot. In Proceedings of the 43rd IEEE Conference on Decision and Control, Nassau, Bahamas, 14–17 December 2004; pp. 1216–1221. [Google Scholar]
- Luo, J.; Zhu, L.; Yan, G. Novel Quadrotor Forward-Flight Model Based on Wake Interference. AIAA J. 2015, 53, 3522–3533. [Google Scholar] [CrossRef]
- Bohorquez, F.; Samuel, P.; Sirohi, J.; Pines, D.; Rudd, L.; Perel, R. Design, analysis and hover performance of a rotary wing micro air vehicle. J. Am. Helicopter Soc. 2003, 48, 80–90. [Google Scholar] [CrossRef]
- Matus-Vargas, A.; Rodriguez-Gomez, G.; Martinez-Carranza, J. Ground effect on rotorcraft unmanned aerial vehicles: A review. Intell. Serv. Robot. 2021, 14, 99–118. [Google Scholar] [CrossRef]
- Lei, Y.; Bai, Y.; Xu, Z.; Gao, Q.; Zhao, C. An experimental investigation on aerodynamic performance of a coaxial rotor system with different rotor spacing and wind speed. Exp. Therm. Fluid Sci. 2013, 44, 779–785. [Google Scholar] [CrossRef]
- Ismail, N.I.; Zulkifli, A.H.; Abdullah, M.Z.; Basri, M.H.; Abdullah, N.S. Computational aerodynamic analysis on perimeter reinforced (PR)-compliant wing. Chin. J. Aeronaut. 2013, 26, 1093–1105. [Google Scholar] [CrossRef]
- Lin, L.; He, M.; Ma, W.; Wang, Q.; Zhai, H.; Deng, C. Dynamic Characteristic Analysis of the Multi-Stage Centrifugal Pump Rotor System with Uncertain Sliding Bearing Structural Parameters. Machines 2022, 10, 473. [Google Scholar] [CrossRef]
- Qin, K.; Ma, G.; Yao, G.; Xi, Y. Airfoil Pneumatic Impact of Missile Exhaust Jet Stream. J. Proj. Rocket. Missiles Guid. 2014, 34, 123–125+195. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).