A New Kinematic Synthesis Model of Spatial Linkages for Designing Motion and Identifying the Actual Dimensions of a Double Ball Bar Test Based on the Data Measured
Abstract
:1. Introduction
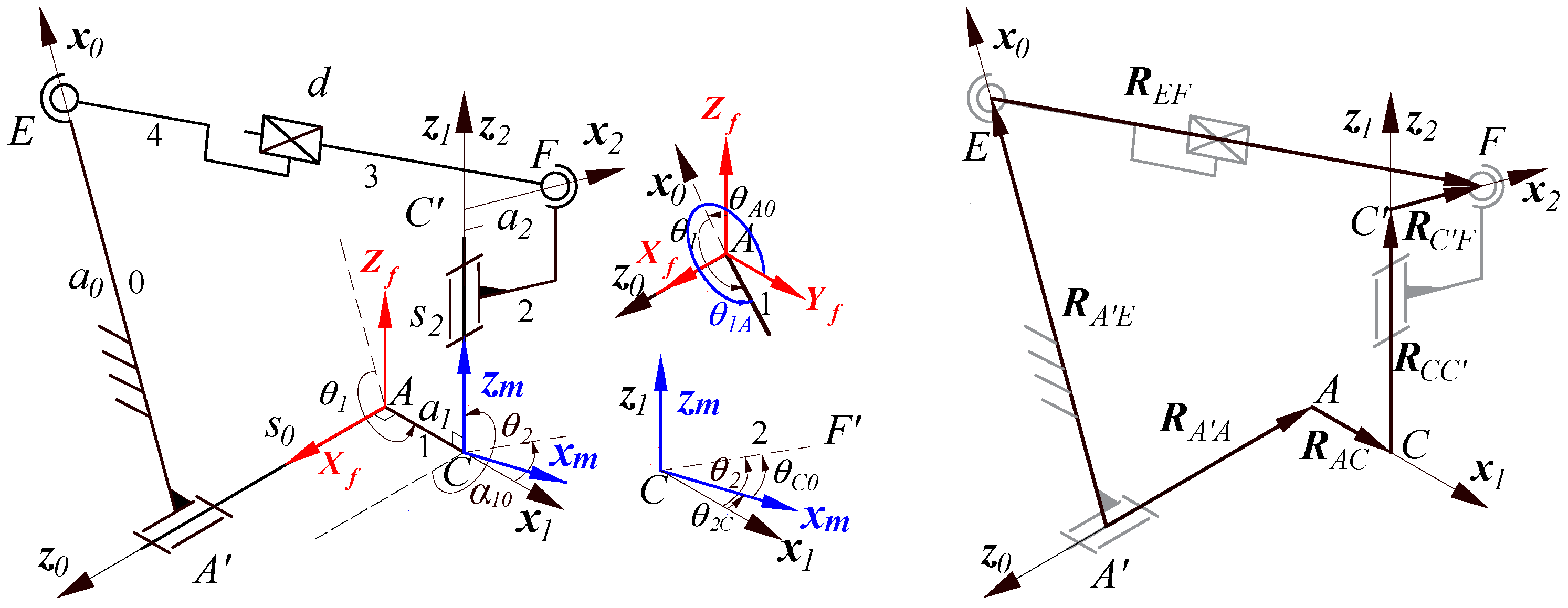
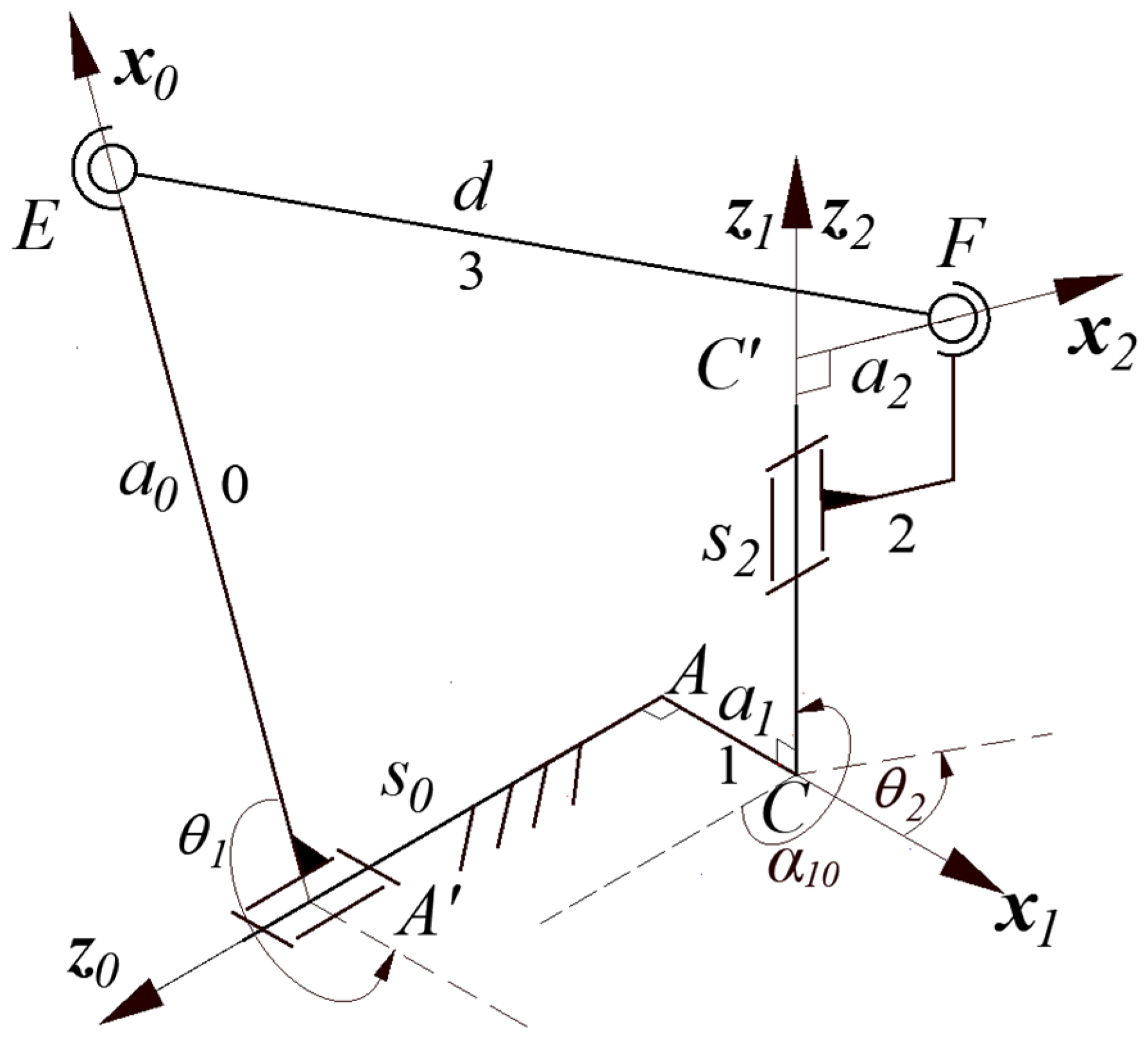
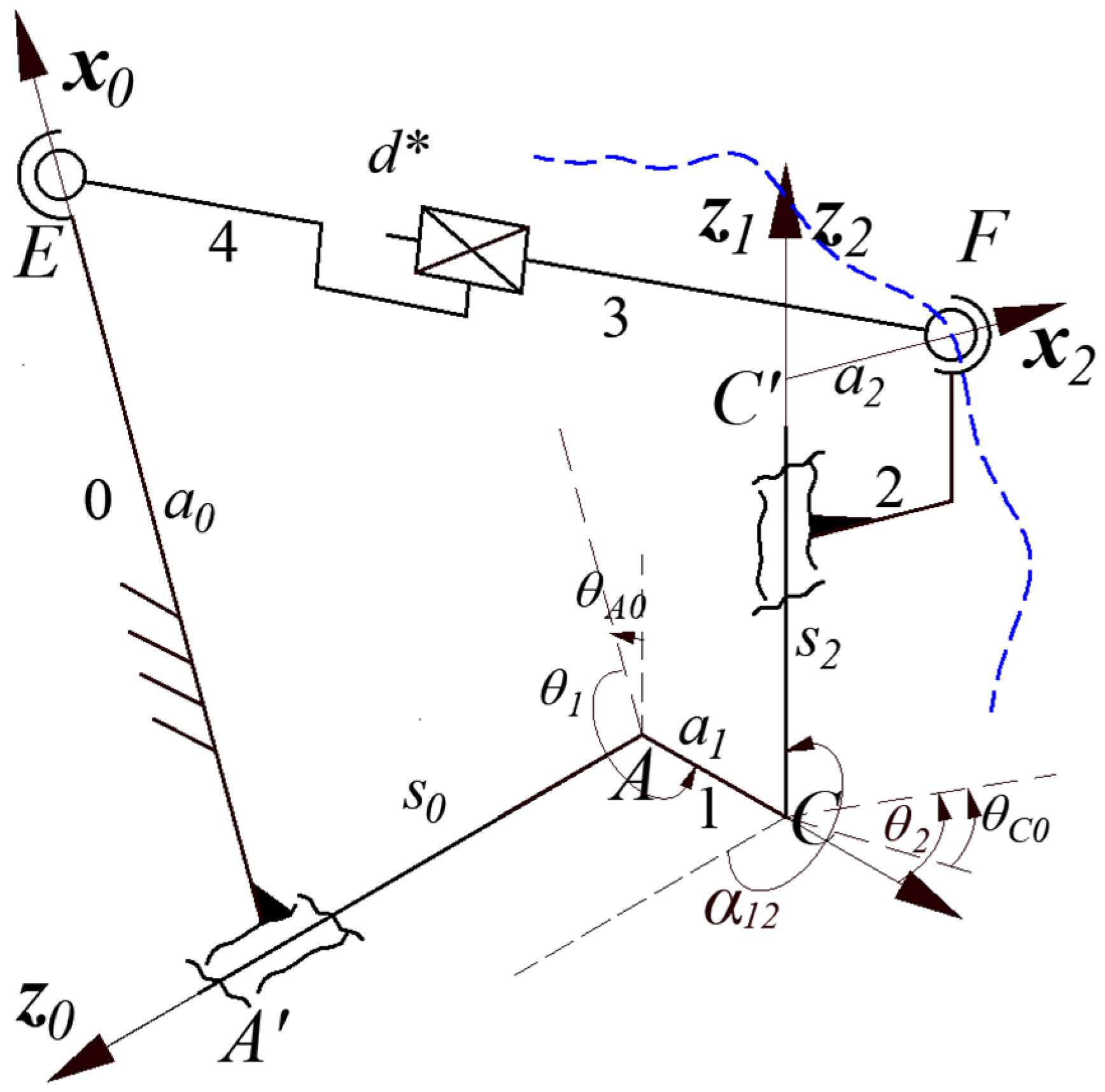
2. The Spatial Five-Bar Linkage of Double Ball Bar Tests of a Two-Axis Rotary Table
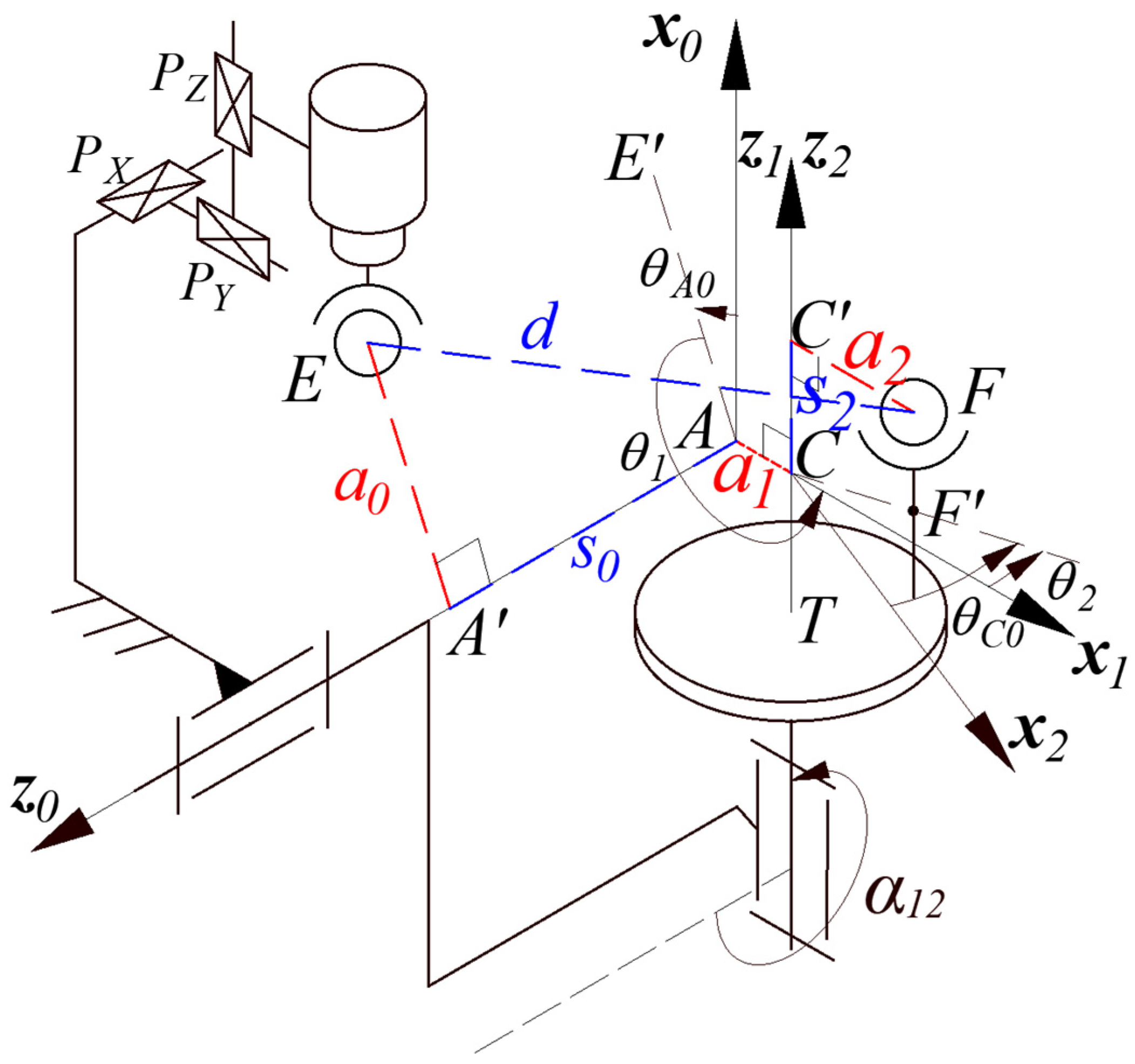
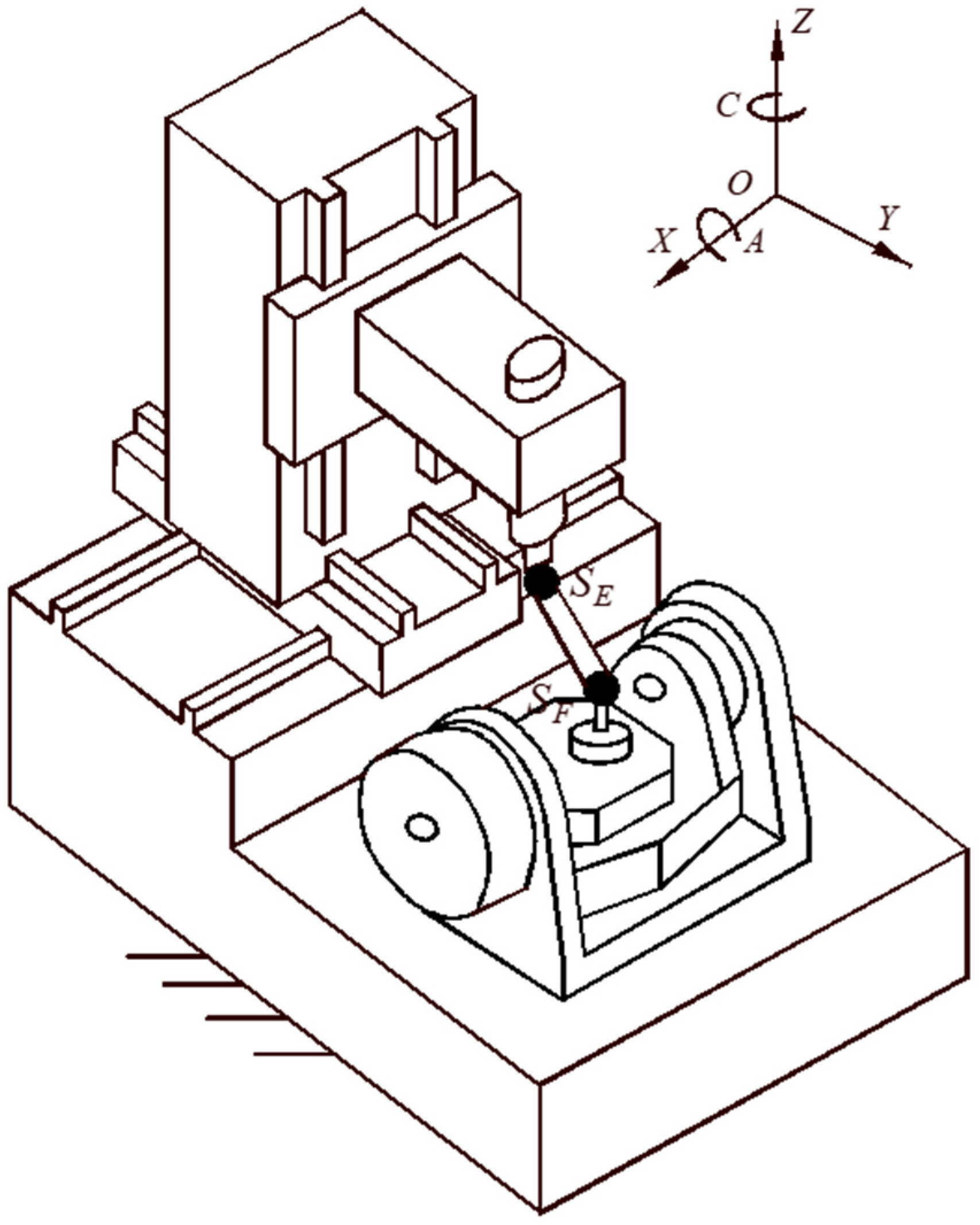
2.1. Double Ball Bar Test of a Two-Axis Rotary Table
2.2. The Mechanism Model for the DBB Test of a Two-Axis Rotary Table
3. Motion Design of Spatial Four-Bar Linkage for the DBB Test of a Two-Axis Rotary Table
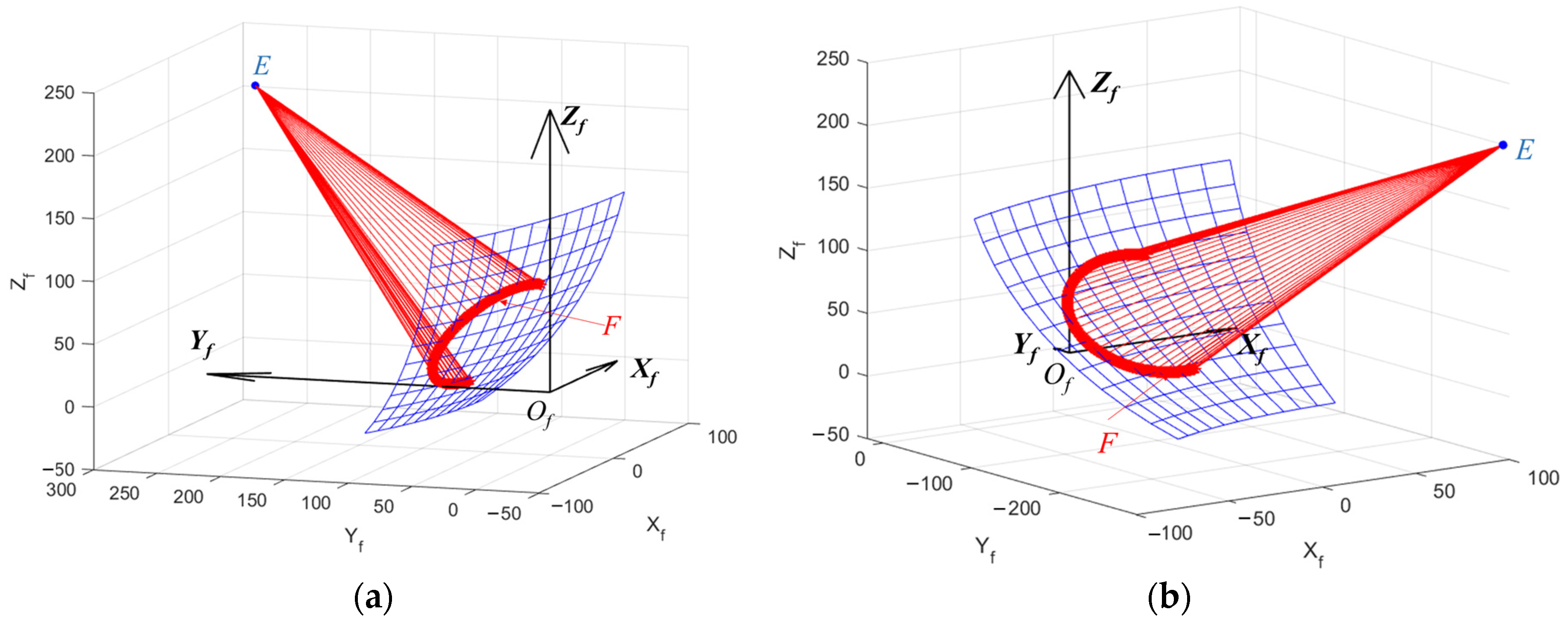
3.1. Motion Function Design for the DBB Test
3.2. Motion Range of the DBB Test of an Ideal Two-Axis Rotary Table
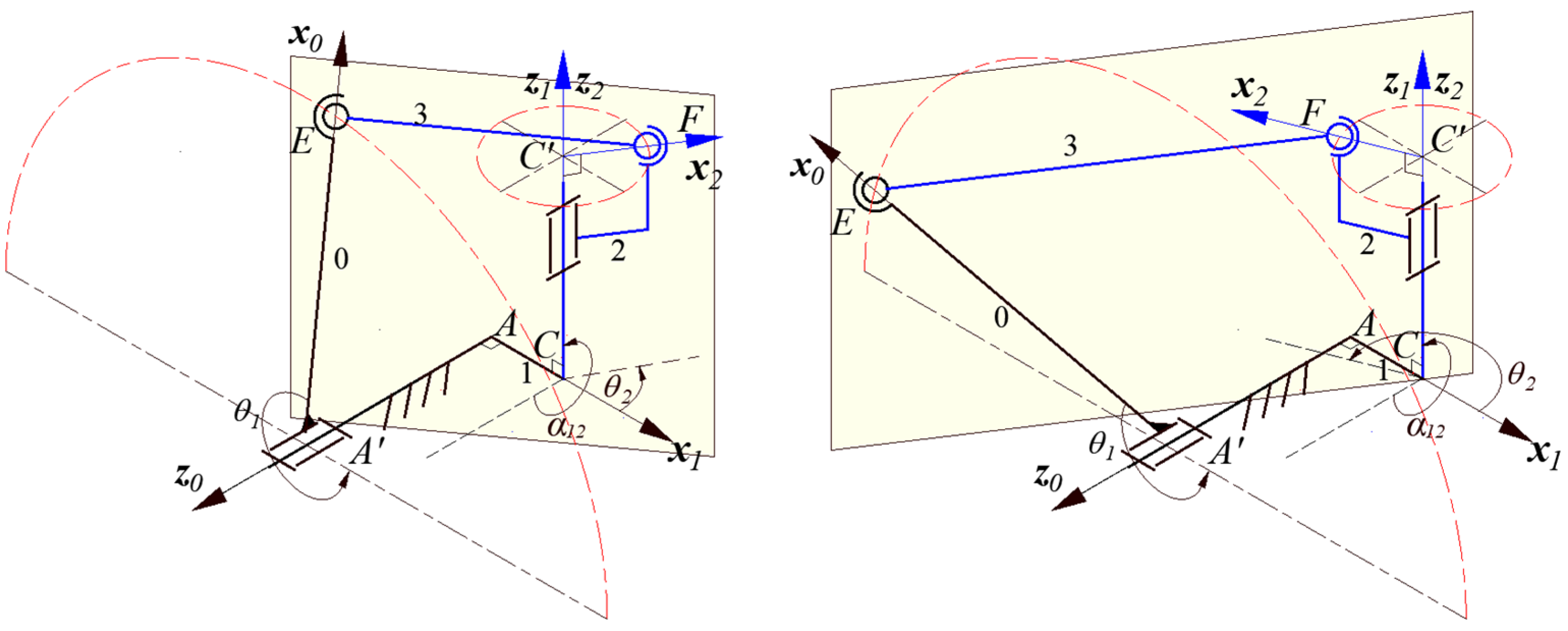
3.3. Kinematic Synthesis of a Spatial Four-Bar Linkage for the DBB Test
4. Actual Parameter Identification of Spatial Five-Bar Linkage for the DBB Test
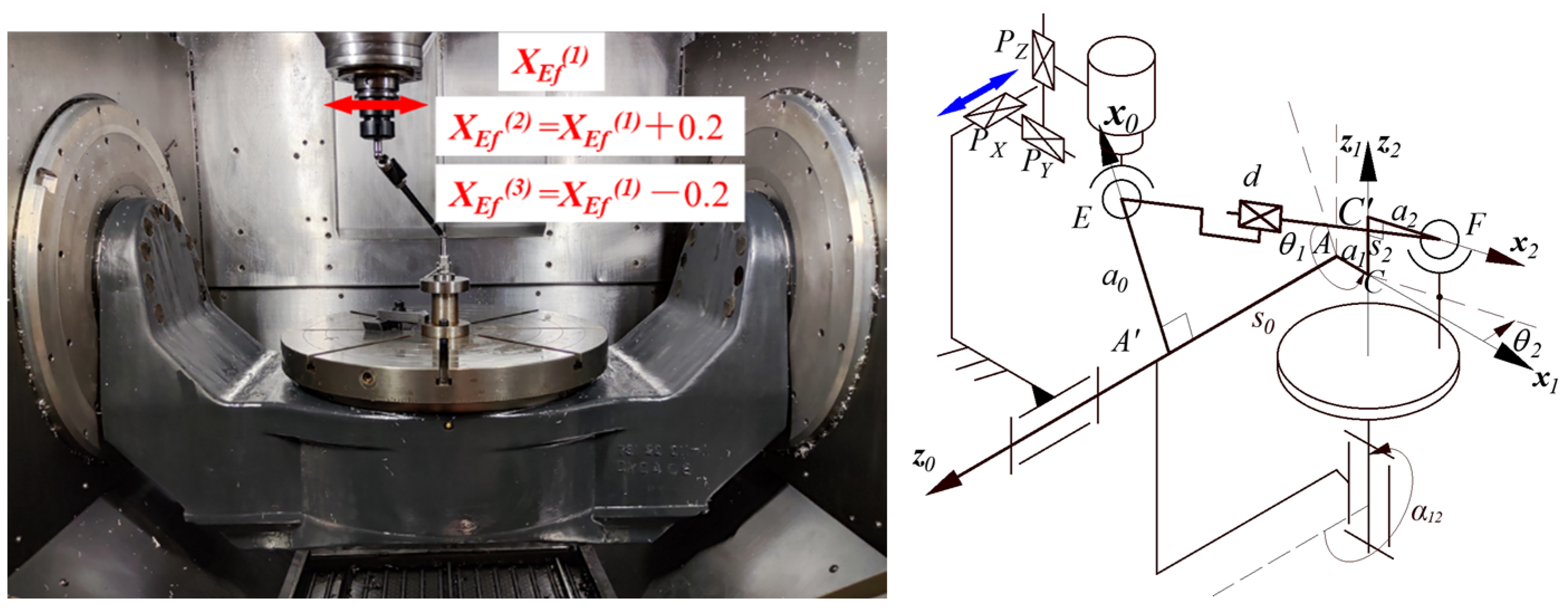
5. Experiments of the Double Ball Bar Test of the Two-Axis Rotary Table
5.1. Measurement Motion Function and Range of the DBB Test
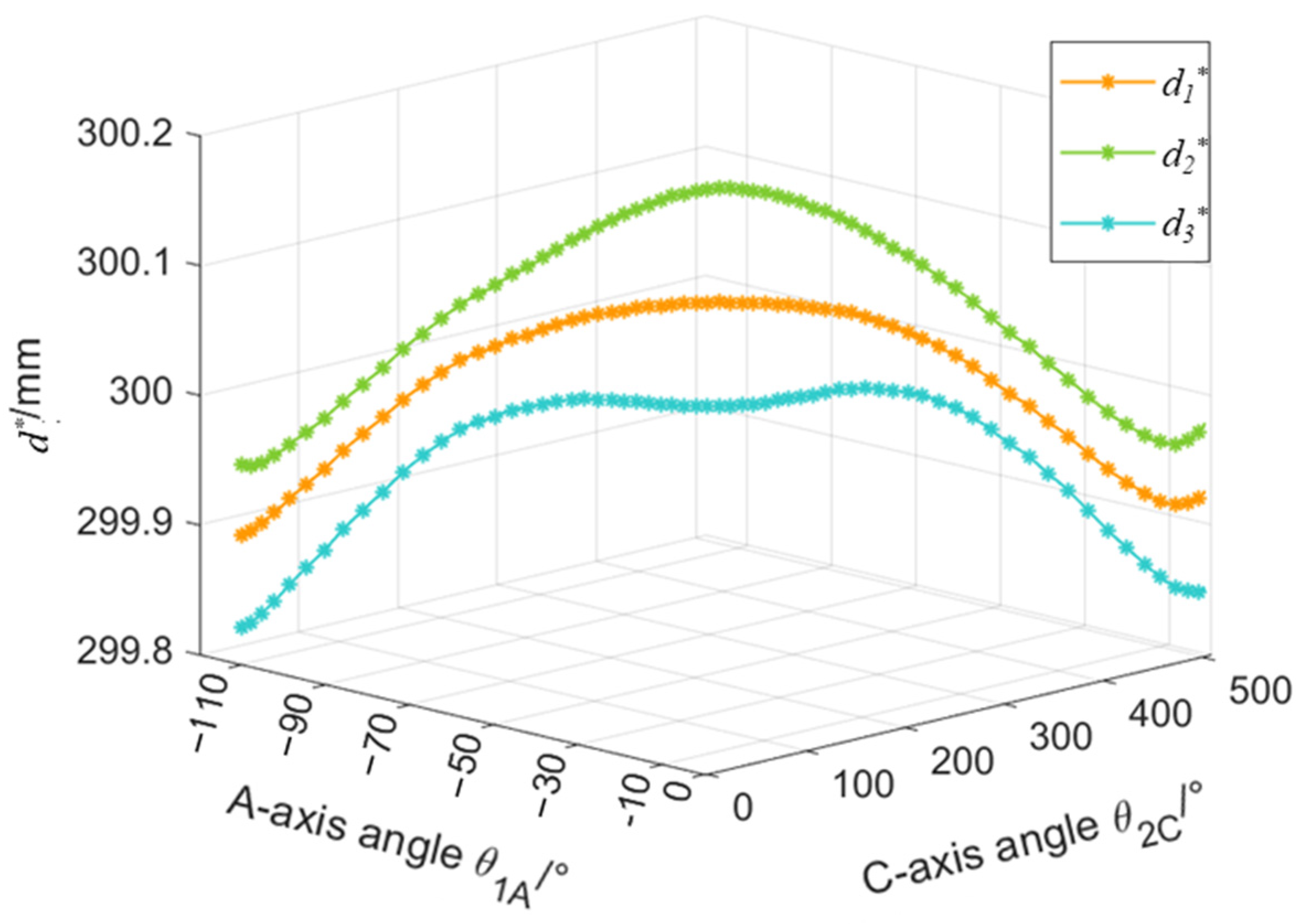
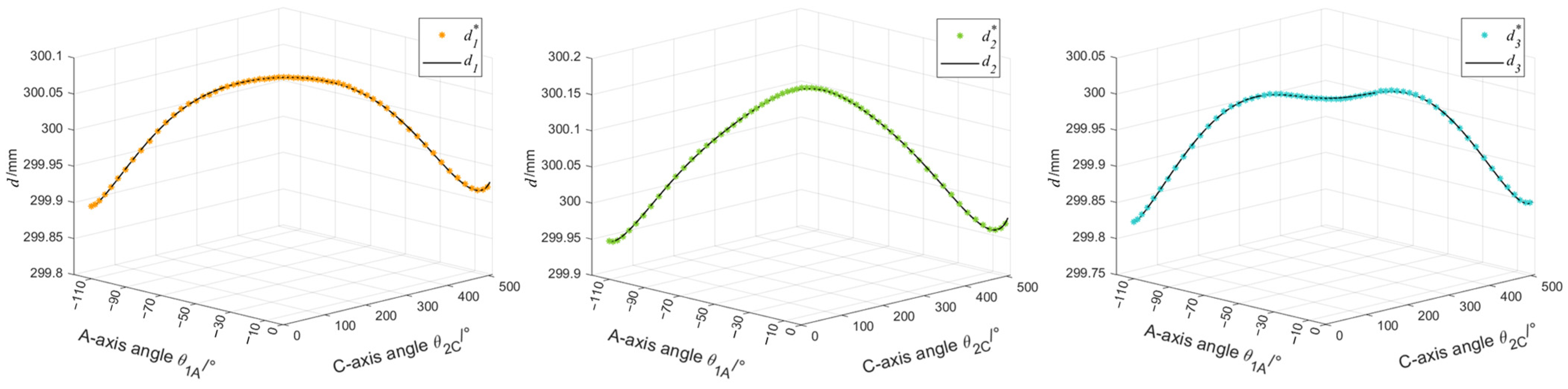
5.2. The Actual Parameter Identification of the DBB Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hunt, K.H. Kinematic Geometry of Mechanisms; Oxford University Press: Oxford, UK, 1978. [Google Scholar]
- McCarthy, J.M.; Soh, C.S. Geometric Design of Linkages, 2nd ed.; Interdisciplinary Applied Mathematics 11; Springer: New York, NY, USA, 2010. [Google Scholar]
- Bryan, J. A simple method for testing measuring machines and machine tools Part 1: Principles and applications. Precis. Eng. 1982, 4, 61–69. [Google Scholar] [CrossRef]
- Bryan, J. A simple method for testing measuring machines and machine tools Part 2: Construction details. Precis. Eng. 1982, 4, 125–138. [Google Scholar] [CrossRef]
- ISO 230-4; Test Code for Machine Tools-Part 4: Circular Tests for Numerically Controlled Machine Tools. ISO: London, UK, 2005.
- ASME B5.54; Methods for Performance Evaluation of Computer Numerically Controlled Machining Centers. American National Standards Institute: Washington, DC, USA, 2005.
- Huang, Y.B.; Fan, K.C.; Lou, Z.F.; Sun, W. A Novel Modeling of Volumetric Errors of Three-Axis Machine Tools Based on Abbe and Bryan Principles. Int. J. Mach. Tools Manuf. 2020, 151, 103527. [Google Scholar] [CrossRef]
- Lee, K.I.; Yang, S.H. Accuracy Evaluation of Machine Tools by Modeling Spherical Deviation Based on Double Ball-Bar Measurements. Int. J. Mach. Tools Manuf. 2013, 75, 46–54. [Google Scholar] [CrossRef]
- Lei, W.T.; Sung, M.P.; Liu, W.L. Double Ballbar Test for the Rotary Axes of Five-Axis CNC Machine Tools. Int. J. Mach. Tools Manuf. 2007, 47, 273–285. [Google Scholar] [CrossRef]
- Lasemi, A.; Xue, D.; Gu, P. Accurate Identification and Compensation of Geometric Errors of 5-Axis CNC Machine Tools Using Double Ball Bar. Meas. Sci. Technol. 2016, 27, 055004. [Google Scholar] [CrossRef]
- Chen, J.; Lin, S.; He, B. Geometric Error Measurement and Identification for Rotary Table of Multi-Axis Machine Tool Using Double Ballbar. Int. J. Mach. Tools Manuf. 2014, 77, 47–55. [Google Scholar] [CrossRef]
- Zhu, S.; Ding, G.; Qin, S. Integrated Geometric Error Modeling, Identification and Compensation of CNC Machine Tools. Int. J. Mach. Tools Manuf. 2012, 52, 24–29. [Google Scholar] [CrossRef]
- Pahk, H.J.; Kim, Y.S.; Moon, J.H. A new technique for volumetric error assessment of CNC machine tools incorporating ball bar measurement and 3D volumetric error model. Int. J. Mach. Tools Manuf. 1997, 37, 1583–1596. [Google Scholar] [CrossRef]
- Zhong, L.; Bi, Q.; Wang, Y. Volumetric accuracy evaluation for five-axis machine tools by modeling spherical deviation based on double ball-bar kinematic test. Int. J. Mach. Tools Manuf. 2017, 122, 106–119. [Google Scholar] [CrossRef]
- Xu, K.; Li, G.; He, K.; Tao, X. Identification of Position-Dependent Geometric Errors with Non-Integer Exponents for Linear Axis Using Double Ball Bar. Int. J. Mech. Sci. 2020, 170, 105326. [Google Scholar] [CrossRef]
- Xia, C.; Wang, S.; Wang, S.; Ma, C.; Xu, K. Geometric error identification and compensation for rotary worktable of gear profile grinding machines based on single-axis motion measurement and actual inverse kinematic model. Mech. Mach. Theor. 2021, 155, 104042. [Google Scholar] [CrossRef]
- Xia, H.-J.; Peng, W.-C.; Ouyang, X.-B.; Chen, X.-D.; Wang, S.-J. Identification of geometric errors of rotary axis on multi-axis machine tool based on kinematic analysis method using double ball bar. Int. J. Mach. Tools Manuf. 2017, 122, 161–175. [Google Scholar] [CrossRef]
- Chai, X.; Zhang, N.; He, L.; Li, Q.; Ye, W. Kinematic Sensitivity Analysis and Dimensional Synthesis of a Redundantly Actuated Parallel Robot for Friction Stir Welding. Chin. J. Mech. Eng. 2020, 33, 1–10. [Google Scholar] [CrossRef]
- Bai, S.; Li, Z.; Angeles, J. Exact Path Synthesis of RCCC Linkages for a Maximum of Nine Prescribed Positions. ASME J. Mech. Robot. 2022, 14, 021011. [Google Scholar] [CrossRef]
- Chen, C.; Angeles, J. A novel family of linkages for advanced motion synthesis. Mech. Mach. Theory 2008, 43, 882–890. [Google Scholar] [CrossRef]
- Zhao, C.; Guo, W. Inverted Modelling: An Effective Way to Support Motion Planning of Legged Mobile Robots. Chin. J. Mech. Eng. 2023, 36, 19. [Google Scholar] [CrossRef]
- Huang, X.; Liu, C.; Xu, H.; Li, Q. Displacement Analysis of Spatial Linkage Mechanisms Based on Conformal Geometric Algebra. J. Mech. Eng. 2021, 57, 39–50. [Google Scholar]
- Denavit, J.; Hartenberg, R.S. A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices. J. Appl. Mech. 1955, 22, 215–221. [Google Scholar] [CrossRef]
- Wang, D.; Wang, W. Kinematic Differential Geometry and Saddle Synthesis of Linkages; John Wiley & Sons: Singapore, 2015. [Google Scholar]
- Wang, D.; Wang, Z.; Wu, Y.; Dong, H.; Yu, S. Invariant errors of discrete motion constrained by actual kinematic pairs. Mech. Mach. Theory 2018, 119, 74–90. [Google Scholar] [CrossRef]


| Technical Parameters | Value | Unit |
|---|---|---|
| X/Y/Z travel | 650/650/450 | mm |
| A-axis motion range | −130~+130 | ° |
| C-axis motion range | 0~360 | ° |
| Table diameter | Φ650 | mm |
| Distance from spindle end face to table | 90~540 | mm |
| Perpendicular distance of AC axis line (a1) | 0 | mm |
| Included angle of AC axis line (α12) | 270 | ° |
| s0/mm | a0/mm | θA0/° | s2/mm | a2/mm | θC0/° | |
|---|---|---|---|---|---|---|
| angle measurement range as −110°~0° | 96.310 | 352.114 | −55.000 | 80.000 | 30.000 | −161.592 |
| angle measurement range as 0°~+110° | 96.310 | 352.114 | 55.000 | 80.000 | 30.000 | −161.592 |
| s0/mm | a0/mm | θA0/° | s2/mm | a2/mm | θC0/° | a1/mm | α12/° | |
|---|---|---|---|---|---|---|---|---|
| Case M1 | 96.865 | 351.891 | −54.995 | 79.871 | 30.063 | −161.531 | −0.023 | 270.093 |
| Case M2 | 97.124 | 351.900 | −54.996 | 79.904 | 30.080 | −161.541 | −0.021 | 270.102 |
| Case M3 | 96.682 | 351.951 | −54.996 | 79.934 | 30.111 | −161.559 | −0.019 | 270.094 |
| Design value | 96.310 | 352.114 | −55.000 | 80.000 | 30.000 | −161.592 | 0 | 270.000 |
| Case M1 | Case M2 | Case M3 | |
|---|---|---|---|
| ΔMA/μm | 1.587 | 1.607 | 1.674 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Z.; Tang, S.; Wang, D. A New Kinematic Synthesis Model of Spatial Linkages for Designing Motion and Identifying the Actual Dimensions of a Double Ball Bar Test Based on the Data Measured. Machines 2023, 11, 919. https://doi.org/10.3390/machines11090919
Liao Z, Tang S, Wang D. A New Kinematic Synthesis Model of Spatial Linkages for Designing Motion and Identifying the Actual Dimensions of a Double Ball Bar Test Based on the Data Measured. Machines. 2023; 11(9):919. https://doi.org/10.3390/machines11090919
Chicago/Turabian StyleLiao, Zuping, Shouchen Tang, and Delun Wang. 2023. "A New Kinematic Synthesis Model of Spatial Linkages for Designing Motion and Identifying the Actual Dimensions of a Double Ball Bar Test Based on the Data Measured" Machines 11, no. 9: 919. https://doi.org/10.3390/machines11090919
APA StyleLiao, Z., Tang, S., & Wang, D. (2023). A New Kinematic Synthesis Model of Spatial Linkages for Designing Motion and Identifying the Actual Dimensions of a Double Ball Bar Test Based on the Data Measured. Machines, 11(9), 919. https://doi.org/10.3390/machines11090919






