ApOL-Application Oriented Workload Model for Digital Human Models for the Development of Human-Machine Systems

Abstract

Since musculoskeletal disorders are one of the most common work-related diseases for assemblers and machine operators, it is crucial to find new ways to alleviate the physical load on workers. Support systems such as exoskeletons or handheld power tools are promising technology to reduce the physical load on the humans. The development of such systems requires consideration of the interactions between human and technical systems. The physical relief effect of the exoskeleton can be demonstrated in experimental studies or by simulation with the digital human model (DHM). For the digital development of these support systems, an application-oriented representation of the workload is necessary. To facilitate digital development, an application-oriented workload model (ApOL model) of an overhead working task is presented. The ApOL model determines the load (forces, torques) onto the DHM during an overhead screw-in task using a cordless screwdriver, based on experimental data. The ApOL model is verified by comparing the simulated results to the calculated values from a mathematical model, using experimental data from three participants. The comparison demonstrates successful verification, with a maximum relative mean-absolute-error (rMAE) of the relevant load components at 11.4%. The presented ApOL model can be utilized to assess the impact of cordless screwdriver design on the human workload and facilitate a strain-based design approach for support systems e.g., exoskeletons.

1. Introduction

According to the European Agency for Safety and Health at Work (EU-OSHA), musculoskeletal disorders (MSDs) are one of the most common work-related health problems in the European Union (EU) [1]. In 2018, the German Federal Institute for Occupational Safety and Health (BAuA) estimated a production loss of EUR 17.2 billion and a loss of gross value added of EUR 30.4 billion in Germany for the year 2016 due to musculoskeletal disorders [2]. In the 28 member states of the European Union, 66% of plant and machine operators and assemblers reported one or more MSD-related health problems in 2015, while 61% of all workers reported that they are exposed to repetitive hand or arm movements and 43% are exposed to tiring and painful positions [1]. To reduce the load on workers in assembly lines, support systems such as exoskeletons can be used e.g. when being exposed to peak loads [3] or for motion assistance when working in ergonomic demanding postures [3,4,5,6,7] such as overhead work. Recent studies show a reduction in muscle activity when working with an exoskeleton above shoulder height [8,9,10,11,12].

To ensure a well-user-centered product, technical systems need to be developed and validated considering the physical human-exoskeleton interaction [13]. In the past, this involved expensive and time-consuming studies, while in recent years a shift from checklists and questionnaires to the integration of digital human factor such as virtual/augmented reality or digital human solutions can be observed [14]. The integration of human factors helps in designing a user-centered product, e.g., by predicting the load on the user [15] or by enhancing the user’s well-being by improving the workspace and reducing the complexity of performed tasks [16]. One possibility to ensure the integration of digital human factors is using digital human models (DHM) [17].

Biomechanical DHM, e.g., musculoskeletal human models (MHM) such as Anybody or OpenSim [18,19], can be used to estimate the strain on humans for specific tasks, when the motion of the human and the external loads on the human are known [20,21,22]. Model-based optimization approaches exist for the development of exoskeletons in which the parameters of the exoskeleton are iteratively adjusted e.g., Jensen et al., varied the spring stiffness of a passive upper limb orthosis to reduce muscle activity of the shoulder [23,24]. A challenge with these MHMs is to model the interaction with technical systems as these interactions usually cause loads on the human. However, the accuracy of these models in representing the real interaction between the human and the support system can vary [25]. Designing user-centered support systems for e.g., assembly lines require a holistic approach where the human, assembly tool, task, and support system are taken into consideration and the interactions between them are appropriately modelled. This kind of modelling comes with several challenges which have not been entirely solved yet. Often in MHM, the loads to determine the stress on the user are modelled in a simple way by using a generic load profile [26] e.g., Molz et al., 2022 modeled the load acting on the hand of the MHM as a constant process force during an overhead screw-in task [27,28]. Uchida et al., 2016 added a massless technical system to the MHM to evaluate the effect of a running support system, they did not consider the load on the human due to the mass of the technical system [29]. Moreover, the spatial dimensions of the technical system are often not considered [9,24], as well as the motion of the user [17], thus overlooking the loads on the human due to mass and inertia forces. As a result, the forces and torques acting on the human are often not modelled in a sufficient way, since in reality the physical load on the user varies over time when performing a task and the dynamic forces must be taken into account.

When, for example, using handheld power tools such as cordless screwdrivers, the torque induced by the screwdriver motor and the push force induced by the user are not constant during the work process [30,31]. Therefore, there is a research gap in application-oriented load models that describe the load on the human during manual tasks with support systems that are not available. To customize exoskeleton support for manual tasks, the process forces and torques need to be modelled application oriented.

In literature, several approaches for measuring human process forces are presented. Kalra et al., 2015 presented a flexible resistive sensor-based measurement system to measure the hand-handle interaction forces under static and dynamic conditions [32]. Furthermore, Landry et al., 2021 propose an algorithm to isolate the push and grip force distribution from force measurement foils during the use of an electric nut runner [33]. Komi et al., 2007 evaluated a flexible sensor for grip force measurements during golf shots [34]. Other approaches derive push or pull forces from ground reaction forces (GRF) in costly and time-consuming experimental studies with prototypes [24,31]. Simulation models of the work tasks provide a reliable and cheaper way to determine these forces and torques.

Another important aspect of the development of support systems is the varying external loads for different users performing the same task which are caused by their individual handling of the power tool [31]. Support systems will then have to be optimized for each user individually, which is expensive and time-consuming. Simulations provide an alternative as they can be used to design robust systems, which are insensitive to noise factors [35]. The workload on the user is then only determined by the task and the technical system itself and not by the individual usage of the system by the user.

In the simulation-based development of strain-optimized human-machine systems, the consideration of application-oriented loads is relevant. To provide more realistic loads on DHM, the inertial forces must be taken into consideration, thus realistic motion data, the mass, mass distribution and spatial dimensions have to be provided. In addition, external loads such as the process torque and the push force must be taken into consideration.

This paper therefore presents a simulation model that fulfills all these requirements. The aim of this model is to provide realistic interaction forces and torques between the handheld power tool and the hand of a musculoskeletal human model (DHM) for an overhead assembly task performed by [31].

The model consists of three sub-models to determine the load onto the user based on the user’s motion and interaction forces and torques. For the verification of the simulation model, two separate steps are taken. First, the simulation results are compared to a mathematical model secondly a simulative parameter study is conducted. With this model, it is possible for the first time to give an accurate estimation of user loads for DHMs for real use cases which enables efficient research on support structures such as exoskeletons.

Following, the model structure, individual sub-models, and combined ApOL model will be explained in detail. In addition, the validation method, validation results, and limitations of the ApOL model will be presented and discussed in the subsequent sections of this paper.

2. Materials and Methods

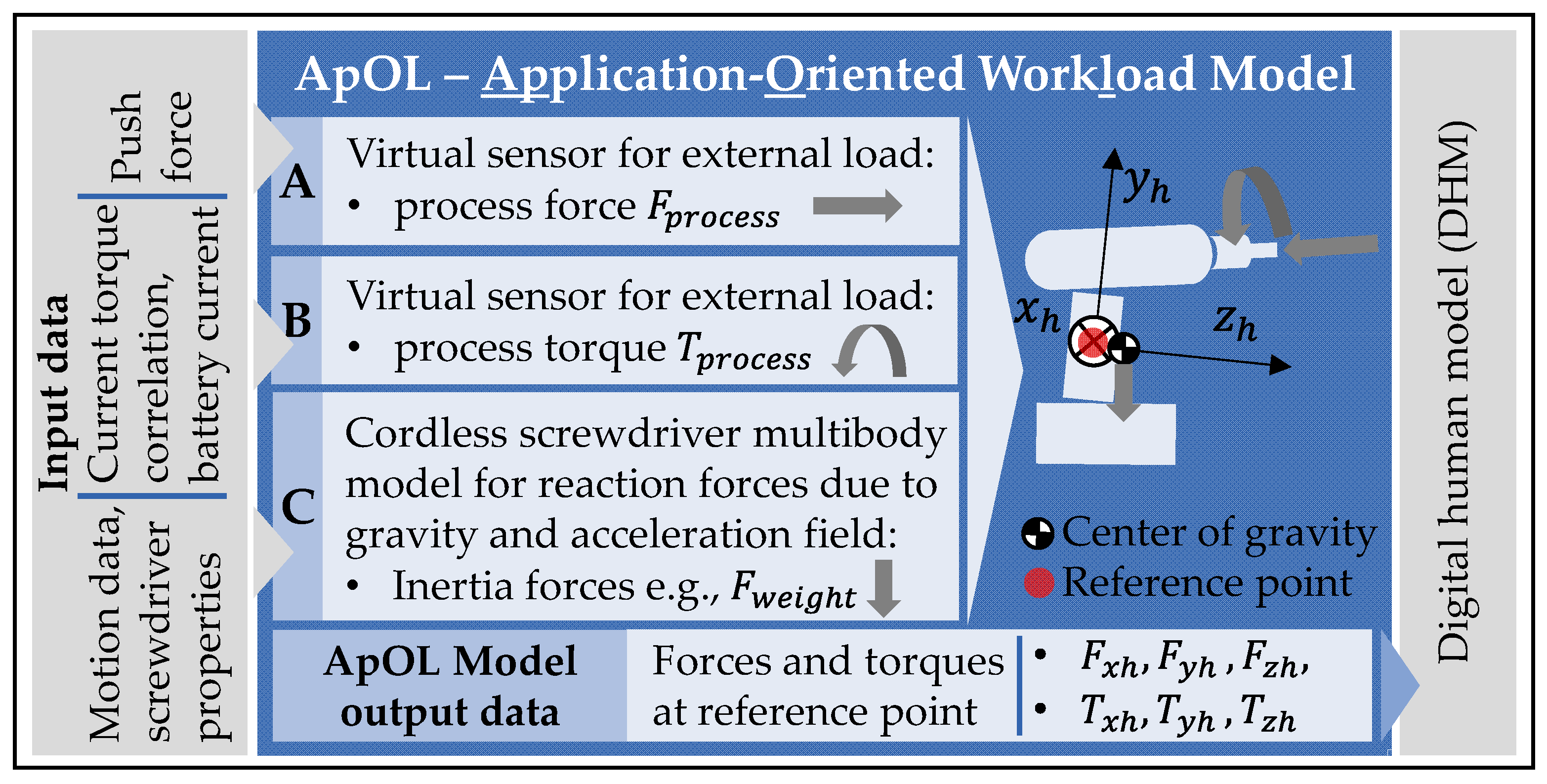
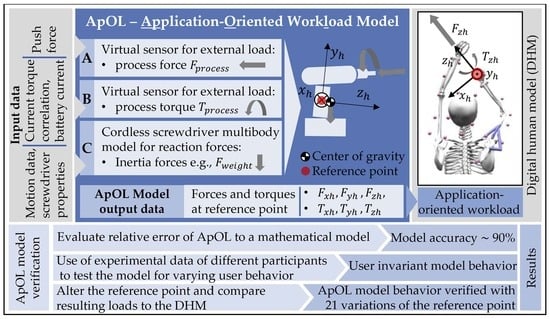
In this paper the application-oriented workload (ApOL) model is developed on the exemplary use case of a cordless screwdriver. The ApOL model combines sub-models A, B, and C to determine the interaction forces and torques onto the DHM based on the process force and torque as well as the motion of the user (see Figure 1). The results of the respective sub-models are forces and torques which represent the loads that act on the screwdriver during application. The workload model uses experimental data from the study described by Sänger et al., 2022 [31] and [30] to determine the reaction forces ($F_{xh}, F_{yh}, F_{zh}$) and torques ($T_{xh}, T_{yh}, T_{zh}$) for the DHM while working with a screwdriver in an overhead screw-in task. To do so, the ApOL model is implemented in MATLAB Simulink and is built up as a rigid body model of the screwdriver where the resulting forces and torques from the three sub-models are applied (see Figure 1). The input data consists of motion data captured by a Vicon motion capture system, GRF, and the battery current of a cordless screwdriver. Sub-model A determines the external process three-dimensional force vector $F_{process}$ based on experimentally determined push forces (calculated from the GRF). Sub-model B uses the battery current from the experimental studies of Sänger et al., 2022 [31] and [30] to estimate the external process torque $T_{process}$ acting onto the screwdriver during the screw-in process. Sub-model C uses the human and screwdriver motion data provided by Sänger et al., 2022 [31] to determine the load onto the DHM based on the screwdriver motion. For this purpose, a model of the screwdriver is built in MATLAB Simulink using the Simscape multibody package.

2.1. Sub-Model A: Virtual Sensor to Determine the External Process Force Based on the Experimental Users Push Force

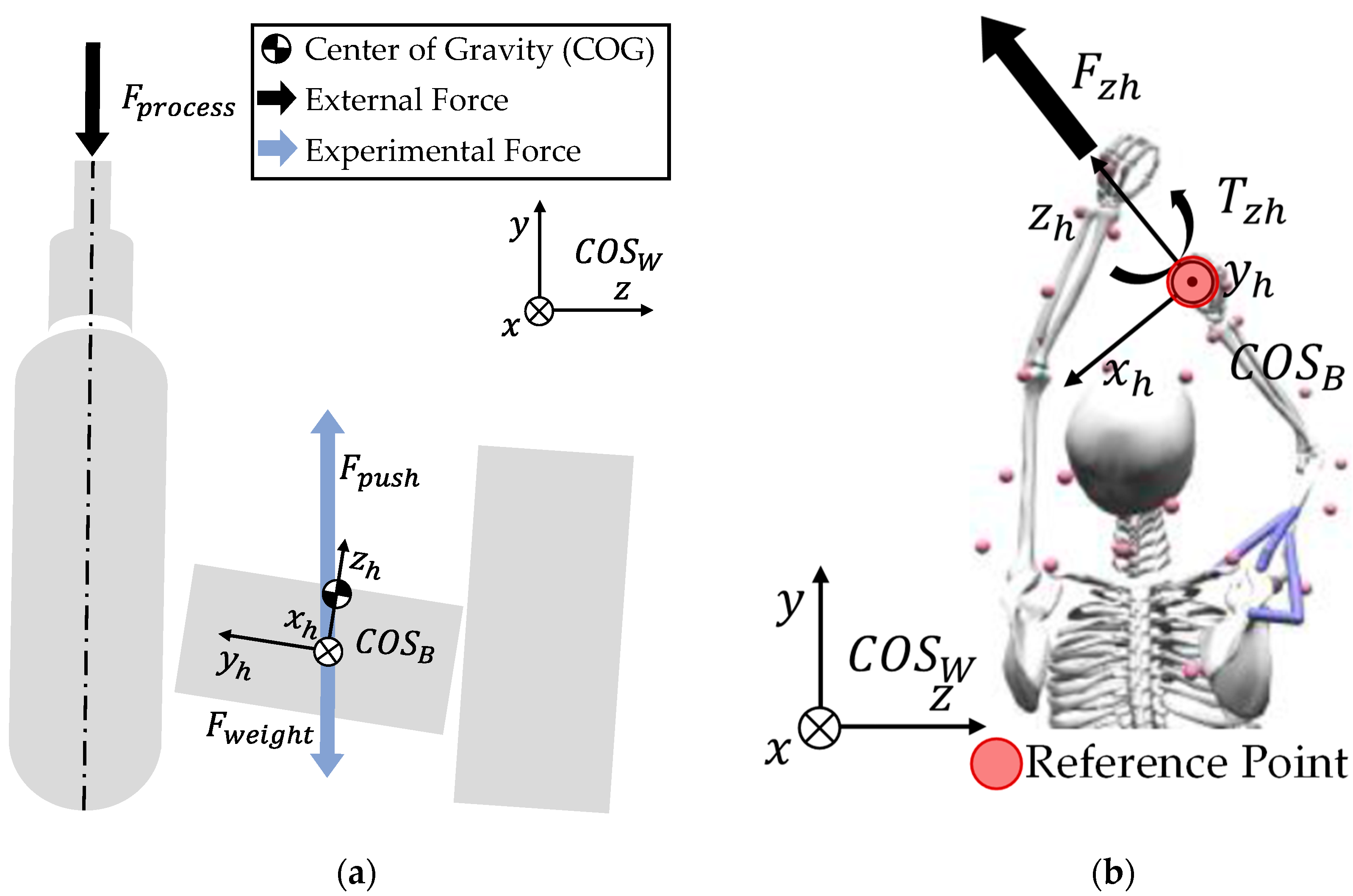
Sub-model A aims at estimating the external process force during a work task. In our example, we chose the case of an electric screwdriver for fastening woodscrews. Here, this process force, $F_{process }$ origins from the interaction of the screwdriver with the workpiece and is necessary for function fulfillment (e.g., force for keeping a drill bit in the screw head).

The data for this sub-model is taken from Sänger et al. 2022 [31], where the push force was investigated on three participants.

The push force $F_{push}$ acting between the handle and the hand for all participants was calculated indirectly from the ground reaction forces of the overhead screw-in task performed by Sänger et al., 2022 [31]. Based on the data the process force acting on the bit of the screwdriver was determined using the following equation:

$${\overrightarrow{F}}_{process }={\overrightarrow{F}}_{push}-{\overrightarrow{F}}_{weight}$$

(1)

This formula assumes a close fit of the directions of the push-force and gravity-force vector. In Figure 2a the relevant forces for determining the user load during the screw-in process are illustrated on which Equation (1) is based on. The result of the sub-model A is the process force $F_{process}$ acting on the bit of the screwdriver during the screw-in process (see Figure 1 and Figure 2a).

2.2. Sub-Model B: Virtual Sensor for Determining the External Process Torque Based on the Battery Current from Experimental Data

To determine the process torque $T_{process}$ from the experimental battery current data in the study by Sänger et al., 2022 [31] the correlation between the process torque and the battery current of the screwdriver must be determined. In the study by Sänger et al., 2023 [30] ten consecutive screw-in processes with the same screwdriver, screw, and wood used by Sänger et al. [31] were performed on a custom build test bench. The screw-in torque and the battery current of the screwdriver, as well as the screw-in depth of the screw, were measured.

After interpolating all torque and battery current data to the same data length, the mean of the battery current and the torque from all ten repetitions was calculated and a correlation analysis using the least squares method was performed.

2.3. Sub-Model C: Virtual Sensor to Determine Interaction Forces on the DHM from Experimental Motion Data

As mentioned above, when determining loads of technical systems onto the user, the force of inertia and the moment of inertia as well as the mass distribution of the technical system and the external loads must be modelled.

To model the influence of the inertia as realistic as possible, real motion data captured by Sänger et al., 2022 [31] during their experiments was used as an input. A detailed demonstration of a movement cycle for the overhead screw-in task is given in [25]. During the movement cycle of the performed overhead task, there are four screwdriver orientations. The initial position is referred to as (O1) holding the screwdriver, while the orientation of the screwdriver while being rotated upwards is referred to as (O2). During the screw-in process, the drilling axle of the screwdriver faces directly upwards (O3). After the screw-in process, the screwdriver is brought to its final position (O4), which is similar to its initial position (O1).

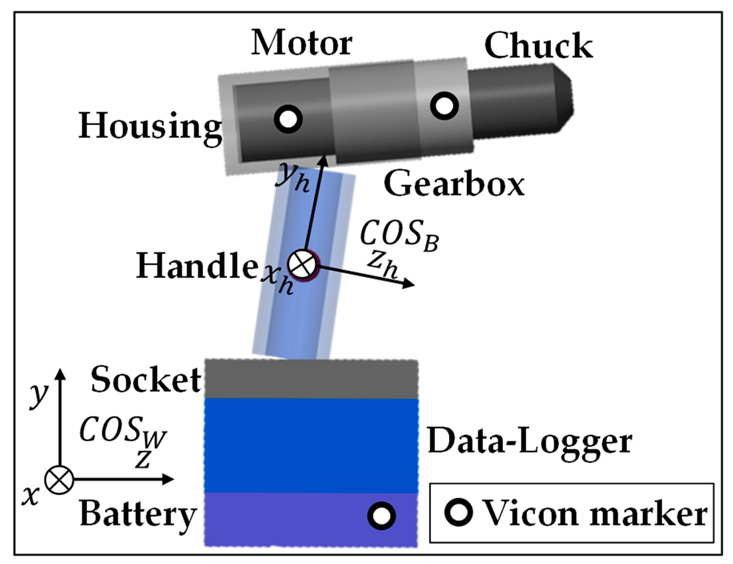
The experimental motion data of the participant and the screwdriver (in total six markers were used for the screwdriver, three on each side) was used as an input for this musculoskeletal human model [36] to determine the three translational degrees of freedom (DoF) and the three rotational DoF of the screwdriver for each motion cycle. The output motion data of the DHM describes the translation and rotation of the body-fixed ${COS}_B$ at the reference point of the screwdriver in relation to the world-fixed ${COS}_W$ (see Figure 2a,b and

Table 1. Simulink screwdriver model and mass the components.

Component	Mass in kg	Simulink Model
Handle	0.09
Battery (3.1 Ah)	0.40
Battery socket	0.09
Data Logger	0.40
Motor	0.41
Gearbox	0.51
Chuck	0.24
Motor and gearbox housing	0.09
Total	2.22

). The experimental data for three participants P3, P4, and P5 from the study by Sänger et al., 2022 [31] were used. In this paper, these participants are labeled as P1, P2, and P3.

The Festool PDC 18/4 screwdriver was modelled in Simscape Multibody using its real geometric parameters and mass (-distribution). Therefore, the components of the screwdriver were disassembled and weighted separately. A list of the modelled components with their weight can be found in Table 1. The visual representation of the model created in MATLAB Simulink as well as the dimensions of the components can be found in Appendix A.

2.4. Application-Oriented Workload Model-ApOL Model

The ApOL model combines sub-models A, B, and C to determine the interaction forces and torques onto the DHM based on the process force and torque as well as the motion of the user (see Figure 1). The ApOL model is implemented in MATLAB Simulink.

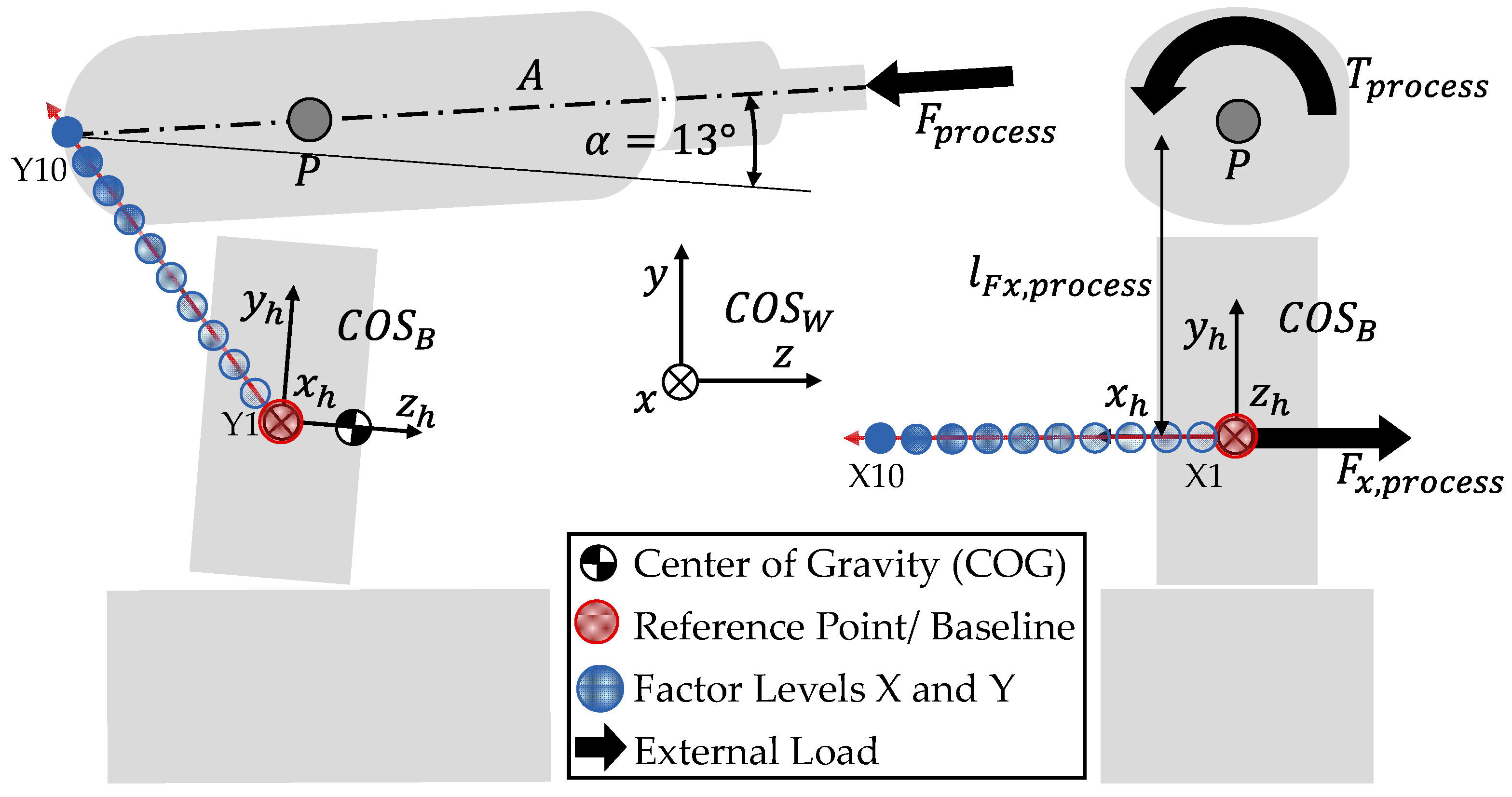
The external torque $T_{process}$ onto the screwdriver were determined by the virtual sensor and the external force $F_{process}$ was provided indirectly by the push force, as described above. These two results from the sub-models A and B were used together with sub-model C to build up the ApOL model.

The loads on the human (forces ($F_{xh}, F_{yh}, F_{zh}$) and torques ($T_{xh}, T_{yh}, T_{zh}$)) are calculated in one point, called the reference point, located at the middle of the handle in the MATLAB Simulink model (see Figure 3). The motion data is also passed into the model at this reference point. The external loads ($F_{process}. T_{process}$) are added to the screwdriver at the point of applied load. The process force $F_{process}$ is applied at the tip of the screwdriver along the drilling axis $A$ while the process torque $T_{process}$ acts around the drilling axis $A$. Since the drilling axis is not parallel to the $z_h$-axis and has an offset of $\alpha =13°$, $F_{process}$ and $T_{process}$ has components in the $y_h$- and $z_h$-axis. During a screw-in process, the user must withstand the process torque $T_{process}$ from the motor by applying a counteraction force at the handle resulting in a counteracting torque. Thus, $T_{process}$ is converted to a force $F_{x,process}$ using the lever $l_{Fx,process}$ between point $P$ on the drilling axis $A$ and reference point. This force acts along the $x_h$-axis of body-fixed coordinate system (${COS}_B$) of the screwdriver. The body-fixed ${COS}_B$ is implemented according to ISO 10068 [37] (see Figure 3). The $z_h$-axis is collinear to the forearm of the user-facing away from him. The $y_h$-axis is colinear to the centerline of the handle, thus the $x_h$-axis is perpendicular to the handle centerline (see Figure 3).

The load on the human (forces and torques) is calculated by MATLAB Simulink in the body-fixed coordinate system ${COS}_B$. To eliminate the noise, a 50th-order one-dimensional median filter was applied using the “medfilt1”-function built into MATLAB.

2.5. Verification of the ApOL Model

For the verification of the ApOL model two separate steps were taken: First the simulation results of the forces ($F_{xh}, F_{yh}, F_{zh}$) and torques ($T_{xh}, T_{yh}, T_{zh}$) are compared to basic analytical considerations of the mathematical model. Second, a parameter study was conducted which shows the influence of the location of the reference point (handle position) on the user load.

Considering the first part of the verification, the comparison between the ApOL simulation model and the mathematical model, the mathematical model consists of the process forces and torques as well as the mass of the screwdriver. Since the direction of the weight force vector changes in the body fixed ${COS}_B$ when the screwdriver is moved around, the calculated values for $F_{process}$ and $T_{process}$ were only determined for the duration of the screw-in process as the screwdriver’s position is fixed upwards (see Section 2.3 motion phase O3). Outside of the screw-in phase, the process force and torque values were set to zero. This is also due to the fact, that the process forces and torques only occur during the screw-in process. The mathematical model calculates the maximum and minimum force ($F_{xh}, F_{yh}, F_{zh}$) and torque ($T_{xh}, T_{yh}, T_{zh}$) values only during the screw-in process. The formulas for the maximum and minimum force and torque values can be found in Appendix A in

Table A2. Mathematical model: formulas for calculated max. and min. values. α describes the angle between the drilling axis and the $z_h$-axis during the screw-in process.

Component	Formula	Formula	Comment
	YB and Y1–Y10	XB and X1–X10	-
$F_{xh,max}$	$T_{process}$/Y9y	$T_{process}$/XBy	-
$F_{xh,min}$	$T_{process}$/YBy	= $F_{xh,max}$	-
$F_{yh,max}=F_{yh,min}$	$F_{process}$∗ sin(α)– $F_{weight}$∗ sin(α)	$F_{process}$∗ sin(α)– $F_{weight}$∗ sin(α)	No Influence of the parameter setup onto$F_{yh}$
$F_{zh,max}=F_{zh,min}$	$F_{process}$∗ cos(α)– $F_{weight}$∗ cos(α)	$F_{process}$∗ cos(α)– $F_{weight}$∗ cos(α)	No Influence of the parameter setup onto $F_{zh}$
$T_{xh,max}$	$F_{process}$∗ YBy	$F_{process}$∗ XBy	-
$T_{xh,min}$	$F_{weight}$∗ YBy	= $T_{xh,max}$	-
$T_{yh,max}$	$T_{process}$∗ sin(α)	$F_{process}$∗cos(α) ∗ X10x + $F_{weight}$∗ cos(α) ∗ X10x	-
$T_{yh,min}$	0 (reference point is not in line with drill axis, weight induces no torque around zh-axis)	$F_{process}$∗cos(α) ∗ XBx	-
$T_{zh,max}$	$T_{process}$∗ cos(α)	$F_{process}*\sin \left(\alpha \right)*$ X10x + $F_{weight} *\sin \left(\alpha \right)*$ X10x	-
$T_{zh,min}$	0 (reference point is not in line with drill axis, weight induces no torque around zh-axis)	$F_{process}*\sin \left(\alpha \right)*$ XBx	-

.

The ApOL model is verified by comparing the forces ${(F}_{xh}, F_{yh}, F_{zh}$) and torques ${(T}_{xh}, T_{yh}, T_{zh})$ of the mathematical model and the ApOL model. The mean-absolute-error (MAE) is calculated since the value of the force/torque is important for the load on the user. In addition, the relative MAE (rMAE) is calculated by dividing the MAE by the corresponding mean force or torque value. The rMAE is used to evaluate the deviation between the participants.

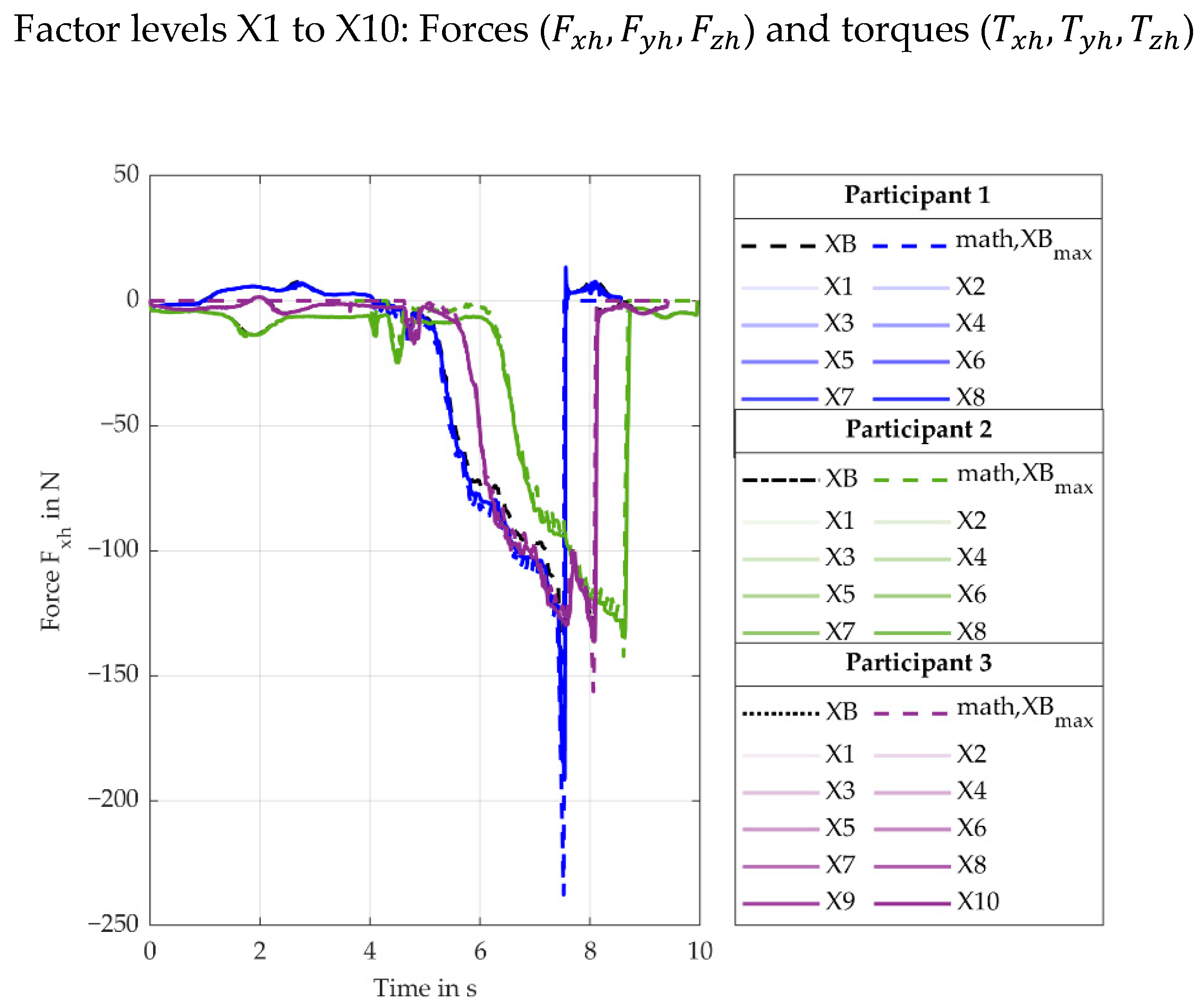
To show the importance of modelling the mass, for $T_{yh}$ in the variation of X1–X10 (X variation), the maximum calculated force, $F_{process}$, without the mass was also calculated.

The second part of the verification of the ApOL model is a parameter study. The parameter study was conducted to further verify the ApOL model. In total 21 cases were analyzed. To verify the model’s behavior, the reference point was altered along the three coordinates axis and the change in the load was analyzed. The initial design of the screwdriver was used as the baseline of the model. Here, x, y, and z coordinates were equal to zero (origin of ${COS}_B$). According to the sub-model C, the center of gravity (COG) is located slightly in front of the baseline point along the $z_h$-axis (see Figure 3). The values of the x-, y-, and z-coordinates describe the displacement of the reference point in relation to the baseline in the body-fixed coordinate system ${COS}_B$.

For the first set of parameters, the values of y- and z-coordinate were varied in ten steps from the baseline (YB) to the drill axis (see

Table 2. Y-variation: Reference point with factor levels YB and Y1–Y10. This variation represents a successive relocation of the original handle of the screwdriver to the backside of the motor assembly, putting the forearm axis in line with the drilling axis.

Factor Level	YB	Y1	Y2	Y3	Y4	Y5	Y6	Y7	Y8	Y9	Y10
y in mm	0	7.4	14.8	22.2	29.6	37.1	44.5	51.9	59.3	66.7	74.1
z in mm	0	$-5.9$	$-11.9$	$-17.8$	$-23.7$	$-29.6$	$-35.6$	$-41.5$	$-47.4$	$-53.3$	$-59.3$

and

Table 3. X-variation: Reference point with factor levels XB and X1–X10. This variation is selected to validate the model’s accuracy in accommodating modifications of the reference point in all three spatial directions.

Factor Level	XB	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10
x in mm	0	10	20	30	40	50	60	70	80	90	100

). The value for the x-coordinate was not changed for these cases. This variation of the reference point represents a successive relocation of the original handle of the screwdriver to the backside of the motor assembly, putting the forearm axis in line with the drilling axis.

For the second set of parameters, only the value of the x-coordinate was varied in ten equal steps from the baseline (XB) to a maximum X10 (see Figure 3). The altered values for these setups can be found in Table 3. The cases are named X1–X10.

3. Results

First, the correlation of the battery current and the process torque ${\mathit{T}}_{\mathit{p}\mathit{r}\mathit{o}\mathit{c}\mathit{e}\mathit{s}\mathit{s}}$ is presented separately since sub-model B can be analyzed independently of the overall ApOL model. Followed by the results of the parameter study and the verification of the ApOL model with the three sub-models A–C in Section 3.2.

3.1. Sub-Model B: Virtual Sensor Battery Current–Process Torque

The correlation of the process torque and the battery current is shown in Figure 4a. The blue curve shows the mean torque values over all 10 screw-in repetitions based on the data by Sänger et al. 2023 [30]. The yellow curve shows the linear correlation later used to determine the process torque ${\mathit{T}}_{\mathit{p}\mathit{r}\mathit{o}\mathit{c}\mathit{e}\mathit{s}\mathit{s}}$ based on the battery current. The correlation consists of two sections. For the first section (Idle Current) up to a current of 2.45 A, the torque equals zero. In the second section (Screw-in Process), from 2.45 A upwards.

The correlation of process torque $T_{process}$ and the battery current ${current}_{bat}$ can be described based on linear correlation as follows:

$$T_{process}=0, {current}_{bat}<2.45 \mathrm{A}$$

(2)

$$T_{process}= 0.75 \frac{\mathrm{Nm}}{\mathrm{A}}\times {current}_{bat}-1.41 \mathrm{Nm}, {current}_{bat}\ge 2.45 \mathrm{A}.$$

(3)

R² of the correlation for the second section (Screw-in Process) is 98%, as it fits very well from 2.45 A up to 24 A. From here, the torque increases stronger than the linear regression model. This can also be seen in Figure 4b, as the residual between the measured torque and the linear regression model shows low values up to a maximum of 0.5 Nm for torques below 12 Nm and a maximum residual of 2.2 Nm for higher torques.

3.2. ApOL Model Implemented in MATLAB-Simulink

In the following section, the results from the ApOL model implemented in MATLAB-Simulink are shown. The results focus on the load components that show a considerable change in their values due to the parameter variation and thus, are used for the verification of the ApOL model. For the factor levels Y1–Y10, this includes the force ${\mathit{F}}_{\mathit{x}\mathit{h}}$ (force direction is perpendicular to handle- and drill-axis) and the torque ${\mathit{T}}_{\mathit{x}\mathit{h}}$ (torque leads to radial/ulnar deviation of the wrist) and for the factor levels of X1–X10, the torques ${\mathit{T}}_{\mathit{y}\mathit{h}}$ (torque leads to extension/flexion of the wrist, torque along the handle axis) and ${\mathit{T}}_{\mathit{z}\mathit{h}}$ (torque leads to pronosupination forearm, torque along the forearm axis). The figures of the other forces ($F_{yh}$, $F_{zh}$) and torques ($T_{xh}$, $T_{yh}$, $T_{zh}$) can be found in Appendix B as they might be of interest to other researchers.

3.2.1. Influence of the Y- and Z-Coordinate (Y Variation) of the Reference Point on the Load Components

An exemplary load curve for the force ${\mathit{F}}_{\mathit{x}\mathit{h}}$ (force direction is perpendicular to handle- and drill-axis) during the whole movement cycle of the screwdriver is shown in Figure 5. The start and the end of the screw-in process are marked as dashed lines at 4 s and as dotted lines at 7.5 s. This period in the signal is referred to as the “screw-in process”. The calculated maximum and minimum values from the mathematical model are shown in red and yellow (see Appendix A Table A2 for formulas). The orientation of the screwdriver during the whole movement cycle is marked with (O1–O4), as explained in Section 2.3.

Since no considerable change in the force signals appears before and after the screw-in process, only the time of the screw-in process is examined. Figure 6 shows section (O3) of the force $F_{xh}$ for the three participants.

The qualitative progression for P1 and P2 are very similar except for a high rise at the end of the screw-in process for P1. P3 differentiates by having a kink towards the end. Equal for all participants are, that the calculated values mark the lower and upper limits with the simulated forces lying between them with rising values from Y1–Y9. Only the load for Y10 is approximately equal to zero. This is a special case in modeling the external load since the torque $T_{process}$ is not modeled as a lateral process force $F_{x,process}$ (see Figure 3). The rMAE and MAE values of all load components is shown in

Table 4. Verification of the ApOL model. The accuracy of the prediction compared to the mathematical model is presented as mean (and standard deviation (SD)) with the mean-absolute-error (MAE) and the relative mean-absolute-error (rMAE) for the X- and Y-variation.

P1−P3	MAE [N], [Nm]	rMAE [%]	MAE [N], [Nm]	rMAE [%]	MAE [N], [Nm]	rMAE [%]
Variations	Fxh		Fyh		Fzh
X	5.1 (3.4)	9.4 (4.6)	1.0 (0.5)	4.7 (2.8)	1.6 (0.2)	1.6 (0.5)
Y	12.0 (4.0)	11.4 (4.6)	1.1 (0.4)	5.1 (2.4)	1.1 (0.2)	3.7 (4.5)
	Txh		Tyh		Tzh
X	0.5 (0.1)	8.1 (2.5)	0.2 (0.1)	1.7 (0.6)	0.1 (0.0)	4.6 (2.7)
Y	0.5 (0.1)	8.5 (4.5)	0.3 (0.1)	16.1 (11.4)	0.3 (0.1)	7.0 (2.6)

.

The MAE the force $F_{xh}$ between the calculated and simulated values for the three participants is 12.0 N with a standard deviation (SD) of 4.0 N and the rMAE is 11.4% (SD 4.6%) (see Table 4).

The torque ${\mathit{T}}_{\mathit{x}\mathit{h}}$ around the $x_h$-axis during the whole motion cycle for all three participants is shown in Figure 7. The qualitative progression of the curves is partly different between the users, as P1 shows two peaks and P2 and P3 both only show one.

Equal for all participants is, that outside of the screw-in process, the simulated values for the baseline (YB) are lowest and increase from Y1–Y10. The calculated values here are equal to zero. Regarding the simulated values during the screw-in process, the absolute values for the baseline are the highest and decrease from Y1–Y6 for P1 and P3 and from Y1–Y7 for P2. Y7 (Y8) marks the zero-crossing for P1 and P3 (P2) and the values of the remaining setups increase from Y7–Y10 (Y8–Y10). The calculated maximum value is slightly lower than the baseline values during the screw-in process. The calculated minimum value is equal to zero outside of the screw-in process and about 1.8 Nm during the screw-in process. The rMAE between the calculated maximum value (math, YBmax) and the baseline is 8.5% (SD 4.5%), while the MAE is 0.5 Nm (SD 0.1 Nm) (see Table 4).

3.2.2. Influence of the X-Coordinate (X-Variation) of the Reference Point on the Load Components

The results of the torque ${\mathit{T}}_{\mathit{y}\mathit{h}}$ (torque along the handle axis) are shown in Figure 8. Similar to Figure 7, the absolute values outside of the screw-in process are lowest for the baseline (XB) and X1 and increase towards X10.

A zero-crossing from positive to negative (negative to positive) can be seen for all three participants before (after) the screw-in process. The calculated values are zero. During the screw-in phase, the baseline shows the lowest absolute values amongst the simulated values. The magnitude of the torque increases from X1 to X10. The maximum calculated value is equal to the values for X10 for all participants. The two signals overlap as shown in the section in Figure 8. The maximum calculated values (math, X10_max) fit the simulated values (X10) with a rMAE of 1.7% (SD 0.6%) (see Table 4). Moreover, similar to Figure 7, the progression of the signals varies between the participants, as P1 shows again two peaks and P2 and P3 show only one peak. The minimum calculated value is equal to zero during the whole movement cycle. Furthermore, shown in Figure 8 is the calculated maximum torque without consideration of the screwdriver’s mass (green line). This signal progression is roughly 2 Nm lower than the calculated values with mass consideration (red line). The rMAE of 15.4% (SD 2.9%) between the calculated values (math, X10_max, noMass, green curve) and the simulated values (X10) occur if the mass of the screwdriver is ignored.

The signal for the torque ${\mathit{T}}_{\mathit{z}\mathit{h}}$ around the $z_h$-axis (torque leads to pronosupination forearm, torque along the forearm axis) (see Figure 9) show some partly similar results to the torque $T_{yh}$.

Besides the baseline and the calculated minimum values, the signals show the lowest value for X1 and increase towards X10 during the whole movement cycle. The calculated minimum value is equal to zero and the baseline (XB) fluctuates around zero with a maximum offset of 0.1 Nm. Before and after the screw-in process, significant changes in the signal can be seen as they show only slightly lower values than during the screw-in process itself. Here, the signals show the same qualitative curve progression as seen in Figure 7 but with positive values. The calculated maximum values are approximately equal to the maximum simulated values from X10 with a maximum offset of 0.2 Nm. The maximum calculated values (math, X10_max) fit the maximum simulated values of $T_{zh}$ with a rMAE of 4.6% (SD 2.7%). The minimum calculated values (math, XB_min) fit the baseline values with sufficient accuracy. The maximum offset is 0.3 Nm.

4. Discussion

First, a short summary of the discussion is given, followed by a detailed discussion in Section 4.1 and Section 4.2. Limitations are given in Section 4.3.

The correlation between the process torque and the battery current shows an acceptable coefficient of determination (R = 98%). Only for torque values higher than 12 Nm, a relative error of 15.2% can be seen, which is still reasonable since these torques only occur for a very short amount of time during the screw-in process.

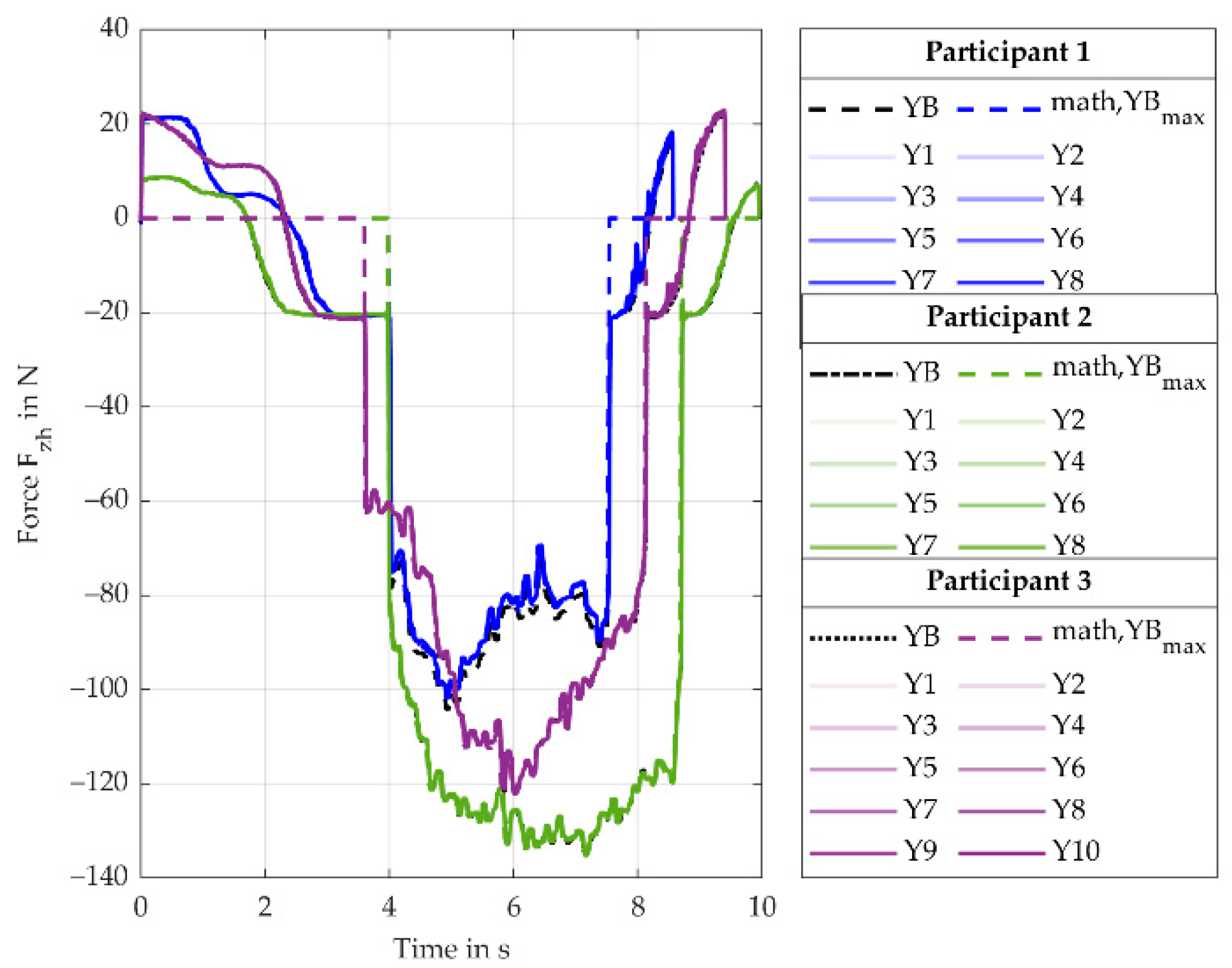
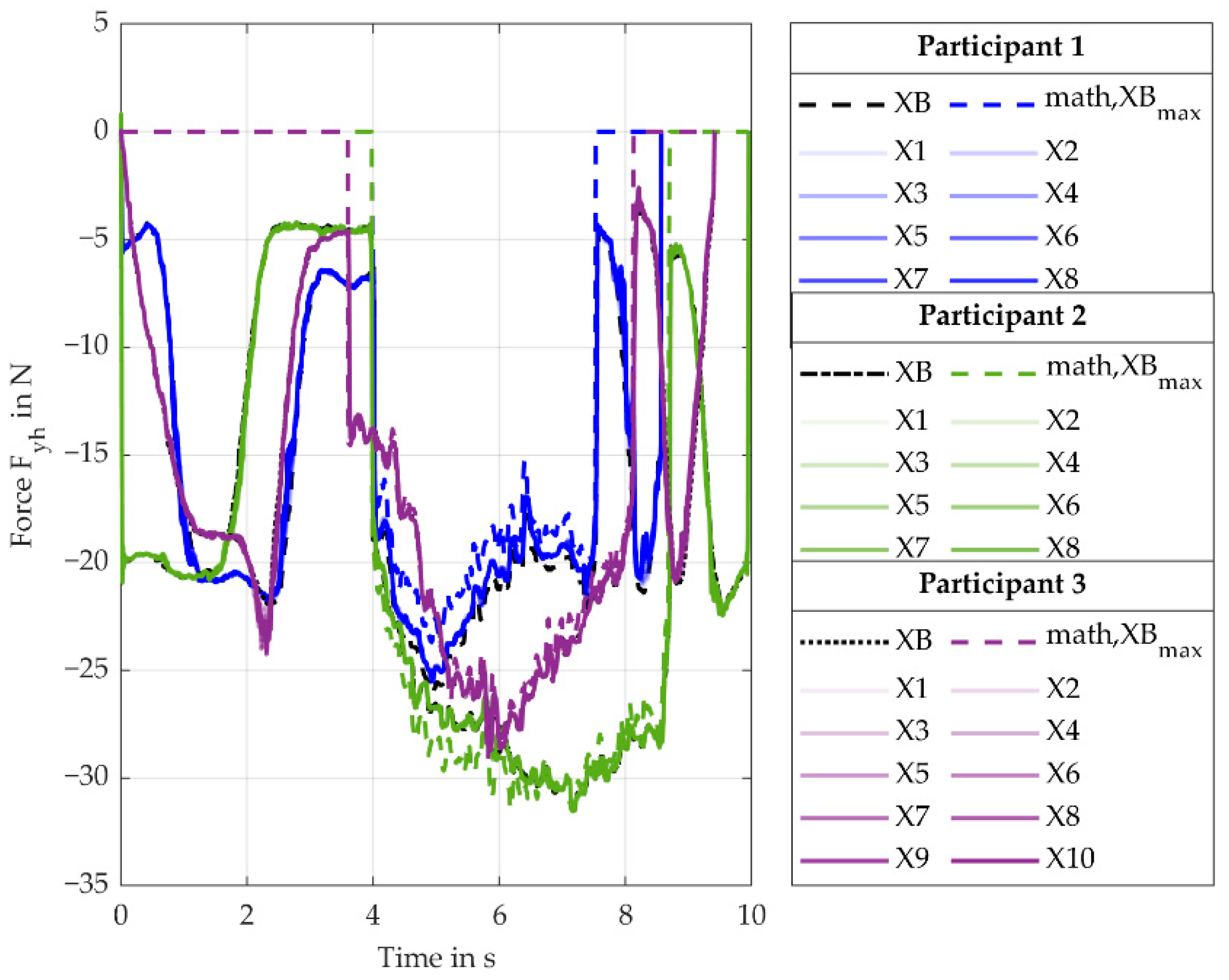
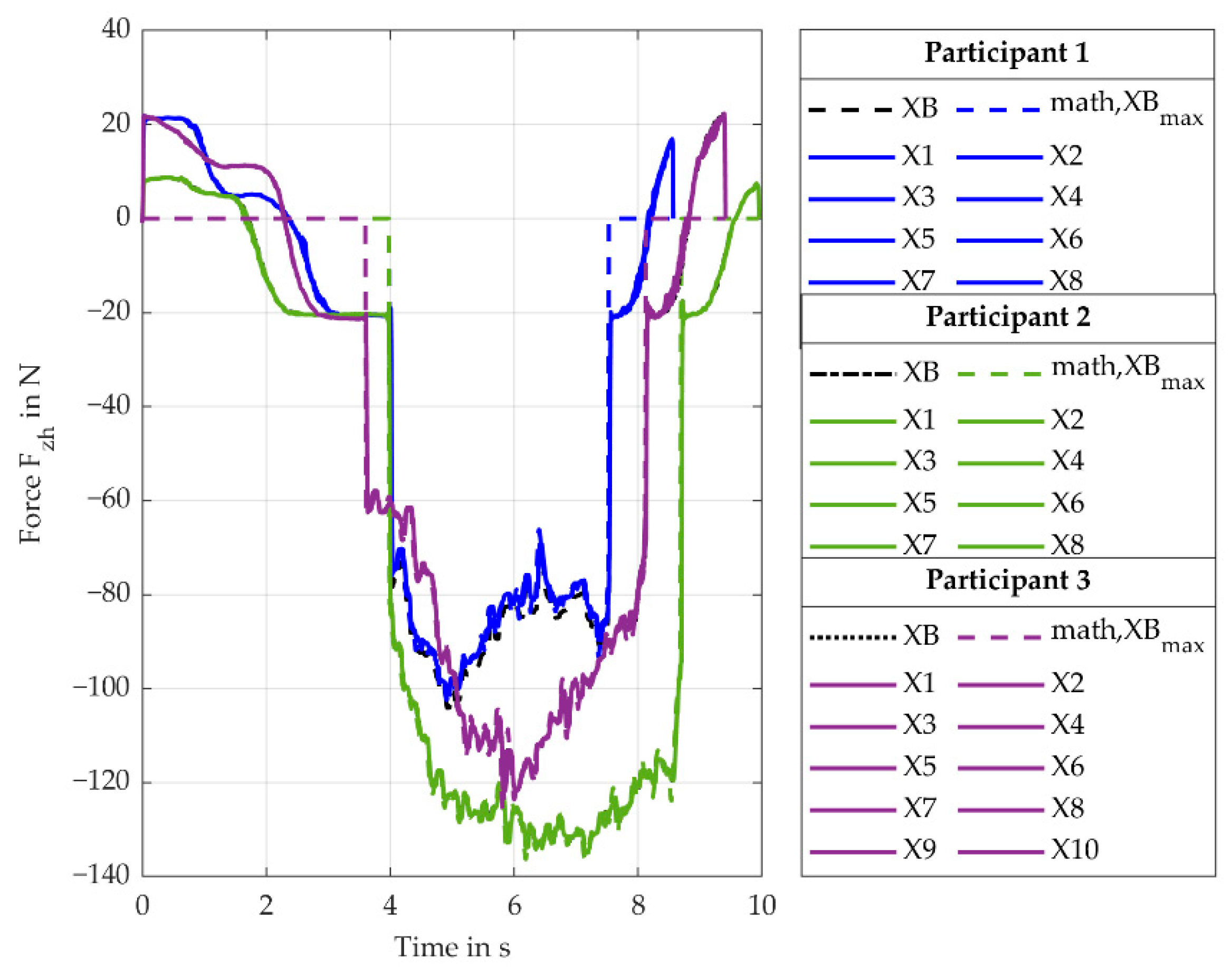
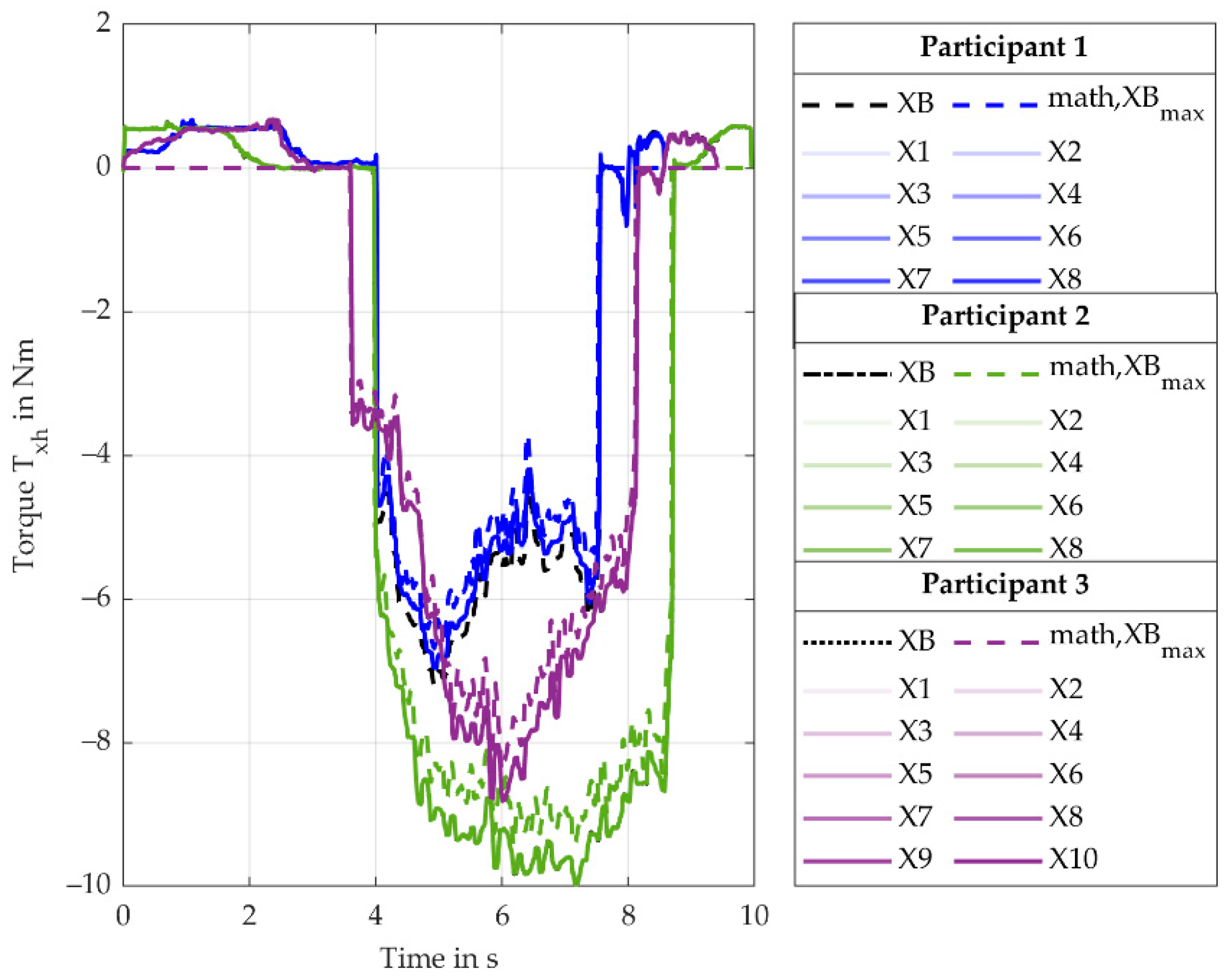
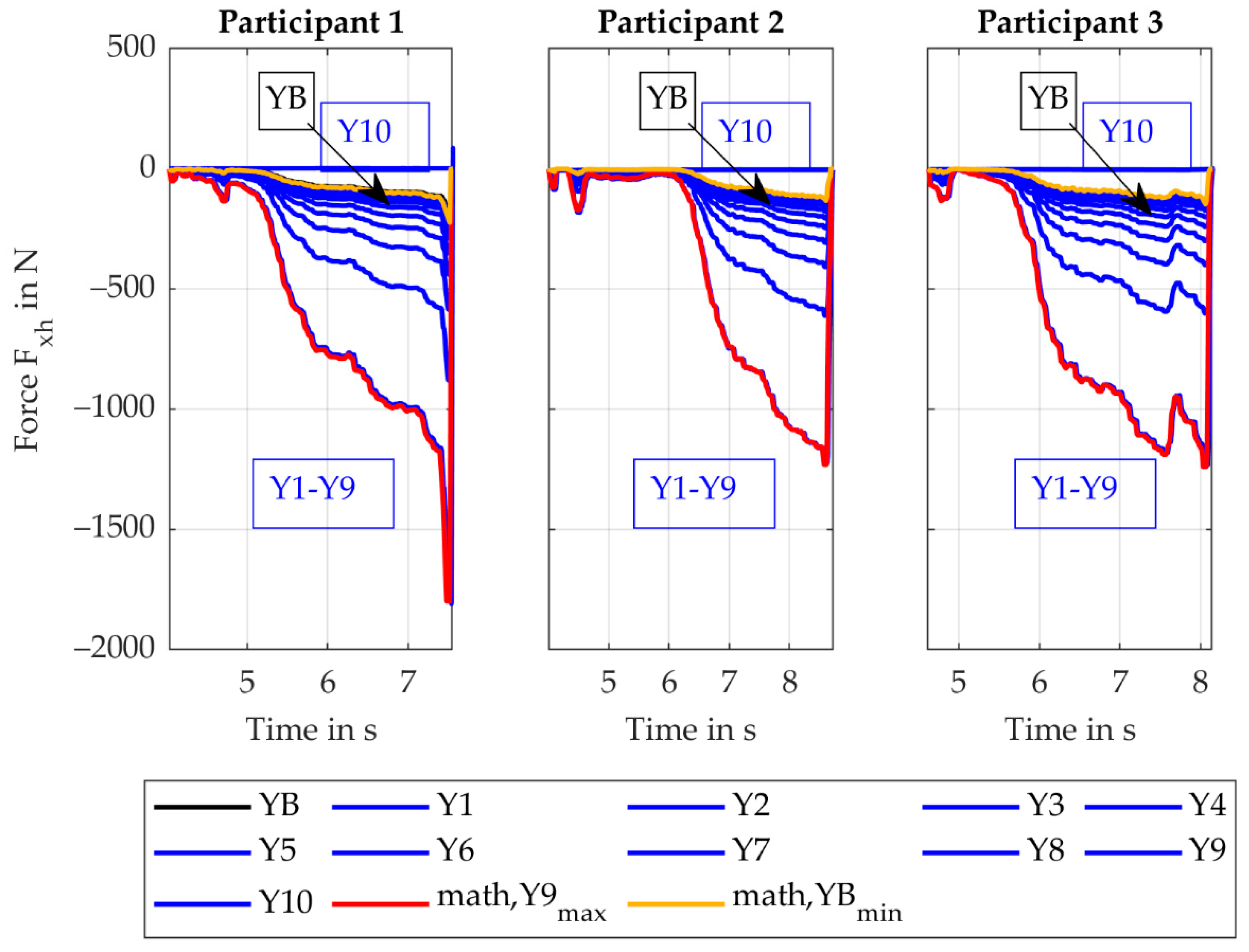
The force ${\mathit{F}}_{\mathit{x}\mathit{h}}$ (force direction is perpendicular to handle- and drill-axis) for the Y-variation behaves as expected and is determined by the simulation model with a rMAE of 11.4% (SD 4.6%). An increase from the baseline (YB) to Y9 fits the assumption of inverse proportionality between $F_{x,process}$ and the lever.

Since the Torque ${\mathit{T}}_{\mathit{x}\mathit{h}}$(torque leads to radial/ulnar deviation of the wrist) for the Y-variation is mainly influenced by $F_{process}$, decreasing the lever reduces the torque. This effect overlays with a torque induced by moving the reference point away from the COG. This results in an increasingly robust design moving from the baseline (YB) to Y10. The ApOL model is able to determine the torque ${\mathit{T}}_{\mathit{x}\mathit{h}}$ with rMAE of 8.5% (SD 4.5%). However, the MAE of the torque $T_{xh}$ is 0.5 Nm (SD 0.1 Nm).

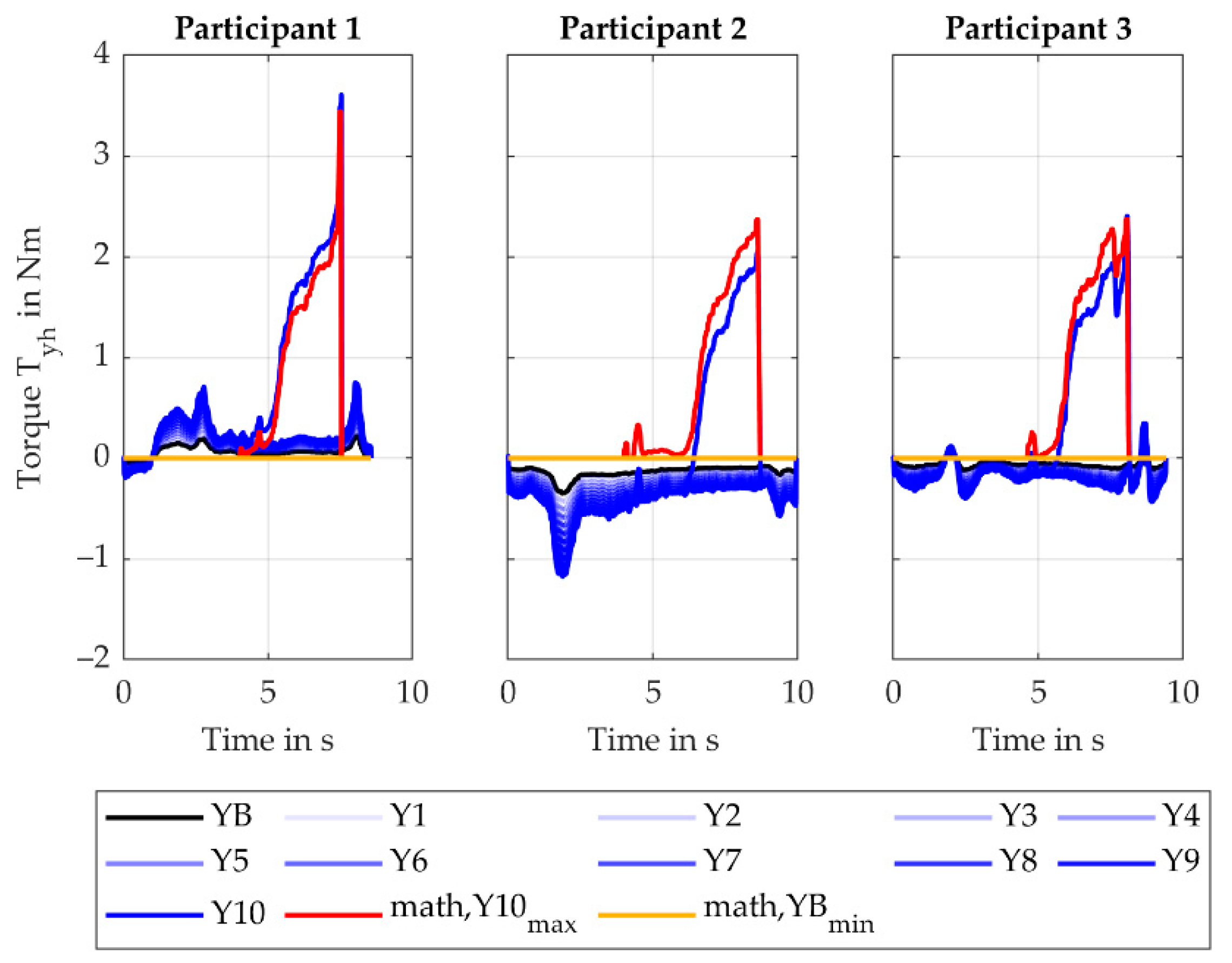
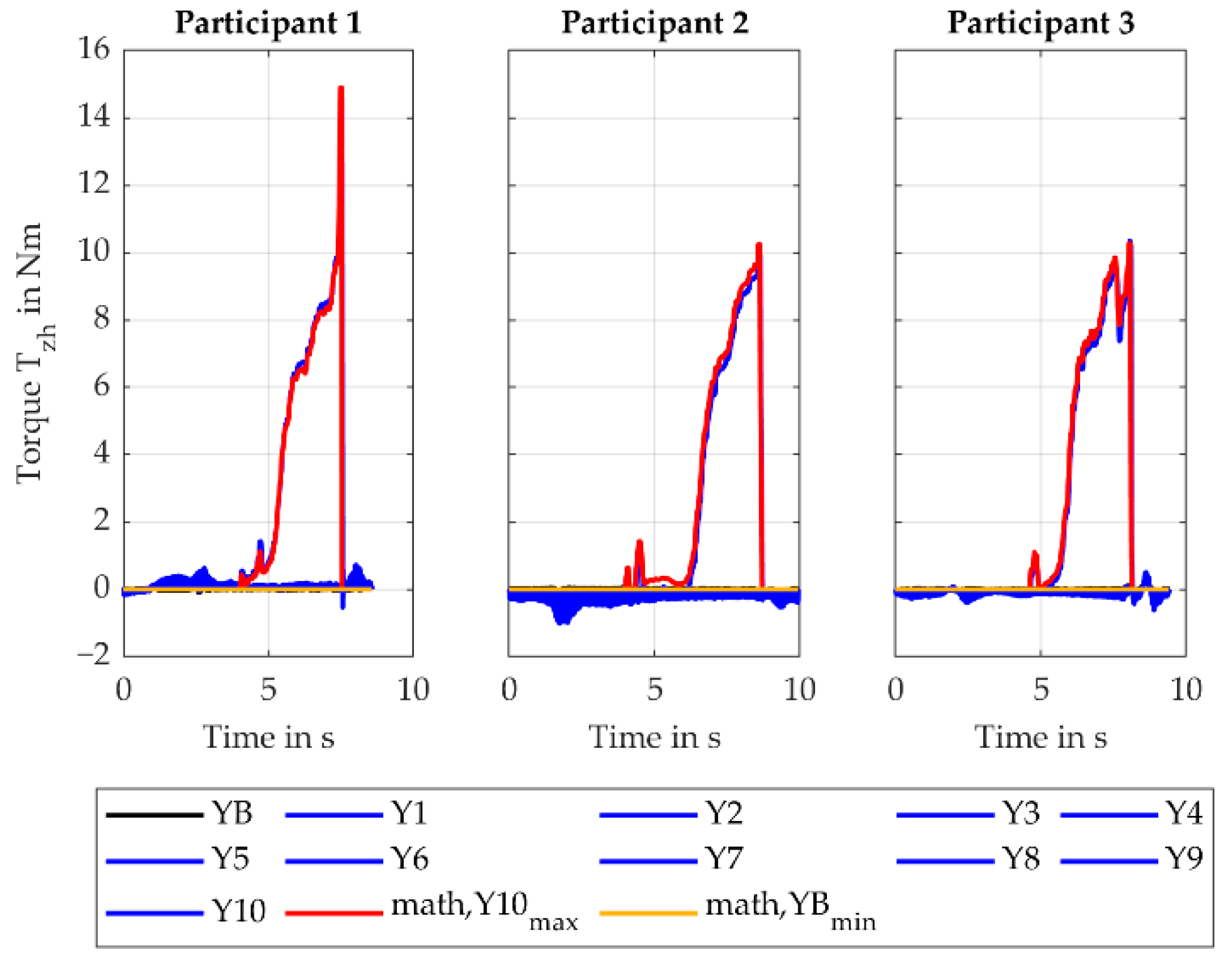
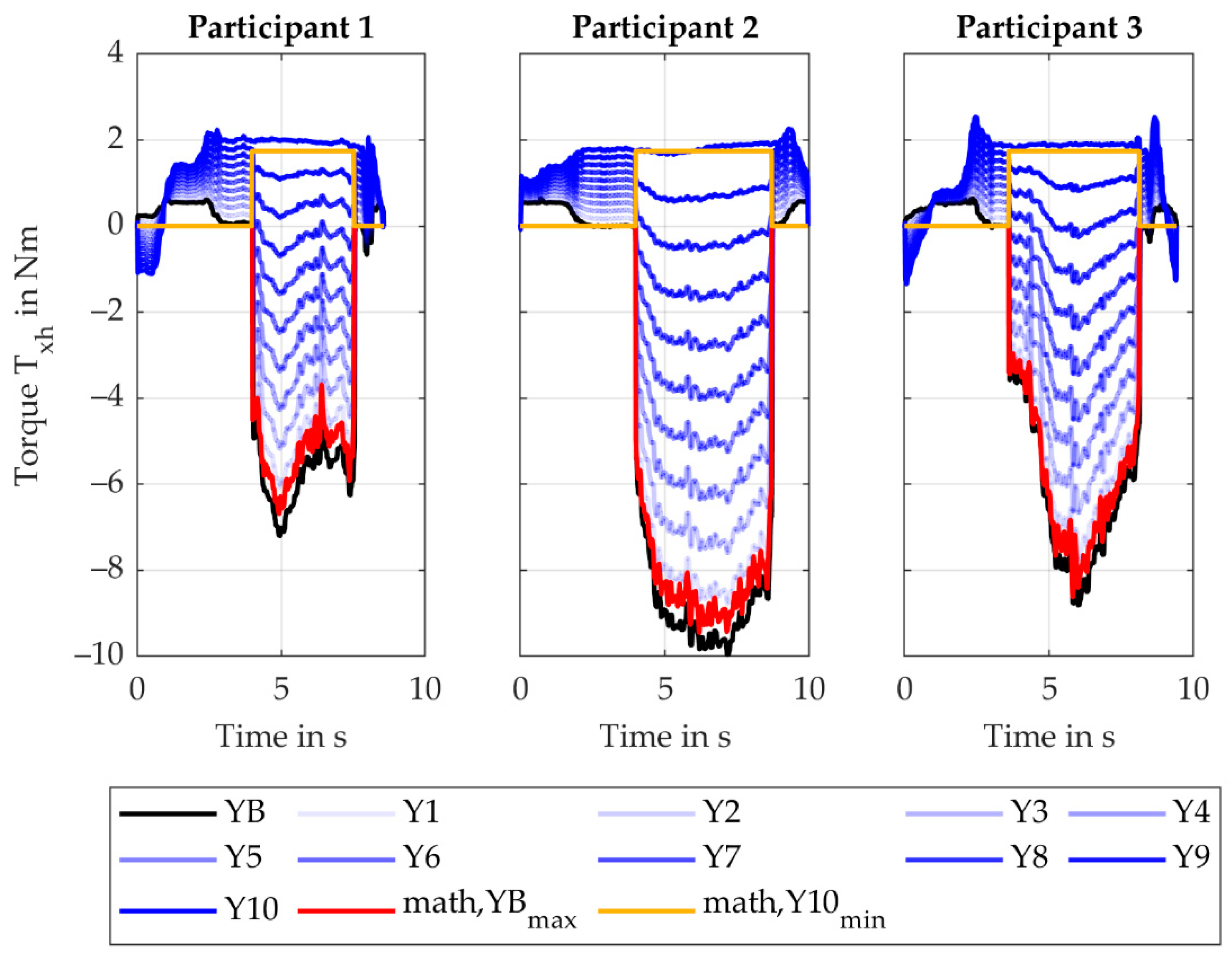
The increase in the torque ${\mathit{T}}_{\mathit{y}\mathit{h}}$ (torque leads to extension/flexion of the wrist, torque along the handle axis) for the X-variation from the XB to X10 is caused by increasing the distance between the reference point and the drill axis. This causes the $z_h$-component of $F_{process}$ to induce an increasing torque. The rMAE of ${\mathit{T}}_{\mathit{y}\mathit{h}}$ is 1.7% (SD 0.6%).

Considering the torque ${\mathit{T}}_{\mathit{z}\mathit{h}}$ (torque leads to pronosupination forearm, torque along the forearm axis) for the X-variation, the increase in torque from the baseline to Y10 is caused by the same effect. Here, the $y_h$-component of $F_{x,process}$ induces the torque causing the resulting absolute values to be smaller. The rMAE is 4.6% (SD 2.7%).

4.1. Virtual Sensor for External Load–Process Torque

For battery currents below 2.45 A, the screw does not bite into the wood [30]. Up to this point, there is no torque that loads the human (see Figure 4a Idle Current). When the screw bites, the torque and the current increase as seen in Figure 4a Screw-in Process). With a R² of 98%, the linear correlation fits the reality on an acceptable level. It has to be taken into account, that higher residuals for the correlation (see Figure 4b) in the high torque area indicate a lower quality of the model for this area. The residuals cause a maximum relative error of 5.1% for values lower than 12 Nm and a maximum relative error of 15.2% for values above 12 Nm. These errors are acceptable as these high torques are only reached for about 100 ms at the end of the screw-in process when the screw is fully sunk into the wood.

4.2. ApOL Model in MATLAB-Simulink

The ApOL model is verified by comparing the simulated values with the calculated ones from the mathematical model. The verification considers the influence of factor level (see Section 2.5) on the forces and torques for the y- and z-coordinates and the x-coordinate separately.

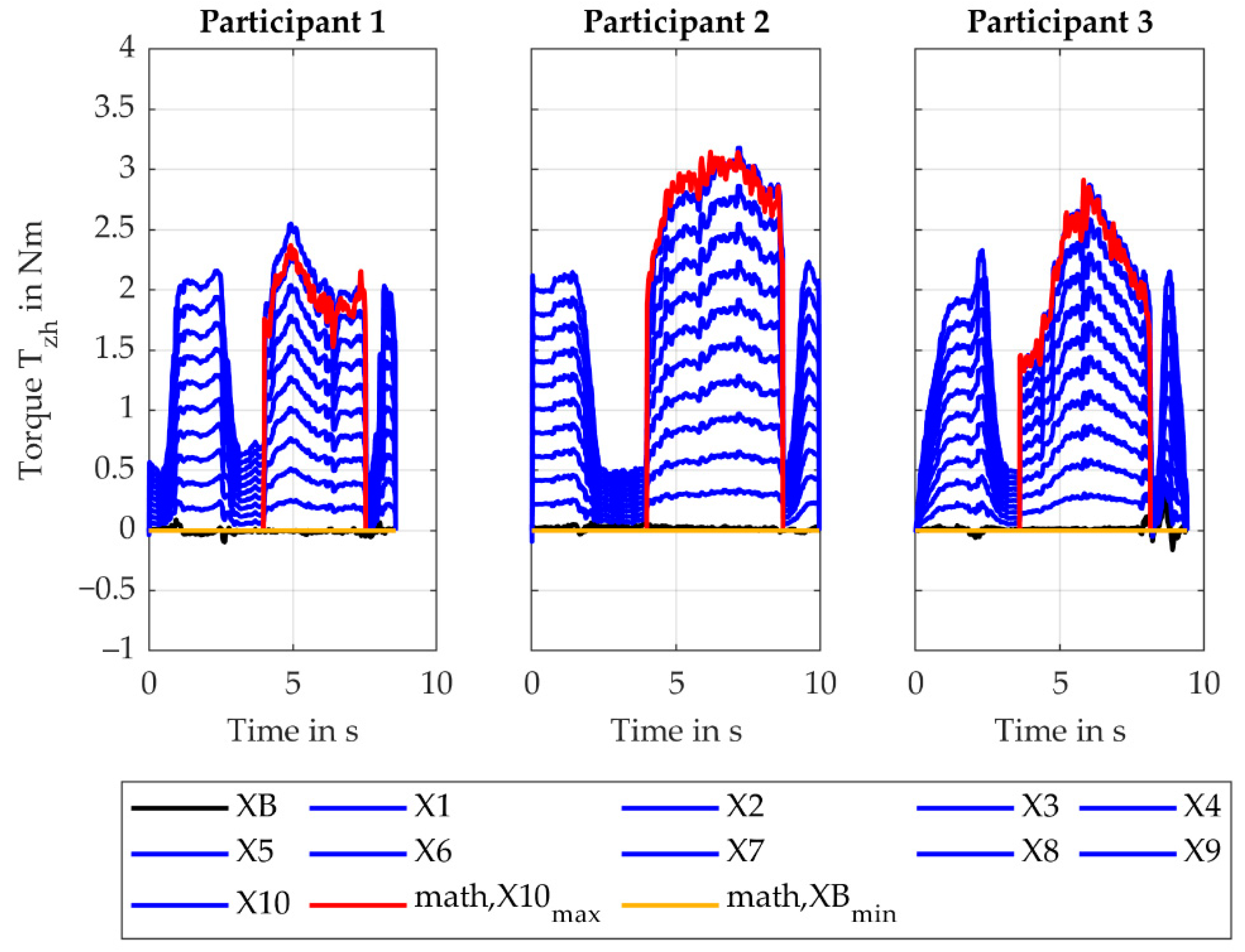
4.2.1. Influence of the Y- and Z-Coordinate of the Reference Point, Factor Levels Y1–Y10

For the variation of the y- and z-coordinates of the reference point, only the force ${\mathit{F}}_{\mathit{x}\mathit{h}}$ (force direction is perpendicular to handle- and drill-axis) and the torque ${\mathit{T}}_{\mathit{x}\mathit{h}}$ (torque leads to radial/ulnar deviation of the wrist) showed a considerable change. The remaining plots are presented in Appendix B.

Considering the force ${\mathit{F}}_{\mathit{x}\mathit{h}}$ (force direction is perpendicular to handle- and drill-axis) in Figure 6, the force behaves as expected. This component is mainly influenced by the process force $F_{x,process}$, which is inversely proportional to the lever, represented by the value of the y coordinate. With a decreasing lever, the force component increases. For Y10, the model assumes that the torque $T_{process}$ is converted to $F_{x,process}$ does not hold, resulting in a force that is approximately zero. Since the maximum (math, Y9_max) and minimum (math, YB_min) calculated values fit the simulated values pretty well, the inertia forces induced by the motion of the user do not influence the results in a considerable way for this setup.

During the screw-in process, the torque ${\mathit{T}}_{\mathit{x}\mathit{h}}$ (torque leads to radial/ulnar deviation of the wrist) is mainly influenced by the process force $F_{process}$. When moving the reference point out of the baseline, the corresponding lever decreases, resulting in a lower torque. The second influence on $T_{xh}$ is the mass of the screwdriver, which induces an increasing torque when moving the reference point away from the baseline and the COG. The two phenomena overlay and result in the torque curves shown in Figure 7. For the calculated minimum (math, Y10_min), only the mass is considered while the progression of the simulated values indicates an influence of $F_{process}$. This is caused by the fact that the screwdriver is not held perfectly upright in Position (C) during the screw-in process by the users, thus inducing an additional load component that is not considered in the mathematical model yet. Outside of the screw-in process, the mass of the screwdriver is mainly responsible for the torque curve. For the baseline, the torque ${\mathit{T}}_{\mathit{x}\mathit{h}}$ is always positive since the COG is located in front of the reference point. Moving the reference point up towards the drilling axle shifts the COG behind the reference point, thus the torque $T_{xh}$ is negative. When the screwdriver is rotated upwards, this changes and so does the torque $T_{xh}$. The same effect occurs after the screw-in process when the screwdriver is lowered. Another characteristic seen in Figure 7 is the robust design of the setup Y10. For the baseline (YB), the main load appears during the screw-in process, and it also varies between the users. Even though they all performed the same task, the load is dependent on the individual handling. For Y10, not only is the load approximately the same for all participants, it also only slightly increases during the screw-in process. This effect is very important, as a robust design eliminates noise factors and helps develop systems that are invariant from the user and the handling of the task. Finding robust designs helps significantly when optimizing support systems for humans.

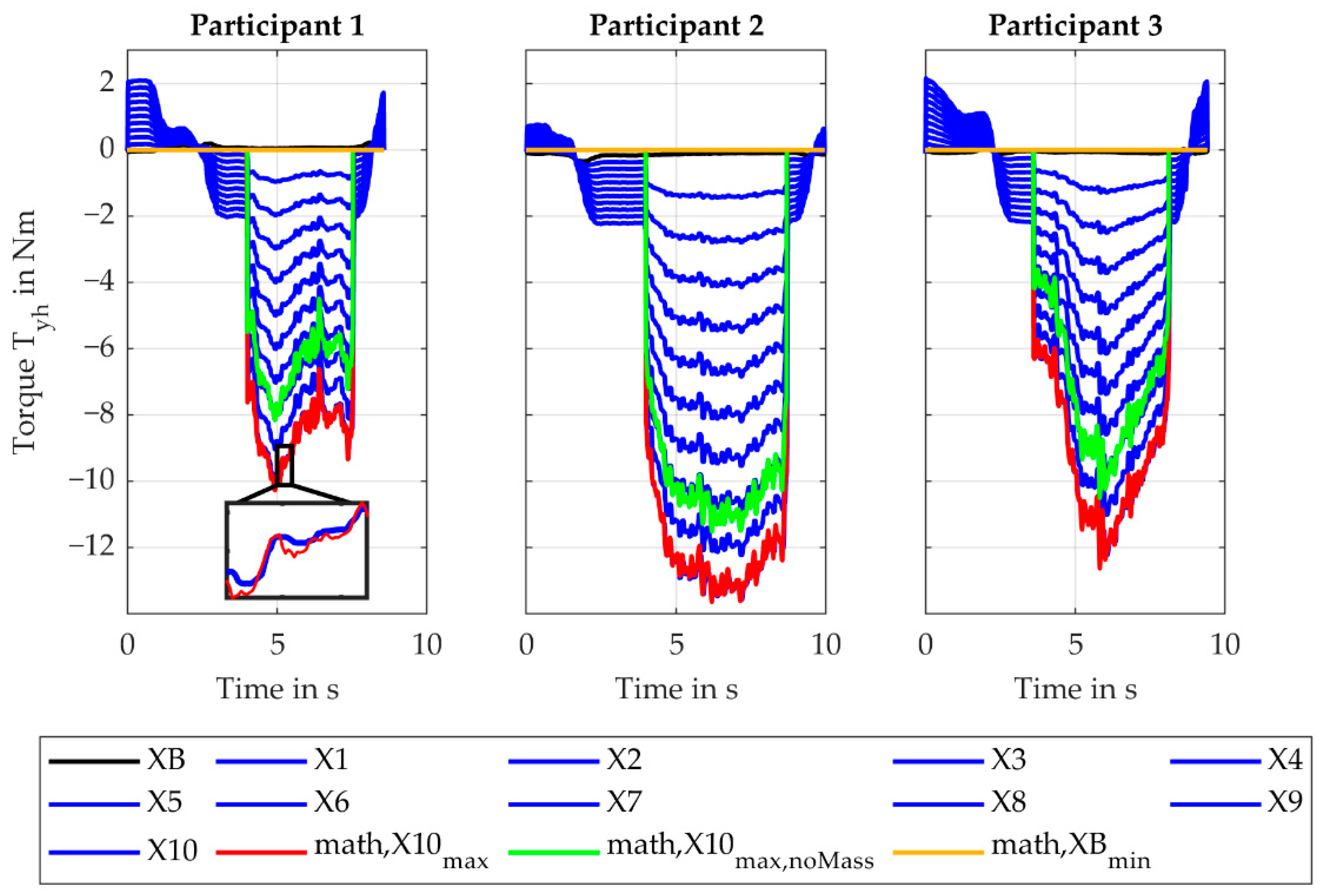
4.2.2. Influence of the X-Coordinate of the Reference Point, Factor Levels X1–X10

For the variation of the x-coordinate of the reference point, only the torques ${\mathit{T}}_{\mathit{y}\mathit{h}}$ (torque leads to extension/flexion of the wrist, torque along the handle axis) and ${\mathit{T}}_{\mathit{z}\mathit{h}}$ (torque leads to pronosupination forearm, torque along the forearm axis) showed a considerable change. The remaining plots are presented in Appendix B.

The torque${\mathit{T}}_{\mathit{y}\mathit{h}}$ (torque leads to extension/flexion of the wrist, torque along the handle axis) (see Figure 8), is only induced due to the screwdriver’s mass outside of the screw-in process. Moving the reference point out of its initial position (XB), the lever towards the COG increases and so does the torque $T_{yh}$. When rotating the screwdriver upwards, the orientation of the COG to the reference point in the space-fixed coordinate system changes, causing the gravity to flip the torque. The same effect in the opposite direction can be seen after the screw-in process. During the screw-in process, the main influence is the process force $F_{process}$ and the weight force. An increase in the x coordinate also increases the lever for these forces, resulting in higher torques $T_{yh}$. The maximum calculated values (math, X10_max) fit the simulated values (X10) with a rMAE of 1.7% (SD 0.6%). If the mass of the screwdriver were ignored, a rMAE of 15.4% (SD 2.9%) between the calculated values (math, X10_max, noMass) (green curve) and the simulated values (X10) would occur. This shows the importance of modelling the mass of the technical system. For the baseline (XB), the process force $F_{process}$ and the weight force induces no torque around the $y_h$-axis. The values for the baseline setup are only influenced by the motion of the user. The minimum calculated values correspond to the baseline (XB) and are equal to zero. The maximum offset between these two curves is 0.4 Nm, thus the motion of the user has very little influence in this case.

The torque ${\mathit{T}}_{\mathit{z}\mathit{h}}$ (torque leads to pronosupination forearm, torque along the forearm axis) is mainly influenced by the process force $F_{process}$ during the screw-in process and by the weight force outside of the screw-in process. For the latter, the weight force induces a torque around the $z_h$-axis. Since the axis are body-fixed, moving the screwdriver from its initial position (O1) to its upward position (O3) decreases this torque. After the screw-in process (O4), the screwdriver is again oriented vertically so the torque increases again. These torque values match the weight force times the corresponding lever. During the screw-in process, the torque $T_{zh}$ increase from Y1 to Y10, as the $y_h$-component of the process force induces a torque around the $z_h$-axis. The maximum calculated values (math, X10_max) fit the maximum simulated values of $T_{zh}$ with a rMAE of 4.6% (SD 2.7%) showing again a successful verification. The minimum calculated values (math, XB_min) fit the baseline values with sufficient accuracy. The maximum offset is 0.4 Nm.

4.3. Limitations of the ApOL Model

The ApOL model allows us to determine interaction torques and forces between the screwdriver and the DHM. Nevertheless, some limitations exist, that have to be considered when looking at the results.

The process force $F_{process}$, the battery current, and the motion data used as input for the ApOL model are subject to inaccuracies and are based on studies performed by students and not professional workers as stated by [31]. This should be taken into account in the product development of support systems for professionals. Since this data was determined based on an overhead task, the data is only valid for this specific use case.

Limiting the virtual sensor for the correlation of process torque and battery current is the constant push force of 100 N applied by the user during the experiment conducted by Sänger et al., 2023 [30]. The authors showed that a constant push force on the test bench does not match reality. Moreover, the relative error discussed in Section 4.1 induced by higher residuals for the linear approximation of the torque for torque values above 12 Nm has to be taken into consideration. This specific correlation is also only applicable to the specific screwdriver, the screws and the wood mentioned in Sänger et al., 2023 [30].

The interaction forces and torques in sub-model C are calculated at the reference point. This sets some limitations to the accuracy of the determined values, since in real life, the loads are transferred on the surface of the handle onto the user. In addition, not considered in the multibody model is the drivetrain of the screwdriver, thus ignoring its inertia forces and torques. Even though the verification of the workload model was successful, a validation of the model is still missing. This could be achieved by measuring the interaction forces of the hand and screwdriver handle or by using this ApOL model for the determination of the user loads as input for musculoskeletal human models and comparing the muscular activities with surface electromyography (s-EMG) measurements from experimental studies.

In the modeling of the external torque $T_{process}$ (resp. $F_{x,process}$, see Figure 3) it was assumed that the process torque $T_{process}$ is compensated by a lateral force $F_{xh}$ applied by the user. This represents a simplification of the human-machine interface between the hand of the DHM and the handle of the screwdriver.

Regarding the verification of the ApOL model, it must be taken into consideration that the analytical values were determined based on the assumption that the screwdriver is held perfectly upright in position (O3). This does not correspond to reality, making the analytical results only limited and comparable to the simulated ones as seen for the torque $T_{xh}$ for the factor levels Y1–Y10.

5. Conclusions

This paper proposes an application-oriented workload (ApOL) model to evaluate interaction forces and torques between a cordless screwdriver and a DHM for an overhead drilling task. The model uses experimental data such as the battery current of the screwdriver, the push force of the user, as well as the motion of the user to determine external loads onto the user at the handle of the screwdriver. For the verification of the ApOL model, analytical results calculated from the process forces and the screwdriver mass during the screw-in process were compared to the simulated results. The verification was successful, as the rMAE between the simulated values and the calculated ones were all below 11.4% except for and $T_{yh}$. For the variation of the y- and z-coordinate (Y variation), the rMAE for all forces ($F_{xh}$ $F_{yh}$, $F_{zh}$) is 11.4% (SD 4.6%) or smaller. For the torques ($T_{xh}$, $T_{yh}$ $T_{zh}$) the maximum rMAE 16.1% (SD 11.4%). However, the maximum MAE of the torques is 0.5 Nm (SD 0.1 Nm).

For the variation of the x-coordinate (X variation), the rMAE is comparable but occasionally lower. The maximum rMAE for the forces ($F_{xh},$ $F_{yh}$, $F_{zh}$) is 9.4% (SD 4.6%) with a maximum MAE of 5.1 N (SD 3.4 N). The maximum rMAE of the toques ($T_{xh}$, $T_{yh}$, $T_{zh}$) is 8.1% (SD 2.5%). Altering the screwdriver setup led to an expected change in the interaction torques and forces estimated at the handle of the screwdriver. For $F_{yh}$, $F_{zh}$, $T_{xh}$, $T_{yh}$, and $T_{zh}$, a noticeable portion of the load occurred outside of the screw-in process, showing the importance of modelling the mass of the technical system. To validate the workload model, the authors recommend a coupled DHM and ApOL model simulation to determine muscle activity and compare the calculated values to experimental surface EMG measurements.

In future work the proposed ApOL model can be used in the early stages of hand- or power tool- development to test different configurations of electric screwdrivers to estimate the load onto the user without the need for a physical prototype of the technical system. This allows the development of load-optimized power tools in a user-centered way, e.g., through optimal weight distribution of the power tool or individual optimization of the handle size. A challenge is the consideration of the anthropometry of the user e.g., hand size and finger length.

Considering the loads, the model can also be used to identify favorable setups for tasks supported by e.g., exoskeletons. This helps in the holistic development of support systems in combination with handheld power tools by modeling realistic interaction forces and torques. For example, setups can be found where the force distribution is shifted to increase the force components supported by the support system, while the force components acting on the user decrease. This helps further reduce stress on the human body and thus prevents musculoskeletal diseases.

The ApOL model can also be used to identify the influence of different drivetrain configurations and the motor controller by simply extending the sub-model C. Besides determining realistic loads, the model showed the ability to identify robust designs of the technical system, which eliminate noise factors and thus help develop systems, where the load is invariant from the user handling of the work task. This is important considering user-invariant loads reduce the cost and effort for the optimization procedure of the support system for each user.