Author Contributions
Conceptualization, L.E.G.-C., L.I.M.-A., A.V.-M., V.P.C. and P.P. (Pierre Payeur); data curation, P.P. (Patricia Portillo); formal analysis, L.E.G.-C.; investigation, P.P. (Patricia Portillo); methodology, L.E.G.-C. and V.P.C.; project administration, L.E.G.-C.; software, P.P. (Patricia Portillo); supervision, L.E.G.-C.; validation, P.P. (Patricia Portillo), L.I.M.-A., A.V.-M. and P.P. (Pierre Payeur); visualization, P.P. (Patricia Portillo); writing—original draft, P.P. (Patricia Portillo); writing—review and editing, L.E.G.-C., L.I.M.-A., A.V.-M., V.P.C. and P.P. (Pierre Payeur). All authors have read and agreed to the published version of the manuscript.
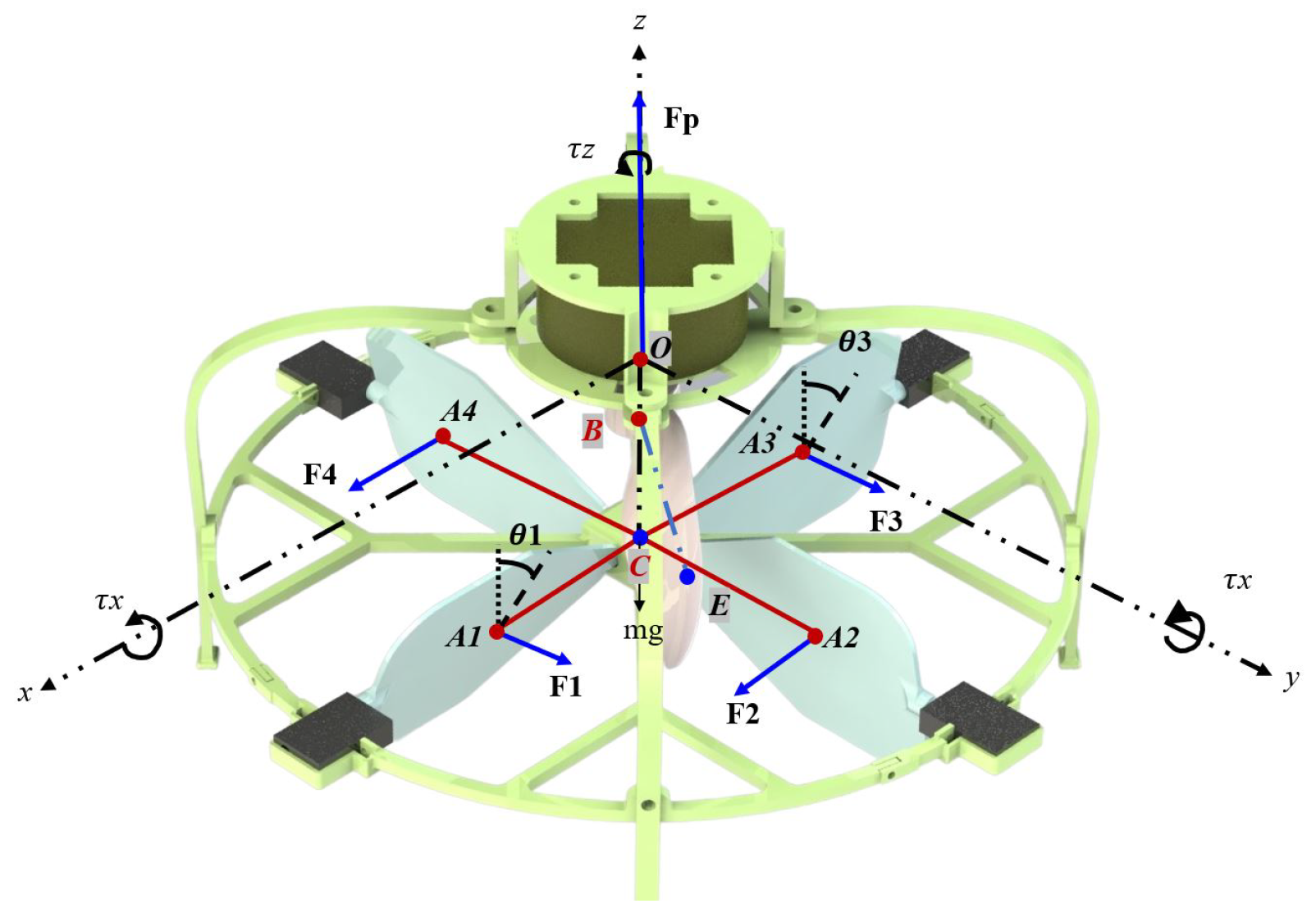
Figure 1.
Acting force diagram of the SR-UAV body frame.
Figure 1.
Acting force diagram of the SR-UAV body frame.
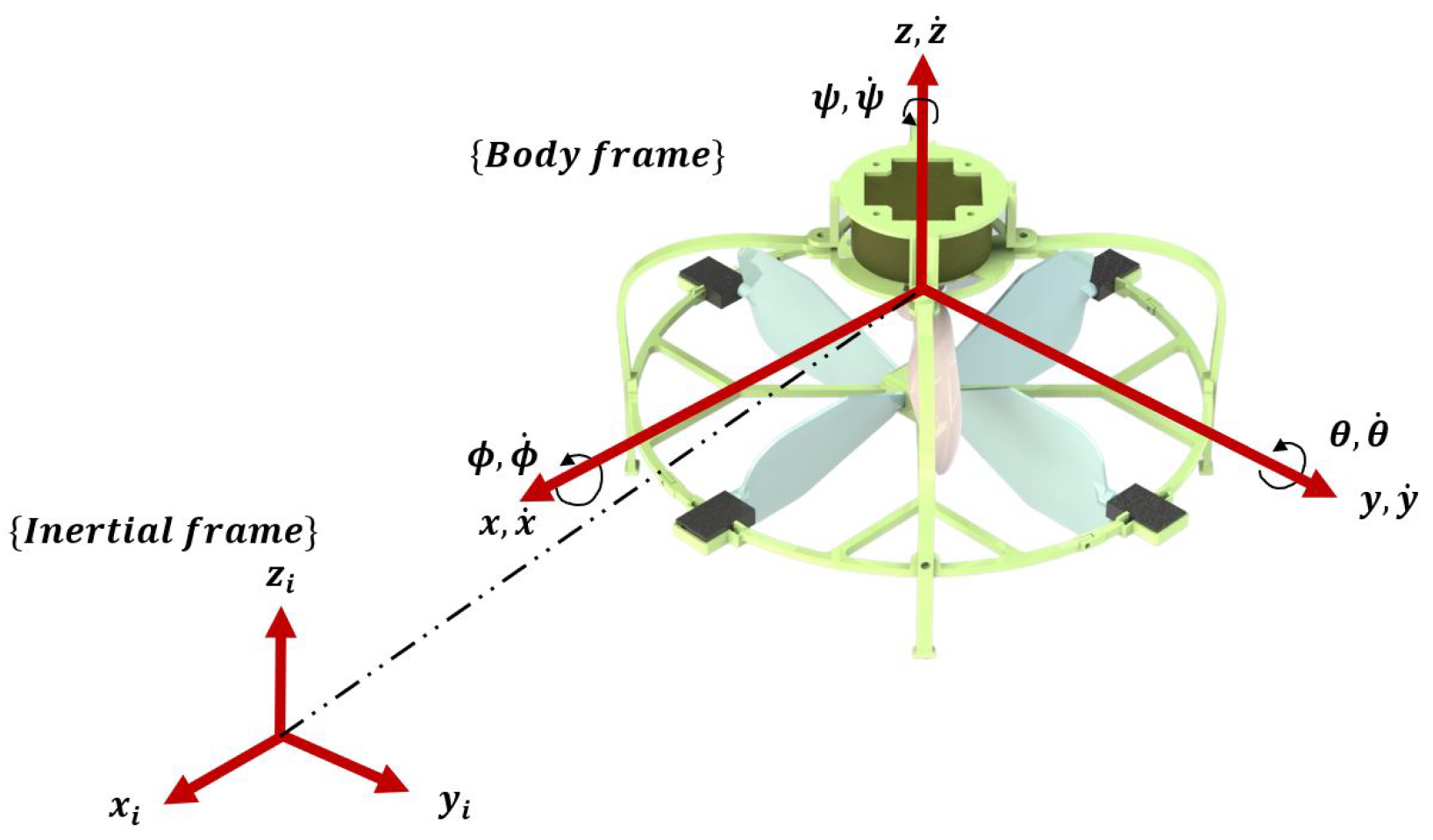
Figure 2.
Inertial and body frame of the SR-UAV.
Figure 2.
Inertial and body frame of the SR-UAV.
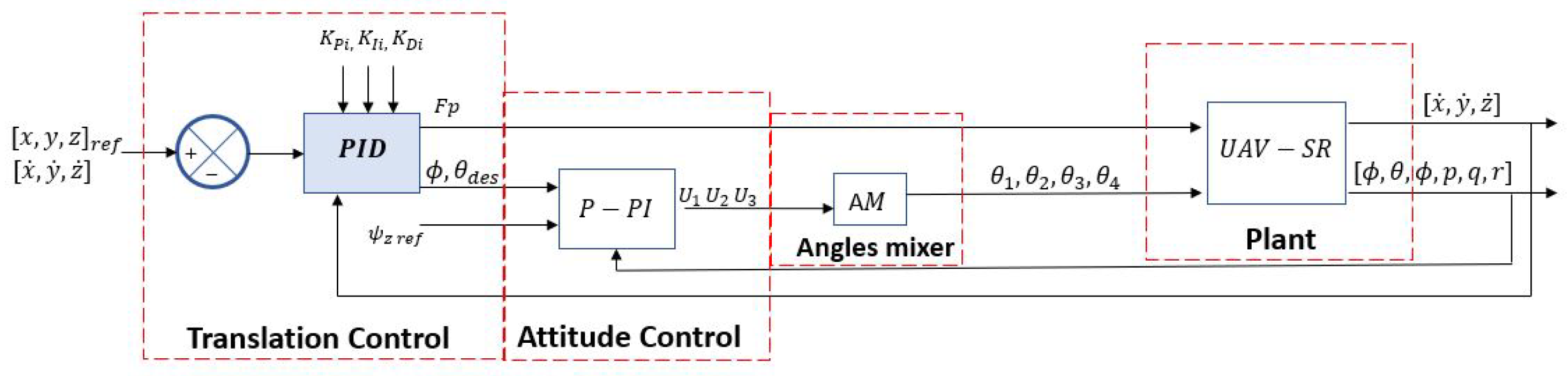
Figure 3.
PID in cascade with a P-PI for translation and attitude control.
Figure 3.
PID in cascade with a P-PI for translation and attitude control.
Figure 4.
P-PI attitude control.
Figure 4.
P-PI attitude control.
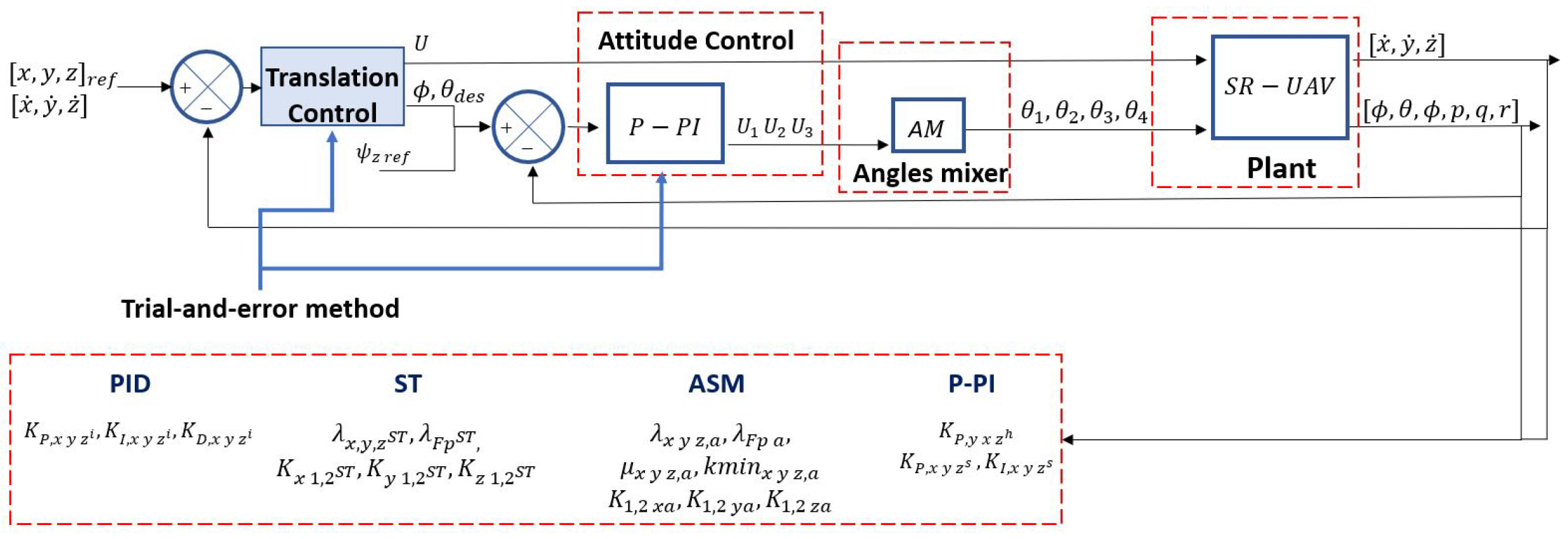
Figure 5.
SR-UAV system control, where Super-Twisting method is used for translational control.
Figure 5.
SR-UAV system control, where Super-Twisting method is used for translational control.
Figure 6.
SR-UAV system control, where Adaptive Sliding Mode method is used for translational control.
Figure 6.
SR-UAV system control, where Adaptive Sliding Mode method is used for translational control.
Figure 7.
Control scheme with the trial-and-error method.
Figure 7.
Control scheme with the trial-and-error method.
Figure 8.
Control scheme with the PSO method.
Figure 8.
Control scheme with the PSO method.
Figure 9.
Helicoidal trajectory for PID, ST, and ASM with trial-and-error tuning compared with reference path. (a) Controller PID-PPI with a helicoidal trajectory. (b) Controller ST-PPI with a helicoidal trajectory. (c) Controller ASM-PPI with a helicoidal trajectory.
Figure 9.
Helicoidal trajectory for PID, ST, and ASM with trial-and-error tuning compared with reference path. (a) Controller PID-PPI with a helicoidal trajectory. (b) Controller ST-PPI with a helicoidal trajectory. (c) Controller ASM-PPI with a helicoidal trajectory.
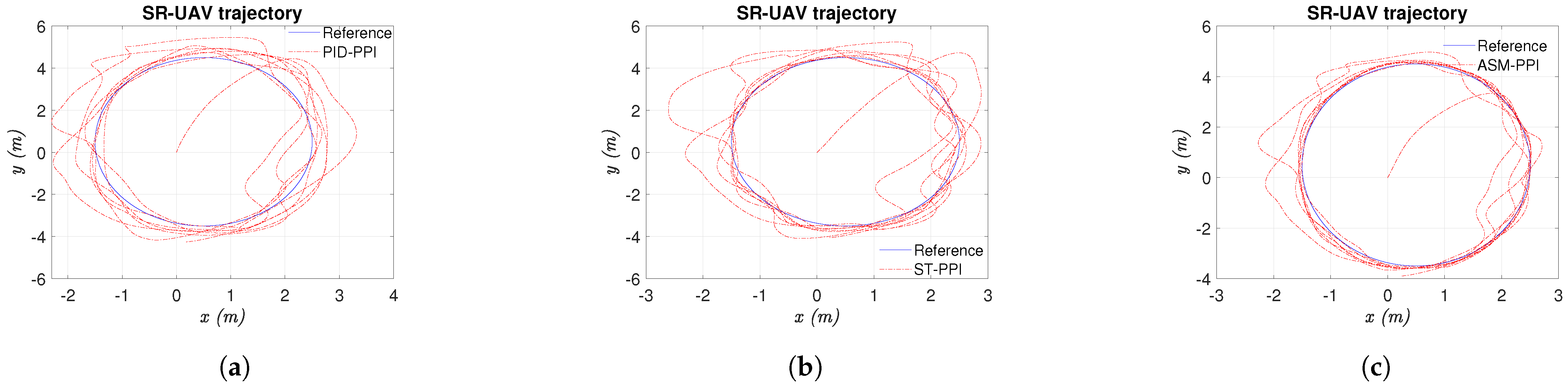
Figure 10.
Helicoidal trajectory for PID, ST, and ASM in 2D compared with trial-and-error tuning. (a) Controller PID-PPI with a helicoidal trajectory in 2D. (b) Controller ST-PPI with a helicoidal trajectory in 2D. (c) Controller ASM-PPI with a helicoidal trajectory in 2D.
Figure 10.
Helicoidal trajectory for PID, ST, and ASM in 2D compared with trial-and-error tuning. (a) Controller PID-PPI with a helicoidal trajectory in 2D. (b) Controller ST-PPI with a helicoidal trajectory in 2D. (c) Controller ASM-PPI with a helicoidal trajectory in 2D.
Figure 11.
Servomotor fin angles for PID, ST, and ASM. (a) Angles of PID-PPI with a helicoidal trajectory. (b) Angles of ST-PPI with a helicoidal trajectory. (c) Angles of ASM-PPI with a helicoidal trajectory.
Figure 11.
Servomotor fin angles for PID, ST, and ASM. (a) Angles of PID-PPI with a helicoidal trajectory. (b) Angles of ST-PPI with a helicoidal trajectory. (c) Angles of ASM-PPI with a helicoidal trajectory.
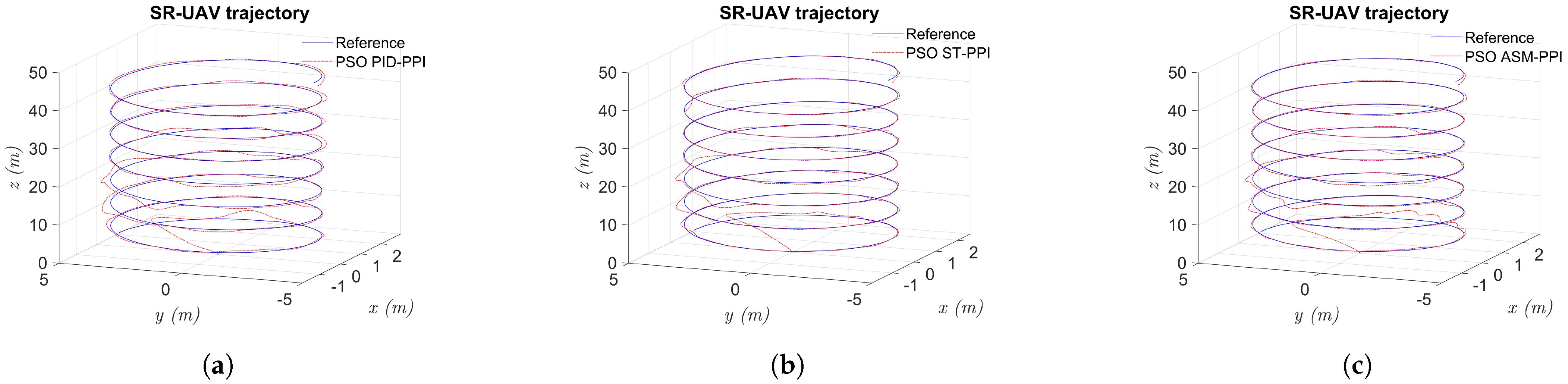
Figure 12.
Helicoidal trajectory for PID, ST, and ASM tuned with PSO and compared with reference path. (a) Controller PID-PPI with PSO gains. (b) Controller ST-PPI with PSO gains. (c) Controller ASM-PPI with PSO gains.
Figure 12.
Helicoidal trajectory for PID, ST, and ASM tuned with PSO and compared with reference path. (a) Controller PID-PPI with PSO gains. (b) Controller ST-PPI with PSO gains. (c) Controller ASM-PPI with PSO gains.
Figure 13.
Helicoidal trajectory for PID, ST, and ASM with PSO in 2D. (a) Controller PID-PPI with PSO gains in 2D. (b) Controller ST-PPI with PSO gains in 2D. (c) Controller ASM-PPI with PSO gains in 2D.
Figure 13.
Helicoidal trajectory for PID, ST, and ASM with PSO in 2D. (a) Controller PID-PPI with PSO gains in 2D. (b) Controller ST-PPI with PSO gains in 2D. (c) Controller ASM-PPI with PSO gains in 2D.
Figure 14.
Servomotor fin angles for PID, ST, and ASM. (a) Angles of controller PID-PPI with PSO. (b) Angles of controller ST-PPI with PSO. (c) Angles of controller ASM-PPI with PSO.
Figure 14.
Servomotor fin angles for PID, ST, and ASM. (a) Angles of controller PID-PPI with PSO. (b) Angles of controller ST-PPI with PSO. (c) Angles of controller ASM-PPI with PSO.
Figure 15.
Sliding surface for ST with trial-and-error. (a) Sliding surface—ST 1(x)—trial and error. (b) Sliding surface—ST 2(y)—trial and error. (c) Sliding surface—ST 3(z)—trial and error.
Figure 15.
Sliding surface for ST with trial-and-error. (a) Sliding surface—ST 1(x)—trial and error. (b) Sliding surface—ST 2(y)—trial and error. (c) Sliding surface—ST 3(z)—trial and error.
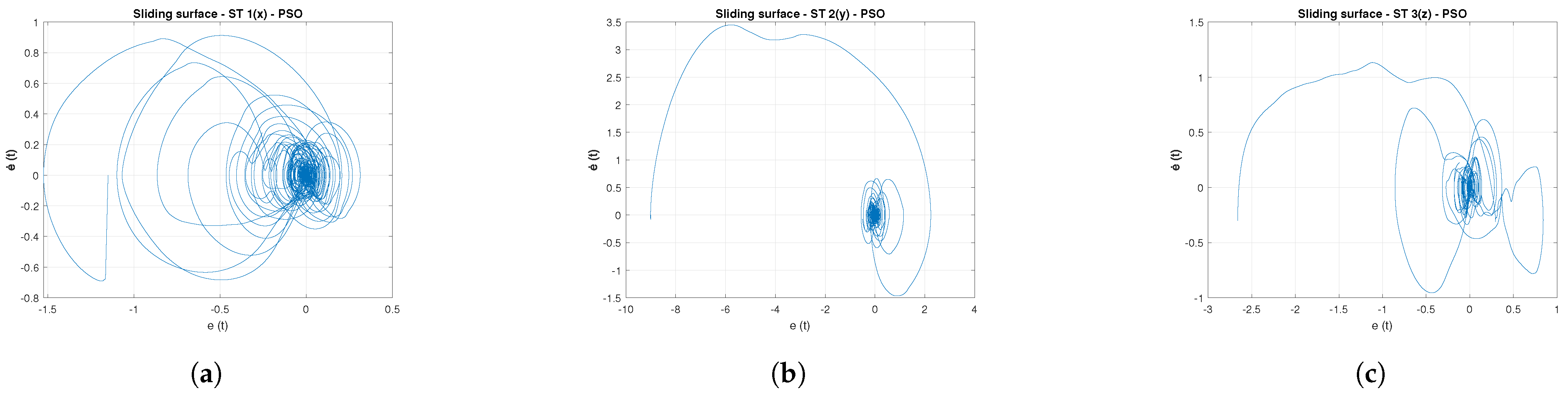
Figure 16.
Sliding surface for ST with PSO. (a) Sliding surface—ST 1(x)—PSO. (b) Sliding surface—ST 2(y)—PSO. (c) Sliding surface—ST 3(z)—PSO.
Figure 16.
Sliding surface for ST with PSO. (a) Sliding surface—ST 1(x)—PSO. (b) Sliding surface—ST 2(y)—PSO. (c) Sliding surface—ST 3(z)—PSO.
Figure 17.
Sliding surface for ASM with trial and error. (a) Sliding surface—ASM 1(x)—trial and error. (b) Sliding surface—ASM 2(y)—trial and error. (c) Sliding surface—ASM 3(z)—trial and error.
Figure 17.
Sliding surface for ASM with trial and error. (a) Sliding surface—ASM 1(x)—trial and error. (b) Sliding surface—ASM 2(y)—trial and error. (c) Sliding surface—ASM 3(z)—trial and error.
Figure 18.
Sliding surface for ASM with PSO. (a) Sliding surface—ASM 1(x)—PSO. (b) Sliding surface—ASM 2(y)—PSO. (c) Sliding surface—ASM 3(z)—PSO.
Figure 18.
Sliding surface for ASM with PSO. (a) Sliding surface—ASM 1(x)—PSO. (b) Sliding surface—ASM 2(y)—PSO. (c) Sliding surface—ASM 3(z)—PSO.
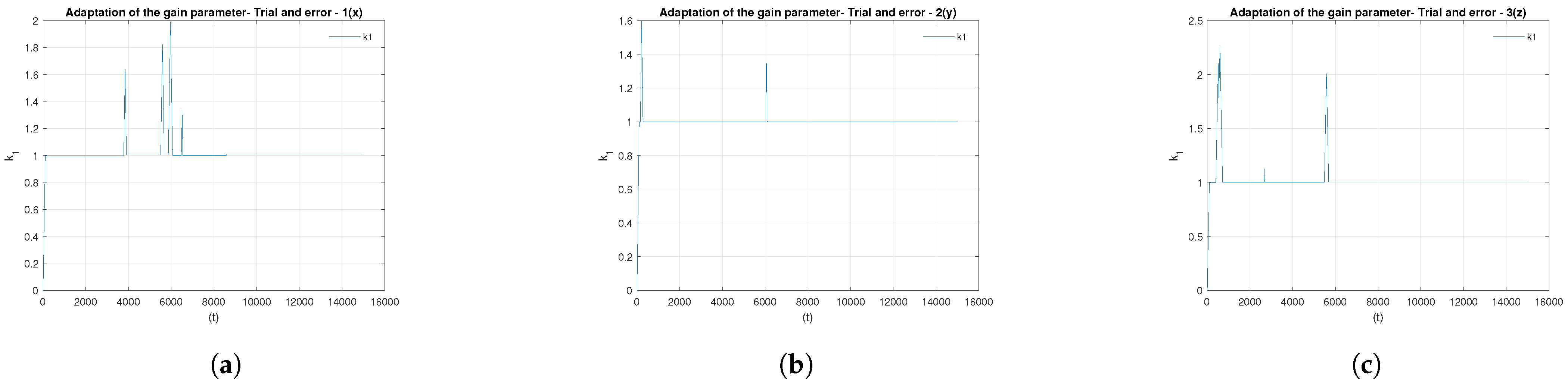
Figure 19.
Adaptation of the gain parameter for ASM with trial-and-error method. (a) Adaptation of the gain parameter—trial and error—1(x). (b) Adaptation of the gain parameter—trial and error—2(y). (c) Adaptation of the gain parameter—trial and error—3(z).
Figure 19.
Adaptation of the gain parameter for ASM with trial-and-error method. (a) Adaptation of the gain parameter—trial and error—1(x). (b) Adaptation of the gain parameter—trial and error—2(y). (c) Adaptation of the gain parameter—trial and error—3(z).
Figure 20.
Adaptation of the gain parameter for ASM with PSO. (a) Adaptation of the gain parameter—PSO—1(x). (b) Adaptation of the gain parameter—PSO—2(y). (c) Adaptation of the gain parameter—PSO—3(z).
Figure 20.
Adaptation of the gain parameter for ASM with PSO. (a) Adaptation of the gain parameter—PSO—1(x). (b) Adaptation of the gain parameter—PSO—2(y). (c) Adaptation of the gain parameter—PSO—3(z).
Table 1.
PID, Super Twisting, and Adaptive Sliding Mode parameters and gains.
Table 1.
PID, Super Twisting, and Adaptive Sliding Mode parameters and gains.
| PID | Super Twisting | Adaptive Sliding Mode |
|---|
| Translation C | Attitude C | Translation C | Attitude C | Translation C | Attitude C |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| - | - | | - | | - |
| - | - | - | - | | - |
| - | - | - | - | | - |
| - | - | - | - | | - |
| - | - | - | - | | - |
| - | - | - | - | | - |
Table 2.
Parameters of the SR-UAV.
Table 2.
Parameters of the SR-UAV.
| Parameters | Values |
|---|
| m | Kg |
| Kgm |
| Kgm |
| |
| |
| m |
| m |
| L | m |
| r | m |
| Nm |
| 15 N |
Table 3.
PID controller gains with trial-and-error tuning.
Table 3.
PID controller gains with trial-and-error tuning.
| Parameters | Values |
|---|
| |
| |
| |
| |
| |
| |
Table 4.
P-PI controller gains with trial-and-error tuning.
Table 4.
P-PI controller gains with trial-and-error tuning.
| Parameters | Values |
|---|
| 7 |
| |
| |
| |
| |
Table 5.
Parameters for ST controller.
Table 5.
Parameters for ST controller.
| Parameters | Values |
|---|
| 2 |
| 1 |
Table 6.
Gains for the ST controller with trial-and-error tuning.
Table 6.
Gains for the ST controller with trial-and-error tuning.
| Parameters | Values |
|---|
| 1 |
| |
| 1 |
Table 7.
Gains for the P-PI controller with trial-and-error tuning.
Table 7.
Gains for the P-PI controller with trial-and-error tuning.
| Parameters | Values |
|---|
| 3 |
| |
| |
| |
| |
Table 8.
Parameters for ASM controller.
Table 8.
Parameters for ASM controller.
| Parameters | Values |
|---|
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
Table 9.
Gains for the ASM controller with trial-and-error tuning.
Table 9.
Gains for the ASM controller with trial-and-error tuning.
| Parameters | Values |
|---|
| 1 |
| 1 |
| 1 |
Table 10.
P-PI controller gains with trial-and-error tuning.
Table 10.
P-PI controller gains with trial-and-error tuning.
| Parameters | Values |
|---|
| 3 |
| |
| |
Table 11.
Gains for PID controller with PSO tuning.
Table 11.
Gains for PID controller with PSO tuning.
| Parameters | Values |
|---|
| 4 |
| |
| |
| |
| 7 |
| 2 |
| |
Table 12.
Gains for the P-PI controller with PSO tuning.
Table 12.
Gains for the P-PI controller with PSO tuning.
| Parameters | Values |
|---|
| |
| |
| |
| 1 |
| |
| |
| |
| |
Table 13.
Parameters for ST controller.
Table 13.
Parameters for ST controller.
| Parameters | Values |
|---|
| 2 |
| |
| |
| 1 |
Table 14.
Parameters for ST controller.
Table 14.
Parameters for ST controller.
| Parameters | Values |
|---|
| |
| |
| |
| |
| |
| |
Table 15.
Gains for the P-PI controller with PSO tuning.
Table 15.
Gains for the P-PI controller with PSO tuning.
| Parameters | Values |
|---|
| |
| |
| |
| |
| |
| |
| |
Table 16.
Gains for the ASM controller with PSO tuning.
Table 16.
Gains for the ASM controller with PSO tuning.
| Parameters | Values |
|---|
| |
| |
| 1 |
| |
| |
| 1 |
| |
Table 17.
Gains for the ASM controller with PSO tuning.
Table 17.
Gains for the ASM controller with PSO tuning.
| Parameters | Values |
|---|
| |
| |
| |
| |
| 1 |
| |
Table 18.
P-PI controller gains with PSO tuning.
Table 18.
P-PI controller gains with PSO tuning.
| Parameters | Values |
|---|
| |
| |
| |
| |
| |
| |
| |
| |
| |
Table 19.
Performance indices with trial-and-error tuning.
Table 19.
Performance indices with trial-and-error tuning.
| Controller | RMSE | Control Effort |
|---|
| | | | |
|---|
| PID-PPI | 0.4433 | 480.5439 | 9.0057 | 8.9537 | 9.0109 | 8.9567 |
| ST-PPI | 0.1801 | 481.3770 | 8.9601 | 8.9581 | 8.9577 | 8.9564 |
| ASM-PPI | 0.1183 | 480.9337 | 8.9743 | 8.9541 | 8.9568 | 8.9715 |
Table 20.
Performance indices with PSO tuning.
Table 20.
Performance indices with PSO tuning.
| Controller | RMSE | Control Effort |
|---|
| | | | |
|---|
| PID-PPI | 0.0421 | 483.1402 | 9.4368 | 9.4386 | 9.2016 | 9.0777 |
| ST-PPI | 0.0181 | 481.9643 | 8.9829 | 9.0097 | 8.9849 | 9.0380 |
| ASM-PPI | 0.0393 | 481.4128 | 9.0753 | 9.0201 | 9.0606 | 9.0708 |