A Compact Three-Dimensional Two-Layer Flexible Hinge
Abstract
1. Introduction
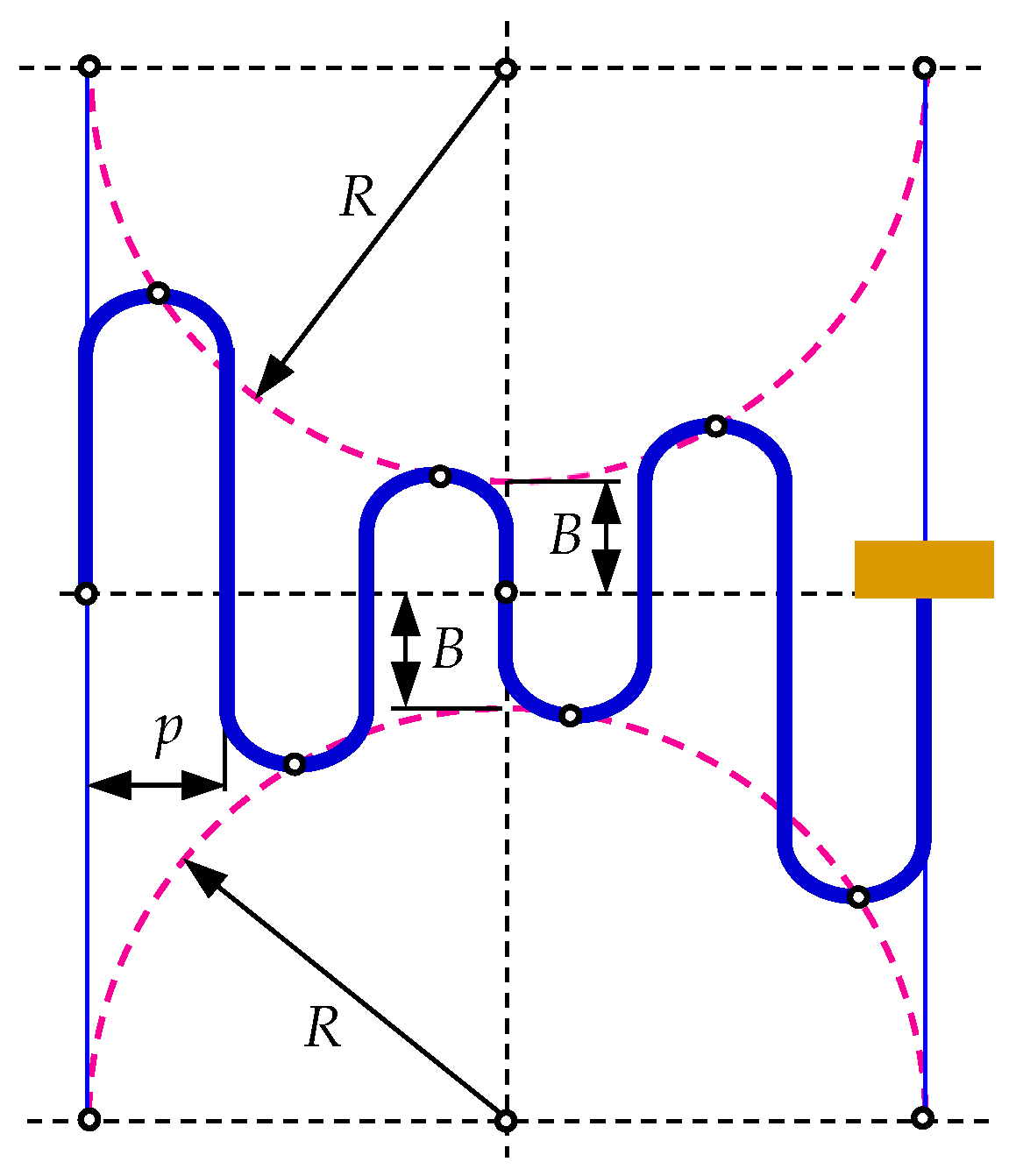
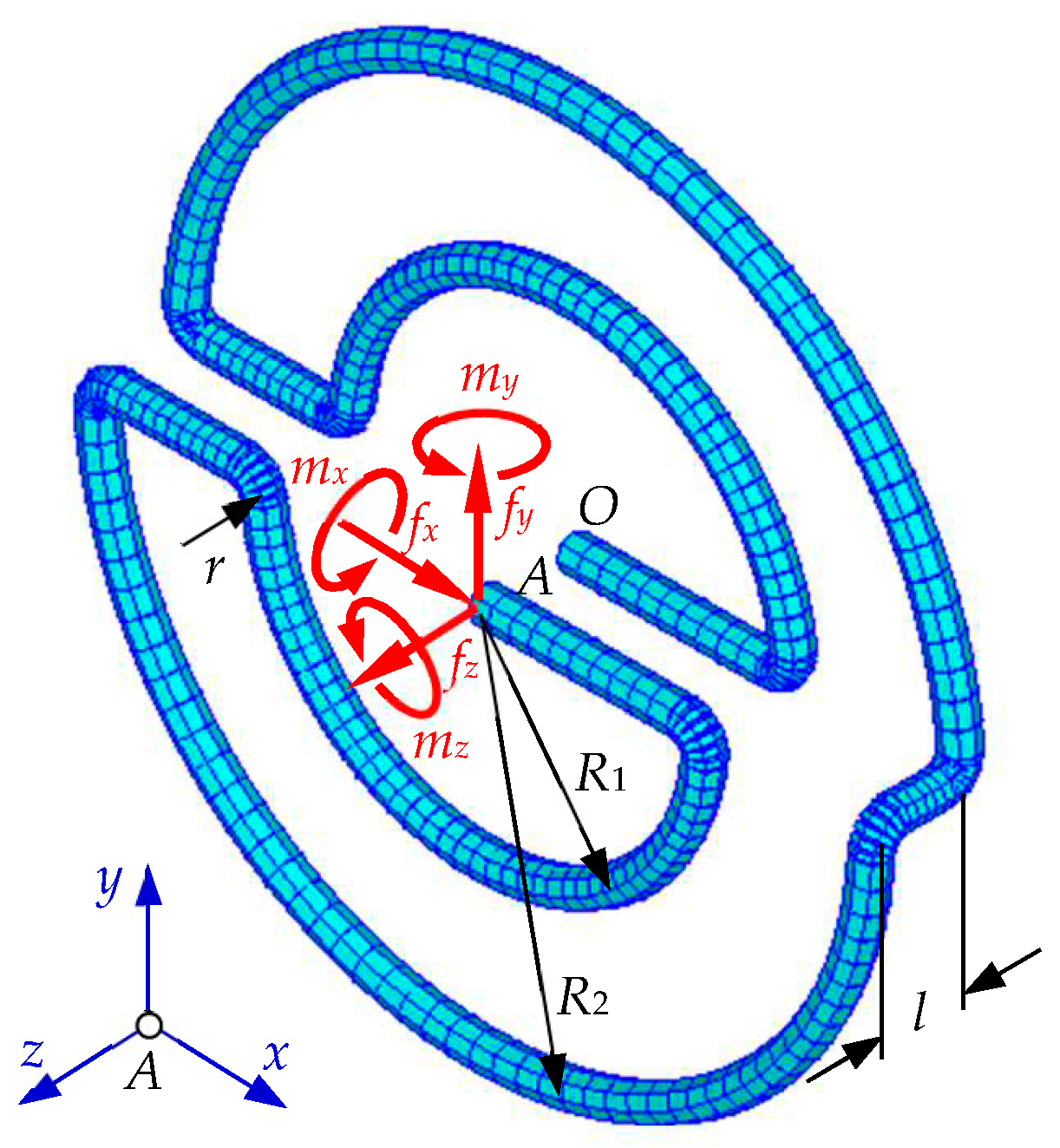
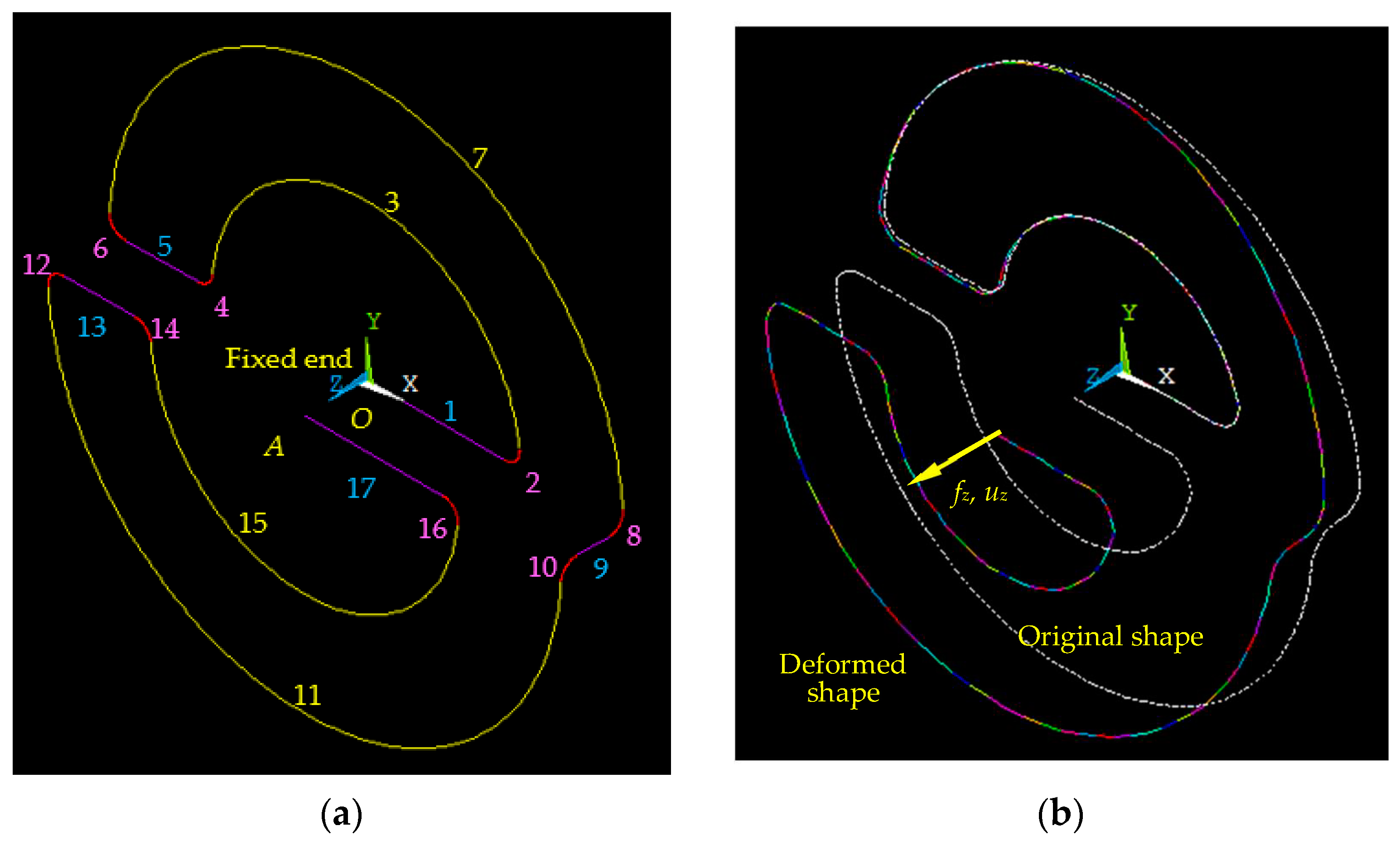
2. New 3D Flexible Hinge Design
3. Analytical Compliance Model
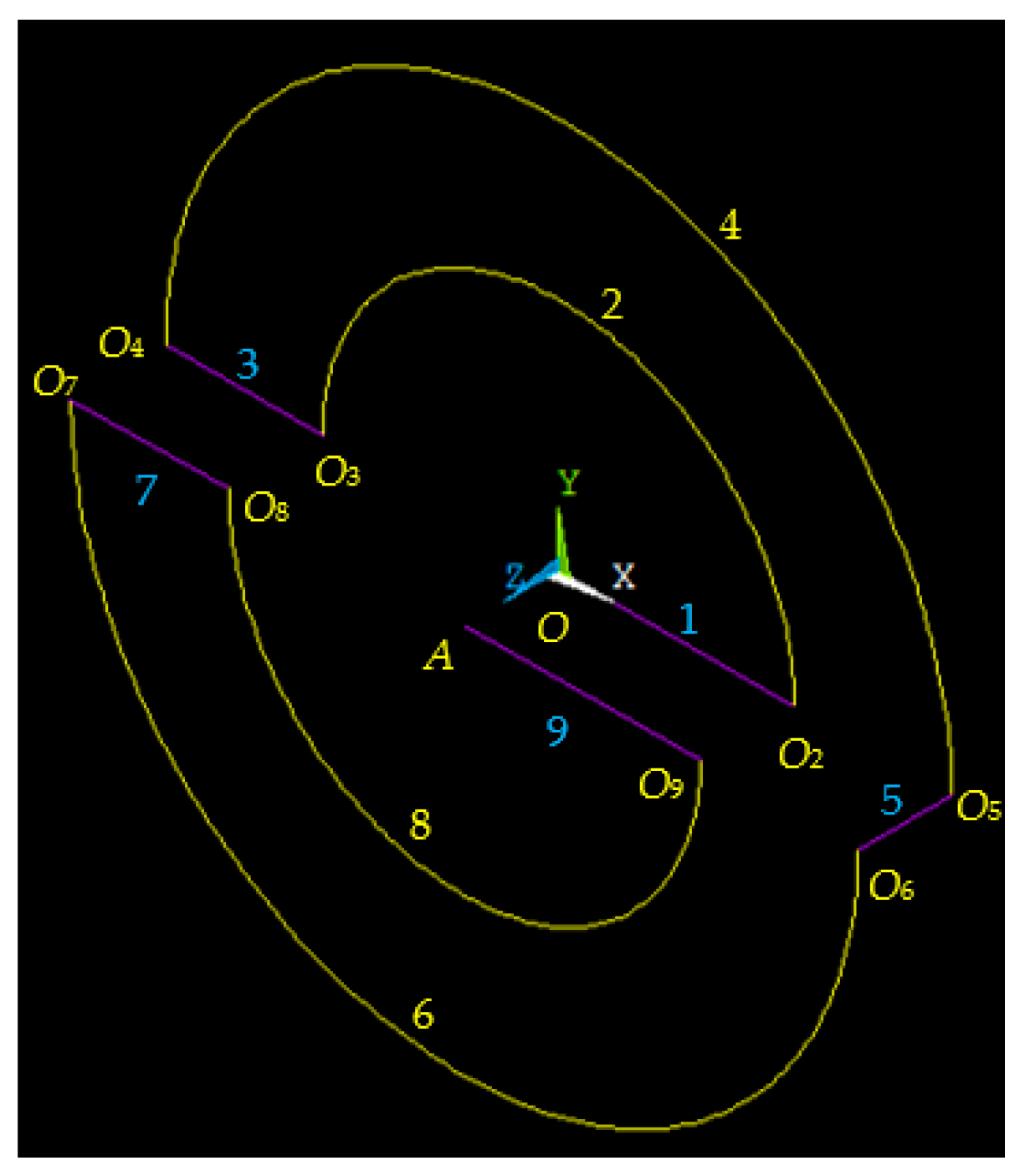
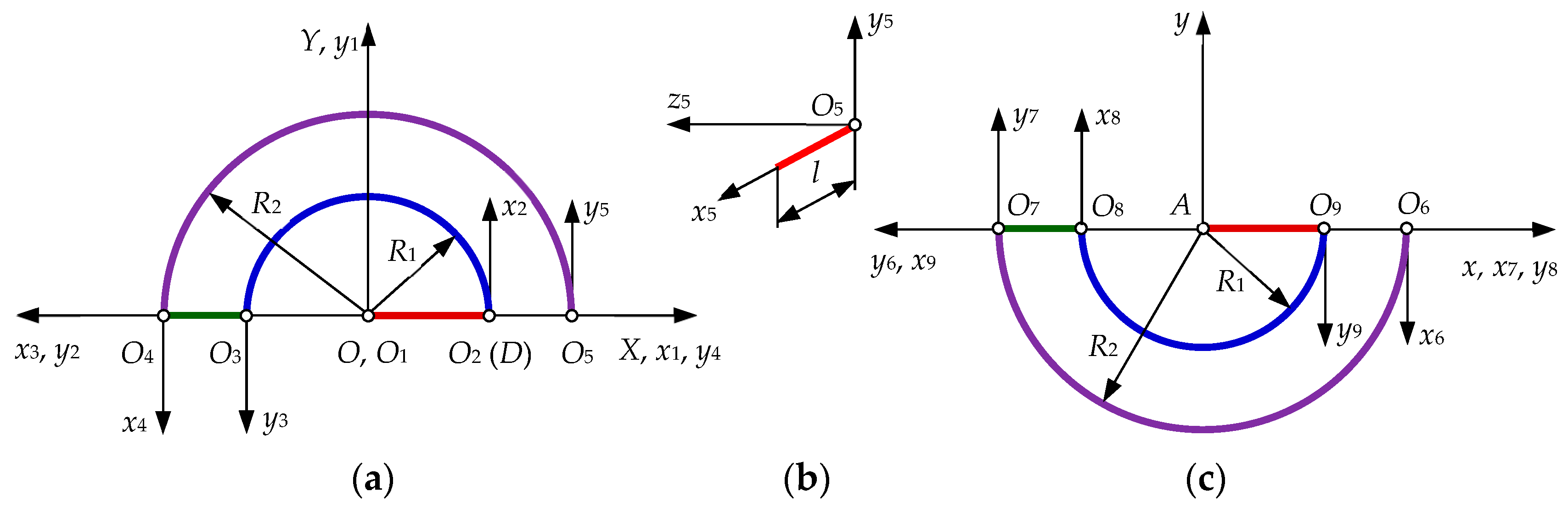
3.1. Model Derivation
3.2. Analytical Compliance Model Finite Element Validation
3.3. Prototype Experimental Testing
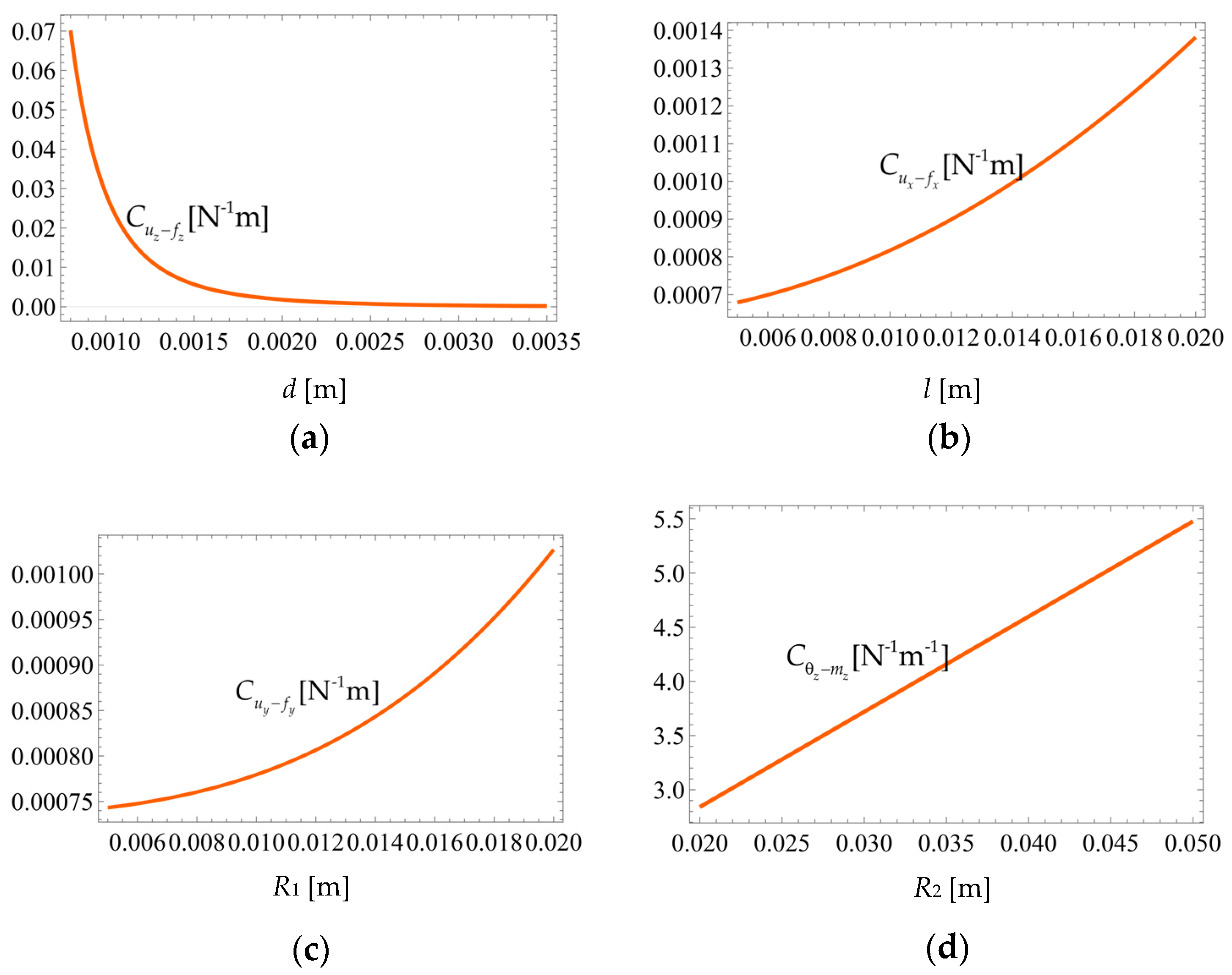
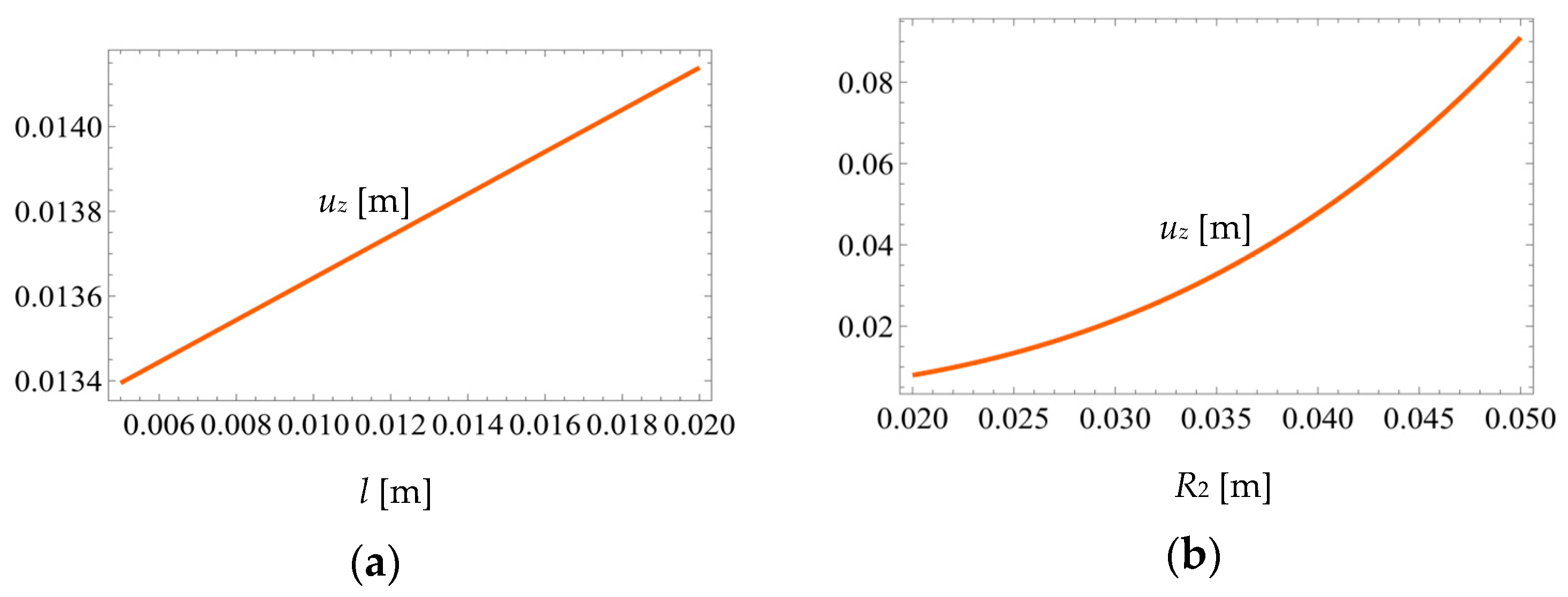
3.4. Geometric Parameters Variation Influence on Compliances
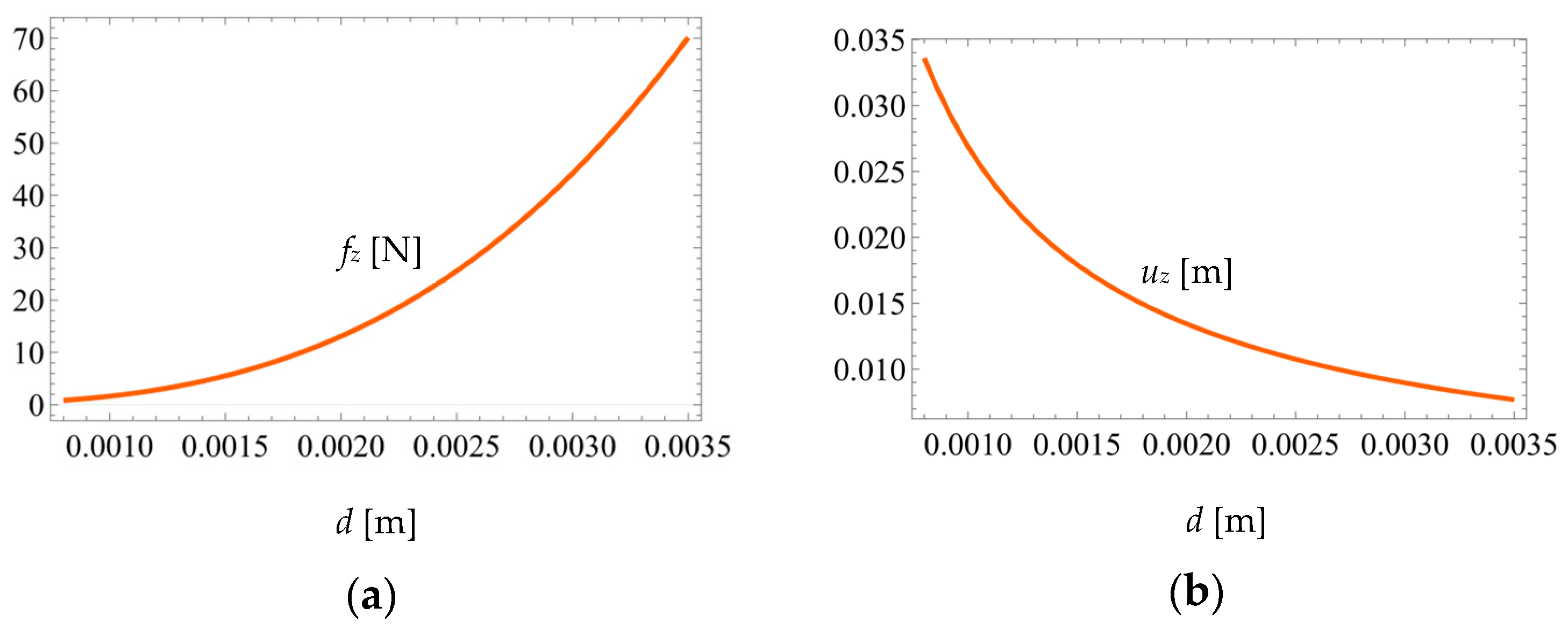
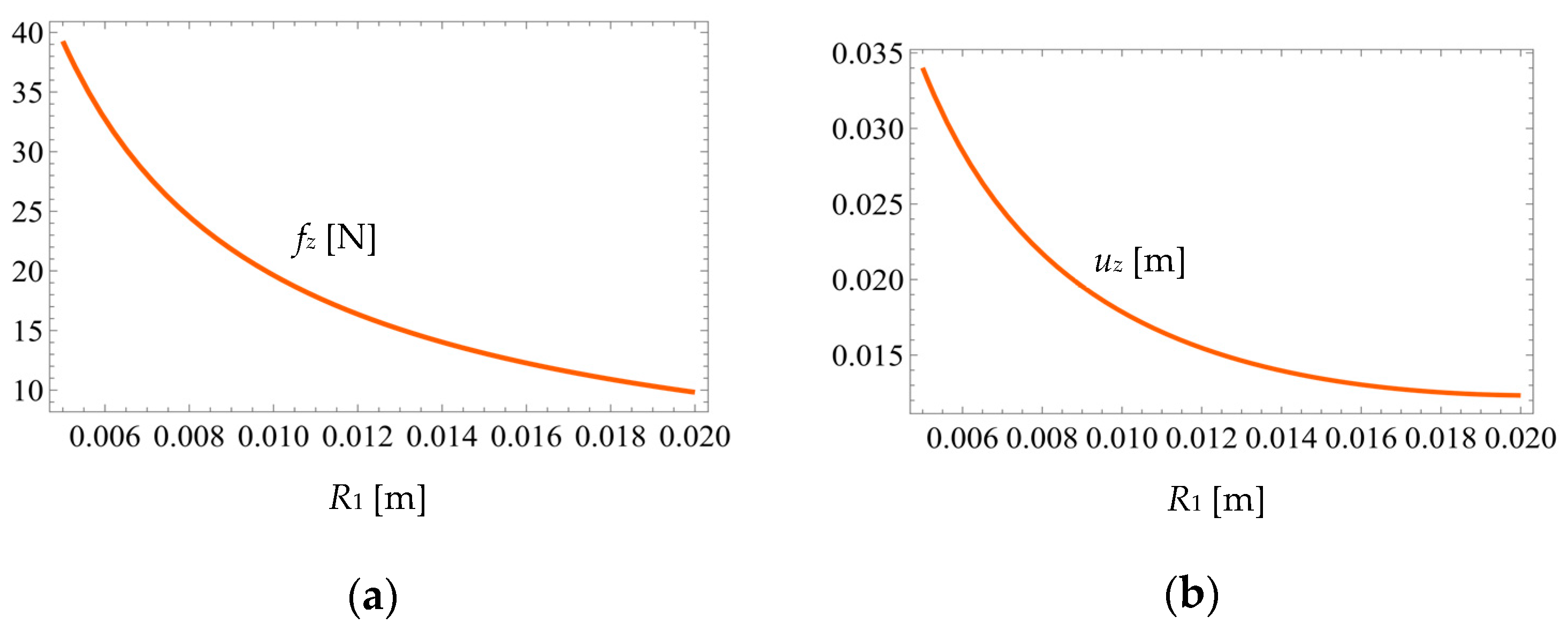
4. Stress Limitations to Load and Displacement with Analytical Compliance Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Segment | Δx | Δz | φ | θ | ψ |
|---|---|---|---|---|---|
| 1 | 0 | −l | 0 | 0 | 0 |
| 2 | R1 | −l | π/2 | 0 | 0 |
| 3 | −R1 | −l | π | 0 | 0 |
| 4 | −R2 | −l | −π/2 | 0 | 0 |
| 5 | R2 | −l | π/2 | −π/2 | −π/2 |
| 6 | R2 | 0 | π/2 | 0 | 0 |
| 7 | −R2 | 0 | 0 | 0 | 0 |
| 8 | −R1 | 0 | −π/2 | 0 | 0 |
| 9 | R1 | 0 | π | 0 | 0 |
References
- Paros, J.M.; Weisbord, L. How to design flexure hinges. Mach. Des. 1965, 37, 151–156. [Google Scholar]
- Smith, S.T. Flexures: Elements of Elastic Mechanisms; Gordon & Breach: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Lobontiu, N. Compliant Mechanisms: Design of Flexure Hinges, 2nd ed.; Taylor and Francis (CRC Press): Boca Raton, FL, USA, 2020. [Google Scholar]
- Wu, Y.; Zhou, Z. Design calculations for flexure hinges. Rev. Sci. Instrum. 2002, 73, 3101–3106. [Google Scholar] [CrossRef]
- Chen, G.; Liu, X.; Gao, H.; Jia, J. A generalized model for conic flexure hinges. Rev. Sci. Instrum. 2009, 80, 055106. [Google Scholar]
- Tian, Y.; Shirinzadeh, B.; Zhang, D. Closed-form compliance equations of filleted V-shaped flexure hinges for compliant mechanism design. Precis. Eng. 2010, 34, 408–418. [Google Scholar] [CrossRef]
- Linβ, S.; Erbe, T.; Zentner, L. On polynomial flexure hinges for increased deflection and an approach for simplified manufacturing. In Proceedings of the 13th World Congress in Mechanism and Machine Science, Guananjuato, Mexico, 19–25 June 2011. [Google Scholar]
- Vallance, R.R.; Haghighian, B.; Marsh, E.R. A unified geometric model for designing elastic pivots. Precis. Eng. 2008, 32, 278–288. [Google Scholar] [CrossRef]
- Li, Q.; Pan, C.; Xu, X. Closed-form compliance equations for power-function-shaped flexure hinge based on unit-load method. Precis. Eng. 2013, 37, 135–145. [Google Scholar]
- Lin, R.; Zhan, X.; Fatikow, S. Hybrid flexure hinges. Rev. Sci. Instrum. 2013, 84, 085004. [Google Scholar] [CrossRef]
- Li, L.; Zhang, D.; Guo, S.; Qu, H. Design, modeling, and analysis of hybrid flexure hinges. Mech. Mach. Theory 2019, 13, 300–316. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Cai, S.; Cui, J. Modeling and analysis of conical-shaped notch flexure hinges based on NURBS. Mech. Mach. Theory 2018, 128, 560–568. [Google Scholar] [CrossRef]
- Hsiao, F.Z.; Lin, T.W. Analysis of a novel flexure hinge with three degrees of freedom. Rev. Sci. Instrum. 2001, 72, 1565–1573. [Google Scholar] [CrossRef][Green Version]
- Lee, V.; Ziegert, J. Hybrid bi-directional flexure joints. In Proceedings of the Proceedings of ASPE 2007 Annual Meeting, Dallas, TX, USA, 14–19 October 2007. [Google Scholar]
- Bi, S.; Zhao, S.; Zhu, X. Dimensionless design graphs for three types of annulus-shaped flexure hinges. Precis. Eng. 2010, 34, 659–666. [Google Scholar]
- Rad, F.P.; Vertechy, R.; Berselli, G.; Parenti-Castelli, V. Analytical compliance analysis and finite element verification of spherical flexure hinges for spatial compliant mechanisms. Mech. Mach. Theory 2016, 101, 168–180. [Google Scholar]
- Bilancia, P.; Berselli, G. An overview of procedures and tools for designing nonstandard beam-based compliant mechanisms. Comput. Aided Des. 2021, 134, 103001. [Google Scholar] [CrossRef]
- Li, J.; Liu, H.; Zhao, H. A compact 2-DOF piezoelectric-driven platform based on “Z-shaped” flexure hinges. Micromachines 2017, 8, 245. [Google Scholar] [CrossRef]
- Qiu, L.; Liu, Y.; Yu, Y.; Bai, Y.B. Design and stiffness analysis of a pitch-varying folded flexure hinge (PFFH). Mech. Mach. Theory 2021, 157, 104187. [Google Scholar]
- Qiu, L.; Li, C.; Dai, S.; Yu, Y. Research on the line-arc-line constant-torque flexure hinge (LAL-CTFH) based on improved pseudo-rigid-body model (PRBM). Mech. Mach. Theory 2002, 174, 104878. [Google Scholar] [CrossRef]
- Abedi, K.; Shakhesi, E.; Seraj, H.; Mahnama, M.; Shirazi, F.A. Design and analysis of a 2-DOF compliant serial micropositioner based on “S-shaped” flexure hinge. Precis. Eng. 2023, 83, 228–236. [Google Scholar] [CrossRef]
- Iandiorio, C.; Salvini, P. Elasto-kinematics and instantaneous invariants of compliant mechanisms based on flexure hinges. Micromachines 2023, 14, 783. [Google Scholar] [CrossRef]
- Cao, L.; Dolovich, A.T.; Chen, A.; Zhang, W. Topology optimization of efficient and strong hybrid compliant mechanisms using a mixed mesh of beams and flexure hinges with strength control. Mech. Mach. Theory 2018, 121, 213–227. [Google Scholar] [CrossRef]
- Lobontiu, N.; Hunter, J.; Keefe, J.; Westenskow, J. Tripod mechanisms with novel spatial Cartesian flexible hinges. Mech. Mach. Theory 2022, 167, 104521–104537. [Google Scholar] [CrossRef]
- Lobontiu, N.; Hunter, J.; Robles, B. New 3D Cartesian flexible hinge and tripod mechanisms: Stress-based maximum load and displacement with compliance model. Rom. J. Tech. Sci. Appl. Mech. 2022, 67, 43–59. [Google Scholar]
- Zolfagharian, A.; Lakhi, M.; Ranjbar, S.; Tadesse, Y.; Bodaghi, M. 3D printing non-assembling compliant joints for soft robotics. Results Eng. 2022, 15, 100558. [Google Scholar] [CrossRef]
- Alshebly, Y.S.; Mustapha, K.B.; Zolfagharian, A.; Bodaghi, M.; Mohamed Ali, M.S.; Almurib, H.A.; Nafea, M. Bioinspired pattern-driven single-material 4D printing for self-morphing actuators. Sustainability 2022, 14, 10141. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Gharaie, S.; Gregory, J.; Bodaghi, M.; Kaynak, A.; Nahavandi, S. A bioinspired compliant 3D-printed soft gripper. Soft Robot. 2022, 9, 680–689. [Google Scholar] [CrossRef] [PubMed]





| Design | d [m] | R1 [m] | R2 [m] | r [m] | l [m] |
|---|---|---|---|---|---|
| 1 | 0.002 | 0.015 | 0.025 | 0.0015 | 0.006 |
| 2 | 0.003 | 0.015 | 0.025 | 0.0015 | 0.006 |
| 3 | 0.003 | 0.02 | 0.035 | 0.002 | 0.008 |
| 4 | 0.003 | 0.02 | 0.04 | 0.0025 | 0.008 |
| Design | Results | [N−1m] | [N−1] | [N−1m] | [N−1m−1] | [N−1m] |
|---|---|---|---|---|---|---|
| 1 | A | 6.99 × 10−4 | 1.098 × 10−2 | 1.797 × 10−3 | 3.28 | 8.647 × 10−3 |
| FEA | 6.998 × 10−4 | 1.081 × 10−2 | 1.773 × 10−3 | 3.227 | 8.4 × 10−3 | |
| e [%] | 0.114 | 1.548 | 1.336 | 1.616 | 2.856 | |
| 2 | A | 1.383 × 10−4 | 2.169 × 10−3 | 3.551 × 10−4 | 0.648 | 1.71 × 10−4 |
| FEA | 1.386 × 10−4 | 2.135 × 10−3 | 3.51 × 10−4 | 0.637 | 1.663 × 10−4 | |
| e [%] | 0.216 | 1.567 | 1.155 | 1.698 | 2.749 | |
| 3 | A | 3.67 × 10−4 | 3.986 × 10−3 | 9.516 × 10−4 | 0.893 | 4.552 × 10−4 |
| FEA | 3.67 × 10−4 | 3.92 × 10−3 | 9.397 × 10−4 | 0.879 | 4.428 × 10−4 | |
| e [%] | 0 | 1.656 | 1.251 | 1.568 | 2.724 | |
| 4 | A | 5.092 × 10−4 | 4.372 × 10−3 | 1.349 × 10−3 | 0.98 | 6.359 × 10−4 |
| FEA | 5.094 × 10−4 | 4.29 × 10−3 | 1.329 × 10−3 | 0.962 | 6.16 × 10−4 | |
| e [%] | 0.039 | 1.876 | 1.483 | 1.837 | 3.129 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lobontiu, N.; Moses, M.; Hunter, J.; Min, D.; Munteanu, M.G. A Compact Three-Dimensional Two-Layer Flexible Hinge. Machines 2023, 11, 825. https://doi.org/10.3390/machines11080825
Lobontiu N, Moses M, Hunter J, Min D, Munteanu MG. A Compact Three-Dimensional Two-Layer Flexible Hinge. Machines. 2023; 11(8):825. https://doi.org/10.3390/machines11080825
Chicago/Turabian StyleLobontiu, Nicolae, Morgan Moses, Jozef Hunter, Daniel Min, and Mircea Gh. Munteanu. 2023. "A Compact Three-Dimensional Two-Layer Flexible Hinge" Machines 11, no. 8: 825. https://doi.org/10.3390/machines11080825
APA StyleLobontiu, N., Moses, M., Hunter, J., Min, D., & Munteanu, M. G. (2023). A Compact Three-Dimensional Two-Layer Flexible Hinge. Machines, 11(8), 825. https://doi.org/10.3390/machines11080825






