Triboelectric Film Sensor for Integrity Monitoring of Bolted Joints

Abstract

In this study, a concept and design of a self-powered sensor that utilizes a triboelectric effect to evaluate the condition of tensile bolted joints was proposed. Based on the fact that the triboelectric charge yields electrostatic voltage induced by the separation of the contacting rough surfaces, the proposed sensor is a film-shaped triboelectric sensor made of inexpensive materials being installed between the objects to be fastened. The principle of the sensor is that it detects microscale relative motions between the contacting surfaces against an external vibratory load when the integrity of the fastened joint is compromised due to a decrease in the bolt’s fastening force. In this study, we designed and fabricated triboelectric sensor and tested it on a tensile bolted joint specimen subjected to inertial vibratory loading, and it was experimentally shown that the output voltage amplitude of the sensor increased as the bolt’s fastening force decreased. In addition, a modeling study was performed to explain the unexpected decrease in voltage amplitude observed at medium preloads, by combining the triboelectric and mechanical models with the experimental results of two different external circuit configurations. Estimation of the triboelectric charge density at the contacting surfaces was performed, which was found to be consistent with the contact mechanics model assumed. Finally, the calculation of the sensor output voltage based on the presented mechanical/triboelectric model was provided, confirming the validity of the modeling study.

1. Introduction

Fastening with bolts, a joining method which facilitates assembly and disassembly, is widely used because of its low fastening costs and high maintainability [1,2]. In a bolted joint, the objects to be fastened are united by a compressive force generated by the tightening of the bolt–nut system, as an equivalent counterforce to the tensile force induced in the shaft of the bolt [3]. Fastening with bolts, however, always carries the risk of losing fastening force during use. In fact, many accidents have occurred in which a certain part of machinery or structure has fallen off due to loosening or improper tightening of bolts, and many of these accidents have been attributed to infrequent or wrong maintenance and inspections.

In recent years, predictive maintenance, or condition-based maintenance, has been introduced to optimize the maintenance interval by monitoring the health condition of the target system in place of preventive maintenance, based on periodic maintenance and inspection. The simplest method for detecting bolt looseness is the percussion test [4]. A quantitative method that has been put into practical use is the axial force meter [5], which calculates the axial force from the echo delay time of ultrasonic waves injected from the head of the bolt. Although these are nondestructive inspection methods, they are not suitable for condition-based maintenance because they require inspection personnel to check each and every fastening part. Therefore, various methods have been proposed to conduct continuous monitoring of the integrity of bolted joints [6]. These can be broadly classified into direct and indirect methods; the former intends to measure the axial force or fastening force of bolts in situ, whereas the latter focuses on the changes in the mechanical properties of the structure, such as natural frequencies, wave propagation, structural impedance, etc., caused by the bolt loosening. The former, however, has not yet reached practical use due to cost issues, whereas the latter is not sensitive enough to capture the loosening phenomenon in its early stage.

There are two main types of loosening: loosening with bolt rotation and loosening without rotation. The former is a phenomenon in which the bolt rotates and the axial force decreases due to shear force acting between the joint surfaces, slip between the surfaces caused by rotational torque, or repeated load acting in the tensile direction on the joint surfaces. In both cases, however, bolt loosening is considered to be accompanied by minute relative movements between the bonding surfaces, such as slipping and localized loosening, as a precursor or initial symptom of the loosening. Therefore, in this study, we intend to develop a sensing method to detect such relative motions. In other words, what we are aiming for in this study is a sensor that produces no output when the joint surfaces are in close contact with each other with sufficient contact pressure, but produces an output when the contact pressure decreases and minute relative motions occur between the surfaces.

As a mechanism for generating such an output, this research proposes a sensing principle based on the triboelectric effect, a phenomenon in which one material takes on a positive charge and the other a negative charge at the contact interface when two different materials come into contact. This phenomenon is caused by the transfer of charge across the contact interface, which can occur between metal and metal, insulator and insulator, and metal and insulator, even though the mechanisms of charging are diverse, such as electron motion, ion motion, and material motion [7,8,9]. When the contacted surfaces are separated, a potential difference is created between them, which causes electrostatic induction. Therefore, a variety of devices that utilize this phenomenon are being actively studied, including inexpensive vibration energy harvesting devices as known as triboelectric nanogenerators (TENGs) [10,11,12,13,14,15,16,17] and self-powered pressure sensors [18,19,20]. Furthermore, various types of triboelectic sensing devices other than pressure sensors have also been presented in the literature. Su et al. reported a methylammonium lead triiodide (MAPbI3) perovskite-based photoenhanced TENG, which can be used as a photodetector based on the joint properties of the photoelectric and triboelectric effects of the perovskite material [21]. A TENG developed by Zhou et al. consisting of flexible and transparent conducting electrodes (FTCE) with high transmittance and low sheet resistance and transparent 3D-hierarchical polydimethylsiloxane (PDMS) with porous pyramid patterns can be used as a self-powered raindrop detection sensor on a window for a smart home [22]. Moreover, Xu et al. use the perovskite material to create a self-powered, light-stimulated, smart e-skin based on both the photoelectric and triboelectric effects of the perovskite material, which can generate an electric signal from low-frequency motion, providing tactile sensing ability [23].

This study aims to use the triboelectric effect to develop a self-powered sensor that monitors the integrity of joints fastened by bolt–nut systems. Based on the fact that the triboelectric charge yields electrostatic voltage upon the separation of the contacted rough surfaces, a sensor that is capable of detecting relative motions between the fastened surfaces on the microscale, such as a decrease in the true contact area, minute misalignment, and separation due to loosening of bolts, is proposed. The potential advantages of this idea are twofold. First, the existence of a variety of material combinations that can exhibit the triboelectric effect, including metals and polymers, makes it possible to fabricate the sensor with inexpensive materials; second, the sensor can be self-powered, as it itself is a source of the induced voltage.

In the following, first the design and fabrication of the proposed sensor are described in Section 2, including operation principle and functionality, material selection, electrode construction, and sensor geometry, followed by experimental verification in Section 3. The modeling study, which accounts for the triboelectric effect, electrostatic induction, tightening mechanics, and contact mechanics between rough surfaces, is presented in Section 4 to explain the experimental results with reasonable consistency. The conclusions are summarized in Section 5.

2. Sensor Design

2.1. Concept

In a sound tensile bolted joint tightened with appropriate tightening torque, the fastening force applied between the fastened objects provides sufficient contact pressure on the interface inside a stressed region, i.e., the cross-section of a frustum of a hollow cone called a pressure cone [3], which allows uniting the surfaces with sufficient true contact area. Note that the contact pressure is not uniformly distributed, but monotonically decreases from its maximum around the hole circumference to a negligible value at the outer edge of the stressed region [24]. This fact makes the contact interface imperfect around the outer edge of the stressed region even in the sound joint. When a dynamic load (vibrations or shocks) in the axial direction is applied, the fluctuation of the applied load makes the imperfect contact pressure fluctuate; thus, the true contact area also fluctuates at the outer edge of the stressed region. This means that there may be relative motions between the rough surfaces of the fastened objects on a microscale (microslip or microslap [25]).

When the bolt loosens, the decrease in the fastening force causes the decrease in the contact pressure, which causes the contact condition to become imperfect in an annulus on the interface, whose inner radius $r_c$ is a specific critical radial distance from the bolt axis. As the fastening force decreases, the larger part of the stressed region becomes imperfect ($r_c$ becomes smaller); thus, the larger part of the stressed region can undergo microslip/microslap under the dynamic load.

The sensor proposed in this study is designed to directly detect these microscale motions by installing a pair of triboelectric material layers between the tightened objects, as Figure 1 shows. It is based on the idea that if the tightened objects undergo the relative motions, so too do the triboelectric material layers. Thanks to the triboelectric effect, these relative motions of the triboelectric layers will induce a potential difference between two materials, becoming synchronized with the dynamic load, which can be measured as a voltage fluctuation.

It should be noted here that inserting such sensor layers between the tightened objects must be done extremely carefully because the mechanical properties of the inserted layers, e.g., stiffness, strength, wear resistance, creep resistance, etc., may directly affect the quality of the joint, or even completely impair its functionality. In practice, the material selection for the sensor layer should be carried out thoughtfully, considering those mechanical properties. However, in order to focus only on the validation of the legitimacy of the above-mentioned concept of the proposed sensor, the appropriateness of the sensor materials in terms of those mechanical properties will not be addressed in this study.

2.2. Design

The proposed sensor has the form of a thin sheet, which is designed to be placed between the fastened objects, as illustrated in Figure 1, to allow direct evaluation of the fastening quality. Details of the design are shown in Figure 2, which depicts that the sensor consists of a pair of thin triboelectric layers, copper electrode layers, and insulation layers, all stacked together in the order indicated in Figure 2a. The electrode layer is attached to each of the triboelectric layers using conductive adhesive. The sensor has a ring shape with a rectangle-shaped electric outlet so that one can measure the voltage difference between the electrodes from outside the joint by soldering a lead wire on this area. The outer diameter of the electrode is set to cover the stressed region on the contact interface, whose diameter is usually approximated by a sum of the diameter of the seating surface of the bolt and the thickness of the clamped objects.

For experimental purposes, we determined specific dimensions of the sensor, as shown in Figure 2b, assuming an M8 bolt–nut system and tightened objects with a thickness of 8 mm made of structural steel (SS400). As described in Section 2.1, the material selection was carried out only focusing on the triboelectric performance without considering their mechanical properties as the joint insertion. We chose polyethylene terephthalate (PET) and polyimide (PI) films as the triboelectric layers, the former of which is to be positively charged while the latter is negative when brought into contact with the other. For the insulation layers, we chose polyimide (PI) films. The material and thickness of all layers are summarized in

Table 1. Material and thickness of sensor layers.

Layers	Material	Thickness
Insulation	PI	0.047 mm
Triboelectric 1	PET	0.05 mm
Triboelectric 2	PI	0.05 mm
Electrodes	Cu	0.07 mm

.

3. Experiments

3.1. Experimental Setup

Experiments to examine the performance of the proposed sensor were conducted using an experimental setup consisting of a test assembly mounted on a shaker, as shown in Figure 3. The test assembly is composed of an upper and lower component jointed by a single M8 bolt–nut with a sensor, under test, inserted between them. The lower component is fixed on the shaker’s head with four M4 bolts to give the assembly a dynamic load in the vertical direction. The upper component has a crown-like shape to effectively give an inertial mass to produce an inertial force as an external dynamic tensile load when it is harmonically excited by the shaker. Thus, this assembly is designed to perform as a dynamically loaded tensile joint with a single bolt. On the joining surface of both components, a circle-shaped tab 1 mm in height with a diameter of 30 mm is machined to explicitly define the contact interface. The M8 bolt was a gauge bolt with a strain gauge embedded inside to measure the axial force of the bolt. In addition, an accelerometer was mounted on the upper component to monitor the acceleration applied to the test assembly.

3.2. Experimental Procedure

In order to investigate the performance of the proposed sensor, axial vibration experiments were carried out with the experimental setup mentioned in Section 3.1 under 13 different preload conditions, i.e., a tightening torque of 0.2 Nm, 0.4 Nm, 0.6 Nm, 0.8 Nm, 1.0 Nm, 1.2 Nm, 1.4 Nm, 2.0 Nm, 3.0 Nm, 5.0 Nm, 10.0 Nm, 15.0 Nm, and 19.0 Nm, where 19.0 Nm is the standard tightening torque of the M8 bolt. The tightening torque was roughly controlled by using a torque wrench when tightening, and the real fastening force was directly measured by the gauge bolt. The experiment started from the minimum preload condition and repeated the same procedure, retightening the gauge bolt step by step. For each preload condition, first, the axial force applied on the gauge bolt was measured, and then a vibration test was performed. In the vibration test, the test assembly was excited for 30 s with a sinusoidal wave at a frequency of 35 Hz. This frequency was chosen with reference to the American National Aeronautics Standard NAS3350, in which an accelerated impacting vibration test in the perpendicular direction is defined to use 30 Hz excitation. The test frequency was slightly modified to avoid the interference with power supply frequencies and maximize the dynamic load on the test assembly within the performance limit of the shaker. It was found that the axial force of the bolt slightly decreased during the vibration test, probably due to the initial self-loosening. This effect, however, was ignored because the decrease rate was very small (less than 0.1% of the maximum preload). To reduce the background noise, the test assembly was electrically grounded to the case voltage of the data recorder. During the vibration tests, the output of the sensor under test and the accelerometer were acquired using a data recorder with a sampling frequency of 2 kHz. The steady-state part of the vibration data for 5 s (from the 25th second to the 30th second) was used for the evaluation of the 35 Hz component in the response. All data processing and analysis were performed offline using MATLAB R2019a Update 3.

4. Results and Discussion

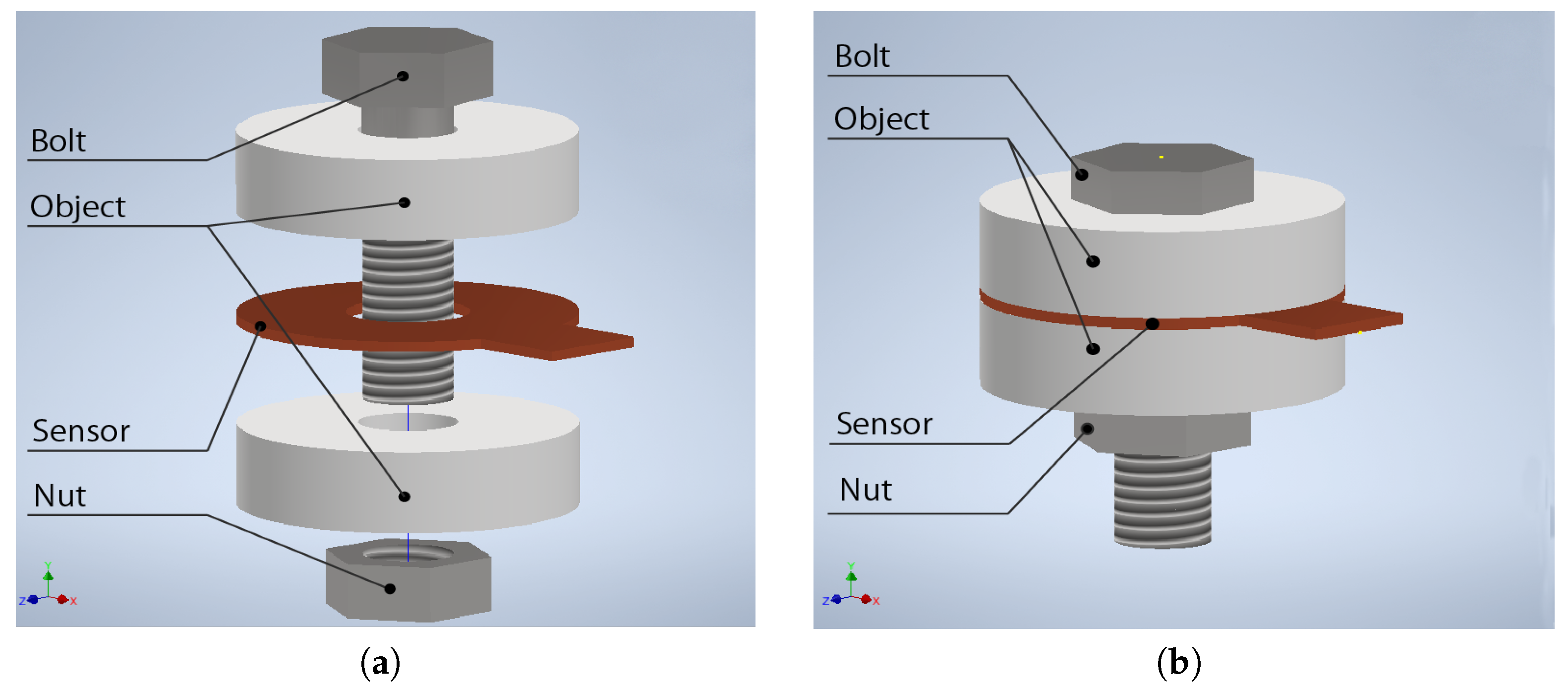
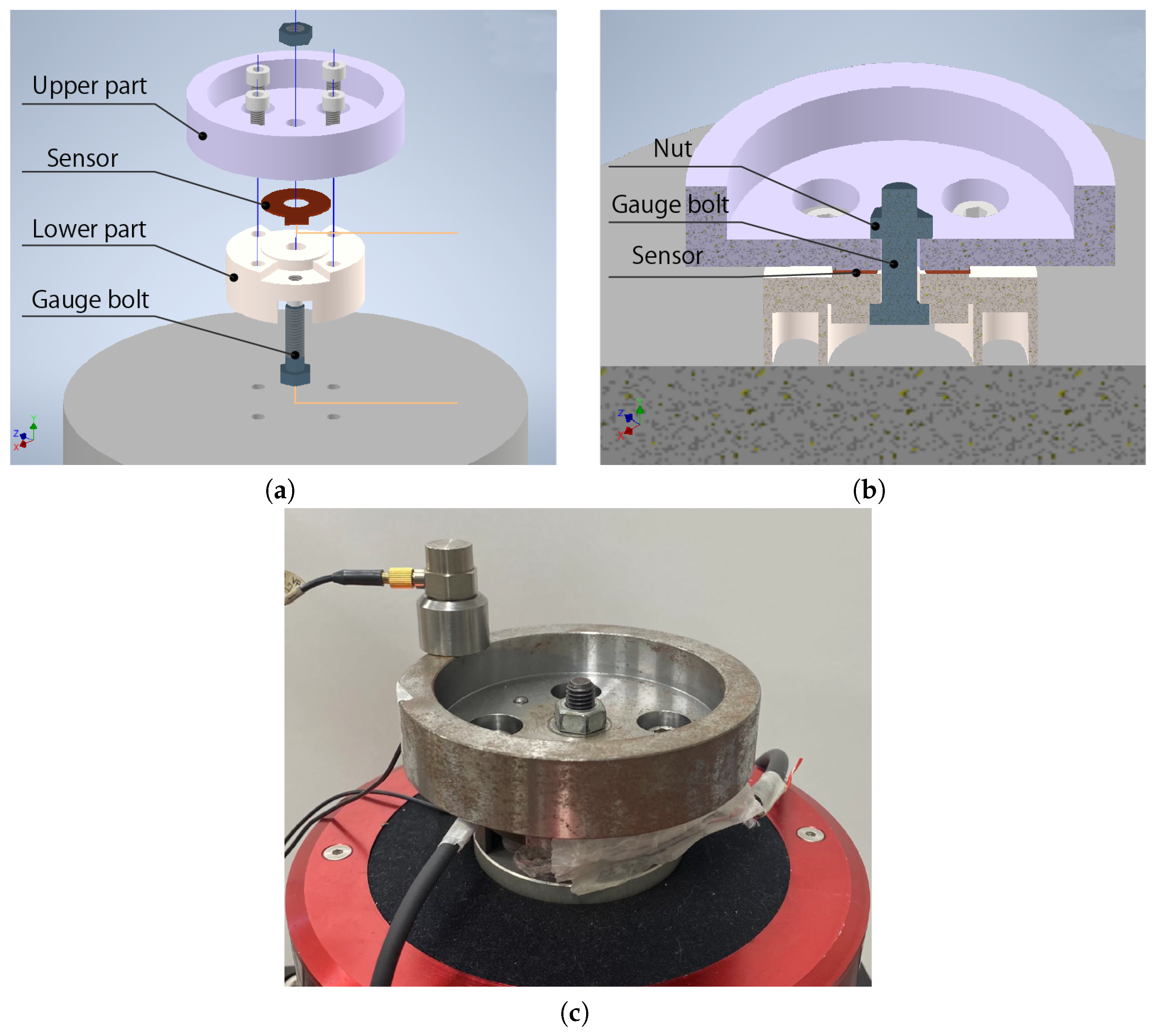
4.1. Experimental Results and Triboelectric Modeling Study

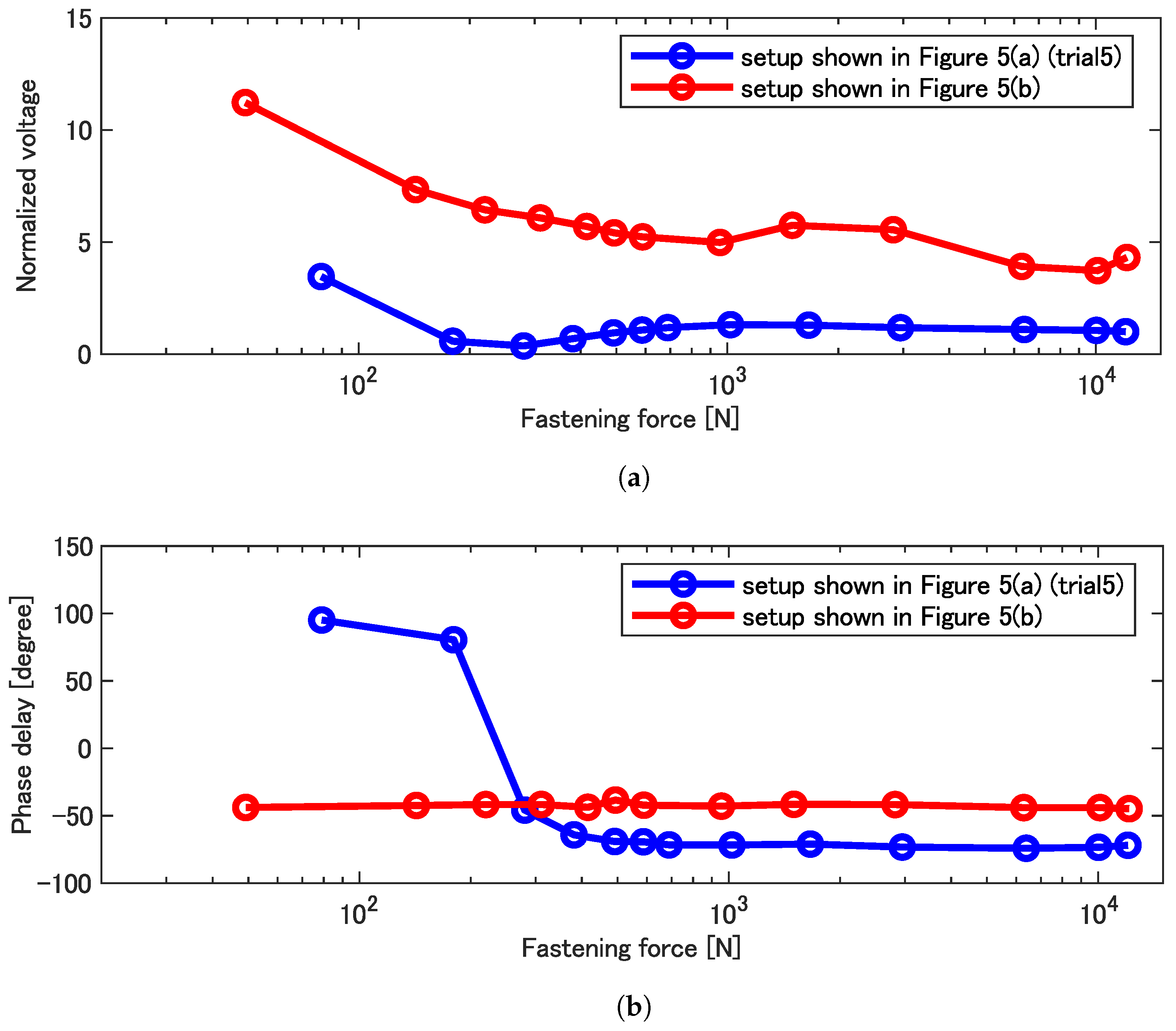
The results of the vibration tests, repeated six times, are plotted in Figure 4, where the absolute values of the 35 Hz component of the sensor output are plotted in Figure 4a against the axial force of the bolt, while the phase delays with respect to the excitation acceleration are shown in Figure 4b. Note that the sensor output was defined as the voltage of the upper triboelectric layer (PET) relative to the lower layer (PI) and normalized by the value for the maximum fastening condition to eliminate the difference in the variation in the voltage level among the trials.

From Figure 4, one can find that the test results have enough repeatability in terms of the relative ratio with respect to the maximum fastening condition when the fastening force is over 500 N. Below 200 N, the amplitude of the sensor output rapidly increases with larger deviation as the fastening force reduces. The reason for this deviation may be the difficulty of controlling the initial contact condition under the loosest bolt fastening force. Contrary to our prior expectation that the amplitude of the sensor output would monotonically increase with the decrease in the fastening force, it exhibits an unexpected “valley” around 300 N accompanied by a phase reversal of almost 180 degrees.

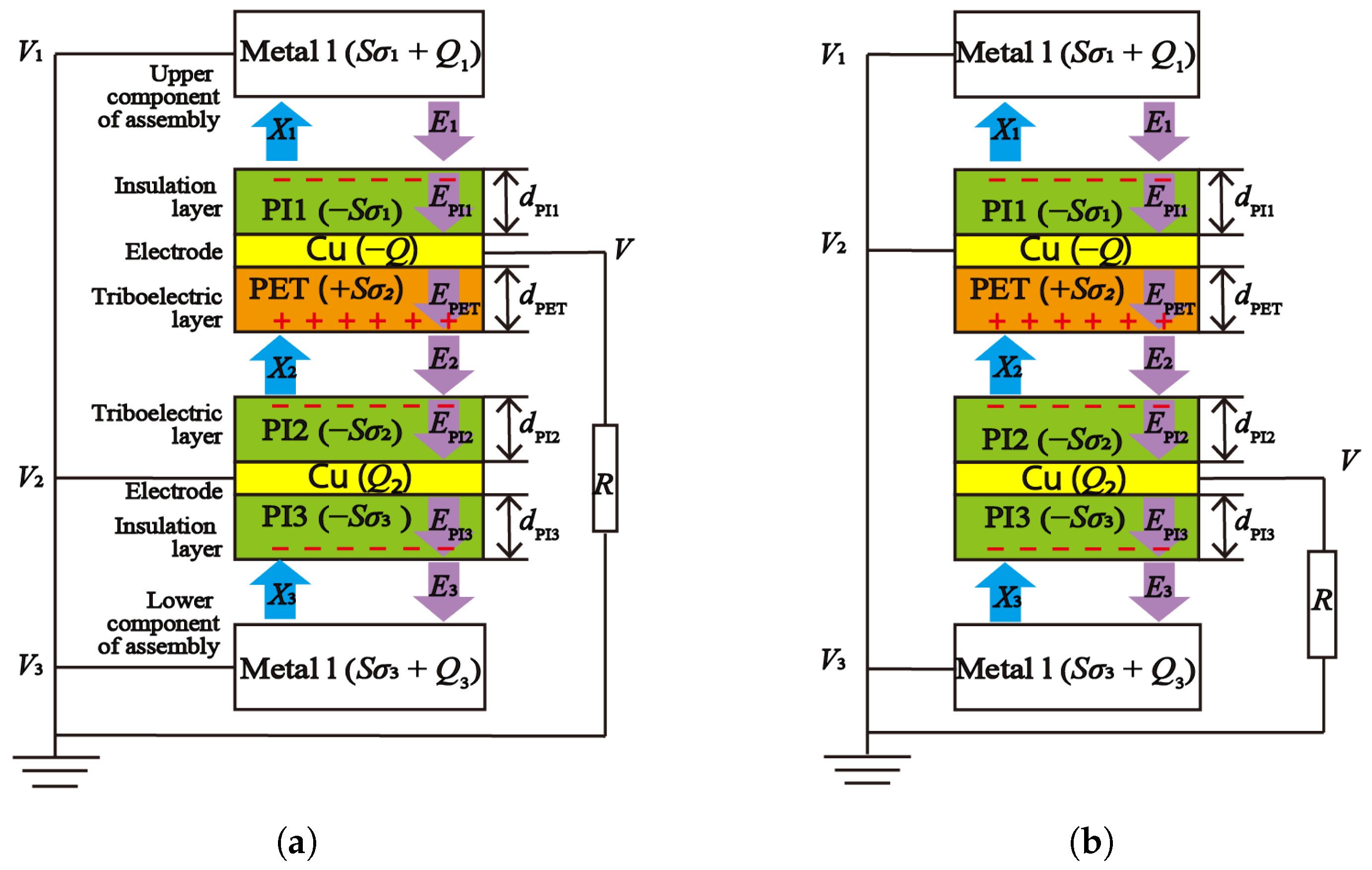
In order to understand the reason for this amplitude dropping phenomenon, and the reason why the phase delay has changed from 100 degrees to approximately −80 degrees, mathematical modeling of the experiments in terms of the triboelectric aspect was conducted. The model is schematically shown in Figure 5a. The white rectangles are the upper and lower components of the assembly, and the layer of the colored rectangles is the sensor. Unlike the standard model of triboelectric devices, our model takes account of the effect of the contact between the upper insulation layer and the upper component of the assembly made of steel (PI1 and Metal1) and the contact between the lower insulation layer and the lower component (PI3 and Metal2), in addition to the contact between the triboelectric layers (PET and PI2). Considering the wiring described in Section 3.2, the electric boundary conditions are set as depicted in the figure, and the measurement apparatus (data recorder) is modeled as an input resistance R.

As shown in Figure 5a, the triboelectric charge density at the contact between the triboelectric layers (PET and PI2) is assumed to be ${\sigma }_2$, where PET is positively charged, while PI2 is negative. Similarly, ${\sigma }_1$ and ${\sigma }_3$ are assumed for the triboelectric charge density between Metal1 and PI1, and between PI3 and Metal2, respectively. Note that, for this metal–polymer contact, the metal layers are supposed to be positively charged. Also, air gaps between every contacted layer should be considered because the sensor is simply sandwiched between the fastened objects. The axial displacements of each air gap are assumed to be $x_1$, $x_2$, and $x_3$, as indicated in the figure.

Then, assuming the electric fields inside the air gaps and the triboelectric layers are all uniform, they are formulated, respectively, from Gauss’s theorem as

$$E_1=\frac{S{\sigma }_1+Q_1}{{\epsilon }_{0}S}$$

(1)

$$E_{\mathrm{PI}1}=\frac{Q_1}{{\epsilon }_0{\epsilon }_{\mathrm{PI}}S}$$

(2)

$$E_{\mathrm{PET}}=\frac{Q_1-Q}{{\epsilon }_0{\epsilon }_{\mathrm{PET}}S}$$

(3)

$$E_2=\frac{Q_1-Q+S{\sigma }_2}{{\epsilon }_{0}S}$$

(4)

$$E_{\mathrm{PI}2}=\frac{Q_1-Q}{{\epsilon }_0{\epsilon }_{\mathrm{PI}}S}$$

(5)

$$E_{\mathrm{PI}3}=\frac{Q_1-Q+Q_2}{{\epsilon }_0{\epsilon }_{\mathrm{PI}}S}$$

(6)

$$E_3=\frac{Q_1-Q+Q_2-S{\sigma }_3}{{\epsilon }_{0}S}$$

(7)

where S denotes the area of the electrode, ${\epsilon }_0$, ${\epsilon }_{\mathrm{PI}}$, and ${\epsilon }_{\mathrm{PET}}$ are the permittivity of vacuum, the relative permittivity of PET and PI, respectively; furthermore, Q, $Q_1$, $Q_2$, and $Q_3$ are the induced charges in the metal entities (electrodes and tightened objects) via the external circuit, which should satisfy Kirchhoff’s law as

$$Q_1+Q_2+Q_3=Q$$

(8)

The voltages of the electrodes are represented by the electric fields as

$$V_1=V+E_{\mathrm{PI}1}{d}_{\mathrm{PI}1}+E_1{x}_1$$

(9)

$$V=V_2+E_{\mathrm{PI}2}{d}_{\mathrm{PI}2}+E_2{x}_2+E_{\mathrm{PET}}{d}_{\mathrm{PET}}$$

(10)

$$V_2=V_3+E_3{x}_3+E_{\mathrm{PI}3}{d}_{\mathrm{PI}3}$$

(11)

where $d_{\mathrm{PI}1}$, $d_{\mathrm{PI}2}$, $d_{\mathrm{PET}}$, $d_{\mathrm{PI}3}$ are the thickness of PI1, PI2, PET, and PI3 layers, respectively. Moreover, the electric boundary conditions are given by

$$V_1=V_2=V_3=0$$

(12)

$$V=R\dot{Q}$$

(13)

The relationship between V and Q can be obtained by eliminating all other voltage and charge variables from Equations (1) to (12) as

$$\begin{array}{cc}\hfill V=& \hfill -\frac{1}{{\epsilon }_{0}S}\frac{\left(\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_2\right)\left(\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+x_1\right)}{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_1+x_2}Q\hfill \\ \hfill & \hfill -\frac{1}{{\epsilon }_0}\frac{\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_2}{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_1+x_2}{\sigma }_1{x}_1\hfill \\ \hfill & \hfill +\frac{1}{{\epsilon }_0}\frac{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+x_1}{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_1+x_2}{\sigma }_2{x}_2\hfill \end{array}$$

(14)

The charge Q in the above equation is derived by solving a differential equation, obtained by eliminating V from Equations (13) and (14) as

$$\begin{array}{cc}\hfill R\dot{Q}=& \hfill -\frac{1}{{\epsilon }_{0}S}\frac{\left(\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_2\right)\left(\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+x_1\right)}{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_1+x_2}Q\hfill \\ \hfill & \hfill -\frac{1}{{\epsilon }_0}\frac{\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_2}{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_1+x_2}{\sigma }_1{x}_1\hfill \\ \hfill & \hfill +\frac{1}{{\epsilon }_0}\frac{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+x_1}{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_1+x_2}{\sigma }_2{x}_2\hfill \end{array}$$

(15)

Considering that $x_1$ and $x_2$ are the distance of the air gaps vibrating in phase, the second and third terms in the right-hand side of Equation (15), which perform as the excitation terms in this differential equation, vary antiphase because they have opposite signs. This means that if the relationship between the magnitude of those terms inverses across a certain fastening condition, it would make the resulting voltage have a valley in the amplitude and a jump in the phase, as observed in Figure 4b.

If the above hypothesis for the reason behind the valley phenomenon in Figure 4a is true, it should disappear if the signs of the second and third terms in the right-hand side of Equation (15) are the same. This is possible by reversing the order of the lamination of the triboelectric layers, or just swapping the lead wires to the measurement apparatus, as depicted in Figure 5b. In this case, the relationship between V and Q is derived as

$$\begin{array}{cc}\hfill V=& \hfill -\frac{1}{{\epsilon }_{0}S}\frac{\left(\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_2\right)\left(\frac{d_{\mathrm{PI}3}}{{\epsilon }_{\mathrm{PI}}}+x_3\right)}{\frac{d_{\mathrm{PI}3}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_3+x_2}Q\hfill \\ \hfill & \hfill -\frac{1}{{\epsilon }_0}\frac{\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_2}{\frac{d_{\mathrm{PI}3}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_3+x_2}{\sigma }_3{x}_3\hfill \\ \hfill & \hfill -\frac{1}{{\epsilon }_0}\frac{\frac{d_{\mathrm{PI}3}}{{\epsilon }_{\mathrm{PI}}}+x_3}{\frac{d_{\mathrm{PI}3}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}+x_3+x_2}{\sigma }_2{x}_2\hfill \end{array}$$

(16)

This time, the signs of the second and third terms of the right-hand side become the same as expected, which should allow the sensor voltage to be pulled more negatively by aligning the polarity of the triboelectric effects at the polymer–polymer contact and the polymer–metal contact.

Figure 6 shows the amplitude and phase delay of the sensor output for the setup shown in Figure 5b in red lines with the trial 1 data for the test using the setup shown in Figure 5a in blue lines. Note that the amplitude is normalized by the value for the maximum fastening condition of trial 1 data for the configuration in Figure 5a for ease of comparison. From the figure, one can find that the sensor output keeps the same phase delay throughout the experiment, not showing the valley in the amplitude and the jump in the phase as expected.

4.2. Modeling of Deformation of Bolt and Fastened Objects Considering Contact Mechanics

In order to gain a better understanding of the relationship between the fastening force and sensor output, a model describing the dynamic variation in the air gaps at the contacting surfaces, involving the fastening mechanics of the bolted joint as well as the contact mechanics, is introduced and combined with the triboelectric model described in the previous section. The purpose of this modeling study is to establish a rational explanation for the experimental results of sensor output shown in Figure 4 and Figure 6 in terms of both the amplitude and phase delay.

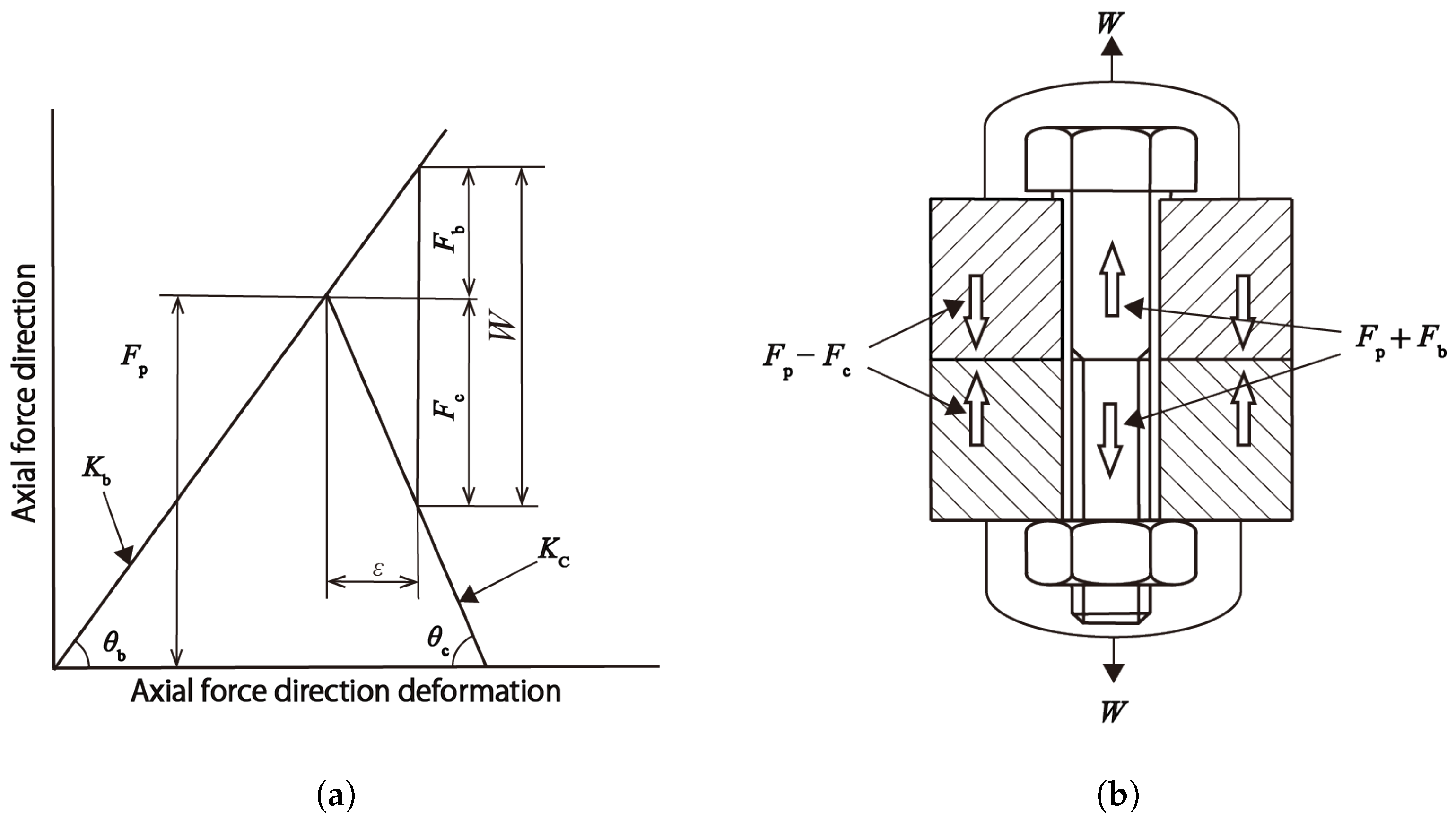
Let us first consider the forces and deflections in a bolted joint. When the bolt and nut are fastened, a tensile force (preload) $F_{\mathrm{p}}$ is generated in the bolt and a compressive force (fastening force) $F_{\mathrm{p}}$ of equal magnitude is generated between the fastened objects. This relationship is illustrated in Figure 7a, usually called a joint diagram [3], in which $K_{\mathrm{b}}$ is the spring constant of the bolt–nut system and $K_{\mathrm{c}}$ is the spring constant of the fastened objects.

When an axial tensile force W is externally applied as depicted in Figure 7b, the grip length $l_{\mathrm{k}}$ (the distance between the contact of the upper object with the bolt seat and the contact of the lower object with the nut seat) is supposed to be extended by $\epsilon$. As a consequence, a tensile internal force $F_{\mathrm{b}}$ is appended to the bolt, resulting in a tensile axial force $(F_{\mathrm{p}}+F_{\mathrm{b}})$, and a compressive internal force $F_{\mathrm{c}}$ is removed from the fastened objects, resulting in a compressive force $(F_{\mathrm{p}}-F_{\mathrm{c}})$. In other words, the tensile load acting on the fastened objects increases the axial force of the bolt, while decreasing the fastening force. The increase and decrease in these forces can be calculated from Figure 7a as follows:

$$F_{\mathrm{b}}=\epsilon tan{\theta }_{\mathrm{b}}=\epsilon K_{\mathrm{b}}$$

(17)

$$F_{\mathrm{c}}=\epsilon tan{\theta }_{\mathrm{c}}=\epsilon K_{\mathrm{c}}$$

(18)

$$W=F_{\mathrm{b}}+F_{\mathrm{c}}=\epsilon (K_{\mathrm{b}}+K_{\mathrm{c}})$$

(19)

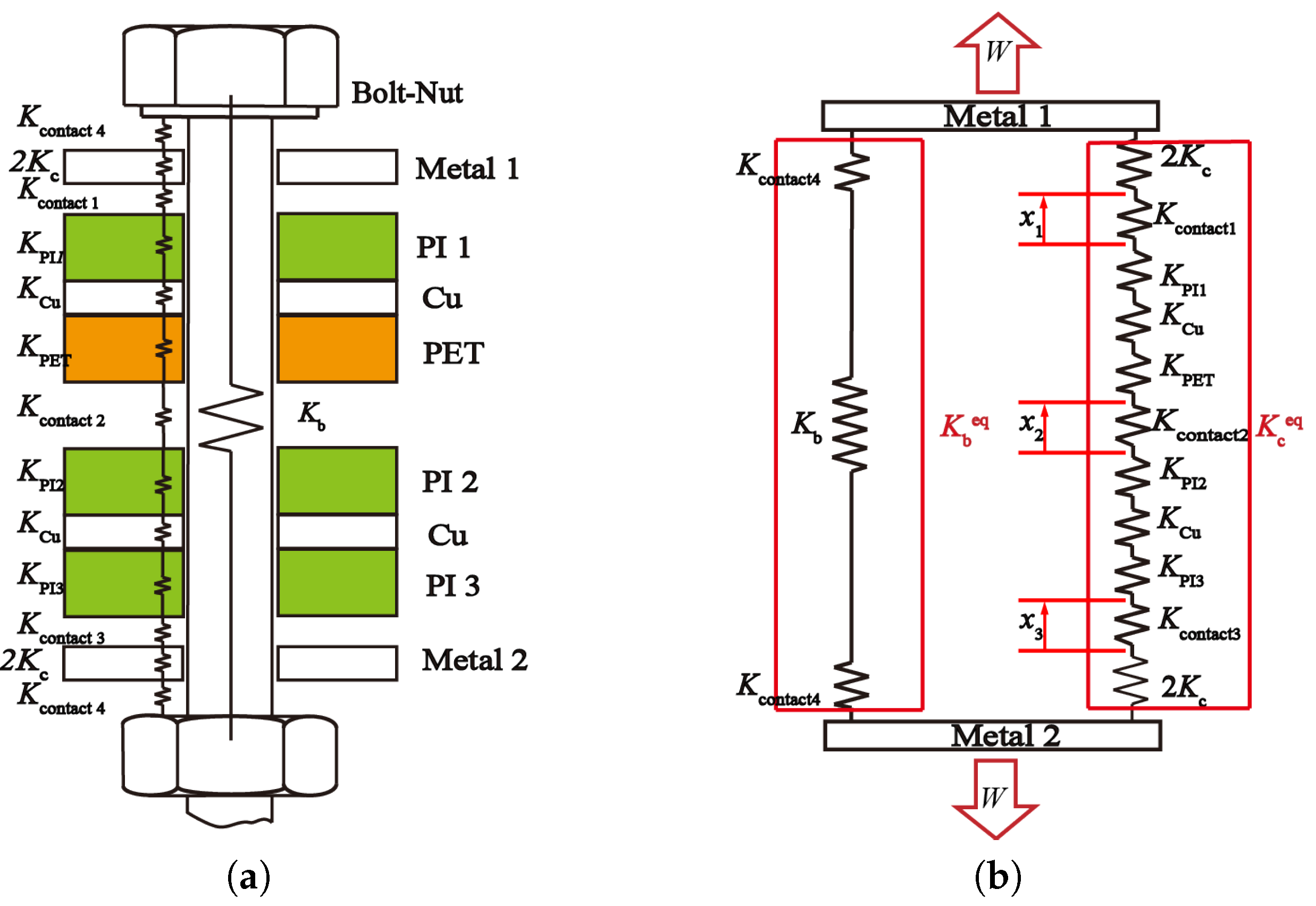
In ordinary models, the spring constants $K_{\mathrm{b}}$ and $K_{\mathrm{c}}$ are calculated just using appropriate formulae of the stiffness of the bolt and fastened objects, or using finite element models of them. In this study, however, we have to take account of the influence of the surface contact mechanics between the bolt sheet and the upper object, fastened objects and the sensor, triboelectric layers inside the sensor, and nut sheet and the lower object to explain the reduction in the stiffness due to the bolt loosening. Therefore, those spring constants $K_{\mathrm{b}}$ and $K_{\mathrm{c}}$ should be replaced by equivalent spring constants $K_{\mathrm{b}}^{\mathrm{eq}}$ and $K_{\mathrm{c}}^{\mathrm{eq}}$ considering the stiffness of the sensor layer and a contact stiffness between the contacting surfaces as well.

Figure 8a shows a model of the bolted joint with the proposed sensor, in which a contact stiffness denoted by $K_{\mathrm{contact}}$ is introduced between each contacting surface, and $K_{\mathrm{PI}}$, $K_{\mathrm{PET}}$, and $K_{\mathrm{Cu}}$ are the spring constants of PI, PET, and the copper electrode, respectively. Note that the contact stiffness between the bolt sheet (or nut sheet) and the fastened object is involved in $K_{\mathrm{b}}^{\mathrm{eq}}$, and the others in $K_{\mathrm{c}}^{\mathrm{eq}}$, because the external load is applied on the fastened objects (labeled as Metal1 and Metal2), as depicted in Figure 8b. Then, the equivalent spring constants are calculated as series composite spring constants of these trains of spring elements as

$$\frac{1}{K_{\mathrm{b}}^{\mathrm{eq}}}=\frac{1}{K_{\mathrm{b}}}+\frac{2}{K_{\mathrm{contact}4}}$$

(20)

$$\frac{1}{K_{\mathrm{c}}^{\mathrm{eq}}}=\frac{1}{K_{\mathrm{c}}}+\frac{1}{K_{\mathrm{contact}1}}+\frac{1}{K_{\mathrm{contact}2}}+\frac{1}{K_{\mathrm{contact}3}}+\frac{1}{K_{\mathrm{PET}}}+\frac{3}{K_{\mathrm{PI}}}+\frac{2}{K_{\mathrm{Cu}}}$$

(21)

The stiffness of the bolt is given by [26]

$$\frac{1}{K_{\mathrm{b}}}=\frac{1}{E_{\mathrm{b}}}\left(\frac{l_{\mathrm{g}}}{A_{\mathrm{g}}}+\frac{l_{\mathrm{s}}}{A_{\mathrm{s}}}+\frac{0.6d}{A_{\mathrm{s}}}\right)$$

(22)

whereas the stiffness of the fastened objects is calculated by VDI 2230 (1986) [27] as

$$K_{\mathrm{c}}=\frac{E_{\mathrm{c}}}{l_{\mathrm{k}}}\frac{\pi }{4}\left[\left(d_{\mathrm{w}}^2-d_{\mathrm{h}}^2\right)+\frac{1}{2}{d}_{\mathrm{w}}{l}_{\mathrm{k}}\left\{{\left(\sqrt[3]{\frac{l_{\mathrm{k}}·d_{\mathrm{w}}}{{(l_{\mathrm{k}}+d_{\mathrm{w}})}^2}}+1\right)}^2-1\right\}\right]$$

(23)

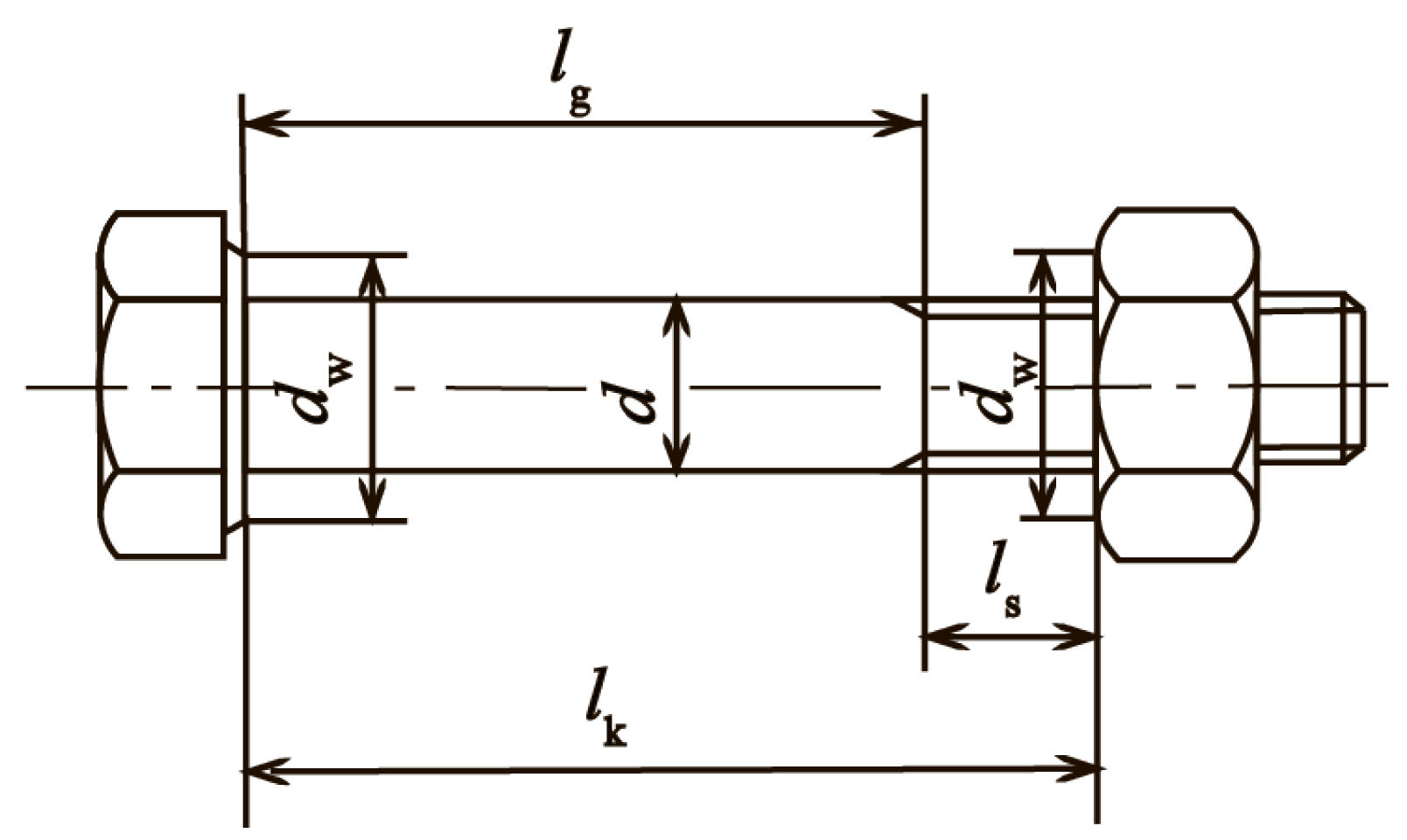
where d, $d_{\mathrm{w}}$, $l_{\mathrm{g}}$, $l_{\mathrm{s}}$, and $l_{\mathrm{k}}$ are the dimensions of the bolts, which are defined in Figure 9, while $d_{\mathrm{h}}$, $A_{\mathrm{s}}$, $E_{\mathrm{b}}$, and $E_{\mathrm{c}}$ denote the diameter of the bolt hole, effective cross-sectional area of the bolt, Young’s modulus of the bolt, and Young’s modulus of the fastened objects, respectively. All the values of those parameters used in the calculations are listed in

Table 2. Valuesof parameters.

Parameter	Value
$E_{\mathrm{b}}$	$2.06\times {10}^{11}$	$\mathrm{N}/{\mathrm{m}}^2$
$E_{\mathrm{c}}$	$2.06\times {10}^9$	$\mathrm{N}/{\mathrm{m}}^2$
d	$8\times {10}^{-3}$	$\mathrm{m}$
$l_{\mathrm{g}}$	$6.3\times {10}^{-3}$	$\mathrm{m}$
$l_{\mathrm{s}}$	$9.7\times {10}^{-3}$	$\mathrm{m}$
$d_{\mathrm{w}}$	$1.3\times {10}^{-2}$	$\mathrm{m}$
$l_{\mathrm{k}}$	$1.6\times {10}^{-2}$	$\mathrm{m}$
$A_{\mathrm{n}}$	$5.024\times {10}^{-5}$	${\mathrm{m}}^2$
$A_{\mathrm{s}}$	$3.378\times {10}^{-5}$	${\mathrm{m}}^2$
$A_{\mathrm{g}}$	$5.024\times {10}^{-5}$	${\mathrm{m}}^2$

.

In the field of contact mechanics, much research has been carried out on the contact of rough surfaces under both elastic and plastic deformation conditions [28,29,30,31], including Hertzian elastic contact theory [32,33], Greenwood and Williamson’s model [34], Bush, Gibson, and Thomas [35], and O’Callaghan and Cameron’s model [36]. Greenwood and Williamson’s model is a widely recognized and influential model in the field of contact mechanics. The model aims to understand the nature of contact between rough surfaces and provides insights into the dependency between the real area of contact, separation, and applied load, in terms of the surface topology, particularly the distribution of the heights of the surface asperities within the contact region.

According to the analysis by Greenwood and Williamson [34], the relationship between the load P on the contacting surfaces and the separation d in the case of rough plane contact assuming a specific distribution of the heights of the surface asperities is

$$P=\frac{4}{3}\eta A_{\mathrm{n}}{E}^{\prime }{\beta }^{\frac{1}{2}}{\sigma }_{\mathrm{s}}^{\frac{3}{2}}{F}_p(d/{\sigma }_{\mathrm{s}})$$

(24)

where $\eta$, $A_{\mathrm{n}}$, and $\beta$ are the surface density of asperities, nominal contact area, and radius of asperity summits, respectively; further, $E^{\prime }={\{(1-{\nu }_1^2)/E_1+(1-{\nu }_2^2)/E_2\}}^{-1}$, ${\sigma }_{\mathrm{s}}={\left({\sigma }_{\mathrm{s}1}^2+{\sigma }_{\mathrm{s}2}^2\right)}^{1/2}$, where ${\nu }_i$, $E_i$, and ${\sigma }_{\mathrm{s}i}$, $i=1,2$, are the Poisson’s ratio, Young’s modulus, and standard deviations of the height distributions of the asperities on surfaces in contact, respectively. And

$$F_p\left(h\right)={\int }_h^{\infty }{(s-h)}^{\frac{3}{2}}{\varphi }^{*}\left(s\right)ds$$

(25)

where ${\varphi }^{*}\left(s\right)$ is the standardized probability density function of the height distribution of the asperities scaled to make its standard deviation unity. Differentiating Equation (24) with respect to $-d$, the contact stiffness is derived as follows:

$$K_{\mathrm{contact}}=\frac{\mathrm{d}P}{\mathrm{d}(-d)}=-\frac{4}{3}\eta A_{\mathrm{n}}{E}^{\prime }{\beta }^{\frac{1}{2}}{\sigma }_{\mathrm{s}}^{\frac{1}{2}}{F}_p^{\prime }(d/{\sigma }_{\mathrm{s}})=-\frac{F_p^{\prime }}{F_p}\frac{P}{{\sigma }_{\mathrm{s}}}$$

(26)

where $F_p^{\prime }$ is the first derivative of $F_p$, and the last equality is derived by applying Equation (24).

From this model, the contact stiffness is found to be proportional to the magnitude of the compressive load on the contact surface if the height distribution is exponential, because $F_p^{\prime }$ is equal to $-F_p$ in this case. Greenwood and Williamson [34] clarified that the area of contact and number of contact spots are also proportional to the load. Furthermore, it was stated that those for the real height distribution, which tends to be Gaussian rather than exponential, can be fairly approximated by the formula for the exponential distribution as long as the real contact area stays small compared with the nominal area [34,37].

When the external force W, i.e., the inertial force $-m{a}_{0}cos\omega t$ in our experiment where m, $a_0$, and $\omega$ are the mass of the upper object, acceleration amplitude, and excitation angular frequency, respectively, is applied to the upper and lower ends of the model as indicated in Figure 8b, the variation in the axial separation between the contacting layers, denoted by $x_1$, $x_2$, and $x_3$, is calculated as follows:

$$x_1=\frac{W}{K_{\mathrm{contact}1}}\frac{K_{\mathrm{c}}^{\mathrm{eq}}}{K_{\mathrm{b}}^{\mathrm{eq}}+K_{\mathrm{c}}^{\mathrm{eq}}}$$

(27)

$$x_2=\frac{W}{K_{\mathrm{contact}2}}\frac{K_{\mathrm{c}}^{\mathrm{eq}}}{K_{\mathrm{b}}^{\mathrm{eq}}+K_{\mathrm{c}}^{\mathrm{eq}}}$$

(28)

$$x_3=\frac{W}{K_{\mathrm{contact}3}}\frac{K_{\mathrm{c}}^{\mathrm{eq}}}{K_{\mathrm{b}}^{\mathrm{eq}}+K_{\mathrm{c}}^{\mathrm{eq}}}$$

(29)

As described in Equation (26) and the following paragraph, the contact stiffness is nearly proportional to the applied compressive load, which is the fastening force in our experiment. Therefore, as the bolt loosens, the contact stiffness $K_{\mathrm{contact}}$ at each contact interface decreases with the decrease in the fastening force, resulting in the decrease in $K_{\mathrm{b}}^{\mathrm{eq}}$ and $K_{\mathrm{c}}^{\mathrm{eq}}$ as well. In consequence, the variation in the separation of the contact interface due to the external force increases.

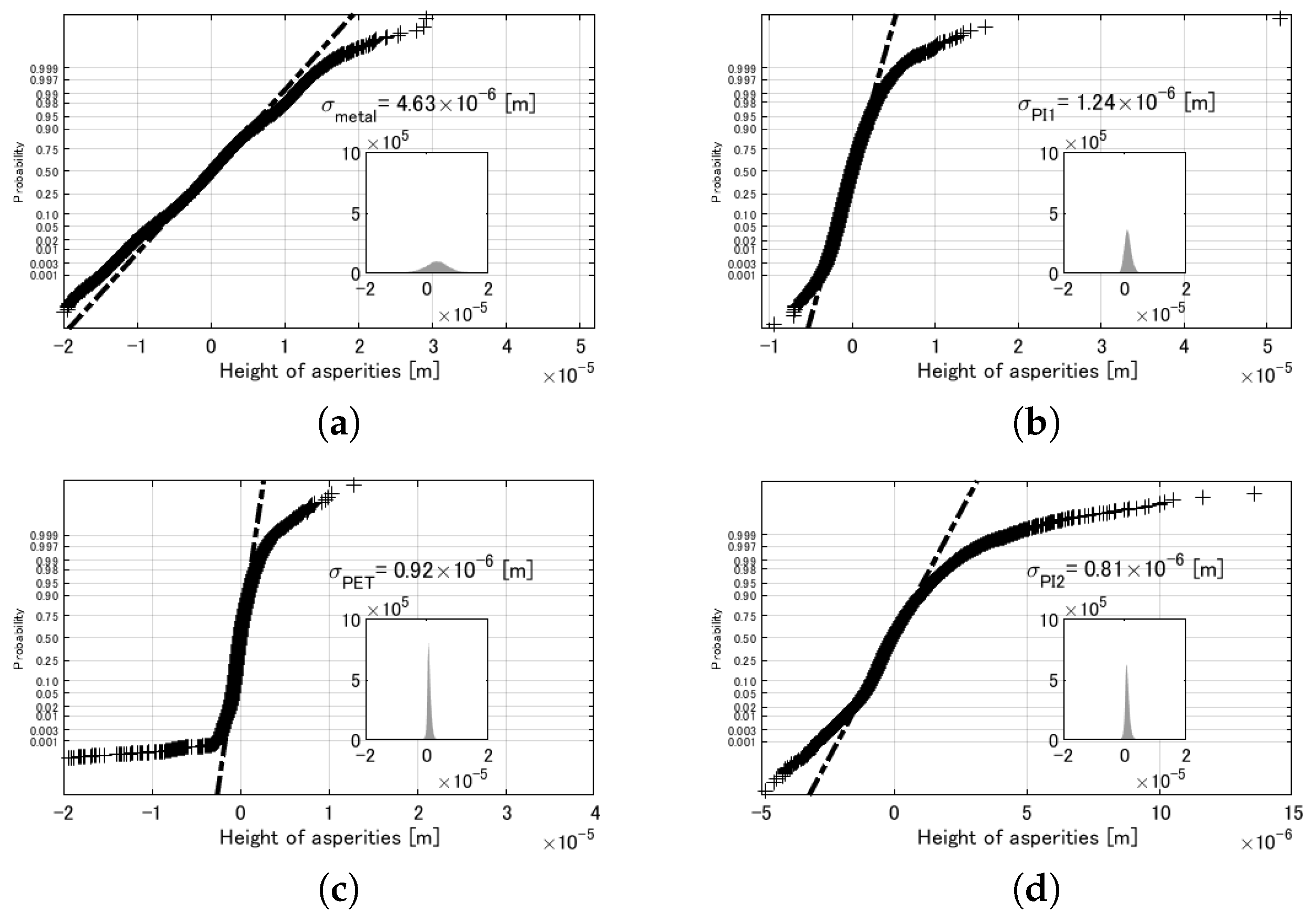
In order to evaluate the actual values of the contact stiffness according to Equation (26), the distribution of the heights of the asperities on each surface of the contacting materials was investigated. We measured the two-dimensional profile of each contacting surface with a laser microscope at three specific locations, and extracted the heights of the local summits from those profiles. Figure 10 shows the normal probability plot of the extracted heights for each surface, displayed with their histogram. From the plots, it was found that the main body of the right part of the distribution is fairly approximated by a Gaussian distribution except for the long right tail, which may contain measurement noise and outliers. Thus, we adopted the standardized normal density as ${\varphi }^{*}$ in Equation (25) and calculated the stiffness of each contact interface by numerically evaluating Equations (25) and (26).

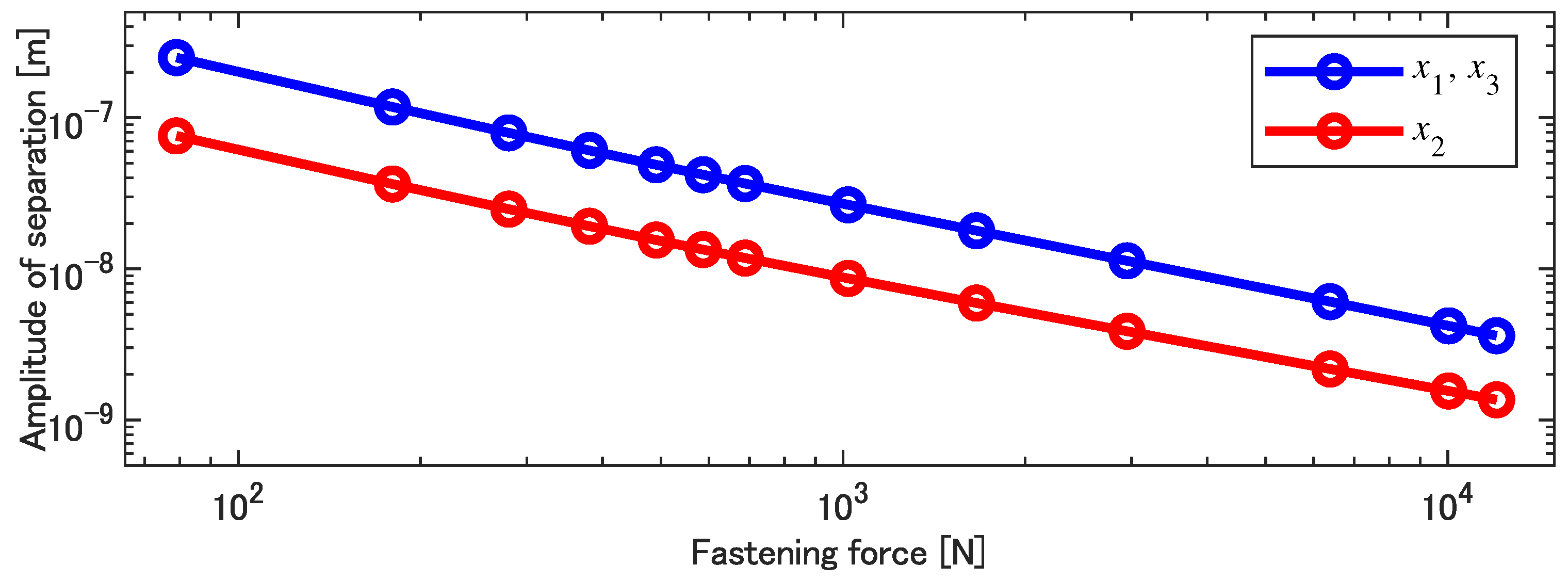
Figure 11 shows the results of the calculation of the amplitude of the variation in the contact separation by Equations (27)–(29). Note that the contact stiffness $K_{\mathrm{contact}1}$ and $K_{\mathrm{contact}3}$ are assumed to be the same because both are the contact between the same Metal and PI, and thus are the calculated amplitudes of $x_1$ and $x_3$. As presented in the figure, it is found that the contact separation amplitudes are almost inversely proportional to the fastening force, and they are on the order of ${10}^{-7}$ m at most for the Metal–PI contact and ${10}^{-8}$ m at most for the PET–PI contact within the experimental conditions.

4.3. Model Validation via Evaluation of Triboelectric Charge Density

Since the value of the contact separation amplitude is negligibly small, as shown in Figure 11, compared with the thickness of the polymer layer in the sensor, which is on the order of ${10}^{-5}$ m, Equation (15) can be reduced to an equation of a first-order lag system as

$$R\dot{Q}=-AQ-B{\sigma }_1{x}_1+C{\sigma }_2{x}_2$$

(30)

where

$$A=\frac{1}{{\epsilon }_{0}S}\frac{(\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}})\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}}{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}}$$

(31)

$$B=\frac{1}{{\epsilon }_0}\frac{\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}}{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}}$$

(32)

$$C=\frac{1}{{\epsilon }_0}\frac{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}}{\frac{d_{\mathrm{PI}1}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PI}2}}{{\epsilon }_{\mathrm{PI}}}+\frac{d_{\mathrm{PET}}}{{\epsilon }_{\mathrm{PET}}}}$$

(33)

Similarly, Equation (16) is reduced to

$$R\dot{Q}=-AQ-B{\sigma }_1{x}_1-C{\sigma }_2{x}_2$$

(34)

because $d_{\mathrm{PI}1}=d_{\mathrm{PI}3}$.

Now assuming a steady-state response, the voltage amplitude is derived as

$$\widehat{V}=\frac{j\omega R}{j\omega R+A}(-B\sigma {\widehat{x}}_1+C{\sigma }_2{\widehat{x}}_2)$$

(35)

for the experimental setup shown in Figure 5a, while

$$\widehat{V}=\frac{j\omega R}{j\omega R+A}(-B\sigma {\widehat{x}}_3-C{\sigma }_2{\widehat{x}}_2)$$

(36)

for the setup shown in Figure 5b, assuming ${\sigma }_1={\sigma }_3=\sigma$, where the values with hat denote the complex amplitude.

Equations (35) and (36) provide a cogent explanation of the experimental results from the following two perspectives. First, the argument of the common part of the above two equations, $\arg \{j\omega R/(j\omega R+A\left)\right\}$, explains the phase delay of the measured voltage from the excitation acceleration. For the given values of R and A, the value of the argument is calculated as 83°. This means that the phase delay of the voltage from the separation variation is −83° if the sign inside the parentheses in the right-hand side of those equations is positive, and 97° when it is negative. Furthermore, assuming that the natural frequency of the experimental setup is sufficiently higher than the excitation frequency, the phase delay of the separation variation from the excitation acceleration should be nearly 180°. In conclusion, the phase delay of the voltage from the excitation acceleration should be 97° when the sign inside the parentheses in the right-hand side of Equation (35) (or Equation (36)) is positive, and −83° if it is negative.

For the experimental results, it is found from Figure 4b that the phase delay from the excitation acceleration for the circuit configuration shown in Figure 5a was around 100° for the fastening force less than 200 N, and around −80° for the fastening force greater than 300 N. These findings are consistent with the above theoretical values and suggest that the magnitude of the first term in the parentheses in Equation (35) is greater than the second term at high fastening forces, while it is smaller at low fastening forces. Moreover, the experimental results shown in Figure 6b indicate that the phase delay for the circuit configuration shown in Figure 5b took a nearly constant value around −45°. Although the value was slightly different from the theoretical value, possibly due to thinning of the polymer layers after the repeated tests, the fact that the observed phase delay showed a negative constant value is consistent with the theoretical findings.

Next, as the values of R, A, B, and C are known, and ${\widehat{x}}_1$, ${\widehat{x}}_2$, and ${\widehat{x}}_3$ are calculated as shown in Figure 11, the values of $\sigma$ and ${\sigma }_2$ are the only unknown values in Equations (35) and (36), which can be estimated by fitting the equations to the experimental values shown in Figure 6 for each fastening force. To do this, the values of the phase delay were idealized by being replaced by the theoretical values based on the above discussion, and combined with the experimental amplitude values. Moreover, because the experimental results from two different configurations shown in Figure 6 had different values for the fastening force, the results of the swapped configuration (red points) were resampled by linear interpolation at the values of the fastening force of the initial configuration (blue points).

The results are plotted in Figure 12, in which regression lines being described below are also drawn. The triboelectric charge density that fits the experimental results increases as the fastening force increases, varying from the order of ${10}^{-5}$ C/m${}^2$ to ${10}^{-4}$ C/m${}^2$ for the Metal–PI contact and from ${10}^{-4}$ C/m${}^2$ to ${10}^{-3}$ C/m${}^2$ for the PET–PI contact. These values are reasonable, as the charge density reported in the literature related to TENG varies in the same range [8,14,15,38]. A closer look at the dependence of the estimated charge density on the fastening force reveals that the triboelectric charge density at the contact between Metal and PI is almost proportional to the fastening force, showing a slight saturating tendency at high loads, whereas the charge density between PET and PI exhibits a different power law at low loads.

The increasing dependency of the estimated charge density on the fastening force can be explained by considering the real contact area at the interface. When the real charge density is ${\sigma }_{\mathrm{r}}$ on the real contact area $A_{\mathrm{r}}$, the nominal charge density ${\sigma }_{\mathrm{n}}$ is given by

$${\sigma }_{\mathrm{n}}=\frac{A_{\mathrm{r}}}{A_{\mathrm{n}}}{\sigma }_{\mathrm{r}}$$

(37)

where $A_{\mathrm{n}}$ is the nominal contact area. Because the real contact area is in general an increasing function of the applied pressure, the increasing dependency on the charge density is understandable.

Moreover, in the elastic contact model of random rough surfaces adopted in this analysis (described in Section 4.2), the real contact area is nearly proportional to the applied load on the interface [34,37]. The estimated charge density at the Metal–PI interface showing almost linear dependency, which was in fact the power of 0.77 according to the regression line shown in Figure 12 with a solid line, is consistent with this model. On the other hand, the different dependency of the charge density at the PET–PI interface in low load conditions suggests the existence of different contact mechanics. To see this tendency, the estimated density was regressed by a bilinear curve, as shown in Figure 12 with a dashed and dotted line, which was specified by first fitting a line to the first seven points, extending it to the abscissa of the eighth point, and then fitting another line starting from the end of the first line to the remaining six points. The resultant power law was 0.29 for low loads and 0.74 for high loads. A possible candidate for a model of the different dependency in low loads is a contact of elastic wavy surfaces, in which the real contact area has a dependence proportional to the 2/3 power of the contact load, as described in the literature [37,39,40].

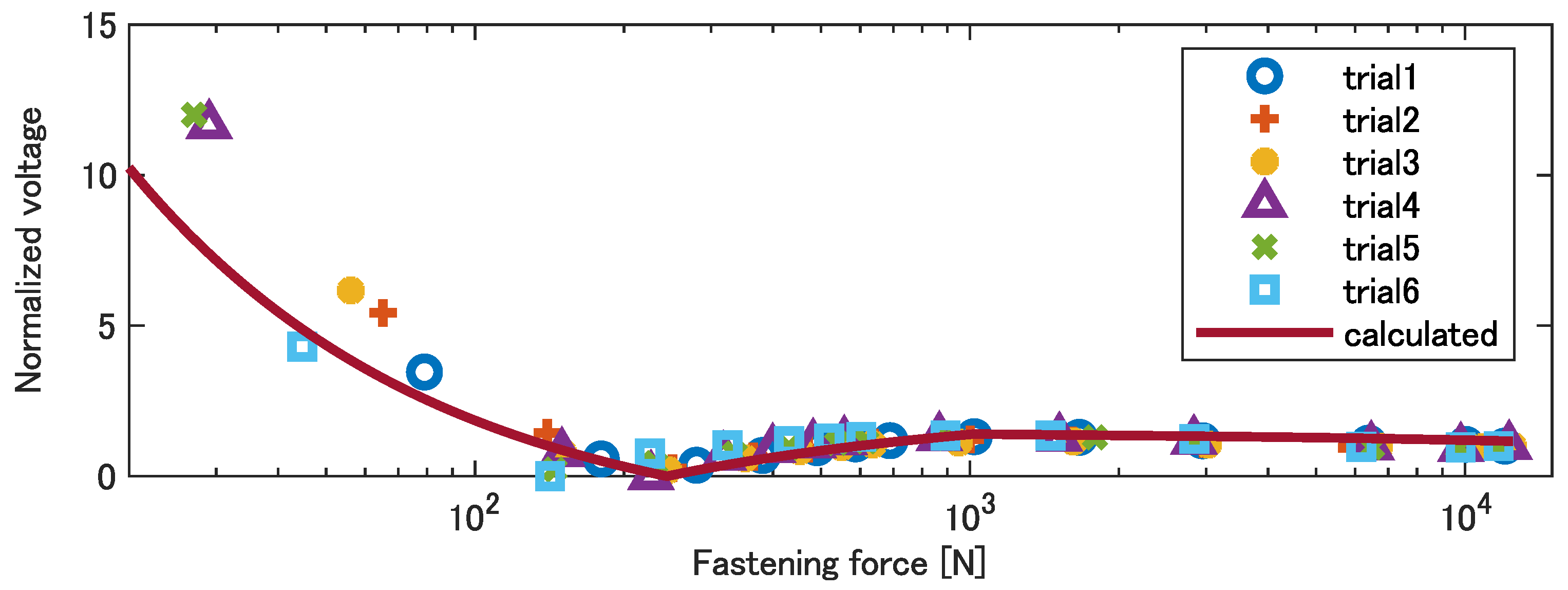
Finally, to verify that the mechanical–triboelectric model presented in this section, taking account of the tightening mechanics of the bolt and the contact mechanics of Metal–PI and PET–PI contacts, can appropriately explain the experimental results, the voltage amplitude of the sensor output for the initial configuration shown in Figure 5a was calculated based on the regression curves indicated in Figure 12. The result is shown in Figure 13 with a solid line accompanied by all the experimental data plotted by markers. As presented in the figure, the model curve has a valley at a location close to the valleys that the experimental data exhibited and shows a good agreement with the experimental results in wide range of the fastening force, except for the lowest load conditions. The relatively large error at the low fastening forces is probably due to the deviation of the initial contact condition under the loosest fastening force, as mentioned in Section 4.1. Introducing additional parameters to express the variation in triboelectric charge density considering the deviation of the real contact area in low load conditions may further improve the model adequacy.

5. Conclusions

In this study, a concept and design of a self-powered sensor that utilizes a triboelectric effect to evaluate the condition of tensile bolted joints was proposed. The proposed sensor is a film-shaped triboelectric sensor made of inexpensive materials being installed between the objects to be fastened. The principle of the sensor is that it detects microscale relative motions between the contacting surfaces against an external vibratory load when the integrity of the fastened joint is compromised due to a decrease in the bolt’s fastening force. The designed and fabricated triboelectric sensor was tested on a tensile bolted joint specimen subjected to inertial vibratory loading, and it was experimentally shown that the output voltage amplitude of the sensor increased as the bolt’s fastening force decreased. To explain the unexpected decrease in the voltage amplitude observed at medium preloads, modeling was performed to account for triboelectric charging not only between the triboelectric material layers within the sensor but also between the polymer–metal contact of the insulating layer and the fastened members, showing that the latter has a significant effect on the sensor voltage. The model and the results of two experiments with different external circuit connections were combined with a mechanical analysis of the bolted joint to estimate the triboelectric charge density at the contact surfaces. The estimated charge densities were found to be consistent with the contact mechanics model assumed. Finally, the calculation of the sensor output voltage for the circuit configuration of the first experiment based on the presented mechanical/triboelectric model using the regression curves for the triboelectric charge density was provided, confirming the validity of the modeling study in terms of the consistency with the experimental results.

There are a wide range of challenges to be overcome in the future. First of all, more experiments and analyses with various conditions, including bolt diameters, fastening force, loading frequencies, and the shape of the contacting interface of the fastened objects, are necessary to see the dependence of the triboelectric charge densities and variation in separations at the contacting surfaces and to verify the performance of the sensor in more realistic situations. Cyclic stability is also essential for the feasibility in practical applications. The investigation of practical methodologies to detect the bolt loosening at an appropriate stage based on the sensor output in real circumstances is another issue to be addressed to design a bolt-loosening detection system based on the proposed sensor. Examination of the comprehensive performance of the detection system as a whole, including sensitivity, resolution, and detectablity, should be focused on after that. Furthermore, we could improve the sensor structure to be more simple and effective, considering the triboelectric effect between the insulating layer of the sensor and the fastened object. More reliable material selection is another important issue to be resolved to ensure the long-term performance of the fastener by exploring more creep-resistant materials, possibly including thermosetting resins, ceramics, and diamond-like carbon-coated metal sheets. Other issues to be addressed include the protection of the sensor against field environment factors such as temperature and humidity, more sensitive loosening detection by optimizing the pattern of the electrodes, and application to multi-bolt joints as well as shear joints.