Development and Experiment of Clamp Type Submarine Cable Inspection Robot
Abstract
:1. Introduction
2. Design Scheme of Submarine Cable Towing Auxiliary Device
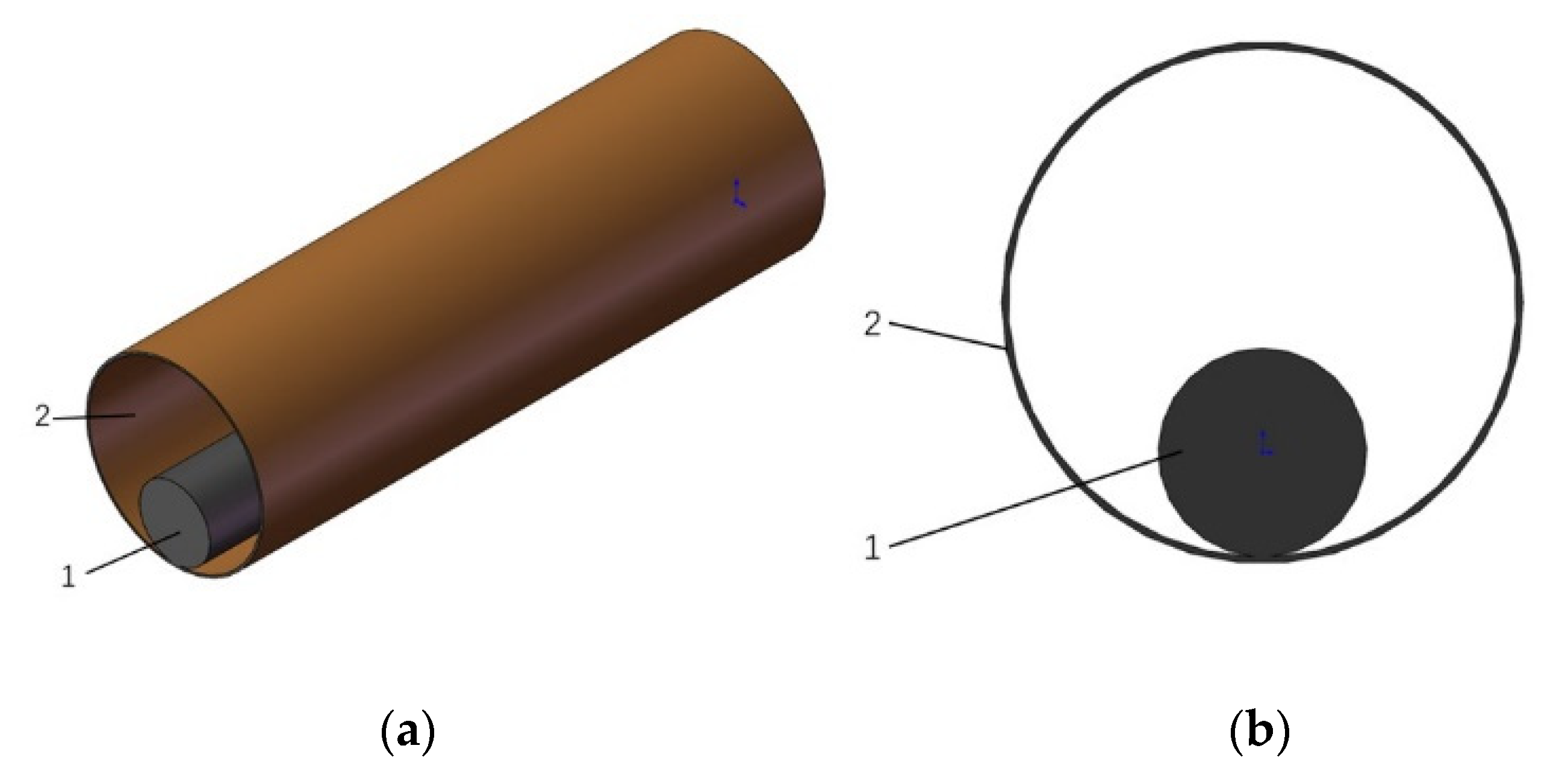
2.1. Detection Robot Parameter Determination and Working Condition Analysis
- inner diameter of the pipeline: D = 614 mm;
- outer diameter of the submarine cable: d = 252 mm;
- pipeline material: welded steel pipe;
- maximum walking speed: v = 10 m/min;
- control distance: 1000 m;
- power supply: AC 220 V power supply;
- operation: detect drag damage along the cable and can take pictures and record.
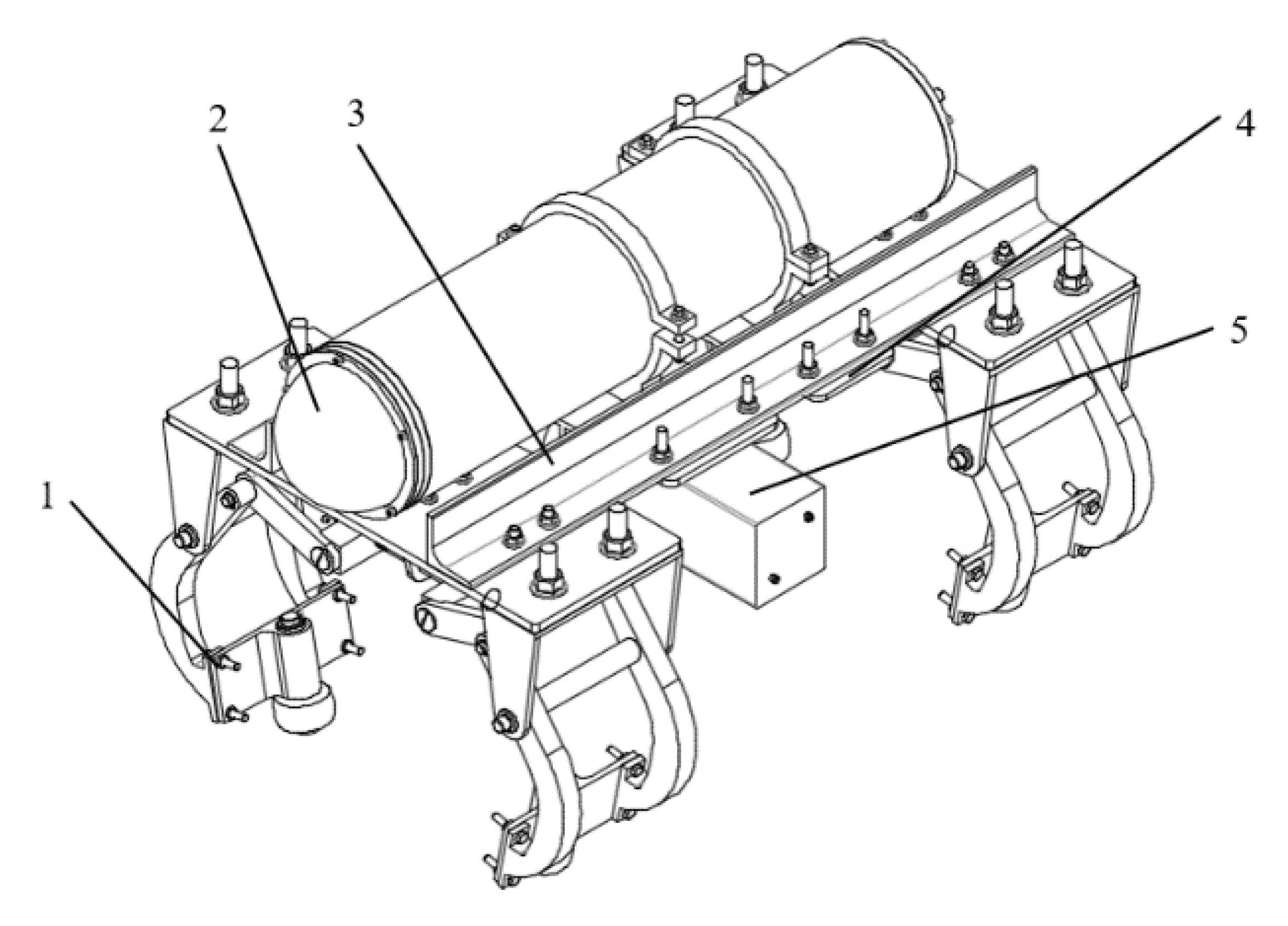
2.2. Structural Design of Inspection Robot
3. Theoretical Analysis of Mechanics of Submarine Cable Towing
3.1. Theoretical Analysis of Mechanics in Submarine Cable Towing Stage
3.2. Theoretical Analysis of Mechanics of Submarine Cable Traction Stage
- (1)
- Use the segment method to calculate and analyze the force of the submarine cable. This method divides the submarine cable into multiple segments according to the pipeline trajectory, and each segment is in the vertical plane, regardless of the direction change in the horizontal plane;
- (2)
- When the pipeline trajectory is bent around the corner point, the curved section of the pipeline is symmetrical about the corner bisector. On both sides of the corner bisector, the submarine cable is tangent to the pipe wall;
- (3)
- There is no mutual influence between the winch effect and the submarine cable bending effect.
- The resistance caused by the weight of the submarine cable outside the pipe;
- The resistance caused when part of the submarine cable in the pipe passes through the straight section;
- The resistance caused when part of the submarine cable in the pipe passes through the bending section.
- (1)
- Resistance caused by the weight of the submarine cable outside the pipe
- (2)
- The resistance of the submarine cable through the straight section
- (3)
- The resistance of the submarine cable through the bending section
4. Finite Element Simulation Analysis of Submarine Cable Traction
4.1. Parameter Determination of Submarine Cable
4.2. Geometric Modeling
4.3. Meshing
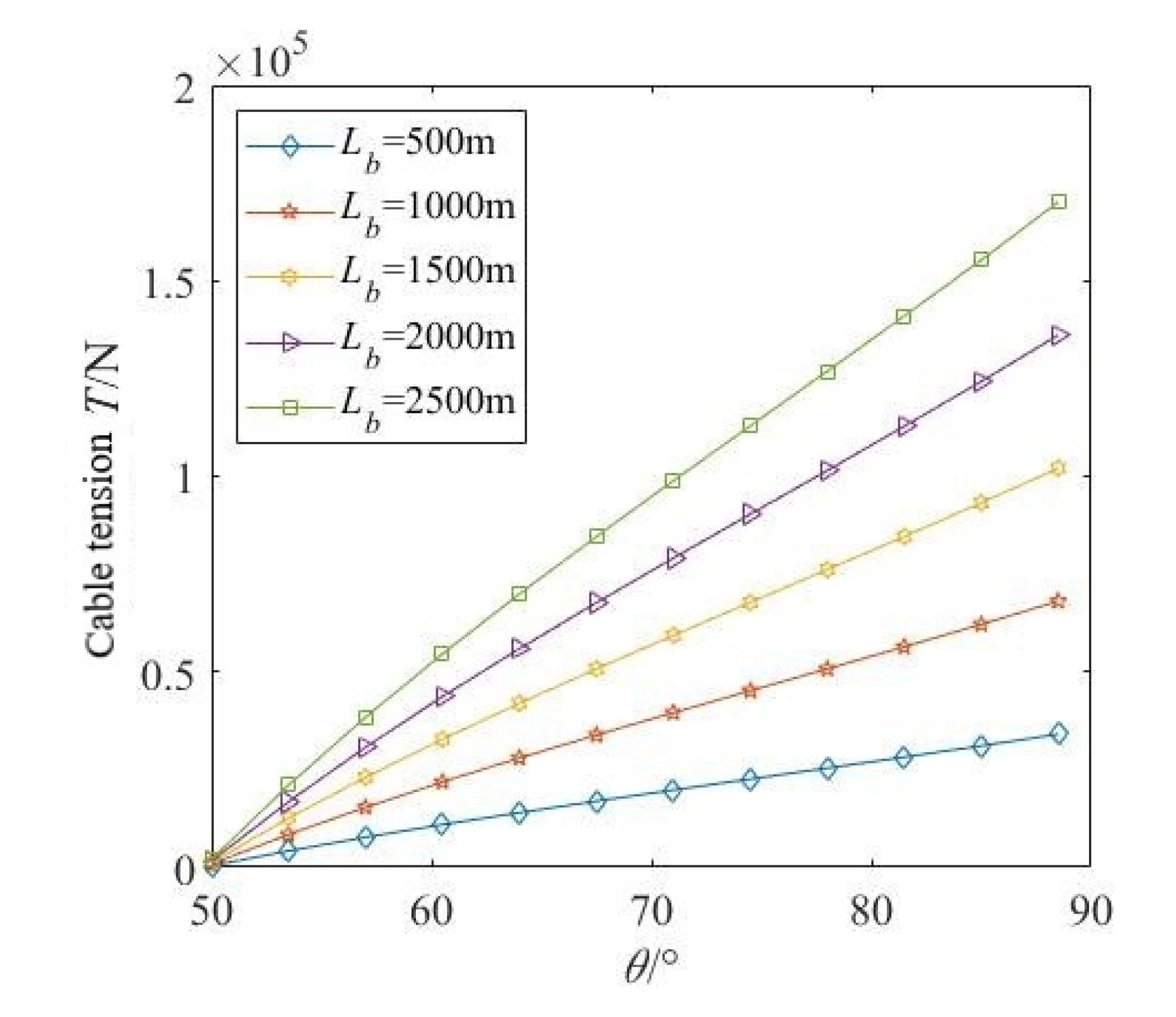
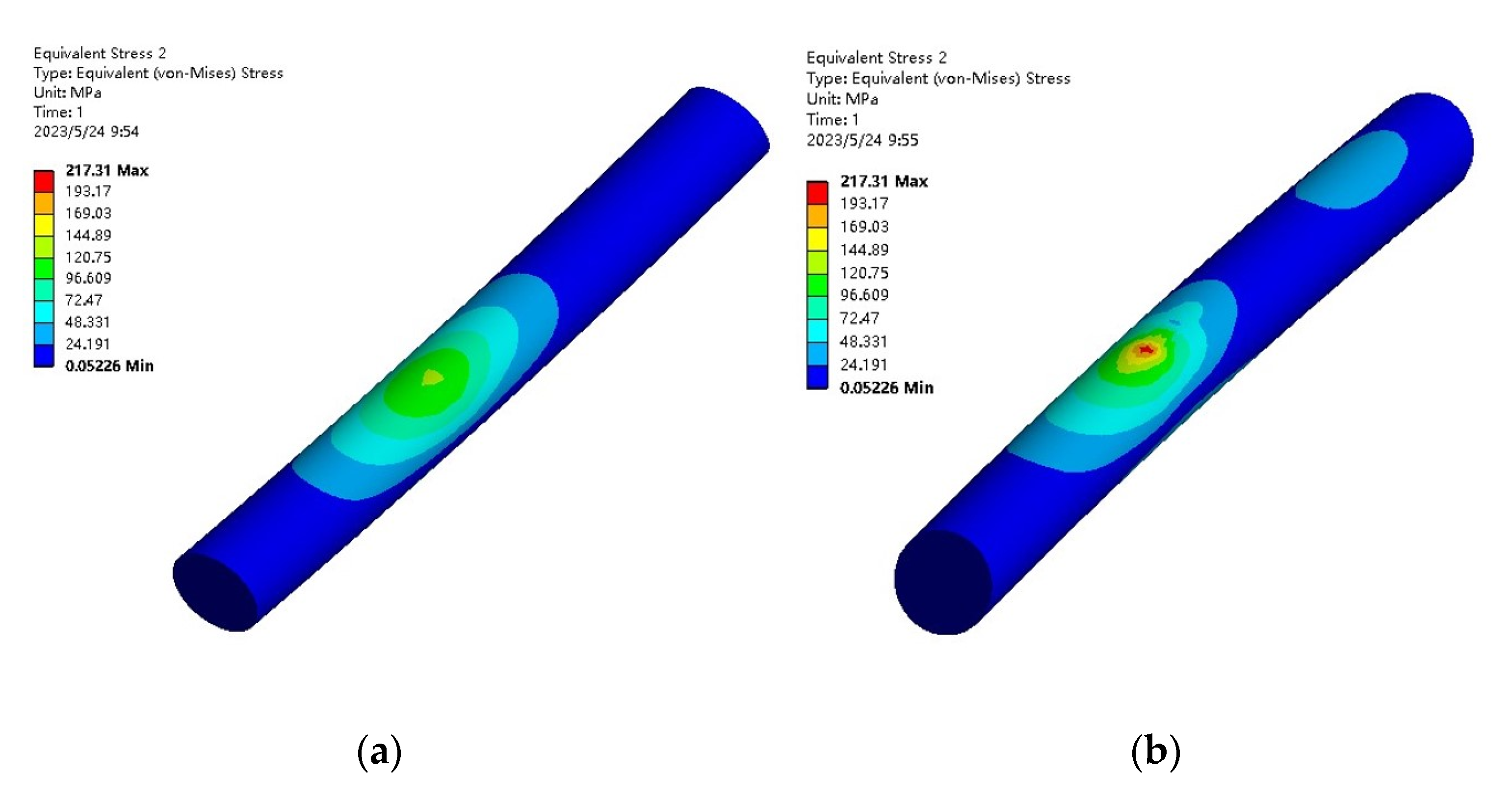
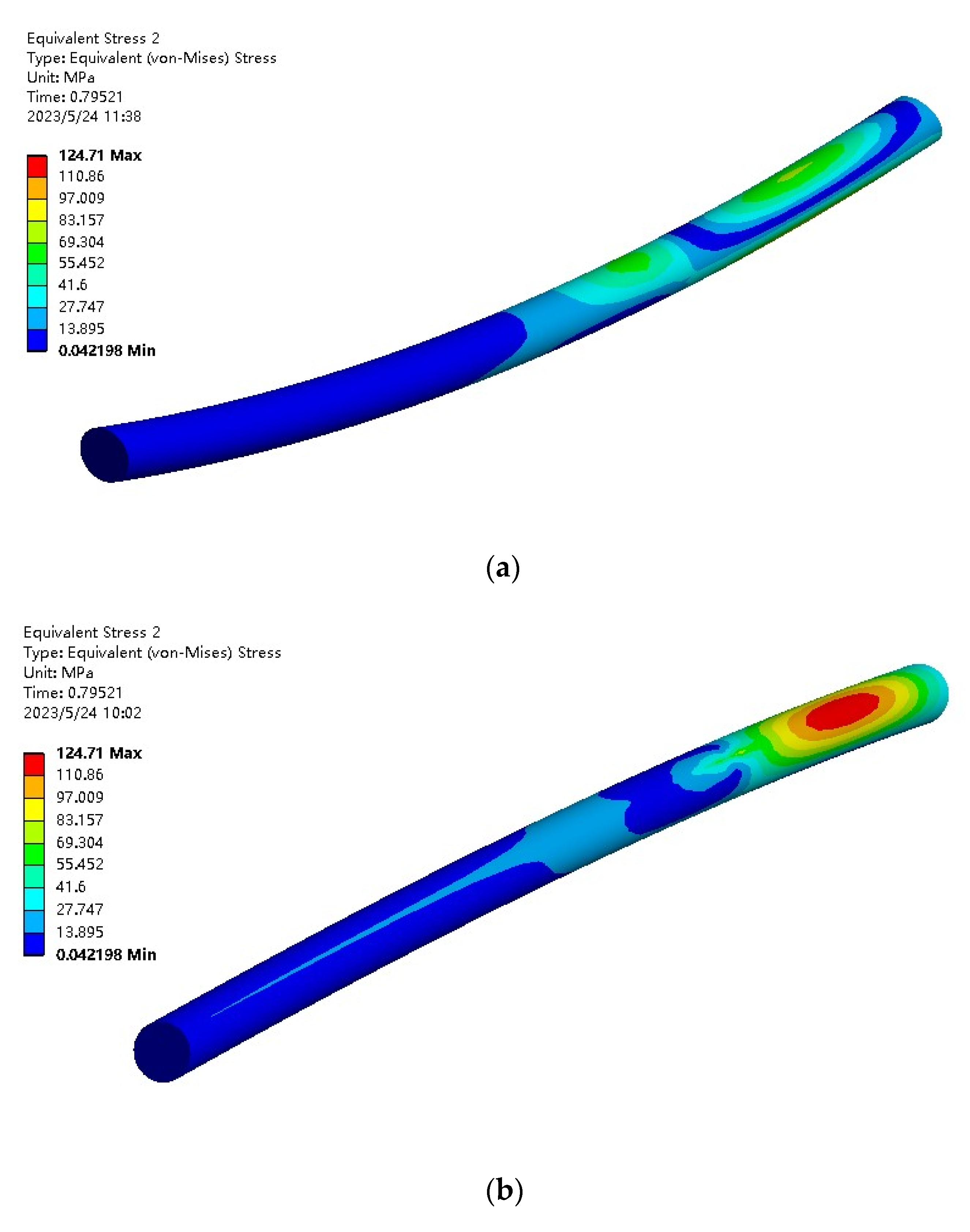
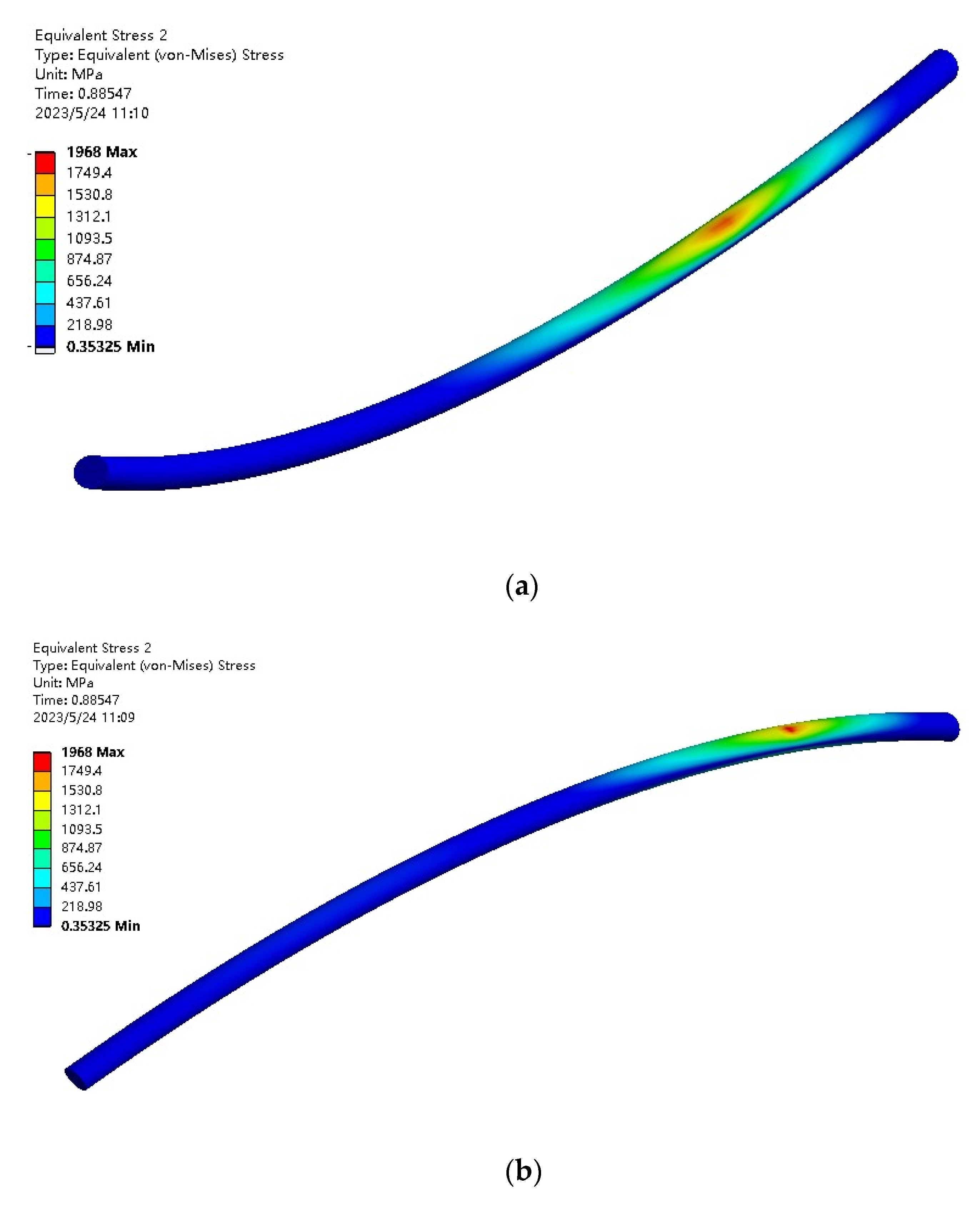
4.4. Simulation Results
- The initial stage of cable towing
- 2.
- Intermediate stage of submarine cable hauling
- 3.
- Submarine cable towing end stage
5. Performance Experiment of Submarine Cable Outer Wall Detection Robot
5.1. Experimental Device Structural Scheme
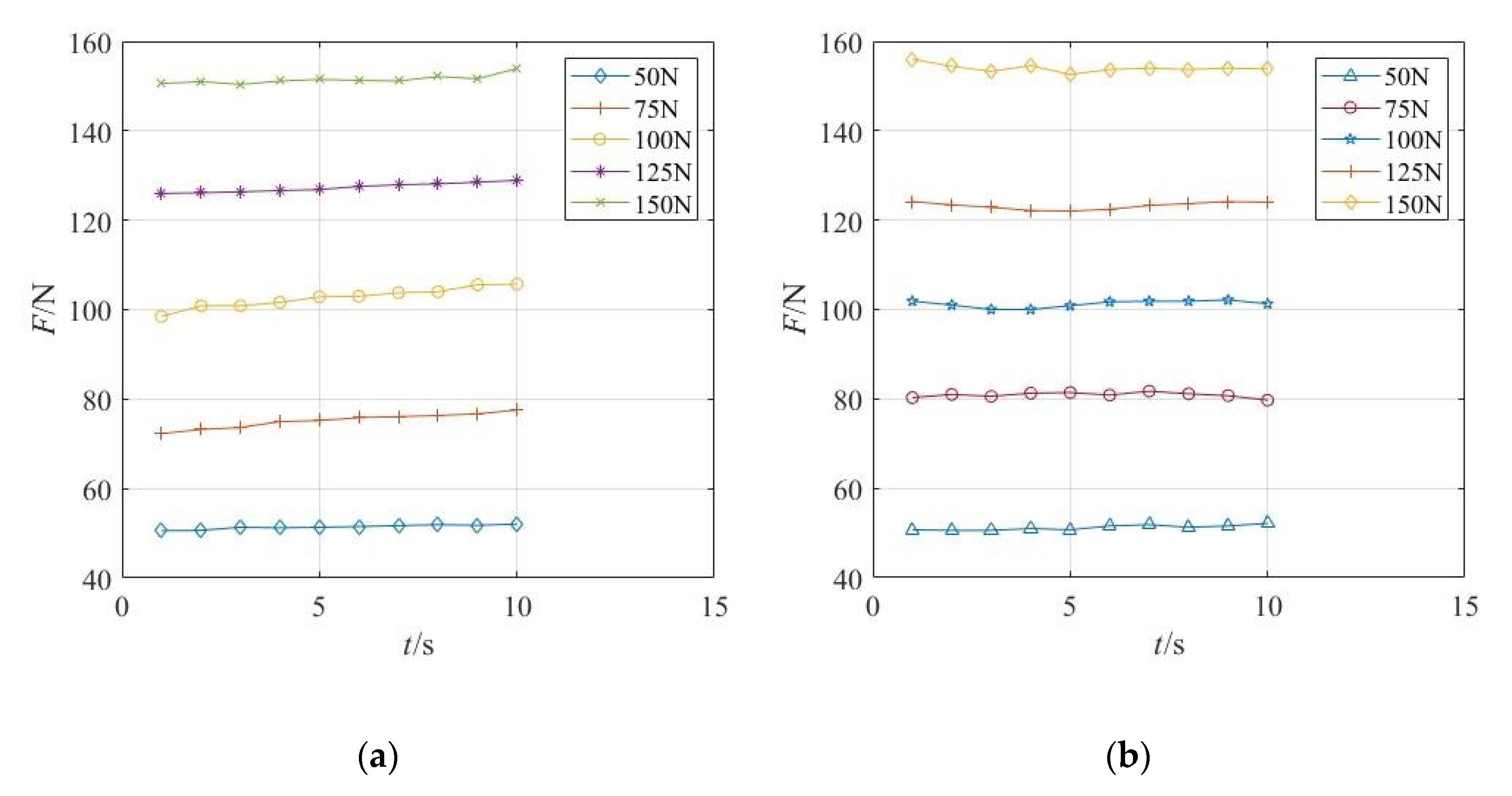
5.2. Experimental Process and Result Analysis
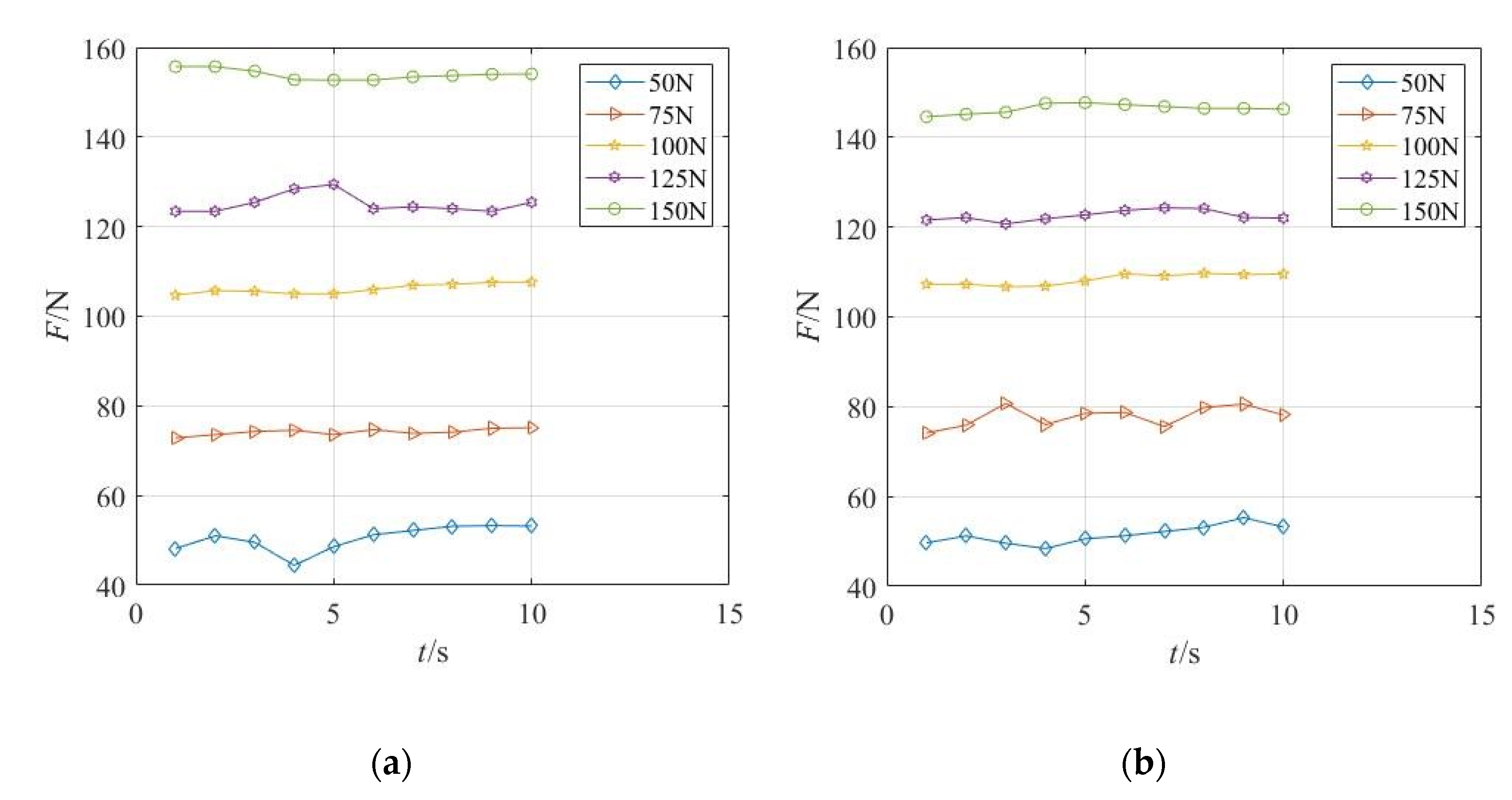
- Walking experiments on horizontal pipes
- 2.
- Walking experiments on inclined pipes
6. Conclusions
- In this paper, a detection robot that walks along the outer wall of the cable inside the submarine casing is designed. It adopts a non-enclosed four-link clamping mechanism and a wheel drive, which is well adapted to the working conditions of the submarine cable in the casing and runs stably. The driving force is strong, and the detection task can be well completed.
- We analyzed the force of the submarine cable towing in the crossing project. The finite element simulation was used to simulate the towing of the submarine cable in the pipeline, and it was confirmed that the most likely location for plastic deformation was the real-time contact surface between the submarine cable and the pipeline.
- We carried out relevant experimental research on the detection robot of the outer wall of the submarine cable. The walking experiments were carried out on the horizontal and inclined pipelines, respectively. The experimental prototype reached the maximum running speed with a clamping force of 50 N, which were 15.15 m/min and 14.28 m/min, respectively. By measuring the relationship between the position of the wheel arm module parts and the change in the submarine cable diameter, the feasibility of measuring the change of cable diameter in real-time by the number of turns of the lead screw is proved.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, B.; Zhang, Q.R.; Wang, T.; Wang, Z. Research on the Bearing Capacity of a Damaged Jacket Repaired by a Grouting Clamp Based on a Type of Wedge Gripping. J. Mar. Sci. Eng. 2020, 8, 973. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, H.; Wang, T.; Wang, Z. Design and Experiment of a Lifting Tool for Hoisting Offshore Single-Pile Foundations. Machines 2021, 9, 29. [Google Scholar] [CrossRef]
- Huang, P.Y.; Hua, X.L.; Hu, T.J.; Zhang, W.L.; Zhang, M.M.; Hu, H. Preliminary Conception of Submarine Cable and Pipeline Corridor Planning. Ocean. Dev. Manag. 2020, 37, 8–11. [Google Scholar]
- Zhou, X.; Jia, X.; Yin, G.Q. Research on sea-to-sea directional drilling crossing technology. Pipeline Technol. Equip. 2015, 3, 43–46. [Google Scholar] [CrossRef]
- Lin, R.R.; Du, N.F. A brief discussion on the application of offshore directional drilling traction pipes to cross submarine cables in submarine pipelines. China Water Transp. 2018, 18, 226–229. [Google Scholar]
- Alvi, M.J.; Izhar, T.; Qaiser, A.A.; Afzaal, M.U.; Anjum, A.; Safdar, A. Pliability assay of conventional gas insulated transmission line and flexible gas insulated transmission line regarding horizontal directional drilling based underground cable laying for metropolitan areas. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe) IEEE, Palermo, Italy, 12–15 June 2018. [Google Scholar] [CrossRef]
- Cho, K.H.; Kim, H.M.; Jin, Y.H.; Liu, F.; Moon, H.; Koo, J.C.; Choi, H.R. Inspection Robot for Hanger Cable of Suspension Bridge: Mechanism Design and Analysis. IEEE/ASME Trans. Mechatron. 2013, 18, 1665–1674. [Google Scholar] [CrossRef]
- Zhang, Z.H.; He, F.J. Design and analysis of an out-of-pipe crawling robot for row pipes. Mech. Transm. 2016, 40, 63–66. [Google Scholar] [CrossRef]
- Hans-Joachim, B. Grabenlose Auswechslung von Erdkabelleitungen. Acta Montan. Slovaca 2007, 12, 237–241. [Google Scholar]
- Wang, Z.Y. Structural Design and Adsorption Performance of Wind Turbine Tower Cleaning Robot; Harbin Engineering University: Harbin, China, 2016; pp. 30–35. [Google Scholar] [CrossRef]
- Almonacid, M.; Saltaren, R.; Aracil, R.; Reinoso, O. Motion planning of a climbing parallel robot. IEEE Trans. Robot. Autom. 2003, 19, 485–489. [Google Scholar] [CrossRef]
- Aracil, R.; Saltarén, R.; Reinoso, O. Parallel robots for autonomous climbing along tubular structures. Robot. Auton. Syst. 2003, 42, 125–134. [Google Scholar] [CrossRef]
- Aracil, R.; Saltaren, R.; Reinoso, O. A climbing parallel robot: A robot to climb along tubular and metallic structures. IEEE Robot. Autom. Mag. 2006, 13, 16–22. [Google Scholar] [CrossRef]
- Choi, C.; Park, B.; Jung, S. The Design and Analysis of a Feeder Pipe Inspection Robot With an Automatic Pipe Tracking System. IEEE/ASME Trans. Mechatron. 2010, 15, 736–745. [Google Scholar] [CrossRef]
- Noohi, E.; Mahdavi, S.S.; Baghani, A.; Ahmadabadi, M.N. Wheel-based climbing robot: Modeling and control. Adv. Robot. 2010, 24, 1313–1343. [Google Scholar] [CrossRef]
- Yuan, X.Q.; Ding, N.; Zhang, T.; Zhen, Z.L. Development of Portable Cable Robot. Mech. Des. Manuf. Eng. 2019, 48, 32–36. [Google Scholar] [CrossRef]
- Khan, M.B.; Chuthong, T.; Do, C.D.; Thor, M.; Billeschou, P.; Larsen, J.C.; Manoonpong, P. iCrawl: An Inchworm-Inspired Crawling Robot. IEEE Access 2020, 8, 200655–200668. [Google Scholar] [CrossRef]
- Ito, K.; Ninomiya, Y. TAOYAKA V: A multi-legged robot, successfully combining walking and climbing mechanisms. Artif. Life Robot. 2021, 26, 97–102. [Google Scholar] [CrossRef]
- Dutta, S.K.; Reddy, B.S.; Dwivedy, S.K. Complibot: A compliant external pipe climbing robot. Mech. Based Des. Struct. Mach. 2023, 2023, 1–30. [Google Scholar] [CrossRef]
- Kawasaki, H.; Murakami, S.; Kachi, H.; Ueki, S. Novel climbing method of pruning robot. In Proceedings of the 2008 SICE Annual Conference, Chofu, Japan, 20–22 August 2008; pp. 160–163. [Google Scholar] [CrossRef]
- Lee, S.H. Design of the out-pipe type pipe climbing robot. Int. J. Precis. Eng. Manuf. 2013, 14, 1559–1563. [Google Scholar] [CrossRef]
- Ho, H.-N.; Kim, K.-D.; Park, Y.-S.; Lee, J.-J. An efficient image-based damage detection for cable surface in cable-stayed bridges. Ndt E Int. 2013, 58, 18–23. [Google Scholar] [CrossRef]
- Zheng, M.; Yang, M.; Yuan, X.; Ding, N. A Light-Weight Wheel-Based Cable Inspection Climbing Robot: From Simulation to Reality. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 1365–1370. [Google Scholar] [CrossRef]
- Gao, Z.Y.; Peng, L.M. The design of the robot body for the detection of the stay cables of the Hangzhou Bay Bridge. Shanxi Archit. 2012, 38, 174–175. [Google Scholar] [CrossRef]
- Md-Yusoff, M.N.S.; Bin Cheah, K.; Mohamad-Wazir, A.R.; Othman, W.A.F.W.; Alhady, S.S.N.; Wahab, A.A.A. Steel Pipe Climbing Robot Development. In Proceedings of the 11th International Conference on Robotics, Vision, Signal Processing and Power Applications, Lecture Notes in Electrical Engineering; Springer: Singapore, 2022; Volume 829. [Google Scholar] [CrossRef]
- Li, D.Q.; Wang, W.L.; Lin, Y.H.; Zhang, Z.S.; Zhang, X.L. Exploration and practice of land-to-sea directional drilling crossing technology in ocean engineering. J. Ocean. Technol. 2020, 39, 95–100. [Google Scholar]
- Yang, N. Tension Analysis of Submarine Cables during Laying Process; Shanghai Jiaotong University: Shanghai, China, 2015; pp. 40–58. [Google Scholar]
- Liu, X.; Ai, Z.J.; Li, H.Y.; Hu, K.; Yu, J.G. Calculation method of back drag force of horizontally oriented crossing stiffness winch. J. Wuhan Univ. 2018, 51, 356–362. [Google Scholar] [CrossRef]
- Salhaoui, M.; Molina-Molina, J.C.; Guerrero-González, A.; Arioua, M.; Ortiz, F.J. Autonomous Underwater Monitoring System for Detecting Life on the Seabed by Means of Computer Vision Cloud Services. Remote Sens. 2020, 12, 1981. [Google Scholar] [CrossRef]




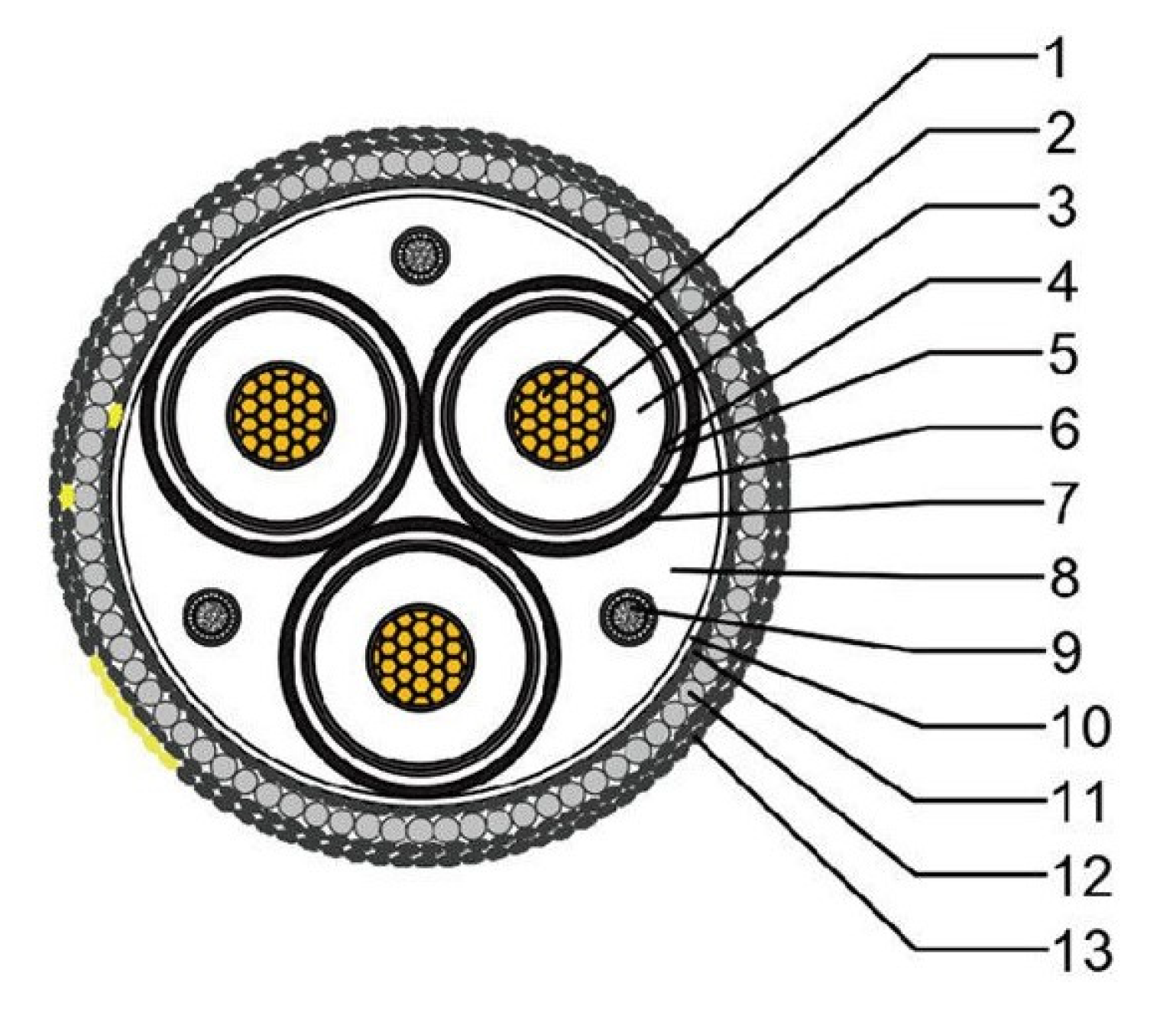










| No | Composition | Nominal Thickness | Reference Outside Diameter (mm) |
|---|---|---|---|
| 1 | Copper conductor + water-blocking tape | / | 29.9 |
| 2 | Conductor shield | 2 | 33.9 |
| 3 | XLPE insulation | 26 | 85.9 |
| 4 | Insulation shield | 1.2 | 88.3 |
| 5 | Semiconducting resistance hose | 0.8 | 90.7 |
| 6 | Lead sheath | 3.6 | 97.9 |
| 7 | PE sheath | 3.3 | 105.5 |
| 8 | padding | / | 227.2 |
| 9 | 48-core single fiber optic cable | / | / |
| 10 | Rubberized cloth bag | 0.3 | 229 |
| 11 | PP rope | 1.5 | 232 |
| 12 | Galvanized steel wire | 6 | 244 |
| 13 | PP outer cover | 4 | 252 |
| Preload force (N) | 50 | 75 | 100 | 125 | 150 |
| Average speed (m/min) | 15.18 | 12.63 | 13.23 | 13.47 | 12.81 |
| Preload force (N) | 50 | 75 | 100 | 125 | 150 |
| Average speed (m/min) | 14.28 | 13.13 | 12.43 | 13.18 | 13.25 |
| Number of Turns | Head Wheel Arm Module | Tail Wheel Arm Module | ||
|---|---|---|---|---|
| X1 (mm) | X2 (mm) | X3 (mm) | X4 (mm) | |
| 1 | 30.02 | 38.47 | 38.71 | 32.38 |
| 2 | 32.06 | 40.31 | 40.55 | 34.73 |
| 3 | 34.05 | 42.33 | 42.41 | 36.65 |
| 4 | 35.90 | 44.28 | 45.02 | 42.34 |
| 5 | 37.85 | 46.45 | 46.30 | 45.05 |
| 6 | 39.94 | 48.23 | 47.65 | 47.50 |
| Average value of Xi change per revolution | 1.98 | 1.95 | 1.79 | 3.02 |
| D | Head Wheel Arm Module | Tail Wheel Arm Module | ||||
|---|---|---|---|---|---|---|
| X1 | Distance from the Center of the Screw | X2 | Distance from the Center of the Screw | X3 | Distance from the Center of the Screw | |
| 252 | 46.50 | 63.50 | 43.58 | 62.58 | 41.91 | 58.91 |
| 254 | 46.49 | 63.49 | 42.44 | 59.44 | 41.41 | 58.41 |
| 256 | 46.25 | 63.25 | 42.88 | 59.88 | 41.31 | 58.31 |
| 258 | 45.57 | 62.57 | 42.77 | 59.77 | 40.86 | 57.86 |
| 262 | 44.50 | 61.50 | 42.07 | 59.07 | 40.44 | 57.44 |
| 266 | 42.59 | 59.59 | 41.69 | 58.69 | 39.11 | 56.11 |
| 268 | 41.23 | 58.23 | 41.35 | 58.35 | 38.23 | 55.23 |
| 272 | 40.06 | 57.06 | 41.61 | 58.61 | 37.53 | 54.53 |
| 274 | 39.68 | 56.68 | 40.90 | 57.90 | 37.25 | 54.25 |
| 276 | 39.30 | 56.30 | 40.05 | 57.05 | 37.00 | 54.00 |
| 282 | 39.03 | 56.03 | 39.46 | 56.46 | 36.59 | 53.59 |
| 288 | 38.21 | 55.21 | 39.57 | 55.57 | 36.05 | 53.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, Y.; Zhang, B. Development and Experiment of Clamp Type Submarine Cable Inspection Robot. Machines 2023, 11, 627. https://doi.org/10.3390/machines11060627
Wang Z, Wang Y, Zhang B. Development and Experiment of Clamp Type Submarine Cable Inspection Robot. Machines. 2023; 11(6):627. https://doi.org/10.3390/machines11060627
Chicago/Turabian StyleWang, Zhuo, Yufan Wang, and Bo Zhang. 2023. "Development and Experiment of Clamp Type Submarine Cable Inspection Robot" Machines 11, no. 6: 627. https://doi.org/10.3390/machines11060627
APA StyleWang, Z., Wang, Y., & Zhang, B. (2023). Development and Experiment of Clamp Type Submarine Cable Inspection Robot. Machines, 11(6), 627. https://doi.org/10.3390/machines11060627





