Analysis and Optimization of Milling Deformations of TC4 Alloy Thin-Walled Parts Based on Finite Element Simulations
Abstract
1. Introduction
2. Milling Analysis of TC4 Alloy Thin-Walled Parts
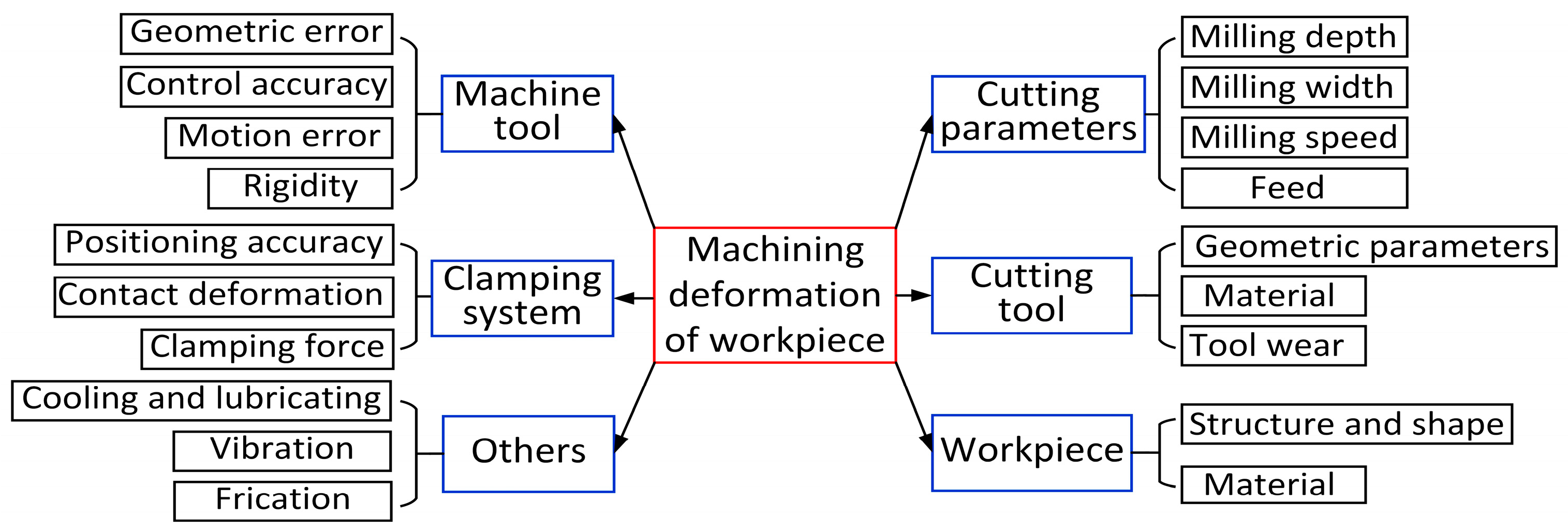
2.1. Analysis of Factors Influencing the Milling Deformation of Thin-Walled Parts
- The influence of the milling cutter
- 2.
- The influence of processing conditions
- 3.
- The influence of milling force
2.2. Proposed Empirical Model for Milling
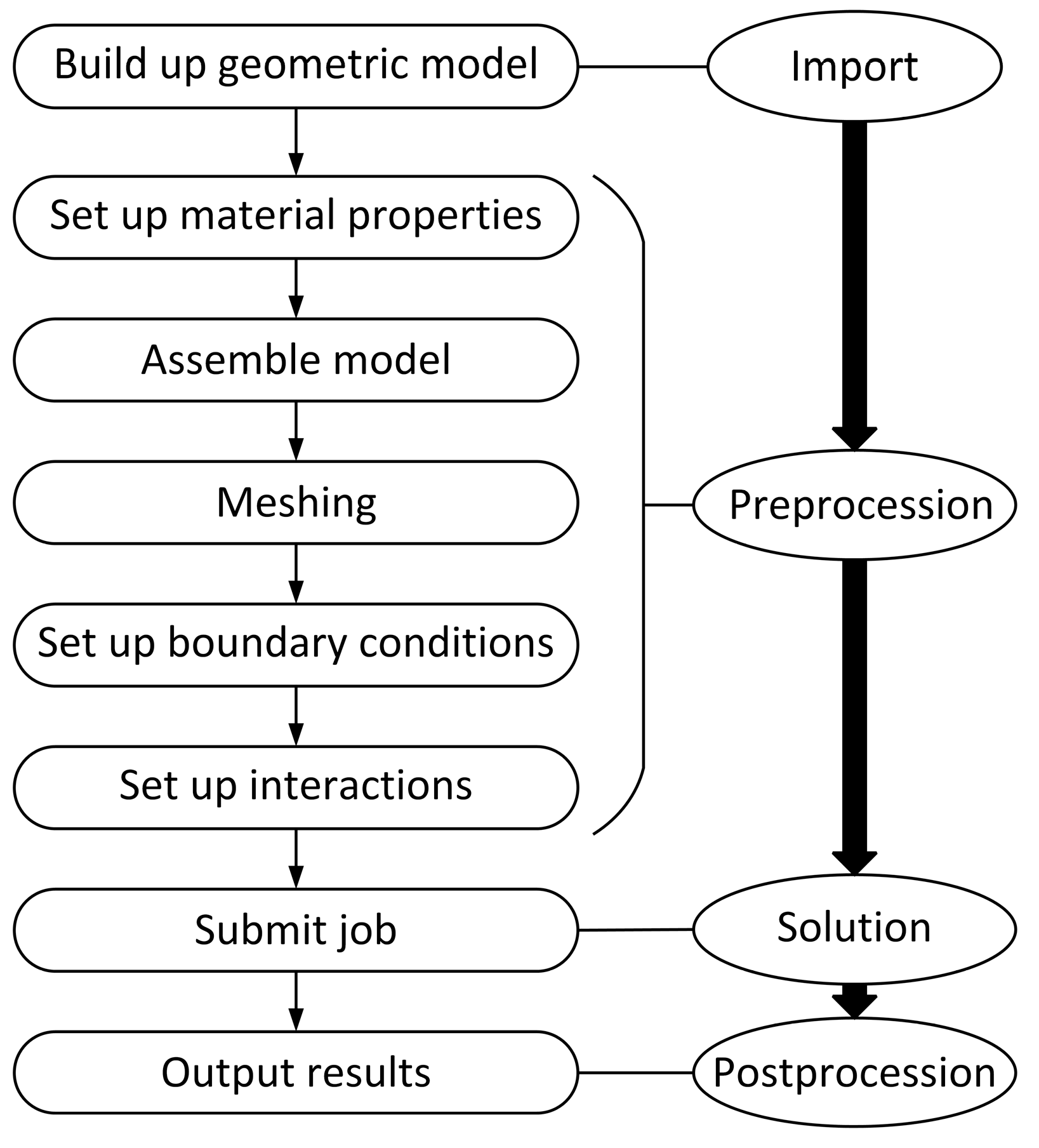
2.3. Principle of Finite Element Model for Milling Thin-Walled Parts
2.3.1. Constitutive Model for Material
2.3.2. Failure Guidelines
2.3.3. Chip Separation Guidelines
3. Finite Element Simulation Tests
3.1. Orthogonal Experimental Design for the Milling of Thin-Walled Parts
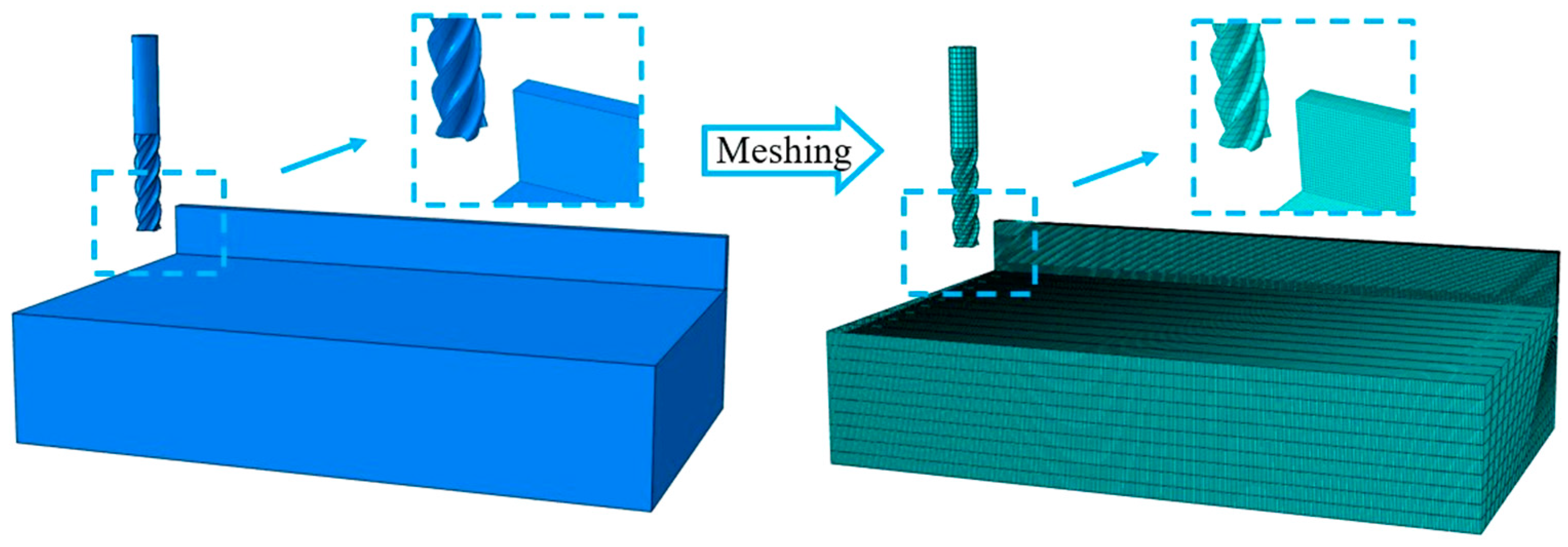
3.2. Establishment of the Finite Element Simulation Model
3.3. The Results of the Finite Element Simulation
- The degree of influence of the eight parameters on the total milling force is as follows: diameter of milling cutter > milling depth > milling width > spindle speed > feed rate per tooth > tilt angle of milling cutter > number of teeth > rake angle of milling cutter;
- The degree of influence of the eight parameters on the maximum nodal deformation is as follows: milling width > milling depth > feed rate per tooth > spindle speed > diameter of milling cutter > tilt angle of milling cutter > rake angle of milling cutter > number of teeth.
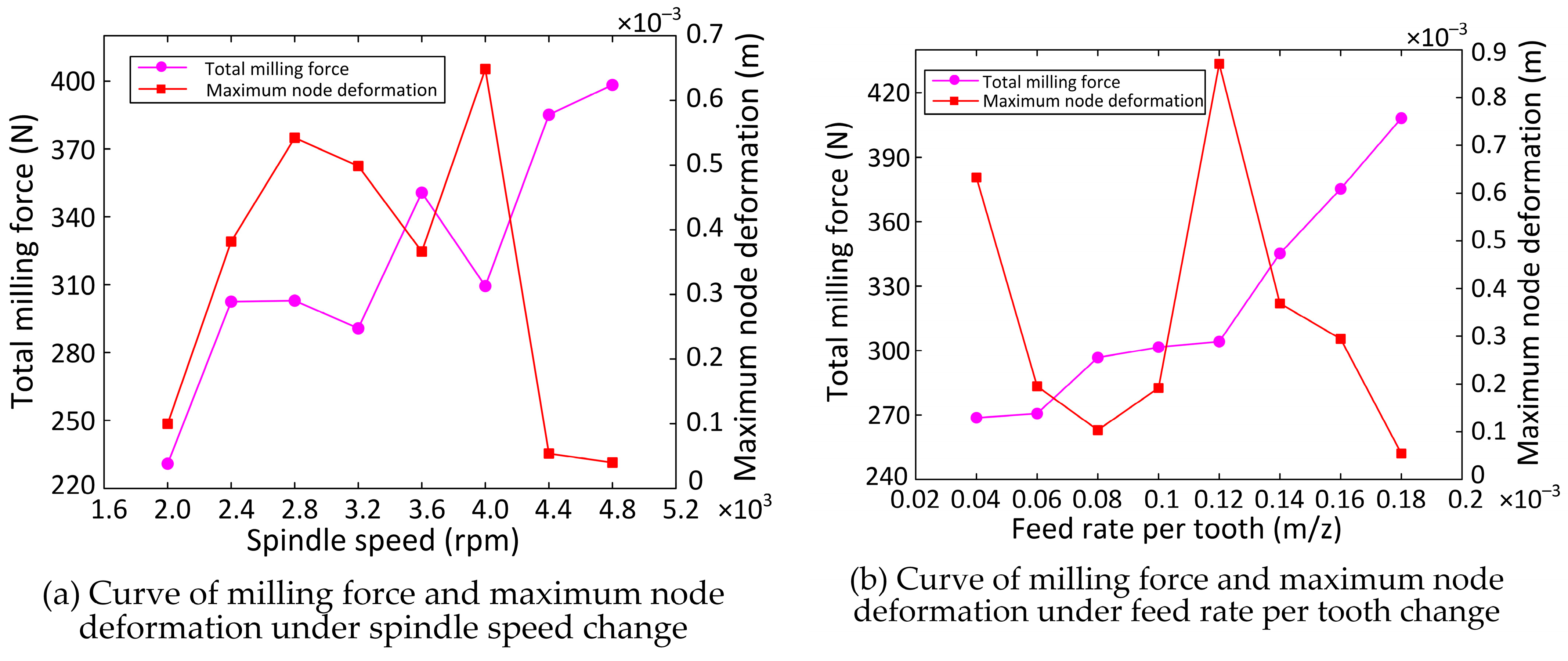
3.4. The Influence of Processing Parameters on the Milling Force and Maximum Node Deformation
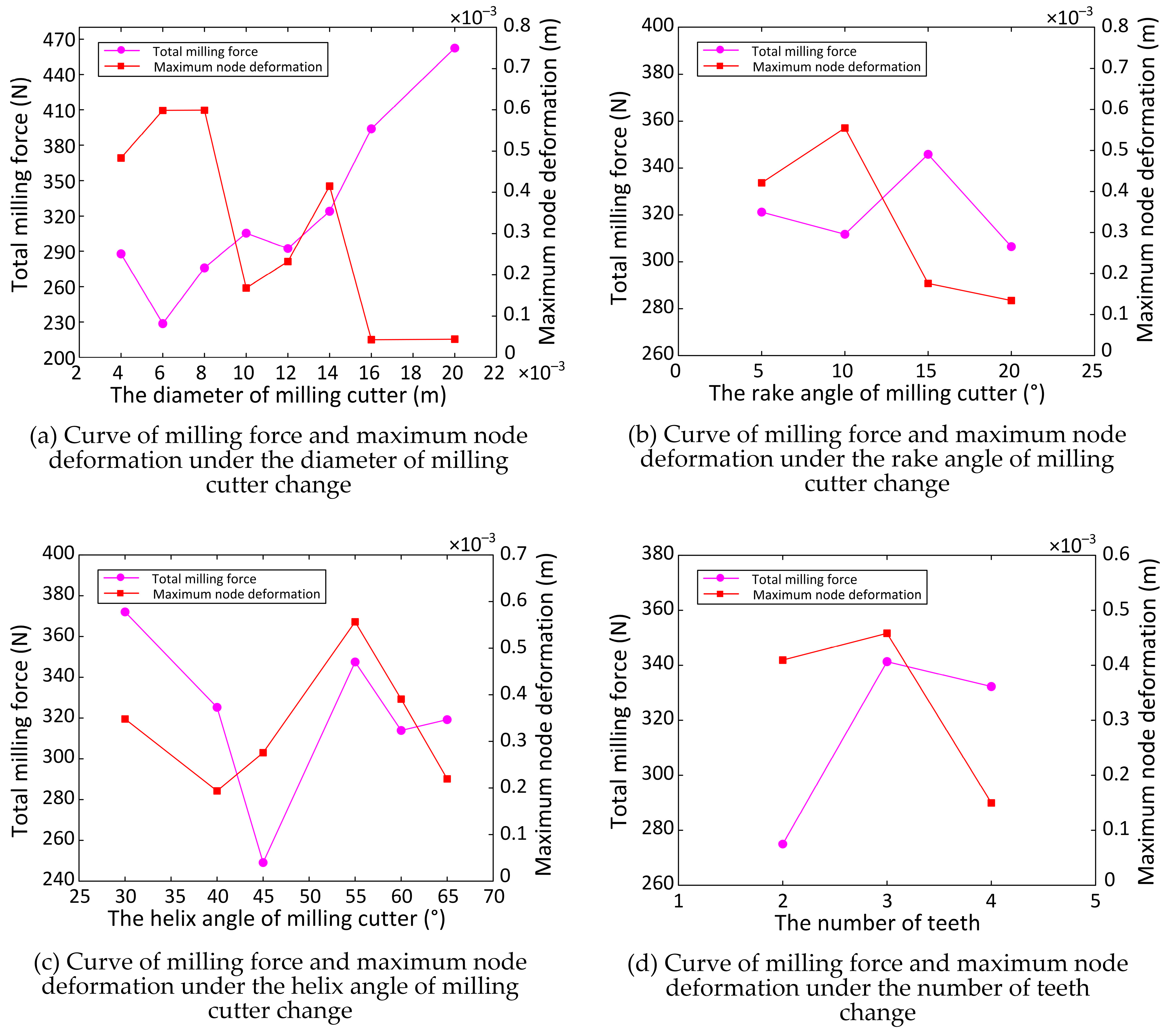
3.5. The Influence of Tool Geometry Parameters on the Milling Force and Maximum Node Deformation
4. Milling Empirical Modeling
4.1. Milling Empirical Formula Fitting
4.2. Milling Empirical Formula Validation
5. Conclusions
- The finite element simulation software ABAQUS v6.16 is used to realize the finite element simulation of milling of thin-walled titanium alloy parts with milling cutters, and the orthogonal experimental design method is used to obtain the milling force and maximum node deformation under various combinations of machining parameters. Given that the data obtained from the finite element simulation software ABAQUS v6.16 are valid, these obtained simulated results can serve as the fundamental data for further optimization of milling parameters;
- In this paper, the optimal parameters obtained from the orthogonal experiment are used in the finite element simulation software ABAQUS v6.16 for finite element simulations. The results indicate that there is a small error between the minimum value of the milling force and the maximum node deformation obtained by the orthogonal experiment and the finite element stimulated results with the optimal parameter combination, proving the reliability of the orthogonal experiment. Based on the finite element simulation results, the empirical functions of milling force and maximum node deformation are obtained by fitting the data in the data-processing software MATLAB R2019a v9.6.0. Some different combinations of process parameters are randomly selected to conduct a validation; the calculated empirical milling forces and maximum node deformations are consistent with the finite element simulated results, showing the feasibility of the established empirical model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ge, M.J.; Shan, G.F.; Yu, J.; Sun, Y.S.; Qin, X.T. Experimental Research on Milling Force Model of Titanium Alloy Thin Wall Workpiece. Tool Eng. 2015, 49, 44–47. (In Chinese) [Google Scholar]
- Hu, M.M.; Zhang, Y.; Li, Z.S.; Yuan, S.W. Modeling and experimental study on the milling force of Titanium Alloy TC4. Mach. Manuf. 2016, 54, 58–61. (In Chinese) [Google Scholar]
- Tang, M. Modeling and simulation analysis of TC4 titanium alloy milling force based on fuzzy neural network. China Met. Equip. Manuf. Technol. 2021, 56, 96–99. (In Chinese) [Google Scholar]
- Qian, L.L. Deformation Prediction and Process Analysis for Titanium Alloy Thin-Walled Workpiece. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2013. (In Chinese). [Google Scholar]
- Pan, H.L. Deflection Prediction and Control in Milling of Thin-Wall Titanium Alloy Components. Master’s Thesis, Shandong University, Jinan, China, 2016. (In Chinese). [Google Scholar]
- Gao, X.; Cheng, X.; Ling, S.; Zheng, G.; Li, Y.; Liu, H. Research on optimization of micro-milling process for curved thin wall structure. Precis. Eng 2022, 73, 296–312. [Google Scholar] [CrossRef]
- Yan, J.H.; Li, L. Multi-objective optimization of milling parameters the trade-offs between energy, production rate and cutting quality. J. Clean. Prod. 2013, 52, 462–471. [Google Scholar] [CrossRef]
- Li, Z.S.; Shi, Y.Y.; Xin, H.M.; Zhao, T.; Yang, C. Technological Parameter Optimization of Disc-Milling Grooving of Titanium Alloy Based on Grey Correlation Degree. J. Northwestern Polytech. Univ. 2018, 36, 139–148. [Google Scholar] [CrossRef]
- Doriana, M.; Addona, D.; Roberto, T. Genetic algorithm-based optimization of cutting parameters in turning processes. Procedia CIRP 2013, 7, 323–328. [Google Scholar]
- Shen, Z.H. Finite Element Simulation and Cutting Parameters Optimization of Milling Deformation for Titanium Alloy Thin-Walled Workpiece. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2009. (In Chinese). [Google Scholar]
- Yue, C.X.; Hu, D.S.; Liu, X.L.; Liu, X.; Chen, Z.T.; Lin, Z. Milling Parameters Optimization of Titanium Alloy Thin-walled Parts Based on Finite Element Simulation. Tool Eng. 2021, 55, 53–60. [Google Scholar]
- Daniyan, I.; Tlhabadira, K.; Mpofu, K.; Adeodu, A. Investigating the geometrical effects of cutting tool on the surface roughness of Titanium Alloy (Ti6Al4V) during milling operation. Procedia CIRP 2021, 99, 157–164. [Google Scholar] [CrossRef]
- Hu, X.; Qiao, H.; Yang, M.; Zhang, Y. Research on Milling Characteristics of Titanium Alloy TC4 with Variable Helical End Milling Cutter. Machines 2022, 10, 537. [Google Scholar] [CrossRef]
- Yue, C.X.; Zhang, J.T.; Liu, X.L.; Chen, Z.T.; Steven, Y.; Wang, L. Research progress on machining deformation of thin-walled parts in milling process. Acta Aeronaut. Astronaut. Sin. 2022, 43, 106–131. (In Chinese) [Google Scholar]
- Sun, Y.J. Parametric Modeling of Milling Titanium Alloy and Prediction of Tool Wear State. Master’s Thesis, Shandong University, Jinan, China, 2014. (In Chinese). [Google Scholar]
- Wang, L.T. Study on Residual Stresses and Distortion Theory of Aeronautica Frame Structure in the Milling. Master’s Thesis, Zhejiang University, Hangzhou, China, 2003. (In Chinese). [Google Scholar]
- Ge, M.J.; Du, Y.B.; Li, B.; Wang, M.; Ma, Y.Y. Milling lest of Titanium Alloy Thin-Walled Parts and Related Milling Force Model. Mech. Eng. Autom. 2018, 5, 136–138. (In Chinese) [Google Scholar]
- Li, T.; Gu, L.Z. Key Techniques of Finite Element Simulation in Metal Cutting Process and Some Considerations. Tool Eng. 2008, 42, 14–18. [Google Scholar]
- Zhang, Y.; Outeiro, J.C.; Mabrouki, T. On the selection of Johnson-Cook constitutive model parameters for Ti-6Al-4 V using three types of numerical models of orthogonal cutting. Procedia CIRP 2015, 31, 112–117. [Google Scholar] [CrossRef]
- Ma, T. Finite Element Simulation Analysis and Machining Process Optimization of TC4 Alloy Thin-Walled Parts Milling. Master’s Thesis, Tiangong University, Tianjin, China, 2018. (In Chinese). [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 2016, 21, 31–48. [Google Scholar] [CrossRef]
- Han, T.X.; Zeng, X.G.; Sheng, Y.; Chen, J.; Chen, H.Y. Study and Application of Dynamic Constitutive Relation for Titanium Alloy. Adv. Titan. Ind. 2016, 33, 17–21. (In Chinese) [Google Scholar]
- Yue, C.X.; Liu, X.; He, G.H.; Li, L.X. Finite Element Simulation Analysis of Thin-Walled Parts Milling Process of Titanium Alloy. Aerosp. Manuf. Technol. 2019, 62, 60–66. (In Chinese) [Google Scholar]
- Hu, Q.W.; Qiao, L.H.; Zhang, H.W. Optimization of Thin-walled Part Milling Parameters Based on Finite Element and Orthogonal Dominance Analysis. J. Mech. Eng. 2013, 49, 176–184. (In Chinese) [Google Scholar] [CrossRef]
- Liu, R.J.; Zhang, Y.W.; Wen, C.W.; Tang, J. Study on the design and analysis methods of orthogonal experiment. Exp. Technol. Manag. 2010, 27, 52–55. (In Chinese) [Google Scholar]




| Material | A (MPa) | B (MPa) | n | c | m |
|---|---|---|---|---|---|
| TC4 | 861 | 331 | 0.34 | 0.03 | 0.8 |
| Materials | d1 | d2 | d3 | d4 | d5 |
|---|---|---|---|---|---|
| TC4 | −0.09 | 0.27 | −0.48 | 0.014 | 3.87 |
| Orthogonal Factors | Orthogonal Levels | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Spindle speed n (r/min) | 2000 | 2400 | 2800 | 3200 | 3600 | 4000 | 4400 | 4800 |
| Feed rate per tooth f (mm/z) | 0.04 | 0.06 | 0.08 | 0.10 | 0.12 | 0.14 | 0.16 | 0.18 |
| Milling depth ap (mm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Milling width ae (mm) | 1 | 1.3 | 1.6 | 1.9 | 2.2 | 2.5 | 2.8 | 3 |
| Diameter of milling cutter d (mm) | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 20 |
| Rake angle of milling cutter γ (°) | 5 | 10 | 15 | 20 | ||||
| Tilt angle of milling cutter λ (°) | 30 | 40 | 45 | 55 | 60 | 65 | ||
| Number of teeth z | 4 | 3 | 2 | |||||
| Experiment Serial Number | Orthogonal Factors | |||||||
|---|---|---|---|---|---|---|---|---|
| Spindle Speed n (r/min) | Feed Rate Per Tooth f (mm/z) | Milling Depth ap (mm) | Milling Width ae (mm) | Diameter of Milling Cutter d (mm) | Rake Angle of Milling Cutter γ (°) | Tilt Angle of Milling Cutter λ (°) | Number of Teeth z | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 3 | 4 | 5 | 2 | 1 | 2 |
| 3 | 1 | 3 | 5 | 7 | 6 | 4 | 2 | 1 |
| 4 | 1 | 4 | 7 | 6 | 2 | 3 | 1 | 3 |
| 5 | 1 | 5 | 6 | 2 | 8 | 4 | 3 | 1 |
| 6 | 1 | 6 | 8 | 3 | 4 | 3 | 5 | 2 |
| 7 | 1 | 7 | 2 | 8 | 3 | 1 | 4 | 2 |
| 8 | 1 | 8 | 4 | 5 | 7 | 2 | 6 | 3 |
| 9 | 2 | 1 | 4 | 3 | 6 | 1 | 2 | 1 |
| 10 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 11 | 2 | 3 | 8 | 5 | 1 | 4 | 2 | 3 |
| 12 | 2 | 4 | 6 | 8 | 5 | 3 | 1 | 3 |
| 13 | 2 | 5 | 7 | 4 | 3 | 4 | 6 | 1 |
| 14 | 2 | 6 | 5 | 1 | 7 | 3 | 4 | 2 |
| 15 | 2 | 7 | 3 | 6 | 8 | 1 | 5 | 2 |
| 16 | 2 | 8 | 1 | 7 | 4 | 2 | 3 | 1 |
| 17 | 3 | 1 | 7 | 5 | 8 | 2 | 4 | 2 |
| 18 | 3 | 2 | 5 | 8 | 4 | 1 | 6 | 1 |
| 19 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 20 | 3 | 4 | 1 | 2 | 7 | 4 | 5 | 1 |
| 21 | 3 | 5 | 4 | 6 | 1 | 3 | 2 | 2 |
| 22 | 3 | 6 | 2 | 7 | 5 | 4 | 3 | 1 |
| 23 | 3 | 7 | 8 | 4 | 6 | 2 | 1 | 2 |
| 24 | 3 | 8 | 6 | 1 | 2 | 1 | 3 | 3 |
| 25 | 4 | 1 | 6 | 7 | 3 | 2 | 5 | 2 |
| 26 | 4 | 2 | 8 | 6 | 7 | 1 | 3 | 1 |
| 27 | 4 | 3 | 2 | 1 | 8 | 3 | 6 | 3 |
| 28 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 1 |
| 29 | 4 | 5 | 1 | 8 | 6 | 3 | 4 | 2 |
| 30 | 4 | 6 | 3 | 5 | 2 | 4 | 1 | 1 |
| 31 | 4 | 7 | 5 | 2 | 1 | 2 | 4 | 3 |
| 32 | 4 | 8 | 7 | 3 | 5 | 1 | 2 | 2 |
| 33 | 5 | 1 | 2 | 6 | 4 | 4 | 5 | 3 |
| 34 | 5 | 2 | 4 | 7 | 8 | 3 | 1 | 3 |
| 35 | 5 | 3 | 6 | 4 | 7 | 1 | 5 | 2 |
| 36 | 5 | 4 | 8 | 1 | 3 | 2 | 2 | 1 |
| 37 | 5 | 5 | 5 | 5 | 5 | 1 | 5 | 1 |
| 38 | 5 | 6 | 7 | 8 | 1 | 2 | 3 | 2 |
| 39 | 5 | 7 | 1 | 3 | 2 | 4 | 6 | 2 |
| 40 | 5 | 8 | 3 | 2 | 6 | 3 | 4 | 1 |
| 41 | 6 | 1 | 3 | 8 | 7 | 4 | 2 | 2 |
| 42 | 6 | 2 | 1 | 5 | 3 | 3 | 6 | 3 |
| 43 | 6 | 3 | 7 | 2 | 4 | 1 | 1 | 2 |
| 44 | 6 | 4 | 5 | 3 | 8 | 2 | 6 | 1 |
| 45 | 6 | 5 | 8 | 7 | 2 | 1 | 4 | 3 |
| 46 | 6 | 6 | 6 | 6 | 6 | 2 | 6 | 1 |
| 47 | 6 | 7 | 4 | 1 | 5 | 4 | 3 | 2 |
| 48 | 6 | 8 | 2 | 4 | 1 | 3 | 5 | 1 |
| 49 | 7 | 1 | 8 | 2 | 5 | 3 | 6 | 1 |
| 50 | 7 | 2 | 6 | 3 | 1 | 4 | 4 | 3 |
| 51 | 7 | 3 | 4 | 8 | 2 | 2 | 5 | 1 |
| 52 | 7 | 4 | 2 | 5 | 6 | 1 | 3 | 2 |
| 53 | 7 | 5 | 3 | 1 | 4 | 2 | 3 | 2 |
| 54 | 7 | 6 | 1 | 4 | 8 | 1 | 2 | 3 |
| 55 | 7 | 7 | 7 | 7 | 7 | 3 | 1 | 1 |
| 56 | 7 | 8 | 5 | 6 | 3 | 4 | 1 | 2 |
| 57 | 8 | 1 | 5 | 4 | 2 | 3 | 3 | 3 |
| 58 | 8 | 2 | 7 | 1 | 6 | 4 | 5 | 3 |
| 59 | 8 | 3 | 1 | 6 | 5 | 2 | 4 | 1 |
| 60 | 8 | 4 | 3 | 7 | 1 | 1 | 6 | 2 |
| 61 | 8 | 5 | 2 | 3 | 7 | 2 | 1 | 2 |
| 62 | 8 | 6 | 4 | 2 | 3 | 1 | 2 | 1 |
| 63 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 64 | 8 | 8 | 8 | 8 | 8 | 4 | 4 | 2 |
| Total Length | Blade Length | Relief Angle | Rake Angle | Tilt Angle | Diameter | Number of Teeth |
|---|---|---|---|---|---|---|
| 60 mm | 20 mm | 12° | 5~20° | 30~65° | 4~20 mm | 2/3/4 |
| Orthogonal Factors | Spindle Speed n (r/min) | Feed Rate per Tooth f (mm/z) | Milling Depth ap (mm) | Milling Width ae (mm) | Diameter of Milling Cutter d (mm) | Rake Angle of Milling Cutter γ (°) | Tilt Angle of Milling Cutter λ (°) | Number of Teeth z |
|---|---|---|---|---|---|---|---|---|
| k1 | 230.856 | 268.704 | 257.297 | 236.255 | 287.797 | 321.219 | 372.065 | 332.252 |
| k2 | 302.557 | 270.698 | 301.482 | 271.599 | 228.708 | 311.754 | 325.272 | 341.314 |
| k3 | 302.997 | 296.751 | 250.593 | 314.861 | 275.924 | 345.877 | 249.115 | 274.982 |
| k4 | 290.700 | 301.589 | 280.414 | 327.837 | 305.396 | 306.481 | 347.522 | |
| k5 | 350.721 | 304.172 | 302.316 | 323.865 | 292.368 | 313.923 | ||
| k6 | 309.389 | 345.217 | 279.587 | 339.793 | 324.056 | 319.238 | ||
| k7 | 385.118 | 375.316 | 448.158 | 352.332 | 393.986 | |||
| k8 | 398.326 | 408.215 | 450.817 | 404.121 | 462.427 | |||
| R | 167.471 | 139.511 | 200.224 | 167.867 | 233.719 | 39.396 | 122.950 | 66.332 |
| Orthogonal Factors | Spindle Speed n (r/min) | Feed Rate per Tooth f (mm/z) | Milling Depth ap (mm) | Milling Width ae (mm) | Diameter of Milling Cutter d (mm) | Rake Angle of Milling Cutter γ (°) | Tilt Angle of Milling Cutter λ (°) | Number of Teeth z |
|---|---|---|---|---|---|---|---|---|
| k1 | 0.100 | 0.633 | 0.0323 | 0.021 | 0.484 | 0.421 | 0.348 | 0.150 |
| k2 | 0.382 | 0.195 | 0.043 | 0.026 | 0.599 | 0.555 | 0.194 | 0.458 |
| k3 | 0.542 | 0.104 | 0.068 | 0.092 | 0.599 | 0.176 | 0.276 | 0.409 |
| k4 | 0.499 | 0.192 | 0.205 | 0.385 | 0.168 | 0.134 | 0.557 | |
| k5 | 0.366 | 0.871 | 0.175 | 0.111 | 0.232 | 0.391 | ||
| k6 | 0.648 | 0.369 | 0.575 | 0.166 | 0.415 | 0.219 | ||
| k7 | 0.054 | 0.294 | 0.534 | 1.144 | 0.043 | |||
| k8 | 0.040 | 0.054 | 0.869 | 0.605 | 0.044 | |||
| R | 0.609 | 0.817 | 0.837 | 1.122 | 0.556 | 0.421 | 0.363 | 0.308 |
| Number | Spindle Speed n (r/min) | Feed Rate per Tooth f (mm/z) | Milling Depth ap (mm) | Milling Width ae (mm) | Diameter of Milling Cutter d (mm) | Rake Angle of Milling Cutter γ (°) | Tilt Angle of Milling Cutter λ (°) | Number of Teeth z | Simulated Value (N) | Calculated Value (N) | Difference Value (N) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3200 | 0.18 | 7 | 1.6 | 12 | 5 | 40 | 3 | 422.01 | 470.19 | −48.18 |
| 2 | 4000 | 0.08 | 7 | 1.3 | 10 | 5 | 30 | 3 | 367.23 | 381.04 | −13.81 |
| 3 | 4400 | 0.04 | 8 | 1.3 | 12 | 15 | 65 | 4 | 357.81 | 391.62 | −33.81 |
| 4 | 4400 | 0.08 | 4 | 3 | 6 | 10 | 60 | 4 | 260.91 | 278.49 | −17.58 |
| 5 | 4800 | 0.10 | 3 | 2.8 | 4 | 5 | 65 | 3 | 239.06 | 195.67 | 43.39 |
| Number | Spindle Speed n (r/min) | Feed Rate per Tooth f (mm/z) | Milling Depth ap (mm) | Milling Width ae (mm) | Diameter of Milling Cutter d (mm) | Rake Angle of Milling Cutter γ (°) | Tilt Angle of Milling Cutter λ (°) | Number of Teeth z | Simulated Value (mm) | Calculated Value (mm) | Difference Value (mm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3200 | 0.18 | 7 | 1.6 | 12 | 5 | 40 | 3 | 0.069 | 0.060 | 0.009 |
| 2 | 4000 | 0.08 | 7 | 1.3 | 10 | 5 | 30 | 3 | 0.055 | 0.042 | 0.013 |
| 3 | 4400 | 0.04 | 8 | 1.3 | 12 | 15 | 65 | 4 | 0.061 | 0.047 | 0.014 |
| 4 | 4400 | 0.08 | 4 | 3 | 6 | 10 | 60 | 4 | 0.199 | 0.215 | −0.016 |
| 5 | 4800 | 0.10 | 3 | 2.8 | 4 | 5 | 65 | 3 | 0.108 | 0.132 | −0.024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Deng, C.; Chen, X.; Zhai, H. Analysis and Optimization of Milling Deformations of TC4 Alloy Thin-Walled Parts Based on Finite Element Simulations. Machines 2023, 11, 628. https://doi.org/10.3390/machines11060628
Tang J, Deng C, Chen X, Zhai H. Analysis and Optimization of Milling Deformations of TC4 Alloy Thin-Walled Parts Based on Finite Element Simulations. Machines. 2023; 11(6):628. https://doi.org/10.3390/machines11060628
Chicago/Turabian StyleTang, Jiaquan, Congying Deng, Xuhui Chen, and Haiyan Zhai. 2023. "Analysis and Optimization of Milling Deformations of TC4 Alloy Thin-Walled Parts Based on Finite Element Simulations" Machines 11, no. 6: 628. https://doi.org/10.3390/machines11060628
APA StyleTang, J., Deng, C., Chen, X., & Zhai, H. (2023). Analysis and Optimization of Milling Deformations of TC4 Alloy Thin-Walled Parts Based on Finite Element Simulations. Machines, 11(6), 628. https://doi.org/10.3390/machines11060628






