Research on Multiphase Flow and Nozzle Wear in a High-Pressure Abrasive Water Jet Cutting Head
Abstract
1. Introduction
2. Methods
2.1. The Continuous Phase
2.2. The Disperse Phase
2.3. Distribution and Erosion of Particle Phase
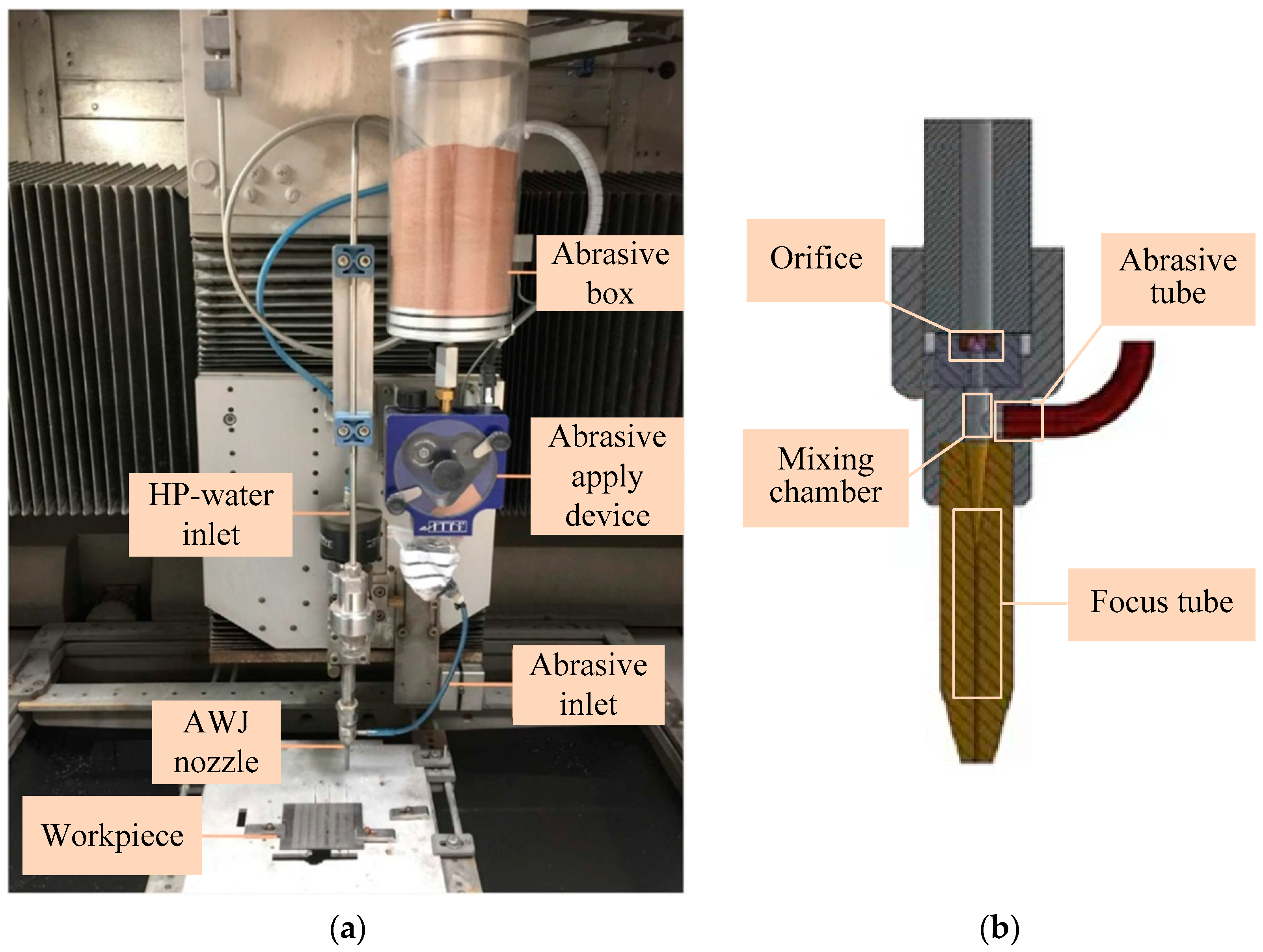
3. CFD Models and Boundary Conditions
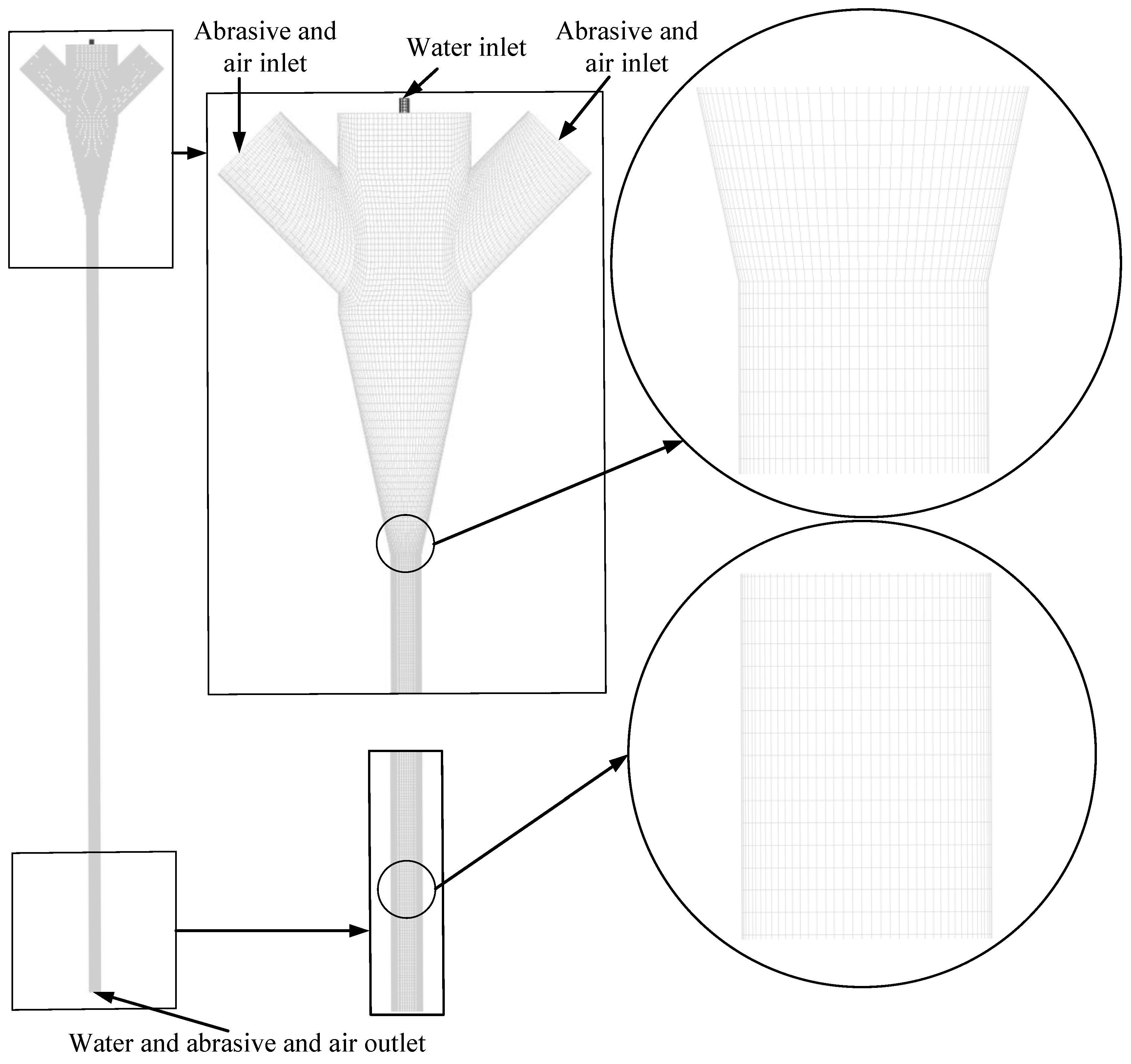
3.1. Geometry and Mesh
3.2. Boundary Conditions and Other Parameters
- The turbulent kinetic energy equation:
- The turbulent dissipation rate equation:
- Water is in a continuous phase and is incompressible.
- The sphericity and roundness of the abrasive are both 0.8 and the average size of the abrasive is 0.135 mm, with a diameter range of 0.1–0.16 mm. The diffusion coefficient is 5.9 and the abrasive mass flow rate is 0.007 g/s, with a density of 2600 kg/m3.
- There is no heat exchange between the particles and the water in the flow, and the temperature remains constant.
3.3. Mesh Independence Verification
4. Results and Discussion
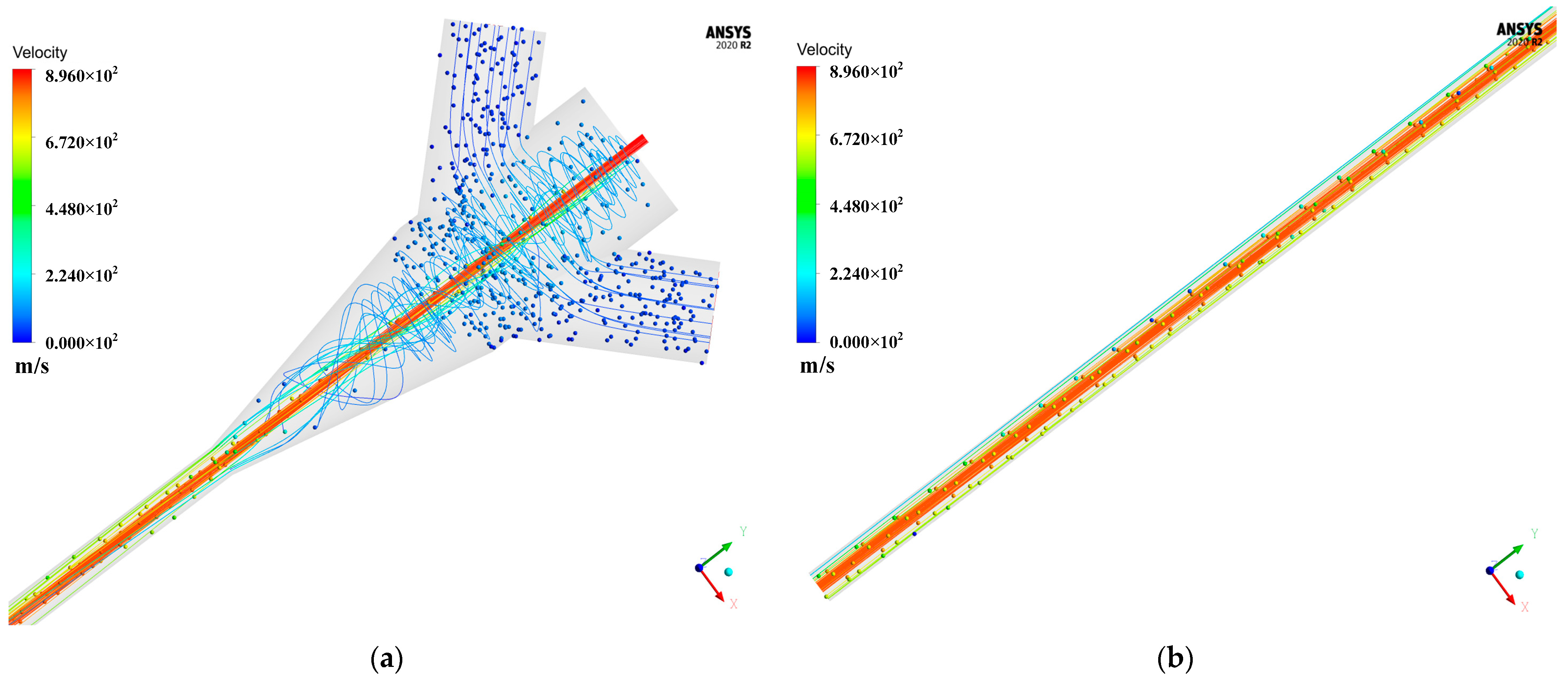
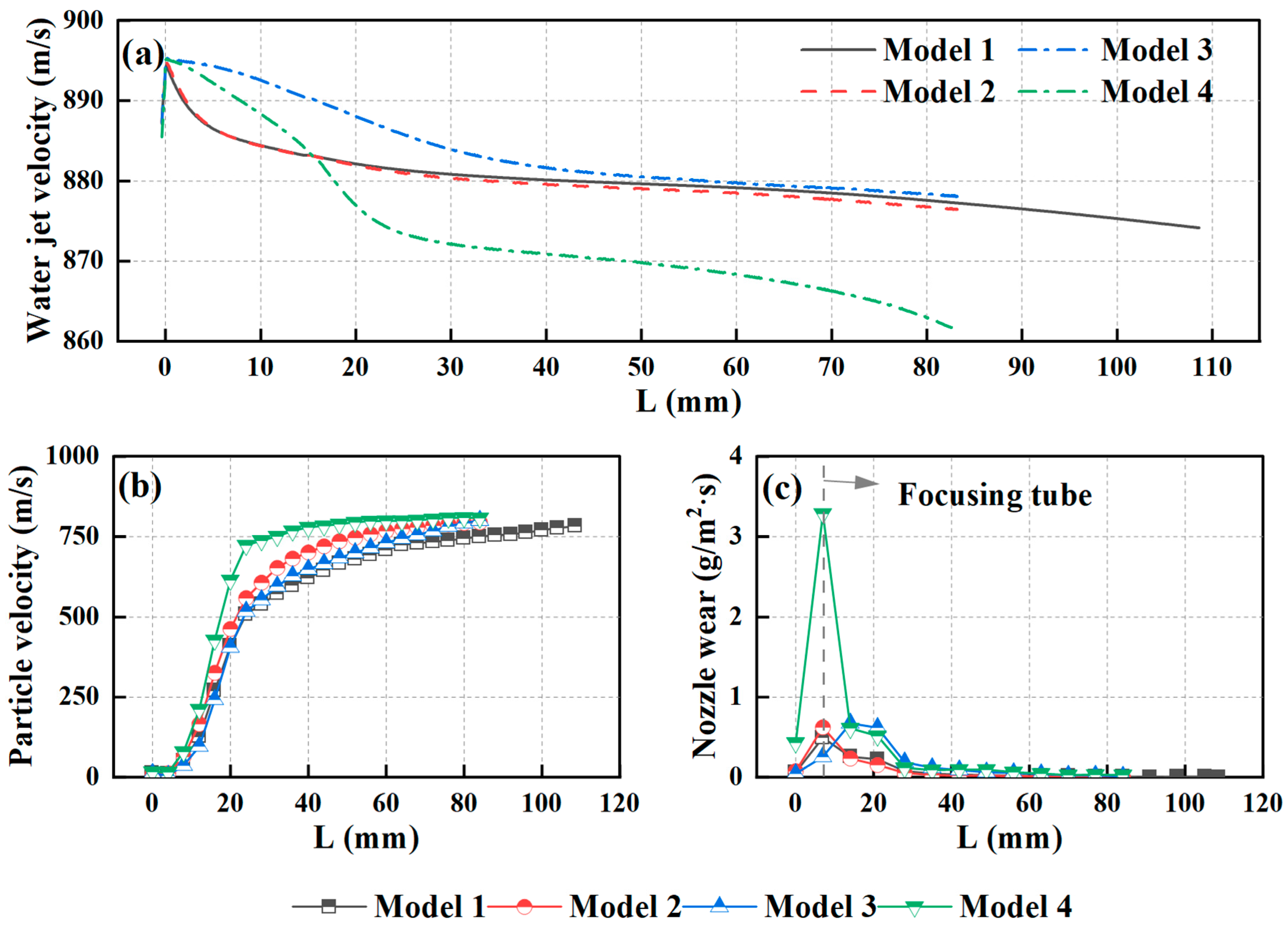
4.1. The Effect of Model Infrastructure on AWJ Performance
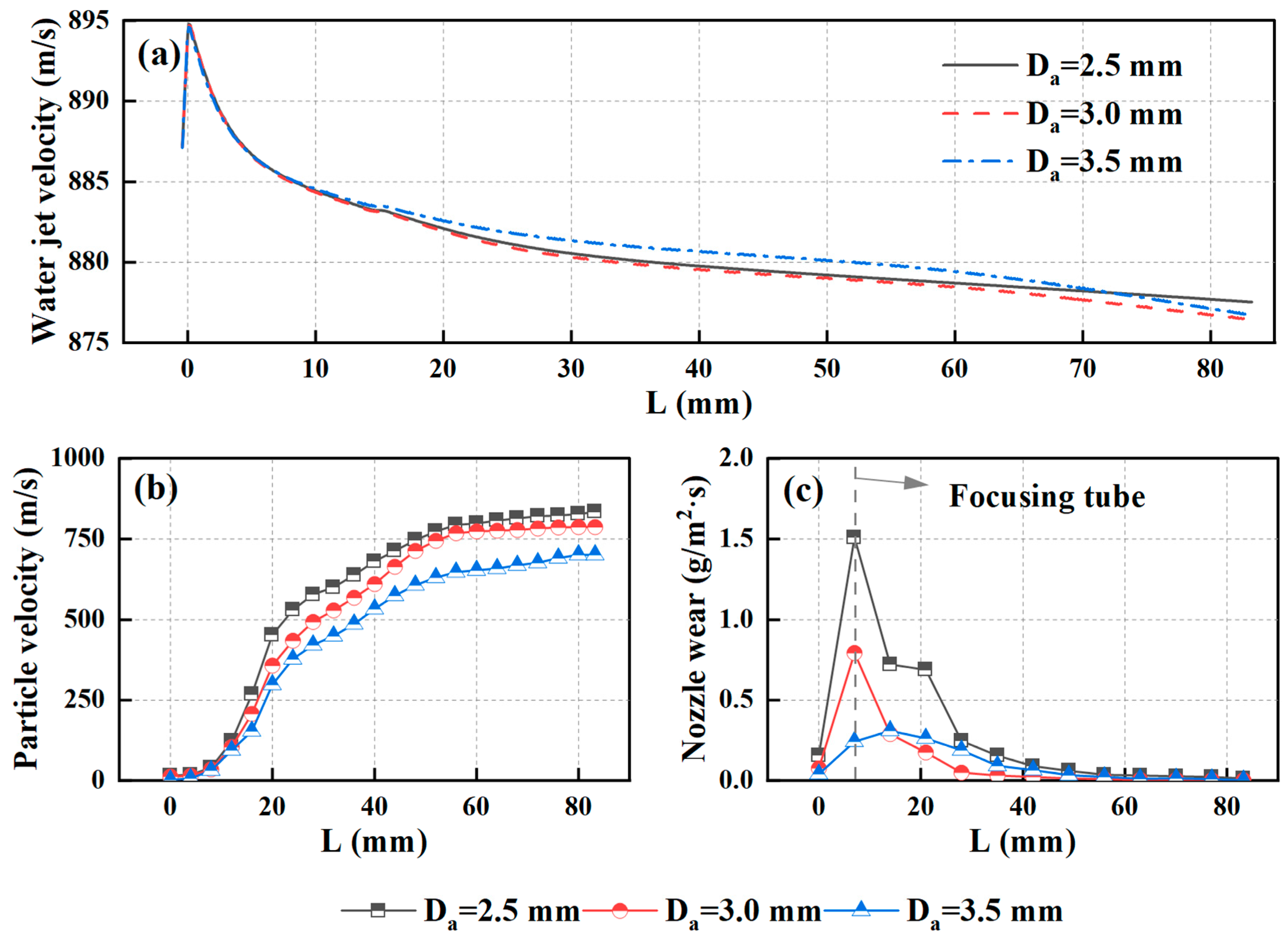
4.2. The Effect of Particle Inlet Size
4.3. The Effect of Mixing Chamber Diameter
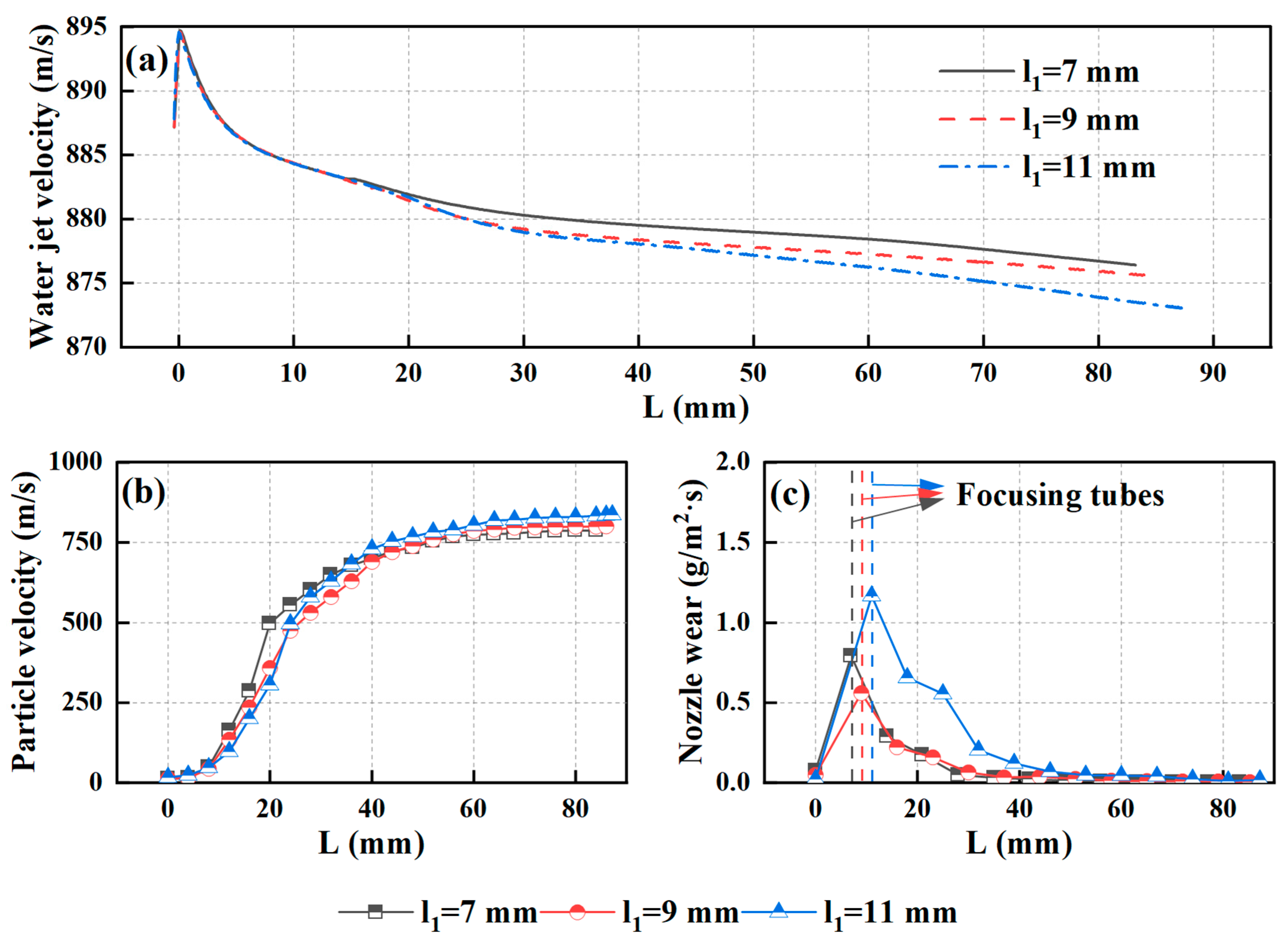
4.4. The Effect of Mixing Chamber Length
5. Conclusions
- The double abrasive tube model can avoid the phenomenon of one-sided wear in the cone cavity of the focusing tube, further reducing the wear on the focusing tube, and a reasonable nozzle model design can fully accelerate the abrasive, reducing the wear of the abrasive on the wall surface and achieving higher machining and erosion capabilities.
- The air inside the nozzle has tangential velocity, and an increase in the air volume flow rate will affect the velocity of the continuous phase (air, water). The tangential velocity of the air decreases along the direction of the flow field as the velocity of the continuous phase increases.
- The size of the abrasive inlet tube affects the initial velocity of the particles, and the outlet velocity of the particles is affected by the initial velocity. By using a smaller abrasive inlet tube size (Da = 2.5 mm), the final velocity of the particle phase can be increased by 16%.
- The size of the mixing chamber affects the velocity of the particles entering the focusing tube, with a smaller mixing chamber width resulting in a 6% lower outlet velocity of the particles compared to other models, while a larger mixing chamber length results in a 7% higher acceleration efficiency of the particles compared to other models.
- The lower the velocity of the abrasive inside the nozzle, the less wear on the model. The tangential velocity of the air and the circumferential velocity of the abrasive affect the wear inside the mixing chamber and the acceleration of the particles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gupta, K.; Gupta, M.K. Developments in nonconventional machining for sustainable production: A state-of-the-art review. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 4213–4232. [Google Scholar] [CrossRef]
- Hou, R.; Huang, C.; Zhu, H. Numerical simulation of multiphase flow field in abrasive waterjet machining. Int. J. Abras. Technol. 2013, 6, 40–57. [Google Scholar] [CrossRef]
- Patel, D.; Tandon, P. Experimental investigations of thermally enhanced abrasive water jet machining of hard-to-machine metals. CIRP J. Manuf. Sci. Technol. 2015, 10, 92–101. [Google Scholar] [CrossRef]
- Henning, A.; Lo, M.; Schubert, E.; Miles, P. Effect of Particle Fragmentation on Cutting Performance in Abrasive Waterjets. In Proceedings of the Advances in Water Jetting, Selected Papers from the International Conference on Water Jet 2019-Research, Development, Applications, Čeladná, Czech Republic, 20–22 November 2019; Springer International Publishing: Cham, Switzerland, 2021; pp. 3–14. [Google Scholar]
- Hashish, M. Cutting with abrasive water jets. Mech. Eng. 1984, 106, 60–69. [Google Scholar]
- Momber, A.W. Energy transfer during the mixing of air and solid particles into a high-speed waterjet: An impact-force study. Exp. Therm. Fluid Sci. 2001, 25, 31–41. [Google Scholar] [CrossRef]
- Axinte, D.A.; Srinivasu, D.S.; Kong, M.C.; Butler-Smith, P.W. Abrasive waterjet cutting of polycrystalline diamond: A preliminary investigation. Int. J. Mach. Tools Manuf. 2009, 49, 797–803. [Google Scholar] [CrossRef]
- Wang, J.; Shanmugam, D.K. Cutting meat with bone using an ultrahigh pressure abrasive waterjet. Meat Sci. 2009, 81, 671–677. [Google Scholar] [CrossRef] [PubMed]
- Alberdi, A.; Rivero, A.; López de Lacalle, L.N.; Etxeberria, I.; Suárez, A. Effect of process parameter on the kerf geometry in abrasive water jet milling. Int. J. Adv. Manuf. Technol. 2010, 51, 467–480. [Google Scholar] [CrossRef]
- Alberdi, A.; Rivero, A.; López de Lacalle, L.N. Experimental Study of the Slot Overlapping and Tool Path Variation Effect in Abrasive Waterjet Milling. J. Manuf. Sci. Eng. 2011, 133, 034502. [Google Scholar] [CrossRef]
- Folkes, J. Waterjet—An innovative tool for manufacturing. J. Mater. Process. Technol. 2009, 209, 6181–6189. [Google Scholar] [CrossRef]
- Bhowmik, S.; Jagadish; Ray, A. Abrasive Water Jet Machining of Composite Materials. In Advanced Manufacturing Technologies: Modern Machining, Advanced Joining, Sustainable Manufacturing; Gupta, K., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 77–97. [Google Scholar]
- Bhattacharyya, B.; Doloi, B. Modern Machining Technology: Advanced, Hybrid, Micro Machining and Super Finishing Technology; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Wang, J. Particle velocity models for ultra-high pressure abrasive waterjets. J. Mater. Process. Technol. 2009, 209, 4573–4577. [Google Scholar] [CrossRef]
- Qiang, Z.; Wu, M.; Miao, X.; Sawhney, R. CFD research on particle movement and nozzle wear in the abrasive water jet cutting head. Int. J. Adv. Manuf. Technol. 2018, 95, 4091–4100. [Google Scholar] [CrossRef]
- Momber, A.W.; Kovacevic, R. Principles of Abrasive Water Jet Machining; Springer: London, UK, 2012. [Google Scholar]
- Long, X.; Ruan, X.; Liu, Q.; Chen, Z.; Xue, S.; Wu, Z. Numerical investigation on the internal flow and the particle movement in the abrasive waterjet nozzle. Powder Technol. 2017, 314, 635–640. [Google Scholar] [CrossRef]
- Nanduri, M.; Taggart, D.G.; Kim, T.J. A Study of Nozzle Wear in Abrasive Entrained Water Jetting Environment. J. Tribol. 1999, 122, 465–471. [Google Scholar] [CrossRef]
- Hashish, M. Observations of Wear of Abrasive-Waterjet Nozzle Materials. J. Tribol. 1994, 116, 439–444. [Google Scholar] [CrossRef]
- Nanduri, M.; Taggart, D.G.; Kim, T.J. The effects of system and geometric parameters on abrasive water jet nozzle wear. Int. J. Mach. Tools Manuf. 2002, 42, 615–623. [Google Scholar] [CrossRef]
- Liu, H.; Wang, J.; Brown, R.J.; Kelson, N. Computational Fluid Dynamics (CFD) Simulation of Ultrahigh Velocity Abrasive Waterjet. Key Eng. Mater. 2002, 233–236, 477–482. [Google Scholar]
- Liu, H.; Wang, J.; Kelson, N.; Brown, R.J. A study of abrasive waterjet characteristics by CFD simulation. J. Mater. Process. Technol. 2004, 153–154, 488–493. [Google Scholar] [CrossRef]
- Prisco, U.; D’Onofrio, M.C. Three-dimensional CFD simulation of two-phase flow inside the abrasive water jet cutting head. Int. J. Comput. Methods Eng. Sci. Mech. 2008, 9, 300–319. [Google Scholar] [CrossRef]
- Yang, M.; Wang, Y.; Kang, C.; Feng, Y. Multiphase flow and wear in the cutting head of ultra-high pressure abrasive water jet. Chin. J. Mech. Eng. 2009, 22, 1. [Google Scholar] [CrossRef]
- Mostofa, M.G.; Kil, K.Y.; Hwan, A.J. Computational fluid analysis of abrasive waterjet cutting head. J. Mech. Sci. Technol. 2010, 24, 249–252. [Google Scholar] [CrossRef]
- Narayanan, C.; Balz, R.; Weiss, D.A.; Heiniger, K.C. Modelling of abrasive particle energy in water jet machining. J. Mater. Process. Technol. 2013, 213, 2201–2210. [Google Scholar] [CrossRef]
- Basha, A.T.; Annoni, M.; Monno, M.; Inzoli, F. Investigation of the hydrodynamic characteristics of abrasive water jet cutting head. Int. J. Mach. Mach. Mater. 2013, 14, 105–122. [Google Scholar] [CrossRef]
- Pozzetti, G.; Peters, B. A numerical approach for the evaluation of particle-induced erosion in an abrasive waterjet focusing tube. Powder Technol. 2018, 333, 229–242. [Google Scholar] [CrossRef]
- Riha, Z.; Zelenak, M.; Soucek, K.; Hlavacek, A. Flow field analysis inside and at the outlet of the abrasive head. Materials 2021, 14, 3919. [Google Scholar] [CrossRef]
- Tazibt, A.; Parsy, F.; Abriak, N. Theoretical analysis of the particle acceleration process in abrasive water jet cutting. Comput. Mater. Sci. 1996, 5, 243–254. [Google Scholar] [CrossRef]
- Hashish, M. Inside AWJ nozzles. In Proceedings of the 12th WJTA Conference, Houston, TX, USA, 7 April 2003; pp. 17–19. [Google Scholar]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Kamarudin, N.H.; Prasada Rao, A.K.; Azhari, A. CFD Based Erosion Modelling of Abrasive Waterjet Nozzle using Discrete Phase Method. IOP Conf. Ser. Mater. Sci. Eng. 2016, 114, 012016. [Google Scholar] [CrossRef]
- Axinte, D.A.; Karpuschewski, B.; Kong, M.C.; Beaucamp, A.T.; Anwar, S.; Miller, D.; Petzel, M. High Energy Fluid Jet Machining (HEFJet-Mach): From scientific and technological advances to niche industrial applications. CIRP Ann. 2014, 63, 751–771. [Google Scholar] [CrossRef]
- Liu, D.; Huang, C.; Wang, J.; Zhu, H.; Yao, P.; Liu, Z. Modeling and optimization of operating parameters for abrasive waterjet turning alumina ceramics using response surface methodology combined with Box–Behnken design. Ceram. Int. 2014, 40, 7899–7908. [Google Scholar] [CrossRef]
- Hoogstrate, A.M.; Susuzlu, T.; Karpuschewski, B. High Performance Cutting with Abrasive Waterjets beyond 400 MPa. CIRP Ann. 2006, 55, 339–342. [Google Scholar] [CrossRef]
- Hoogstrate, A.M.; Karpuschewski, B.; van Luttervelt, C.A.; Kals, H.J.J. Modelling of high velocity, loose abrasive machining processes. CIRP Ann. 2002, 51, 263–266. [Google Scholar] [CrossRef]
- Wadell, H. Sphericity and Roundness of Rock Particles. J. Geol. 1933, 41, 310–331. [Google Scholar] [CrossRef]
- Lefebvre, A.H.; McDonell, V.G. Atomization and Sprays; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Soyama, H. Effect of nozzle geometry on a standard cavitation erosion test using a cavitating jet. Wear 2013, 297, 895–902. [Google Scholar] [CrossRef]
- Pătîrnac, I.; Ripeanu, R.G.; Laudacescu, E. Abrasive flow modelling through active parts water jet machine using CFD simulation. IOP Conf. Ser. Mater. Sci. Eng. 2020, 724, 012001. [Google Scholar] [CrossRef]
- Biswas, R.; Strawn, R.C. Tetrahedral and hexahedral mesh adaptation for CFD problems. Appl. Numer. Math. 1998, 26, 135–151. [Google Scholar] [CrossRef]
- Zapata-Cautillo, J.A.; Cholango-Gavilanes, A.I.; Nieto-Londoño, C.; Zapata-Benabithe, Z. Numerical and comparative study of the turbulence effect on elbows and bends for sanitary water distribution. Rev. Fac. De Ing. 2019, 28, 101–118. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Jia, P.; Liu, H.; Yun, F.; Li, Z.; Wang, L. Orthogonal Experimental Design Based Nozzle Geometry Optimization for the Underwater Abrasive Water Jet. Machines 2022, 10, 1243. [Google Scholar] [CrossRef]
- Xiong, P.; Chen, X.Y.; Sun, H.J.; Zhong, J.P.; Zhen, C.P. Effect of internal leakage on torque converter characteristics. Adv. Mech. Eng. 2020, 12, 1687814020959969. [Google Scholar] [CrossRef]
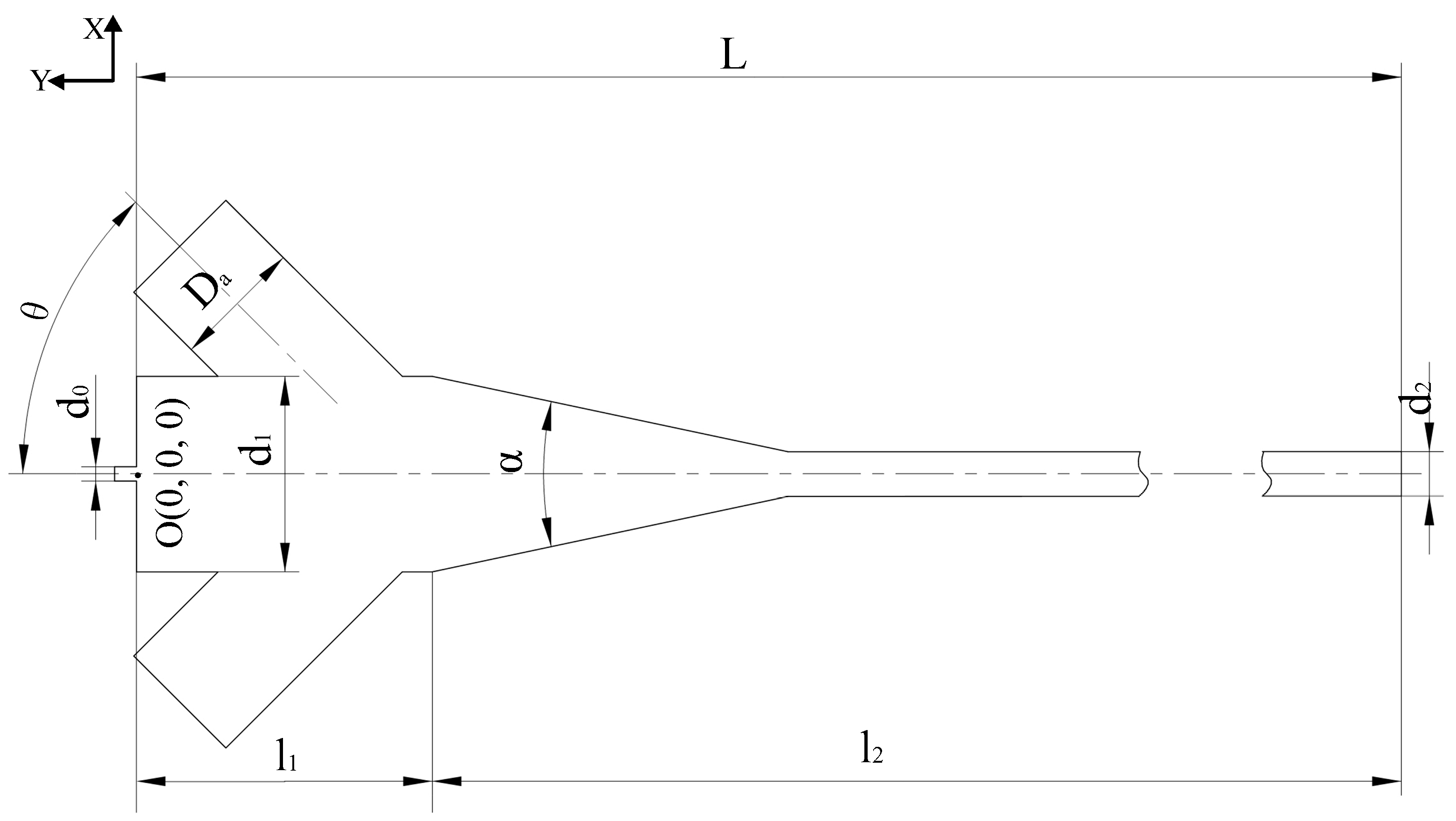

| Parameters | Values |
|---|---|
| Particle inlet angular θ (°) | 45 |
| Converging part angular α (°) | 24 |
| Orifice diameter d0 (mm) | 0.28, 0.33 |
| Mixing chamber diameter d1 (mm) | 4, 4.5, 5 |
| Focusing tube diameter d2 (mm) | 0.76, 1.02 |
| Abrasive inlet diameter Da (mm) | 2.5, 3, 3.5 |
| Mixing chamber length l1 (mm) | 7, 9, 11 |
| Focusing tube length l2 (mm) | 76.2, 101.6 |
| Boundary Conditions | Parameter Settings | Boundary Conditions | Parameter Settings |
|---|---|---|---|
| Fluid method | Unsteady | Discrete format | Second order upwind |
| Turbulence model | Realizable k–ε | Time step | 0.0001 s |
| Wall condition | No slip wall | Liquid density | 998.2 kg/m3 |
| Multiphase flow model | VOF model | Liquid viscosity | 0.001003 Pa·s |
| Calculation method | SIMPLE | Gas density | 1.225 kg/m3 |
| Operating pressure | 400 MPa | Gas viscosity | 1.7894 × 10−5 Pa·s |
| Operating Pressure (MPa) | Model 2 | Model 3 | ||
|---|---|---|---|---|
| Outlet Velocity (m/s) | Maximum Wear Rate (g/m2·s) | Outlet Velocity (m/s) | Maximum Wear Rate (g/m2·s) | |
| 200 | 618.07 | 0.0003 | 620.64 | 0.0009 |
| 250 | 692.04 | 0.0005 | 693.63 | 0.0010 |
| 300 | 759.13 | 0.0009 | 760.01 | 0.0021 |
| 350 | 818.95 | 0.0010 | 821.23 | 0.0035 |
| 400 | 874.31 | 0.0011 | 878.13 | 0.0045 |
| 450 | 925.81 | 0.0013 | 929.83 | 0.0060 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, X.; Fu, L.; Wu, L.; Zuo, W. Research on Multiphase Flow and Nozzle Wear in a High-Pressure Abrasive Water Jet Cutting Head. Machines 2023, 11, 614. https://doi.org/10.3390/machines11060614
Zou X, Fu L, Wu L, Zuo W. Research on Multiphase Flow and Nozzle Wear in a High-Pressure Abrasive Water Jet Cutting Head. Machines. 2023; 11(6):614. https://doi.org/10.3390/machines11060614
Chicago/Turabian StyleZou, Xiang, Liandong Fu, Lin Wu, and Wenhao Zuo. 2023. "Research on Multiphase Flow and Nozzle Wear in a High-Pressure Abrasive Water Jet Cutting Head" Machines 11, no. 6: 614. https://doi.org/10.3390/machines11060614
APA StyleZou, X., Fu, L., Wu, L., & Zuo, W. (2023). Research on Multiphase Flow and Nozzle Wear in a High-Pressure Abrasive Water Jet Cutting Head. Machines, 11(6), 614. https://doi.org/10.3390/machines11060614






