Influence of the Rotor Geometry on Efficiency and Torque Ripple of Switched Reluctance Motor Controlled by Optimized Torque Sharing Functions †
Abstract
1. Introduction
2. Torque Sharing Functions and Motor Geometry
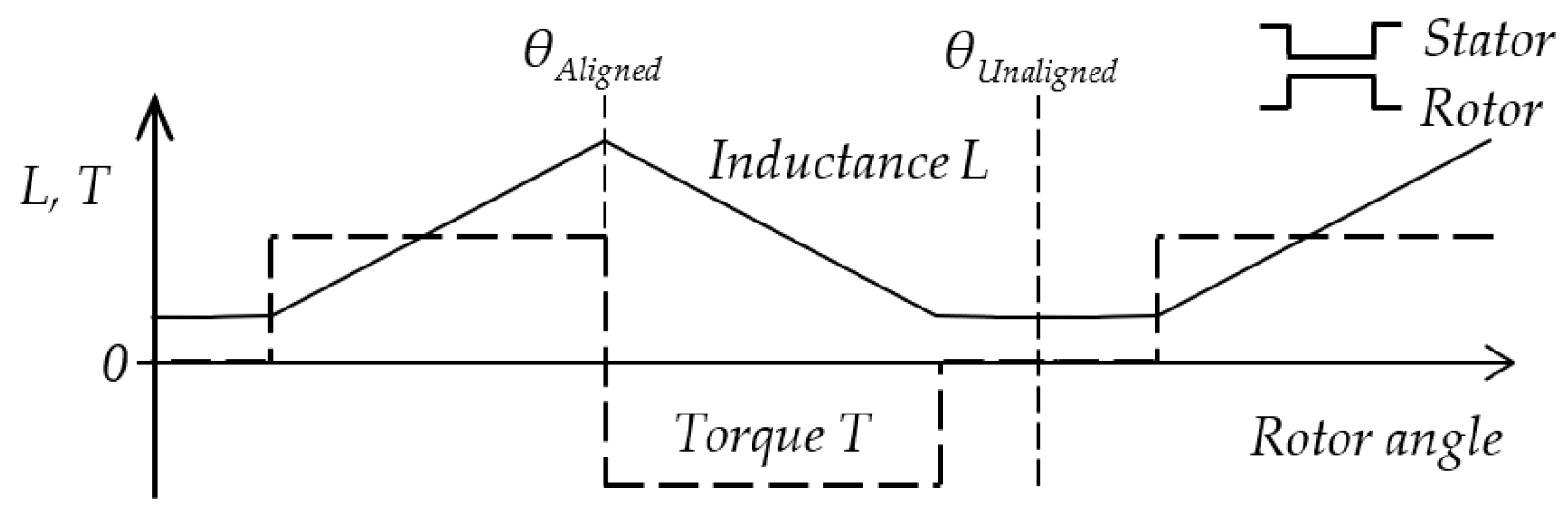
2.1. Reluctance Torque
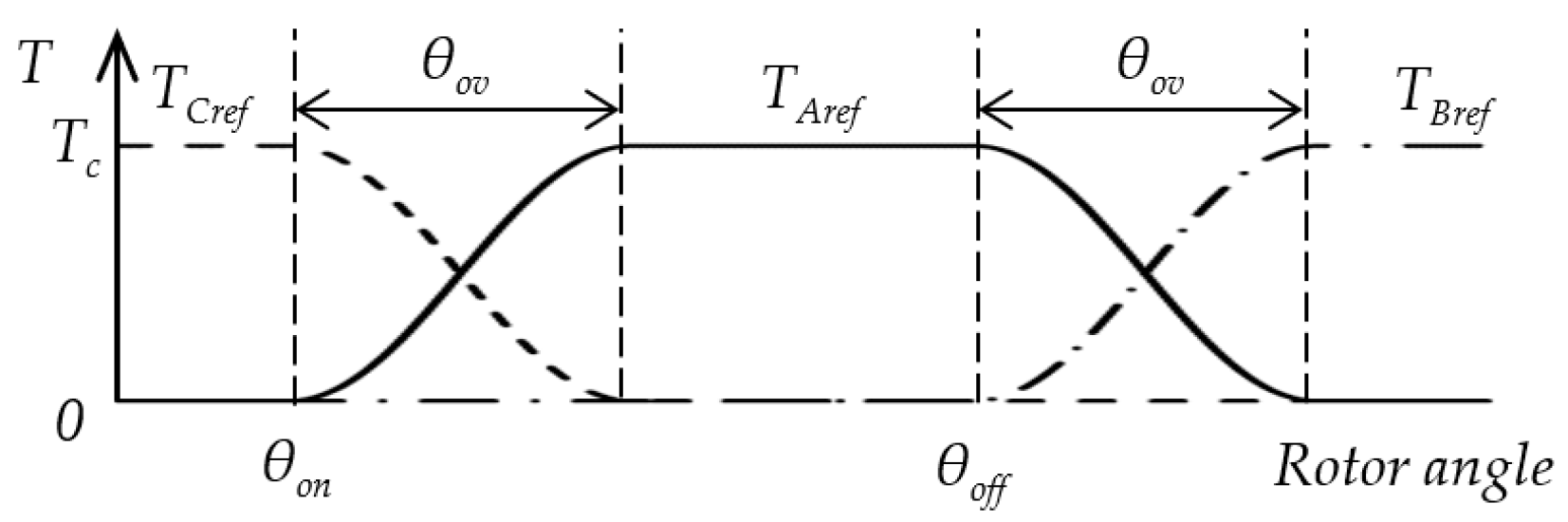
2.2. Torque Sharing Functions
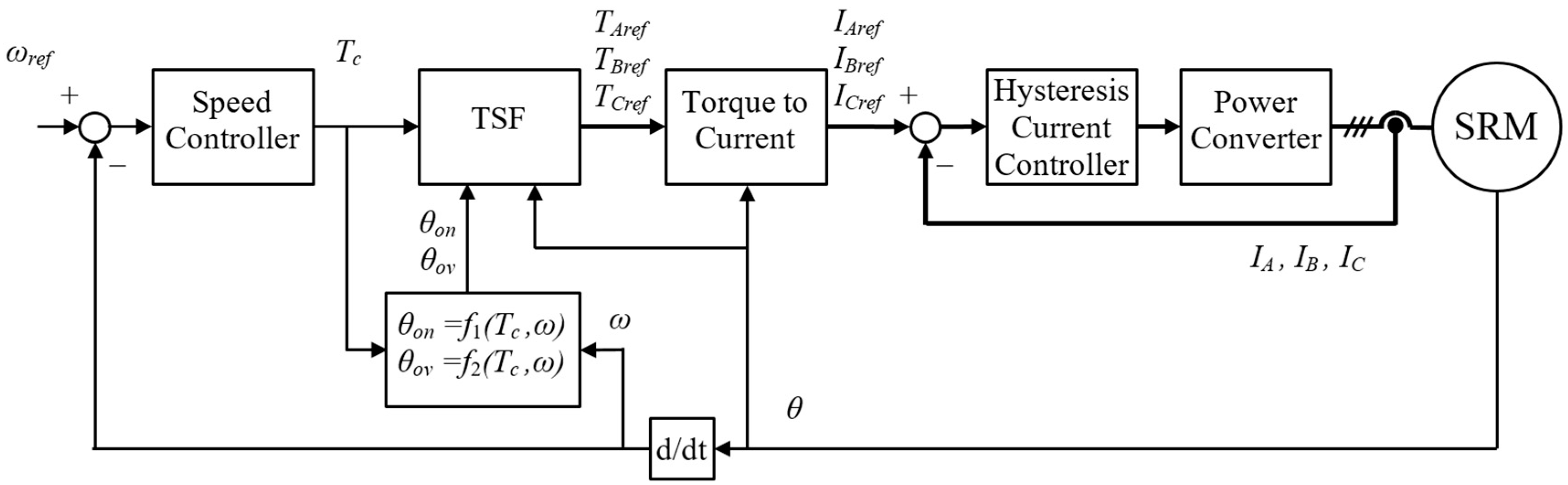
2.3. The Influence of Motor Geometry on TSF Control
3. Optimization of Torque Sharing Function Parameters
- Relative torque ripple Trip:
- Torque ripple RMS TripRMS:where T is the instantaneous torque during the time interval (t1, t2).
- Motor efficiency η
- Weighted criterion Wcrit:where w1 and w2 are relative weights.
- Building and verification of FEM model for given SRM;
- Determining the range and number of discrete values of load torque, speed, θon, and θov for a given geometry;
- Planning and execution of simulation experiments for each torque-speed combination;
- Executing a set of experiments for all combinations of θon and θov values, recording values of selected objective functions;
- Creating an interpolation function fint(θon,θov) for each objective function;
- Finding a minimum of fint and recording optimal values of θon and θov for actual torque-speed combinations for each objective function at given geometry.
- Interpolating θon = f1(Tc,ω) and θov = f2(Tc,ω) from optimal values recorded in the previous step.
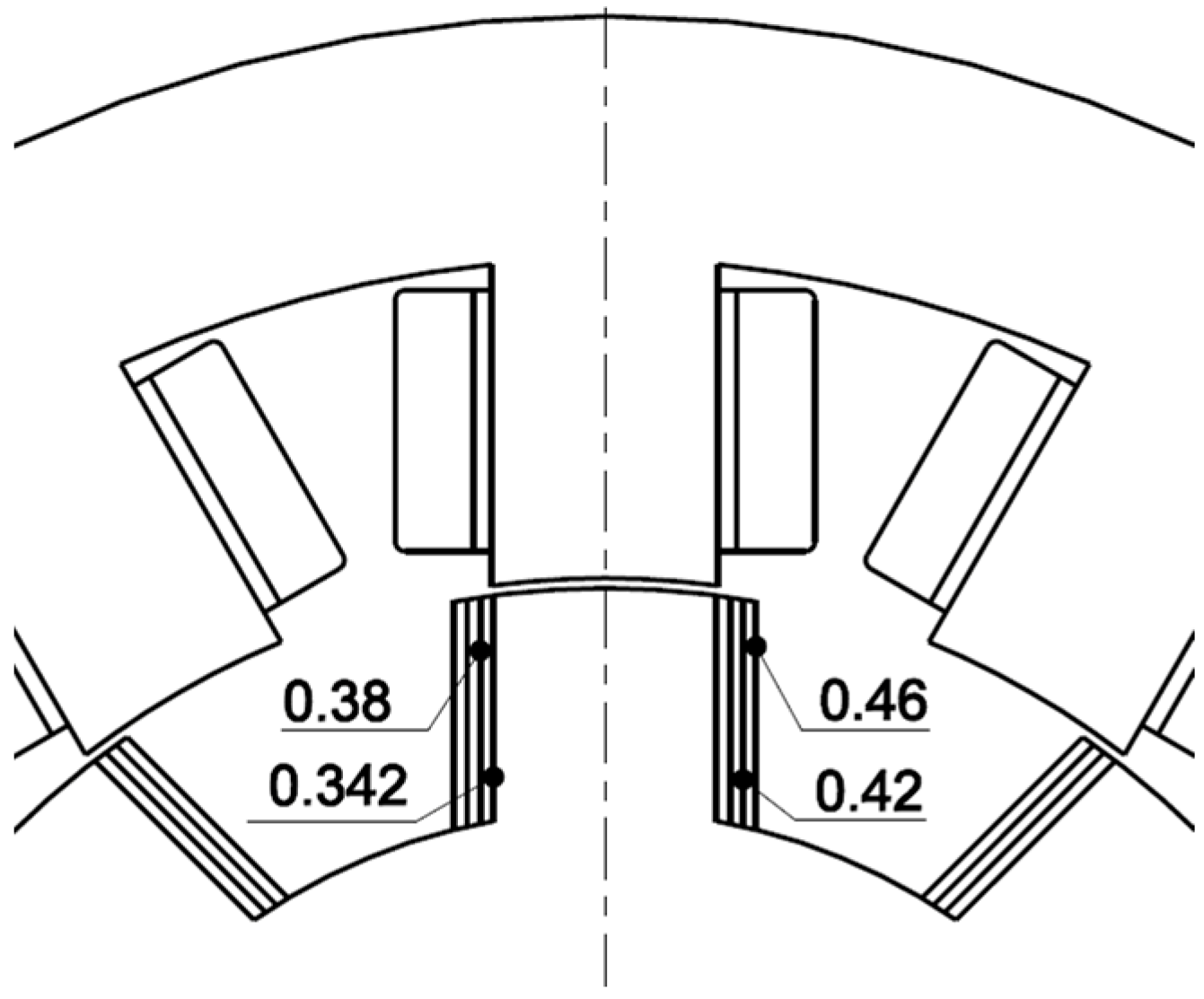
4. Rotor Pole Embrace
- Creation of the FEM model for each pole embrace value.
- Calculation of the look-up tables for Torque to the Current block.
- Running TSF optimization for each geometry (Section 3).
- Analyzing results, finding optimal value of pole embrace and corresponding functions f1 and f2.
5. Results from Experiments and Simulation
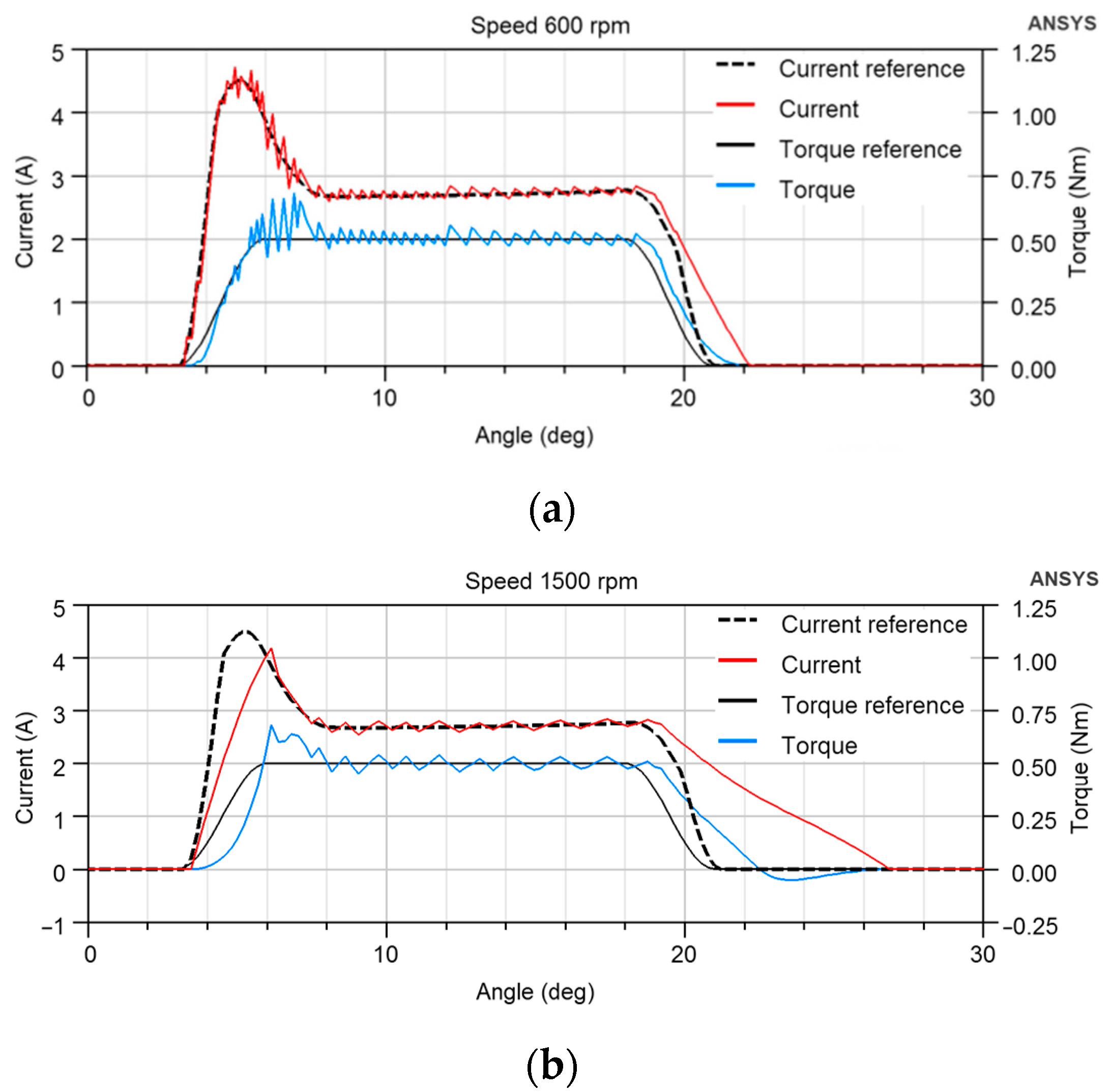
5.1. FEM Model Verification
5.2. Optimization of TSF
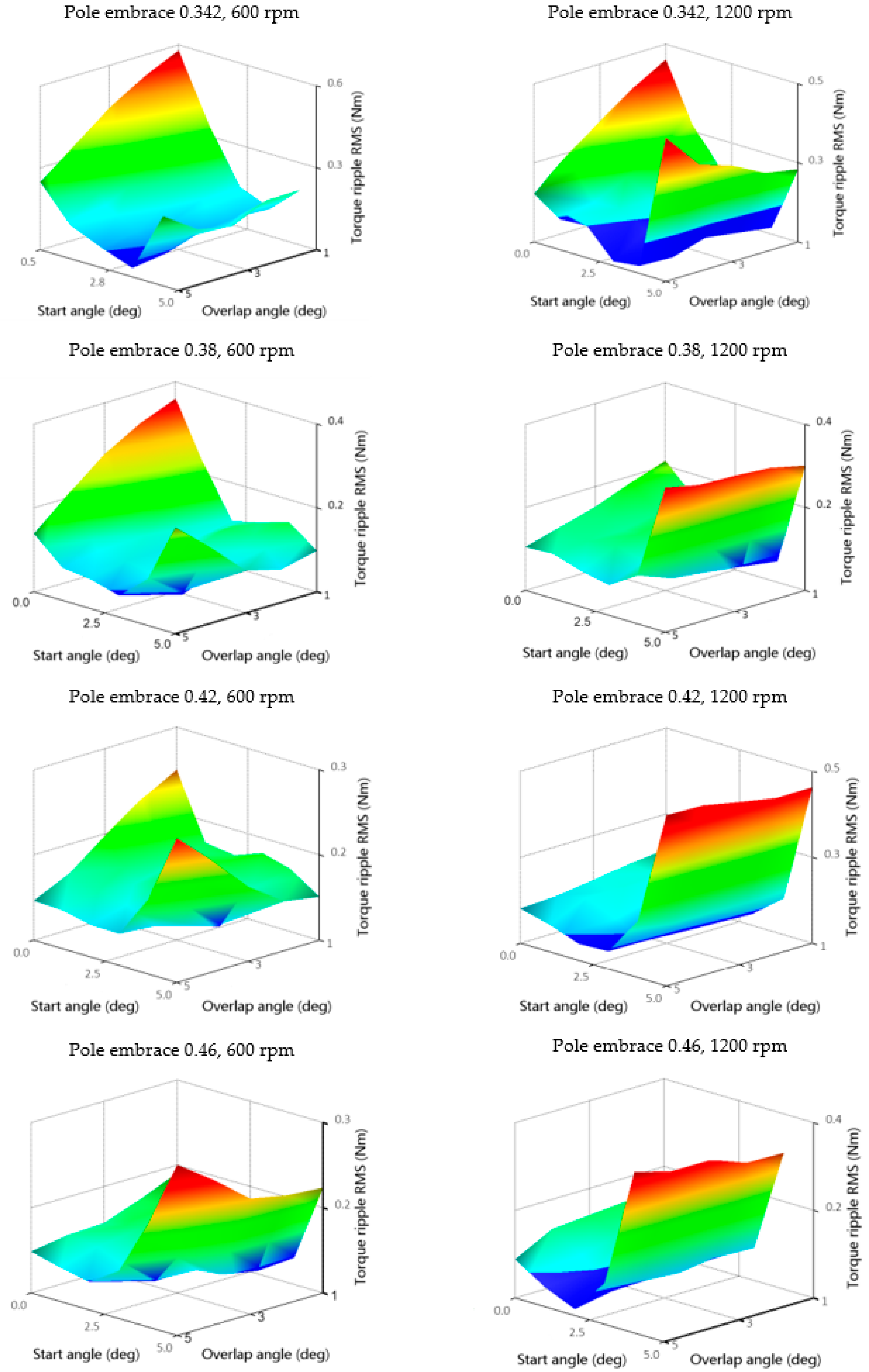
5.3. Effect of Changing Rotor Embrace on TSF Control
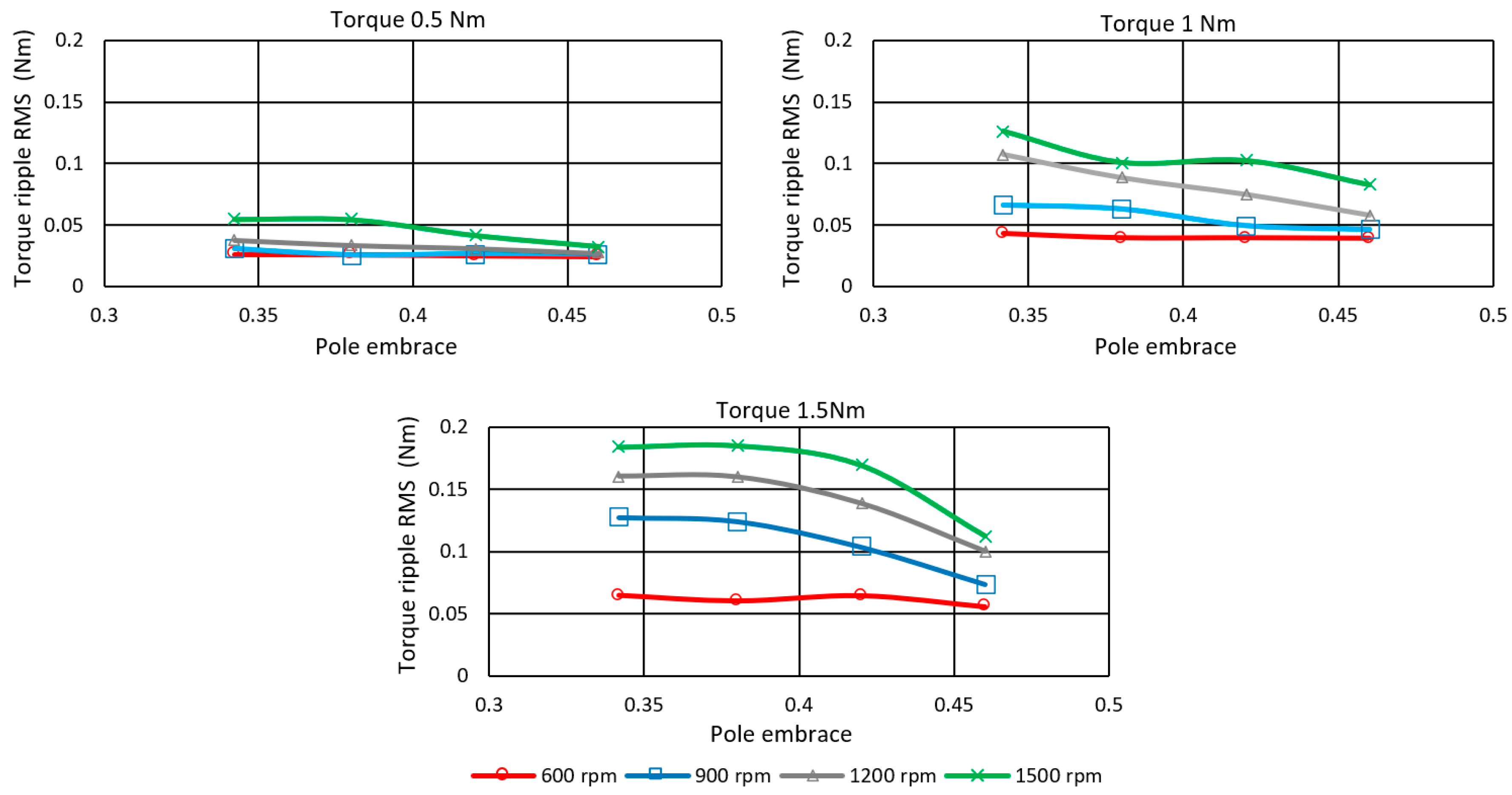
5.4. Influence of Rotor Geometry on Efficiency and Torque Ripple
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miller, T.J.E. Optimal design of switched reluctance motors. IEEE Trans. Ind. Electron. 2002, 49, 15–27. [Google Scholar] [CrossRef]
- Tursini, M.; Villani, M.; Fabri, G.; Di Leonardo, L. A switched-reluctance motor for aerospace application: Design, analysis and results. Electr. Power Syst. Res. 2017, 142, 74–83. [Google Scholar] [CrossRef]
- Belhadi, M.; Krebs, G.; Marchand, C.; Hannoun, H.; Mininger, X. Geometrical optimization of SRM on operating mode for automotive application. Electr. Eng. 2018, 100, 303–310. [Google Scholar] [CrossRef]
- Gan, C.; Wu, J.; Sun, Q.; Kong, W.; Li, H.; Hu, Y. A Review on Machine Topologies and Control Techniques for Low-Noise Switched Reluctance Motors in Electric Vehicle Applications. IEEE Access 2018, 6, 31430–31443. [Google Scholar] [CrossRef]
- Rahman, K.M.; Fahimi, B.; Suresh, G.; Rajarathnam, A.V.; Ehsani, M. Advantages of switched reluctance motor applications to EV and HEV: Design and control issues. IEEE Trans. Ind. Appl. 2000, 36, 111–121. [Google Scholar] [CrossRef]
- Saxena, S.; Le Floch, C.; MacDonald, J.; Moura, S. Quantifying EV battery end-of-life through analysis of travel needs with vehicle powertrain models. J. Power Sources 2015, 282, 265–276. [Google Scholar] [CrossRef]
- 360 Market Updates: Global Switched Reluctance Motors Market Research Report 2020. 7 January 2020. Available online: https://www.360marketupdates.com/global-switched-reluctance-motors-market-14837961 (accessed on 31 May 2022).
- Hamouda, M.; Amin, A.R.A.; Gouda, E. A New Constructed Geometry of a Switched Reluctance Motor for Reduced Torque Ripple. Mansoura Eng. J. 2015, 40, 22–35. [Google Scholar] [CrossRef]
- Peniak, A.; Makarovic, J.; Rafajdus, P.; Vavrus, V.; Makys, P.; Buhr, K.; Fajtl, R. Design and optimization of switched reluctance motor for electrical vehicles. Electr. Eng. 2017, 99, 1393–1401. [Google Scholar] [CrossRef]
- Di Barbaa, P.; Mognaschia, M.E.; Przybylskib, M.; Rezaeia, N.; Slusarekb, B.; Wiak, S. Geometry optimization for a class of switched-reluctance motors: A bi-objective approach. Int. J. Appl. Electromagn. Mech. 2018, 56, 107–122. [Google Scholar] [CrossRef]
- Lee, J.; Seo, J.H.; Kikuchi, N. Topology optimization of switched reluctance motors for the desired torque profile. Struct. Multidiscip. Optim. 2010, 42, 783–796. [Google Scholar] [CrossRef]
- Byun, J.; Hahn, S. Topology Optimization of Switched Reluctance Motor Using Mutual Energy Method. Int. J. Appl. Electromagn. Mech. 2001, 13, 421–426. [Google Scholar] [CrossRef]
- Ye, W.; Ma, Q.S.; Zhang, P.M. Improvement of the Torque-Speed Performance and Drive Efficiency in an SRM Using an Optimal Torque Sharing Function. Appl. Sci. 2018, 8, 720. [Google Scholar] [CrossRef]
- Zhang, M.; Bahri, I.; Mininger, X.; Vlad, C.; Xie, H.Q.; Berthelot, E. A New Control Method for Vibration and Noise Suppression in Switched Reluctance Machines. Energies 2019, 12, 1554. [Google Scholar] [CrossRef]
- Li, H.; Bilgin, B.; Emadi, A. An Improved Torque Sharing Function for Torque Ripple Reduction in Switched Reluctance Machines. IEEE Trans. Power Electron. 2019, 34, 1635–1644. [Google Scholar] [CrossRef]
- Ye, J.; Bilgin, B.; Emadi, A. An Offline Torque Sharing Function for Torque Ripple Reduction in Switched Reluctance Motor Drives. IEEE Trans. Energy Convers. 2015, 30, 726–735. [Google Scholar] [CrossRef]
- Xue, X.D.; Cheng, K.W.E.; Ho, S.L. Optimization and Evaluation of Torque-Sharing Functions for Torque Ripple Minimization in Switched Reluctance Motor Drives. IEEE Trans. Power Electron. 2009, 24, 2076–2090. [Google Scholar] [CrossRef]
- Ro, H.-S.; Lee, K.-G.; Lee, J.-S.; Jeong, H.-G.; Lee, K.-B. Torque Ripple Minimization Scheme Using Torque Sharing Function Based Fuzzy Logic Control for a Switched Reluctance Motor. J. Electr. Eng. Technol. 2015, 10, 118–127. [Google Scholar] [CrossRef]
- Üstün, O.; Önder, M. An Improved Torque Sharing Function to Minimize Torque Ripple and Increase Average Torque for Switched Reluctance Motor Drives. Electr. Power Components Syst. 2020, 48, 667–681. [Google Scholar] [CrossRef]
- Xia, Z.; Bilgin, B.; Nalakath, S.; Emadi, A. A New Torque Sharing Function Method for Switched Reluctance Machines With Lower Current Tracking Error. IEEE Trans. Ind. Electron. 2021, 68, 10612–10622. [Google Scholar] [CrossRef]
- Ferková, Ž.; Bober, P. An off-line Optimization of Torque Sharing Functions for Switched Reluctance Motor Control. In Proceedings of the 2021 IEEE International Workshop of Electronics, Control, Measurement, Signals and their application to Mechatronics (ECMSM), Liberec, Czech Republic, 21–22 June 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Abhijith, V.; Hossain, M.J.; Lei, G.; Sreelekha, P.A.; Monichan, T.P.; Rao, S.V. Hybrid Switched Reluctance Motors for Electric Vehicle Applications with High Torque Capability without Permanent Magnet. Energies 2022, 15, 7931. [Google Scholar] [CrossRef]

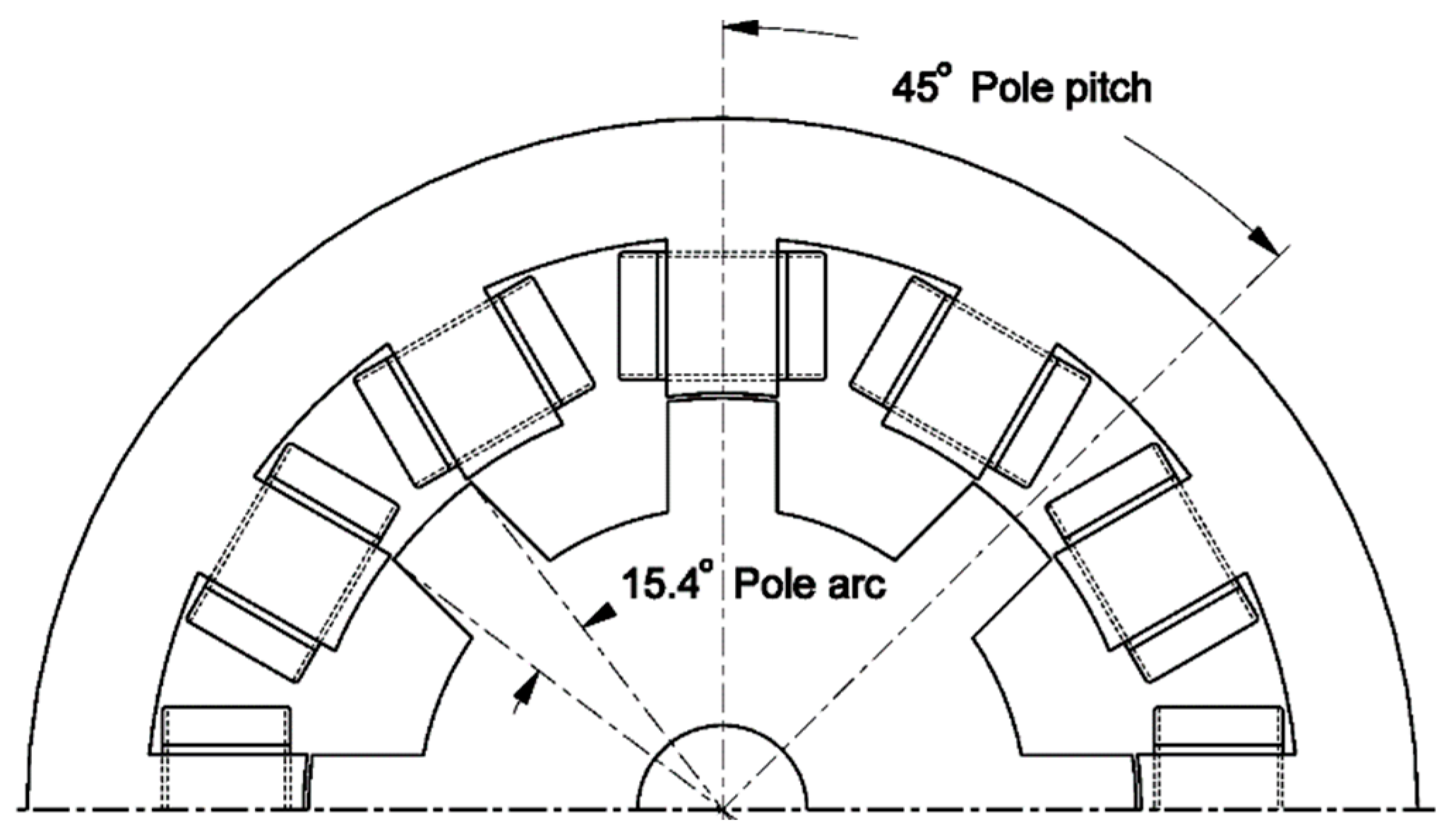

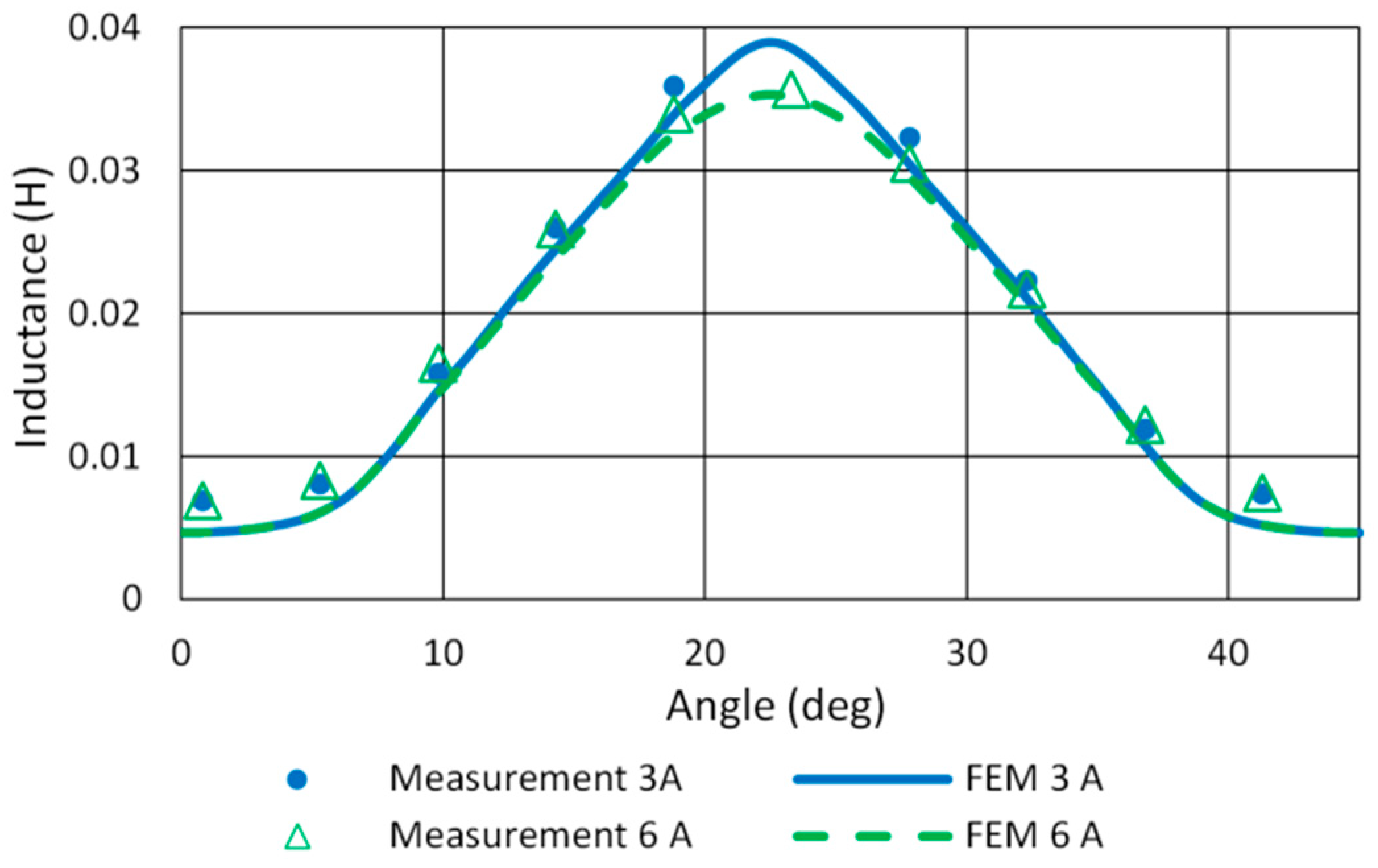




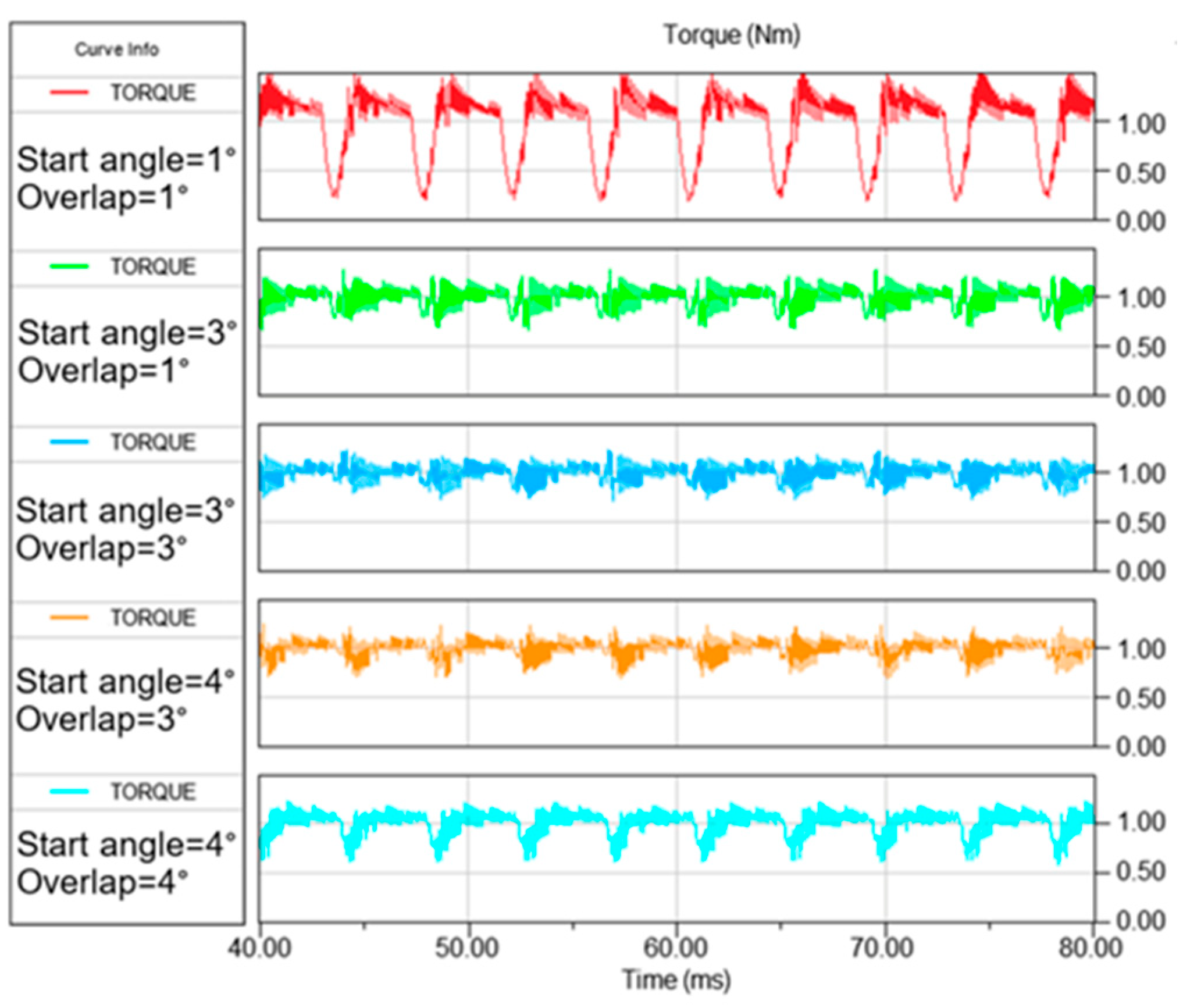



| Specification | Value |
|---|---|
| Voltage | 120 V |
| Current | 2.5 A per phase/max. 6 A |
| Number of stator poles | 12 |
| Number of rotor poles | 8 |
| Stator outer diameter | 139.5 mm |
| Stator inner diameter | 83.5 mm |
| Rotor outer diameter | 82.9 mm |
| Motor length | 47 mm |
| Stator pole arc | 15.8° |
| Rotor pole arc | 15.4° |
| Rotor pole embrace | 0.342 |
| Pole Arc | Pole Embrace |
|---|---|
| 15.4° | 0.342 value for existing motor |
| 17.1° | 0.38 |
| 18.9° | 0.42 |
| 20.7° | 0.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferková, Ž.; Bober, P. Influence of the Rotor Geometry on Efficiency and Torque Ripple of Switched Reluctance Motor Controlled by Optimized Torque Sharing Functions. Machines 2023, 11, 613. https://doi.org/10.3390/machines11060613
Ferková Ž, Bober P. Influence of the Rotor Geometry on Efficiency and Torque Ripple of Switched Reluctance Motor Controlled by Optimized Torque Sharing Functions. Machines. 2023; 11(6):613. https://doi.org/10.3390/machines11060613
Chicago/Turabian StyleFerková, Želmíra, and Peter Bober. 2023. "Influence of the Rotor Geometry on Efficiency and Torque Ripple of Switched Reluctance Motor Controlled by Optimized Torque Sharing Functions" Machines 11, no. 6: 613. https://doi.org/10.3390/machines11060613
APA StyleFerková, Ž., & Bober, P. (2023). Influence of the Rotor Geometry on Efficiency and Torque Ripple of Switched Reluctance Motor Controlled by Optimized Torque Sharing Functions. Machines, 11(6), 613. https://doi.org/10.3390/machines11060613







