Enriched Finite Element Method Based on Interpolation Covers for Structural Dynamics Analysis
Abstract
1. Introduction
2. Formula of the E-FEM
2.1. Theory of the E-FEM
2.2. 3D Structural Element Construction Theory of the E-FEM
2.3. Dynamics Controlling Equations for Linear Elastic Solids
2.4. The Eigenvalue Problem of Free Vibration Analysis
2.5. The Dynamic Problem of Forced Vibration Analysis
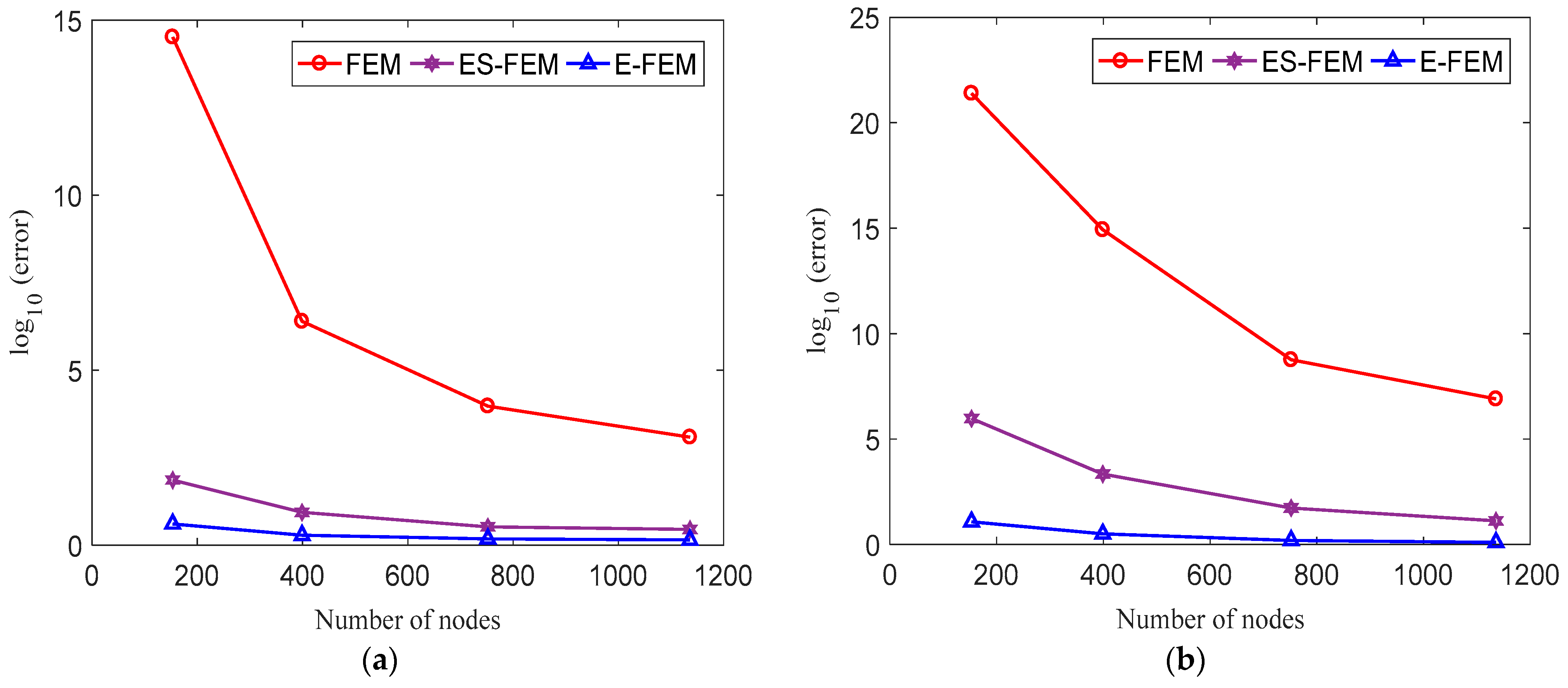
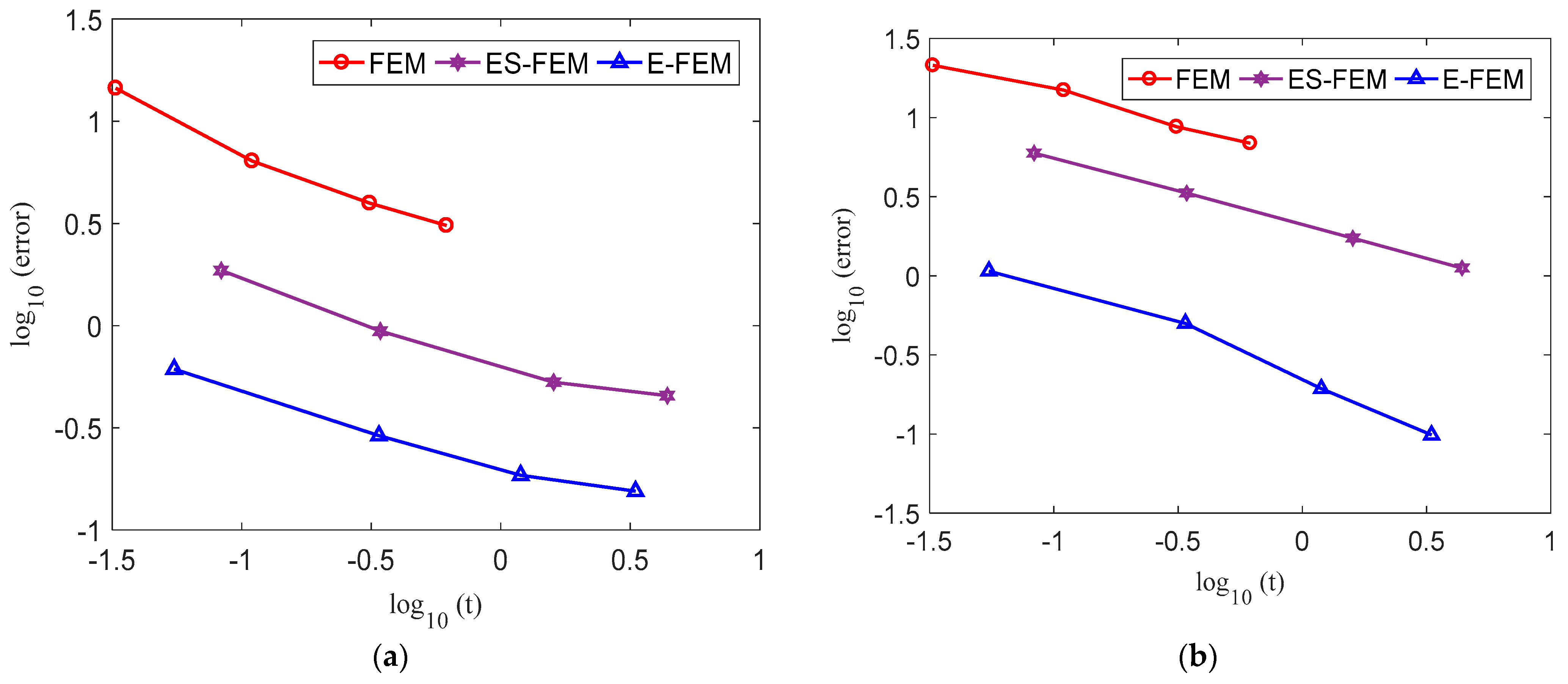
3. Analysis of 2D Examples
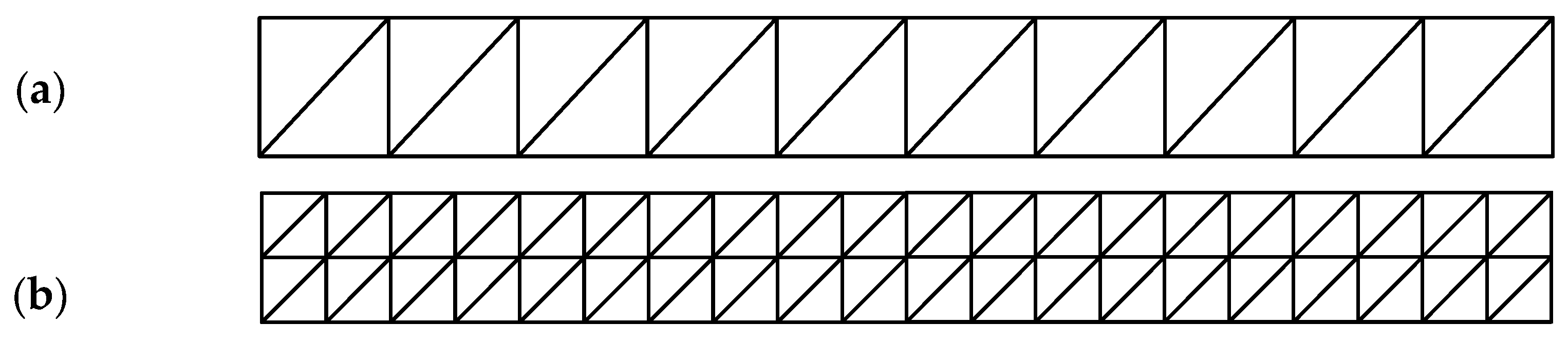
3.1. The Cantilever Beam
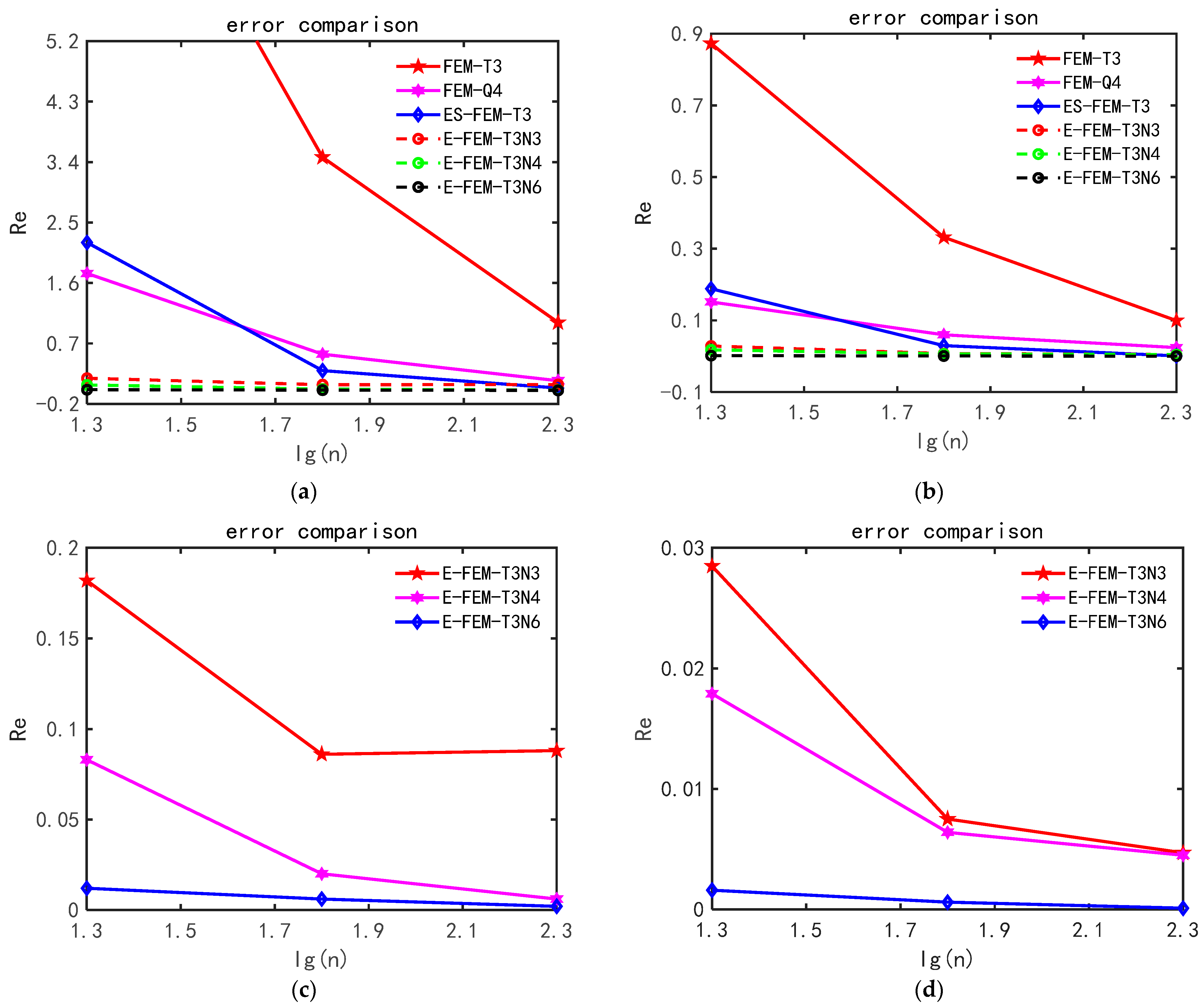
3.1.1. Convergence Study
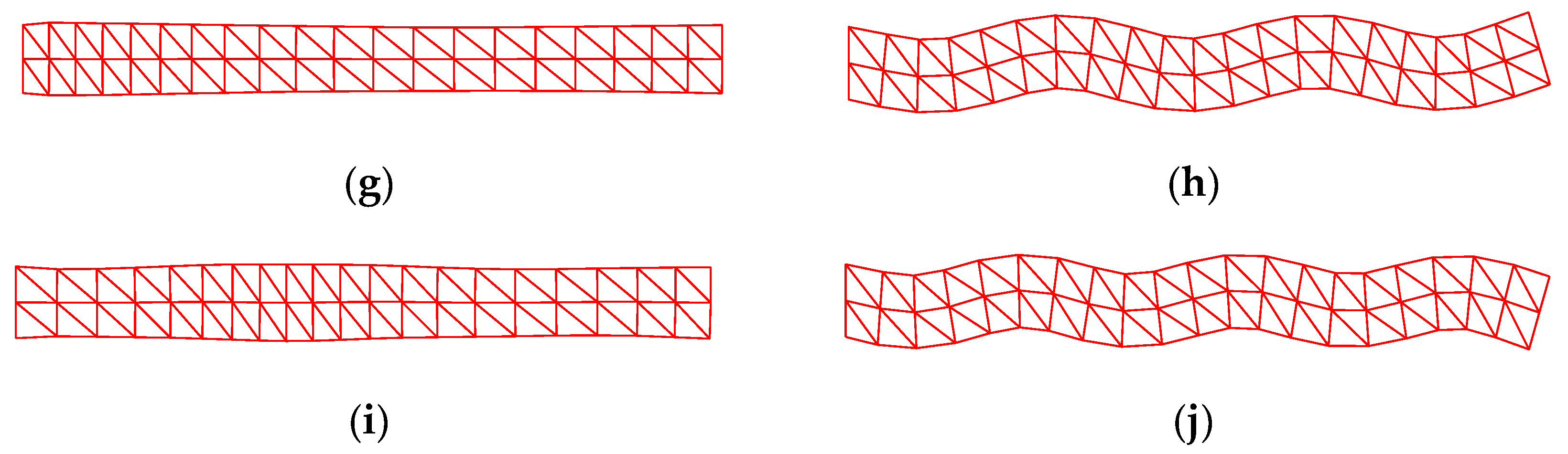
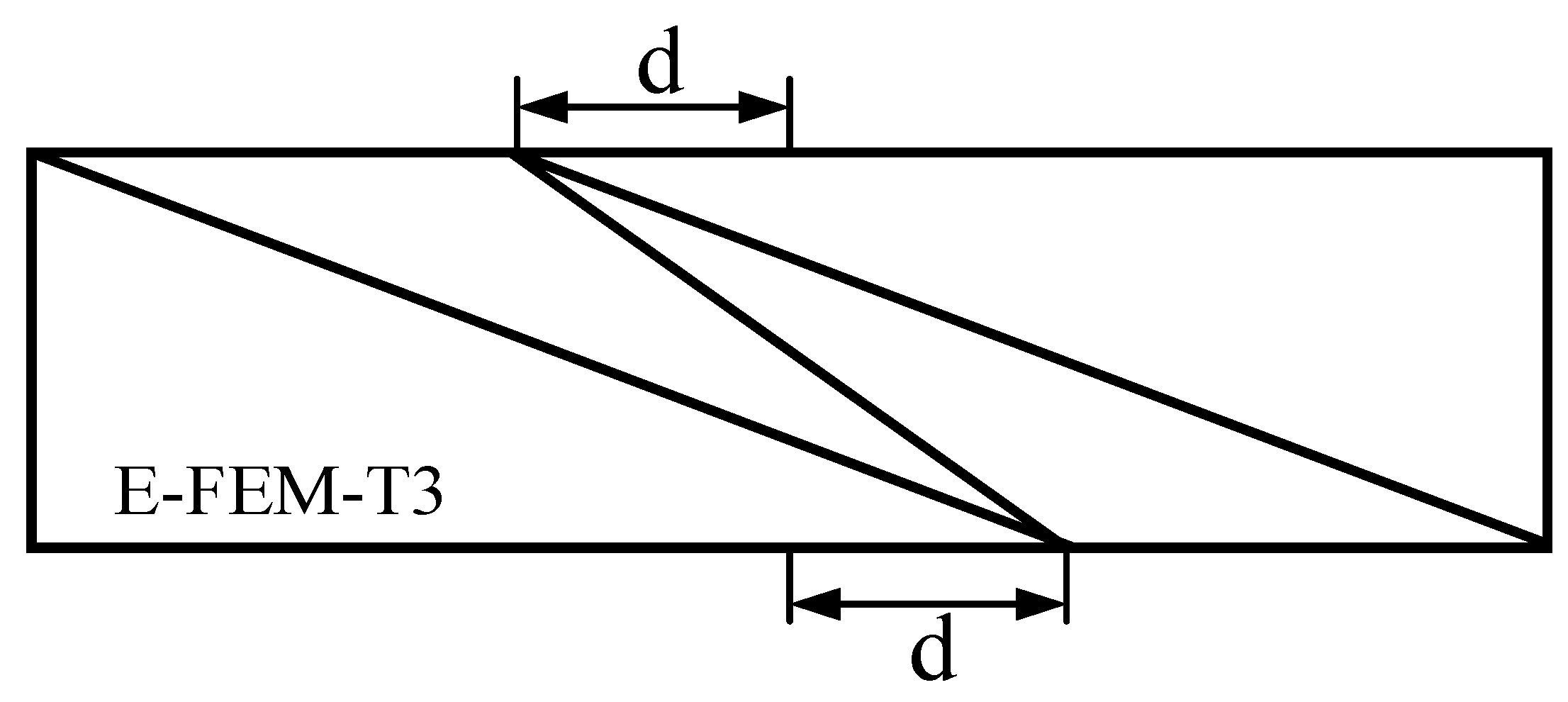
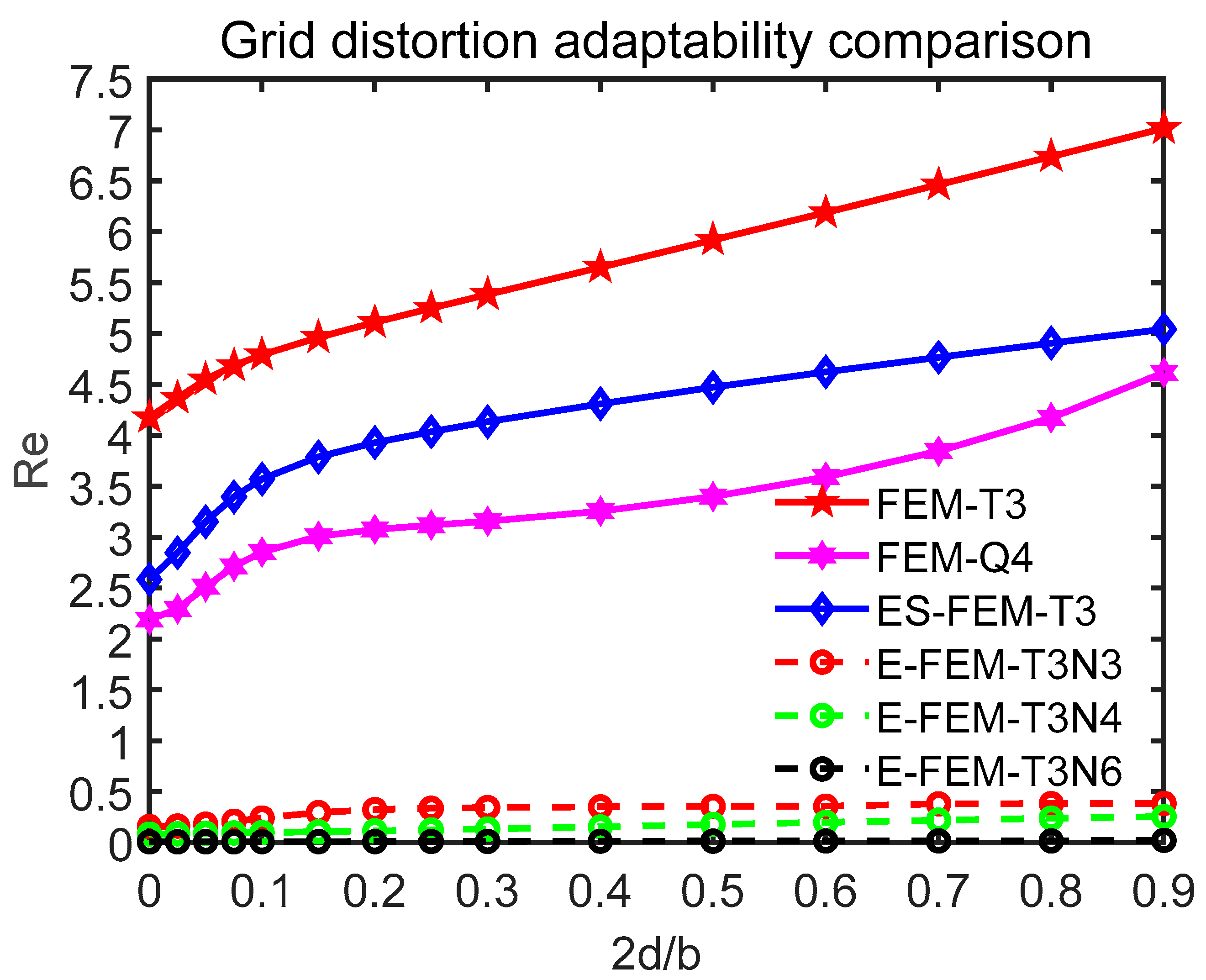
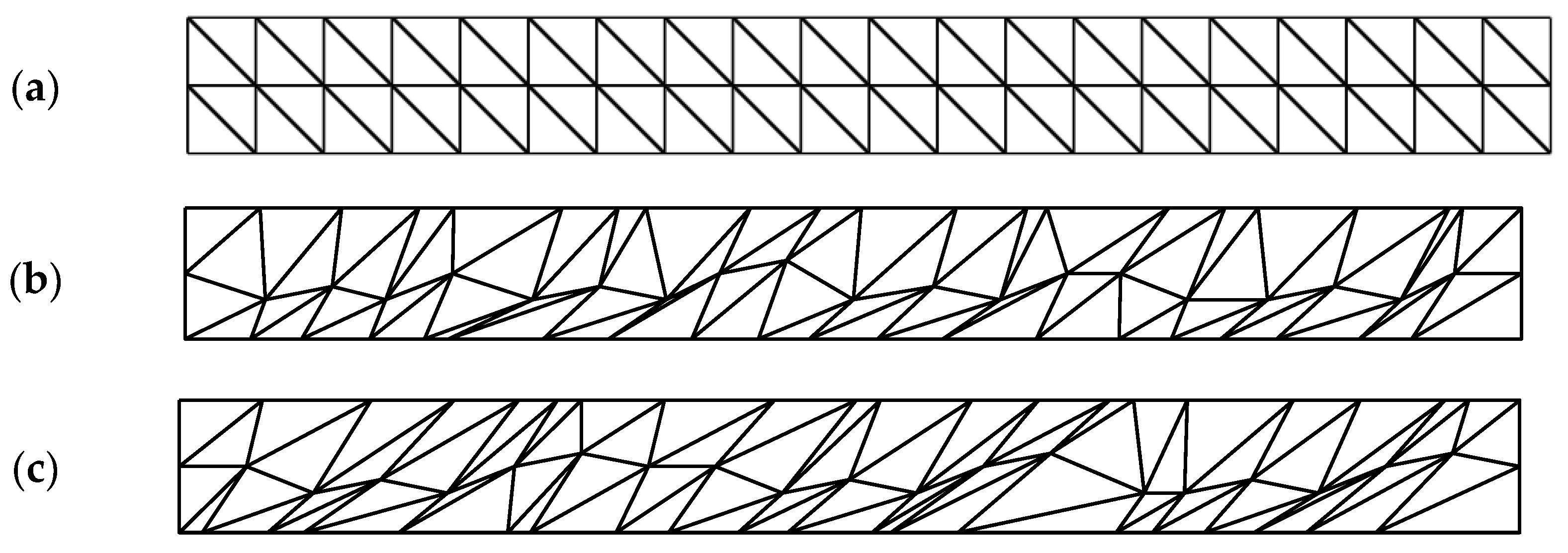
3.1.2. Grid Distortion Sensitivity Study
3.1.3. Forced Vibration Study
3.2. A Shear Wall
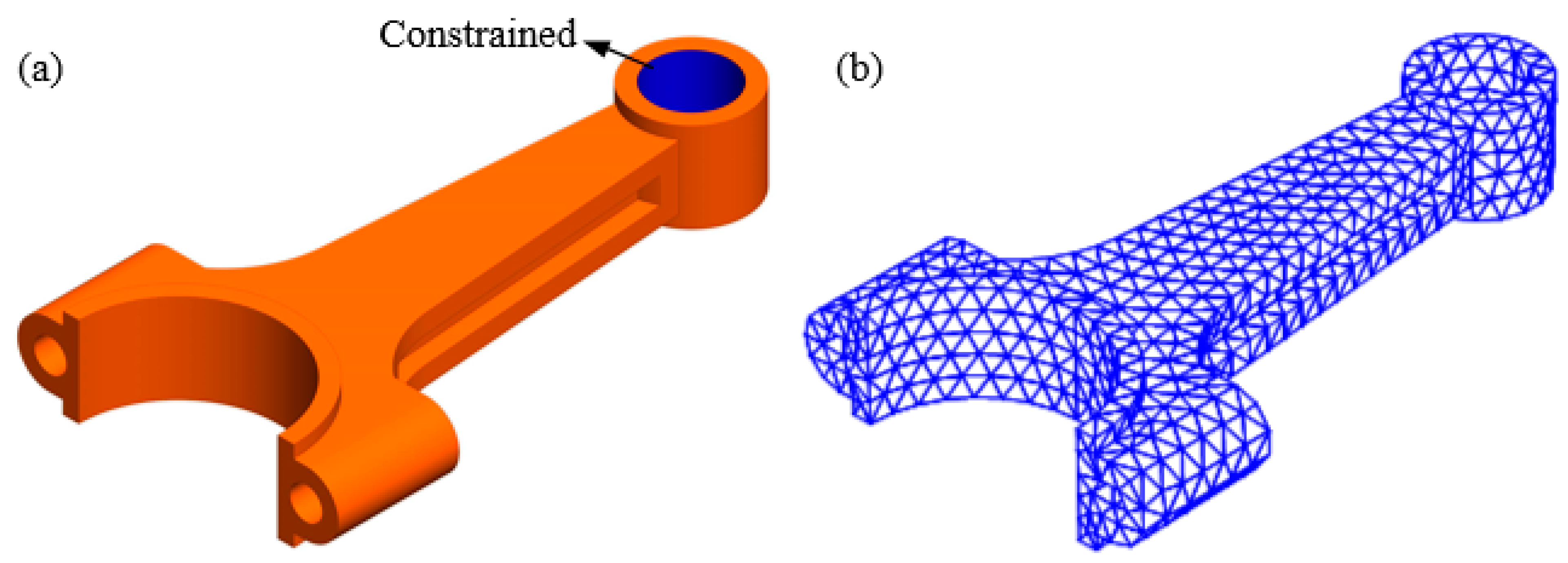
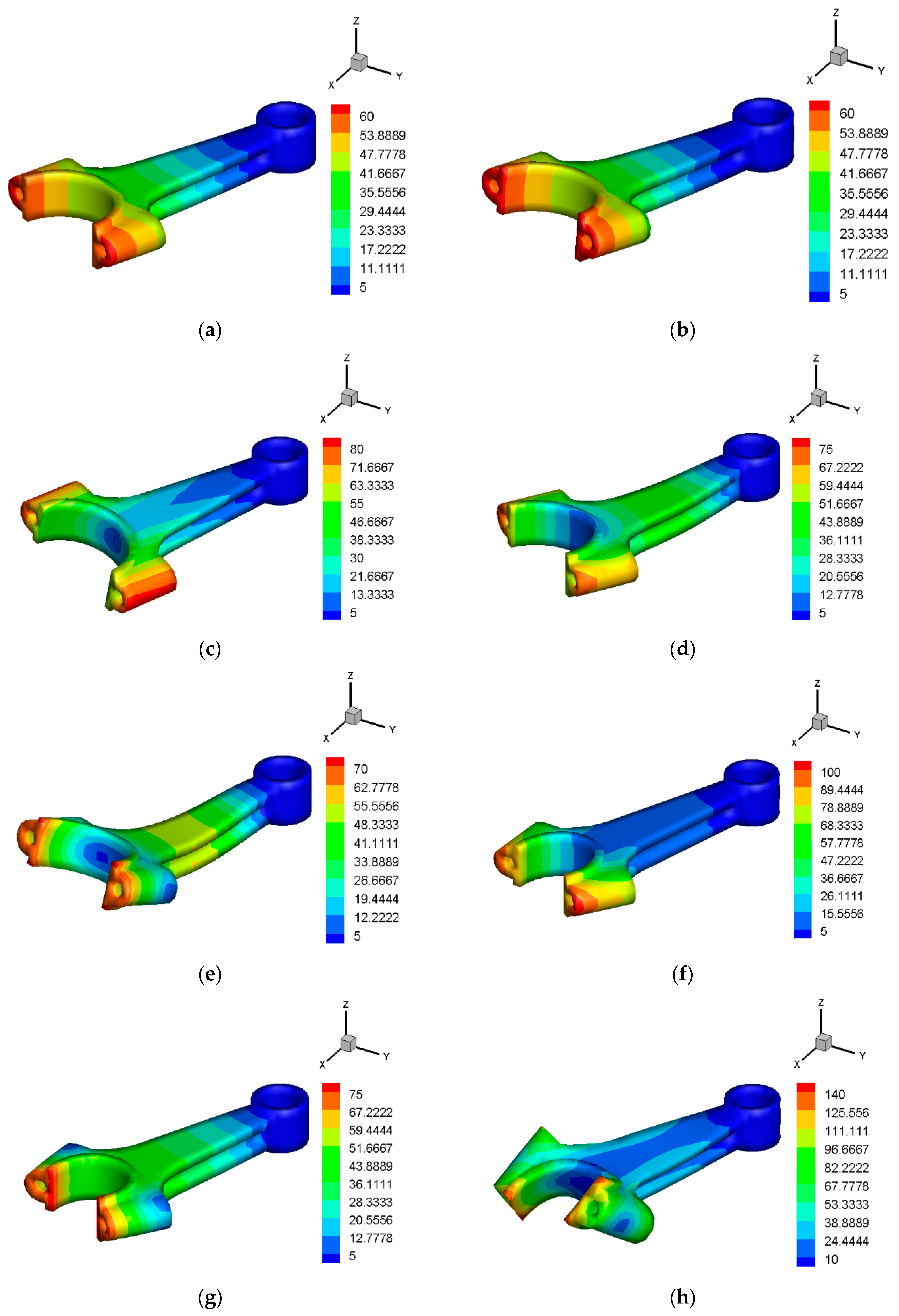
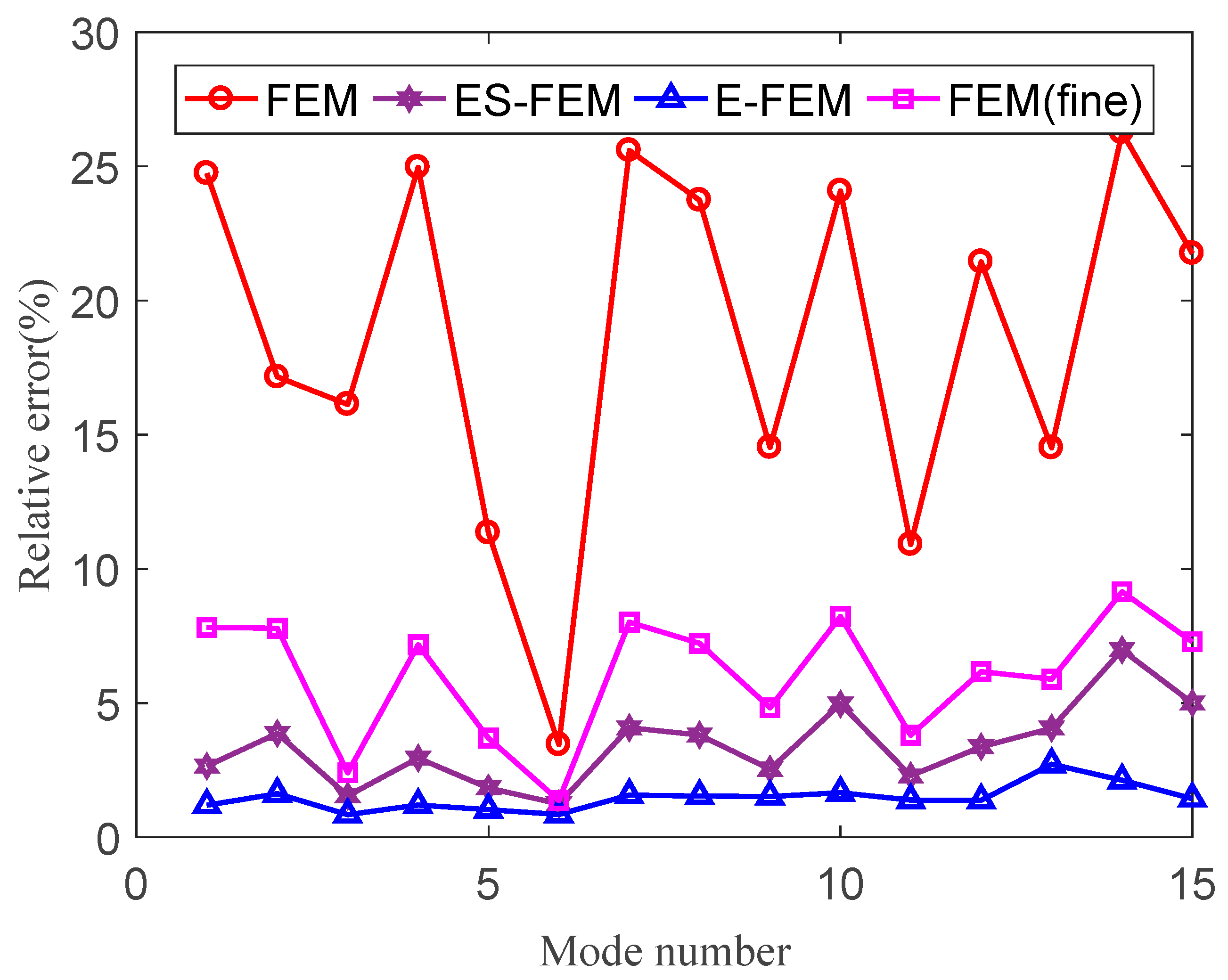
3.3. A Connecting Rod
4. Analysis of 3D Examples
4.1. The Cantilever Beam
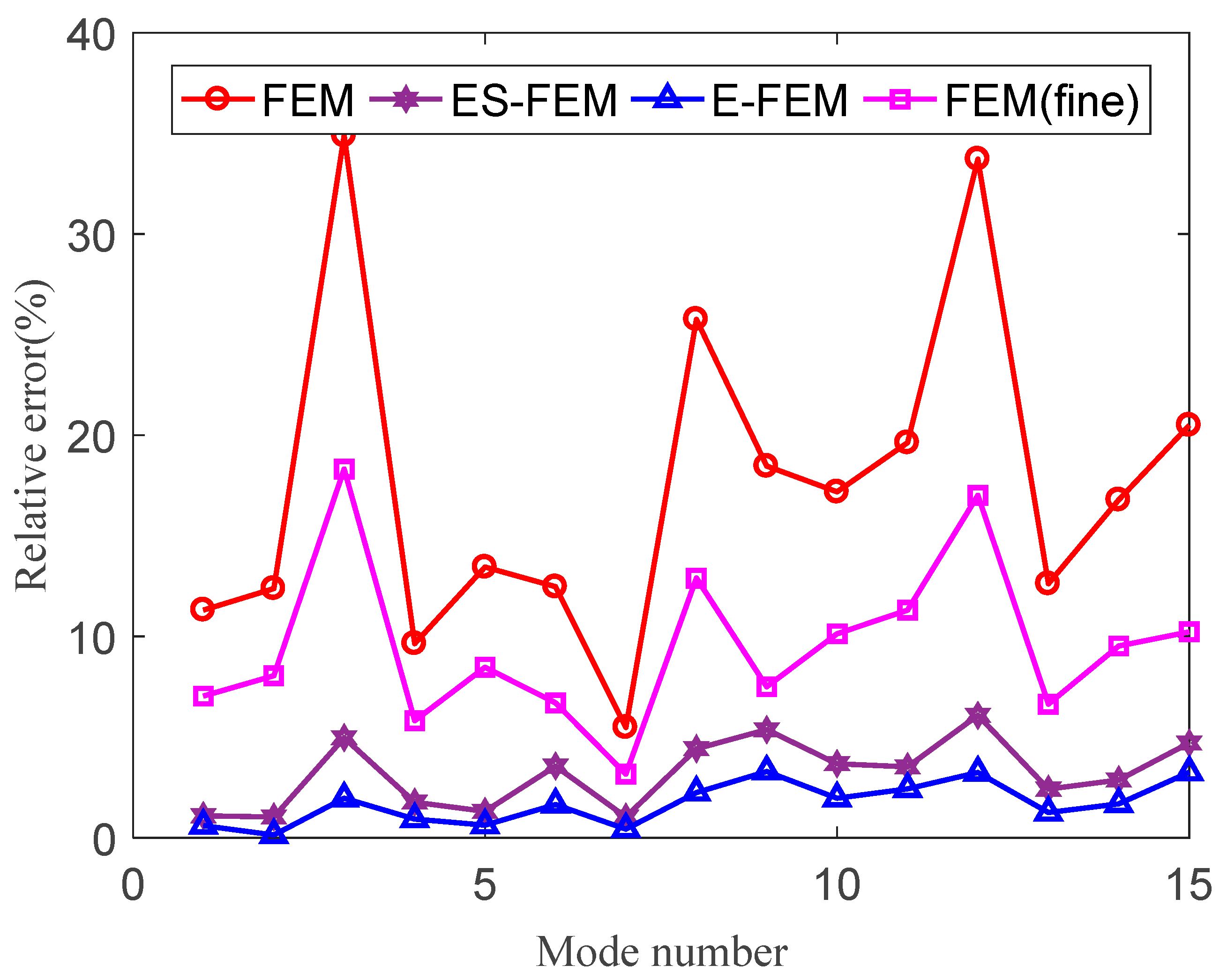
4.2. Engine Connecting Rod
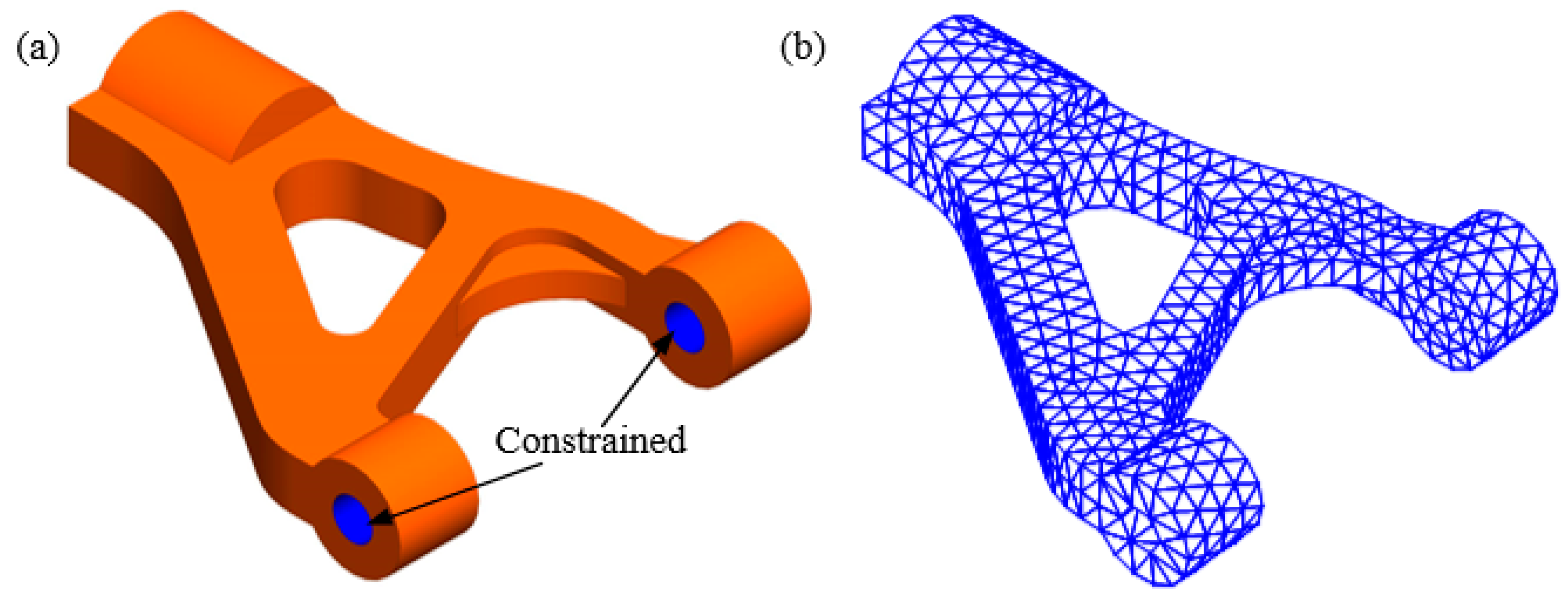
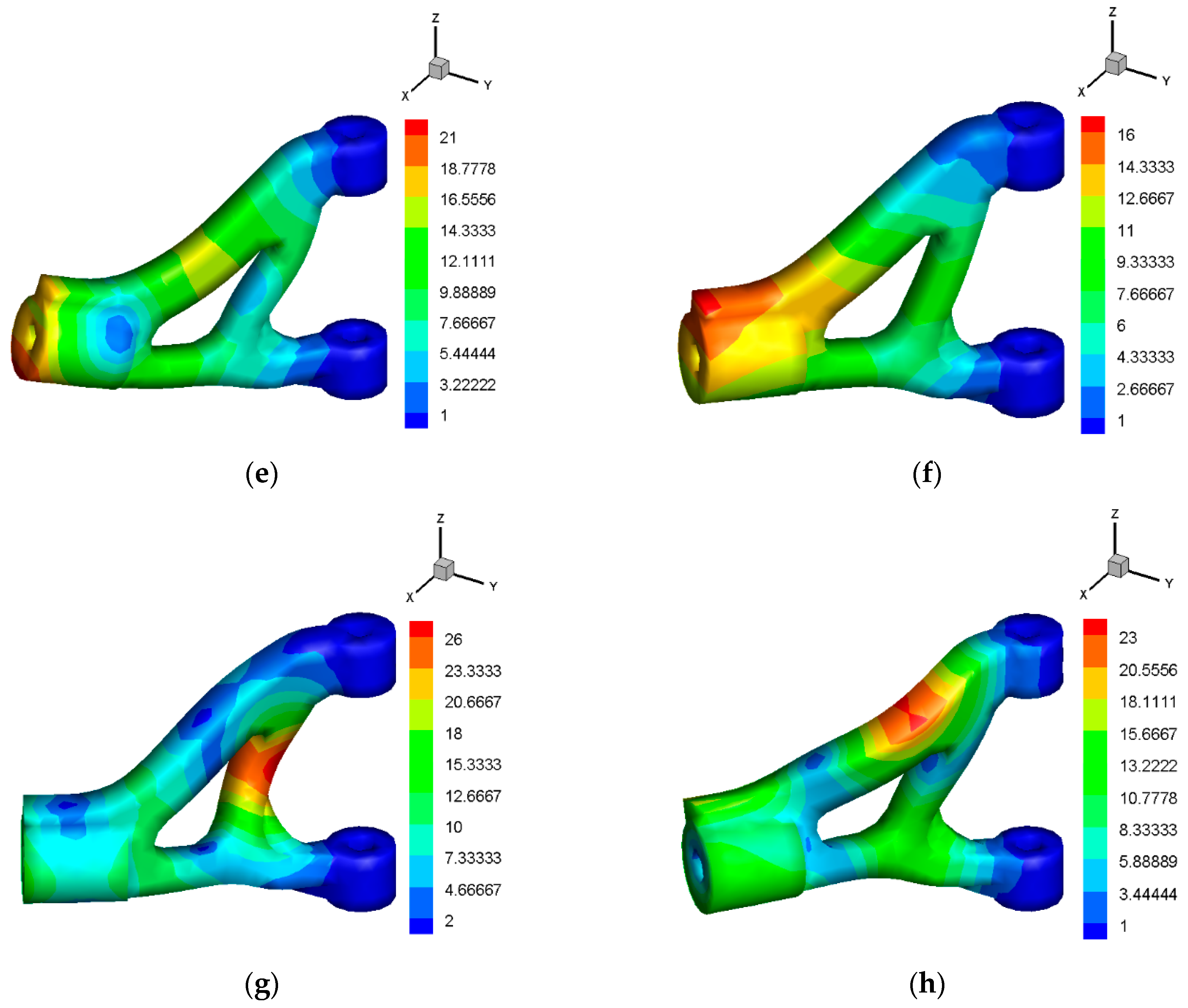
4.3. Automobile Front Suspension Arm
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- To, M. A further study of hybrid strain-based three-node flat triangular shell elements. Finite Elem. Anal. Des. 1998, 31, 135–152. [Google Scholar]
- Chen, L.; Liu, G.R.; Zeng, K.; Zhang, J. A novel variable power singular element in g space with strain smoothing for bi-material fracture analyses. Eng. Anal. Bound. Elem. 2011, 35, 1303–1317. [Google Scholar] [CrossRef]
- Liu, G.R.; Dai, K.Y.; Nguyen, T.T. A Smoothed Finite Element Method for Mechanics Problems. Comput. Mech. 2007, 39, 859–877. [Google Scholar] [CrossRef]
- Liu, G.R.; Nguyen-Thoi, T. Smoothed Finite Element Methods, 1st ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Nguyen-Xuan, H.; Rabczuk, T.; Nguyen-Thoi, T.; Tran, T.; Nguyen-Thanh, N. Computation of limit and shakedown loads using a node-based smoothed finite element method. Int. J. Numer. Methods. Eng. 2012, 90, 287–310. [Google Scholar] [CrossRef]
- Bordas, S.; Rabczuk, T.; Hung, N.X.; Nguyen, V.P.; Natarajan, S.; Bog, T.; Hiep, N.V. Strain smoothing in FEM and XFEM. Comput. Struct. 2010, 88, 1419–1443. [Google Scholar] [CrossRef]
- Liu, G.R. A G space theory and a weakened weak (W2) form for a unified formulation of compatible and incompatible methods: Part I Theory. Int. J. Numer. Methods. Engrg. 2010, 81, 1093–1126. [Google Scholar] [CrossRef]
- Liu, G.R. A G space theory and a weakened weak (W2) form for a unified formulation of compatible and incompatible methods: Part II applications to solid mechanics problems. Int. J. Numer. Methods. Engrg. 2010, 81, 1127–1156. [Google Scholar] [CrossRef]
- Liu, M.Y.; Gao, G.J.; Zhu, H.F.; Jiang, C.; Liu, G.R. A cell-based smoothed finite element method (CS-FEM) for three-dimensional incompressible laminar flows using mixed wedge-hexahedral element. Eng. Anal. Bound. Elem. 2021, 133, 269–285. [Google Scholar] [CrossRef]
- Liu, G.R.; Nguyen-Thoi, T.; Nguyen-Xuan, H.; Lam, K.Y. A node-based smoothed finite element method (NS-FEM) for upper bound solutions to solid mechanics problems. Comput. Struct. 2009, 87, 14–26. [Google Scholar] [CrossRef]
- Duarte, C.A.; Babuška, I.; Oden, J.T. Generalized finite element methods for three dimensional structural mechanics problems. Comput. Struct. 2000, 77, 215–232. [Google Scholar] [CrossRef]
- Liu, G.R.; Nguyen-Thoi, T.; Lam, K.Y. An edge-based smoothed finite element method (ES-FEM) for static, free and forced vibration analyses of solids. J. Sound Vib. 2009, 320, 1100–1130. [Google Scholar] [CrossRef]
- Li, W.; Chai, Y.B.; Lei, M.; Li, T.Y. Numerical investigation of the edge-based gradient smoothing technique for exterior Helmholtz equation in two dimensions. Comput. Struct. 2017, 182, 149–164. [Google Scholar] [CrossRef]
- Chai, Y.B.; You, X.Y.; Li, W.; Huang, Y.; Yue, Z.J.; Wang, M.S. Application of the edge-based gradient smoothing technique to acoustic radiation and acoustic scattering from rigid and elastic structures in two dimensions. Comput. Struct. 2018, 203, 43–58. [Google Scholar] [CrossRef]
- Zeng, W.; Liu, G.R. Smoothed Finite Element Methods (S-FEM): An Overview and Recent Developments. Arch. Comput. Methods. Eng. 2016, 25, 397–435. [Google Scholar] [CrossRef]
- Liu, G.R. The smoothed finite element method (S-FEM): A framework for the design of numerical models for desired solutions. Front. Struct. Civ. Eng. 2019, 13, 456–477. [Google Scholar] [CrossRef]
- Kim, J.; Bathe, K.J. The finite element method enriched by interpolation covers. Comput. Struct. 2013, 116, 35–49. [Google Scholar] [CrossRef]
- Jeon, H.M.; Lee, P.S.; Bathe, K.J. The MITC3 shell finite element enriched by interpolation covers. Comput. Struct. 2014, 134, 128–142. [Google Scholar] [CrossRef]
- Jun, H.; Yoon, K.; Lee, P.S.; Bathe, K.J. The MITC3+ shell element enriched in membrane displacements by interpolation covers. Comput. Methods Appl. Mech. Eng. 2018, 337, 458–480. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, G.Y.; Lu, H.; Zong, Z. A cell-based smoothed point interpolation method (CS-PIM) for 2D thermoelastic problems. Int. J. Numer. Methods Heat. Fluid. Flow. 2017, 27, 1249–1265. [Google Scholar] [CrossRef]
- Kim, J.; Bathe, K.J. Towards a procedure to automatically improve finite element solutions by interpolation covers. Comput. Struct. 2014, 131, 81–97. [Google Scholar] [CrossRef]
- Wu, F.; Zhou, G.; Gu, Q.Y.; Chai, Y.B. An enriched finite element method with interpolation cover functions for acoustic analysis in high frequencies. Eng. Anal. Bound. Elem. 2021, 129, 67–81. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, J.; Liu, M.; Li, M.; Chai, Y. Evaluation of the transient performance of magneto-electro-elastic based structures with the enriched finite element method. Compos. Struct. 2021, 280, 114888. [Google Scholar] [CrossRef]
- Li, Y.; Dang, S.; Li, W.; Chai, Y. Free and forced vibration analysis of two-dimensional linear elastic solids using the finite element methods enriched by interpolation cover functions. Mathematics 2022, 10, 456. [Google Scholar] [CrossRef]
- Khoei, A.R.; Bahmani, B. Application of an enriched FEM technique inthermo-mechanical contact problems. Comput. Mech. 2018, 62, 1127–1154. [Google Scholar] [CrossRef]
- Khoei, A.R.; Vahab, M.; Hirmand, M. An enriched–FEM technique for numerical simulation of interacting discontinuities in naturally fractured porous media. Comput. Methods Appl. Mech. Eng. 2017, 17, 169–232. [Google Scholar] [CrossRef]
- Wu, C.T.; Koishi, M. Three-dimensional meshfree-enriched finite element formulation for micromechanical hyper elastic modeling of particulate rubber composites. Int. J. Numer. Methods Eng. 2012, 91, 1137–1157. [Google Scholar] [CrossRef]
- Yang, Y.T.; Xu, D.D.; Zheng, H. Application of the three-node triangular element with continuous nodal stress for free vibration analysis. Comput. Struct. 2016, 169, 69–80. [Google Scholar] [CrossRef]
- Dai, K.Y.; Liu, G.R. Free and forced vibration analysis using the smoothed finite element method (SFEM). J. Sound Vib. 2007, 301, 803–820. [Google Scholar] [CrossRef]
- Chen, J.S.; Wu, C.T.; Yoon, S.; You, Y. A stabilized confirming nodal integration for Galerkin meshfree methods. Int. J. Numer. Methods Eng. 2001, 53, 2587–2615. [Google Scholar] [CrossRef]
- Ham, S.; Bathe, K.J. A finite element method enriched for wave propagation problems. Comput. Struct. 2012, 94, 1–12. [Google Scholar] [CrossRef]
- Chai, Y.B.; Bathe, K.J. Transient wave propagation in inhomogeneous media with enriched overlapping triangular elements. Comput. Struct. 2020, 237, 106273. [Google Scholar] [CrossRef]
- Li, Y.; Liu, G.R.; Yue, J.H. A novel node-based smoothed radial point interpolation method for 2D and 3D solid mechanics problems. Comput. Struct. 2018, 196, 157–172. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y.T. An Introduction to Meshfree Methods and Their Programming; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Gui, Q.; Zhou, Y.; Li, W.; Chai, Y.B. Analysis of two-dimensional acoustic radiation problems using the finite element with cover functions. Appl. Acoust. 2022, 185, 108408. [Google Scholar] [CrossRef]
- Chai, Y.B.; Li, W.; Liu, Z.Y. Analysis of transient wave propagation dynamics using the enriched finite element method with interpolation cover functions. Appl. Math. Comput. 2022, 412, 126564. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y.T. A local radial point interpolation method (LRPIM) for free vibration analyses of 2-D solids. J. Sound Vib. 2001, 246, 29–46. [Google Scholar] [CrossRef]
- Gu, Y.; Lei, J. Fracture mechanics analysis of two-dimensional cracked thin structures (from micro- to nano-scales) by an efficient boundary element analysis. Results Math. 2021, 11, 100172. [Google Scholar] [CrossRef]
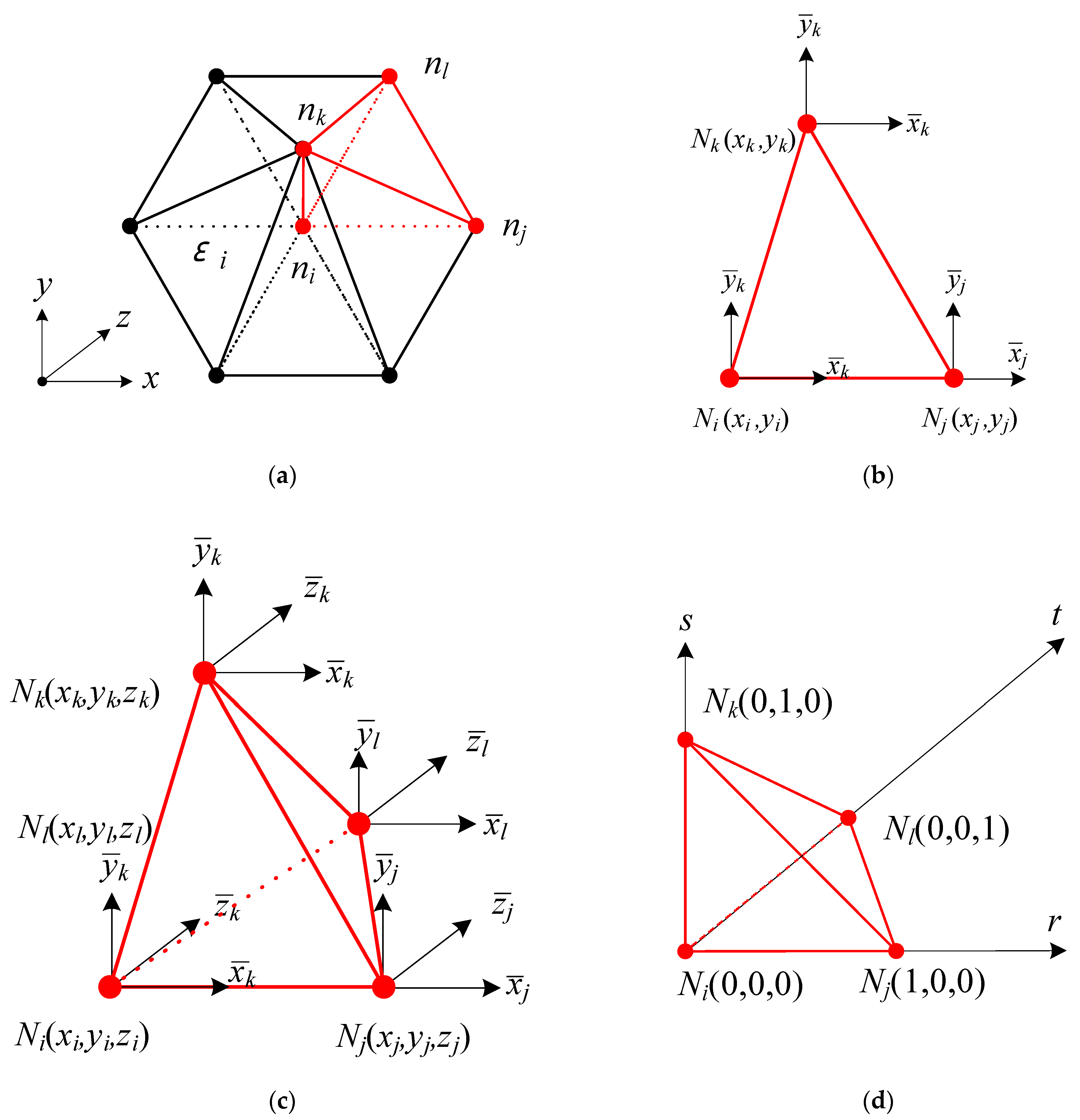



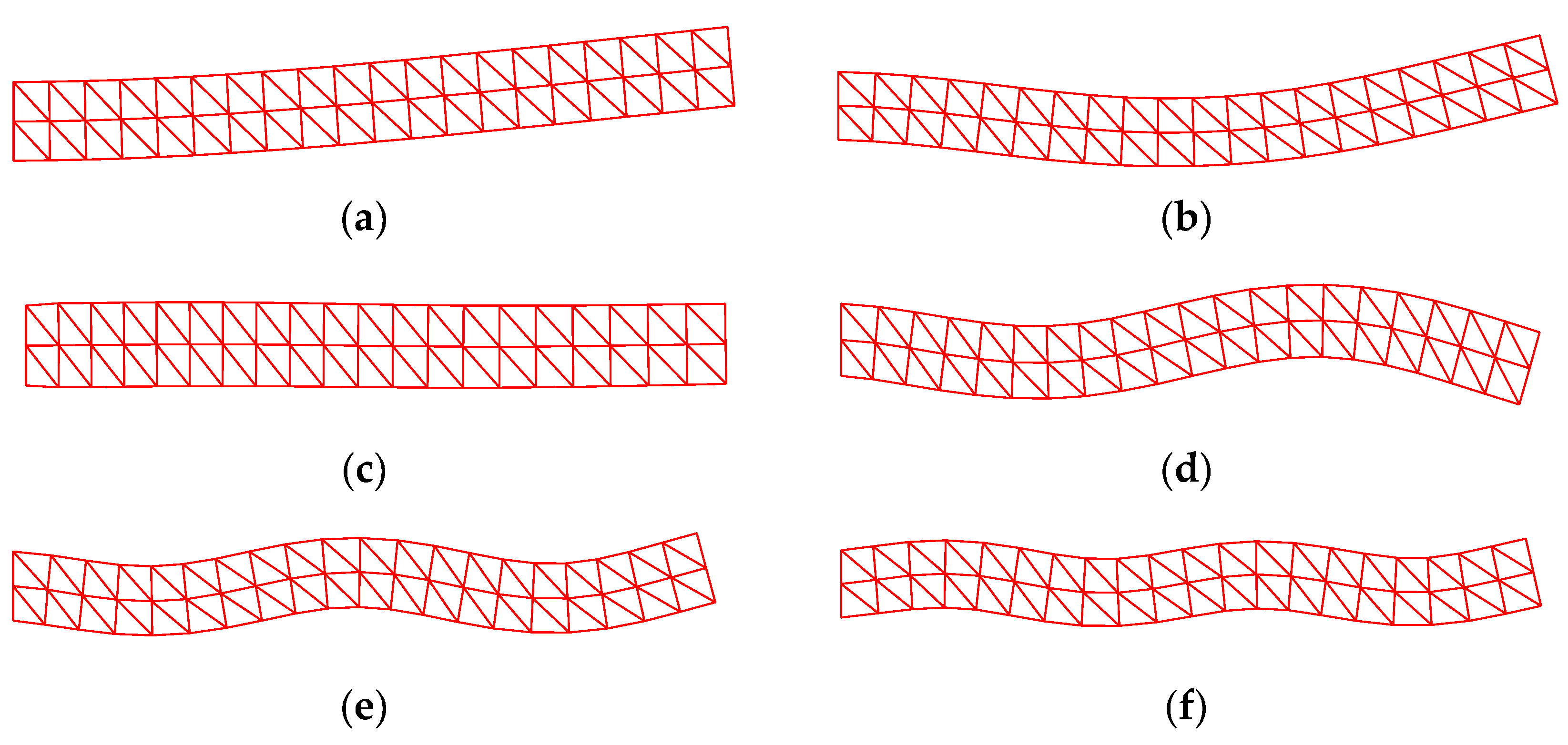


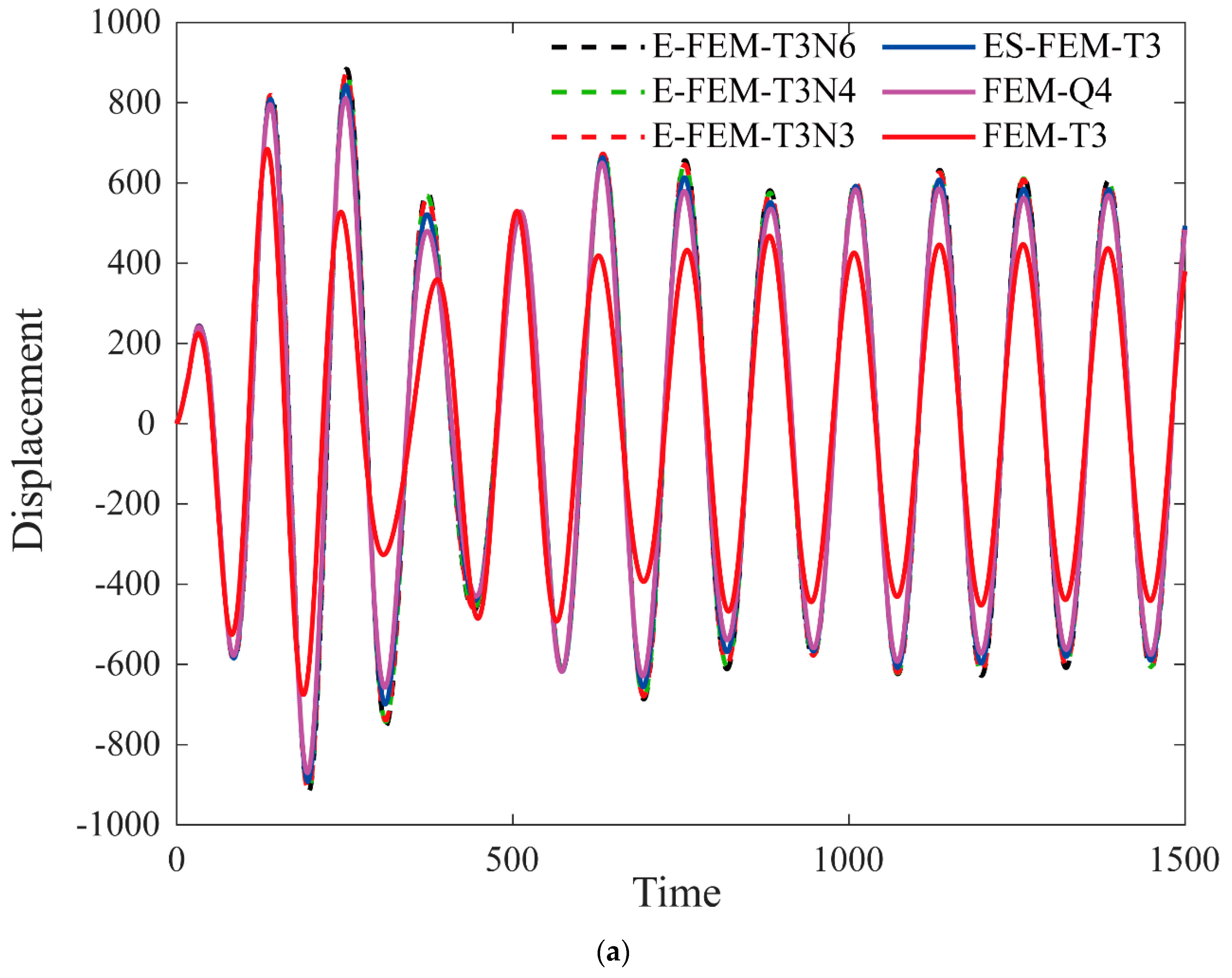
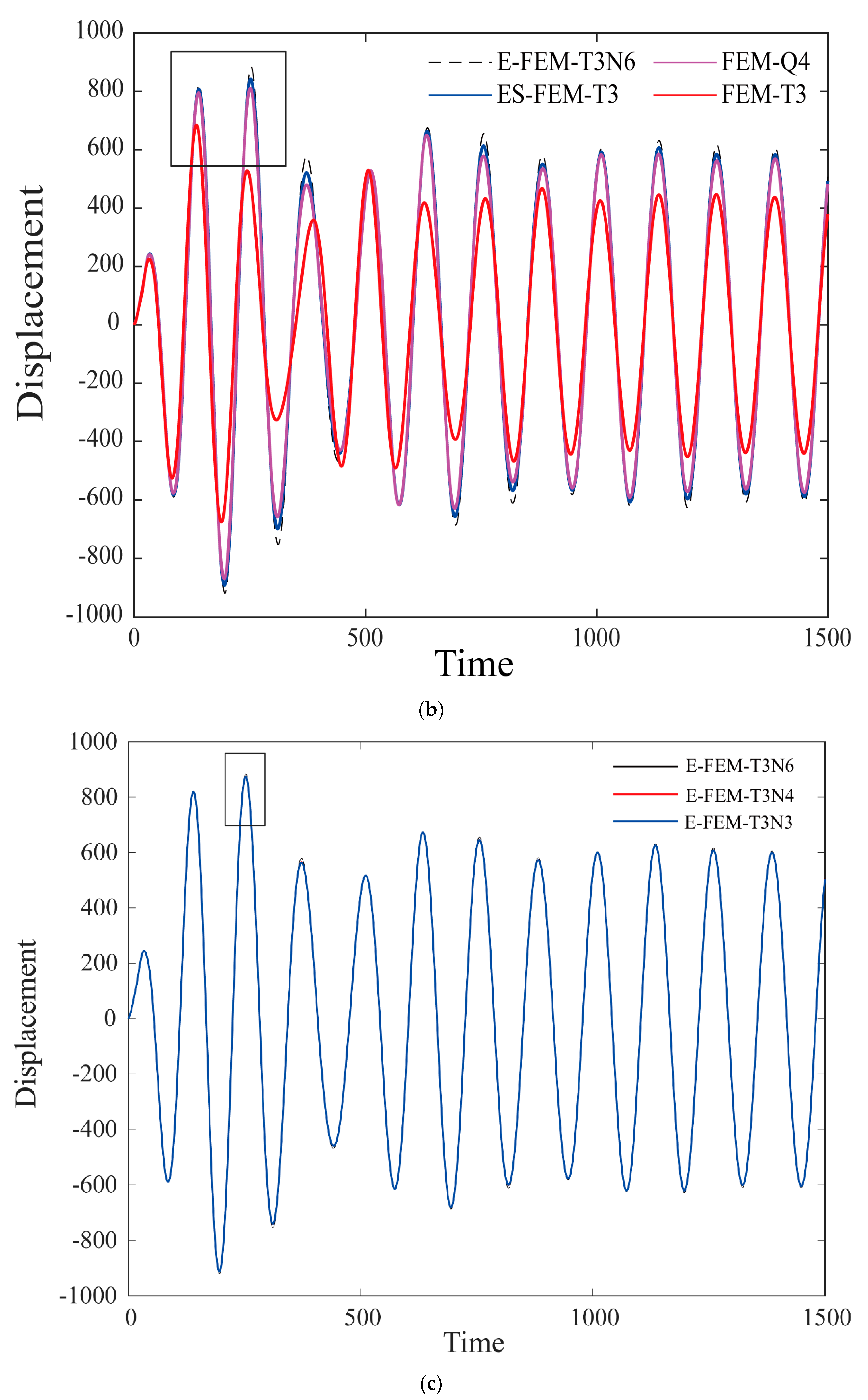
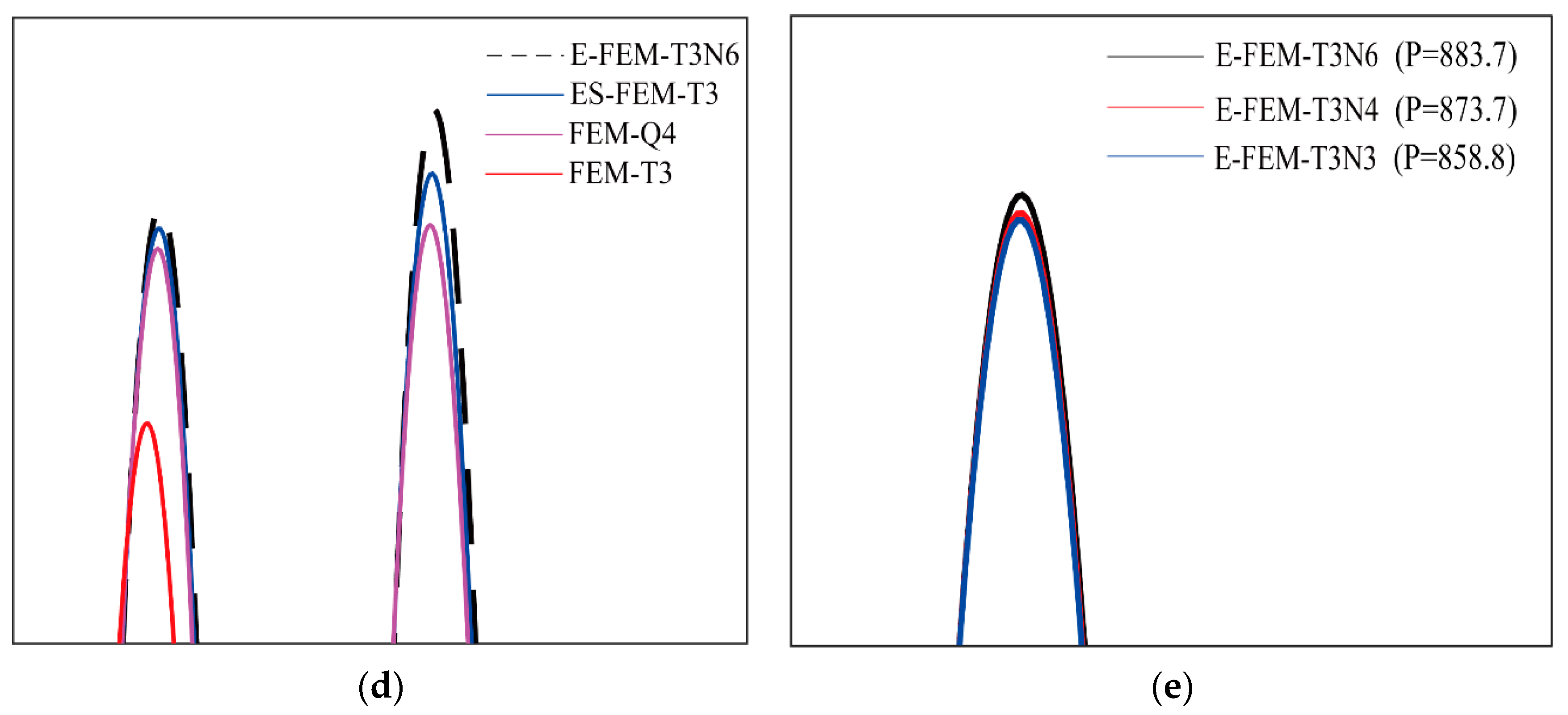



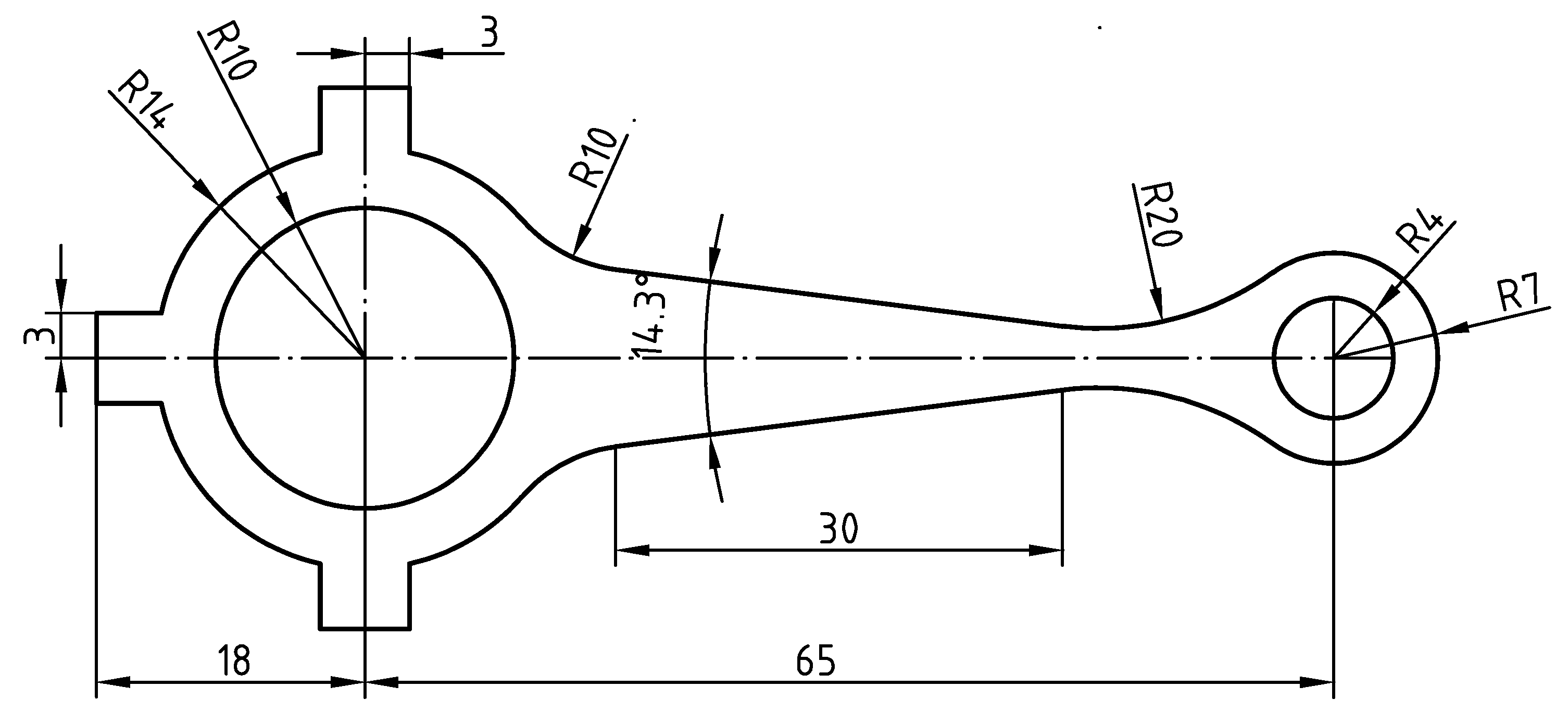
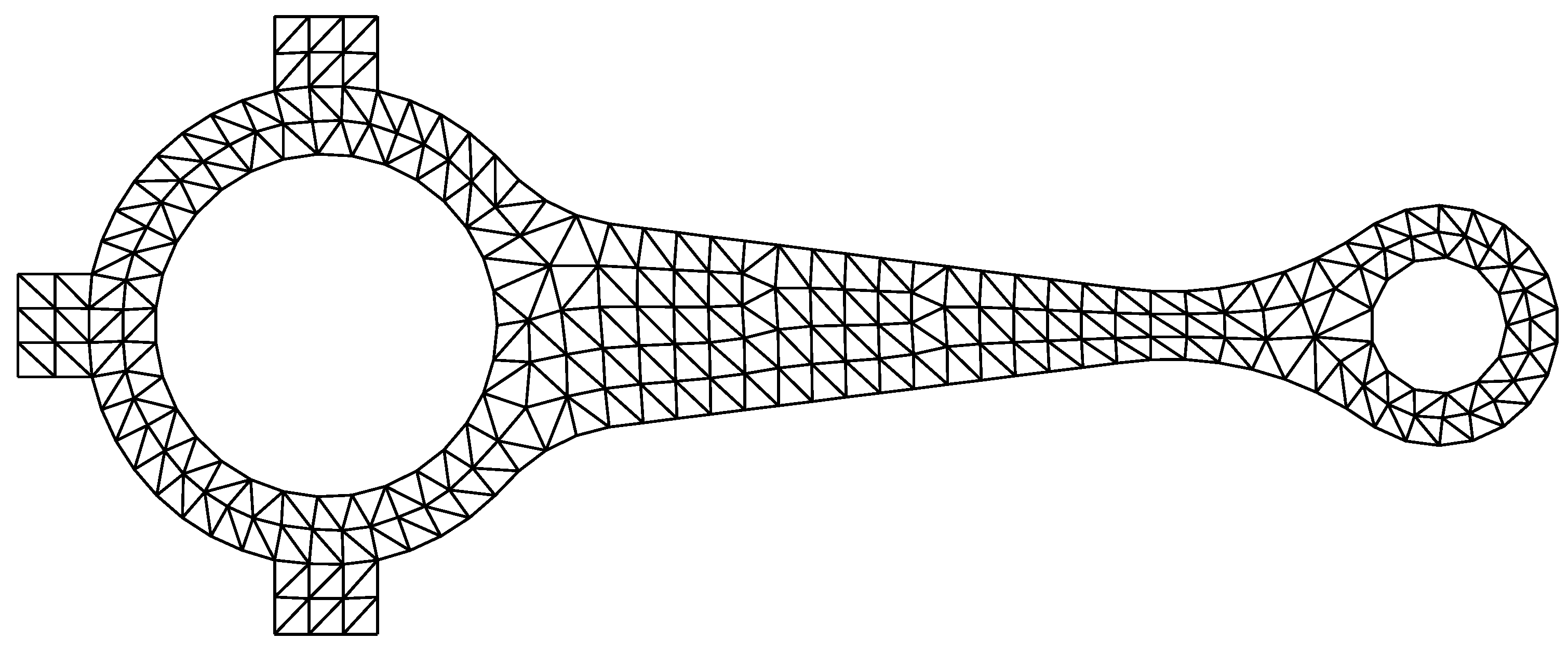
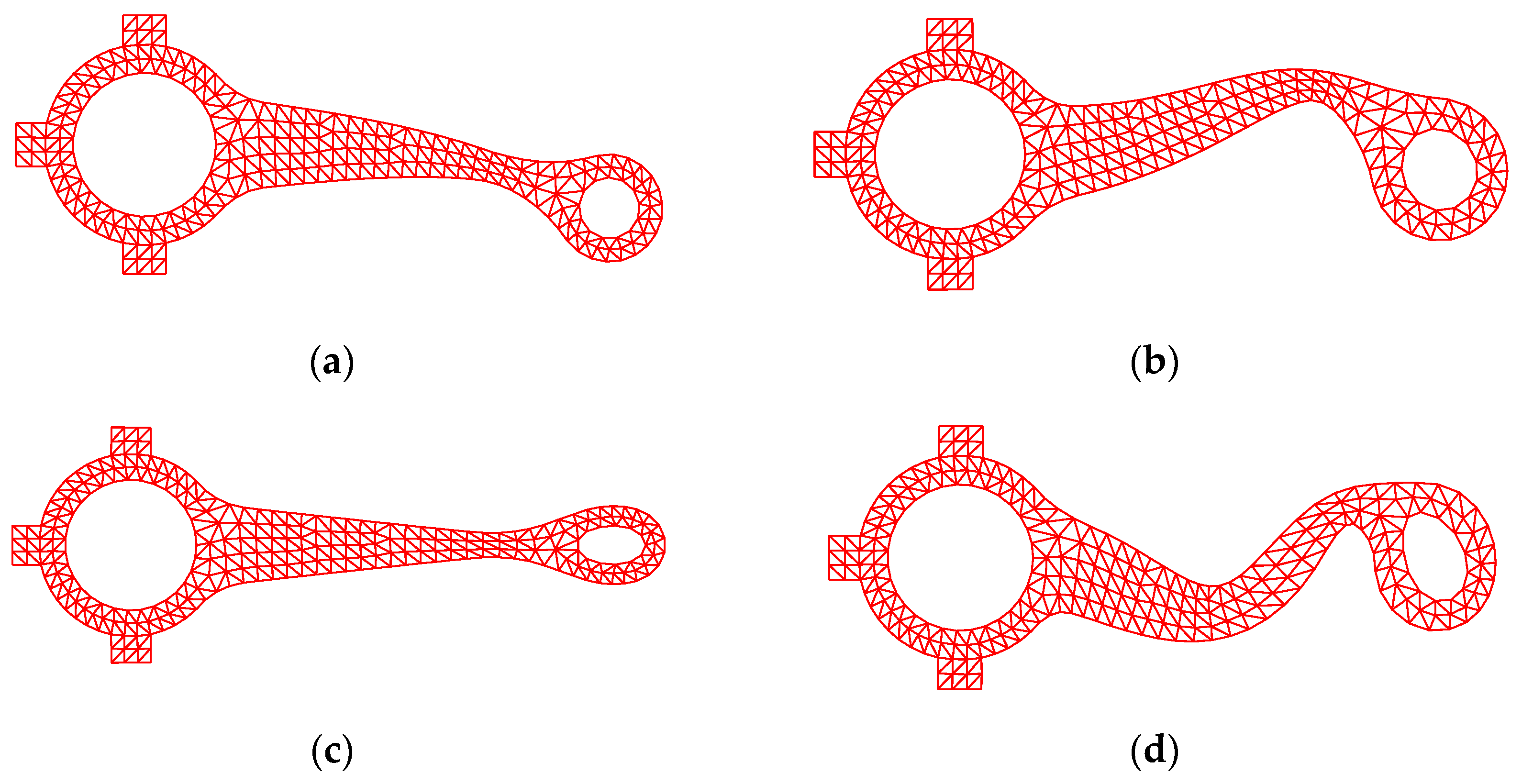
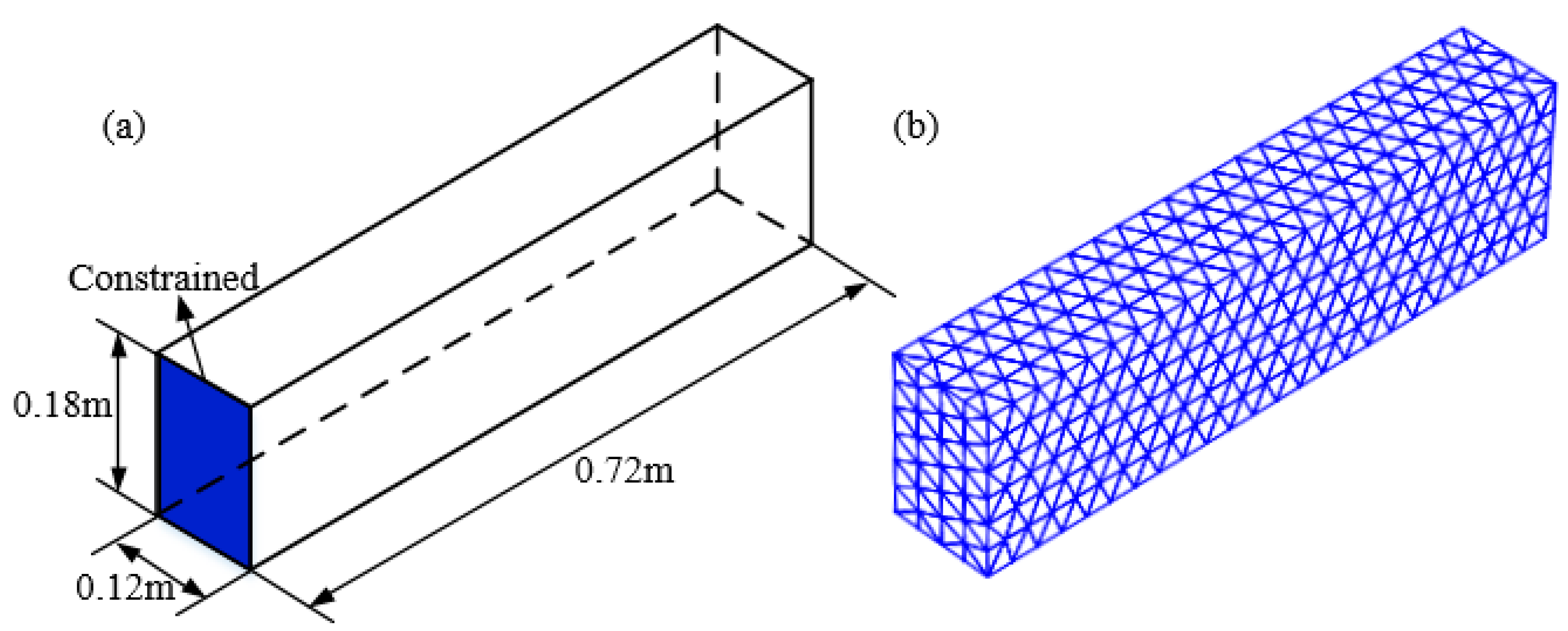
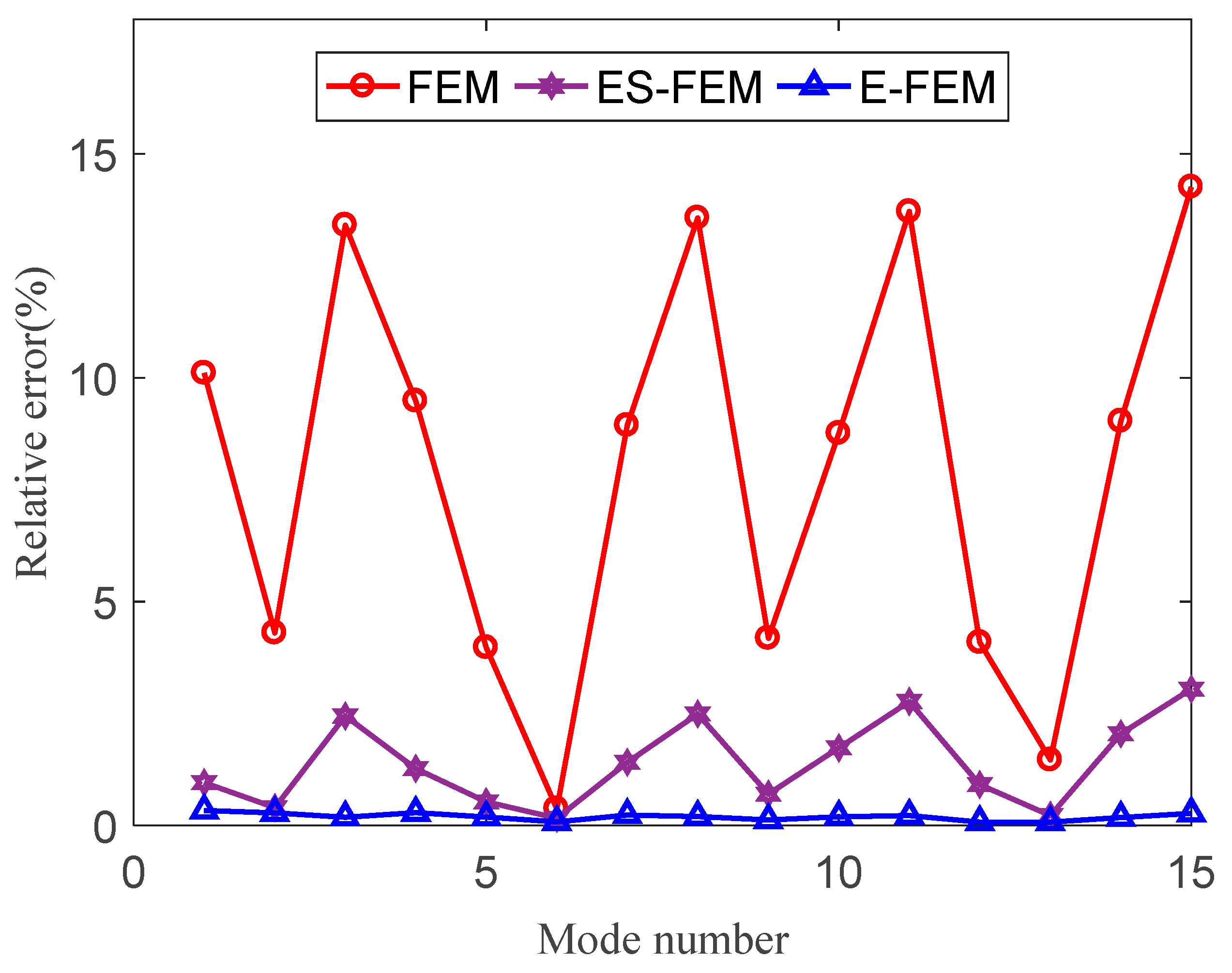
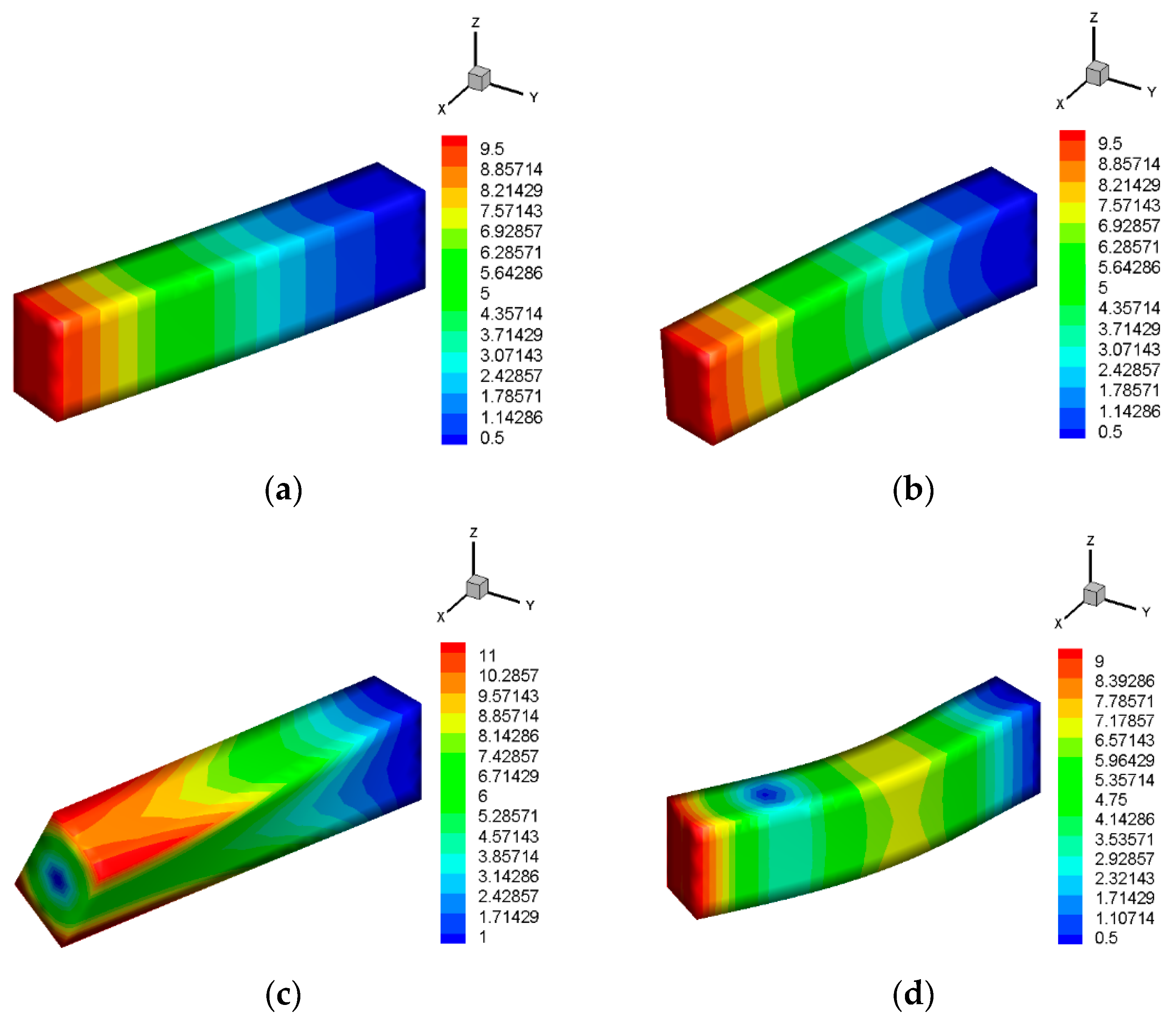
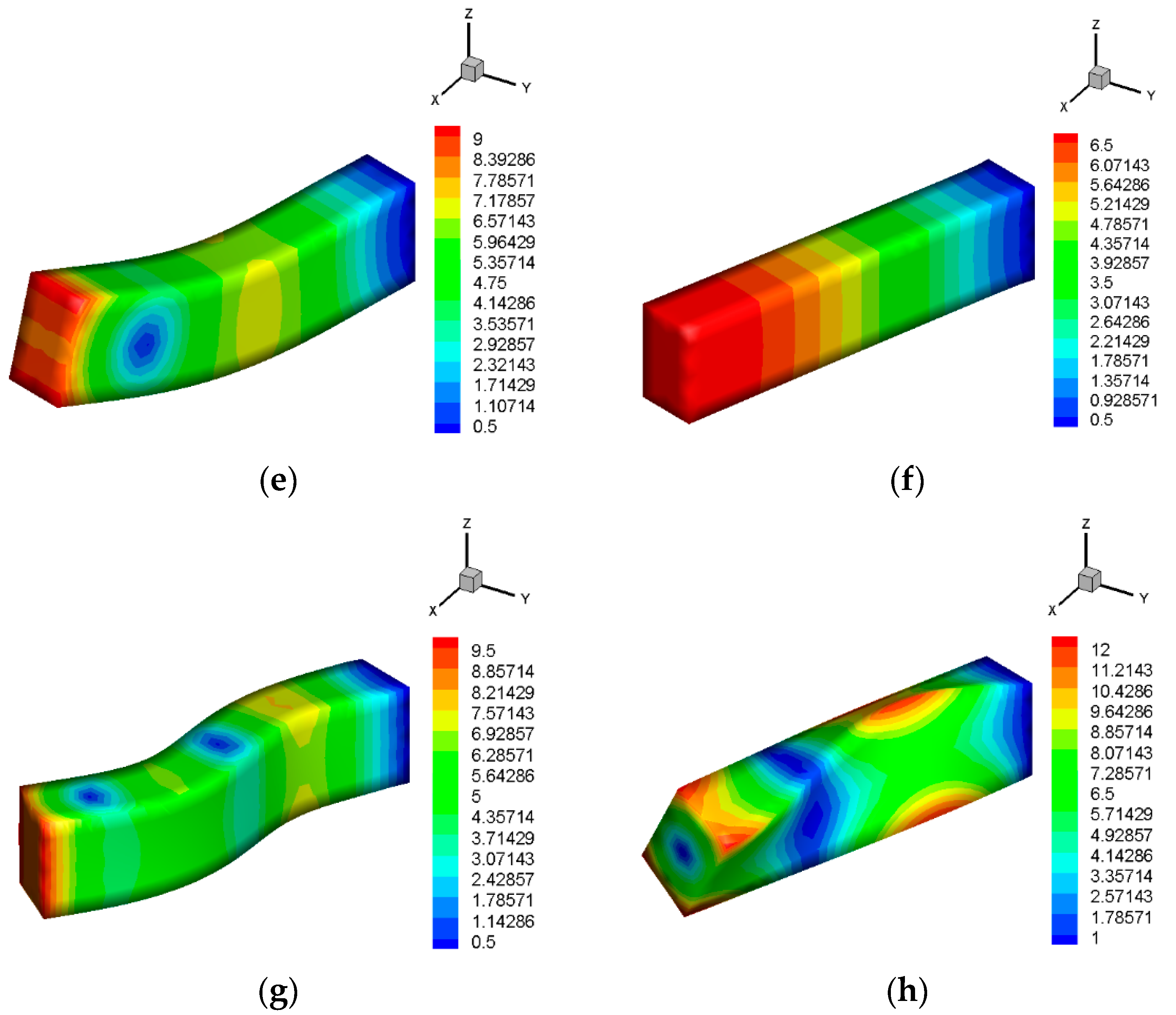

| Order | FEM-T3 | FEM-Q4 | ES-FEM-T3 | E-FEM- T3N3 | E-FEM- T3N4 | E-FEM- T3N6 | References |
|---|---|---|---|---|---|---|---|
| 1708 | 992 | 1048 | 826 | 826 | 823 | 822 | |
| 9689 | 5791 | 6018 | 4997 | 4973 | 4938 | 4932 | |
| 12,908 | 12,834 | 12,833 | 12,834 | 12,833 | 12,827 | 12,824 | |
| 24,331 | 14,830 | 15,177 | 13,311 | 13,174 | 13,014 | 12,993 | |
| 39,193 | 26,183 | 26,362 | 24,523 | 24,111 | 23,670 | 23,611 | |
| 42,944 | 38,140 | 37,724 | 37,946 | 37,051 | 36,149 | 36,010 | |
| 64,559 | 38,824 | 38,559 | 38,482 | 38,473 | 38,453 | 38,444 | |
| 67,691 | 51,924 | 50,349 | 53,047 | 51,413 | 49,865 | 49,578 | |
| 90,810 | 62,345 | 60,827 | 64,059 | 64,032 | 63,990 | 63,913 | |
| 98,302 | 64,846 | 61,520 | 69,457 | 66,800 | 64,440 | 63,975 |
| Order | FEM-T3 | FEM-Q4 | ES-FEM-T3 | E-FEM-T3N3 | E-FEM-T3N4 | E-FEM-T3N6 | References |
|---|---|---|---|---|---|---|---|
| 1120 | 870 | 853 | 824 | 824 | 823 | 822 | |
| 6644 | 5199 | 5078 | 4945 | 4942 | 4935 | 4932 | |
| 12,852 | 12,830 | 12,828 | 12,828 | 12,827 | 12,825 | 12,824 | |
| 17,307 | 13,640 | 13,246 | 13,038 | 13,024 | 13,001 | 12,993 | |
| 31,173 | 24,685 | 23,783 | 23,729 | 23,687 | 23,629 | 23,611 | |
| 38,686 | 37,477 | 35,784 | 36,259 | 36,165 | 36,041 | 36,010 | |
| 47,342 | 38,378 | 38,298 | 38,455 | 38,454 | 38,448 | 38,444 | |
| 64,769 | 51,322 | 48,533 | 50,037 | 49,858 | 49,628 | 49,578 | |
| 65,365 | 63,585 | 61,527 | 63,996 | 63,991 | 63,975 | 63,913 | |
| 84,519 | 65,731 | 63,182 | 64,678 | 64,373 | 63,992 | 63,975 |
| Order | FEM-T3 | FEM-Q4 | ES-FEM-T3 | E-FEM-T3N3 | E-FEM-T3N4 | E-FEM-T3N6 | Reference |
|---|---|---|---|---|---|---|---|
| 907 | 835 | 827 | 823 | 823 | 823 | 822 | |
| 5431 | 5004 | 4950 | 4936 | 4935 | 4933 | 4932 | |
| 12,834 | 12,827 | 12,826 | 12,825 | 12,825 | 12,824 | 12,824 | |
| 14,286 | 13,174 | 13,006 | 13,002 | 13,000 | 12,994 | 12,993 | |
| 25,949 | 23,926 | 23,554 | 23,631 | 23,626 | 23,614 | 23,611 | |
| 38,511 | 36,462 | 35,778 | 36,046 | 36,035 | 36,014 | 36,010 | |
| 39,612 | 38,431 | 38,408 | 38,448 | 38,447 | 38,445 | 38,444 | |
| 54,647 | 50,150 | 49,029 | 49,638 | 49,619 | 49,584 | 49,578 | |
| 64,236 | 63,883 | 62,867 | 63,980 | 63,969 | 63,919 | 63,913 | |
| 70,685 | 64,561 | 63,774 | 64,007 | 63,985 | 63,976 | 63,975 |
| FEM-T3 | FEM-Q4 | ES-FEM-T3 | E-FEM- T3N3 | E-FEM- T3N4 | E-FEM- T3N6 | References | |
| 0.000 | 4256 | 2623 | 2947 | 870 | 851 | 829.0 | 822 |
| 0.025 | 4413 | 2710 | 3163 | 875 | 853 | 829.5 | 822 |
| 0.050 | 4560 | 2889 | 3413 | 890 | 856 | 829.7 | 822 |
| 0.075 | 4674 | 3052 | 3614 | 913 | 860 | 830.0 | 822 |
| 0.100 | 4762 | 3169 | 3758 | 939 | 863 | 830.3 | 822 |
| 0.150 | 4902 | 3296 | 3937 | 983 | 870 | 830.8 | 822 |
| 0.200 | 5023 | 3352 | 4052 | 1007 | 877 | 831.5 | 822 |
| 0.250 | 5137 | 3386 | 4141 | 1018 | 884 | 832.3 | 822 |
| 0.300 | 5248 | 3417 | 4221 | 1024 | 892 | 833.0 | 822 |
| 0.400 | 5468 | 3498 | 4366 | 1030 | 909 | 834.0 | 822 |
| 0.500 | 5688 | 3617 | 4499 | 1033 | 928 | 835.0 | 822 |
| 0.600 | 5910 | 3776 | 4623 | 1035 | 946 | 835.7 | 822 |
| 0.700 | 6134 | 3984 | 4741 | 1037 | 963 | 836.4 | 822 |
| 0.800 | 6361 | 4252 | 4856 | 1039 | 978 | 837.2 | 822 |
| 0.900 | 6591 | 4617 | 4968 | 1040 | 992 | 841.2 | 822 |
| Order | FEM-T3 | ES-FEM-T3 | E-FEM- T3N3 | E-FEM- T3N4 | E-FEM- T3N6 | References |
|---|---|---|---|---|---|---|
| 1376 | 947 | 825 | 824 | 823 | 822 | |
| 8554 | 5663 | 4960 | 4946 | 4936 | 4932 | |
| 12,870 | 12,827 | 12,828 | 12,828 | 12,825 | 12,824 | |
| 21,883 | 14,726 | 13,112 | 13,036 | 13,004 | 12,993 | |
| 38,777 | 27,242 | 23,975 | 23,715 | 23,637 | 23,611 | |
| 40,231 | 38,194 | 36,927 | 36,214 | 36,059 | 36,010 | |
| 62,931 | 39,798 | 38,458 | 38,456 | 38,449 | 38,444 | |
| 67,377 | 54,754 | 51,329 | 49,958 | 49,668 | 49,578 | |
| 86,597 | 62,901 | 64,010 | 63,996 | 63,982 | 63,913 | |
| 94,872 | 72,378 | 66,640 | 64,569 | 64,080 | 63,975 |
| Order | FEM-T3 | ES-FEM-T3 | E-FEM- T3N3 | E-FEM- T3N4 | E-FEM- T3N6 | References |
|---|---|---|---|---|---|---|
| 1584 | 1029 | 825 | 824 | 822 | 822 | |
| 9522 | 6227 | 4978 | 4944 | 4936 | 4932 | |
| 12,887 | 12,826 | 12,828 | 12,828 | 12,825 | 12,824 | |
| 24,124 | 15,611 | 13,283 | 13,030 | 13,002 | 12,993 | |
| 39,120 | 29,557 | 24,373 | 23,704 | 23,635 | 23,611 | |
| 47,170 | 38,019 | 37,259 | 36,235 | 36,078 | 36,010 | |
| 67,566 | 46,072 | 38,460 | 38,455 | 38,448 | 38,444 | |
| 74,501 | 61,371 | 53,065 | 49,995 | 49,708 | 49,578 | |
| 97,634 | 63,573 | 64,021 | 63,993 | 63,981 | 63,913 | |
| 102,709 | 76,854 | 70,025 | 64,674 | 64,180 | 63,975 |
| Order | FEM-T3 | FEM-Q4 | ES-FEM-T3 | E-FEM- T3N3 | E-FEM- T3N4 | E-FEM- T3N6 | References |
|---|---|---|---|---|---|---|---|
| 0.1081 | 0.1044 | 0.1032 | 0.1021 | 0.1019 | 0.1014 | 0.1011 | |
| 0.3681 | 0.3580 | 0.3553 | 0.3520 | 0.3515 | 0.3504 | 0.3497 | |
| 0.3855 | 0.3839 | 0.3836 | 0.3830 | 0.3828 | 0.3826 | 0.3825 | |
| 0.6312 | 0.6029 | 0.5916 | 0.5839 | 0.5823 | 0.5788 | 0.5767 | |
| 0.8094 | 0.7773 | 0.7677 | 0.7587 | 0.7579 | 0.7549 | 0.7532 | |
| 0.9503 | 0.9275 | 0.9214 | 0.9135 | 0.9119 | 0.9103 | 0.9094 | |
| 1.0352 | 1.0061 | 0.9983 | 0.9898 | 0.9882 | 0.9865 | 0.9857 | |
| 1.1459 | 1.1247 | 1.1158 | 1.1106 | 1.1045 | 1.1021 | 1.1007 | |
| 1.2045 | 1.1673 | 1.1552 | 1.1450 | 1.1434 | 1.1404 | 1.1389 | |
| 1.2276 | 1.1944 | 1.1844 | 1.1760 | 1.1750 | 1.1720 | 1.1724 |
| Order | FEM-T3 | FEM-Q4 | ES-FEM-T3 | E-FEM- T3N3 | E-FEM- T3N4 | E-FEM- T3N6 | References |
|---|---|---|---|---|---|---|---|
| 158.4 | 144.6 | 140.9 | 144.8 | 142.1 | 141.2 | 140.7 | |
| 709.6 | 650.5 | 630.6 | 643.4 | 635.4 | 631.8 | 622.6 | |
| 1541.1 | 1535.2 | 1525.7 | 1555.4 | 1543.8 | 1535.4 | 1522.5 | |
| 1760.1 | 1644.7 | 1585.7 | 1578.5 | 1569.6 | 1565.5 | 1563.9 | |
| 3220.1 | 3028.4 | 2871.2 | 2897.3 | 2877.6 | 2857.3 | 2839.1 | |
| 3873.4 | 3797.9 | 3628.6 | 3586.1 | 3496.4 | 3484.1 | 3468.1 | |
| 4832.3 | 4503.2 | 4104.1 | 4259.5 | 4151.6 | 4040.5 | 3986.3 | |
| 5478.4 | 5274.7 | 4932.2 | 4996.4 | 4866.8 | 4846.3 | 4821.2 | |
| 5760.9 | 5473.5 | 4994.5 | 5017.9 | 4977.8 | 4957.9 | 4936.5 | |
| 6495.1 | 6177.8 | 5953.1 | 6251.6 | 6131.9 | 6081.5 | 6050.5 |
| Order | FEM | ES-FEM | E-FEM | Reference |
|---|---|---|---|---|
| 207.73 | 190.47 | 189.30 | 188.67 | |
| 286.97 | 276.23 | 275.90 | 275.14 | |
| 1060.39 | 957.89 | 936.74 | 935.04 | |
| 1155.80 | 1069.11 | 1058.69 | 1055.70 | |
| 1445.77 | 1397.85 | 1393.07 | 1390.50 | |
| 1786.54 | 1782.74 | 1781.27 | 1779.90 | |
| 2823.05 | 2627.97 | 2597.55 | 2591.50 | |
| 3187.11 | 2876.26 | 2811.92 | 2806.40 | |
| 3318.56 | 3207.69 | 3189.32 | 3185.40 | |
| 4798.67 | 4488.68 | 4420.82 | 4412.30 | |
| 5323.91 | 4811.58 | 4692.26 | 46,820 | |
| 5343.23 | 5180.15 | 5137.22 | 5133.40 | |
| 5373.71 | 5307.97 | 5299.98 | 5296.20 | |
| 6963.50 | 6517.56 | 6397.92 | 6386.80 | |
| 7500.03 | 6764.03 | 6581.80 | 6564.10 |
| Order | FEM | ES-FEM | E-FEM | FEM (Fine) | Reference |
|---|---|---|---|---|---|
| 582.14 | 528.66 | 525.51 | 541.21 | 522.99 | |
| 620.30 | 557.66 | 552.29 | 570.38 | 551.98 | |
| 1420.51 | 1105.39 | 1071.56 | 1160.39 | 1053.10 | |
| 3848.07 | 3571.62 | 3539.52 | 3624.49 | 3509.70 | |
| 4650.39 | 4152.56 | 4121.00 | 4256.49 | 4099.30 | |
| 5092.29 | 4688.78 | 4599.24 | 4751.62 | 4527.90 | |
| 8137.86 | 7794.29 | 7744.57 | 7881.27 | 7715.50 | |
| 10,191.39 | 8462.14 | 8271.87 | 8877.15 | 8104.20 | |
| 10,948.29 | 9737.92 | 9521.96 | 10,126.97 | 9242.10 | |
| 11,277.62 | 9977.75 | 9800.76 | 10,134.92 | 9624.20 | |
| 12,190.94 | 10,549.44 | 10,423.65 | 10,812.64 | 10,191.00 | |
| 15,146.03 | 12,015.30 | 11,664.54 | 12,570.43 | 11,327.00 | |
| 17,553.76 | 15,962.76 | 15,766.72 | 16,389.37 | 15,587.00 | |
| 19,701.50 | 17,353.71 | 17,125.72 | 17,825.40 | 16,870.00 | |
| 21,737.13 | 18,887.72 | 18,588.77 | 19,513.86 | 18,040.00 |
| Order | FEM | ES-FEM | E-FEM | FEM (Fine) | Reference |
|---|---|---|---|---|---|
| 193.75 | 159.44 | 157.18 | 167.46 | 155.32 | |
| 993.98 | 881.23 | 862.16 | 914.48 | 848.42 | |
| 1089.25 | 952.41 | 945.81 | 960.43 | 937.93 | |
| 1188.08 | 978.71 | 962.14 | 1018.88 | 950.71 | |
| 1877.99 | 1717.52 | 1703.89 | 1748.93 | 1686.60 | |
| 2134.42 | 2088.82 | 2080.74 | 2091.49 | 2063.20 | |
| 2675.84 | 2217.36 | 2163.85 | 2301.22 | 2130.50 | |
| 2792.76 | 2342.92 | 2291.51 | 2419.86 | 2256.90 | |
| 3279.08 | 2935.65 | 2906.53 | 3001.27 | 2863.10 | |
| 3790.99 | 3206.87 | 3105.93 | 3306.54 | 3055.20 | |
| 3857.71 | 3557.73 | 3526.29 | 3610.49 | 3478.20 | |
| 5209.41 | 4433.95 | 4348.32 | 4554.320 | 4289.50 | |
| 5422.11 | 4927.43 | 4863.51 | 5013.80 | 4734.90 | |
| 6159.29 | 5218.63 | 4981.44 | 5324.24 | 4878.10 | |
| 6637.36 | 5724.11 | 5529.93 | 5848.54 | 5451.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Q.; Han, H.; Zhou, G.; Wu, F.; Ju, Z.; Hu, M.; Chen, D.; Hao, Y. Enriched Finite Element Method Based on Interpolation Covers for Structural Dynamics Analysis. Machines 2023, 11, 587. https://doi.org/10.3390/machines11060587
Gu Q, Han H, Zhou G, Wu F, Ju Z, Hu M, Chen D, Hao Y. Enriched Finite Element Method Based on Interpolation Covers for Structural Dynamics Analysis. Machines. 2023; 11(6):587. https://doi.org/10.3390/machines11060587
Chicago/Turabian StyleGu, Qiyuan, Hongju Han, Guo Zhou, Fei Wu, Zegang Ju, Man Hu, Daliang Chen, and Yaodong Hao. 2023. "Enriched Finite Element Method Based on Interpolation Covers for Structural Dynamics Analysis" Machines 11, no. 6: 587. https://doi.org/10.3390/machines11060587
APA StyleGu, Q., Han, H., Zhou, G., Wu, F., Ju, Z., Hu, M., Chen, D., & Hao, Y. (2023). Enriched Finite Element Method Based on Interpolation Covers for Structural Dynamics Analysis. Machines, 11(6), 587. https://doi.org/10.3390/machines11060587







