Abstract
Since the stagnation point is subject to straining motion, this 3D experiment is an effort to simulate the stagnation plane, which applies to studying the particle erosion in rotary machine blades, such as wind turbines, gas turbines, and compressors. Wind turbine blade erosion, caused by particles such as sand, ice, insects, raindrops, and snowflakes, can significantly impact turbine efficiency, as with other rotary machines. Previous research has indicated that flow geometry and gravity can influence particle dynamics statistics. The current study’s laboratory experiment simulates the airfoil’s stagnation plane to investigate how floating particles cause erosion. The experiment involves seeding tracers and inertial particles in a strained turbulent flow with specific turbulent intensity, strain rate, and the presence of gravity. It is conducted on initially homogeneous turbulence undergoing a sudden axisymmetric expansion. The flow was generated in . The Lagrangian particle tracking technique based on the 4-frame best estimate method was employed to measure the velocity field. The obtained results are with two different mean strain rates and Reynolds–Taylor microscales in the presence of gravity, which has not been considered in most numerical studies in a particle-laden turbulent flow. It provides a transparent window to investigate how particles of different sizes with distinct strain rates flow and their relationship to the turbulence intensity affects the erosion. Two most important issues are observed in the presence of gravity: Increasing the turbulence intensity from to 160 led to a 10–23% increase in the erosion ratio, depending on the particle type and the flow strain rate. Likewise, a doubled mean strain rate of the flow (caused by deformation/shear flow) resulted in a 3–10% increase in erosion, depending on the particle type and Reynolds number. Moreover, the influence of gravity could potentially play a significant role in this observation.
Keywords:
rotary machine; erosion; particle-laden turbulent; stagnation point; blade; airfoil; turbine; compressor 1. Introduction
The problem of blade erosion in turbomachines is of utmost importance for their effective utilization. In wind turbines, erosion at the leading edge is predominantly caused by ice, rain, hail, or airborne particles, such as dust, sand, pollutants, and insects. The outer region of the turbine blade experiences a higher relative velocity compared to the inner part, which is why leading-edge erosion mainly occurs in this region [1]. The aerodynamic properties of a wind turbine blade significantly impact its performance. Erosion unevenly removes portions of the blade surface, resulting in changes to the profile’s surface and subsequent reduction in aerodynamic performance. This loss of structural integrity in the blade surface is a driving factor for decreased performance [2]. The decrease in turbine efficiency and the need for expensive on-site repairs are the direct consequences of blade erosion. Turbine operators also face economic consequences, including reduced production and reliability. Recent studies indicate that offshore turbines experience accelerated leading-edge erosion due to environmental factors. This issue of leading-edge erosion in wind turbine blades is particularly critical in the first few years of commissioning, given their 25-year service life [2].
The deleterious effects of solid particle erosion in gas turbines are a significant area of concern in the field. The ingestion of airborne particles, such as sand, dust, and wind ash, in the turbine operation environment cannot be avoided, rendering it an inevitable challenge for gas turbine systems. The resulting impact of these particles on gas turbine components, particularly rotor blades and stator vanes, can lead to severe and destructive outcomes, ultimately resulting in a decline in the turbine’s overall performance and structural integrity [3,4].
The erosion of last-stage blades in steam turbines remains a significant challenge in the field, which can lead to a reduction in overall turbine efficiency and structural damage [5]. Extensive research efforts have been devoted to mitigating this issue, including approaches such as erosion protection, low-pressure erosion, and erosion prediction. Among these strategies, a prominent solution that has received considerable attention is the utilization of materials with high erosion resistance. This approach has shown promising results in enhancing the durability and reliability of steam turbine blades, ultimately contributing to improved turbine performance and operational longevity [5].
High-pressure compressors and jet engine fans are heavily impacted by erosion caused by solid particles, as reported in [6,7]. Thin airfoils in the erosion areas are particularly affected by the high-momentum solid particles, leading to a change in the airfoil’s shape, as noted in service experience reports [8]. Erosion’s destructive effects, including pitting and cutting back of leading edges and thinning of trailing edges, results in a shortened chord length of axial compressor blades, as reported in [9]. Moreover, this factor increases the surface roughness [10]. In general, erosion caused by solid particles involves particle transport in fluid flow [11], particle-wall interaction [12], particle fracture [13], and material loss. To investigate the particle behavior leading to erosion using numerical methods, complex numerical models are required to simulate turbulent flows [14].
The majority of studies investigating surface erosion primarily examine the influence of erosion levels on turbomachinery performance [15,16]. Some studies employ numerical methods or experiments to quantify the extent of damage and its associated effects [17]. Additionally, there are research efforts dedicated to developing coatings and materials aimed at minimizing the impact of erosion and preventing a decline in machinery efficiency [17,18]. However, there exists a gap in the examination of particle size as a factor in leading-edge erosion, specifically in relation to blades and impellers. Deshun et al. [19] highlighted the significance of the Stokes number as a critical measure for assessing the effects of particles on wind turbine airfoil erosion.
The motivation behind this study stems from the predominant use of numerical methods in investigating airfoil and blade erosion, which often face limitations in computational techniques when dealing with large problem sizes. To address this issue, the current study introduces a fresh empirical approach to analyzing surface erosion on rotary components, with particular emphasis on the particle scale near the stagnation point. By incorporating various influential factors, including turbulence intensity, strain deformation, gravity, and particle size, the aim is to understand their effects comprehensively. In addition, the proposed approach puts forward a quantitative measurement technique based on the impact of particles on the surface. This methodology provides a metric scale that enables researchers to assess the erosion process in a more objective manner, considering the number of particles that make contact with the surface versus those that do not. Overall, this study offers a novel perspective by bridging the gap between numerical methods and empirical approaches, allowing for a more detailed analysis of surface erosion on rotary components. By considering multiple parameters and implementing a quantitative measurement strategy, a deeper understanding of erosion phenomena can be achieved.
As mentioned above, particle-laden turbulence is a matter causing surface erosion in the turbomachine components. Therefore, it is essential to be able to examine the particle motion in turbulent flow conditions around the streamlined body and stagnation point, which is the primary area where particles collide with the surface. The findings of this study may offer insights into effective strategies for mitigating particle erosion and identifying potential solutions to this issue or enhancing available strategies. The idea of the current study is based on these three concepts: (a) the stagnation point is subject to strain flow motion [20,21], (b) the turbulent flow and particle effects [22,23], and (c) the presence of gravity affects the particle motion [24,25,26]. The current study proposes an empirical simulation for particles in turbulent flow dealing with different strain rates and turbulence intensity to examine the leading-edge erosion and similar areas [27,28]. Furthermore, this experiment was conducted with the presence of gravity, which is overlooked in most numerical simulations; there is a considerable lack of information about its effects [29]. The suggested method applies to a wide range of fundamental and industrial applications. Hence, this paper is organized as follows: The applied methodology and theory are presented in Section 2. The experiment is explained in Section 3. The results and discussion are represented in Section 4, and Section 5 provides the conclusions.
2. Methods
The fluid flow in the operation of the rotary machine is in the range of turbulent flow [30,31]. It is well known that statistics properties are applicable in turbulent flow studies [32,33]. In order to simulate a stagnation plane in turbulent flow, the applied theory is described in this section. Moreover, the methodology to perform the experiment, generate seeded particles flow, and define initial conditions is described.
2.1. Theory
The stagnation point is subjected to strained flow [34,35]. In order to examine the motion of the particles in the stagnation point area, the current study develops a turbulent flow model in the form of strained flow with a specified mean strain rate and turbulence intensity in the presence of gravity, which its effects are unknown numerically [36,37,38]. In Figure 1, a schematic representation of the generated turbulent flow is depicted. It sketches a container filled with water, which serves as the fluid. The water within the container possesses a specific turbulence intensity that has been selected for this study. The measurement area, positioned at the center of the container, exhibits a nearly homogeneous flow. To induce the desired flow characteristics, the flow within this region is altered through compression using two circular plates. These plates are adjusted at a specific rate to deform the flow, effectively simulating a stagnation plane within the measurement area. The primary objective of this experimental setup is to investigate the movement of particles within the designated measurement area under controlled conditions. By simulating the stagnation plane, the experiment aims to analyze and understand the behavior of particles in this particular region. Equation (1) describes the mean flow field in strained turbulent flow [30,39]:
where is the primary strain rate in the y- direction, and S is the mean strain rate in the two other x- and z-directions (The strain rate is a measure of the velocity gradient within a flow.). The variables x, y, and z are locations. This study creates three-dimensional (3D) flow and applies two-dimensional (2D) techniques to measure the flow features; therefore, properties in the z-direction have not been addressed. Equation (1) determines the laminar flow; however, it is well known that in turbulent flow, the velocity fluctuates.
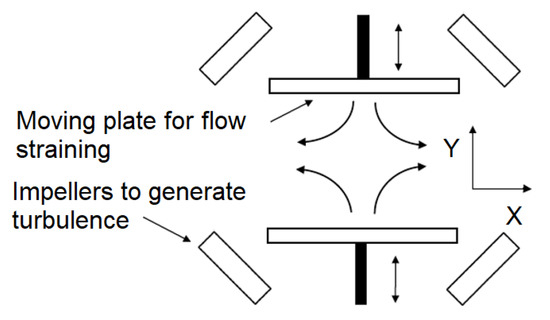
Figure 1.
A sketch of the straining turbulent flow simulation [21].
2.2. Turbulent Flow Characterizations
The turbulence flow statistics were used to extract the flow field properties. To analyze the trajectories of particles in the flow field, the Lagrangian particle tracking (LPT) technique was used. Accordingly, the velocity fluctuations and can be calculated as
where U is the measured (total) velocity, is the mean velocity, and the subscript i refers to the component of the velocity, in the x-, y- (or z)-direction.
To identify the Reynolds–Taylor microscale range in the experiment, it is essential to calculate the flow characteristics, such as the turbulent energy dissipation rate, integral length scale (the integral length scale is regarded as a characteristic scale for the largest motions present in a turbulent flow), Kolmogorov length, and time scales (the Reynolds–Taylor microscale is a length scale employed to describe turbulent fluid flow dynamics. The Taylor microscale represents an intermediate-length scale where the influence of fluid viscosity becomes significant, affecting the dynamics of turbulent eddies in the flow). The current study applies a procedure based on Hassanian et al. [40] to obtain this data. To perform the procedure, it must be noted that the experiment must be conducted with tracer particles and without strain deformation initially. Then the particle image velocimetry (PIV) [41] technique must be applied using a second-order longitudinal velocity structure function [30,40]. The detail of the procedure can be found in [40,42]. In this study, the flow cases properties in the experiments have been measured as follows; turbulent energy dissipation rate m/s (the trbulent energy dissipation rate refers to the rate at which the turbulence kinetic energy is converted into internal thermal energy); Kolmogorov time scale ms (the Kolmogorov scale represents the smallest scales in turbulent fluid flow, where the viscosity becomes dominant and the turbulence kinetic energy is dissipated into thermal energy).
2.3. Stokes Number
Current work uses LPT to track the particle in the generated turbulent flow. Therefore, the Stokes number must be considered for particles. The Stokes number specifies whether a particle introduced to the flow will follow the flow streamline or not. This identification is defined by Equation (3) [43].
where is the Stokes’ relaxation time, is the Kolmogorov time scale, and is the Stokes number. The Kolmogorov scale is based on the flow quantities before applying the strain. The Stokes’ relaxation time is, in turn, calculated by Equation (4) [40,43]
where is the particle density, is a spherical particle diameter, and is the dynamic fluid viscosity that, in this experiment, is water. Both the Stokes’ relaxation time and the Kolmogorov time scale are required in Equation (3). The relaxation time for particles is calculated based on the particle property from Equation (4). A Stokes number significantly greater than 1 () describes particles that are unaffected by a fluid velocity change and continue their original trajectory; if , the particle will follow the fluid’s local velocity. To evaluate both types of particles used in this experiment to the actual erosion particle, the non-dimensional time scale is determined as below:
where is the non-dimensional time scale, is the strain rate time scale and is the mean strain rate. To apply this definition, the Stokes’ relaxation time for any particle type is calculated from the physical properties, and then the non-dimensional time scale ratio is achieved. In this study, hail, raindrops, sand and insects were compared to seeded particles in similar flow conditions for flow around the S809 airfoil from the experiment [44] that was conducted with a wind speed flow 14 m/s, angle of attack 10 degrees, chord length 150 mm, and strain rate in the x-direction [21].
Table 1 shows estimates of the time scales from different particle types expected in the real wind turbine flow and other turbomachines. The last two rows show the same dimensionless timescale in our experiment. Although it is clear that our experiment does not directly match the particles identified in the table, it is still clear that our experiment lies in the region of interest in terms of the parameter space.

Table 1.
The non-dimensional time scale calculated for mean velocity flow around the S809 airfoil from experiment [44] with speed flow 14 m/s, angle of attack 10 degrees, chord length 150 mm, and strain rate in the x-direction [21,45].
2.4. Stagnation Plane Definition
As discussed above, the flow near the stagnation point in the experiment is similar to that near objects with stagnation points, such as the leading edge of a turbine blade, compressor blade, and rotor vane. The particle collision study with the stagnation plane is based on the following concepts and methods:
- In the Lagrangian particle tracking method (LPT), the path line of each particle can be followed from the time it entered the study area to the time it left.
- When particles encircle the streamlined body, two-particle states can be observed; the particles either pass the stagnation plane or continue their path without crossing the stagnation plane.
The stagnation plane location is identified initially by observing all the trajectories that were measured in the fluid. A stagnation coordinate is where the flow and particles have almost zero velocity. It must be noted that the coordinate of the stagnation point for every flow case is expected to be unique. Based on the two previous concepts, we must examine whether each particle passed the stagnation plane location or not to study the collision of particles. The number of particles entering and leaving the study area can be counted. The ratio of the counted particles passing the stagnation plane to the number of particles counted can be obtained as a normalized measure. In this case, a higher ratio for each flow case indicates more particles colliding with the surface and more erosion. The effects of various factors on the erosion rate are evaluated by changing the turbulence intensity, mean strain rate, and particle size in the presence of gravity.
3. Apparatus
The experiment was performed in a water tank with eight impellers mounted in the cube’s corners and pointed into the center of the tank (see Figure 2). They rotated at particular speeds, measured in the , and simulated the turbulent flow. This flow facility produced a nearly stationary homogeneous isotropic turbulence near the center of the tank, where the measurements were conducted. The water tank (60 cm× 60 cm × 60 cm) had 20 mm thick acrylic walls (transparent Plexiglas XT) that enabled optical access to the data. An aluminum frame held the components of the turbulence box together. The fluid was seeded with tracer particles and inertial particles with median diameters 8–10 m and 210–250 m, respectively. The specific gravity for the tracers was 1.1 g/cm (hollow glass) and 2.5 g/cm (solid glass) for the inertial particles. The tank had two circular flat disks which were located up and down; they moved toward each other vertically in the center of the tank and generated a specified mean strain rate. The flow cases were examined with two mean strain rates: −4 and −8 s, mainly in the y-direction. Based on the Equation (1), the strain rates in the two other directions were 2 s and 4 s, respectively. The measurement area was located in the center of the tank with a size of 24.5 × 24.5 mm (Figure 3). The Lagrangian particle tracking (LPT) technique was applied to track the particle and extract the particle dynamics features.

Figure 2.
A photo of the facility used in the experiment. A tank containing water seeded with tracer and inertial particles separately; impellers generate turbulence flow, while two circular plates cause strain deformation with a particular mean strain rate. The laser sheet has been synchronized with a high-speed camera to record the frames.
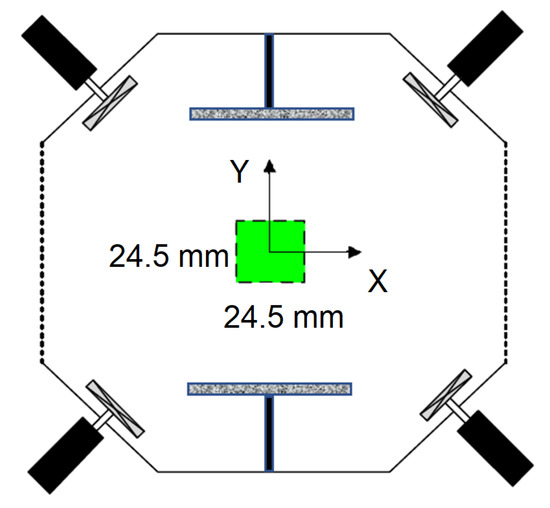
Figure 3.
A side-view sketch of the facility illustrates the measurement area location, size, and coordinate system [21].
Lagrangian particle tracking (LPT) is a non-intrusive optical technique commonly employed in experimental fluid dynamics. It involves capturing images of particles suspended in a fluid and tracking the individual particles within a small interrogation window. In the case of 2-dimensional LPT, the flow field is observed within a thin plane illuminated by a laser sheet, allowing for the measurement of particle motion in that specific slice of the flow. By seeding the flow of interest with low-density particles, each particle can be tracked individually over several frames. This tracking enables the reconstruction of fluid particle motion, which can be used to calculate both Eulerian (fixed point) and Lagrangian (particle-based) quantities. In this study, a single camera was used to reconstruct particle tracks in two dimensions, providing valuable information about the initial turbulence and Lagrangian statistics of the turbulent flow. The construction of particle tracks in 2D-LPT involves two main tasks. Firstly, the images captured by the camera are processed to determine the two-dimensional positions of the particles within the camera’s image space. Secondly, the tracking algorithm, based on the principle of the 4-frame best estimate pioneered by Ouelette et al. [42], is applied to establish the paths followed by the particles over time using a sequence of images.
A single high-speed CMOS camera with a 105 mm focal length lens was used to record the LPT images, and was set at 512 × 512 pixels resolution; the detection system was set at 10 kHz (10,000 frames per second (fps)) for well-resolved particle velocity and acceleration statistics. This very high temporal resolution (0.1–0.2 ms) is considerably smaller than the Kolmogorov time (16.6–31.6 ms) of the smallest eddies present in the flow; therefore, the properties of the dissipation range in the flow are solved. For the illumination of the tracer particles, an Nd-YAF laser (527 nm) was used and synchronized at the same sampling frequency as the camera. The laser was set at internal mode, 14 A Q-switch current, and a pulse width of 2.5 s. To obtain accurate statistics of the particle-laden turbulent flow, the recording process was repeated 20 times for each flow case. It must be noted that the current study used the LPT measurement techniques based on Ouelette et al. [42] Hassanian et al. [40].
4. Results and Discussion
This study aimed to apply an LPT technique [40,42] to follow particles in particle-laden turbulent flow and to simulate a stagnation plane in the 2D measurement of a 3D experiment in order to examine the erosion of turbomachine components encountering float particles. The suggested approach is based on the stagnation point subject to strain deformation. Thus, a turbulence flow with controlled intensity was conducted and seeded with tracer and inertial particles. As explained in the apparatus section, the flow underwent strain with the designed mechanism. For every flow case, it is a stagnation area where the flow and particles get almost zero velocity. The coordinate of the stagnation point for every flow case is unique. In this work, the statistics of the particle fluid are applied. Because the measurement is 2D, the stagnation area has x- and y-coordinates. Since the straining motion is mainly in the y-direction, the stagnation plane should be assumed horizontally along the x-axis. The particles floating in the flow have two scenarios in the conducted experiment: particles from the upper or lower side of the stagnation plane are affected by the flow features and cross the stagnation plane. Others will stream in a way that will not scratch the stagnation plane. The particles are affected by the following variables: the turbulence intensity, strain rate, and the presence of gravity. The Stokes number of the inertial particles in this study is not significant, and we do not expect to see ballistic behavior, but particles of comparable Stokes numbers are seen to coagulate efficiently in local regions of high-strain turbulent flow fields [46]. In the literature, it is sometimes noted that the particles in particle-laden flow interact and are affected by Brownian motion [47,48]. However, these items could be disregarded based on the particle size analyzed in this study. This section presents the erosion ratio affected by variants of the strain rate and turbulence intensity besides gravity. The particle assessment displayed in Table 1 specifies the range of the particle similarity to actual airborne raindrops, ice, sand, etc.
4.1. Particle Characterization
Based on the Stokes number definition in the method section, the Stokes number for tracer and inertial particles is in the range of – and 0.113–0.307, respectively. It must be noted that the particle Stokes numbers are based on the Kolmogorov timescale of the flow before the straining motion is applied to the turbulent field. As is described in the Methods section, a non-dimensional time scale is defined and applied to compare the particles in the current study to actual particle impacts (Table 1). For flow around the S809 airfoil from the experiment, with [44] speed flow 14 m/s, angle of attack 10 degrees, chord length 150 mm, strain rate in the x-direction, the inertial particle in this study has a near range of non-dimensional time scale to hail, raindrops, and sand. Therefore, the inertial particles used in this study could behave the same as raindrops and sand in analogous conditions. For example, it can be assumed that the used inertial particles can have impacts similar to raindrops on the wind turbine for leading-edge erosion. Hence, it is possible to use different-sized inertial particles to simulate another airborne particle. Furthermore, the tracer particle and insects have the same range of non-dimensional time scales.
4.2. Particle Leading to Erosion and Stagnation Plane
LPT allows tracking every single particle and counting the whole number of particles. To specify the stagnation plane coordinate, it is essential to find the location where the particles have velocity ≈ 0. The coordinates of the stagnation plane for each flow case are shown in Table 2. The location of the stagnation point was determined by tracking the movement of tracer particles along the flow streamline. The coordinates reported in this measurement are based on the assumption that the center of the measurement area is the origin point.

Table 2.
The coordinates of the stagnation plane were measured in 2D for each flow case and where the particles have velocity ≈ 0. Tracer particles were used to seed the flow and both the turbulence intensity and strain rate were varied.
Once the location of the stagnation plane is specified, it is possible to determine how many particles crossed the stagnation plane during the experiments and how many did not pass. The normalized particle number is an appropriate scale, a ratio of the crossed particle number to the whole of the particles during the experiment. This definition provides an index that we callthe erosion ratio (ER); when the turbulence intensity, strain rate, or both change, it shows whether the erosion ratio is increasing or decreasing and, therefore, examines the effect of the strain rate and the turbulence intensity on the erosion. Figure 4 is a sketch presenting a view of the assumed stagnation plane in the location of the stagnation area and the scenarios possible for particle motion. It must be noted in the actual condition, for example, for the airflow around the wind turbine blade, gas turbine, and compressor, there are different sizes and types of particles, such as ice and sand, and some interaction is expected between the particles. Thus, this issue could not be resolved in this study. Moreover, the humidity is another impact factor. Considering the wind turbine and the airborne particles, when there is rainy weather or high humidity, the solid float particle gets wet, and their behavior and impact cannot be determined in this work. Nevertheless, the employed method could be developed to address the points highlighted.
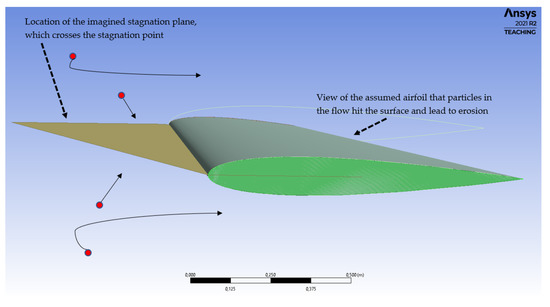
Figure 4.
In view of the assumed stagnation plane, the location crosses the stagnation point on the airfoil. Particles have two scenarios, some pass the stagnation plane, and others do not. Image used courtesy of ANSYS, Inc. Canonsburg, PA, USA [49].
4.3. Erosion Caused by Turbulence and Flow Strain
The study investigated particle-laden turbulent flow at two distinct strain rates, and erosion ratios were calculated for each flow case. Figure 5 illustrates the erosion ratio for different strain rates at a constant turbulence intensity. Doubling the strain rate for both tracer and inertial particles at resulted in a significant increase in the erosion ratio for the tracer. Conversely, at , an increase in the mean strain rate led to a reduction in erosion for both particles, but the effect was more pronounced for the inertial particle. Notably, when the same particles were subjected to varying turbulence intensities, changes in the rate did not exhibit a corresponding trend in erosion.
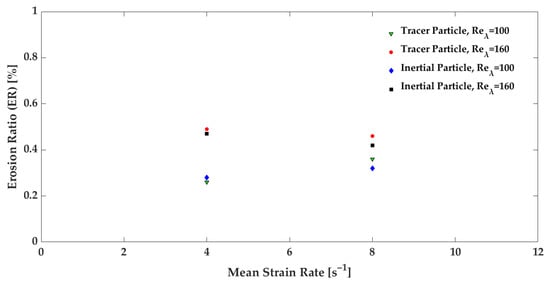
Figure 5.
Flow cases with two different are affected by the strain rate, and both variables make the erosion ratio vary.
The particle erosion affected by the turbulence intensity in the stagnation area of the simulated surface in the flow is illustrated in Figure 6. It is evident that the turbulence intensity has a significant impact on particle erosion, regardless of the strain rate. Lower strain rate flows were more susceptible to erosion for both the tracer and inertial particles. Conversely, flows with higher strain rates exhibited less sensitivity to the turbulence intensity, resulting in relatively less erosion.
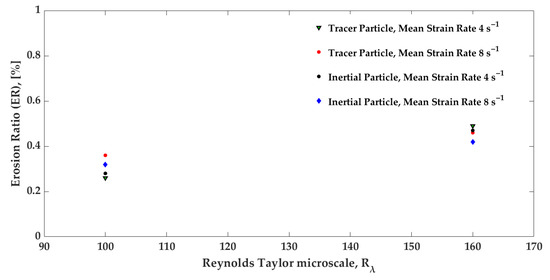
Figure 6.
Flow cases with two different mean strain rates are affected by the turbulence intensity, and both variables vary the erosion ratio.
Table 3 provides a quantitative measurement of erosion ratios. When combined with the observations from Figure 5 and Figure 6, it is evident that increasing both the flow strain and the turbulence intensity leads to more erosion. However, the impact is more pronounced for tracer particles than inertial particles. It should be noted that this experiment was conducted with the influence of gravity, which could not be quantitatively measured, but the distinct behavior of the tracer and inertial particles may be attributed to the effects of gravity. Previous studies have suggested that inertial particles are more influenced by gravity [40]. Based on the results presented in Table 3, increasing the turbulence intensity from to 160 resulted in a 10–23% increase in the erosion ratio, depending on the particle type and the flow strain rate. Similarly, an increase in the flow strain (due to deformation/shear flow) resulted in a 3–10% increase in erosion, depending on the particle type and Reynolds number.

Table 3.
The erosion ratio of two types of particles has been varied and is affected by the mean strain rate (deformation/shear of the flow) and the turbulence intensity.
5. Conclusions
The erosion of rotary machine components by floating particles is a critical problem that often results in decreased efficiency and damage to the machinery. In the present study, an empirical approach was developed and implemented to simulate a 3D particle-laden turbulent flow using two types of particles and to investigate the effects of the flow characteristics and boundary conditions on the particle-induced erosion of rotary parts through 2D measurement. The simulation involved a turbulent flow with a known turbulence intensity within the range of 100 < < 160 and a specified strain rate (representative of flow deformation/shear) of 4 and 8 s in the y-direction. The particle movement in the flow was extracted using the Lagrangian particle tracking technique. The experiment was conducted under the influence of gravity to replicate real-world conditions. The measurement techniques used in the experiment were based on the work of Ouelette et al. [42] and Hassanian et al. [40].
To quantify particle erosion, a stagnation plane coordinate is defined, and the count of particles that pass or do not pass through this plane is recorded. A normalized metric is then calculated by taking the ratio of the number of particles that pass the plane to the total number of particles in the flow. This metric is used to compare erosion under different flow conditions.
The findings indicate that an increase in the flow strain rate and turbulence intensity has a significant impact on tracer particles, with the strain rate exhibiting less sensitivity to turbulence intensity than the flow with a lower strain rate. Additionally, the study revealed that gravity had a greater impact on the inertial particles than the tracers, resulting in distinct erosion effects. The study highlights that particle size, turbulence intensity, flow fluctuations, flow deformation (caused by shear, deformation, or boundary conditions), and gravity are all important factors that affect the erosion of rotary machine components.
The experiment conducted in this study aimed to simulate a stagnation plane and to investigate the erosion caused by floating particles on various components of rotary machines, such as wind turbine airfoils, steam turbine blades, compressor blades, pump impellers, hydraulic turbine blades, and marine propellers. However, there is potential for further expansion of this experiment to explore the effects of different particle sizes and flow characteristics, including higher turbulence intensity and various flow deformations. The influence of gravity on inertial particles in turbulent flows remains an open research area. By employing the empirical approach proposed in this study, it is possible to gain insight into the role of gravity in erosion, specifically considering the particle size. While the shear flow resulting from boundary conditions or external forces can be investigated using the well-established 2D particle tracking approach, there is a plan for future research to enhance the setup by employing two cameras for recording 3D measurements. This advancement will allow for a more comprehensive examination of the effects and provide a transparent window into understanding the impact of gravity on erosion.
Author Contributions
R.H.: conceptualization, methodology, software, validation, formal analysis and writing—original draft; M.R.: methodology, writing—review and editing and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results was conducted in the Center of Excellence (CoE) Research on AI and Simulation-Based Engineering at Exascale (RAISE); the EuroCC and the EuroCC 2 projects received funding from EU’s Horizon 2020 Research and Innovation Framework Programme and European Digital Innovation Hub Iceland (EDIH-IS) under grant agreement no. 951733, no. 951740, no. 101101903 and no. 101083762 respectively.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Acknowledgments
We thank Ármann Gylfason from Reykjavik University for his technical comments on the experiment conducted at the Laboratory of Fundamental Turbulence Research (LFTR) at Reykjavik University. We also acknowledge Lahcen Bouhlali from Reykjavik University for his experimental work in data preparation.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LPT | Lagrangian Particle Tracking |
| PTV | Particle Tracking Velocimetry |
| PIV | Particle Image Velocimetry |
References
- Schramm, M.; Rahimi, H.; Stoevesandt, B.; Tangager, K. The Influence of Eroded Blades on Wind Turbine Performance Using Numerical Simulations. Energies 2017, 10, 1420. [Google Scholar] [CrossRef]
- Herring, R.; Dyer, K.; Martin, F.; Ward, C. The increasing importance of leading edge erosion and a review of existing protection solutions. Renew. Sustain. Energy Rev. 2019, 115, 109382. [Google Scholar] [CrossRef]
- Bonu, V.; Jeevitha, M.; Praveen Kumar, V.; Srinivas, G.; Siju; Barshilia, H.C. Solid particle erosion and corrosion resistance performance of nanolayered multilayered Ti/TiN and TiAl/TiAlN coatings deposited on Ti6Al4V substrates. Surf. Coat. Technol. 2020, 387, 125531. [Google Scholar] [CrossRef]
- Bonu, V.; Jeevitha, M.; Praveen Kumar, V.; Barshilia, H.C. Nanolayered multilayer Ti/TiN coatings: Role of bi-layer thickness and annealing on solid particle erosion behaviour at elevated temperature. Surf. Coat. Technol. 2019, 357, 204–211. [Google Scholar] [CrossRef]
- Ahmad, M. An Overview of Droplet Impact Erosion, Related Theory and Protection Measures in Steam Turbines. In Cavitation; Borek, W., Tański, T., Król, M., Eds.; IntechOpen: Rijeka, Croatia, 2018. [Google Scholar] [CrossRef]
- Brandes, T.; Koch, C.; Staudacher, S. Estimation of Aircraft Engine Flight Mission Severity Caused by Erosion. J. Turbomach. 2021, 143, 111001. [Google Scholar] [CrossRef]
- Lorenz, M.; Klein, M.; Hartmann, J.; Koch, C.; Staudacher, S. Prediction of Compressor Blade Erosion Experiments in a Cascade Based on Flat Plate Specimen. Front. Mech. Eng. 2022, 8, 925395. [Google Scholar] [CrossRef]
- Sallee, G.P. Performance Deterioration Based on Existing (Historical) Data; JT9D Jet Engine Diagnostics Program; Contractor Report (CR) CR-135448; NASA, Pratt & Whitney Aircraft Group: Cleveland, OH, USA, 1987. [Google Scholar]
- Grant, G.; Tabakoff, W. Erosion Prediction in Turbomachinery Resulting from Environmental Solid Particles. J. Aircr. 1975, 12, 471–478. [Google Scholar] [CrossRef]
- Balan, C.; Tabakoff, W. Axial flow compressor performance deterioration. In Proceedings of the 20th Joint Propulsion Conference, Cincinnati, OH, USA, 11–13 June 1984. [Google Scholar] [CrossRef]
- Ghenaiet, A. Study of Sand Particle Trajectories and Erosion Into the First Compression Stage of a Turbofan. J. Turbomach. 2012, 134, 051025. [Google Scholar] [CrossRef]
- Bons, J.P.; Prenter, R.; Whitaker, S. A Simple Physics-Based Model for Particle Rebound and Deposition in Turbomachinery. J. Turbomach. 2017, 139, 081009. [Google Scholar] [CrossRef]
- Sommerfeld, H.; Koch, C.; Schwarz, A.; Beck, A. High velocity measurements of particle rebound characteristics under erosive conditions of high pressure compressors. Wear 2021, 470–471, 203626. [Google Scholar] [CrossRef]
- Kopper, P.; Beck, A.; Ortwein, P.; Krais, N.; Kempf, D.; Koch, C. High-order large eddy simulation of particle-laden flow in a T106C low-pressure turbine linear cascade. In Proceedings of the 8th European Conference for Aeronautics and Space Sciences, Madrid, Spain, 1–4 July 2019. [Google Scholar] [CrossRef]
- Vimalakanthan, K.; van der Mijle Meijer, H.; Bakhmet, I.; Schepers, G. Computational fluid dynamics (CFD) modeling of actual eroded wind turbine blades. Wind Energy Sci. 2023, 8, 41–69. [Google Scholar] [CrossRef]
- Law, H.; Koutsos, V. Leading edge erosion of wind turbines: Effect of solid airborne particles and rain on operational wind farms. Wind Energy 2020, 23, 1955–1965. [Google Scholar] [CrossRef]
- Pryor, S.C.; Barthelmie, R.J.; Cadence, J.; Dellwik, E.; Hasager, C.B.; Kral, S.T.; Reuder, J.; Rodgers, M.; Veraart, M. Atmospheric Drivers of Wind Turbine Blade Leading Edge Erosion: Review and Recommendations for Future Research. Energies 2022, 15, 8553. [Google Scholar] [CrossRef]
- López, J.C.; Kolios, A.; Wang, L.; Chiachio, M. A wind turbine blade leading edge rain erosion computational framework. Renew. Energy 2023, 203, 131–141. [Google Scholar] [CrossRef]
- Li, D.; Zhao, Z.; Li, Y.; Wang, Q.; Li, R.; Li, Y. Effects of the particle Stokes number on wind turbine airfoil erosion. Appl. Math. Mech. 2018, 39, 639–652. [Google Scholar] [CrossRef]
- Lee, C.M.; Gylfason, Á.; Perlekar, P.; Toschi, F. Inertial particle acceleration in strained turbulence. J. Fluid Mech. 2015, 785, 31–53. [Google Scholar] [CrossRef]
- Hassanian, R. An Experimental Study of Inertial Particles in Deforming Turbulence Flow, in Context to Loitering of Blades in Wind Turbines. Doctoral Dissertation, Reykjavik University, Reykjavik, Iceland, 2020. [Google Scholar]
- Toschi, F.; Bodenschatz, E. Lagrangian Properties of Particles in Turbulence. Annu. Rev. Fluid Mech. 2009, 41, 375–404. [Google Scholar] [CrossRef]
- Batchelor, G.K. The Theory of Homogeneous Turbulence; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Arabnejad, M.H.; Amini, A.; Farhat, M.; Bensow, R.E. Numerical and experimental investigation of shedding mechanisms from leading-edge cavitation. Int. J. Multiph. Flow 2019, 119, 123–143. [Google Scholar] [CrossRef]
- Petersen, A.J.; Baker, L.; Coletti, F. Experimental study of inertial particles clustering and settling in homogeneous turbulence. J. Fluid Mech. 2019, 864, 925–970. [Google Scholar] [CrossRef]
- Lee, J.; Lee, C. The effect of wall-normal gravity on particle-laden near-wall turbulence. J. Fluid Mech. 2019, 873, 475–507. [Google Scholar] [CrossRef]
- Ayyalasomayajula, S.; Warhaft, Z. Nonlinear interactions in strained axisymmetric high-Reynolds-number turbulence. J. Fluid Mech. 2006, 566, 273–307. [Google Scholar] [CrossRef]
- Gualtieri, P.; Meneveau, C. Direct numerical simulations of turbulence subjected to a straining and destraining cycle. Phys. Fluids 2010, 22, 065104. [Google Scholar] [CrossRef]
- Brandt, L.; Coletti, F. Particle-Laden Turbulence: Progress and Perspectives. Annu. Rev. Fluid Mech. 2022, 54, 159–189. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Tanuma, T. Advances in Steam Turbines for Modern Power Plants; Woodhead Publishing: Sawston, UK, 2017. [Google Scholar]
- Davidson, P.A. Turbulence: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- John, L.; Lumley, H.T. A First Course in Turbulence; MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Taherkhani, B.; Anaraki, A.P.; Kadkhodapour, J.; Farahani, N.K.; Tu, H. Erosion Due to Solid Particle Impact on the Turbine Blade: Experiment and Simulation. J. Fail. Anal. Prev. 2019, 19, 1739–1744. [Google Scholar] [CrossRef]
- Hunt, J.C.R. A theory of turbulent flow round two-dimensional bluff bodies. J. Fluid Mech. 1973, 61, 625–706. [Google Scholar] [CrossRef]
- Ireland, P.J.; Bragg, A.D.; Collins, L.R. The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects. J. Fluid Mech. 2016, 796, 617–658. [Google Scholar] [CrossRef]
- Baker, L.J.; Coletti, F. Particle–fluid–wall interaction of inertial spherical particles in a turbulent boundary layer. J. Fluid Mech. 2021, 908, A39. [Google Scholar] [CrossRef]
- Xiao, W.; Jin, T.; Luo, K.; Dai, Q.; Fan, J. Eulerian–Lagrangian direct numerical simulation of preferential accumulation of inertial particles in a compressible turbulent boundary layer. J. Fluid Mech. 2020, 903, A19. [Google Scholar] [CrossRef]
- Hassanian, R.; Helgadóttir, Á.; Riedel, M. Deep Learning Forecasts a Strained Turbulent Flow Velocity Field in Temporal Lagrangian Framework: Comparison of LSTM and GRU. Fluids 2022, 7, 344. [Google Scholar] [CrossRef]
- Hassanian, R.; Helgadottir, A.; Bouhlali, L.; Riedel, M. An Experiment Generates a Specified Mean Strained Rate Turbulent Flow: Dynamics of Particles. Phys. Fluids 2023, 35, 015124. [Google Scholar] [CrossRef]
- Kompenhans, M.R.J.; Willert, C.E.; Scarano, F.; Kähler, C.J.; Wereley, S.T. Particle Image Velocimetry; Springer International Publishing AG: Cham, Switzerland, 2018. [Google Scholar]
- Ouellette, N.T.; Xu, H.; Bodenschatz, E. A quantitative study of three-dimensional Lagrangian particle tracking algorithms. Exp. Fluids 2006, 40, 301–313. [Google Scholar] [CrossRef]
- Cengel, Y.; Cimbala, J. Fluid Mechanics: Fundamentals and Applications; McGraw Hill: New York, NY, USA, 2017. [Google Scholar]
- Gomes, A.O.; Brito, R.F.; Rosa, H.; RosaShow, H.; Campos, J.C.C.; Tibiriçá, Á.M.B.; Casanova, P. Experimental Analysis of an S809 Airfoil. In Proceedings of the ENCIT 2014, 15th Brazilian Congress of Thermal Sciences and Engineering, Belem, Brazil, 10–13 November 2014. [Google Scholar] [CrossRef]
- Kühsel, S.; Brückner, A.; Schmelzle, S.; Heethoff, M.; Blüthgen, N. Surface area–volume ratios in insects. Insect Sci. 2017, 24, 829–841. [Google Scholar] [CrossRef] [PubMed]
- Collins, L.R.; Keswani, A. Reynolds number scaling of particle clustering in turbulent aerosols. New J. Phys. 2004, 6, 119. [Google Scholar] [CrossRef]
- Zaichik, L.I.; Alipchenkov, V.M. The effect of Brownian motion on collisions between aerosol particles in turbulent flow. High Temp. 2008, 46, 502–511. [Google Scholar] [CrossRef]
- Lin, J.Z.; Huang, L.Z. Review of some researches on nano- and submicron Brownian particle-laden turbulent flow. J. Hydrodyn. Ser. B 2012, 24, 801–808. [Google Scholar] [CrossRef]
- Ansys Workbench Teaching Version; Ansys Inc.: Canonsburg, PA, USA, 2021.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).