Simulative and Experimental Investigation of the Ring Creeping Damage Mechanism Considering the Training Effect in Large-Sized Bearings
Abstract
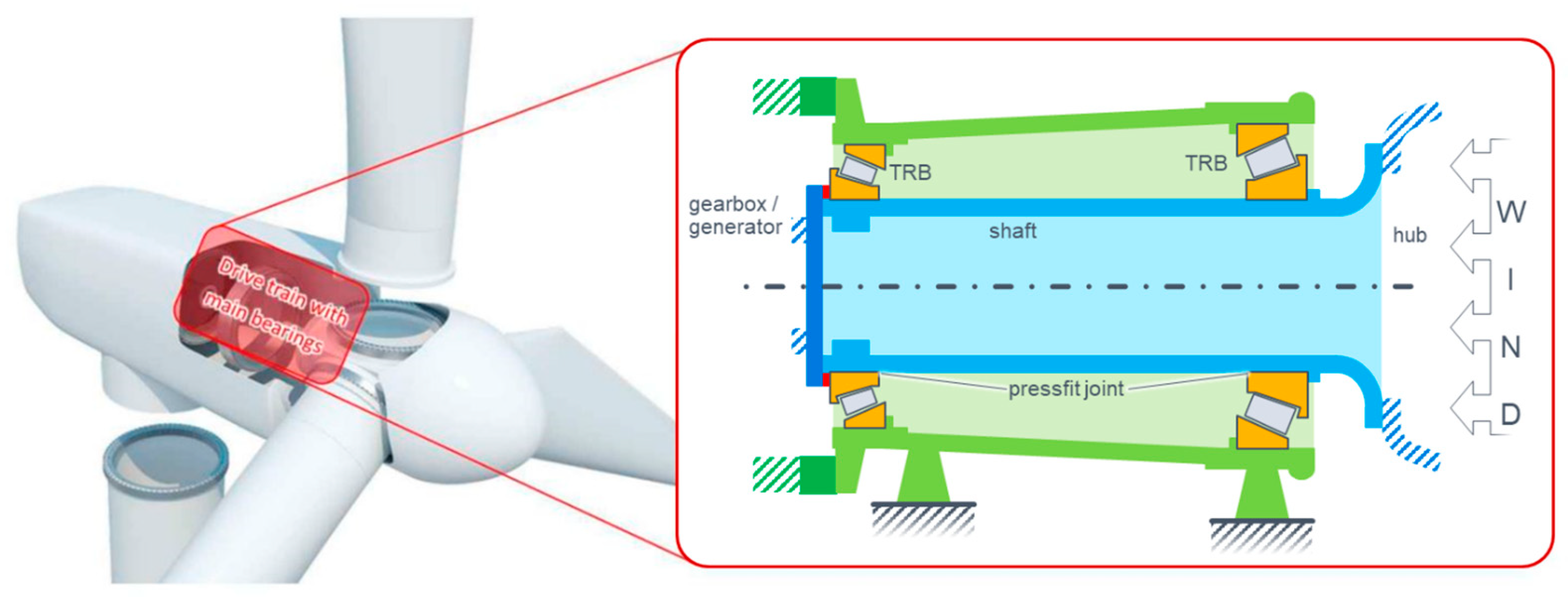
:1. Introduction
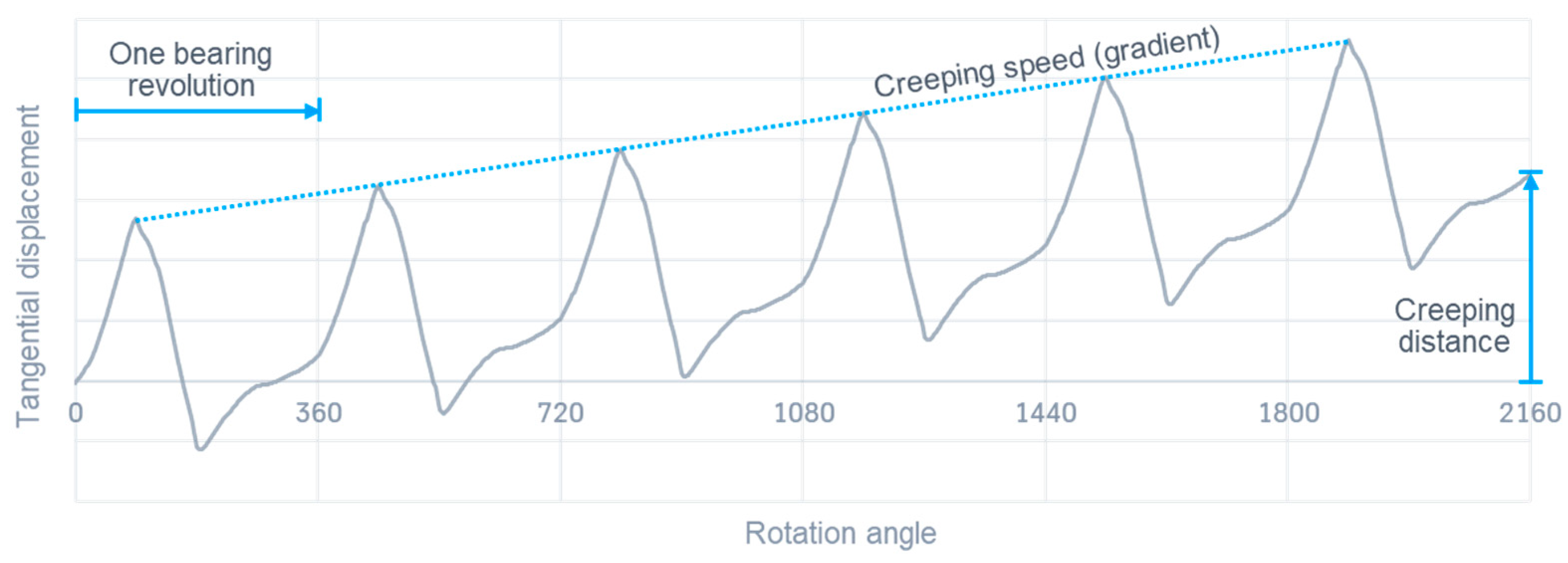
2. Developed Procedure
3. Experimental Investigations
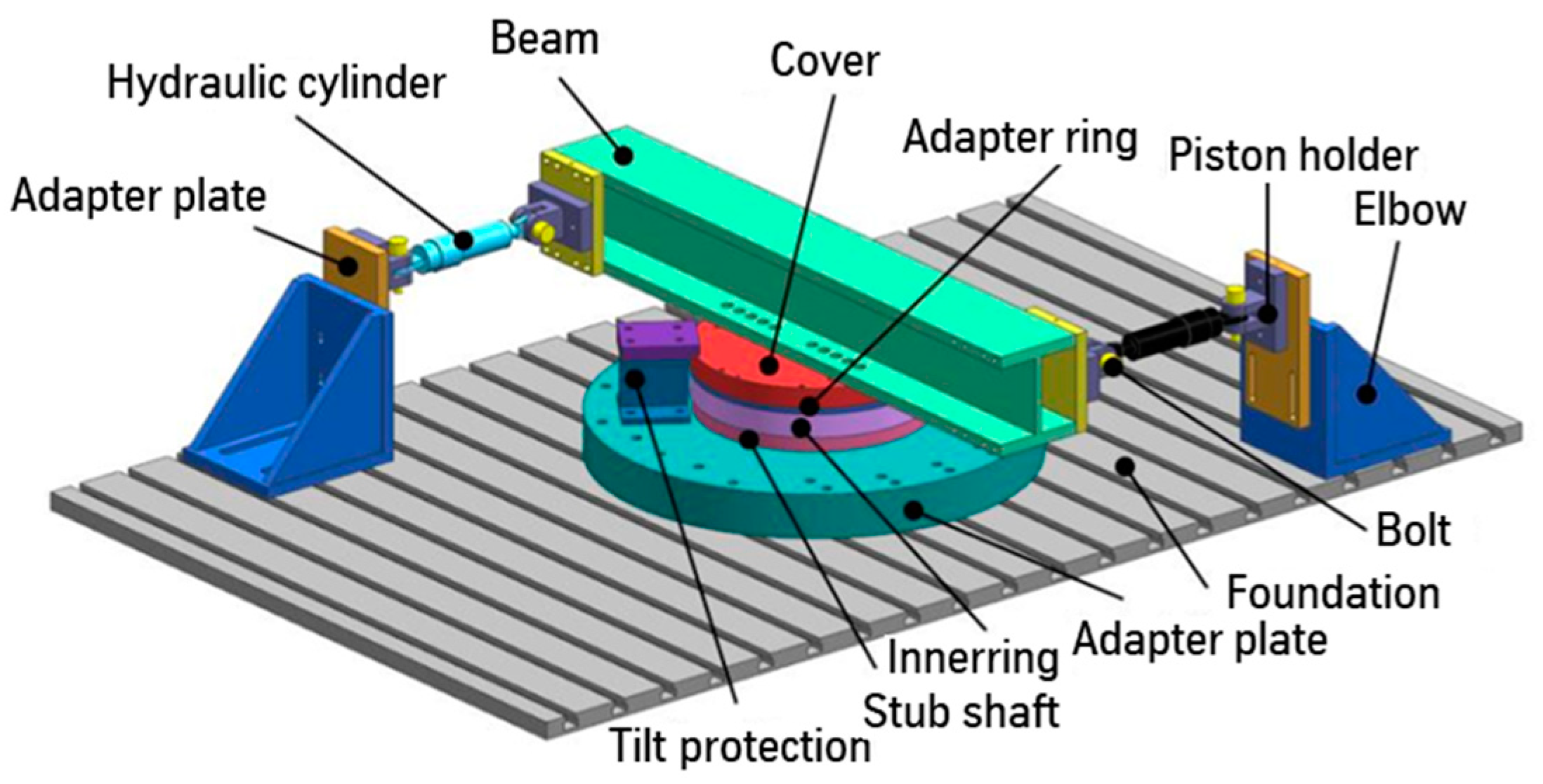
3.1. Creeping Test Rig
3.2. Coefficient of Friction (COF) Test Rig
4. Numerical Simulation Method
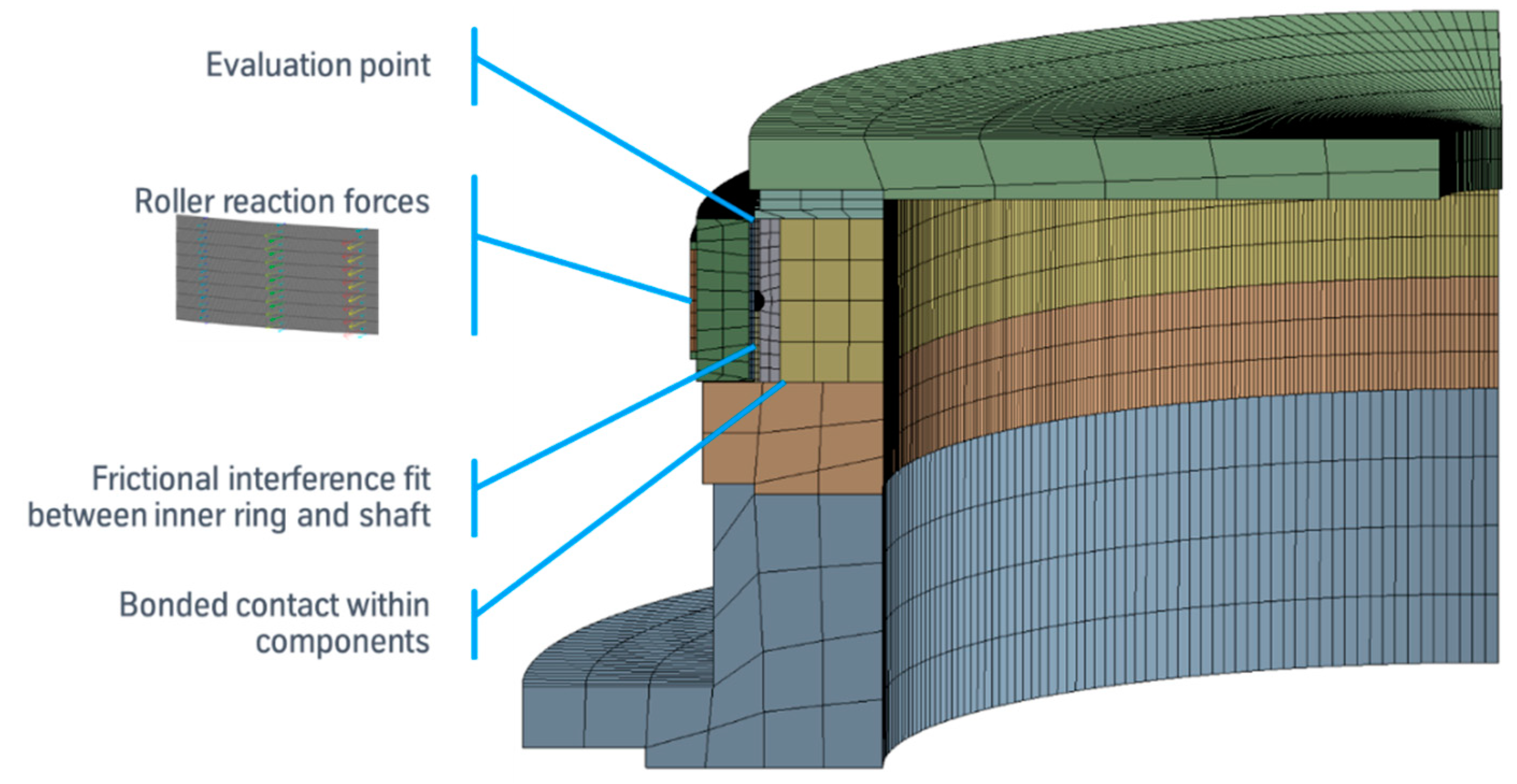
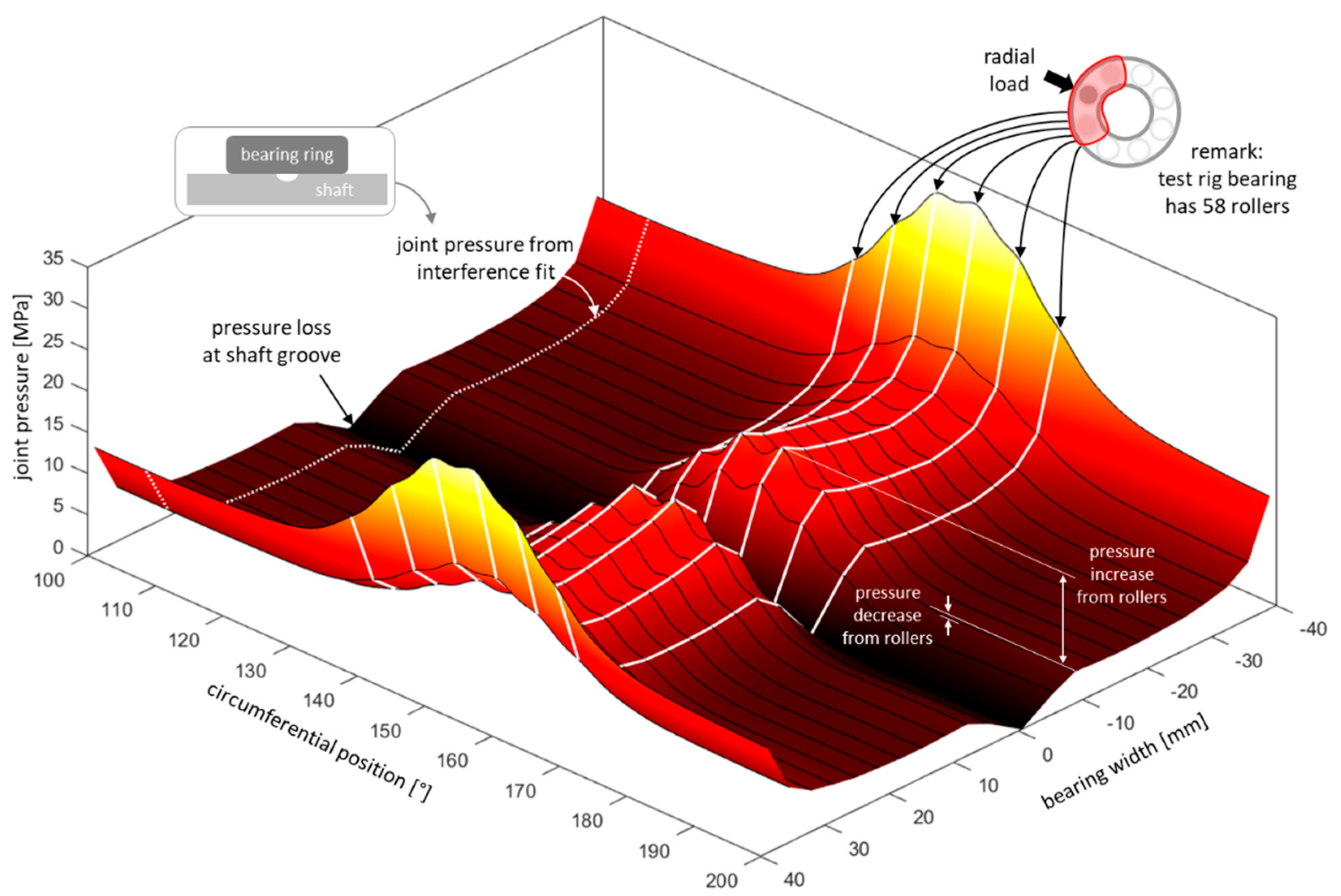
4.1. Finite Element Model Setup
- Boundary conditions of the interference fit: The interference between the bearing ring and the shaft is not modeled geometrically. Instead, it is integrated into the contact condition as an initial penetration that is zeroed out gradually. During this first step, the friction is deactivated so that a condition without frictional shear stress ensues;
- Frictional contact condition and external load: The contact condition in the joint is set from frictionless to frictional by using the trained COF. The initial load distribution of the bearing is applied as radial forces. As an alternative or in addition, any other external loads that occur (periodically) can also be applied. Thus, it is possible to simulate structural-induced creeping as well;
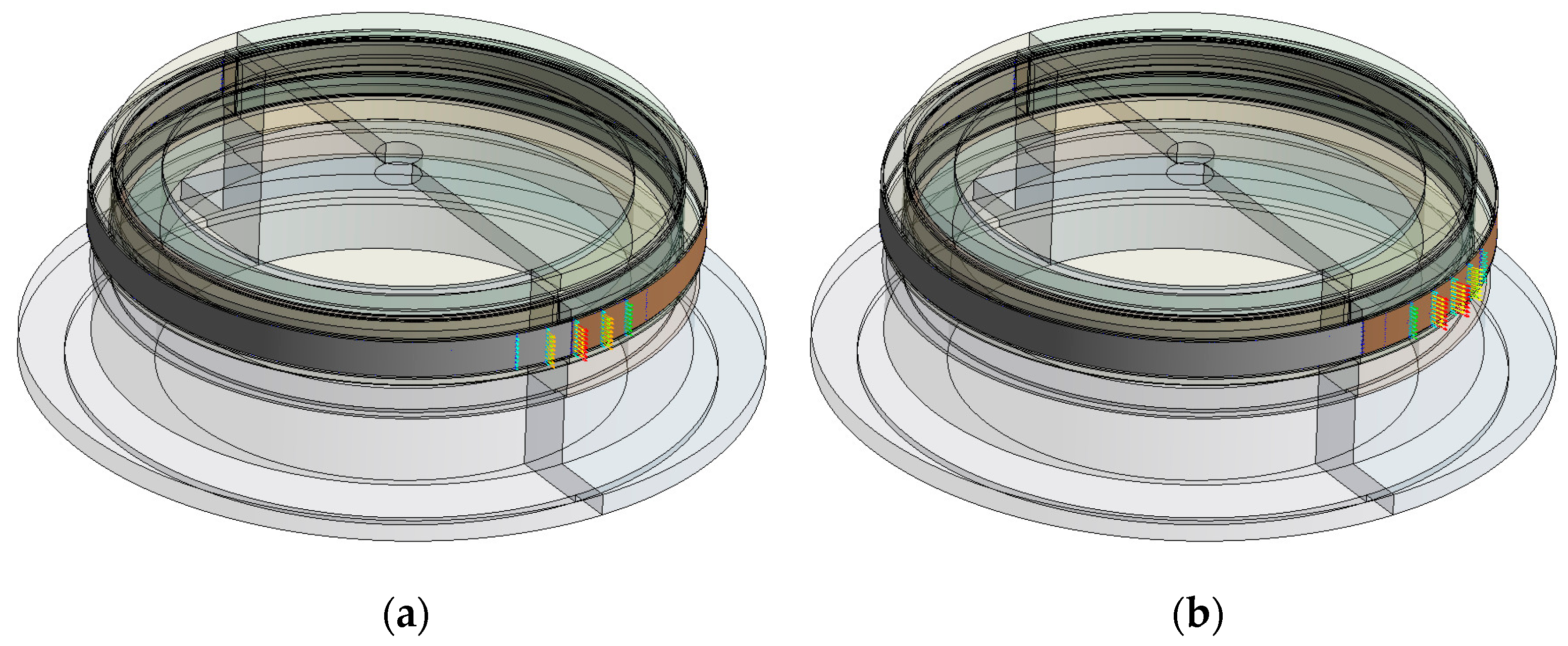
- Load stepwise rotation of the roller forces: During this calculation sequence, the previously stationary bearing model is set in motion by rotating the radial forces by a defined angle at each load step. This stepwise rotation of the load distribution isshown in Figure 10 for two different calculation increments.
4.2. Exemplary Simulation Results
4.3. Comparison of Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Becker, D.; Lüneburg, B.; Billenstein, D.; Handreck, T.; Müller, P.; Neidnicht, M.; Volmer, G.; Schlüter, D.; Netz, T.; Rollmann, J. Design and calculation process for large-sized multi-MW blade bearing applications based on advanced multi-bearing FE-analyses. In Proceedings of the 4th Bearing World, Würzburg, Germany, 5–6 July 2022. [Google Scholar]
- Lüneburg, B.; Becker, D.; Rollmann, J.; Terwey, T.; Michalek, I.; Mevius, L.; Neidnicht, M. Advanced design and qualification of dual taper roller main bearing arrangements for multi-MW wind turbines. In Proceedings of the 4th Bearing World, Würzburg, Germany, 5–6 July 2022. [Google Scholar]
- Heuser, L.; Bager, C. Preload Adjustment and Creeping Prevention of large size Tapered Roller Bearings. In Proceedings of the 4th Bearing World, Würzburg, Germany, 5–6 July 2022. [Google Scholar]
- Liewen, C.; Neidnicht, M.; Billenstein, D. Untersuchung zum Ringwandern an Großwälzlagern. In Proceedings of the 5th VDI-Conference “Schadensmechanismen an Lagern”, Aachen, Germany, 28–29 June 2022. [Google Scholar]
- Schlüter, F.; Jacobs, G.; Bosse, D.; Brügge, T.; Schlegel, F. Correlation of Planetary Bearing Outer Ring Creep and Gear Load Distribution in a Full-Size Wind Turbine. J. Phys. 2020, 1452, 012062. [Google Scholar] [CrossRef]
- Babbick, T.; Maiwald, A.; Vidner, J.; Sauer, B.; Leidich, E. Beanspruchungsgerechte Auslegung von Wälzlagersitzen unter Berücksichtigung von Schlupf- und Wandereffekten (FVA479II, Nr. 956; AiF: IGF-Nr. 15652 BG), 1st ed.; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Hasse, A.; Rieg, F. Einfluss der Nachgiebigkeit von Lagergehäuse und deren Anschlusskonstruktion auf das Wanderverhalten von Wälzlagern (FVA479IX, Forschungsantrag), 1st ed.; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2018. [Google Scholar]
- Aul, E.; Walther, V.; Sauer, B.; Leidich, E. Wandernde Wälzlager-Innen- und Außenringe unter verschiedenen Einsatzbedingungen (FVA479I, Nr. 852), 1st ed.; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2008. [Google Scholar]
- Liebrecht, J.; Maiwald, A.; Marquart, M.; Sauer, B.; Leidich, E. Ringwandern bei Angestellten Lagern und Radiallagern unter Kombinierten Belastungen (FVA479III, Nr. 1097; AiF: IGF-Nr. 16987 BG), 1st ed.; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2014. [Google Scholar]
- Thiele, S.; Pörsch, S.; Liebrecht, J.; Schiemann, T.; Marquart, M.; Sauer, B.; Leidich, E. Definition und Auslegung von Konstruktiven und Tribologischen Abhilfemaßnahmen Gegen Tangentiale Wanderbewegungen von Wälzlagerringen (FVA479IV, Nr. 1153; AiF: IGF-Nr. 16985 BG), 1st ed.; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2015. [Google Scholar]
- Nützel, F.; Rieg, F. Erweiterung des FEA-Solvers im FVA-Programm SimWag (FVA479V, Nr. 1155), 1st ed.; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2015. [Google Scholar]
- Dimov, G.; Schiemann, T.; Kiekbusch, T.; Sauer, B.; Leidich, E. Untersuchungen des Wanderverhaltens von Wälzlagern in Schrägverzahnten Planetenrädern (FVA479VI, Nr. 1281; AiF: IGF-Nr. 18311 BG), 1st ed.; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2018. [Google Scholar]
- Viebahn, F.; Schiemann, T.; Rieg, F.; Leidich, E. Auslegung von Abhilfemaßnahmen mit SimWag2.1 (FVA479VII, Nr. 1249), 1st ed.; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2017. [Google Scholar]
- Zimmermann, M.; Viebahn, F.; Schiemann, T.; Rieg, F.; Leidich, E. Erweiterung des Gültigkeitsbereichs zur Berechnung von Wälzlagerwandern mit Spielpassungen in SimWag2.2 (FVA479VIII, Nr. 1448), 1st ed.; Forschungsvereinigung Antriebstechnik e.V.: Frankfurt am Main, Germany, 2021. [Google Scholar]
- Leidich, E.; Maiwald, A. FE Simulations of Irreversible Relative Movements (creeping) in Rolling Bearing Sets. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 23–25 October 2013. [Google Scholar]
- Niwa, T. A Creep Mechanism of Rolling Bearings. NTN Tech. Rev. 2013, 81, 100–103. [Google Scholar]
- Murata, J.; Onizuka, T. Generation Mechanism of Inner Race Creep. Koyo Eng. J. 2005, 166E, 40–45. [Google Scholar]
- Zhan, J.; Takaemura, H.; Yukawa, K. A study on Bearing Creep Mechanism with FEM Simulation. In Proceedings of the International Mechanical Engineering Congress and Exposition, Seattle, WA, USA, 11–15 November 2007. [Google Scholar]
- Maiwald, A. Specific creeping phenomena of roller bearings used in lightweight constructions. In Proceedings of the 4th Bearing World, Würzburg, Germany, 5–6 July 2022. [Google Scholar]
- Gnauert, J.; Schlüter, F.; Jacobs, G.; Bosse, D.; Witter, S. Simulative investigation of ring creep on a planetary bearing of a wind turbine gearbox. Forsch. Ing. 2021, 85, 219–227. [Google Scholar] [CrossRef]
- Radaj, D.; Vormwald, M. Ermüdungsfestigkeit, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 138–140. [Google Scholar]
- Heydt, J. Untersuchungen zum Dynamischen Verhalten von Topologisch Optimierten Pressverbänden bei Umlaufbiegung. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 29 February 2021. [Google Scholar]
- Deutsches Institut für Normung e.V. (Ed.) DIN 7190-1:2017-02 Interference Fits (Part 1: Calculation and Design Rules for Cylindrical Self-Locking Pressfits), 2017-02 ed.; Beuth-Verlag: Berlin, Germany, 2017; pp. 1–47. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Billenstein, D.; Neidnicht, M.; Becker, D.; Liewen, C.; Rollmann, J.; Lüneburg, B. Simulative and Experimental Investigation of the Ring Creeping Damage Mechanism Considering the Training Effect in Large-Sized Bearings. Machines 2023, 11, 543. https://doi.org/10.3390/machines11050543
Billenstein D, Neidnicht M, Becker D, Liewen C, Rollmann J, Lüneburg B. Simulative and Experimental Investigation of the Ring Creeping Damage Mechanism Considering the Training Effect in Large-Sized Bearings. Machines. 2023; 11(5):543. https://doi.org/10.3390/machines11050543
Chicago/Turabian StyleBillenstein, Daniel, Martin Neidnicht, Daniel Becker, Christian Liewen, Jörg Rollmann, and Bernd Lüneburg. 2023. "Simulative and Experimental Investigation of the Ring Creeping Damage Mechanism Considering the Training Effect in Large-Sized Bearings" Machines 11, no. 5: 543. https://doi.org/10.3390/machines11050543
APA StyleBillenstein, D., Neidnicht, M., Becker, D., Liewen, C., Rollmann, J., & Lüneburg, B. (2023). Simulative and Experimental Investigation of the Ring Creeping Damage Mechanism Considering the Training Effect in Large-Sized Bearings. Machines, 11(5), 543. https://doi.org/10.3390/machines11050543




